Influence of Temperature on the Frictional Properties of Water-Lubricated Surfaces
Abstract
:1. Introduction
2. Results and Discussion
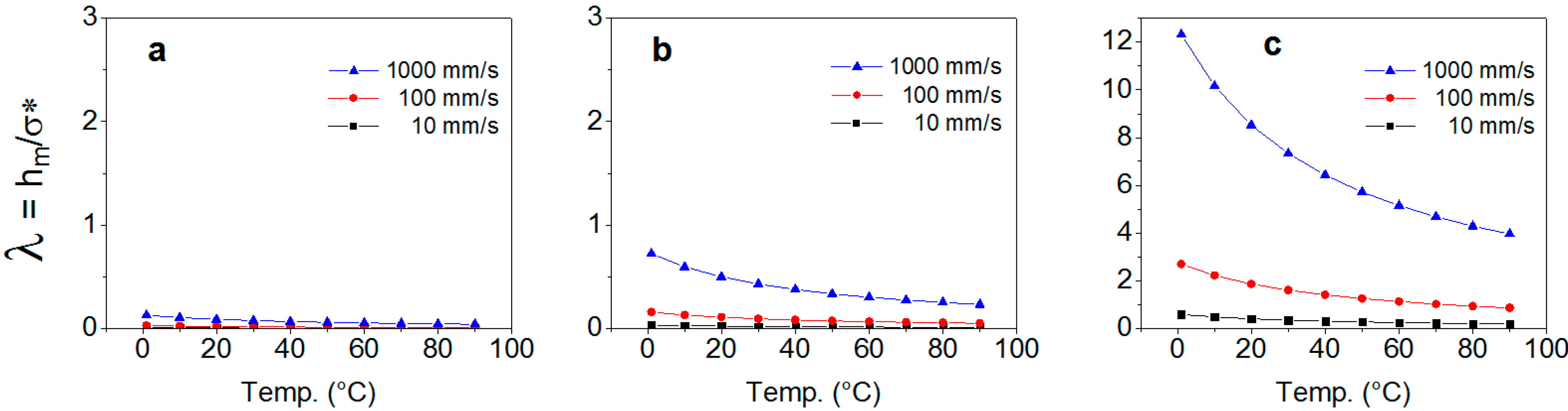
2.1. Theoretically Predicted Lubricating Properties: Lubricating Film Thickness

2.2. Theoretically Predicted Lubricating Properties: Consideration of Surface Properties
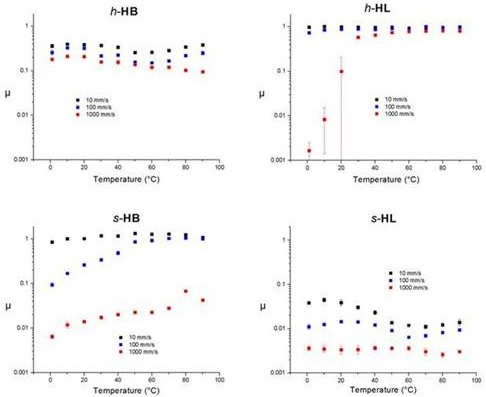
2.3. Experimentally Determined Friction Forces
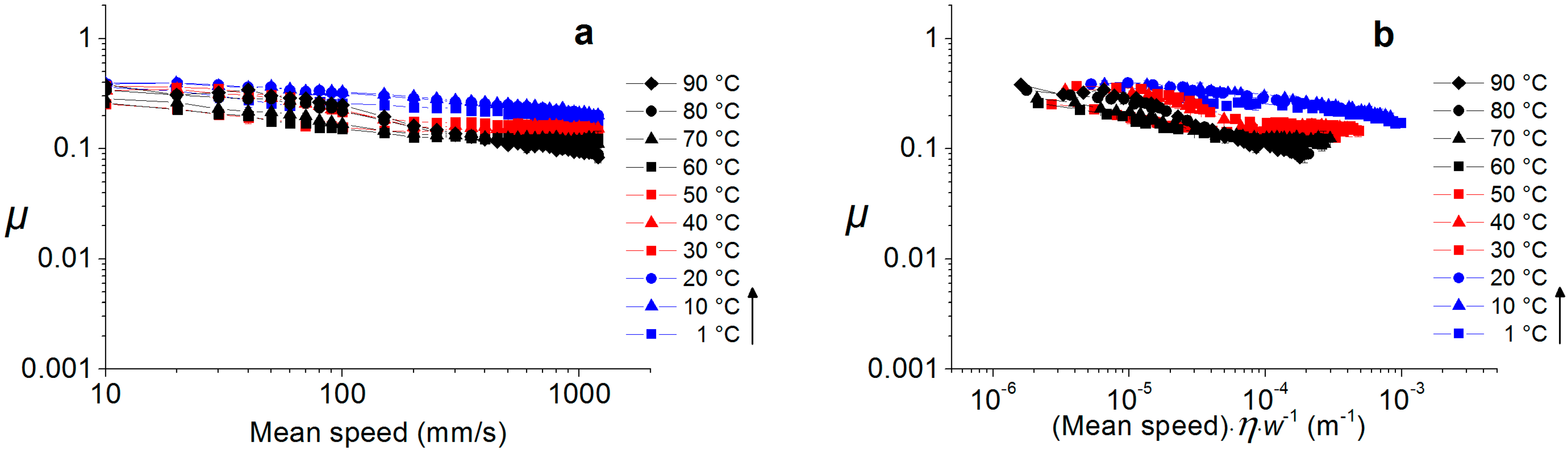
2.3.1. Hard Interfaces
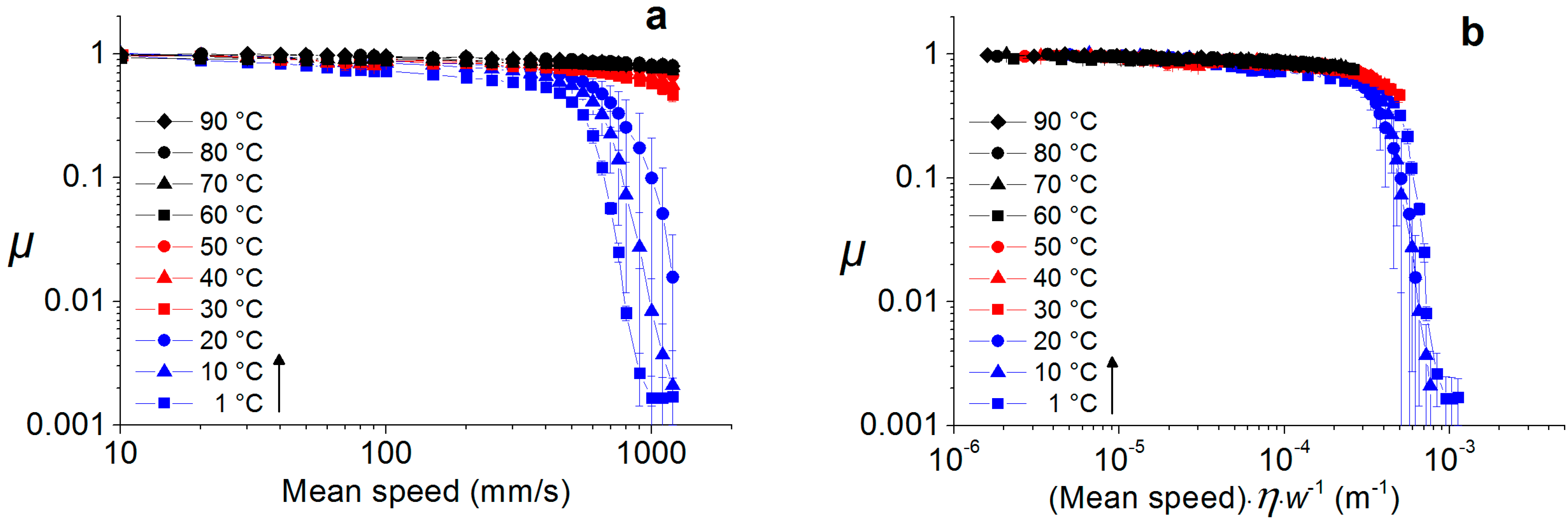
2.3.2. Soft Interfaces

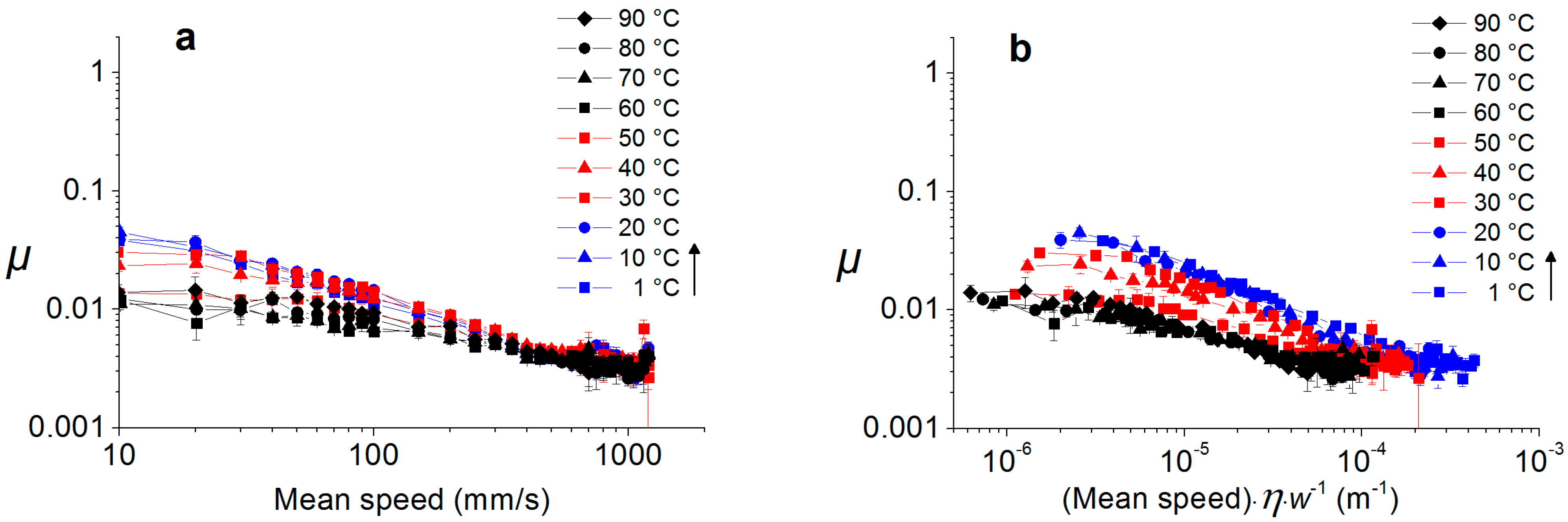
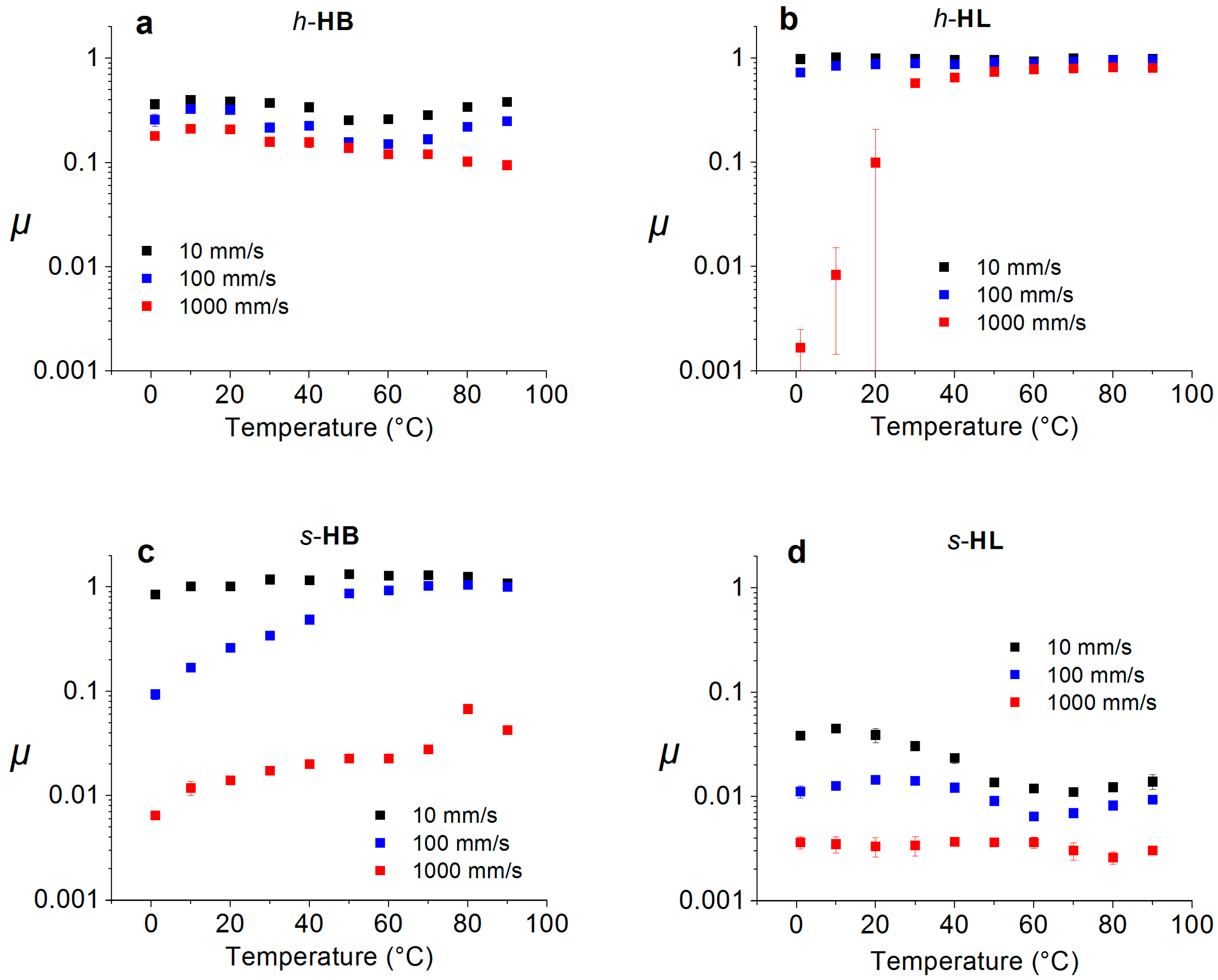
2.4. Temperature Dependence of Water-Lubricated Tribocontacts
3. Experimental Section
3.1. Tribopairs
| Substrate | Young’s Modulus (MPa) | Poisson’s Ratio | Hardness (MPa) | Roughness, Rq, (nm) | Asperity Diameter Average (nm) | Static Water Contact Angle (°) | ||
|---|---|---|---|---|---|---|---|---|
| Disc | Ball | Disc | Ball | |||||
| PDMS | 2.0 [39] (7.0) a,[40] | 0.5 [39] | 2.2 f | 1.6 ± 0.3 2.9 ± 0.7 (plasma tr.) | HB: 121.4 ± 36.4 HL: 116.9 ± 50.6 | No asperities | HB: 1448 ± 300 HL: 2189 ± 246 | pristine: 105.6 ± 2.2 e plasma tr.: <2 |
| POM | 3,100 [41] | 0.35 [41] | 354 [41],h | 223 ± 51 Wear track: 133 ± 44 | 659 ± 179 414 ± 180 | 5086 ± 504 | 4743 ± 1419 | pristine: 84.8 ± 2.9 c |
| Steel (AISI E 52100) | 210,000 [41] | 0.3 [41] | 8,319 [41] | - | 26.1 ± 5.5 Wear track: | 116 ± 17 | pristine: 57.5 ± 0.7 b plasma tr.: <2 | |
| Glass | 73,000 [42] | 0.17 [42] | 7,848 [41] | 2.9 ± 0.3 Wear track: | - | 73 ± 49 | pristine: 32.9 ± 3.3 plasma tr.: <2 | |
3.2. Hydrophilization of Substrates
3.3. Lubricant
3.4. MTM (Mini-Traction Machine)
| Hydrophobic | Hydrophilic | |
|---|---|---|
| Soft | PDMS †-PDMS † | PDMS-PDMS |
| Load | 5 N | 5 N |
| E′ | 2.07 | 2.07 |
| Pressure | 0.24 MPa | 0.24 MPa |
| σ* | 121.4 nm | 116.9 nm |
| ψ | 0.22 | 0.27 |
| Hard | Steel †-glass † | POM-POM |
| Load | 2 N | 2 N |
| E′ | 56,700 MPa | 1766 MPa |
| Pressure | 160 MPa | 16 MPa |
| σ* | 26.3 nm | 695 nm |
| ψ | 5.8 | 1.9 |
| T, Temperature | η, Viscosity |
|---|---|
| (°C) | (mPa·s) |
| 0 | 1.793 |
| 1 * | 1.750 * |
| 10 | 1.307 |
| 20 | 1.002 |
| 30 | 0.798 |
| 40 | 0.653 |
| 50 | 0.547 |
| 60 | 0.467 |
| 70 | 0.404 |
| 80 | 0.354 |
| 90 | 0.315 |
| 100 | 0.282 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Dedinaite, A.; Pettersson, T.; Mohanty, B.; Claesson, P.M. Lubrication by organized soft matter. Soft Matter 2010, 6, 520–1526. [Google Scholar]
- Dai, Z.; Tong, J.; Ren, L. Researches and developments of biomimetics in tribology. Chin. Sci. Bull. 2006, 51, 2681–2689. [Google Scholar] [CrossRef]
- Ahlroos, T.; Hakala, T.J.; Helle, A.; Linder, M.B.; Holmberg, K.; Mahlberg, R.; Laaksonen, P.; Varjus, S. Biomimetic approach to water lubrication with biomolecular additives. Proc. IMechE. Part J 2011, 225, 1013–1022. [Google Scholar] [CrossRef]
- Lee, S.; Spencer, N.D. Achieving ultra-low friction by aqueous, brush-assisted lubrication. In Superlubricity; Erdemir, A., Martin, J.-M., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 365–396. [Google Scholar]
- Klein, J. Hydration lubrication. Friction 2013, 1, 1–23. [Google Scholar] [CrossRef]
- Neville, A.; Morina, A.; Liskiewicz, T.; Yan, Y. Synovial joint lubrication—Does nature teach more effective engineering lubrication strategies? Proc. IMechE Part C 2007, 221, 1223–1230. [Google Scholar] [CrossRef]
- Crockett, R. Tribology of natural articular joints. In Aqueous Lubrication: Natural and Biomimetic Approaches; Spencer, N.D., Ed.; Elsevier: World Scientific, IISc Press: Singapore, 2014; pp. 1–32. [Google Scholar]
- Wang, B.; Sun, J.; Wu, Y. Lubricating performances of nano organic-molybdenum as additives in water-based liquid during cold rolling. Adv. Mater. Res. 2011, 337, 550–555. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, D. Comparative investigation on the tribological behavior of reinforced plastic composite under natural seawater lubrication. Mater. Design 2013, 51, 983–988. [Google Scholar] [CrossRef]
- Lee, S.; Müller, M.; Vörös, J.; Pasche, S.; de Paul, S.; Textor, M.; Ratoi, M.; Spikes, H.A.; Spencer, N.D. Boundary lubrication of oxide surfaces by poly(L-lysine)-g-poly(ethylene glycol) (PLL-g-PEG) in aqueous media. Tribol. Lett. 2003, 15, 231–239. [Google Scholar] [CrossRef]
- Ratoi, M.; Spikes, H.A. Lubricating properties of aqueous surfactant solutions. Tribol. Trans. 1999, 42, 479–486. [Google Scholar] [CrossRef]
- Chinas-Castillo, F.; Lara-Romero, J.; Alonso-Nunez, G.; Lopez-Velazquez, A. Tribology of aqueous thiomolybdate and thiotungstate additives in low-pressure contacts. Tribol. Trans. 2013, 56, 366–373. [Google Scholar] [CrossRef]
- Penga, Y.; Hua, Y.; Wang, H. Tribological behaviors of surfactant-functionalized carbon nanotubes as lubricant additive in water. Tribol. Lett. 2007, 25, 247–253. [Google Scholar] [CrossRef]
- Mens, J.W.M.; de Gee, A.W. Friction and wear behavior of 18 polymers in contact with steel in environments of air and water. Wear 1991, 149, 255–268. [Google Scholar] [CrossRef]
- Hsu, J.-P.; Lin, S.-H. Temperature dependence of the viscosity of nonpolymeric liquids. J. Chem. Phys. 2003, 118, 172–178. [Google Scholar] [CrossRef]
- Bair, S.; Jarzynski, J.; Winer, W.O. The temperature, pressure and time dependence of lubricant viscosity. Tribol. Int. 2001, 34, 461–468. [Google Scholar] [CrossRef]
- CRC. Handbook of Chemistry and Physics, 89th ed.; Taylor and Francis Group LLC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Tripaldi, G.; Vettor, A.; Spikes, H.A. Friction behavior of ZDDP films in the mixed, boundary/EHD regime. SAE Trans. 1996, 105, 1819–1830. [Google Scholar]
- Dardin, A.; Hedrich, K.; Müller, M.; Ksenija, T.-M.; Spikes, H.A. Influence of Polyalkylmethacrylate Viscosity Index Improvers on the Efficiency of Lubricants. SAE Tech. Paper 2003. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Minimum film thickness in elliptical contacts for different regimes of fluid-film lubrication. In Proceedings of the 5th Leeds-Lyon symposium on tribology; Mechanical Engineering Publication: Bury St Edmunds, Suffolk, UK, 1979; pp. 22–27. [Google Scholar]
- Esfahanian, M.; Hamrock, B.J. Fluid-film lubrication regimes revisited. Tribol. Trans. 1991, 34, 628–632. [Google Scholar] [CrossRef]
- Lee, S.; Spencer, N.D. Aqueous lubrication of polymers: Influence of surface modification. Tribol. Int. 2005, 38, 922–930. [Google Scholar] [CrossRef]
- Kumikov, V.K.; Khokonov, K.B. On the measurement of surface free energy and surface tension of solid metals. J. Appl. Phys. 1983, 54, 1346–1350. [Google Scholar] [CrossRef]
- Wu, S. Surface and interfacial tensions of polymer melts II. J. Phys. Chem. 1970, 74, 632–638. [Google Scholar] [CrossRef]
- Lui, M.; Sun, J.; Chen, Q. Influences of heating temperature on mechanical properties of polydimethylsiloxane. Sens. Actuators A 2009, 151, 42–45. [Google Scholar] [CrossRef]
- Hutchings, I.M. Tribology: Friction and Wear of Engineering Materials; Elsevier: London, UK, 1992. [Google Scholar]
- Stachowiak, G.; Batchelor, A.W. Engineering Tribology, 3rd ed.; Butterworth-Heinemann: Burlington, MA, USA, 2005. [Google Scholar]
- Cassin, G.; Heinrich, E.; Spikes, H.A. The influence of surface roughness on the lubrication properties of adsorbing and non-adsorbing biopolymers. Tribol. Lett. 2001, 11, 95–102. [Google Scholar] [CrossRef]
- Bongaerts, J.H.H.; Fourtouni, K.; Stokes, J.R. Soft-tribology: Lubrication in a compliant PDMS–PDMS contact. Tribol. Int. 2007, 40, 1531–1542. [Google Scholar] [CrossRef]
- Glovnea, R.P.; Forrest, A.K.; Olver, A.V.; Spikes, H.A. Measurement of sub-nanometer lubricant films using ultra-thin film interferometry. Tribol. Lett. 2003, 15, 217–230. [Google Scholar] [CrossRef]
- Guo, F.; Wong, P.L.; Fu, Z.; Ma, C. Interferometry measurement of lubricating films in slider-on-disc contacts. Tribol. Lett. 2010, 39, 71–79. [Google Scholar] [CrossRef]
- Bongaerts, J.H.H.; Day, J.P.R.; Marriott, C.; Pudney, P.D.A.; Willamson, A.M. In situ confocal Raman spectroscopy of lubricants in a soft elastohydrodynamic tribological contact. J. App. Phys. 2008, 104. [Google Scholar] [CrossRef]
- Gohar, R.; Rahnejat, H. Fundamentals of Tribology; Imperial College Press: London, UK, 2012. [Google Scholar]
- Onset of plastic bulk deformation due to shear stress under normal load can be judged by Tresca yield criterion (sphere on plane with ideal smoothness), , where pm is the mean pressure, Y is the elastic limit and H is the hardness of the softer of the two materials in contact. The thresholds for PDMS-PDMS, POM-POM, and steel-glass are 0.8, 142 and 3140 MPa, respectively, that the contact pressures in this study are sufficiently lower than these thresholds.
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A 1966, 295, 300–319. [Google Scholar] [CrossRef]
- De Vicente, J.; Stokes, J.R.; Spikes, H.A. The frictional properties of Newtonian fluids in rolling-sliding soft-EHL contact. Tribol. Lett. 2005, 20, 273–286. [Google Scholar] [CrossRef]
- De Vicente, J.; Stokes, J.R.; Spikes, H.A. Soft lubrication of model hydrocolloids. Food Hydrocoll. 2006, 20, 483–491. [Google Scholar] [CrossRef]
- Nalam, P.C.; Clasohm, J.N.; Mashaghi, A.; Spencer, N.D. Macrotribological studies of Poly(L-lysine)-graft-poly(ethylene glycol) in aqueous glycerol mixtures. Tribol. Lett. 2010, 37, 541–552. [Google Scholar] [CrossRef]
- Mark, J.E. Polymer Data Handbook; Oxford University Press, Inc.: New York, NY, USA, 1999. [Google Scholar]
- The effective Young’s modulus of composite layers in the antiparallel direction of the layers is calculated from the relation: E = (f1/E1 + f2/E2)−1, where fx is volume fraction the material and Ex is the bulk Young’s modulus. For the case of 2 mm PDMS layer on a 5 mm thick steel disc the effective Young’s modulus is: ((0.2/0.7)/2 MPa + (0.5/0.7)/207 GPa)−1 = 7.0 MPa.
- MatWeb Homepage. Available online: http://www.matweb.com (accessed on 1 May 2014).
- Callister, W.D.J. Material Science and Engineering, an Introduction, 7th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2007. [Google Scholar]
- Mata, A.; Fleischman, A.J.; Roy, S. Characterization of polydimethylsiloxane (PDMS) properties for biomedical micro/nanosystems. Biomed. Microdev. 2005, 7, 281–293. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Røn, T.; Lee, S. Influence of Temperature on the Frictional Properties of Water-Lubricated Surfaces. Lubricants 2014, 2, 177-192. https://doi.org/10.3390/lubricants2040177
Røn T, Lee S. Influence of Temperature on the Frictional Properties of Water-Lubricated Surfaces. Lubricants. 2014; 2(4):177-192. https://doi.org/10.3390/lubricants2040177
Chicago/Turabian StyleRøn, Troels, and Seunghwan Lee. 2014. "Influence of Temperature on the Frictional Properties of Water-Lubricated Surfaces" Lubricants 2, no. 4: 177-192. https://doi.org/10.3390/lubricants2040177
APA StyleRøn, T., & Lee, S. (2014). Influence of Temperature on the Frictional Properties of Water-Lubricated Surfaces. Lubricants, 2(4), 177-192. https://doi.org/10.3390/lubricants2040177