Hydraulic Electromechanical Regenerative Damper in Vehicle–Track Dynamics: Power Regeneration and Wheel Wear for High-Speed Train
Abstract
1. Introduction
1.1. Regenerative Damper
1.2. Wear Depth
2. Modelling Systems
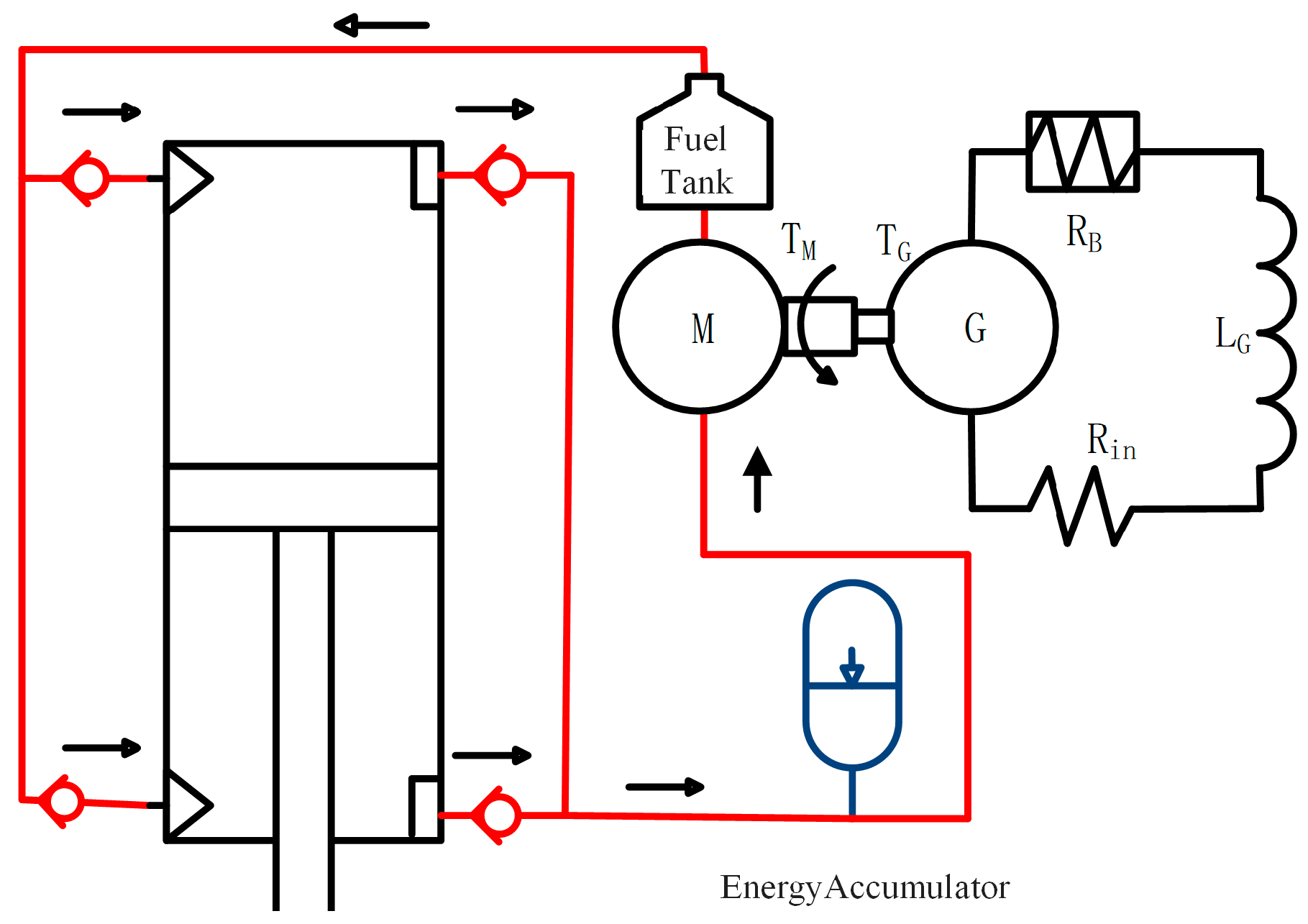
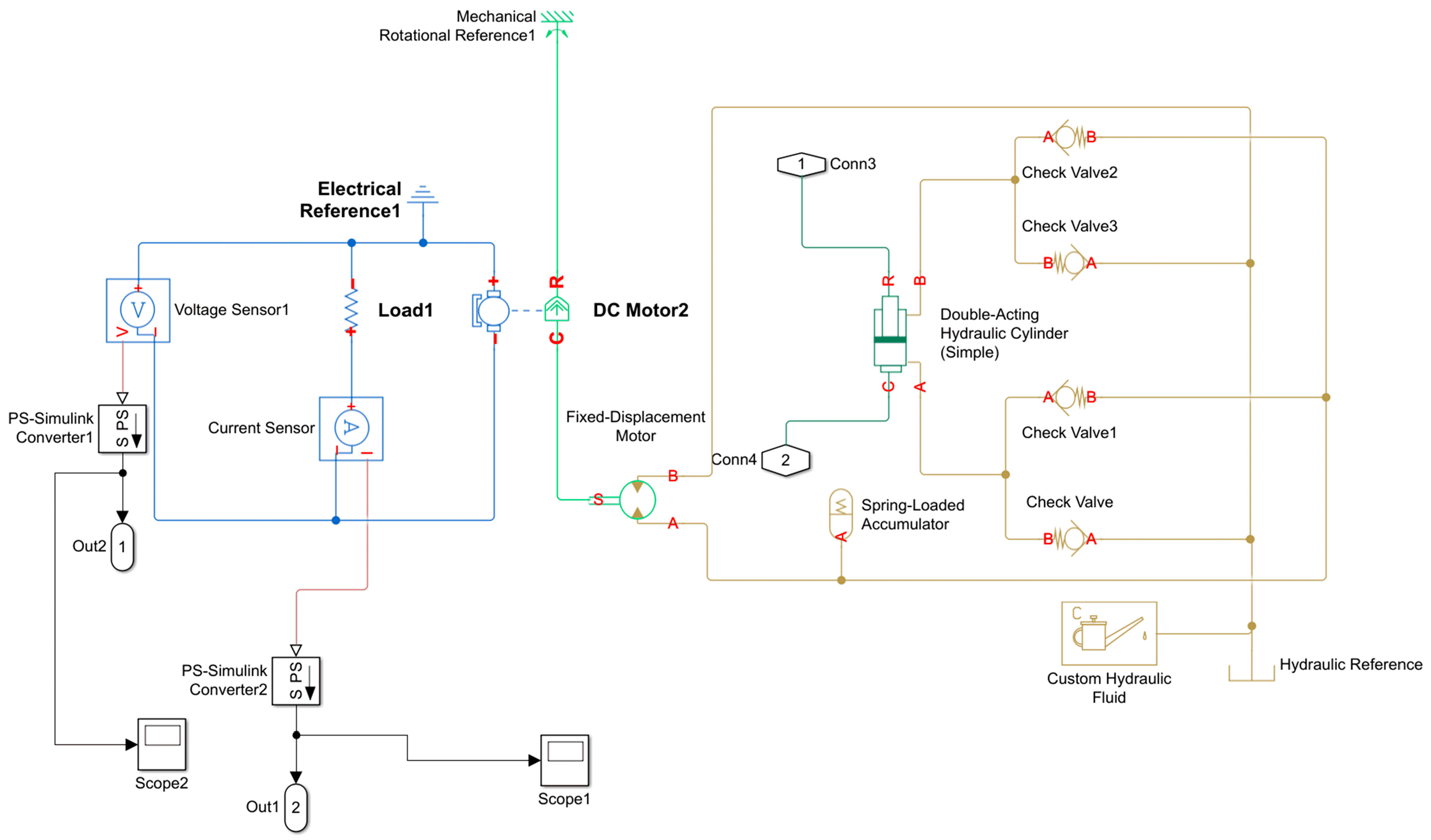
2.1. Modelling of the Hydraulic Electromechanical Regenerative Damper (HERD)
- Dynamics of hydraulic rectifier
- 2.
- Hydraulic cylinder flow and pressure Loss
- 3.
- Pressure loss characteristics of the check valve
- 4.
- Pressure drops in pipelines
- 5.
- Operating pressure difference in hydraulic motor
- 6.
- Hydraulic motor power, generated voltage, and current
- 7.
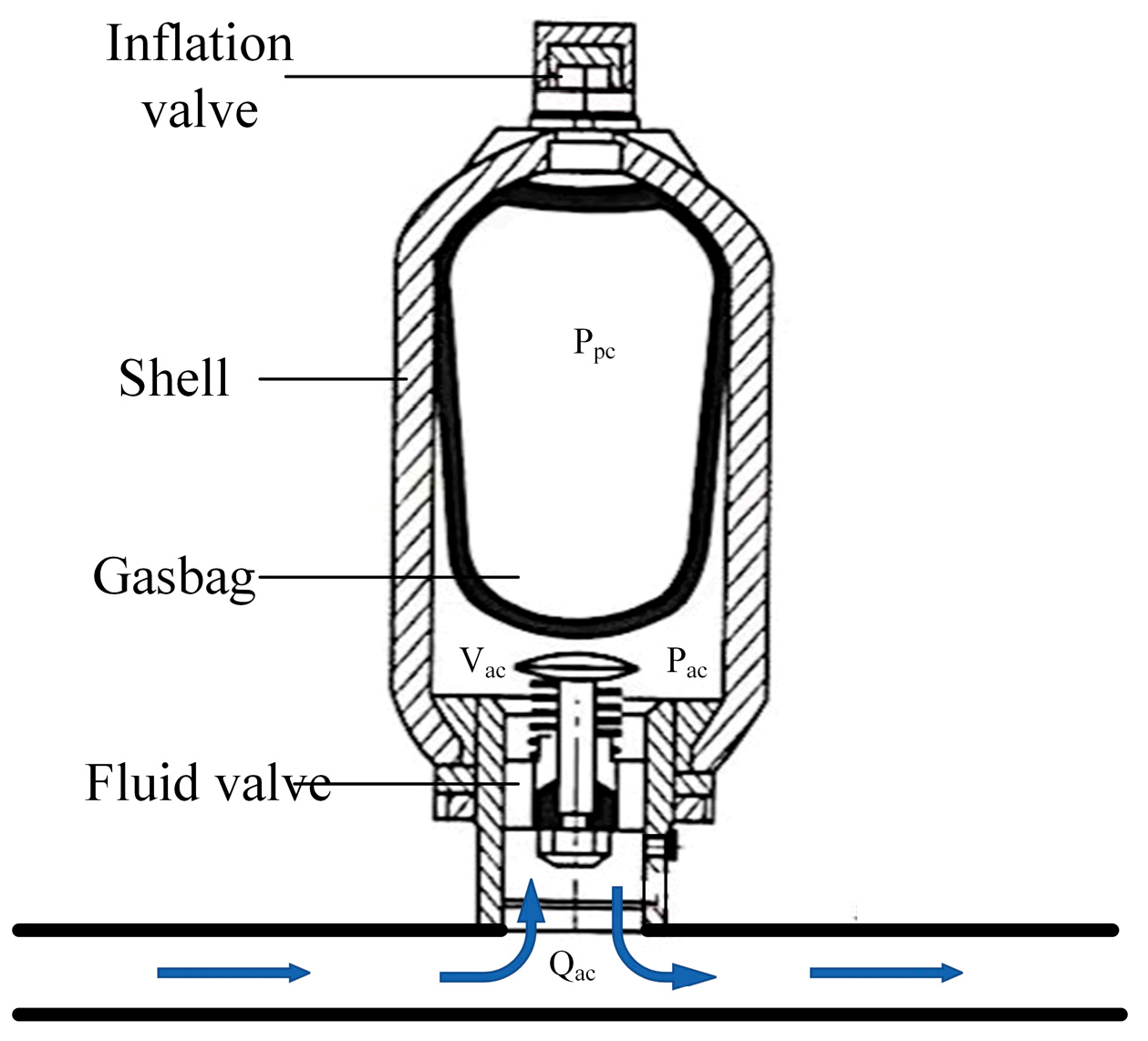
- Model of the accumulator
- 8.
- Damping force of the hydraulic cylinder
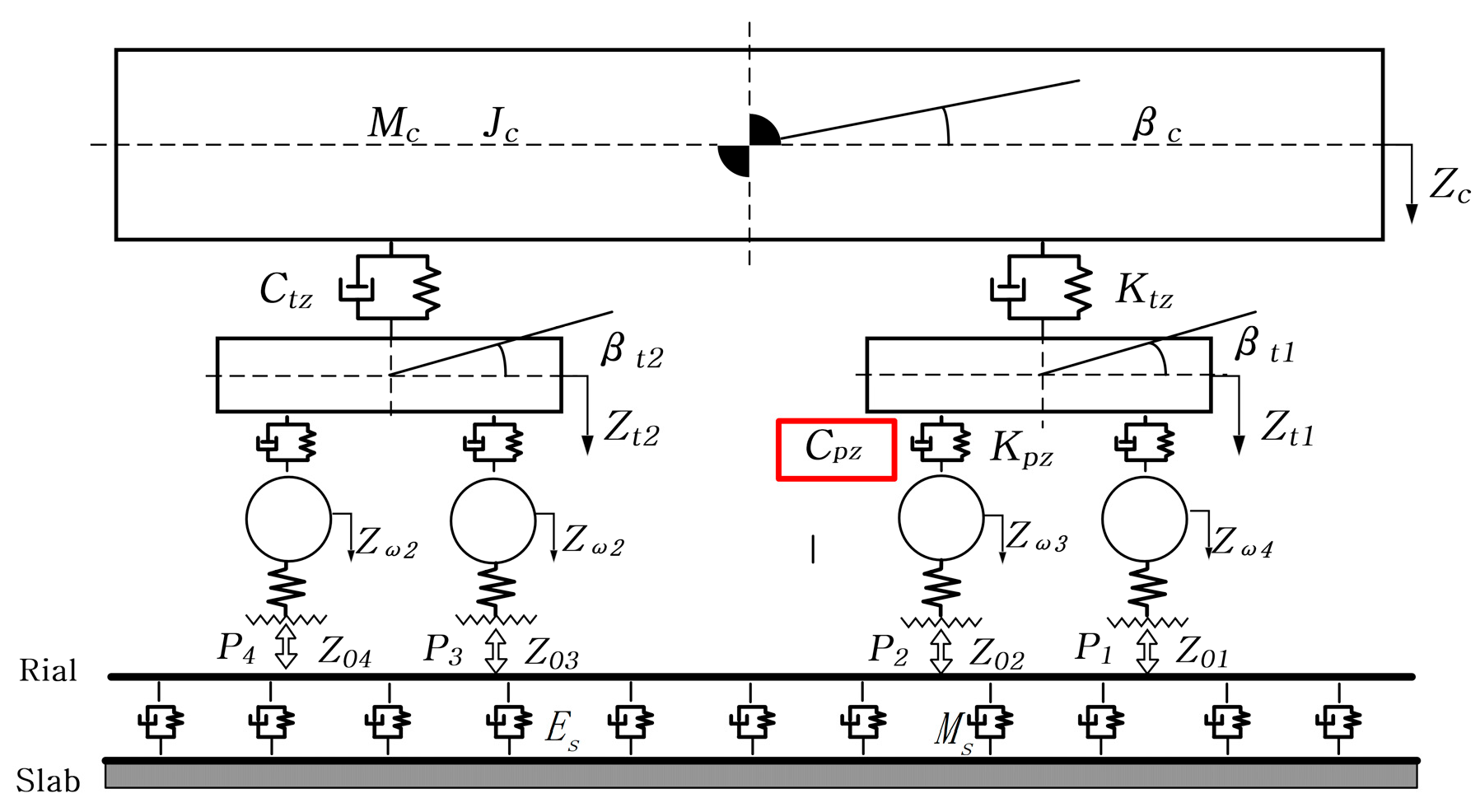
2.2. Vehicle Dynamics Coupled Model
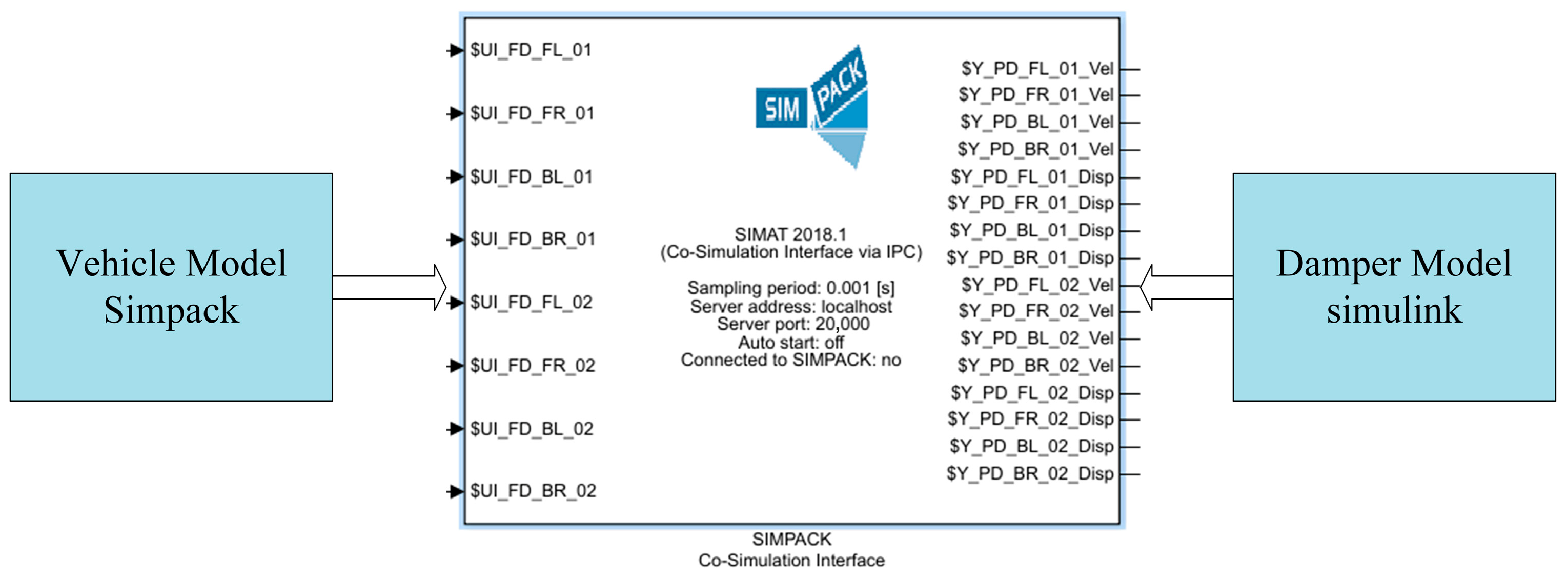
2.3. Co-Simulation Approach
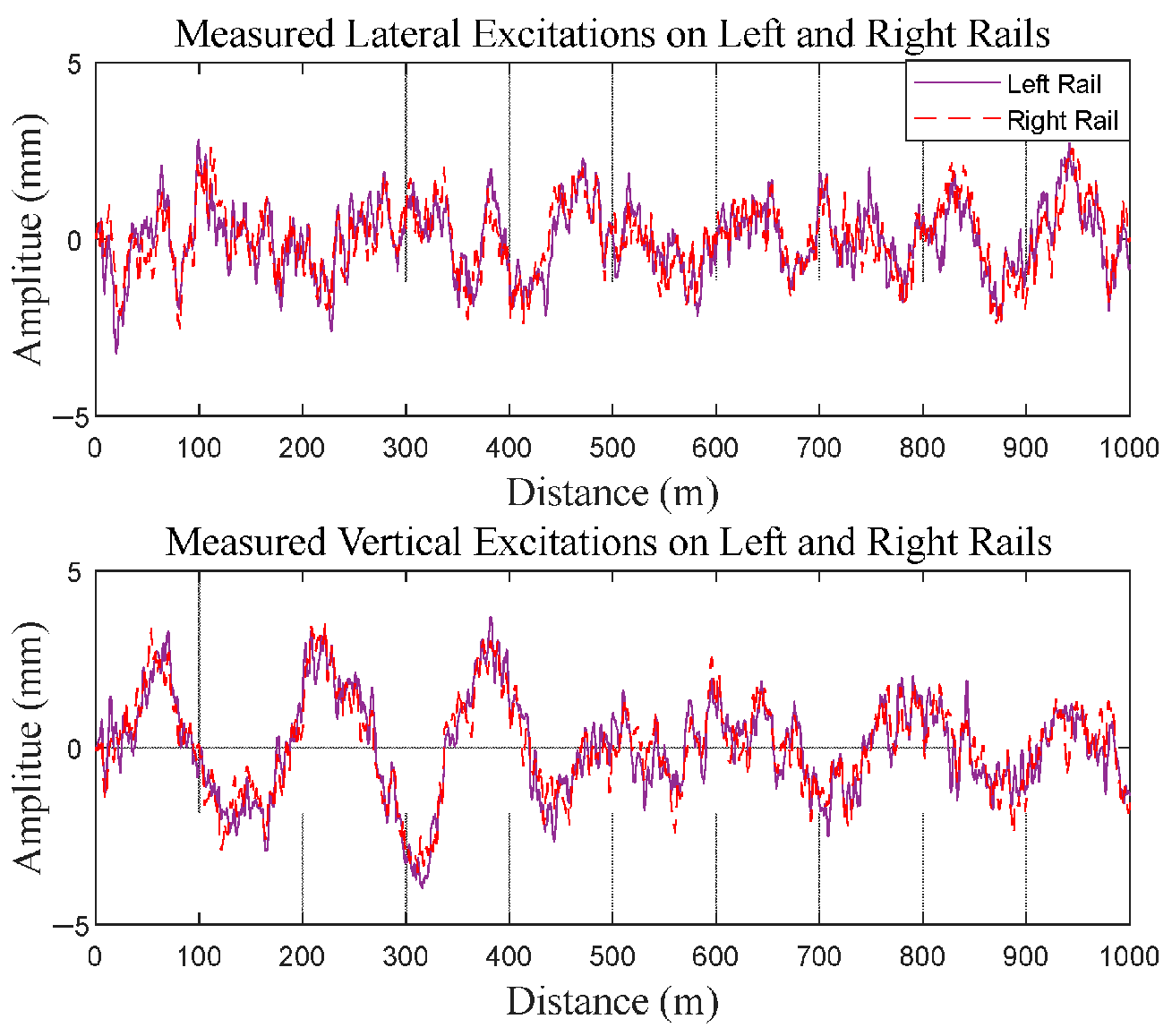
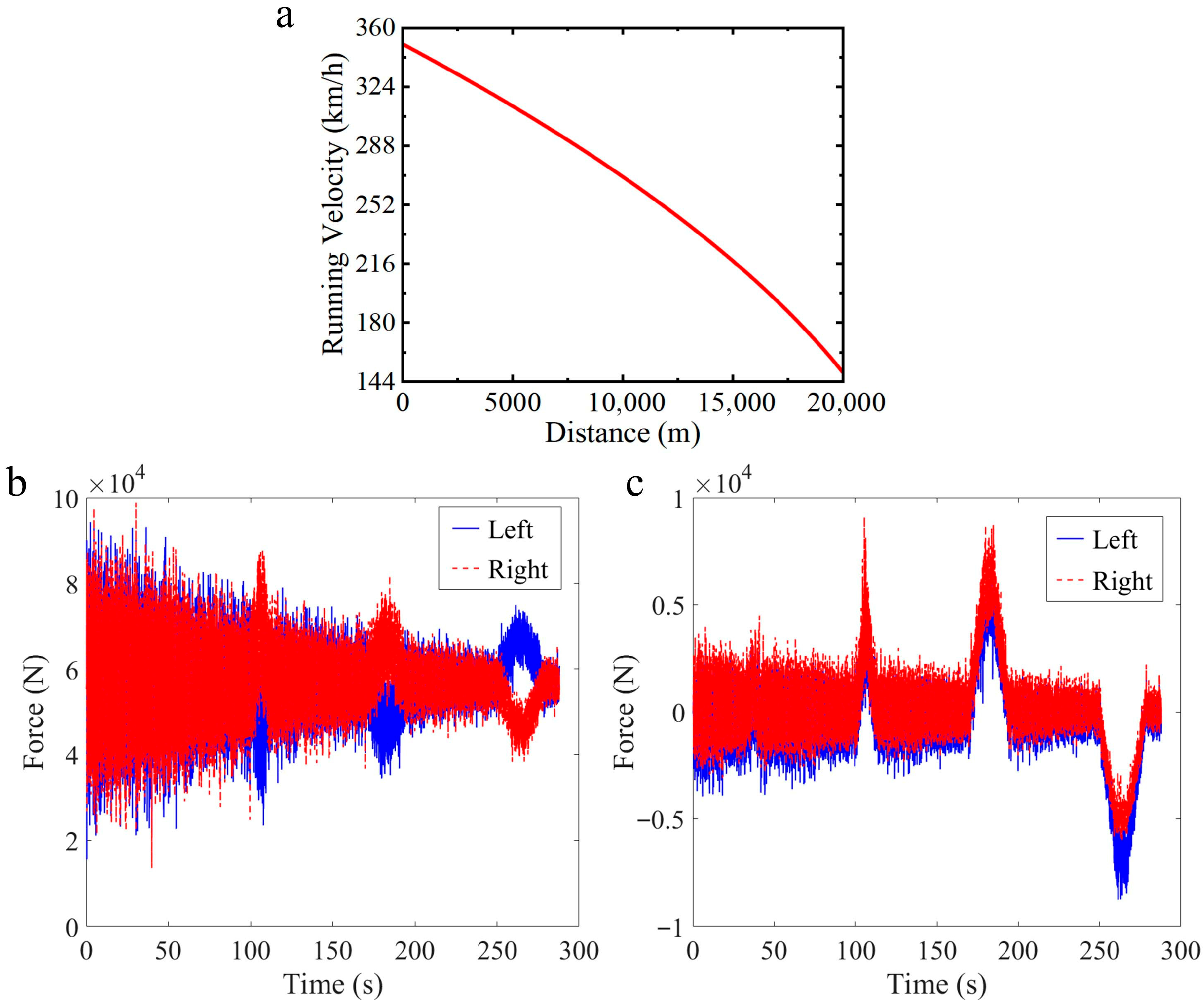
2.4. Track Irregularity
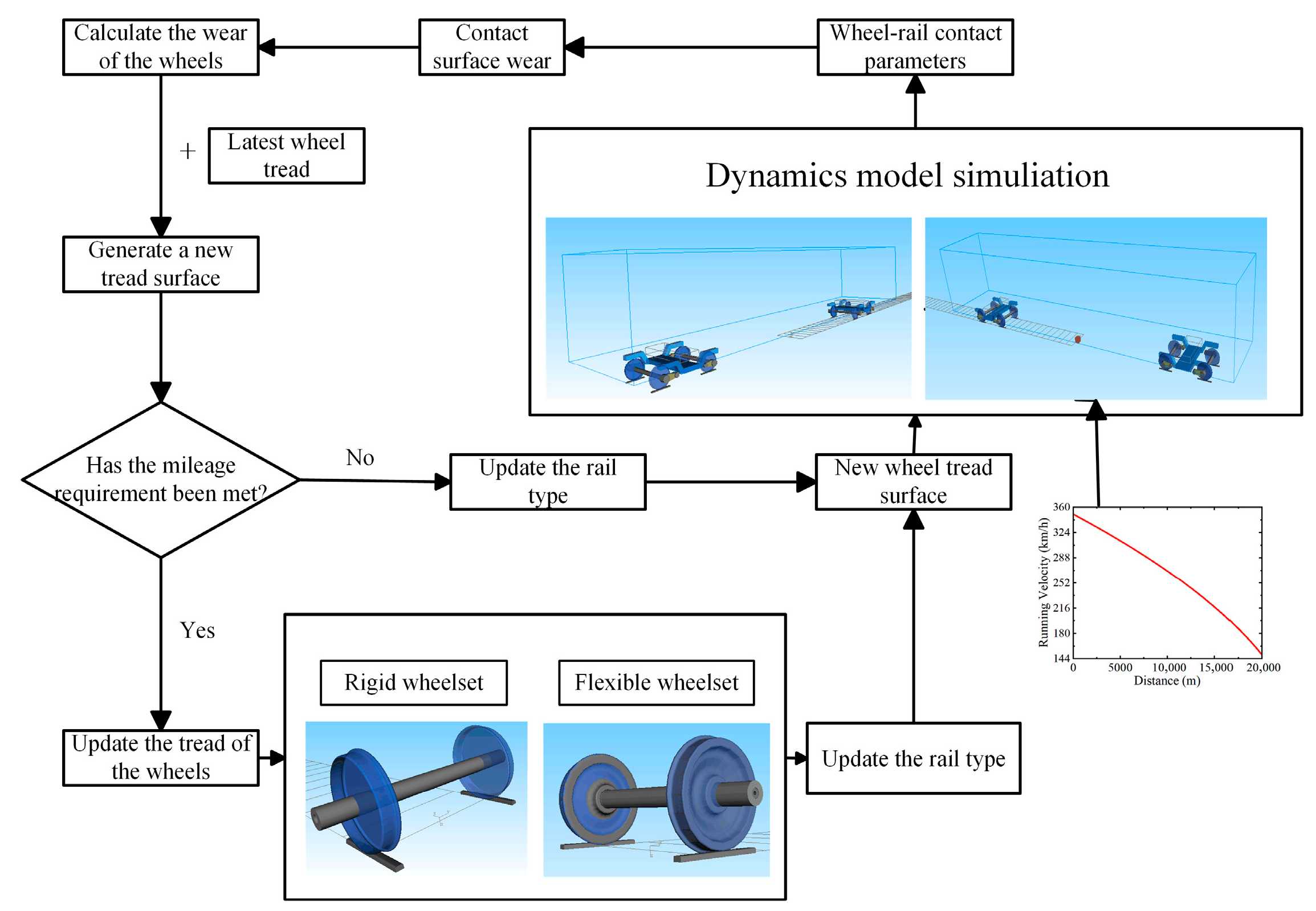
3. Simulation and Analysis
3.1. Damping Characteristics of the Damper
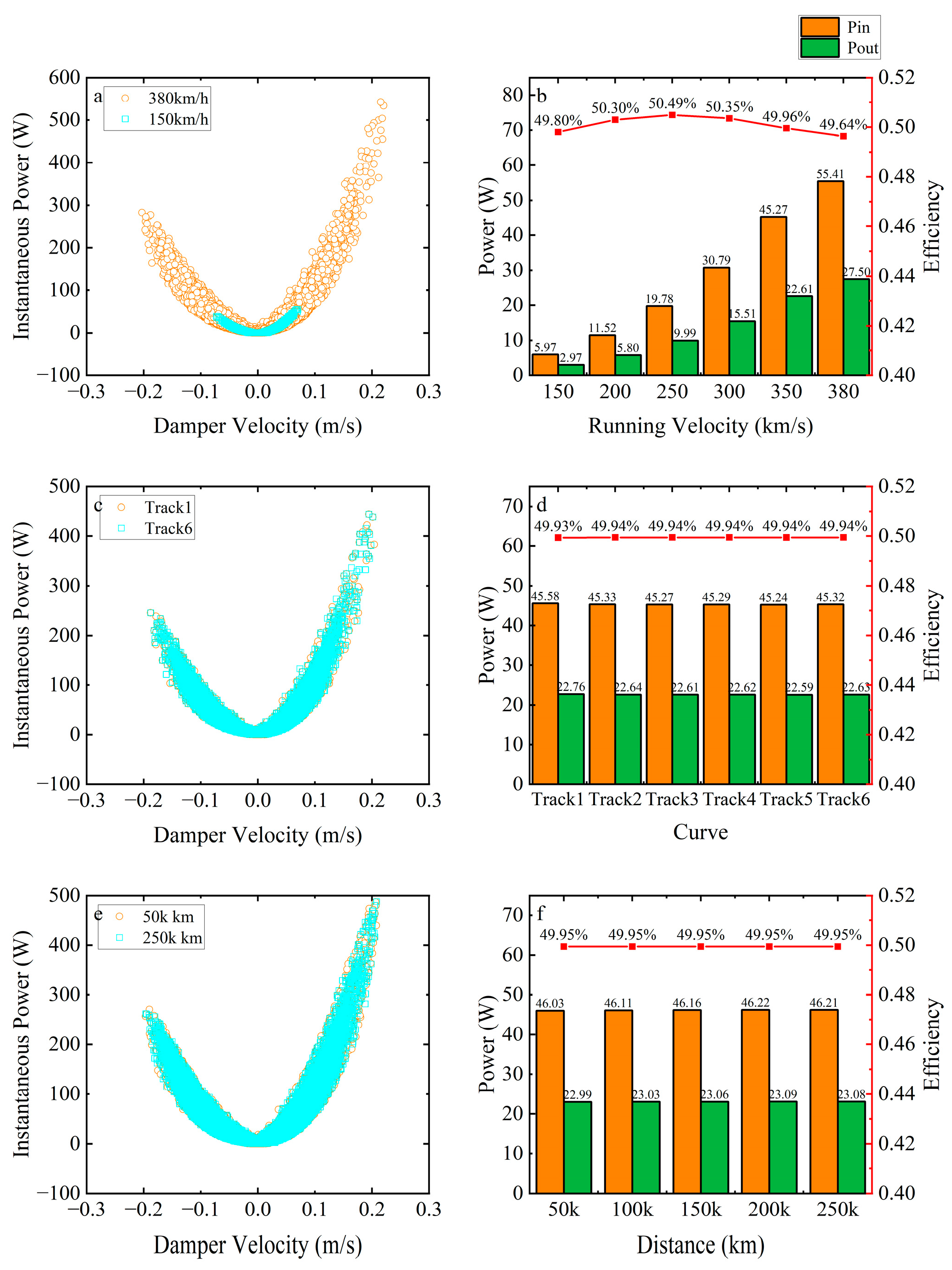
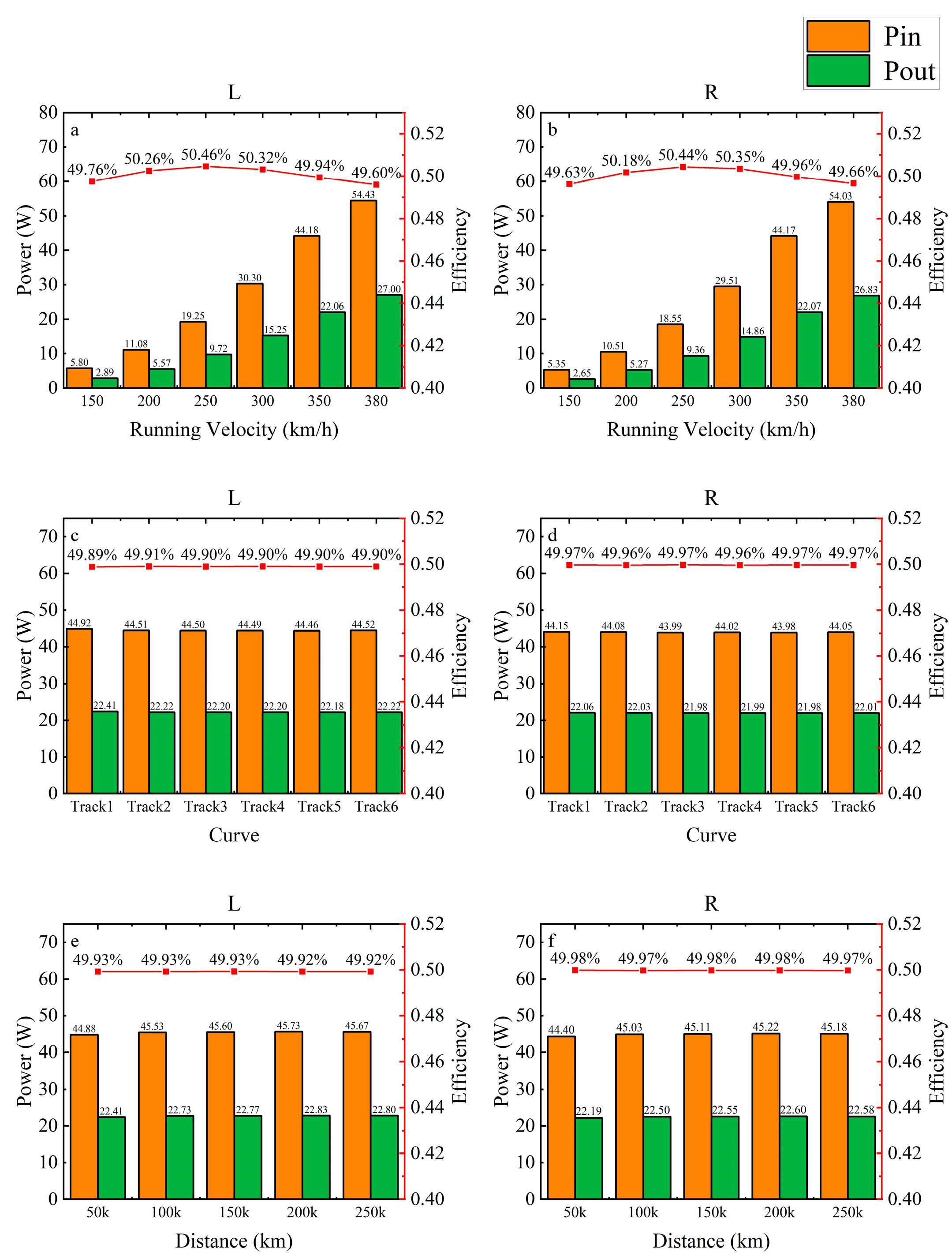
3.2. Power Regeneration Potential
3.3. Prediction of Wear Depth
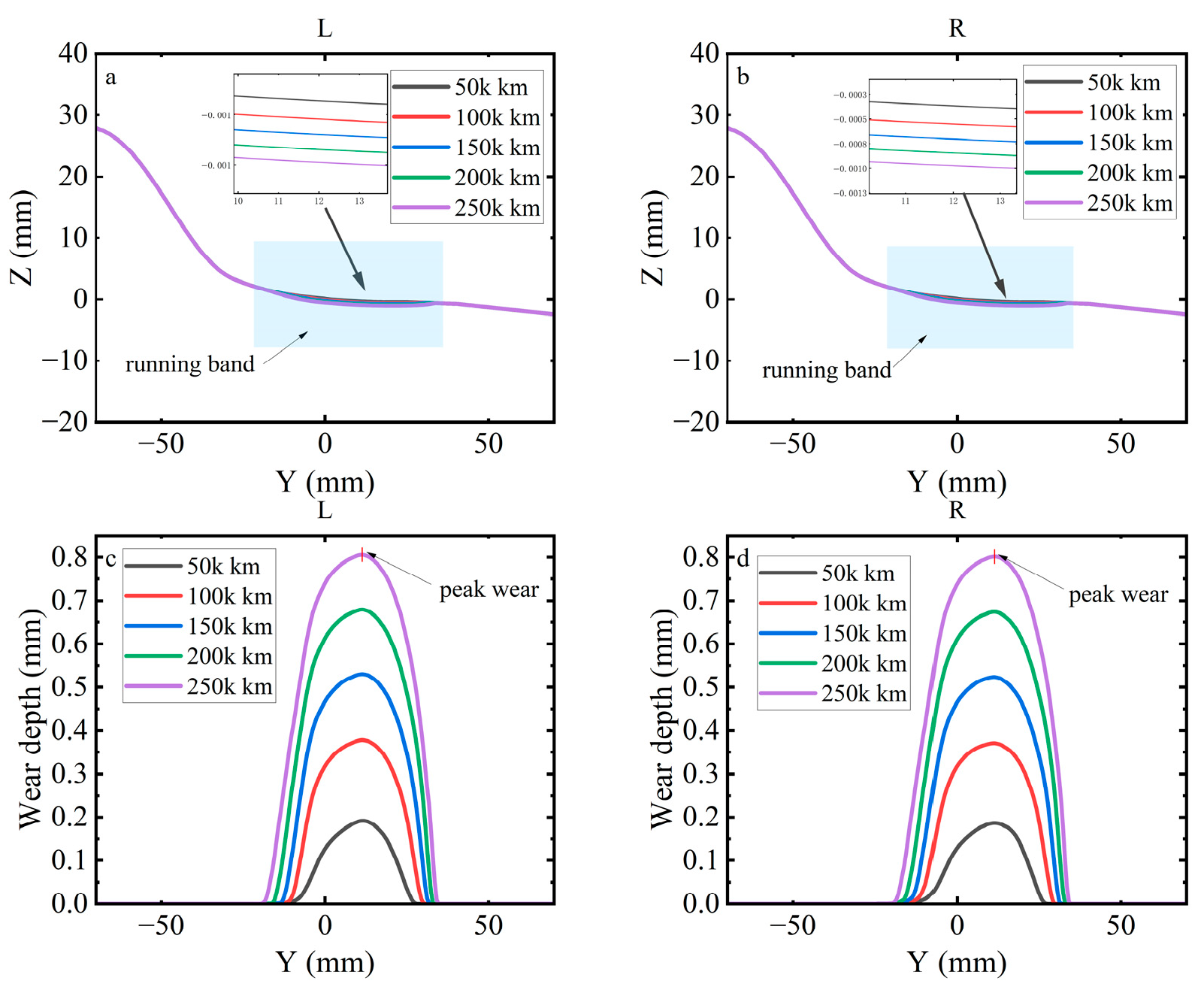
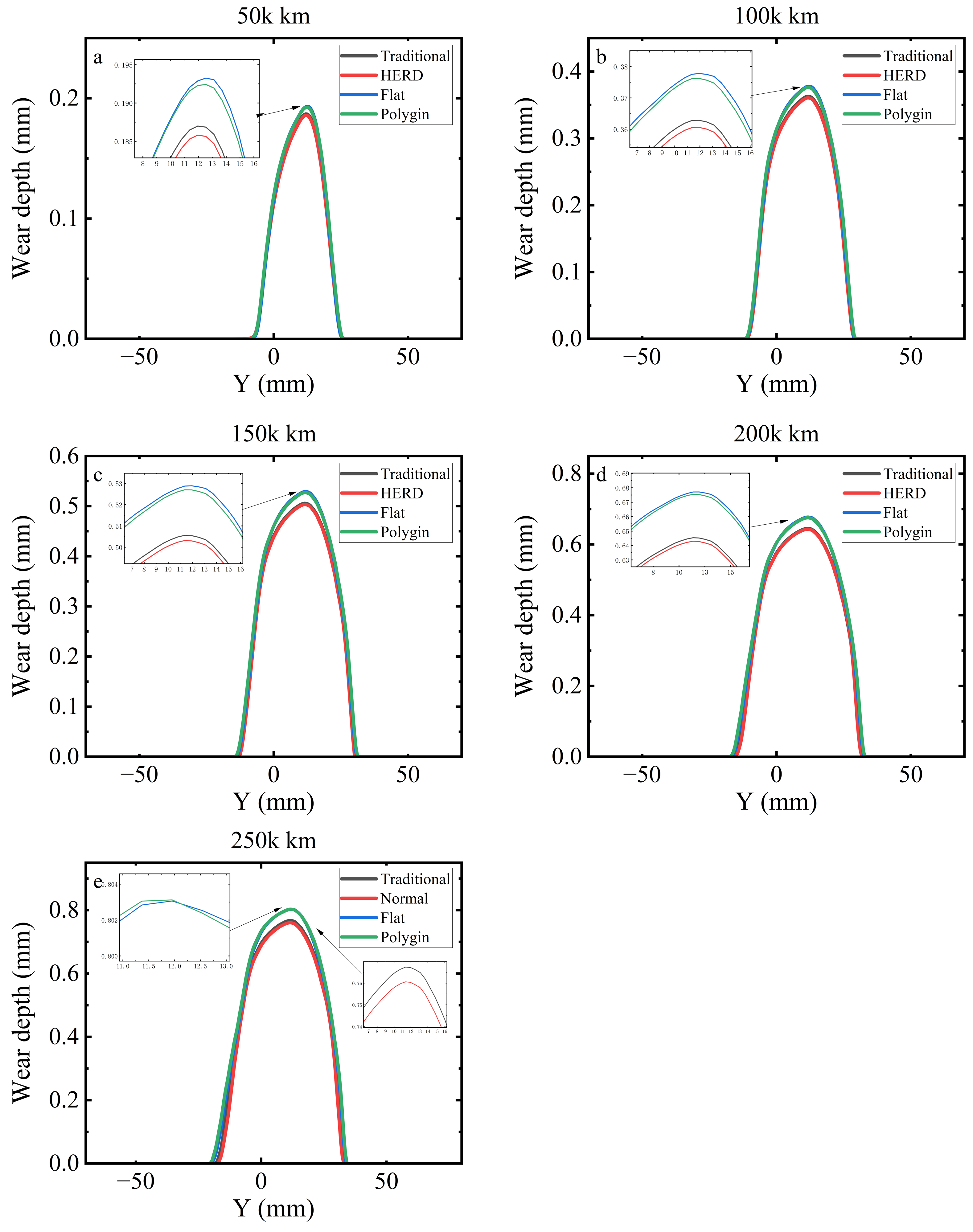
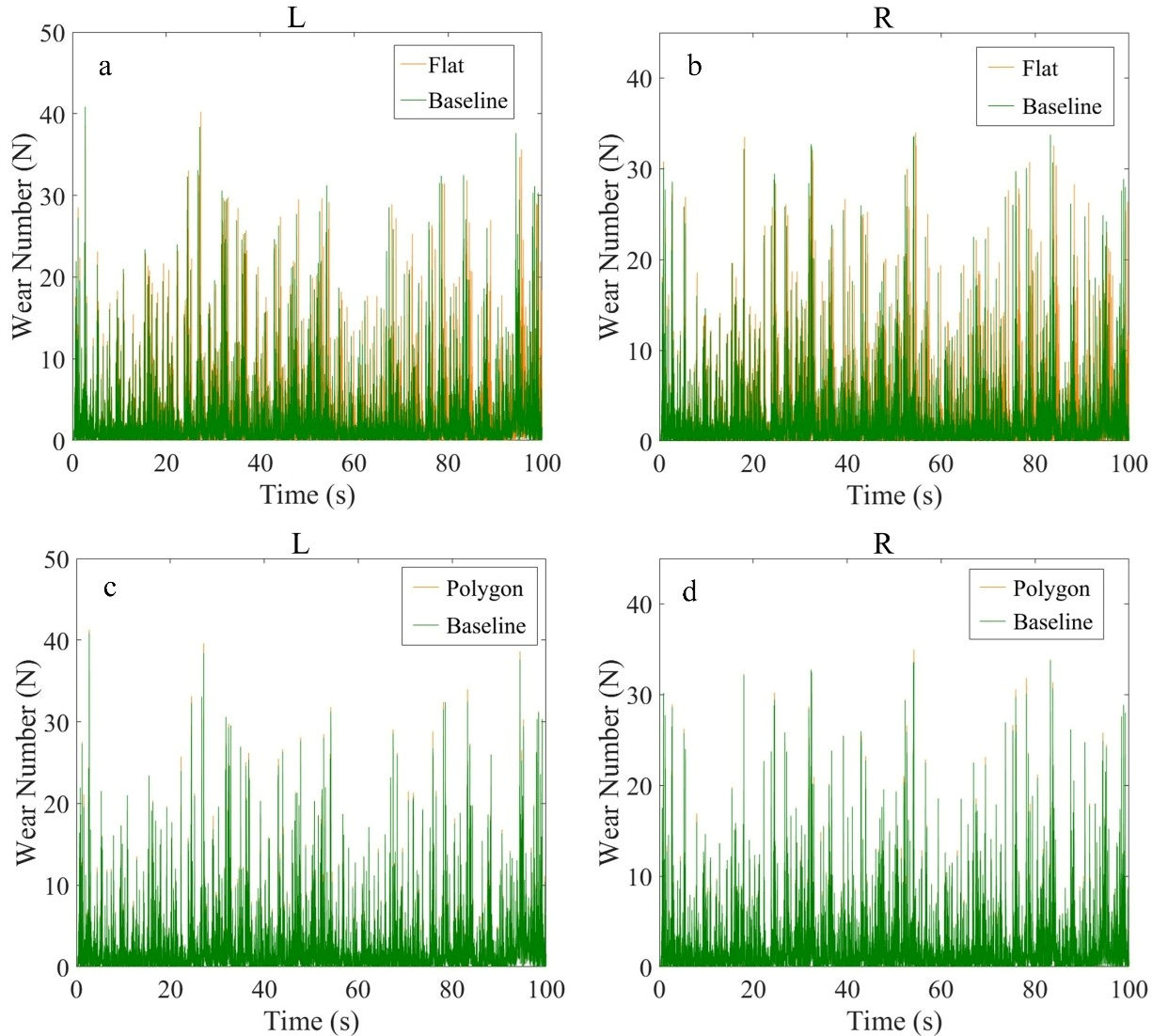
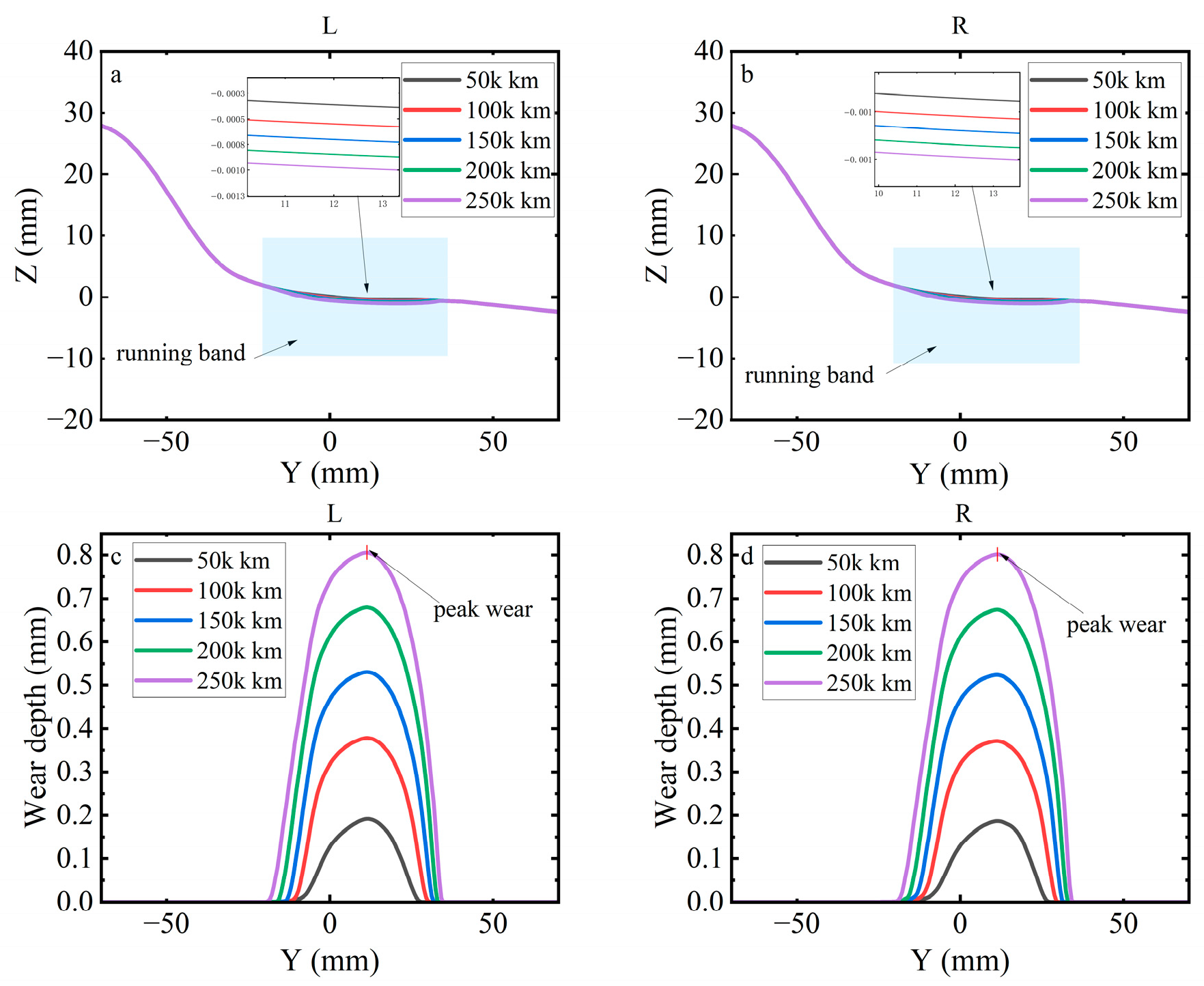
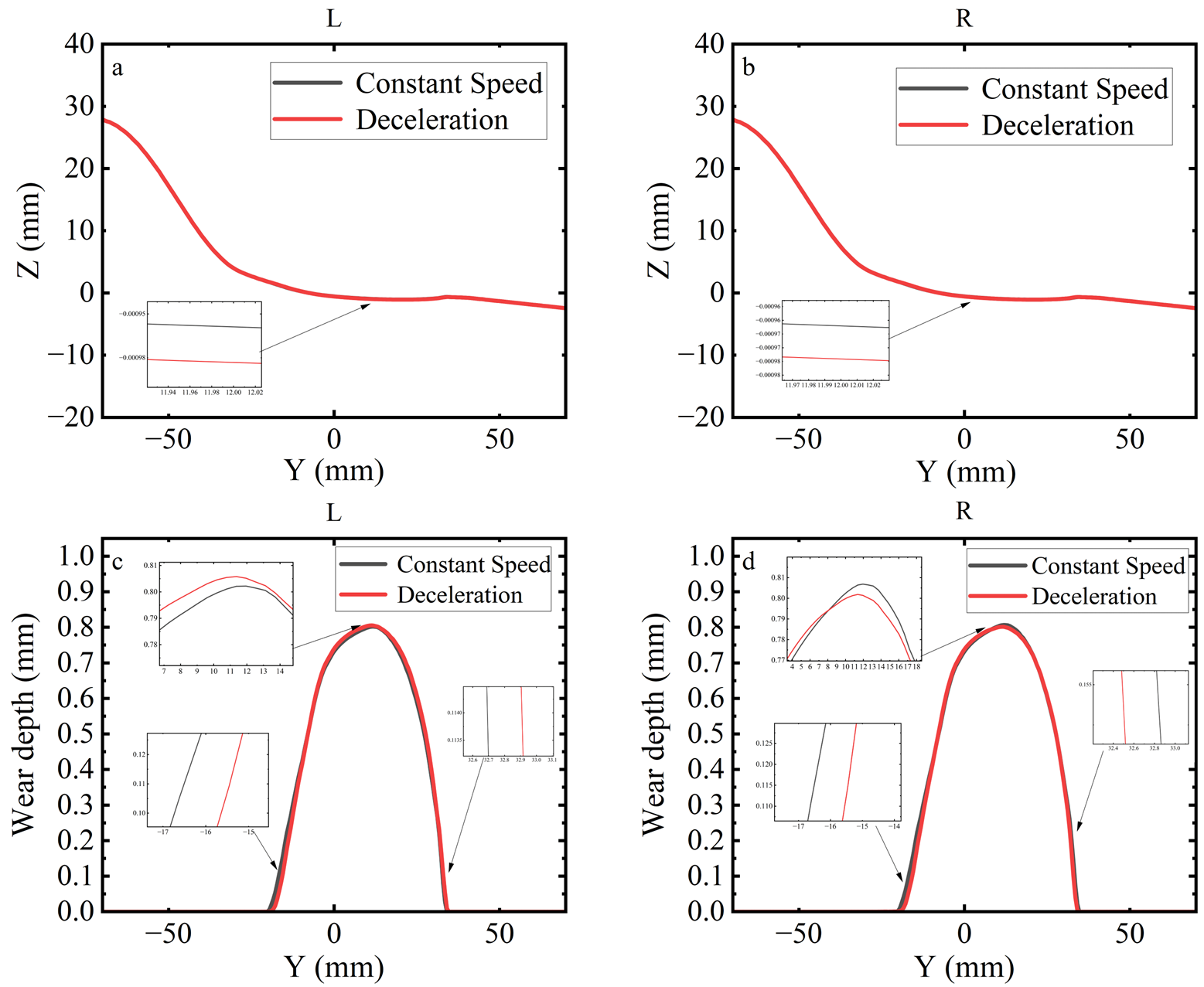
3.3.1. Wear Depth Under Complex Excitations
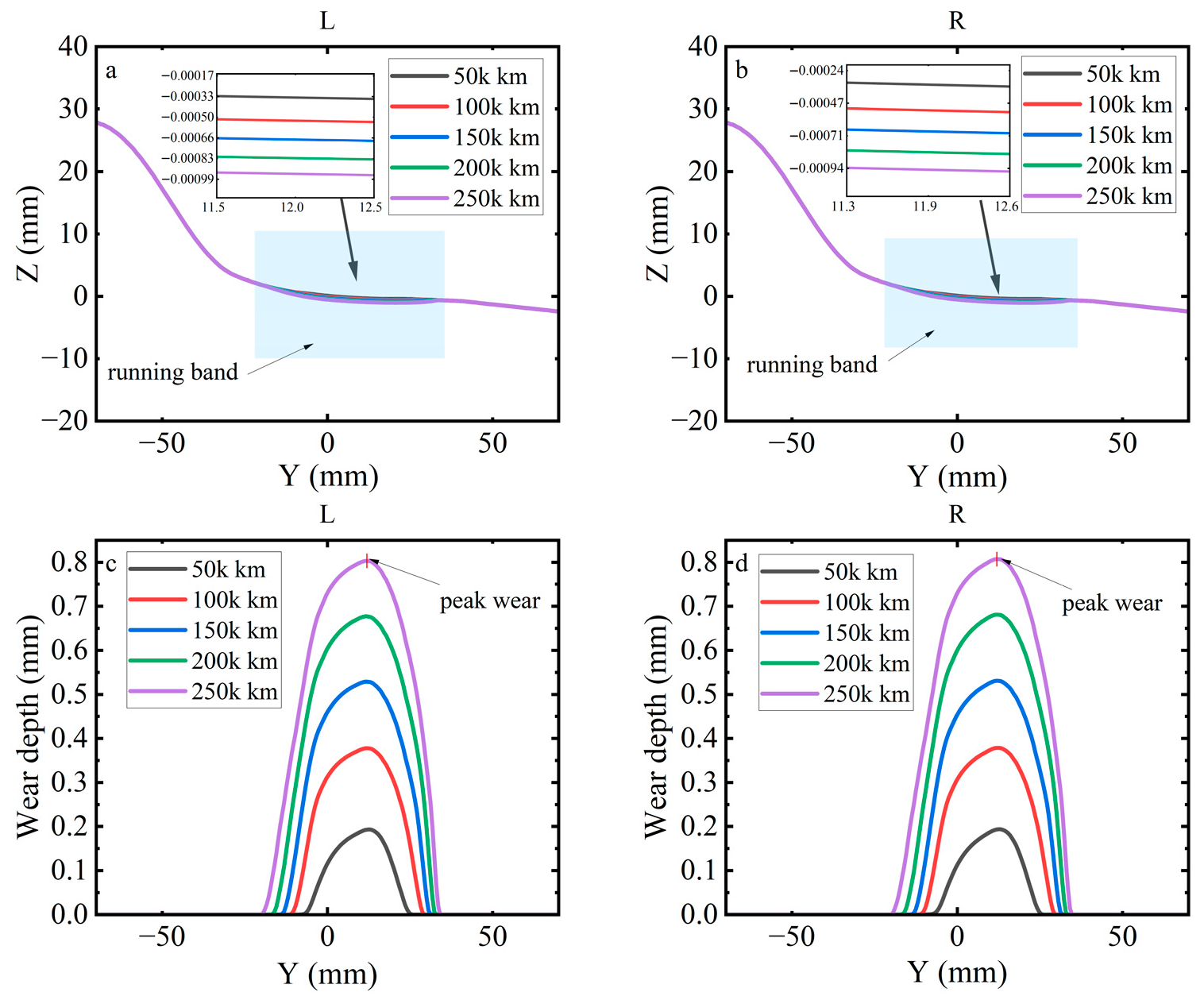
3.3.2. Analysis of Wear Depth Under Braking Conditions
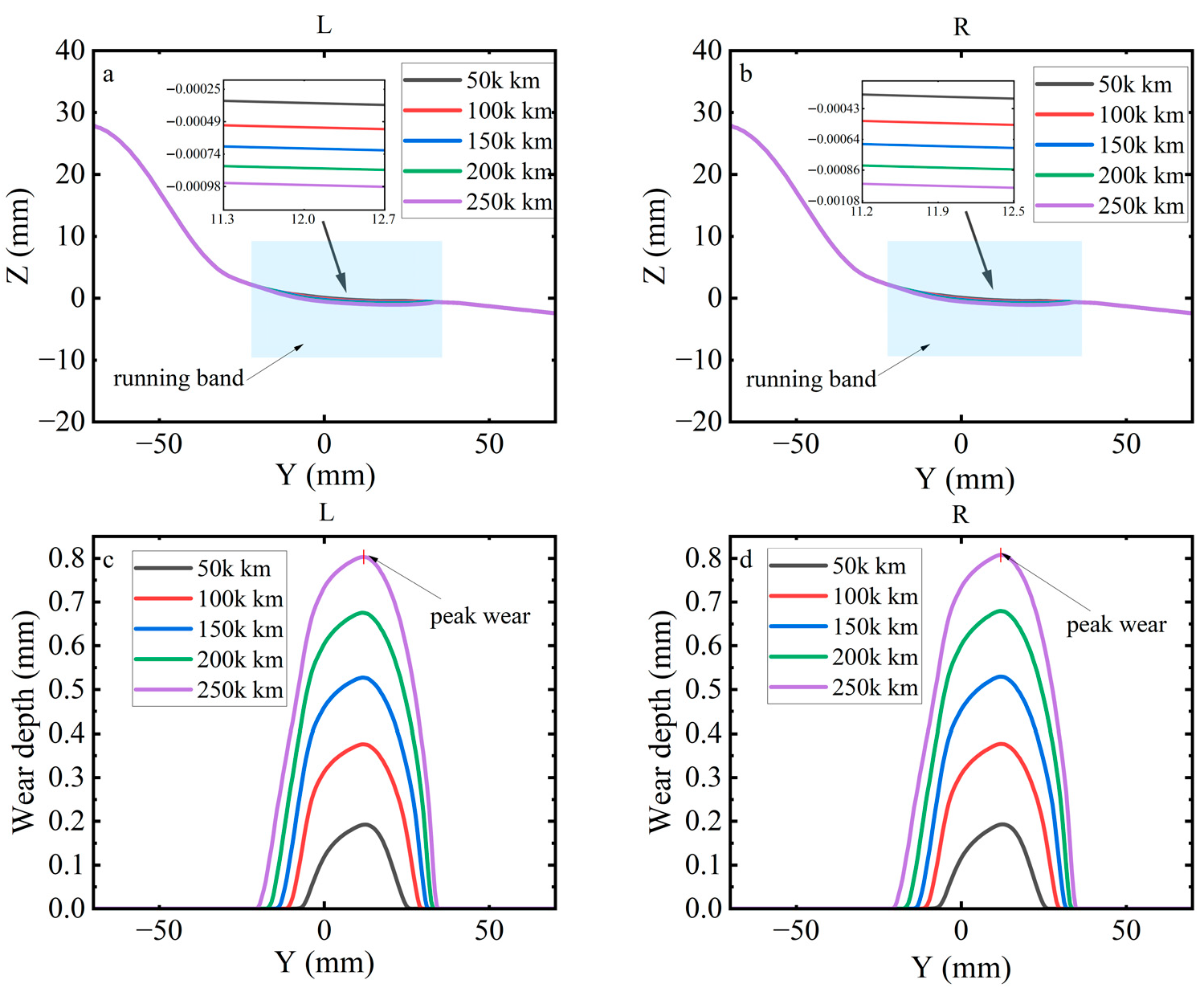
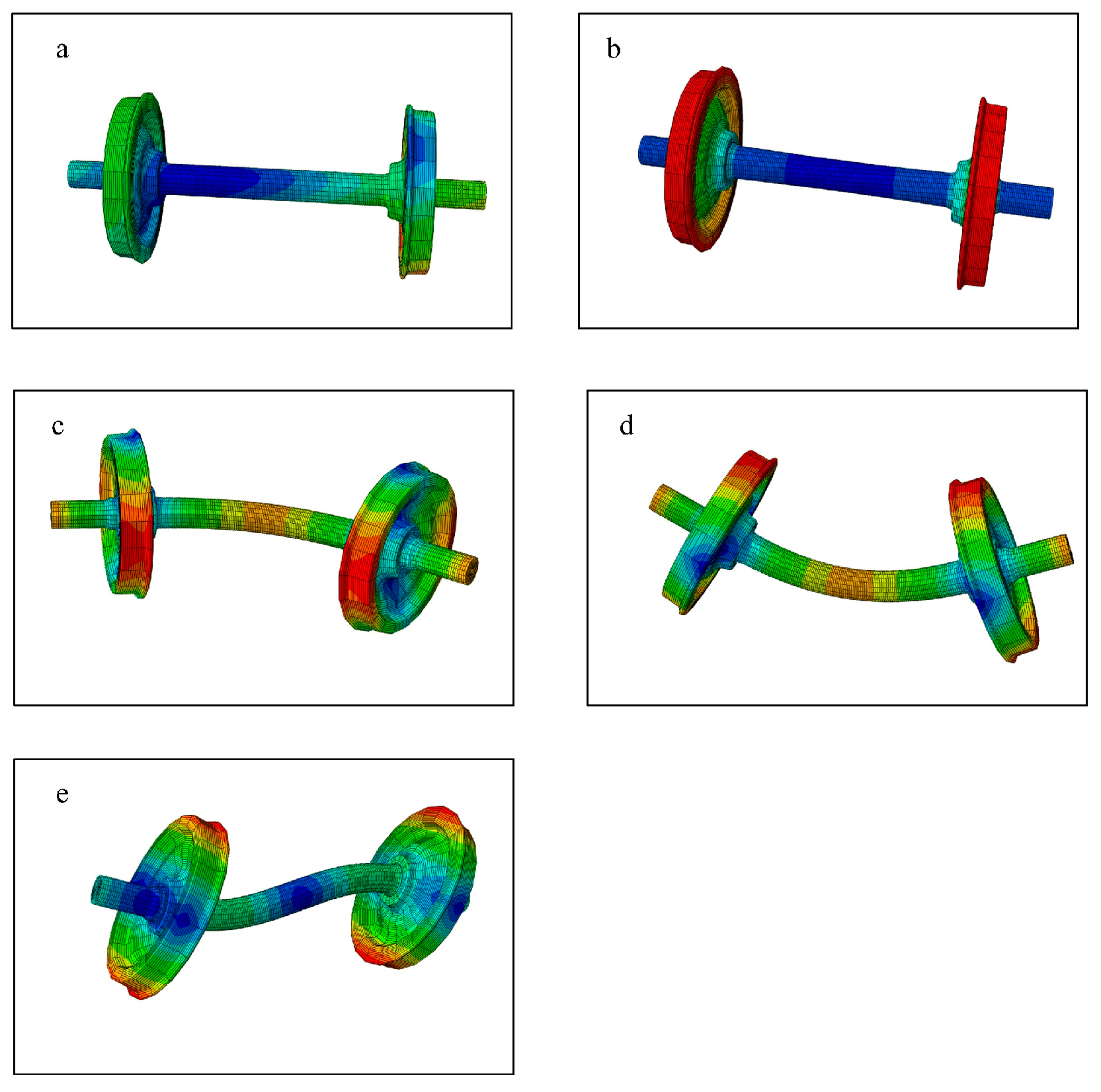
3.3.3. Effect of Flexible Wheelsets on Wear Depth

4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alhumaid, S.; Hess, D.; Guldiken, R. A Noncontact Magneto–Piezo Harvester-Based Vehicle Regenerative Suspension System: An Experimental Study. Energies 2022, 15, 4476. [Google Scholar] [CrossRef]
- Alhumaid, S.; Hess, D.; Guldiken, R. Energy Regeneration from Vehicle Unidirectional Suspension System by a Non-Contact Piezo-Magneto Harvester. Eng. Res. Express 2021, 3, 015033. [Google Scholar] [CrossRef]
- Shi, X.; Yu, Q.; Wu, Z.; Li, J.-Y.; Zhu, S. Active Control for Vehicle Suspension Using a Self-Powered Dual-Function Active Electromagnetic Damper. J. Sound Vib. 2024, 569, 117976. [Google Scholar] [CrossRef]
- Xie, Y.; Tan, B.; Liu, J.; Li, H.; Tan, X. Research on Switchable Energy-Regenerative Suspension System. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA.
- Dong, L.; Yang, F.; He, A.; Guo, Z.; Yu, J.; Zuo, J. Investigation on Energy-Regenerative Shock Absorber with Adjustable Damping and Power for Freight Wagons. Energy Convers. Manag. 2022, 254, 115228. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, H.; Yu, J.; Hu, G. Energy Harvesting Potential Assessment and Systematic Design for Energy-Regenerative Shock Absorbers on Railway Freight Wagons. J. Intell. Mater. Syst. Struct. 2024, 35, 270–290. [Google Scholar] [CrossRef]
- Kopylov, S.; Chen, Z.; Abdelkareem, M.A.A. Implementation of an Electromagnetic Regenerative Tuned Mass Damper in a Vehicle Suspension System. IEEE Access 2020, 8, 110153–110163. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, F.; Jiang, R.; Tu, Z.; Zuo, L. Modeling and Onboard Test of an Electromagnetic Energy Harvester for Railway Cars. Appl. Energy 2019, 250, 568–581. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, G.; Guo, Y. Research on Damping and Energy Recovery Characteristics of a Novel Mechanical-Electrical-Hydraulic Regenerative Suspension System. Energy 2023, 271, 127022. [Google Scholar] [CrossRef]
- Liu, P.; Kou, F.; Chen, Y.; Wang, G.; Lv, W.; Xing, L. A Novel Hybrid Electromagnetic-Hydraulically Interconnected Actuator Suspension: Dynamic Modeling, Bench Test and Ride Analysis. Mech. Syst. Signal Process. 2025, 236, 113028. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, C.; Gao, J.; Zheng, P. Modelling, Validation and Parameter Sensitivity of Regenerative Hydraulic-Electric Shock Absorber. Eng. Comput. 2022, 39, 1348–1373. [Google Scholar] [CrossRef]
- Galluzzi, R.; Tonoli, A.; Amati, N.; Curcuruto, G.; Conti, P.; Greco, G.; Nepote, A. Regenerative Shock Absorbers and the Role of the Motion Rectifier. In Proceedings of the SAE 2016 World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2016. [Google Scholar]
- Guo, S.; Xu, L.; Liu, Y.; Guo, X.; Zuo, L. Modeling and Experiments of a Hydraulic Electromagnetic Energy-Harvesting Shock Absorber. IEEE ASME Trans. Mechatron. 2017, 22, 2684–2694. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Zhan, M.; Guo, K.; Zhao, F.; Liu, Z. Study on a Novel Hydraulic Pumping Regenerative Suspension for Vehicles. J. Frankl. Inst. 2015, 352, 485–499. [Google Scholar] [CrossRef]
- Du, L.; Chen, X. Design of a Novel Electro-Hydraulic Energy-Recovery Shock Absorber for Vehicles. J. Machinery 2018, 56, 647. [Google Scholar]
- Demetgul, M.; Guney, I. Design of the Hybrid Regenerative Shock Absorber and Energy Harvesting from Linear Movement. J. Clean Energy Technol. 2017, 5, 81–84. [Google Scholar] [CrossRef]
- Cai, Q.; Hua, Y.; Zhu, S. Energy-Harvesting Adaptive Vibration Damping in High-Speed Train Suspension Using Electromagnetic Dampers. Int. J. Struct. Stab. Dyn. 2021, 21, 2140002. [Google Scholar] [CrossRef]
- Deubel, C.; Schneider, S.J.; Prokop, G. Effect of Shock Absorber Friction on Vehicle Vertical Dynamics. SAE Int. J. Veh. Dyn. Stab. NVH 2024, 8, 155–177. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Z. Evaluation of Power Regeneration in Primary Suspension for a Railway Vehicle. Front. Mech. Eng. 2020, 15, 265–278. [Google Scholar] [CrossRef]
- Hua, Y.; Cai, Q.; Zhu, S. Energy-Regenerative Semiactive Lateral Suspension Control in High-Speed Trains Using Electromagnetic. IEEE Trans. Veh. Technol. 2022, 71, 4801–4812. [Google Scholar] [CrossRef]
- Isacchi, G.; Ripamonti, F. A Robust and Fail-Safe Semi-Active Vertical Damper to Improve Ride Comfort. Veh. Syst. Dyn. 2024, 1–23. [Google Scholar] [CrossRef]
- Zhang, B.; Luo, M.; Tan, C.A. Ride Comfort and Energy Harvesting of Inflatable Hydraulic-Electric Regenerative Suspension System for Heavy-Duty Vehicles. J. Mech. Sci. Technol. 2024, 38, 2277–2289. [Google Scholar] [CrossRef]
- Sang, H.; Zeng, J.; Wang, Q.; Huang, C.; Mu, J.; Qi, Y.; Kang, W.; Liang, Y. Theoretical Study on Wheel Wear Mechanism of High-Speed Train under Different Braking Modes. Wear 2024, 540–541, 205262. [Google Scholar] [CrossRef]
- Sang, H.; Zeng, J.; Qi, Y.; Mu, J.; Gan, F. Study on Wheel Wear Mechanism of High-Speed Train in Accelerating Conditions. Wear 2023, 516–517, 204597. [Google Scholar] [CrossRef]
- Song, R.; Lu, C.; Sun, L.; Zhang, Z.; Chen, D.; Shen, G. Analysis of Wheel Wear and Wheel-Rail Dynamic Characteristics of High-Speed Trains under Braking Conditions. Shock Vib. 2024, 2024, 9618500. [Google Scholar] [CrossRef]
- Liu, B.; Bruni, S.; Lewis, R. Numerical Calculation of Wear in Rolling Contact Based on the Archard Equation: Effect of Contact Parameters and Consideration of Uncertainties. Wear 2022, 490–491, 204188. [Google Scholar] [CrossRef]
- Zhu, A.; Zhu, A.; Ma, C.; Yang, J.; Hou, X.; Li, H.; Sun, P. The Effect of High-Speed Train Meet on Wheel Wear at Different Speeds. Ind. Lubr. Tribol. 2021, 73, 1019–1027. [Google Scholar] [CrossRef]
- Luo, R.; Shi, H.; Teng, W.; Song, C. Prediction of Wheel Profile Wear and Vehicle Dynamics Evolution Considering Stochastic Parameters for High-Speed Train. Wear 2017, 392–393, 126–138. [Google Scholar] [CrossRef]
- Wang, S.; Guo, H.; Zhang, S.; Barton, D.; Brooks, P. Analysis and Prediction of Double-Carriage Train Wheel Wear Based on SIMPACK and Neural Networks. Adv. Mech. Eng. 2022, 14, 16878132221078491. [Google Scholar] [CrossRef]
- Myśliński, A.; Chudzikiewicz, A. Power Dissipation and Wear Modeling in Wheel–Rail Contact. Appl. Sci. 2023, 14, 165. [Google Scholar] [CrossRef]
- Apezetxea, I.S.; Perez, X.; Alonso, A. Experimental Validation of a Fast Wheel Wear Prediction Model. Wear 2021, 486–487, 204090. [Google Scholar] [CrossRef]
- Hao, K.; Yang, W.; Zhang, D.; Pei, X.; Wang, C.; Xi, Y. Research on Wheel Wear Simulation and Wheel-Rail Contact Relationship of Heavy-Haul Freight Wagon. Int. J. Mechatron. Appl. Mech. 2024, 18, 33–43. [Google Scholar] [CrossRef]
- Liu, X.; Song, Y. Research on the Influence of Wheel Polygons on Vehicle Dynamics Performance. In Proceedings of the Seventh International Conference on Traffic Engineering and Transportation System (ICTETS 2023), Chongqing, China, 22–24 September 2023; SPIE: Dalian, China, 2024; p. 187. [Google Scholar]
- Fang, S.; Feng, J. Research on the Prediction of Polygonal Wear of Metro Wheels. In Proceedings of the Eighth International Conference on Traffic Engineering and Transportation System (ICTETS 2024), Dalian, China, 20–22 September 2024; SPIE: Dalian, China, 2024; p. 174. [Google Scholar]
- Xu, Z.; Li, X.; He, X.; Wang, Z.; Ma, J.; Fan, H. Impact of Wheel Polygonization on Vehicle Vibration and Wheel-Rail Interaction Forces. Noise Vib. Worldw. 2025, 09574565251359155. [Google Scholar] [CrossRef]
- Shi, J. Study on the Influence of Wheel Flat Scar on the Dynamic Performance of Metro Vehicles. Smart Rail Transit. 2024, 64. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Chanson, H. Bernoulli Theorem, Minimum Specific Energy, and Water Wave Celerity in Open-Channel Flow. J. Irrig. Drain. Eng. 2009, 135, 773–778. [Google Scholar] [CrossRef][Green Version]
- Henry Darcy and the Making of a Law—Brown—2002—Water Resources Research—Wiley Online Library. Available online: https://agupubs.onlinelibrary.wiley.com/doi/10.1029/2001WR000727 (accessed on 16 September 2025).[Green Version]
- Li, W.; An, G. Application of Kirchhoff’s Voltage Law in Circuit Analysis. J. Electron. Sci. Technol. 2013, 26, 136–138. [Google Scholar] [CrossRef]
- Wang, R.; Gu, F.; Cattley, R.; Ball, A.D. Modelling, Testing and Analysis of a Regenerative Hydraulic Damper System. Energies 2016, 9, 386. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Wang, R.; Feng, G. A Simulation Approach for Analysis of the Regenerative Potential of High-Speed Train Suspensions. Energies 2024, 17, 3496. [Google Scholar] [CrossRef]
- Enblom, R. Deterioration Mechanisms in the Wheel–Rail Interface with Focus on Wear Prediction: A Literature Review. Veh. Syst. Dyn. 2009, 47, 661–700. [Google Scholar] [CrossRef]
- Krause, H.; Poll, G. Wear of Wheel-Rail Surfaces. Wear 1986, 113, 103–122. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R.; Crosbee, D.; Allen, P.; Ye, Y.; Zhang, W. Wheel wear analysis of motor and unpowered car of a high-speed train. Wear 2020, 444–445, 203126. [Google Scholar]






| Key Component | Parameter | Symbol | Value | Units |
|---|---|---|---|---|
| Hydraulic Cylinder | Piston area | 0.005 | ||
| Piston ring area | 0.0041 | |||
| Hydraulic Motor | Motor displacement | 30 | ||
| Mechanical efficiency | 0.95 | - | ||
| Generator | Torque coefficient | 0.93 | ||
| Internal inductance | 0.03 | |||
| Internal inductance | 20 | |||
| Internal resistance | 20 | |||
| Spring-loaded Accumulator | Accumulator port area | 0.0038 | - | |
| Specific heat ratio of charged gas | 0.78 | - |
| Major Parameter | Value | Unit | Title 1 | Title 2 | Title 3 |
|---|---|---|---|---|---|
| Carboy mass | 34.934 × 103 | kg | entry 1 | data | data |
| Bogie mass | 3.12 × 103 | kg | entry 2 | data | data |
| Wheel mass | 1.7518 × 103 | kg | |||
| Primary vertical stiffness | 1176 × 103 | N/m | |||
| Primary vertical damping | 19.6 × 103 | N·s /m |
| Percentage (%) | Superelevation (mm) | Transition (m) | |
|---|---|---|---|
| 3000 | 2.0 | 150 | 380 |
| 7000 | 6.7 | 150 | 540 |
| 8000 | 5.3 | 135 | 500 |
| 9000 | 7.5 | 125 | 490 |
| 10,000 | 4.3 | 115 | 430 |
| 12,000 | 2.3 | 100 | 370 |
| Category | Parameter | Value | Unit |
|---|---|---|---|
| HERD | Piston area | 0.005 | |
| Motor displacement | 30 | ||
| Generator torque coefficient | 0.93 | ||
| Vehicle | Carbody mass | 34.934 × 103 | |
| Bogie mass | 3.12 × 103 | ||
| Wheel mass | 1.7518 × 103 | ||
| Primary vertical stiffness | 1176 × 103 | ||
| Primary vertical damping | 19.6 × 103 |
| Regeneration Efficiency (%) | Distance (km) | Wheel Wear (mm) | |
|---|---|---|---|
| Conventional damper | 45.27~45.28 | 200,000 | 0.66 |
| 250,000 | 0.78 | ||
| HERD | 49.93~49.94 | 200,000 | 0.64 |
| 250,000 | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Wang, R.; Yin, Z.; Sun, T.; Lyu, H. Hydraulic Electromechanical Regenerative Damper in Vehicle–Track Dynamics: Power Regeneration and Wheel Wear for High-Speed Train. Lubricants 2025, 13, 424. https://doi.org/10.3390/lubricants13090424
He Z, Wang R, Yin Z, Sun T, Lyu H. Hydraulic Electromechanical Regenerative Damper in Vehicle–Track Dynamics: Power Regeneration and Wheel Wear for High-Speed Train. Lubricants. 2025; 13(9):424. https://doi.org/10.3390/lubricants13090424
Chicago/Turabian StyleHe, Zifei, Ruichen Wang, Zhonghui Yin, Tengchi Sun, and Haotian Lyu. 2025. "Hydraulic Electromechanical Regenerative Damper in Vehicle–Track Dynamics: Power Regeneration and Wheel Wear for High-Speed Train" Lubricants 13, no. 9: 424. https://doi.org/10.3390/lubricants13090424
APA StyleHe, Z., Wang, R., Yin, Z., Sun, T., & Lyu, H. (2025). Hydraulic Electromechanical Regenerative Damper in Vehicle–Track Dynamics: Power Regeneration and Wheel Wear for High-Speed Train. Lubricants, 13(9), 424. https://doi.org/10.3390/lubricants13090424






