Crushing Removal Conditions and Experimental Research on Abrasive Water Jets Impacting Rock
Abstract
1. Introduction
2. Movement of Abrasive Particles in Abrasive Water Jets
2.1. Accelerated Motion Process of Abrasive Particles
- (1)
- Abrasive particles in contraction section of nozzle
- (2)
- Abrasive particles within straight-line segment of nozzle
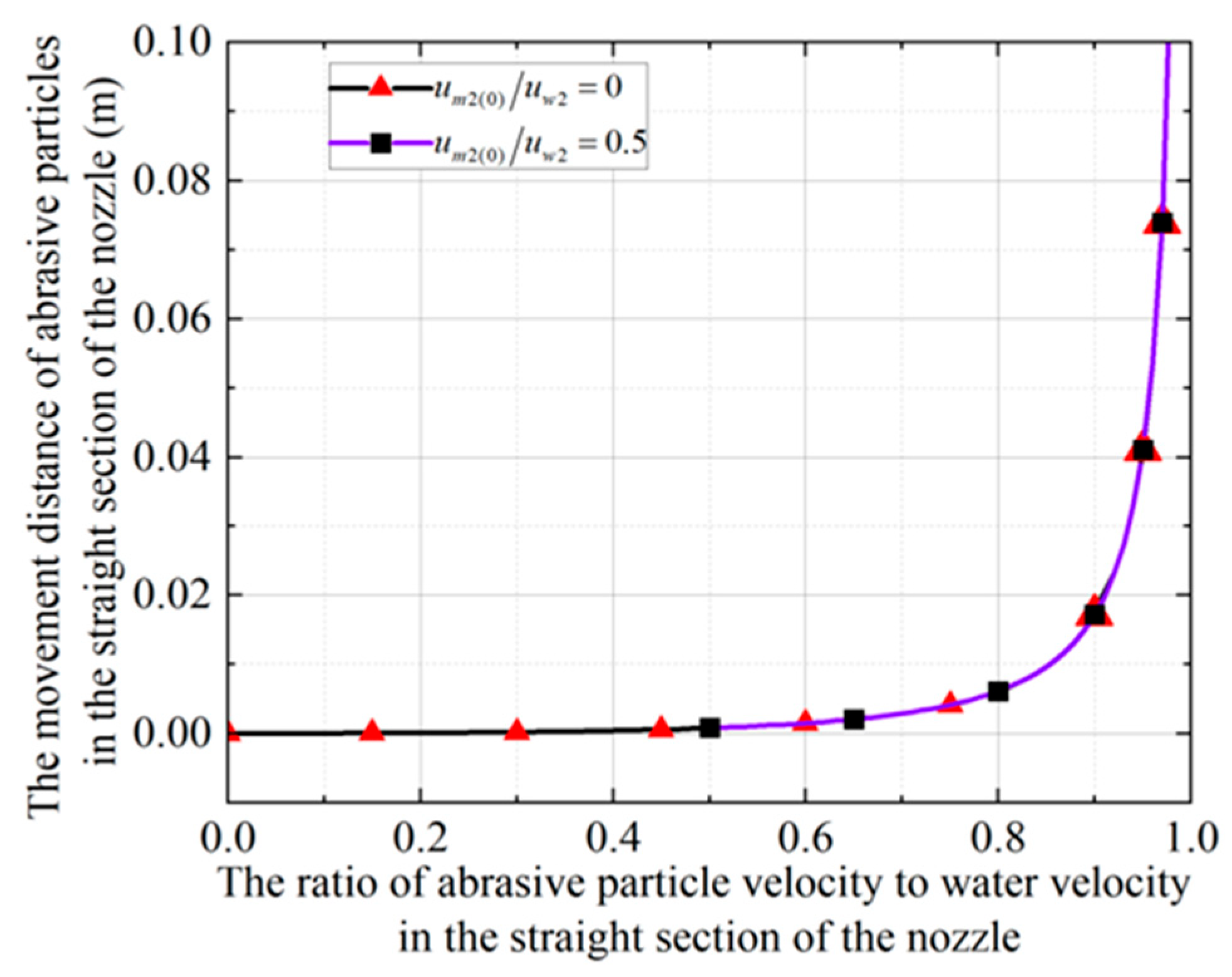
2.2. Decelerating Motion Process of Abrasive Particles
3. Establishment of Mathematical Model of Abrasive Particle Impact on Rock Breaking
3.1. Conditional Assumptions in Modeling
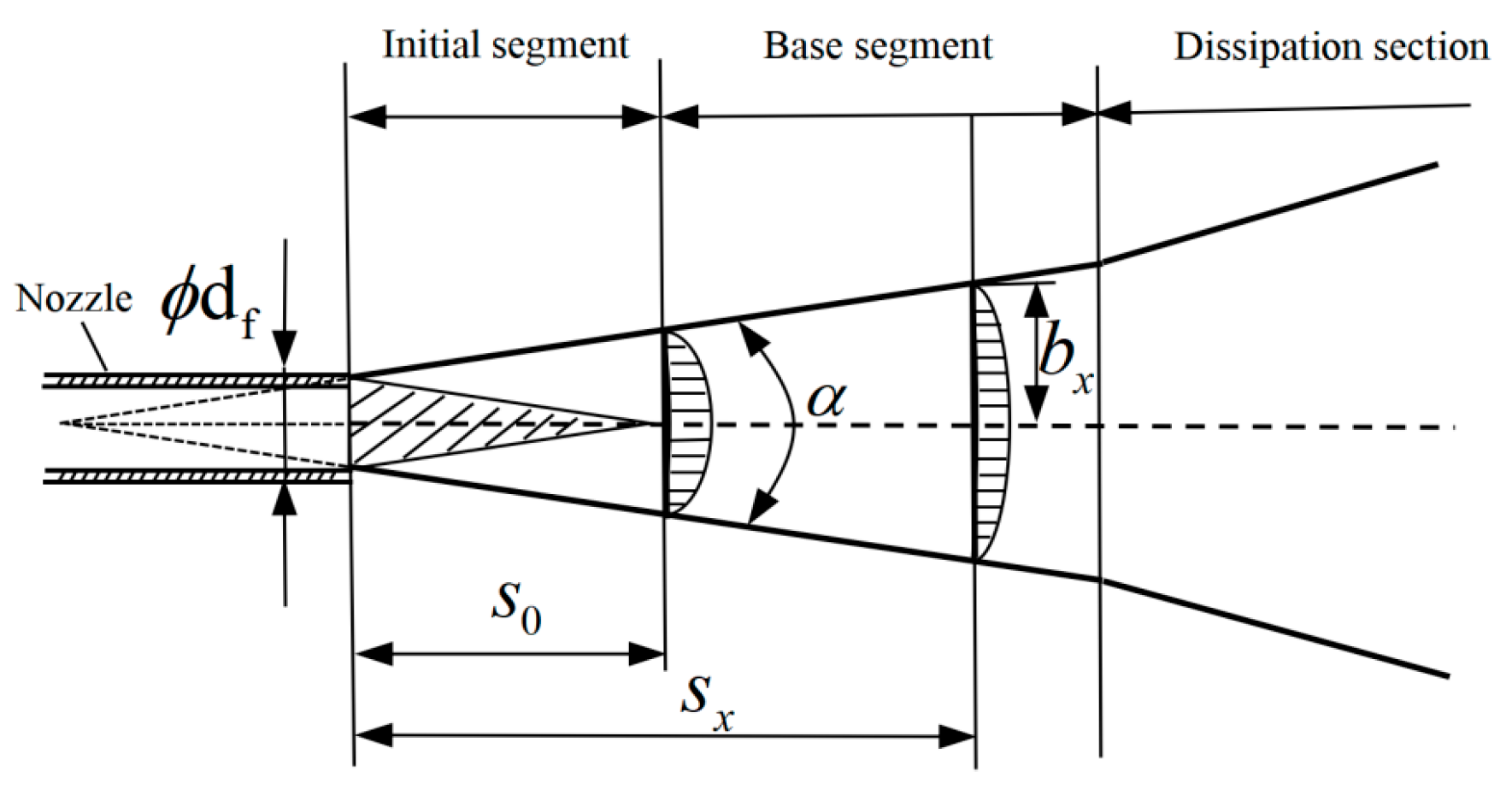
3.2. Theoretical Analysis of Abrasive Particles Impacting Rock
3.2.1. Theoretical Modeling of Single Abrasive Particle Impact on Rock Breaking
3.2.2. Calculation of Maximum Concentrated Force of Abrasive Particles Impacting Rock
3.2.3. Maximum Contact Stress of Abrasive Particles Impacting Rock
3.2.4. Conditions for Crushing Removal by Abrasive Particles Impacting Rock
4. Simulation Analysis
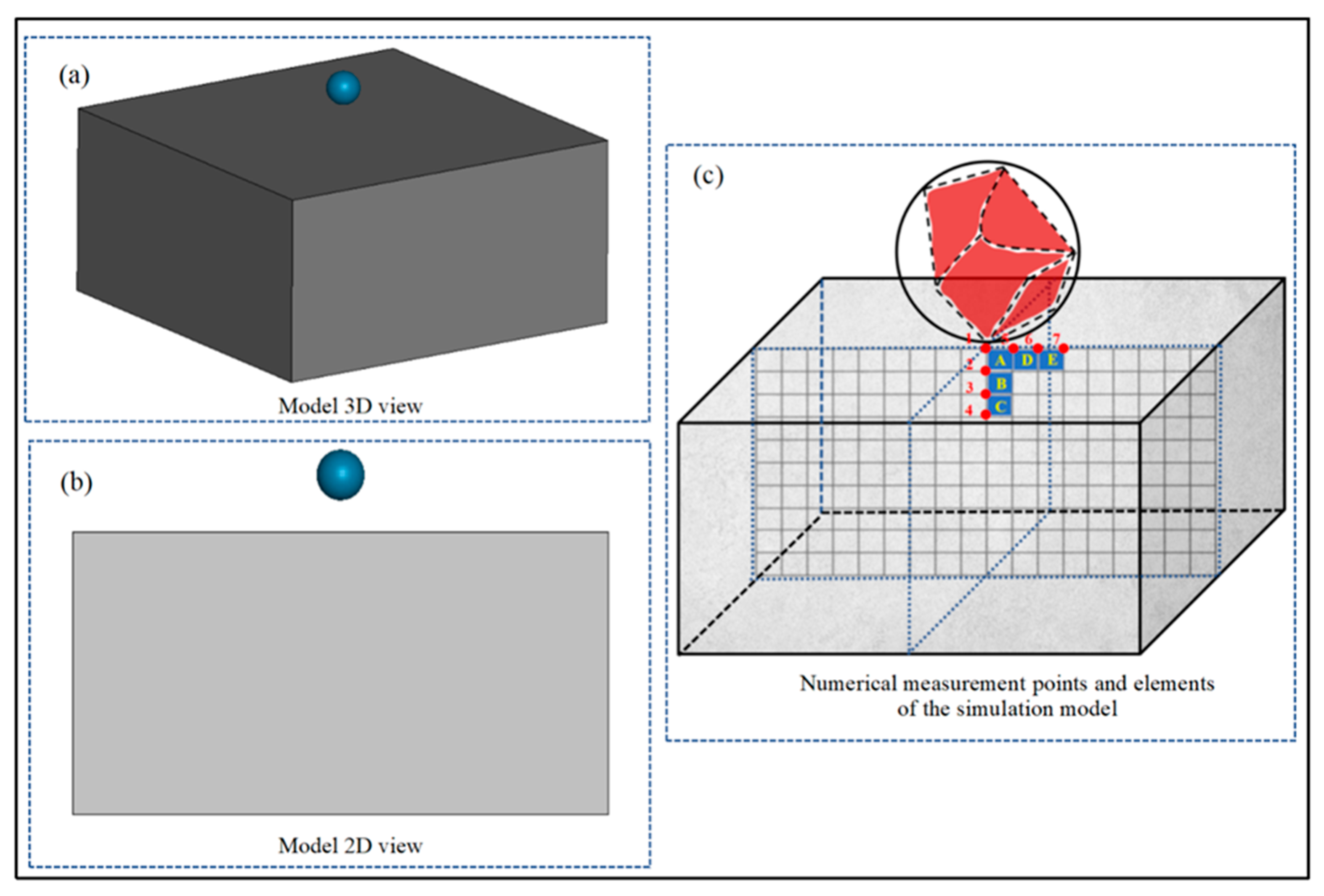
4.1. Numerical Model Establishment
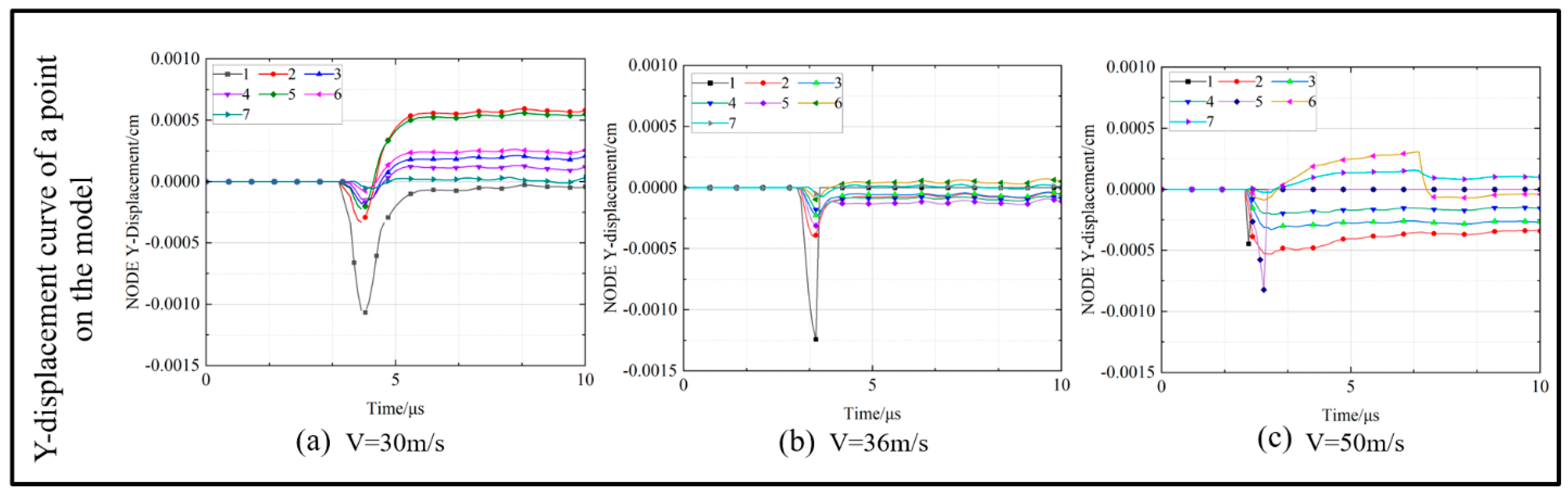
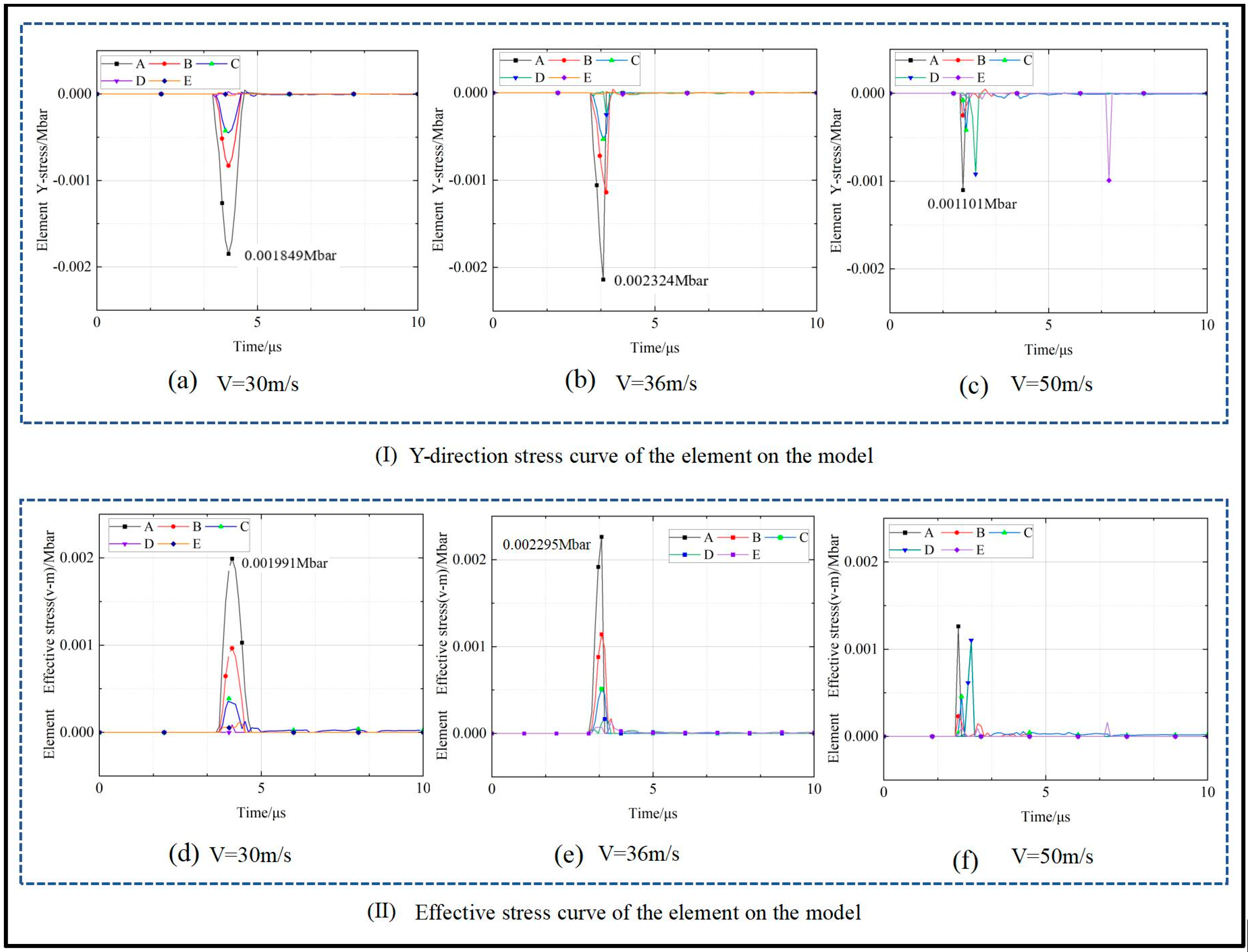
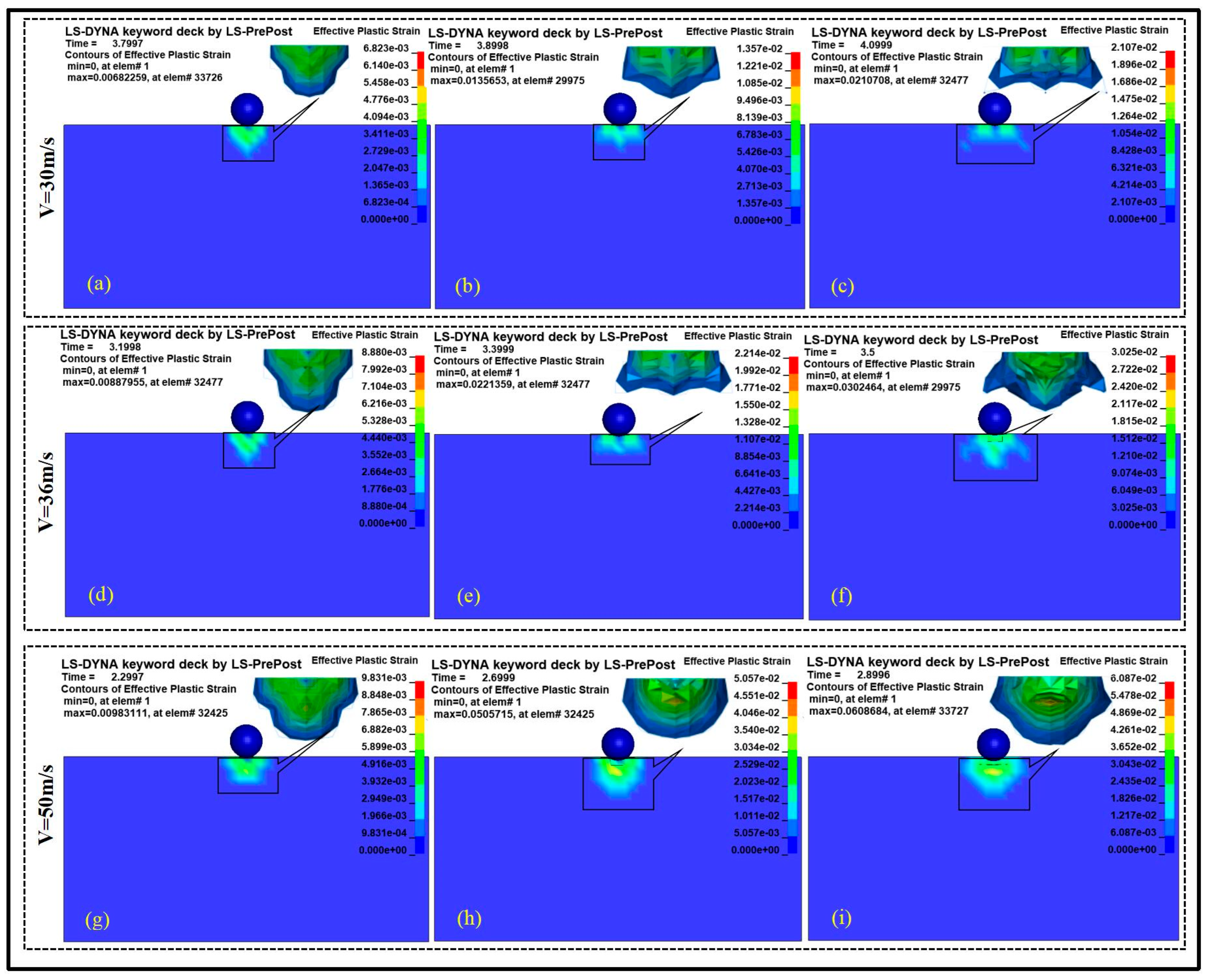
4.2. Simulation Analysis of the Abrasive Impact on Rock
- (1)
- Displacement change rule of marking points under different impact velocities
- (2)
- Stress cloud diagrams and stress variation law of rock under different impact velocities
- (3)
- Effective plastic strain cloud diagram and strain variation law of rock under different impact velocities
5. Abrasive Water Jet Impact Rock-Breaking Experiment
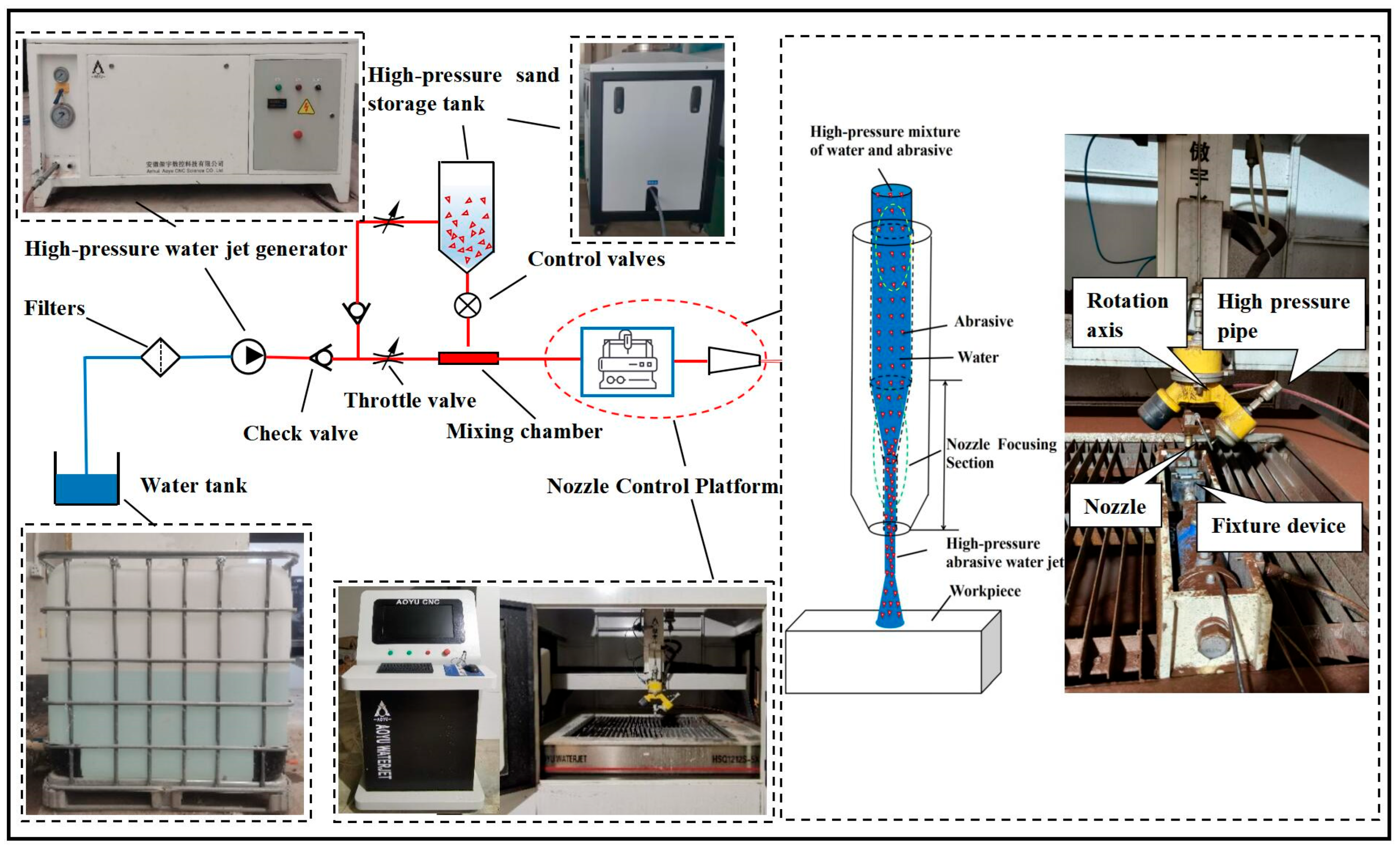
5.1. Experimental Equipment and Materials
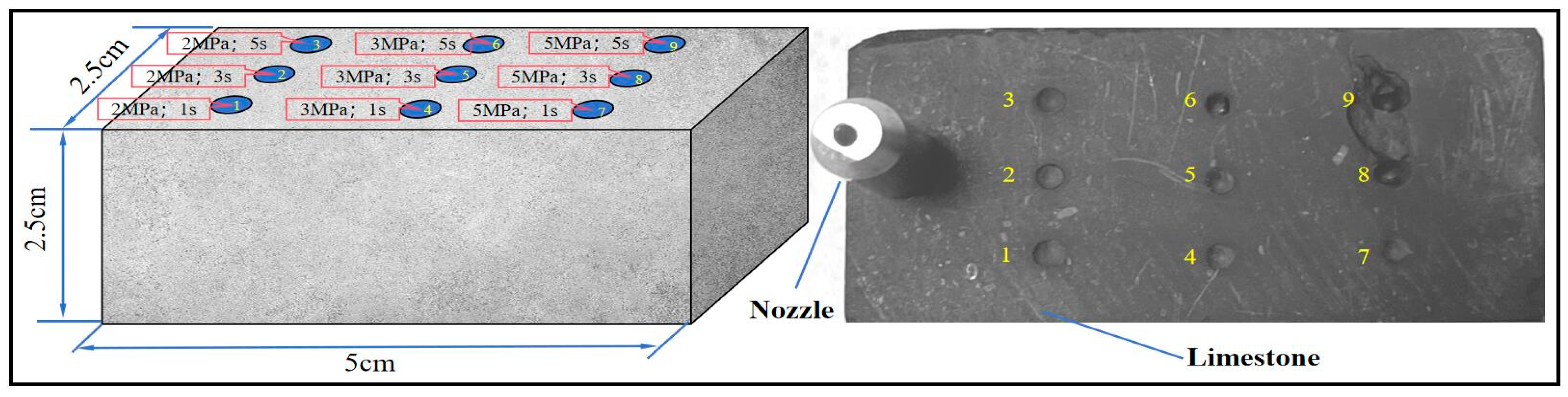
5.2. Experimental Program
5.3. Analysis of Experimental Results
6. Conclusions
- (1)
- The acceleration and deceleration mechanism of abrasive particles was studied by applying high-pressure water jet theory, and a mathematical calculation model for the velocity change during the whole process of abrasive particle impact was established. Based on cavity expansion theory, the mechanism of single abrasive particles impacting rocks was studied, and a mathematical model for the radius of each expansion area was established. Knowledge of contact mechanics and rock mechanics was used to study the elastic contact force of single abrasive particles colliding with rocks, and the concentrated force acting on the abrasive particles and the maximum compressive stress on the rock were obtained. On the basis of the above, a mathematical model of the rock-crushing removal conditions by abrasive water jet impact was established, and the parameter thresholds of the rock-crushing removal conditions by jets were obtained.
- (2)
- Based on the simulation of the environment and the rock-related parameters, the mathematical model of the rock-crushing removal conditions was verified by numerical simulation. The research results show that the theoretical value of the velocity of the jet impact when limestone undergoes crushing removal is no less than 36 m/s, and the theoretical value of the required jet pressure is no less than 2.7 MPa. Through numerical simulation, the displacement change law of the marked points on the rock at different impact velocities was obtained, as well as the stress cloud diagram of the rock in the impact direction and the change law of the marked element stress.
- (3)
- Based on the equipment test conditions and the rock-related parameters, erosion of the rock surface at 2 MPa, 3 MPa, and 5 MPa pressure for different time periods was carried out by replacing the 2.7 MPa pressure calculated by the mathematical model with the 3 MPa pressure used as the benchmark for limestone crushing removal. The results of the study showed that, when the pressure was 2 MPa, no significant erosion pit damage was formed on the limestone surface, and a smooth morphology due to wear was present only in the impact area; meanwhile, the wear amount or depth did not change significantly with a continuous increase in the erosion time. When the pressure is 3 MPa, erosion pit damage begins to occur on the limestone surface, and a broken scratch morphology due to crushing removal was present in the impact area. Moreover, there was a significant change in the depth of the erosion pits with the continued increase in the erosion time, indicating that, under these pressure conditions, the jet can cause the erosion of limestone, which is more obvious when the pressure is 5 MPa. In summary, the impact rock-breaking effect in the experiment was consistent with the corresponding relationship between the test pressure and the theoretical pressure, and the error between the test reference pressure and the theoretical pressure was within reasonable limits, which confirms that the mathematical model of the rock-crushing removal conditions has good accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| The nozzle diameter | |
| The diameter of abrasive particles | |
| The density of abrasive particles | |
| The density of water | |
| The velocity of abrasive particles in the nozzle contraction section | |
| The velocity of water in the nozzle contraction section | |
| The water resistance coefficient | |
| The fluid pressure on abrasive particles | |
| The velocity of abrasive particles in the straight section of the nozzle | |
| The velocity of water in the straight section of the nozzle | |
| The velocity of abrasive particles at the inlet of the nozzle straight section | |
| The pump driving pressure | |
| The velocity flow coefficient of the nozzle | |
| The length of the initial phase | |
| The spray distance along the axis | |
| The spherical radius of the cavity area | |
| The outer diameter of the rock crushing area | |
| The outer diameter of the cracking area | |
| The outer diameter of the elastic deformation area | |
| The abrasive particle impact velocity | |
| The radial coordinate in the Euler coordinate system of the rock | |
| The density of the rock | |
| The radial stress in the Euler coordinate system | |
| , | The cyclic stress in the Euler coordinate system |
| The radial displacement of a micro-point on the rock | |
| The Young’s modulus of the rock | |
| The Poisson’s ratio of the rock | |
| The tensile strength of the rock | |
| The correction factor for the rock crushing radius | |
| The uniaxial compressive strength of the rock | |
| The depth of compression | |
| The concentrated stress | |
| The Poisson’s ratio of abrasive particles | |
| The Young’s modulus of abrasive particles | |
| The shape correction coefficient of abrasive particles | |
| The radius of abrasive particles | |
| The abrasive particle mass | |
| The relative velocity between the abrasive particles and rock | |
| The relative velocity of the abrasive particles and the rock before collision | |
| The relative velocity of the abrasive particles and the rock after collision | |
| The relative displacement of the abrasive particles and rock before impact | |
| The relative displacement of the abrasive particles and rock after impact | |
| The radius of the circular domain of the pressure distribution | |
| The radius from a point in the circular domain to the center of the circular domain | |
| The radial stress in the cylindrical coordinate system | |
| The circumferential stress in the cylindrical coordinate system | |
| The axial stress in the cylindrical coordinate system |
References
- Saraçyakupoğlu, T. Abrasive Water Jet (AWJ) Applications in the Aviation Industry. Int. J. Mech. Prod. Eng. Res. Dev. 2019, 9, 347–356. [Google Scholar]
- Xue, Y.; Si, H.; Xu, D.; Yang, Z. Experiments on the microscopic damage of coal induced by pure water jets and abrasive water jets. Powder Technol. 2018, 332, 139–149. [Google Scholar] [CrossRef]
- Wang, G.; Qiao, S.; Wang, G.; Jiang, H.; Singh, J. Cutting depth of pile materials subjected to the abrasive waterjet and its prediction model. Tunn. Undergr. Space Technol. 2022, 124, 104473. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Huang, Z.; Cheng, K.; Hu, J.; Li, W. Experimental Investigation into the Effect of Process Parameters on the Drilling Performance for Swirling Impeller Abrasive Water Jet. Rock Mech. Rock Eng. 2023, 56, 8833–8850. [Google Scholar] [CrossRef]
- Wang, F.; Wang, R.; Zhou, W.; Chen, G. Numerical simulation and experimental verification of the rock damage field under particle water jet impacting. Int. J. Impact Eng. 2017, 102, 169–179. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, F.; Li, H.; Chen, Y.; Wang, F.; Guo, C. Experimental investigation of hard rock breaking using a conical pick assisted by abrasive water jet. Rock Mech. Rock Eng. 2020, 53, 4221–4230. [Google Scholar] [CrossRef]
- Oh, T.M.; Cho, G.C. Rock cutting depth model based on kinetic energy of abrasive waterjet. Rock Mech. Rock Eng. 2016, 49, 1059–1072. [Google Scholar] [CrossRef]
- Aydin, G.; Karakurt, I.; Amiri, M.R.; Kaya, S. Improvement of rock cutting performance through two-pass abrasive waterjet cutting. Sustainability 2022, 14, 12704. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, D.; Zhou, X.; Xiao, N.; Guo, C. Rock breaking performance of TBM disc cutter assisted by high-pressure water jet. Appl. Sci. 2020, 10, 6294. [Google Scholar] [CrossRef]
- Ge, Z.; Zhang, H.; Zhou, Z.; Cao, S.; Zhang, D.; Liu, X.; Chao, T. Experimental study on the characteristics and mechanism of high-pressure water jet fracturing in high-temperature hard rocks. Energy 2023, 270, 126848. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, S.; Ge, Z.; Zhou, Z. Research progress and strategic thinking of coal mine water jet technology to enhance coal permeability in China. J. China Coal Soc. 2022, 47, 3189–3211. [Google Scholar] [CrossRef]
- Wei, J.; Cai, Y.; Liu, Y.; Yu, D.; Huang, Y.; Li, X.; Gao, M. Progress and trends in non-tool rock breaking theory and technology. J. China Coal Soc. 2024, 49, 801–832. [Google Scholar]
- Huang, B.; Zhao, X.; Chen, S.; Liu, J. Theory and technology of controlling hard roof with hydraulic fracturing in underground mining. Chin. J. Rock Mech. Eng. 2017, 36, 2954–2970. [Google Scholar] [CrossRef]
- Xia, Y.; Lu, C.; Yang, G.; Su, S.; Pang, L.; Ding, G.; Su, B. Experimental study on axial fracture cutting and fracturing of abrasive jet in boreholes within hard rock roofs. J. Min. Strat. Control Eng. 2020, 2, 33522. [Google Scholar]
- Pan, J.; Ma, W.; Liu, S.; Gao, J. A prevention technology of rock burst based on directional presplitting of water jet prefabricated slot in hard roof. Chin. J. Rock Mech. Eng. 2021, 40, 1591–1602. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, F.; Zhao, T.; Yang, K.; Wu, W.; Jiang, G. Theoretical and applied research on hydraulic slit-fracture joint roof control and pressure relief of hard roof in goaf roadway. J. China Coal Soc. 2024, 49, 4739–4751. [Google Scholar]
- Gupta, K. Introduction to Abrasive Water Jet Machining. In Abrasive Water Jet Machining of Engineering Materials; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–11. [Google Scholar]
- Jiang, H.; Du, C.; Dong, J. Investigation of rock cutting dust formation and suppression using water jets during mining. Powder Technol. 2017, 307, 99–108. [Google Scholar] [CrossRef]
- Li, M.; Ni, H.; Wang, G.; Wang, R. Simulation of thermal stress effects in submerged continuous water jets on the optimal standoff distance during rock breaking. Powder Technol. 2017, 320, 445–456. [Google Scholar] [CrossRef]
- Yuan, R.; Chen, C.; Zai, P.; Hou, Z. Investigation on the wear characteristics of slurry abrasive flow to key passage parts of the pump body. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 331. [Google Scholar] [CrossRef]
- Muthuramalingam, T.; Vasanth, S.; Vinothkumar, P.; Geethapriyan, T.; Mohamed Rabik, M. Multi criteria decision making of abrasive flow oriented process parameters in abrasive water jet machining using Taguchi–DEAR methodology. Silicon 2018, 10, 2015–2021. [Google Scholar] [CrossRef]
- Natarajan, Y.; Murugasen, P.K.; Sundarajan, L.R.; Arunachalam, R. Experimental investigation on cryogenic assisted abrasive water jet machining of aluminum alloy. Int. J. Precis. Eng. Manuf.-Green Technol. 2019, 6, 415–432. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, R.; Zhang, X.; Zai, P.; Deng, J. Research progress in abrasive water jet processing technology. Micromachines 2023, 14, 1526. [Google Scholar] [CrossRef]
- Monno, M.; Pellegrini, G.; Ravasio, C. Effect of workpiece heat treatment on surface quality of AWJ kerf. Int. J. Mater. Prod. Technol. 2015, 51, 345–358. [Google Scholar] [CrossRef]
- Farmer, I.W.; Attewell, P.B. Rock penetration by high velocity water jet: A review of the general problem and an experimental study. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. Pergamon 1965, 2, 135–153. [Google Scholar] [CrossRef]
- Jiang, H.; Du, C.; Liu, S. The effects of impact velocity on energy and size distribution of rock crushing. J. China Coal Soc. 2013, 38, 604–609. [Google Scholar] [CrossRef]
- Momber, A.W. Deformation and Fracture of Rocks Due to High-Speed Liquid Impingement. Int. J. Fract. 2004, 130, 683–704. [Google Scholar] [CrossRef]
- Momber, A.W. The Response of Geo-Materials to High-Speed Liquid Drop Impact. Int. J. Impact Eng. 2016, 89, 83–101. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, J.W.; Xu, Z.Y.; Li, Z.F. Comparison of the Rock Breakage Pressure of Abrasive Water Jets and Abrasive Air Jets. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 1–11. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, C.; Wei, J.; Zhang, J. Comparison analysis on the rock breakage pressure induced by abrasive water jets and abrasive gas jets. J. China Coal Soc. 2018, 43, 2510–2517. [Google Scholar] [CrossRef]
- Hu, M.; Li, B.; Zhang, B.; Nie, L.; Liu, Z.; Cao, W. Effect of Rock Stress Evolution on Failure under Transverse Plain Water Jet. Geotech. Geol. Eng. 2020, 38, 3941–3954. [Google Scholar] [CrossRef]
- Chen, X.; Deng, S.; Guan, J.; Hua, W. Experiment and simulation research on abrasive water jet nozzle wear behavior and anti-wear structural improvement. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2023–2033. [Google Scholar] [CrossRef]
- Nanduri, M.; Taggart, D.G.; Kim, T.J. The effects of system and geometric parameters on abrasive water jet nozzle wear. Int. J. Mach. Tools Manuf. 2002, 42, 615–623. [Google Scholar] [CrossRef]
- Morsi, S.A.J.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Du, M.; Guo, Y.; Wang, H.; Dong, H.; Liang, W.; Wu, H.; Ke, Y. Modeling of the cutting front profile in abrasive water jet machining based on the energy balance approach. Precis. Eng. 2023, 79, 210–220. [Google Scholar] [CrossRef]
- Abrmovich, G.; Schindel, L. General Properties of Turbulent Jets; MIT Press: Cambridge, MA, USA, 1963; pp. 3–49. [Google Scholar]
- Bush, W.B.; Krishnamurthy, L. Asymptotic analysis of the fully developed region of an incompressible, free, turbulent, round jet. J. Fluid Mech. 1991, 223, 93–111. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Huang, Z.; Kuru, E.; Guo, C.; Hu, J. Numerical Investigation of Abrasive Water Jet Rock Damage Characteristics That Considers the Shape, the Interaction and the Fragmentation of Abrasive Particles. Rock Mech. Rock Eng. 2024, 58, 2105–2131. [Google Scholar] [CrossRef]
- Li, Z.; Ge, Z.; Zhou, Z.; Mi, J.; Liu, L.; Shangguan, J.; Shao, C. Numerical simulation and experimental verification of heterogeneous granite impacted by abrasive water jet based on SPH-FEM coupling algorithm. Powder Technol. 2023, 416, 118233. [Google Scholar] [CrossRef]
- Huang, F.; Zhao, Z.; Li, D.; Mi, J.; Wamg, R. Investigation of the breaking manifestations of bedded shale impacted by a high-pressure abrasive water jet. Powder Technol. 2022, 397, 117021. [Google Scholar] [CrossRef]
- Feng, L.; Dong, X.; Li, Z.; Liu, J.; Sun, Z. Modeling of waterjet abrasion in mining processes based on the smoothed particle hydrodynamics (SPH) method. Int. J. Comput. Methods 2020, 17, 1950075. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Liu, C.; Chen, H.; Xiong, W.; Tan, M. Research progress of target resistance model of cavity expansion theory and its application. Explos. Shock. Waves. 2021, 41, 101101. [Google Scholar] [CrossRef]
- Deng, Y.J.; Chen, X.W.; Yao, Y. Study on the cavity expansion response of the concrete target under penetration. Sci. Sin. Phys. Mech. Astron. 2020, 50, 024606. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, F. A dynamic spherical cavity-expansion theory for concrete materials. Explos. Shock Waves 2009, 29, 95–100. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Tzou, D.Y. A spherical cavity-expansion penetration model for concrete targets. Int. J. Solids Struct. 1997, 34, 4127–4146. [Google Scholar] [CrossRef]
- Satapathy, S. Dynamic spherical cavity expansion in brittle ceramics. Int. J. Solids Struct. 2001, 38, 5833–5845. [Google Scholar] [CrossRef]
- Cao, G.N. Second order homogeneous variable coefficient differential equation and Riccati equation. J. Xi’an Univ. Sci. Technol. 2004, 2, 247–249. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. The Hertzian contact surface. J. Mater. Sci. 1999, 34, 129–137. [Google Scholar] [CrossRef]
- Greenwood, J.A. Analysis of elliptical Hertzian contacts. Tribol. Int. 1997, 30, 235–237. [Google Scholar] [CrossRef]
- Momber, A.W.; Kovacevic, R. Principles of Abrasive Water Jet Machining; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, MA, USA, 1985. [Google Scholar] [CrossRef]
- Borrvall, T.; Riedel, W. The RHT concrete model in LS-DYNA. In Proceedings of the 8th European LS-DYNA User Conference, Strasbourg, France, 23–24 January 2011. [Google Scholar]
- Wang, Z.L.; Huang, Y.P.; Li, S.Y.; Xiong, F. SPH-FEM coupling simulation of rock blast damage based on the determination and optimization of the RHT model parameters. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 570, p. 042035. [Google Scholar]
- Wang, H.; Wang, Z.; Wang, J.; Wang, S.; Wang, H.; Yin, Y.; Li, F. Effect of confining pressure on damage accumulation of rock under repeated blast loading. Int. J. Impact Eng. 2021, 156, 103961. [Google Scholar] [CrossRef]
- Xu, L.; Xu, X.; Sun, Y.; Lu, T. Evaluation of Rock Brittleness Based on Complete Stress-Strain Curve. Mathematics 2022, 10, 4470. [Google Scholar] [CrossRef]
- Chen, G.; Jiang, W.; Sun, X.; Zhao, C.; Qin, C. Quantitative evaluation of rock brittleness based on crack initiation stress and complete stress-strain curves. Bull. Eng. Geol. Environ. 2019, 78, 5919–5936. [Google Scholar] [CrossRef]
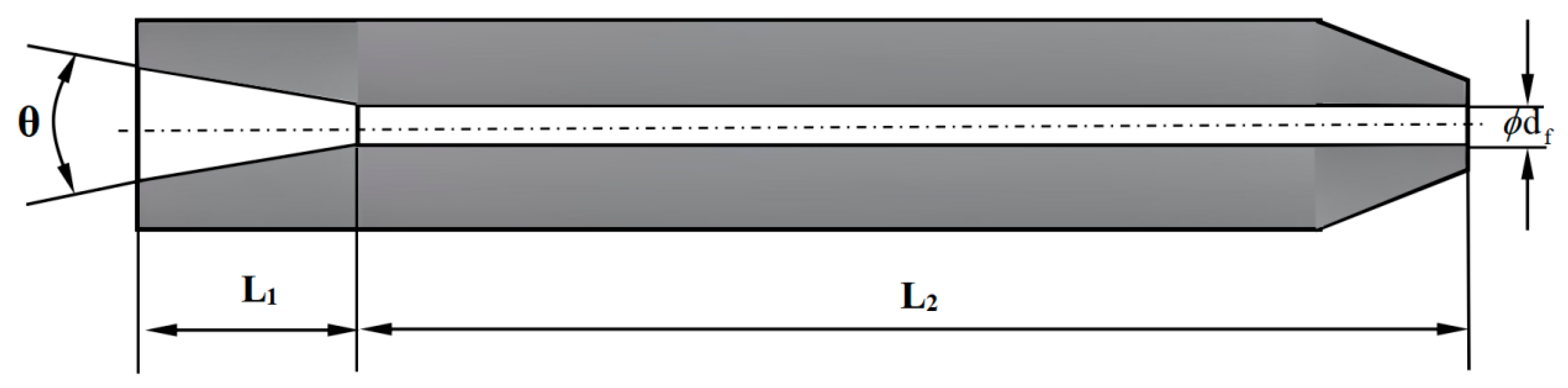





| Contraction Angle (o) | Length of Contraction Section (mm) | Straight Section of Cylinder (mm) | Outlet Diameter (mm) |
|---|---|---|---|
| Material | Density (kg/m3) | Poisson’s Ratio | Average Particle Size (mm) | Elastic Modulus (GPa) |
|---|---|---|---|---|
| Garnet | 4200 | 0.25 | 0.18 | 240 |
| Water | 998 |
| Density (kg/m3) | Poisson’s Ratio | Compressive Strength (MPa) | Tensile Strength (MPa) | Modulus of Elasticity (GPa) |
|---|---|---|---|---|
| 2900 | 0.16 | 202.2 | 3.7 | 28.1 |
| Parameter and Symbol | Value | Parameter and Symbol | Value |
|---|---|---|---|
| Mass density () | 2900 | Compressive strain rate dependence exponent | 0.025 |
| Elastic shear modulus () | 10.68 | Tensile strain rate dependence exponent | 0.02 |
| Parameter for polynomial EOS | 0.9 | Compressive yield surface parameter | 0.53 |
| Parameter for polynomial EOS | 0.9 | Tensile yield surface parameter | 0.7 |
| Parameter for polynomial EOS () | 22.5 | Shear modulus reduction factor | 0.5 |
| Failure surface parameter | 1.92 | Damage parameter | 0.04 |
| Failure surface parameter | 0.76 | Damage parameter | 1 |
| Compressive strength () | 200 | Minimum damaged residual strain | 0.01 |
| Relative shear strength | 0.3 | Residual surface parameter | 2.24 |
| Relative tensile strength | 0.02 | Residual surface parameter | 0.854 |
| Lode angle dependence factor | 0.6805 | Hugoniot polynomial coefficient () | 22.5 |
| Lode angle dependence factor | 0.0105 | Hugoniot polynomial coefficient () | 20.25 |
| Parameter for polynomial EOS () | 0 | Hugoniot polynomial coefficient () | 2.1 |
| Reference compression strain rate | 3.0 × 10−11 | Crush pressure () | 0.092 |
| Reference tensile strain rate | 3.0 × 10−12 | Compaction pressure () | 130 |
| Break compressive strain rate | 3.0 × 1019 | Porosity exponent | 3 |
| Break tensile strain rate | 3.0 × 1019 | Note: The system unit is g-cm-μs. |
| No. | Pressure | Impact Time | Target Distance | Abrasive Flow | Nozzle Diameter | Impact Angle | Abrasive Particle Diameter | Cutting Material |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 Mpa | 1 s | 10 mm | 120 g/min | 1 mm | 90° | 0.18 mm | Limestone |
| 2 | 2 Mpa | 3 s | ||||||
| 3 | 2 Mpa | 5 s | ||||||
| 4 | 3 Mpa | 1 s | ||||||
| 5 | 3 Mpa | 3 s | ||||||
| 6 | 3 Mpa | 5 s | ||||||
| 7 | 5 Mpa | 1 s | ||||||
| 8 | 5 Mpa | 3 s | ||||||
| 9 | 5 Mpa | 5 s |
| Impact Time | 1 s | 3 s | 5 s | |
|---|---|---|---|---|
| Impact Pressure | ||||
| 2 MPa | Mark No. | 1 | 2 | 3 |
| Depth (mm) | 0.71 | 0.76 | 0.84 | |
| 3 MPa | Mark No. | 4 | 5 | 6 |
| Depth (mm) | 1.49 | 1.60 | 2.05 | |
| 5 MPa | Mark No. | 7 | 8 | 9 |
| Depth (mm) | 1.65 | 3.15 | 3.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yuan, R.; Zhang, X.; Zai, P.; Fan, J.; Deng, J. Crushing Removal Conditions and Experimental Research on Abrasive Water Jets Impacting Rock. Lubricants 2025, 13, 348. https://doi.org/10.3390/lubricants13080348
Wang H, Yuan R, Zhang X, Zai P, Fan J, Deng J. Crushing Removal Conditions and Experimental Research on Abrasive Water Jets Impacting Rock. Lubricants. 2025; 13(8):348. https://doi.org/10.3390/lubricants13080348
Chicago/Turabian StyleWang, Hongqi, Ruifu Yuan, Xinmin Zhang, Penghui Zai, Junkai Fan, and Junhao Deng. 2025. "Crushing Removal Conditions and Experimental Research on Abrasive Water Jets Impacting Rock" Lubricants 13, no. 8: 348. https://doi.org/10.3390/lubricants13080348
APA StyleWang, H., Yuan, R., Zhang, X., Zai, P., Fan, J., & Deng, J. (2025). Crushing Removal Conditions and Experimental Research on Abrasive Water Jets Impacting Rock. Lubricants, 13(8), 348. https://doi.org/10.3390/lubricants13080348





