Static Characteristic Analysis of Multi-Layer Foil Thrust Bearing: Considering Parameter Effects

Abstract

A modified static characteristic model for the multi-layer foil thrust bearing (MLFTB) is established. In this model, the finite difference method and the thick plate element are implemented, the compressible Reynolds equation is linearized by the Newton–Raphson method, and the evolution law of the static characteristics with the geometric and operational parameters is derived by iterative solution. The results indicate that the bearing capacity could be generally decreased by around 3.15% when considering the slip boundary condition, which should not be neglected. Also, when under the rigorous wedge effect, the pressure peak near the mini clearance exhibits an obvious double peak shape. The bearing capacity can be slightly enhanced by an increase in the tilt angle of the thrust disk. In comparison to data in the literature, the current model shows satisfactory precision for the multi-layer foil thrust bearing. It aims to provide effective predictive means and theoretical reference for MLFTB.

1. Introduction

As a significant type of mechanical supporting element, the foil thrust bearing offers inherent advantages of good operational stability [1], low frictional power loss [2], high-speed adaptability [3], and non-pollution [4]. It plays a significant role in engineering applications, for instance, in micro gas turbines [5,6], turbochargers [7,8], and turbo-expanders [9,10] in refrigeration systems [11]. The foil thrust bearing was developed to sustain the axial loading function of a rotor, and the static characteristics, especially the load capacity, are one of the main focuses of a foil thrust bearing. The bump-foil type [12,13], protuberant foil type [14,15], and viscoelastic supporting foil type [16,17] are the common types of foil thrust bearings. Nevertheless, faced with the challenge of high machining precision restrictions and the difficulty of the assembling process, some researchers have tried to enhance the bearing capacity through parametric studies and geometric modifications [18,19,20].

Compared with former concave or plane wedges, both the valid area of the high-pressure zone and the load capacity of the bearing can be effectively enhanced using the convex-type wedge-shaped clearance [21,22]. By introducing multi-layer foils, which not only significantly improve the bearing capacity but also offer the advantage of inherently simple fabrication, the door to a potentially brighter future has been opened [23,24]. Consequently, the multi-layer foil thrust bearing (MLFTB), as exhibited in Figure 1, has attracted the attention of numerous researchers [25,26,27]. Iordanoff [28] established the numerical method for investigating the parameter effects of characteristic clearance on bearing capacity. It is based on the Reynolds equation coupled with the empirical formula for foil deformation. The results suggest that a tiny change in the parameters of clearance can lead to multiple variations in bearing capacity. Hou et al. [29] compared the bearing capacity under different geometric parameters of the top foil, and they suggested that there could be an optimal height of the wedge shape, which can intensify bearing capacity. The parameter effects of bearing call for more interest from researchers, and different numerical methods have been introduced in the simulation of MLFTB.

Larsen [30] pointed out that both easy programming and simplicity of use are significant. It provides valuable advice for promoting the directions of bearing numerical models, which can be efficient and effective. Under the so-called Reissner–Mindlin-type shell theory, Lehn et al. [31] handled the bump foil and set up the numerical model for the foil thrust bearing. They claimed that the unequal deformation of the bump foil may affect the bearing capacity. The advantages of the finite difference method (FDM), including ease of use, simple programming, and high efficiency in the simulation of bearings, are increasingly acknowledged by researchers. Later, Hu et al. [32] set up a fully coupled elastic-hydrodynamic model via both the finite volume method (FVM) and the finite element method (FEM). The commercial FEM software COMSOL was adopted. It shows that when under a certain clearance, the higher bearing speed could lead to a larger bearing capacity, which indicates that the so-called hardening effect of the gas film could be formed. Based on the so-called NASTRAN solver, Zhang et al. [33] successfully derived the distributions of foil deformations of bearings. They compared the results with those of the traditional type foil thrust bearing and believed that the multi-layer structure has better adaptability for changing bearing load, and the probability of collision and abrasion can be largely decreased. After that, Xu et al. [34] established the numerical models for bearings and compared the simulated results, derived by FDM, with the experimental data. It validates that with appropriate modification, the simplified model can also possess good precision and high efficiency. In comparison with the results in the literature and test data, the model was proven to be more applicable for the bearings under heavy load conditions.

Notably, the tiny wedge-shaped clearance is at the micrometer scale, and the slip effect could be involved in the strong stress flow of the foil thrust bearing. Some researchers are interested in slip-flow, and the influence of the slip effect on the bearing capacity becomes one of the concerns [35,36,37,38]. Bruckner et al. [36] adopted the Knudsen (Kn) number into the Reynolds equation to forecast the hydrodynamic property of gas foil bearings. Later, the gas rarefaction coefficients were introduced by Park et al. [37] in the calculation of static characteristics. Jiang et al. [18,38] established the numerical model of the gas foil bearing at the multiscale, upon which the conditions of high Kn numbers (Kn > 0.1) were explored. It was found that the compression action on the gas film could be significantly weakened by the slip effect. Nevertheless, due to the complexity of multi-layer structure, the influence of slip-effect under fluid-structure interactions and foil deformation calls for further development.

Apart from numerical simulation, some experimental research has been reported. Radil et al. [39] carried out experiments for bearing capacity and found that there could be an optimal choice for the clearance of film thickness. Later, Dykas [40] carried out experimental research and revealed that the bearing capacity is sensitive to the parametric variation of the wedge-shaped clearance. However, due to the difficulty of the test rig and rigorous experimental conditions, few reports have shown how the distributions of pressure and film thickness are in the tiny wedge-shaped clearance, and there is a lack of models to clarify the fluid-elastic mechanism of bearing capacity.

In contrast to the former types, the flow channels of the multi-layer structures of MLFTB are more complicated, and the stiffnesses of foils could be different. Consequently, the interactions and inner mechanisms between the parameters and the static characteristics, especially under the conditions of slip and tilting, need to be clarified. In addition, the accuracy, calculating efficiency, and programming simplicity of numerical models for the static characteristics of MLFTB need to be promoted. It will be beneficial to the design of MLFTB if further investigation of the elastohydrodynamic mechanism and parameter effects of static characteristics can be made.

In the current study, a modified static characteristics model for the MLFTB is established. In this model, the FDM and the thick plate element are implemented, and the compressible Reynolds equation is linearized by the Newton–Raphson method. The evolution law of the static characteristics with geometric and operational parameters was derived by iterative solution. The slip effect is taken into consideration. The results indicate that the bearing capacity could be generally decreased by around 3.15% when the slip boundary condition was considered, which should not be neglected. Also, when under the rigorous wedge effect, the pressure peak near the mini clearance exhibits an obvious double peak shape. In comparison with the literature data and test results, the current model shows satisfactory precision for the MLFTB. It is designed to provide effective and efficient prediction methods, as well as theoretical guidance for this essential type of bearing.

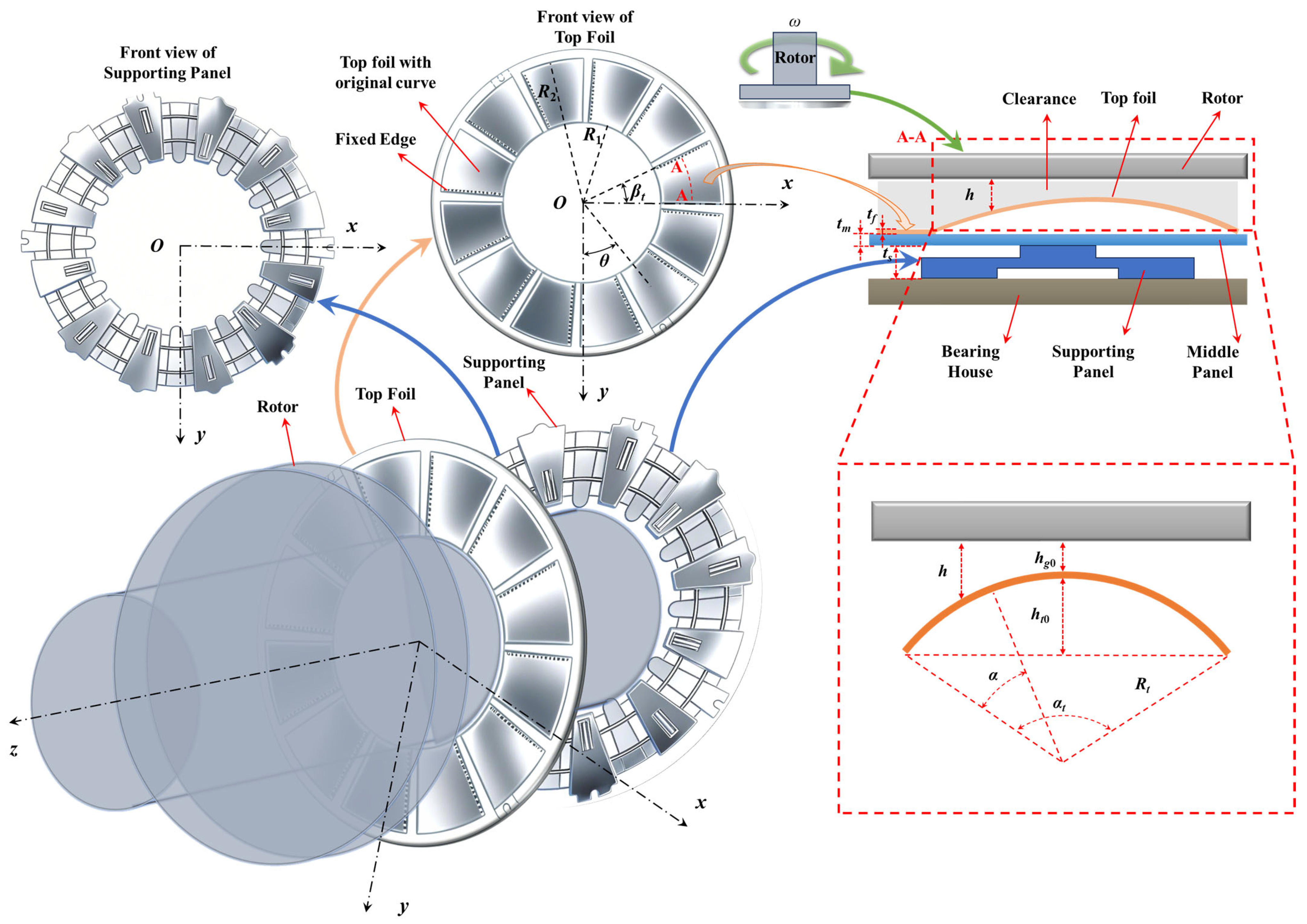
2. Numerical Models

The schematic of the MLFTB can be depicted in Figure 1. In the present investigation, the FDM and the thick plate element are implemented, the compressible Reynolds equation is linearized by the Newton–Raphson method to forecast the distributions of lubricating gas film, and the evolution law of the static characteristics with the geometric and operational parameters was derived by iterative solution, with the dimensionless pressure, dimensionless film thickness and bearing capacity being included.

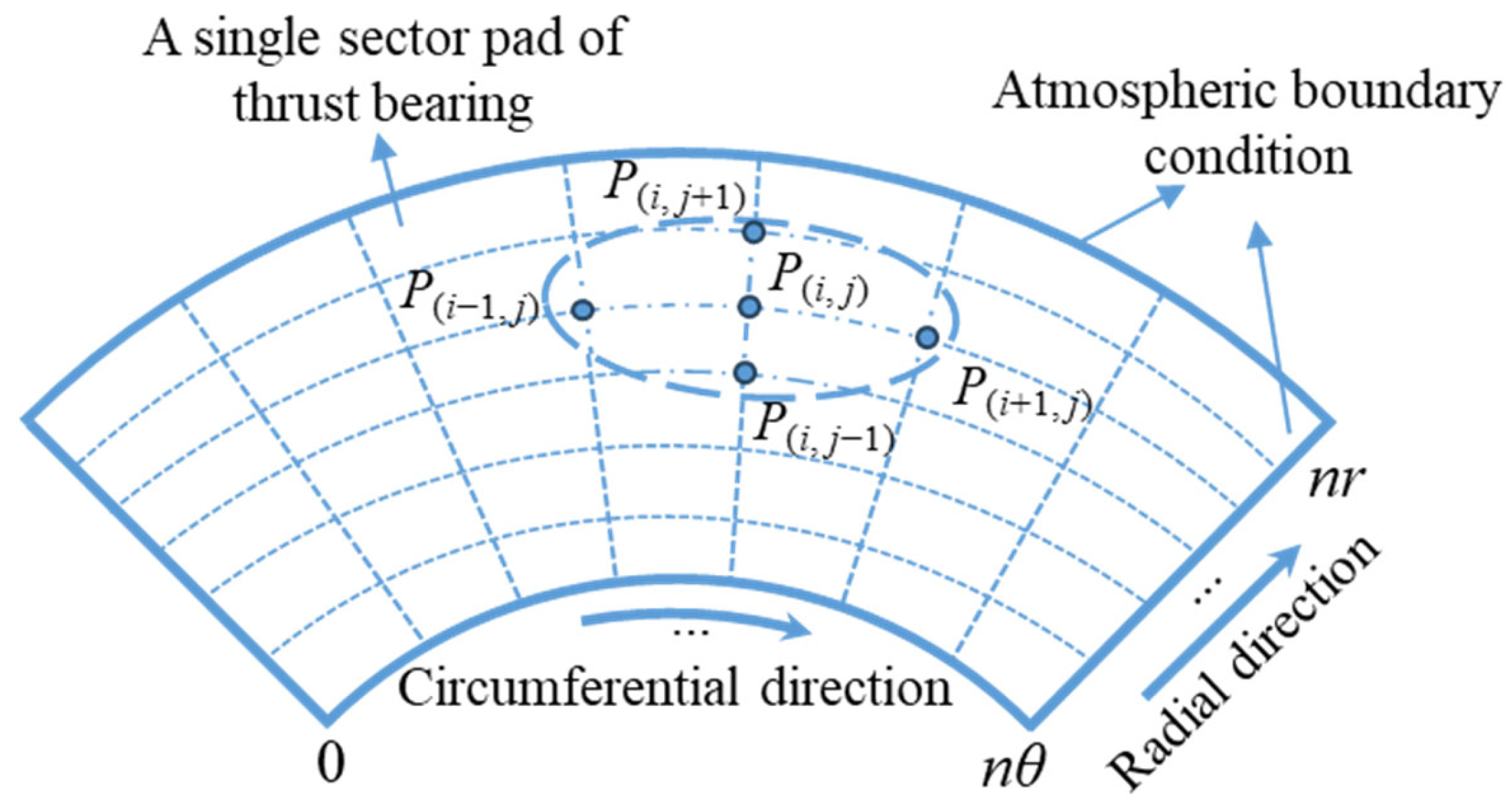
2.1. Reynolds Equation

In the present research, the lubricating gas is assumed to be the isothermal ideal gas. The dimensionless compressible Reynolds equation can be introduced to calculate the pressure distributions of MLFTB, which is as follows [33]:

$${\displaystyle \frac{1}{R^2}}{\displaystyle \frac{\partial }{\partial \theta }}\left[\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right){\displaystyle \frac{\partial P}{\partial \theta }}\right]+{\displaystyle \frac{1}{R}}{\displaystyle \frac{\partial }{\partial R}}\left[R\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right){\displaystyle \frac{\partial P}{\partial R}}\right]=\Lambda {\displaystyle \frac{\partial \left(PH\right)}{\partial \theta }}$$

(1)

where

$$\theta ={\displaystyle \frac{x}{R}}; P={\displaystyle \frac{p}{p_a}}; H={\displaystyle \frac{h}{t_s}};\Lambda ={\displaystyle \frac{6\mu \omega }{p_a}}{\left({\displaystyle \frac{R}{t_s}}\right)}^2; a=\left(2-{\sigma }_v\right){\sigma }_v$$

The symbols a and σ_v represent the surface coefficient and the accommodation coefficient of the tangential momentum, respectively. The symbol ${\overline{Kn}}_0$ refers to the Knudsen number, which can be expressed as follows:

$$\overline{Kn}=\mu \sqrt{{\displaystyle \frac{\pi R_g}{2}}}{\displaystyle \frac{\sqrt{T_0}}{t_s{p}_a}}$$

(2)

It is decided by the environment pressure p_a, the height of the supporting plate t_s, and the reference temperature T₀. Additionally, R_g is the gas constant; as for air, there is $R_g=287.1 \mathrm{J}/(\mathrm{k}\mathrm{g}·\mathrm{K})$.

2.2. Gas Film Thickness Equation

The dimensionless gas film thickness could be expressed as follows:

$$H={\displaystyle \raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$t_s$}\right.}=\left(h_0+u\right)/t_s=H_0+U$$

(3)

where H₀ represents the original film thickness, u represents the foil deformation in the axial direction. As for the current MLFTB, the H₀ is decided by the folding and the flare angle α_t at the inner and outer radiuses of a sector can be expressed as follows:

$${\displaystyle \frac{2h_{t0}}{{\beta }_t{R}_i}}={\displaystyle \frac{1-cos\left({\alpha }_t/2\right)}{sin\left({\alpha }_t/2\right)}} \left(i=1, 2\right)$$

(4)

where h_t0 is the pitch of the arch of foil at the inner and outer radiuses, β_t is the flare angle of the sector of the bearing house. R_i is the inner (when i = 1) and outer (when i = 2) radiuses, respectively. When under a certain h_t0, the height distribution of the single sector will be easily determined.

On account of the stiffness of the foil, the thick plate element [41,42] is adopted to establish the FEM models of the top foil, the middle foil, and the supporting panels. The schematic is illustrated in Figure 2 [34,41].

Practically, the element stiffness matrices can be divided into two parts, the bending stiffness k_f and the shear stiffness k_t, which are as follows:

$$\left[{\mathit{k}}_e\right]=\left[{\mathit{k}}_f\right]+\left[{\mathit{k}}_s\right]$$

(5)

where

$$\left[{\mathit{k}}_f\right]={\int }_A{\displaystyle \frac{h^3}{12}}{\left[{\mathit{B}}_f\right]}^T\left[D\right]\left[B_f\right]dA$$

(6)

and

$$\left[{\mathit{k}}_s\right]={\int }_A\kappa h{\left[{\mathit{B}}_s\right]}^T\left[D_s\right]\left[B_s\right]dA$$

(7)

The strain matrix $\left[B_f\right]$ is of the following form:

$$\left[{\mathit{B}}_f\right]=\left[B_f^1 B_f^2 B_f^3 B_f^4 \right]dA$$

(8)

where

$$B_f^j=\left[\begin{array}{ccc}0& 0& -{\displaystyle \frac{\partial N_i}{\partial y}}\\ 0& {\displaystyle \frac{\partial N_j}{\partial y}}& 0\\ 0& {\displaystyle \frac{\partial N_j}{\partial x}}& -{\displaystyle \frac{\partial N_i}{\partial y}}\end{array}\right]$$

(9)

The strain matrix $\left[B_s\right]$ is of the following form:

$$\left[{\mathit{B}}_s\right]=\left[B_s^1 B_s^2 B_s^3 B_s^4 \right]dA$$

(10)

where

$$B_s^j=\left[\begin{array}{ccc}{\displaystyle \frac{\partial N_j}{\partial x}}& 0& -N_j\\ {\displaystyle \frac{\partial N_j}{\partial y}}& N_j& 0\end{array}\right]$$

(11)

where the functions N_j are defined as follows:

$$N_j={\displaystyle \frac{1}{4}}\left(1+{\xi }_j\xi \right)\left(1+{\eta }_j\eta \right)$$

(12)

Introducing Equation (12) into Equations (9) and (11), the following equations can be obtained:

$$B_f^j=\left[\begin{array}{ccc}0& 0& -{\displaystyle \frac{{\xi }_j\left(1+{\eta }_j\eta \right)}{4a}}\\ 0& {\displaystyle \frac{\left(1+{\xi }_j\xi \right){\eta }_j}{4b}}& 0\\ 0& {\displaystyle \frac{{\xi }_j\left(1+{\eta }_j\eta \right)}{4a}}& -{\displaystyle \frac{\left(1+{\xi }_j\xi \right){\eta }_j}{4b}}\end{array}\right]$$

(13)

and

$$B_s^j=\left[\begin{array}{ccc}{\displaystyle \frac{{\xi }_j\left(1+{\eta }_j\eta \right)}{4a}}& 0& {\displaystyle \frac{\left(1+{\xi }_j\xi \right)\left(1+{\eta }_j\eta \right)}{4}}\\ {\displaystyle \frac{\left(1+{\xi }_j\xi \right){\eta }_j}{4b}}& -{\displaystyle \frac{\left(1+{\xi }_j\xi \right)\left(1+{\eta }_j\eta \right)}{4}}& 0\end{array}\right]$$

(14)

Substituting Equation (13) and Equation (14) into Equation (8) and Equation (10), respectively, and the resulting matrices into Equations (8) and (10), then the element stiffness matrix defined in Equation (5) can be derived.

Assuming the foils are connected in parallel, the overall stiffness matrix can be expressed as [41]:

$${\mathit{K}}_{all}{\mathit{U}}_{all}={\mathit{F}}_{all}$$

(15)

where ${\mathit{F}}_{all}=\left\{\dots , \right.\left.F_{pi},0, 0, \dots \right\}$, F_pi (i = 1, 2, …), and it is related to the gas pressure film of each node. Additionally, ${\mathit{U}}_{all}=\left\{{\dots ,w}_i, \right.\left.{ \theta }_{ri},{\theta }_{ti}, \dots \right\}$, θ_ri, θ_ti(i = 1, 2, …), which corresponds to the movement of the foil at each node. Through extracting each node’s lateral shift w_i, the deformation of the foil u_f can be obtained.

2.3. Gas Film Thickness Equation at Tilted Thrust Disc

In the engineering application, sometimes the thrust disc could be tilted, and the distributions of gas film thickness and pressure can be influenced. To research this situation, the thrust disc at the tilted condition and the relative position of the bearing pad are illustrated in Figure 3. It is assumed that the tilting condition of the thrust disc can be described through the rotating angles Θ_x and Θ_y, which are around the x and y coordinates, respectively.

Because the values of the Θ_x and Θ_y are quite small, they can be approximated and be regarded as

$${\Theta }_x\approx sin{\Theta }_x, {\Theta }_y\approx sin{\Theta }_y$$

(16)

The angle ξ in Figure 3b is the angle of the node from the positive x-axis. Defining the foil number as N, select one random sector of the pad and set one fixed side of it as the positive direction of the x-axis. Starting with this pad and number the other pads in an anticlockwise direction, and ξ can be described as follows:

$$\xi =\left(i-1\right){\displaystyle \frac{2\pi }{N}}\theta$$

(17)

Then, when considering the tilting condition of the thrust disc, the distribution of film thickness of each pad can be expressed as follows:

$$H=H_0+G\left(\theta \right)+{\Theta }_x^{*}Rsin\xi -{\Theta }_y^{*}Rsin\xi +U$$

(18)

where

$$G\left(\theta \right)=\left\{\begin{array}{c}{h}_{t0}\left(1-{\displaystyle \frac{\theta }{b{\beta }_t}}\right),0<\theta <b{\beta }_t\\ 0, b{\beta }_t\le \theta \le {\beta }_t\end{array}\right.$$

(19)

and b is the pitch ratio,

where

$$R={\displaystyle \frac{r}{R_2}}; {\Theta }_x^{*}={\Theta }_x{\displaystyle \frac{R_2}{h-h_{g0}}}; {\Theta }_y^{*}={\Theta }_y{\displaystyle \frac{R_2}{h-h_{g0}}}$$

(20)

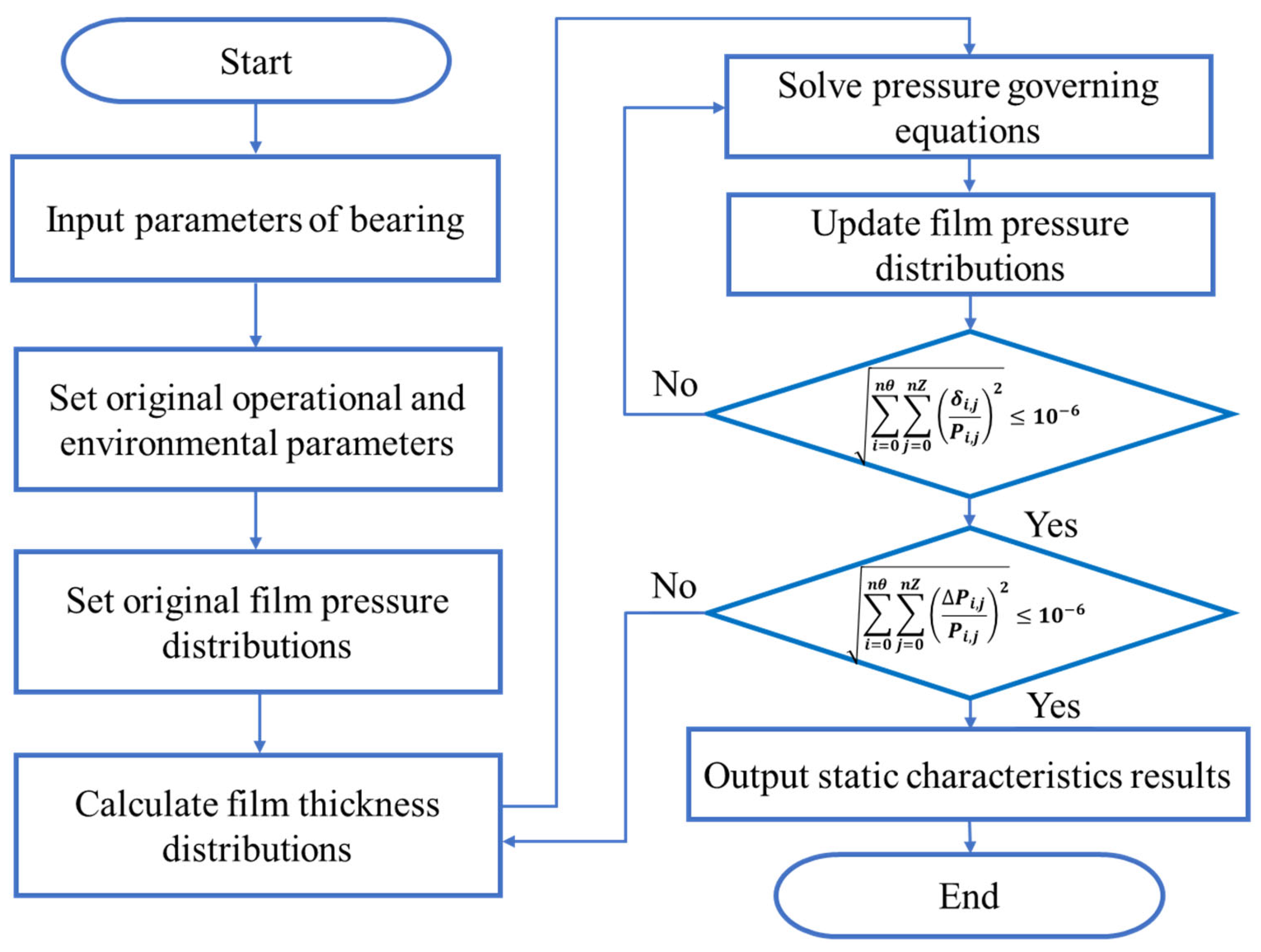
2.4. The Solution Processes of the Static Characteristics

The Newton–Raphson method [43] is adopted, and Formula (1) can be linearized and transferred into the following expression:

$$F={\displaystyle \frac{1}{R^2}}{\displaystyle \frac{\partial }{\partial \theta }}\left[\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right){\displaystyle \frac{\partial P}{\partial \theta }}\right]+{\displaystyle \frac{1}{R}}{\displaystyle \frac{\partial }{\partial R}}\left[R\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right){\displaystyle \frac{\partial P}{\partial R}}\right]-\Lambda {\displaystyle \frac{\partial \left(PH\right)}{\partial \theta }}$$

(21)

According to the Newton iteration method, the following relationships exist:

$$\left\{\begin{array}{c}F\left(P^n\right)+F^{\prime }\left(P^n\right){\delta }^n=0\\ {\delta }^n=P^{n+1}-P^n\end{array}\right.$$

(22)

where n is the iterations. Construct the composite function $F\left(P+\beta \delta \right)$, take a derivative concerning β, and define $\beta =0,$ then Formula (22) can be transferred into the following:

$${\left.{\displaystyle \frac{dF\left(P+\beta \delta \right)}{d\beta }}\right|}_{\beta =0}=F^{\prime }\left(P\right)\delta =-F\left(P\right)$$

(23)

For simple programming and easy use, the central difference form is adopted, and expressions of $P$, $\theta$, and $R$ can be written as follows:

$$\left\{\begin{array}{c}{\left({\displaystyle \frac{\partial P}{\partial \theta }}\right)}_{i, j}={\displaystyle \frac{P_{i+1, j}-P_{i-1, j}}{2∆\theta }}\\ {\left({\displaystyle \frac{\partial P}{\partial R}}\right)}_{i, j}={\displaystyle \frac{P_{i, j+1}-P_{i, j-1}}{2∆R}}\\ {\left({\displaystyle \frac{{\partial }^{2}P}{\partial R^2}}\right)}_{i, j}={\displaystyle \frac{P_{i+1, j}-2P_{i, j}+P_{i-1, j}}{{\left(∆\theta \right)}^2}}\\ {\left({\displaystyle \frac{{\partial }^{2}P}{\partial R^2}}\right)}_{i, j}={\displaystyle \frac{P_{i, j+1}-2P_{i, j}+P_{i, j-1}}{{\left(∆R\right)}^2}}\end{array}\right.$$

(24)

With the FDM being introduced, Formula (1) can be transformed into a linearized equation, which can be expressed as follows:

$$A_{i,j}{\delta }_{i-1,j}+B_{i,j}{\delta }_{i+1,j}+C_{i,j}{\delta }_{i,j}+D_{i,j}{\delta }_{i,j-1}+E_{i,j}{\delta }_{i,j+1}={-S}_{i,j}$$

(25)

where A_i,j, B_i,j, C_i,j, D_i,j, E_i,j, and S_i,j are related to P, which can be written as the following expressions:

$$A_{i,j}=-{\displaystyle \frac{H^3}{2∆\theta R^2}}{\displaystyle \frac{\partial P}{\partial \theta }}-{\displaystyle \frac{1}{2∆\theta R^2}}{\displaystyle \frac{\partial }{\partial \theta }}\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right)+{\displaystyle \frac{\Lambda H}{2∆\theta }}+{\displaystyle \frac{P{H}^3+6a{\overline{Kn}}_0{H}^2}{∆{\theta }^2{R}^2}}$$

(26)

$$B_{i,j}={\displaystyle \frac{H^3}{2∆\theta R^2}}{\displaystyle \frac{\partial P}{\partial \theta }}-{\displaystyle \frac{1}{2∆\theta R^2}}{\displaystyle \frac{\partial }{\partial \theta }}\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right)-{\displaystyle \frac{\Lambda H}{2∆\theta }}+{\displaystyle \frac{P{H}^3+6a{\overline{Kn}}_0{H}^2}{∆{\theta }^2{R}^2}}$$

(27)

$$C_{i,j}={\displaystyle \frac{1}{R^2}}{\displaystyle \frac{\partial }{\partial \theta }}\left(H^3{\displaystyle \frac{\partial P}{\partial \theta }}\right)+{\displaystyle \frac{1}{R}}{\displaystyle \frac{\partial }{\partial R}}\left(H^{3}R{\displaystyle \frac{\partial P}{\partial R}}\right)-\Lambda {\displaystyle \frac{\partial H}{\partial \theta }}-2\left({\displaystyle \frac{1}{∆R^2}}+{\displaystyle \frac{1}{∆{{\theta }^{2}R}^2}}\right)\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right)$$

(28)

$$D_{i,j}=-{\displaystyle \frac{H^3}{2∆R}}{\displaystyle \frac{\partial P}{\partial R}}+{\displaystyle \frac{1}{2R∆R}}{\displaystyle \frac{\partial }{\partial R}}\left[R\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right)\right]+{\displaystyle \frac{P{H}^3+6a{\overline{Kn}}_0{H}^2}{∆R^2}}$$

(29)

$$E_{i,j}={\displaystyle \frac{H^3}{2∆R}}{\displaystyle \frac{\partial P}{\partial R}}+{\displaystyle \frac{1}{2R∆R}}{\displaystyle \frac{\partial }{\partial R}}\left[R\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right)\right]+{\displaystyle \frac{P{H}^3+6a{\overline{Kn}}_0{H}^2}{∆R^2}}$$

(30)

$$S_{i,j}={\displaystyle \frac{1}{R^2}}{\displaystyle \frac{\partial }{\partial \theta }}\left[\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right){\displaystyle \frac{\partial P}{\partial \theta }}\right]+{\displaystyle \frac{1}{R}}{\displaystyle \frac{\partial }{\partial R}}\left[R\left(P{H}^3+6a{\overline{Kn}}_0{H}^2\right){\displaystyle \frac{\partial P}{\partial R}}\right]-\Lambda {\displaystyle \frac{\partial }{\partial \theta }}\left(PH\right)$$

(31)

The boundary conditions can be written as follows:

$$\left\{\begin{array}{c}P\left(:,0\right)=1\\ P\left(:,nr\right)=1\\ P\left(0,:\right)=1\\ P\left(n\theta ,:\right)=1\end{array}\right.$$

(32)

The bearing capacity can be calculated through the expressions listed below:

$$\overline{W}={\sum }_{i=1}^N{\int }_0^{{\beta }_t}{\int }_{{\displaystyle \frac{R_1}{R_2}}}^1\left(P-1\right)RdRd\theta$$

(33)

$$W=p_0{R}_2^2\overline{W}$$

(34)

2.5. Calculation Flow Chart of Static Characteristic

The calculation procedure of the static characteristics of the MLFTB is shown in Figure 4. Both the mesh structures and the computational domains of the pad of MLFTB are depicted in Figure 5. The original parameters will be set up, and the distributions of pressure and film thickness will be calculated and judged. The iterations will not be stopped until the convergence criteria expressed as Formula (35) are satisfied. Then the static characteristics results of MLFTB can be obtained.

The conditions of the convergence criteria are set as follows:

$$\left\{\begin{array}{c}\sqrt{\sum _{i=0}^{n\theta }\sum _{j=0}^{nr}{\left({\displaystyle \frac{{\delta }_{i,j}}{P_{i,j}}}\right)}^2}\le {10}^{-6}\\ \sqrt{\sum _{i=0}^{n\theta }\sum _{j=0}^{nr}{\left({\displaystyle \frac{{∆P}_{i,j}}{P_{i,j}}}\right)}^2}\le {10}^{-6}\end{array}\right.$$

(35)

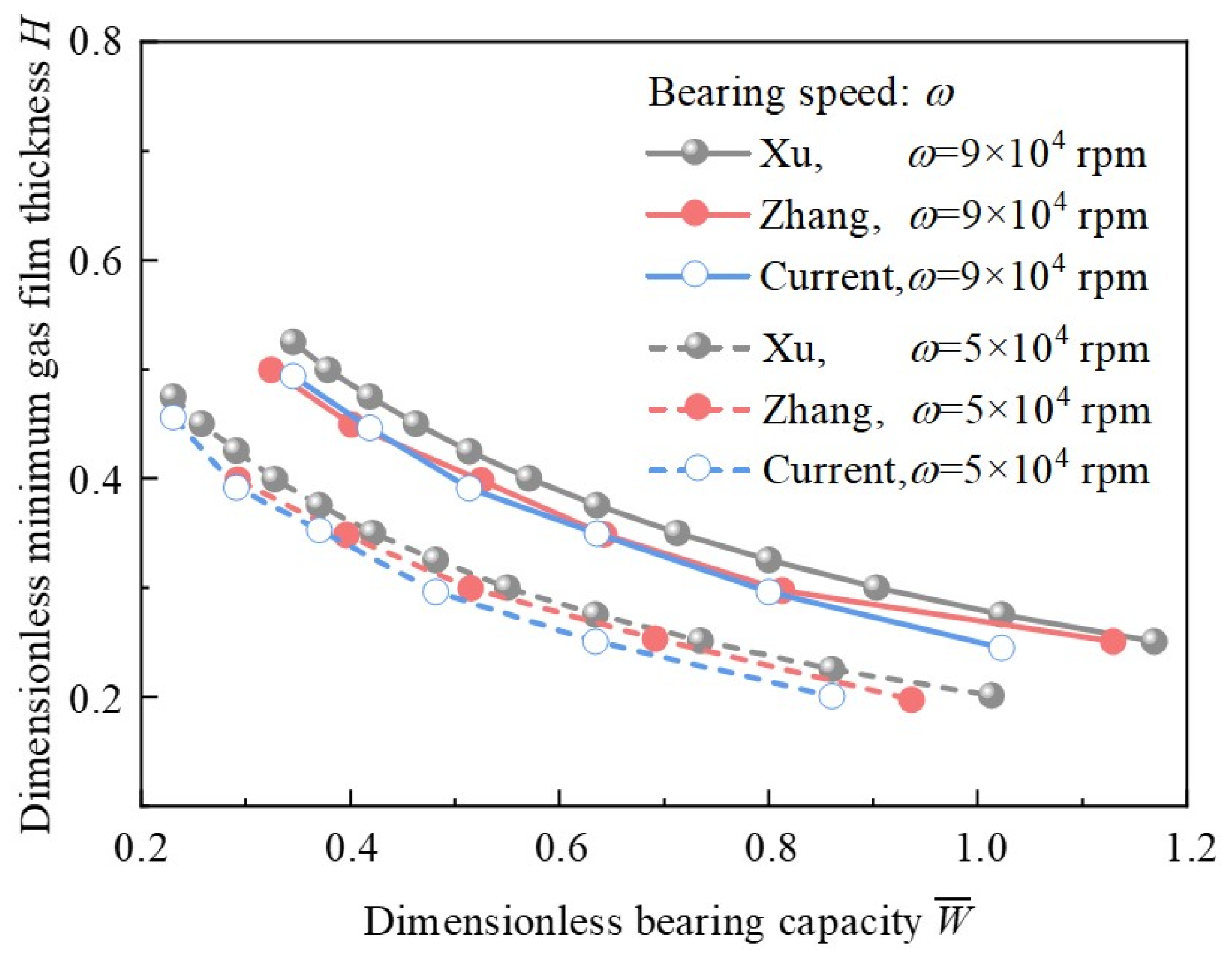
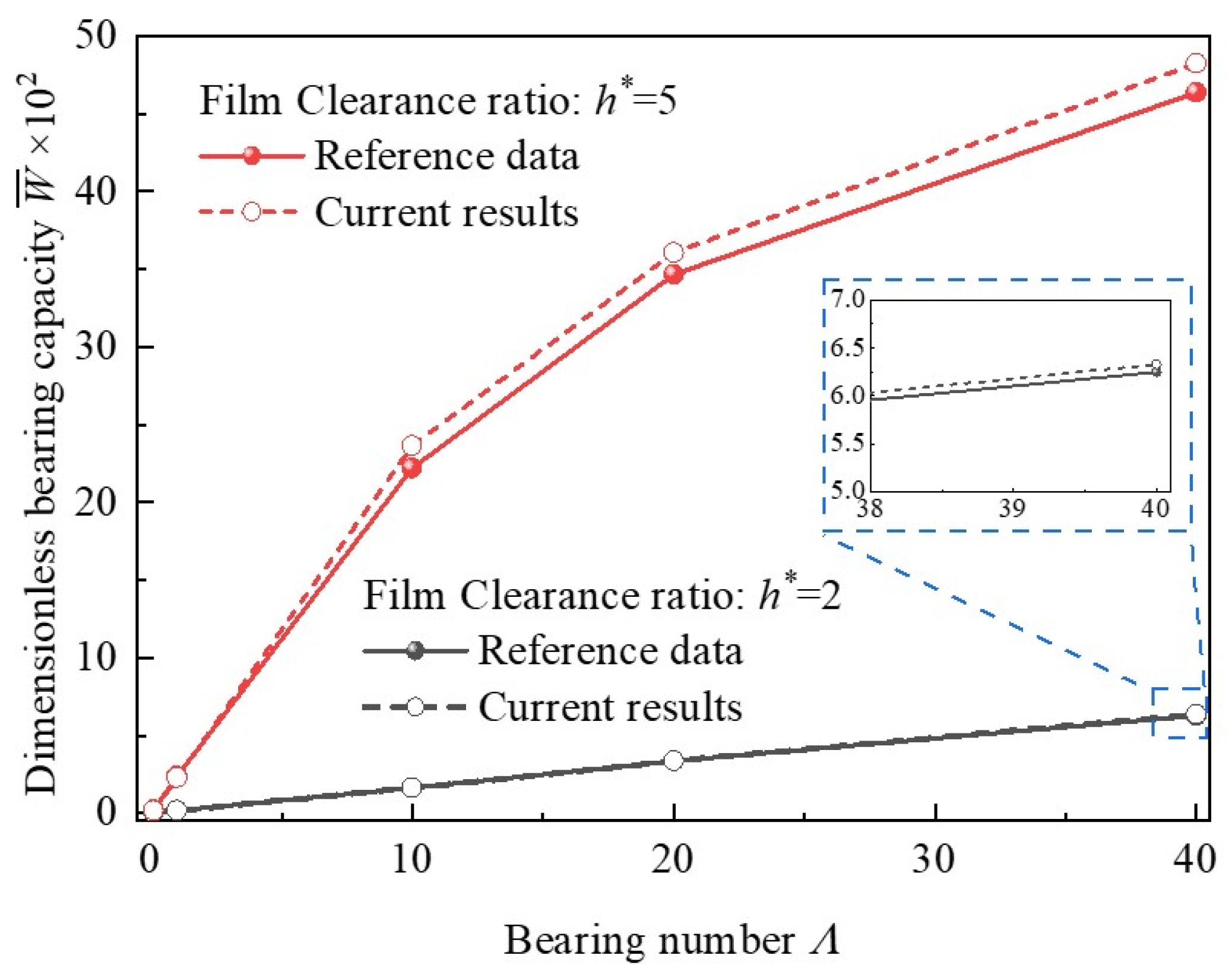
2.6. Validation of Model

To certain the accuracy and efficiency of the present models, they were adopted to simulate the variation of the minimum film thickness versus bearing capacity at different bearing speeds. As depicted in Figure 6, comparisons between the numerical results and the data in the literature [33,34] are made. The parameters and operating conditions are kept the same as those in the literature [33,34]. In Figure 7, the lines labeled with small hollow circles are the results derived from the current model. In contrast, the lines signed by small balls and solid circles represent the data in the literature [33] and literature [34], respectively. The variations of results by present models are in high consistency with those of the literature [33,34]. Additionally, the maximum deviation between the current results and the simulated results in the literature [33,34] is less than 3.6%. It demonstrates that the current model obtains credible reliability and precision.

To better ensure the validity of the present model, the calculated bearing capacities versus different bearing numbers are compared with data in the literature [44]. In literature [44], the film clearance ratio is defined as $h^{*}=h_1/h_2$, where h₁ represents the inlet film thickness of one sector of the bearing pad, and h₂ represents the nominal design clearance. The relevant parameters are set identically to those in the literature [44]. As depicted in Figure 7, the variation discipline of results derived from the present model is in accordance with that of the literature. Additionally, the maximum deviation is less than 8%, which means the present model is reliable and accurate. Additionally, the relevant parameters for the current investigation are exhibited in

Table 1. Relevant bearing parameters for current research.

Parameter Name	Value
Outer radius of top foil (R2)	57.15 × 10−3 m
Inner radius of top foil (R1)	29.75 × 10−3 m
Thickness of top foil (tf)	2.0 × 10−4 m
Thickness of middle panel (tm)	1.1 × 10−4 m
Thickness of supporting panel (ts)	8.2 × 10−4 m
Foil elastic modulus (Eb)	2.2 × 1011 Pa
Foil number (N)	8~16
Ambient pressure (pa)	1.01325 × 105 Pa
Foil Poisson’s ratio (υb)	0.3
Bearing speed (ω)	3.0 × 104~1.2 × 104 rpm
Clearance between thrust disc and bearing (hg0)	6.0 × 10−6 m~14.0 × 10−6 m
Dynamic viscosity of gas (μ)	1.932 × 10−5 Pa·s

.

To reduce the influence of grid division on the results, the results of grid independence of the number of elements have been verified, which is depicted in Figure 8 below. Based on the verification of grid independence, the final mesh quantity was chosen as $nr\times n\theta =20\times 30$.

3. Results and Discussion

In this section, the effects of the clearance, bearing speed, foil number, and tilt angle on the pressure and film thickness distributions and bearing capacity are presented in Section 3.1, Section 3.2, Section 3.3, and Section 3.4, respectively. Based on the Knudsen (Kn) number and slip model, the differences between the slip effect and no-slip effect are compared and discussed in detail. When ignoring the deviation of the shaft in the direction of gravity, the distributions of pressure and film thickness can be regarded as periodic and symmetric. To better observe the distributions of flow fields of this type of MLFTB, one sector (one period) of the pad is selected, and the distributions of pressure and film thickness at different parameters are illustrated in Figure 9 and Figure 10, respectively. As seen in Figure 9, the pressure of lubrication gas is increased from the ambient pressure to the maximum pressure immediately. In contrast, the film thickness shrinks from the original position to the minimum film thickness, correspondingly, that is where the first convergent wedge of foil exists. Subsequently, the pressure is decreased and then increased at a small amplitude; meanwhile, the film thickness will first increase and then decline to the second minimum peak values. It is the position where the second convergent wedge of foil lies. It can be induced by forced deformation of the upward-convex structure of the supporting panel. Thus, the characteristics of double-peak pressure values and double-valley film thickness values of MLFTBs in the current research differ from those of the traditional foil thrust bearing [31]. Further, the second peak of pressure or valley of film thickness can be led by the deformed upward-convex structure on the supporting panel of MLFTBs.

Compared with Figure 10, it can be found that when at a smaller clearance between the thrust disc and the bearing, the variations of the distributions of pressure and film thickness along both the circumferential direction and the radial direction are much more intensive. It can be seen that the gas film pressure in the area close to the outer radius of the bearing is relatively large. It can be attributed to the linear velocity at the outer radius of the rotor, which is greater, and to the aerodynamic pressure effect of the lubricant gas, which is stronger. In contrast, due to the convergence gap in the slope section, the film thickness will be originally circumferentially decreased to a small value. Later, after being influenced by the deformation of the top foil in the middle portion of the horizontal section, the film thickness will be increased.

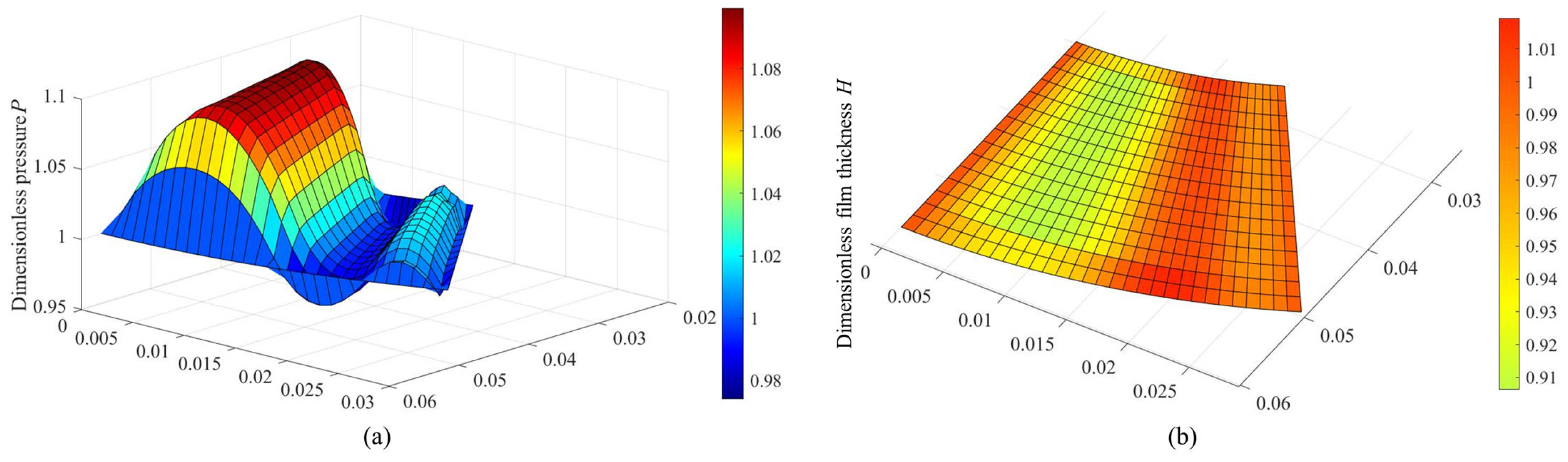
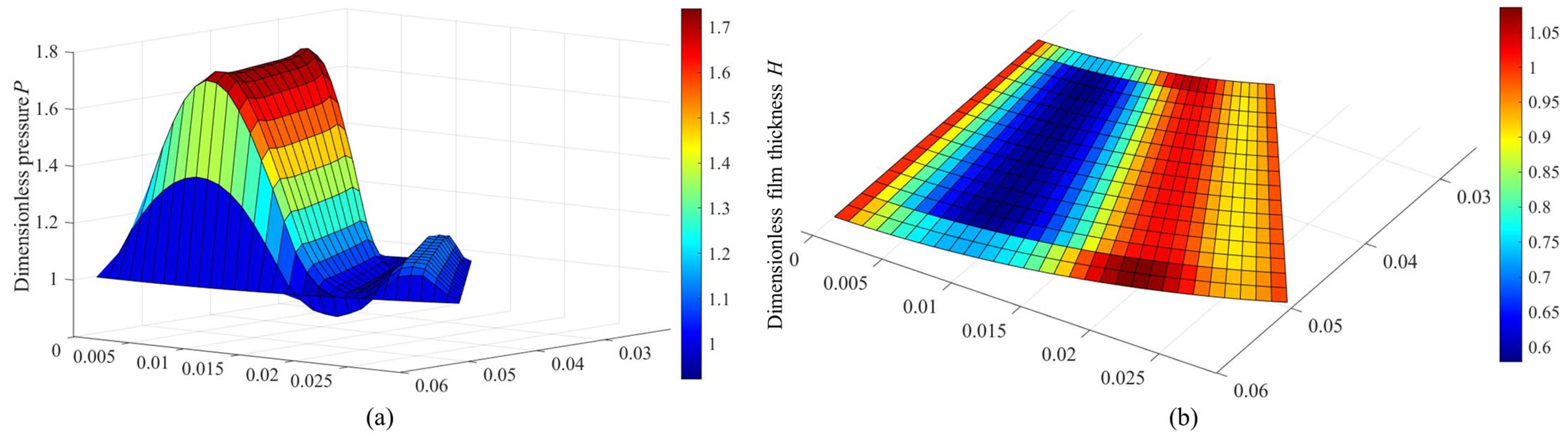
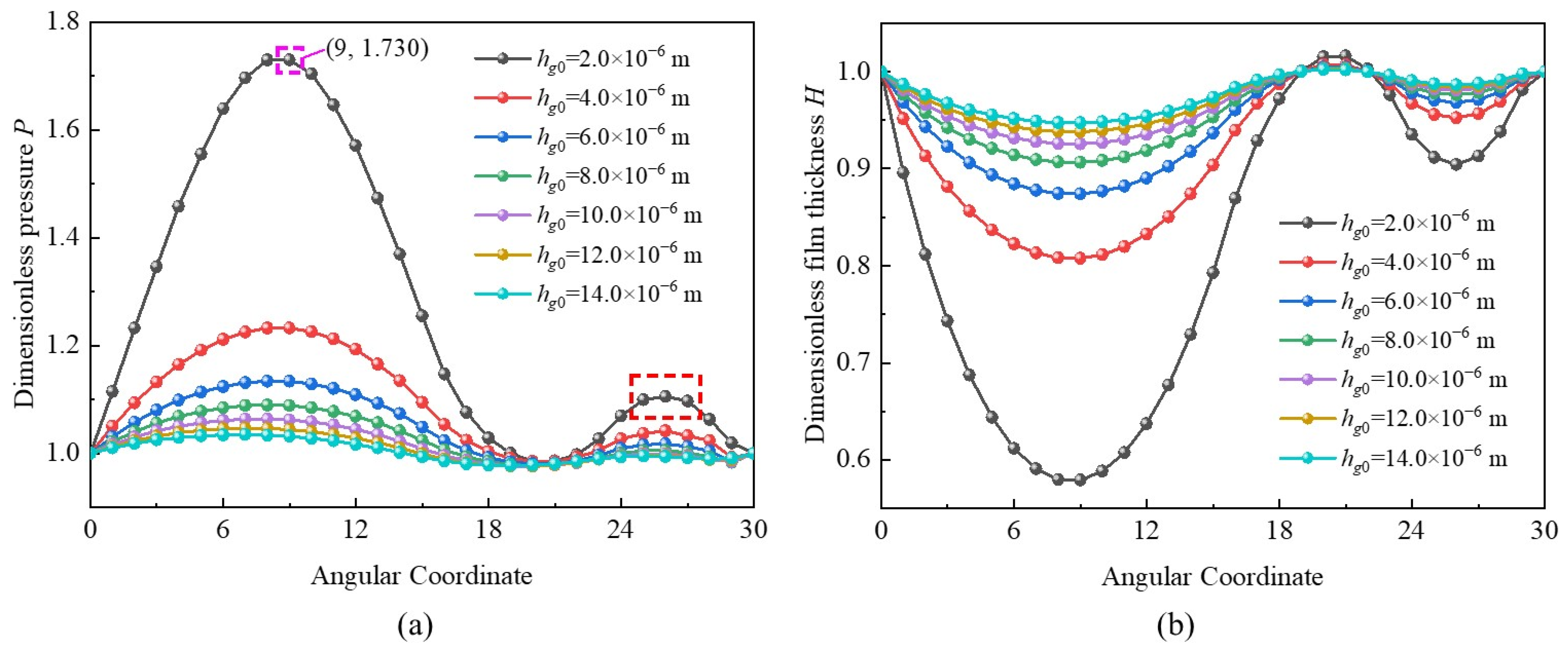
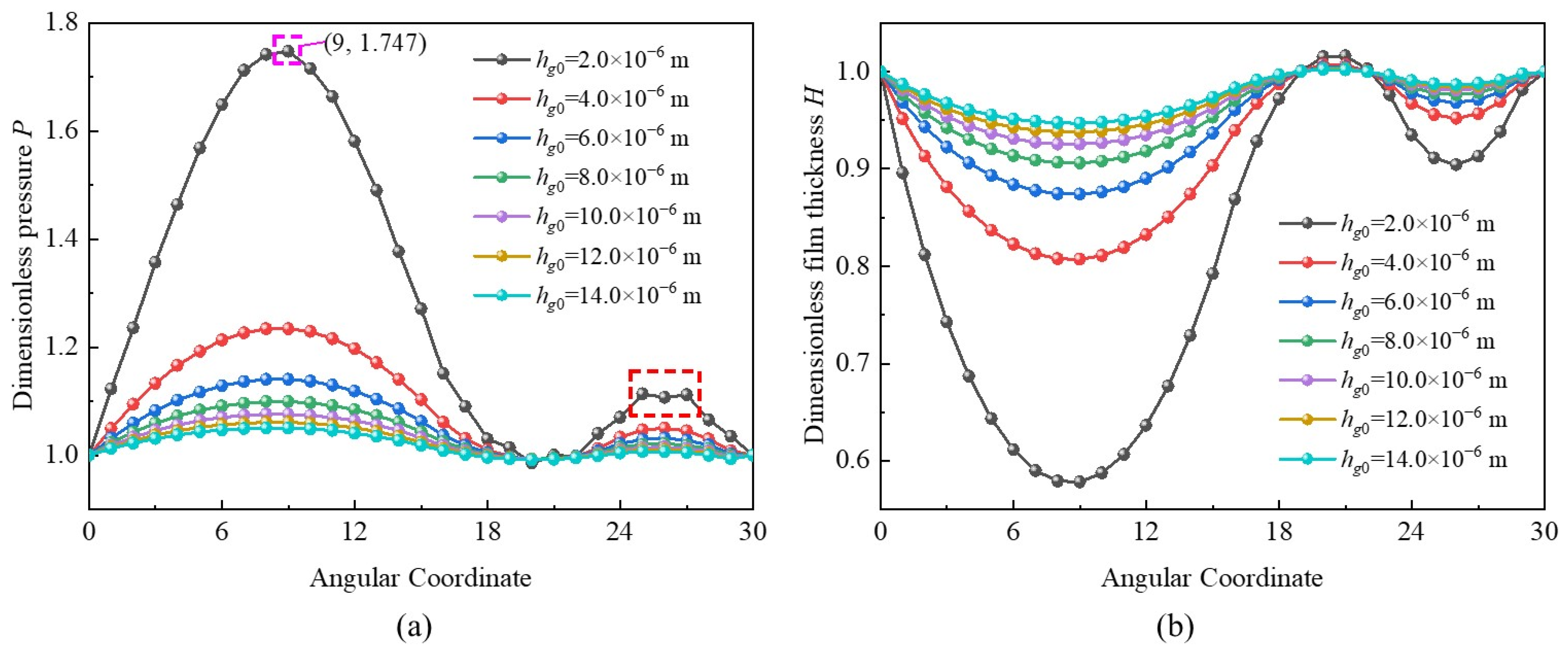
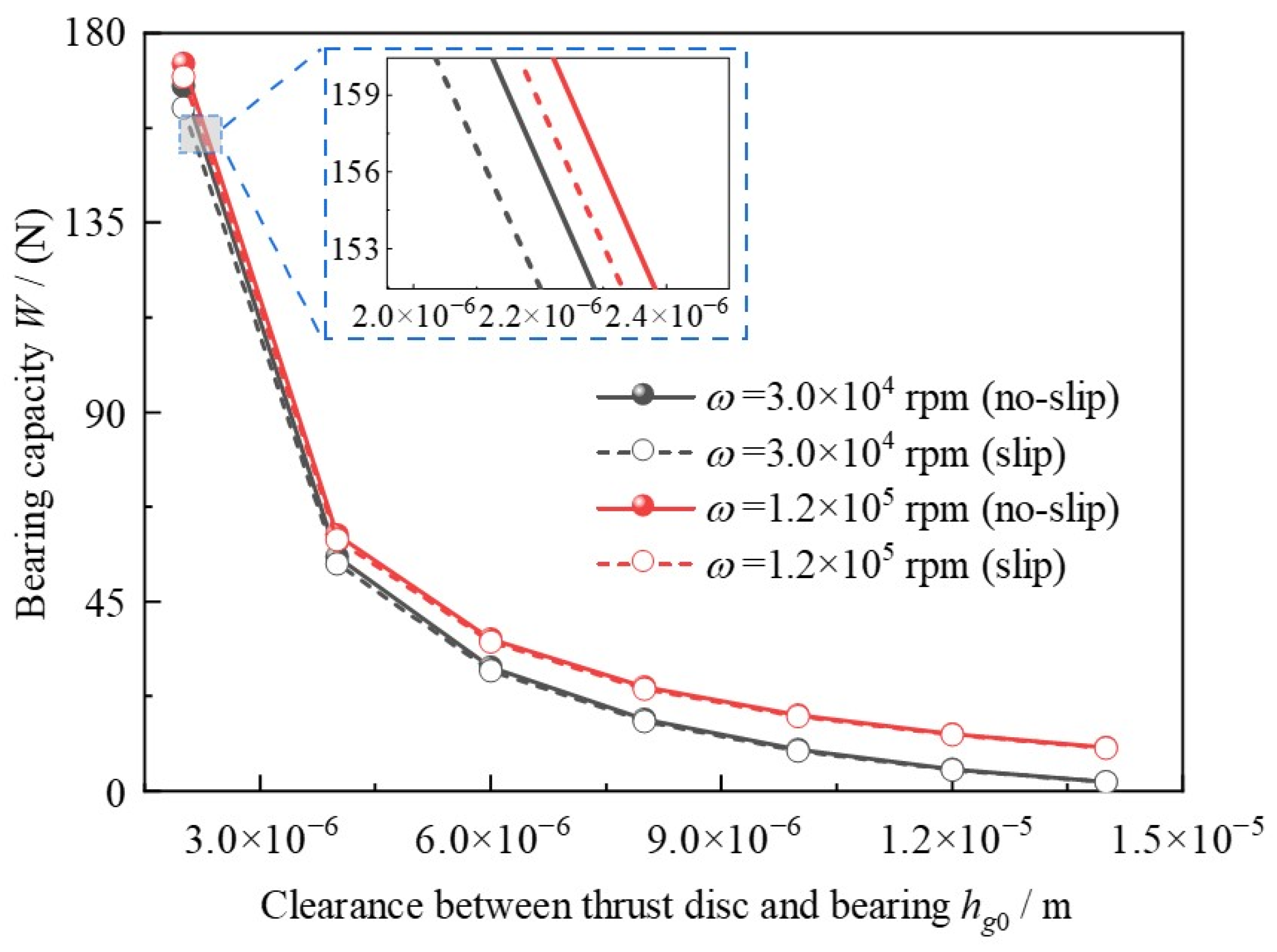
3.1. Effects of Clearance

Primarily, the effects of the significant parameter of clearance on the pressure and film thickness distributions, and bearing capacities were first simulated. The clearance between the thrust disc and bearing is increased from h_g0 = 2.0 × 10⁻⁶ m to h_g0 = 14.0 × 10⁻⁶ m. Other parameters are as follows: bearing speed ω = 3.0 × 10⁴ rpm and foil number N = 12. To better observe the variation of static characteristics of MLFTBs, the distribution of pressure and film thickness in the mid-panel of the pad is illustrated in Figure 11a and Figure 11b, respectively.

As illustrated in Figure 11a, with the rise of the clearance between the thrust disc and bearing, the maximum peaks of pressure will be rapidly decreased at a declining amplitude. At the same time, the double-peak pressure phenomenon has receded. It implies that the aerodynamic pressure effect of the convergent-wedge shape is weakened. It can be explained that when it is at a small clearance with a high-pressure load, a large normal deformation of the convex part of the supporting panel (as illustrated in Figure 1) can occur. The pressure can be decreased first and then increased. As a consequence, the obvious “double peak” can appear, which is the so-called “double wedge effect” [34].

As seen from Figure 12a, when it comes to a larger bearing speed ω = 12.0 × 10⁴ rpm, the overall variations trend of pressure are similar and the maximum peak of pressure increases, nevertheless, as for the small clearance condition of h_g0 = 2.0 × 10⁻⁶ m, the second peak of pressure becomes flattening (labeled by orange dashed square box). It can be attributed to the fact that, under higher bearing speed and less clearance conditions, the aerodynamic pressure effect in the clearance will be strengthened, and the normal force acting on the convex panel of the supporting panel can be intensified. However, when it exceeds a certain scope, there will not be enough deformation allowance of the convex to support the foil; instead of remaining at the distinct pressure peak, the platform of high pressure near the second peak can emerge. It can be supported by the research content of the literature [33].

In comparison, as seen from Figure 11b and Figure 12b, the minimum valleys of distributions of film thickness at the mid-panel will be increased, and the variation amplitudes will be reduced. In addition, the double-valley characteristic will also become less obvious. It can be considered as a result of the faded aerodynamic pressure effect at larger clearance.

Subsequently, the relationships between the bearing capacity and clearance under the slip effect and the no-slip effect are compared and depicted in Figure 13. As seen in Figure 13, with the increase of clearance, the bearing capacity will initially rapidly decrease and then slowly decline. When it is under smaller clearance or higher bearing capacity, the aerodynamic pressure effect will become stronger, and the bearing capacity can be strengthened more obviously.

In addition, the bearing capacity under the slip effect will be decreased in comparison to the no-slip effect. For instance, the maximum deviation for the condition of ω = 3.0 × 10⁴ rpm is about −3.05%, meanwhile, that of ω = 12.0 × 10⁴ rpm is less intense, which is around −1.90%. It indicates that the slip effect should not be neglected when it is under small clearance with low bearing speed. It can also be supported by the investigation results in the literature [33].

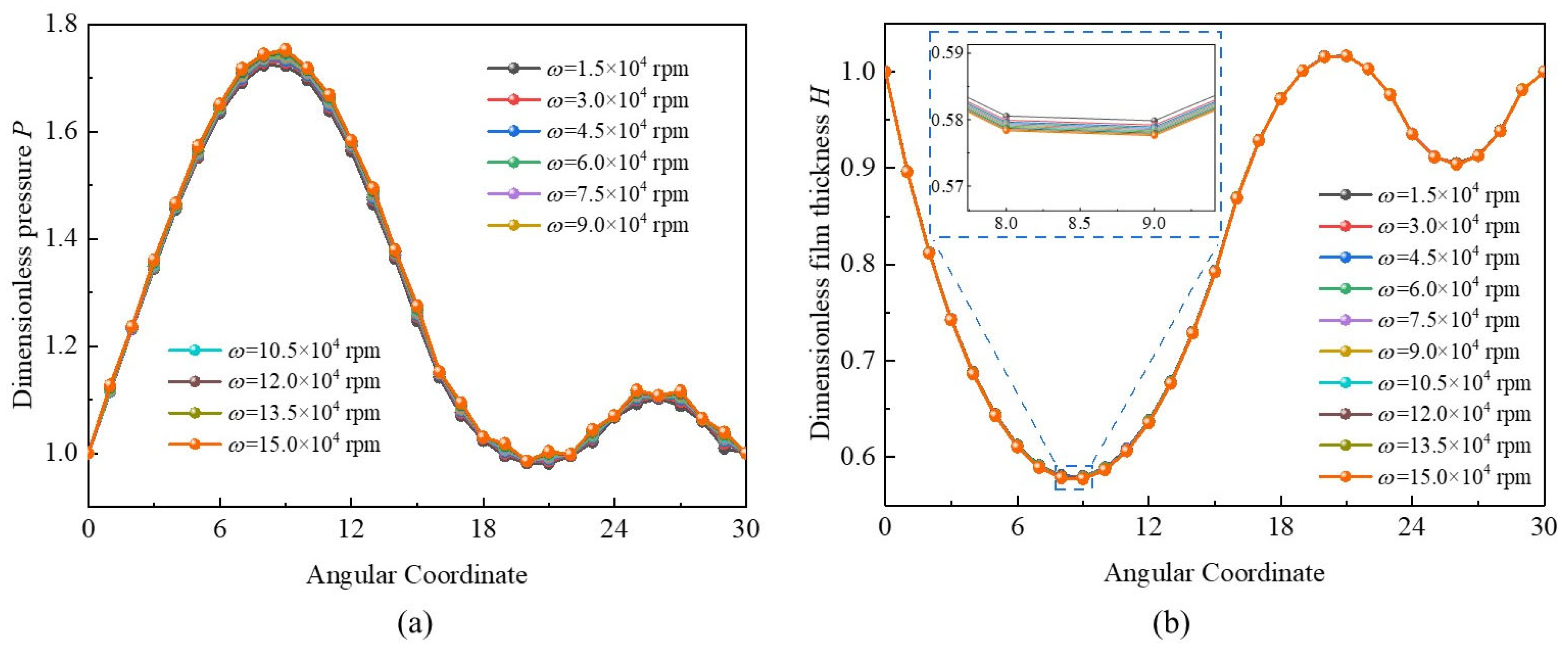
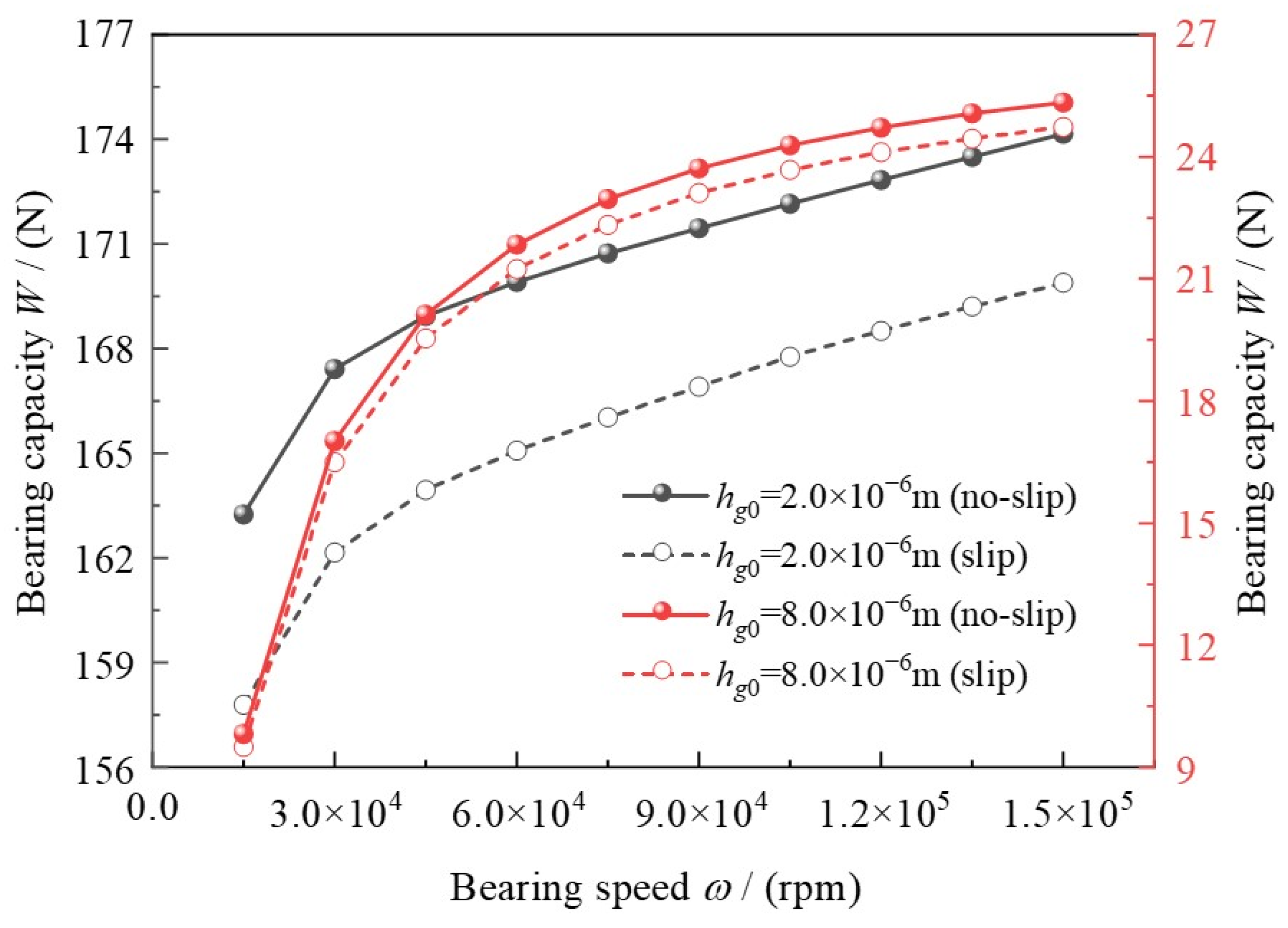
3.2. Effects of Bearing Speed

In this section, the influences of the bearing speed on the static characteristics are explored. The bearing speed is increased from ω = 1.5 × 10⁴ rpm to ω = 15.0 × 10⁴ rpm. Meanwhile, the typical combinations of clearance between thrust disc and bearing h_g0 = 8.0 × 10⁻⁵ m and h_g0 = 2.0 × 10⁻⁵ m are selected, and other parameters such as E_b = 2.2 × 10¹¹ Pa and N = 12 are kept the same. The variation laws are illustrated in Figure 14 and Figure 15, respectively.

As shown in Figure 14a, as the bearing speed rises from ω = 1.5 × 10⁴ rpm to ω = 15.0 × 10⁴ rpm, the maximum pressure peaks will increase with a declining amplitude, and the double-peak phenomenon appears. In contrast, as seen in Figure 14b, the differences in film thickness are slight. As a comparison, the distribution of pressure under clearance of h_g0 = 2.0 × 10⁻⁵ m at different bearing speeds is shown in Figure 15a. However, when it is at a lower clearance, the effect of bearing speed is not as influential as that of a larger clearance. It can be due to the existing stronger compressing effect at lower clearance. Similarly, as shown in Figure 15b, with the increase of bearing speed, the distributions of valleys are slightly decreased, whereas the variations are not obvious.

In the meantime, the influences of bearing speed on the bearing capacity of MLFTBs under different boundary conditions, for instance, the slip effect and no-slip effect boundary conditions, are depicted in Figure 16. When it is at large clearance, such as h_g0 = 8.0 × 10⁻⁵ m, the variation of bearing capacity with bearing speed is more obvious than that at low clearance, for instance, h_g0 = 2.0 × 10⁻⁵ m.

Furtherly, when compared with no-slip effect conditions, the slip effect makes more distinguishable differences in the bearing capacity at lower clearance and bearing speed. As for h_g0 = 8.0 × 10⁻⁵ m, the maximum deviation is about −2.90%, and as for h_g0 = 2.0 × 10⁻⁵ m, that is about −3.15%. The variation tendency is consistent with that interesting phenomenon observed in Figure 13.

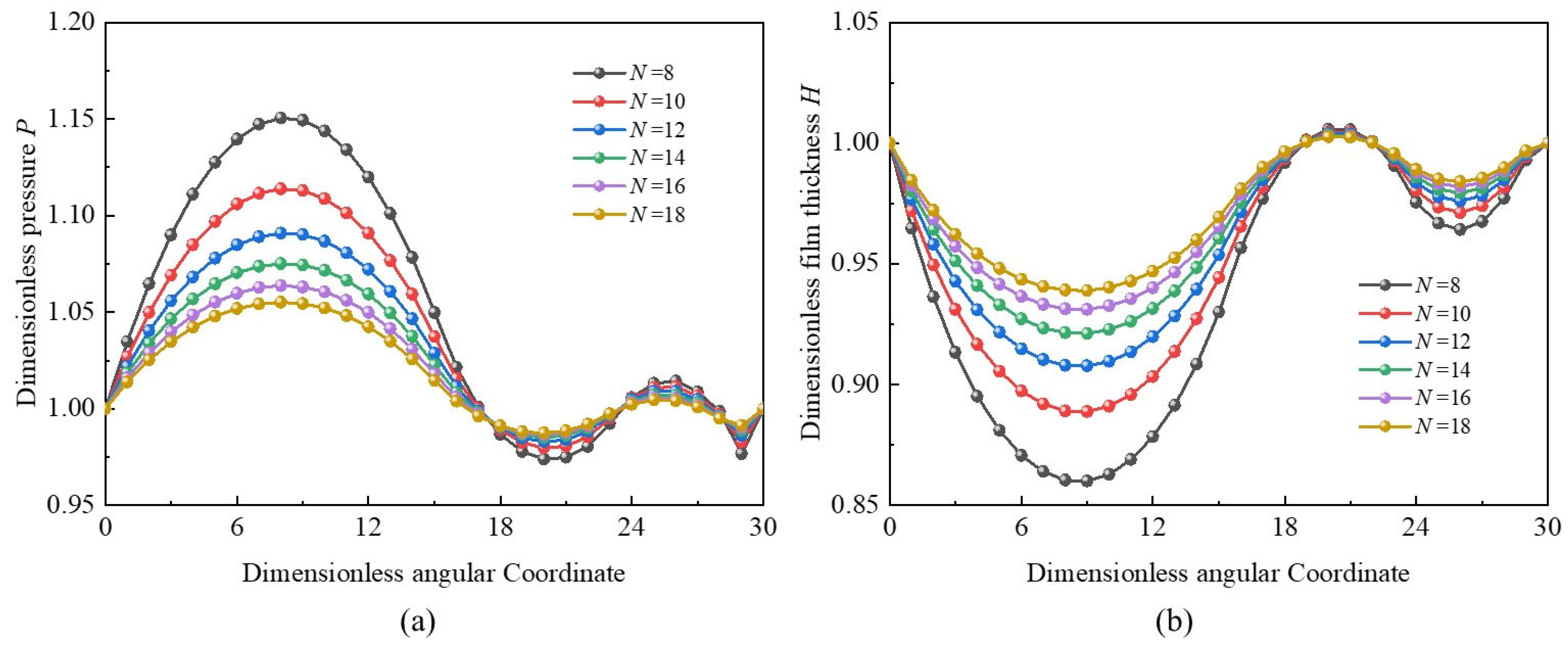
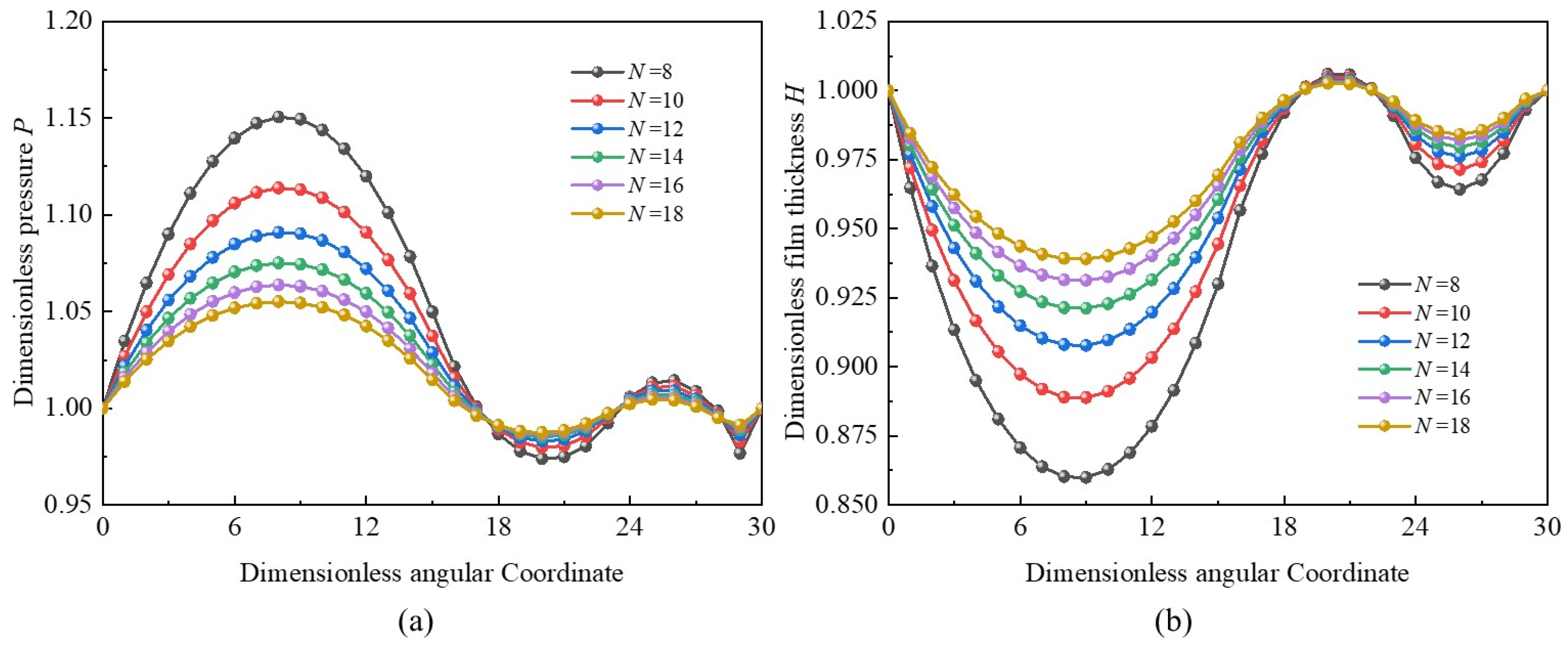
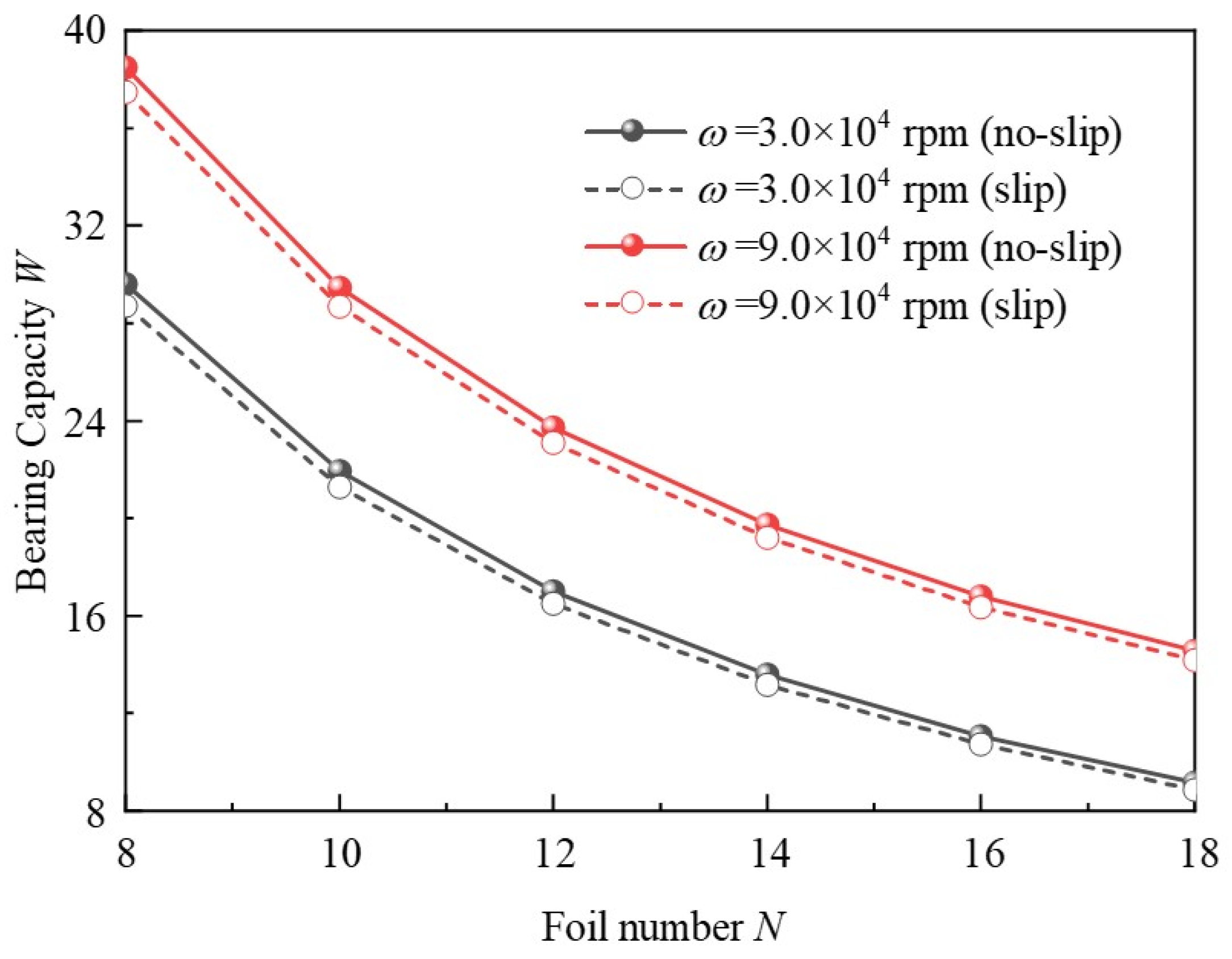
3.3. Effects of Foil Number

In this section, the effects of foil number on the static characteristics are discussed. As seen in Figure 17 and Figure 18, the different conditions of foil numbers from N = 8 to N = 18 with typical combinations of bearing speeds ω = 3.0 × 10⁴ rpm and ω = 9.0 × 10⁴ rpm are selected, and the other parameters are h_g0 = 8.0 × 10⁻⁵ m and E_b = 2.2 × 10¹¹ Pa. Seen from Figure 17a and Figure 18a, within the present investigation scope, the double-peak structure of the pressure distributions will remain, while the pressure peaks will be increased with the rise of the foil numbers. The main difference is that when under higher bearing speed, the distinctions of the second pressure peak will be more distinct. The reason for this phenomenon can be that, under the same original clearance condition, the load capacity of each foil will be enlarged at a smaller foil number [45].

The variation in film thickness is depicted in Figure 17b and Figure 18b. As shown in Figure 17b and Figure 18b, the distributions of film thickness keep the double-valley structure. However, the amplitude decreases as the foil number increases. Additionally, the area of the second valley is shrinking, which indicates that the elastic deformation of the foil that contacts the supporting panel is decreasing. Consequently, the film thickness becomes larger. Additionally, the distinction of distributions of film thickness under different bearing speeds is not obvious.

To better understand the influence of foil number, the variation of bearing capacity at different foil numbers is investigated and illustrated in Figure 19. Within the research scope, the bearing capacity will be decreased with the rise of the foil number. It can be attributed to when at a large foil number, the span of the adjacent pair of convex panels on the supporting panel will be narrowed, and the structural stiffness will be reduced. Thus, the deformation of the foil can be weakened, and the aerodynamic pressure effect will be less intense. Consequently, the bearing capacity can be reduced at a larger foil number.

The variations of bearing capacity under different boundary conditions are considered. As depicted in Figure 19, compared with the no-slip effect, the bearing capacity under the slip effect condition can be decreased. As for the bearing speed ω = 3.0 × 10⁴ rpm, the maximum deviation for the slip condition is about −3.00%; meanwhile, that of bearing speed ω = 9.0 × 10⁴ rpm is less intense, which is around −2.60%.

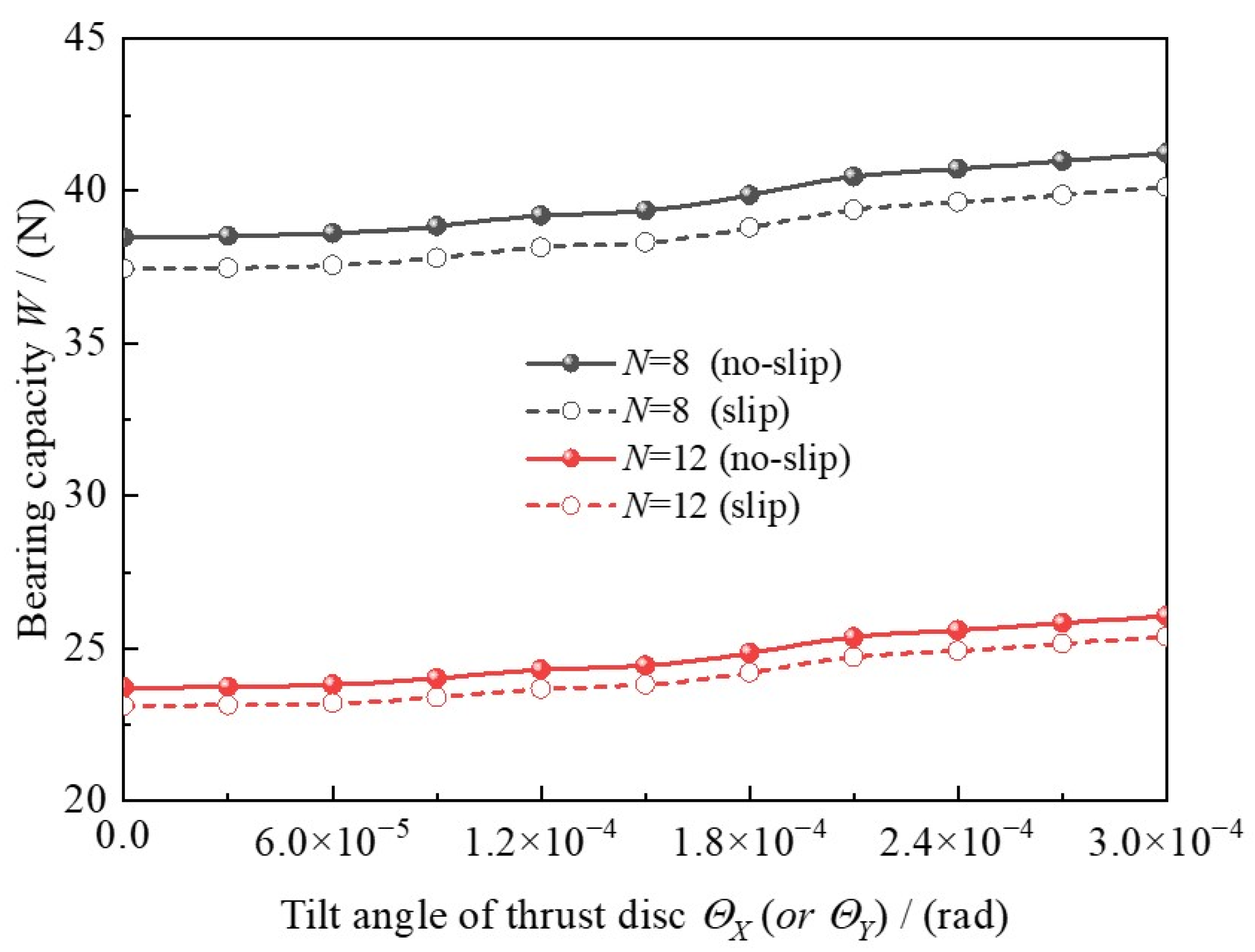
3.4. Effects of Tilt Angle

In this section, the effects of the tilt angle of the thrust disc on the load capacity will be explored. The different slip and no-slip boundary conditions are emphasized. The tilt angle of thrust disc Θ_X (or Θ_Y) is increased from 0.0 to 3.0 × 10⁻⁴ rad, and two typical combinations of foil numbers N = 8 and N = 12 are selected. The other parameters are set as h_g0 = 8.0 × 10⁻⁶ m and ω = 9.0 × 10⁴ rpm. As depicted in Figure 20, within the research scope, the bearing capacity will be slightly enhanced with the increase in the tilt angle of the thrust disc. However, the overall variation tendency is quite gentle, and it exhibits good anti-tilting performance in the MLFTBs.

Compared with the no-slip boundary conditions, the bearing capacity at the slip boundary conditions will be decreased. As for the foil number N = 8, the maximum deviation for the condition is about −2.70%, and for N = 12, that is around −2.60%. It indicates that when the thrust disc tilts, the effect of slip boundary conditions can be slightly reduced by increasing the foil number.

4. Conclusions

In the present research, an effective modified numerical model with high computational efficiency for the static characteristics of the MLFTB is established. The FDM and the thick plate element are implemented, and the compressible Reynolds equation is linearized by the Newton–Raphson method. The evolution law of the static characteristics with geometric and operational parameters was derived by iterative solution and comprehensively discussed. The main conclusions are as follows:

(1)

The numerical model reinforces the static characteristics analysis of the MLFTB. The parameter effects can be directly and efficiently acquired by numerical methods with high calculation accuracy.

(2)

The results indicate that bearing capacity could be generally decreased by around 3.15% when the slip boundary condition is considered, especially under small clearance and low bearing speed, which should not be neglected.

(3)

The so-called “double wedge effect” characteristic of MLFTB with double-peak pressure and double-valley film thickness differs from the traditional foil thrust bearing with top and bump foils. However, it can disappear when hg0 > 12.0 × 10⁻⁶ m.

The increase in tilt angle could result in a slight enhancement of bearing capacity, and the large foil number can slightly decrease the slip effect. The MLFTB exhibits good anti-tilting performance.

(4)

In summary, these findings concentrate on the influences of parameters on the static characteristics. Moreover, investigating the impact of aerodynamic heat performance may contribute to insights into MLFTB and lead to better properties.