Dynamic Characteristic Analysis of Angular Contact Ball Bearings with Two-Piece Inner Rings in Aero-Engine Main Shafts Under Unsteady-State Conditions

Abstract

The dynamic interactions among the internal components of aero-engine main shaft bearings under unsteady-state conditions are intricate, involving clearance collisions, contact, friction, and lubrication. The dynamic characteristics of bearings significantly influence the performance and stability of mechanical systems. This study establishes a rigid–flexible coupling dynamic model for angular contact ball bearings with two-piece inner rings based on Hertz contact theory and lubrication theory. It systematically analyzes the dynamic characteristics of bearings under the coupling effects of acceleration, deceleration, and impact load. This study explores the influence of various loads, bearing speeds, and groove curvature radius coefficients on the dynamic characteristics of bearings. The findings indicate that the uniform speed phase of a bearing is highly responsive to impact load, followed by the deceleration phase, while the acceleration phase shows lower sensitivity to impact load. The groove curvature radius coefficient significantly affects the contact stress between the ball and its corresponding raceway, with contact stress increasing as the groove curvature radius coefficient rises. As the axial load decreases and the radial load, bearing speed, and groove curvature radius coefficient increase, there is a rise in pocket force, guiding force, and maximum equivalent stress of the flexible cage. Impact load leads to short-term intense fluctuations in the thickness of the bearing oil film, which can be alleviated by an increase in axial load. The oil film thickness firstly increases and then decreases with respect to the groove curvature radius coefficient. Furthermore, variations in bearing speed notably influence the thickness of the bearing oil film. This study analyzes the dynamic characteristics of bearings under the coupling effects of acceleration, deceleration, and impact load, offering insights for the design and optimization of angular contact ball bearings with two-piece inner rings.

1. Introduction

Among the most common types of main shaft bearings used in aero-engines are cylindrical roller bearings, three-point contact ball bearings with two-piece inner rings, and four-point contact ball bearings with two-piece inner rings. The focus of this study is on three-point contact ball bearings with two-piece inner rings, also known as angular contact ball bearings with two-piece inner rings. These bearings feature a compact structure and have the capability to bear bidirectional axial loads simultaneously. They are often employed as the frontal support for the high-pressure compressor of an aero-engine, playing a crucial role in ensuring the stable operation of the engine. In demanding working environments such as the high-temperature and high-pressure conditions found in aircraft engines, angular contact ball bearings with two-piece inner rings are required to handle high speeds and loads while maintaining high-precision positioning and operational stability. However, in practical applications, bearings frequently encounter various unsteady-state conditions, including rapid acceleration, deceleration, impact loads, and more. These conditions impose more stringent requirements on the dynamic characteristics of the bearings.

Since Stribeck [1] initiated the study of ball bearing statics based on Hertz contact theory, numerous scholars have conducted extensive theoretical and experimental research on the dynamic properties of bearings. The dynamic properties of bearings under steady-state conditions have thus garnered significant attention and have been studied extensively. Jones [2] proposed race control theory to address the challenges associated with the dynamic analysis of rolling bearings. Subsequently, Walters [3] and Gupta [4] established dynamic analysis models for bearings, describing their motion states at any given moment by introducing differential equations of motion. Hagiu et al. [5] investigated the stiffness and damping characteristics of high-speed angular contact ball bearings, considering thin film squeeze effects and Hertz contact elastic deformation. Li et al. [6] established a rigid–flexible coupling analysis model to investigate the wear issue of the pocket hole in high-speed ball bearing cages and its impact on the dynamic characteristics of the bearing. Gu et al. [7] formulated a time-varying nonlinear dynamic model for angular contact ball bearings and analyzed the influence of wear on their dynamic characteristics based on their model. Deng et al. [8] established dynamic equations for cages to investigate the influence of bearing operating conditions and structural parameters on the dynamic characteristics of the cage. Wang et al. [9] considered the interactions between the rolling elements and the raceways, the cage, and the lubricant and established a dynamic model of angular contact ball bearings under high-speed conditions, researching the skidding characteristics of angular contact ball bearings. Xie et al. [10] combined the quasi-dynamics of an angular contact ball bearing with the elastic deformation of its cage to analyze the temporal variation in the interaction forces between the bearing components and the equivalent stress at a node on the cage’s side wall. Liu et al. [11] investigated how different factors influence the slip rate and friction power consumption of the cage within an angular contact ball bearing at ultra-low temperatures by formulating the dynamic equations for angular contact ball bearings equipped with elliptical pocket cages. Bian et al. [12] created a multi-body dynamics model that includes the rolling elements, the cage, and the rings to examine how the linear velocity of the rolling elements and the cage’s slip rate vary under varying external loads and rotational speeds. Weinzapfel [13] and Ashtekar [14] respectively established dynamic models for bearings that consider cage flexibility, employing the discrete element method alongside a hybrid approach using explicit finite element methods and discrete element techniques to investigate how flexible cages influence the bearing’s dynamic properties. Chen et al. [15] developed a time-varying stiffness model for a zero-clearance four-point contact ball bearing, focusing specifically on the pitch bearings used in wind turbines. Their study explored variations in bearing stiffness resulting from the combined effects of axial and radial loads.

As rolling bearings advance toward higher speeds, heavier loads, and increased precision, it has become crucial to investigate their dynamic behaviors under unsteady-state conditions, which encompass fluctuating speeds, changing accelerations, and import loads. Tu et al. [16] examined the impact of operational parameters on the dynamic characteristics of angular contact ball bearings during deceleration by developing a multi-rigid-body dynamics model. Yao et al. [17] delved into the multi-body contact dynamics of angular contact ball bearings under varying working conditions, focusing on the intricate dynamic characteristics of rolling bearings in rotating machinery systems. This study considered factors such as gap rubbing, lubrication drag effects, and multi-body dynamic contact relationships. Chen et al. [18] argued that the dynamic interactions involving collisions and friction among bearing components during acceleration and deceleration are complex. Consequently, experimental research was conducted to scrutinize the dynamic characteristics of the cage in an angular contact ball bearing during these processes. Jacobs et al. [19] designed a test platform to assess the condition of a bearing under dynamic loads, studying the impacts of complex varying loads on the dynamic characteristics of rolling bearings. Govardhan et al. [20] established a quasi-dynamic model that incorporates harmonic and periodic impact loads to analyze the load characteristics of internal components in a bearing subjected to dynamic loads. Liu et al. [21] developed a dynamic model for rolling bearings with a flexible cage divided into spring-connected segments, integrating nonlinear contact forces and friction. Comparative analyses with rigid-cage models explored skidding dynamics under acceleration, radial loads, and stiffness variations, emphasizing transient load-zone interactions. Tu et al. [22] established a coupled dynamics model of rolling bearings and examined variations in contact characteristics, including amplitude, frequency, and distribution of collision force, under conditions of uniform motion, acceleration, deceleration, and fluctuations in rotational speed.

Most existing research concentrates on the dynamic characteristics of ball bearings under steady-state or variable conditions. The combined effects of acceleration, deceleration, and impact loads on the dynamic behavior of an angular contact ball bearing with a two-piece inner ring have not been thoroughly explored. The actual operating environment of aero-engines is complex, particularly during startup, shutdown, and maneuvering flights. Frequent speed changes and impact loads jointly result in alterations to the dynamic characteristics of bearings, such as contact stress and load distribution. These changes cannot be accurately represented in bearing dynamics models that consider only steady-state conditions or single-variable operating conditions. Furthermore, although the acceleration and deceleration phases constitute a relatively small portion of the actual operating time, failures of aero-engine main shaft bearings frequently occur during these phases. Given the high reliability requirements of aero-engines, failures at any stage can potentially lead to severe consequences. Therefore, studying the dynamic characteristics of bearings during the acceleration and deceleration phases is significantly important for enhancing the reliability and lifespan of spindle bearings.

This study aims to investigate the dynamic characteristics of bearings under impact loads during phases of acceleration, uniform speed, and deceleration (referred to as unsteady-state conditions). By taking a specific type of aero-engine angular contact ball bearing with a two-piece inner ring as a case study, flexible processing of the cage is conducted to establish a rigid–flexible coupling dynamic model of the bearings. The research examines the influence of unsteady-state conditions, varying loads, bearing speeds, and groove curvature radius coefficients on the dynamic characteristics of the bearing. It reveals the phased differences in bearing dynamic behavior under unsteady-state conditions, thereby offering a theoretical basis for bearing design and optimization.

2. Rigid–Flexible Coupling Dynamics Model

A schematic diagram of the structure of an angular contact ball bearing with a two-piece inner ring is presented in Figure 1, comprising a complete outer ring, a two-piece inner ring, a ball, and a cage that is guided by the outer ring. The design of the bearing’s outer ring closely resembles that of a deep groove ball bearing, featuring a complete circular raceway in the outer ring, while the inner raceway is constructed with left and right half-groove structures. This configuration can be conceptualized as a complete inner ring of a deep groove ball bearing with a thickness h space removed. In the unloaded and clearance-free natural state of the bearing, the ball has one contact point with the outer ring, one contact point with the left half of the inner ring, and one contact point with the right half of the inner ring. The angle α_D represents the shim angle at the two contact points between the ball and the inner ring.

The internal action model of an angular contact ball bearing with a two-piece inner ring is highly complex. This model is established under the following assumptions:

(1)

In the model, the geometric deformation of each rigid component only occurs at the local contact positions, and the contact deformation conforms to the Hertz contact theory.

(2)

The geometric centers of all bearing components coincide with their centers of mass, without considering the influence of machining errors.

2.1. Bearing Analysis Coordinate System

In order to establish a bearing analysis model, it is essential to analyze the motion and forces acting on the bearing in different coordinate systems. Figure 2 illustrates a schematic diagram of the coordinate system for an angular contact ball bearing with a two-piece inner ring.

The coordinate system established in this study is as follows:

(1)

The global coordinate system is defined as $S=\left\{O;X,Y,Z\right\}$, where $O$ positioned at the geometric center of a bearing. The X-axis coincides with the bearing’s axial center line, and the Y-axis and Z-axis lie within the radial plane, oriented horizontally and vertically, respectively. It is important to note that this coordinate system remains fixed and does not move with the bearing.

(2)

The coordinate systems of the ball centroid and the cage pocket hole are, respectively, $S_{bj}=\left\{O_{bj};x_{bj},y_{bj},z_{bj}\right\}$ and $S_{pj}=\left\{O_{pj};x_{pj},y_{pj},z_{pj}\right\}$. $O_{bj}$ and $O_{pj}$, respectively, coincide with the ball’s centroid and the center of the pocket hole where the ball resides. The $x_{bj}$ axis aligns with the global coordinate system’s X-axis. The $y_{bj}$ axis points in the radial direction. The $z_{bj}$ axis indicates the direction of the ball’s circumferential movement. The ball coordinate system moves with the position of the ball centroid. The $x_{pj}$ axis runs parallel to $x_{bj}$ axes of ball coordinate system, $y_{pj}$ and $z_{pj}$ axes are in the radial plane of the bearing and are in the radial and tangent directions. The cage pocket hole coordinate system undergoes both movement and rotation in synchrony with the cage.

(3)

The centroid coordinate systems for the inner ring and cage are denoted as $S_i=\left\{O_i;x_i,y_i,z_i\right\}$ and $S_c=\left\{O_c;x_c,y_c,z_c\right\}$, respectively. Here, $O_i$ and $O_c$ denote the centroid’s centers of the inner ring and the cage, respectively. The $x_i$, $y_i$, and $z_i$ axes are aligned with the X, Y, and Z axes, as are the $x_c$, $y_c$, and $z_c$ axes. It is important to note that the cage centroid coordinate system is dynamic, moving alongside the cage’s centroid.

(4)

The contact surface coordinate system is $S_H=\left\{O_H;\xi ,\eta \right\}$. The observed contact surface’s center serves as the origin for this coordinate system. The $\xi$ axis is the semiminor axis of the contact ellipse, and its direction points to the rolling direction of the contacting object. The $\eta$ axis is the semimajor axis of the contact ellipse and is perpendicular to the rolling direction.

2.2. Interaction Force Between Ball and Raceways

2.2.1. Normal Contact Force

When an angular contact ball bearing with a two-piece inner ring operates, the axial force causes the inner ring to undergo axial displacement, which typically does not result in a three-point contact situation. The left figure presents a schematic diagram of the contact axial plane in the axial plane of bearing under load. The right figure provides a detailed illustration of the locations of the center of curvature for both the inner and outer raceways, in addition to the ball center, before and after loading. Figure 3 depicts the geometric relationships of the contact angle, deformation, and displacement of the ball and the raceway following their mutual interaction.

As illustrated in Figure 3, after the bearing is loaded, the relative distance between raceway groove curvature centers can be described as follows:

$$A_{xj}=B{D}_w\sin {\alpha }_0+{\delta }_a$$

(1)

$$A_{yj}=B{D}_w\cos {\alpha }_0+{\delta }_r\cos {\phi }_j$$

(2)

where $A_{xj}$ and $A_{yj}$ represent the distances in the x and y directions of the center of curvature of the inner and outer ring raceways, respectively. The diameter of the ball is denoted by $D_w$; ${\alpha }_0$ signifies the initial contact angle; ${\delta }_a$ and ${\delta }_r$ are the axial and radial displacements of the center of curvature of the inner ring raceway, respectively; and $B=f_i+f_e-1$, where $f_i$ and $f_e$ are the curvature radius coefficients of the inner and outer ring raceways, respectively.

The contact angles between the ball and the inner and outer raceways after loading are, respectively, as follows:

$${\alpha }_{ij}=\arctan \left(V_{xj}/V_{yj}\right)$$

(3)

$${\alpha }_{ej}=\arctan \left[\left(A_{xj}-V_{xj}\right)/\left(A_{yj}-V_{yj}\right)\right]$$

(4)

where $V_{xj}$ and $V_{yj}$ are the position parameters of the ball’s center of mass relative to the center of curvature of raceways after loading, which are related to bearing deformation and speed.

The contact deformations ${\delta }_{ij}$ and ${\delta }_{ej}$ of the ball with the inner and outer raceways are, respectively, as follows:

$${\delta }_{ij}=\sqrt{V_{xj}^2+V_{yj}^2}-\left(f_i-0.5\right)D_w$$

(5)

$${\delta }_{ej}=\sqrt{{\left(A_{xj}-V_{xj}\right)}^2+{\left(A_{yj}-V_{yj}\right)}^2}-\left(f_e-0.5\right)D_w$$

(6)

The relationship between the contact load and elastic deformation of the inner and outer rings based on Hertz contact theory can be calculated as follows [23]:

$$Q_{ij}=K_{ij}{\left({\delta }_{ij}\right)}^{3/2}$$

(7)

$$Q_{ej}=K_{ej}{\left({\delta }_{ej}\right)}^{3/2}$$

(8)

where $Q_{ij}$ and $Q_{ej}$ represent the contact loads between the ball and the inner and outer raceways, respectively; and $K_{ij}$ and $K_{ej}$ are the load–deformation constants of the ball with the inner and outer rings.

2.2.2. Oil Film Traction Force

In the elastohydrodynamic lubrication state, the friction force between the contact surface of the ball and the raceway is the traction force of the lubricating oil. The dragging force ${\stackrel{⃑}{T}}_{e\left(i\right)j}$ on the contact surface is two-dimensional; its components $T_{\xi e\left(i\right)j}$ and $T_{\eta e\left(i\right)j}$ are divided into n slices along the long axis direction of the contact area. The unit dragging forces $T_{m\xi e\left(i\right)j}$ and $T_{m\eta e\left(i\right)j}$ (where m = 1, 2, …, n) of the slices are as follows [10]:

$${\stackrel{⃑}{T}}_{e\left(i\right)j}=T_{\xi e\left(i\right)j}\stackrel{⃑}{i}+T_{\eta e\left(i\right)j}\stackrel{⃑}{k}$$

(9)

$$T_{\xi e\left(i\right)j}=\sum _{m=1}^n{T}_{m\xi e\left(i\right)j}$$

(10)

$$T_{\eta e\left(i\right)j}=\sum _{m=1}^n{T}_{m\eta e\left(i\right)j}$$

(11)

Under full oil film conditions, the traction force $T_{m\xi e\left(i\right)j}$ or $T_{m\eta e\left(i\right)j}$ on each unit is the elastohydrodynamic oil film traction force:

$$T_{m\xi \left(\eta \right)e\left(i\right)j}={\left({\mu }_{EHDm}{Q}_m\right)}_{\xi \left(\eta \right)e\left(i\right)j}$$

(12)

where $Q_m$ represents the normal contact load on a slice and ${\mu }_{EHDm}$ denotes the elastohydrodynamic oil film traction coefficient.

In this study, the lubricating oil used is 4106 aviation lubricating oil specified by the project. The primary reason for using 4106 lubricating oil is that it complies with the U.S. military standard MIL-L-23699C specification [24] and is widely used in aero-engines. It possesses excellent high and low-temperature performance, oxidation resistance, and lubricity, meeting the lubrication requirements of aero-engine main shaft bearings under high temperatures and long-term operation. The relevant parameter information of the lubricating oil is shown in the first table in Section 4. The calculation formula for its elastohydrodynamic lubrication oil film traction coefficient, ${\mu }_{EHDm}$, is presented as follows [25]:

$${\mu }_{EHDm}=\left(a+b\times s\right)\times e^{-c\times s}+d$$

(13)

$$a=2.7968\times {10}^{-15}{\overline{Q}}^{0.5796}{\overline{U}}^{-0.5551}{\overline{T}}_o^{-0.5498}$$

(14)

$$b=1.6581\times {10}^{-28}{\overline{Q}}^{0.5687}{\overline{U}}^{-0.3537}{\overline{T}}_o^{-1.3936}$$

(15)

$$c=3.8718\times {10}^{-18}{\overline{Q}}^{0.2928}{\overline{U}}^{-0.5124}{\overline{T}}_o^{-0.8009}$$

(16)

$$d=2.2910\times {10}^{-20}{\overline{Q}}^{0.7423}{\overline{U}}^{-0.6713}{\overline{T}}_o^{-0.8022}$$

(17)

$$\overline{Q}={\displaystyle \frac{Q_{e\left(i\right)j}}{E^{*}{R^{*}}^2}},\overline{U}={\displaystyle \frac{{\eta }_o{U}^{*}}{E^{*}{R}^{*}}},{\overline{T}}_o={\displaystyle \frac{{\eta }_o{K}_o{T}_o}{{\left(E^{*}{R}^{*}\right)}^2}}$$

(18)

$$R^{*}={\displaystyle \frac{R_e{R}_i}{R_e+R_i}},{\displaystyle \frac{1}{E^{*}}}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1-{\upsilon }_b^2}{E_b}}+{\displaystyle \frac{1-{\upsilon }_{i\left(e\right)}^2}{E_{i\left(e\right)}}}\right)$$

(19)

$$s={\displaystyle \frac{\mathit{\Delta }U}{U_R}},\mathit{\Delta }U=U_{ij}-U_{ej},U_R={\displaystyle \frac{U_{ej}+U_{ij}}{2}}$$

(20)

where $K_o$ is the thermal conductivity coefficient of the lubricating oil; $R_i$ and $R_e$ are the curvature radius; $U_{ij}$ and $U_{ej}$ are the linear velocities of the ball and raceways at the contact point, respectively; and ${\eta }_o$ is the dynamic viscosity coefficient of the lubricating oil at atmospheric pressure and ambient temperature.

For an angular contact ball bearing with a two-piece inner ring, an external preload is typically applied during operation to prevent gyroscopic rotation of the ball. Consequently, no relative sliding occurs in the $\eta$ direction between the ball and the contact surface, leading to the conclusion that $T_{\eta e\left(i\right)j}=0$.

2.3. Interaction Force Between Ball and Cage Pocket

2.3.1. Normal Force

The normal acting force between the ball and the pocket hole is determined based on the position of the ball within the pocket hole. Figure 4 illustrates two scenarios: one where the center, $O_p$, of the pocket hole is ahead of the center $O_b$ of the ball and another where $O_p$ is behind $O_b$. In this study, when $O_p$ is ahead, $Z_{cj}$ is positive; conversely, when $O_p$ is behind, $Z_{cj}$ is negative. A positive $Z_{cj}$ thus indicates that the cage applies a force on the ball, causing it to move, while a negative $Z_{cj}$ signifies that the ball exerts a force on the cage, resulting in its movement.

The normal force $Q_{cj}$ between the ball and the cage pocket [26] is calculated as follows:

$$Q_{cj}=\left\{\begin{array}{c}{K}_c·Z_{cj} \left(Z_{cj}\le C_p\right)\\ K_c·C_p+K_n·{\left(Z_{cj}-C_p\right)}^{1.5} \left(Z_{cj}>C_p\right)\end{array}\right.$$

(21)

where $K_c$ is the linear approximation constant determined based on the test data for a ball bearing, with $K_c=11/C_p$; $C_p$ is the cage pocket clearance, with $C_p=0.5\left(D_p-D_w\right)$; $D_p$ is the cage pocket diameter; and $K_n$ is load–deformation constant at the contact point.

2.3.2. Hydrodynamic Friction Force

The fluid at the entrance of the contact surface enters the contact surface during pumping action, thus generating rolling friction resistance $P_{R\xi \left(\eta \right)j}$ and sliding friction resistance $P_{S\xi \left(\eta \right)j}$ on the surface of a moving ball. As illustrated in Figure 5, the center of the contact surface is assumed to be at the intersection of the cage pocket surface and the average diameter of the cage.

The rolling friction forces ($P_{R\xi j}$ and $P_{R\eta j}$) and sliding friction forces ($P_{S\xi j}$ and $P_{S\eta j}$) acting on the surface of the ball can be expressed as [27]:

$$P_{R\xi j}=0.5C_{O_{p}j}{\overline{P}}_{Rj}\cos {\theta }_{pj}$$

(22)

$$P_{R\eta j}=0.5C_{O_{p}j}{\overline{P}}_{Rj}\sqrt{R_{p\xi }/R_{p\eta }}\sin {\theta }_{pj}$$

(23)

$$P_{S\xi j}={\overline{P}}_{Sj}{\eta }_o{\mu }_{sp\xi j}\sqrt{R_{p\xi }{R}_{p\eta }}$$

(24)

$$P_{S\eta j}={\overline{P}}_{Sj}{\eta }_o{\mu }_{sp\eta j}\sqrt{R_{p\xi }{R}_{p\eta }}$$

(25)

In this formula,

$$C_{O_{p}j}={\eta }_o{\mu }_{p\xi j}\sqrt{R_{p\xi }{R}_{p\eta }\left[{\left(3+2k_p\right)}^{-2}+{\mu }_{p\eta j}^2{\left(3+2k_p^{-1}\right)}^{-2}{k}_p^{-1}/{\mu }_{p\xi j}^2\right]}$$

(26)

where ${\mu }_{p\xi j}$ denotes the dragging speed of the lubricating oil between the ball and the pocket surface in the $\xi$ direction. $R_{p\xi }$ indicates the effective radius of the curvature between the ball and the pocket surface in the $\xi$ direction, while $R_{p\eta }$ refers to the effective radius of the curvature between the ball and the pocket surface in the $\eta$ direction. Additionally, ${\mu }_{p\eta j}$ represents the dragging speed of the lubricating oil between the ball and the pocket surface in the $\eta$ direction. Furthermore, ${\mu }_{sp\xi j}$ and ${\mu }_{sp\eta j}$ denote the relative speeds of the lubricating oil between the ball and the pocket surface in the $\xi$ and $\eta$ directions, respectively.

2.4. Interaction Force Between Cage and Guiding Ring

The lubricant’s hydrodynamic effect creates an interaction between the cage and the guiding ring. Based on the geometric characteristics between the cage and the guide ring, the mathematical model of the interaction force between the cage and the guide ring can be established using the theory of short sliding bearings [28,29]. The forces acting on the cage include the radial forces $F_{cy}^{\prime }$ and $F_{cz}^{\prime }$ and the frictional torque $M_{cx}^{\prime }$, as illustrated in Figure 6.

In Figure 6, the point $O_c$ is positioned at the center of mass of the cage, and the $y_c$ axis passes through the point of minimum oil film thickness $h_0$ (calculate the minimum oil film thickness and the central oil film thickness in the contact area between the ball and the raceway based on the elliptical point contact oil film thickness calculation formula in reference [30]) and forms an angle ${\mathsf{\Psi }}_c$ with the Y-axis of the inertial coordinate system. When guided by the outer ring, ${\mathsf{\Psi }}_c={\mathsf{\Psi }}_c^{\prime }$. The hydrodynamic oil film’s frictional torque $M_{cx}^{\prime }$ acting on the cage’s surface is as follows [29]:

$$F_{cy}^{\prime }=-{\eta }_o{\mu }_o{L}^3{\epsilon }^2/\left[C_g^2{\left(1-{\epsilon }^2\right)}^2\right]$$

(27)

$$F_{cz}^{\prime }=\pi {\eta }_o{\mu }_o{L}^3\epsilon /\left[4C_g^2{\left(1-{\epsilon }^2\right)}^{3/2}\right]$$

(28)

$$M_{cx}^{\prime }=2\pi {\eta }_o{V}_1{R}_1^{3}L/\left(C_g\sqrt{1-{\epsilon }^2}\right)$$

(29)

where ${\mu }_o$ is the dragging speed of the lubricating oil, with ${\mu }_o=R_1\left({\omega }_{e\left(i\right)}+{\omega }_c\right)$, where $R_1$ denotes the radius of the surface where the cage centers; $L$ indicates the width of this surface; the relative eccentricity of the cage center is expressed as $\epsilon$, with $\epsilon =e/C_g$, where $e$ indicates the eccentricity of center of cage; and the relative sliding velocity between guiding surface and centering surface is given by $V_1$, with $V_1=R_1\left({\omega }_{e\left(i\right)}-{\omega }_c\right)$.

2.5. Rigid–Flexible Coupling Dynamics Differential Equations

This model considers the outer ring as fixed, while the inner ring rotates at a constant speed around its axis. The center of mass experiences displacement in the direction of radial force. The ball revolves with the cage while simultaneously rotating around its own axis.

2.5.1. Ball Dynamics Differential Equation

Figure 7 illustrates the force acting on the j-th ball. The calculation of all forces in the figure can be found in reference [31]. Based on Newton’s law and Euler’s equation, the dynamic differential equation governing the behavior of the ball was established.

$$\left\{\begin{array}{c}{m}_b{\ddot{x}}_{bj}=Q_{ij}\sin {\alpha }_{ij}-Q_{ej}\sin {\alpha }_{ej}+T_{\eta ij}\cos {\alpha }_{ij}-T_{\eta ej}\cos {\alpha }_{ej}-F_{R\eta ij}\cos {\alpha }_{ij}\\ +F_{R\eta ej}\cos {\alpha }_{ej}-F_{H\eta ej}\cos {\alpha }_{ej}+F_{H\eta ij}\cos {\alpha }_{ij}+P_{S\xi j}+P_{R\xi j}\\ m_b{\ddot{y}}_{bj}=Q_{ij}\cos {\alpha }_{ij}-Q_{ej}\cos {\alpha }_{ej}+T_{\eta ej}\sin {\alpha }_{ej}-T_{\eta ij}\sin {\alpha }_{ij}-F_{R\eta ej}\sin {\alpha }_{ej}\\ +F_{R\eta ij}\sin {\alpha }_{ij}-F_{H\eta ij}\sin {\alpha }_{ij}\cos {\alpha }_{ej}+F_{H\eta ej}\sin {\alpha }_{ej}+F_{\eta j}-P_{S\eta j}-P_{R\eta j}\\ m_b{\ddot{z}}_{bj}=T_{\xi ej}-T_{\xi ij}+F_{R\xi ij}-F_{R\xi ej}-F_{H\xi ij}+F_{H\xi ej}+Q_{cj}-F_{dj}-F_{\tau j}\\ I_b{\dot{\omega }}_{bjx}=\left(F_{R\xi ij}-T_{\xi ij}\right){\displaystyle \frac{D_w}{2}}\cos {\alpha }_{ij}+\left(F_{R\xi ej}-T_{\xi ej}\right){\displaystyle \frac{D_w}{2}}\cos {\alpha }_{ej}+\left(P_{S\eta j}+P_{R\eta j}\right)\\ {\displaystyle \frac{D_w}{2}}-J_x{\dot{\omega }}_{bjx}\\ I_b{\dot{\omega }}_{bjy}-I_b{\omega }_{bjz}{\dot{\theta }}_{bj}=\left(F_{R\xi ij}-T_{\xi ij}\right){\displaystyle \frac{D_w}{2}}\sin {\alpha }_{ij}+\left(F_{R\xi ej}-T_{\xi ej}\right){\displaystyle \frac{D_w}{2}}\sin {\alpha }_{ej}\\ +G_{yj}-\left(P_{S\xi j}+P_{R\xi j}\right){\displaystyle \frac{D_w}{2}}-J_y{\dot{\omega }}_{bjy}\\ I_b{\dot{\omega }}_{bjz}+I_b{\omega }_{bjy}{\dot{\theta }}_{bj}=\left(T_{\eta ij}-F_{R\eta ij}\right){\displaystyle \frac{D_w}{2}}+\left(T_{\eta ej}-F_{R\eta ej}\right){\displaystyle \frac{D_w}{2}}-G_{zj}-J_z{\dot{\omega }}_{bjz}\end{array}\right.$$

(30)

where $m_b$ denotes the ball’s mass; ${\ddot{x}}_{bj}$, ${\ddot{y}}_{bj}$, and ${\ddot{z}}_{bj}$ represent the acceleration components of the ball’s center of mass; $T_{\eta ij}$, $T_{\xi ij}$, $T_{\eta ej}$, and $T_{\xi ej}$ are the components of the traction force in the directions of the long and short semi-axes at the contact points between the ball and the inner and outer raceways, respectively; $F_{\eta j}$ and $F_{\tau j}$ are the components of the ball’s inertial force; $I_b$ signifies the ball’s moment of inertia; $J_x$, $J_y$, and $J_z$ are the components of the moment of inertia of the ball; ${\omega }_{bjx}$, ${\omega }_{bjy}$, ${\omega }_{bjz}$, ${\dot{\omega }}_{bjx}$, ${\dot{\omega }}_{bjy}$, and ${\dot{\omega }}_{bjz}$ are the components of the ball’s angular velocity and angular acceleration, respectively; ${\dot{\theta }}_{bj}$ is the orbital velocity of the ball; and $G_{yj}$ and $G_{zj}$ are the components of the inertial torque of the ball.

2.5.2. Inner Ring Dynamics Differential Equation

Based on Newton’s law and Euler’s equation, the dynamic differential equation governing the behavior of the inner ring was established.

$$\left\{\begin{array}{c}{m}_i{\ddot{x}}_i=F_x+{\displaystyle \sum _{j=1}^Z}\left(Q_{ij}\sin {\alpha }_{ij}-F_{R\eta ij}\cos {\alpha }_{ij}\right)\\ m_i{\ddot{y}}_i=F_y+{\displaystyle \sum _{j=1}^Z}\left[\left(Q_{ij}\cos {\alpha }_{ij}+F_{R\eta ij}\sin {\alpha }_{ij}\right)\cos {\phi }_j+\left(T_{\xi ij}-F_{R\xi ij}\right)\sin {\phi }_j\right]\\ m_i{\ddot{z}}_i=F_z-{\displaystyle \sum _{j=1}^Z}\left[\left(Q_{ij}\cos {\alpha }_{ij}+F_{R\eta ij}\sin {\alpha }_{ij}\right)\sin {\phi }_j+\left(T_{\xi ij}-F_{R\xi ij}\right)\cos {\phi }_j\right]\\ I_{iy}{\dot{\omega }}_{iy}-\left(I_{iz}-I_{ix}\right){\omega }_{iz}{\omega }_{ix}=M_y+{\displaystyle \sum _{j=1}^Z}\left[\begin{array}{c}{r}_j\left(Q_{ij}\sin {\alpha }_{ij}-F_{R\eta ij}\cos {\alpha }_{ij}\right)\sin {\phi }_j\\ +{\displaystyle \frac{D_w}{2}}{f}_i{T}_{\xi ij}\sin {\alpha }_{ij}\cos {\phi }_j\end{array}\right]\\ I_{iz}{\dot{\omega }}_{iz}-\left(I_{ix}-I_{iy}\right){\omega }_{ix}{\omega }_{iy}=M_z+{\displaystyle \sum _{j=1}^Z}\left[\begin{array}{c}{r}_j\left(Q_{ij}\sin {\alpha }_{ij}-F_{R\eta ij}\cos {\alpha }_{ij}\right)\cos {\phi }_j\\ -{\displaystyle \frac{D_w}{2}}{f}_i{T}_{\xi ij}\sin {\alpha }_{ij}\sin {\phi }_j\end{array}\right]\end{array}\right.$$

(31)

where $m_i$ denotes the mass of the inner ring; ${\ddot{x}}_i$, ${\ddot{y}}_i$, and ${\ddot{z}}_i$ are the displacement acceleration components for the inner ring; $F_x$, $F_y$, $F_z$, $M_y$, and $M_z$ are the support force and support torque components of a bearing on the rotor; $I_{ix}$, $I_{iy}$, and $I_{iz}$ refer to the main moment of inertia components for the inner ring; ${\omega }_{ix}$, ${\omega }_{iy}$, ${\omega }_{iz}$, ${\dot{\omega }}_{iy}$, and ${\dot{\omega }}_{iz}$ indicate the components of angular velocity and angular acceleration of the inner ring; $r_j=0.5d_m-0.5D_w{f}_i\cos {\alpha }_{ij}$; and ${\phi }_j$ is the positional angle of the ball.

2.5.3. Cage Rigid–Flexible Coupling Dynamics Differential Equation

The cage exhibits six complete degrees of freedom, resulting in a relatively complex motion. The primary forces acting on the cage are the pocket and guiding forces, as illustrated in Figure 4, Figure 5 and Figure 6. According to Newton’s laws of motion, the translational dynamic equation for the center of mass of the cage can be derived as follows:

$$m_c{\ddot{x}}_c=\sum _{j=1}^n\left(P_{S\eta j}+P_{R\eta j}+Q_{cxj}\right)$$

(32)

$$m_c{\ddot{y}}_c=\sum _{j=1}^n\left[\left(P_{S\xi j}+P_{R\xi j}\right)\cos {\phi }_j+Q_{cyj}\right]+F_{cy}$$

(33)

$$m_c{\ddot{z}}_c=\sum _{j=1}^n\left[\left(P_{S\xi j}+P_{R\xi j}\right)\sin {\phi }_j-Q_{czj}\right]+F_{cz}$$

(34)

where $m_c$ represents the mass of cage; ${\ddot{x}}_c$, ${\ddot{y}}_c$, and ${\ddot{z}}_c$ denote the acceleration components of the cage’s center of mass; and $Q_{cxj}$, $Q_{cyj}$, and $Q_{czj}$ are the component forces of the collision force between the ball and the cage in the X, Y, and Z directions.

The rotational dynamic equation of the cage can be described using the classical Euler dynamic equation:

$$I_{cx}{\dot{\omega }}_{cx}=\sum _{j=1}^n\left[\left(P_{S\xi j}+P_{R\xi j}\right){\displaystyle \frac{D_w}{2}}-Q_{cj}{\displaystyle \frac{d_m}{2}}\right]+M_{cx}+\left(I_{cy}-I_{cz}\right){\omega }_{cy}{\omega }_{cz}$$

(35)

$$I_{cy}{\dot{\omega }}_{cy}=\sum _{j=1}^n\left[\left(P_{S\eta j}+P_{R\eta j}\right){\displaystyle \frac{d_m}{2}}\sin {\phi }_j\right]+\left(I_{cz}-I_{cx}\right){\omega }_{cz}{\omega }_{cx}$$

(36)

$$I_{cz}{\dot{\omega }}_{cz}=\sum _{j=1}^n\left[\left(P_{S\eta j}+P_{R\eta j}\right){\displaystyle \frac{d_m}{2}}\cos {\phi }_j\right]+\left(I_{cx}-I_{cy}\right){\omega }_{cx}{\omega }_{cy}$$

(37)

where $I_{cx}$, $I_{cy}$, and $I_{cz}$ represent the moments of inertia of the cage; ${\omega }_{cx}$, ${\omega }_{cy}$, and ${\omega }_{cz}$ represent the angular velocities of the cage; ${\dot{\omega }}_{cx}$, ${\dot{\omega }}_{cy}$, and ${\dot{\omega }}_{cz}$ represent the angular accelerations of the cage; and $d_m$ represents the pitch diameter of the bearing.

In this study, the cage is treated as a flexible body. First, the cage is discretized, and a modal analysis is conducted. Subsequently, the dynamic differential equations of a flexible cage are derived using the modified Craig–Bampton modal synthesis method [32,33] and Lagrange’s equations, as follows:

$$M_{flex}\ddot{\zeta }+{\dot{M}}_{flex}\dot{\zeta }-{\displaystyle \frac{1}{2}}{\left[{\displaystyle \frac{\mathit{\partial }{M}_{flex}}{\mathit{\partial }\zeta }}\dot{\zeta }\right]}^T\dot{\zeta }+K_2\zeta +f_g+D\dot{\zeta }+{\left[{\displaystyle \frac{\mathit{\partial }C}{\mathit{\partial }\zeta }}\right]}^T\lambda =Q_{flex}$$

(38)

where $M_{flex}$ and ${\dot{M}}_{flex}$ represent the generalized mass matrix of the flexible cage and its time derivative, respectively:

$$M_{flex}=\left[\begin{array}{ccc}{M}_{tt}& M_{tr}& M_{tm}\\ M_{tr}^T& M_{rr}& M_{rm}\\ M_{tm}^T& M_{rm}^T& M_{mm}\end{array}\right]$$

(39)

where the subscripts t, r, and m denote the translational, rotational, and modal degrees of freedom of cage, respectively. $\zeta$, $\dot{\zeta }$, and $\ddot{\zeta }$ represent the generalized coordinates of flexible cage and their time derivatives:

$$\mathsf{\zeta }={\left[\begin{array}{ccc}X& \Psi & q\end{array}\right]}^T$$

(40)

where $X$ represents the displacement coordinates of the flexible cage retainer in the inertial coordinate system; $\Psi$ denotes the Euler angles that reflect its orientation; and $q$ stands for the modal coordinates. $K_2$ is the generalized stiffness matrix of a flexible cage, while $D$ is the damping matrix, defined as $D=\beta \sqrt{K_2{M}_{flex}}$, where $\beta$ is the damping constant. The term $f_g$ represents the gravitational force acting on a flexible cage. The constraint equation is given by $\mathrm{C}\left(\dot{\zeta },\zeta ,t\right)=0$, and $\lambda$ represents the Lagrange multiplier associated with this constraint. $Q_{flex}$ denotes the generalized force applied to the flexible cage, which comprises three components: generalized translational force, generalized torque (represented by Euler angles), and generalized modal force [27]:

$$Q_{flex}={\left[\begin{array}{ccc}{F}_T& T_R& F_M\end{array}\right]}^T$$

(41)

$$F_T=A\sqrt{F_y^2+F_z^2}$$

(42)

$$F_{\mathrm{y}}=\sum _{j=1}^n\left[\left(P_{S\eta j}-P_{R\eta j}\right)\cos {\phi }_j+Q_{cyj}\right]+F_{cy}$$

(43)

$$F_{\mathrm{z}}=\sum _{j=1}^n\left[\left(P_{S\eta j}-P_{R\eta j}\right)\sin {\phi }_j-Q_{czj}\right]+F_{cz}$$

(44)

$$T_R=B\left\{\sum _{j=1}^n\left[\left(P_{S\eta j}-P_{R\eta j}\right){\displaystyle \frac{D_w}{2}}-Q_{cj}{\displaystyle \frac{d_m}{2}}\right]+M_{cx}\right\}$$

(45)

$$F_M={\Phi }^T{F}_T+{\Phi }^{*T}A{M}_{cx}$$

(46)

where A and B represent the Euler transformation matrices of the bearing coordinate system, where the force and torque act relative to the global coordinate system. The symbols $\Phi$ and ${\Phi }^{*}$ denote the modal covariance matrices that apply to the translational and rotational degrees of freedom of the node.

3. Simulation Model and Test Verification

3.1. Rigid–Flexible Coupling Dynamics Simulation Model

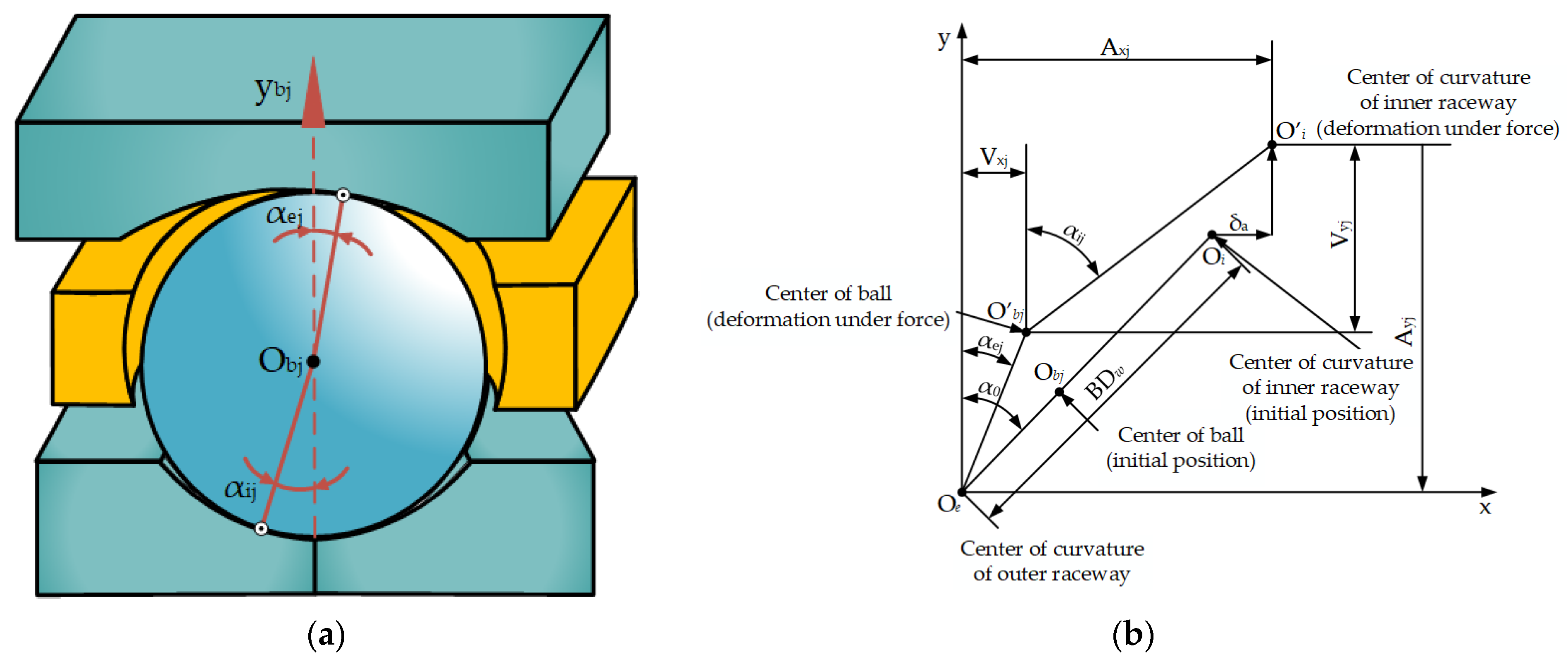
This study focuses on angular contact ball bearings with two-piece inner rings, which are utilized in aero-engine main shafts. The geometric parameters of a bearing are presented in

Table 1. Bearing geometric parameters.

Parameters	Value
Outside diameter	199 mm
Bore diameter	135 mm
Width	29.5 mm
Pitch circle diameter	167 mm
Ball diameter	22 mm
Number of balls	20
Outer groove curvature radius coefficient fe	0.515
Inner groove curvature radius coefficient fi	0.52
Cage outside diameter	178.45 mm
Cage bore diameter	161.15 mm
Cage width	28.3 mm

. Based on the interaction force model between bearing components described in Section 2, a user subroutine was written in FORTRAN language to calculate the interaction forces between bearing components. The user subroutine was compiled and a dynamic link library (DLL) file was generated, which was then linked with the ADAMS solver module. Furthermore, secondary development of ADAMS was carried out using the CMD commands in the ADAMS system to develop a parameterized rigid–flexible coupling multi-body dynamics simulation analysis module for bearings in order to simulate and solve the rigid–flexible coupling dynamics model of the angular contact ball bearing with a two-piece inner ring. Different lubricant properties can be specified in the parameterized interface of the dynamics simulation analysis module as needed. Additionally, the dynamic simulation analysis module can be configured as needed to have the outer ring fixed with the inner ring rotating or the inner ring fixed with the outer ring rotating.

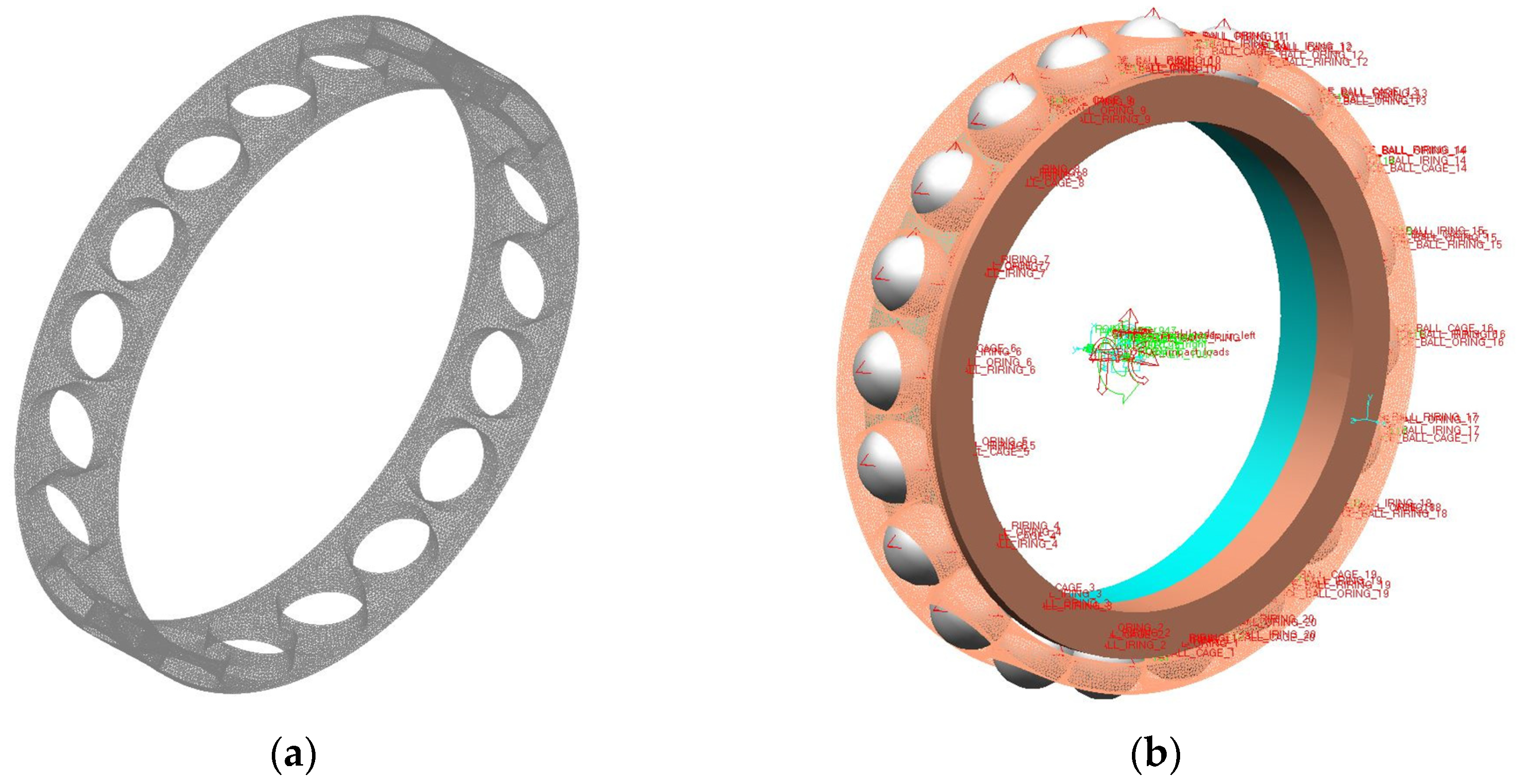
The construction and solution process of the rigid–flexible coupling dynamics model is illustrated in Figure 8. Based on considering the interaction relationships among bearing components, the bearing geometric parameters are input into the dynamic simulation analysis software ADAMS (2019 version). A rigid-body dynamic model is constructed through the developed parameterized rigid–flexible coupling dynamic simulation analysis module. The rigid cage is imported into the finite element analysis software ABAQUS (2024 version) for flexible treatment, and then the generated MNF file of the flexible cage is imported into the dynamic simulation analysis software ADAMS. The MNF, which stands for Modal Neutral File, acts as an interface file between finite element software ABAQUS and the multi-body dynamics software ADAMS and is utilized to export the modal information of the flexible cage—including its nodes, elements, mass matrix, stiffness matrix, and modal shapes—after the flexibility treatment. This process allows for the incorporation of the elastic deformation effects of the cage in multi-body dynamics simulations. In the parametric rigid–flexible coupling dynamics simulation analysis module, the flexible cage replaces the rigid cage in the rigid-body dynamics model, and the connection between the flexible cage and other components is established through dummy bodies. Constraint forces are established among bearing components to construct the rigid–flexible coupling dynamics model. Input simulation parameters such as operating condition parameters including load, impact load and acceleration and deceleration conditions, material parameters of bearing components, and lubricant parameters for simulation analysis. In the solving process, the FORTRAN user subroutine reads the system state values at the beginning of each time step in ADAMS by calling the function subroutine SYSARY, calculates the force terms of the dynamic differential equations, and then passes them to the ADAMS solver through the array RESULT, completing the integration solution of the dynamic differential equations for each time step. In Figure 9, the left figure depicts the flexible cage, while the right figure depicts the rigid–flexible coupled dynamic simulation model.

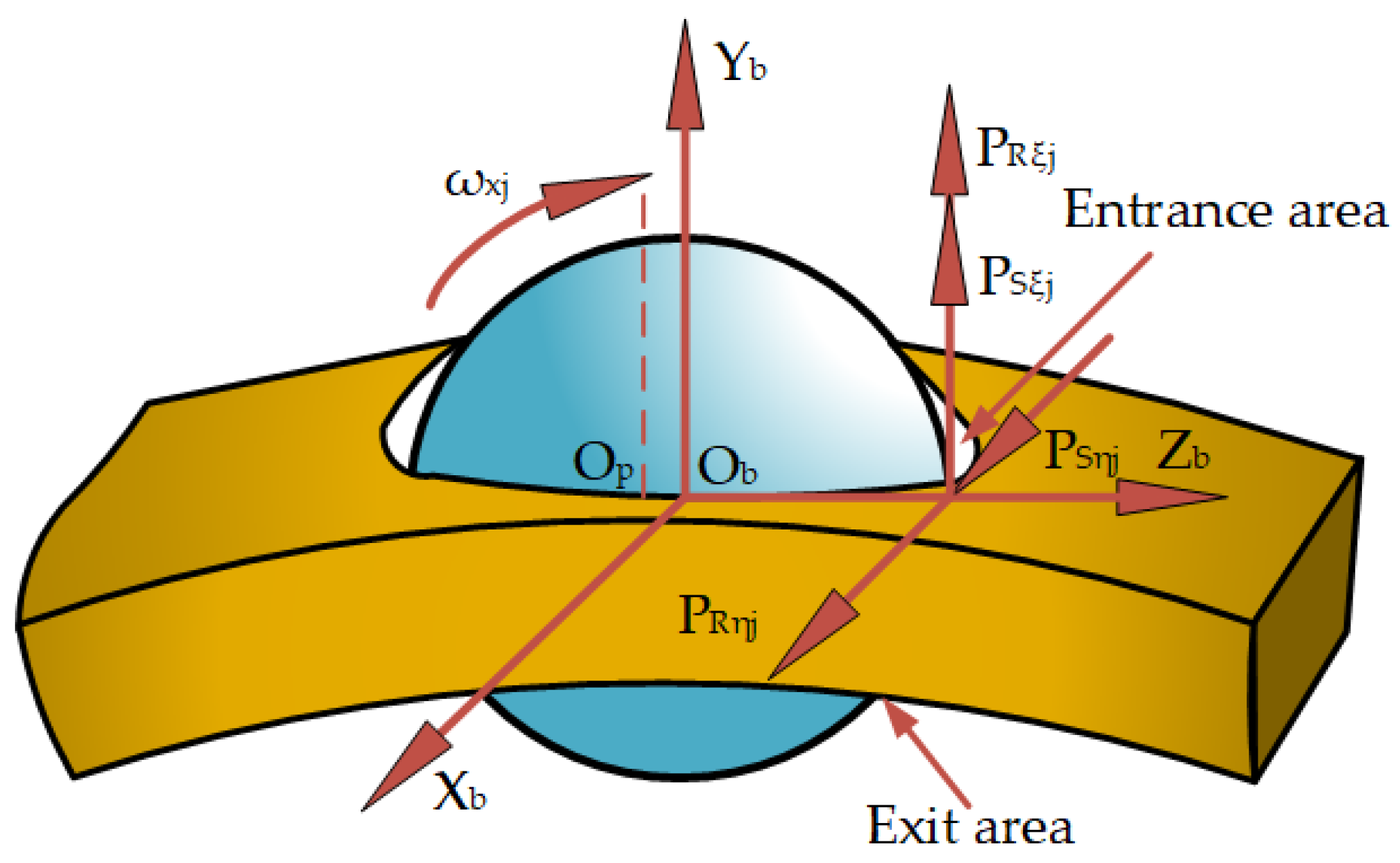
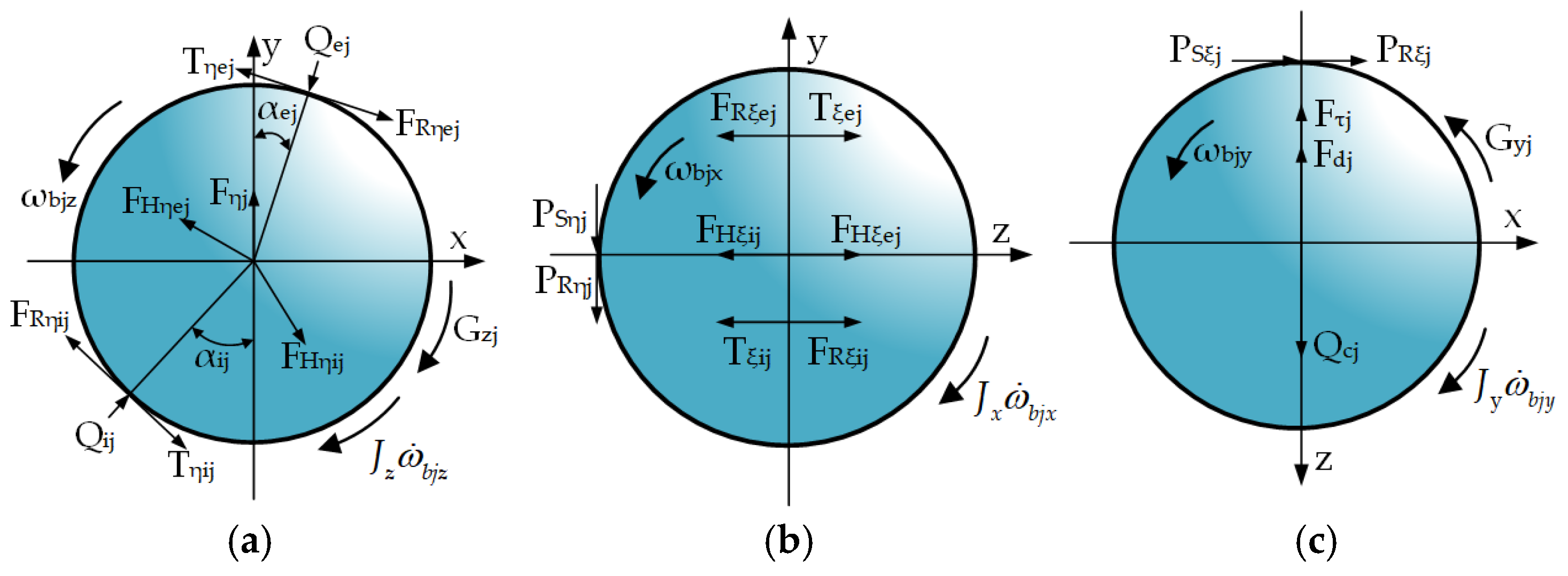
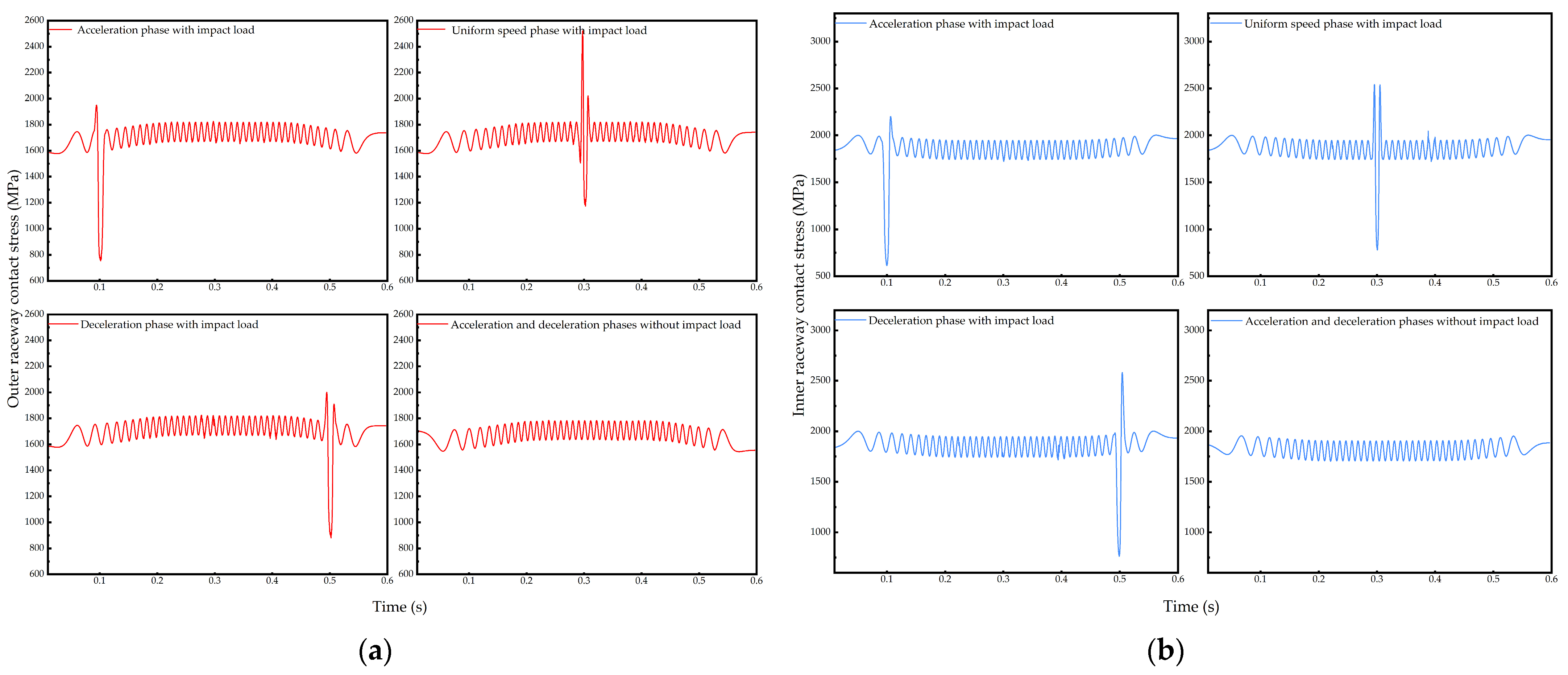
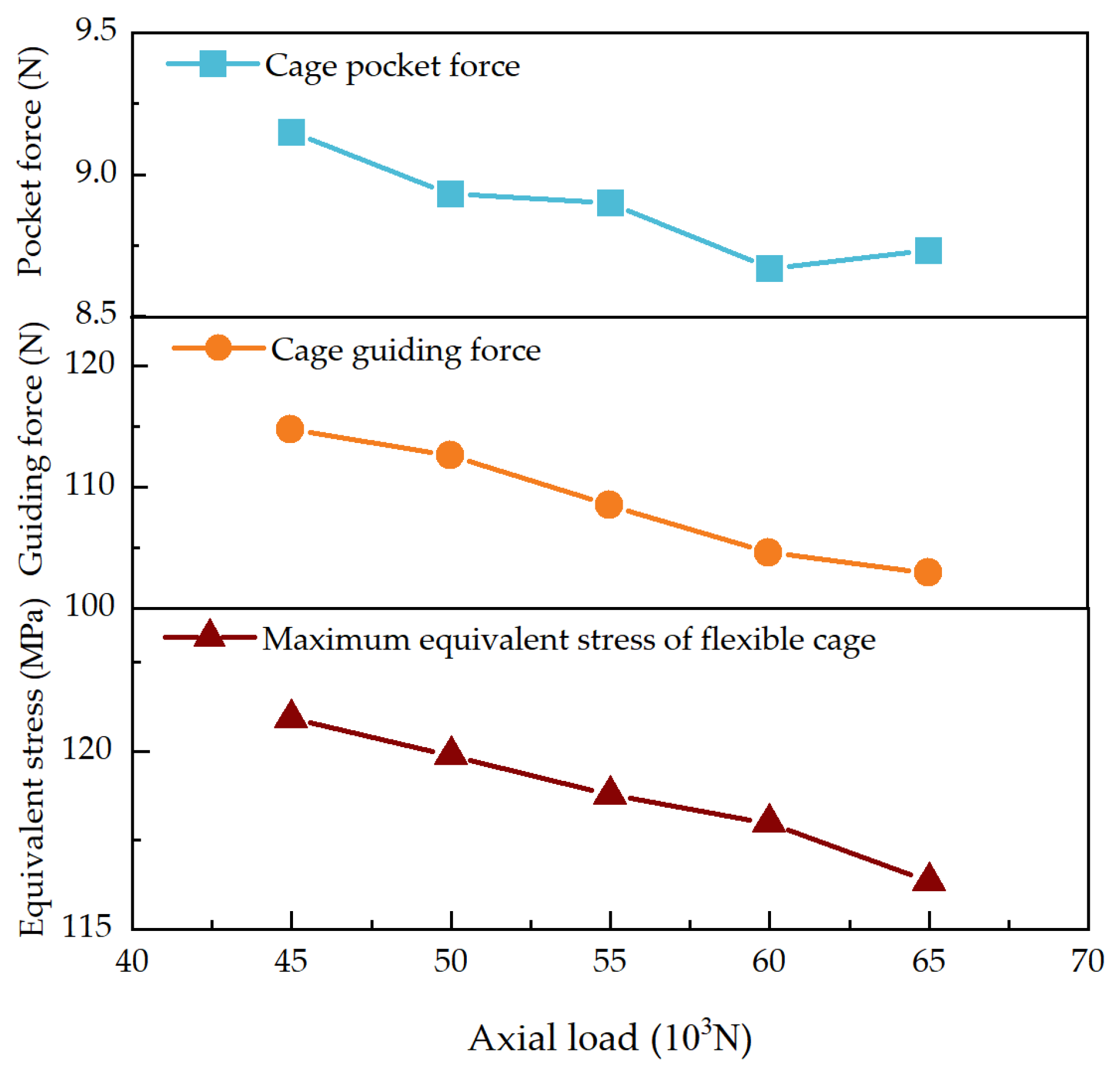
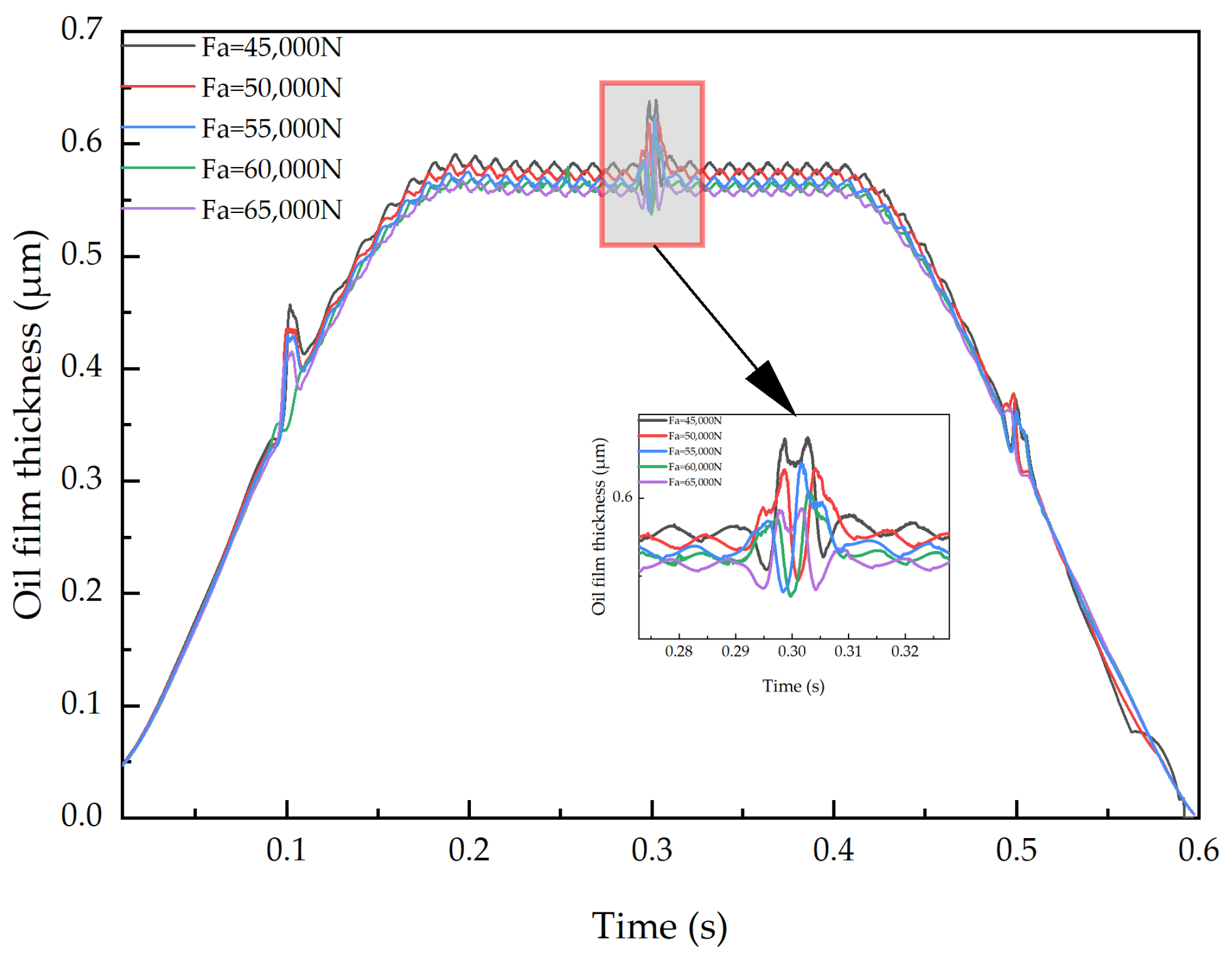
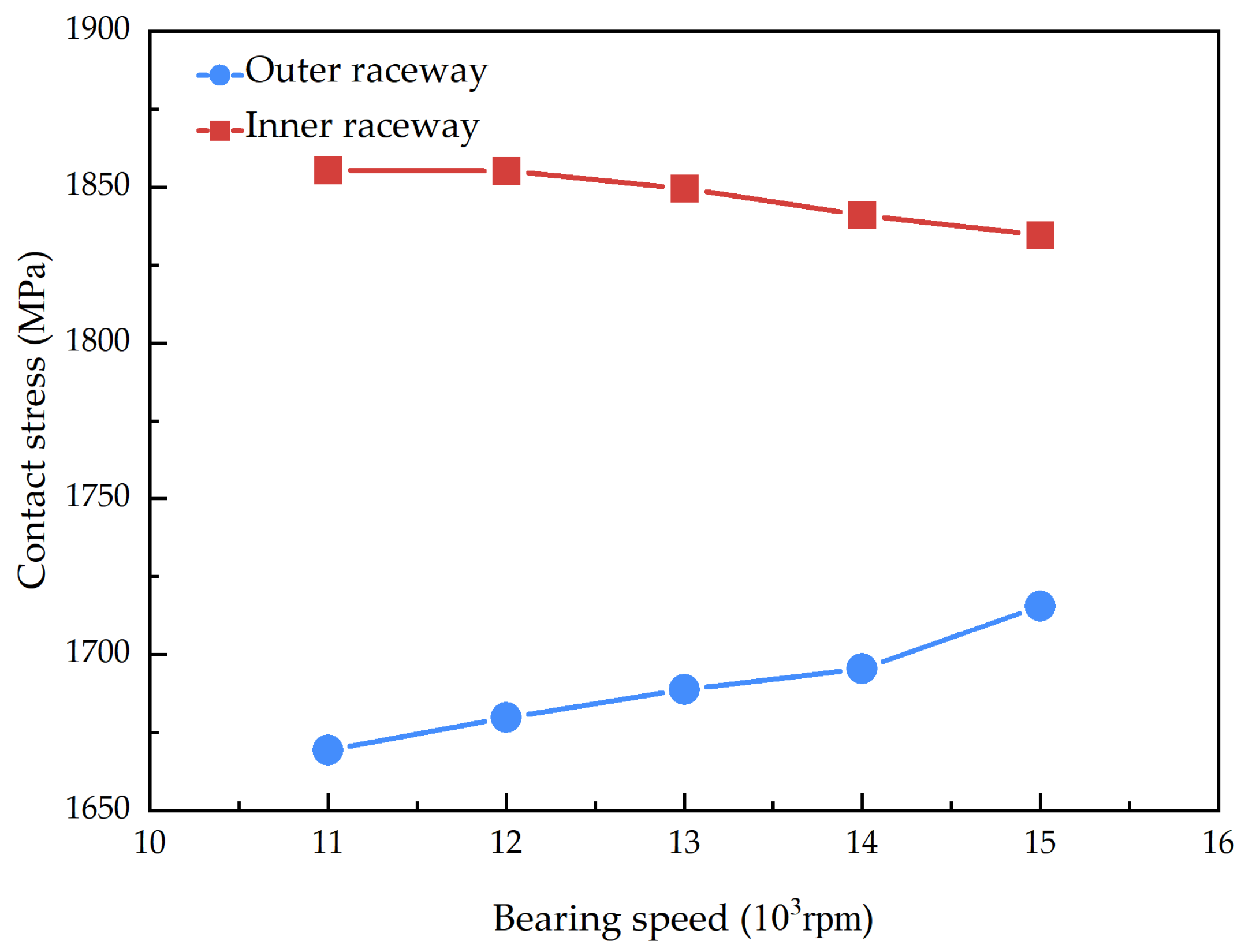
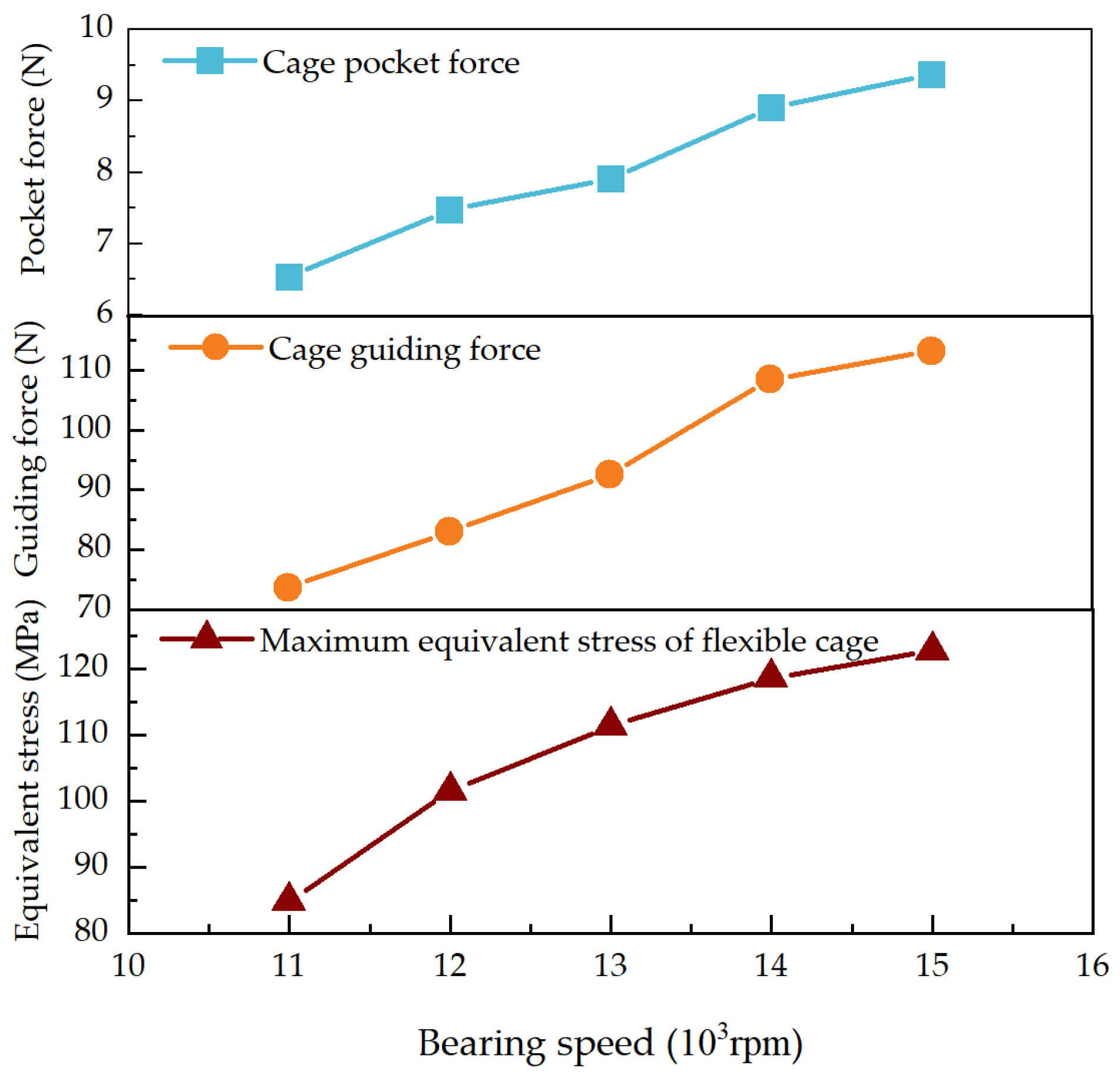
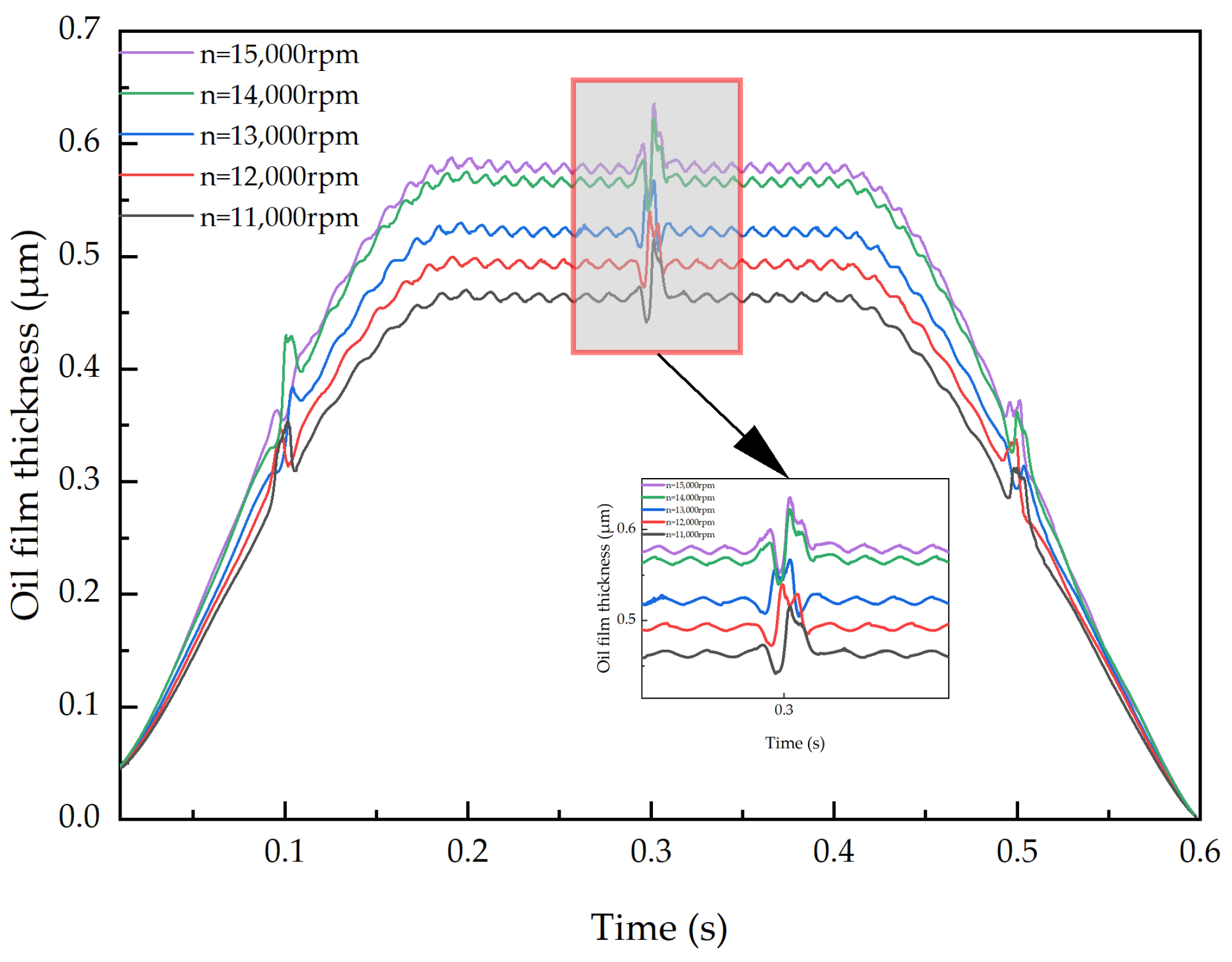
Utilizing the dynamic simulation analysis program, a simulation analysis of the dynamic model was conducted to obtain the interaction and motion states among the various components of a bearing. This includes parameters such as the contact stress between the balls and the inner and outer raceways, the collision force between the balls and the cage, the guiding force between the cage and the ring, the maximum equivalent stress of a flexible cage, and the cage slip rate. Additionally, the lubrication condition of the bearing can be assessed at any moment, including the thickness of the bearing oil film.

3.2. Test Verification

To verify the accuracy of the dynamic simulation model for bearing rigid–flexible coupling established, a cage slip rate test was executed on an angular contact ball bearing with a two-piece inner ring. The bearing test was performed using a dynamic performance test machine designed for an aero-engine main shaft bearing cage. The overall performance indicators of the test device are presented in

Table 2. Overall performance indicators of the test apparatus.

Performance Indicators	Scope and Values
Inner diameter size of the test bearing	60~200 mm
Spindle speed	0~15,000 rpm
Additional radial load	0~15,000 N
Additional axial load	0~20,000 N
Oil supply temperature	23~200 °C

. The main components of the test apparatus are illustrated in Figure 10, which primarily include an axial loading device, a radial loading device, an oil tank, an oil fuel pump, an oil return pump, an electric spindle, a water tank, a control cabinet, a data acquisition instrument, and a computer.

The test bearing was subjected to both radial and axial test loads via hydraulic loading, with the load magnitude controlled by a proportional pressure-reducing valve. The motor is coupled to the test spindle, ensuring accurate test loading while preventing any additional loads on the motor end. The test machine features both high-temperature and room-temperature lubrication systems. The high-temperature system supplies oil to the test bearing, with a maximum oil supply temperature of 200 °C, while the pressure is regulated by a pressure-reducing valve to meet the test requirements.

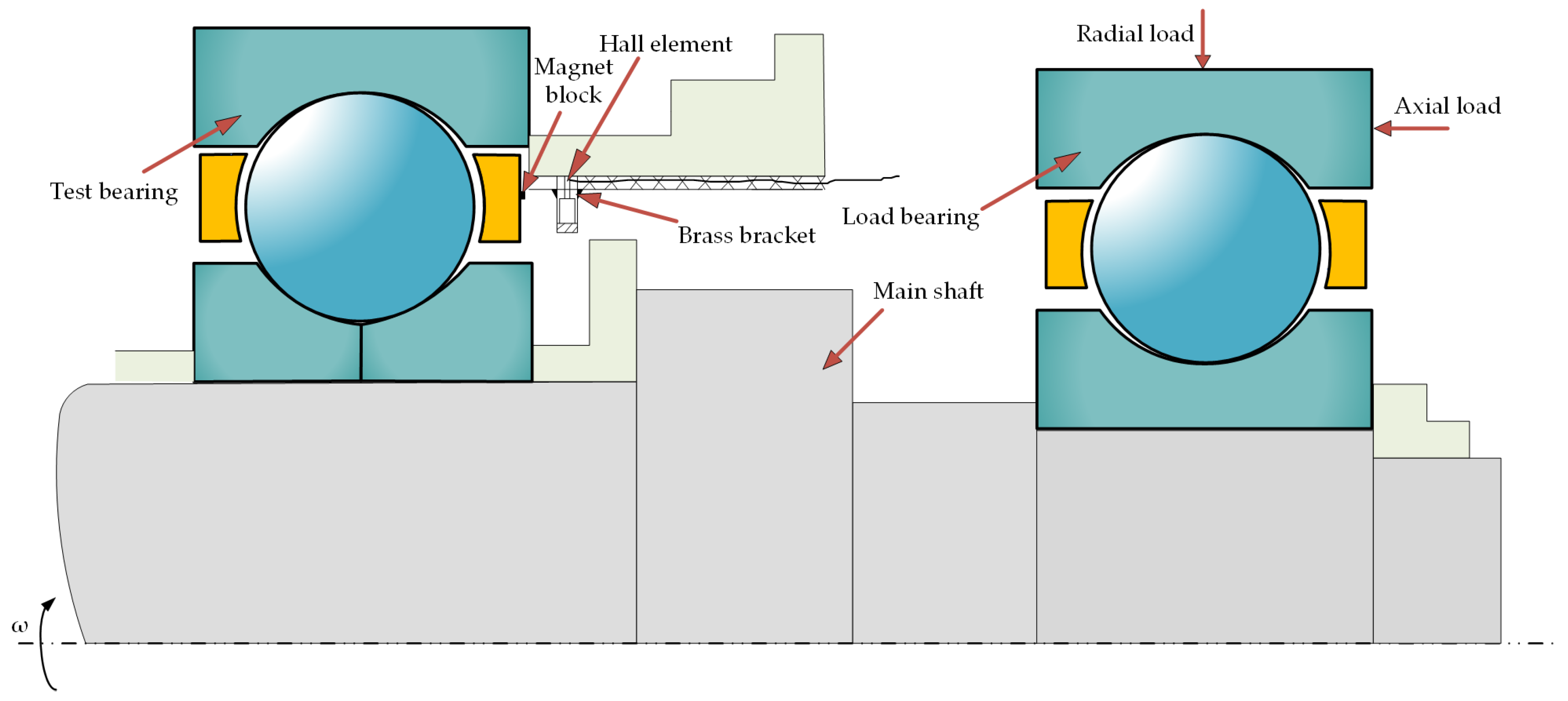
A diagram of the physical installation of the test bearing is illustrated in Figure 11. A cantilever structure was utilized, with the loading bearing positioned at the cantilever end of the spindle, while the test bearing was situated at the fulcrum of the spindle and the supporting bearing was placed at the left end of the spindle. Both the load bearing and the supporting bearing adopt deep groove ball bearings to ensure the system has sufficient precision and longevity.

The test apparatus mainly consists of the main body of the test apparatus, electrical control device, hydraulic loading device, lubrication device, computer monitoring and data acquisition system, etc.

The main body of the test apparatus is installed on a cast iron base. The electrical control device is mainly composed of a frequency converter and control circuit and is controlled through the electrical control cabinet, which is responsible for providing a power supply to the test apparatus and controlling the speed of the electric spindle to simulate the working conditions of the aero-engine main shaft bearing at different speeds. The hydraulic loading device includes an axial loading device and a radial loading device, mainly loaded by hydraulic pressure.

The lubrication device mainly consists of an oil tank, oil returning pump, and oil feed pump, primarily used for lubricating the test bearing. The oil supply and return pipes of the test bearing in the test apparatus are led out through the side wall on the same side of the base. The test bearing is lubricated via under-race lubrication and features a self-contained oil return chamber. The oil returning pump, driven by the oil return motor, pumps the lubricating oil back to the oil tank. The computer monitoring and data acquisition system primarily consists of a computer and data acquisition instrument, which are mainly used for setting, processing, and recording test parameters. Additionally, it can monitor the test process and automatically shut down in case of anomalies (such as excessive vibration or high temperature of the test apparatus) to ensure the safety of the test apparatus and the test bearing.

Figure 12 shows the schematic diagram of the test principle. The axial and radial loads are directly applied to the load bearing through the axial and radial loading devices in Figure 10, and then transmitted to the test bearing. When a radial load is applied to the outer ring of the load bearing, since the loading bearing is mounted at the cantilever end of the spindle and the test bearing is mounted at the fulcrum of the spindle, the radial load on the test bearing can be calculated through force balance analysis based on the mounting positions of the load bearing and the test bearing on the spindle. Both the load bearing and the supporting bearing at the two ends of the spindle are deep groove ball bearings, with the supporting bearing having a larger axial clearance and the outer ring of the load bearing not being fixed. When an axial load is applied to the outer ring of the load bearing, the load bearing transmits the axial load to the spindle, while the supporting bearing is not preloaded. Therefore, the axial load applied to the load bearing entirely acts on the test bearing. The test spindle is connected to the electric spindle in Figure 10 through a coupling. The rotation of the electric spindle drives the rotation of the test spindle and the test bearing. The cage is embedded with magnets, and the rotational speed of the cage during the test is measured by magneto-sensitive Hall elements.

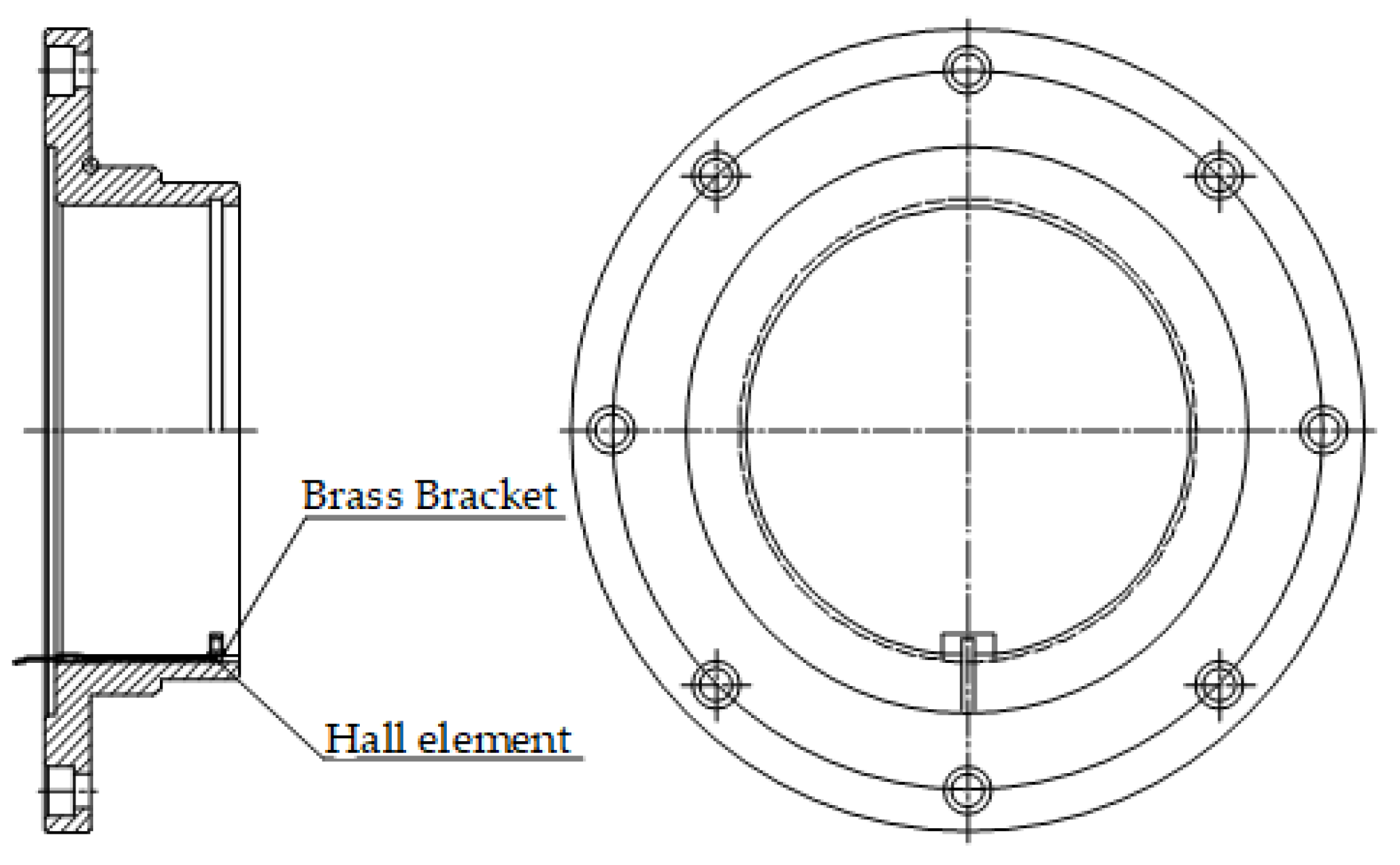
The installation position of the Hall element on the retainer is shown in Figure 13. The measuring element is located within the brass material bracket on the inner side of the compression end cover, and the collected information is output through three signal transmission lines arranged in adjacent grooves.

Figure 14 illustrates the mounting positions of the magnet blocks. Two magnet blocks were symmetrically positioned on the cage reference surface at intervals of 180°, and they were installed in opposite directions. The sensing device is the Hall element. The working principle is as follows: during testing, the magnet blocks rotate at high speeds with the cage, generating pulse signals as they pass by the sensor. The rotational speed is displayed by a digital instrument that receives pulse signals, and the received signals are connected to the industrial control computer via a serial port, automatically displaying and saving the rotational speed. During the usage process, the cage rotation speed determined by the aforementioned method can be compared and calibrated using a dedicated tachometer stroboscope. Measurement uncertainties include the improper adjustment of the Hall element’s measurement distance during installation and the potential demagnetization of the magnetic block in high-temperature environments, which may affect the accuracy of the measurement results. Under the temperature conditions of this test, the magnetic block can function normally, and the installation position of the Hall element is measured during installation to ensure that the measurement distance of the Hall element is met.

The cage slip rate is calculated using the following formula:

$$S={\displaystyle \frac{n_m-n_r}{n_m}}\times 100\%$$

(47)

where $n_r$ is the measured cage speed; $n_m$ is the theoretically calculated cage speed, with $n_m={\displaystyle \frac{1}{2}}{n}_i\left(1-{\displaystyle \frac{D_w\cos \alpha }{d_m}}\right)$, where $n_i$ is inner ring speed; $D_w$ is the ball diameter; $\alpha$ is the contact angle; and $d_m$ is the pitch diameter of the bearing.

The cage slip test was conducted based on the parameters of the test bearing, as shown in

Table 3. Test bearing parameters.

Parameters	Value
Outside diameter	199 mm
Bore diameter	135 mm
Width	29.5 mm
Cage outside diameter	178.45 mm
Cage bore diameter	161.15 mm
Cage width	28.3 mm

. The lubricating oil utilized in the test was 4106 aviation lubricating oil, and the relevant parameter information of the lubricant is shown in the first table in Section 4. The working condition parameters of the test group were then measured and are detailed in

Table 4. Test group working condition parameters.

Test Conditions	Group	Axial Load/N	Radial Load/N	Speed/rpm	Time/s
1	1	1100	200	4000	120
	2			5000	120
	3			6000	120
	4			8000	120
	5			10,000	120
	6			12,000	120
2	7	1500	500	4000	120
	8			5000	120
	9			6000	120
	10			8000	120
	11			10,000	120
3	12	2000	1000	4000	120
	13			5000	120
	14			6000	120
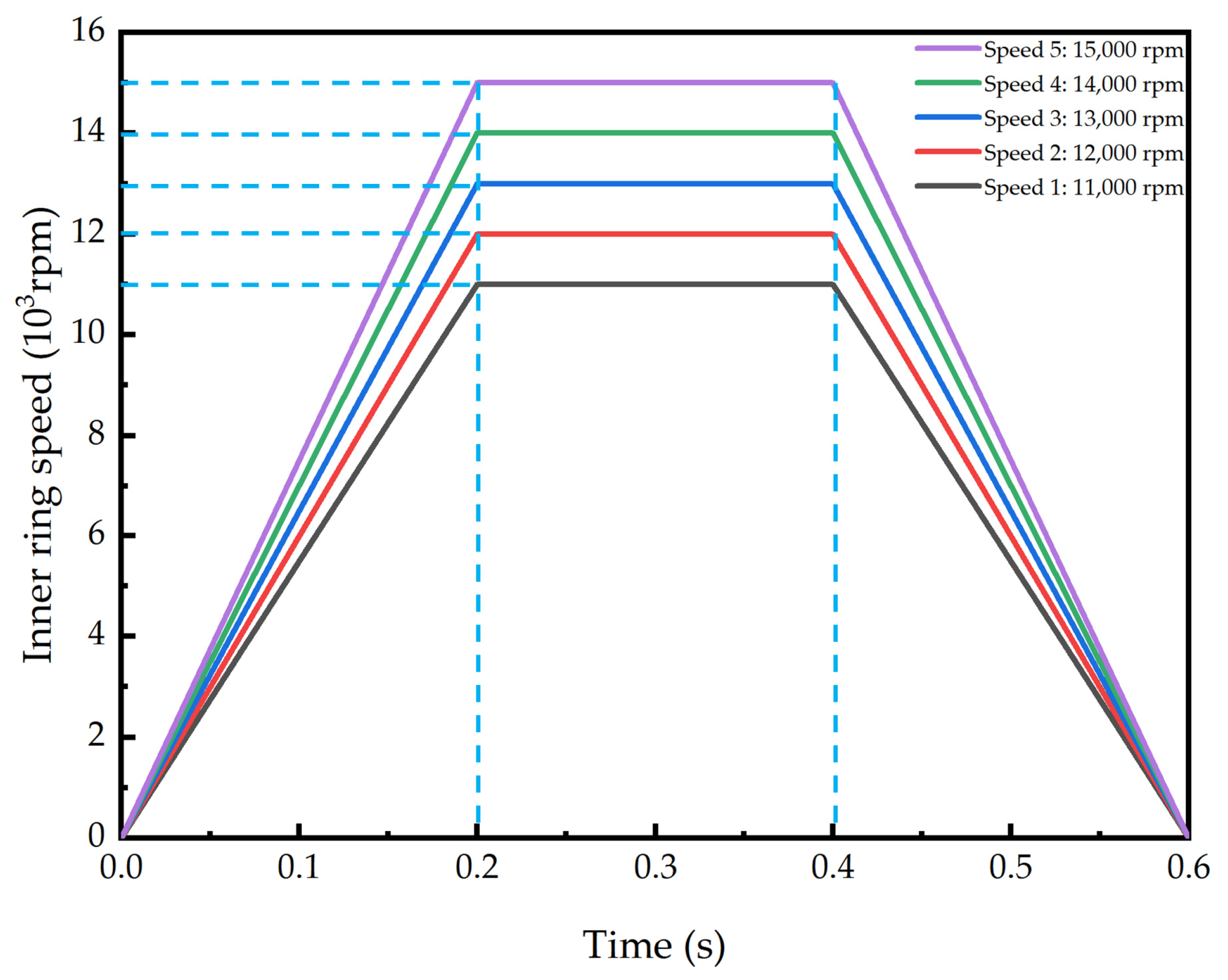
	15			8000	120

. The test time was set as follows: considering the limitations of the test apparatus and the safety of the test, after reaching the designated initial speed of 4000 rpm and maintaining stable operation for 120 s, the acceleration and deceleration test was initiated, the durations for both acceleration and deceleration were 10 s. Following this, subsequent acceleration and deceleration tests after ensuring stable operation for 110 s were commenced. The test is conducted in three cycles, and the average of the results from these three cycles is taken as the final result of the test. Considering the small degree of dispersion in the results of the three cycles, the final result of the test is deemed reliable.

Although consistency in each cycle test was meticulously maintained in this study, with the inlet oil temperature of the lubricant precisely controlled during the test process and the bearing accurately loaded via a precise hydraulic load device, there still exist certain uncertainties. Factors such as variations in the ambient temperature of the test environment, the initial phase of the bearing balls, and the distribution state of the internal lubricant within the bearing may have some influence on the test results.

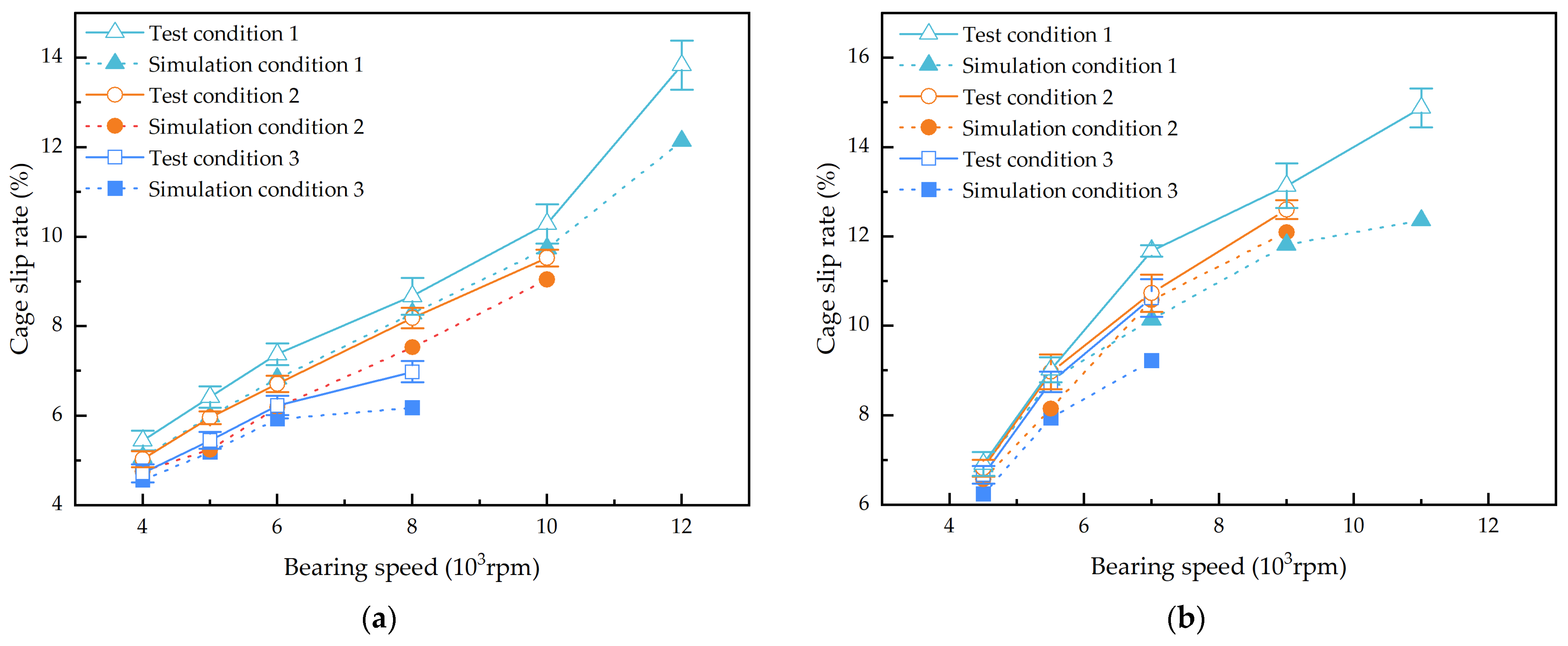
Figure 15 presents the comparison results of the cage slip rate between the test and the simulation. The trends of the simulation and test results are evidently consistent. The cage slip rate gradually increases with the bearing speed, and the overall numerical difference between the two is minimal, thereby verifying the accuracy of the established model. This model can be employed for subsequent analyses of the dynamic characteristics of the bearing. In Figure 15, the simulated slip rate is slightly lower than the experimental slip rate. The primary sources of error are attributed to two factors: first, the theoretical simulation model employs partial theoretical assumptions and empirical formulas, and cumulative errors are generated during the numerical integration process; second, the measurement of the cage speed is also influenced by factors such as the vibration of the test device, leading to a deviation between the slip rate and the theoretical calculation.

The test data and simulation results of the cage slip rate under three load conditions were further compared, and the error percentages for both steady-state and unsteady-state conditions were calculated separately, as presented in

Table 5. Error between test and simulation results of cage slip rate under steady-state conditions.

Test Conditions	Group	Speed/rpm	Test Slip Rate/%	Simulation Slip Rate/%	Slip Rate Error/%
1	1	4000	5.45	5.08	6.79
	2	5000	6.42	5.99	6.70
	3	6000	7.38	6.83	7.45
	4	8000	8.67	8.29	4.38
	5	10,000	10.29	9.74	5.35
	6	12,000	13.84	12.14	12.28
2	7	4000	5.03	4.76	5.37
	8	5000	5.96	5.25	11.91
	9	6000	6.71	6.19	7.75
	10	8000	8.18	7.53	7.95
	11	10,000	9.52	9.04	5.04
3	12	4000	4.72	4.57	3.18
	13	5000	5.45	5.19	4.77
	14	6000	6.23	5.93	4.82
	15	8000	6.98	6.18	11.46

and

Table 6. Error between test and simulation results of cage slip rate under unsteady-state conditions.

Test Conditions	Group	Speed/rpm	Test Slip Rate/%	Simulation Slip Rate/%	Slip Rate Error/%
1	1	4000–5000	6.91	6.86	0.72
	2	5000–6000	9.02	8.79	2.55
	3	6000–8000	11.68	10.14	13.18
	4	8000–10,000	13.14	11.82	10.05
	5	10,000–12,000	14.88	12.36	16.94
2	6	4000–5000	6.82	6.57	3.67
	7	5000–6000	8.97	8.14	9.25
	8	6000–8000	10.73	10.58	1.4
	9	8000–10,000	12.6	12.09	4.05
3	10	4000–5000	6.67	6.24	6.45
	11	5000–6000	8.74	7.94	9.155
	12	6000–8000	10.62	9.22	13.185

.

As shown in Table 5 and Table 6, the maximum error between the simulation results and the test results for the cage slip rate does not exceed 20%, indicating that the simulation results are consistent with the test results within a 20% error margin. Under the test operating conditions, this simulation analysis model can predict the cage slip rate measured in the tests.

4. Bearing Dynamic Characteristic Analysis Under Unsteady-State Conditions

This study establishes a rigid–flexible coupled dynamic simulation model for angular contact ball bearings with two-piece inner rings in an aero-engine main shaft, using angular contact ball bearings with two-piece inner rings as an example to analyze its dynamic characteristics. The geometric parameters of a bearing are presented in Table 1, while the operational, lubricating oil, and material parameters are detailed in

Table 7. Operational, lubricating oil, and material parameters.

Parameter Type		Parameter	Value
Operational parameters		Axial load	55,000 N
		Radial Load	4000 N
Lubricating oil parameters		Density (g/cm3) (20 °C)	0.8922
		Viscosity–temperature coefficient (°C−1)	0.031531
		Thermal conductivity coefficient (N/s·°C)	0.0965788
		Viscosity–pressure coefficient (10−8 Pa−1)	1.85
		Dynamic viscosity (Pa·s)	0.055
Material parameters	Ball and rings	Material	M50
		Density (kg/m3)	7810
		Modulus of Elasticity (GPa)	210
		Poisson’s Ratio	0.3
	Cage	Material	40CrNiMoA
		Density (kg/m3)	7870
		Modulus of Elasticity (GPa)	209
		Poisson’s Ratio	0.295

.

This study compares and analyzes the dynamic characteristics of a bearing under steady and unsteady-state conditions and explores the influence of unsteady-state conditions on these dynamic characteristics. It examines the effects of various loads, bearing speeds, and groove curvature radius coefficients on the dynamic characteristics of a bearing under unsteady-state conditions, thereby providing a reference for bearing design and optimization.

4.1. Modal Analysis of a Flexible Cage

To obtain information such as modal shapes, mass matrix, and stiffness matrix, a modal analysis is conducted on the flexible cage. Based on the results of this analysis, a rigid–flexible coupled dynamic simulation model of angular contact ball bearings with a two-piece inner ring was constructed. This model allows the elastic deformation of the flexible cage to be taken into consideration during a dynamic simulation analysis. Compared to the traditional rigid model that ignores cage deformation, even minor deformation of the flexible cage during actual bearing operation can affect the overall dynamic performance of the bearing. This study calculates the first 26 orders of free vibration frequencies and modes of the cage.

Table 8. Natural frequency of the cage.

Mode	Natural Frequency	Mode	Natural Frequency	Mode	Natural Frequency
7	484.77 Hz	14	2455.6 Hz	21	6160.6 Hz
8	484.77 Hz	15	2622.8 Hz	22	6160.6 Hz
9	813.59 Hz	16	2622.8 Hz	23	6552.9 Hz
10	813.59 Hz	17	4226.1 Hz	24	6552.9 Hz
11	1370.3 Hz	18	4226.1 Hz	25	6692.1 Hz
12	1370.3 Hz	19	4469.8 Hz	26	6692.0 Hz
13	2455.6 Hz	20	4469.8 Hz	27	7113.5 Hz

presents the natural frequencies corresponding to each order of vibration mode. From a numerical perspective, the minimum natural frequency of the cage is 484.77 Hz. Consequently, resonance is unlikely to occur in the low-frequency range.

Figure 16 presents the calculated typical vibration modes of the cage component. Calculation results indicate that cage vibrations exhibit characteristics typical of ring components. Specifically, the 7th, 11th, 15th, and 17th modal orders correspond to the bending vibrations of the cage in the ring plane, where the bending stiffness of the cage in this plane is relatively low. The 14th and 20th modal orders represent the bending–torsion coupling vibrations of the cage. The 24th and 25th modal orders primarily reflect the overall tilting of the cage’s end face and out-of-plane torsion. Finally, the 26th modal order is identified as a high-frequency irregular vibration mode, which arises from the influence of the cage pocket.

4.2. Effect of Unsteady-State Conditions on Bearing Dynamic Characteristics

During the operational phases of an aero-engine, acceleration and deceleration occur, leading to the bearing experiencing impact loads due to various maneuvering behaviors. Based on research into the typical maneuvering states of the engine, simplified impact load and speed spectra were evaluated and formulated. During each phase of acceleration, uniform speed, and deceleration, the impact load duration is 0.02 s with a magnitude of 50,000 N. Based on a simplified velocity spectrum, the acceleration and deceleration phases are set at 0.2 s. Simulation analysis of different durations for the uniform speed phase reveals that setting the duration to 0.2 s adequately reflects the dynamic characteristics of the bearing under impact loads. Additionally, choosing a constant speed time of 0.2 s leads the bearing to reach a stable state, and extending the duration of the uniform speed phase does not alter the bearing’s condition. Thus, the uniform speed phase duration is fixed at 0.2 s. The acceleration, deceleration conditions, and impact load conditions under unsteady-state conditions investigated in this study are illustrated in Figure 17 and Figure 18.

Unless otherwise specified, the bearing speed conditions employed in the simulation analysis of this study were all derived from the speed 4 in Figure 17. During the actual operation of aviation engines, acceleration and deceleration constitute relatively small proportions of the overall function. Therefore, this study focuses on the uniform speed phase to investigate the influence of varying loads, bearing speeds, and groove curvature radius coefficients on the bearing oil film thickness under the effect of impact load.

In order to comparatively analyze the impact of unsteady-state conditions on the dynamic characteristics of bearings, this paper also conducts simulation analysis on steady-state conditions. Considering the unsteady-state conditions of bearings under the combined action of acceleration, deceleration, and impact loads, the study investigates the differences in the dynamic characteristics of bearings under steady-state and unsteady-state conditions. Under steady-state conditions, the bearing operates at a uniform speed of 14,000 rpm, adhering to the working conditions outlined in Table 4, for a duration of 0.6 s without any impact load.

Figure 19 illustrates the variations in contact stress between the ball and both the outer and inner raceways over time under steady- and unsteady-state conditions. In the steady-state condition, the maximum contact stress for the outer raceway is 1839.9 MPa, with an average value of 1707 MPa. Conversely, the maximum contact stress for the inner raceway reaches 1933.8 MPa, with an average of 1805.2 MPa. Under the unsteady-state condition, the peak contact stress for the outer raceway rises to 2679.4 MPa, representing a 45.63% increase compared with under the steady-state condition, while its average value is 1717.6 MPa. The peak contact stress for the inner raceway increases to 2793.8 MPa, a 44.47% increase from the steady-state condition, with an average value of 1840.1 MPa. The contact stress in both the outer and inner raceways exhibits periodic changes resembling sinusoidal fluctuations under the steady-state condition due to the influence of radial load. In contrast, under the unsteady-state condition, when subjected to impact load, the amplitude of contact stress in both raceways increases instantaneously before returning to periodic changes similar to sinusoidal fluctuations. Notably, the contact stress in the inner raceway consistently exceeds that of the outer raceway in both the steady and unsteady-state working conditions.

The curves depicting the collision force between the ball and the cage (hereafter referred to as the cage pocket force) as a function of time under both steady-state and unsteady-state conditions are illustrated in Figure 20. Under steady-state conditions, the maximum value of the cage pocket force is 613.9 N, with an average value of 8.41 N. In contrast, under unsteady-state conditions, the peak value of the cage pocket force reaches 1052.7 N, reflecting a 71.47% increase compared with under the steady-state condition, while the average value is 8.72 N. During steady-state conditions, while the ball enters the load-bearing area, the relative velocity between the ball and cage changes, leading to a collision between them. Conversely, under unsteady-state conditions, the application of an impact load on the bearing induces an additional impact force on the ball, resulting in an increased collision force.

Figure 21 illustrates the time-dependent curves of the cage guiding force under both steady- and unsteady-state conditions. In the steady-state condition, the maximum cage guiding force is 719.1 N, while the average value is 140.3 N. In contrast, during the unsteady-state conditions, the peak cage guiding force reaches 987.1 N, representing a 37.28% increase compared with that in the steady-state conditions, and the average value is 152 N. Under steady-state conditions, the interaction between the ball and the cage, along with the influence of the centrifugal force acting on the cage, causes a change in the relative position of the cage within the bearing, leading to collisions between the cage and rib of the guiding ring. Conversely, under unsteady-state conditions, the impact load exerts a significant force on the ball, resulting in an increased collision force between the ball and the cage, a decrease in the running stability of the cage, and an increase in the guiding force between the cage and the ring.

By comparing and analyzing the contact stress between the ball and the outer and inner raceways, as well as the pocket and guiding forces of the cage under both steady and unsteady-state conditions, as illustrated in Figure 19, Figure 20 and Figure 21, the interaction among bearing elements was concluded to be enhanced under unsteady-state conditions compared with under steady-state conditions.

4.3. Influence of Impact Load on Acceleration and Deceleration Phases

This study compares and analyzes the variation in the dynamic characteristics of a bearing under three conditions in the absence of impact load: acceleration, uniform speed, and deceleration. Furthermore, it investigates the influence of impact load on the dynamic characteristics of a bearing during each phase.

Figure 22 illustrates the influence of impact load on the dynamic characteristics of a bearing during the acceleration, uniform speed, and deceleration phases. In the absence of impact load during these phases, the maximum contact stress between the ball and outer and inner raceways is 1853.5 MPa and 1957.2 MPa, respectively. Additionally, the maximum pocket force of the cage is 537.3 N, while the maximum guiding force of the cage is 754.7 N.

As illustrated in Figure 22, during the acceleration, uniform speed, and deceleration phases of a bearing, the presence of impact load causes the maximum values of the interactions between bearing elements to exceed those observed during the acceleration and deceleration phases without impact load. Notably, the maximum difference between the impact observed in the uniform speed phase and the maximum value recorded without impact during the acceleration and deceleration phases is the largest, whereas the maximum difference between the impact in the acceleration phase and the maximum value without impact during the acceleration and deceleration phases is the smallest. Overall, the uniform speed phase of a bearing exhibits the highest sensitivity to impact load, followed by the deceleration phase, while the acceleration phase demonstrates the least sensitivity.

4.4. Influence of Parameters Variations on Bearing Dynamic Characteristics

4.4.1. Axial Load

Under unsteady-state conditions, while keeping the other structural parameters of the bearing unchanged, considering that axial load borne by the aero-engine main shaft bearings is typically in the range of tens of thousands of newtons, based on the load spectrum of an aero-engine main shaft bearing, the axial load range is selected to be 45,000~65,000 N. This study investigates the influence of varying the axial load within the range of 45,000 to 65,000 N on the dynamic characteristics of a bearing, specifically when the radial load is set at 4000 N.

Figure 23 illustrates the influence of varying axial loads on the contact stress of both the outer and inner raceways. As depicted, as the axial load increases, the contact stress of outer and inner raceways exhibits an upward trend, with the amplitude of change in the contact stress of the inner raceway being greater than that of the outer raceway. This phenomenon occurs because, as the axial load increases, the contact load between the ball and the outer and inner raceways also rises, leading to an increase in the contact stresses of both raceways.

Figure 24 illustrates the effect of axial load variations on the pocket force, guiding force, and maximum equivalent stress of a flexible cage. It is evident from Figure 24 that as the axial load increases, the pocket force, guiding force, and maximum equivalent stress of the flexible cage all exhibit decreasing trends. This phenomenon occurs because the axial load restricts the axial offset of the ball. As the axial load increases, the axial offset of the ball diminishes, which further reduces the impact between the ball and the pocket. Consequently, the stability of the cage improves, leading to a reduction in both the pocket and guiding forces of the cage. Furthermore, as the axial load increases, the bearing load range expands, resulting in a more uniform load distribution. This allows the ball and the cage to maintain a relatively stable state, thereby causing a corresponding decrease in the maximum equivalent stress of the flexible cage.

Figure 25 illustrates the oil film thickness under varying axial loads. As depicted in Figure 25, the oil film thickness exhibits a decreasing trend with an increase in axial load. This phenomenon occurs because, as the axial load rises, the pressure in the contact area between the ball and the raceway increases significantly, resulting in rapid expulsion of the lubricating oil from the contact area and a subsequent reduction in oil film thickness. Furthermore, as the axial load increases, the fluctuation range of oil film thicknesses during the impact load in the uniform speed phase decreases from 0.1144 μm at an axial load of 45,000 N to 0.0614 μm at an axial load of 65,000 N, indicating that a larger axial load is effective in diminishing the influence of impact load.

4.4.2. Radial Load

Under unsteady-state conditions, with other structural parameters of a bearing remaining unchanged and an axial load of 55,000 N, based on the load spectrum of an aero-engine main shaft bearing, the radial load range was selected to be 4000~8000 N. This study investigated the effect of varying radial loads within the range of 4000 to 8000 N on the dynamic characteristics of a bearing.

Figure 26 illustrates the influence of varying radial loads on the contact stress of the outer and inner raceways. As shown in Figure 26, the contact stress of both raceways increases with the rise in radial load, with the inner raceway experiencing a more pronounced increase. This phenomenon occurs because, as the radial load increases, the contact load between the ball and both the outer and inner raceways also rises, thereby leading to an increase in the contact stress between these raceways.

Figure 27 illustrates the impact of radial load variations on the pocket force, guiding force, and maximum equivalent stress of a flexible cage. As depicted in Figure 27, an increase in radial load correlates with increases in the pocket force, guiding force, and maximum equivalent stress of the flexible cage. Moreover, the range of changes in the maximum equivalent stress of the flexible cage consistently expands with an increase in radial load. This phenomenon occurs because, as the radial load increases, the rotational speed of the ball decreases when it traverses the loading area. Consequently, the frequency of collisions between the ball and the pocket increases drastically, leading to an increase in the force exerted on the cage pocket. This reduction in the operational stability of the cage intensifies the collisions between the cage and the guiding ring, resulting in an increase in the guiding force of the cage, which subsequently contributes to a rise in the maximum equivalent stress of the flexible cage.

In addition, as can be seen from Figure 24 and Figure 27, when the axial or radial load increases while the other load (axial or radial) remains constant, the overall load on the bearing increases, but the trends in the cage equivalent stress, cage pocket force, and cage guiding force are opposite. This is because when the overall load increases, i.e., the radial load remains unchanged while the axial load increases, as the axial load increases, the load on all balls increases, the load distribution of the bearing tends to be uniform, and the balls and the cage are in a relatively stable state of motion, reducing the collision frequency between the balls and the cage pockets, thereby enhancing the stability of the cage, which results in a decrease in the cage pocket force, cage guiding force, and the maximum equivalent stress of the cage. However, when the overall load increases, i.e., the axial load remains unchanged while the radial load increases, as the radial load increases, the load on the balls within the range of the radial load direction increases, while the load on the balls in the opposite direction decreases, leading to an uneven load distribution on the bearing. When the balls move from the non-load-bearing zone to the load-bearing zone, the relative speed difference between the balls and the cage changes, causing more frequent collisions between the balls and the cage pockets, thereby reducing the operational stability of the cage, and consequently increasing the cage pocket force, guiding force, and the maximum equivalent stress. Therefore, although the overall bearing load increases, appropriately increasing the axial or radial load results in opposite trends for the cage pocket force, guiding force, and maximum equivalent stress.

Figure 28 illustrates the oil film thickness under varying radial loads. It is evident from the figure that as the radial load increases, the peak oil film thickness exhibits only slight variations. Specifically, the oil film thickness under a 4000 N radial load increases by 2.13% compared with that under an 8000 N radial load, suggesting that under the influence of impact load, the peak and average values of oil film thickness do not change significantly relative to the variation in radial load.

4.4.3. Bearing Speed

Under unsteady-state conditions, while keeping other structural parameters of the bearing constant, this study investigates the dynamic characteristics of a bearing with an axial load of 55,000 N and a radial load of 4000 N, as the speed varies within the range of 11,000 to 15,000 rpm based on the speed spectrum.

Figure 29 illustrates the influence of bearing speed on the contact stress of outer and inner raceways. As shown in Figure 29, with an increase in bearing speed, the contact stress of the inner raceway exhibits a decreasing trend, while that of the outer raceway shows an increasing trend. This phenomenon occurs because, as bearing speed increases, the centrifugal force acting on the ball also increases, causing the ball to shift toward the outer raceway. Consequently, this shift results in an increase in the contact stress of the outer raceway and a decrease in the contact stress of the inner raceway.

Figure 30 illustrates the influence of changes in bearing speed on the pocket force, guiding force, and maximum equivalent stress of a flexible cage. As shown in Figure 30, all forces increase with rising bearing speed. This phenomenon can be attributed to the following factors: As bearing speed increases, the centrifugal force acting on the ball also increases, causing it to deviate toward the outer raceway. This deviation results in a decrease in the drag force between the ball and the inner raceway. Consequently, the speed difference between the ball and the cage widens, leading to an increase in the cage pocket force. Additionally, as a result of centrifugal force, the space separating the cage from the outer guiding ring reduces, leading to more frequent collisions between the cage and the guiding ring. Consequently, the cage guiding force intensifies. Moreover, at elevated speeds, the cage encounters considerable centrifugal force, which helps to elevate the maximum equivalent stress experienced by the flexible cage.

Figure 31 illustrates the oil film thickness at various bearing speed. As shown, the oil film thickness increases with bearing speed. This increase occurs because changes in bearing speed affect the entrainment speed between the ball and rings. When the bearing speed rises, the relative motion between the ball and the raceway accelerates, resulting in an increased entrainment speed. Consequently, the lubricating oil is drawn into the contact area more rapidly, generating a stronger fluid dynamic pressure and significantly enhancing the oil film thickness.

4.4.4. Groove Curvature Radius Coefficient

The groove curvature radius coefficient is defined as the ratio of the groove curvature radius to the ball diameter. In this study, the ball diameter remained unchanged, while the groove curvature radius coefficient was altered by varying the groove curvature radius. Under unsteady-state conditions, while maintaining the other structural parameters of the bearing constant, an axial load of 55,000 N and a radial load of 4000 N were applied. Considering the working environment and high reliability requirements of aero-engine main shaft bearings, the inner groove curvature radius coefficient was selected within the range of 0.515 to 0.535, and the outer groove curvature radius coefficient was chosen to be between 0.51 and 0.53. By varying the groove curvature radius coefficient—where the outer groove curvature radius coefficient ranges from 0.51 to 0.53, and the inner groove curvature radius coefficient ranges from 0.515 to 0.535—this study investigates the impact of changes in the groove curvature radius coefficient on the dynamic characteristics of a bearing.

Figure 32 illustrates the impact of the groove curvature radius coefficient on raceway contact stress. It is evident from Figure 32 that raceway contact stress increases as the groove curvature radius coefficient rises. When the groove curvature radius coefficient varies, the contact stress of the corresponding raceway exhibits a significant range of variations. This phenomenon occurs because, as the groove curvature radius coefficient increases, the contact angle between the ball and both the outer and inner raceways decreases. Consequently, the contact load between the ball and these raceways increases, resulting in heightened contact stress in both the outer and inner raceways. Additionally, the contact area between the ball and the corresponding raceway diminishes with an increase in the groove curvature radius coefficient, further amplifying the variation range of the corresponding raceway contact stress.

Figure 33 illustrates the influence of changes in the groove curvature radius coefficient on the pocket force, guiding force, and maximum equivalent stress of a flexible cage. As shown in Figure 33, all forces increase with the rising groove curvature radius coefficient. As the groove curvature radius coefficient increases, the constraint that the raceway places on the ball diminishes, resulting in an increase in the displacement of the ball. This change alters the relative positions of the ball and the cage pocket, which in turn increases the force on the cage pocket. Consequently, the running stability of the cage declines, the guiding force of the cage increases, and the maximum equivalent stress of the flexible cage rises.

Figure 34 illustrates the oil film thickness as a function of different groove curvature radius coefficients. As depicted in the figure, the oil film thickness initially increases and then decreases with an increase in groove curvature radius coefficient. This trend occurs because the curvature of the groove determines the degree of fit between the ball and the raceway. As the groove curvature radius coefficient increases, the curvature of the groove decreases, leading to a reduction in the contact area and the degree of tightness between the ball and the raceway, which facilitates the formation of a continuous oil film. However, with a further increase in groove curvature radius coefficient, the oil film thickness experiences significant fluctuations due to impact load. If the groove curvature radius coefficient continues to increase, the center of the contact position between the ball and the groove gradually shifts toward the groove bottom, the contact angle between the ball and the raceway decreases, the load value on a single rolling element increases, and the oil film thickness decreases. Therefore, selecting an appropriate groove curvature radius coefficient based on the actual working conditions is essential.

5. Conclusions

This study focuses on aero-engine main shaft angular contact ball bearings with two-piece inner rings as the research subject. Considering the unsteady conditions during engine operation, speed and impact load spectra were developed to account for unsteady factors such as acceleration, deceleration, and impact load simultaneously. Through a force analysis, a lubrication assessment, and a cage flexibility analysis within the bearing, a rigid–flexible coupling dynamic model of bearings was established. The dynamic characteristics of a bearing under unsteady-state conditions were compared and analyzed. Additionally, this study emphasized the effects of varying loads, speeds, and groove curvature radius coefficients on the dynamic characteristics of bearings. The following conclusions were drawn:

(1)

This study examined the unsteady-state conditions of aero-engine main shaft bearings and the flexibility of cages. By considering the internal stress and lubrication conditions of the bearing and utilizing multi-body system dynamics along with the modified Craig–Bampton modal synthesis method, a rigid–flexible coupling dynamic model of angular contact ball bearing with a two-piece inner ring was established and validated through the cage slippage test.

(2)

The cage underwent a flexibility and modal analysis. The results indicate that its vibration modes primarily consist of in-plane bending, out-of-plane torsion, bending–torsion coupling, and irregular deformation. The minimum natural frequency of the cage was 484.77 Hz. Resonance typically does not occur in the low-frequency range. Therefore, this model utilizes the first 26 modal frequencies derived from the calculated modal natural frequencies.

(3)

Based on the formulated unsteady bearing speed and impact load spectrum, a simulation analysis was conducted. The results indicate that under unsteady-state conditions, the interactions among the bearing elements are significantly enhanced compared with those in steady-state conditions. Furthermore, the uniform speed phase of a bearing is highly sensitive to impact load, followed by the deceleration phase, while the acceleration stage exhibits less sensitivity to impact load.

(4)

During the simulation of unsteady-state conditions, the groove curvature radius coefficient has a significant impact on the contact stress between the ball and its corresponding raceway, and the contact stress between the ball and the raceways increases as the groove curvature radius coefficient increases. As the axial load decreases, the radial load, bearing speed, groove curvature radius coefficient, pocket force, guiding force, and maximum equivalent stress of the flexible cage increase.

(5)

Impact load can cause short-term and intense fluctuations in the thickness of the bearing oil film. An increase in axial load can mitigate this effect. Additionally, changes in bearing speed significantly influence the thickness of the bearing oil film. Overall, the thickness of the oil film first increases and then decreases with respect to the groove curvature radius coefficient. Appropriate parameter values should be selected based on the actual working conditions.

Compared to traditional steady-state or single-variable condition models, this model can more reflect the dynamic characteristics of angular contact ball bearings with two-piece inner rings on the aero-engine main shaft under the coupled effects of acceleration, deceleration, and impact loads during actual operation. It provides a reference for the impact resistance optimization of angular contact ball bearings with two-piece inner rings on the aero-engine.

This study focused on angular contact ball bearings with two-piece inner rings, also known as three-point contact ball bearings with two-piece inner rings, used in aero-engine spindles. Considering the structural similarity, the model construction and simulation analysis methods adopted in this study are also applicable to two-point contact ball bearings and three-point contact ball bearings of other sizes and geometries. For four-point contact ball bearings, after modifying the contact model according to the characteristics of four-point contact, the model construction and simulation analysis methods of this study can also be applied. However, whether the conclusions drawn in this study can be extended to other bearing sizes, geometries, or different types of ACBBs still requires further research.