Dynamic Precision and Reliability of Multi-Link Linkages with Translational Pair Clearance
Abstract
1. Introduction
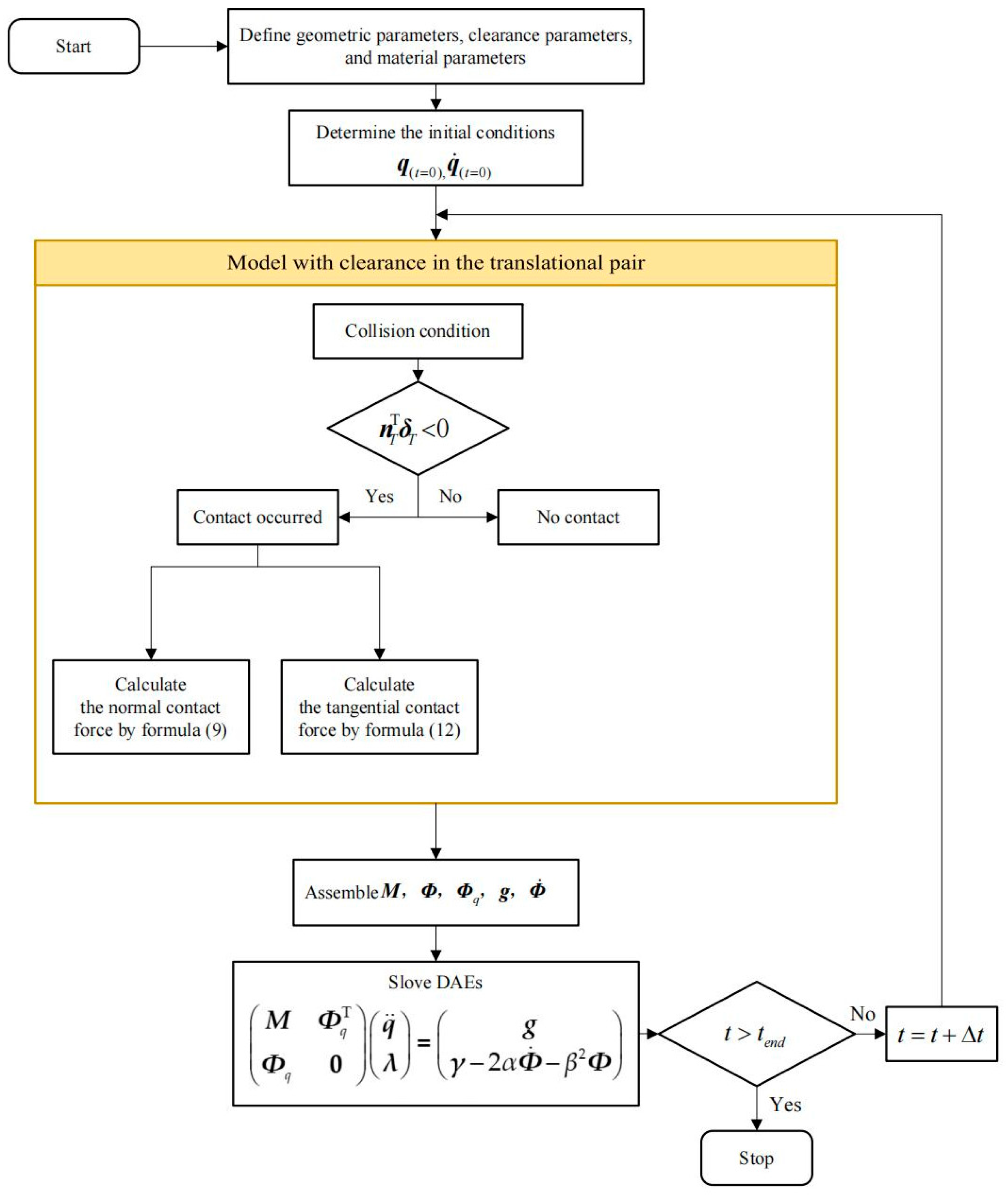
2. Dynamic Model of Mechanisms with Translational Pair Clearance
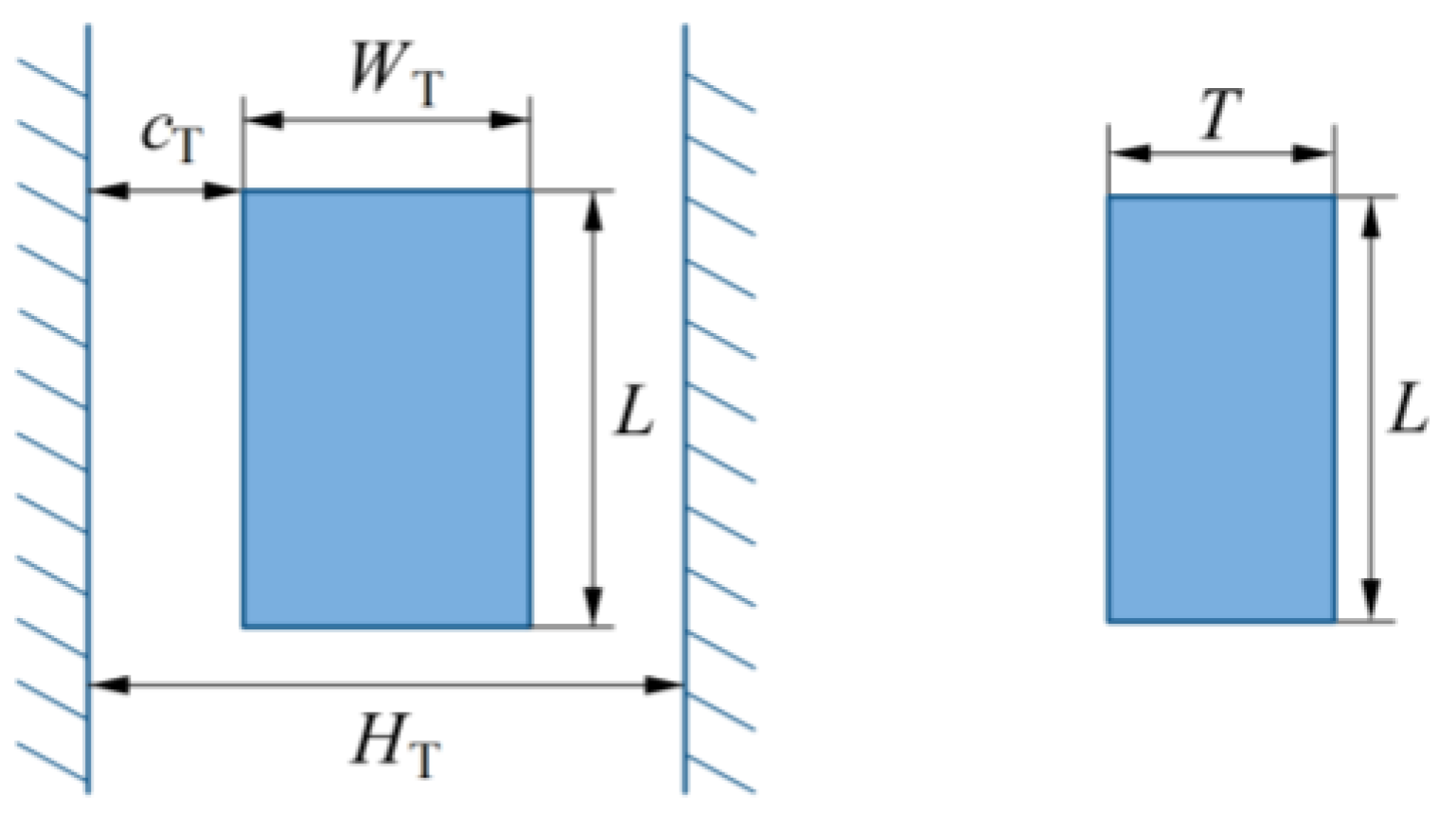
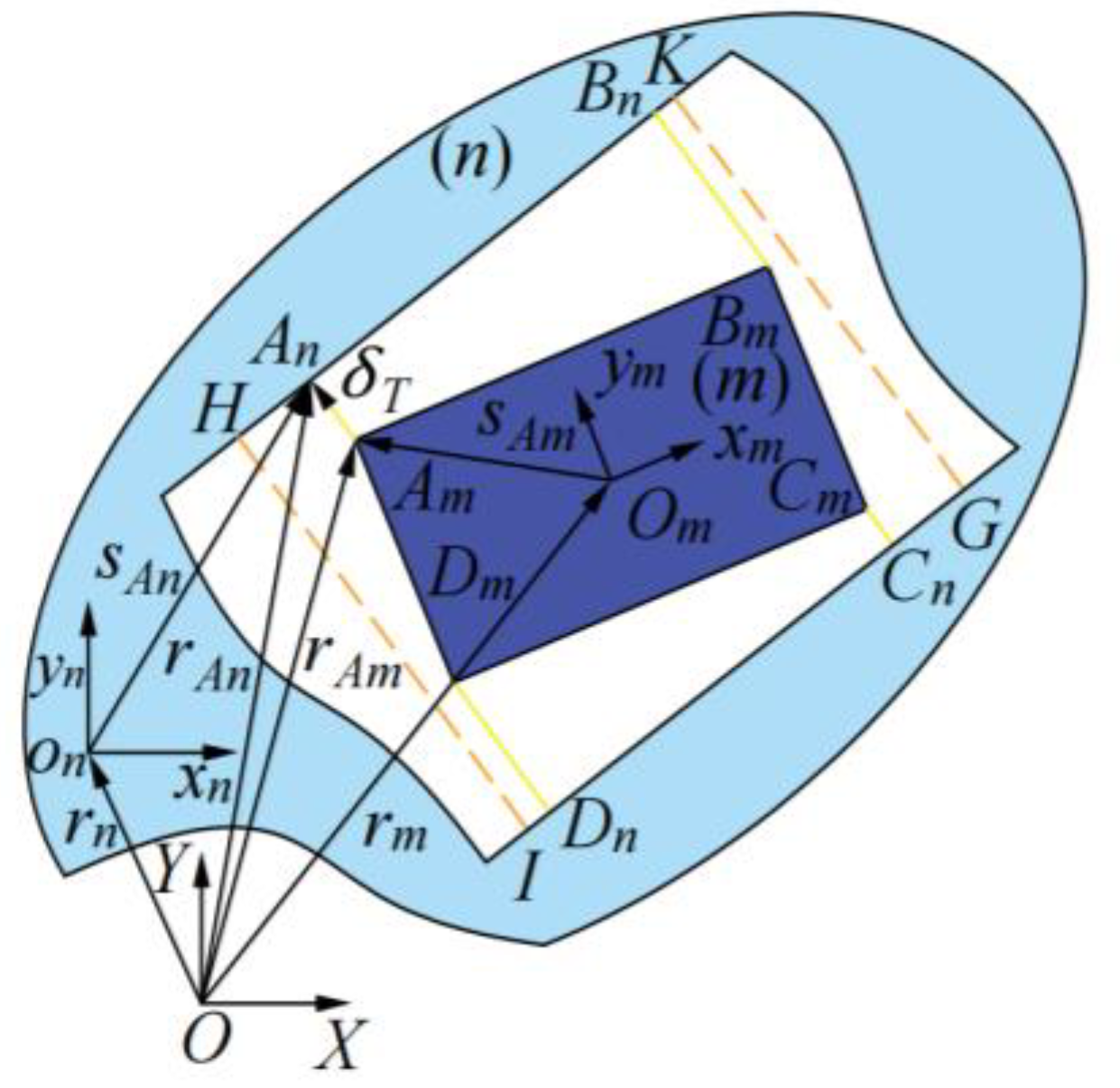
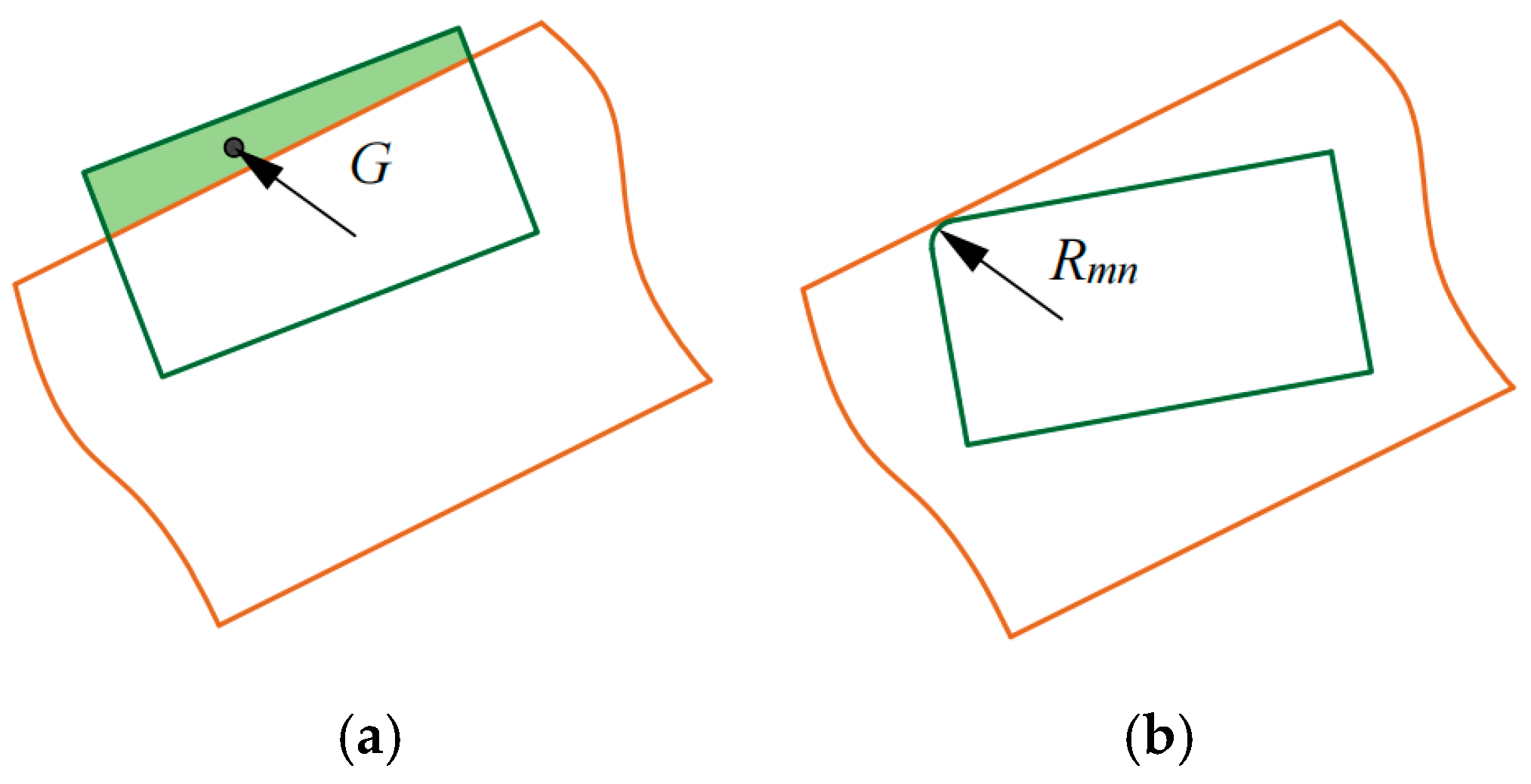
2.1. Establishment of the Translational Pair Clearance Motion Model
2.1.1. Establishment of the Normal Collision Force Model
2.1.2. Formulation of the Tangential Friction Force Model
2.2. Dynamic Model of Mechanisms with Translational Pairs
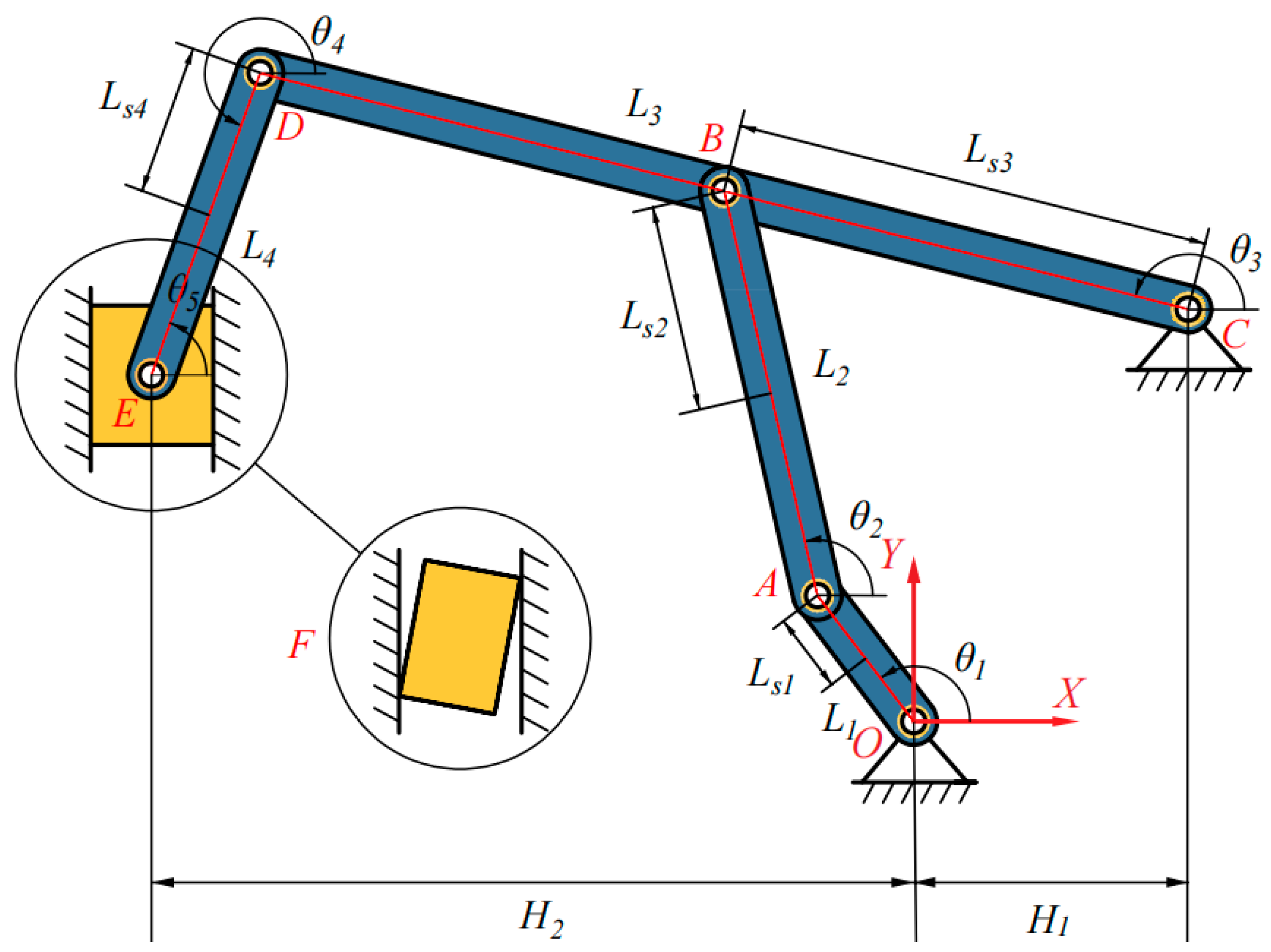
2.2.1. Structural Characteristics of the Press Mechanism’s Linkage System
2.2.2. Dynamic Model of the Six-Bar Linkage Considering the Clearance of Translational Pairs
3. Reliability Model Development
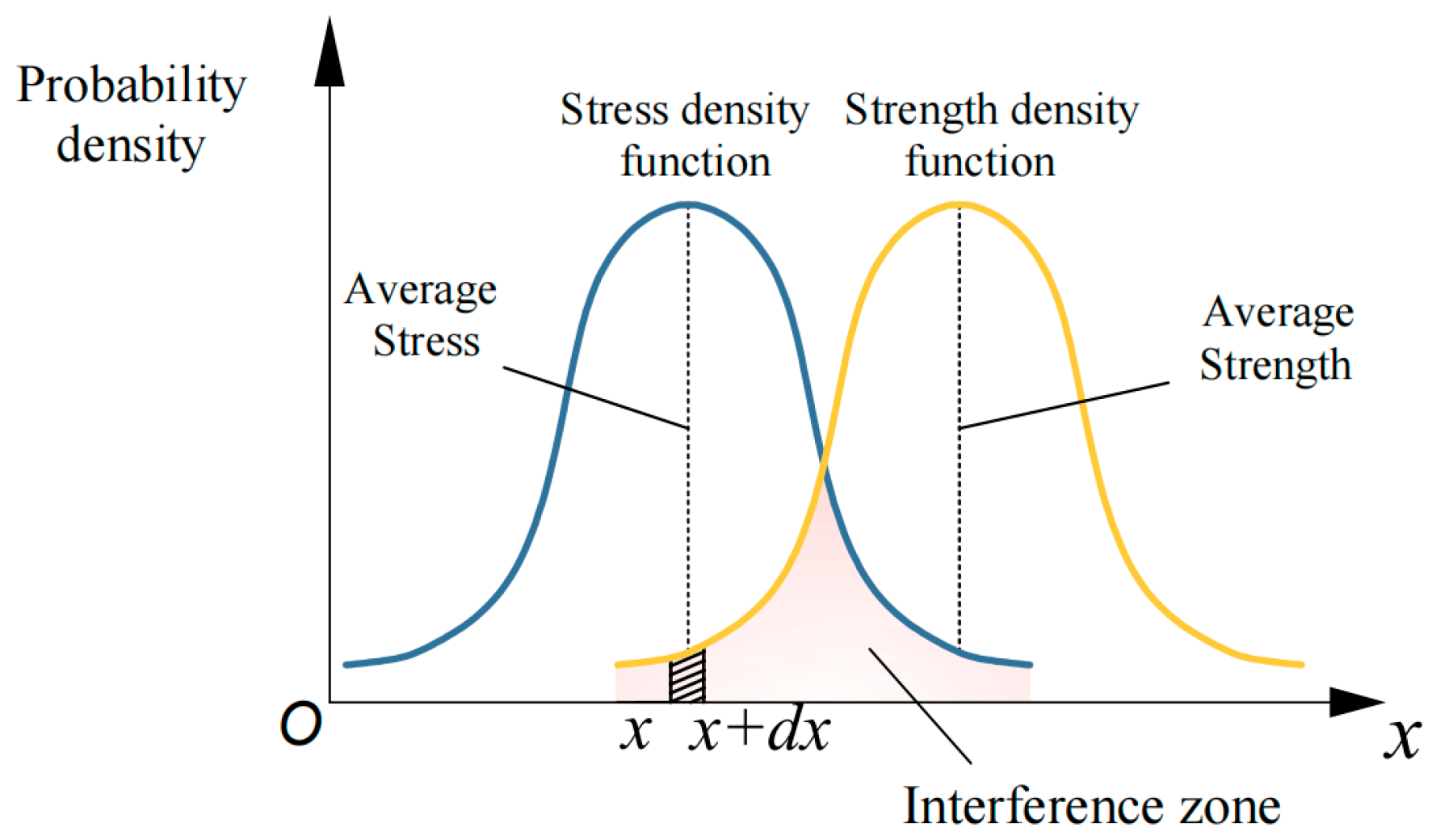
3.1. Kinematic Fidelity Reliability Analysis for Planar Multi-Link Systems with Joint Clearances
3.1.1. First-Order Second-Moment Method
3.1.2. Dynamic Accuracy Reliability Model of Mechanisms
4. Analysis of the Dynamic Behavior and Nonlinear Features Incorporating Clearances in Rigid Body Systems
4.1. Simulation Parameters and Simulation Process
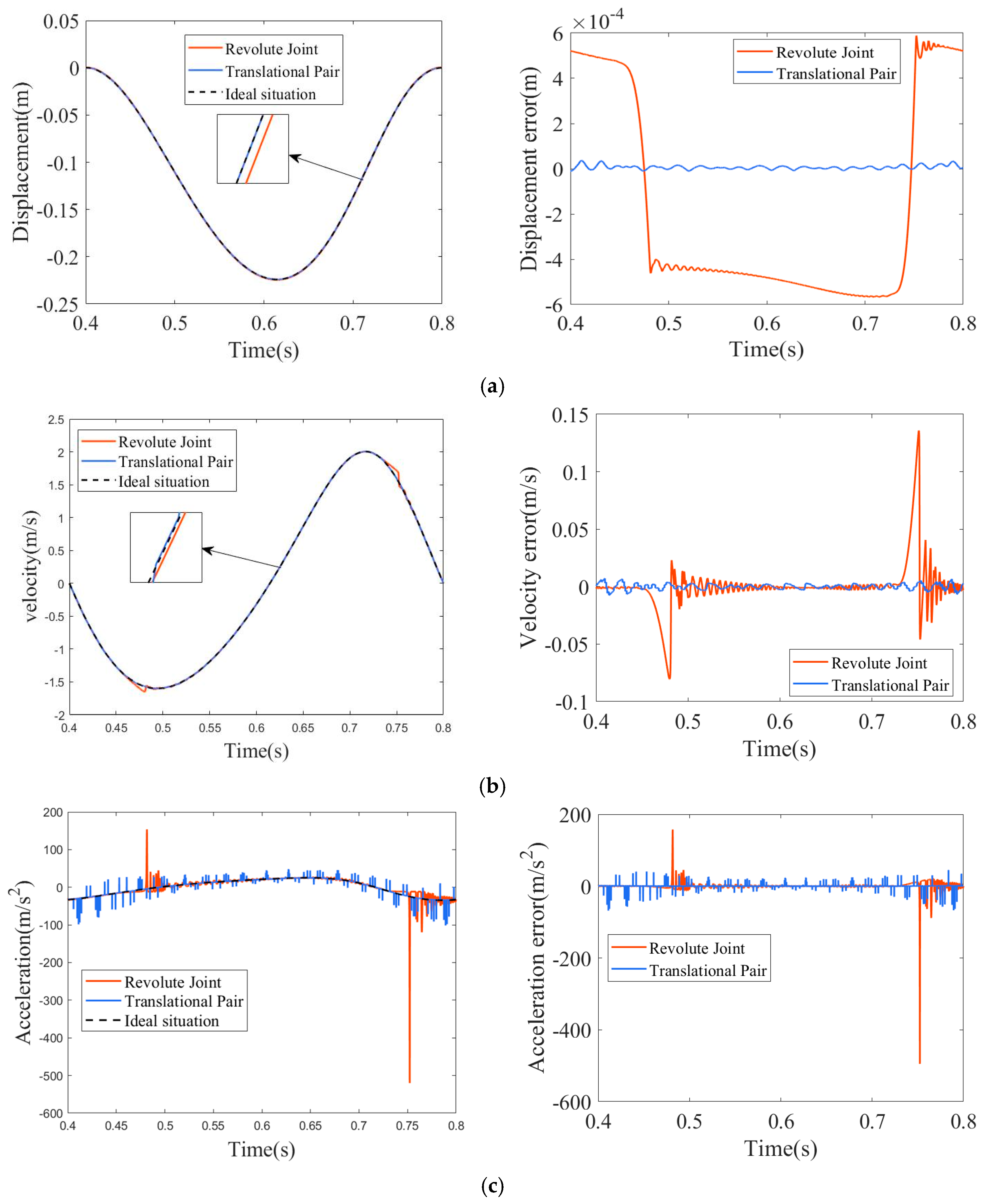
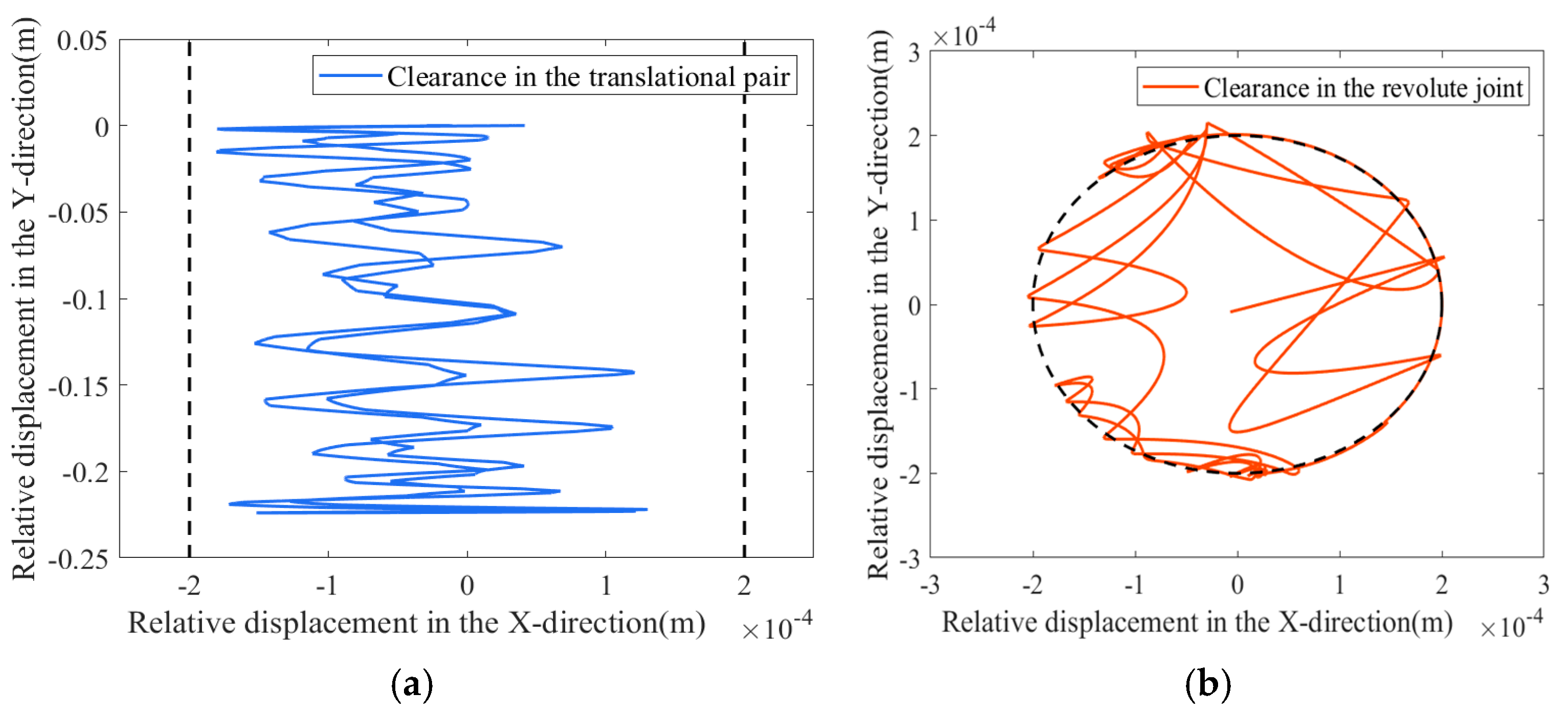
4.2. The Impact of Different Types of Single Joint Clearances on the Mechanism
4.3. The Influence of Varying Material Parameters on Dynamic Performance
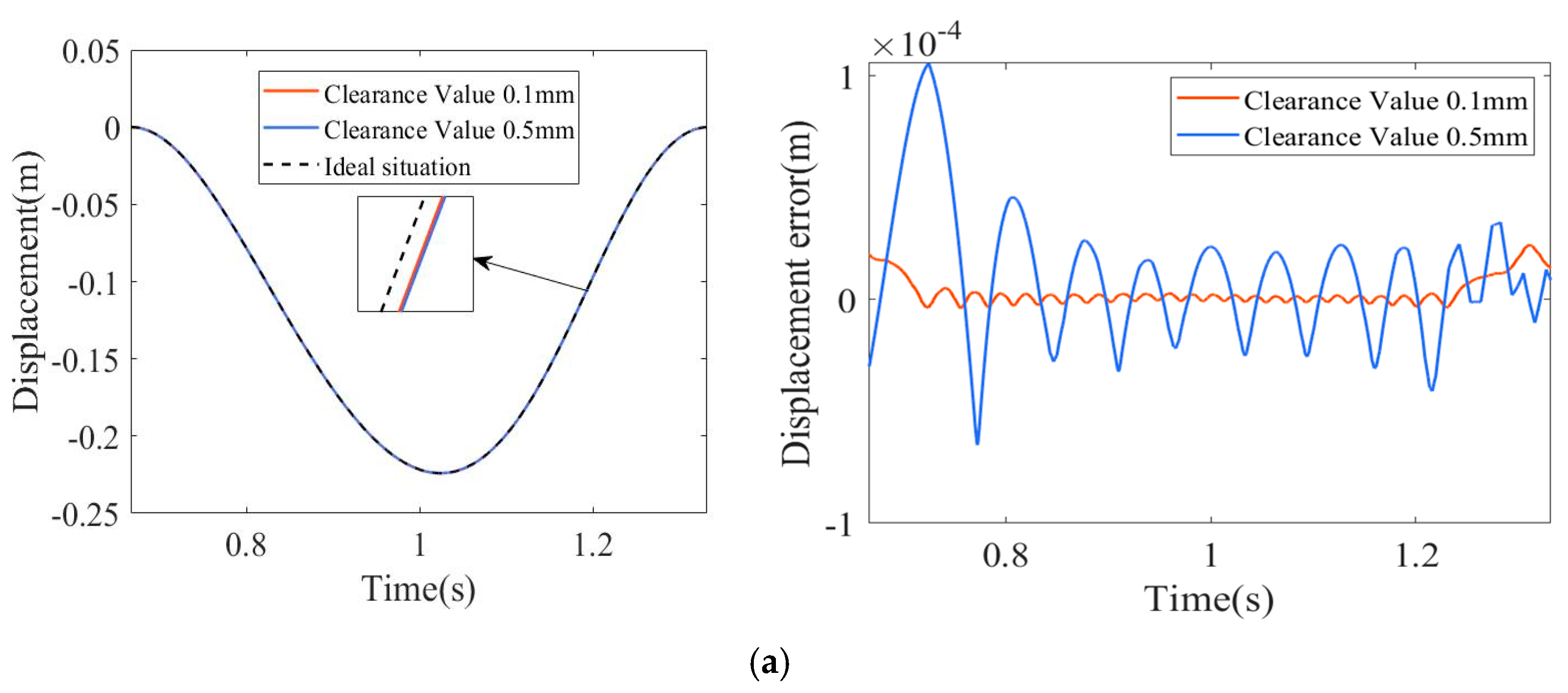
4.4. Impact of Clearance Magnitude on Dynamic Behavior
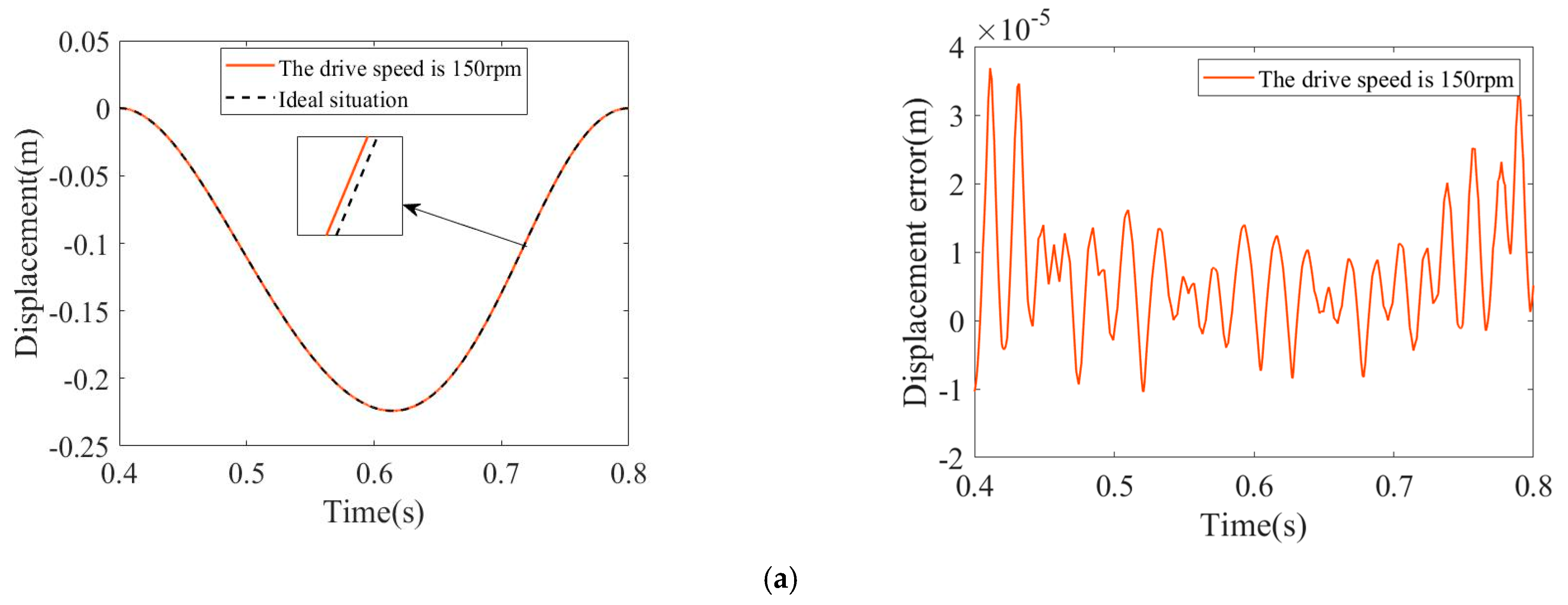
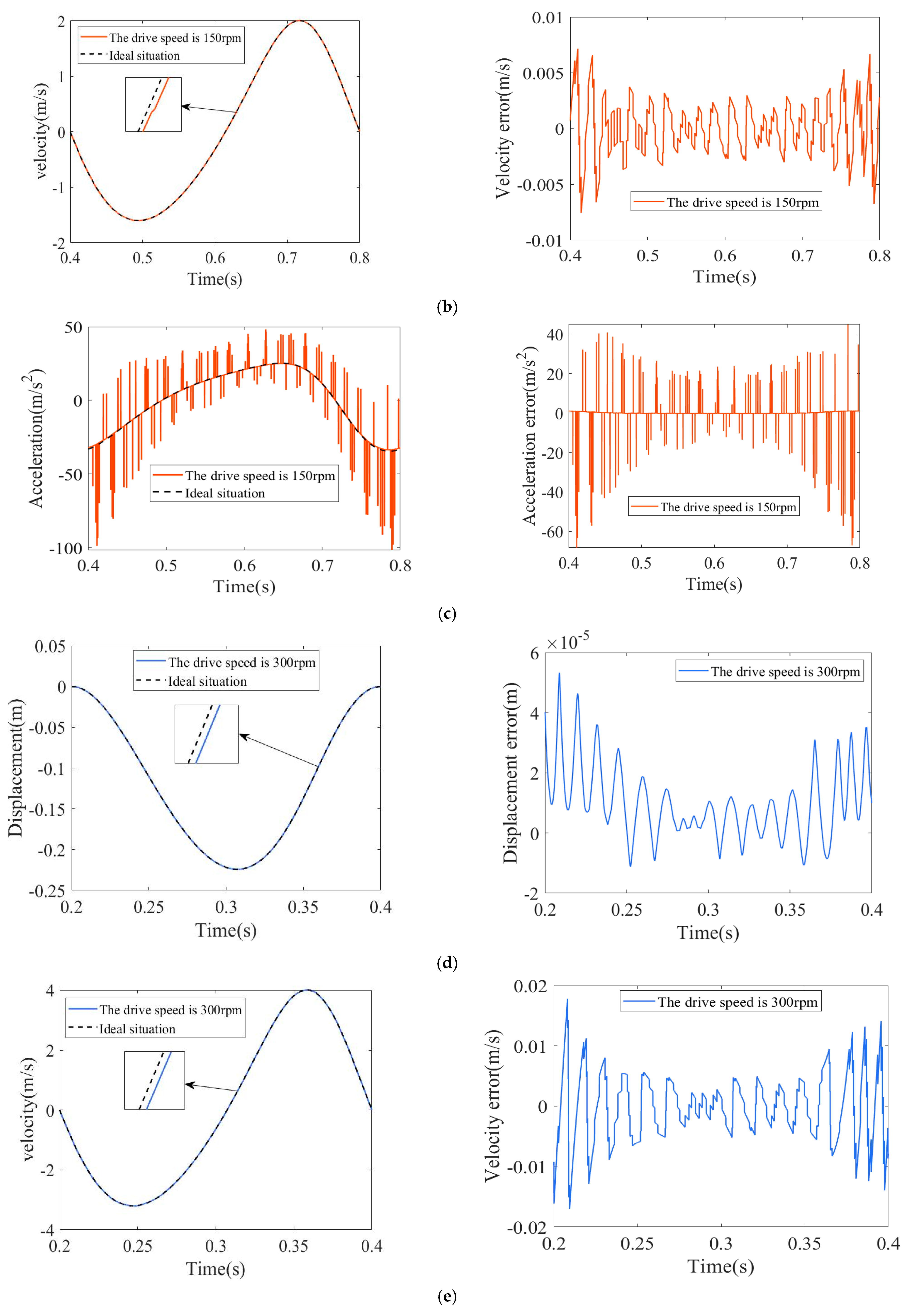
4.5. The Impact of Different Driving Speeds on the Dynamic Response of Rigid Body Mechanisms with Clearances
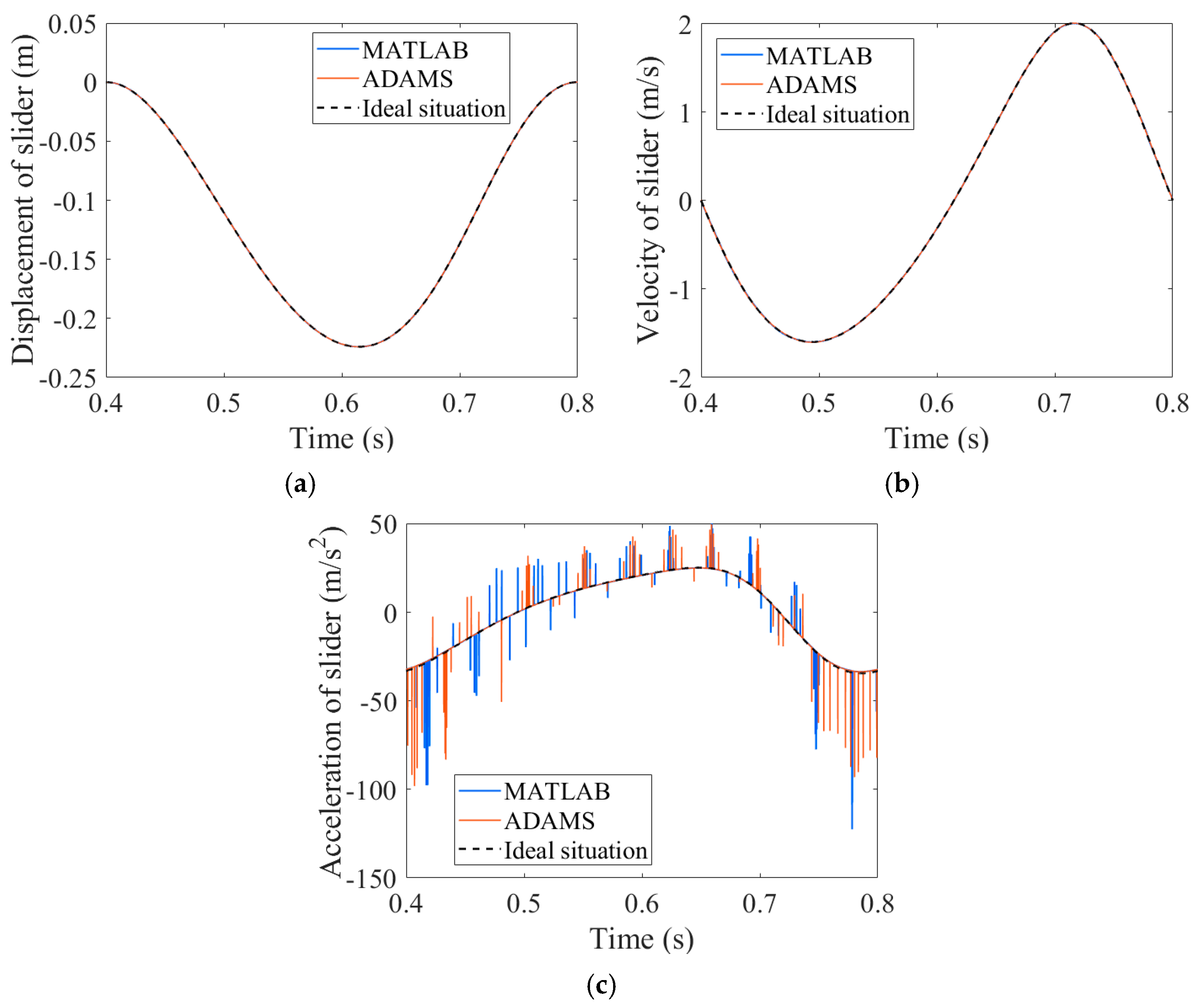
4.6. Virtual Prototype Model of a Mechanism with Translational Pair Clearance
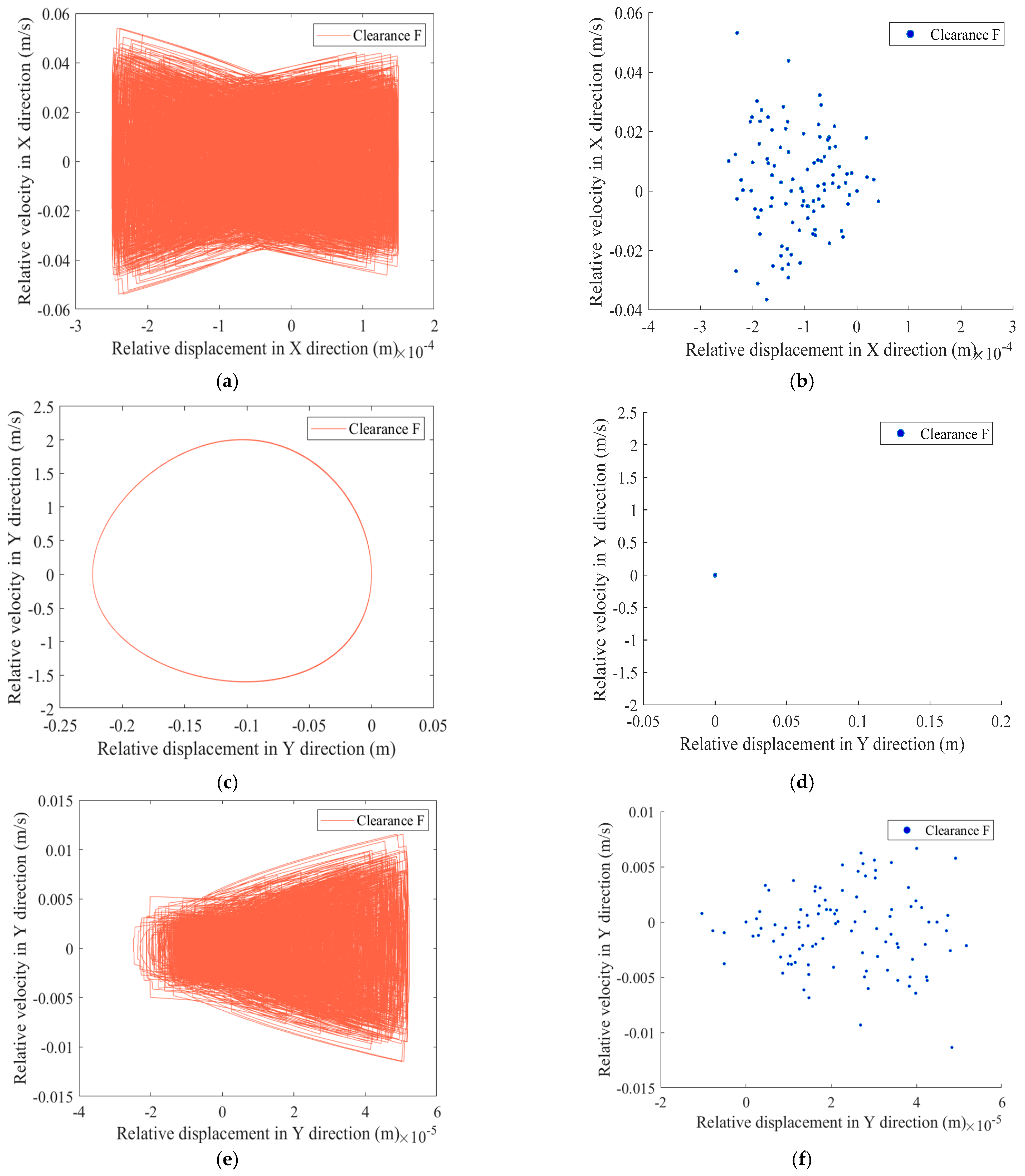
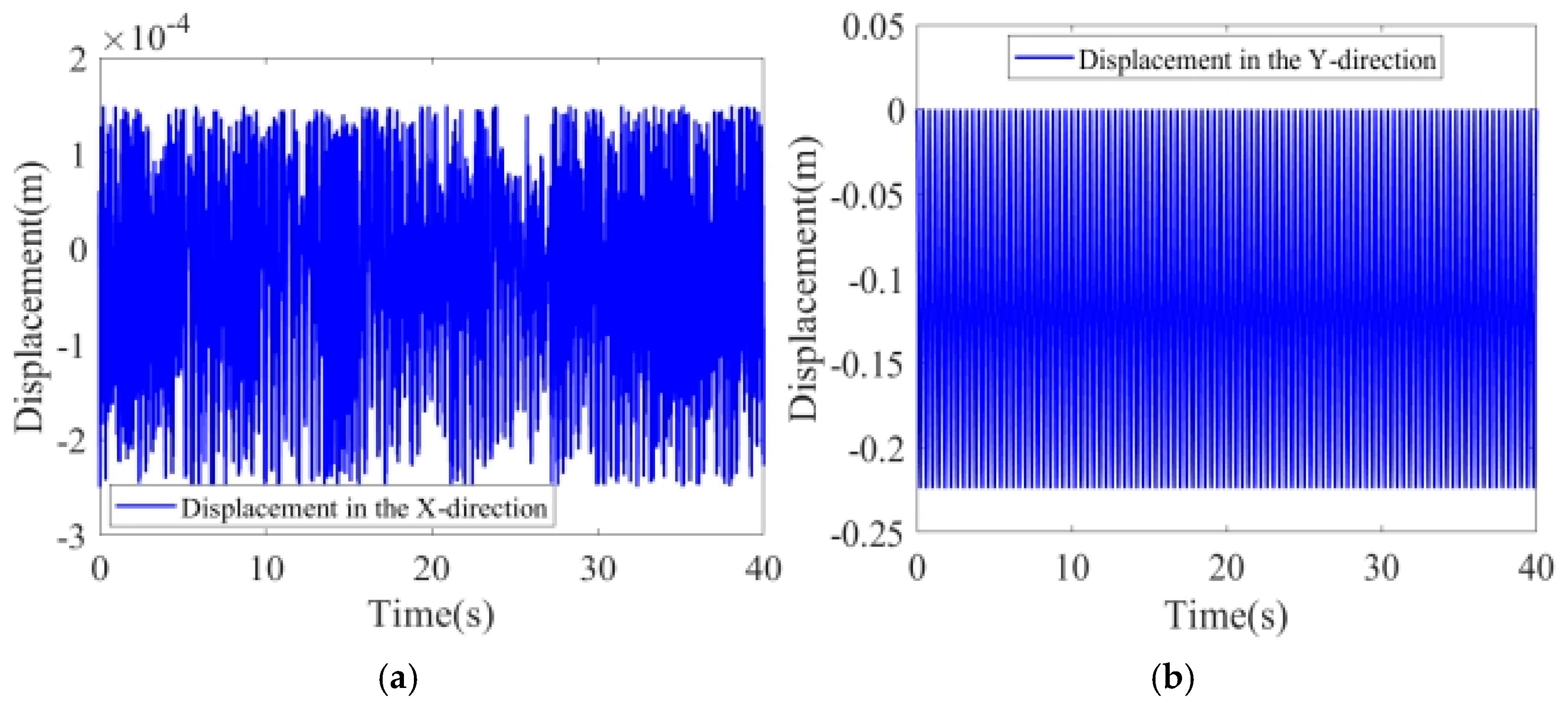
4.7. Nonlinear Characteristics Analysis of Clearance-Containing Mechanisms
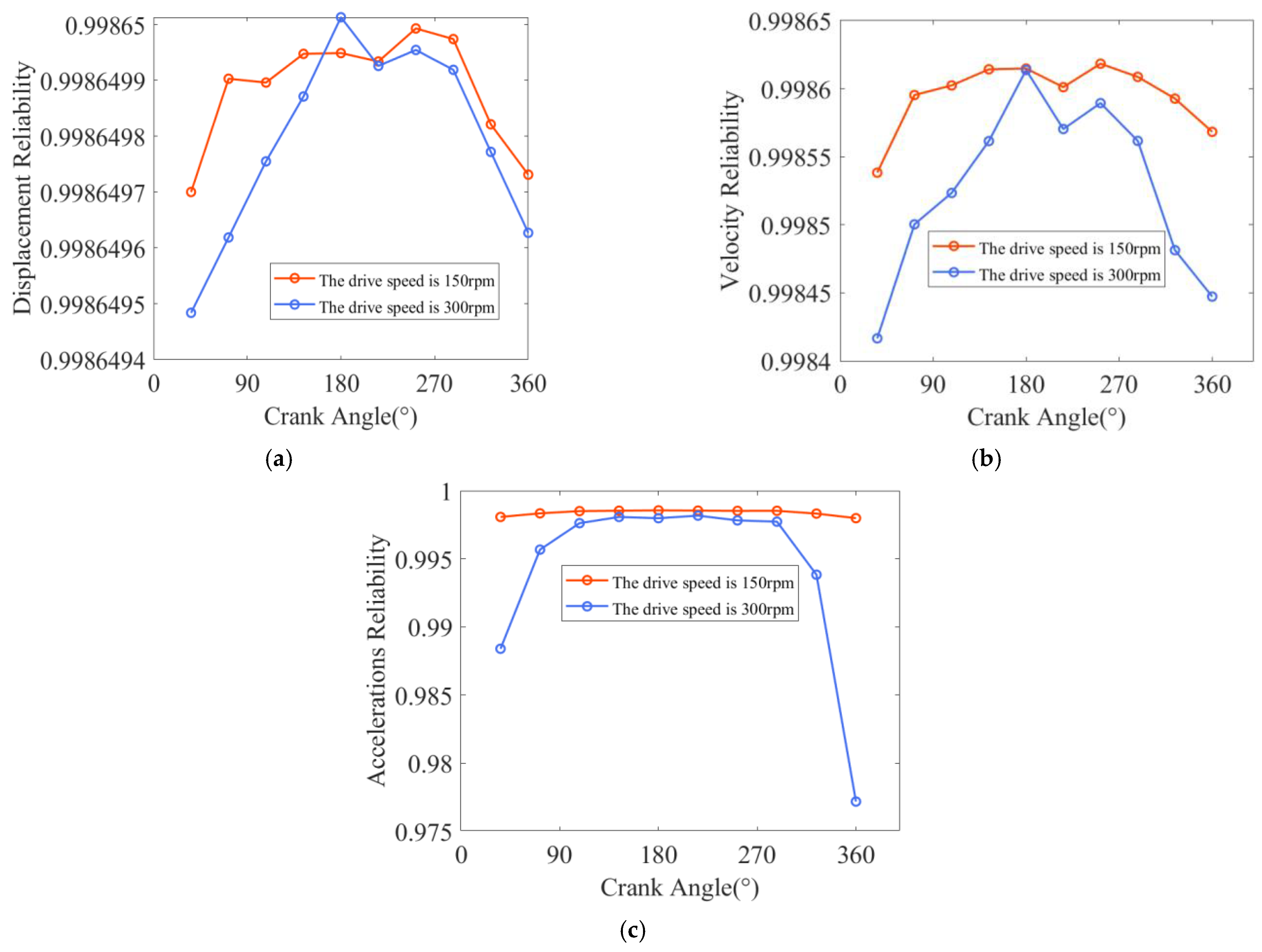
5. Impact on Dynamic Accuracy and Reliability
Operational Reliability Under Variable Clearance Dimensions and Actuation Speeds
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, X.L.; Yao, E.R. Dynamic characteristics analysis of multi-link mechanism with clearances considering uncertain parameters. Mech. Based Des. Struct. Mech. 2024, 52, 9947–9974. [Google Scholar] [CrossRef]
- Jia, P.; Li, D.L.; Zhang, Y.K. A novel reconfigurable parallel mechanism constructed with spatial metamorphic four-link mechanism. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 4120–4132. [Google Scholar] [CrossRef]
- Ming, P. Research on the Core Technology and the Development Tendency of Modern Precision Machinery Manufacturing. In Proceedings of the 4th International Conference on Mechanical Materials and Manufacturing Engineering (MMME), Wuhan, China, 15–16 October 2016; Atlantis Press: Wuhan, China, 2016; pp. 806–809. [Google Scholar]
- Shi, Y.; Song, B.F.; Yu, T.X. Kinetic Reliability Analysis of Space Four-Links Mechanism Considering Wear. In Proceedings of the 2016 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bali, Indonesia, 4–7 December 2016; IEEE: Bali, Indonesia, 2016. [Google Scholar]
- Tian, C.X.; Fang, Y.F.; Guo, S. Structural synthesis of a class of 2R2T hybrid mechanisms. Chin. J. Mech. Eng. 2016, 29, 703–709. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, J.; Lyu, S. Error Analysis of a Deployable Scissor-Like Mechanism with Joint Clearances. In Advances in Mechanism and Machine Science, Proceedings of the IFToMM WC 2023, Tokyo, Japan, 5–10 November 2023; Springer: Cham, Switzerland, 2024; pp. 385–394. [Google Scholar]
- Zhang, H. Effects of Mixed Joint Clearances on Dynamic Characteristic of Six-bar Mechanism. Mech. Sci. Technol. Aerosp. Eng. 2020, 39, 852–857. [Google Scholar]
- Zhao, F.Q.; Gao, Z.Y.; Chen, S.Q. Dynamics Analysis of the Double Push Rod Limb-Leg Mechanism with Clearance Joint. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 1799–1827. [Google Scholar] [CrossRef]
- Chen, X.L.; Jiang, S.Y. Dynamic response and chaos in planar multi-link mechanism considering revolute clearances. Arch. Appl. Mech. 2020, 90, 1919–1941. [Google Scholar] [CrossRef]
- Bai, Z.F.; Ning, Z.Y.; Zhou, J.S. Study on Wear Characteristics of Revolute Clearance Joints in Mechanical Systems. Micromachines 2022, 13, 1018. [Google Scholar] [CrossRef]
- Huang, J.; Hu, B.; Sun, S.L.; Xiao, M.T.; Peng, C.W.; Wang, H.B. Mesh Stiffness and Nonlinear Dynamic Model for a Gear Drive with Revolute Pair Clearance. Processes 2023, 11, 230. [Google Scholar] [CrossRef]
- Muvengei, O.; Kihiu, J.; Ikua, B. Dynamic analysis of planar multi-body systems with LuGre friction at differently located revolute clearance joints. Multibody Syst. Dyn. 2012, 28, 369–393. [Google Scholar] [CrossRef]
- Olyaei, A.A.; Ghazavi, M.R. Stabilizing slider-crank mechanism with clearance joints. Mech. Mach. Theory 2012, 53, 17–29. [Google Scholar] [CrossRef]
- Li, X.F.; Zhao, D.; Xie, F.Q.; Wu, S.J.; Li, X.Y. Experimental investigations of the dynamic responses of a multi-link mechanism with revolute clearance joints. Adv. Mech. Eng. 2021, 13, 16878140211012541. [Google Scholar] [CrossRef]
- Lin, Y.P.; Wang, J.C.; Zhang, J.L.; An, M.X.; Jiang, S. Research on the Dynamic and Reliability of Planar Multi-Link Mechanisms with Multiple Clearances. Mech. Solids 2024, 59, 1537–1558. [Google Scholar] [CrossRef]
- Marques, F.; Isaac, F.; Dourado, N. An enhanced formulation to model spatial revolute joints with radial and axial clearances. Mech. Mach. Theory 2017, 116, 123–144. [Google Scholar] [CrossRef]
- Isaac, F.; Marques, F.; Dourado, N. A finite element model of a 3D dry revolute joint incorporated in a multibody dynamic analysis. Multibody Syst. Dyn. 2019, 45, 293–313. [Google Scholar] [CrossRef]
- Bai, Z.F.; Liu, T.X.; Li, J.Y.; Zhao, J.J. Numerical and experimental study on dynamic characteristics of planar mechanism with mixed clearances. Mech. Based Des. Struct. Mach. 2023, 51, 6142–6165. [Google Scholar] [CrossRef]
- Yang, L.X.; Zhang, X.M.; Huang, Y.J. Dynamic analysis of open-loop mechanisms with multiple spatial revolute clearance joints. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 593–610. [Google Scholar] [CrossRef]
- Brutti, C.; Coglitore, G.; Valentini, P.P. Modeling 3D revolute joint with clearance and contact stiffness. Nonlinear Dyn. 2011, 66, 531–548. [Google Scholar] [CrossRef]
- Farahan, S.B.; Ghazavi, M.R.; Rahmanian, S. Bifurcation in a planar four-bar mechanism with revolute clearance joint. Nonlinear Dyn. 2017, 87, 955–973. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Q.Z.; Zeng, H.; Meng, L.C.; Luo, Z.; Han, Q.K. Analysis of the Dynamic of Vector Nozzle Adjustment Mechanism Considering the Effect of Joint Clearance. J. Vib. Eng. Technol. 2024, 12, 6137–6154. [Google Scholar] [CrossRef]
- Wu, X.Z.; Sun, Y.; Wang, Y.; Chen, Y. Dynamic analysis of the double crank mechanism with a 3D translational clearance joint employing a variable stiffness contact force model. Nonlinear Dyn. 2020, 99, 1937–1958. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, X.L. Test study and nonlinear dynamic analysis of planar multi-link mechanism with compound clearances. Eur. J. Mech. A/Solids 2021, 88, 104260. [Google Scholar] [CrossRef]
- Wang, S.P.; Cui, Y.; Wang, C.E. Dynamics Analysis and Chaos Identification of Compound Pendulum Jaw Crusher with Joint Clearance. Appl. Sci. 2023, 13, 238. [Google Scholar] [CrossRef]
- Ahmedalbashir, M.; Romdhane, L.; Lee, J. Dynamics of a four-bar mechanism with clearance and springs-Modeling and experimental analysis. J. Mech. Sci. Technol. 2017, 31, 1023–1033. [Google Scholar] [CrossRef]
- Liu, S.; Cui, Y.; Fu, Y.; Li, B.; Lv, B.L.; Qian, Y.H. Modeling of lubricated translational joints in rigid-partially flexible multibody systems and its application in two-stroke marine diesel engines. Tribol. Int. 2022, 165, 107244. [Google Scholar] [CrossRef]
- Erkaya, S.; Dogan, S.; Ulus, S. Effects of joint clearance on the dynamics of a partly compliant mechanism: Numerical and experimental studies. Mech. Mach. Theory 2015, 88, 125–140. [Google Scholar] [CrossRef]
- Zheng, X.D.; Li, J.; Wang, Q.; Liao, Q.M. A methodology for modeling and simulating frictional translational clearance joint in multibody systems including a flexible slider part. Mech. Mach. Theory 2019, 142, 103603. [Google Scholar] [CrossRef]
- Dong, X.Y.; Sun, Y.; Wu, X.Z.; Wang, R.D. Dynamic modeling and performance analysis of toggle-linkage presses considering mixed clearances and flexibility. Int. J. Non-Linear Mech. 2022, 147, 104243. [Google Scholar] [CrossRef]
- Akhadkar, N.; Acary, V.; Brogliato, B. Multibody systems with 3D revolute joints with clearances: An industrial case study with an experimental validation. Multibody Syst. Dyn. 2018, 42, 249–282. [Google Scholar] [CrossRef]
- Tan, H.Y.; Li, L.; Huang, Q.; Jiang, Z.D.; Li, Q.X.; Zhang, Y.M.; Yu, D.L. Influence of two kinds of clearance joints on the dynamics of planar mechanical system based on a modified contact force model. Sci. Rep. 2023, 13, 20569. [Google Scholar] [CrossRef]
- Jiang, S.; Lin, Y.P.; Liu, J.N.; Xiao, L.J.; Zhang, S.S. Dynamics Optimization Research and Dynamics Accuracy and Reliability Analysis of a Multi-Link Mechanism with Clearances. Machines 2022, 10, 698. [Google Scholar] [CrossRef]
- Xiang, W.W.K.; Yan, S.Z.; Wu, J.N.; Niu, W.D. Dynamic response and sensitivity analysis for mechanical systems with clearance joints and parameter uncertainties using Chebyshev polynomials method. Mech. Syst. Signal Process. 2020, 138, 106596. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, F.; Li, Y.Y. Reliability optimization design of a planar multi-body system with two clearance joints based on reliability sensitivity analysis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 1369–1382. [Google Scholar] [CrossRef]
- Chen, X.L.; Gao, S. Dynamic response and dynamic accuracy reliability of planar mechanism with multiple lubricated clearances. Multibody Syst. Dyn. 2023, 57, 1–23. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, X.M.; Zhang, H.D.; Chen, G.C. Unified motion reliability analysis and comparison study of planar parallel manipulators with interval joint clearance variables. Mech. Mach. Theory 2019, 138, 58–75. [Google Scholar] [CrossRef]
- Geng, X.Y.; Wang, X.J.; Wang, L.; Wang, R.X. Non-probabilistic time-dependent kinematic reliability assessment for function generation mechanisms with joint clearances. Mech. Mach. Theory 2016, 104, 202–221. [Google Scholar] [CrossRef]
- Zhang, J.F.; Du, X.P. Time-dependent reliability analysis for function generation mechanisms with random joint clearances. Mech. Mach. Theory 2015, 92, 184–199. [Google Scholar] [CrossRef]
- Wu, J.N.; Yan, S.Z.; Zuo, M.J. Evaluating the reliability of multi-body mechanisms: A method considering the uncertainties of dynamic performance. Reliab. Eng. Syst. Saf. 2016, 149, 96–106. [Google Scholar] [CrossRef]
- Li, Y.; Shang, D.Y.; Fan, X.; Liu, Y. Motion Reliability Analysis of the Delta Parallel Robot considering Mechanism Errors. Math. Probl. Eng. 2019, 2019, 3501921. [Google Scholar] [CrossRef]
- Yang, Q.; Ma, H.K.; Ma, J.C.; Sun, Z.L.; Li, C.L. Sensitivity Analysis of Reliability of Low-Mobility Parallel Mechanisms Based on a Response Surface Method. Appl. Sci. 2021, 11, 9002. [Google Scholar] [CrossRef]
- Jia, Y.H.; Chen, X.L.; Zhang, L.Z.; Ning, C.S. Dynamic characteristics and reliability analysis of parallel mechanism with clearance joints and parameter uncertainties. Meccanica 2023, 58, 813–842. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, X.M.; Jian, Z.C.; Zhang, H.D. Error modelling and motion reliability analysis of a planar parallel manipulator with multiple uncertainties. Mech. Mach. Theory 2018, 124, 55–72. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.; Claro, J.C.P. Translational Joints With Clearance in Rigid Multibody Systems. J. Comput. Nonlinear Dyn. 2008, 3, 11007. [Google Scholar] [CrossRef]
- Li, J.L.; Huang, H.Z.; Yan, S.Z.; Yang, Y.Q. Kinematic accuracy and dynamic performance of a simple planar space deployable mechanism with joint clearance considering parameter uncertainty. Acta Astronaut. 2017, 136, 34–45. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavic, J.; Boltezar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Hou, Y.L.; Wang, Y.; Jing, G.N.; Deng, Y.J.; Zeng, D.X.; Qiu, X.S. Chaos phenomenon and stability analysis of RU-RPR parallel mechanism with clearance and friction. Adv. Mech. Eng. 2018, 10, 1687814017746253. [Google Scholar] [CrossRef]
- Li, Y.Y.; Wang, C.; Huang, W.H. Dynamics analysis of planar rigid-flexible coupling deployable solar array system with multiple revolute clearance joints. Mech. Syst. Signal Proc. 2019, 117, 188–209. [Google Scholar] [CrossRef]
- Baumgarte, J. Stabilization of constraints and integrals of motion in dynamical systems. Comput. Methods Appl. Mech. Eng. 1972, 1, 1–16. [Google Scholar] [CrossRef]
- Chen, X.L.; Gao, S. Dynamic accuracy reliability modeling and analysis of planar multi-link mechanism with revolute clearances. Eur. J. Mech. A/Solids 2021, 90, 104317. [Google Scholar] [CrossRef]
- Chen, X.L.; Wang, T.; Gao, S. Dynamic response errors and accuracy reliability for mechanism with multiple lubrication clearance joints. Arch. Appl. Mech. 2023, 93, 525–550. [Google Scholar] [CrossRef]
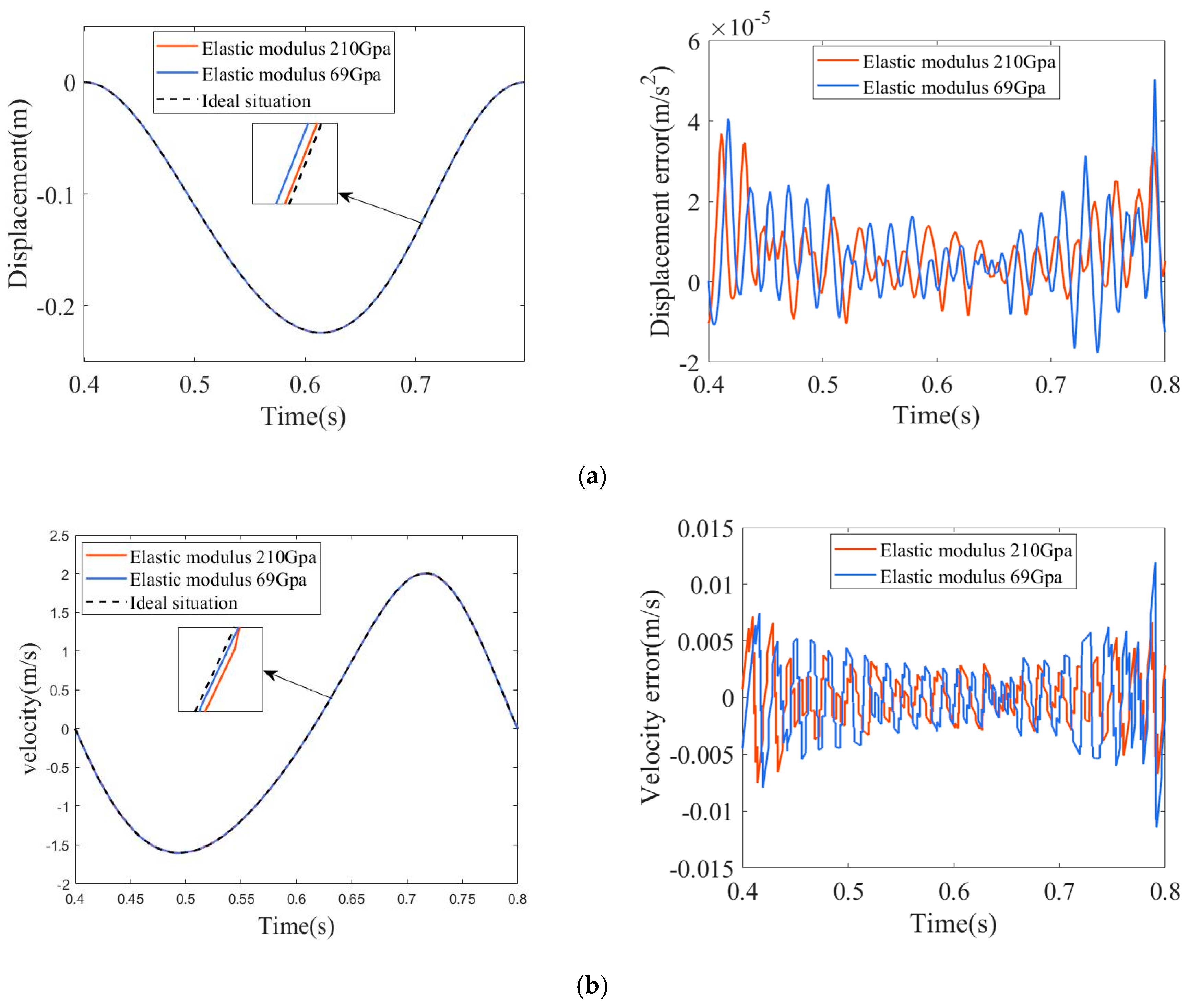
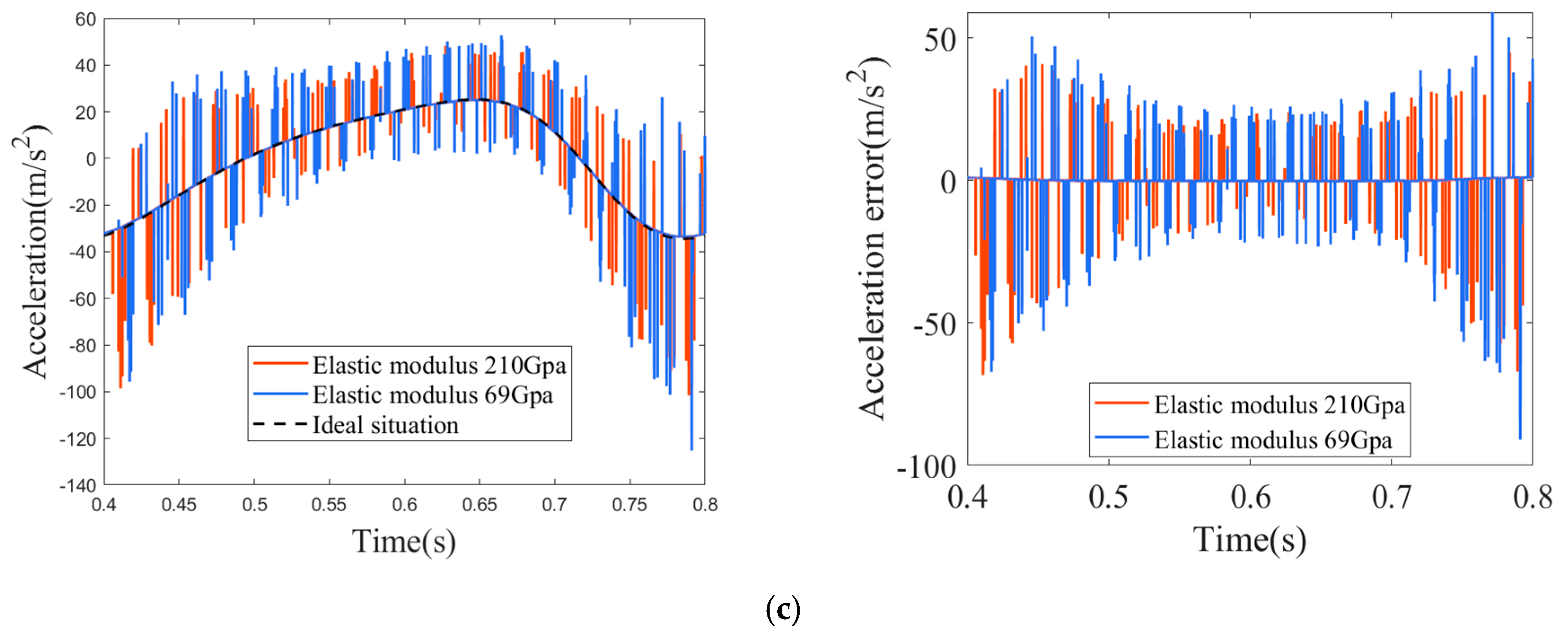
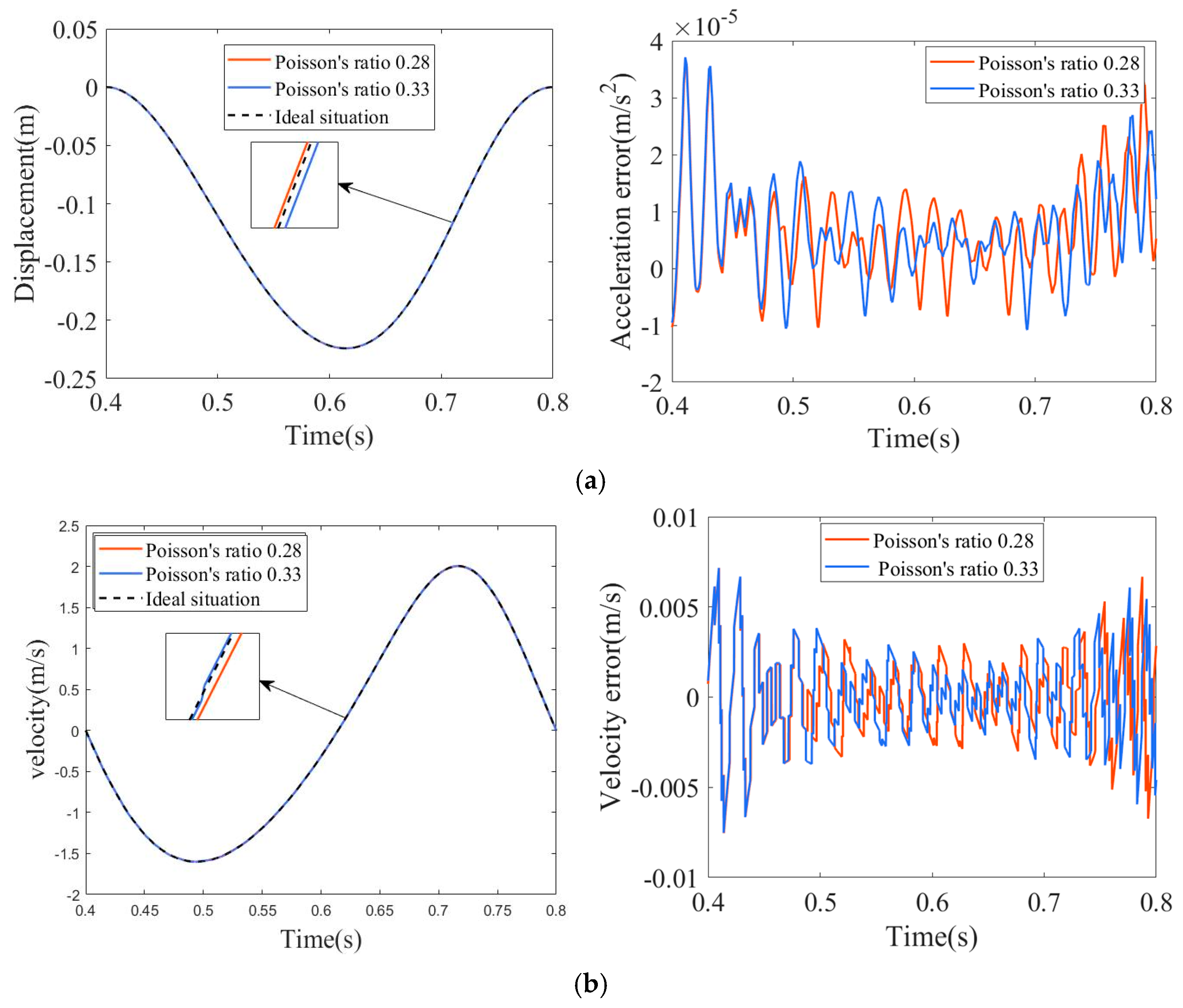
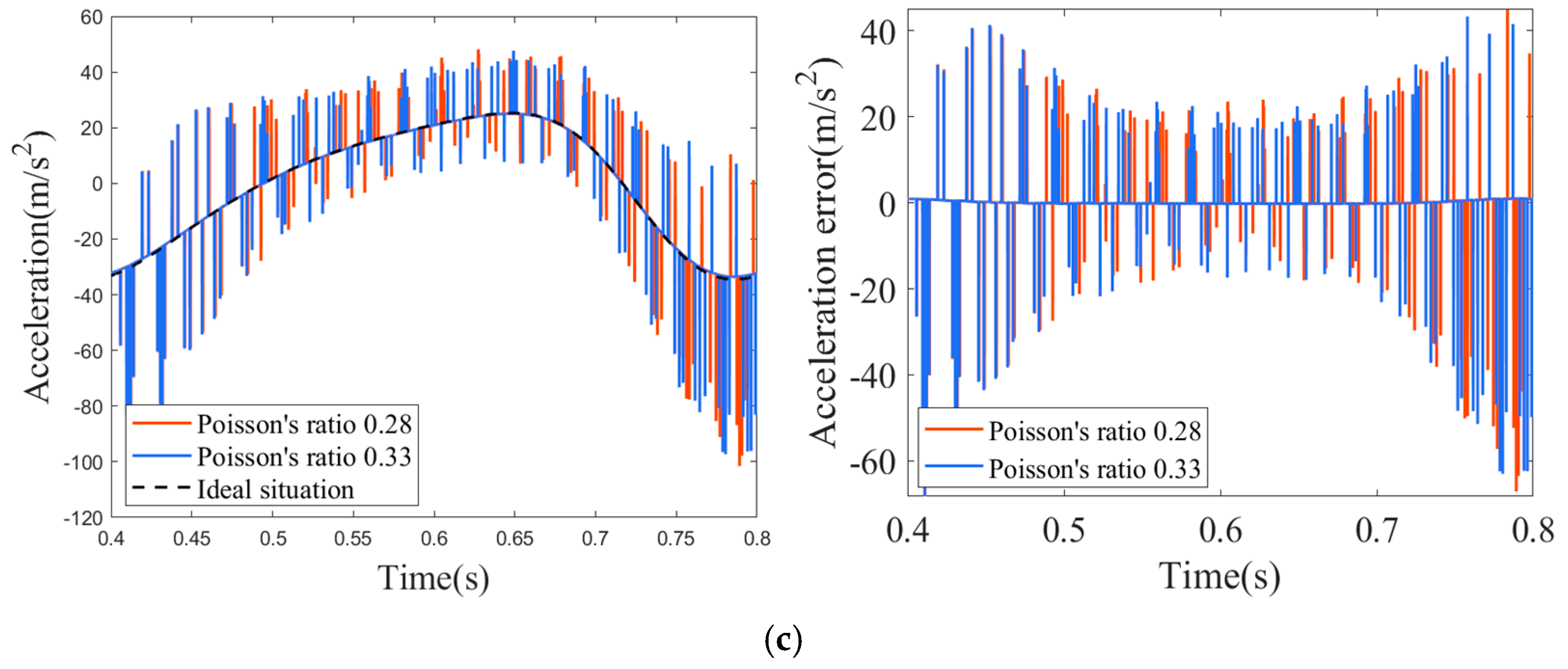



| Component | Length of Rod () | Centroid Position Length () | Mass () | Moment of Inertia () |
|---|---|---|---|---|
| Crank 1 | 0.045 () | 0.225 () | 0.02 () | 0.0101 () |
| Rod 2 | 0.29 () | 0.145 () | 0.115 () | 0.8060 () |
| Rod 3 | 0.79 () | 0.395 () | 0.31 () | 16.1230 () |
| Rod 4 | 0.24 () | 0.12 () | 0.096 () | 0.4608 () |
| Slider 5 | —— | —— | 0.1703 () | 0.0263 () |
| Parameter | Parameter Values |
|---|---|
| Slider length () | 0.07 |
| Slider width () | 0.05 |
| Slider thickness () | 0.05 |
| Maximum static friction speed () | 0.0001 |
| Transitional velocity for kinetic friction () | 0.001 |
| Restitution coefficient | 0.9 |
| Elastic modulus () | 210 |
| Poisson’s ratio , | 0.28 |
| Frictional coefficient | 0.15 |
| 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Q.; Cai, M.; Lian, Y.; Zhu, J.; Jiang, S. Dynamic Precision and Reliability of Multi-Link Linkages with Translational Pair Clearance. Lubricants 2025, 13, 246. https://doi.org/10.3390/lubricants13060246
Zuo Q, Cai M, Lian Y, Zhu J, Jiang S. Dynamic Precision and Reliability of Multi-Link Linkages with Translational Pair Clearance. Lubricants. 2025; 13(6):246. https://doi.org/10.3390/lubricants13060246
Chicago/Turabian StyleZuo, Quanzhi, Mingyang Cai, Yuyang Lian, Jianuo Zhu, and Shuai Jiang. 2025. "Dynamic Precision and Reliability of Multi-Link Linkages with Translational Pair Clearance" Lubricants 13, no. 6: 246. https://doi.org/10.3390/lubricants13060246
APA StyleZuo, Q., Cai, M., Lian, Y., Zhu, J., & Jiang, S. (2025). Dynamic Precision and Reliability of Multi-Link Linkages with Translational Pair Clearance. Lubricants, 13(6), 246. https://doi.org/10.3390/lubricants13060246





