Optimization of Micro-Texture Parameters for Machine Tool Guide Rail Combination Based on Response Surface Methodology and Research on Its Anti-Friction and Lubrication Performance
Abstract
:1. Introduction
2. Materials and Methods
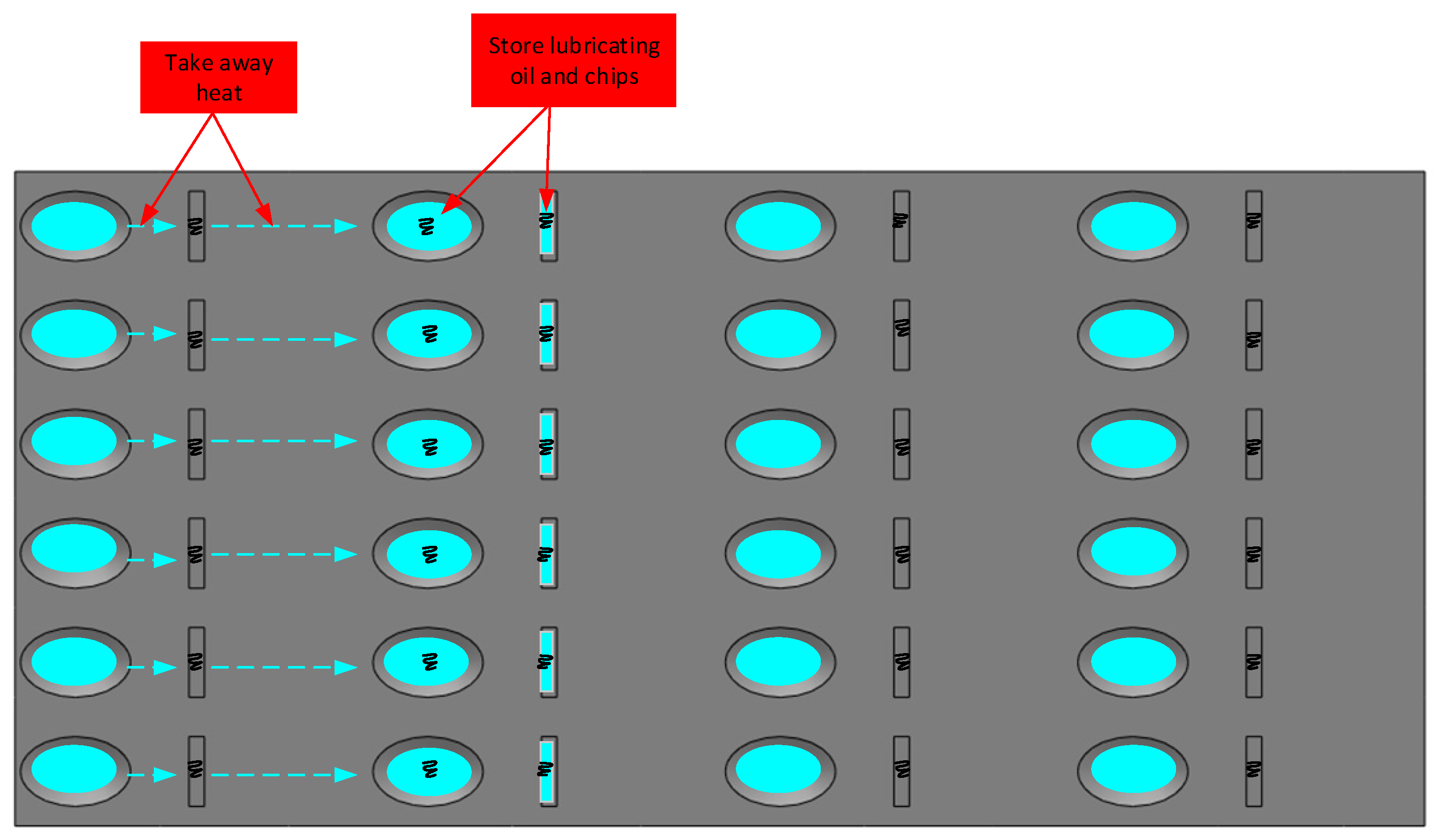
2.1. Selection of Biomimetic Design Prototypes
2.2. Fluid Lubrication Theory
- —friction, N;
- —velocity gradient along the direction of lubricating oil film thickness, S-1;
- —shear stress of lubricating oil, Pa;
- —friction coefficient, which is the ratio of frictional force to bearing pressure;
- T1—average temperature, °C;
- S—oil film area, mm2;
- D—integration region ;
- W—bearing capacity, N.
2.3. Analysis of the Coupling Mechanism of Composite Biomimetic Micro-Textures
3. Design and Scheme Optimization of Biomimetic Micro-Textured Guide Rail Friction Pairs
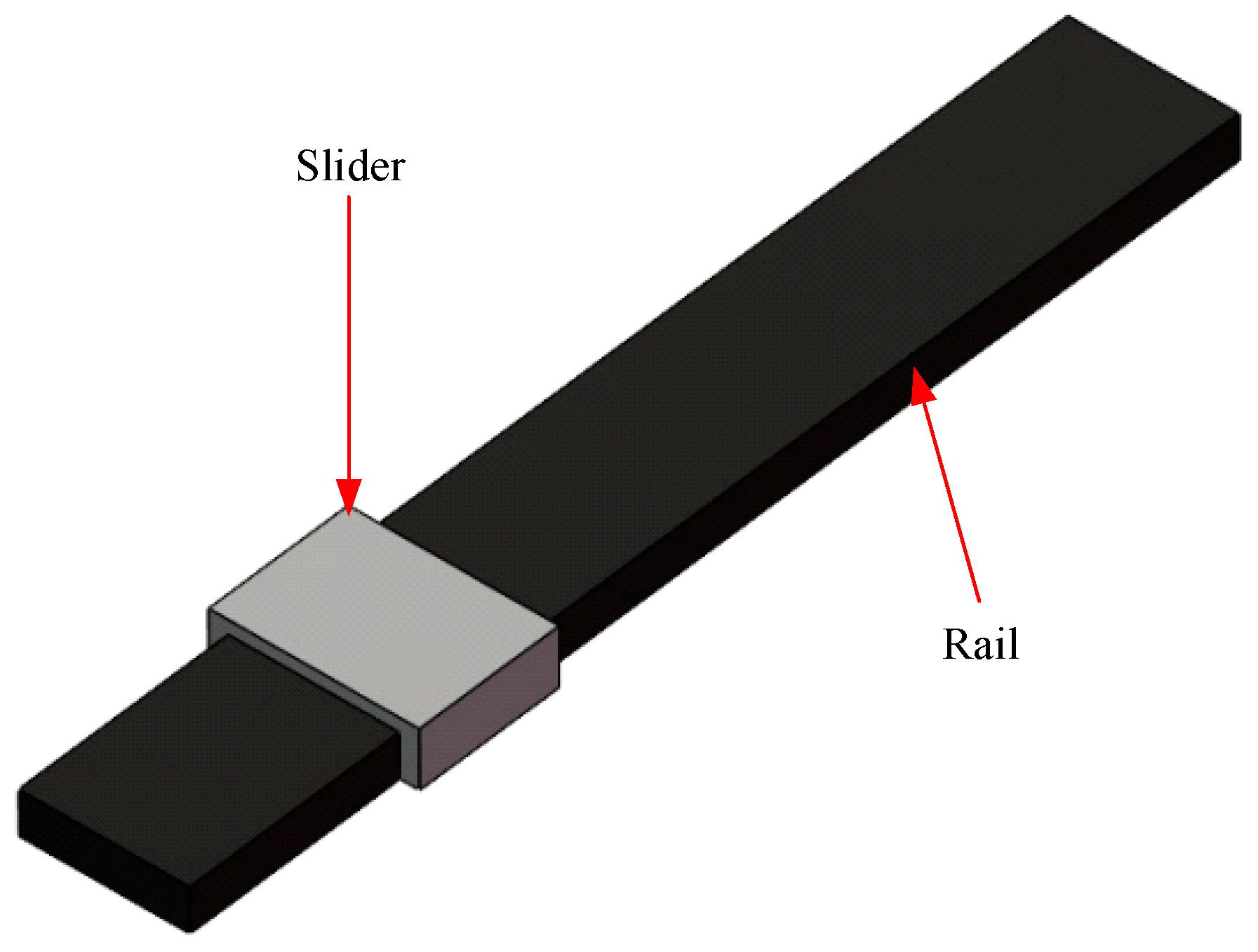
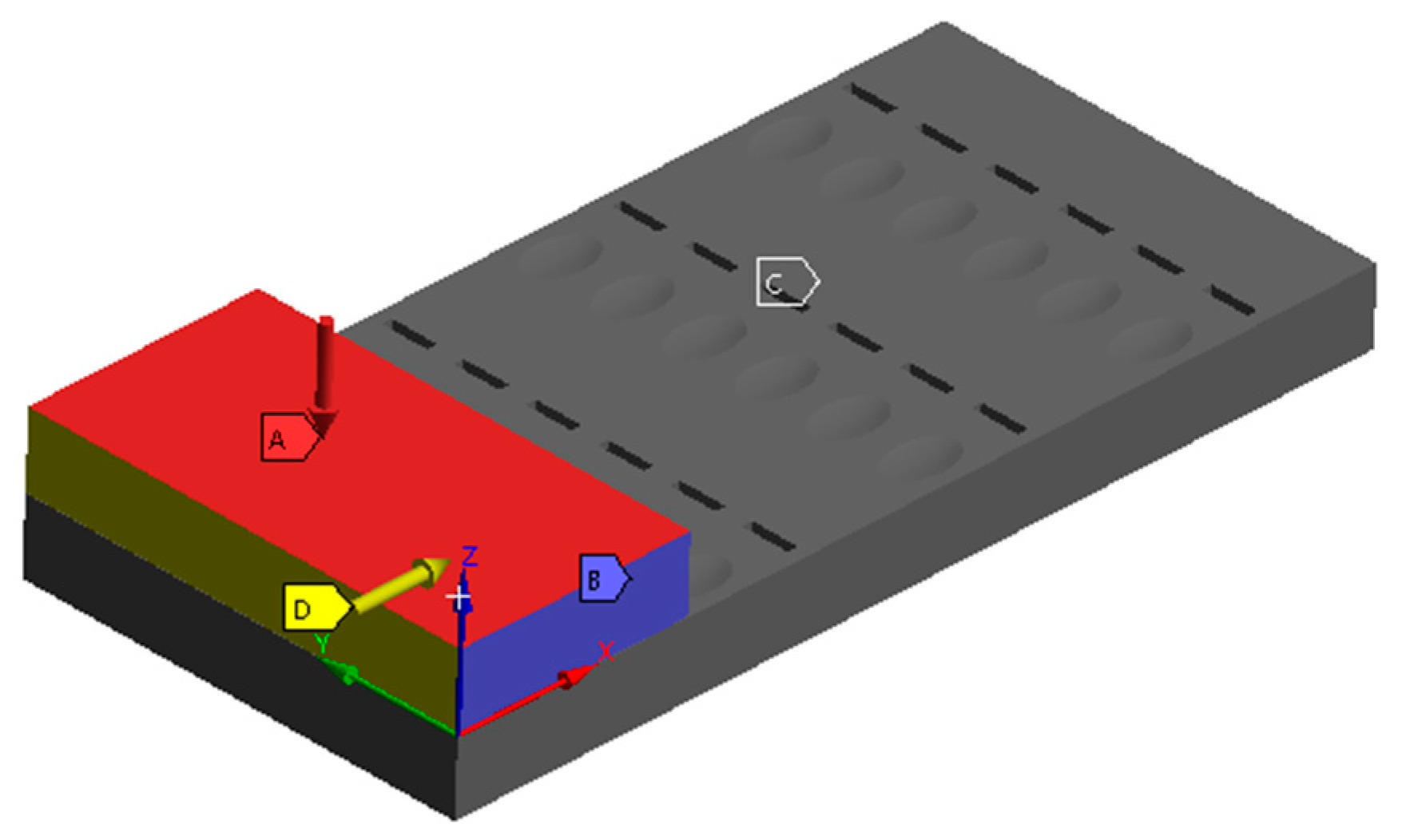
3.1. Determination of Prototype Guides
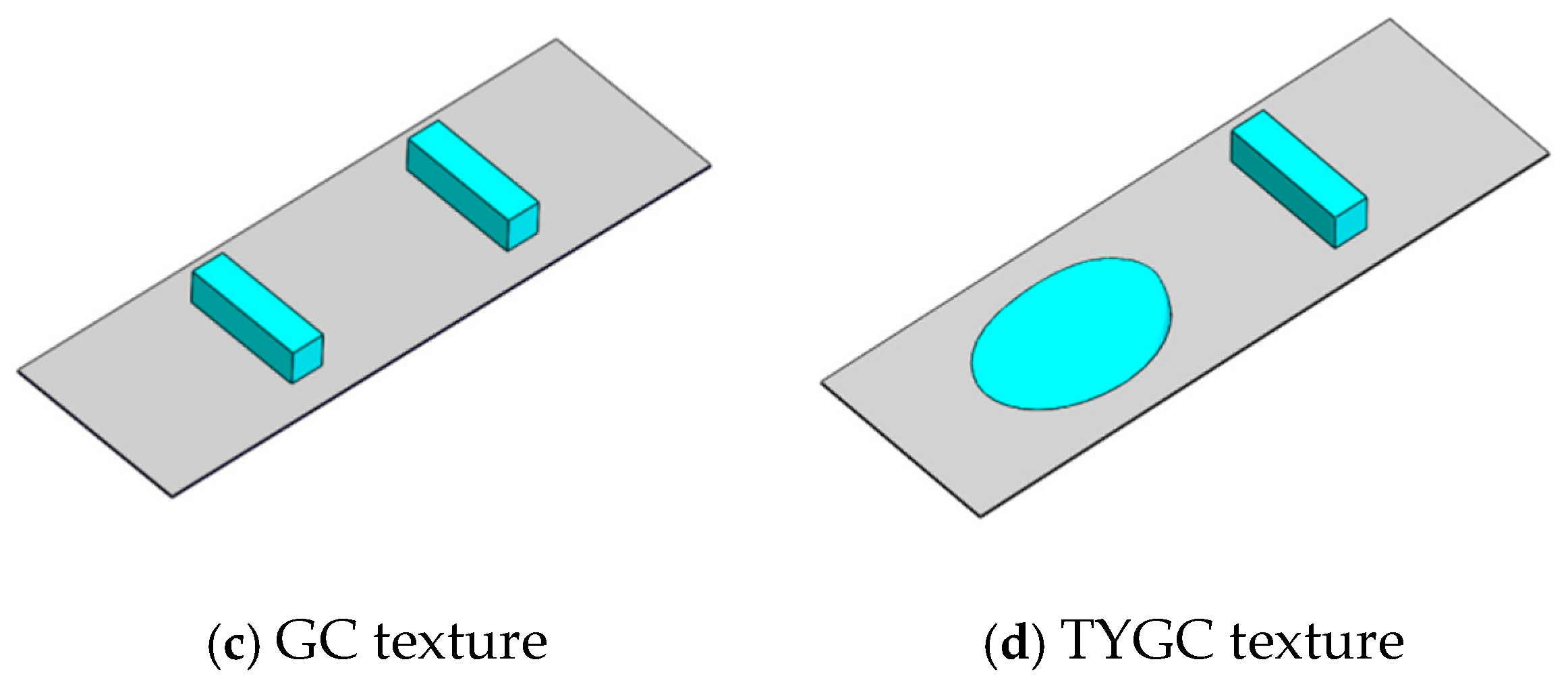
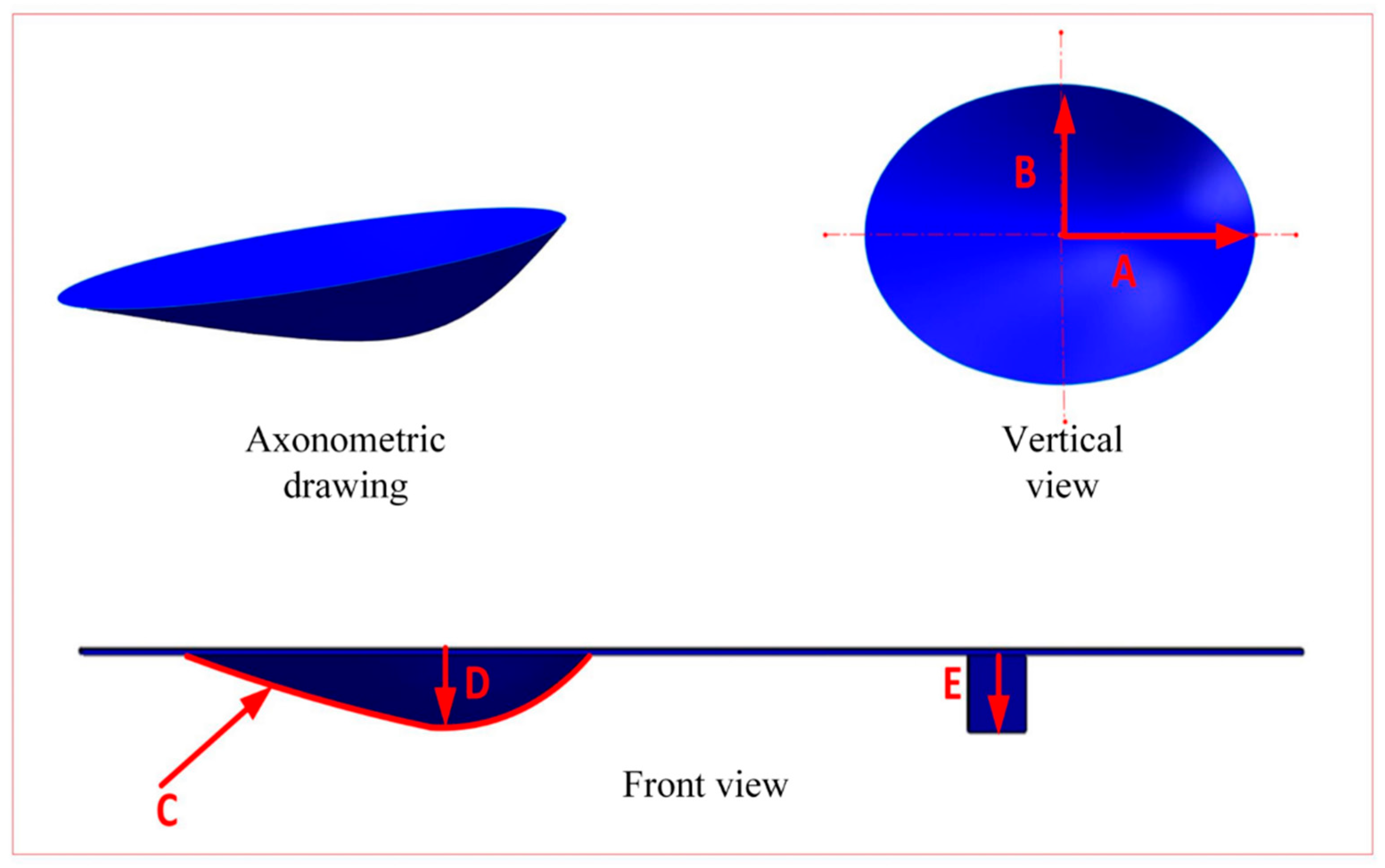
3.2. Surface Biomimetic Micro-Texture Design
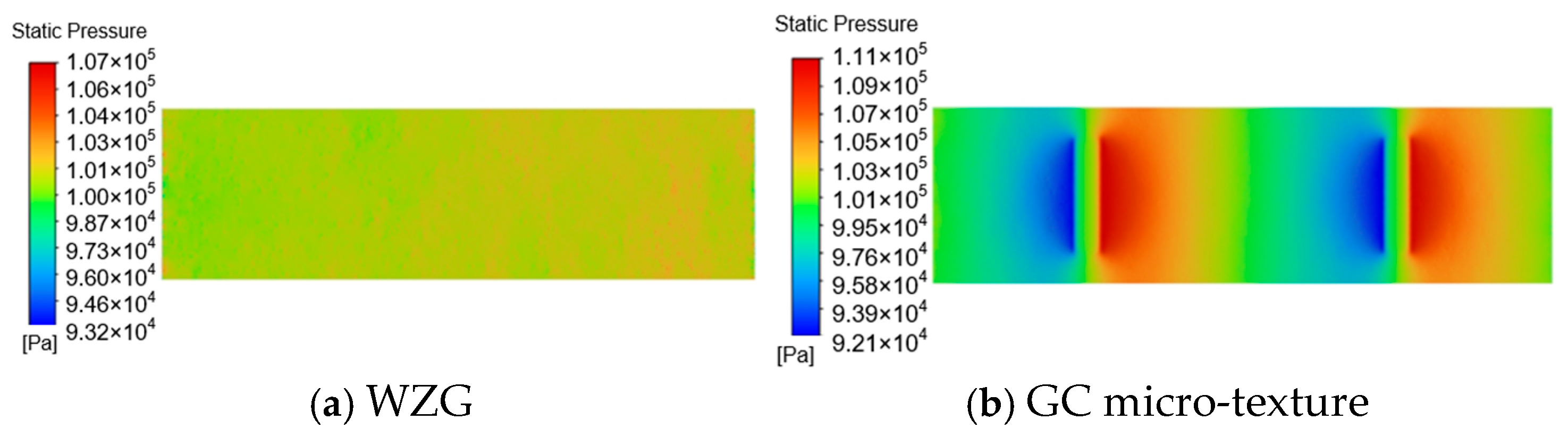
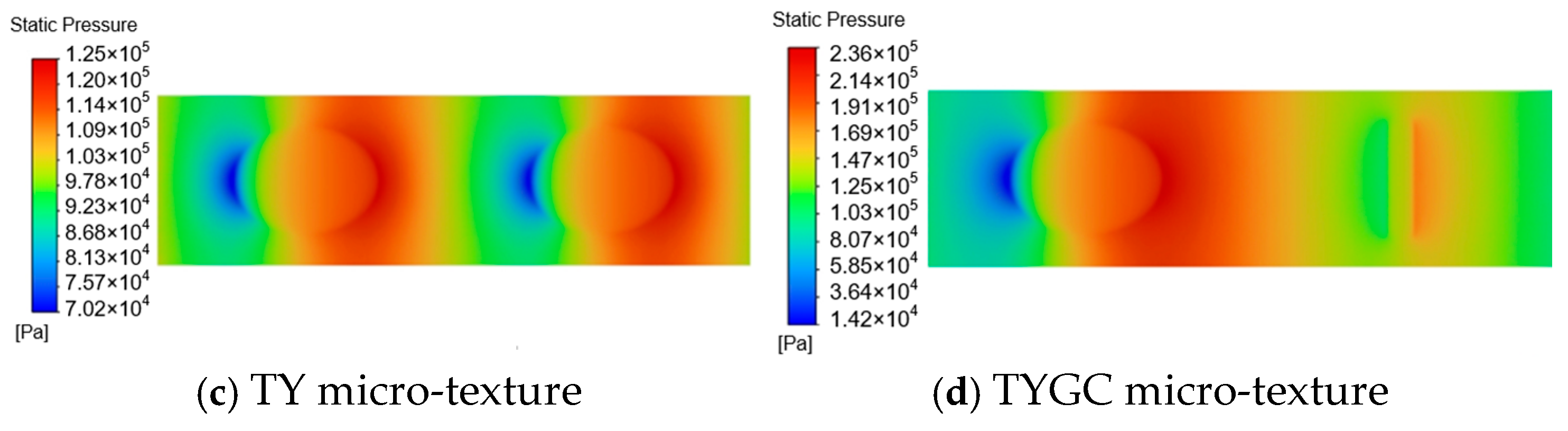
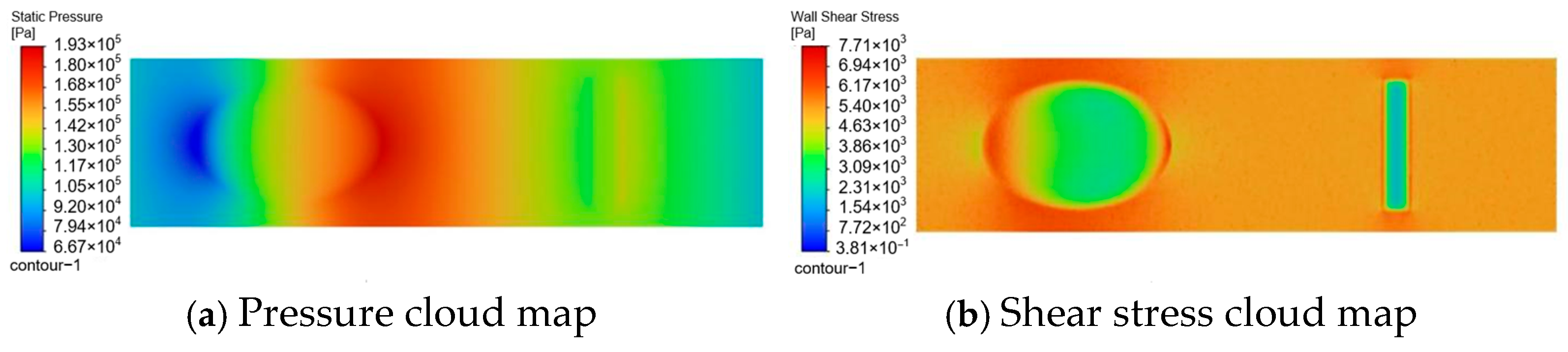
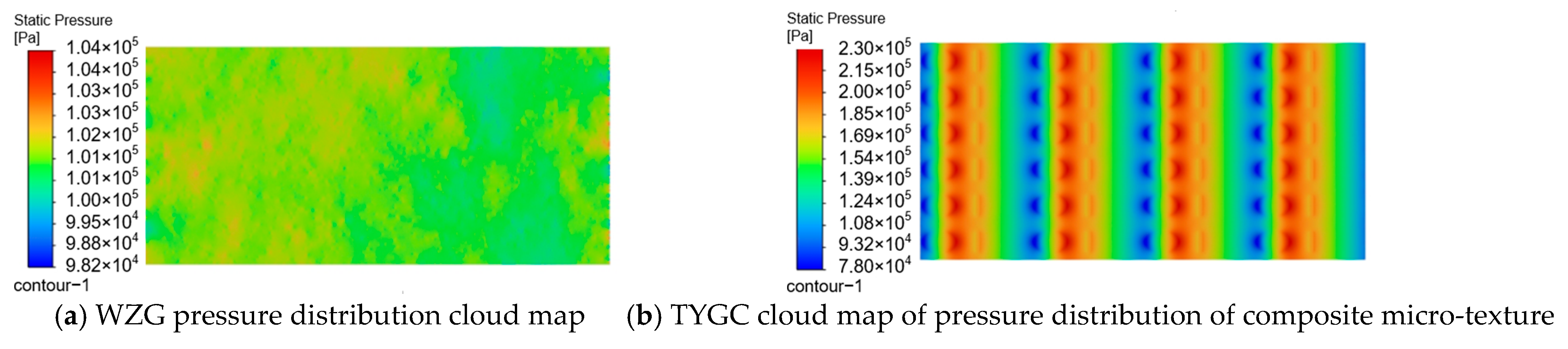
3.3. Simulation Result Analysis
4. Optimization of the Design of Combined Biomimetic Micro-Texture Parameters
4.1. Optimization of the Size Parameters for Composite Microstructures
4.2. Response Surface Methodology Scheme Design
5. Optimization of the Distribution Parameters and Performance Influence of Composite Micro-Textures
5.1. Distributed Parameter Optimization Design
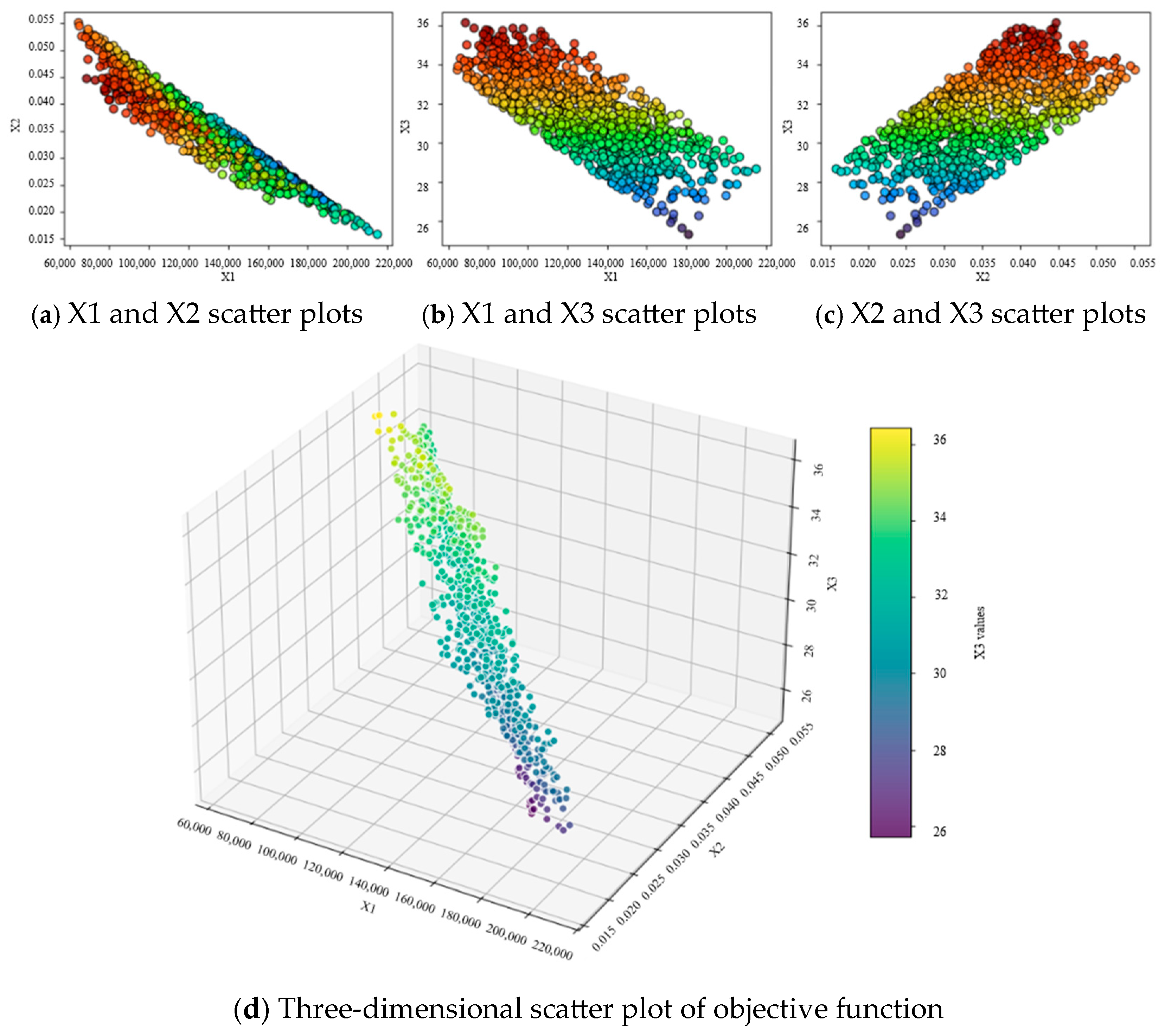
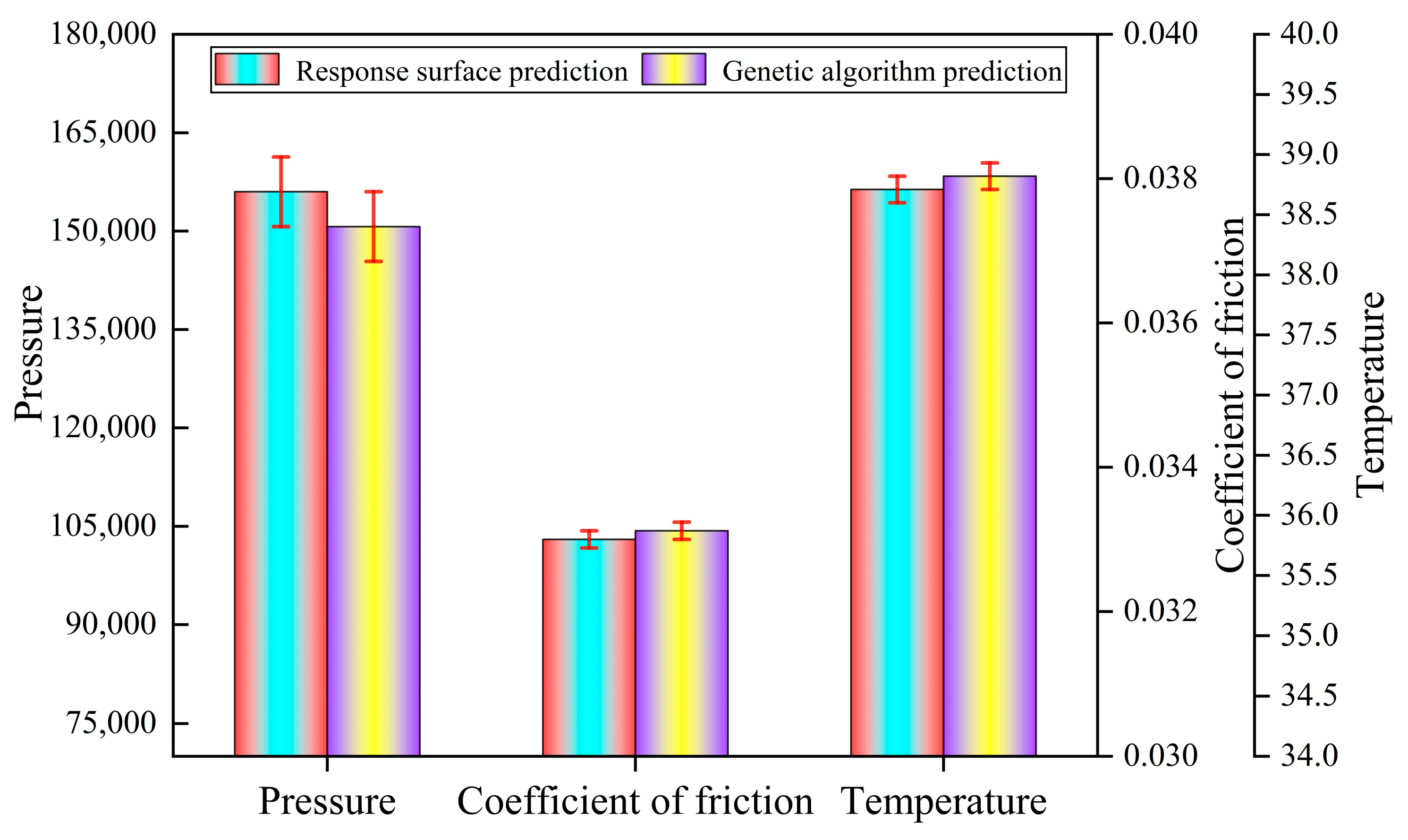
5.2. Genetic Algorithm Design and Validation
- X1(P)—micro-textured sliding slider guide rail pair bearing pressure;
- X2(P)—coefficient of friction;
- X3(P)—temperature;
- P1, P2, P3—micro-texture shape parameters A, B, and C.
5.3. Comparative Analysis of Combined Biomimetic Micro-Texture Oil Film Performance
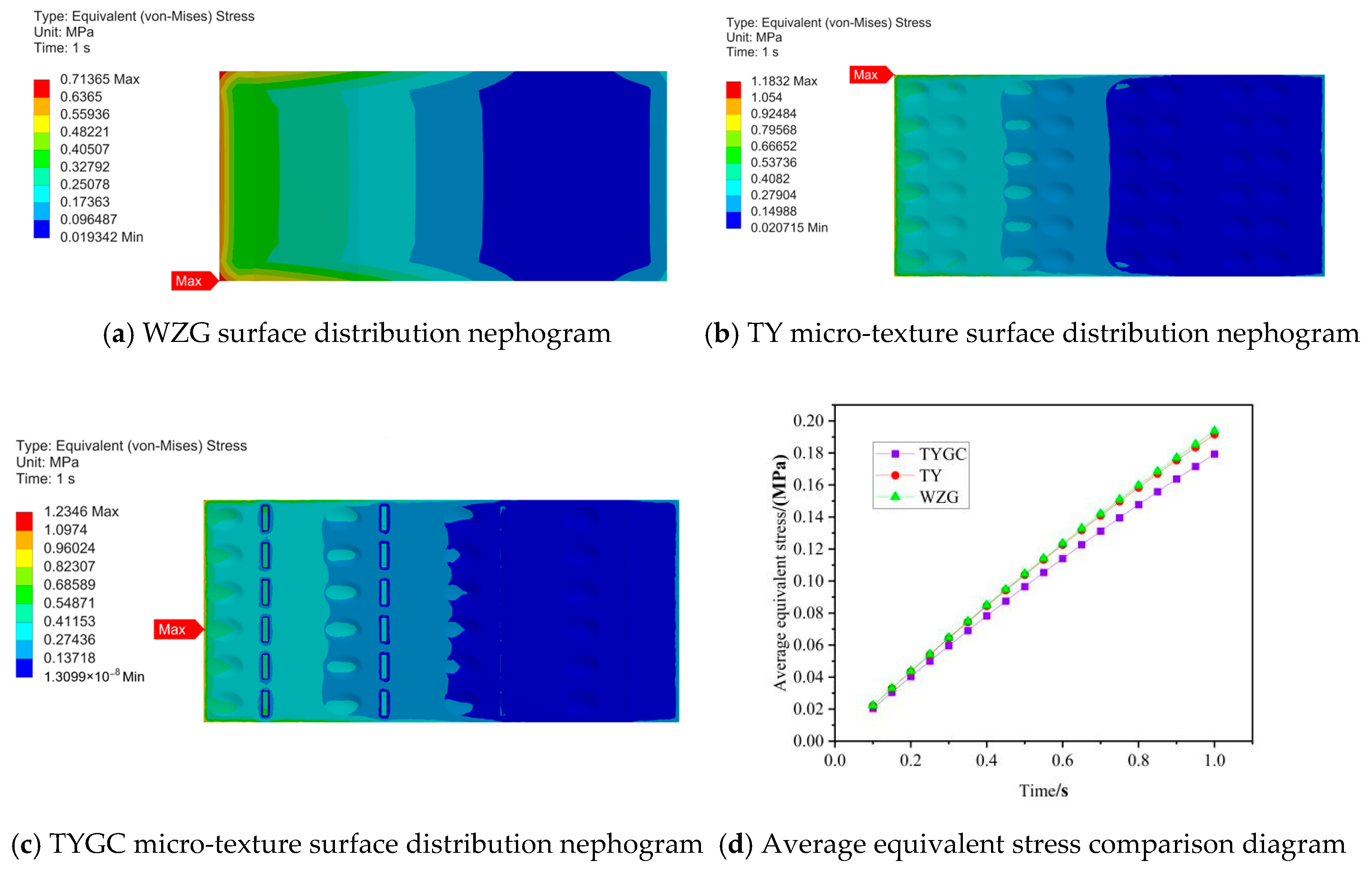
6. Simulation Analysis of the Contact Stress of Micro-Texture Guide Rails Under Oil Depletion Conditions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Hu, Y.; Tan, Y.; Zhang, L. Research on the Accuracy Maintenance of Machine Tool Sliding Guides under Boundary Lubrication Conditions. Mach. Tool Hydraul. 2020, 48, 93–96. [Google Scholar]
- Ogawa, H.; Sasaki, S.; Korenaga, A.; Miyake, K.; Nakano, M.; Murakami, T. Effects of surface texture size on the tribological properties of slideways. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 885–890. [Google Scholar] [CrossRef]
- Wos, S.; Koszela, W.; Pawlus, P. The effect of both surfaces textured on improvement of tribological properties of sliding elements. Tribol. Int. 2017, 113, 182–188. [Google Scholar] [CrossRef]
- Pang, Z.; Zhou, H.; Xie, G.; Cong, D.; Meng, C.; Ren, L. Effect of bionic coupling units’ forms on wear resistance of gray cast iron under dry linear reciprocating sliding condition. Opt. Laser Technol. 2015, 70, 89–93. [Google Scholar] [CrossRef]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G.; Etsion, I. The effect of laser texturing of steel surfaces and speed-load parameters on the transition of lubrication regime from boundary to hydrodynamic. Tribol. Trans. 2004, 47, 299–307. [Google Scholar] [CrossRef]
- Dykha, O.; Dytyniuk, V.; Kovtun, O.; Fasolia, V.; Hetman, M. Improving the wear resistance of guides: Tribological analysis, surface texture and lubricants. Probl. Tribol. 2025, 30, 51–59. [Google Scholar] [CrossRef]
- Atwal, J.C.; Pandey, R.K. Film thickness and friction investigations in a fluid film thrust bearing employing a new conceived micro-texture on pads. J. Tribol. 2021, 143, 061801. [Google Scholar] [CrossRef]
- Fu, Y.; Ji, J.; Bi, Q. The Influence of Partially Textured Slider with Oriented Parabolic Grooves on the Behavior of Hydrodynamic Lubrication. Tribol. Trans. 2012, 55, 210–217. [Google Scholar] [CrossRef]
- Wang, H.; Xie, X.; Hua, X.; Yin, B.; Du, H.; Xu, S.; Qiu, B.J. The effect of laser surface texturing to inhibit stick-slip phenomenon in sliding contact. Adv. Mech. Eng. 2019, 11, 1687814019874635. [Google Scholar] [CrossRef]
- He, Y.; Fu, Y.; Wang, H.; Yang, J. Inhibiting mechanism of micro dimples on the stick-slip of sliding guideway: Combined numerical analysis with tribological tests. Tribol. Int. 2021, 162, 107144. [Google Scholar] [CrossRef]
- He, Y.; Fu, Y.; Wang, H.; Yang, J. Enhancing anti-stick-slip performance by laser surface texturing on sliding guideway surface. J. Manuf. Process. 2022, 75, 1089–1099. [Google Scholar] [CrossRef]
- He, Y.; Yang, J.; Wang, H.; Gu, Z.; Fu, Y. Micro-dimple and micro-bulge textures: Influence of surface topography types on stick--slip behavior under starved lubrication. Appl. Surf. Sci. 2022, 585, 152501. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, J.; Wang, H.; He, Y. Effect of laser-textured micro dimples on inhibition of stick-slip phenomenon of sliding guideway. Ind. Lubr. Tribol. 2022, 74, 34–44. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, T.; Zhou, H.; Chen, Z.; Yang, W.; Ren, L. Effects of different bionic units coupling on the sliding wear of gray cast iron. Surf. Coat. Technol. 2017, 309, 96–105. [Google Scholar] [CrossRef]
- Ji, J.; Dong, B.; Fu, H.; Wang, W.; Zhang, Y. Hydrodynamic lubrication of textured infinitely long slider with cross-hatched texture. Meccanica 2019, 54, 2067–2079. [Google Scholar] [CrossRef]
- Han, H.; Wu, S.; Wu, G.; Fu, Y.; Zhu, W.; Song, C.; Zhang, X. Research on Laser Biomimetic micro texture to improve the friction characteristics of sliding guide. Appl. Laser 2018, 38, 436–441. [Google Scholar]
- Xie, X. Research on Friction Reduction and Anti Creep of Sliding Guide Rail Based on Laser Composite Micro Texture Technology; Jiangsu University: Zhenjiang, China, 2018. [Google Scholar]
- Zhang, D.; Zhao, F.; Gao, F.; Duan, J. Effect of two-layer groove texture on surface lubrication characteristics ofmachine tool guide rail. China Mech. Eng. 2018, 29, 1661–1665. [Google Scholar]
- Zhang, D.; Zhao, F.; Li, Y.; Li, P.; Zeng, Q.; Dong, G. Study on tribological properties of multi-layer surface texture on Babbitt alloys surface. Appl. Surf. Sci. 2016, 390, 540–549. [Google Scholar] [CrossRef]
- Zhu, K.; Jin, J.; Sun, J. Study on lubrication characteristics of parallel slider with surface texture. Metrol. Test. Technol. 2016, 43, 90–92. [Google Scholar]
- Zhang, Y. Study on the Influence of Micro Texture on the Friction and Wear Characteristics of Guide Rail; Shandong University: Jinan, China, 2021. [Google Scholar]
- Fan, Y.; Chen, M.; Hao, M.; Wang, S.; Du, Y.; Xia, J.; Guan, X. Research on the improvement of sliding guide surface creep phenomenon by composite lubrication structure. China Mech. Eng. 2024, 35, 1740–1746+1761. [Google Scholar]
- Yue, H. Study on the Effect of Surface Texture on the Friction and Lubrication Characteristics of Sliding Guide; Shandong University: Jinan, China, 2022. [Google Scholar]
- Chen, C. Research on Anti Creep and Friction Reduction Technology of Laser Micro Texture on Sliding Guide Surface; Jiangsu University: Jinan, China, 2022. [Google Scholar]
- Ahmed, Y.S.; Paiva, J.M.; Arif, A.; Amorim, F.L.; Torres, R.D.; Veldhuis, S. The effect of laser micro-scale textured tools on the tool-chip interface performance and surface integrity during austenitic stainless-steel turning. Appl. Surf. Sci. 2020, 510, 145455. [Google Scholar] [CrossRef]
- Qi, Z.; Chen, X.; Liu, Y.; Wang, L. Optimization of Texture Parameters for Combination Micro textured Cutting Tools. Equip. Mach. 2023, 32–36+52. [Google Scholar]
- Tang, Z.; Liu, S.; Liu, J.; Jiang, S.; Liao, J. Study on the Triboelectric Properties of Composite Micro textured Aluminum Alloy Surface. Lubr. Seal. 2022, 47, 84–91. [Google Scholar]
- Zhang, W. Research on Design and Sealing Performance of Tail Shaft Transmission System of Large Depth AUV Platform; Harbin Engineering University: Harbin, China, 2018. [Google Scholar]
- Wang, X.; Wang, J.; Han, W. Study on friction reduction characteristics of surface micro texture under boundary lubrication. Lubr. Seal. 2007, 36–39. [Google Scholar]
- Yin, B.; Qian, Y.; Dong, F.; Lu, Z. Simulation and experimental study on Tribological Properties of grooved texture. Lubr. Seal. 2012, 37, 9–13. [Google Scholar]
- Dai, J.; Zhang, H.; Zhang, Y.; Hua, X.; Fu, Y. Research on the Low Reynolds Number k–ε Model of Lubrication Field in Trapezoidal Groove Texture Friction Pair. J. Jiangsu Univ. Sci. Technol. (Nat. Sci. Ed.) 2018, 32, 351–356. [Google Scholar]
- Liu, C.; Li, W.; Lu, X.; Zhao, B. Effects of double parabolic profiles with groove textures on the hydrodynamic lubrication performance of journal bearing under steady operating conditions. Mech. Ind. 2020, 21, 301. [Google Scholar] [CrossRef]
- Reynolds, O.I.V. On the theory of lubrication and its application to Mr. Beauchamp tower’sexperiments, including an experimental determination of the viscosity of olive oil. Philos. Ofthe R. Soc. Oflondon 1886, 157–234. [Google Scholar]
- Yu, Y.; Wang, Z. Want golden dragons, etc Multi objective optimization design of micro texture for machine tool sliding guide rails. Aerosp. Manuf. Technol. 2022, 65, 36–44. [Google Scholar]
- Meng, F.M.; Wang, Q.J.; Hua, D.; Liu, J. A simple method to calculate contact factor used in average flow model. J. Tribol. 2010, 132, 483–485. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Huang, L.; Qu, R.; Nojima, Y. A Pareto Front grid guided multi-objective evolutionary algorithm. Appl. Soft Comput. 2023, 136, 110095. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J.; Hua, X.; Li, L.; Sun, Y.; Zhu, Y. Simulation study on friction reduction and anti crawling of sliding guide based on laser composite texture technology. Lubr. Seal. 2025, 1, 1–9. [Google Scholar]



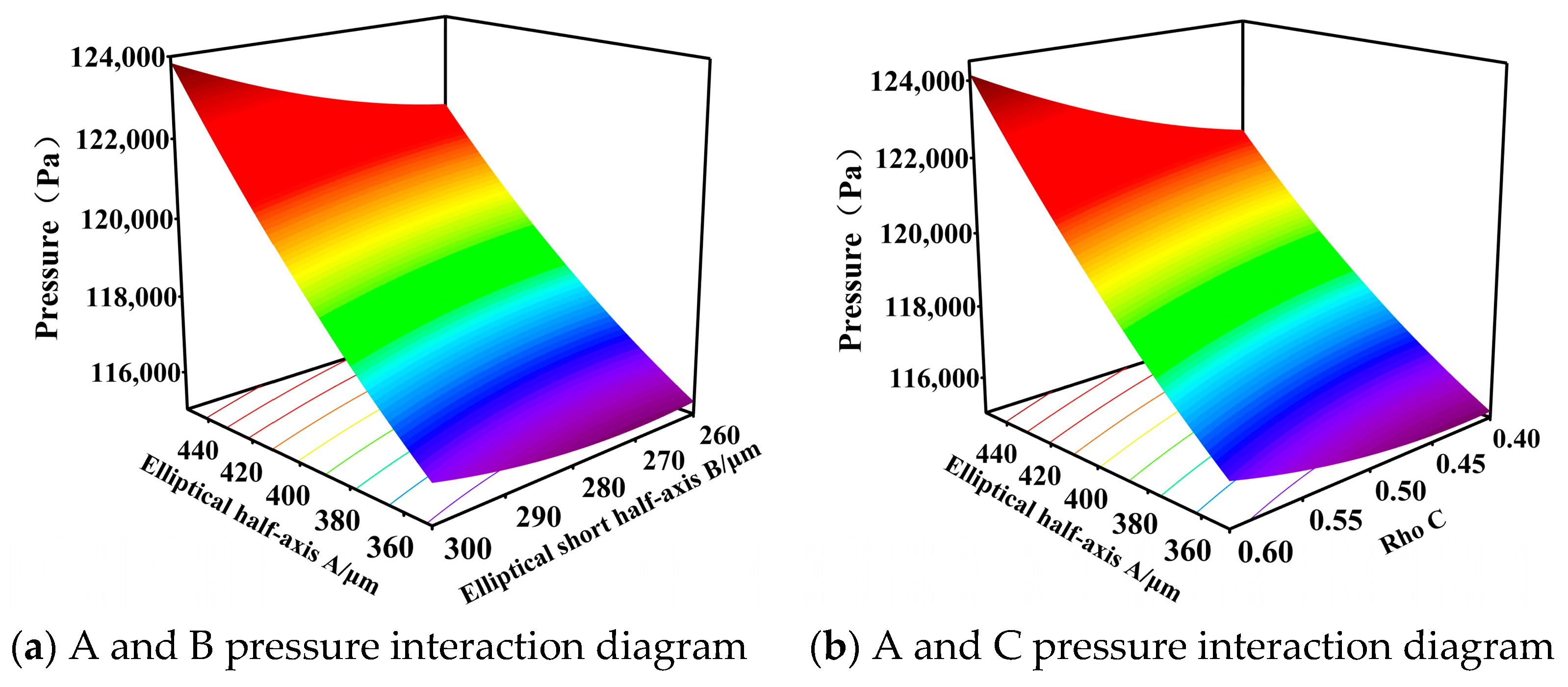
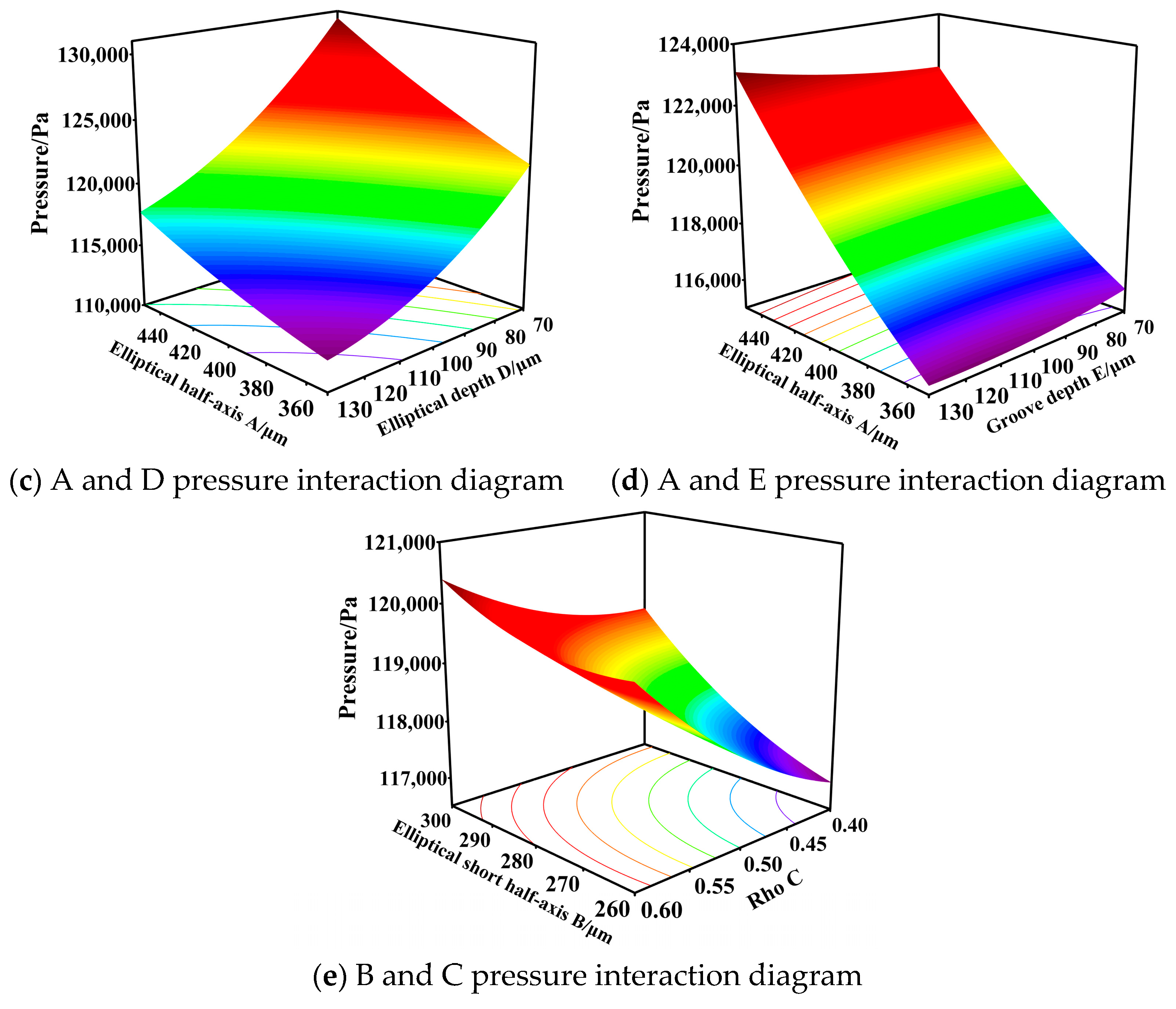
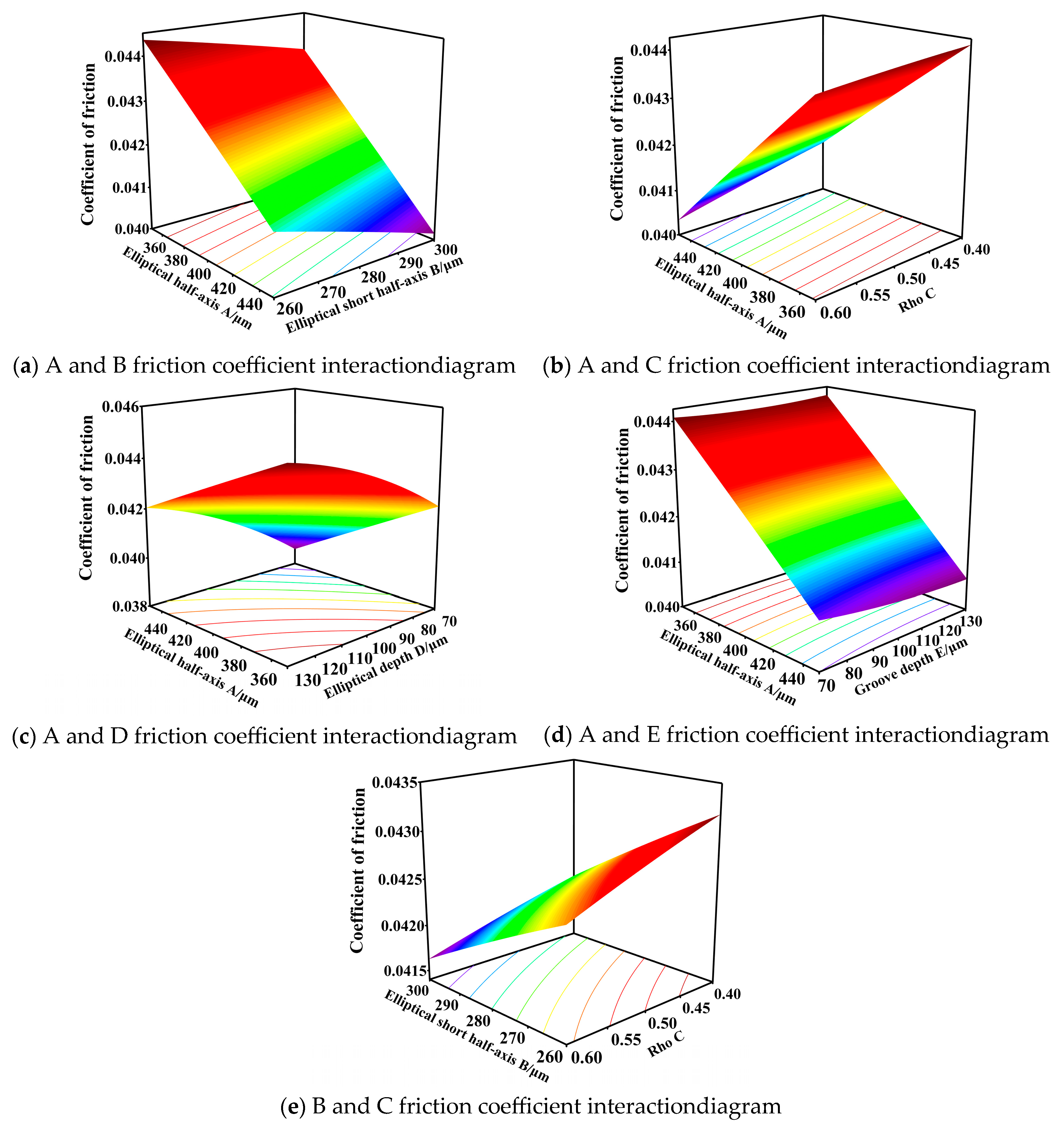


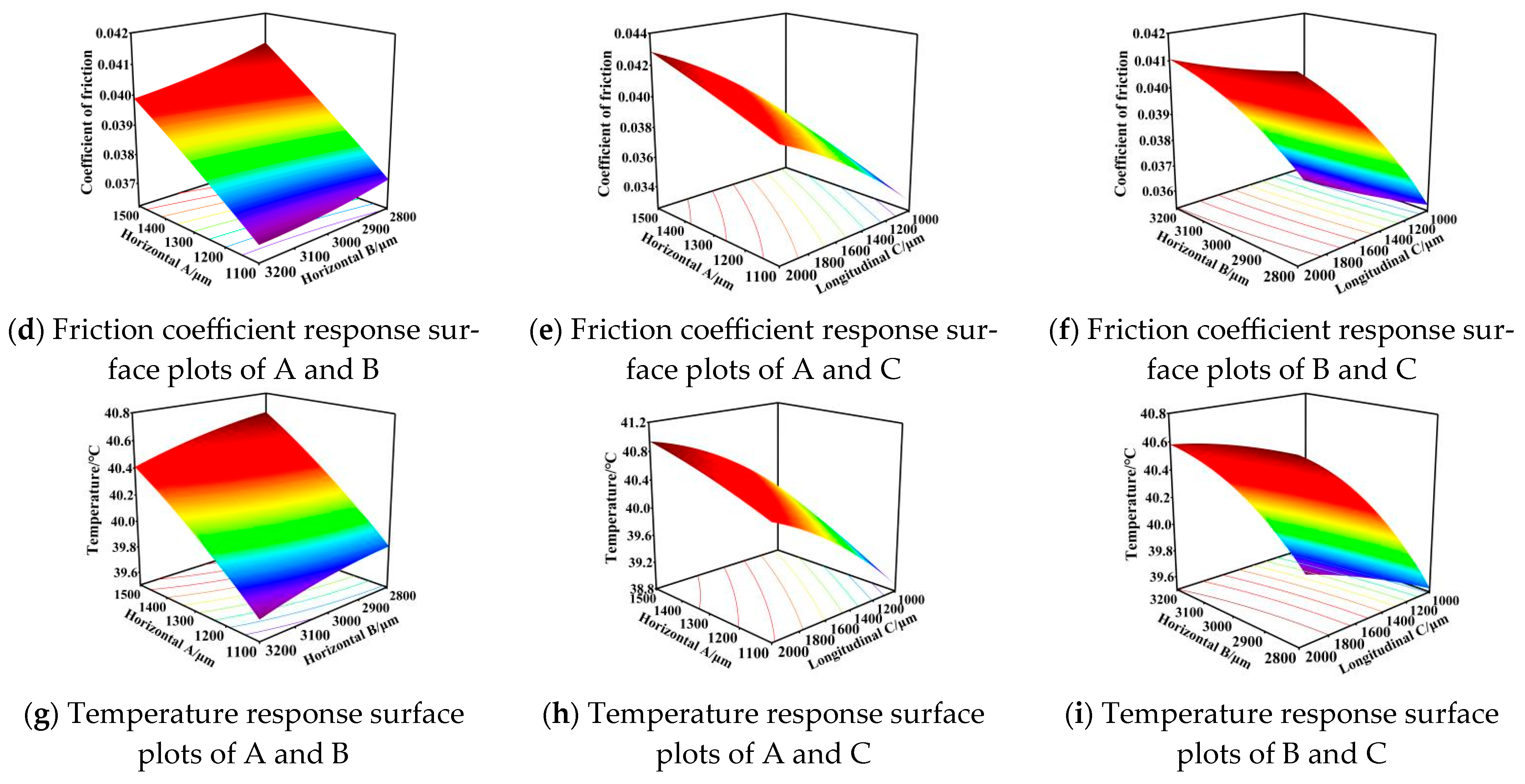





| Input Parameter | Output Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Number | A/μm | B/μm | C | D/μm | E/μm | Pressure/Pa | Coefficient of Friction |
| 1 | 450 | 300 | 0.4 | 130 | 130 | 119,821 | 0.0417 |
| 2 | 350 | 300 | 0.6 | 70 | 130 | 120,280 | 0.0416 |
| 3 | 400 | 280 | 0.3 | 100 | 100 | 117,957 | 0.0429 |
| 4 | 350 | 300 | 0.6 | 70 | 70 | 124,046 | 0.0417 |
| 5 | 450 | 300 | 0.6 | 130 | 70 | 120,909 | 0.0413 |
| 6 | 400 | 280 | 0.5 | 100 | 100 | 119,512 | 0.0422 |
| 7 | 350 | 300 | 0.6 | 130 | 70 | 114,263 | 0.0444 |
| 8 | 400 | 280 | 0.5 | 100 | 100 | 119,663 | 0.0425 |
| 9 | 350 | 260 | 0.6 | 130 | 70 | 113,576 | 0.0452 |
| 10 | 450 | 300 | 0.6 | 70 | 130 | 133,832 | 0.0371 |
| 11 | 450 | 260 | 0.4 | 130 | 130 | 116,932 | 0.0428 |
| 12 | 450 | 260 | 0.4 | 70 | 70 | 124,893 | 0.0408 |
| 13 | 400 | 280 | 0.5 | 100 | 100 | 118,547 | 0.0426 |
| 14 | 400 | 280 | 0.5 | 160 | 100 | 113,117 | 0.0442 |
| 15 | 350 | 300 | 0.6 | 130 | 130 | 114,427 | 0.0449 |
| 16 | 400 | 320 | 0.5 | 100 | 100 | 121,019 | 0.0414 |
| 17 | 450 | 300 | 0.4 | 70 | 130 | 131,395 | 0.0385 |
| 18 | 400 | 280 | 0.5 | 100 | 100 | 117,598 | 0.0423 |
| 19 | 450 | 260 | 0.4 | 130 | 70 | 115,793 | 0.0429 |
| 20 | 500 | 280 | 0.5 | 100 | 100 | 127,110 | 0.0391 |
| 21 | 450 | 300 | 0.4 | 70 | 70 | 131,153 | 0.0386 |
| 22 | 350 | 300 | 0.4 | 130 | 70 | 112,860 | 0.0448 |
| 23 | 400 | 240 | 0.5 | 100 | 100 | 118,835 | 0.0432 |
| 24 | 350 | 260 | 0.4 | 130 | 130 | 112,424 | 0.0457 |
| 25 | 350 | 300 | 0.4 | 70 | 130 | 122,588 | 0.0417 |
| 26 | 400 | 280 | 0.7 | 100 | 100 | 121,982 | 0.0417 |
| 27 | 350 | 260 | 0.6 | 130 | 130 | 113,662 | 0.0451 |
| 28 | 400 | 280 | 0.5 | 100 | 160 | 119,841 | 0.0425 |
| 29 | 350 | 300 | 0.4 | 130 | 130 | 113,085 | 0.0447 |
| 30 | 450 | 300 | 0.4 | 130 | 70 | 117,654 | 0.0419 |
| 31 | 400 | 280 | 0.5 | 100 | 40 | 118,992 | 0.0428 |
| 32 | 450 | 260 | 0.6 | 130 | 70 | 118,925 | 0.0422 |
| 33 | 400 | 280 | 0.5 | 100 | 100 | 116,348 | 0.0424 |
| 34 | 450 | 300 | 0.6 | 70 | 70 | 133,532 | 0.0380 |
| 35 | 400 | 280 | 0.5 | 100 | 100 | 118,542 | 0.0425 |
| 36 | 450 | 300 | 0.6 | 130 | 130 | 120,057 | 0.0412 |
| 37 | 350 | 260 | 0.4 | 70 | 70 | 121,067 | 0.0430 |
| 38 | 300 | 280 | 0.5 | 100 | 100 | 113,834 | 0.0455 |
| 39 | 450 | 260 | 0.6 | 70 | 70 | 131,936 | 0.0389 |
| 40 | 450 | 260 | 0.6 | 130 | 130 | 119,043 | 0.0423 |
| 41 | 400 | 280 | 0.5 | 100 | 100 | 117,456 | 0.0425 |
| 42 | 400 | 280 | 0.5 | 40 | 100 | 137,567 | 0.0373 |
| 43 | 450 | 260 | 0.4 | 70 | 130 | 129,779 | 0.0394 |
| 44 | 450 | 260 | 0.6 | 70 | 130 | 131,999 | 0.0389 |
| 45 | 350 | 260 | 0.4 | 70 | 130 | 121,295 | 0.0429 |
| 46 | 350 | 260 | 0.6 | 70 | 70 | 123,701 | 0.0426 |
| 47 | 350 | 300 | 0.4 | 70 | 70 | 123,291 | 0.0422 |
| 48 | 400 | 280 | 0.5 | 100 | 100 | 119,256 | 0.0423 |
| 49 | 350 | 260 | 0.4 | 130 | 70 | 111,138 | 0.0453 |
| 50 | 350 | 260 | 0.6 | 70 | 130 | 121,799 | 0.0424 |
| Input Parameter | Output Parameters | |||||
|---|---|---|---|---|---|---|
| Number | A/μm | B/μm | C/μm | Pressure/Pa | Coefficient of Friction | Temperature/°C |
| 1 | 1100 | 3000 | 2000 | 134,091 | 0.0396 | 40.34 |
| 2 | 1300 | 2800 | 2000 | 127,051 | 0.0417 | 40.71 |
| 3 | 1500 | 3000 | 1000 | 139,623 | 0.0367 | 39.88 |
| 4 | 1500 | 2800 | 1500 | 127,596 | 0.0410 | 40.62 |
| 5 | 1300 | 3000 | 1500 | 135,924 | 0.0386 | 40.10 |
| 6 | 1500 | 3200 | 1500 | 131,976 | 0.0399 | 40.39 |
| 7 | 1300 | 3000 | 1500 | 135,795 | 0.0387 | 40.23 |
| 8 | 1100 | 3000 | 1000 | 154,464 | 0.0332 | 38.85 |
| 9 | 1100 | 2800 | 1500 | 140,551 | 0.0372 | 39.84 |
| 10 | 1500 | 3000 | 2000 | 124,185 | 0.0428 | 40.98 |
| 11 | 1100 | 3200 | 1500 | 143,376 | 0.0367 | 39.68 |
| 12 | 1300 | 3000 | 1500 | 135,865 | 0.0387 | 40.23 |
| 13 | 1300 | 3200 | 1000 | 148,539 | 0.0347 | 39.28 |
| 14 | 1300 | 3200 | 2000 | 129,935 | 0.0411 | 40.56 |
| 15 | 1300 | 2800 | 1000 | 143,832 | 0.0355 | 39.55 |
| 16 | 1300 | 3000 | 1500 | 135,265 | 0.0387 | 40.23 |
| 17 | 1300 | 3000 | 1500 | 135,865 | 0.0387 | 40.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Yan, B.; Zheng, M.; Mu, H.; Liu, C.; Wang, D.; Li, X.; Li, Q.; Jiang, H.; Wang, F.; et al. Optimization of Micro-Texture Parameters for Machine Tool Guide Rail Combination Based on Response Surface Methodology and Research on Its Anti-Friction and Lubrication Performance. Lubricants 2025, 13, 243. https://doi.org/10.3390/lubricants13060243
Cui Y, Yan B, Zheng M, Mu H, Liu C, Wang D, Li X, Li Q, Jiang H, Wang F, et al. Optimization of Micro-Texture Parameters for Machine Tool Guide Rail Combination Based on Response Surface Methodology and Research on Its Anti-Friction and Lubrication Performance. Lubricants. 2025; 13(6):243. https://doi.org/10.3390/lubricants13060243
Chicago/Turabian StyleCui, Youzheng, Bingyang Yan, Minli Zheng, Haijing Mu, Chengxin Liu, Dongyang Wang, Xinmiao Li, Qingwei Li, Hui Jiang, Fengjuan Wang, and et al. 2025. "Optimization of Micro-Texture Parameters for Machine Tool Guide Rail Combination Based on Response Surface Methodology and Research on Its Anti-Friction and Lubrication Performance" Lubricants 13, no. 6: 243. https://doi.org/10.3390/lubricants13060243
APA StyleCui, Y., Yan, B., Zheng, M., Mu, H., Liu, C., Wang, D., Li, X., Li, Q., Jiang, H., Wang, F., & Hu, Q. (2025). Optimization of Micro-Texture Parameters for Machine Tool Guide Rail Combination Based on Response Surface Methodology and Research on Its Anti-Friction and Lubrication Performance. Lubricants, 13(6), 243. https://doi.org/10.3390/lubricants13060243






