Dynamic Motion of a Vane in Six Degrees of Freedom and Its Effect on Wear in a Rotary-Vane Compressor Considering Fluid Lubrication
Abstract
1. Introduction
2. Method of Analysis
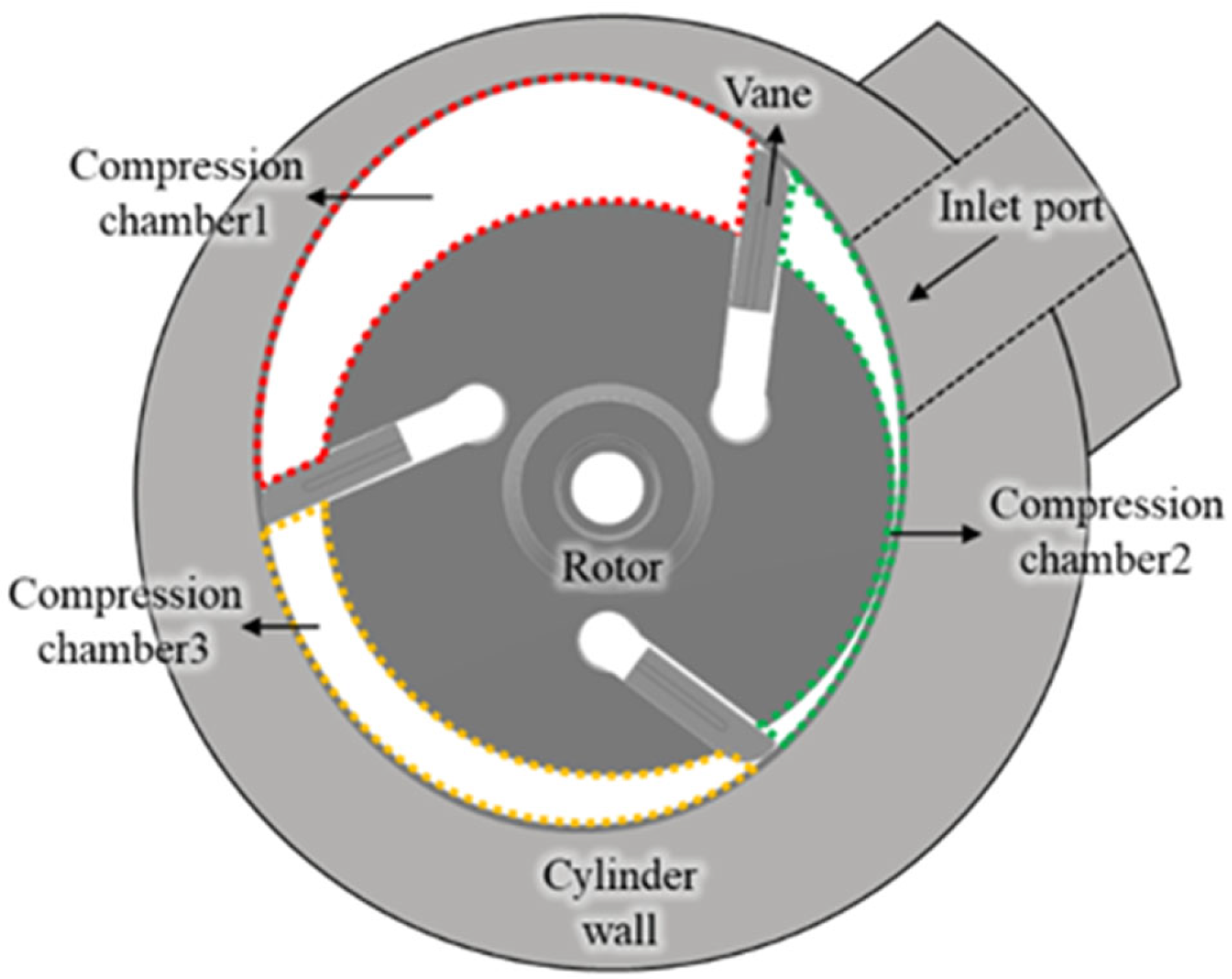
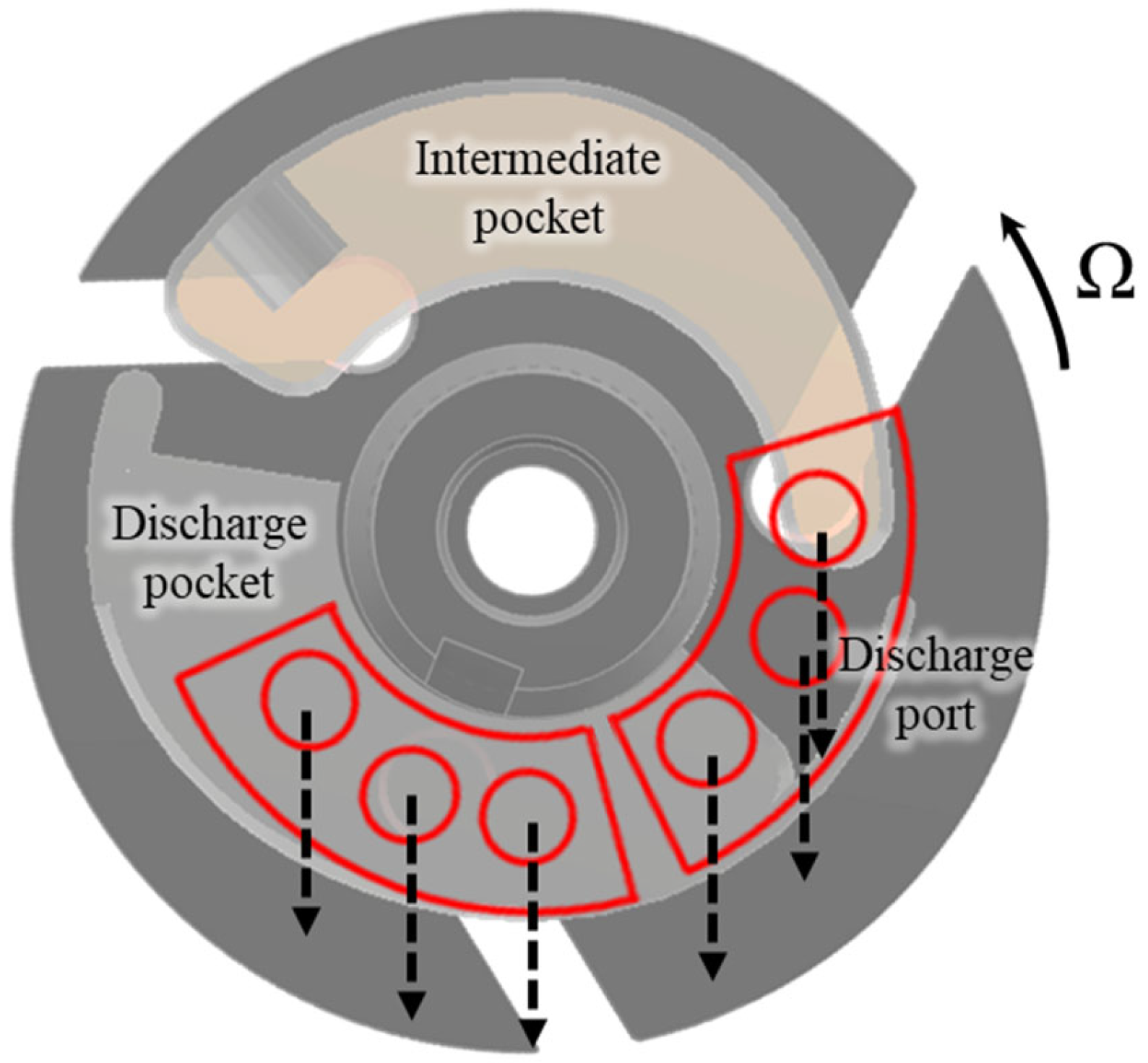
2.1. A Rotary-Vane Compressor
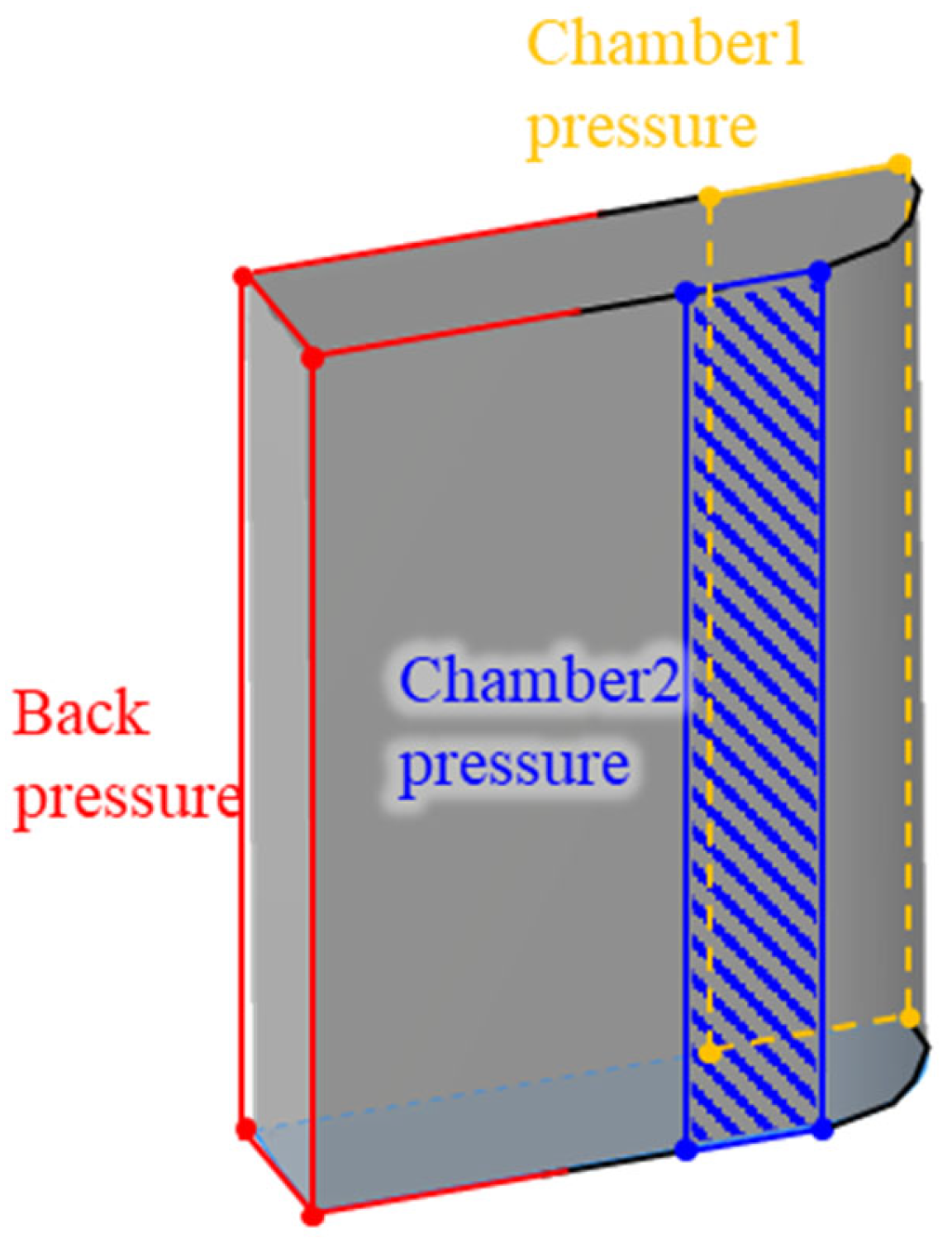
2.2. Gas Pressure of the Compression Chamber
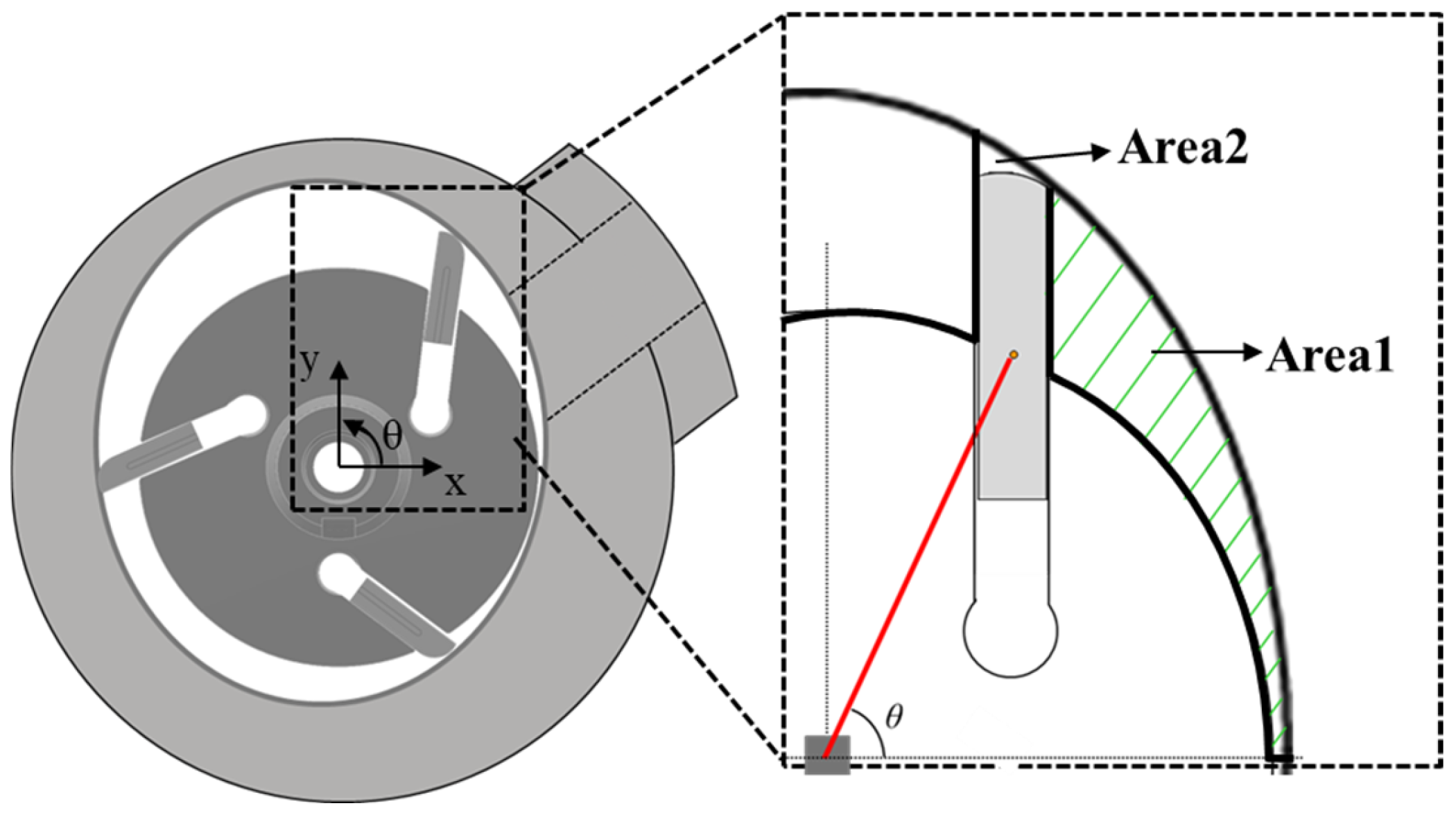
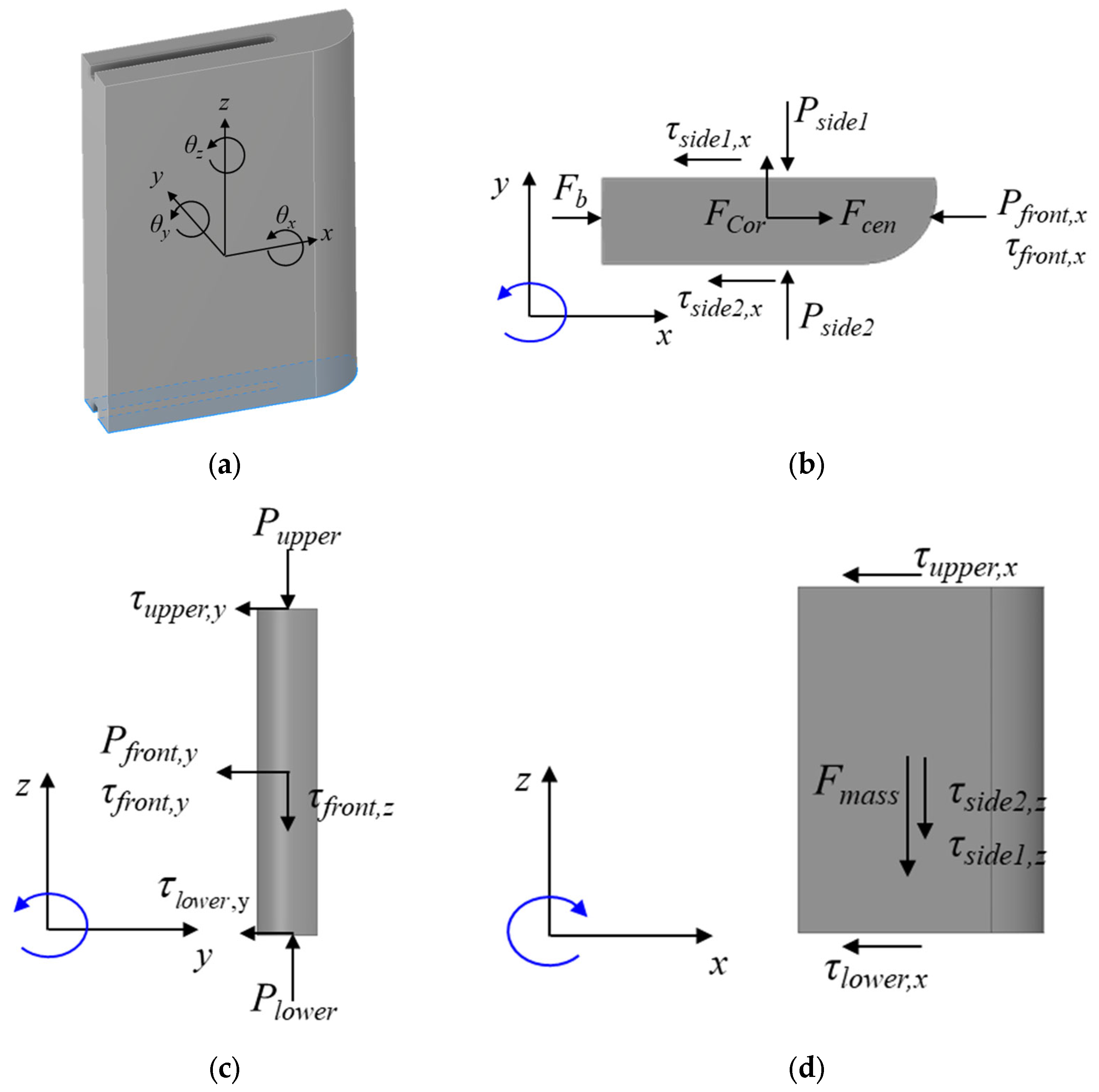
2.3. Pressure and Shear Stress Due to Fluid Lubrication
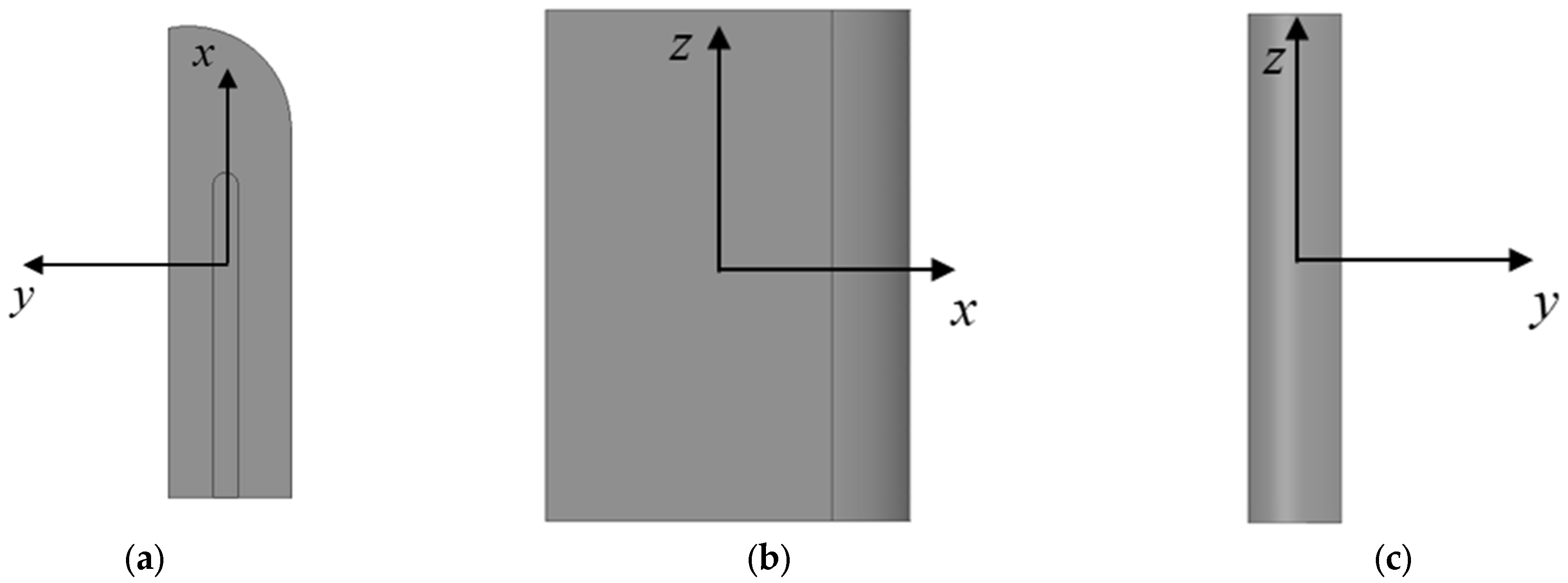
2.4. Motion of the Vane in Six Degrees of Freedom
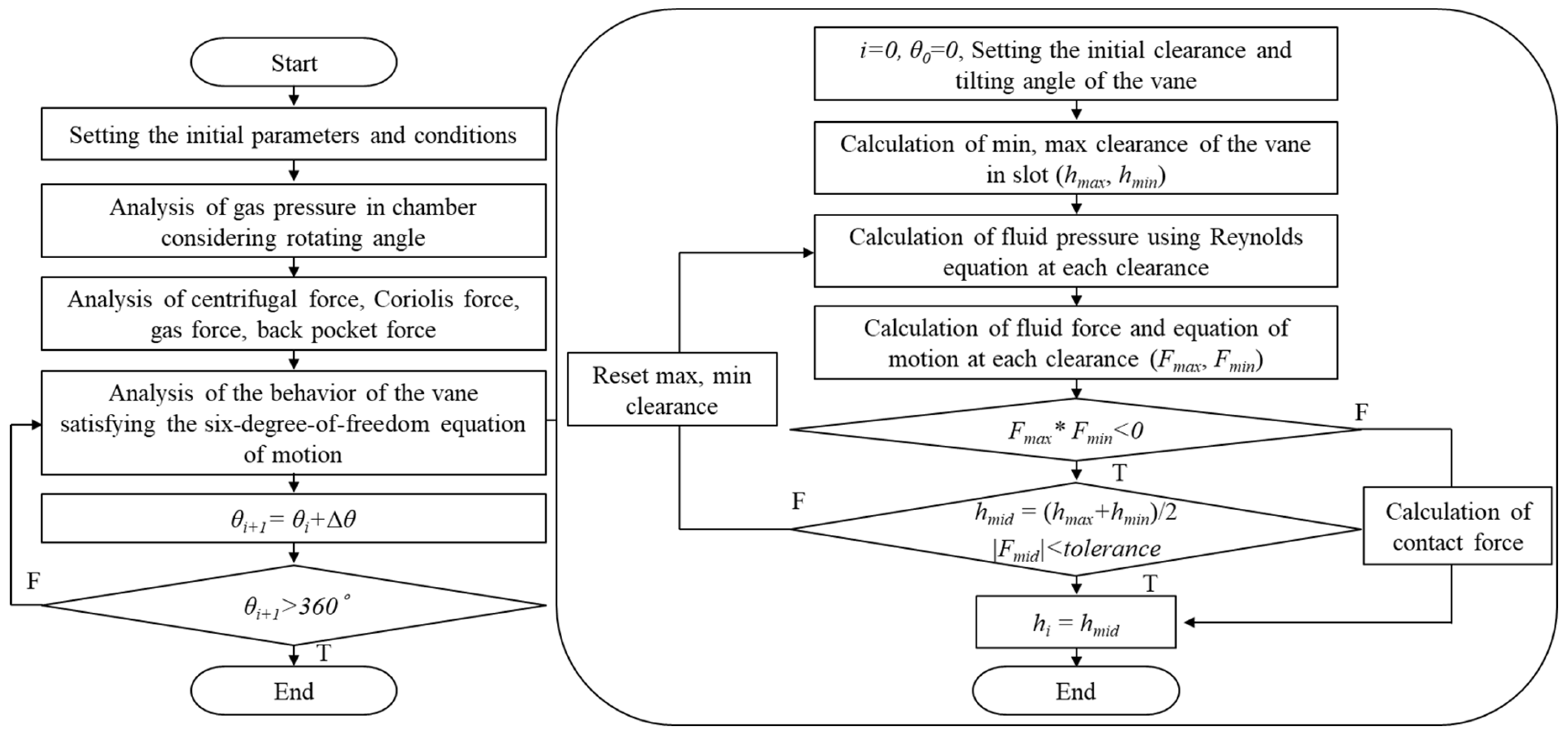
2.5. Numerical Algorithm
3. Simulation Results
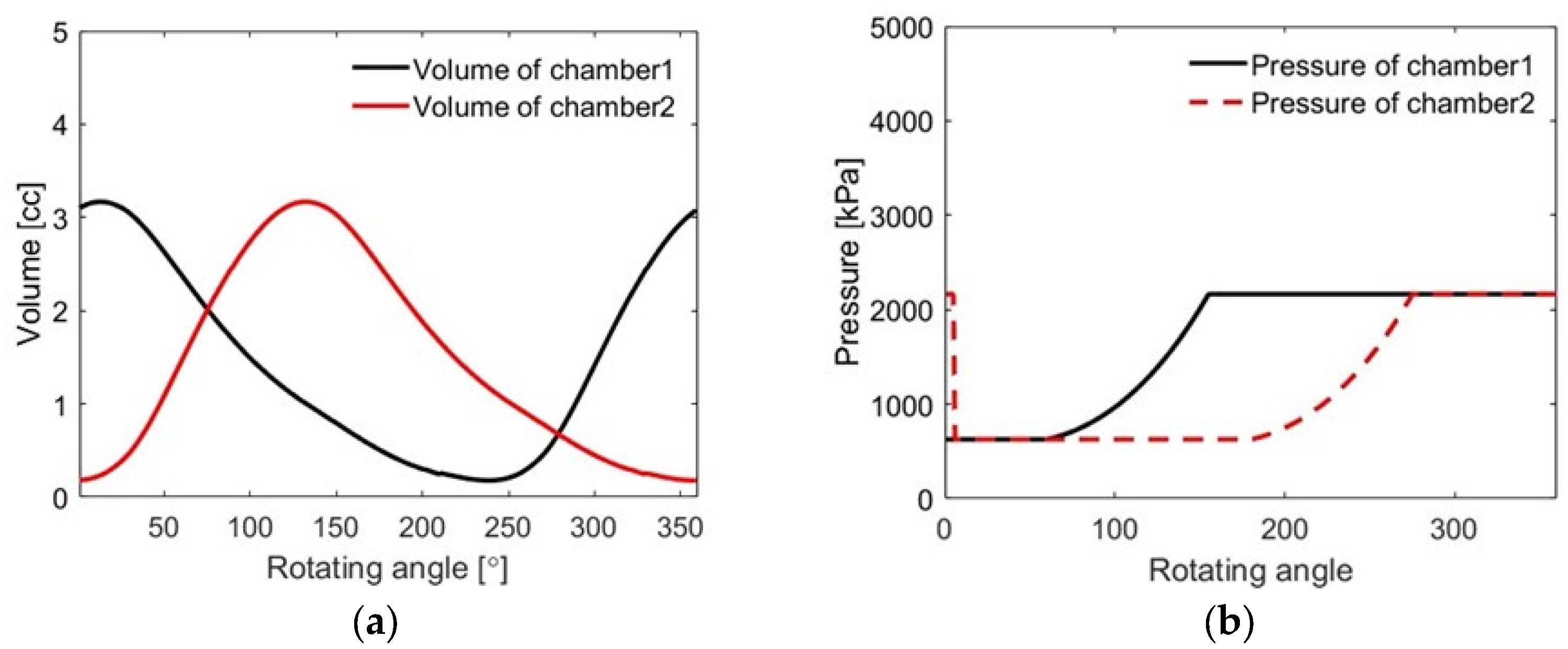
3.1. Simulated Pressure of the Compression Chamber
3.2. Simulated Pressure of the Fluid Lubricant
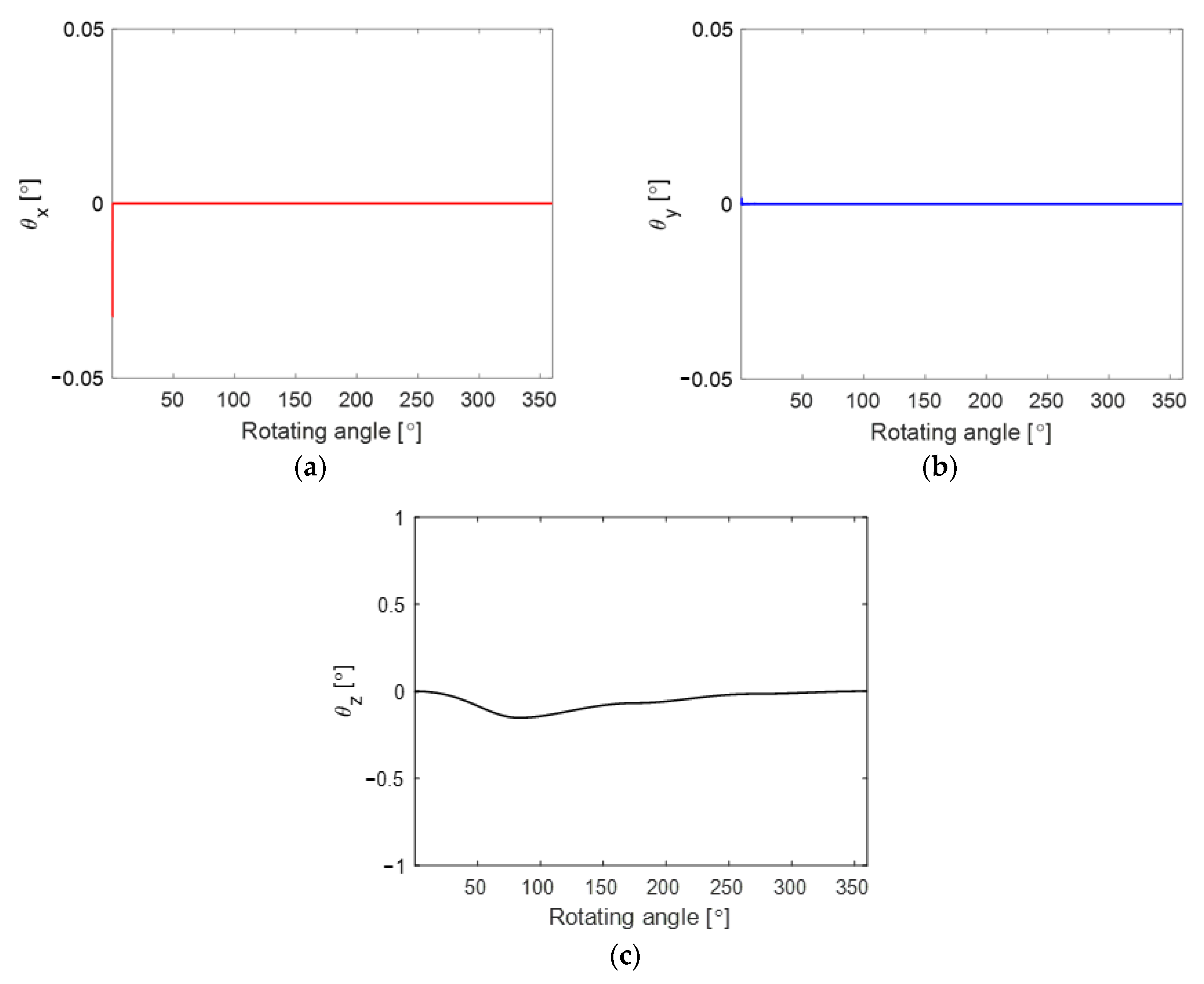
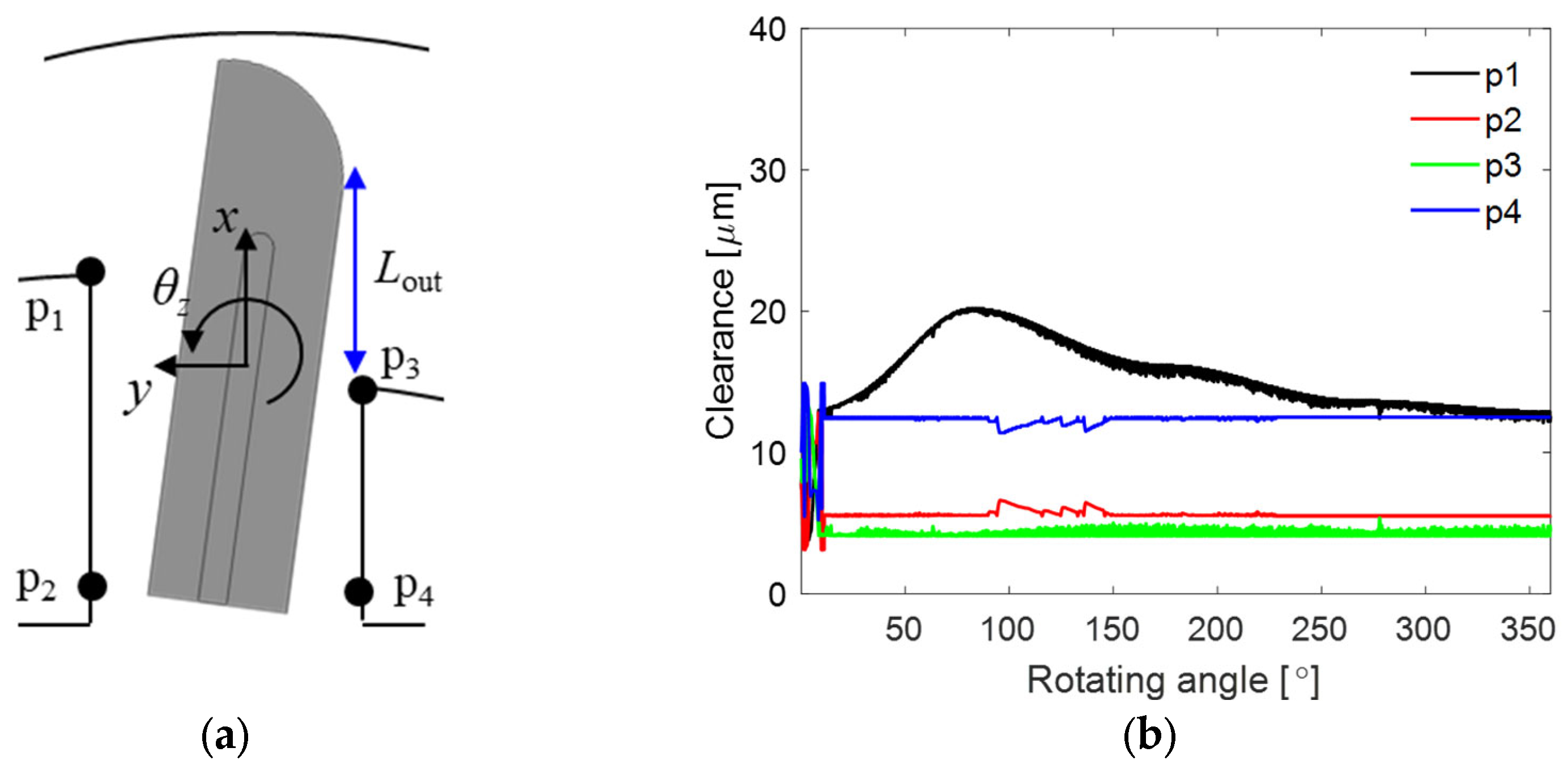
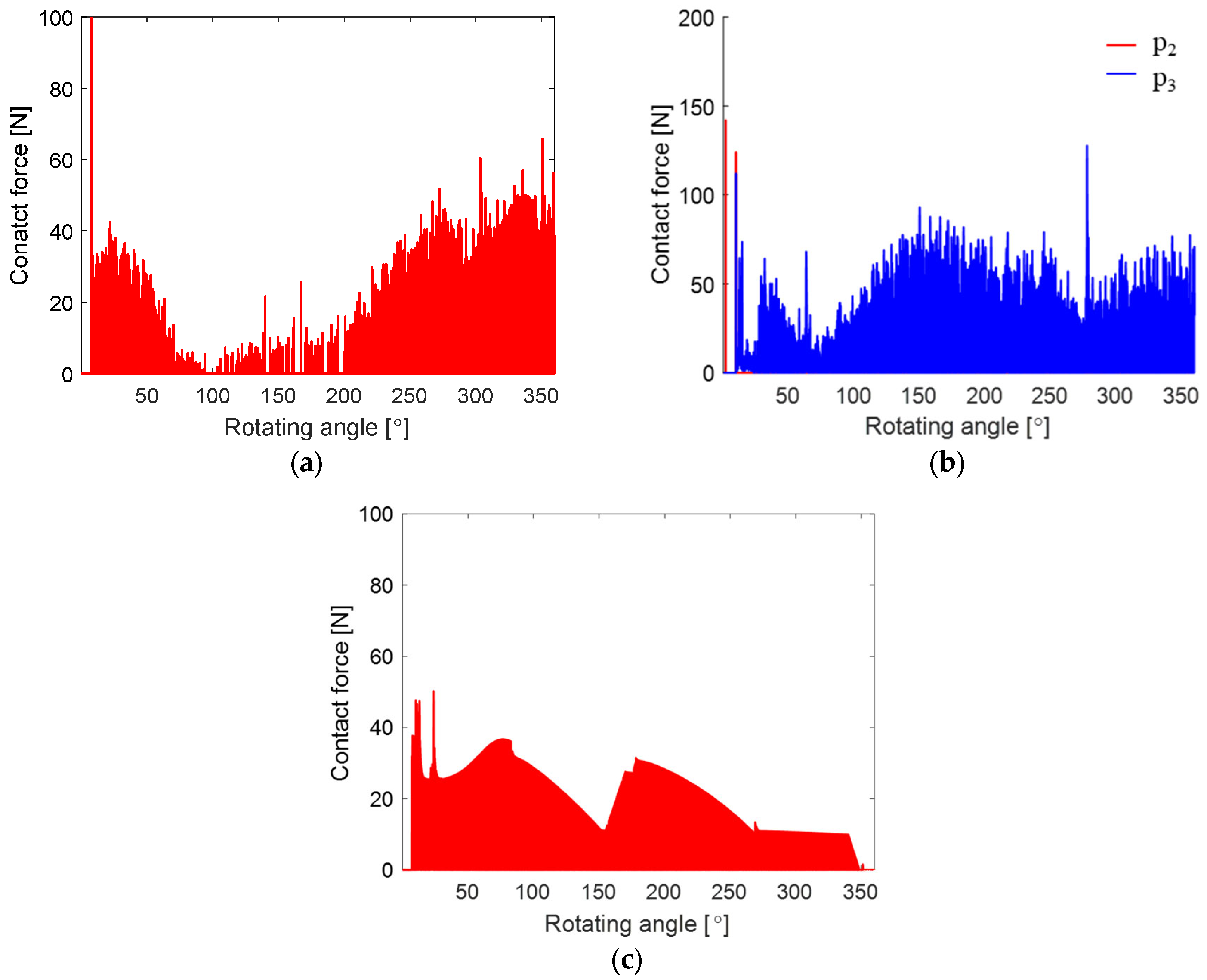
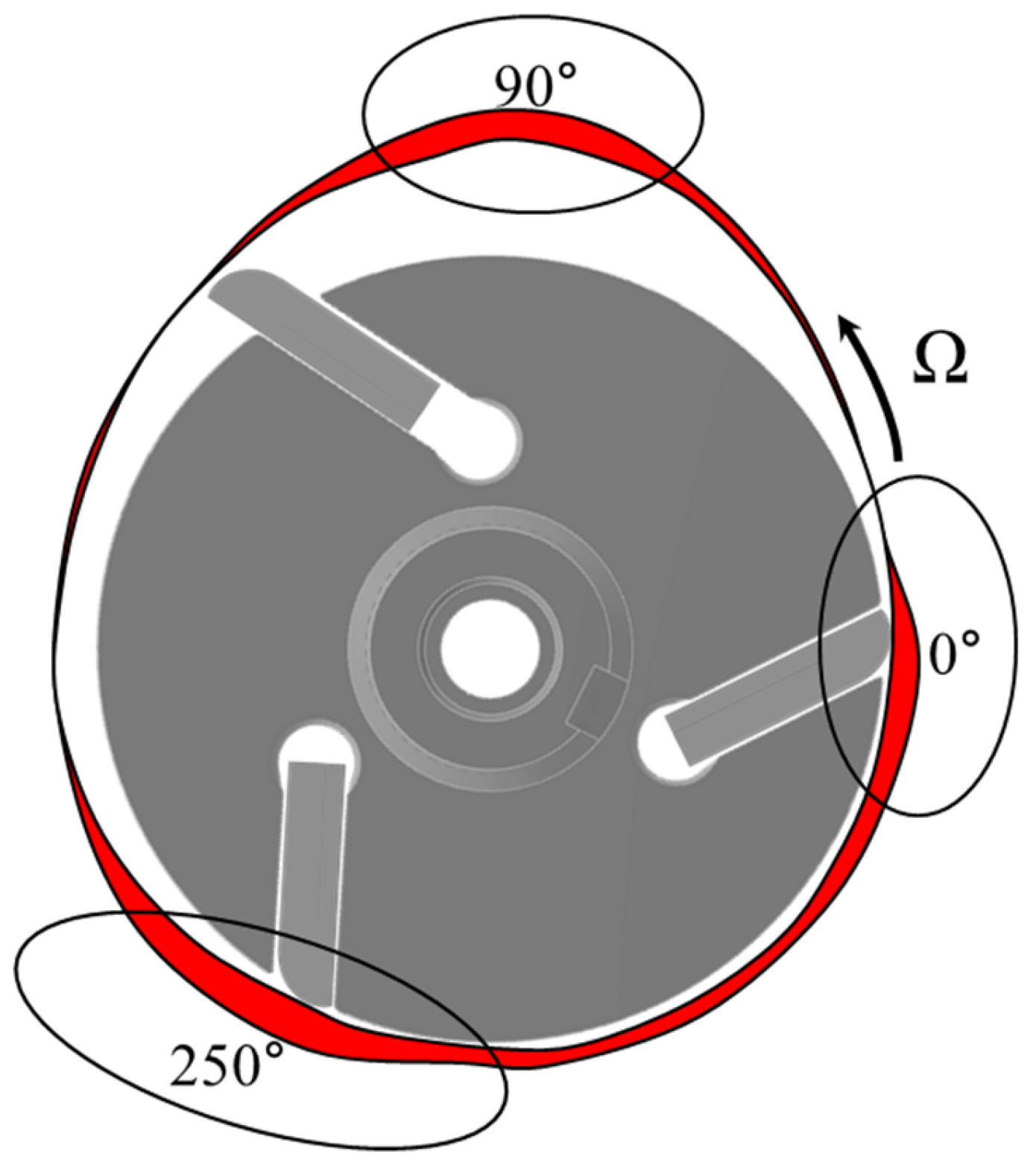
3.3. Simulated Motion of the Vane in Six Degrees of Freedom and Contact Force
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| pocket force | |
| centrifugal force | |
| contact force | |
| Coriolis force | |
| numerical error in z-direction | |
| weight force | |
| numerical error at maximum clearance | |
| numerical error at intermediate clearance | |
| numerical error at minimum clearance | |
| heat capacity ratio | |
| height of vane | |
| distance from rotor center to vane center | |
| thickness of vane | |
| contact torque | |
| gas pressure in the chamber | |
| discharge and intermediate pocket pressure | |
| inlet and discharge gas pressure | |
| pressure acting on the side1, side2, front, upper, and lower surface | |
| gas density in the chamber | |
| inlet gas density | |
| inlet gas temperature | |
| shear force acting on the side1, side2, front, upper, and lower surface | |
| volume of the chamber | |
| inlet gas volume | |
| distance from mass center | |
| Greek symbols | |
| rotating speed of rotor | |
References
- Aw, K.; Ooi, K. A review on sliding vane and rolling pistion compressors. Machines 2021, 9, 125. [Google Scholar] [CrossRef]
- Yoshimura, T.; Ono, K.; Inagaki, K.; Kotsuka, H.; Korenaga, A. Analysis of lubricating characteristics of rotary compressors for domestic refrigerators. Trans. ASME 1999, 121, 510–516. [Google Scholar] [CrossRef]
- Wang, F.; Sun, Z.; Fiebig, W.; Xu, B.; Stelson, K. Lubrication and fluid film study on the vane tip in a vane pump hydraulic transmission considering a fluid and structure interaction. J. Tribol. 2021, 143, 121803. [Google Scholar] [CrossRef]
- Teh, Y.; Ooi, K. Theoretical study of a novel refrigeration compressor—Part I: Design of the revolving vane (RV) compressor and its frictional losses. Int. J. Refrig. 2009, 32, 1092–1102. [Google Scholar] [CrossRef]
- Teh, Y.; Ooi, K. Experimental study of the revolving vane (RV) compressor. Appl. Therm. Eng. 2009, 29, 3235–3245. [Google Scholar] [CrossRef]
- Shakya, P.; Ooi, K. Introduction to coupled vane compressor: Mathematical modelling with validation. Int. J. Refrig. 2020, 117, 23–32. [Google Scholar] [CrossRef]
- Hawaj, O. Theoretical modeling of sliding vane compressor with leakage. Int. J. Refrig. 2009, 32, 1555–1562. [Google Scholar] [CrossRef]
- Dai, Y.; Zhu, H.; Bianchi, G.; Rane, S.; Ye, F. Numerical investigation on flow characteristics and working performance in oil-injected sliding vane rotary compressors. Int. J. Refrig. 2025, 171, 202–216. [Google Scholar] [CrossRef]
- Choo, W.; Ooi, K. Analysis of the novel multi-vane Revolving Vane compressor—Theoretical modelling and experimental investigations. Int. J. Refrig. 2021, 131, 592–603. [Google Scholar] [CrossRef]
- Choo, W.; Ooi, K. Analysis of the novel multi-vane revolving vane compressor investigation of vane chattering phenomenon through instantaneous working chamber pressure measurements. Int. J. Refrig. 2022, 134, 207–218. [Google Scholar] [CrossRef]
- Tan, K.; Ooi, K. Journal bearings design for a novel revolving vane compressor. Int. J. Refrig. 2011, 34, 94–104. [Google Scholar] [CrossRef]
- Tan, K.; Ooi, K. A novel revolving vane compressor with a fixed-vane. Int. J. Refrig. 2011, 34, 1980–1988. [Google Scholar] [CrossRef]
- Liu, R.; Jing, L.; Meng, X.; Lyu, B. Mixed elastohydrodynamic analysis of a coupled journal-thrust bearing system in a rotary compressor under high ambient pressure. Tribol. Int. 2021, 159, 106943. [Google Scholar] [CrossRef]
- Sarip, A.; Musa, M. Friction analysis on vane of an existing and of a novel multi vane rotary compressor. Appl. Mech. Mater. 2013, 284–287, 763–767. [Google Scholar] [CrossRef]
- Li, L.; Zhao, Y.; Guo, B.; Shu, P.; Shen, J.; He, S. Wrap of cylinder and its effect on main features of rotary vane compressor for automobile air conditioning system. Int. J. Refrig. 2003, 26, 566–574. [Google Scholar] [CrossRef]
- Li, R.; Jing, L.; Meng, X.; Lui, Z.; Zhang, R. Numerical analysis of vane–slot friction pair in a rolling piston compressor considering deformation and groove design. Tribol. Int. 2021, 162, 107124. [Google Scholar] [CrossRef]
- Fang, C.; Meng, X.; Xie, Y. A Piston tribodynamic model with deterministic consideration of skirt surface grooves. Tribol. Int. 2017, 110, 232–251. [Google Scholar] [CrossRef]
- Geng, K.; Geng, A.; Wang, X.; Zheng, X.; Wei, W.; Zhao, T.; Lei, Y.; He, Y. Frictional characteristics of the vane–chute pair in a rolling piston compressor based on the second-order motion. Tribol. Int. 2019, 133, 111–125. [Google Scholar] [CrossRef]
- Wen, C.; Liu, Z.; Wen, X.; Gao, K.; Guan, J.; Bai, P.; Meng, Y.; Tian, Y. Dynamic modeling and characteristics analysis of sliding vane in a high-speed rotary compressor considering groove distribution and multi-body coupling. Tribol. Int. 2024, 194, 109505. [Google Scholar] [CrossRef]
- Hu, X.; Qu, Z.; Yang, X.; Sun, J. Theoretical study on frictional losses of a novel automotive swing vane compressor. Int. J. Refrig. 2013, 36, 758–767. [Google Scholar] [CrossRef]
- Bianchi, G.; Cipollone, R. Friction power modeling and measurements in sliding vane rotary compressor. Appl. Therm. Eng. 2015, 84, 276–285. [Google Scholar] [CrossRef]
- Bianchi, G.; Cipollone, R. Theoretical modeling and experimental investigations for the improvement of the mechanical efficiency in sliding vane rotary compressor. Appl. Energy 2015, 142, 95–107. [Google Scholar] [CrossRef]
- Yang, X.; Dong, C.; Qu, Z. Design and dynamic analysis of a novel double-swing vane compressor for electric vehicle air conditioning systems. Int. J. Refrig. 2017, 76, 52–62. [Google Scholar] [CrossRef]
- Zhou, H.; Qu, Z.; Yang, H.; Yu, B. Dynamic model and numerical simulation for synchronal rotary compressor. J. Fluids Eng. 2009, 131, 041102. [Google Scholar] [CrossRef]
- Nederstigt, P.; Pecnik, R. Generalised isentropic relations in thermodynamics. Energies 2023, 16, 2281. [Google Scholar] [CrossRef]
- Hamrock, B. Fundamentals of Fluid Film Lubrication, 2nd ed.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Beer, F.; Johnston, E., Jr.; Cornwell, P. Vector Mechanics for Engineers Dynamics, 9th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Priest, M.; Dowson, D.; Taylor, C. Predictive wear modelling of lubricated piston rings in a diesel engine. Wear 1999, 231, 89–101. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Rotating speed (Hz) | 60 |
| Inlet gas temperature (°C) | 30 |
| Inlet gas pressure (kPa) | 627 |
| Discharge gas pressure (kPa) | 2164 |
| Intermediate pocket pressure (kPa) | 1687 |
| Discharge pocket pressure (kPa) | 2409 |
| Heat specific ratio | 1.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, G.; Park, Y.; Jang, G. Dynamic Motion of a Vane in Six Degrees of Freedom and Its Effect on Wear in a Rotary-Vane Compressor Considering Fluid Lubrication. Lubricants 2025, 13, 228. https://doi.org/10.3390/lubricants13050228
Hong G, Park Y, Jang G. Dynamic Motion of a Vane in Six Degrees of Freedom and Its Effect on Wear in a Rotary-Vane Compressor Considering Fluid Lubrication. Lubricants. 2025; 13(5):228. https://doi.org/10.3390/lubricants13050228
Chicago/Turabian StyleHong, Gwanghee, Youngjun Park, and Gunhee Jang. 2025. "Dynamic Motion of a Vane in Six Degrees of Freedom and Its Effect on Wear in a Rotary-Vane Compressor Considering Fluid Lubrication" Lubricants 13, no. 5: 228. https://doi.org/10.3390/lubricants13050228
APA StyleHong, G., Park, Y., & Jang, G. (2025). Dynamic Motion of a Vane in Six Degrees of Freedom and Its Effect on Wear in a Rotary-Vane Compressor Considering Fluid Lubrication. Lubricants, 13(5), 228. https://doi.org/10.3390/lubricants13050228






