Research on Impact Resistance of Double-Decker Ball Bearing Based on Bionic Loofah Structure
Abstract
1. Introduction
2. Bionic Loofah Double-Decker Ball Bearing Adapter Ring Structure Design
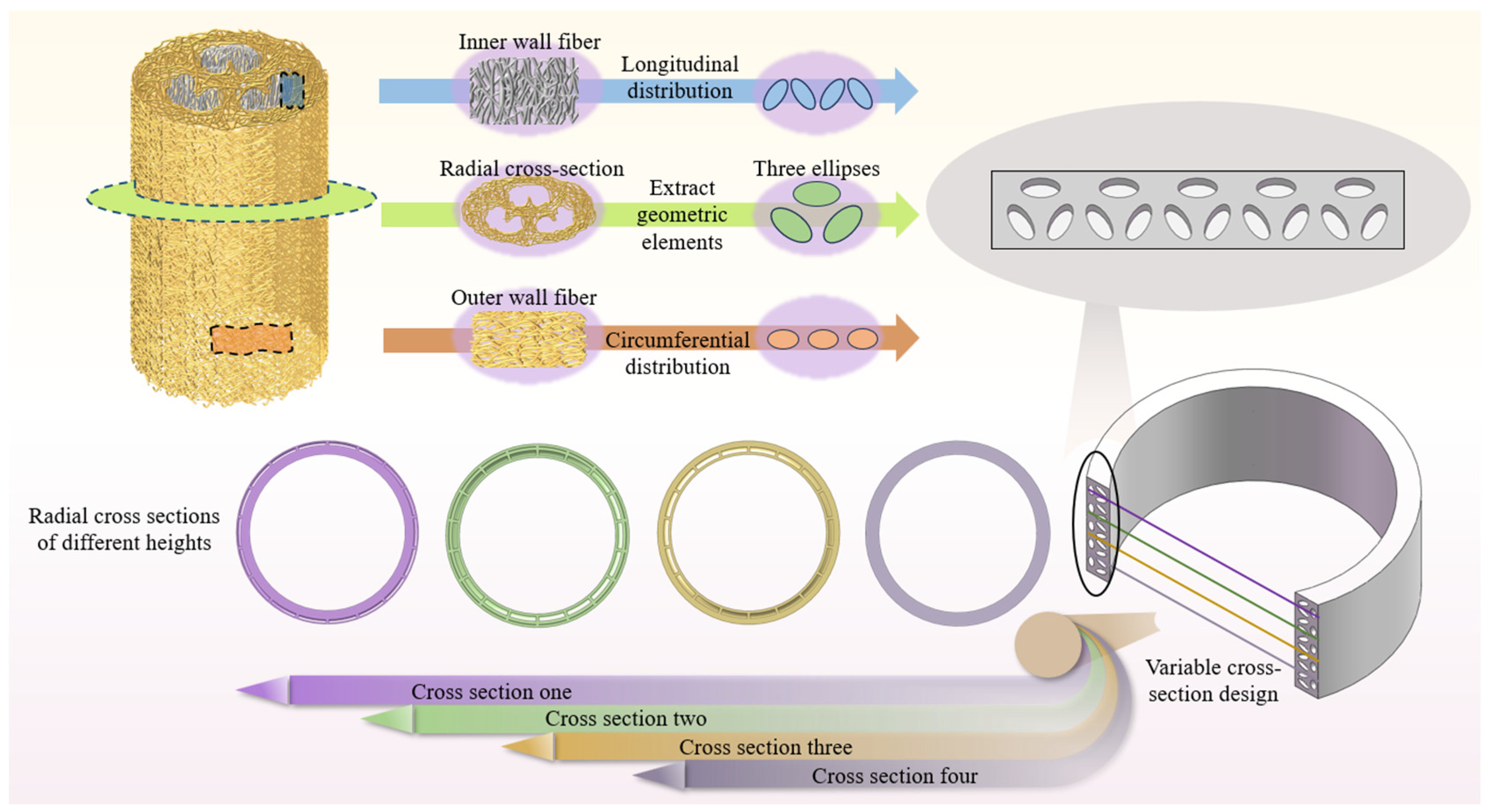
2.1. Structural Prototype Analysis of Loofahs
2.2. Bionic Design of Adapter Ring Structure
2.3. Analysis of Energy Absorption in Bionic Structures
3. Finite Element Analysis of Double-Decker Ball Bearing
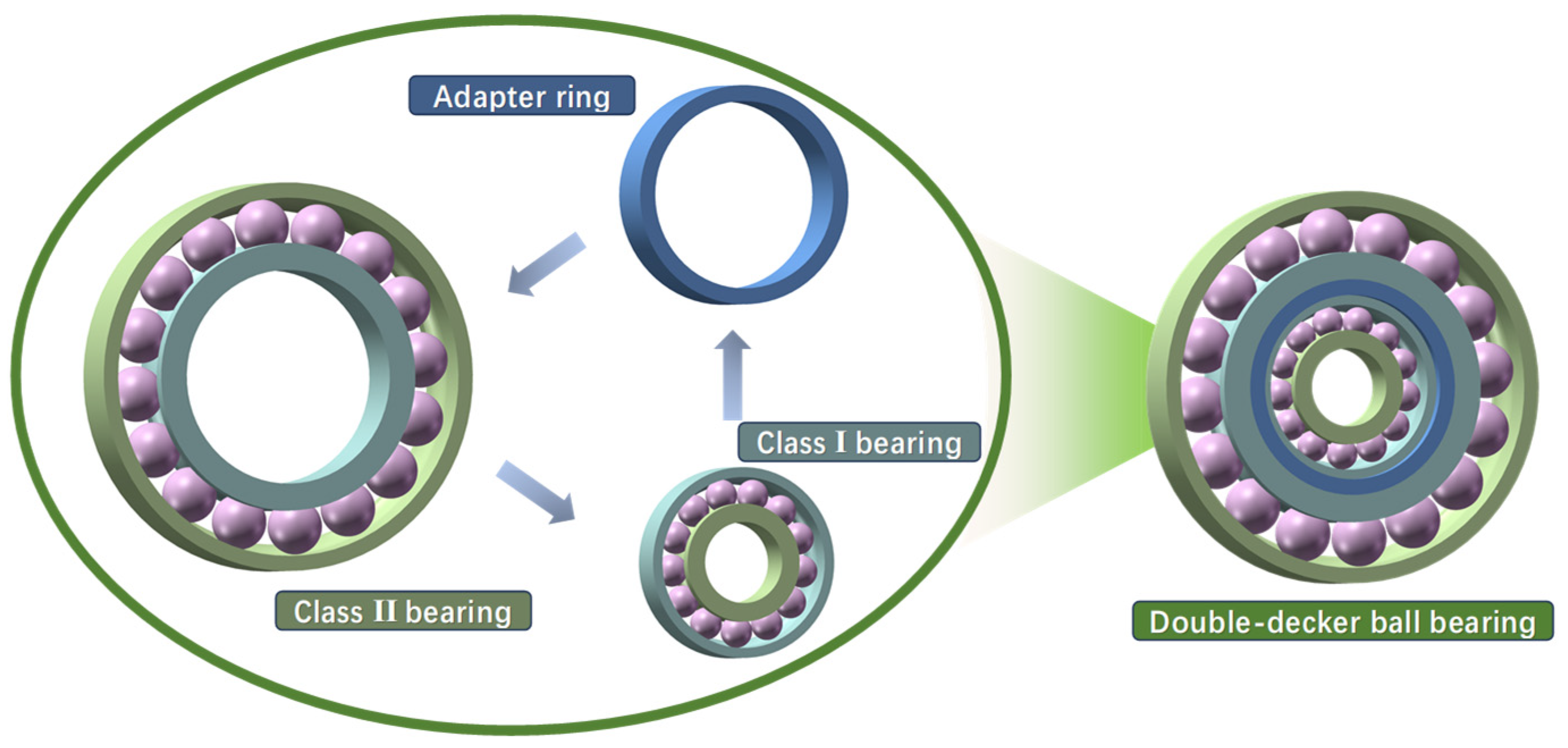
3.1. Selection of Double-Decker Ball Bearing Type
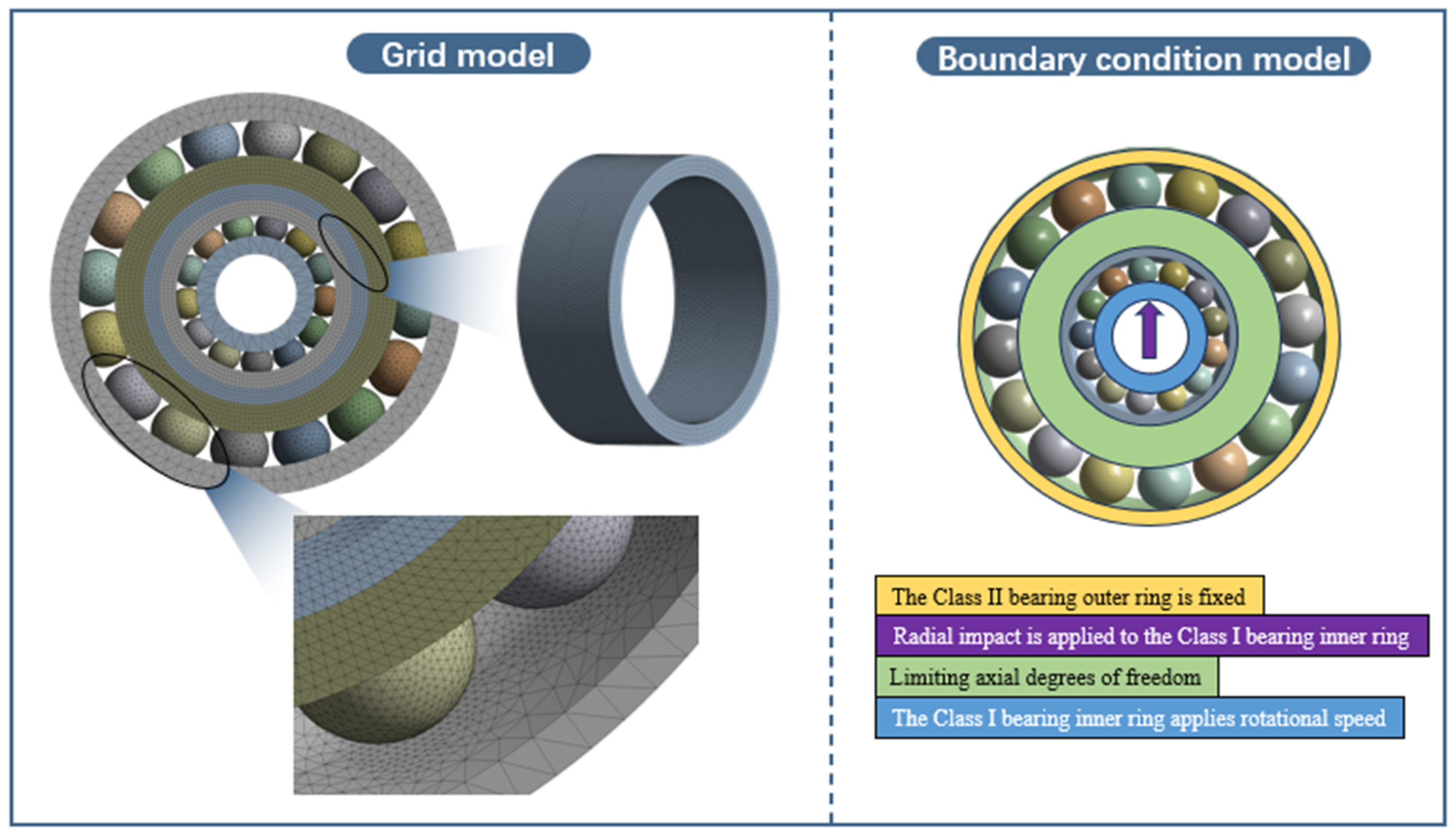
3.2. Finite Element Model Analysis Setup for Double-Decker Ball Bearing
- (1)
- Constrain the degrees of freedom of the nodes on the outer surface of the outer ring of the Class II bearing in all directions.
- (2)
- Constrain the axial translational degrees of freedom of the bearing balls and raceways in the Class I bearing, bearing balls and inner raceway in the Class II bearing, and the adapter ring.
- (3)
- Release the radial translational degrees of freedom of the bearing balls and raceways in the Class I bearing, bearing balls and inner raceway in the Class II bearing, and the adapter ring.
- (4)
- Apply a rotational speed on the inner surface of the inner ring of the Class I bearing, and apply an impact acceleration in the positive z-axis direction on the inner surface of the inner ring of the Class I bearing.
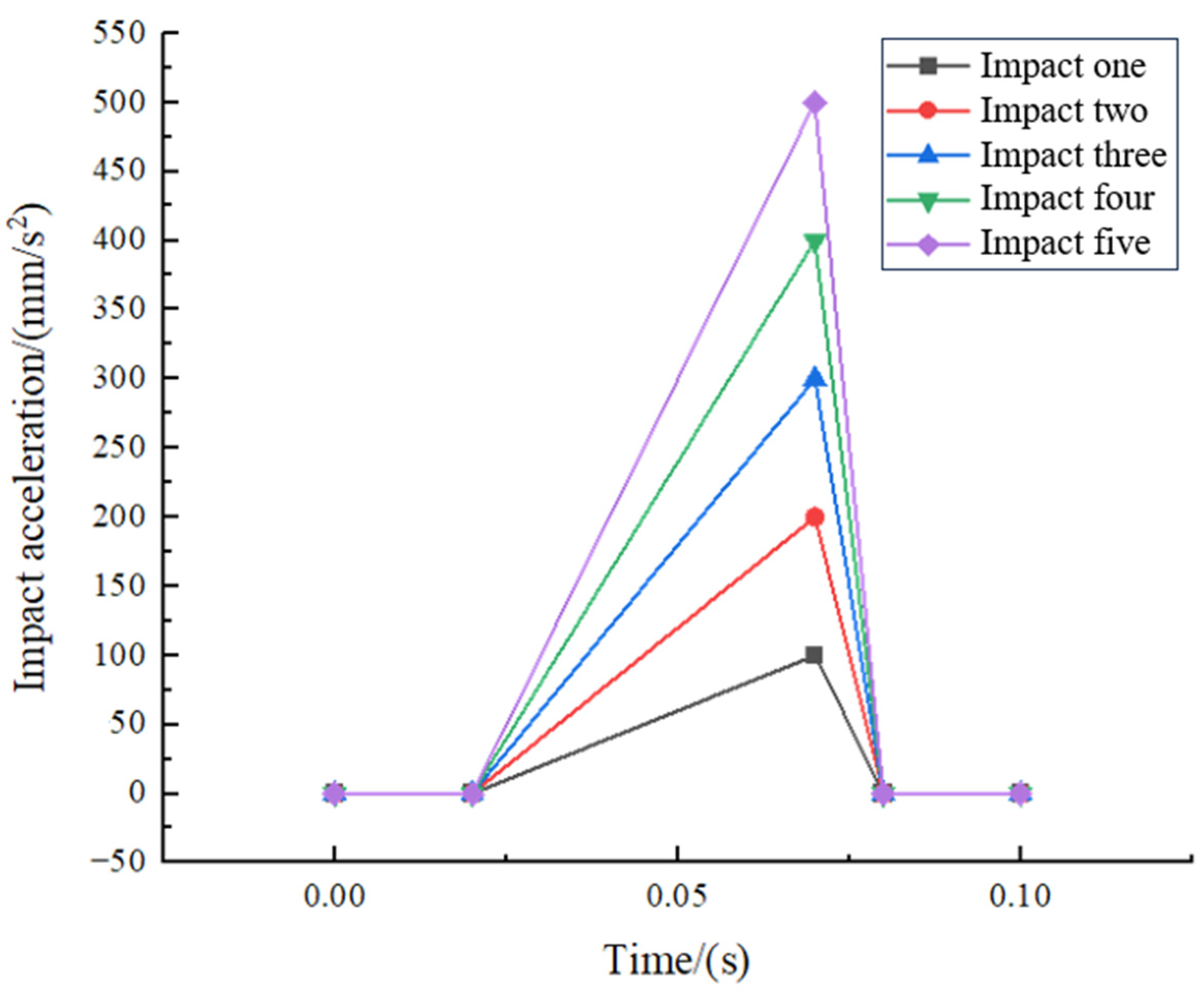
3.3. Simulation Result Analysis
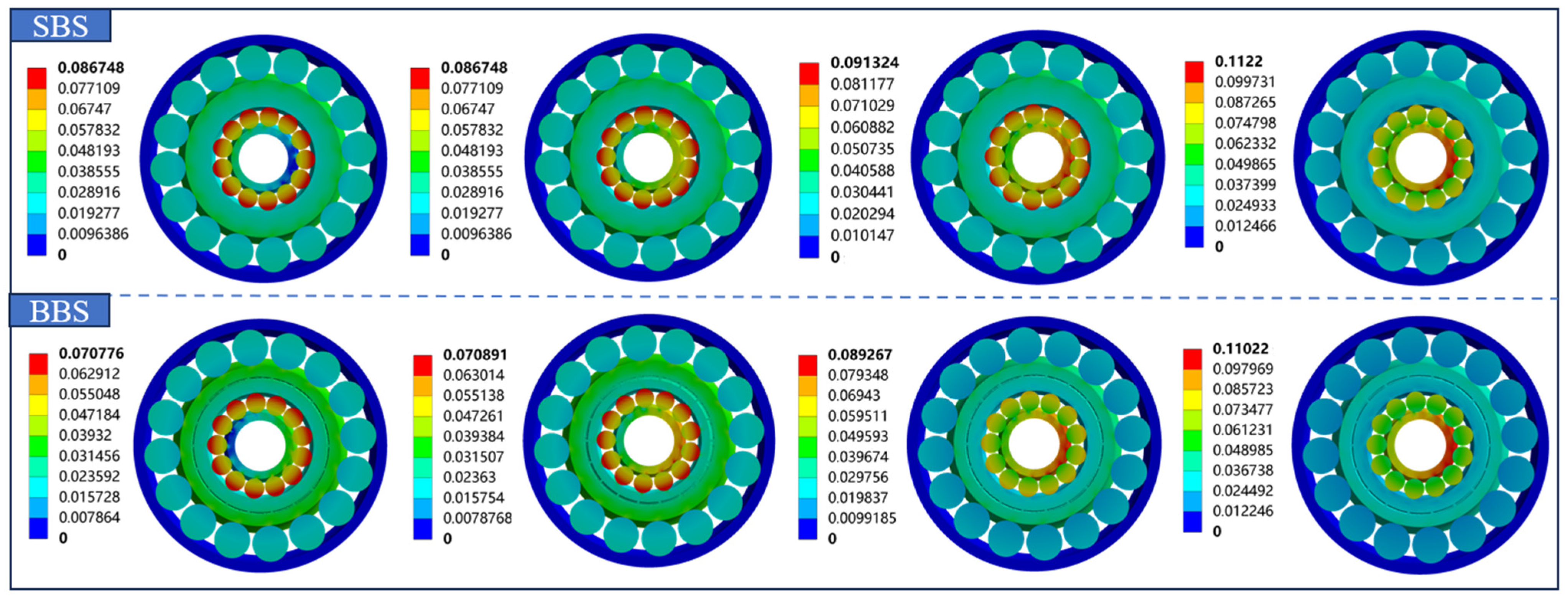
3.3.1. Deformation Analysis
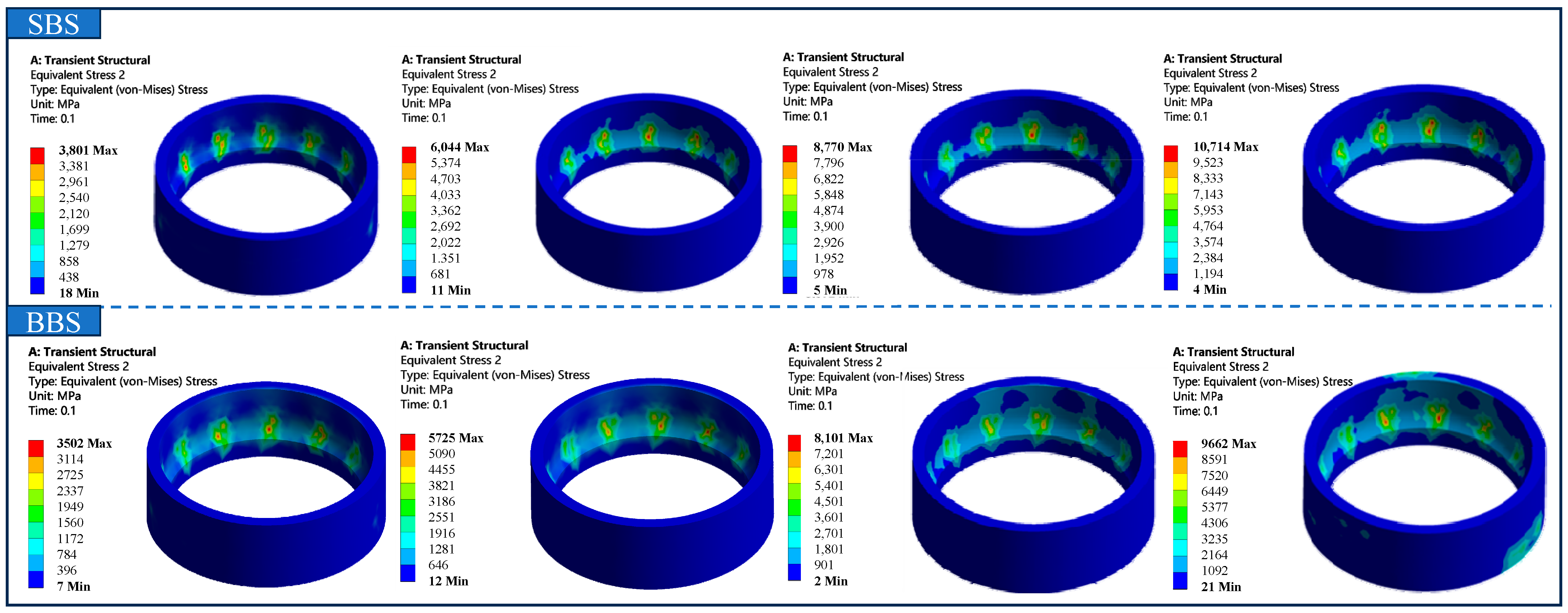
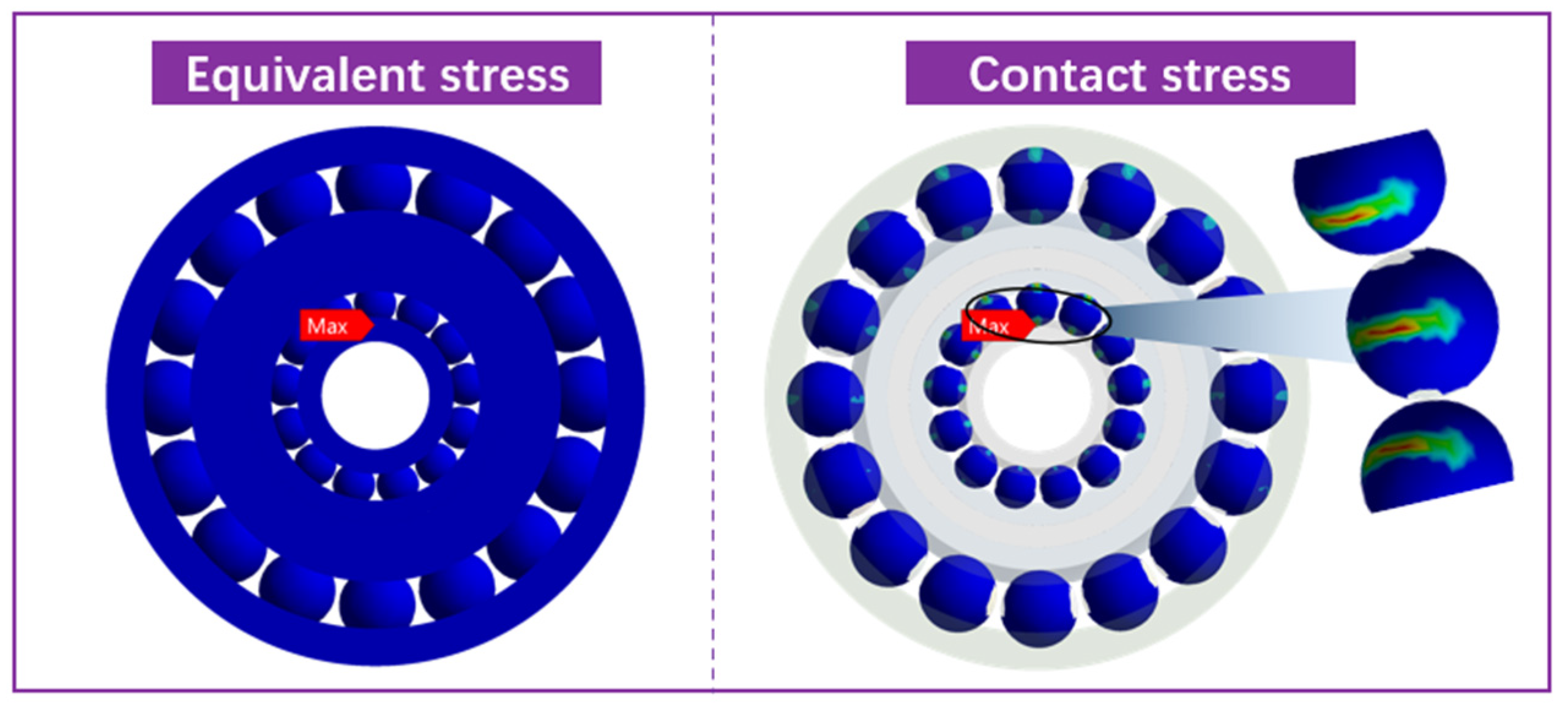
3.3.2. Equivalent Stress Analysis
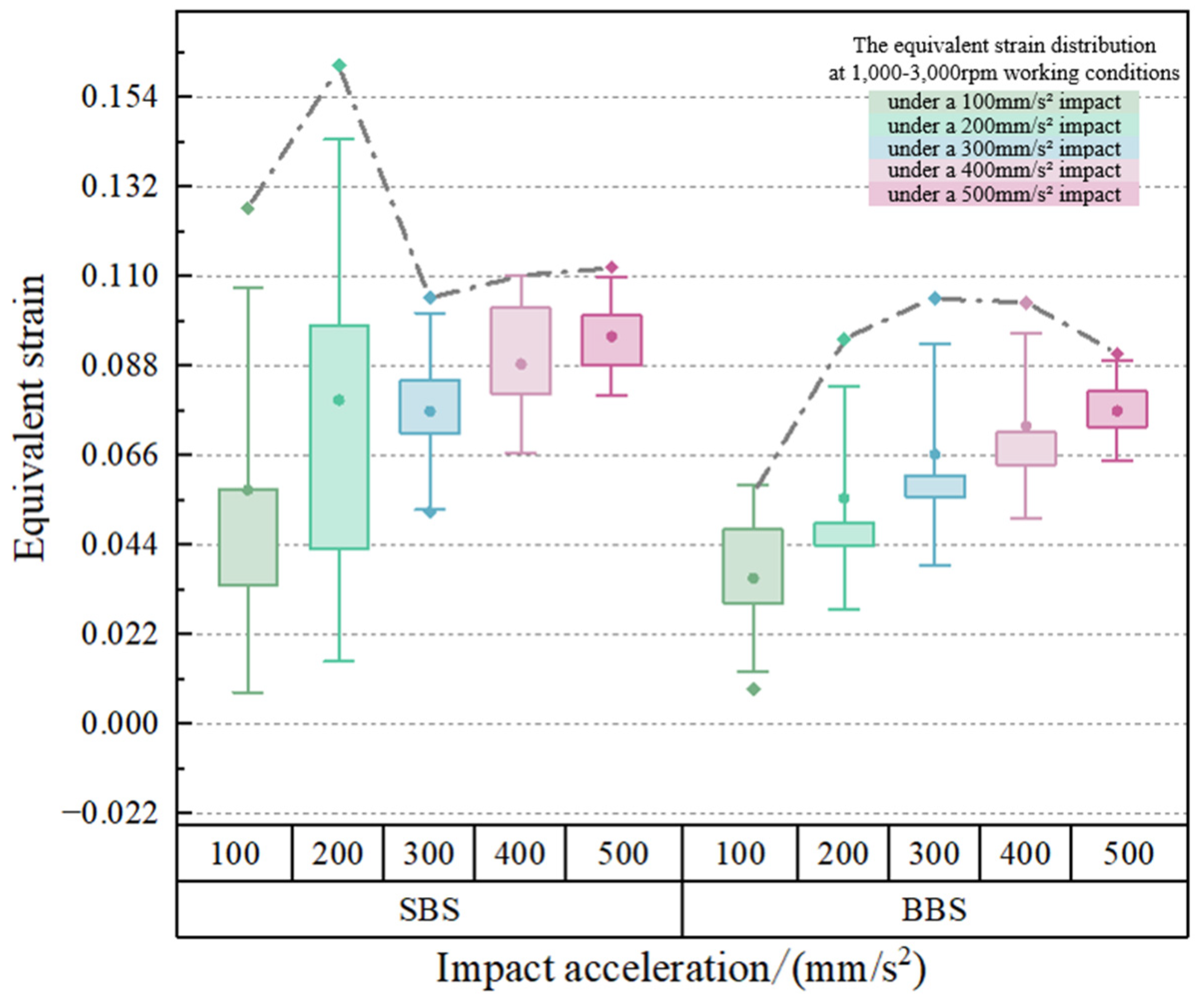
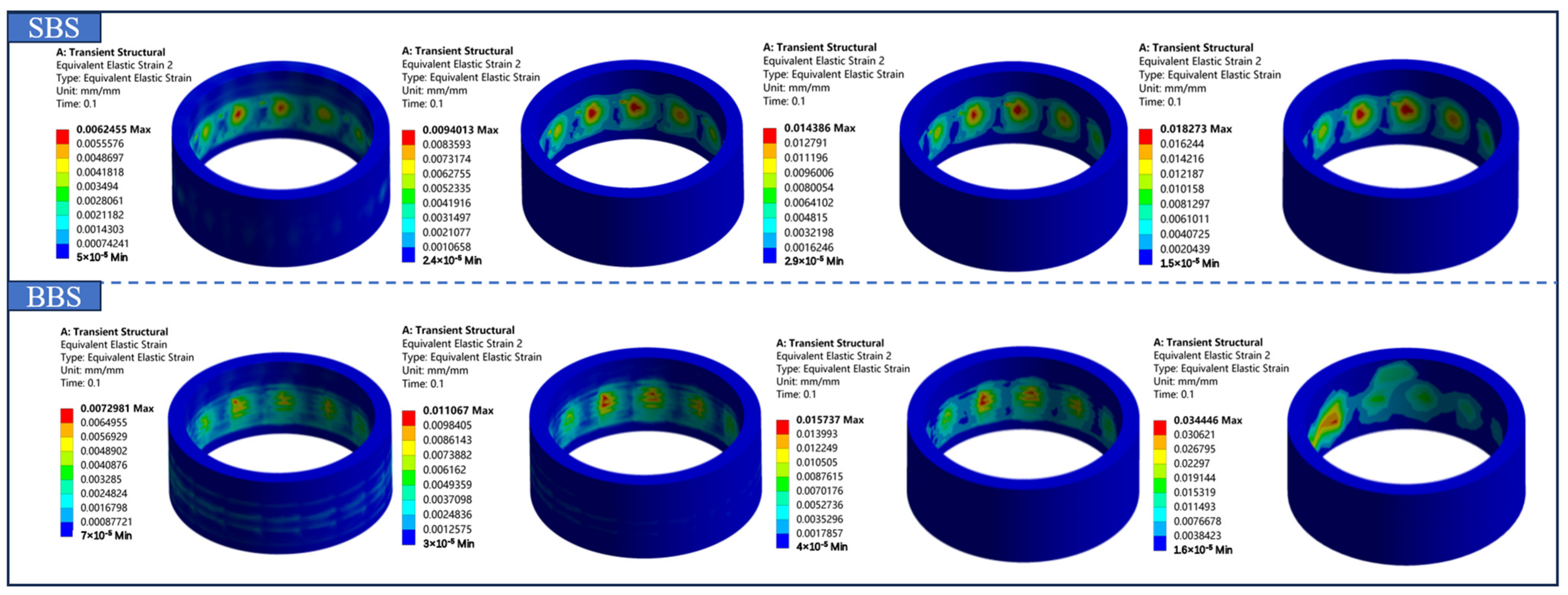
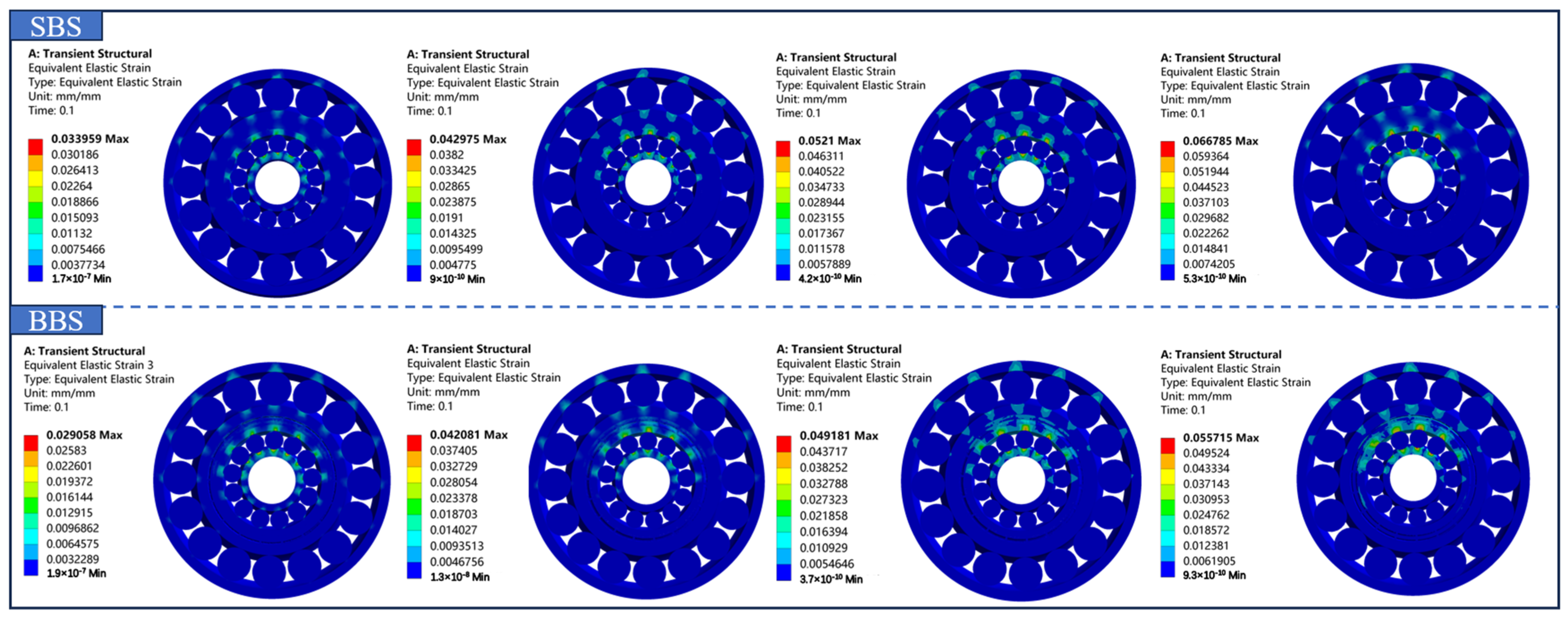
3.3.3. Equivalent Strain Analysis
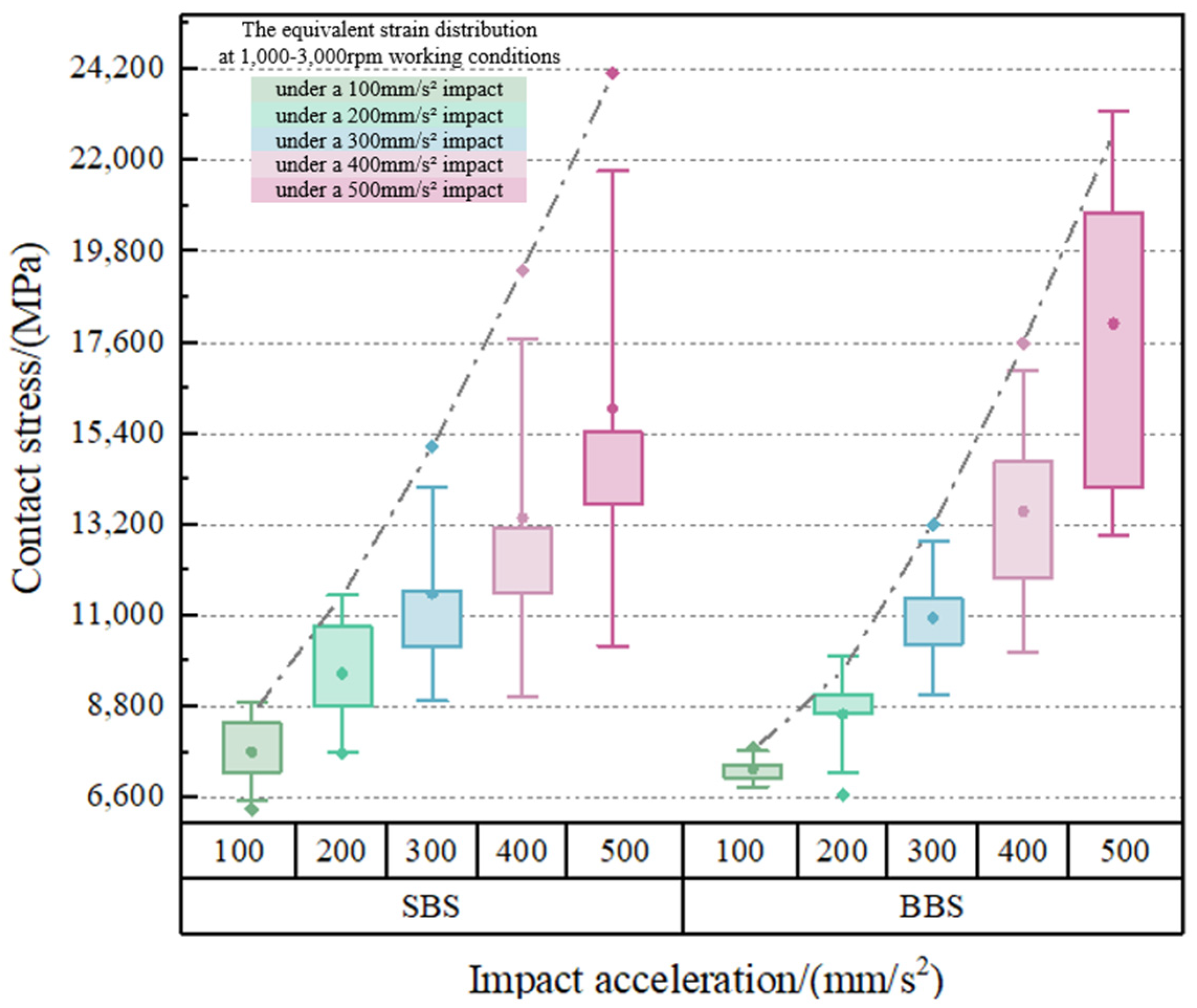
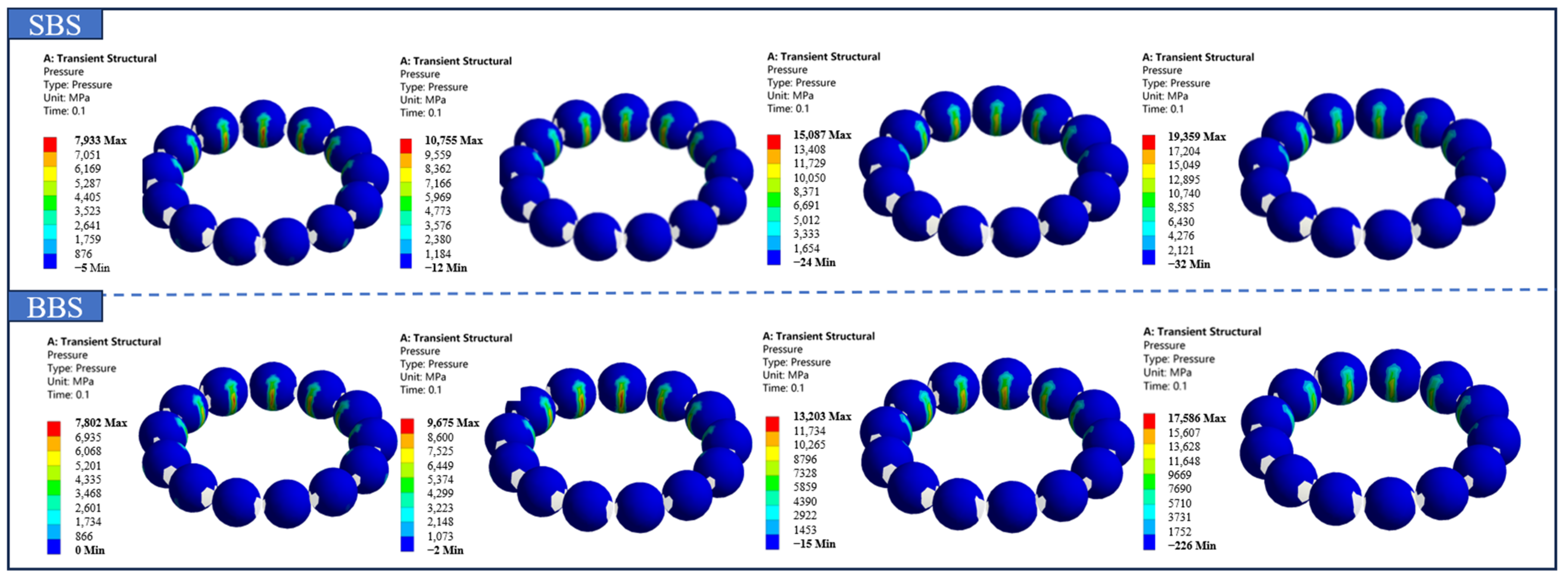
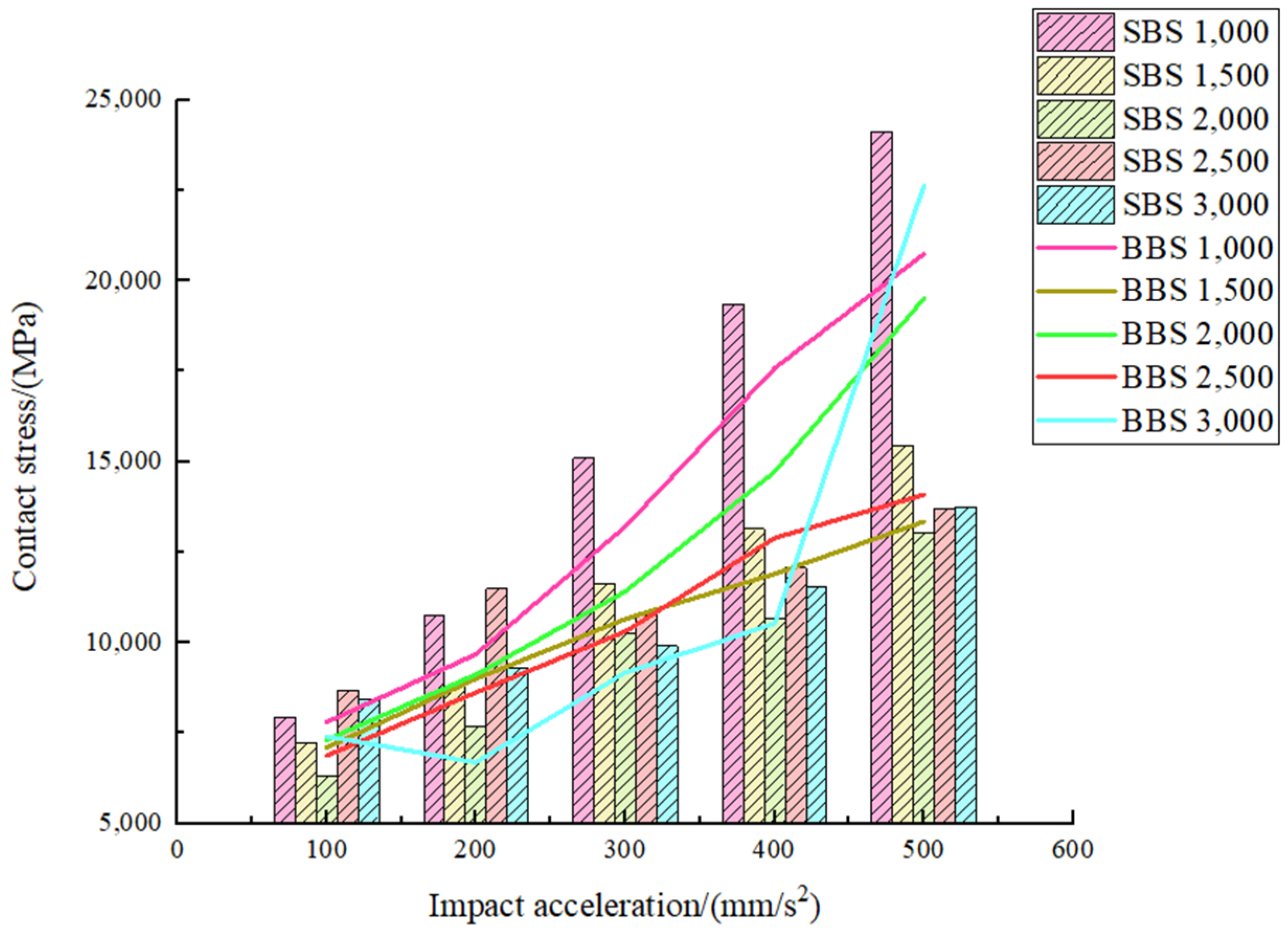
3.3.4. Contact Stress Analysis
3.3.5. Safety Factor Analysis
4. Bionic Loofah Adapter Ring Performance Analysis
5. Conclusions
- (1)
- Through the combination of biomimetic porous design and solid design in this study, we successfully achieved weight reduction in the double-decker ball bearing structure. By adopting a novel biomimetic loofah structure design, the weight of the bearing adapter ring was reduced by 25.26%.
- (2)
- The new bearing structure under the simulation condition of 1000 rpm~3000 rpm in this paper has some improvement in the aspects of deformation, equivalent stress, equivalent strain, contact stress, and safety factor compared with the original double-decker ball bearing structure.
- (3)
- The maximum equivalent stress and the maximum contact stress of double-decker ball bearings appear in the contact between the inner ring of the class Ⅰ bearing and the rolling elements, and the contact stress shows a nonlinear decreasing trend with the increase in bearing speed.
- (4)
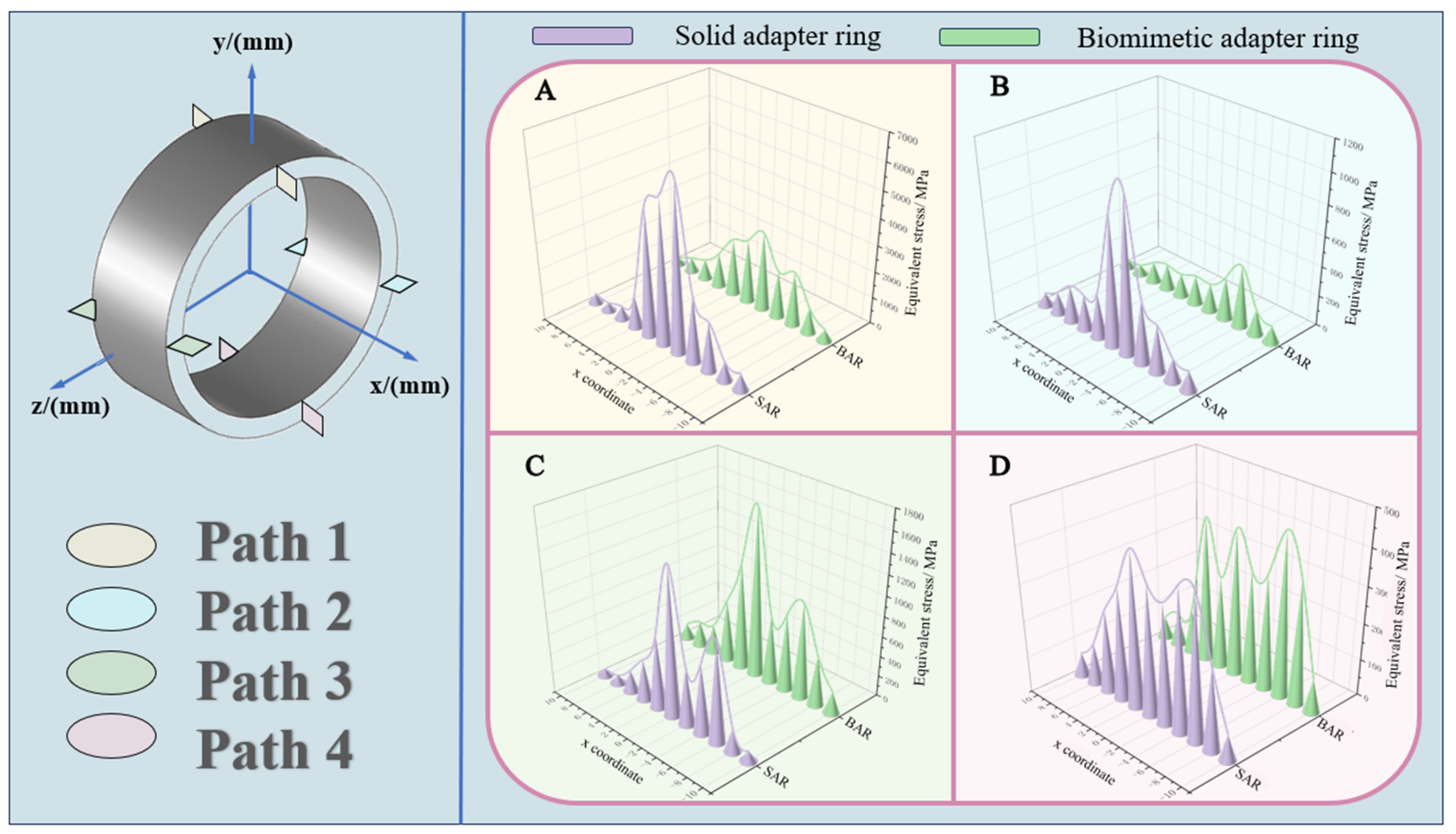
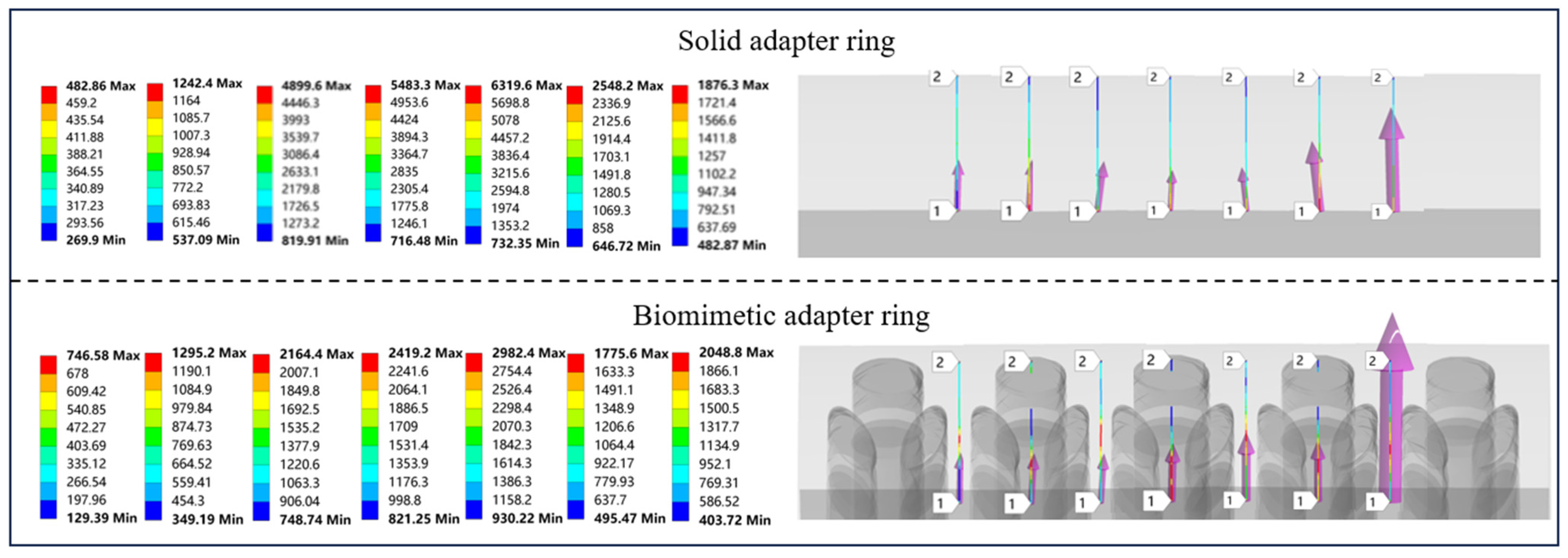
- Under radial impact load, the overall stress in the bionic loofah adapter ring in the axial direction first rises and then declines according to the law of distribution. Compared to the solid adapter ring structure, the overall distribution of stress in the bionic adapter ring structure is more uniform, the stress changes are smaller, and the stress concentration degree is lower.
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, F.; Ding, N. A review of bearing failure Modes, mechanisms and causes. Eng. Fail. Anal. 2023, 152, 107518. [Google Scholar] [CrossRef]
- Chen, R.; Li, J.; Wang, Y. Study on the Time-Varying Stiffness Characteristics of Four-Point Contact Ball Bearings. Lubricants 2025, 13, 118. [Google Scholar] [CrossRef]
- Li, Z.; Zhong, Z.; Zhang, Z. Rolling Bearing Dynamics Simulation Information-Assisted Fault Diagnosis with Multi-Adversarial Domain Transfer Learning. Lubricants 2025, 13, 116. [Google Scholar] [CrossRef]
- Anderson, W.J. Tribology for Aerospace Application; Society of Tribologists and Lubrication Engineers: Park Ridge, IL, USA, 1973; pp. 526–528. [Google Scholar]
- Prashad, H. A new generation double decker high precision rolling element bearing concept, development and investigations. Tribol. Trans. 2001, 44, 203–208. [Google Scholar] [CrossRef]
- Prashad, H. Relative comparison of stiffness and damping properties of double decker high precision and conventional rolling-element bearings. Tribol. Int. 2002, 35, 265–269. [Google Scholar] [CrossRef]
- Prashad, H. Experimental evaluation of the stress distribution on the outer surface of the outer race of conventional and double decker high precision bearings. Tribotest 2003, 9, 249–260. [Google Scholar] [CrossRef]
- Prashad, H. A theoretical approach to evaluating the performance characteristics of double-decker high precision bearings. Tribotest 2004, 10, 251–263. [Google Scholar] [CrossRef]
- Prashad, H. Centrifugal forces on double decker high precision and conventional ball bearings. J. Inst. Eng. India Part C Mech. Eng. Div. 2005, 86, 109. [Google Scholar]
- Zhu, Y.; Xu, L. Mechanical research of double-decker ball bearing. J. Aerosp. Power 2011, 26, 1914–1920. [Google Scholar]
- Zhu, Y.; Zhang, Y.; Jin, C. Research on the mechanical properties of a new “I” type double-decker ball bearing. J. Tribol. 2016, 138, 021102. [Google Scholar] [CrossRef]
- Zhu, Y.; Jin, C.; Xu, L. Dynamic responses of rotor drops onto double-decker catcher bearing. Chin. J. Mech. Eng. 2013, 26, 104–113. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, Z. The use of double-decker catcher bearing with face-to-face installed inner layer bearings. Mod. Phys. Lett. B 2017, 31, 1740012. [Google Scholar] [CrossRef]
- Jin, C.; Zhu, Y.; Xu, L. The thermodynamic properties of a new type catcher bearing used in active magnetic bearings system. Appl. Therm. Eng. 2015, 82, 253–263. [Google Scholar] [CrossRef]
- Hu, J.; Qiao, X.; Lv, Q. Research on a numerical calculation for ball bearings based on a finite initial value search method. Math. Probl. Eng. 2021, 2021, 6617131. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, B.; Zhang, X. Study on speed transfer characteristics of double-deck ball bearing based on generalized four-terminal parameter method. Nonlinear Dyn. 2022, 110, 3273–3302. [Google Scholar] [CrossRef]
- Pape, F.; Coors, T.; Poll, G. Investigations on tailored forming components as tribologically loaded machine elements. Forsch. Ingenieurwesen Eng. Res. 2018, 82, 311–318. [Google Scholar] [CrossRef]
- Coors, T.; Mildebrath, M.; Büdenbender, C. Investigations on tailored forming of AISI 52100 as rolling bearing raceway. Metals 2020, 10, 1363. [Google Scholar] [CrossRef]
- Zheng, L.; Zuo, Y.; Li, X. Biomimetic swallow nest structure: A lightweight and high-strength thermal insulation material. ACS Nano 2022, 16, 8116–8127. [Google Scholar] [CrossRef]
- Huang, Z.; Li, X.; Guan, X. Biomimetic lightweight design of legged robot hydraulic drive unit shell inspired by geometric shape of fish bone rib structure. J. Bionic Eng. 2024, 21, 1238–1252. [Google Scholar] [CrossRef]
- Zou, M.; Xu, S.; Wei, C. A bionic method for the crashworthiness design of thin-walled structures inspired by bamboo. Thin-Walled Struct. 2016, 101, 222–230. [Google Scholar] [CrossRef]
- Yang, X.; Xi, X.; Pan, Q. In-plane dynamic crushing of a novel circular-celled honeycomb nested with petal-shaped mesostructure. Compos. Struct. 2019, 226, 111219. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, X.; Okabe, Y. Beetle elytron plate and the synergistic mechanism of a trabecular-honeycomb core structure. Sci. China Technol. Sci. 2019, 62, 87–93. [Google Scholar] [CrossRef]
- Jiang, B.; He, C.; Zhao, N. Ultralight metal foams. Sci. Rep. 2015, 5, 13825. [Google Scholar] [CrossRef]
- Pape, F.; Noelke, C.; Kaierle, S. Influence of foaming agents on laser based manufacturing of closed-cell Ti foam. Procedia Mater. Sci. 2014, 4, 97–102. [Google Scholar] [CrossRef]
- Yu, C.; Xu, L.; Yu, X. Research on the mechanical properties of “Z” type double-decker ball bearings. J. Tribol. 2014, 136, 011102. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Xie, Y.; Huang, X. Mechanical properties of luffa sponge. J. Mech. Behav. Biomed. Mater. 2012, 15, 141–152. [Google Scholar] [CrossRef]
- Chen, Q.; Shi, Q.; Gorb, S. A multiscale study on the structural and mechanical properties of the luffa sponge from Luffa cylindrica plant. J. Biomech. 2014, 47, 1332–1339. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Xie, Y.; Huang, X. Behaviour of luffa sponge material under dynamic loading. Int. J. Impact Eng. 2013, 57, 17–26. [Google Scholar] [CrossRef]
- Zampieri, A.; Mabande, G.; Selvam, T. Biotemplating of Luffa cylindrica sponges to self-supporting hierarchical zeolite macrostructures for bio-inspired structured catalytic reactors. Mater. Sci. Eng. C 2005, 26, 130–135. [Google Scholar] [CrossRef]
- Chen, B.; Zou, M.; Liu, G. Experimental study on energy absorption of bionic tubes inspired by bamboo structures under axial crushing. Int. J. Impact Eng. 2018, 115, 48–57. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, B.; Hong, J. Effect of preload on ball-raceway contact state and fatigue life of angular contact ball bearing. Tribol. Int. 2017, 114, 365–372. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Pan, J. Review on anti-shock criteria for equipments in some primary navy countries. J. Ship Mech. 2011, 15, 1322–1334. [Google Scholar]




| Parameters | Bearing Type | |
|---|---|---|
| 7204 | 7211 | |
| Number of spheres Z | 13 | 16 |
| Breadth B/mm | 14 | 21 |
| Sphere diameter Dw/mm | 7.938 | 14.288 |
| Inside diameter d/mm | 20 | 55 |
| Outside diameter D/mm | 47 | 100 |
| Contact angle α/° | 25 | 25 |
| Material | Density/(kg/m3) | Modulus of Elasticity/GPa | Poisson’s Ratio |
|---|---|---|---|
| AISI 52100 | 7810 | 200 | 0.3 |
| Path 1 | Path 2 | Path 3 | Path 4 | |
|---|---|---|---|---|
| Stress range of solid adapter ring/MPa | 6009.75 | 956.44 | 1397.08 | 361.656 |
| Stress range of biomimetic adapter ring/MPa | 2742.55 | 355.9 | 1516.44 | 388.258 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Zhang, X.; Wang, P.; Zhang, X.; Zhang, Y.; Zhang, J.; Zhao, B.; Liu, J. Research on Impact Resistance of Double-Decker Ball Bearing Based on Bionic Loofah Structure. Lubricants 2025, 13, 205. https://doi.org/10.3390/lubricants13050205
Hu J, Zhang X, Wang P, Zhang X, Zhang Y, Zhang J, Zhao B, Liu J. Research on Impact Resistance of Double-Decker Ball Bearing Based on Bionic Loofah Structure. Lubricants. 2025; 13(5):205. https://doi.org/10.3390/lubricants13050205
Chicago/Turabian StyleHu, Jing, Xin Zhang, Puyi Wang, Xinming Zhang, Yiwen Zhang, Jingran Zhang, Baoyan Zhao, and Jingru Liu. 2025. "Research on Impact Resistance of Double-Decker Ball Bearing Based on Bionic Loofah Structure" Lubricants 13, no. 5: 205. https://doi.org/10.3390/lubricants13050205
APA StyleHu, J., Zhang, X., Wang, P., Zhang, X., Zhang, Y., Zhang, J., Zhao, B., & Liu, J. (2025). Research on Impact Resistance of Double-Decker Ball Bearing Based on Bionic Loofah Structure. Lubricants, 13(5), 205. https://doi.org/10.3390/lubricants13050205





