Leakage Flow Characteristics of Novel Two-Stage Brush Seal with Pressure-Equalizing Hole
Abstract
1. Introduction
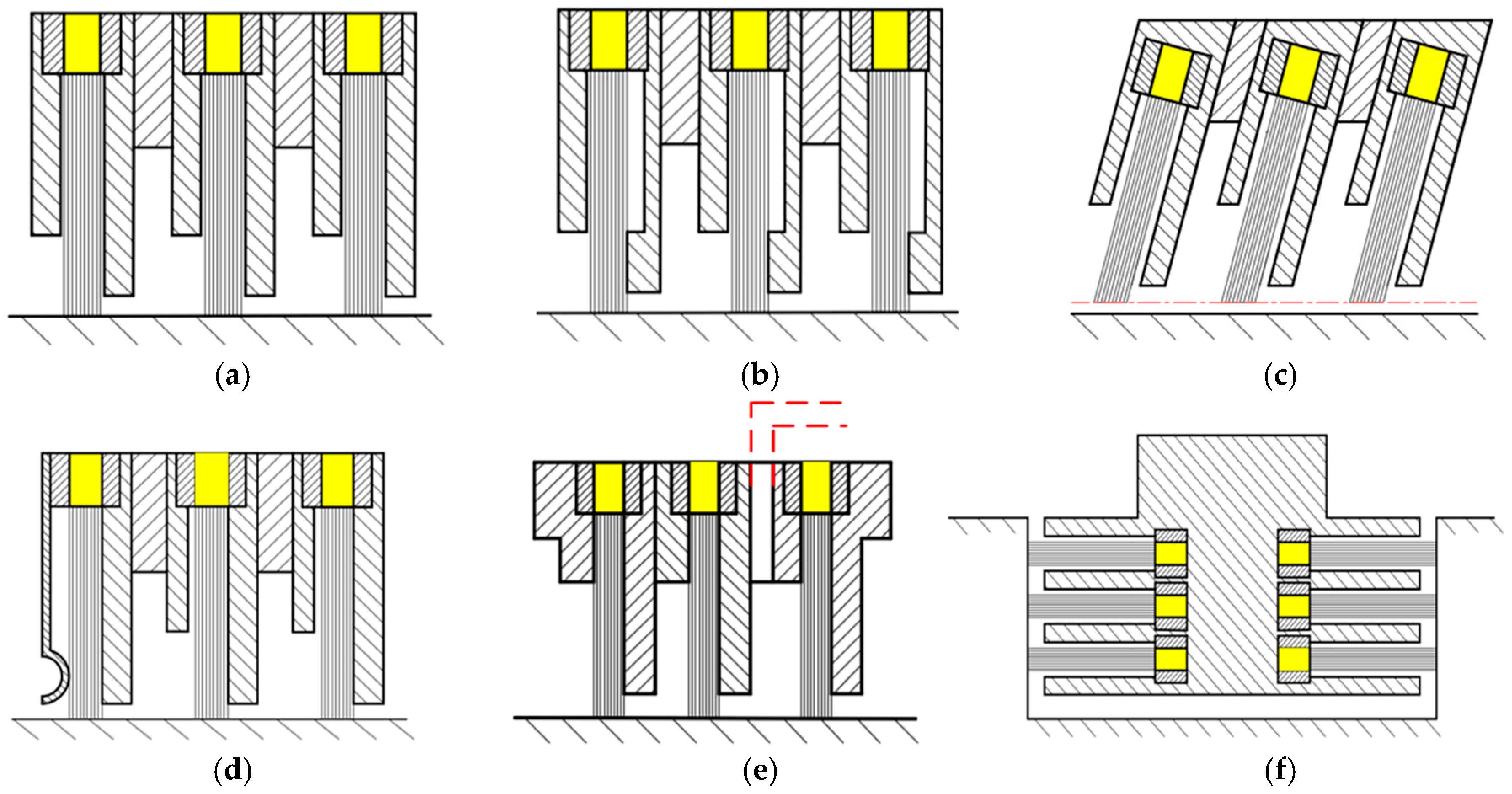
2. NBS Structure Design
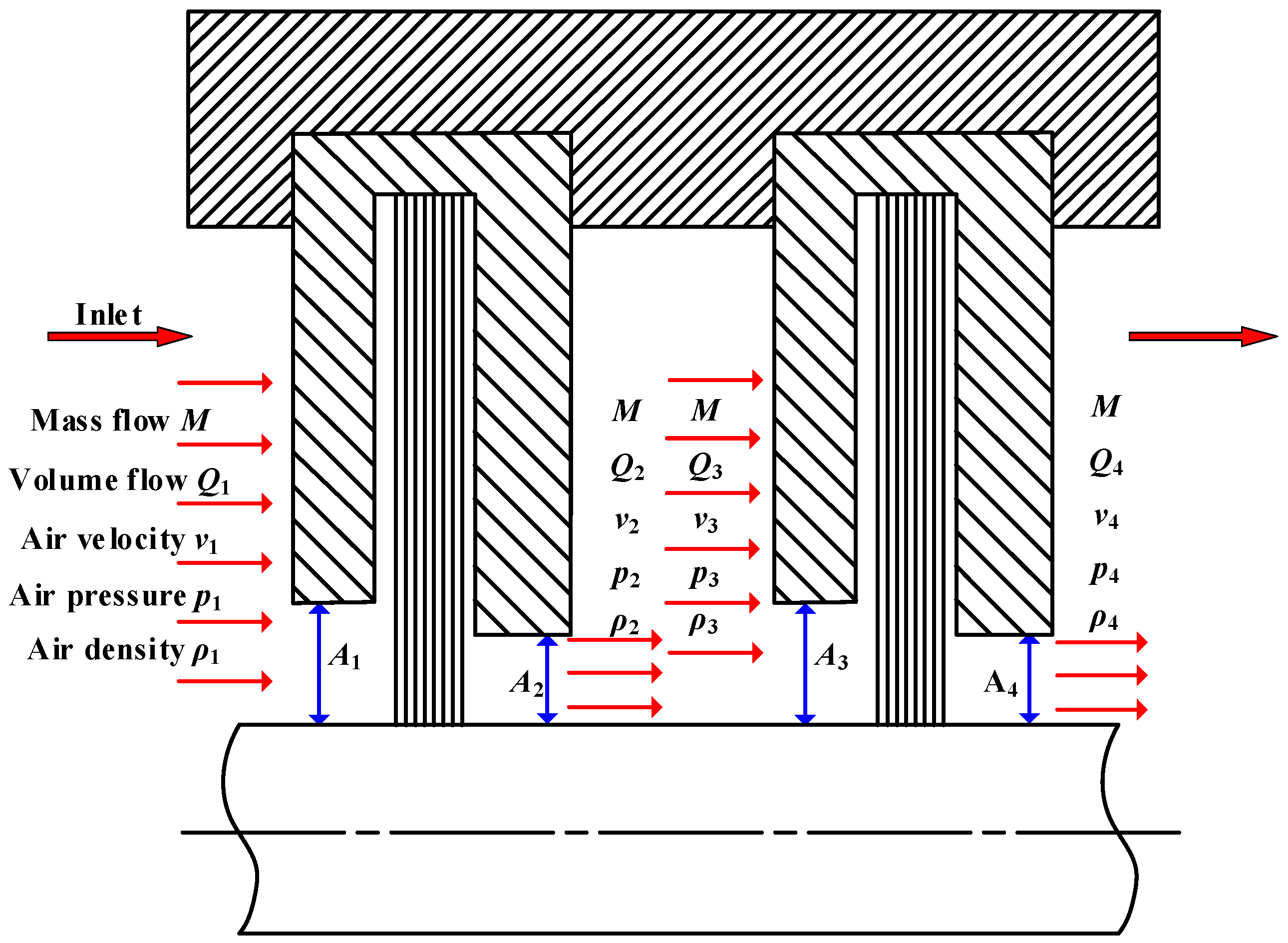
2.1. Pressure Drop Imbalance Theory of the CBS
2.2. Design Principle of the NBS
3. Calculation Model
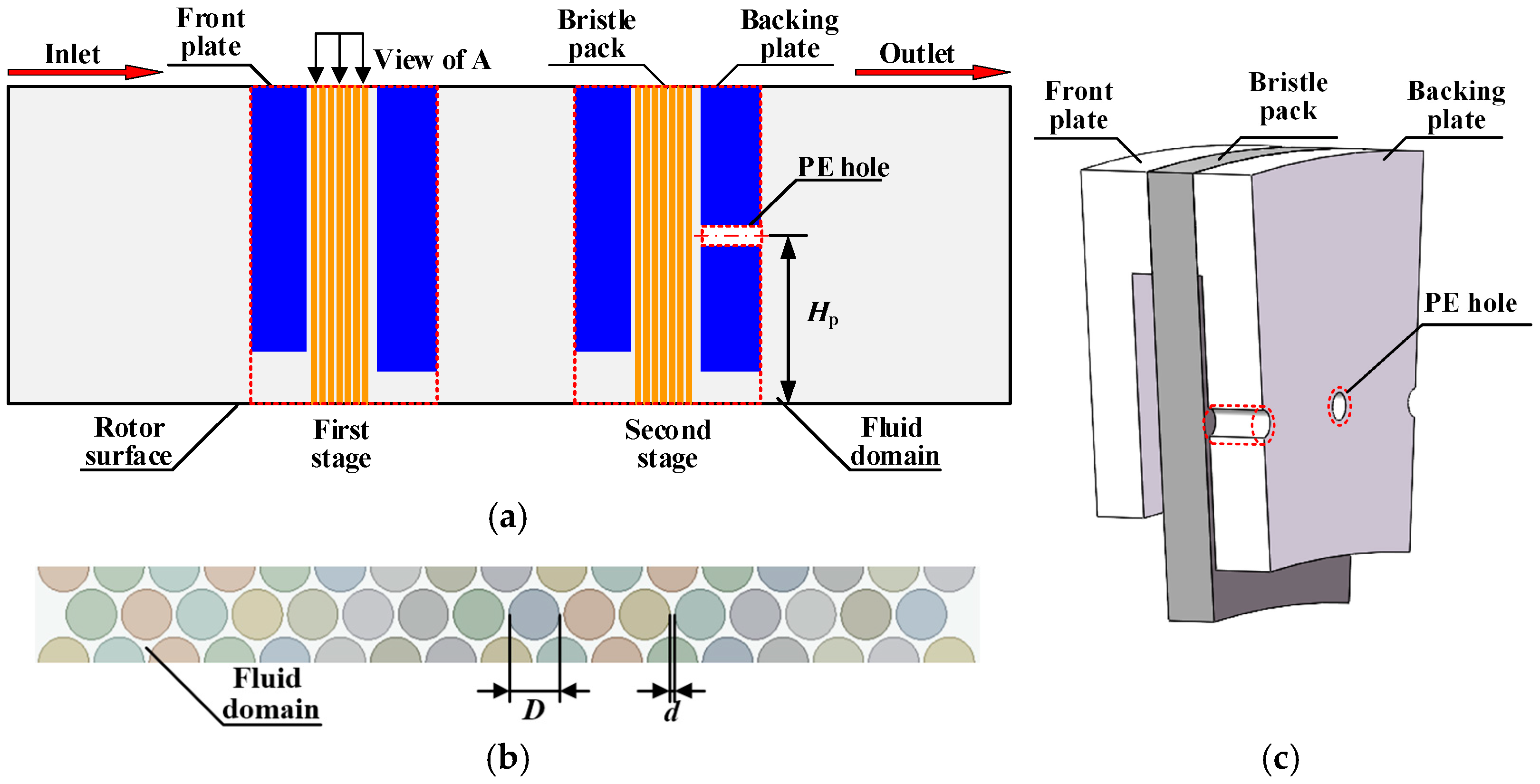
3.1. Numerical Model of NBS
3.2. Meshing
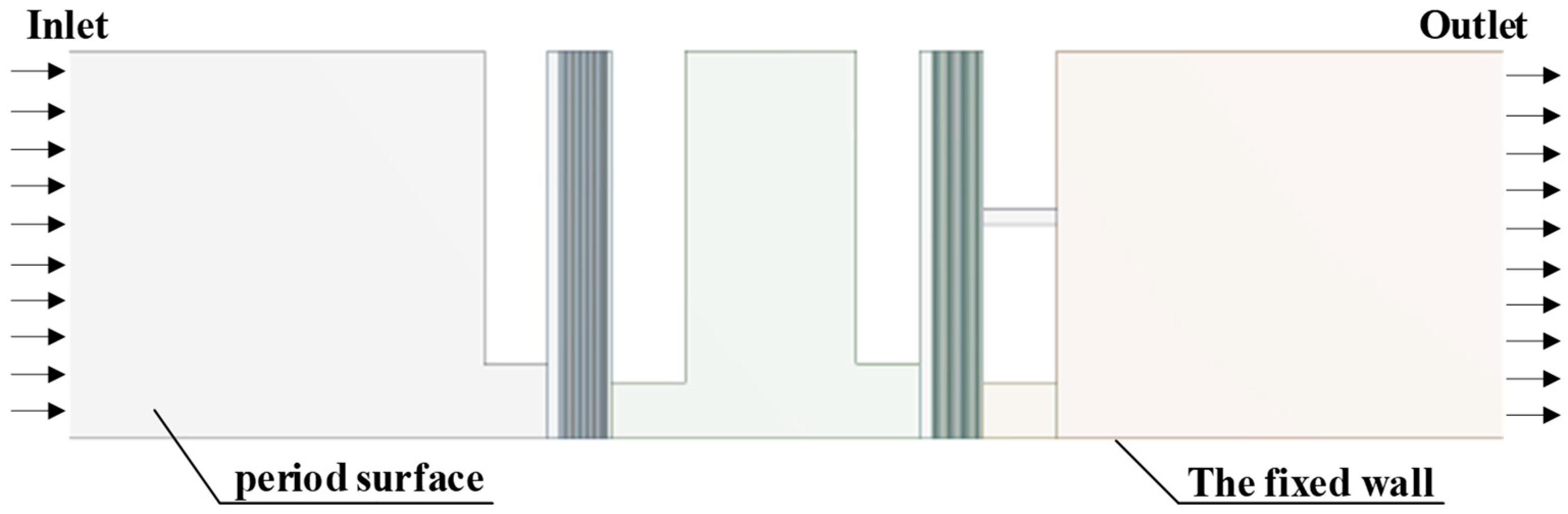
3.3. Boundary Conditions
3.4. Validation of the Numerical Model
4. Analysis of the Effects of Structural Parameters on the Inter-Stage Pressure Drop Balance of NBS
4.1. Effects of PE Hole Diameter on Inter-Stage Pressure
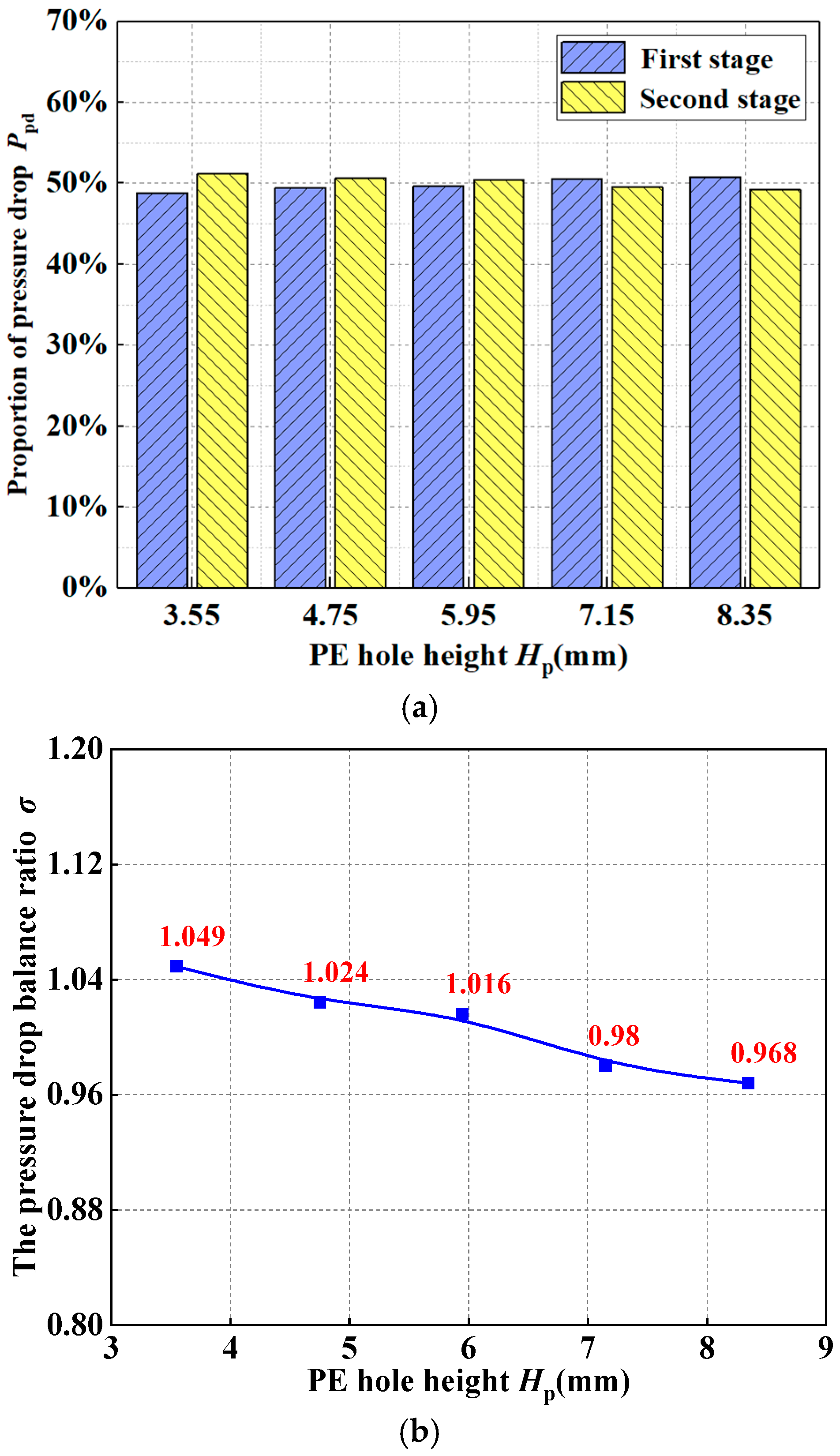
4.2. Effects of PE Hole Height on Inter-Stage Pressure
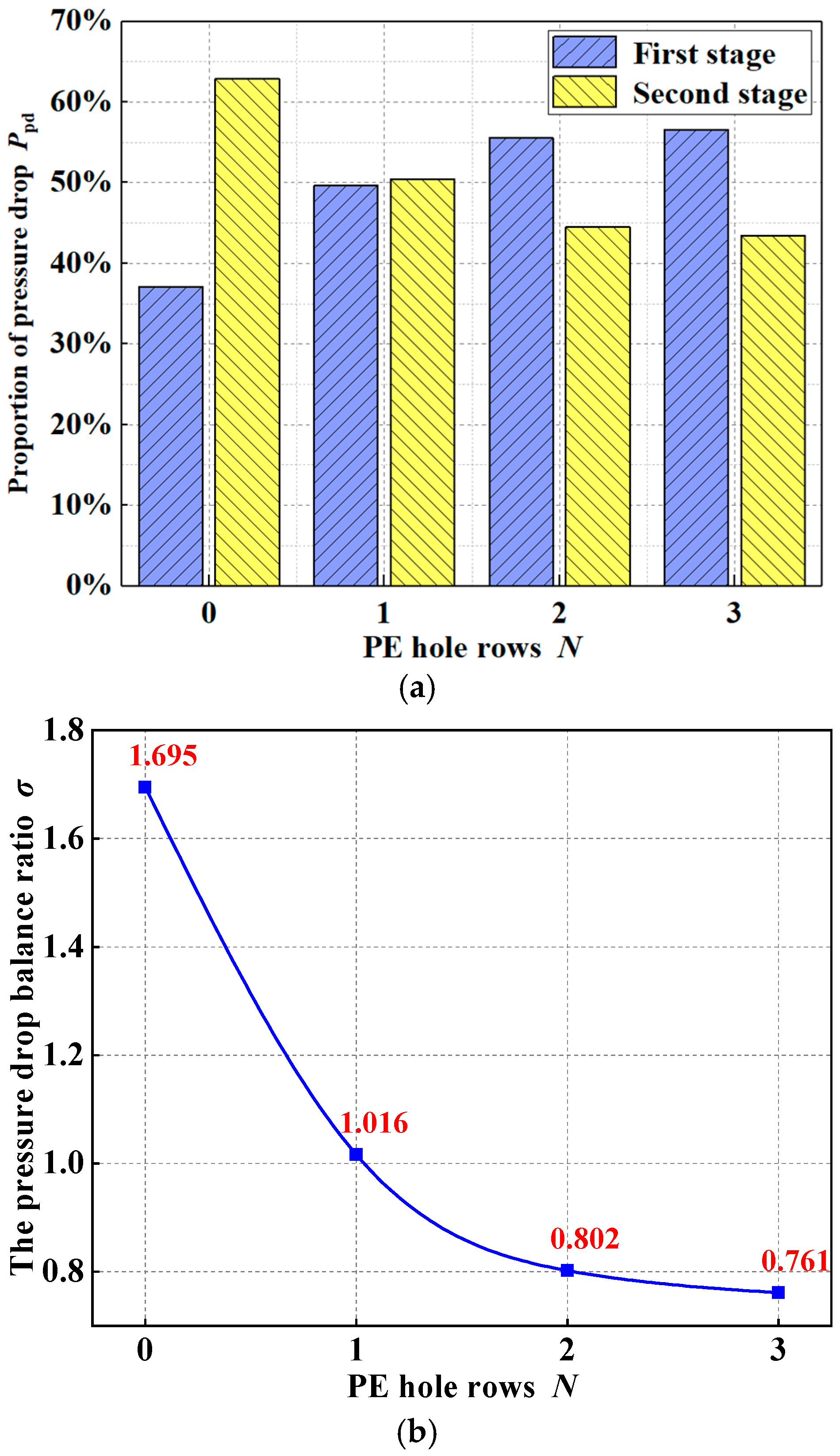
4.3. Effects of PE Hole Rows on Inter-Stage Pressure
4.4. Analysis of Pressure Distribution Characteristics of NBS
5. Analysis of Flow Field of NBS
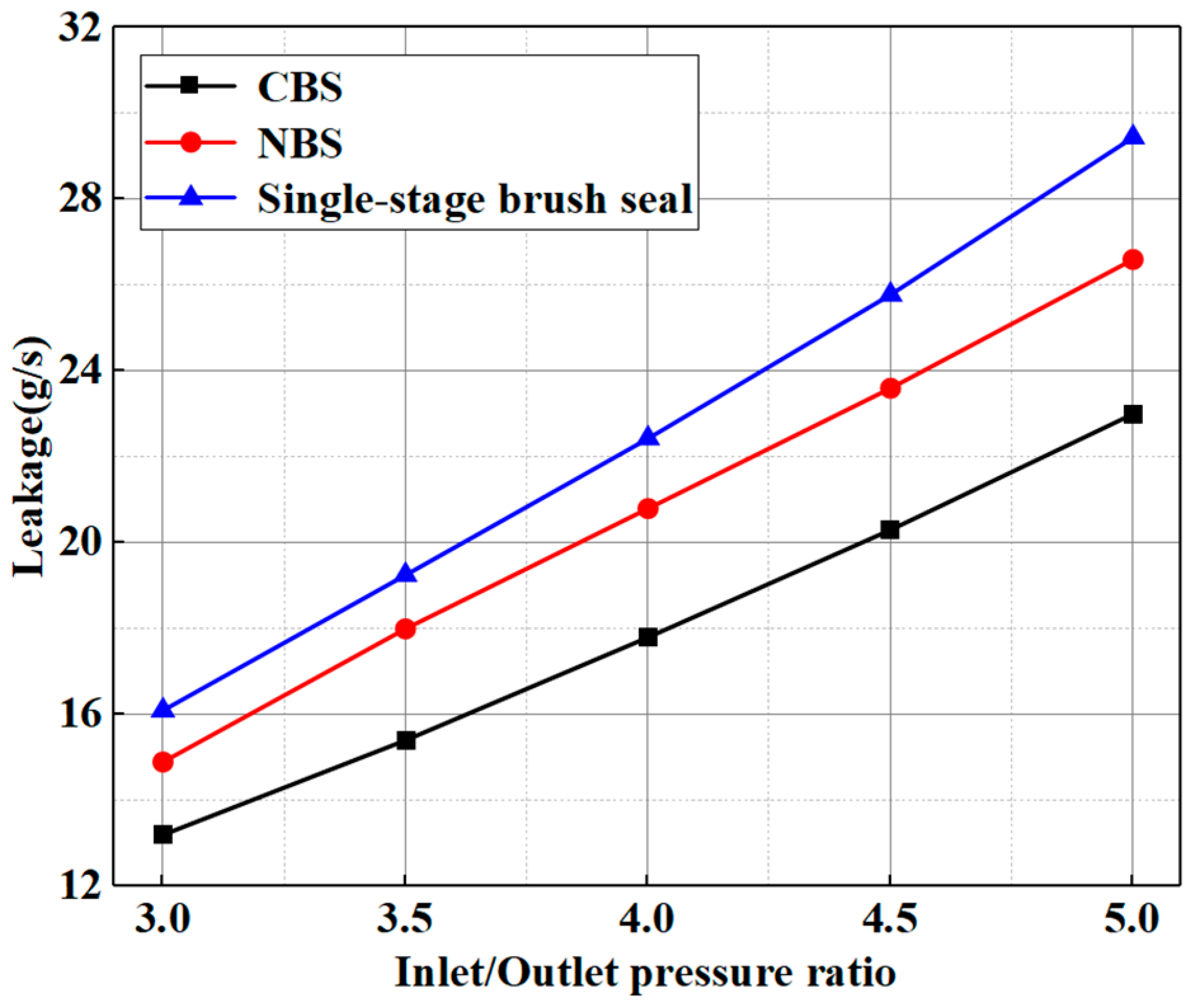
5.1. Analysis of Leakage Characteristics of NBS
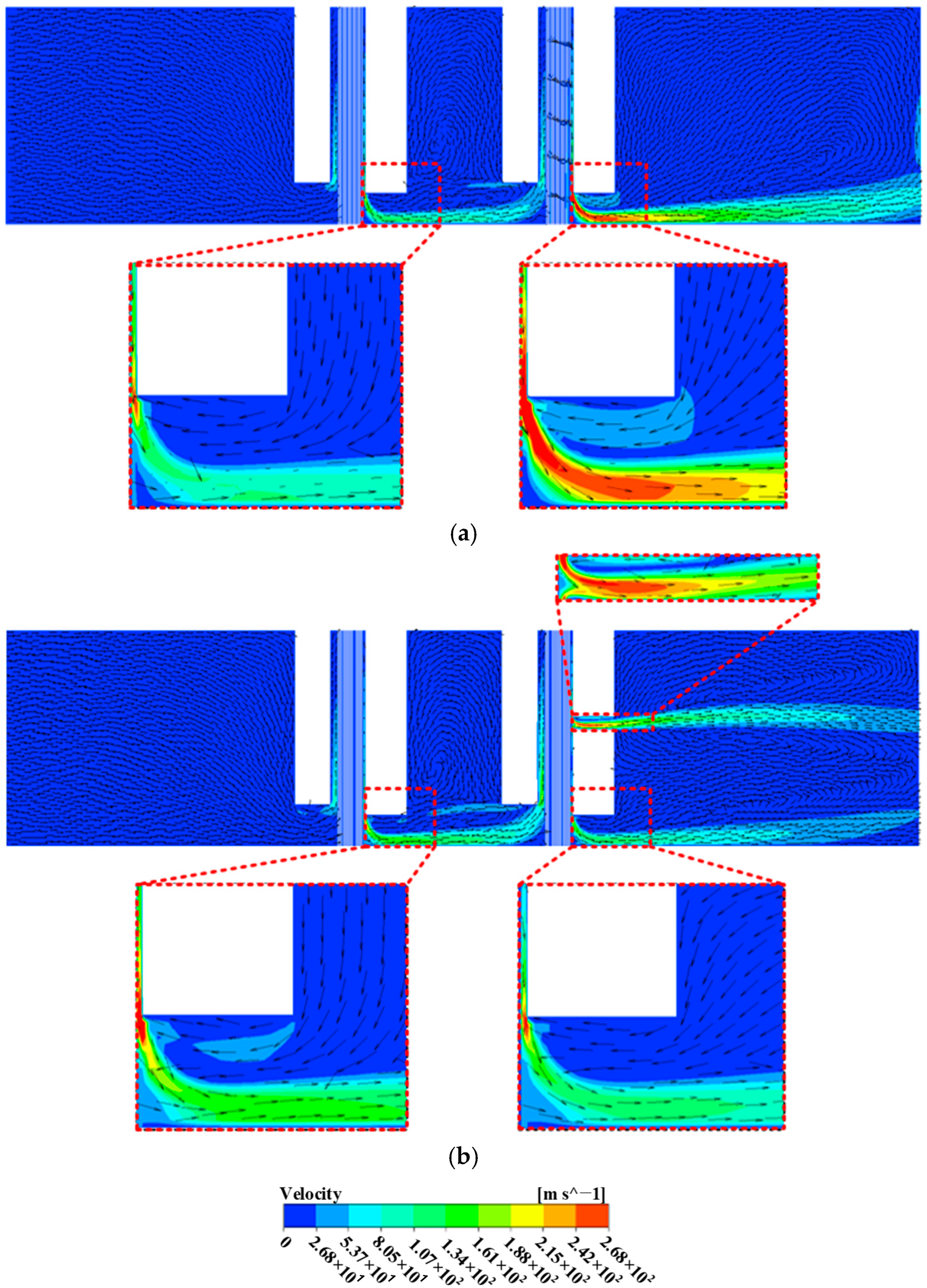
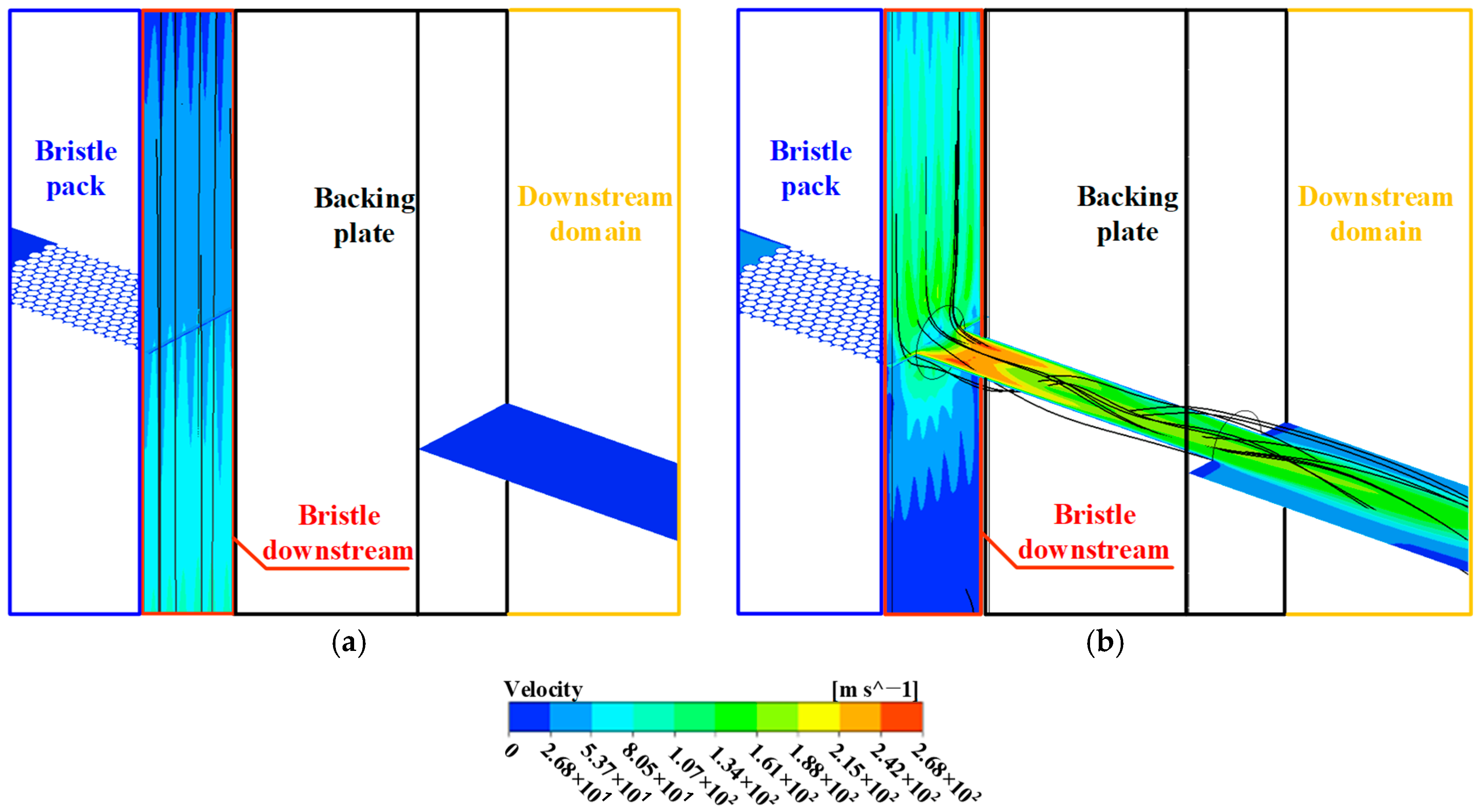
5.2. Analysis of Air Velocity Distribution Characteristics of NBS
6. Conclusions
- (1)
- The NBS increased the effective flow area of the second-stage brush seal, and the inter-stage pressure drop was more even. Therefore, the NBS effectively balanced the inter-stage pressure drop of the CBS. Under the structural parameters studied in this paper, the pressure drop balance ratio of the NBS is improved by 45.6~67.9% compared to the CBS.
- (2)
- The PE hole diameter, rows and PE hole height were found to enhance the pressure drop uniformity. The pressure drop balance ratio was greatly affected by the PE hole diameter and rows, and was less affected by the PE hole height. When the PE hole diameter was 0.4 mm, the height was 5.95 mm and the number of rows was 1, the NBS had the best pressure drop balance.
- (3)
- The PE hole expands the air outlet channel and outflow area, resulting in a 12.9~16.8% increase in NBS leakage relative to CBS. However, this phenomenon does not only constitute damage. On the contrary, the PE hole alleviates the problem of uneven pressure drop between CBS stages, which is beneficial to improve the service life of the two-stage brush seal. From a comprehensive perspective, the solution based on nature proposed in this paper has a certain practicability in practical engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| CBS | common two-stage brush seal |
| NBS | novel two-stage pressure-equalizing brush seal |
| ΔP1, ΔP2 | pressure drop of the first stage and second stage of the two-stage brush seal, MPa |
| σ | pressure drop balance ratio |
| L | ratio between passage areas at inlet and outlet of the stage |
| ΔQ1, ΔQ2 | volume flow increment of first stage and second stage of the two-stage brush seal |
| Hf | height of front plate to rotor, mm |
| Hb | height of backing plate to rotor, mm |
| D | bristle diameter, mm |
| d | bristle gap, mm |
| W | axial width of bristle pack, mm |
| l | bristle length, mm |
| Lf | axial width of front plate, mm |
| Lb | axial width of backing plate, mm |
| Dp | PE hole diameter, mm |
| Hp | PE hole height, mm |
| N | PE hole rows |
| Rp | pressure ratio |
| Ppd | proportion of pressure drop |
References
- Fuchs, A.; Haidn, O.J. Effects of Uncertainty and Quasi-Chaotic Geometry on the Leakage of Brush Seals. J. Turbomach. 2019, 141, 021003. [Google Scholar] [CrossRef]
- Ha, Y.; Ha, T.; Byun, J.; Lee, Y. Leakage effects due to bristle deflection and wear in hybrid brush seal of high-pressure steam turbine. Tribol. Int. 2020, 150, 106325. [Google Scholar] [CrossRef]
- Hildebrandt, M.; Schwitzke, C.; Bauer, H.J. Analysis of Heat Flux Distribution during Brush Seal Rubbing Using CFD with Porous Media Approach. Energies 2021, 14, 1888. [Google Scholar] [CrossRef]
- Wei, Y.; Ran, X.H.; Sun, T.; Liu, S.L.; Zhang, H.L.; Zhao, D.F. Dynamic characteristics analysis of a vertical Jeffcott rotor-brush seal system. J. Chin. Inst. Eng. 2022, 45, 245–254. [Google Scholar] [CrossRef]
- Chupp, R.E.; Ghasripoor, F.; Turnquist, N.A.; Demiroglu, M.; Aksit, M.F. Advanced seals for industrial turbine applications: Dynamic seal development. J. Propul. Power 2002, 18, 1260–1266. [Google Scholar] [CrossRef]
- Changizi, A.; Stiharu, I.; Outirba, B.; Hendrick, P. Mathematical model of brush seals for gas turbine engines: A nonlinear analytical solution. Adv. Mech. Eng. 2021, 13, 16878140211043396. [Google Scholar] [CrossRef]
- Liu, Y.X.; Dong, W.L.; Chew, J.; Pekris, M.; Yue, B.Z.; Kong, X.Z. Flow Conditioning to Control the Effects of Inlet Swirl on Brush Seal Performance in Gas Turbine Engines. Front. Energy Res. 2022, 9, 815152. [Google Scholar] [CrossRef]
- Lee, J.J.; Kang, S.Y.; Kim, T.S.; Byun, S.S. Thermo-economic analysis on the impact of improving inter-stage packing seals in a 500 MW class supercritical steam turbine power plant. Appl. Therm. Eng. 2017, 121, 974–983. [Google Scholar] [CrossRef]
- Addis, M.E.; Dalton, W.S. Brush-Seal Designs for Elastic Fluid Turbines. U.S. Patent No. 6,318,728, 20 November 2001. [Google Scholar]
- Tseng, W.Y.; Bristol, B.L.; Hetico, R.R.; Glynn, C.C. Brush Seal. U.S. Patent No. 5,568,931, 29 October 1996. [Google Scholar]
- Tanimura, K. Apparatus for Sealing a Channel. EP Patent No. 2,305,956, 28 February 2018. [Google Scholar]
- Naert, A.; Durieu, F. Turbomachine Axial Compressor Seal with a Brush Seal. U.S. Patent No. 20,150,063,990, 5 March 2015. [Google Scholar]
- Chupp, R.E.; Dowler, C.A. Performance Characteristics of Brush Seals for Limited-Life Engines. J. Eng. Gas Turbines Power 1993, 115, 390–396. [Google Scholar] [CrossRef]
- Hendricks, R.C.; Griffin, T.A.; Kline, T.R.; Kline, R.C.; Arvind, P.; Dvandra, S. Relative Performance Comparison Between Baseline Labyrinth and Dual Brush Compressor Discharge Seals in a T-700 Engine Test. In Proceedings of the ASME 1994 International Gas Turbine and Aeroengine Congress and Exposition, The Hague, The Netherlands, June 13–16 1994; pp. 1–21. [Google Scholar] [CrossRef]
- Pugachev, A.O.; Deckner, M. Experimental and theoretical rotordynamic stiffness coefficients for a three-stage brush seal. Mech. Syst. Signal Process. 2012, 31, 143–154. [Google Scholar] [CrossRef]
- Qiu, B.; Li, J.; Yan, X. Investigation into the flow behavior of multi-stage brush seals. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 228, 416–428. [Google Scholar] [CrossRef]
- Yang, J.; Huang, S.Q.; Suo, S.F.; Wang, A.M. Investigating the frictional force distributions and inter-stage imbalance of a two-stage brush seal. AIP Adv. 2020, 10, 035323. [Google Scholar] [CrossRef]
- Zhao, H.; Li, Y.L.; Sun, D.; Li, Y.; Wen, S.F.; Sun, J.S. Inter-Stage Pressure Drop of Multi-Stage Brush Seal with Differentiated Structure. J. Eng. Gas Turbines Power 2023, 145, 071001. [Google Scholar] [CrossRef]
- Sun, D.; Yang, Y.X.; Zhao, H.; Zhang, J.Y.; Yang, Z.M.; Zhang, J.H. Influence factors of frictional heat between bristles and rotor for a multi-stage brush seal. Tribol. Int. 2024, 198, 109841. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids 1992, 4, 1510–1520. [Google Scholar] [CrossRef]


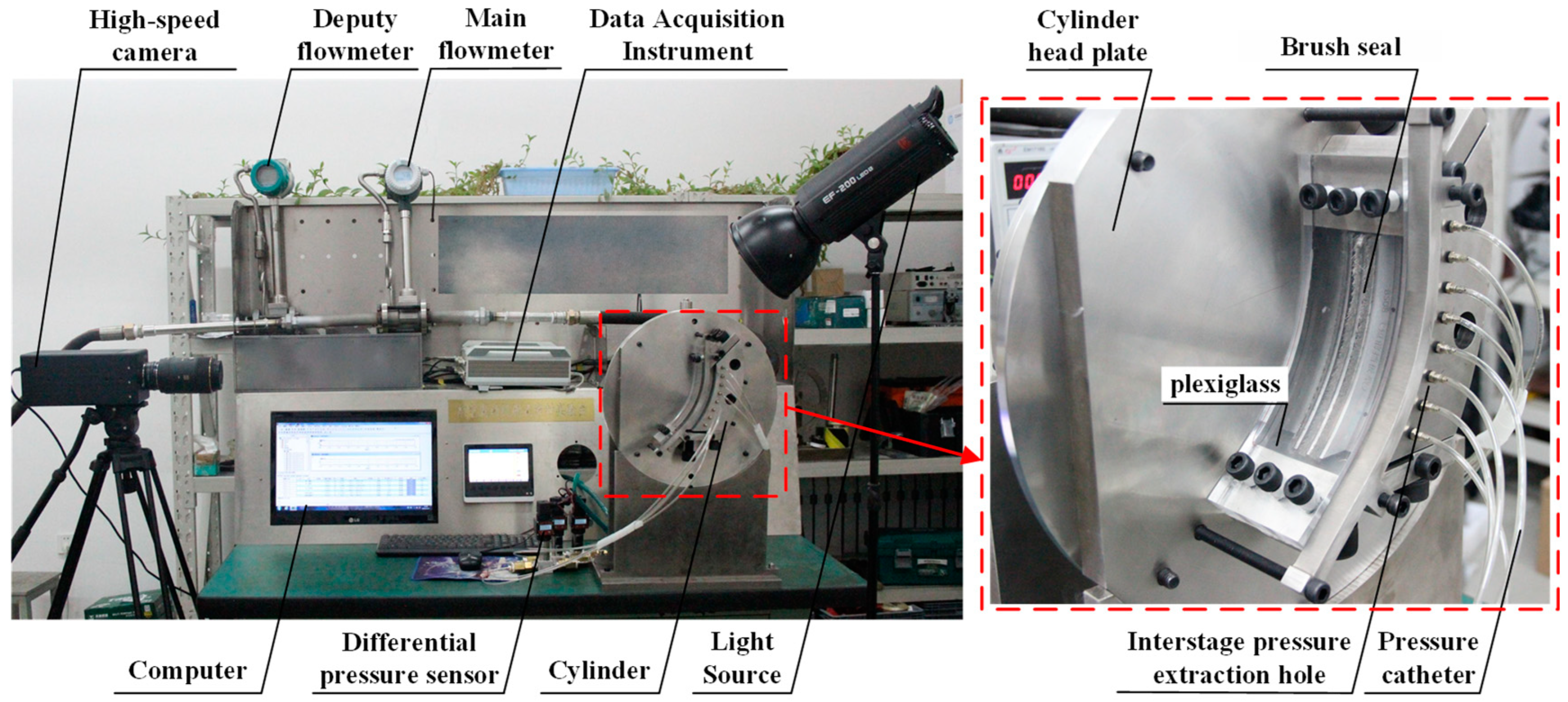
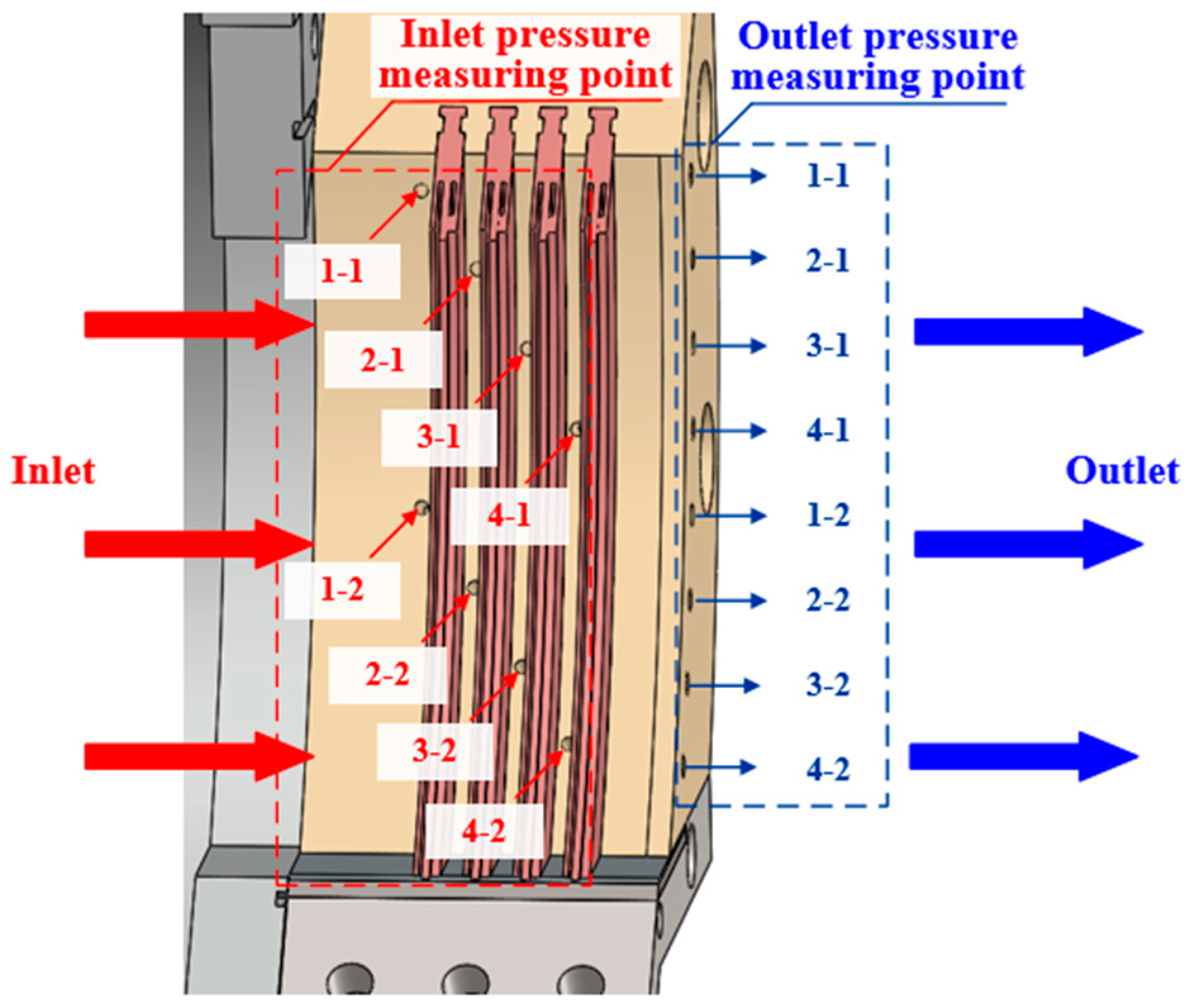


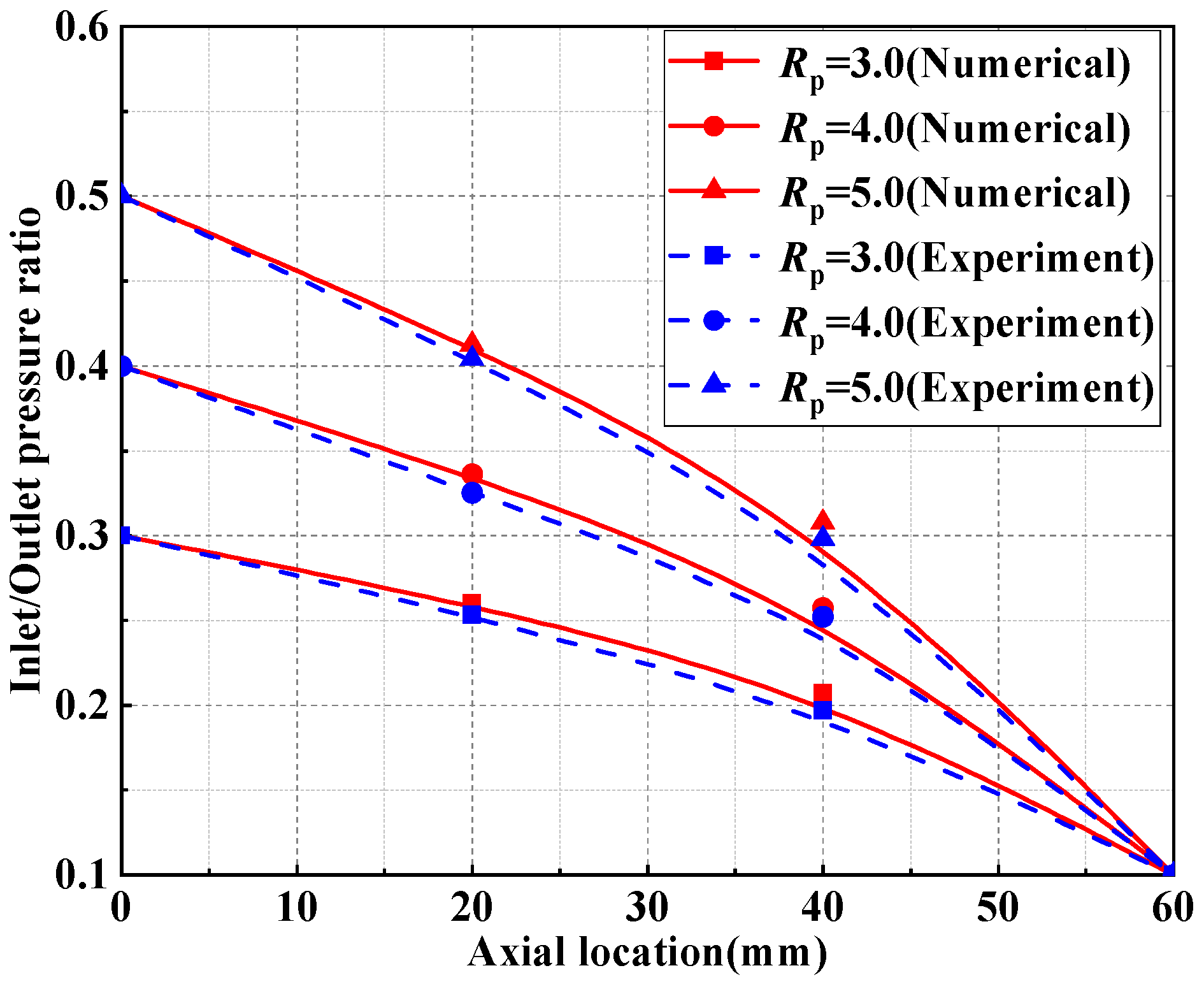



| Structural Parameters | Values |
|---|---|
| Height of front plate to rotor Hf (mm) | 2.0 |
| Height of backing plate to rotor Hb (mm) | 1.5 |
| Bristle diameter D/mm | 0.08 |
| Bristle gap d/mm | 0.008 |
| Axial width of bristle pack W/mm | 1.5 |
| Bristle length l/mm | 10.4 |
| Axial width of front plate Lf/mm | 1.5 |
| Axial width of backing plate Lb/mm | 2 |
| PE hole diameter Dp/mm | 0.2, 0.4, 0.6, 0.8 |
| PE hole height Hp/mm | 3.55, 4.75, 5.95, 7.15, 8.35 |
| PE hole rows N | 1, 2, 3 |
| Number of Grids/Ten Thousand | Leakage (g/s) |
|---|---|
| 301 | 14.62 |
| 382 | 14.43 |
| 458 | 14.08 |
| 546 | 13.84 |
| 590 | 13.84 |
| Working Condition Parameters | Values |
|---|---|
| Fluid | Ideal air |
| Turbulence model | RNG k-ε |
| Inlet total pressure/MPa | 0.3, 0.4, 0.5 |
| Outlet static pressure/MPa | 0.1 |
| Inlet temperature/K | 290 |
| Rotational speed/(r·min−1) | 3000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xu, H.; Zhang, J.; Sun, D.; Yang, Z. Leakage Flow Characteristics of Novel Two-Stage Brush Seal with Pressure-Equalizing Hole. Lubricants 2025, 13, 190. https://doi.org/10.3390/lubricants13040190
Li Y, Xu H, Zhang J, Sun D, Yang Z. Leakage Flow Characteristics of Novel Two-Stage Brush Seal with Pressure-Equalizing Hole. Lubricants. 2025; 13(4):190. https://doi.org/10.3390/lubricants13040190
Chicago/Turabian StyleLi, Yu, Huanze Xu, Jinghan Zhang, Dan Sun, and Zemin Yang. 2025. "Leakage Flow Characteristics of Novel Two-Stage Brush Seal with Pressure-Equalizing Hole" Lubricants 13, no. 4: 190. https://doi.org/10.3390/lubricants13040190
APA StyleLi, Y., Xu, H., Zhang, J., Sun, D., & Yang, Z. (2025). Leakage Flow Characteristics of Novel Two-Stage Brush Seal with Pressure-Equalizing Hole. Lubricants, 13(4), 190. https://doi.org/10.3390/lubricants13040190





