The Impact of Surface Roughness on the Friction and Wear Performance of GCr15 Bearing Steel
Abstract
:1. Introduction
2. Experimental Methods
3. Results and Discussion
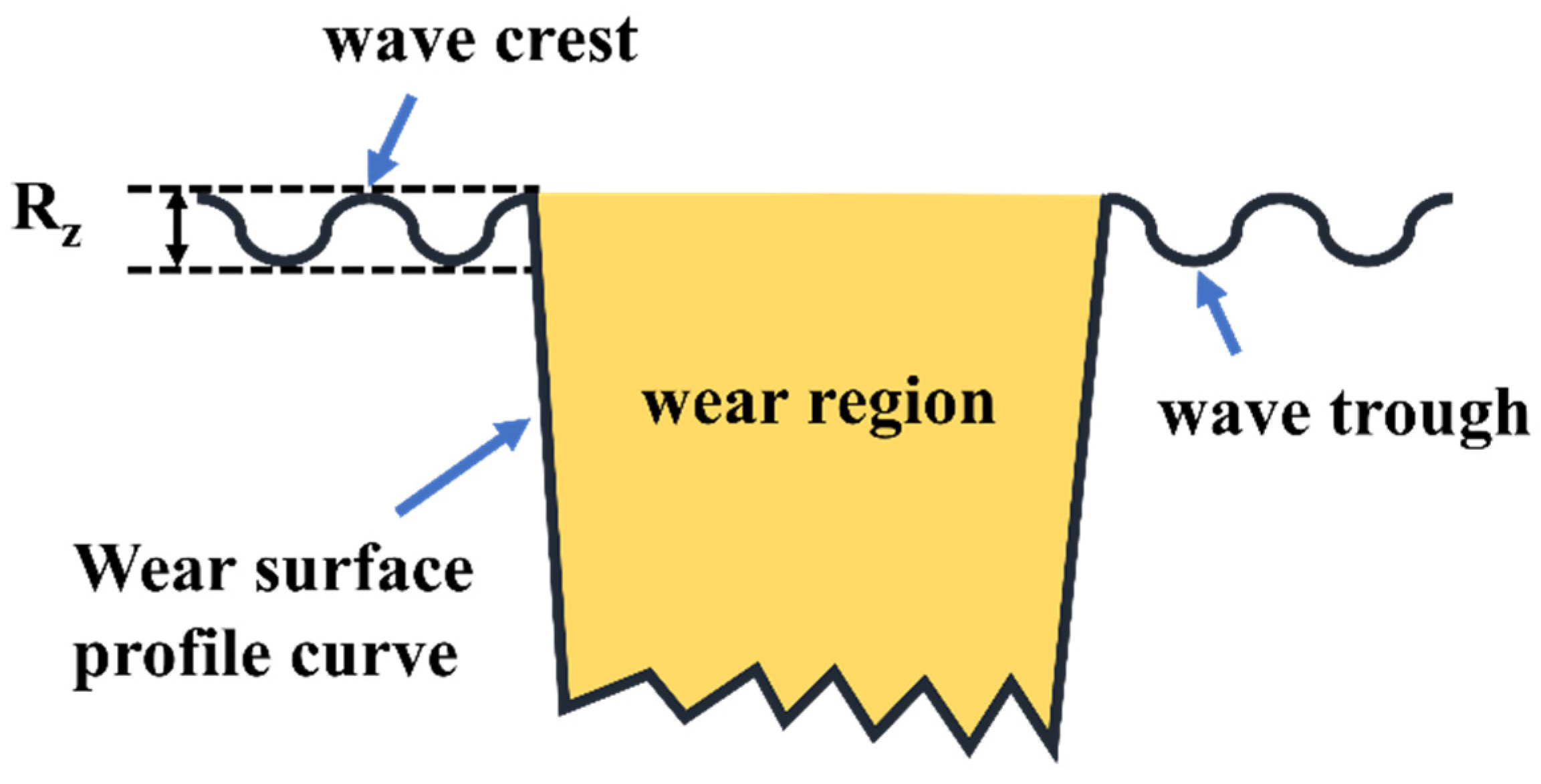
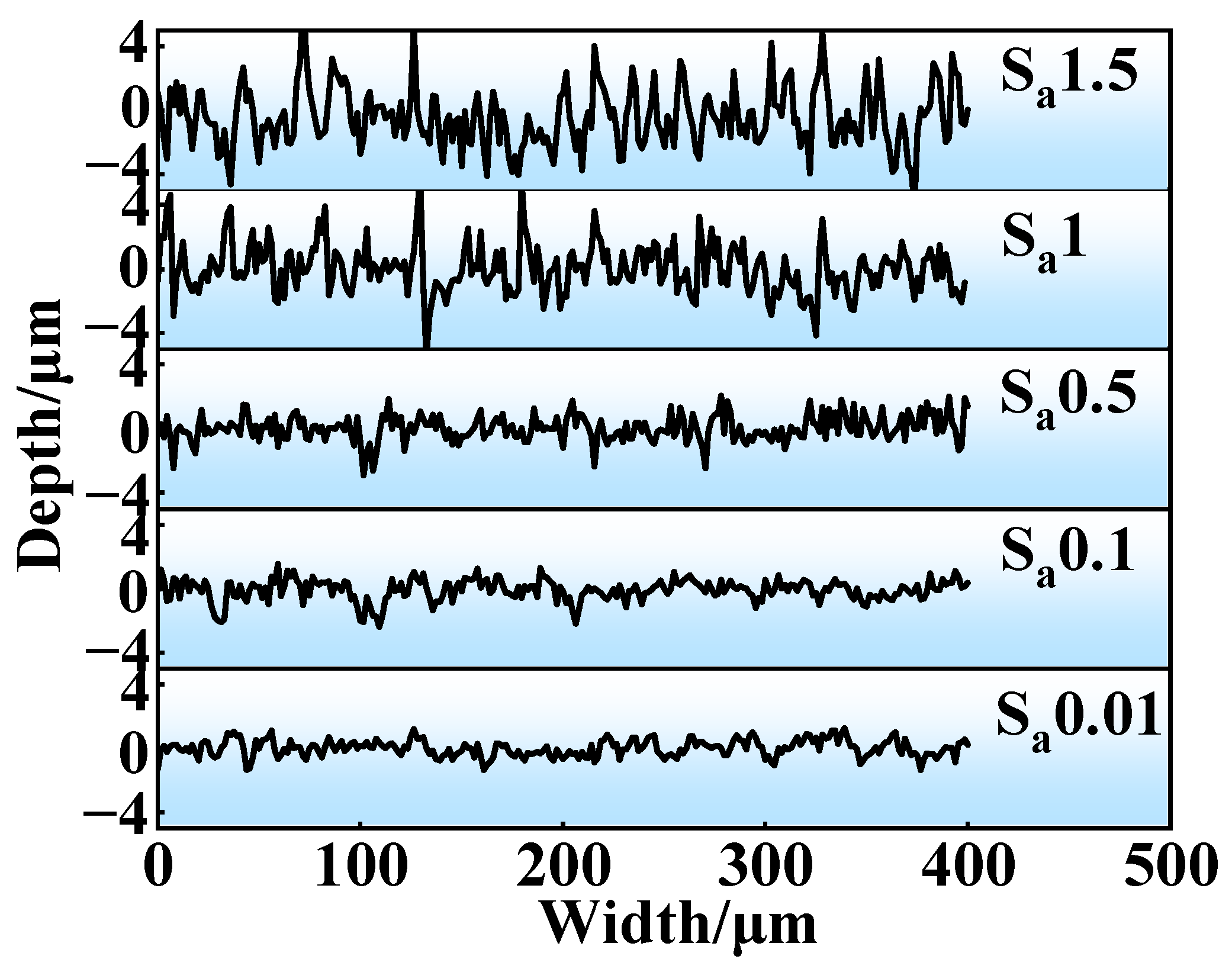
3.1. Microscopic Morphology
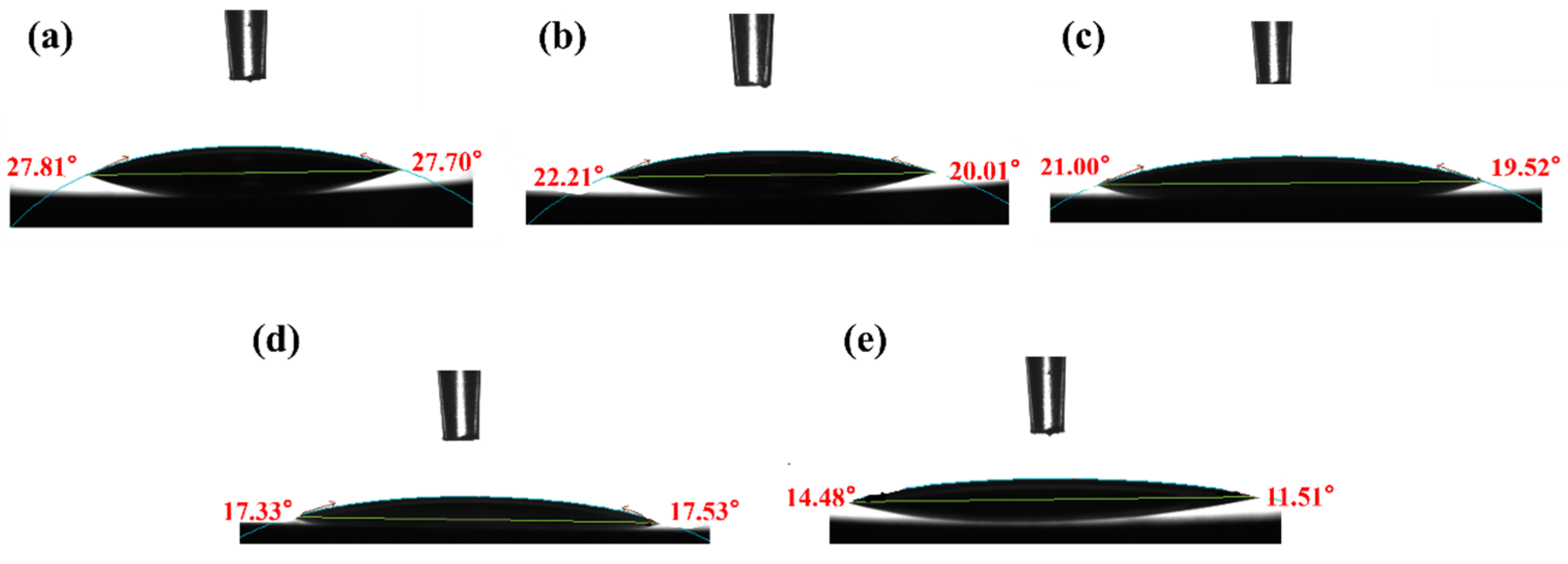
3.2. Contact Angle
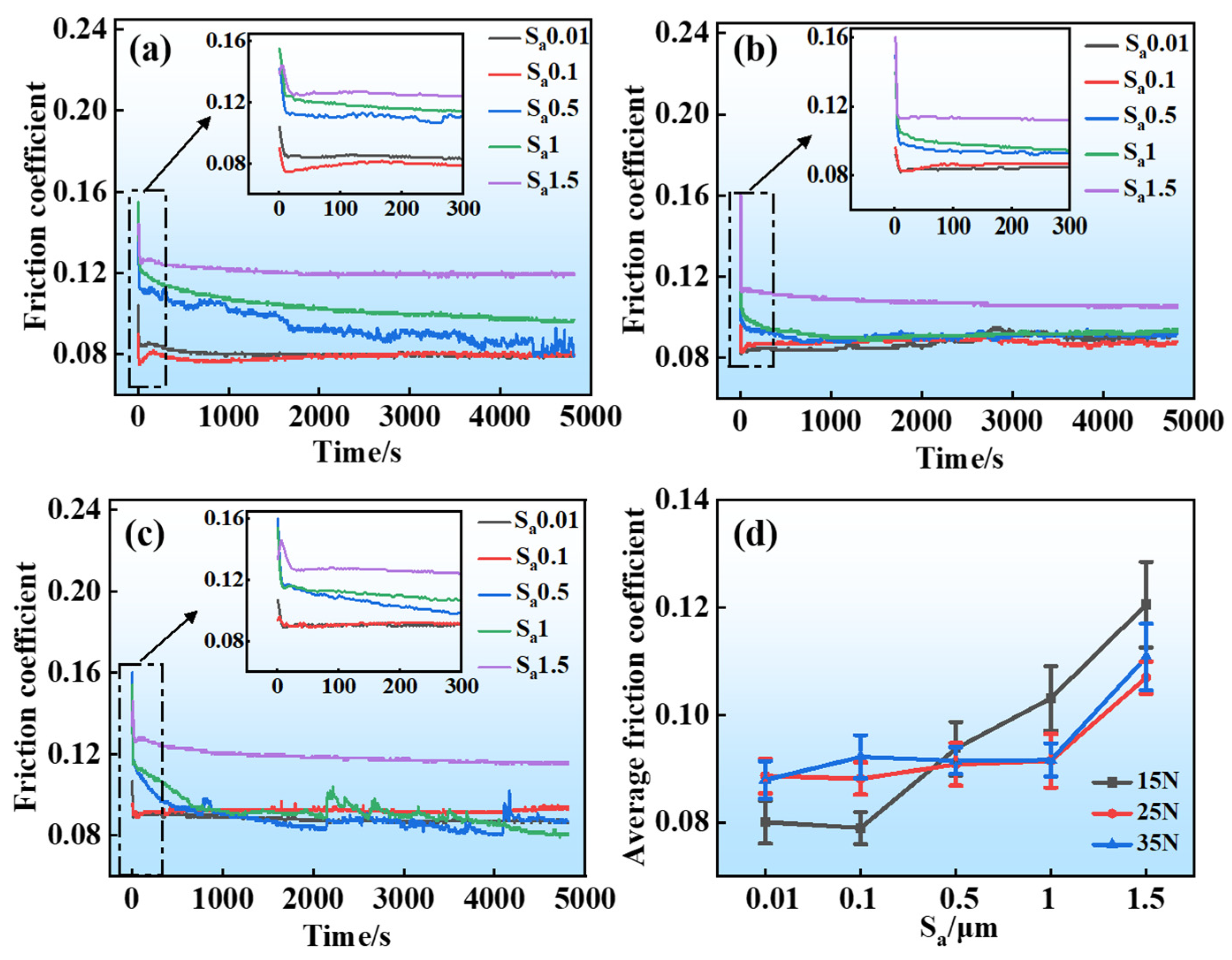
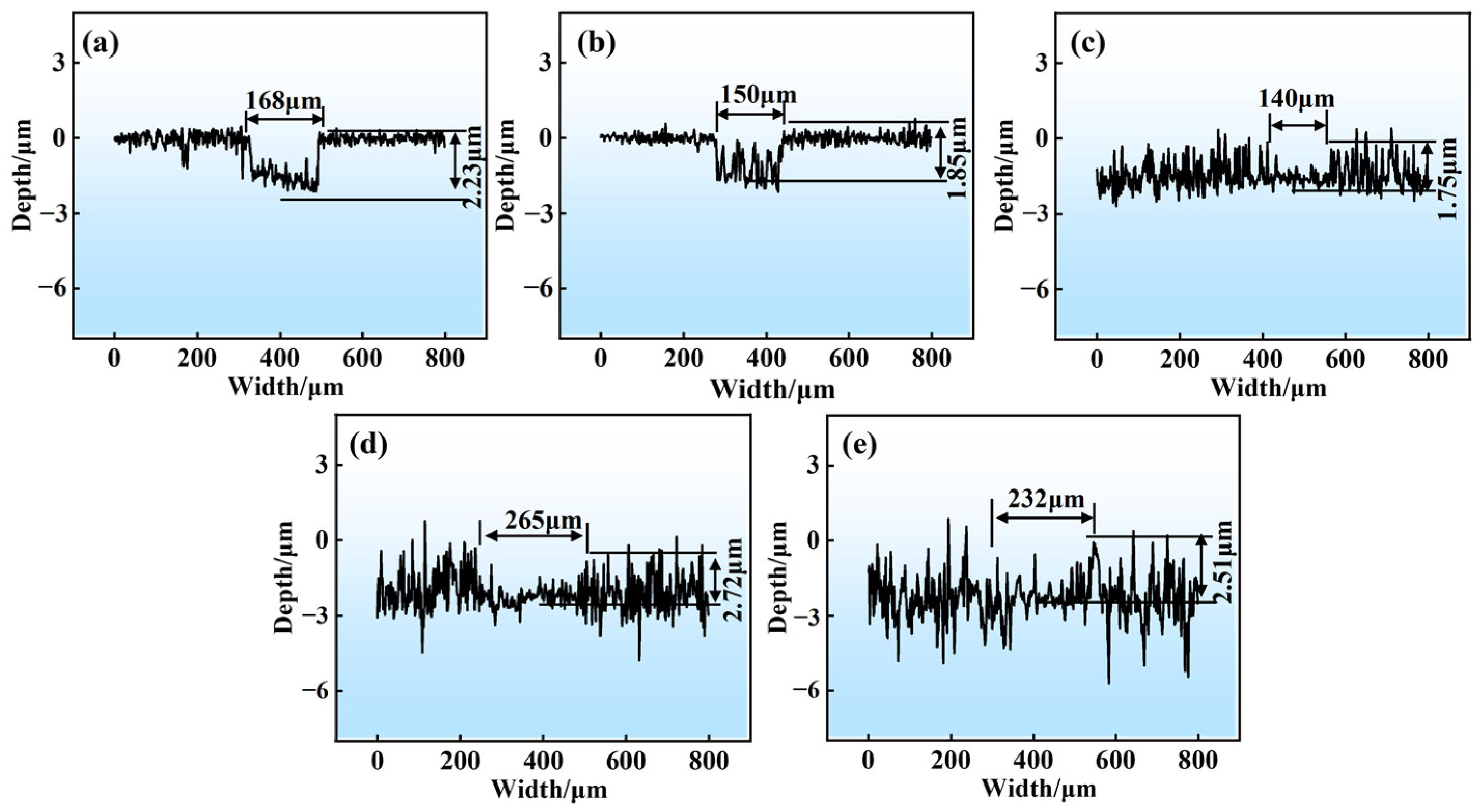
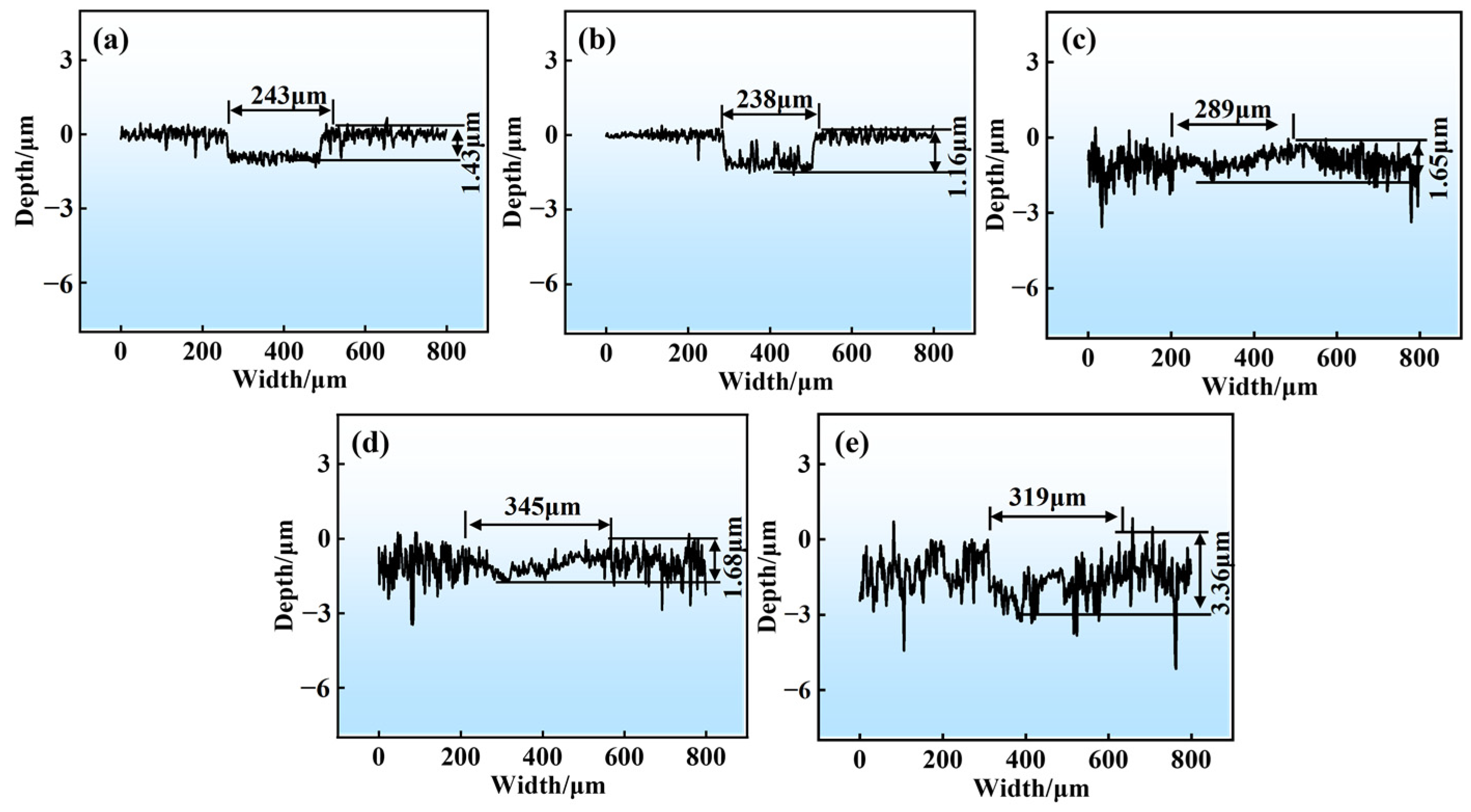
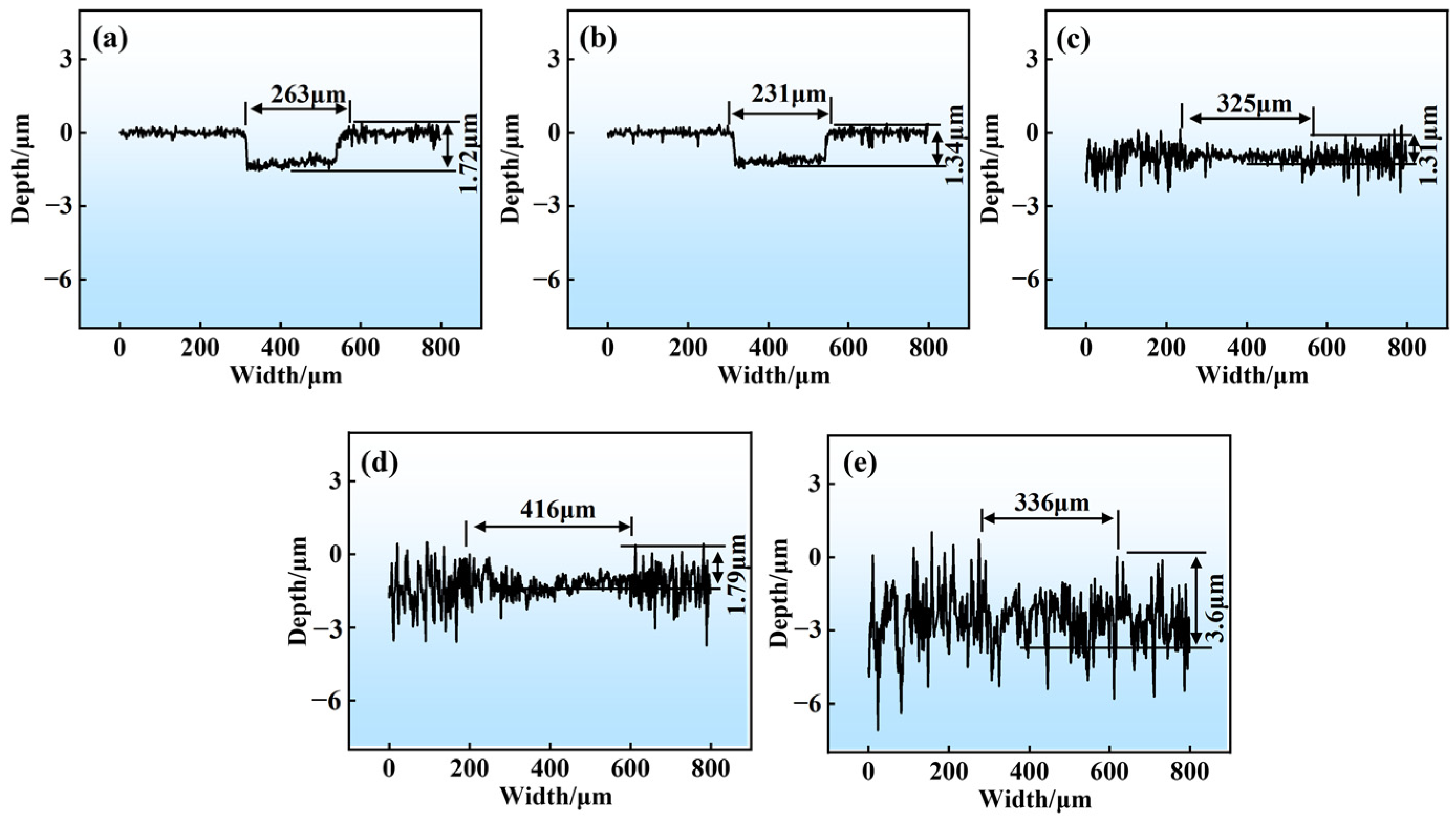
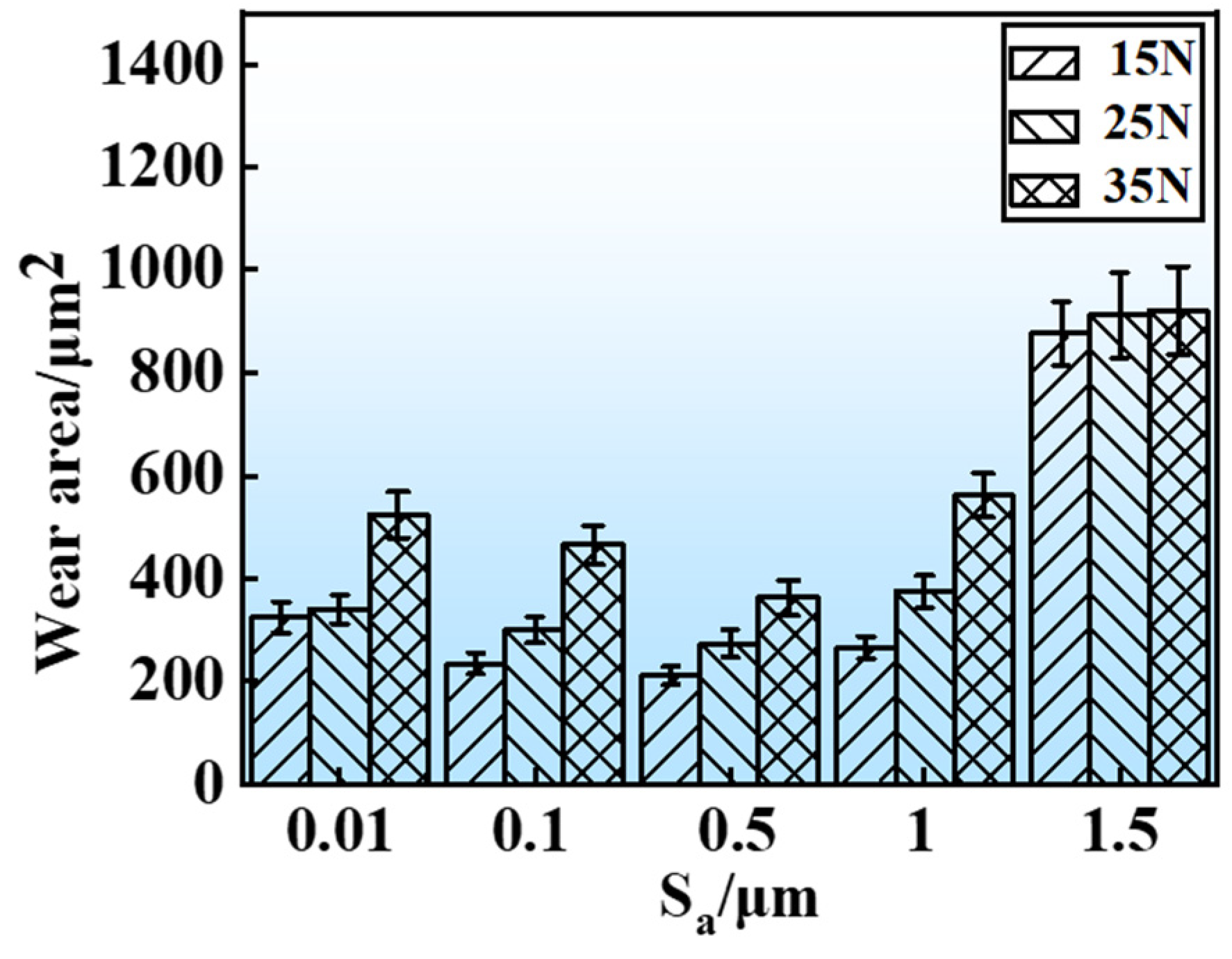
3.3. Friction and Wear Performance
3.4. Wear Mechanism
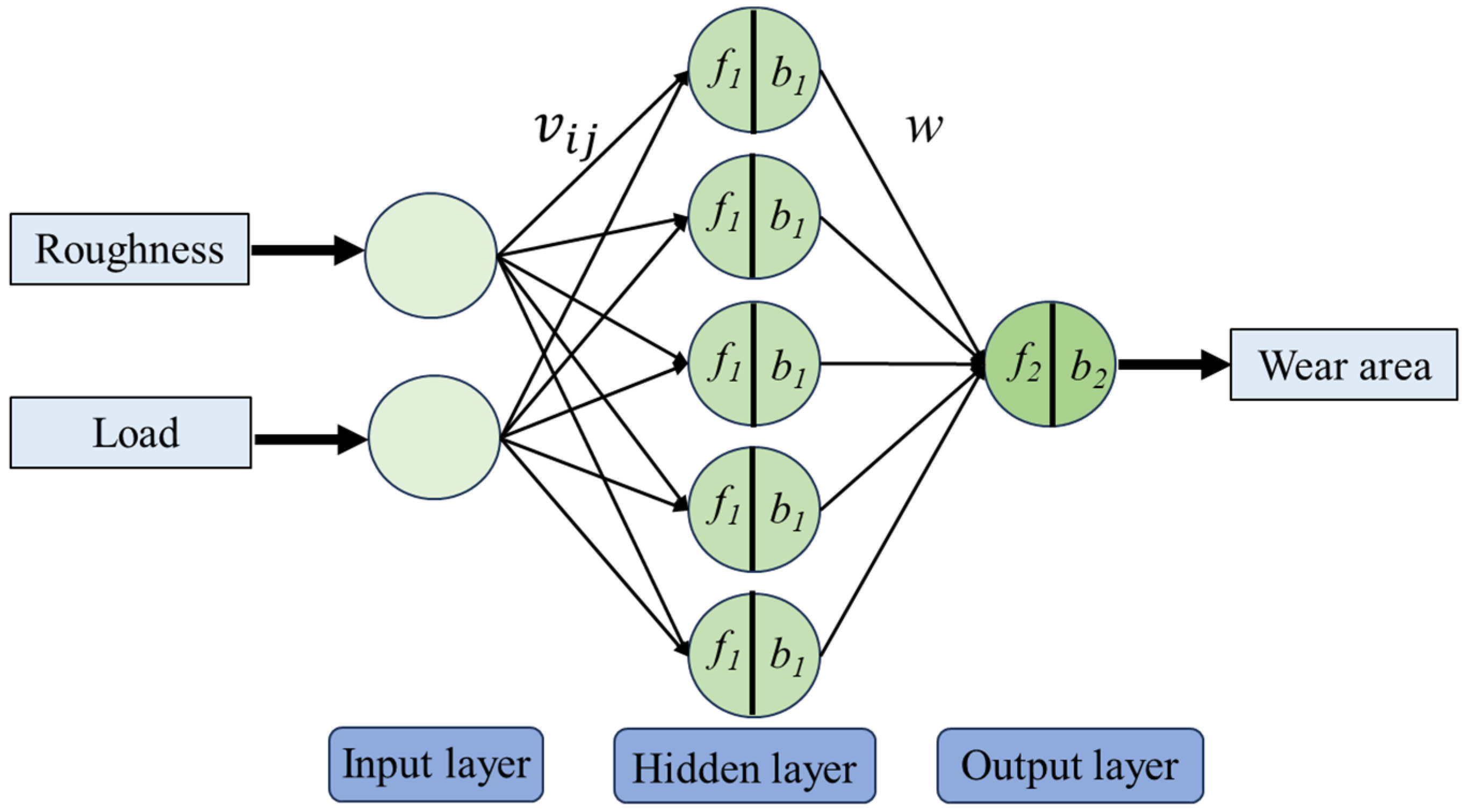
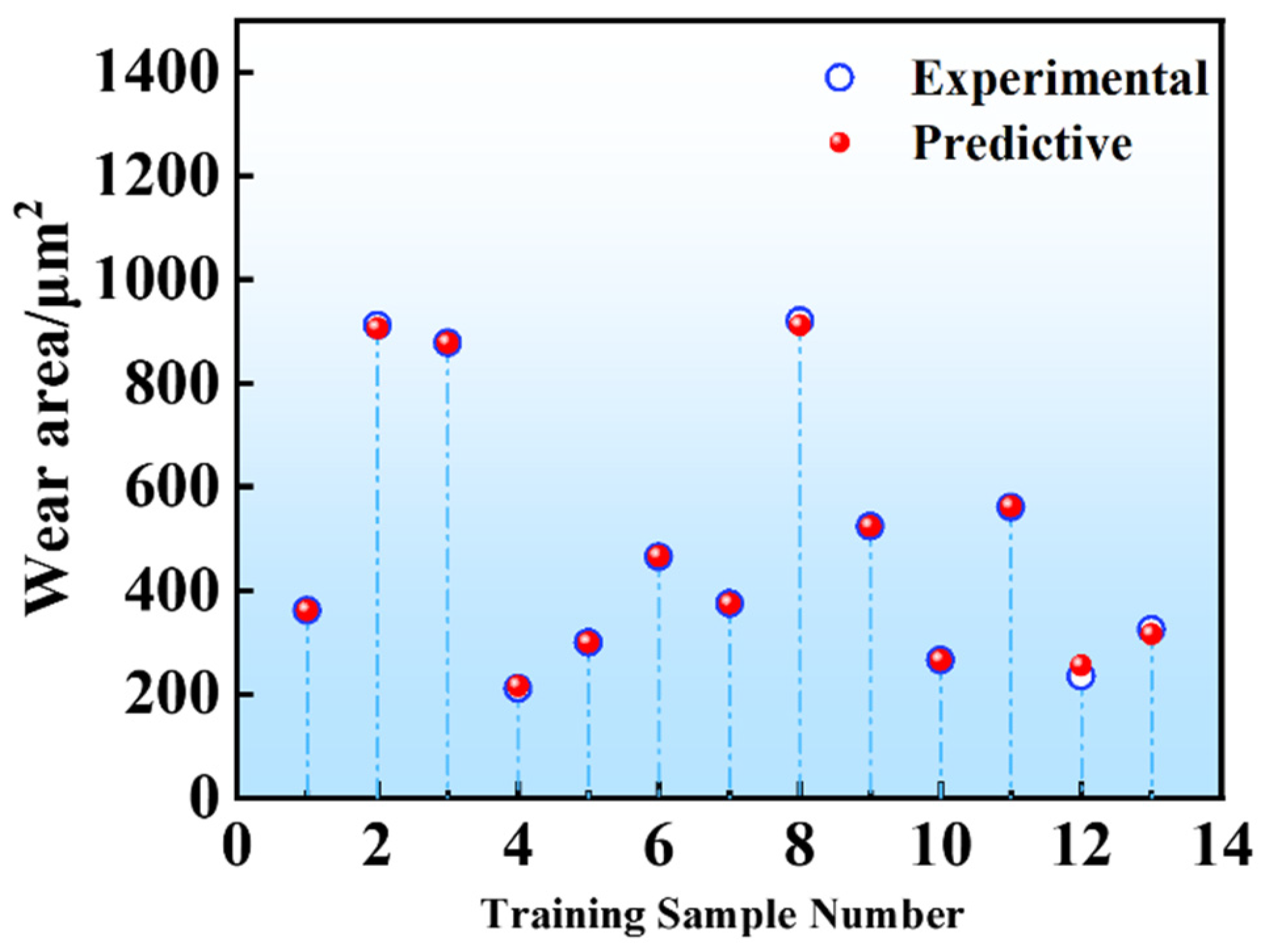
3.5. Wear Performance Prediction and Experimental Validation of GCr15 Bearing Steel
4. Conclusions
- (1)
- The surface asperities of GCr15 steel samples with various surface roughness values (Sa = 0.01 μm, 0.1 μm, 0.5 μm, 1 μm, and 1.5 μm) are uniformly distributed, with no intersecting or disordered scratches observed. As Sa increases from 0.01 μm to 1.5 μm, the Rz correspondingly increases, whereas the contact angle of the samples gradually decreases.
- (2)
- With increasing Sa, the mean friction coefficient of GCr15 steel gradually rises under oil-lubricated conditions, whereas the specimen’s wear area first decreases and then increases. Minimal wear area and optimal wear resistance are observed in the specimen at Sa = 0.5 μm. Additionally, higher loads lead to larger wear areas of the materials and abrasive wear is the main mechanism.
- (3)
- A BPNN model was developed to characterize the correlation between wear areas and experimental parameters (surface roughness Sa and applied load). Through independent validation tests, the mean predictive deviation of the proposed BPNN framework was determined to be 10.64%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Jiang, Z.; Li, L.; Wang, P.; Li, D.; Xue, W.; Duan, D. Wear behavior and damage characterization for AISI 52100 bearing steels: Effect of hardness and spherical carbides. J. Mater. Res. Technol. 2024, 30, 8359–8370. [Google Scholar] [CrossRef]
- Shi, W.; Sun, B.; Chen, L. Low friction and high load-carrying capacity of a slider bearing with an inhomogeneous surface affinity. J. Phys. Conf. Ser. 2020, 1654, 012035. [Google Scholar] [CrossRef]
- Cao, Z.X.; Liu, T.Q.; Yu, F.; Cao, W.; Zhang, X.; Weng, Y. Carburization induced extra-long rolling contact fatigue life of high carbon bearing steel. Int. J. Fatigue 2020, 131, 105351. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, Y.; Du, S. Preliminary research on response of GCr15 bearing steel under cyclic compression. Materials 2020, 13, 3443. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, S.Y.; He, W.Z.; Wang, Z.; Xia, Z. Research for the bearing fit effect on the vibration characteristics of spindle rotor-bearing system. J. Mech. Sci. Technol. 2023, 37, 6257–6270. [Google Scholar] [CrossRef]
- Wang, X.M.; Meng, Q.L.; Zhang, T.X. Sensitivity analysis of rolling bearing fatigue life under cyclic loading. J. Mech. Sci. Technol. 2022, 36, 5689–5698. [Google Scholar] [CrossRef]
- Abd-Alsamieh, M. Ultrathin film formation under combined effect of surface roughness and surface force for elastohydrodynamic lubrication of point contact problems. Ind. Lubr. Tribol. 2022, 74, 597–608. [Google Scholar] [CrossRef]
- Kumar, S.; Charitatos, V. Influence of surface roughness on droplet evaporation and absorption: Insights into experiments from lubrication-theory-based models. Langmuir 2022, 38, 15889–15904. [Google Scholar] [CrossRef]
- Hu, L.; Pueh, L.H.; Wang, D.F.; Wang, Z. Fatigue failure of high precision spindle bearing under extreme service conditions. Eng. Fail. Anal. 2024, 158, 107951. [Google Scholar] [CrossRef]
- Yu, F.; Chen, X.P.; Xu, H.F.; Dong, H.; Weng, Y.; Cao, W. Current status of metallurgical quality and fatigue performance of rolling bearing steel and development direction of high-end bearing steel. Acta Met. Sin 2020, 56, 513–522. [Google Scholar]
- Wang, C.; Zhang, Y.B. Surface roughness effect in hydrodynamic thrust bearing with ultra low clearance. Int. J. Eng. Model. 2023, 36, 61–74. [Google Scholar]
- Sanchez Garrido, D.; Leventini, S.; Martini, A. Effect of temperature and surface roughness on the tribological behavior of electric motor greases for hybrid bearing materials. Lubricants 2021, 9, 59. [Google Scholar] [CrossRef]
- Mohd Yusof, N.F.; Ripin, Z.M. In-situ surface wear assessment using a bearing area curve technique. Tribol.-Mater. Surf. Interfaces 2022, 16, 235–244. [Google Scholar] [CrossRef]
- He, P.Y.; Lu, S.W.; Wang, Y.; Li, R.; Li, F. Analysis of the best roughness surface based on the bearing area curve theory. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 527–540. [Google Scholar] [CrossRef]
- Yuan, Z.; Jiang, Z.; Zhou, Z.; Wang, H.; Li, J.; Cai, Z.; Xing, Z.; Ding, C.; Piao, Z. Effect of surface roughness on friction and wear behavior of GCr15 bearing steel under different loads. Surf. Sci. Technol. 2024, 2, 28. [Google Scholar] [CrossRef]
- Zhao, Z.; Xie, X.C.; Tang, G.B.; Padhiar, M.A.; Xiao, J.; Liang, Z. Study on the effect of the strengthen grinding process surface coverage on the micro-morphology, micro-hardness, roughness, and residue stress of GCr15 bearing steels. J. Manuf. Process. 2023, 99, 362–372. [Google Scholar] [CrossRef]
- Byotra, D.; Sharma, S. Effect of texture shapes and additives in lubricants on the dynamic characteristics of the hydrodynamic journal bearing. Ind. Lubr. Tribol. 2023, 75, 1031–1044. [Google Scholar] [CrossRef]
- Xia, Z.F.; Wu, D.; Zhang, X.C.; Wang, J.; Han, E.-H. Rolling contact fatigue failure mechanism of bearing steel on different surface roughness levels under heavy load. Int. J. Fatigue 2024, 179, 108042. [Google Scholar] [CrossRef]
- Shi, X.J.; Lu, X.Q.; Feng, Y.; Qiu, Z. Tribo-dynamic analysis for aero ball bearing with 3D measured surface roughness. Eng. Fail. Anal. 2022, 131, 105848. [Google Scholar] [CrossRef]
- Feng, Y.; Qiu, Z.Y.; Shi, X.J.; Lu, X.; Sun, W.; Hua, D.; Sun, H. Coupling mechanism of wear and mixed lubrication for gas turbine ball bearing considering real rough surfaces. J. Mech. Eng. 2021, 59, 330–340. [Google Scholar]
- Singh, J.; Singh, S.; Vasudev, H.; Katiyar, J.K. Artificial neural network model for wear characteristic analysis of WC-10Co4Cr and Stellite 6 thermal spray coatings. Tribol. Int. 2024, 199, 109924. [Google Scholar] [CrossRef]
- Sheikh, K.A.; Khan, M.M. Predictive modeling of abrasive wear in in-situ TiC reinforced ZA37 alloy: A machine learning approach. Tribol. Int. 2025, 202, 110291. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Liu, Z.; Zhang, C.; Zhao, Y.; Yan, X. Prediction model for bearing surface friction coefficient in bolted joints based on GA-BP neural network and experimental data. Tribol. Int. 2025, 201, 110217. [Google Scholar] [CrossRef]
- Liu, Z.Y.; He, T.T.; Tian, J.; Jin, Z.; Song, G.; Du, S.; Zhang, Y. Investigation on the material damage and correlation analysis of GCr15SiMn bearing steel under unsteady lubrication based on poor information. Mater. Today Commun. 2025, 43, 111608. [Google Scholar] [CrossRef]
- He, T.T.; Song, G.A.; Shao, R.N.; Du, S.; Zhang, Y. Sliding friction and wear properties of GCr15 steel under different lubrication conditions. J. Mater. Eng. Perform. 2022, 31, 7653–7661. [Google Scholar] [CrossRef]
- Kumar, H.; Gupta, V.; Bharath, V.; Tiwari, M.; Paul, S.K.; Agrawal, L.; Singh, A.P.; Jain, A. Effect of surface roughness on the friction moment in a lubricated deep groove ball bearing. Lubricants 2024, 12, 443. [Google Scholar] [CrossRef]
- Kempepatil, R.S.; Al-Dossari, M.; Hiremath, A.G.; Patil, J.; Alqahtani, A.; Tawade, J.V.; Saydaxmetova, S.; Khan, M.I. Influence of roughness patterns and slip velocity on the lubrication of MHD-affected secant curved annular plates. Int. Commun. Heat Mass Transf. 2025, 160, 108401. [Google Scholar] [CrossRef]
- Khan, S.A.; Oliveira, J.; Ferreira, F.; Emami, N.; Ramalho, A. Surface roughness influence on tribological behavior of HiPIMS DLC coatings. Tribol. Trans. 2023, 66, 565–575. [Google Scholar] [CrossRef]
- Cai, L.; Wang, J.L.; Zheng, H.T. An experimental study on oil-air lubrication of sliding friction wlement. Appl. Mech. Mater. 2010, 34, 181–185. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, L.; Li, R.; Xu, X.; Hong, H.; Lin, H.; Chen, J. Quantification of interfacial energies associated with membrane fouling in a membrane bioreactor by using BP and GRNN artificial neural networks. J. Colloid Interface Sci. 2020, 565, 1–10. [Google Scholar] [CrossRef]
- Song, C.; Liu, Z.; Zhang, Y.; Sun, C.; Liu, Z.; Zhang, Y. Generation conditions of rolling current-carrying associated arc on Cu-Cu pairs and the surface damage mechanisms. Eng. Fail. Anal. 2024, 159, 108103. [Google Scholar]
- Khalfallah, A.; Khalfallah, A.; Benzarti, Z. Identification of elastoplastic constitutive model of GaN thin films using instrumented nanoindentation and machine learning technique. Coatings 2024, 14, 683. [Google Scholar] [CrossRef]





| C | Mn | Si | P | S | Cr | Cu | Ni | Mo | Ti | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.96 | 0.32 | 0.24 | 0.008 | 0.001 | 1.40 | 0.22 | 0.08 | 0.03 | 0.0024 | Bal. |
| Sa/μm | Machining Process |
|---|---|
| 0.01 | Grinding with the grits of 240, 400, 800, 1000, 1200, 1500, and 2000, respectively and then polishing sequentially with W 0.5 polishing diamond paste |
| 0.1 | Grinding with the grits of 240, 400, 800, 1000, 1200, 1500, and 2000, respectively and then polishing sequentially with W 3.5 polishing diamond paste |
| 0.5 | Grinding with the grits of 240, 400, 800, and 1000, respectively |
| 1.0 | Grinding with the grits of 240, 400, and 800, respectively |
| 1.5 | Grinding with the grits of 240 and 400, respectively |
| Number | Measured Surface Roughness Values (Sa/μm) | Average Value (Sa/μm) | ||||
|---|---|---|---|---|---|---|
| 1 | 0.015 | 0.013 | 0.009 | 0.012 | 0.009 | 0.01 |
| 2 | 0.13 | 0.11 | 0.08 | 0.13 | 0.09 | 0.1 |
| 3 | 0.54 | 0.48 | 0.45 | 0.53 | 0.51 | 0.5 |
| 4 | 0.98 | 0.91 | 1.15 | 0.92 | 0.96 | 1 |
| 5 | 1.35 | 1.7 | 1.65 | 1.46 | 1.41 | 1.5 |
| Area | Fe | C | O | Cr | Si |
|---|---|---|---|---|---|
| 1 | 85.5 | 9.2 | 3.7 | 1.4 | 0.1 |
| 2 | 87.1 | 7.8 | 2.9 | 1.9 | 0.3 |
| 3 | 86.6 | 8.2 | 3.0 | 1.9 | 0.3 |
| 4 | 85.8 | 10.1 | 2.4 | 1.3 | 0.4 |
| Training Sample Number | Sa (μm) | Load (N) | Wear Area (μm2) |
|---|---|---|---|
| 1 | 0.5 | 35 | 362 |
| 2 | 1.5 | 25 | 912 |
| 3 | 1.5 | 15 | 877 |
| 4 | 0.5 | 15 | 211 |
| 5 | 0.1 | 25 | 299 |
| 6 | 0.1 | 35 | 465 |
| 7 | 1 | 25 | 374 |
| 8 | 1.5 | 35 | 921 |
| 9 | 0.01 | 35 | 524 |
| 10 | 1 | 15 | 265 |
| 11 | 1 | 35 | 561 |
| 12 | 0.1 | 15 | 234 |
| Testing Data | Sa (μm) | Load (N) | Experimental (μm2) | Predictive (μm2) | Relative Error |
|---|---|---|---|---|---|
| 1 | 0.01 | 25 | 341 | 365.51 | 7.19% |
| 2 | 0.5 | 25 | 273 | 234.48 | 14.1% |
| Average relative error | 10.64% | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, T.; Chen, W.; Liu, Z.; Gong, Z.; Du, S.; Zhang, Y. The Impact of Surface Roughness on the Friction and Wear Performance of GCr15 Bearing Steel. Lubricants 2025, 13, 187. https://doi.org/10.3390/lubricants13040187
He T, Chen W, Liu Z, Gong Z, Du S, Zhang Y. The Impact of Surface Roughness on the Friction and Wear Performance of GCr15 Bearing Steel. Lubricants. 2025; 13(4):187. https://doi.org/10.3390/lubricants13040187
Chicago/Turabian StyleHe, Tiantian, Wenbo Chen, Zeyuan Liu, Zhipeng Gong, Sanming Du, and Yongzhen Zhang. 2025. "The Impact of Surface Roughness on the Friction and Wear Performance of GCr15 Bearing Steel" Lubricants 13, no. 4: 187. https://doi.org/10.3390/lubricants13040187
APA StyleHe, T., Chen, W., Liu, Z., Gong, Z., Du, S., & Zhang, Y. (2025). The Impact of Surface Roughness on the Friction and Wear Performance of GCr15 Bearing Steel. Lubricants, 13(4), 187. https://doi.org/10.3390/lubricants13040187





