Effects of Gait Patterns on the Viscoelastic Squeeze-Film Lubrication of Hip Replacements

Abstract

The present study investigated the influence of various gait patterns on the viscoelastic squeeze-film lubrication characteristics of UHMWPE-based artificial hip replacements. Different gait loads (slow walking, normal walking, slow running) measured by Bergmann et al. were adopted in the present lubrication simulation. A comprehensive squeeze-film lubrication model for UHMWPE hip replacement was developed and numerically solved to determine the spatial distributions of film thickness and pressure profiles. The results showed that physiological loads had a negligible impact on the minimum film thicknesses during the stand phases. However, they significantly enhanced the minimum film thicknesses in both the elastic (1.16–1.31 times) and viscoelastic models (1.43–2.85 times) during the swing phases when compared to constant loads. This improvement was notably more pronounced in the viscoelastic model than in the elastic model. The slow-running gait, characterized by its higher frequency, demonstrated a more pronounced enhancement in squeeze-film lubrication of UHMWPE artificial hip joints compared to both normal-walking and slow-walking gaits. Specifically, the minimum film thicknesses during slow running were found to be 1.15 to 1.35 times greater than those observed during normal walking and 1.33 to 1.66 times greater than those during slow walking, highlighting the superior lubrication performance in the slow running case.

1. Introduction

Lubrication performance plays a significant role in the longevity of artificial hip replacements. An effective lubricant film can help reduce asperity contact and eliminate wear particles. Therefore, understanding the lubrication mechanism is extremely important in the design of artificial hip joints. Because the in vivo measurement of lubricant-film thickness in hip replacements is very hard to achieve, numerical simulation plays a significant role in investigating the lubrication performance of hip replacements.

As a major type of fluid film lubrication, squeeze-film lubrication plays a significant role when the hip replacement is subject to heavy loads and low speeds. Jagatia et al. [1] assumed a constant applied load and investigated the elastic squeeze-film lubrication performance of artificial hip replacements. The applied load was also considered as time-dependent, with variations such as sinusoidal variations [2] and normal gait patterns [3]. It was found that for the squeeze-film lubrication problems, a lubricant pocket could be predicted, which is preferable for lubrication enhancement in UHMWPE artificial hip joints. Physiological loads had more positive effects on the lubrication performance of hip implants compared with the constant load. However, all these studies were conducted under the assumption of elastic deformation of the UHMWPE liner.

In lubrication analyses of artificial joints, the assumption of purely elastic material properties generally suffices for hard-on-hard bearing pairs. However, there is a prevalence of viscoelastic behavior in both biological systems (e.g., articular cartilage) and engineering materials (e.g., UHMWPE liner) [4]. Lu et al. [5,6] have examined the impact of UHMWPE viscoelasticity on hip replacement lubrication performance under both normal walking and constant loading conditions. Furthermore, Rohde and Yoo et al. [7,8] have conducted studies on viscoelastic squeeze-film lubrication in UHMWPE artificial hip joints subjected to sinusoidal loading patterns. Recently, a boundary approach was developed by Putignano [9] to obtain the viscoelastic deformation field. By coupling with a finite difference solver, a line contact squeeze-film lubrication model was further investigated by Putignano and Campanale [10], highlighting the significance of considering the viscoelasticity of the lubricated solid. Subsequent advancements include the numerical framework developed by Zhao et al. [11] for calculating viscoelastic deformations in contact solids. A point-contact viscoelastic lubrication (VEHL) model was constructed and the impacts of key viscoelastic parameters were explored by Zhao et al. [11], providing valuable insights into the effects of viscoelastic solids on soft point-contact lubrication performance. Further sophistication was introduced by He et al. [12] who investigated a VEHL model comprising a rigid sphere interacting with a viscoelastic layer bonded to an elastic half-space, while accounting for various geometrical and material parameters. These studies collectively demonstrate that the inherent viscoelastic properties of lubricated solids significantly influence lubrication performance.

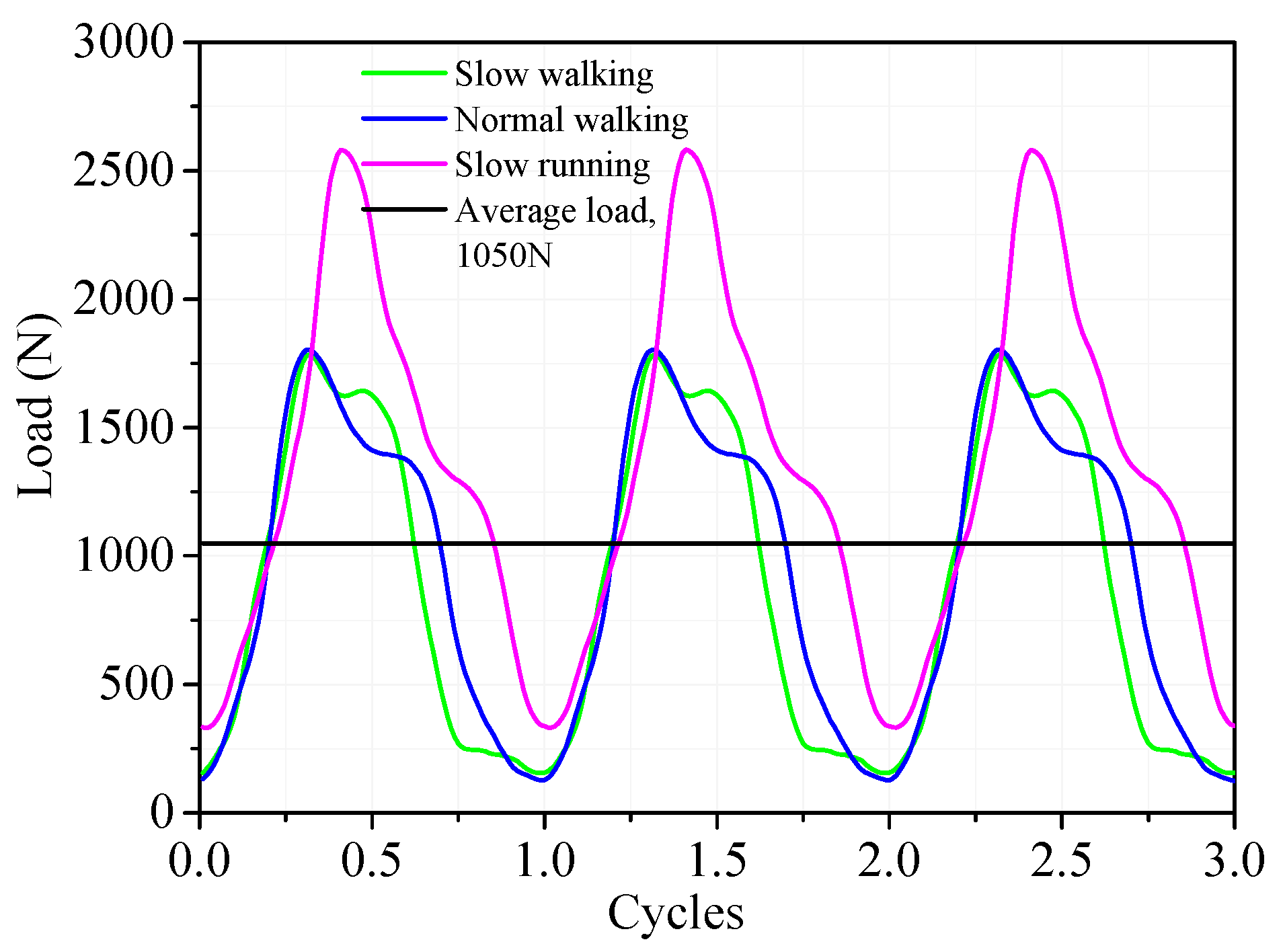
While these investigations have provided valuable insights, it is crucial to emphasize that artificial hip joints operate under diverse physiological motion patterns, including slow walking, normal walking, and fast walking, etc. These activities exhibit substantially different characteristics in terms of loading magnitudes and frequencies. Previous biomechanical studies conducted by Bergmann et al. [13] have quantified these differences, demonstrating that the resultant hip joint force can reach up to three times body weight during normal walking and five times body weight during slow running. Correspondingly, dominant loading frequencies vary considerably across different activities, with characteristic frequencies of 1Hz for normal walking and 1.7 Hz for slow running [10]. Nevertheless, the influence of gait patterns on viscoelastic lubrication behavior in soft artificial hip joint systems remains poorly understood. A comprehensive understanding of these gait-dependent lubrication mechanisms could offer valuable insights for optimizing the design parameters and enhancing the clinical performance of soft artificial hip joint prostheses.

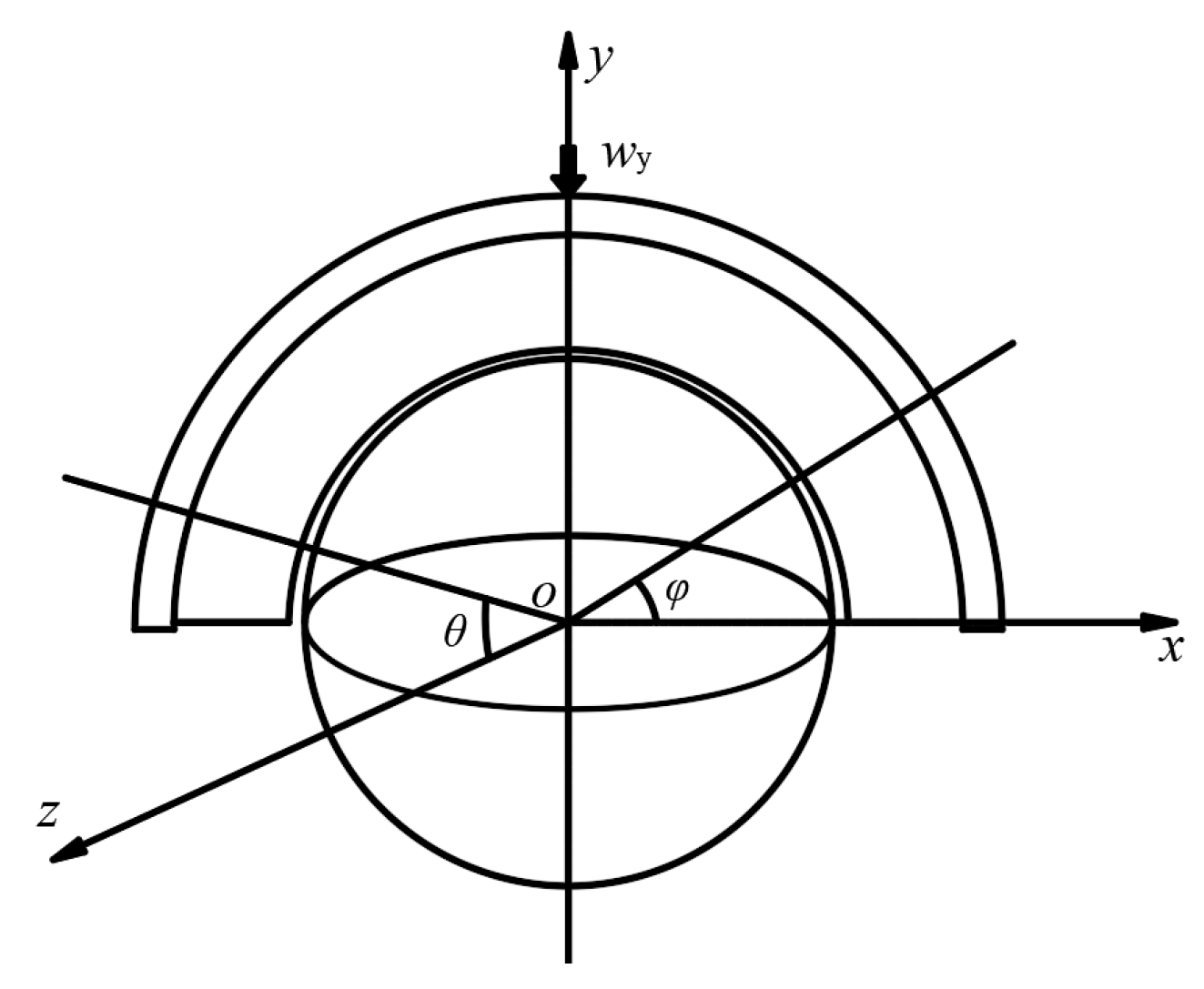
Consequently, this study was designed to systematically examine the impact of diverse gait patterns such as slow walking, normal walking and slow running on the viscoelastic squeeze-film lubrication characteristics of UHMWPE-based artificial hip joint systems. To achieve this, a comprehensive numerical framework was developed: the spherical Reynolds equation was numerically solved using a multi-grid method, with the Gauss–Seidal relaxation iteration technique being implemented at each grid level. Instantaneous elastic deformation was accurately computed using the finite element method, while viscoelastic deformation was subsequently determined by incorporating the creep compliance function into the analysis.

2. Materials and Methods

2.1. Materials

In this investigation, a hard-on-soft artificial hip replacement configuration was implemented, comprising a metal or ceramic femoral head articulating against a UHMWPE acetabular cup.

Table 1. Materials and geometrical parameters adopted in the numerical simulation.

Parameters	Values
Femoral radius, RH	14 mm
Radial clearance, c	40 μm
Thickness of UHMWPE liner	9.5 mm
Instantaneous elastic modulus of UHMWPE	700 MPa
Poisson’s ratio of UHMWPE	0.4
Viscosity of 25% bovine serum solution	0.01 Pa·s

summarizes the essential geometrical and mechanical properties of the prosthetic components, along with the viscosity parameters of the lubricant. To facilitate comparative analysis, the UHMWPE liner was modeled using both linear elastic and standard linear viscoelastic material formulations. The theoretical framework governing the viscoelastic behavior of UHMWPE has been comprehensively established in a prior study [6].

2.2. Lubrication Model

The artificial hip replacement was simulated using a ball-in-socket model, as illustrated in Figure 1. Because the investigation specifically focused on the squeeze-film lubrication phenomena, the analysis was restricted to unidirectional motion along the y-axis direction. Given the significant challenges associated with in vivo measurement of joint forces, the physiological load data experimentally determined by Bergmann et al. [13] were incorporated into the numerical simulation framework. Three gaits (i.e., slow walking, normal walking and slow running) (Figure 2) were adopted to investigate the effects of gait patterns. The maximum loads were 1784 N, 1802 N, and 2580 N and the gait frequencies were 0.75 Hz, 1 Hz, and 1.7 Hz for slow walking, normal walking and slow running, respectively. The comparable maximum loads observed between normal and slow walking gaits indicate that the primary distinguishing factor lies in their frequency characteristics, thereby enabling frequency-based analysis to examine gait-related effects. Slow running gaits, characterized by increased higher frequencies and heavier loads, can be further utilized to systematically assess the amplified influences of frequency on lubrication performance. To systematically evaluate the influence of loading magnitudes on the viscoelastic squeeze-film lubrication characteristics of soft artificial hip joints, a comparative reference case was introduced, wherein the applied load was reduced to half of the slow walking condition (w/2) while preserving identical gait frequency parameters. Furthermore, for comparative analysis in the lubrication simulation, the mean constant load (1050 N) derived from these gait patterns was implemented as a baseline reference.

Given the exclusive focus on squeeze-film motion in this investigation, the time-dependent Reynolds equation [5] was formulated in spherical coordinates as

$$\sin \theta {\displaystyle \frac{\partial }{\partial \theta }}\left({\displaystyle \frac{h^3}{\eta }}\sin \theta {\displaystyle \frac{\partial p}{\partial \theta }}\right)+{\displaystyle \frac{\partial }{\partial \phi }}\left({\displaystyle \frac{h^3}{\eta }}{\displaystyle \frac{\partial p}{\partial \phi }}\right)=12R_c^2{\sin }^2\theta {\displaystyle \frac{\partial h}{\partial t}}$$

(1)

where p represents the hydrodynamic pressure distribution; h denotes the lubricant film thickness; R_c corresponds to the radius of the UHMWPE acetabular cup; t indicates the temporal variable; η signifies the viscosity of the periprosthetic synovial fluid; and φ and θ represent the spherical coordinate parameters, as defined in Figure 1.

The resultant load acting on the acetabular cup was balanced via the integration of hydrodynamic pressures [5]:

$$f_x=R_c^2{\int }_0^{\pi }{\int }_0^{\pi }p{\sin }^2\theta \cos \phi d\theta d\phi =0$$

(2)

$$f_y=R_c^2{\int }_0^{\pi }{\int }_0^{\pi }p{\sin }^2\theta \sin \phi d\theta d\phi =w_y(t)$$

(3)

The film thickness encompasses both the undeformed gap between the two bearing surfaces and the viscoelastic deformation induced by the current and historical hydrodynamic pressures [5]:

$$h\left(\phi ,\theta ,t\right)=c-e_x\sin \theta \cos \phi -e_y\sin \theta \sin \phi +\delta (\phi ,\theta ,t)$$

(4)

where δ is the viscoelastic deformation of the UHMWPE cup; c is the radial clearance between the cup and the head; e_x and e_y are eccentricities of the femoral head.

2.3. Numerical Methods

To enhance numerical stability, all governing equations were non-dimensionalized and subsequently discretized using the finite difference method. Specifically, the left Poiseuille terms were approximated using central differencing, while the right squeeze-film term was treated using first-order backward differencing. The Reynolds equation was solved using a multi-grid method, adopting a numerical approach consistent with established methodologies reported in prior research [6]. The numerical simulation was implemented in Fortran and compiled using Intel Visual Fortran Compiler. The computational methodology for determining viscoelastic deformation has been comprehensively described and verified in prior research [6]. In this computational approach, a unit pressure was applied on the central element of the cup’s inner surface, and the corresponding displacement coefficients along the longitudinal line were determined using finite element method (FEM) analysis using ABAQUS 6.14 (Dassault Systèmes Simulia Corp, Providence, RI, USA). These coefficients were subsequently utilized to derive a displacement influence function via curve fitting techniques. The derived function enabled the calculation of instantaneous elastic deformation coefficients for all nodal points on the cup’s inner surface. These elastic coefficients were then integrated with a creep compliance function to determine the viscoelastic coefficients at discrete time intervals throughout the gait cycle. To ensure consistency, each gait cycle was uniformly discretized into 100 time steps across all three gait patterns, with the assumption of a constant pressure distribution within each time increment. The computational accuracy of both the elastic and viscoelastic deformations was rigorously verified through comparative analysis with results obtained from independent finite element simulations [6].

3. Results

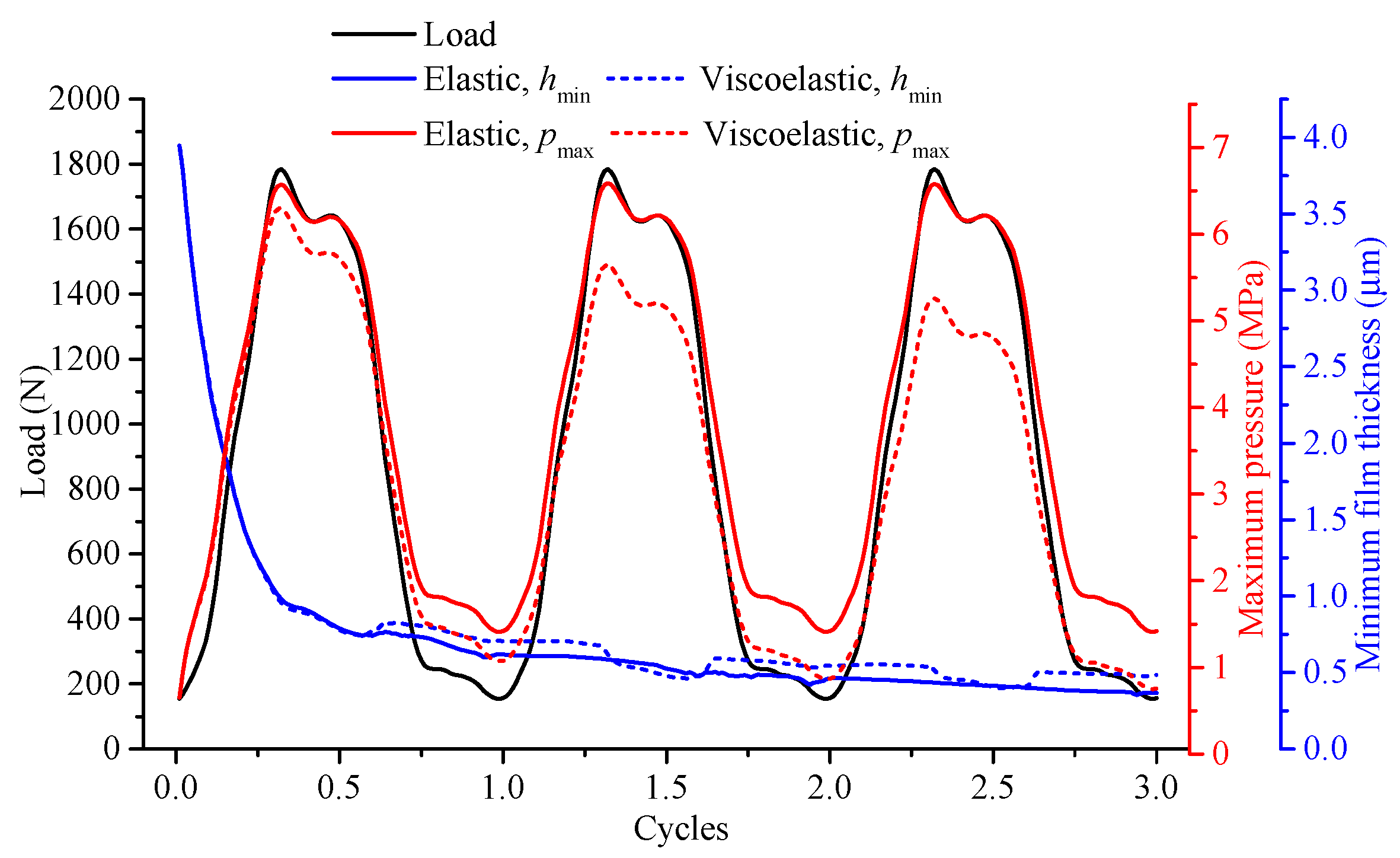
The loads, maximum pressures and minimum film thicknesses under the slow walking condition are shown in Figure 3. The maximum pressures in the elastic model at loading peaks were consistently around 6.58 MPa, corresponding to the peak load of 1784 N. In contrast, the viscoelastic model exhibited maximum pressures of 6.30 MPa, 5.65 MPa, and 5.26 MPa at the three loading peaks. Compared with the elastic model, these values decreased by 4.25%, 14.13% and 20%, respectively, in the viscoelastic cases.

The minimum film thicknesses of the elastic and viscoelastic models were nearly identical at the beginning of the squeeze motion. Then, divergence appeared as the motion progressed. The minimum film thicknesses in the viscoelastic model were larger than those in the elastic model under light-loaded periods. Conversely, during heavy-loading periods, the minimum film thicknesses in the viscoelastic model were smaller, with these differences diminishing as the squeeze motion continued.

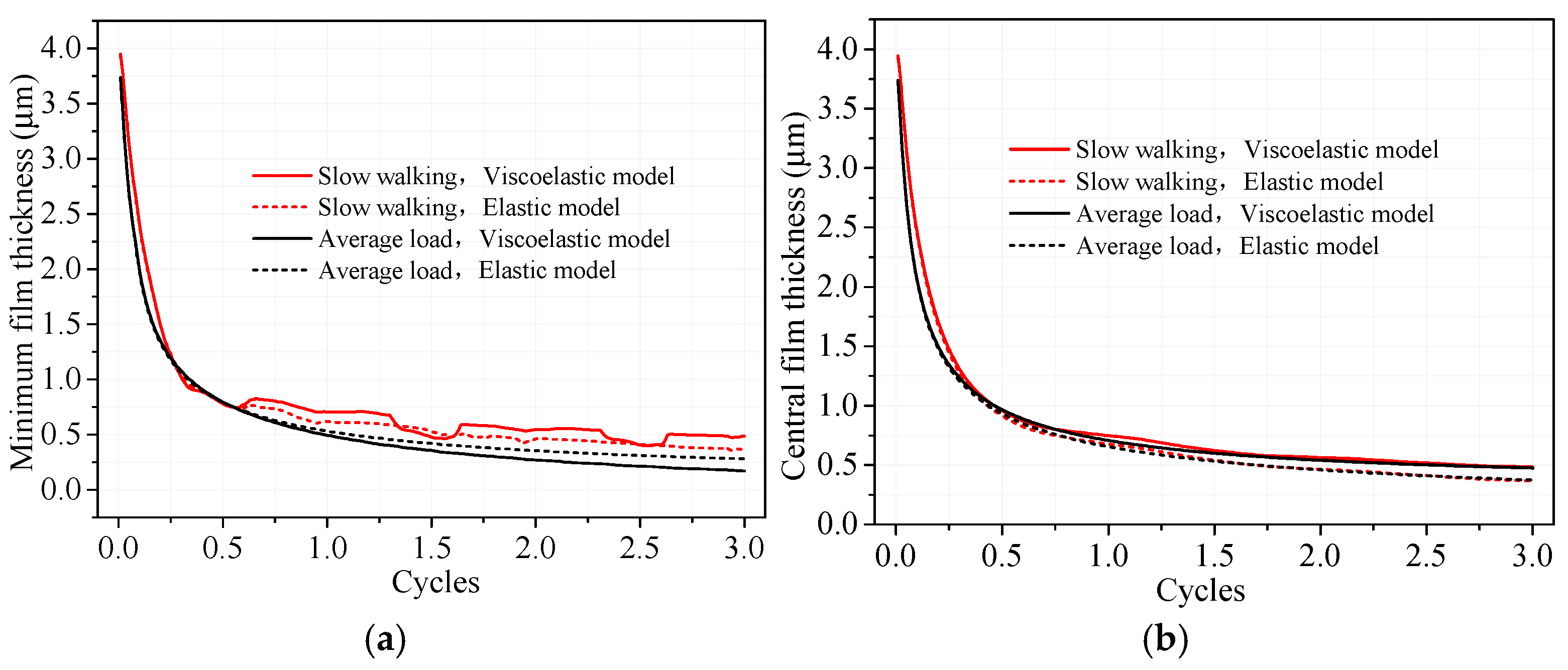
The viscoelasticity of the UHMWPE cup exhibited different influences on the squeeze-film lubrication of artificial hip replacements under constant and physiological loadings (Figure 4). For constant loading, the viscoelastic model showed a reduction in minimum film thickness and an increase in central film thickness (Figure 4). In contrast, under physiological loading, UHMWPE viscoelasticity positively influenced the minimum film thickness while having negligible effects on the central film thickness of hip implants. In addition, the physiological loads had negligible effects on the minimum film thicknesses during the stand phases and improved the minimum film thicknesses in both the elastic (1.16~1.31 times) and viscoelastic models (1.43~2.85 times) during the swing phases compared with constant loads, which indicated that the viscoelastic model demonstrated a more remarkable improvement than the elastic model.

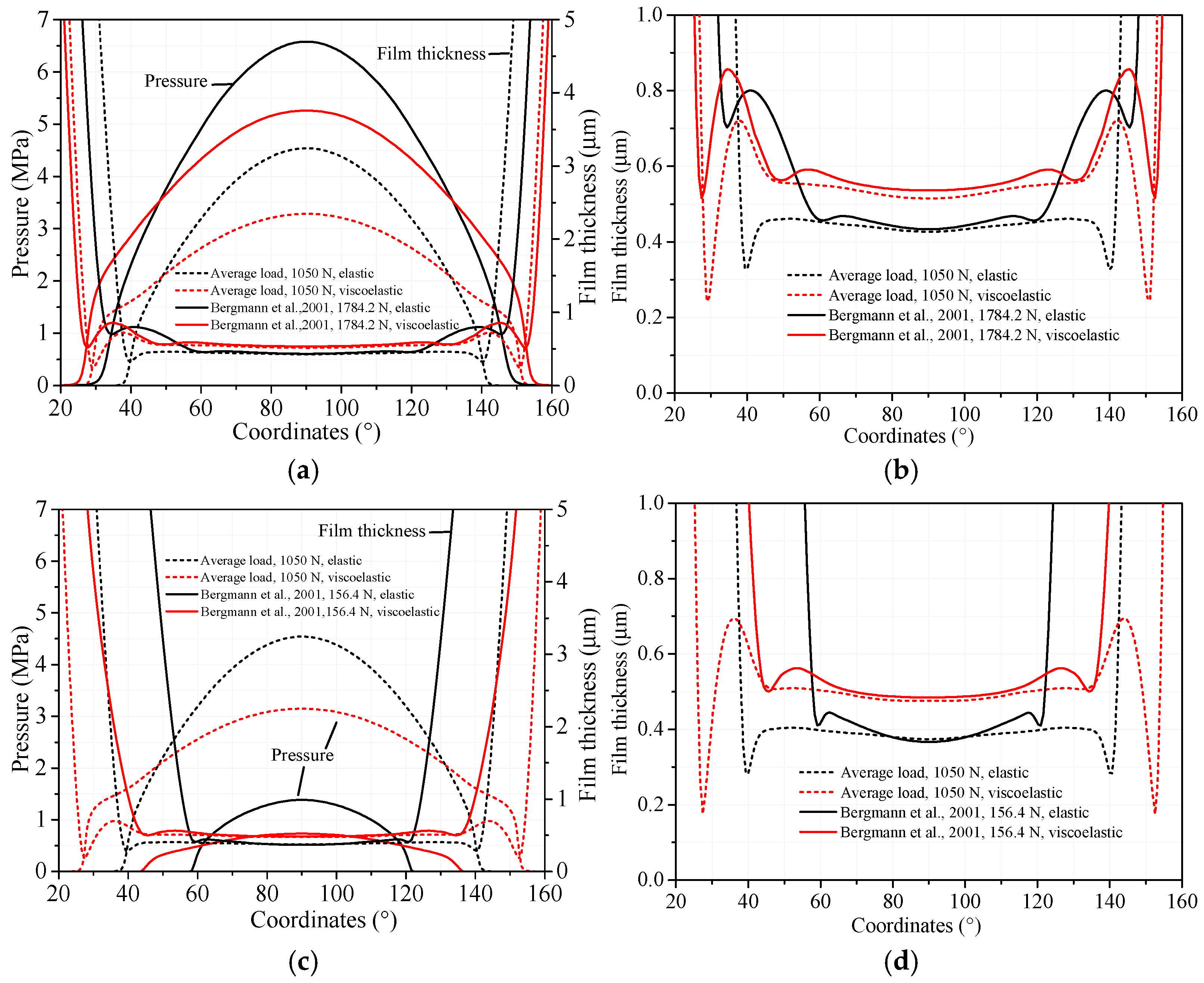
The effects of physiological loads on the lubrication performance of artificial hip implants can be further confirmed by the cross-sectional film thickness and pressure distributions at 2.31 T and 3.0 T (Figure 5). For the viscoelastic case, at t = 2.31 T, the maximum cross-sectional pressure was 5.26 MPa for the physiological load (1784 N) and 3.16 MPa for the average load (1050 N). The central film thicknesses were 0.54 μm and 0.52 μm, respectively. The minimum film thicknesses appeared at the edge of the contact area for both loading conditions, measuring 0.51 μm and 0.24 μm for the physiological and average loads, respectively. At t = 3.0 T, the central film thicknesses were all around 0.48 μm for the physiological (156.4 N) and average loads (1050 N). However, the minimum film thicknesses were notably different, i.e., 0.48 μm and 0.18 μm for the viscoelastic model under the physiological (156.4 N) and constant loads (1050 N), respectively.

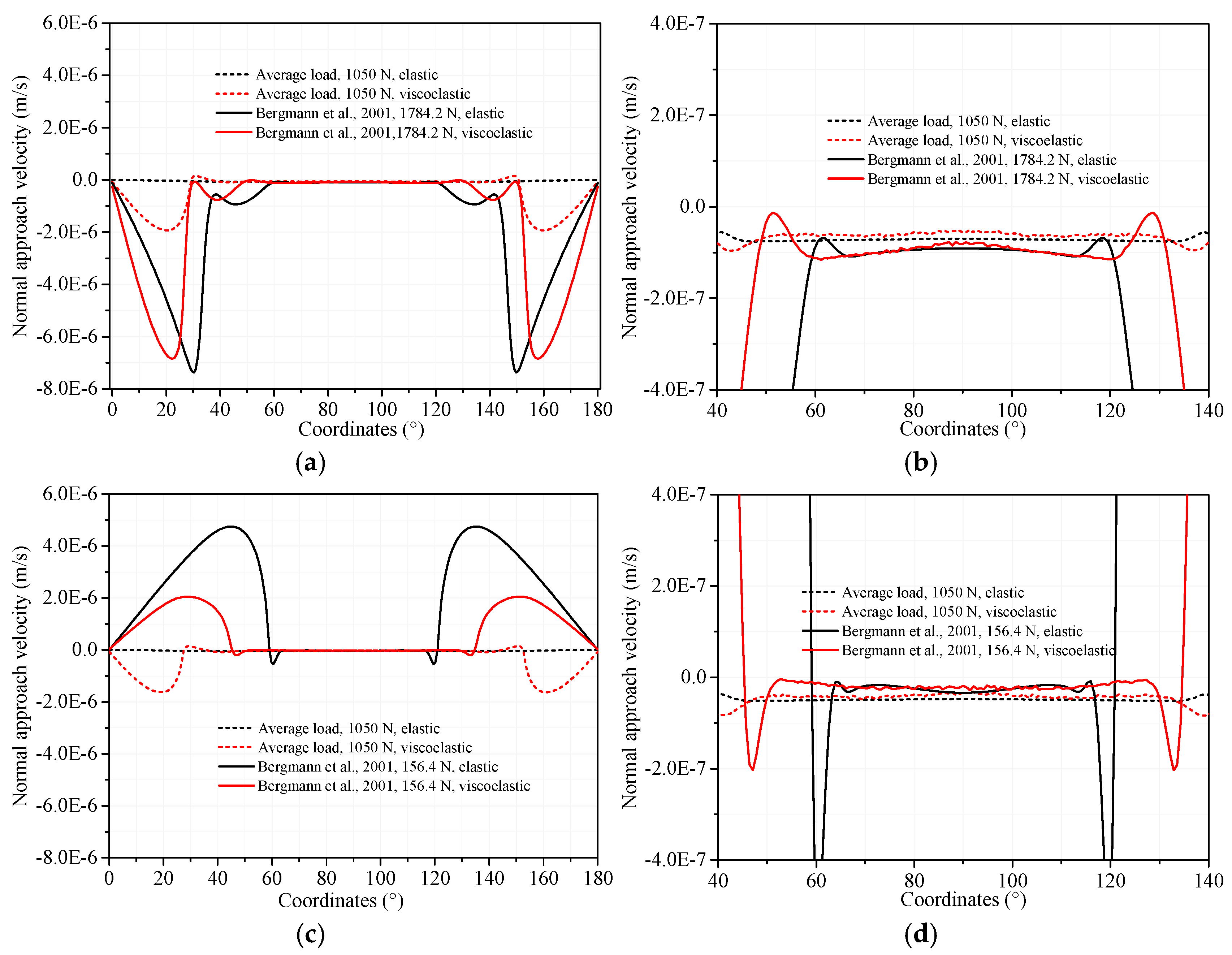
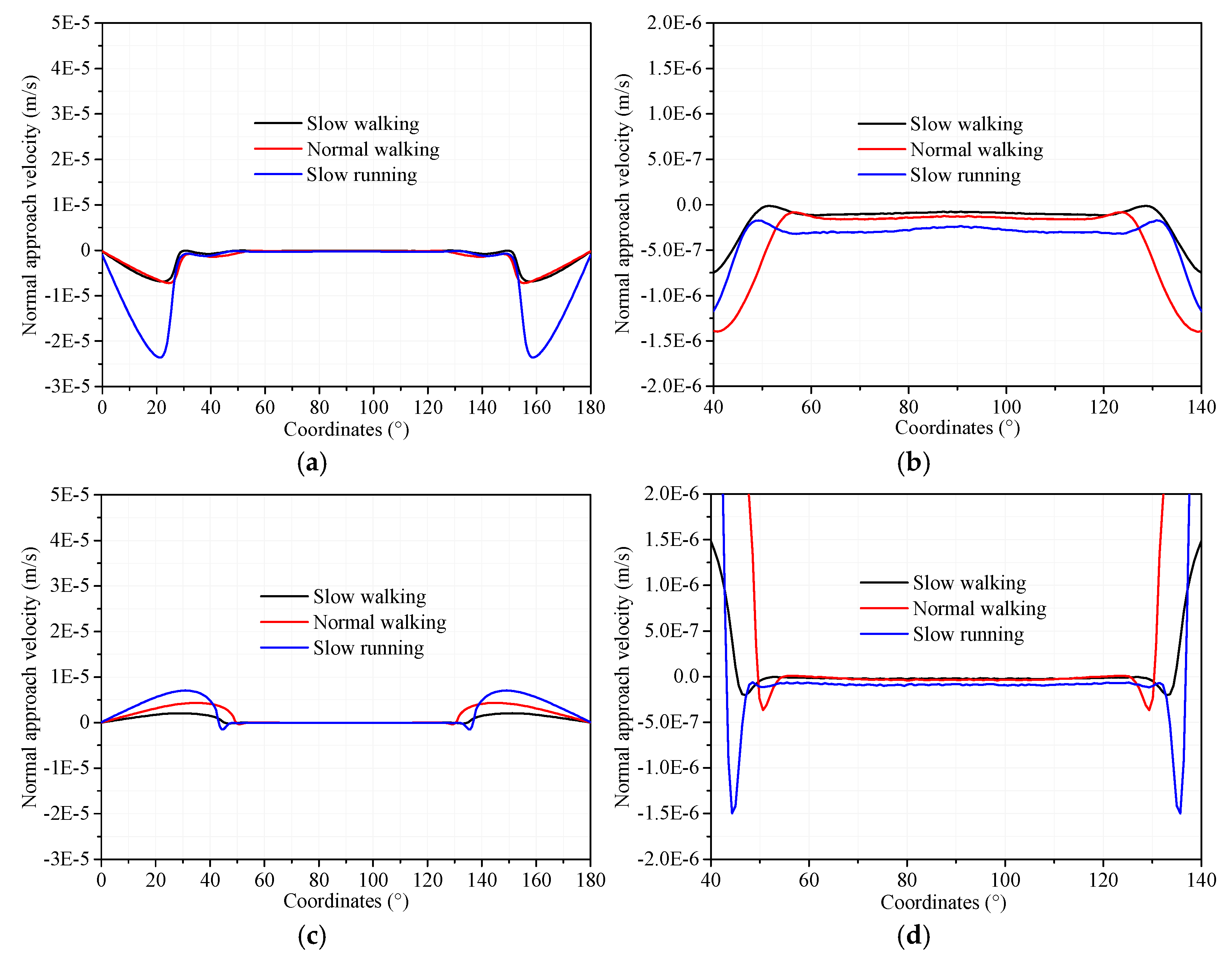
The cross-sectional normal approach velocity and its locally magnified plot are shown in Figure 6 for the average load and slow walking cases. The normal approach velocity of the physiological loading case was generally higher than in the constant loading case for both the elastic and viscoelastic models. Under constant loading, the variation in the normal approach velocity of the elastic model was minimal. The normal approach velocity of the viscoelastic model was lower than that of the elastic model at the central position, but higher at the edge of the contact area. Under physiological loading, the normal approach velocity was comparable for the elastic and viscoelastic models at the central position, while at the edge of the contact area, the elastic model displayed a higher normal approach velocity than the viscoelastic model.

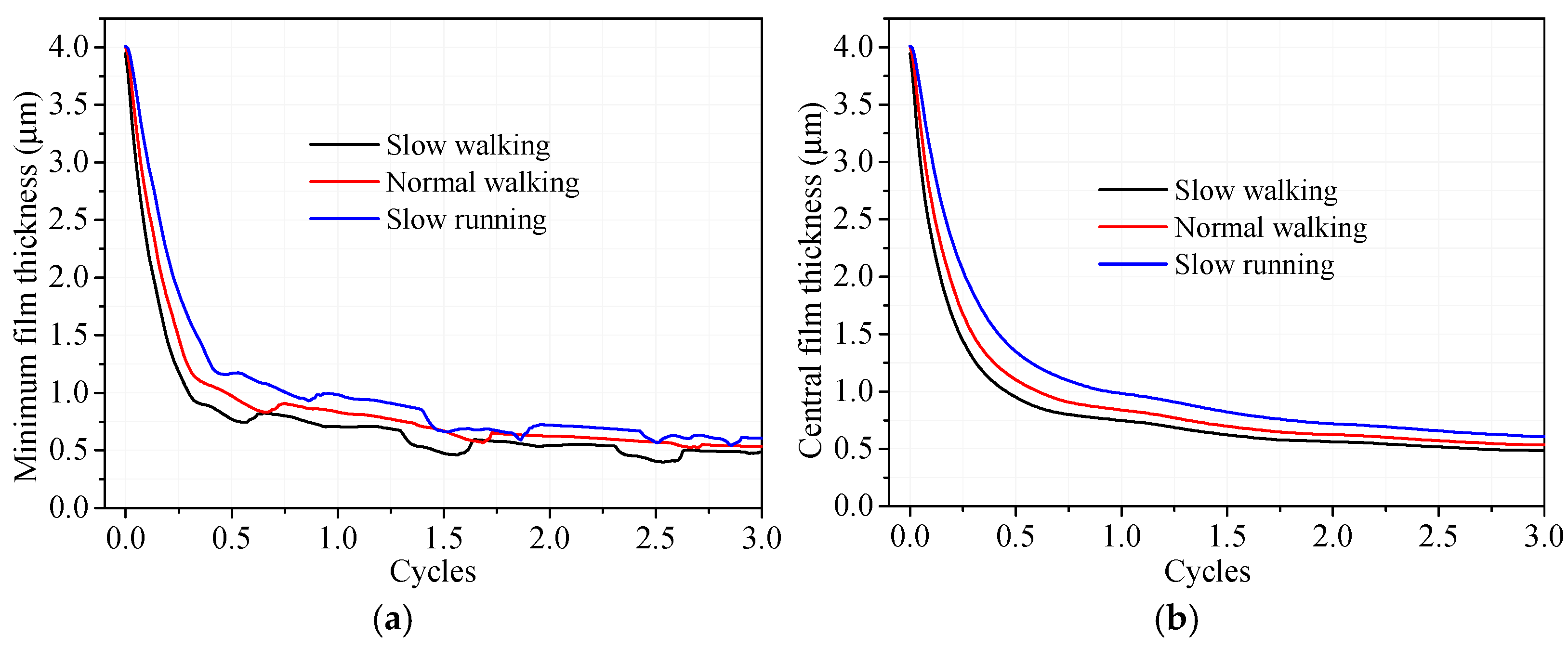
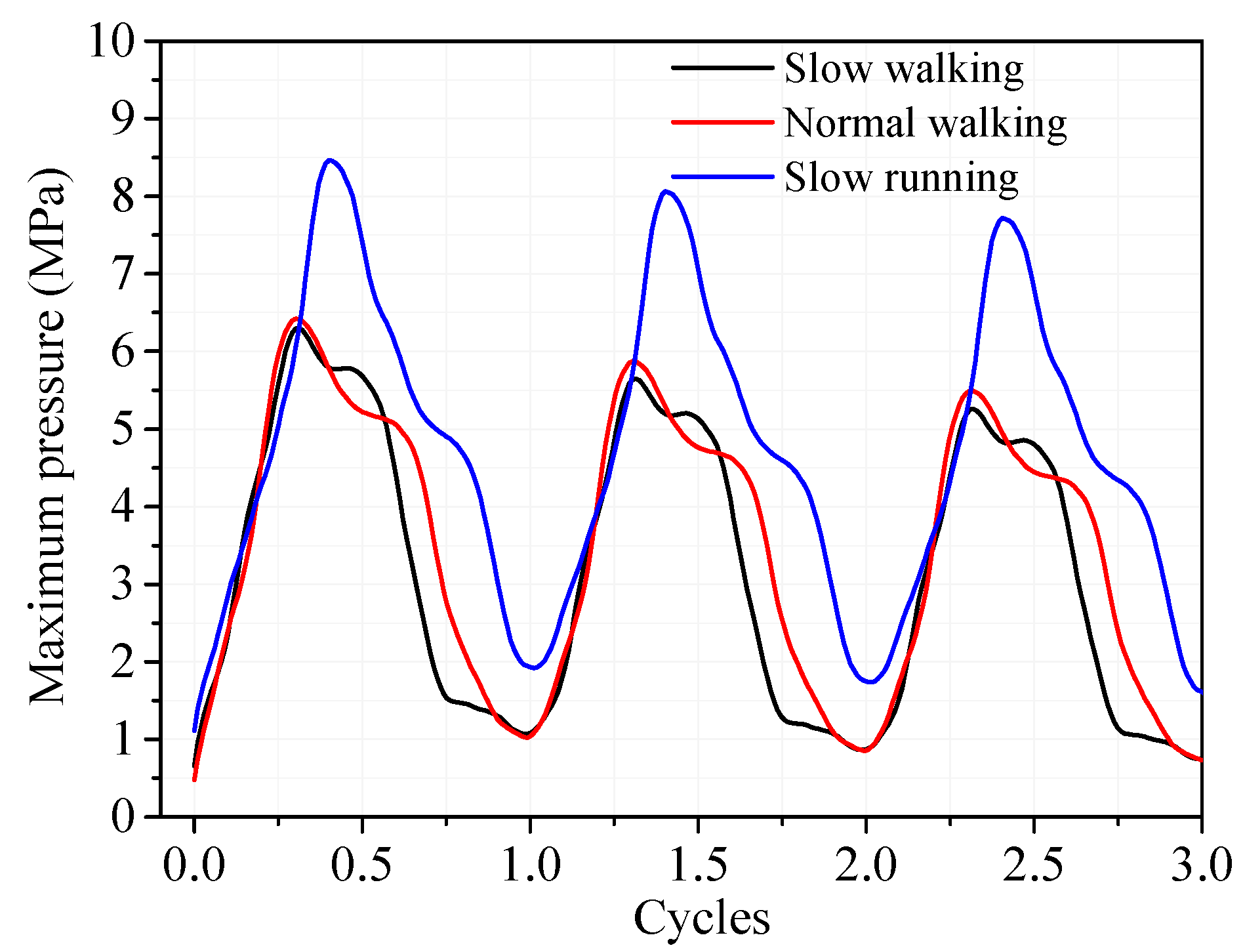
The minimum and central film thicknesses and maximum pressures of the three different physiological gait loads over three cycles are shown in Figure 7 and Figure 8. The minimum and central film thicknesses were largest under the slow running gait, followed by normal walking, and smallest under the slow walking gait. The minimum film thicknesses of slow running were 1.15~1.35 times greater than those of normal walking and 1.33~1.66 times greater than those of slow walking. For example, at time step of 2.31 T, the minimum film thicknesses were 0.684 μm, 0.593 μm and 0.513 μm for the slow running, normal walking and slow walking cases, respectively. At a time step of 3.0 T, the minimum film thicknesses were 0.605 μm, 0.534 μm and 0.485 μm for the slow running, normal walking and slow walking cases, respectively. Due to the similar maximum loads in normal and slow walking conditions, the corresponding maximum pressures at the three loading peaks were approximately 6.30 MPa, 5.65 Mpa, and 5.26 Mpa for both cases. In contrast, the three maximum pressure peaks were significantly higher for the slow running condition, measuring 8.47 Mpa, 8.06 Mpa, and 7.72 Mpa.

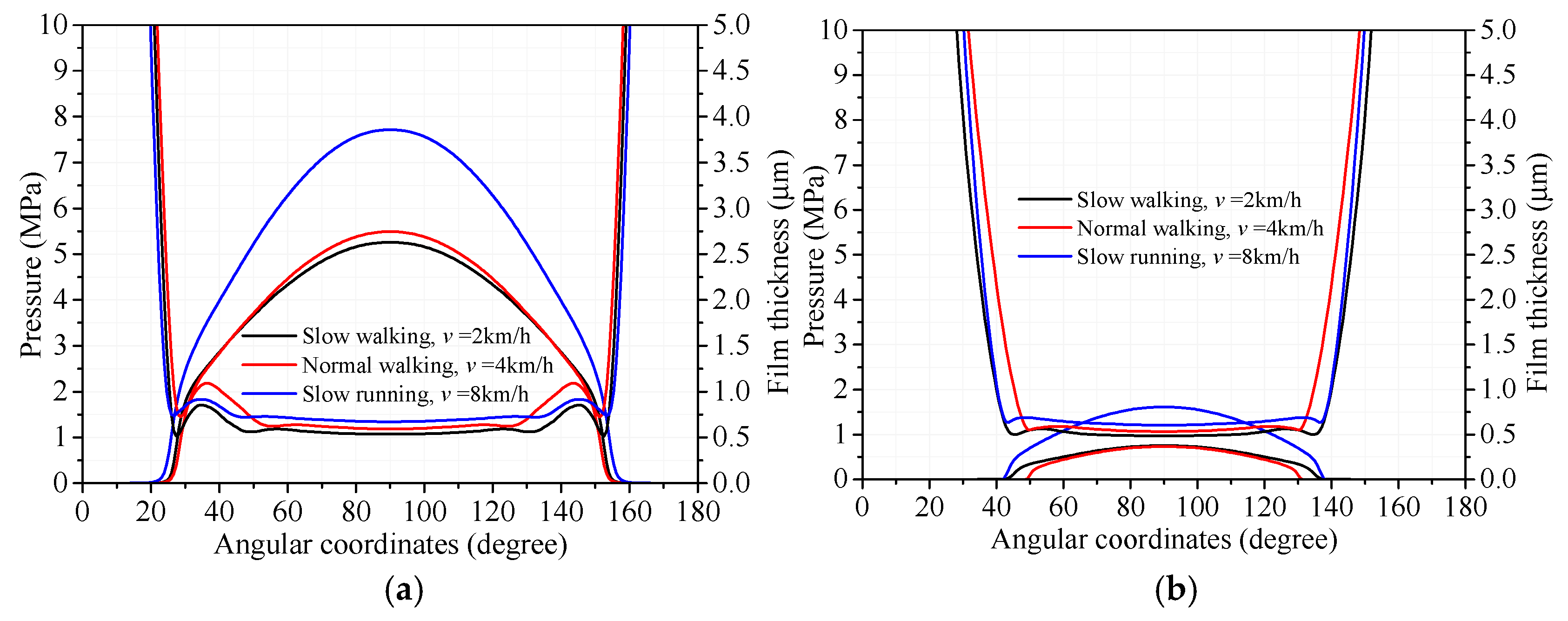
The influence of gait patterns on the viscoelastic squeeze-film lubrication of UHMWPE hip replacements was further examined by comparing the cross-sectional film thickness and pressure distributions at two distinct time instances (Figure 9). Overall, the film thicknesses were highest under slow running conditions and lowest for the slow walking gait, consistent with the trend shown in Figure 7.

The cross-sectional normal approach velocity and its locally magnified plot at instants of 2.31 T and 3.0 T for the three gait patterns are shown in Figure 10. At the central position of the contact area, the normal approach velocity under the slow running condition was higher than in the normal walking and slow walking cases. The normal approach velocity of the slow walking case was generally similar to that of the normal walking case. At the edge of the contact area, the normal approach velocity of the slow running case was remarkably greater than the other gait patterns.

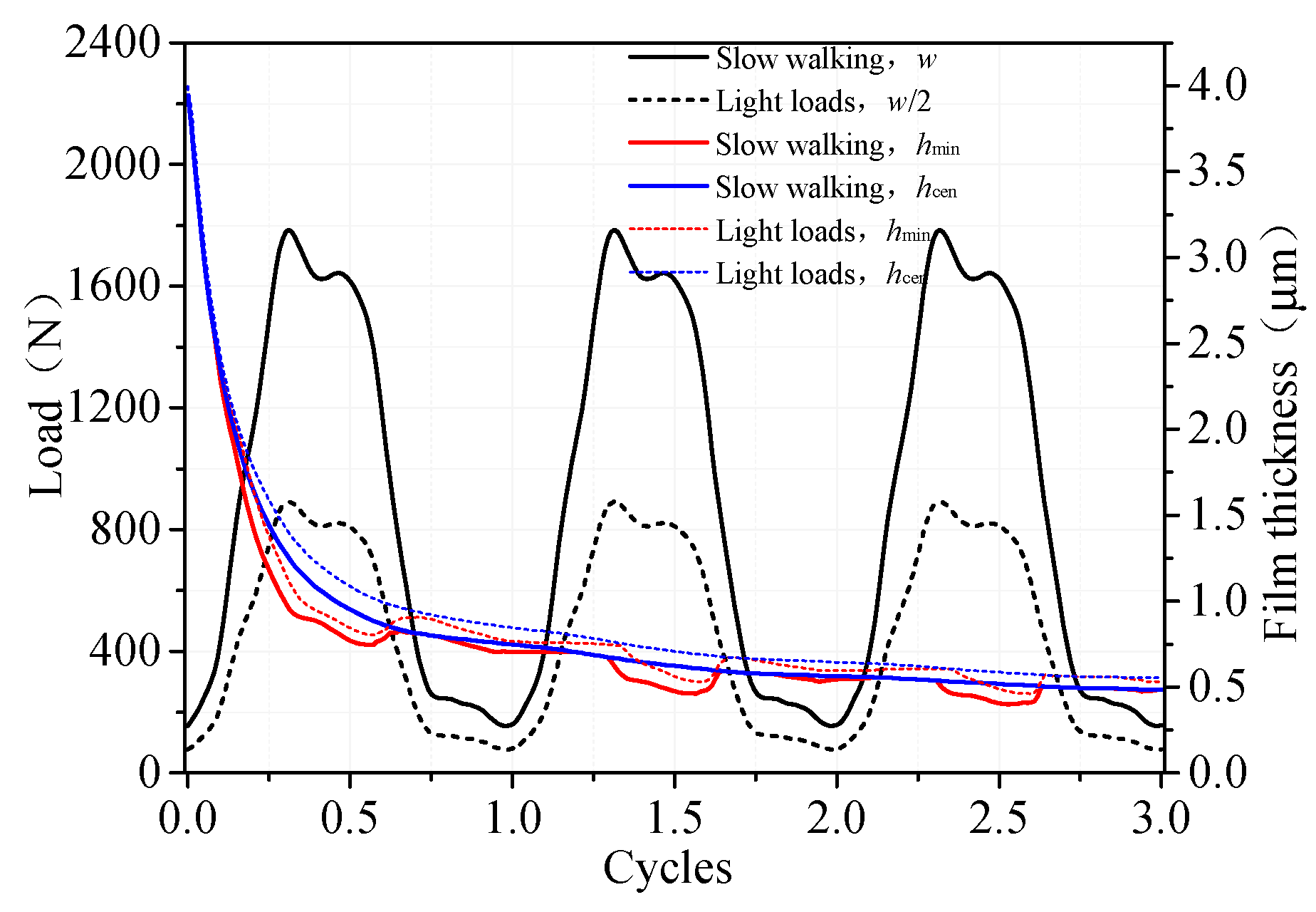
The comparison of minimum and central film thicknesses between the slow walking case and a lighter loading condition, where the load is half that of the slow walking case, is shown in Figure 11. The minimum and central film thicknesses under slow walking were much smaller than those of the lighter loading case. For example, the minimum film thicknesses at 2.31 T were 0.51 μm and 0.6 μm for the slow walking and the lighter loading cases, respectively.

4. Discussion

Previous studies have examined the transient viscoelastic lubrication of UHMWPE artificial hip joints under normal walking conditions [6] and the viscoelastic squeeze-film lubrication performance under constant loading [5]. However, artificial hip joints are subjected to various gait patterns in daily lives, which can significantly impact their lubrication performance. Therefore, different gaits, such as slow running, normal walking and slow walking, as measured by Bergmann et al. [13], were analyzed to investigate their influences on the viscoelastic squeeze-film lubrication of UHMWPE hip replacements.

In the elastic model, deformation was determined by the present loading patterns due to the instantaneous elastic property of the UHMWPE liner. Consequently, the maximum pressures under identical loads were similar in the elastic model. However, the viscoelastic model presented a distinct scenario. The time-dependent properties of the materials in this model meant that deformation was not solely influenced by the current pressure distributions but also by the loading history. Consequently, at the same instant, the viscoelastic model exhibited greater deformation compared to the elastic model. This increased viscoelastic deformation led to an expansion of the contact area, which, in turn, generally resulted in a reduction in pressure distributions.

The viscoelasticity of the UHMWPE liner played different roles in the lubrication of artificial hip joints when subjected to constant and physiological loads. Under the constant loading condition, the lubricant was squeezed out from the contact area continuously and the squeeze-film effect was negligible in both the elastic and viscoelastic models, which was also demonstrated in a previous study [2]. In order to investigate the effect of physiological load on the viscoelastic squeeze-film action, the normal approach velocities of the slow walking case were compared with those of the constant load case. At the central contact area, the squeeze-film effect of the average loading case was similar to that of the slow walking condition. However, at the edge of the contact zone where the minimum film thickness occurred, it was more significant in the physiological loading case for both the elastic and viscoelastic models. Therefore, compared with constant loading, physiological loading contributed to a greater minimum film thickness. Under the physiological loading conditions considered in this study, the normal approach velocity of the elastic model was consistently higher than that of the viscoelastic model, resulting in more pronounced squeeze-film effects in the elastic case. However, the accumulated viscoelastic deformation in the viscoelastic model led to a larger contact area, which subsequently reduced the pressure distribution and increased film thickness. This occurred even though the squeeze-film effects were less significant in the viscoelastic model, highlighting the critical role of time-dependent material properties in influencing lubrication behavior.

Gait patterns had significant influences on the viscoelastic squeeze-film lubrication of UHMWPE artificial hip joints. Despite the much heavier loads, the minimum film thickness under slow running was much thicker than in normal walking and slow walking cases. It should be noted that the load magnitudes of the slow and normal walking cases were similar, but the loading frequencies were different (0.75 Hz and 1 Hz for the slow and normal walking gaits, respectively). If the frequencies were the same, increasing loads would have a negative effect on the lubrication of UHMWPE artificial hip joints in terms of receding the lubricant film thickness (Figure 11). Therefore, gait frequency played a significant role in the lubrication performance of UHMWPE artificial hip joints, i.e., increasing gait frequency would enhance the lubricant film thickness. This is because with the increase in gait frequency, the normal approach velocity increased, causing an enhancement in the squeeze-film effects. Therefore, the lubrication performance of the UHMWPE hip joint was improved by the increase in gait frequency. Although the heavier loads of the slow running gait might reduce film thickness, the squeeze-film action caused by high frequencies contributed more to the film thickness of UHMWPE artificial hip joints.

The present study has several limitations that warrant consideration. Firstly, it is well-established that the film thickness developed in artificial hip joints is insufficient to separate the bearing surfaces [14]. Consequently, UHMWPE artificial hip joints typically operate under mixed lubrication conditions, where surface roughness plays a crucial role. However, our current analyses were conducted under the assumption of smooth bearing surfaces and relied on a fluid film lubrication framework. A more accurate approach would involve implementing a mixed lubrication model that accounts for the actual surface roughness of the UHMWPE liner. In such a model, the contact area could be classified into distinct zones: full-film lubrication regions and asperity contact zones, based on the lubrication status. This approach would yield a composite pressure distribution comprising both asperity contact pressures and fluid-film pressures, with film thickness diminishing to zero in asperity contact zones. Secondly, synovial fluid exhibits complex time-dependent behaviors due to its unique properties, particularly viscoelasticity. The actual properties of a synovial fluid are substantially more complex than those of a Newtonian fluid. To ensure numerical stability and achieve satisfactory convergence in our calculations, we simplified the synovial fluid as a Newtonian fluid with a relatively high viscosity value. However, when considering lower viscosity values, the lubrication model should be appropriately adjusted to a mixed lubrication framework. Otherwise, the convergence and numerical efficiency will encounter challenges. Thirdly, as time advances, the calculation of viscoelastic deformation necessitates the consideration of the cumulative impact of all preceding deformations, resulting in a significant escalation in computational complexity and resource requirements. Consequently, the present investigation was limited to analyzing only three cycles.

Despite the acknowledged limitations, this study provides substantial evidence regarding the critical influence of both gait patterns and UHMWPE liner viscoelasticity on squeeze-film lubrication in artificial hip joints. Furthermore, squeeze-film lubrication is the only lubrication mechanism under heavy loads and low speed conditions. The insights derived from elucidating the role of UHMWPE viscoelasticity across various gait patterns contribute significantly to the fundamental understanding of lubrication mechanisms in soft-bearing artificial hip joints. These findings offer valuable theoretical support and practical implications for the optimization of joint design, particularly in addressing the complex mechanical environment encountered in clinical applications.

While viscoelasticity has been extensively investigated in dry contact mechanics [4,9,15], its role in lubrication phenomena remains relatively underexplored. Future research directions in VEHL should incorporate several critical factors to enhance understanding and model fidelity. These include the surface roughness characteristics of UHMWPE liners, the complex rheological properties of biological lubricants, the interaction between UHMWPE liners and synovial fluid, and the mechanical behavior of high-performance polyethylene, etc. The aforementioned outlook can be elaborated in detail through the following aspects: Firstly, the development of comprehensive viscoelastic boundary and mixed lubrication models for soft artificial hip joints represents a crucial next step toward elucidating actual lubrication mechanisms. Secondly, given the complex nature of synovial fluid, which exhibits both protein aggregation phenomena and non-Newtonian behavior, there is a pressing need to establish more sophisticated rheological models. Such advanced modeling approaches would enable more accurate characterization of lubrication mechanisms in artificial joint systems. Thirdly, non-zero wall slip between the UHMEPE liner and synovial fluid increases the complexity of the analysis, which should be investigated further. Fourthly, recent advancements in material science such as highly cross-linking technology, which enhances the mechanical performance of polyethylene significantly, should be considered in future studies. Finally, to address the limitation of calculation efficiency, future studies should also focus on developing more efficient numerical algorithms capable of accurately modeling squeeze-film lubrication behavior over extended cycles.

5. Conclusions

A viscoelastic squeeze-film lubrication model for artificial hip replacements was developed, incorporating different gait loads measured by Bergmann et al., such as slow walking, normal walking and slow running conditions. The main conclusions are as follows:

• In both elastic and viscoelastic models, physiological loads significantly enhanced the squeeze-film lubrication of artificial hip joints compared to constant loads, with the viscoelastic model showing greater effects than the elastic model.
• Among the tested gait conditions, slow running produced the strongest viscoelastic squeeze-film lubrication in UHMWPE artificial hip joints, followed by normal walking, with slow walking exhibiting the weakest viscoelastic squeeze-film effect.
• High gait frequencies significantly enhanced the viscoelastic squeeze-film lubrication of artificial hip joints, even under heavy loads such as those experienced during slow running.