Wear Prediction and Chaos Identification of Rigid Flexible Coupling Multi-Link Mechanisms with Clearance
Abstract
1. Introduction
2. Establishment of Irregular Wear Model
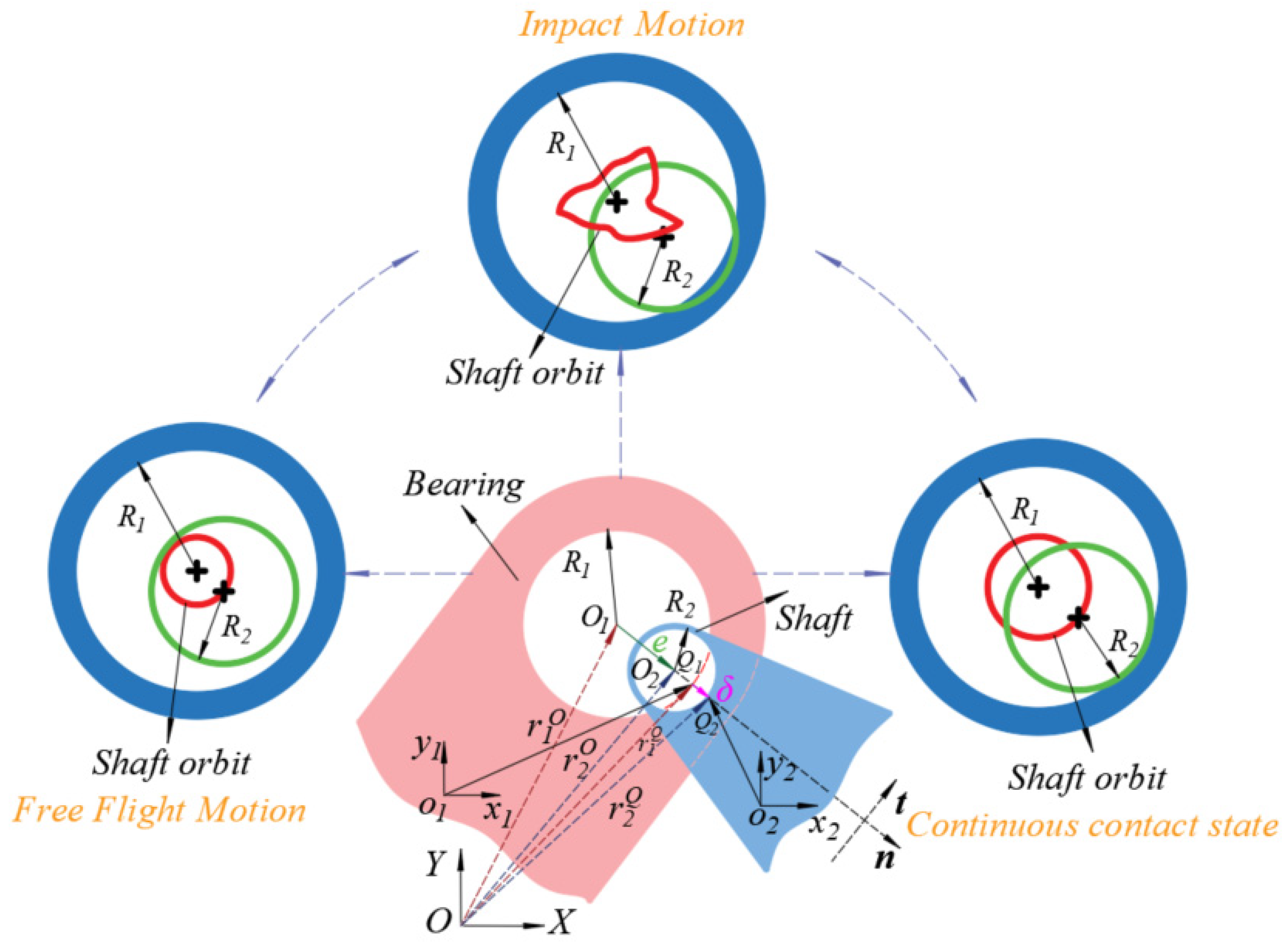
2.1. Establishment of Ideal Revolute Clearance Model
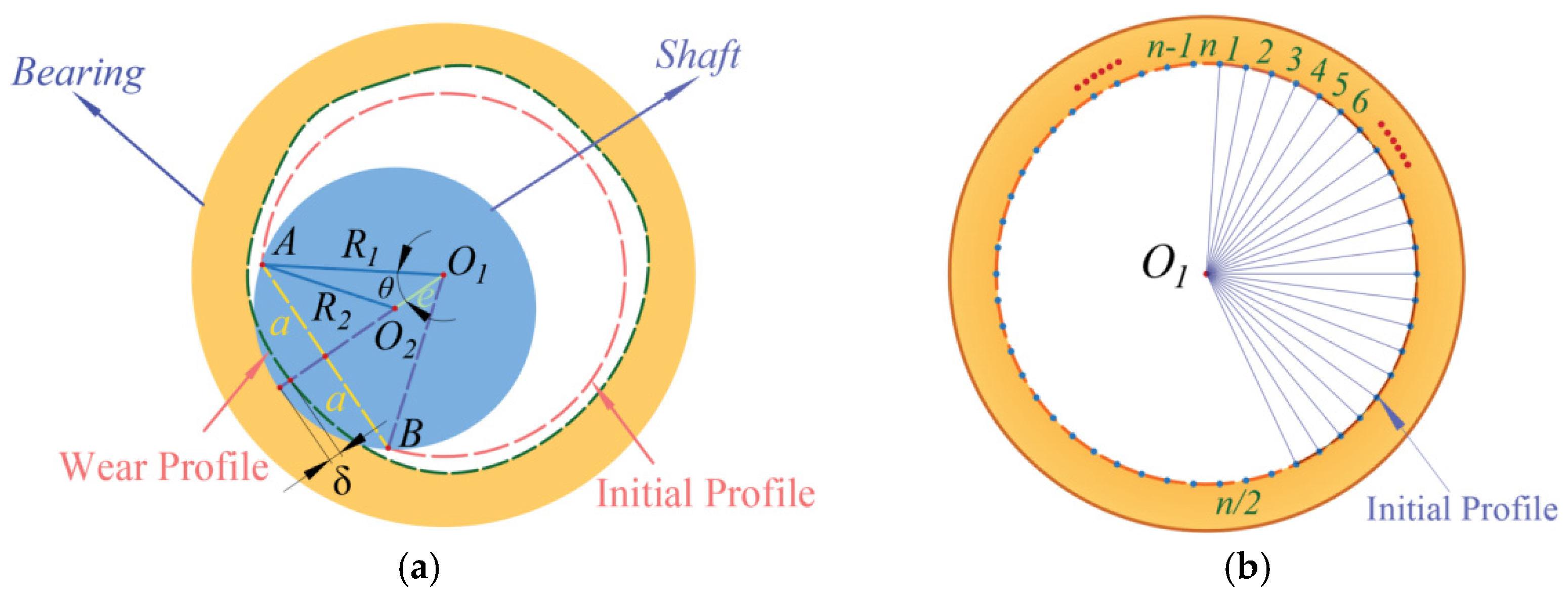
2.2. Establishment of the Wear Clearance Model
3. Establishment of Flexible Beam Element Model
4. Dynamic Model for Mechanism with Irregular Wear Clearance
4.1. Establishment of Dynamic Model for Mechanism with Irregular Wear Clearance
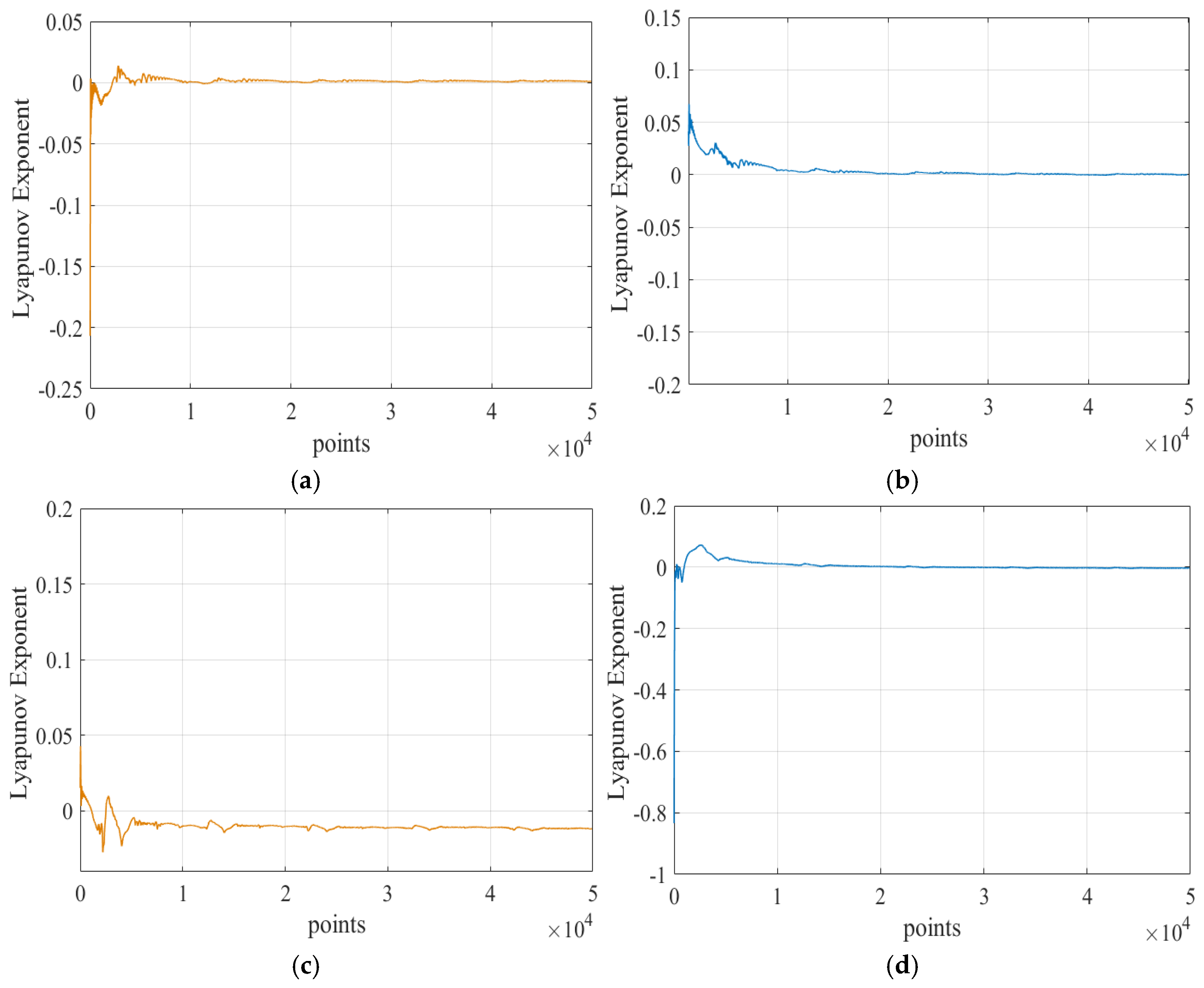
4.2. Establishment of Chaos Characteristics Identification Model
5. Dynamic Analysis of Mechanical System
5.1. Simulation Parameters
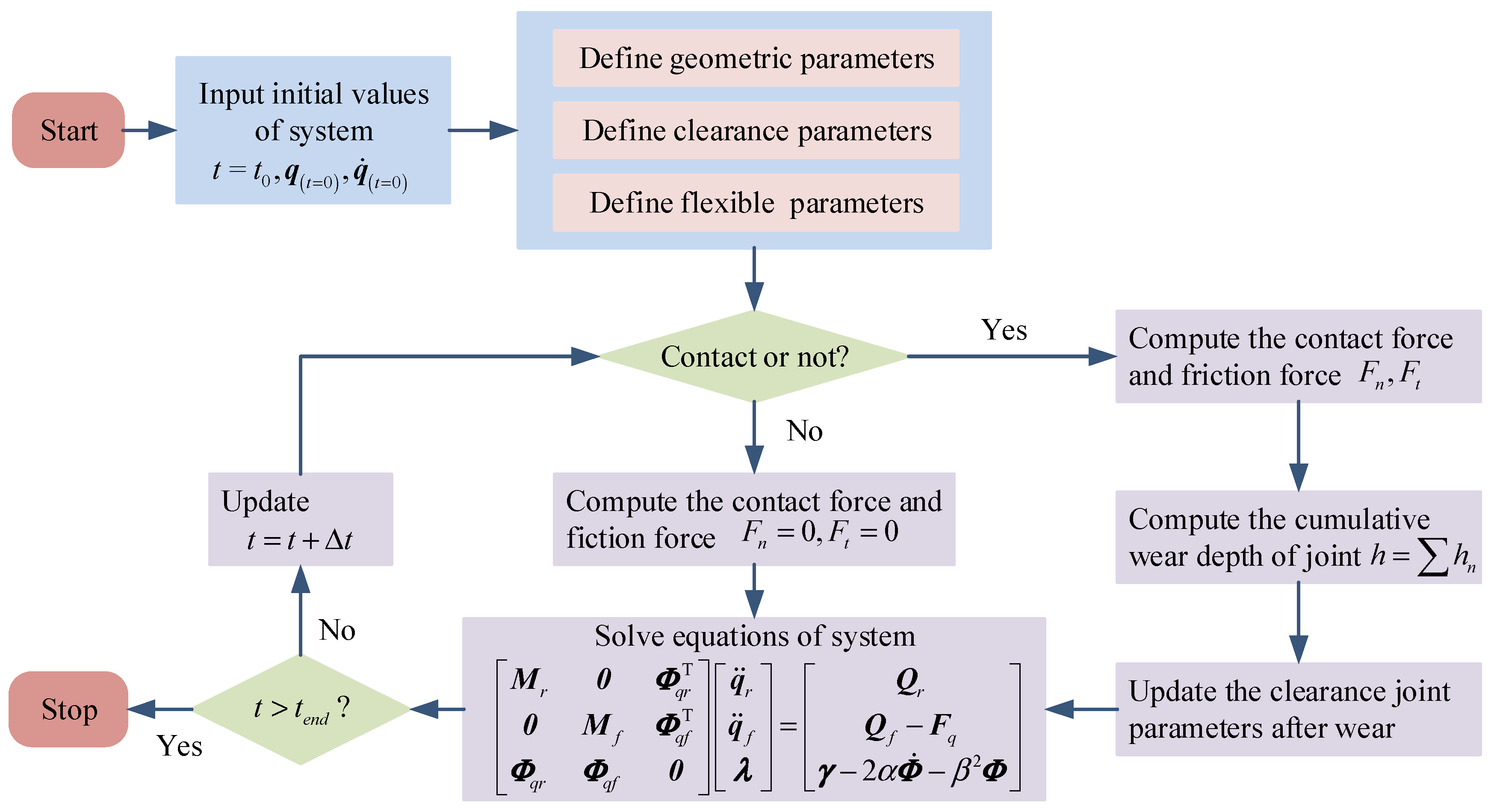
5.2. Solution Flowchart
- Start simulation with given initial values of system for positions and velocities .
- Define the geometric parameters, clearance parameters, and flexible parameters of the system to ensure the model accurately reflects the physical characteristics of the mechanism.
- Determine whether the contact exists between the joint element. If there is contact, calculate the contact force Fn and friction force Ft, further compute the wear depth, and update the parameters of the clearance joint. If no contact exists, set the contact force Fn and friction force Ft to zero.
- Solve the dynamic response of the system based on Equation (38).
- Determine whether the current time exceeds the end time. If yes, terminate the computational process, if no, update the current time to and obtain the new generalized positions and velocities of the system in the next step.
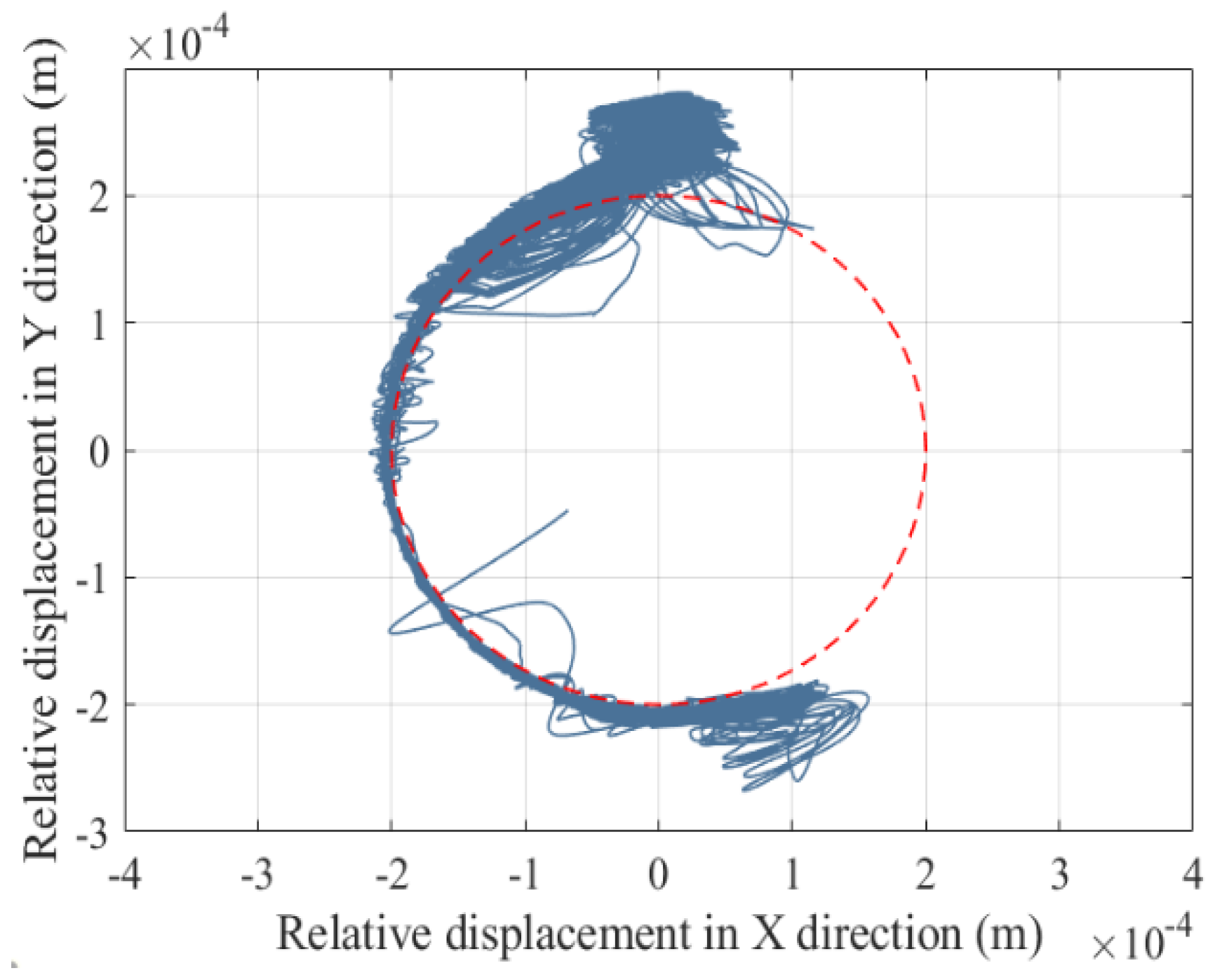
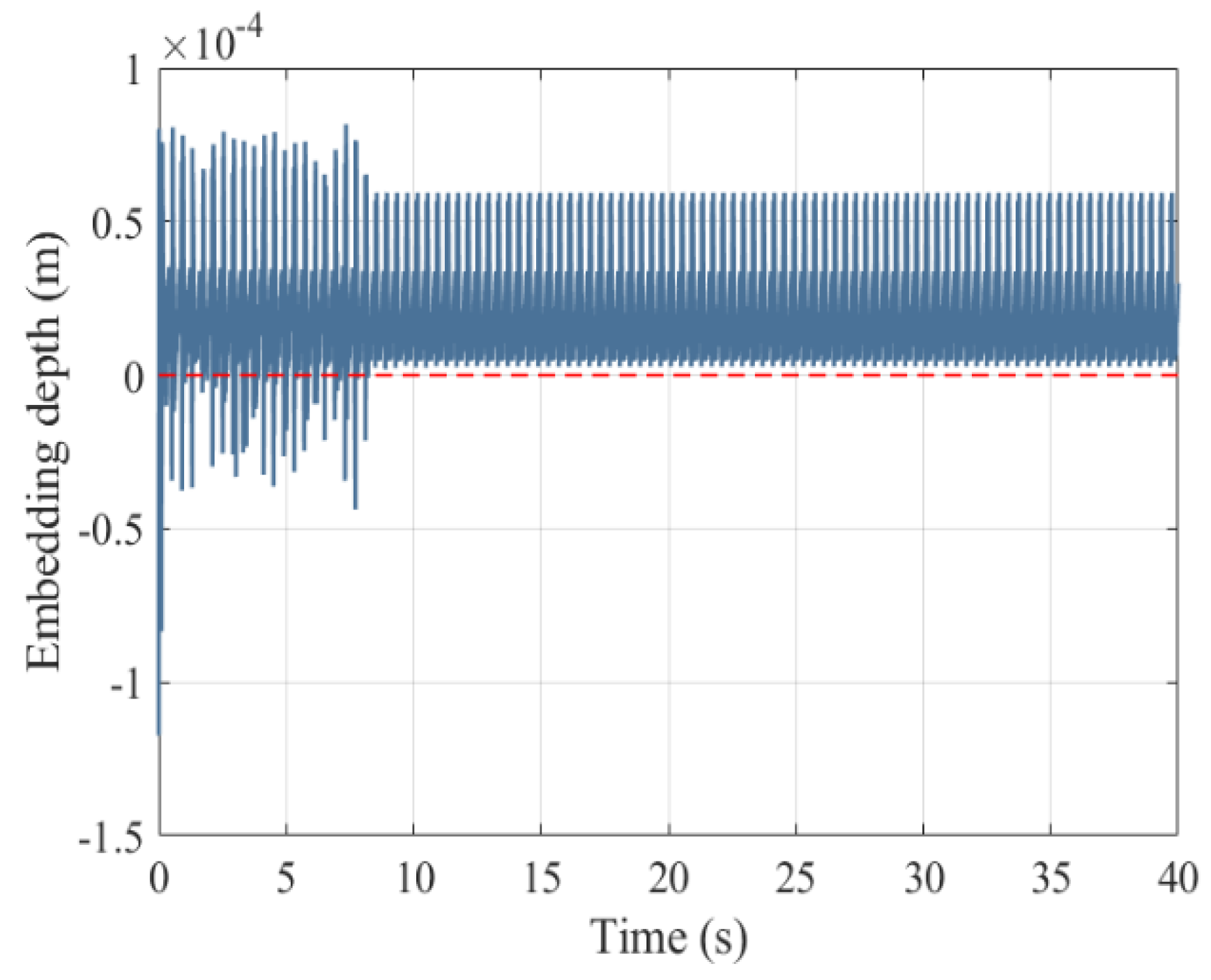
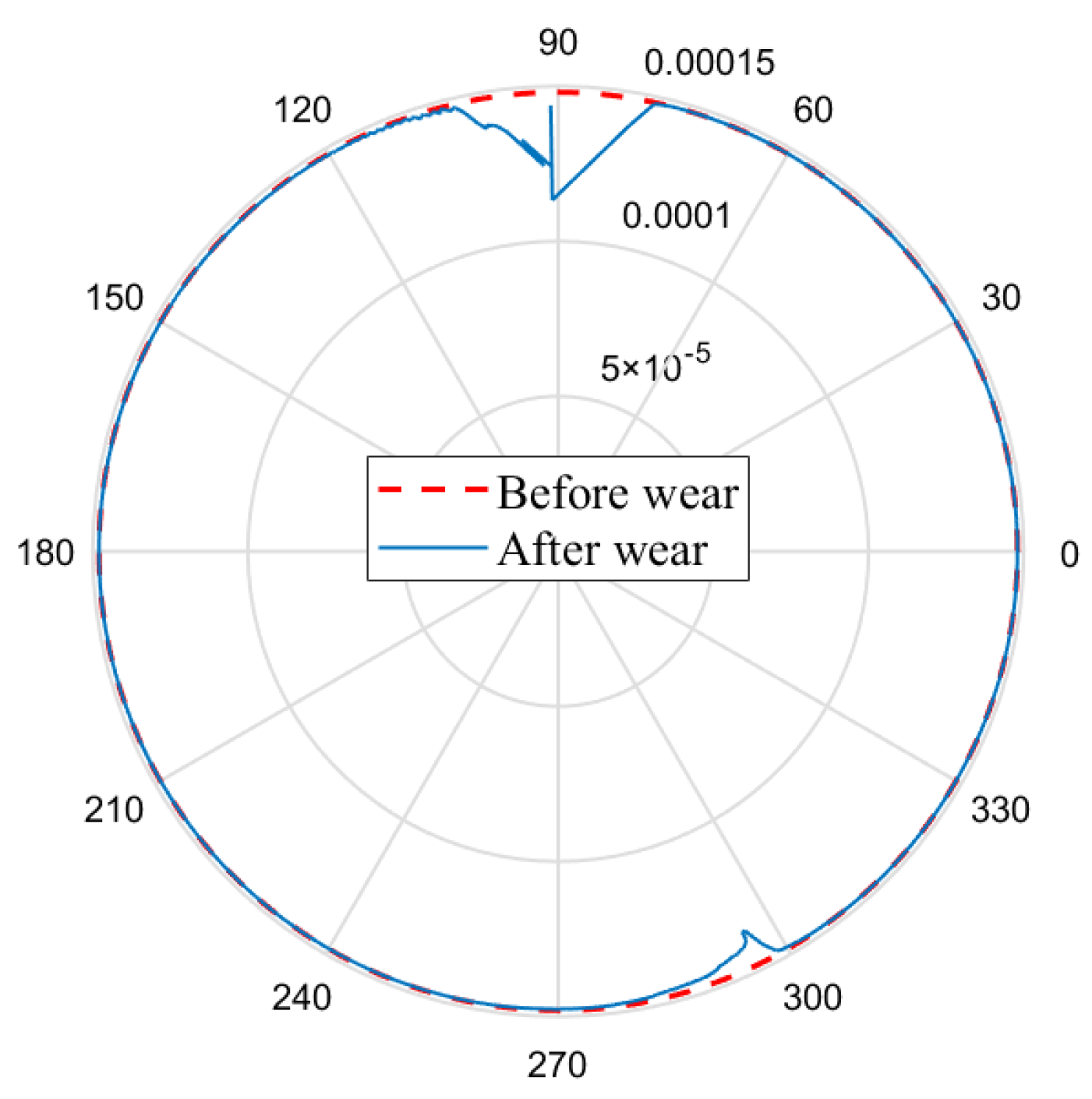
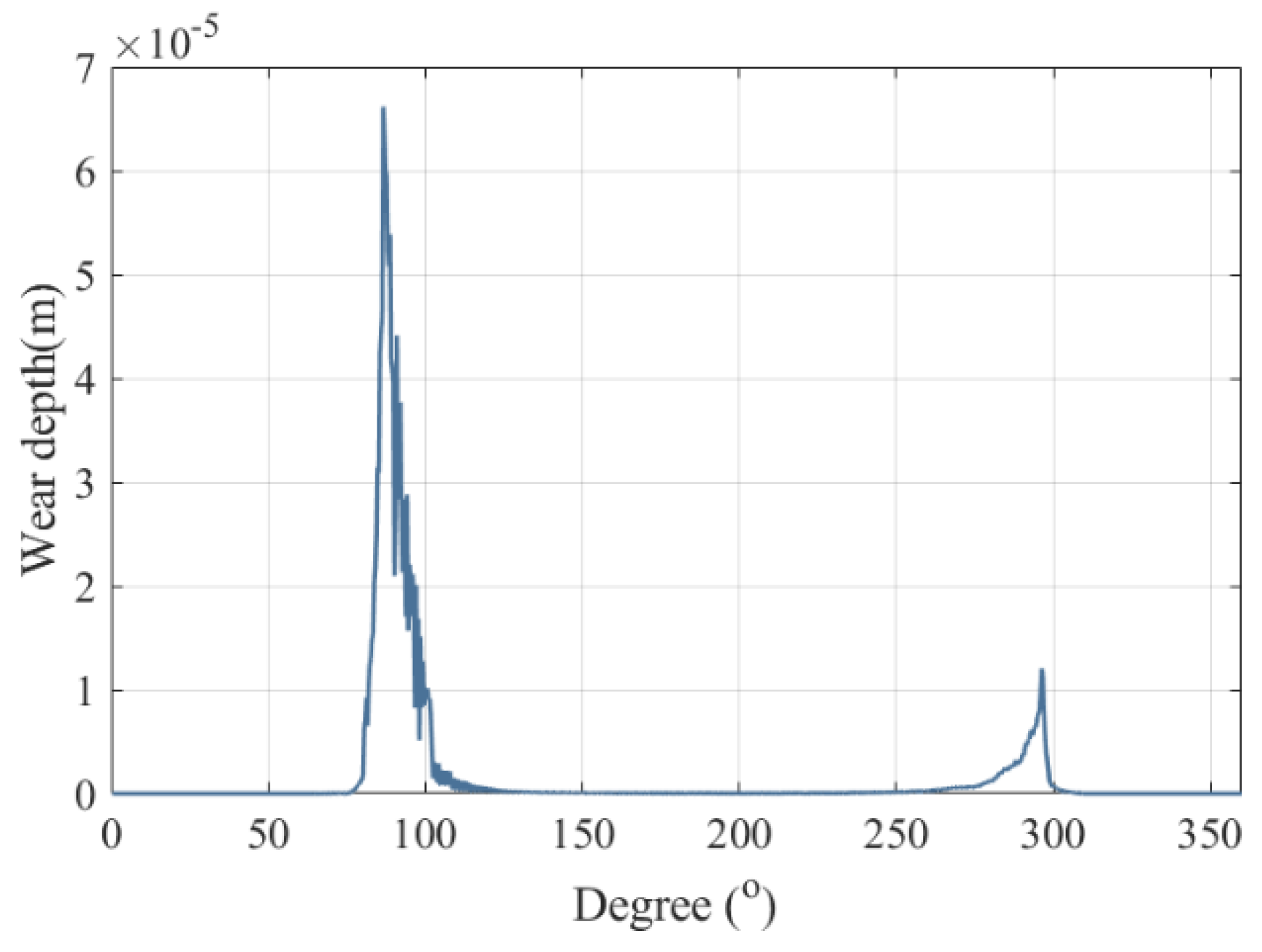
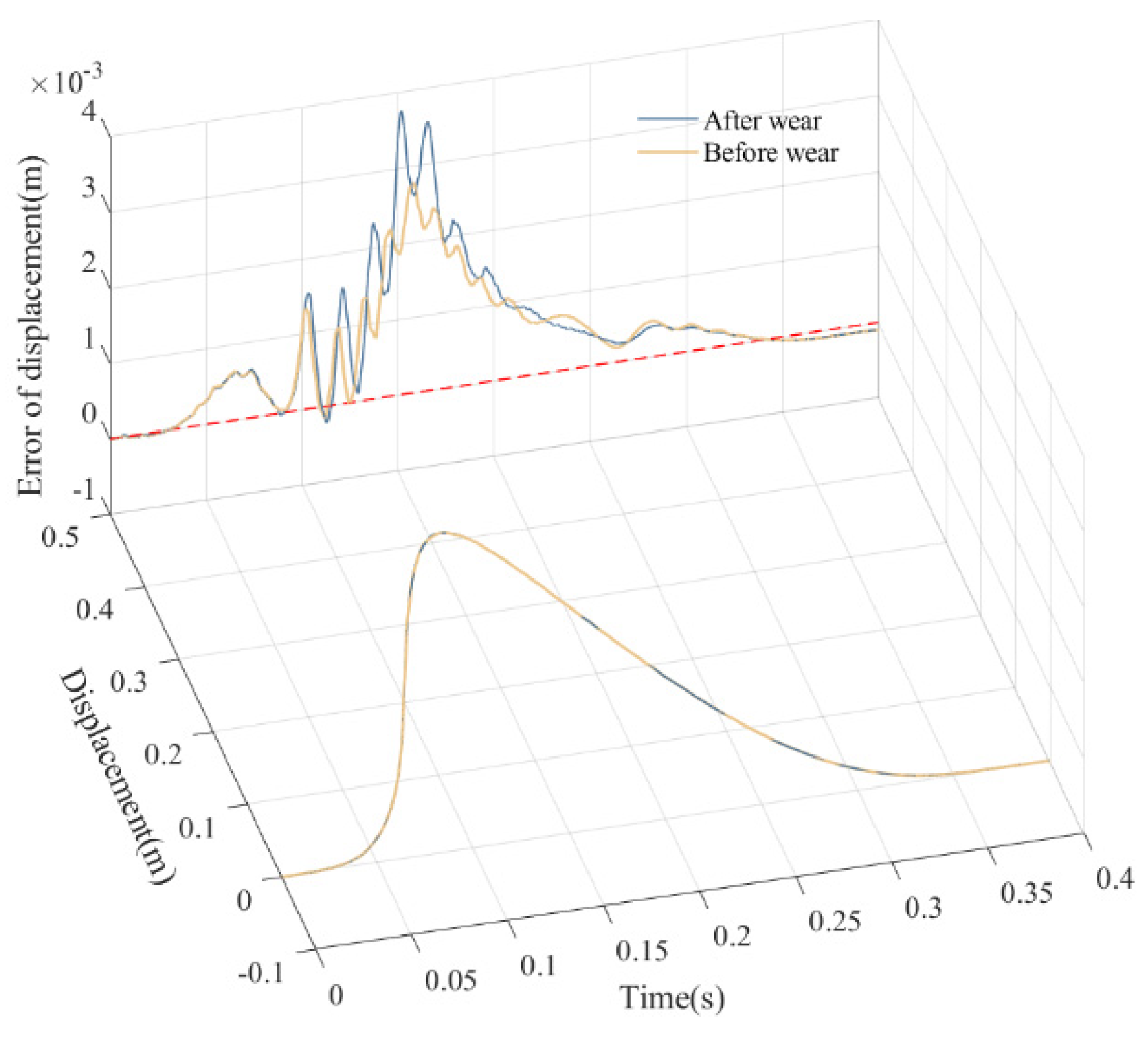
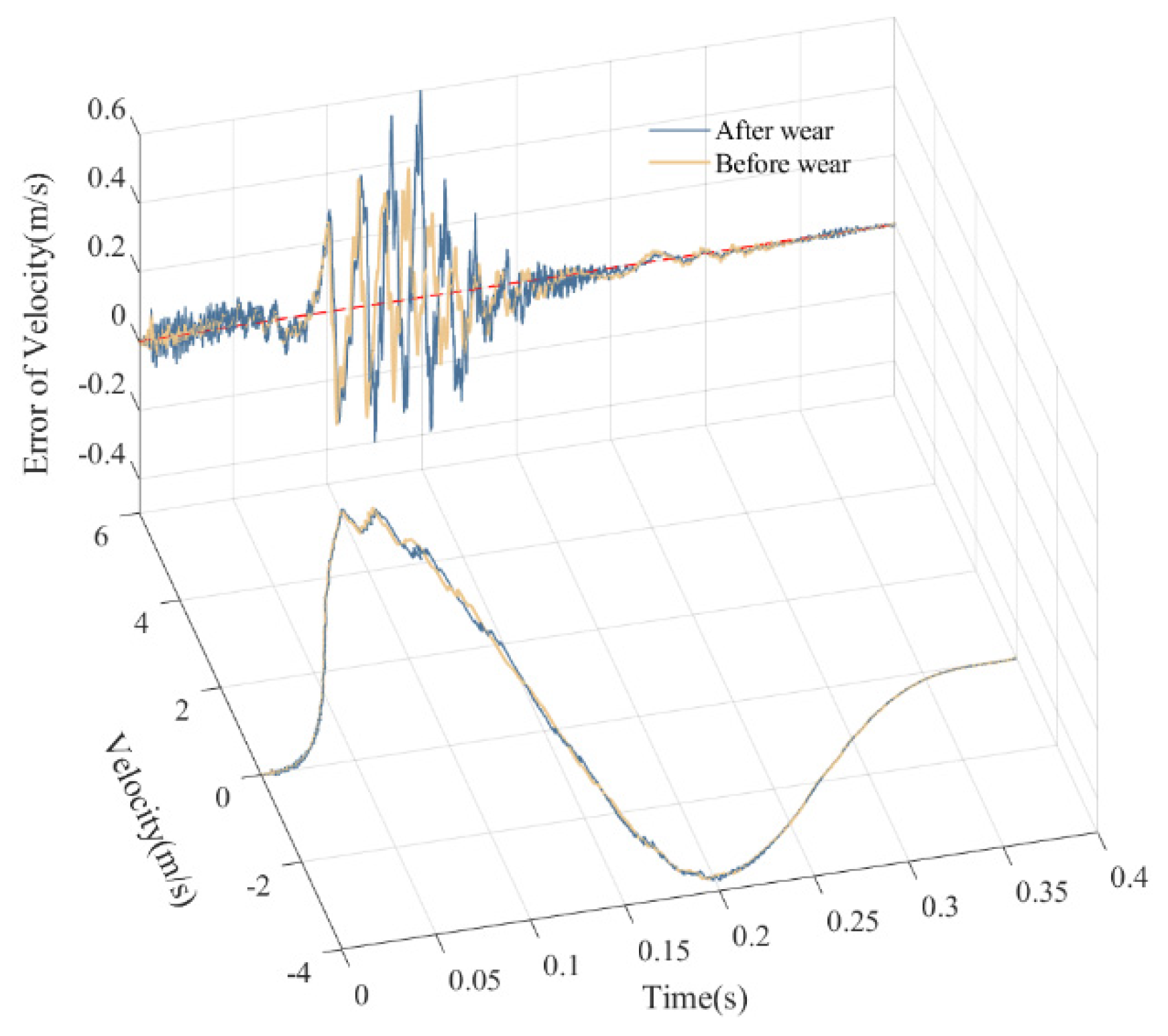
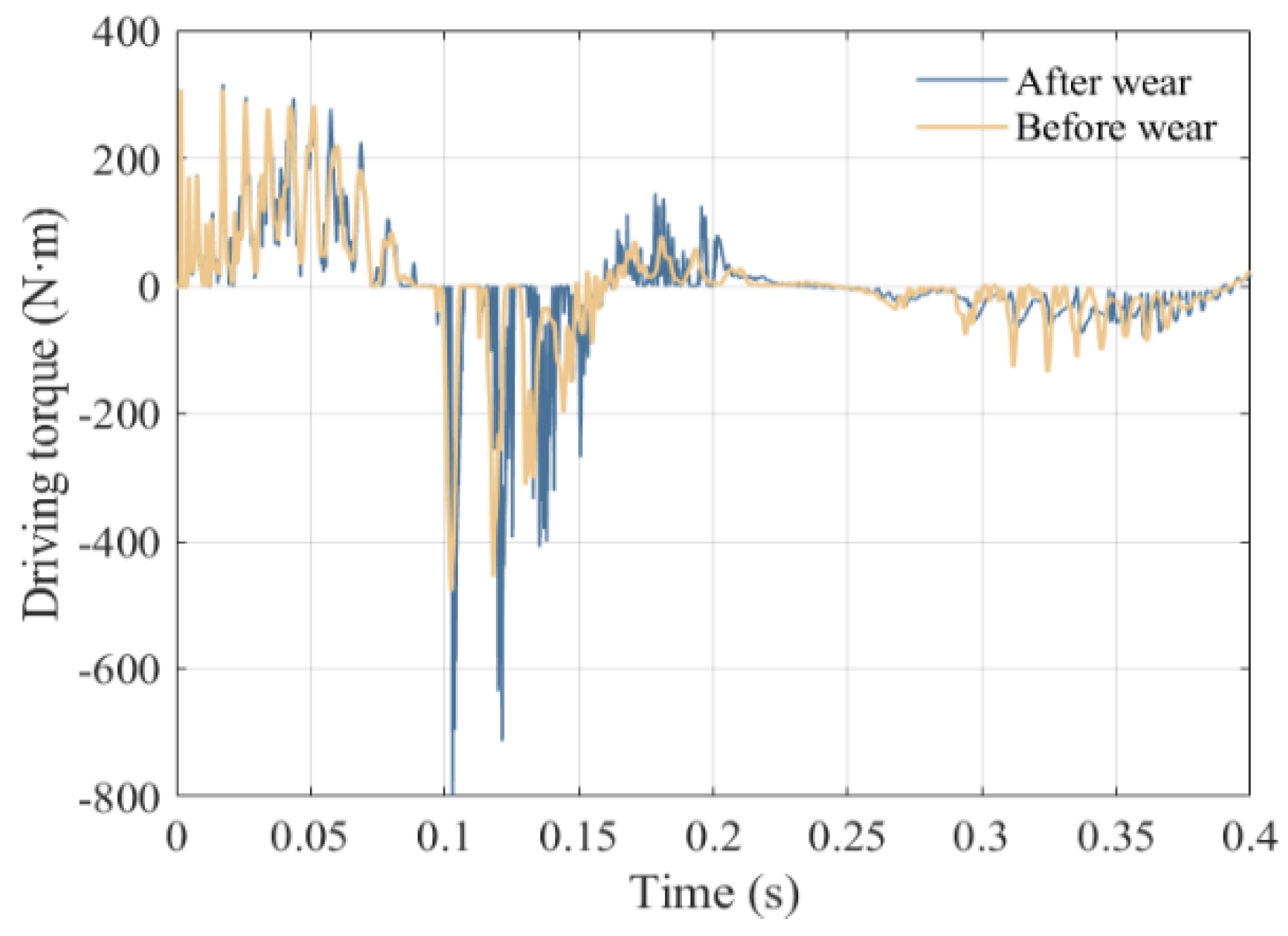
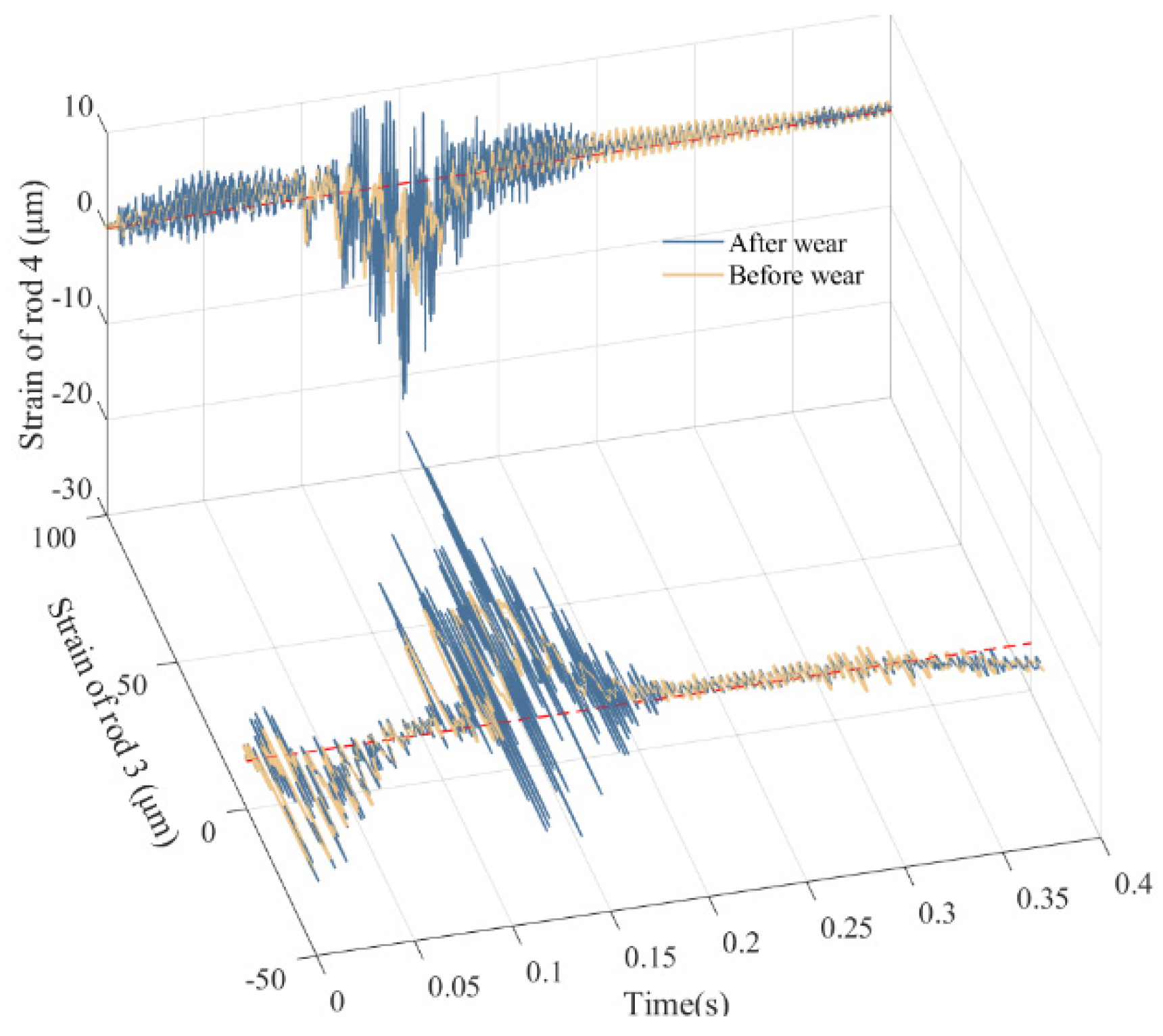
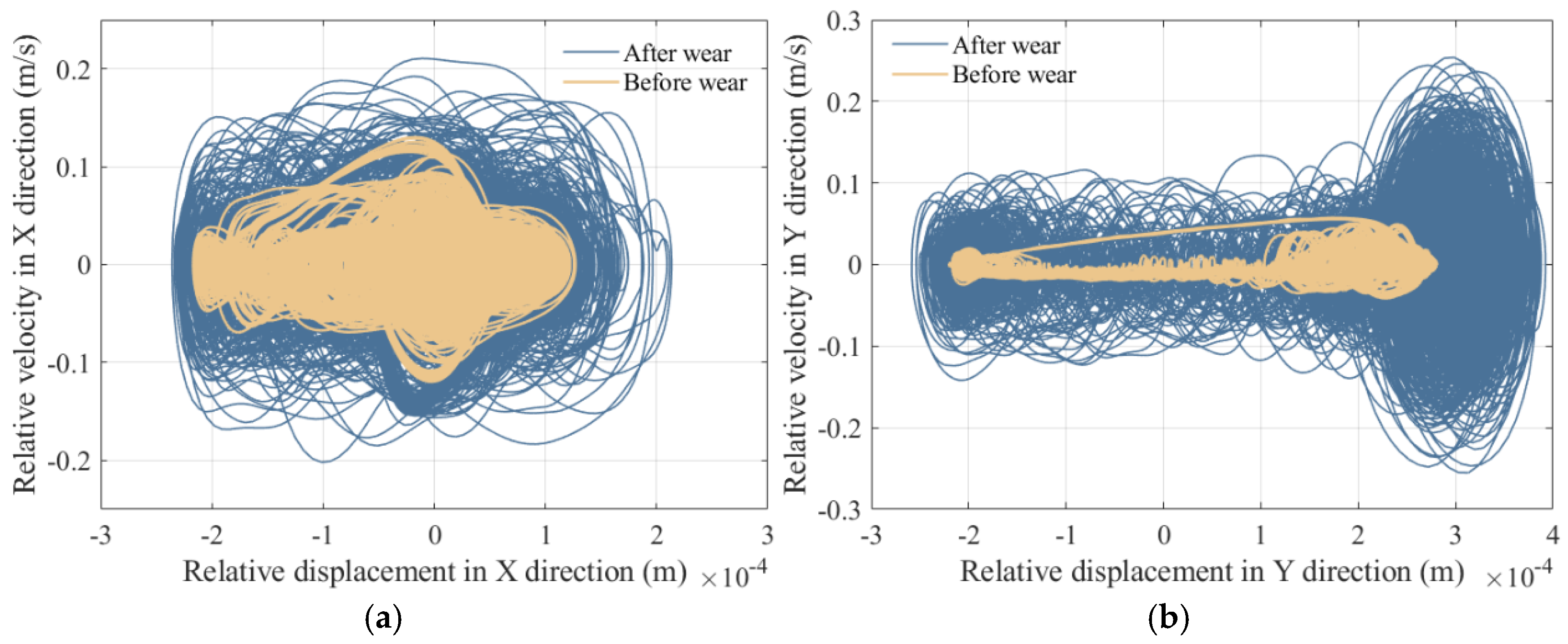
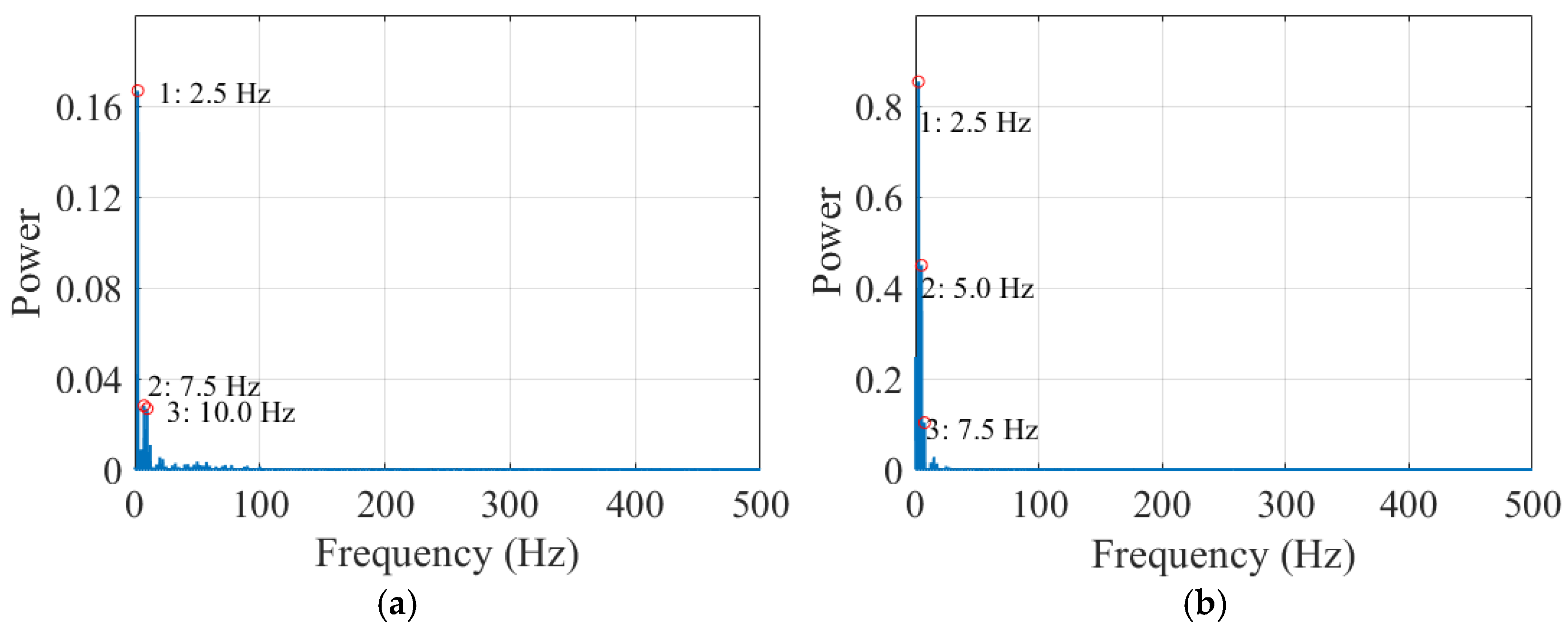
5.3. Comparative Analysis of Mechanism Dynamics Before and After Wear
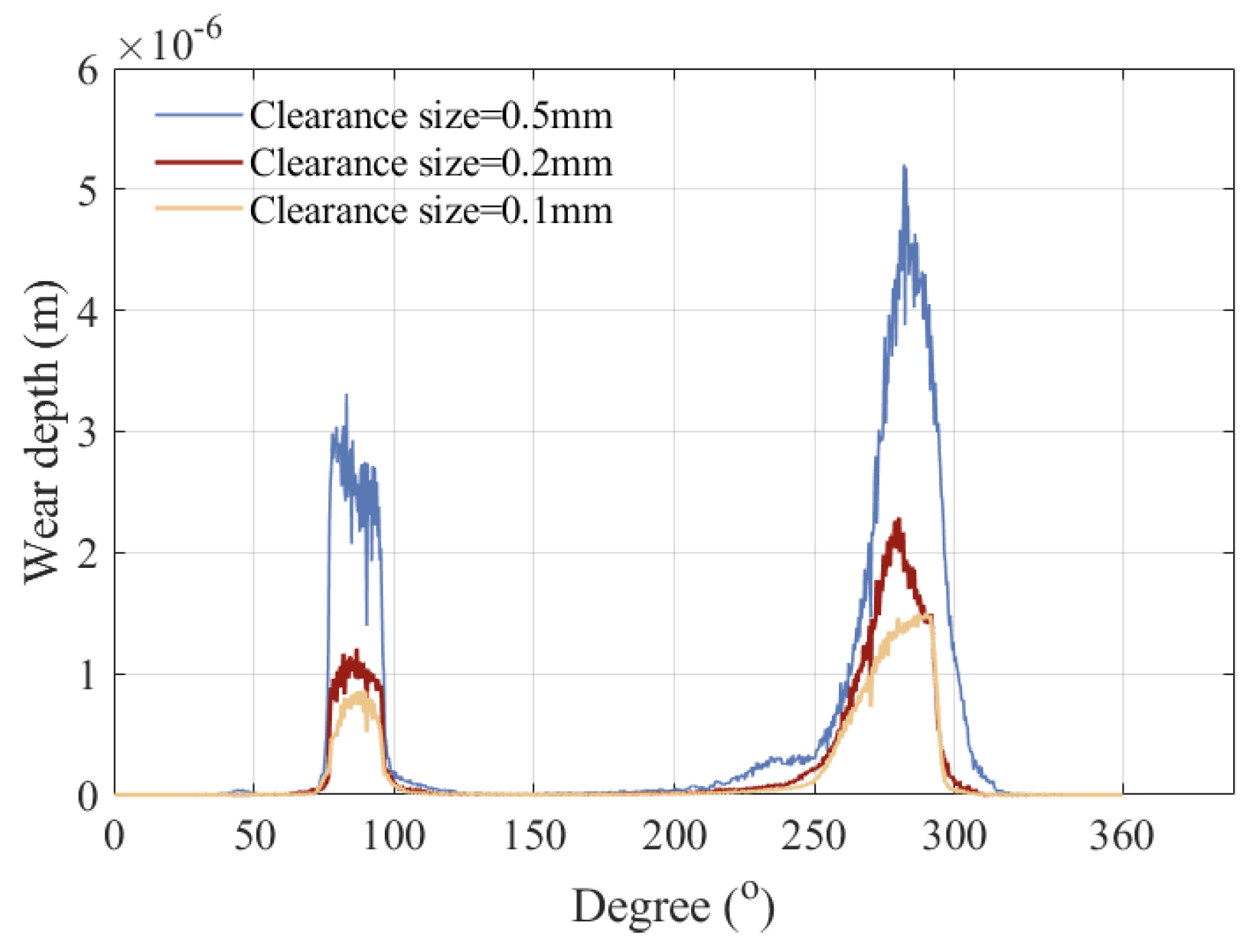
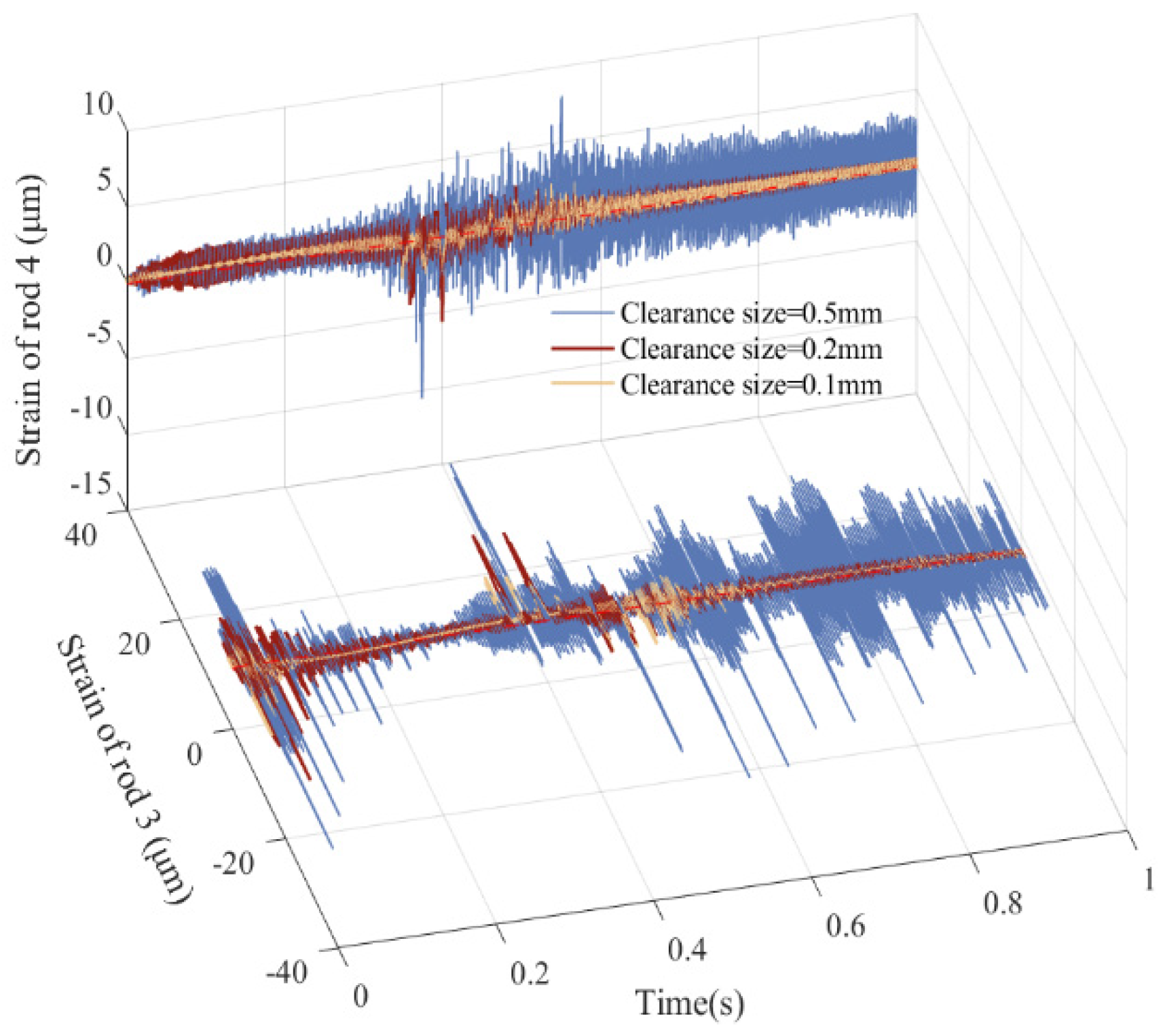
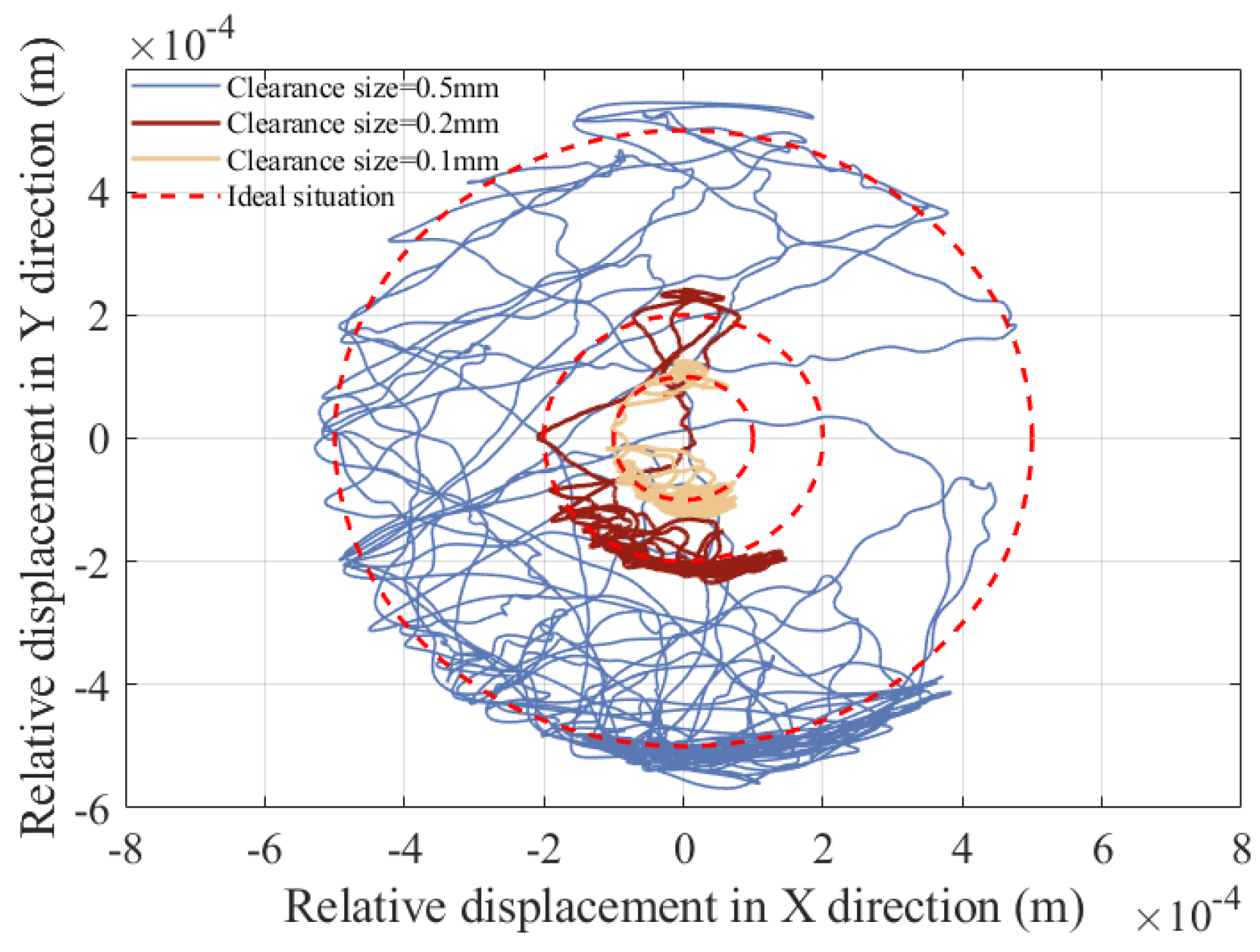
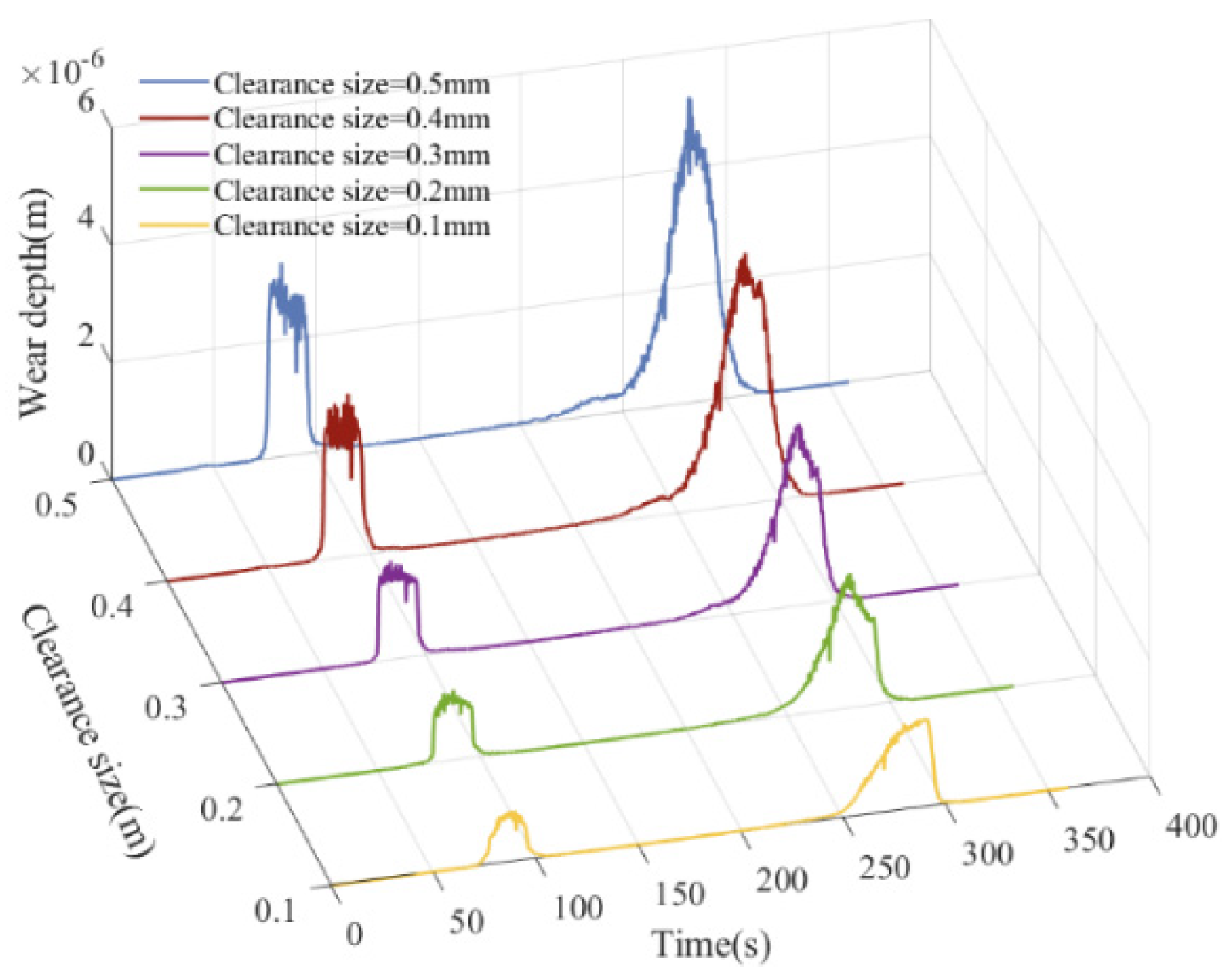
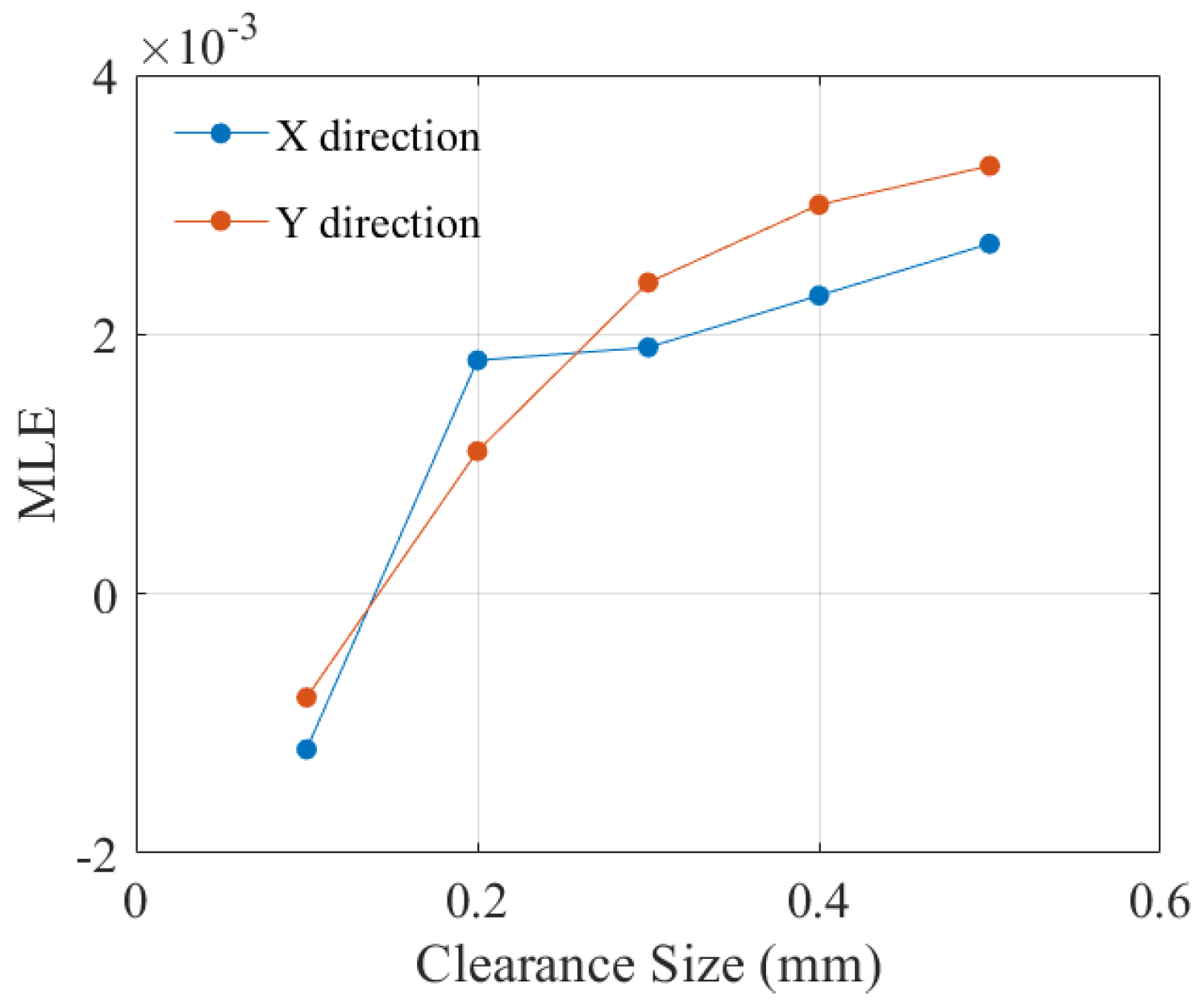
5.4. Influence of Different Clearance Sizes on Dynamics
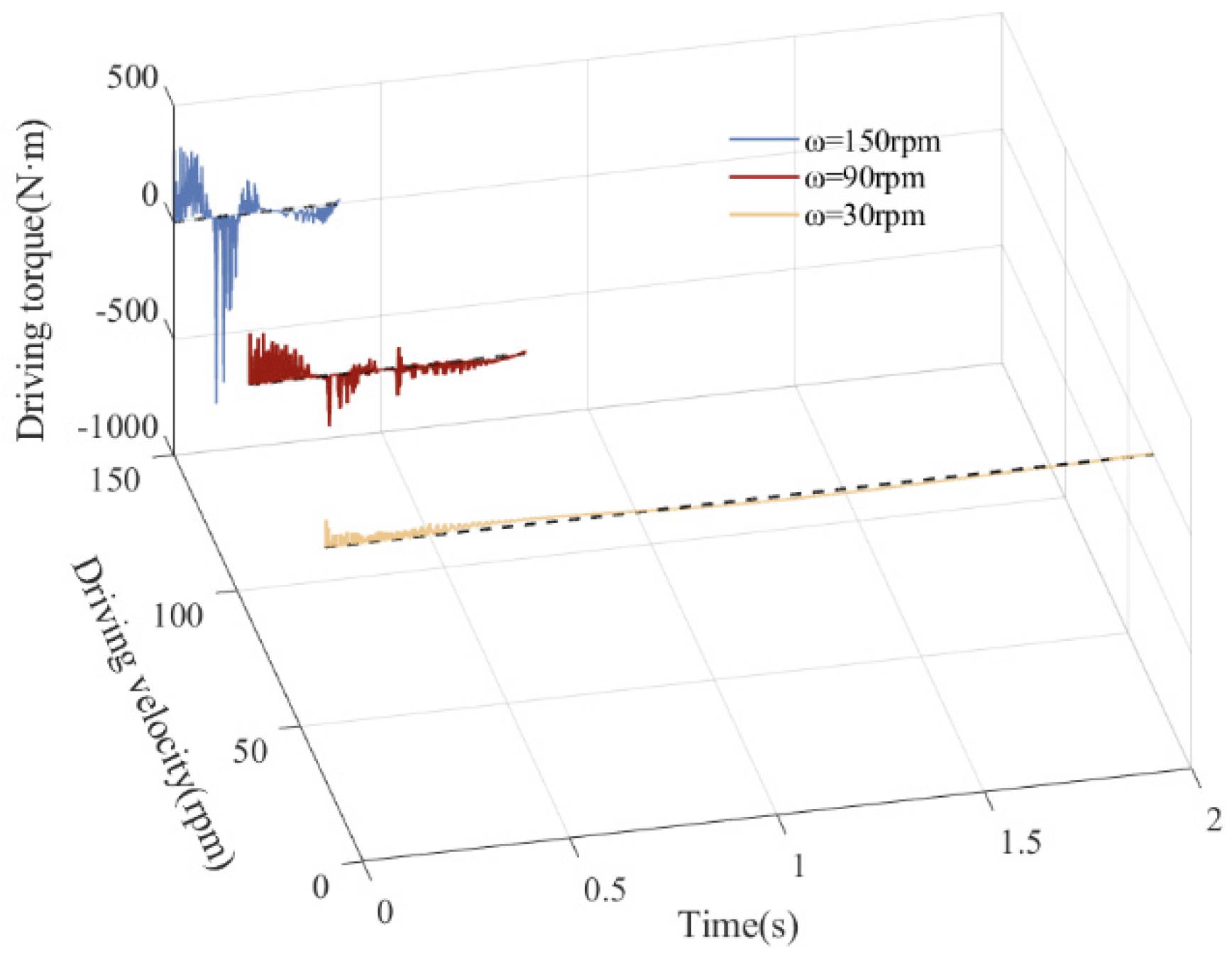
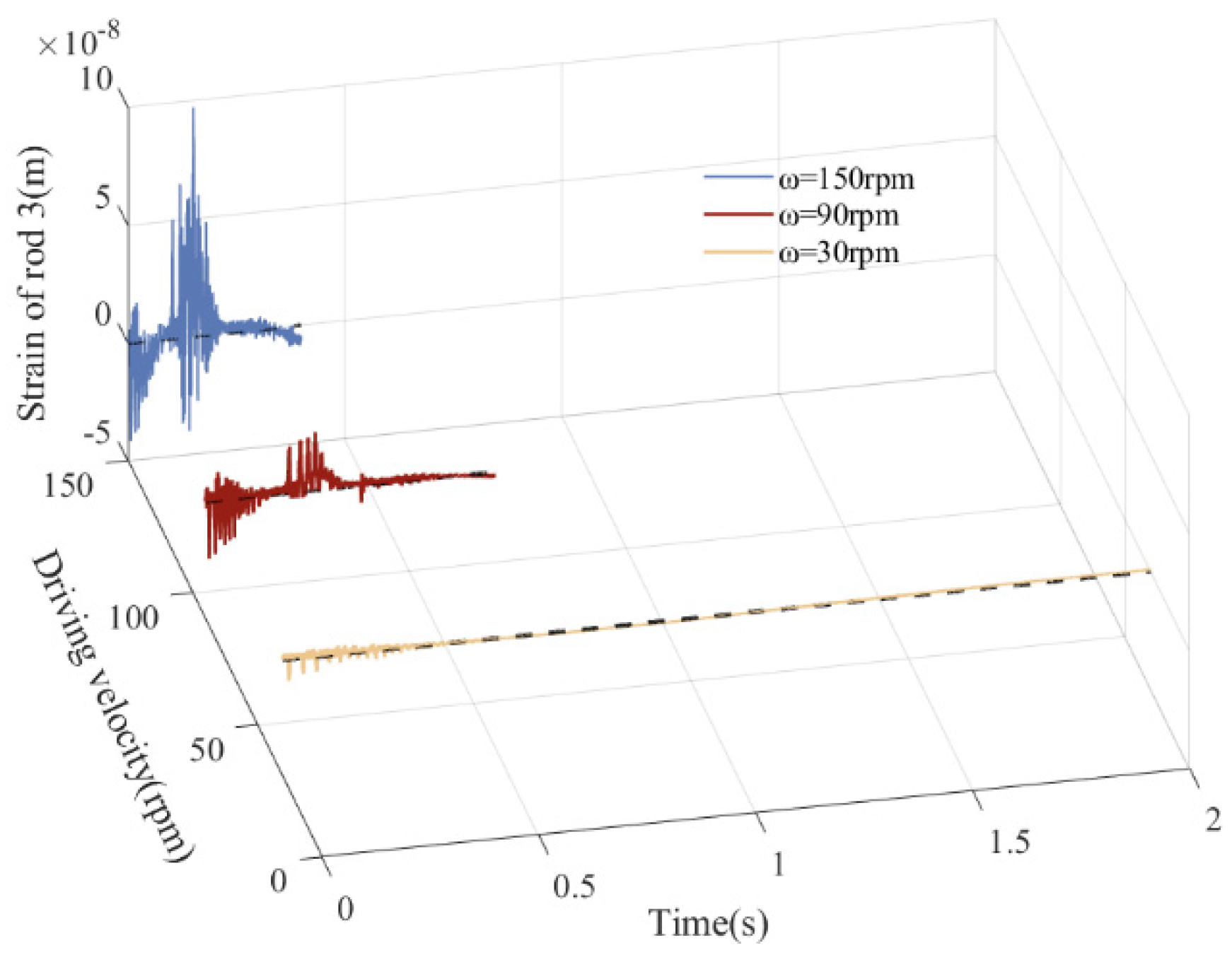
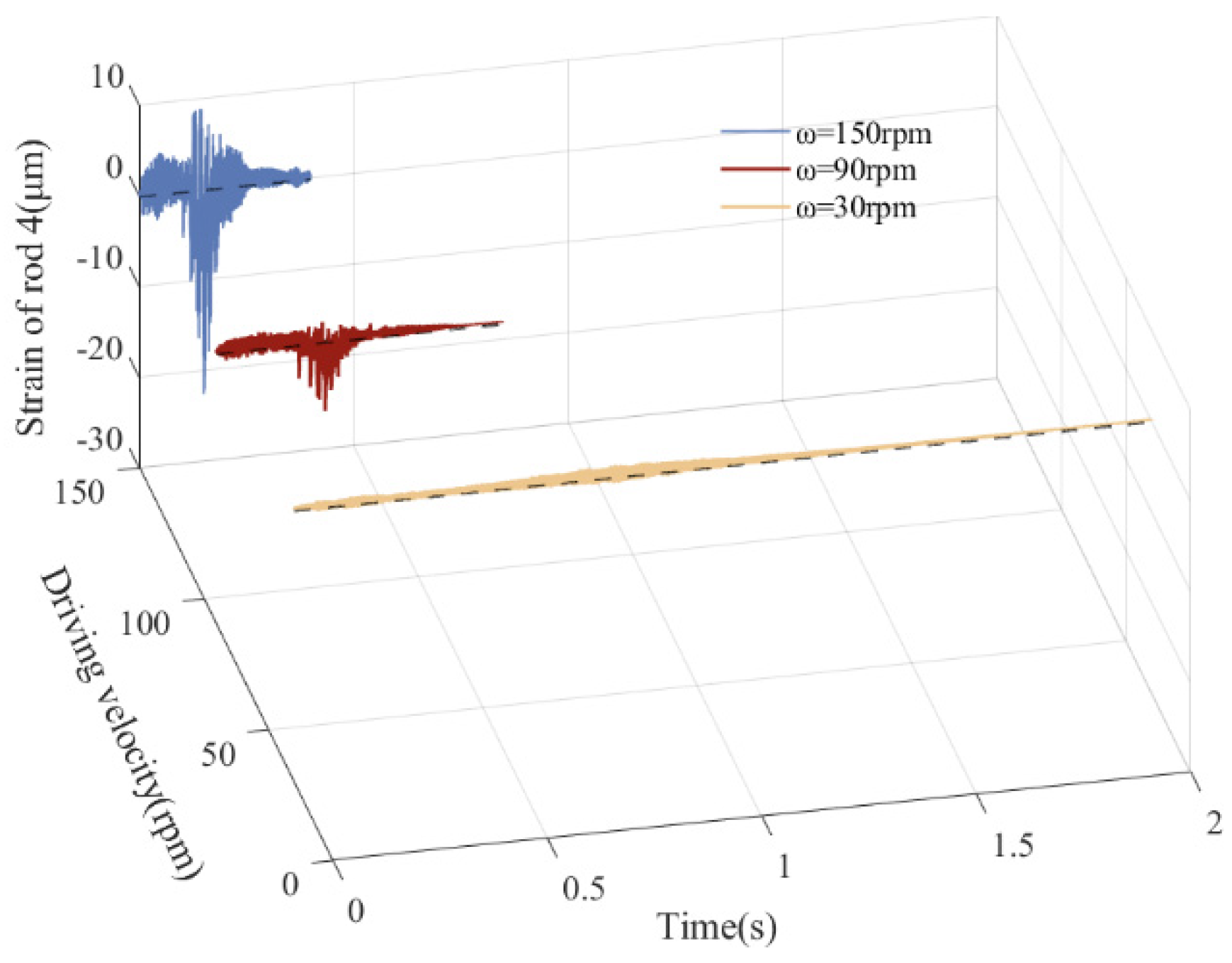
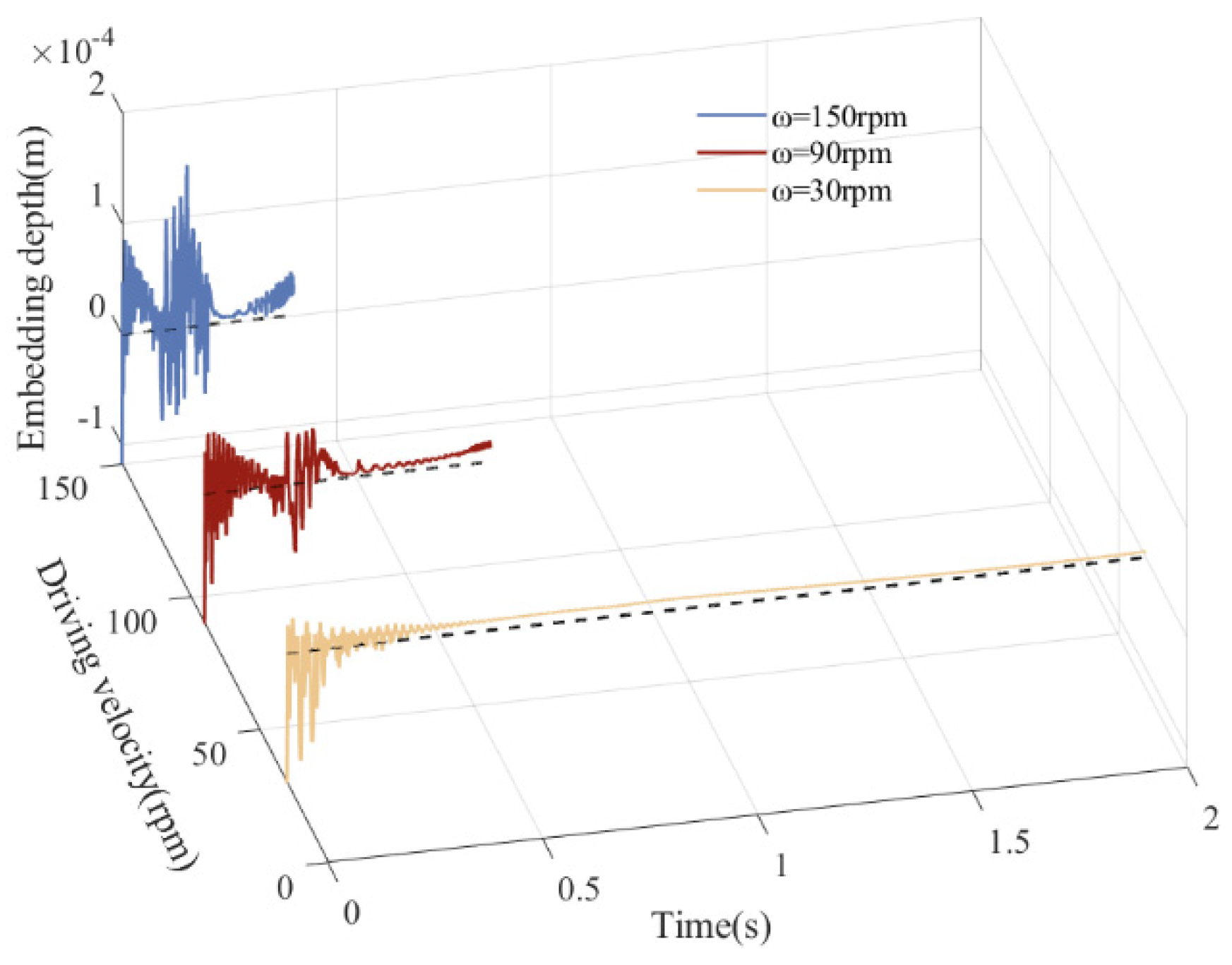
5.5. Influence of Various Driving Velocities on Dynamics
6. Conclusions
- (1)
- A 2D beam element model was developed using the ANCF, integrating the Archard wear model to characterize irregular wear patterns, thereby establishing a flexible multibody dynamics framework for multi-link mechanisms with clearance joints. This framework enables systematic chaos identification and nonlinear dynamic analysis.
- (2)
- A comparative analysis of before and after wear dynamic responses revealed localized wear concentration in the [75°, 132°] and [252°, 310°] intervals of kinematic pairs, attributed to stress concentration and dynamic load redistribution. After wear, the maximum contact force amplitude of the joint increased by 1.54 times.
- (3)
- This study investigated the nonlinear effects of wear-induced clearances in rigid–flexible coupled systems under varying operational conditions. The results indicate that enlarged clearances accelerate the transition from periodic to chaotic motion due to intensified wear. System dynamics exhibit higher sensitivity to driving speed variations than clearance size, with rotational speeds below 90 rpm effectively suppressing wear severity and stabilizing motion.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | contact half width |
| Aw | contact area |
| c | clearance joint value |
| ce | material’s recovery coefficient |
| cd | dynamic correction coefficient |
| cf | coefficient of friction |
| clearance size at discrete region n | |
| D | hysteresis damping factor |
| hysteresis damping factor after wear | |
| e | eccentricity vector |
| ef | absolute node coordinates |
| E1, E2 | elastic modulus of the bearing and shaft |
| E* | Young’s modulus |
| Fe | elastic force of a flexible beam element |
| Ff | elastic force of flexible components |
| Fn | contact force |
| contact force at clearance joint after wear | |
| friction force at clearance joint after wear | |
| h | wear depth |
| hn | wear depth within discrete area code |
| k | wear coefficient |
| stiffness coefficient | |
| Kl | compressive stiffness of the unit |
| Kt | bending stiffness of the unit |
| stiffness coefficient after wear | |
| l | unit length |
| L | axial contact length of hinge |
| M | total number of iterations in the calculation of Lyapunov exponent |
| Me | mass matrix of elastic beam elements |
| Mr | mass matrix of the rigid components |
| Mf | mass matrix of flexible components |
| q | generalized coordinates of entire system |
| qf | generalized coordinate of flexible components |
| qr | generalized coordinate of the system’s rigid components |
| Qe | generalized force of the flexible beam element |
| Qf | total external force of flexible components |
| Qr | total external force of the rigid components |
| contact points | |
| r | absolute position vector of any point on element |
| position vectors of contact points | |
| curvature radius at the discrete region n of the bearing and shaft | |
| s | slip distance |
| S | shape function |
| v0, v1 | speed limit value |
| V | wear volume |
| x | local coordinate of any point before deformation |
| X(ti) | time series |
| Y(ti) | time series reconstructed from phase space |
| parameter of Baumgarte stabilization algorithm | |
| parameter of Baumgarte stabilization algorithm | |
| right side of acceleration constraint equations | |
| δ | penetration depth |
| relative normal contact velocity, | |
| elative embedding depth at the discrete region n | |
| l | strain of unit |
| Lagrange multiplier | |
| right side of velocity constraint equations | |
| υ1, υ2 | Poisson’s ratios of bearing and shaft |
| maximum Lyapunov exponent | |
| Φ | constraint equation of mechanism |
| Φq | Jacobian matrix of constraint equation |
| Φqr | derivative of constraint equation with respect to generalized coordinates of rigid components |
| Φqf | derivative of constraint equation with respect to generalized coordinates of flexible components |
| Φt | differentiation of the constraint equation with respect to time |
| ANCF | Absolute Nodal Coordinate Formulation |
| L-N | Lankarani and Nikravesh |
| MLE | maximum Lyapunov exponent |
References
- Millan, P.; Pagaimo, J.; Magalhães, H.; Ambrósio, J. Clearance joints and friction models for the modelling of friction damped railway freight vehicles. Multibody Syst. Dyn. 2023, 58, 21–45. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Liu, Y.; Geng, X.; Cui, C. Parameter optimization for torsion spring of deployable solar array system with multiple clearance joints considering rigid-flexible coupling dynamics. Chin. J. Aeronaut. 2022, 35, 509–524. [Google Scholar] [CrossRef]
- Xu, L.; Han, Y.; Dong, Q.; Jia, H. An approach for modelling a clearance revolute joint with a constantly updating wear profile in a multibody system: Simulation and experiment. Multibody Syst. Dyn. 2019, 45, 457–478. [Google Scholar] [CrossRef]
- Korayem, M.H.; Ghariblu, H. Analysis of Wheeled Mobile Flexible Manipulator Dynamic Motions with Maximum Load Carrying Capacitie. Robot. Auton. Syst. 2004, 48, 63–76. [Google Scholar] [CrossRef]
- Bai, Z.; Ning, Z.; Zhou, J. Study on Wear Characteristics of Revolute Clearance Joints in Mechanical Systems. Micromachines 2022, 13, 1018. [Google Scholar] [CrossRef]
- Wang, G.; Liu, H. Three-Dimensional Wear Prediction of Four-Degrees-of-Freedom Parallel Mechanism with Clearance Spherical Joint and Flexible Moving Platform. J. Tribol. 2018, 140, 031611. [Google Scholar] [CrossRef]
- Chaturvedi, E.; Sandu, C.; Sandu, A. A nonsmooth dynamics framework for simulating frictionless spatial joints with clearances. Multibody Syst. Dyn. 2024, 63, 3–37. [Google Scholar] [CrossRef]
- Wang, C.; Le, T.D.; Huynh, N.T. Optimal rigid-flexible dynamic of space slider-crank mechanism with clearance joints. Sādhanā 2023, 48, 44. [Google Scholar] [CrossRef]
- Cirelli, M.; Autiero, M.; Belfiore, N.P.; Paoli, G.; Pennestrì, E.; Valentini, P.P. Review and comparison of empirical friction coefficient formulation for multibody dynamics of lubricated slotted joints. Multibody Syst. Dyn. 2024, 63, 83–104. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Y.; Zhang, X.; Cao, S.; Liu, Z. Dynamic characteristic of rudder loop with rough revolute joint clearance. Nonlinear Dyn. 2024, 112, 3179–3194. [Google Scholar] [CrossRef]
- Bai, Z.; Liu, T.; Li, J.; Zhao, J. Numerical and experimental study on dynamic characteristics of planar mechanism with mixed clearances. Mech. Based Des. Struct. Mach. 2023, 51, 6142–6165. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, Y.; Yang, J. Dynamic modeling and analysis of vehicle scissor door mechanism with mixed clearance based on a hybrid contact force model. Multibody Syst. Dyn. 2024, 61, 509–538. [Google Scholar] [CrossRef]
- Chouaibi, Y.; Chebbi, A.H.; Affi, Z.; Romdhane, L. Precision comparison of two 3-DoF translational parallel manipulators based on the orientation errors due to joint clearances. Robotica 2022, 40, 3751–3767. [Google Scholar] [CrossRef]
- Korayem, M.H.; Ghariblu, H.; Basu, A. Dynamic Load Carrying Capacity of Mobile-Base Flexible Joint Manipulators. Int. J. Adv. Manuf. Technol. 2005, 25, 62–70. [Google Scholar] [CrossRef]
- Song, N.; Peng, H.; Kan, Z. Nonsmooth strategy for rigid-flexible multibody system considering different types of clearance joints and lubrication. Multibody Syst. Dyn. 2022, 55, 341–374. [Google Scholar] [CrossRef]
- Wang, Z.; Jin, G.; Liang, D.; Wei, Z.; Chang, B.; Zhou, Y. Nonlinear analysis of complex mechanisms with multi-clearances considering dry friction and lubricated joints. Nonlinear Dyn. 2023, 111, 10911–10938. [Google Scholar] [CrossRef]
- Jiang, J.; Yang, W.; Wei, H.; Peng, B. Distribution Analysis of Multiple Limit Cycles of Vehicle Shimmy System with Consideration of Joint Clearances. Mech. Solids 2022, 57, 1467–1474. [Google Scholar] [CrossRef]
- Wu, X.; Sun, Y.; Wang, Y.; Chen, Y. Passive chaos suppression for the planar slider-crank mechanism with a clearance joint by attached vibro-impact oscillator. Mech. Mach. Theory 2022, 174, 104882. [Google Scholar] [CrossRef]
- Yang, L.; Li, J.; Zhou, X.; Jiang, C. Optimized trajectory tracking control of the clearance manipulator based on improved PSO algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 6424–6439. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhuang, X.; Yu, T. Time-dependent reliability analysis of planar mechanisms considering truncated random variables and joint clearances. Probabilistic Eng. Mech. 2024, 75, 103552. [Google Scholar] [CrossRef]
- Jiang, X.; Bai, Z. Dynamic analysis for mechanical system with clearance joint considering dependent interval parameters. Mech. Based Des. Struct. Mach. 2024, 52, 2726–2748. [Google Scholar] [CrossRef]
- Jia, Y.; Chen, X.; Zhang, L.; Ning, C. Dynamic characteristics and reliability analysis of parallel mechanism with clearance joints and parameter uncertainties. Meccanica 2023, 58, 813–842. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, Y.; Chen, J. Dynamics analysis of planar mechanical system considering revolute clearance joint wear. Tribol. Int. 2013, 64, 85–95. [Google Scholar] [CrossRef]
- Su, Y.; Chen, W.; Tong, Y.; Xie, Y. Wear prediction of clearance joint by integrating multi-body kinematics with finite-element method. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 815–823. [Google Scholar] [CrossRef]
- Zhuang, X.; Yu, T.; Sun, Z.; Song, K. Wear prediction of a mechanism with multiple joints based on ANFIS. Eng. Fail. Anal. 2021, 119, 104958. [Google Scholar] [CrossRef]
- Mukras, S.; Kim, N.H.; Mauntler, N.A.; Schmitz, T.L.; Sawyer, W.G. Analysis of planar multibody systems with revolute joint wear. Wear 2010, 268, 643–652. [Google Scholar] [CrossRef]
- López-Lombardero, M.; Cuadrado, J.; Cabello, M.; Martinez, F.; Dopico, D.; López-Varela, A. A multibody-dynamics based method for the estimation of wear evolution in the revolute joints of mechanisms that considers link flexibility. Mech. Mach. Theory 2024, 2024, 105583. [Google Scholar] [CrossRef]
- Wang, Z.; Jin, G.; Wei, Z.; Liang, D.; Chang, B.; Zhou, Y. Research on irregular wear mechanism of planar multi-body mechanical system with multi-clearance joints. Adv. Mech. Eng. 2022, 14, 1–16. [Google Scholar] [CrossRef]
- Ordiz, M.; Cuadrado, J.; Cabello, M.; Retolaza, I.; Martinez, F.; Dopico, D. Prediction of fatigue life in multibody systems considering the increase of dynamic loads due to wear in clearances. Mech. Mach. Theory 2021, 160, 104293. [Google Scholar] [CrossRef]
- Li, B.; Wang, M.; Gantes, C.J.; Tan, U.-X. Modeling and simulation for wear prediction in planar mechanical systems with multiple clearance joints. Nonlinear Dyn. 2022, 108, 887–910. [Google Scholar] [CrossRef]
- Jiang, D.; Han, Y.; Wang, K.; Jiang, S.; Cui, W.; Song, B. Functional degradation reliability analysis for non-uniform wear of multi-rotating joints of mechanical structures. Eng. Fail. Anal. 2024, 157, 107934. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, Z.; Dai, X. Modeling and prediction of wear at revolute clearance joints in flexible multibody systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 317–329. [Google Scholar] [CrossRef]
- Gao, S.; Fan, S.W.; Fan, S. Optimization research on dynamic behavior for mechanism with clearance joint and wear. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 6871–6891. [Google Scholar] [CrossRef]
- Zhuang, X.; Yu, T.; Liu, J.; Song, B. Kinematic reliability evaluation of high-precision planar mechanisms experiencing non-uniform wear in revolute joints. Mech. Syst. Signal Process. 2022, 169, 108748. [Google Scholar] [CrossRef]
- Zhuang, X. Time-dependent kinematic reliability of a dual-axis driving mechanism for satellite antenna considering non-uniform planar revolute joint clearance. Acta Astronaut. 2022, 197, 91–106. [Google Scholar] [CrossRef]
- Liu, J.; Xue, S.; Zhang, K.; Pang, H. Failure modeling and reliability analysis for motion mechanism with clearance joints under plastic deformation and wear. Eksploat. I Niezawodn. Maint. Reliab. 2023, 25, 169920. [Google Scholar] [CrossRef]
- Hou, Y.; Deng, Y.; Zeng, D. Dynamic modelling and properties analysis of 3RSR parallel mechanism considering spherical joint clearance and wear. J. Cent. South Univ. 2021, 28, 712–727. [Google Scholar] [CrossRef]
- Askari, E.; Flores, P. Coupling multi-body dynamics and fluid dynamics to model lubricated spherical joints. Arch. Appl. Mech. 2020, 90, 2091–2111. [Google Scholar] [CrossRef]
- Marques, F.; Isaac, F.; Dourado, N.; Flores, P. An enhanced formulation to model spatial revolute joints with radial and axial clearances. Mech. Mach. Theory 2017, 116, 123–144. [Google Scholar] [CrossRef]
- Jin, G.; Wang, Z.; Liang, D.; Wei, Z.; Chang, B.; Zhou, Y. Modeling and dynamics characteristics analysis of six-bar rocking feeding mechanism with lubricated clearance joint. Arch. Appl. Mech. 2023, 93, 2831–2854. [Google Scholar] [CrossRef]
- Lou, J.; Li, C. An improved model of contact collision investigation on multi-body systems with revolute clearance joints. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 2103–2112. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, M.; Liu, Y.; Huang, Y. Dynamics analysis and wear prediction of rigid-flexible coupling deployable solar array system with clearance joints considering solid lubrication. Mech. Syst. Signal Process. 2022, 162, 108059. [Google Scholar] [CrossRef]
- Erkaya, S.; Ibrahim, U. Modeling and simulation of joint clearance effects on mechanisms having rigid and flexible links. J. Mech. Sci. Technol. 2014, 28, 2979–2986. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov Exponents from a Time Series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]

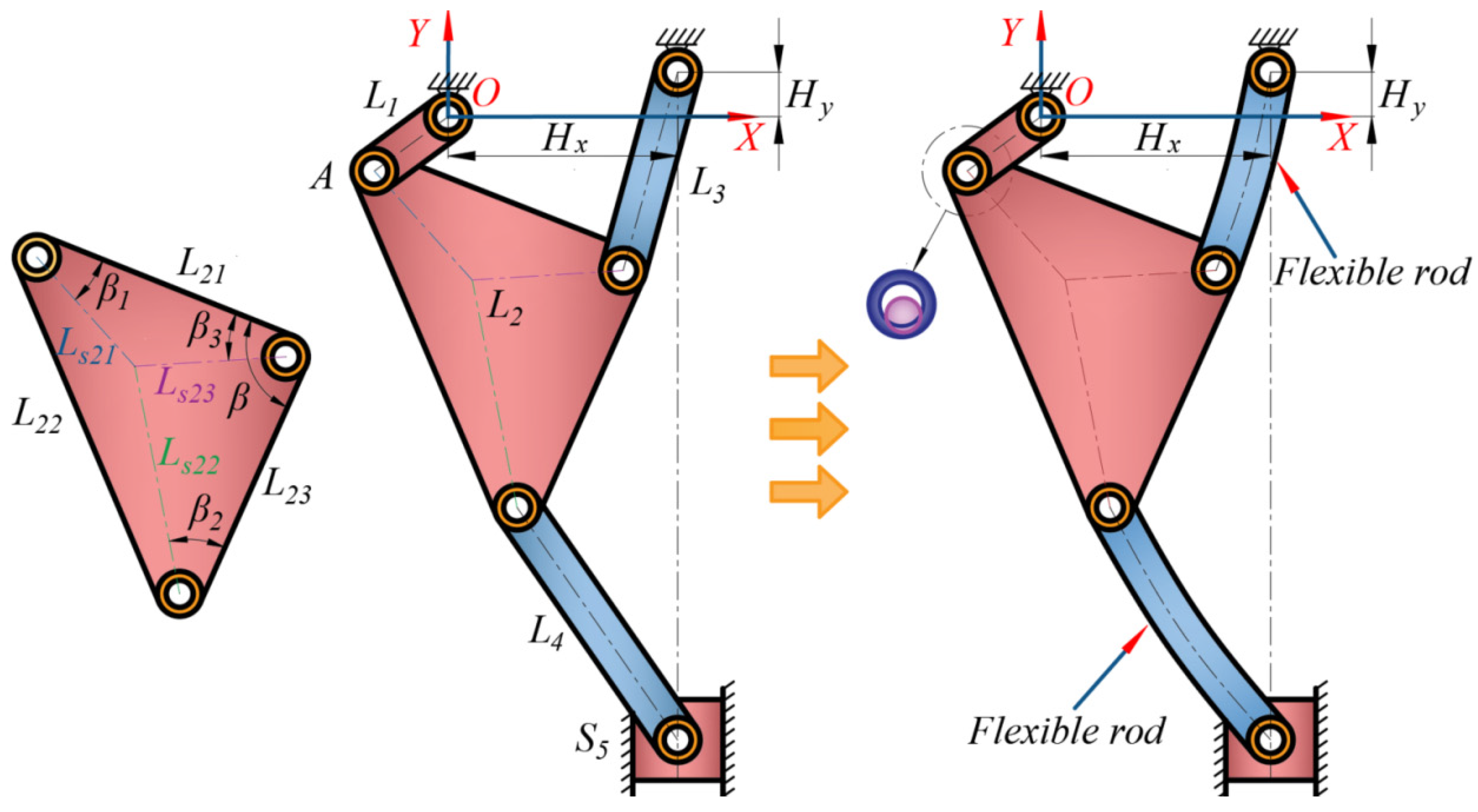




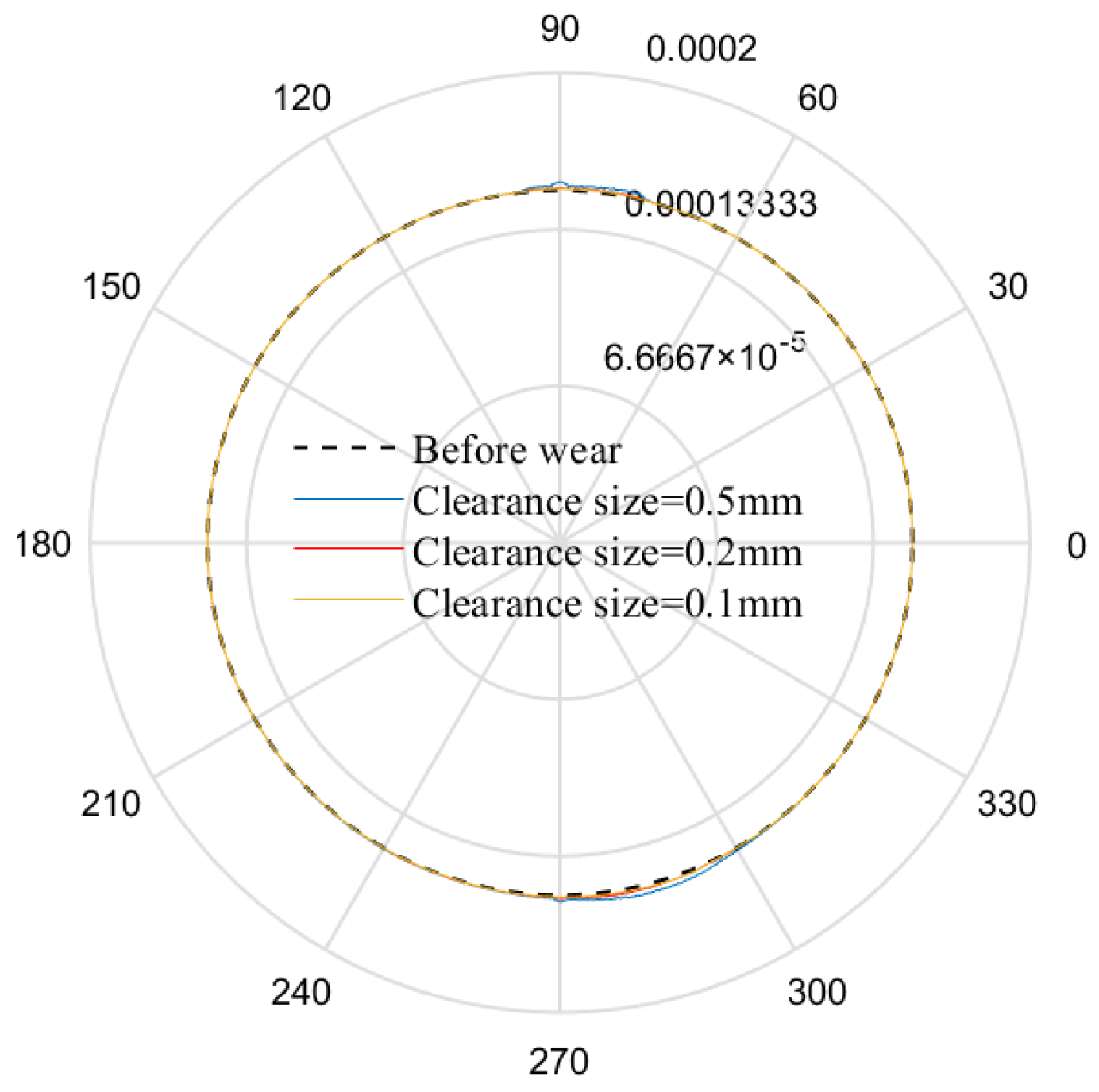
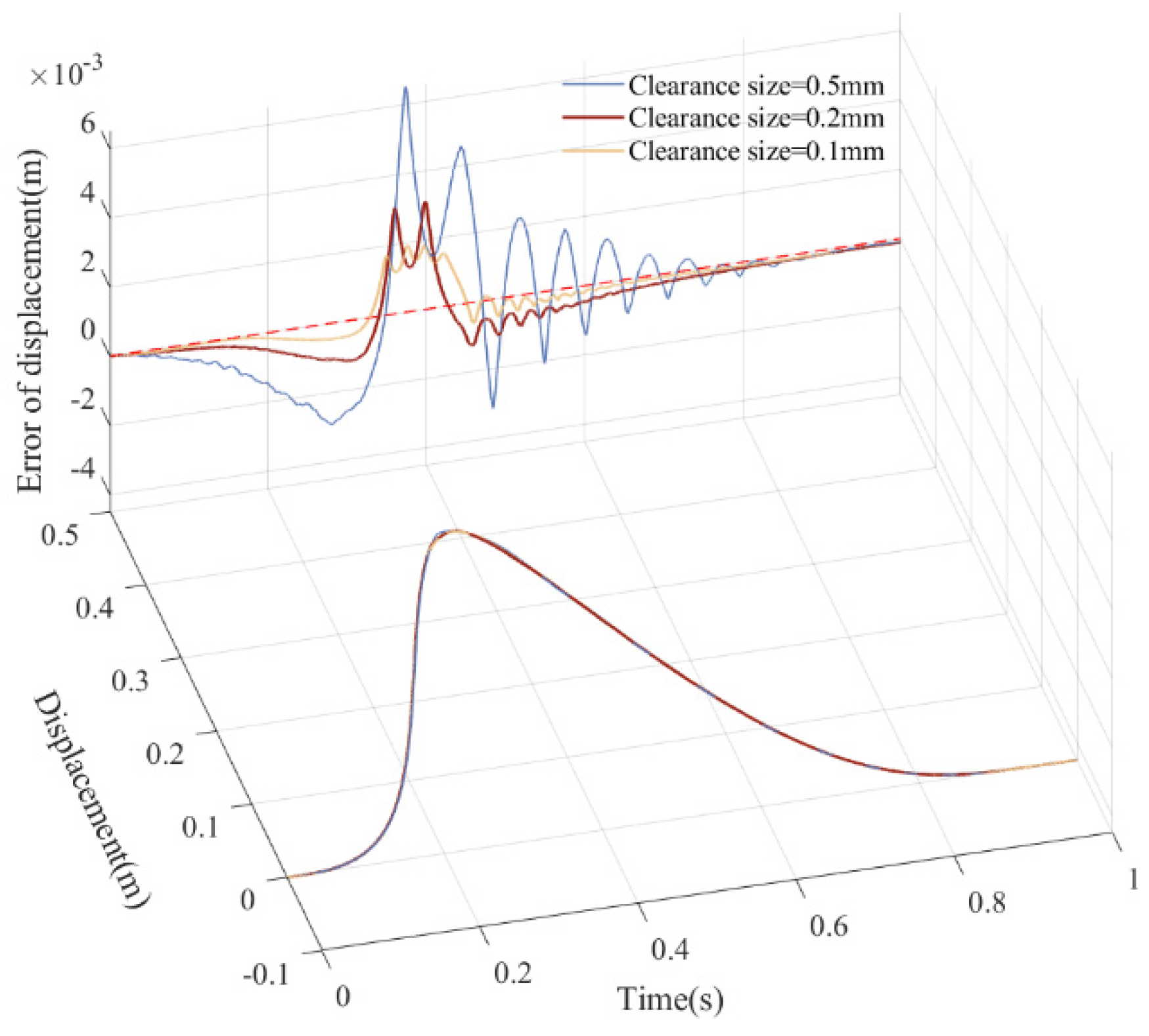
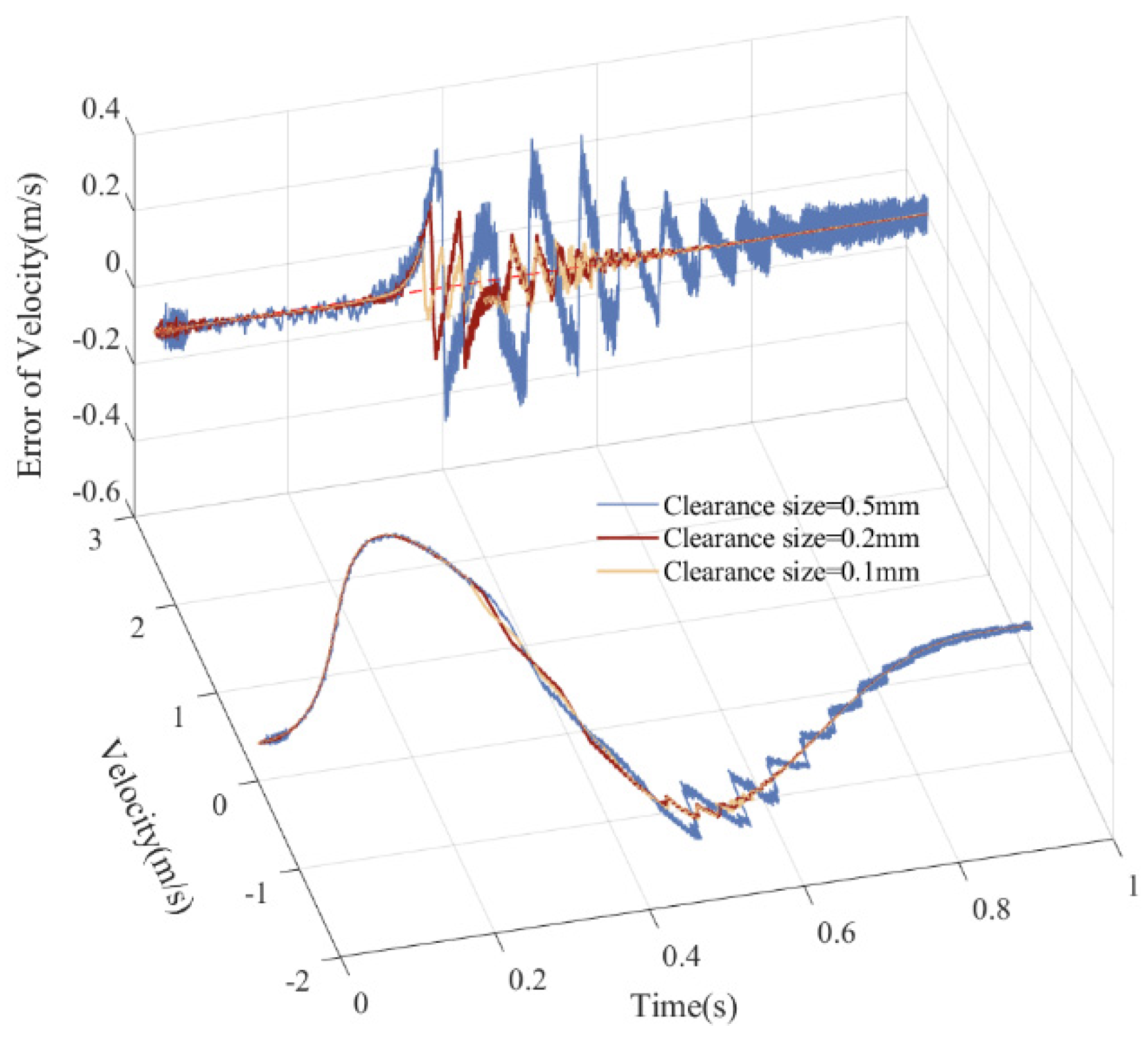

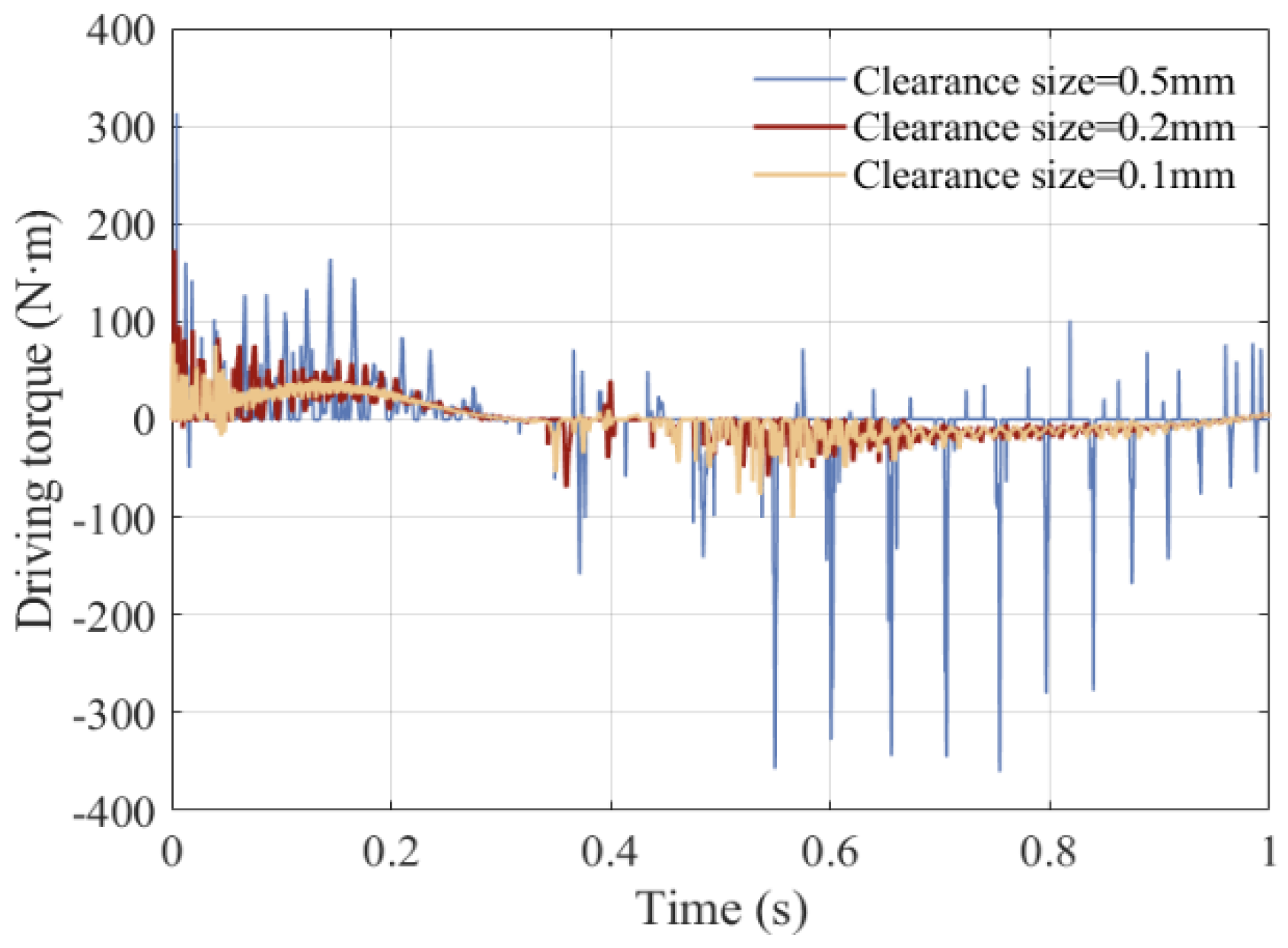
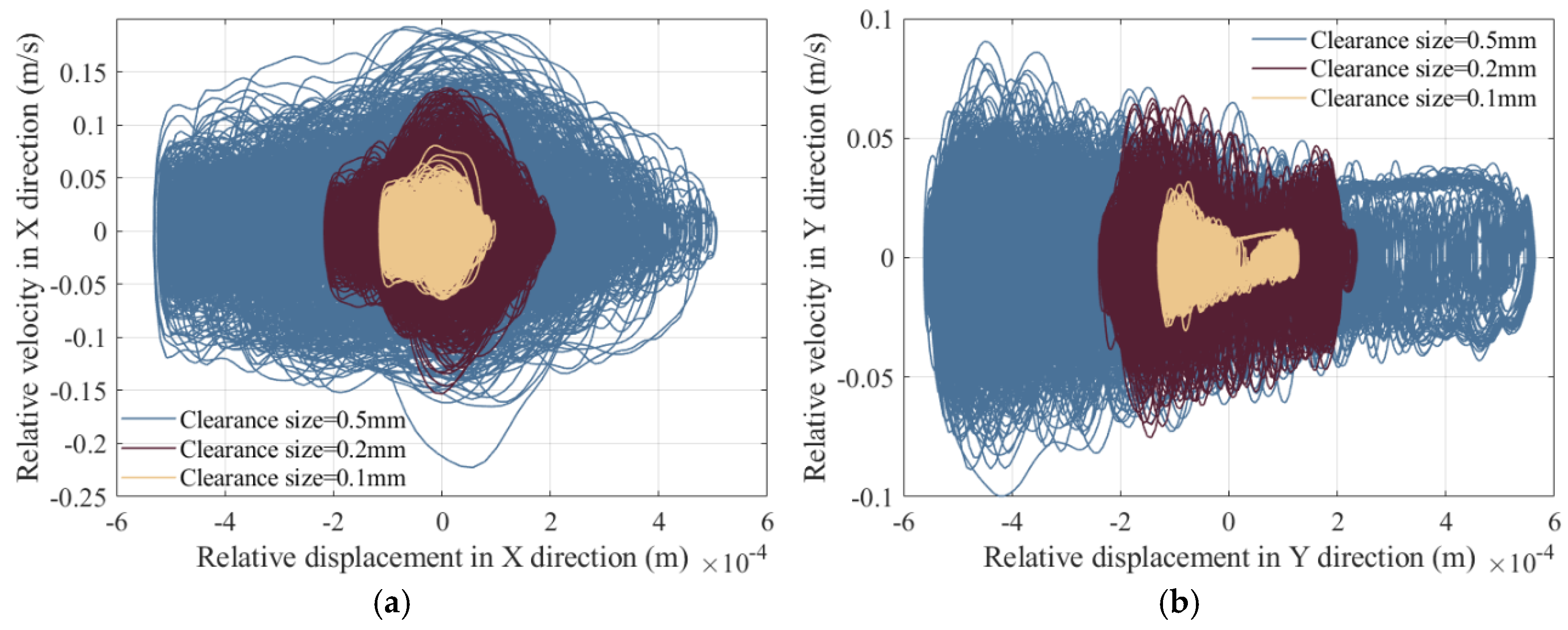
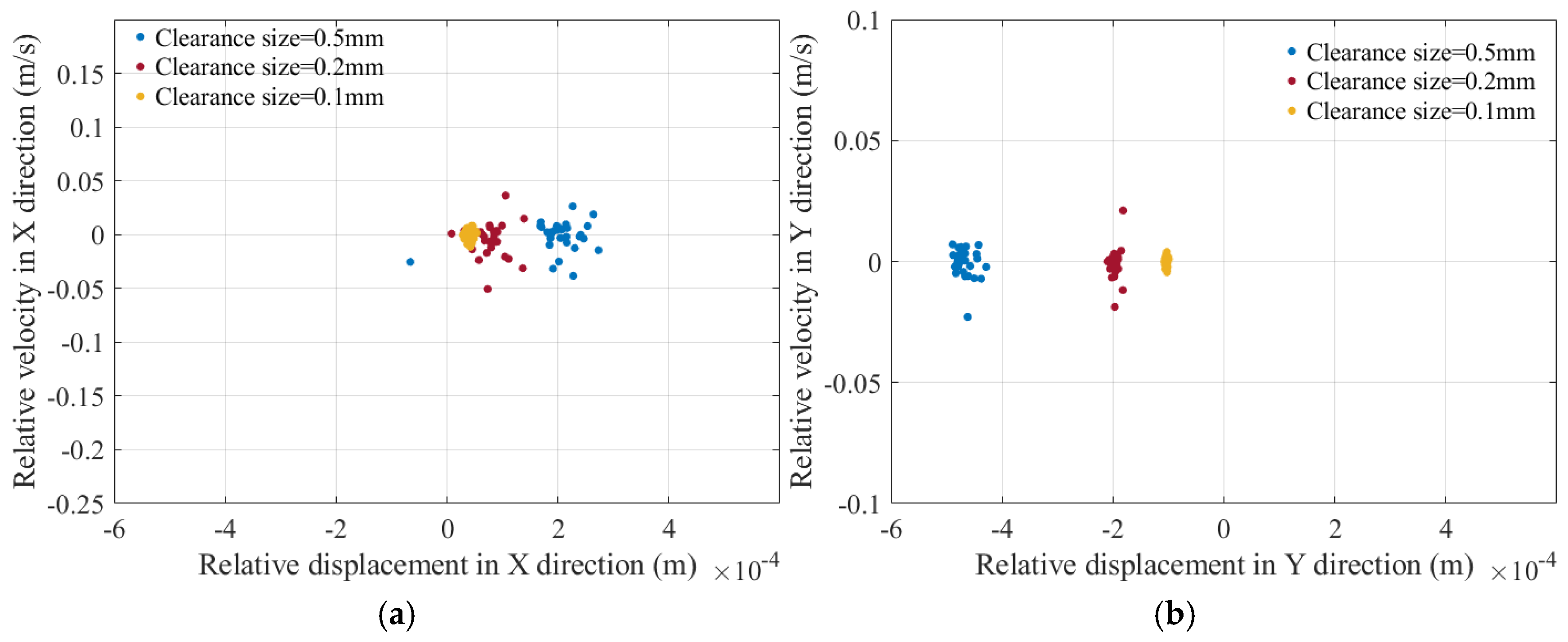
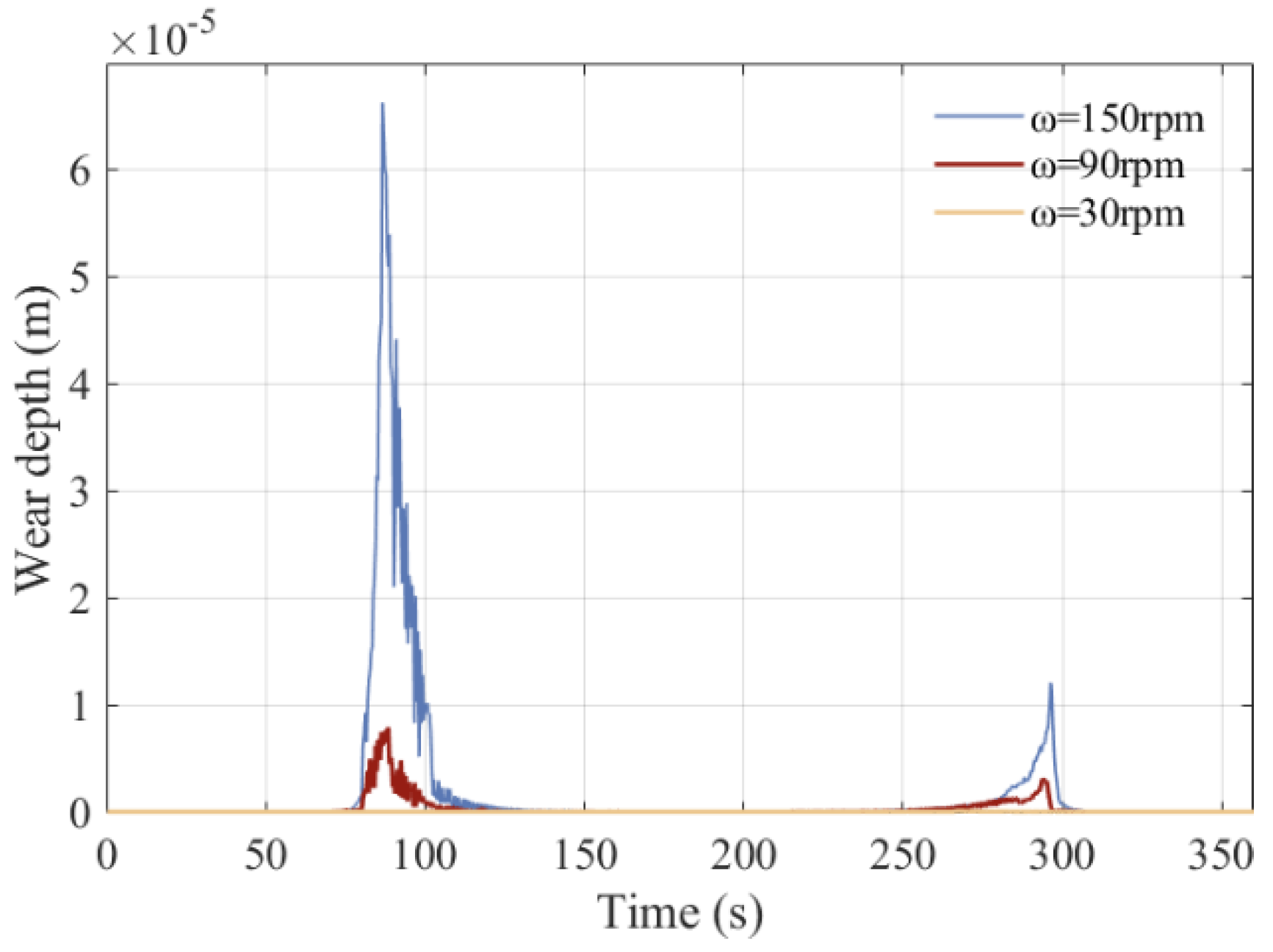

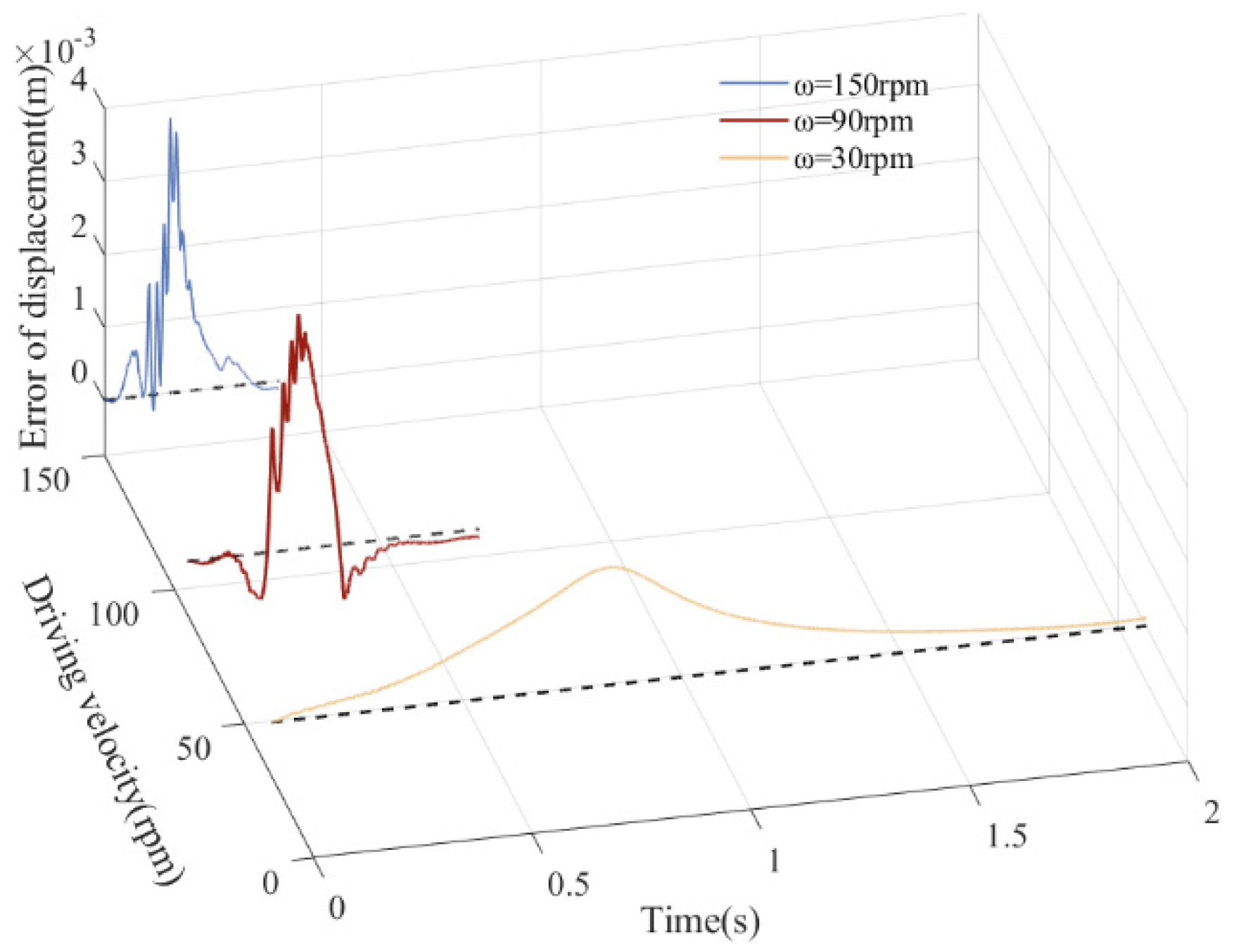


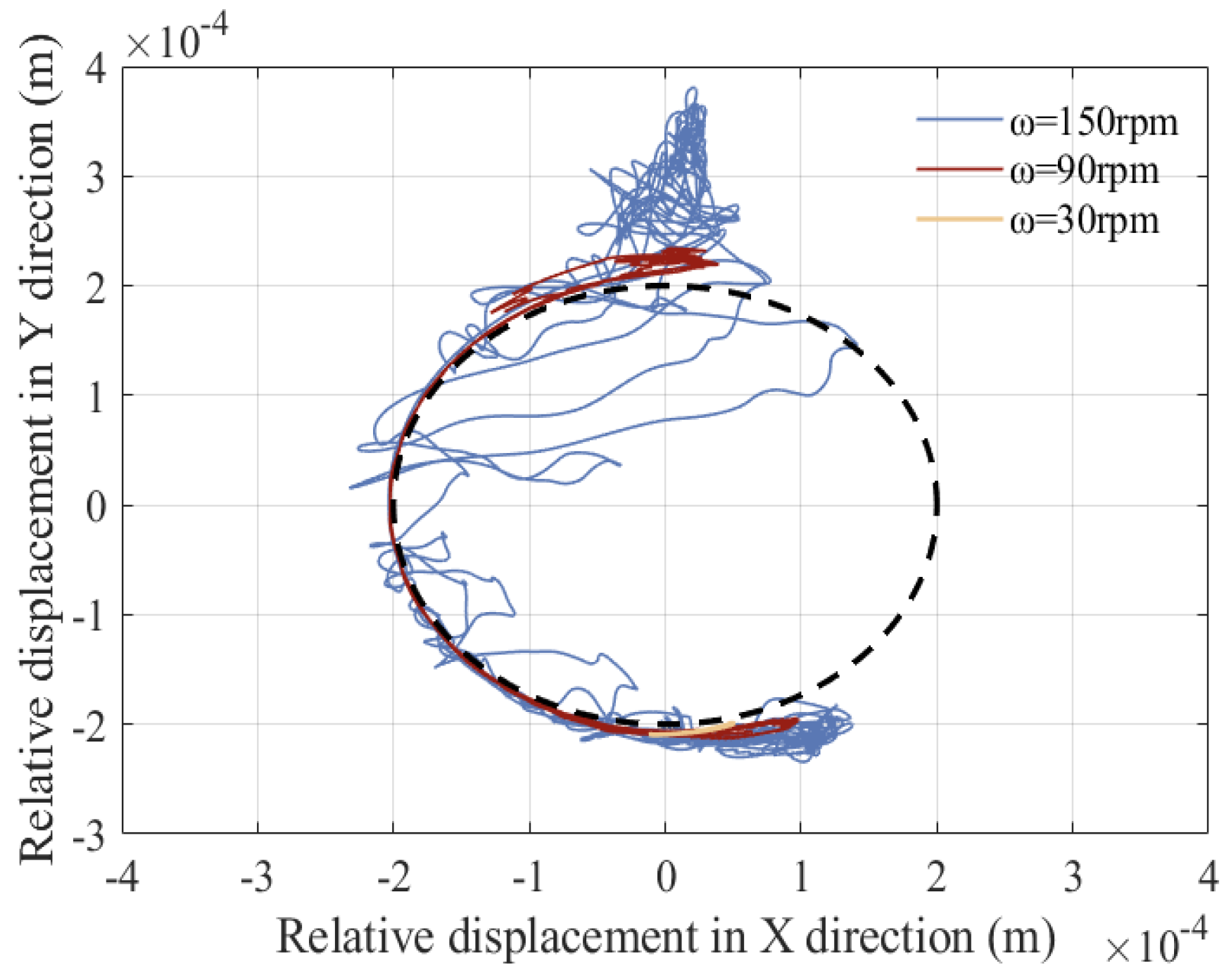
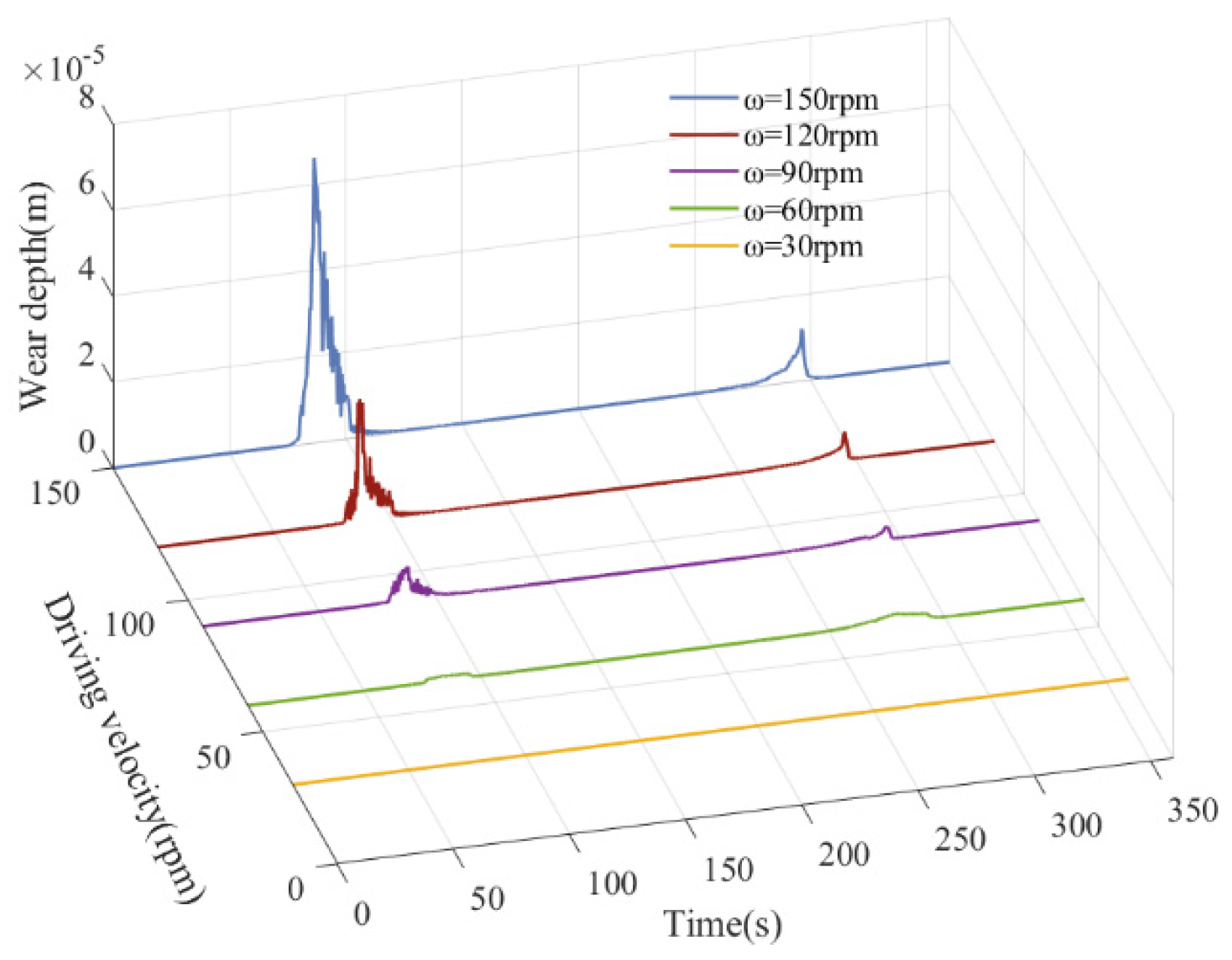


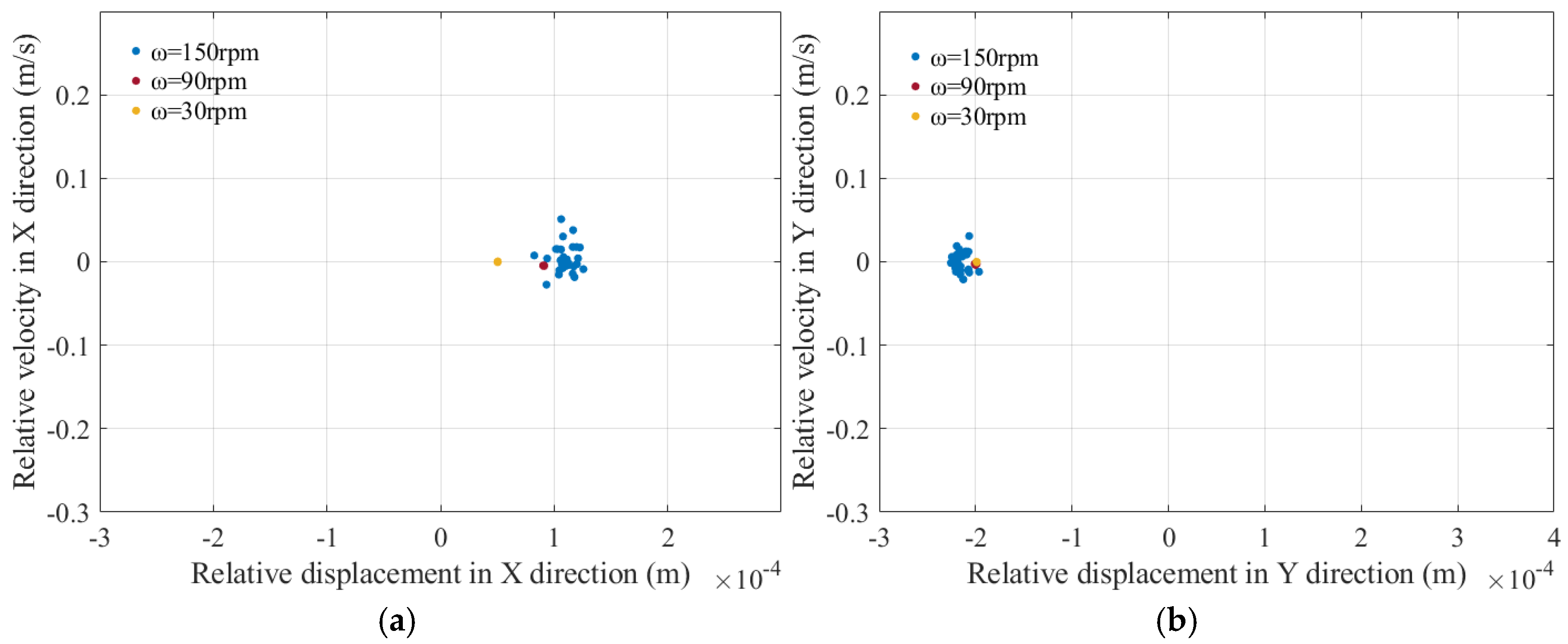
| Parameter | Values | Parameter | ||
|---|---|---|---|---|
| Mass of crank 1 (m1/kg) | 0.738 | Moment of inertia of crank 1 (J1/kg·m3) | 1.977 × 10−9 | |
| Mass of triangle plate 2 (m2/kg) | 21.483 | Moment of inertia of triangle plate 2 (J2/kg·m3) | 1348.94 × 10−9 | |
| Mass of rod 3 (m3/kg) | 4.708 | Moment of inertia of rod 3 (J3/kg·m3) | 546.91 × 10−9 | |
| Mass of rod 4 (m4/kg) | 3.663 | Moment of inertia of rod 4 (J4/kg·m3) | 69.26 × 10−9 | |
| Mass of slider 5 (m5/kg) | 0.922 | Moment of inertia of slider 5 (J5/kg·m3) | 1.059 × 10−9 | |
| Length of crank 1 (L1/mm) | 75 | Dimensions of the rack (Hx/mm) | 350 | |
| Length of triangle plate 2 | (L21/mm) | 555.14 | Dimensions of the rack (Hy/mm) | 60 |
| (L22/mm) | 985 | Second moment of area (I/m4) | 3.33 × 10−8 | |
| (L23/mm) | 473.66 | Cross section area (A/m2) | 0.05 × 0.02 | |
| Length of rod 3 (L3/mm) | 584 | Density (ρ/kg/m3) | 780 | |
| Length of rod 4 (L4/mm) | 450 | Wear coefficient (k) | 1.827 × 10−13 [23] | |
| Bearing radius (R1/mm) | 15 | Axial contact length of joint (L/mm) | 11 | |
| Restitution coefficient (ce) | 0.9 | Baumgarte feedback parameter α | 50 | |
| Poisson ratio (ν1, ν2) | 0.3 | Baumgarte feedback parameter β | 50 | |
| Friction coefficient (cf) | 0.15 [22] | Integral tolerance | 0.00001 [43] | |
| Elastic modulus (E1, E2/GPa) | 207 | Integral step/s | (2π/ω)/10,000 | |
| Parameter | 4 | 8 | 12 | 16 | 20 | 24 |
|---|---|---|---|---|---|---|
| Strain of rod 3 (μm) | 33.17 | 42.41 | 46.20 | 43.41 | 45.38 | 44.26 |
| Strain of rod 4 (μm) | −22.02 | −15.14 | −12.23 | −13.33 | −12.50 | −13.56 |
| Parameter | Displacement Error (mm) | Speed Error (m/s) | Contact Force (kN) | Embedding Depth(mm) | Strain of Rod 3 (μm) | Strain of Rod 4 (μm) | Driving Torque (N·m) |
|---|---|---|---|---|---|---|---|
| Before wear | 2.771 | 0.3825 | 9.182 | 0.0803 | 43.41 | −13.33 | −478.5 |
| After wear | 3.765 | 0.6016 | 23.33 | 0.146 | 97.14 | −22.6 | −799.7 |
| Parameter | Displacement Error (mm) | Speed Error (m/s) | Contact Force (kN) | Embedding Depth (mm) | Strain of Rod 3 (μm) | Strain of Rod 4 (μm) | Driving Torque (N·m) |
|---|---|---|---|---|---|---|---|
| 0.1 mm | 1.917 | 0.1316 | 2.441 | 0.031 | −12.49 | −2.419 | −100.5 |
| 0.2 mm | 3.124 | 0.2317 | 3.846 | 0.045 | −21.03 | −5.662 | 173.7 |
| 0.5 mm | 6.532 | 0.3655 | 6.853 | 0.066 | −33.31 | −10.51 | −357.3 |
| Parameter | Displacement Error (mm) | Speed Error (m/s) | Contact Force (kN) | Embedding Depth (mm) | Strain of Rod 3 (μm) | Strain of Rod 4 (μm) | Driving Torque (N·m) |
|---|---|---|---|---|---|---|---|
| 30 rpm | 1.607 | 0.011 | 2.14 | 0.0305 | −9.086 | 1.283 | 116.9 |
| 90 rpm | 3.216 | 0.23 | 6.12 | 0.0538 | 24.57 | −7.623 | 219.1 |
| 150 rpm | 3.765 | 0.6016 | 23.33 | 0.146 | 97.14 | −22.6 | −799.7 |
| Parameter | Status | Time Delay | Embedding Dimensions | MLE |
|---|---|---|---|---|
| X direction | Before wear | 24 | 5 | 0.001 |
| After wear | 24 | 6 | 0.0042 | |
| Y direction | Before wear | 10 | 11 | −0.01 |
| After wear | 12 | 10 | 0.0047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Meng, K.; Jiang, S.; Kang, J. Wear Prediction and Chaos Identification of Rigid Flexible Coupling Multi-Link Mechanisms with Clearance. Lubricants 2025, 13, 130. https://doi.org/10.3390/lubricants13030130
Jia Y, Meng K, Jiang S, Kang J. Wear Prediction and Chaos Identification of Rigid Flexible Coupling Multi-Link Mechanisms with Clearance. Lubricants. 2025; 13(3):130. https://doi.org/10.3390/lubricants13030130
Chicago/Turabian StyleJia, Yonghao, Kai Meng, Shuai Jiang, and Jing Kang. 2025. "Wear Prediction and Chaos Identification of Rigid Flexible Coupling Multi-Link Mechanisms with Clearance" Lubricants 13, no. 3: 130. https://doi.org/10.3390/lubricants13030130
APA StyleJia, Y., Meng, K., Jiang, S., & Kang, J. (2025). Wear Prediction and Chaos Identification of Rigid Flexible Coupling Multi-Link Mechanisms with Clearance. Lubricants, 13(3), 130. https://doi.org/10.3390/lubricants13030130





