Comparative Study of Friction Models in High-Speed Machining of Titanium Alloys
Abstract
1. Introduction
2. Modelling and Simulation
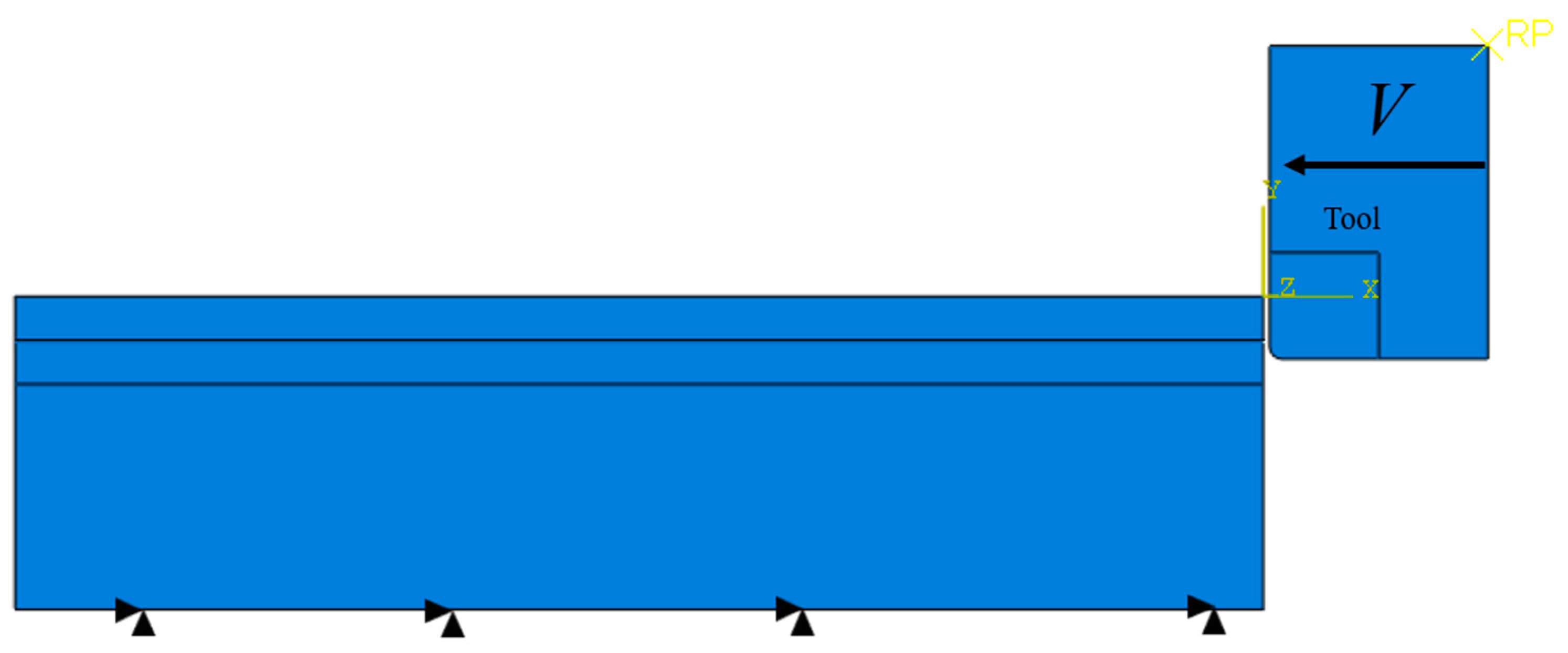
2.1. Orthogonal Cutting Model
2.2. Constitutive Model
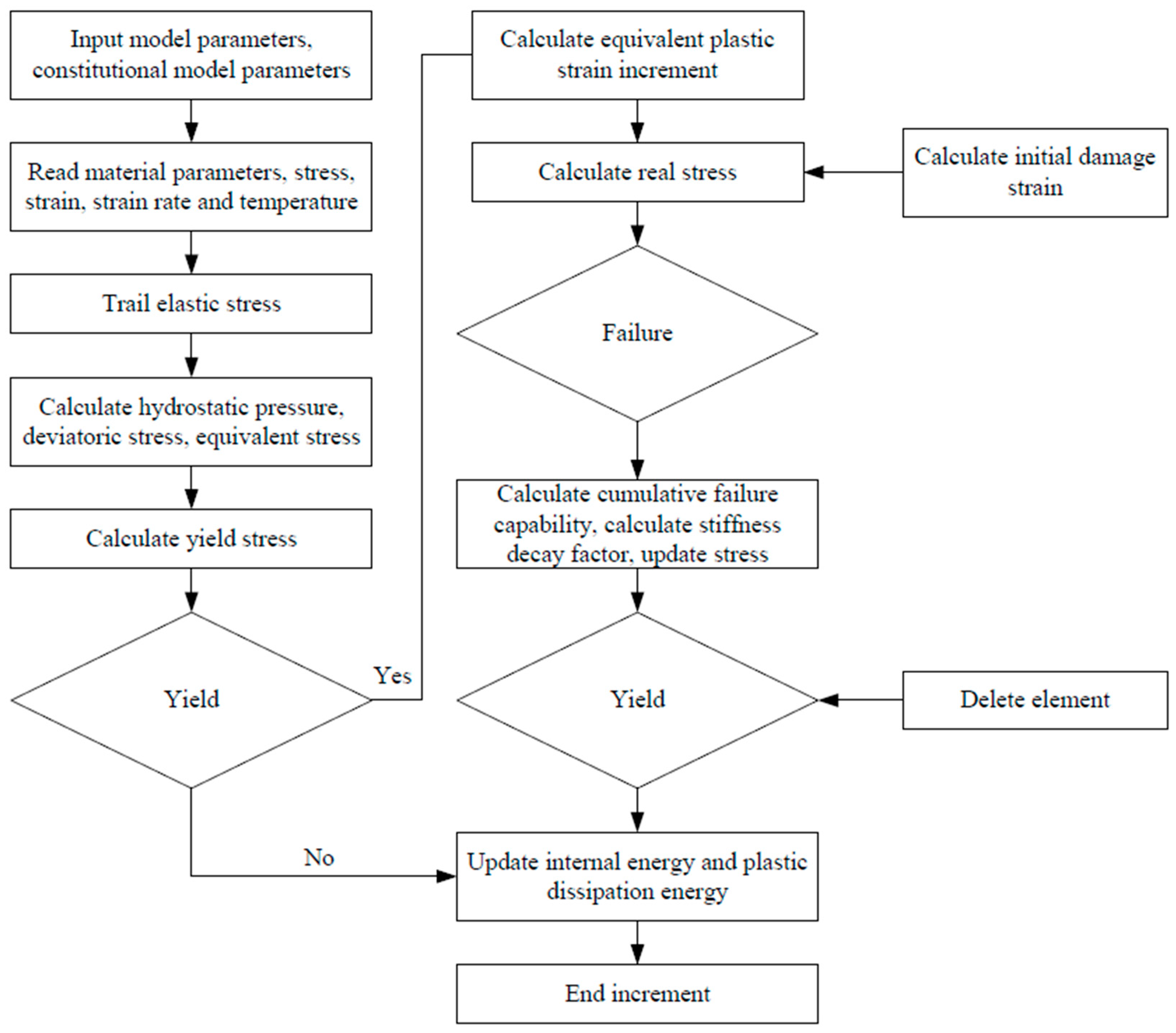
2.3. Damage Model
2.4. Tool–Chip Friction Model
2.4.1. Contact Modelling
2.4.2. Zorev’s Friction Model
2.4.3. Velocity-Dependent Friction Model
2.4.4. Temperature Dependent Friction Model
3. Experimental Orthogonal Cutting Tests
4. Results and Discussion
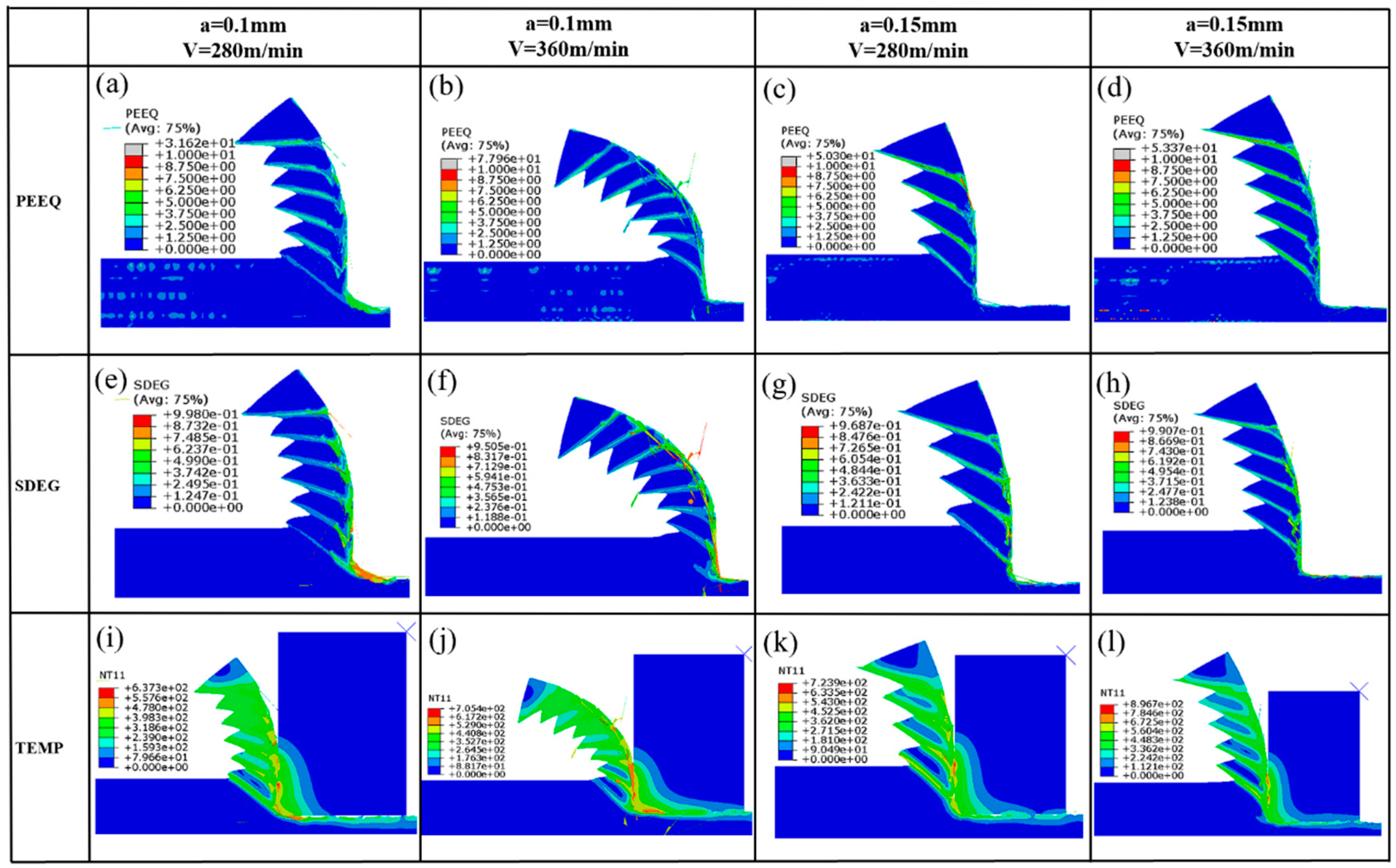
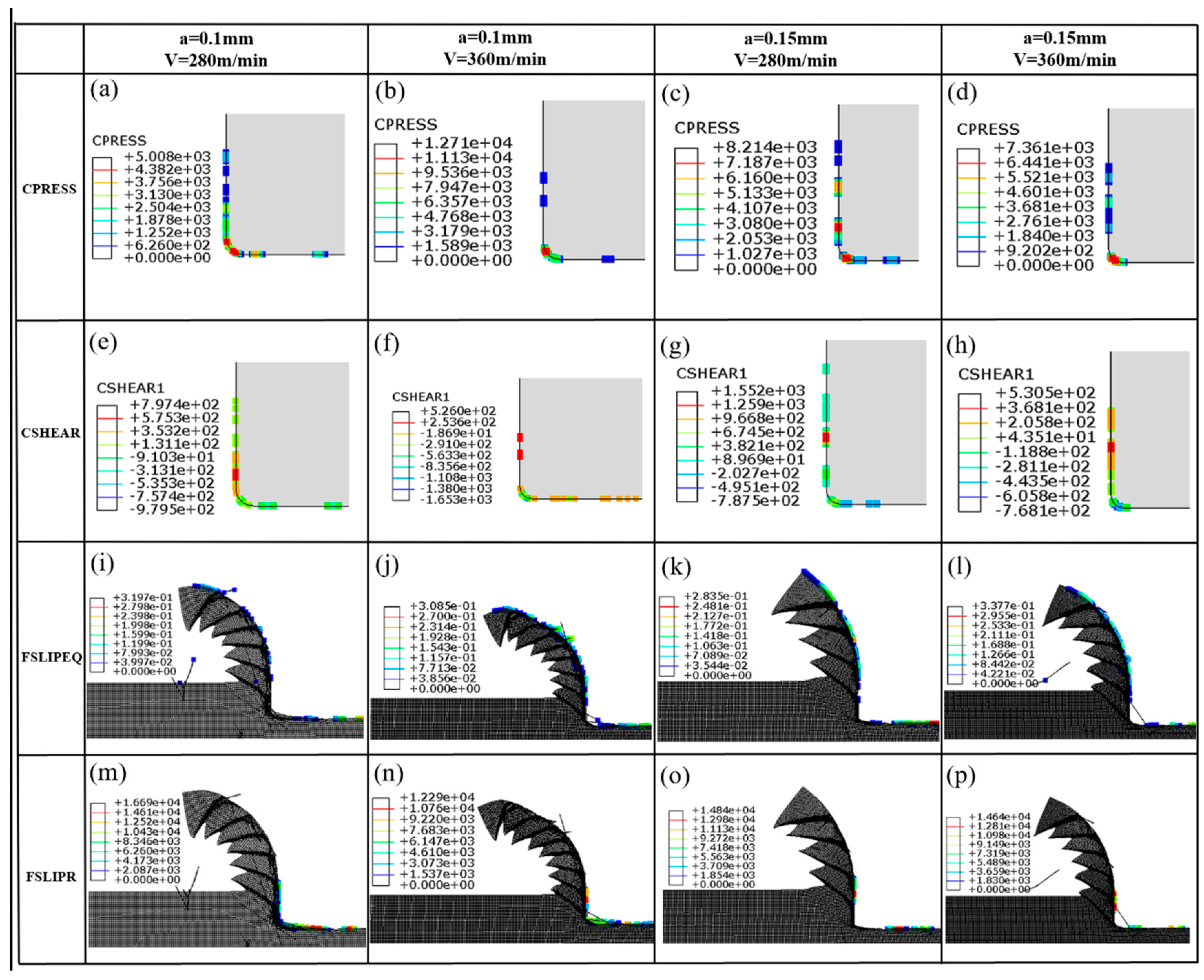
4.1. Results
4.2. Discussion
5. Conclusions
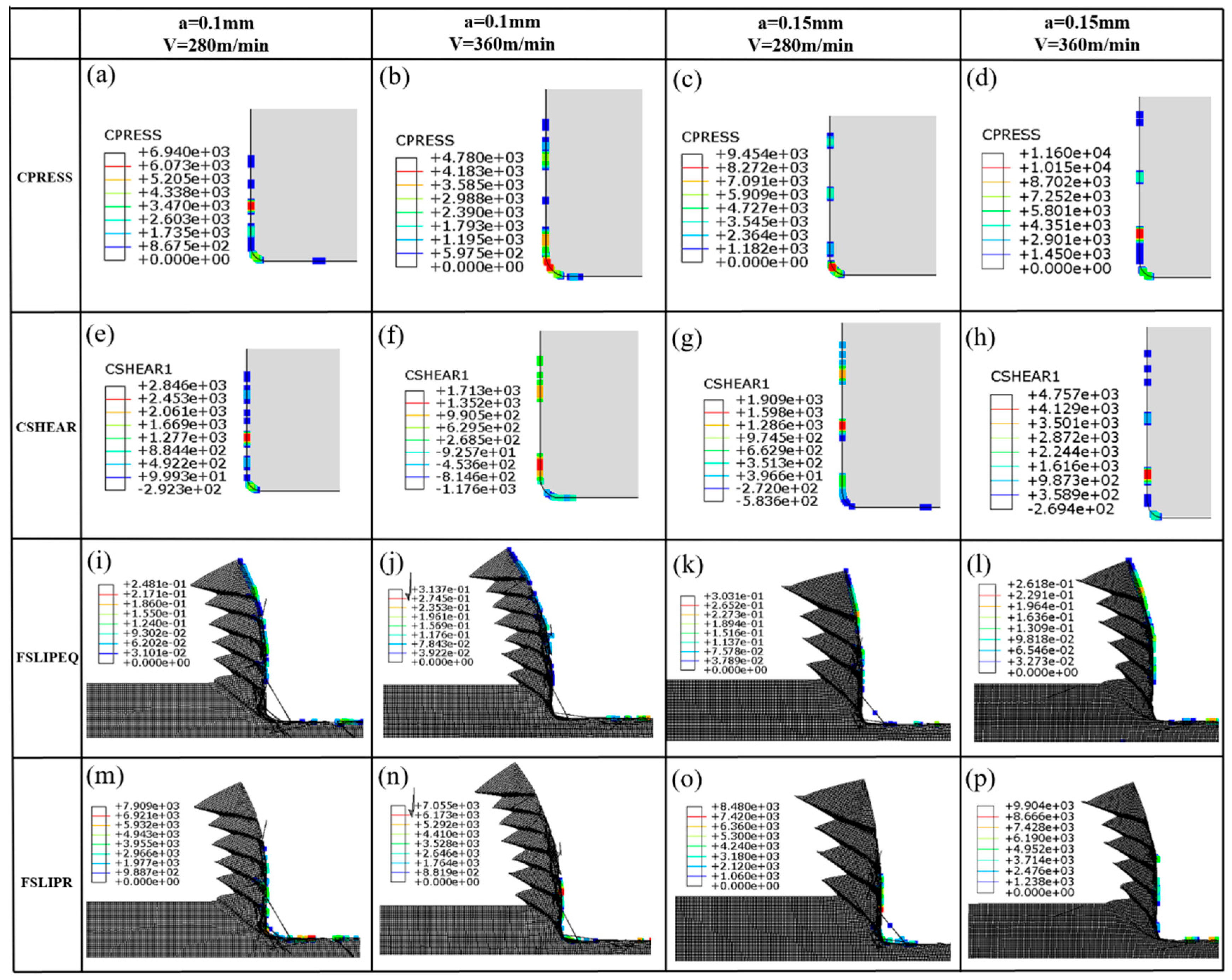
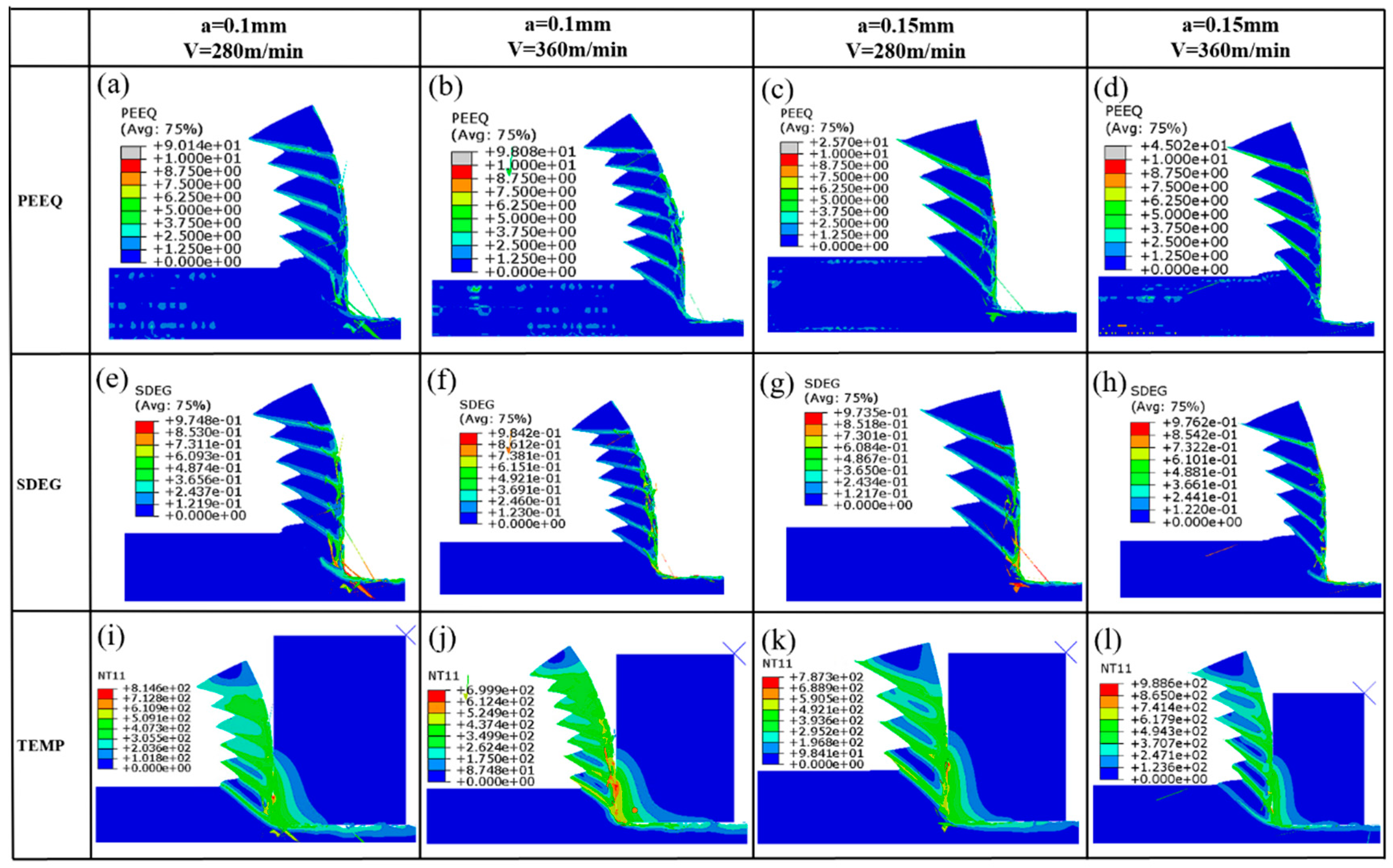
- Friction models exert direct influence on factors such as the relative sliding velocity at the contact interface, cumulative sliding distance, contact pressure, and frictional shear stress. These factors, in turn, modify the generation of frictional heat and subsequently impact the temperature distribution. Additionally, diverse friction models play a role in shaping the process of chip formation, leading to variations in chip morphology and the frequency of sawtooth patterns. The plastic strain of the chip and its stiffness degradation are primarily influenced by the material constitutive model and damage model. The formation of sawtooth-shaped chips is also greatly affected by these models. Compared to the constitutive model, friction models have a lesser impact on the aforementioned parameters.
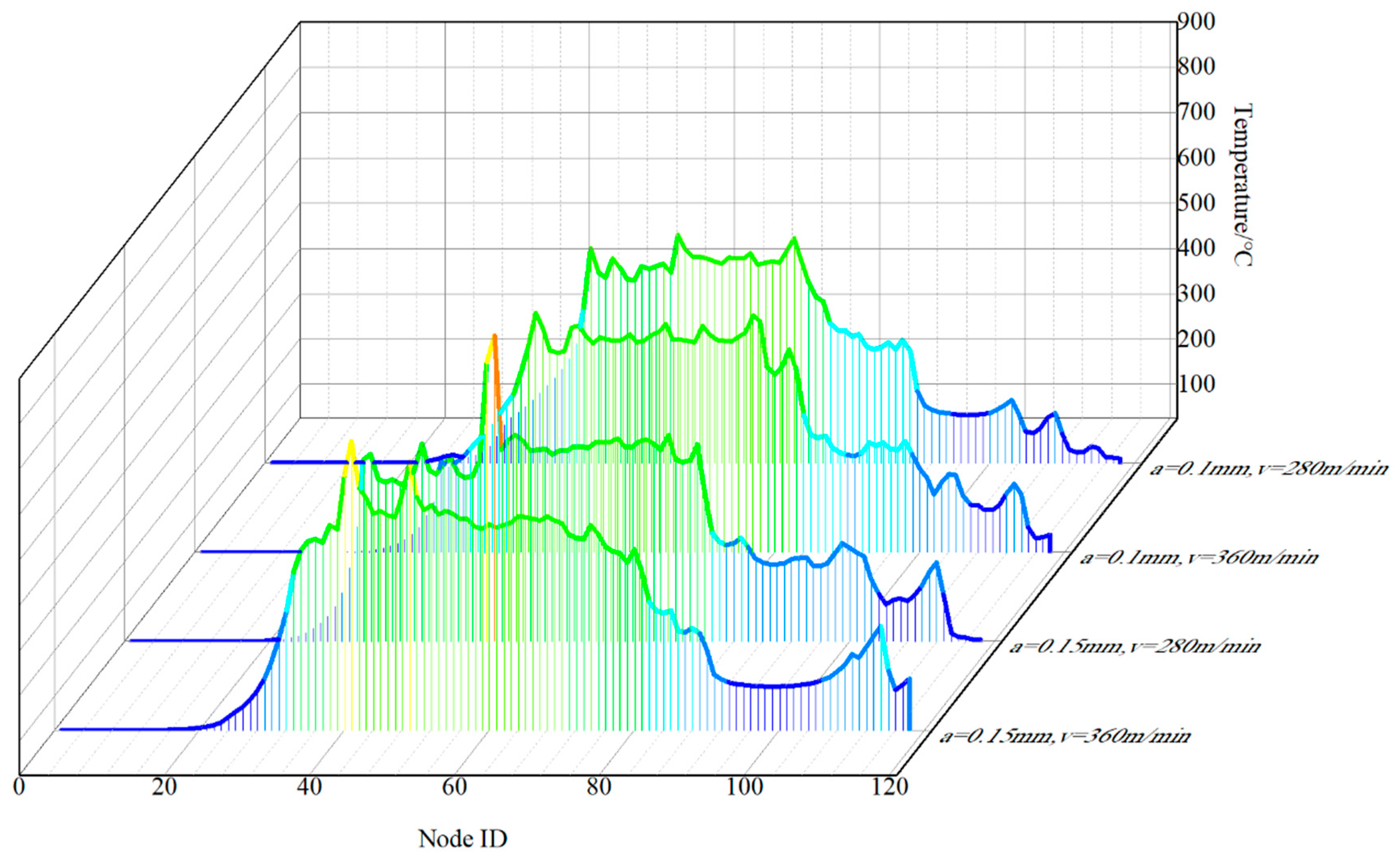
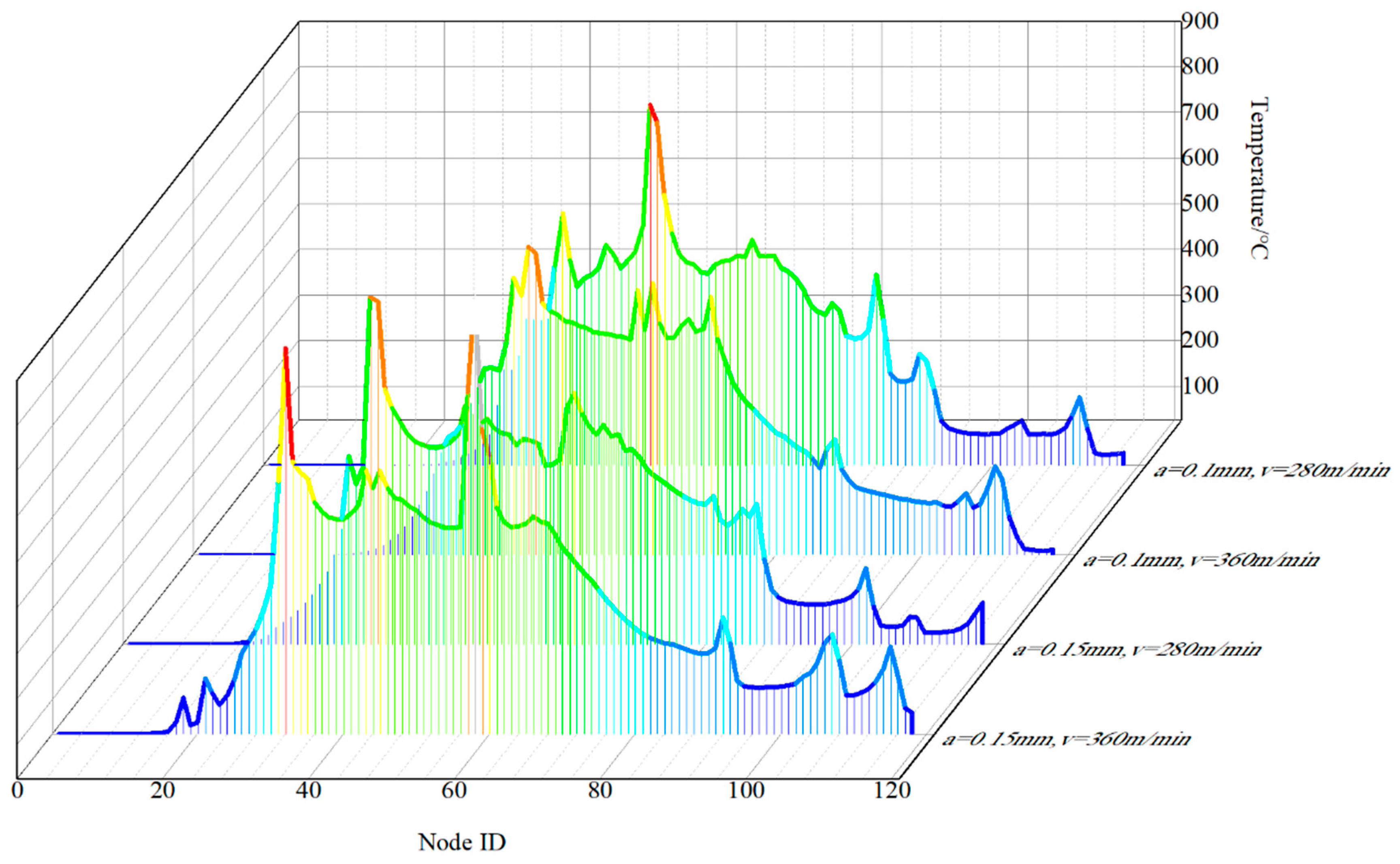
- Friction models play a crucial role in shaping the temperature distribution across the tool surface, with specific operating conditions also influencing this distribution. Adjusting the friction coefficient enables the fine-tuning of parameters such as the contact length between the tool and chip, the extent of high-temperature regions on the tool surface, and the overall fluctuation of temperature during the cutting process. Notably, the friction coefficient displays a heightened sensitivity to sliding speed, while the temperature distribution exhibits a greater sensitivity to the choice of friction model compared to variations in operating conditions.
- Irrespective of enhancements to parameters such as the friction coefficient or the maximum friction shear stress, and irrespective of the incorporation of velocity or temperature-dependent factors, these adjustments impact the fluctuation range, periodicity, and local peaks of the cutting force prediction curves. They contribute to improving prediction accuracy within specific operational contexts to a certain extent. However, it is noteworthy that despite these refinements, the general trend of error fluctuations observed across these friction models remains consistent. Moreover, the predictive accuracy of these models tends to diminish with increasing cutting depth.
- This study provides valuable contributions to both industry and academia by improving the understanding of friction’s impact on titanium alloy machining. The research enhances machining efficiency by optimizing cutting conditions through better understanding of friction’s influence on factors like chip formation, cutting forces, and temperature distribution. This can lead to improved tool life, reduced energy consumption, and better material processing. The study’s insights into friction models can improve predictive capabilities for cutting forces, helping manufacturers optimize machining strategies, reduce trial-and-error experiments, and lower operational costs. Additionally, adjusting friction coefficients to minimize wear and heating can lead to significant material cost reductions. The use of an advanced Johnson–Cook model, which accounts for dynamic recrystallization and softening, advances material behavior simulations, contributing to more accurate predictions in machining. The comparison of different friction models (Zorev’s, velocity-dependent, and temperature-dependent) deepens the academic understanding of friction’s role in machining, providing a foundation for future research. Moreover, the study opens avenues for further exploration into complex cutting phenomena, such as tool wear and chip formation, helping to refine material models and simulation techniques for more accurate predictions in real-world manufacturing. Overall, the study provides practical solutions for industry optimization and theoretical advancements for future research in machining processes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ezugwu, E.O.; Bonney, J.; Yamane, Y. An overview of the machinability of aeroengine alloys. J. Mater. Process. Technol. 2003, 134, 233–253. [Google Scholar] [CrossRef]
- Ezugwu, E.O.; Wang, Z.M. Titanium alloys and their machinability—A review. J. Mater. Process. Technol. 1997, 68, 262–274. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Wang, B. State-of-the-art of surface integrity induced by tool wear effects in machining process of titanium and nickel alloys: A review. Measurement 2019, 132, 150–181. [Google Scholar] [CrossRef]
- Uçak, N.; Çiçek, A.; Outeiro, J.; Aslantas, K.; Çetin, B. Constitutive modelling of Ti-6Al-4V alloy fabricated by laser powder bed fusion and its application to micro cutting simulation. Mech. Mater. 2023, 185, 104756. [Google Scholar] [CrossRef]
- Xi, Y.; Bermingham, M.; Wang, G.; Dargusch, M. SPH/FE modeling of cutting force and chip formation during thermally assisted machining of Ti-6Al-4V alloy. Comput. Mater. Sci. 2014, 84, 188–197. [Google Scholar] [CrossRef]
- Mane, S.; Karagadde, S.; Joshi, S.S.; Kapoor, S.G. Evaluation of an Adhesive Friction Coefficient under Extreme Contact Conditions and Its Application to the Machining Process. Tribol. Trans. 2020, 63, 841–856. [Google Scholar] [CrossRef]
- Dixit, U.; Guduru, R.K.; Rashid, A. Tool wear assessment in dry machining of Ti-6Al-4V using Taguchi approach. Int. J. Interact. Des. Manuf. (IJIDeM) 2024, 1–18. [Google Scholar] [CrossRef]
- Afzal, M.Z.; Khan, S.A.; Raza, S.F.; Naveed, R.; Anwar, S.; Farooq, M.U. Exploring novel PVD coated wiper inserts’ chip breaker designs and feed rates on tool wear and in-depth hole integrity of Ti-6Al-4V alloy when drilling in a dry environment. J. Manuf. Process. 2024, 131, 1667–1685. [Google Scholar] [CrossRef]
- Du, M.; Cheng, Z.; Wang, S. Finite element modeling of friction at the tool-chip-workpiece interface in high speed machining of Ti-6Al-4V. Int. J. Mech. Sci. 2019, 163, 105100. [Google Scholar] [CrossRef]
- Ni, J.; Su, Z.; Tong, K.; Meng, Z.; Li, Z. High performance machining simulation of curved edge broach with surface material constitutive model and tool-chip friction. J. Manuf. Process. 2024, 111, 64–74. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Zhao, L.; Li, G.; Zhang, C.; Zhang, J.; Sun, T. Coupled thermo-mechanical sticking-sliding friction model along tool-chip interface in diamond cutting of copper. J. Manuf. Process. 2021, 70, 578–592. [Google Scholar] [CrossRef]
- Joo, J.; Kim, J.; Yang, S.M.; Park, H.W.; Kim, D.Y. Tool wear evolution and chip formation of the Ti-6Al-4V end milling under cryogenic cooling and minimum quantity lubrication conditions. Int. J. Adv. Manuf. Technol. 2024, 130, 589–602. [Google Scholar] [CrossRef]
- Mohammed, M.; Pervaiz, S.; Deiab, I. A novel finite element model for thermally induced machining of Ti-6Al-4V. Simul. Model. Pract. Theory 2024, 134, 102928. [Google Scholar]
- Zorev, N. Interrelationship between shear processes occurring along tool face and on shear plane in metal cutting. Proc. Int. Res. Prod. Eng. Conf. 1963, 42–49. [Google Scholar]
- Avevor, Y.; Vincent, J.; Faure, L.; Moufki, A.; Philippon, S. An ALE approach for the chip formation process in high speed machining with transient cutting conditions: Modeling and experimental validation. Int. J. Mech. Sci. 2017, 130, 546–557. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, J.; Outeiro, J.; Xu, B.; Zhao, W. Multiscale simulation of grain refinement induced by dynamic recrystallization of Ti-6Al-4V alloy during high speed machining. J. Mater. Process. Technol. 2020, 286, 116834. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Li, G.; Xu, Z.; Zhang, H.; Zhang, J.; Hartmaier, A.; Fang, F.; Yan, Y.; Sun, T. Anisotropy-Related Machining Characteristics in Ultra-Precision Diamond Cutting of Crystalline Copper. Nanomanuf. Metrol. 2020, 3, 123–132. [Google Scholar] [CrossRef]
- Özel, T.; Zeren, E. Determination of work material flow stress and friction for FEA of machining using orthogonal cutting tests. J. Mater. Process. Technol. 2004, 153–154, 1019–1025. [Google Scholar] [CrossRef]
- Usui, E.; Shirakashi, T. Mechanics of Machining from Descriptive to Predictive Theory, on the Art of Cutting Metals 75 Years Later; ASME: New York, NY, USA, 1982. [Google Scholar]
- Afrasiabi, M.; Saelzer, J.; Berger, S.; Iovkov, I.; Klippel, H.; Röthlin, M.; Zabel, A.; Biermann, D.; Wegener, K. A Numerical-Experimental Study on Orthogonal Cutting of AISI 1045 Steel and Ti-6Al-4V Alloy: SPH and FEM Modeling with Newly Identified Friction Coefficients. Metals 2021, 11, 1683. [Google Scholar] [CrossRef]
- Johnson, R.; Cook, W.K. A constitutive model and data for metals subjected to large strains high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- Tan, J.Q.; Zhan, M.; Liu, S.; Huang, T.; Guo, J.; Yang, H. A modified Johnson–Cook model for tensile flow behaviors of 7050-T7451 aluminum alloy at high strain rates. Mater. Sci. Eng. A 2015, 631, 214–219. [Google Scholar] [CrossRef]
- Kumar, C.S.; Zeman, P.; Polcar, T. A 2D finite element approach for predicting the machining performance of nanolayered TiAlCrN coating on WC-Co cutting tool during dry turning of AISI 1045 steel. Ceram. Int. 2020, 46, 25073–25088. [Google Scholar] [CrossRef]
- Aridhi, A.; Perard, T.; Valiorgue, F.; Courbon, C.; Rech, J.; Brosse, A.; Girinon, M.; Truffart, B.; Karaouni, H. Comparison of the CEL and ALE approaches for the simulation of orthogonal cutting of 15-5PH and 42CrMo4 materials. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 237, 1726–1736. [Google Scholar] [CrossRef]
- Dumanić, I.; Jozić, S.; Bagavac, P.; Bajić, D. Orthogonal cutting simulation of EN AW 6082 T6 alloy using a coupled Eulerian-Lagrangian approach. Heliyon 2023, 9, e14821. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Liu, Z. Shear localization sensitivity analysis for Johnson–Cook constitutive parameters on serrated chips in high speed machining of Ti-6Al-4V. Simul. Model. Pract. Theory 2015, 55, 63–76. [Google Scholar] [CrossRef]
- Ducobu, F.; Arrazola, P.J.; Rivière-Lorphèvre, E.; Filippi, E. On the selection of an empirical material constitutive model for the finite element modeling of Ti-6Al-4V orthogonal cutting, including the segmented chip formation. Int. J. Mater. Form. 2021, 14, 361–374. [Google Scholar] [CrossRef]
- Wu, S.; Chen, F.; Wang, C.L. Machining mechanism and stress model in cutting Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 2024, 131, 2625–2639. [Google Scholar] [CrossRef]
- Liu, L.; Wu, W.; Zhao, Y.; Cheng, Y. Subroutine Embedding and Finite Element Simulation of the Improved Constitutive Equation for Ti-6Al-4V during High-Speed Machining. Materials 2023, 16, 3344. [Google Scholar] [CrossRef]
- Zhu, B.; Xiong, L.; Xu, M. Double-edged cutting simulation with a new combined constitutive model for AISI 1045 steel. J. Mater. Process. Technol. 2022, 302, 117496. [Google Scholar] [CrossRef]
- Lei, M.; Sun, G.; Yang, G.; Wen, B. A computational mechanical constitutive modeling method based on thermally-activated microstructural evolution and strengthening mechanisms. Int. J. Plast. 2024, 173, 103881. [Google Scholar] [CrossRef]
- Wagoner Johnson, A.J.; Bull, C.W.; Kumar, K.S.; Briant, C.L. The influence of microstructure and strain rate on the compressive deformation behavior of Ti-6Al-4V. Metall. Mater. Trans. A 2003, 34, 295–306. [Google Scholar] [CrossRef]
- Ullah, I.; Akinlabi, E.T.; Songmene, V.; Kouam, J.; Sadeghifar, M. A multiscale finite element modeling for predicting the surface integrity induced by thermo-mechanical loads during high-speed milling of Ti-6Al-4V. CIRP J. Manuf. Sci. Technol. 2024, 52, 246–263. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, D.; Yao, C. Investigation of the grain refinement mechanism in machining Ti-6Al-4V: Experiments and simulations. J. Manuf. Process. 2023, 94, 479–496. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; He, Z.; Kong, X. The advance of research on constitutive model used in finite element simulation of metal cutting. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 4921–4945. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Tao, Z.; Lovell, M.R.; Yang, J.C. Evaluation of interfacial friction in material removal processes: The role of workpiece properties and contact geometry. Wear 2004, 256, 664–670. [Google Scholar] [CrossRef]
- Moufki, A.; Molinari, A.; Dudzinski, D. Modelling of orthogonal cutting with a temperature dependent friction law. J. Mech. Phys. Solids 1998, 46, 2103–2138. [Google Scholar] [CrossRef]
- Usui, E.; Shirakashi, T.; Kitagawa, T. Analytical Prediction of Three Dimensional Cutting Process. 1977. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=52d3283ff779c1ebb1f32da1b70b6de2&site=xueshu_se (accessed on 10 January 2025).
- Özel, T.; Altan, T. Determination of workpiece flow stress and friction at the chip–tool contact for high-speed cutting. Int. J. Mach. Tools Manuf. 2000, 40, 133–152. [Google Scholar] [CrossRef]
- Fu, J.; Wang, F.L. Cr12MoVPhysical simulation and experimental research on Cr12MoV cutting machining. Mod. Manuf. Eng. 2014, 93–98. [Google Scholar] [CrossRef]
- He, Z. Experimental Study on Serrated Chip and Cutting Force in High Speed Cutting of Ti-6Al-4V. Master’s Thesis, Tianjin University of Technology and Education, Tianjin, China, 2022. [Google Scholar]
- Zhang, N.; Klippel, H.; Kneubühler, F.; Afrasiabi, M.; Kuffa, M.; Wegener, K. Investigation of friction modeling on numerical Ti6Al4V cutting simulations. Int. J. Mech. Sci. 2024, 274, 109231. [Google Scholar] [CrossRef]



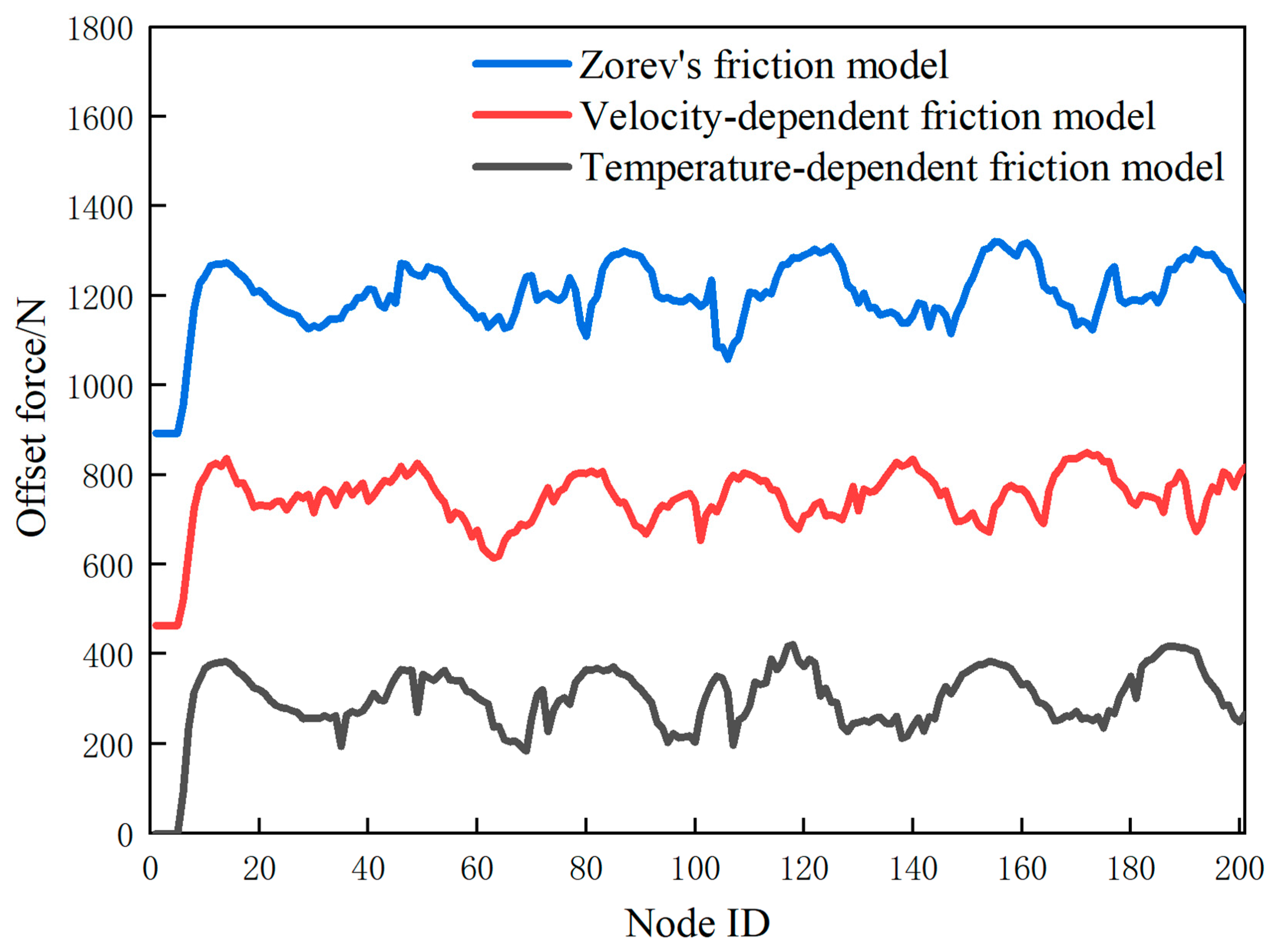
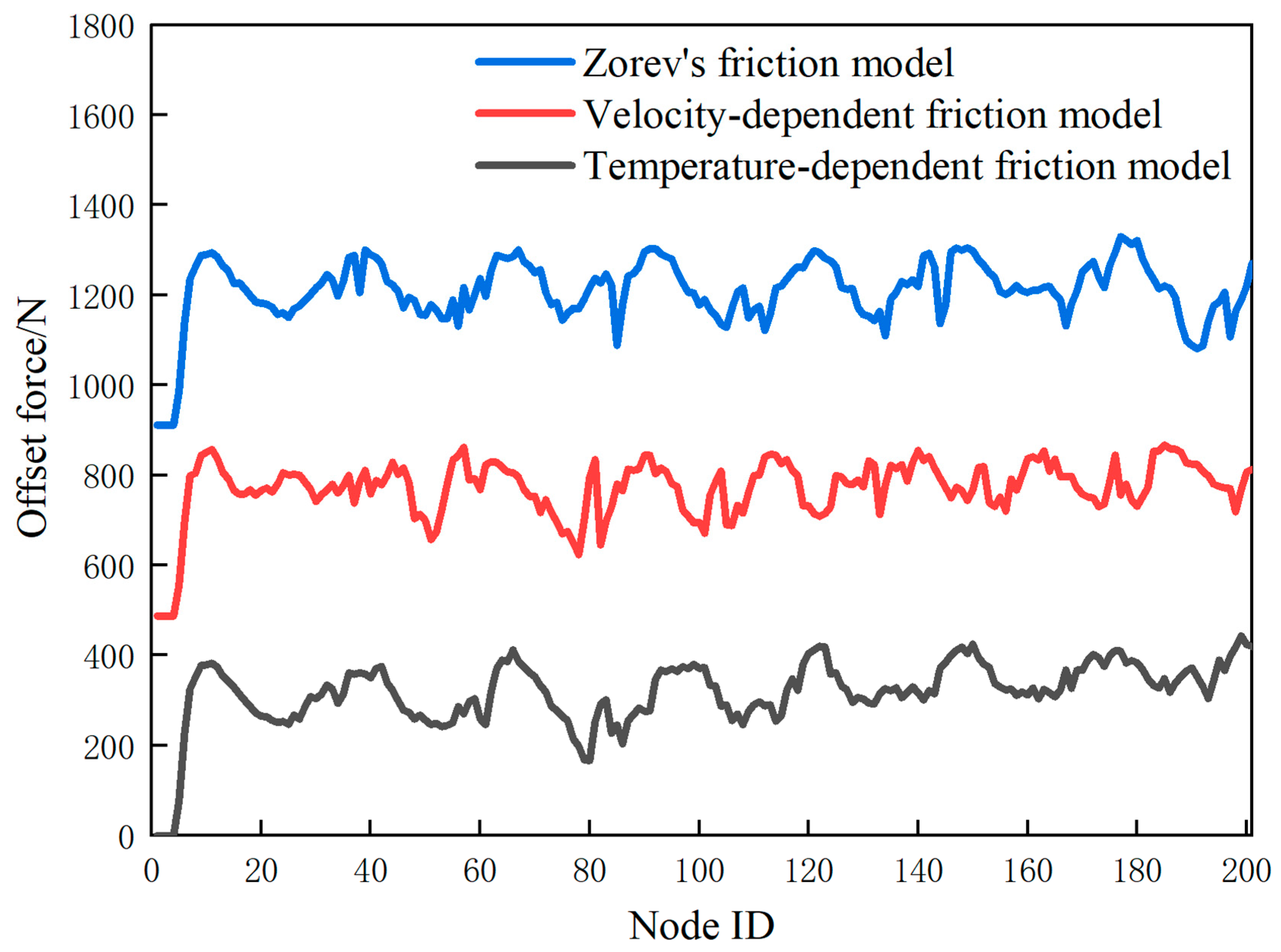
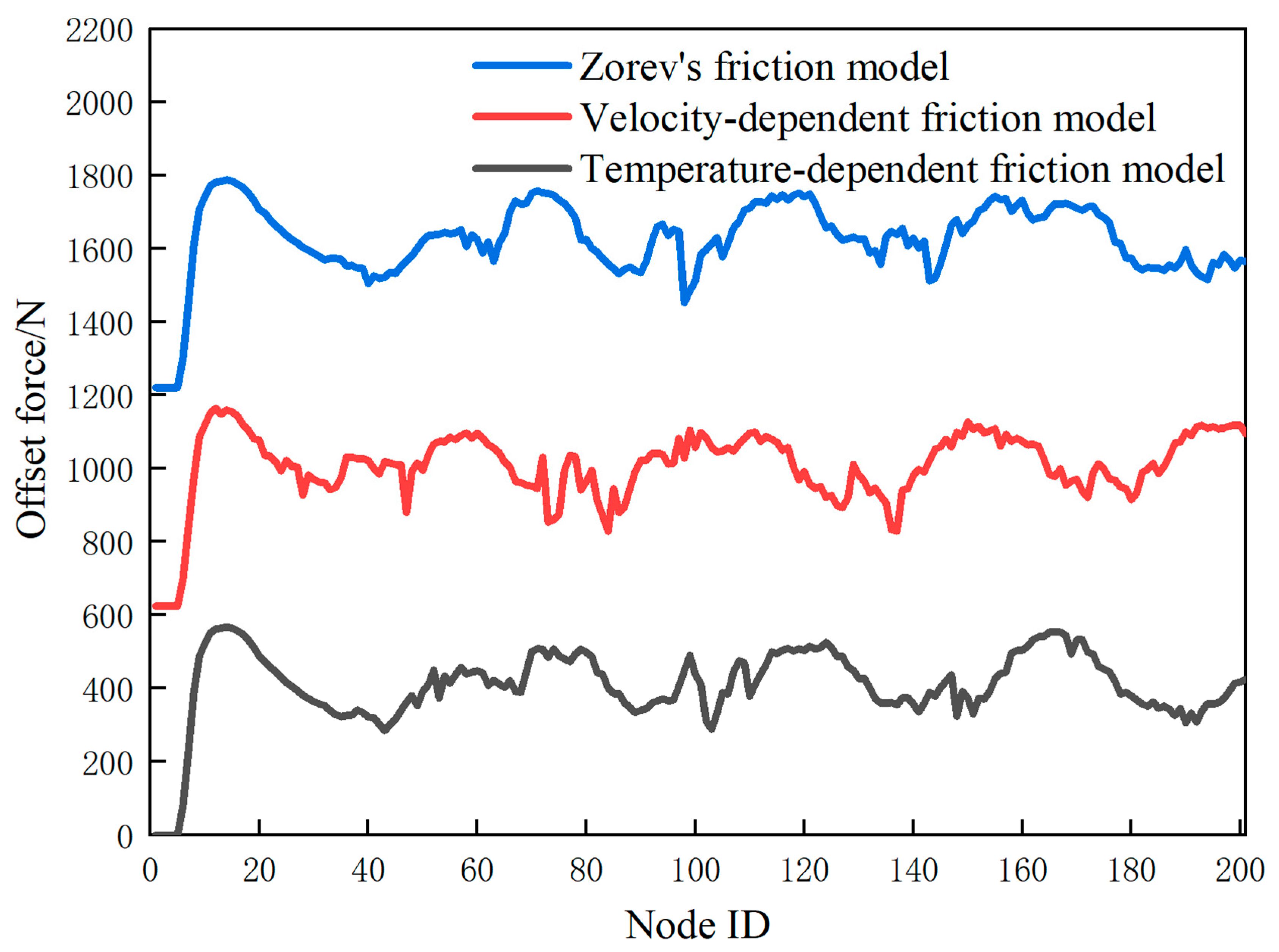
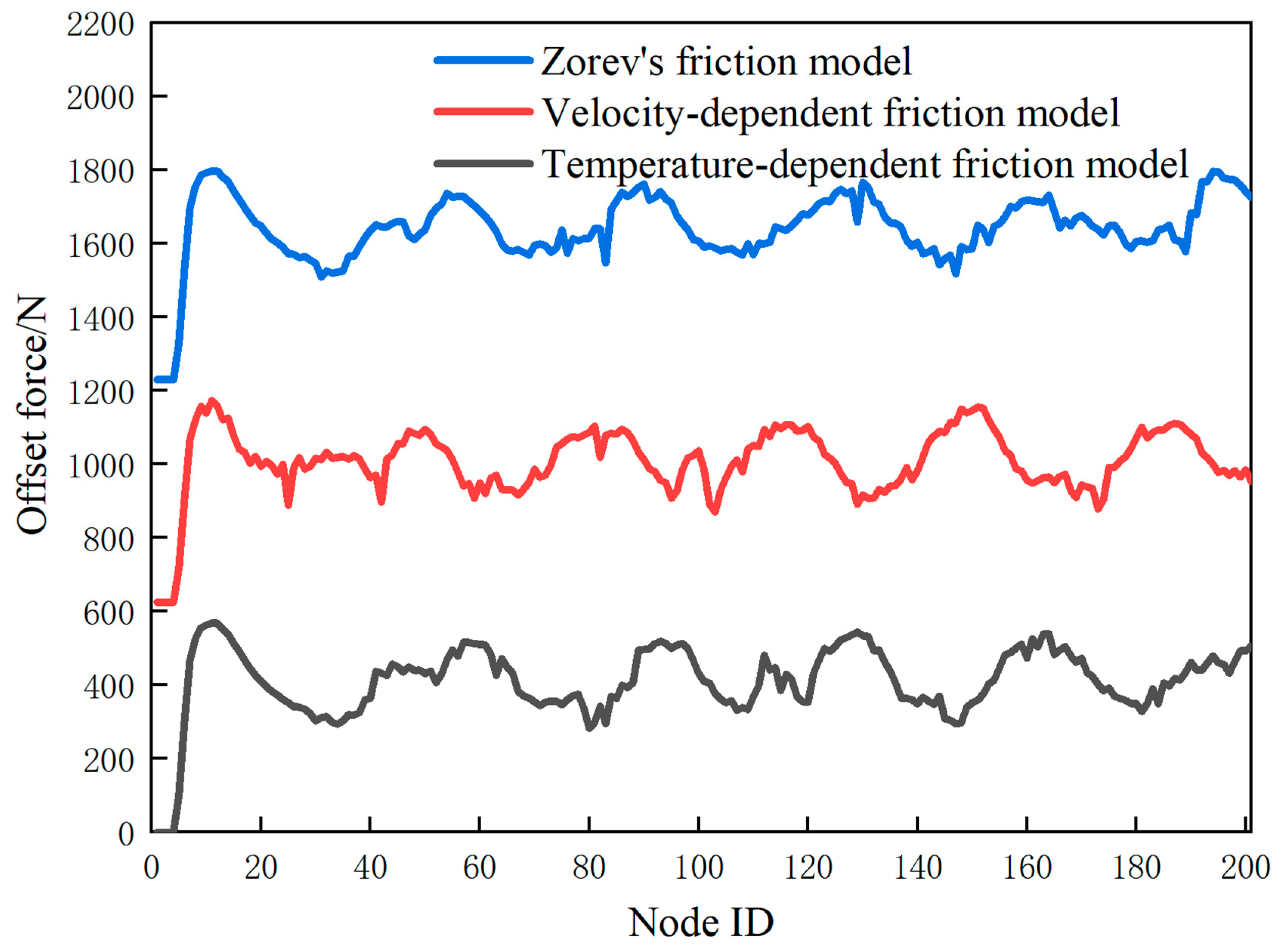
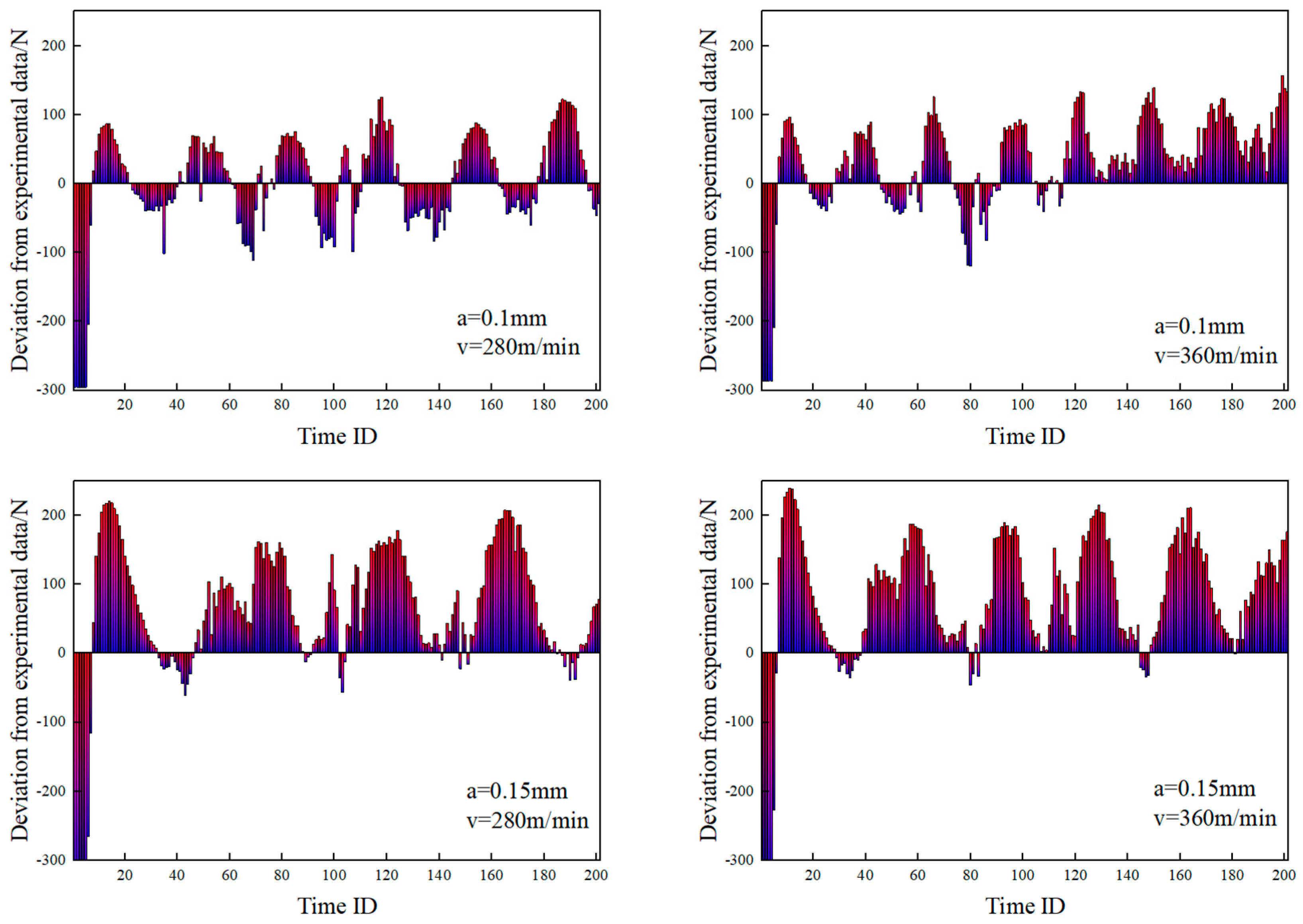
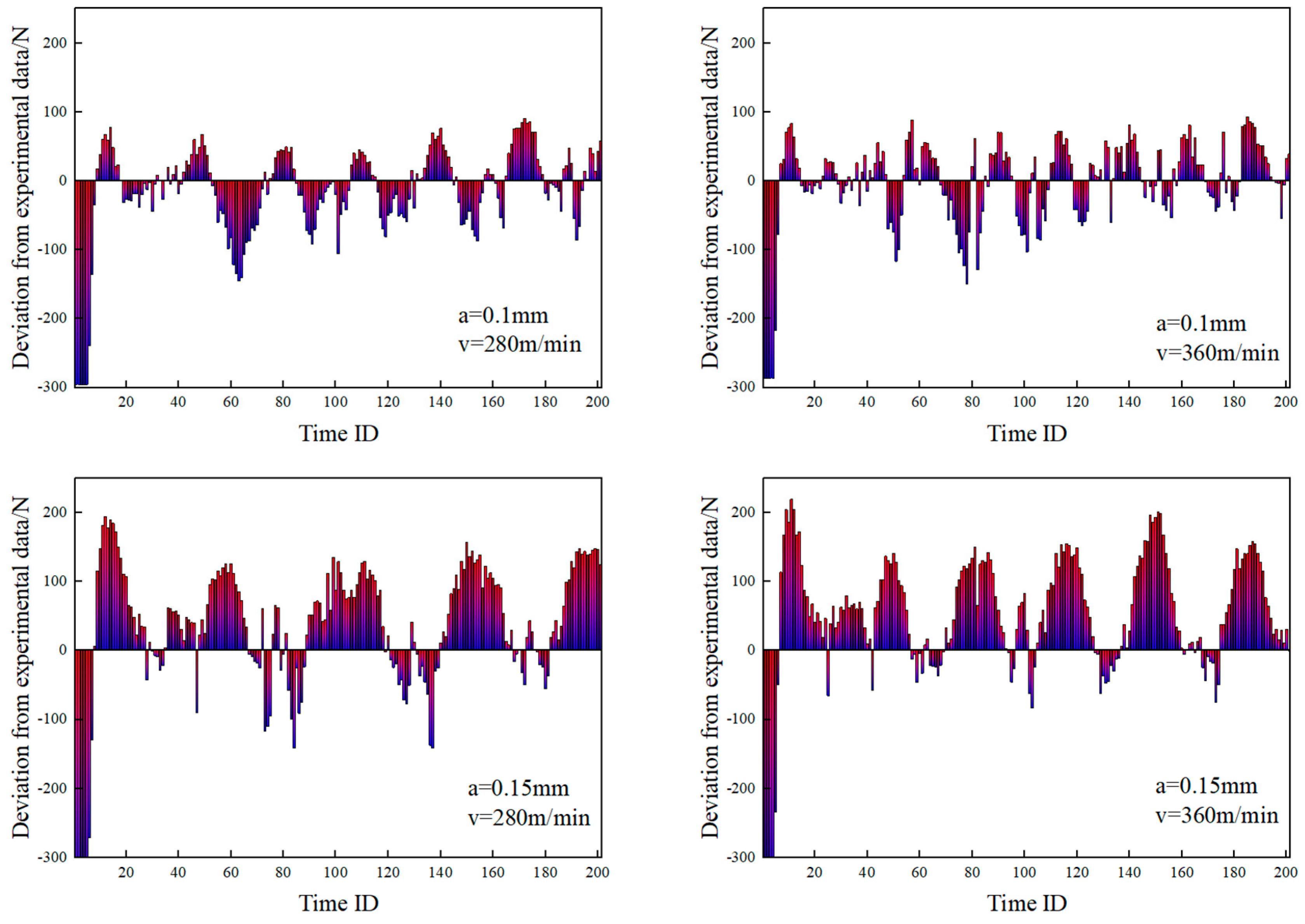
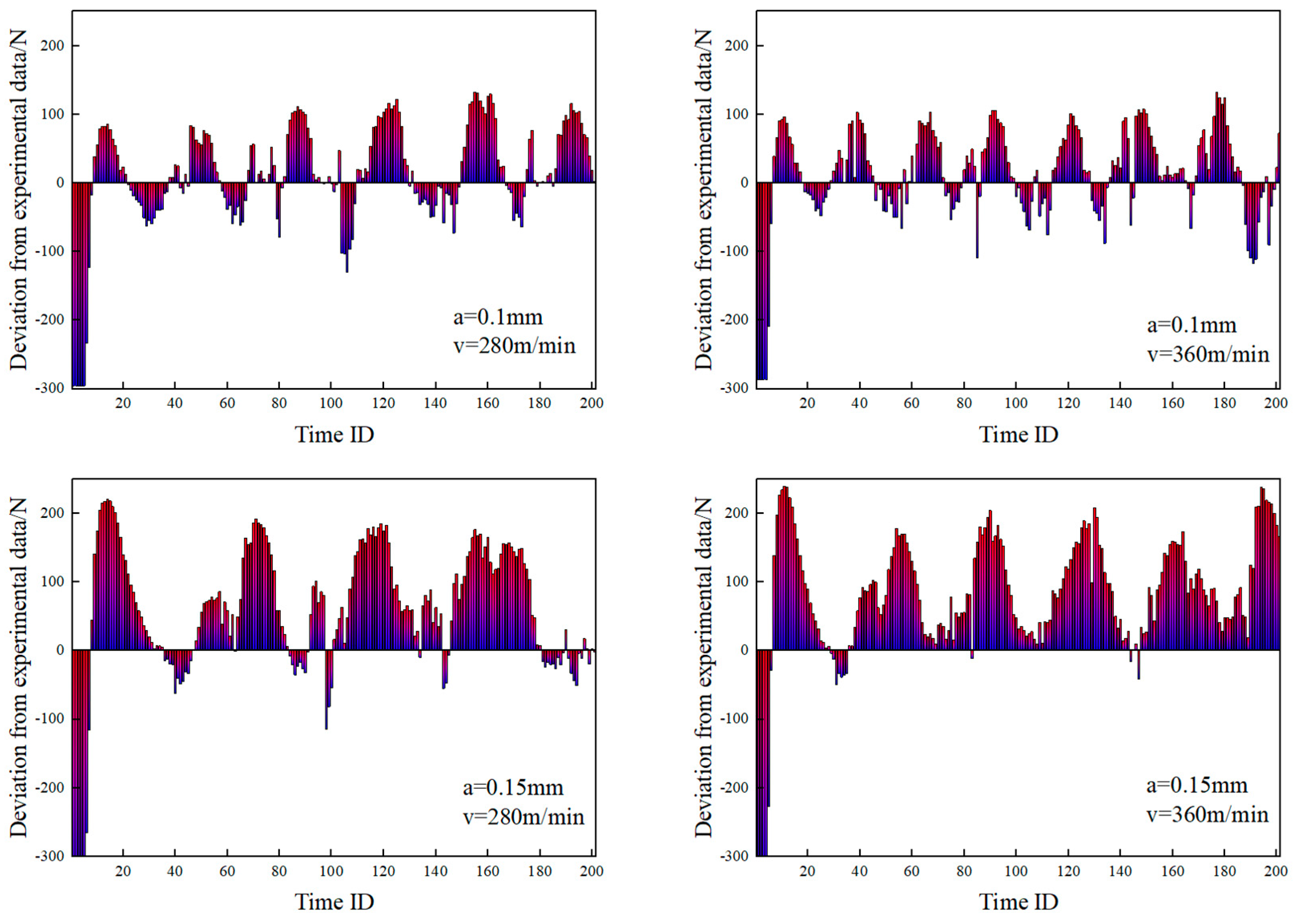
| Cutting Speed /m/min | Cutting Depth /mm | Friction Model | Constitutional Model |
|---|---|---|---|
| 280 | 0.10 | Modified velocity-dependent friction model | Modified J-C model considering dynamic recrystallization and stress softening |
| 280 | 0.15 | ||
| 360 | 0.10 | ||
| 360 | 0.15 | ||
| 280 | 0.10 | Temperature-dependent friction model | |
| 280 | 0.15 | ||
| 360 | 0.10 | ||
| 360 | 0.15 | ||
| 280 | 0.10 | Zorev’s friction model | |
| 280 | 0.15 | ||
| 360 | 0.10 | ||
| 360 | 0.15 |
| Conductivity (W m−1 K−1) | Density (kg m−3) | Elastic (GPa) | Expansion (K−1) | Specific Heat (J kg−1 K−1) |
|---|---|---|---|---|
| 6.8 | 4440 | 109 | 9.1 × 10−6 | 611 |
| A (MPa) | B (MPa) | n | C | m | a | b | d | r | s | (°C) | (°C) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 923.2 | 673.5 | 0.466 | 0.0167 | 1 | 2 | 5 | 1 | 2 | 0.05 | 1620 | 20 |
| D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|
| −0.09 | 0.25 | −0.5 | 0.014 | 3.87 |
| Components | Al | V | Fe | Si | C | N | H | O | Ti |
|---|---|---|---|---|---|---|---|---|---|
| Mass fraction/% | 5.5–6.75 | 3.5–4.5 | 0.3 | 0.1 | 0.1 | 0.05 | 0.015 | 0.2 | other |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, F.; Zhong, R.; Zhu, W.; Zhou, R.; Guo, L.; Wang, Y. Comparative Study of Friction Models in High-Speed Machining of Titanium Alloys. Lubricants 2025, 13, 113. https://doi.org/10.3390/lubricants13030113
Yi F, Zhong R, Zhu W, Zhou R, Guo L, Wang Y. Comparative Study of Friction Models in High-Speed Machining of Titanium Alloys. Lubricants. 2025; 13(3):113. https://doi.org/10.3390/lubricants13030113
Chicago/Turabian StyleYi, Fan, Ruoxi Zhong, Wenjie Zhu, Run Zhou, Li Guo, and Ying Wang. 2025. "Comparative Study of Friction Models in High-Speed Machining of Titanium Alloys" Lubricants 13, no. 3: 113. https://doi.org/10.3390/lubricants13030113
APA StyleYi, F., Zhong, R., Zhu, W., Zhou, R., Guo, L., & Wang, Y. (2025). Comparative Study of Friction Models in High-Speed Machining of Titanium Alloys. Lubricants, 13(3), 113. https://doi.org/10.3390/lubricants13030113




