Tribo-Dynamic Behavior of Double-Row Cylindrical Roller Bearings Under Raceway Defects and Cage Fracture
Abstract
1. Introduction
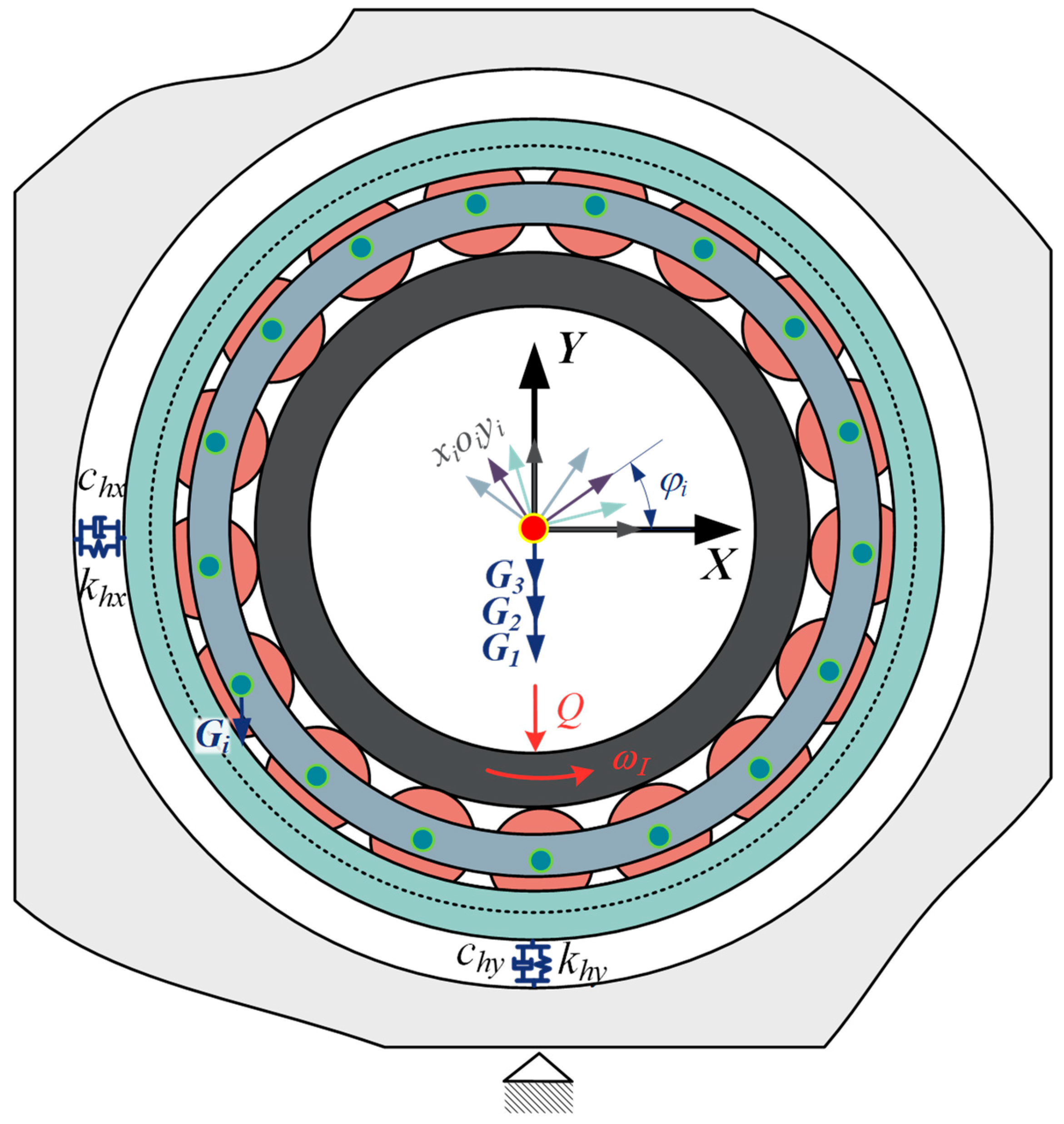
2. Mathematical Modeling for Defective DCRBs
2.1. Modeling for Defects of DCRB
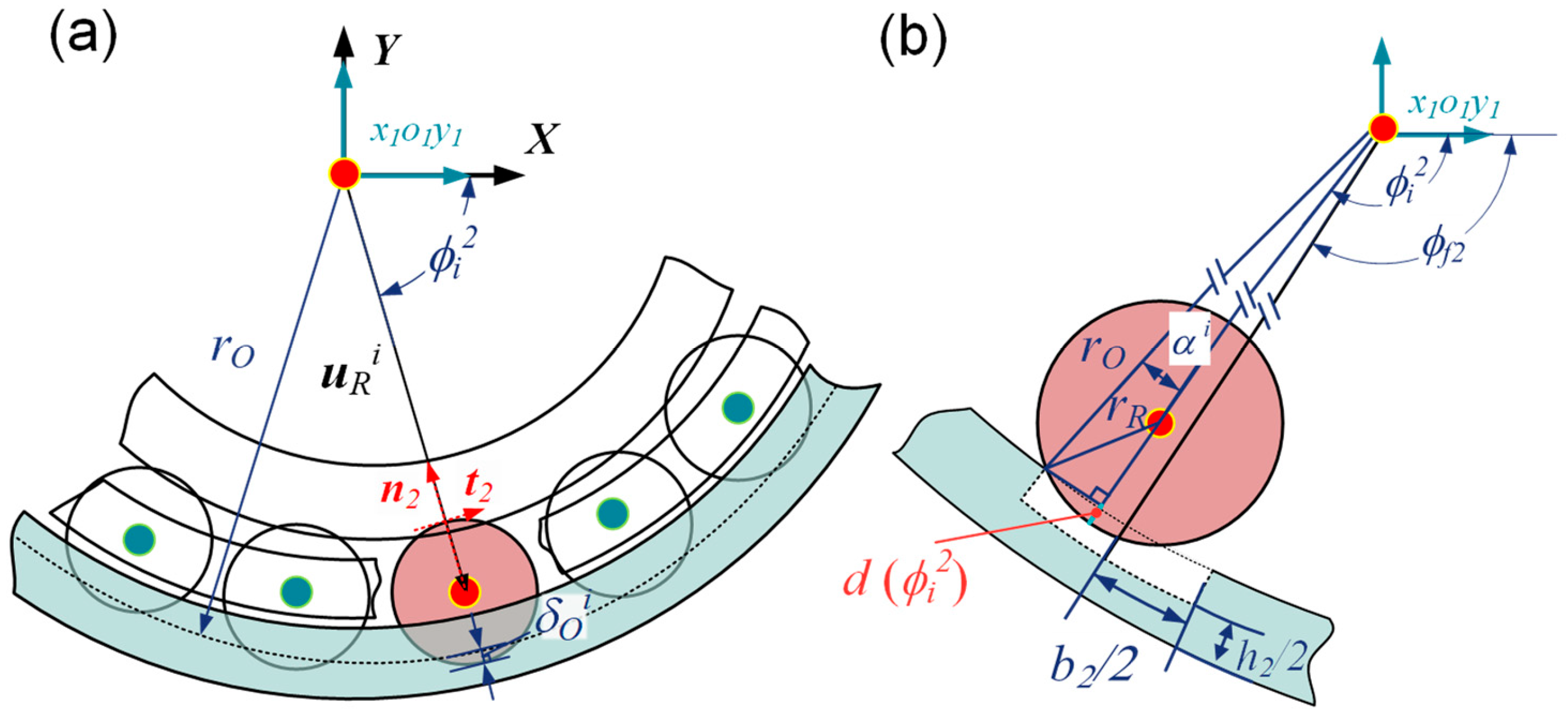
2.1.1. Modeling for Localized Defect on Inner Raceway
2.1.2. Modeling for Localized Defect on Outer Raceway
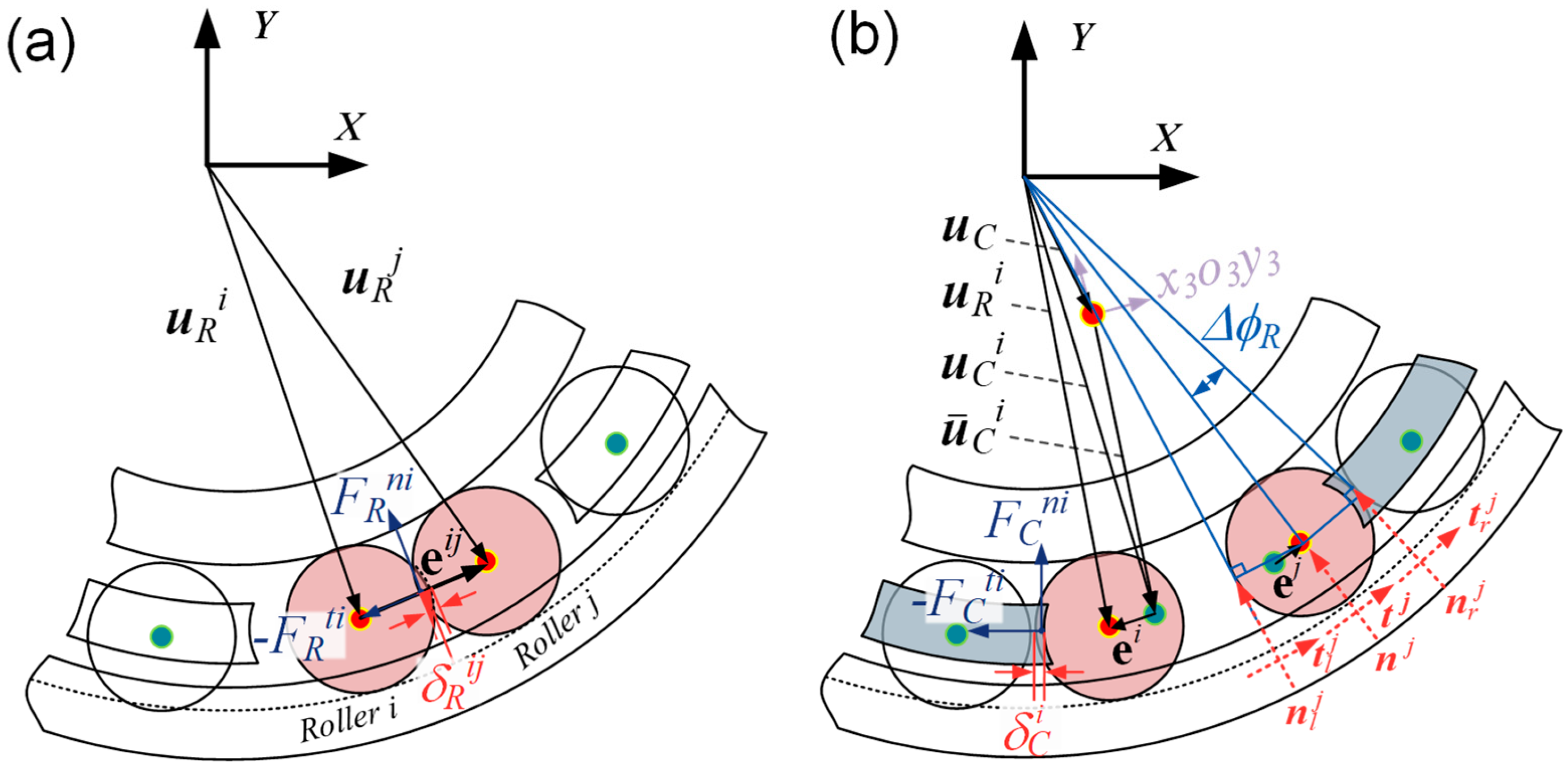
2.1.3. Modeling for Cage Fracture
2.1.4. The Generalized Motion of the Roller
2.2. Modeling of DCRBs Multibody System
2.2.1. Multibody System DAEs
2.2.2. The Dynamics Equations of the DCRB Multibody System
- The geometric center of each bearing component coincides with its center of mass.
- All bearing components are considered rigid bodies, without accounting for elastic deformation.
- The installation of bearing components does not consider human-induced errors, apart from the clearance allowance.
- Contact between bearing components involves dry friction, ignoring the effects of frictional heat generation.
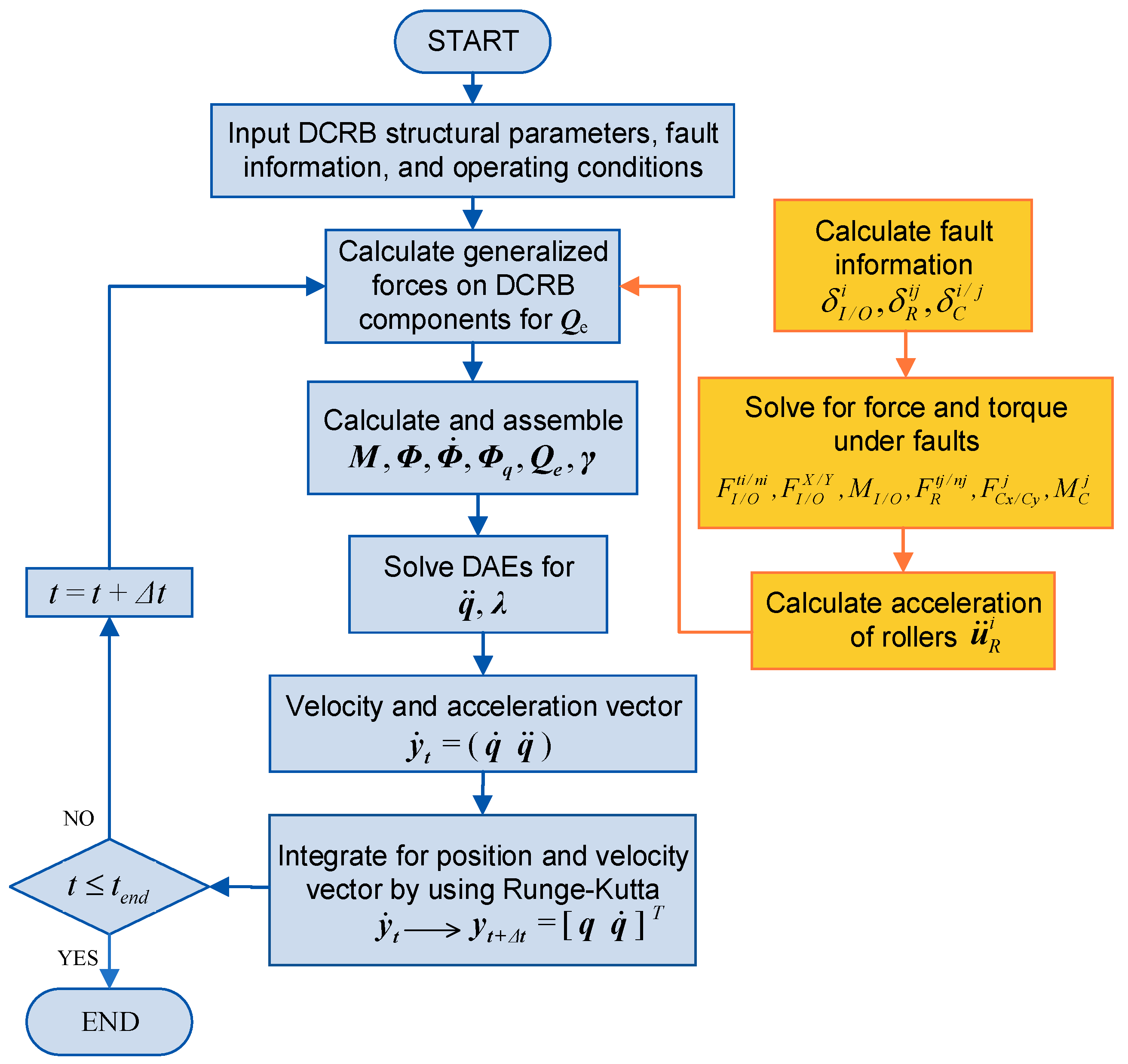
2.3. Model Solution Process and Model Validation
2.3.1. Model Solution Process
2.3.2. Model Validation
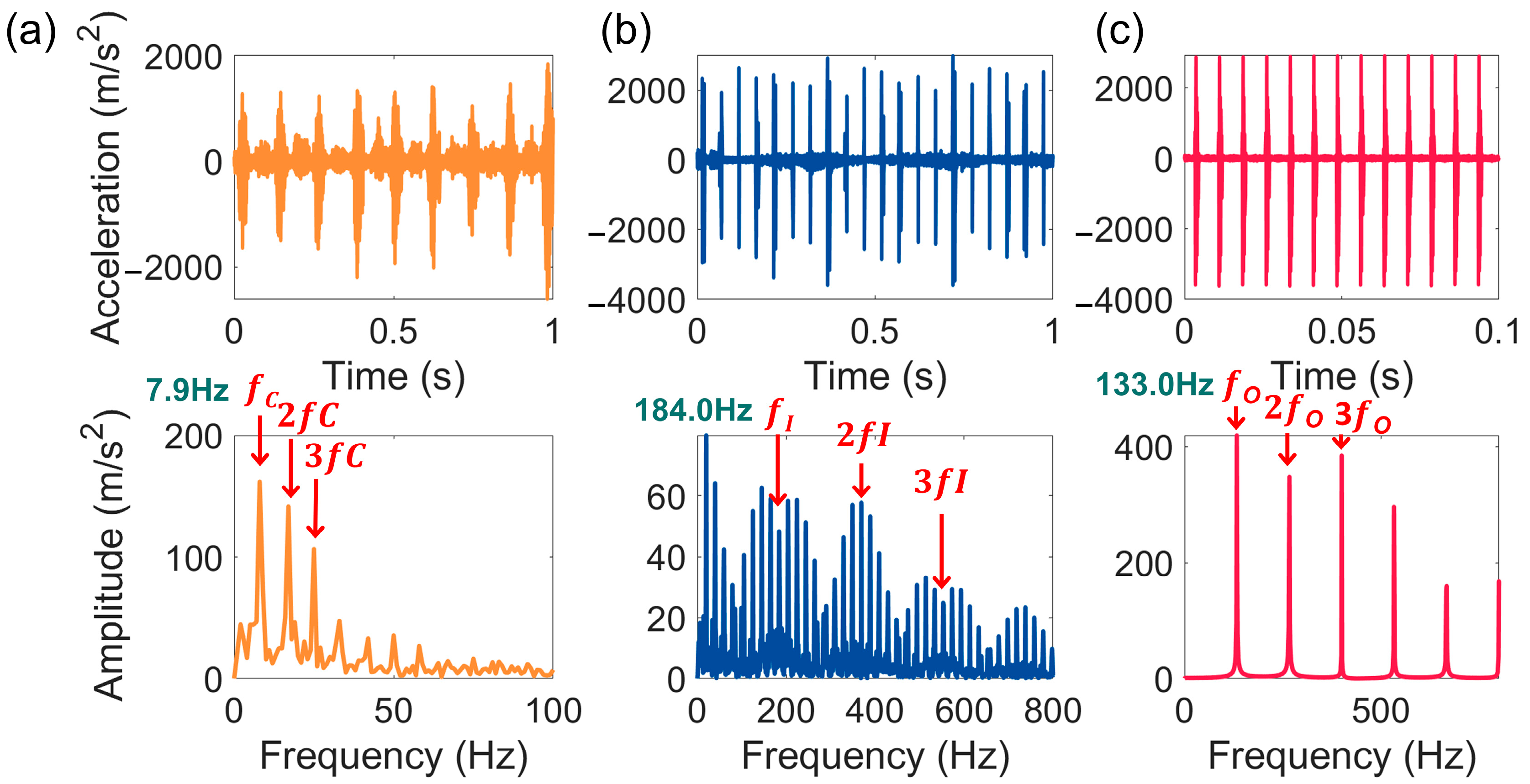
3. Results and Discussion
3.1. Analysis of the Tribological Behavior of Defective DCRBs
3.2. Analysis of the Dynamic Response of Defective DCRBs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Planar transformation matrix; | |
| Derivative of with respect to ; | |
| b1/2 | Width of inner/outer raceway defect (m); |
| Radial clearance between roller and cage pocket (m); | |
| Damping of the outer ring and the bearing housing (Ns/m); | |
| dO, dI, dR | Diameters of the outer raceway, inner raceway and roller (m); |
| dM | Pitch diameter (m); |
| Effective depth of roller and inner/outer raceway (m); | |
| Stick–slip effect coefficient; | |
| Ei, Ej | Elastic modulus of cylinder i and j (GPa); |
| Composite elastic modulus (GPa); | |
| Calculated frequency of outer ring/inner ring/cage (Hz); | |
| Fn | Indentation contact force (N); |
| Contact force acting on inner ring (N); | |
| Contact force acting on outer ring (N); | |
| Contact force that roller j acting on cage (N); | |
| Normal and tangential components of contact force between the inner raceway and roller i (N); | |
| Normal and tangential components of contact force between the outer raceway and roller i (N); | |
| Normal and tangential components of contact force between left/right pocket side and roller j (N); | |
| Normal and tangential components of contact force that roller j acting on roller i (N); | |
| Normal and tangential components of contact force between roller i and cage pocket (N); | |
| Moment of inertia around the central axis of the outer ring (kg·m2); | |
| Stiffness of the outer ring and the bearing housing (N/m); | |
| L | Cylinder length (m); |
| M | Mass matrix of a multibody system; |
| Mass of roller i (kg); | |
| nr | Number of rollers; |
| Unit vector along the contact force between the inner/outer raceway and roller i; | |
| Q | Radial load (N); |
| Radial load on rolling element (N); | |
| Generalized external force vector (N); | |
| Equivalent radius (m); | |
| Ri, Rj | Radii of cylinder i and j (m); |
| rO, rI, rR | Radii of the outer raceway, inner raceway and roller (m); |
| t | Time (s); |
| Unit vector along the contact force between the inner/outer raceway and roller i; | |
| U | Non-dimension parameter of velocity; |
| Sliding velocity of contact surfaces for roller i relative to roller j (m/s); | |
| Sliding velocity of contact surfaces for roller i relative to pocket (m/s); | |
| Relative velocity between the inner/outer raceway and roller (m/s); | |
| Displacement vectors of roller i and inner ring (m); | |
| Relative displacement vector of roller i (m)s; | |
| Global translation position vector of the reference frame origin on body i (m); | |
| vi, vj | Poisson’s ratio of cylinder i and j; |
| vs | Stribeck velocity (m/s); |
| W | Non-dimension parameter of load; |
| w | Contact load (N). |
| Greek letters | |
| γ | External generalized force vector; |
| δ | Indentation depth (m); |
| Contact deformation between inner/outer raceway and roller i (m); | |
| Contact deformation for roller i relative to roller j (m); | |
| Contact deformation for roller i relative to pocket (m); | |
| λ | Vector of Lagrange multipliers; |
| Static and kinetic friction coefficients; | |
| Rotation displacement of the reference frame along with the rotation of body i (rad); | |
| Φq | Jacobian matrix of constraint equations; |
| Constraint equations of multibody system; | |
| Azimuth angle of roller i with respect to inner/outer ring center (rad); | |
| Ψ | Angular position of the roller to the y axis (rad); |
| ωI | Angular velocity of inner ring (rpm); |
| ωC | Angular velocity of cage (rpm). |
| Coordinate systems | |
| XOY | Global coordinate system in the outer ring center; |
| xioiyi | Reference coordinate system fixed on the body i. |
| Abbreviations | |
| DCRB | Double-row cylindrical roller bearing. |
References
- Xu, H.; Ma, H.; Wen, B.; Yang, Y.; Li, X.; Luo, Z.; Han, Q.; Wen, B. Dynamic characteristics of spindle-bearing with tilted pedestal and clearance fit. Int. J. Mech. Sci. 2024, 261, 108683. [Google Scholar] [CrossRef]
- Tingarikar, G.; Choudhury, A. Vibration Analysis-Based Fault Diagnosis of a Dynamically Loaded Bearing with Distributed Defect. Arab. J. Sci. Eng. 2022, 47, 8045–8058. [Google Scholar] [CrossRef]
- Patel, S.P.; Upadhyay, S.H. Influence of roller defect and coupled roller–inner–outer race defects on the performance of cylindrical roller bearing. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2019, 233, 731–746. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Shi, Z. Dynamic modelling of the defect extension and appearance in a cylindrical roller bearing. Mech. Syst. Signal Process. 2022, 173, 109040. [Google Scholar] [CrossRef]
- Tu, W.; Yu, W.; Shao, Y.; Yu, Y. A nonlinear dynamic vibration model of cylindrical roller bearing considering skidding. Nonlinear Dyn. 2021, 103, 2299–2313. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Li, X.; Xiao, S.; Gu, F.; Shi, Z. Effects of Wear on Lubrication Performance and Vibration Signatures of Rotor System Supported by Hydrodynamic Bearings. Lubricants 2023, 11, 107. [Google Scholar] [CrossRef]
- Tofighi-Niaki, E.; Safizadeh, M.S. Dynamic of a Flexible Rotor-Bearing System Supported by Worn Tilting Journal Bearings Experiencing Rub-Impact. Lubricants 2023, 11, 212. [Google Scholar] [CrossRef]
- Wu, Z.; Tang, H.; Li, Y.; Ren, Y.; Chen, L.; Kumar, A. Simulation and experimental analysis of rotor-bearing system with rolling element bearing fault in axial piston pump under churning condition. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2022, 237, 98–113. [Google Scholar] [CrossRef]
- Li, N.; Zhang, J.; Meng, X.; Han, Q.; Zhai, J. Dynamic response and failure analysis of bearing under the impact of vibration excitation. Eng. Fail. Anal. 2023, 154, 107640. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, H.; Fan, Y.; Shangguan, L.; Yang, Y. A Review of Research on Wind Turbine Bearings’ Failure Analysis and Fault Diagnosis. Lubricants 2023, 11, 14. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Ding, S.; Xu, Y.; Zhang, Y.; Xia, M. Dynamic modeling and vibration analysis of double row cylindrical roller bearings with irregular-shaped defects. Nonlinear Dyn. 2023, 112, 2501–2521. [Google Scholar] [CrossRef]
- Shinde, P.V.; Desavale, R.G. Application of dimension analysis and soft competitive tool to predict compound faults present in rotor-bearing systems. Measurement 2022, 193, 110984. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z.; Zi, Y.; Zhang, M.; Tang, T. Dynamic Effect Analysis of Cryogenic Solid-Lubricated Ball Bearings with Geometrical-Frictional Defects. Lubricants 2024, 12, 84. [Google Scholar] [CrossRef]
- Deng, W.; Li, Z.; Li, X.; Chen, H.; Zhao, H. Compound fault diagnosis using optimized MCKD and sparse representation for rolling bearings. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Denni, M.; Biboulet, N.; Abousleiman, V.; Lubrecht, A.A. Dynamic study of a roller bearing in a planetary application considering the hydrodynamic lubrication of the roller/cage contact. Tribol. Int. 2020, 149. [Google Scholar] [CrossRef]
- Wang, P.; Yang, Y.; Ma, H.; Xu, H.; Li, X.; Luo, Z.; Wen, B. Vibration characteristics of rotor-bearing system with angular misalignment and cage fracture: Simulation and experiment. Mech. Syst. Signal Process. 2023, 182, 109545. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Liu, Y.; Liu, H. Dynamic characteristics of ball bearing with flexible cage lintel and wear. Eng. Fail. Anal. 2020, 117, 104956. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, J.; Li, H.; Zhang, Q.; Xiao, G. Dynamic simulation of a planet roller bearing considering the cage bridge crack. Eng. Fail. Anal. 2022, 131, 105849. [Google Scholar] [CrossRef]
- Luo, Y.; Tu, W.; Fan, C.; Zhang, L.; Zhang, Y.; Yu, W. A study on the modeling method of cage slip and its effects on the vibration response of rolling-element bearing. Energies 2022, 15, 2396. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavič, J.; Boltežar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Muvengei, O.; Kihiu, J.; Ikua, B. Dynamic analysis of planar multi-body systems with LuGre friction at differently located revolute clearance joints. Multibody Syst. Dyn. 2012, 28, 369–393. [Google Scholar] [CrossRef]
- Ju, C. Modeling Friction Phenomena and Elastomeric Dampers in Multibody Dynamics Analysis; Georgia Institute of Technology: Atlanta, GA, USA, 2009. [Google Scholar]
- Kermani, M.; Patel, R.; Moallem, M. Friction identification in robotic manipulators: Case studies. In Proceedings of the Proceedings of 2005 IEEE Conference on Control Applications, 2005, CCA 2005, Toronto, ON, Canada, 28–31 August 2005; pp. 1170–1175. [Google Scholar]
- De Wit, C.C.; Lischinsky, P. Adaptive friction compensation with partially known dynamic friction model. Int. J. Adapt. Control Signal Process. 1997, 11, 65–80. [Google Scholar] [CrossRef]
- Pereira, C.; Ramalho, A.; Ambrosio, J. An enhanced cylindrical contact force model. Multibody Syst. Dyn. 2015, 35, 277–298. [Google Scholar] [CrossRef]
- Baumgarte, J. Stabilization of constraints and integrals of motion in dynamical systems. Comput. Methods Appl. Mech. Eng. 1972, 1, 1–16. [Google Scholar] [CrossRef]
- Tan, D.; Chen, Z. On a general formula of fourth order Runge-Kutta method. J. Math. Sci. Math. Educ. 2012, 7, 1–10. [Google Scholar]






| Parameters | Value | Parameters | Value |
| Inner raceway radius rI (m) | 78.86 × 10−3 | Mass of cage mC (kg) | 2.459 |
| Outer raceway radius rO (m) Pitch radius rM (m) | 109.14 × 10−3 94 × 10−3 | Inertial moment of cage IC (kg·m2) | 2.19 × 10−2 |
| Roller radius rR (m) | 15 × 10−3 | Mass of roller mR (kg) | 2.48 × 10−1 |
| Roller length lR (m) Roller number nr (m) | 48 × 10−3 16 × 2 | Inertial moment of roller IR (kg·m2) | 6.15 × 10−5 |
| Elastic modulus E (GPa) Poisson’s radio ν (-) | 207.5 0.3 | Stiffness of the outer ring and the bearing housing khx, khy (N/m) | 212 × 106 |
| Mass of outer ring mO (kg) Inertial moment of outer ring IO (kg·m2) | 1.349 × 101 1.66 × 10−1 | Damping of the outer ring and the bearing housing chx, chy (Ns/m) | 1.0 × 105 |
| Mass of inner ring mI (kg) | 7.316 | ||
| Inertial moment of inner ring II (kg·m2) | 3.82 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.; Zhao, X.; Hao, W.; Miao, C.; Hu, X.; Fang, C. Tribo-Dynamic Behavior of Double-Row Cylindrical Roller Bearings Under Raceway Defects and Cage Fracture. Lubricants 2025, 13, 80. https://doi.org/10.3390/lubricants13020080
Fan L, Zhao X, Hao W, Miao C, Hu X, Fang C. Tribo-Dynamic Behavior of Double-Row Cylindrical Roller Bearings Under Raceway Defects and Cage Fracture. Lubricants. 2025; 13(2):80. https://doi.org/10.3390/lubricants13020080
Chicago/Turabian StyleFan, Longqing, Xingwang Zhao, Wei Hao, Chaoyang Miao, Xiuyuan Hu, and Congcong Fang. 2025. "Tribo-Dynamic Behavior of Double-Row Cylindrical Roller Bearings Under Raceway Defects and Cage Fracture" Lubricants 13, no. 2: 80. https://doi.org/10.3390/lubricants13020080
APA StyleFan, L., Zhao, X., Hao, W., Miao, C., Hu, X., & Fang, C. (2025). Tribo-Dynamic Behavior of Double-Row Cylindrical Roller Bearings Under Raceway Defects and Cage Fracture. Lubricants, 13(2), 80. https://doi.org/10.3390/lubricants13020080






