Abstract
In this paper, the stability of the split doublet mode pair in a disc brake squeal is analytically investigated. A reduced-order doublet mode model is derived based on the formulation of annular plate vibration, sliding contact kinematics, and the assumed mode method. The solution is approximated using a two-mode expansion for the doublet mode pair. The time-varying motion of the slightly asymmetric rotating disc is described through the moving mode shape function method. A stability analysis of the frequency split between the doublet mode pair is performed by calculating the characteristic multipliers using the Floquet theory. The stability boundary is determined within the domain of frequency split variations and other parameters. Finally, the influence of mode splitting on the squeal behaviour of the asymmetric disc is analysed and discussed.
1. Introduction
Brake noise and vibration phenomena occurring during brake engagement are commonly referred to as squeal, groan, moan, and similar terms. Among these, squeal is typically defined as a high-frequency noise problem occurring above 1 kHz during low-speed operations. Due to its high frequency, squeal is widely recognised as the most annoying issue for passengers. Squeal manifests intermittently or even randomly, making it difficult to capture repeatable signals under identical test conditions [1,2,3,4]. Microscopic aspects, such as wear and contact debris, are potential contributors to the intermittency of squeal occurrence, as they alter the friction coefficient at the brake contact interface and its friction–velocity slope [5,6,7].
Brake squeal presents a significant challenge for the automotive industry and has been extensively investigated through finite element (FE) analysis, analytical modelling, and experimental studies. The onset of brake squeal is commonly assumed to be caused by the linear instability of the linearised equations of motion at equilibrium [1,2,3,4]. The complex eigenvalues of the system, derived from analytical approaches, have provided comprehensive explanations of the squeal mechanism [8,9,10,11]. Experimental investigations have also been widely conducted to analyse brake squeal behaviour [12,13,14,15,16,17,18].
In analytical models, the disc brake system is often represented as a symmetric circular plate subjected to frictional stresses [9,10,11]. The rotation of the disc introduces velocity-dependent gyroscopic and friction-damping matrices. Kang’s comprehensive model [11] demonstrated that gyroscopic destabilisation is a critical mechanism for point contact, while mode-coupling becomes predominant for distributed contact areas. The relative contributions of mode-coupling and gyroscopic effects to dynamic instability are summarised in Table 1 of reference [11].

Table 1.
The system parameters of the annular disc system.
Most analytical models assume a brake disc subjected to stationary friction loads over the brake pad contact area. While friction is generated as the disc rotates, the rotation effect is often neglected in brake squeal simulations, as squeal primarily occurs at low speeds. Neglecting the rotation of the disc introduces two major limitations:
(1) Velocity-dependent terms, including gyroscopic destabilisation and friction damping, cannot be investigated [19].
(2) Rotation angle-dependent terms, including the frequency split of the disc, cannot be analysed [20,21,22], which is the central focus of this paper.
The frequency split effect associated with disc rotation may reveal rich insights into nonlinear brake squeal signals, which can exhibit time-periodic and chaotic characteristics. Despite its potential importance, accurate models that account for disc rotation and frequency split are rare. This paper aims to derive these rotational effects, including gyroscopic actions and geometric asymmetry, in the equations of motion.
Geometric asymmetry, a related factor, has drawn attention for its impact on the dynamic behaviour of symmetric-like vibrating structures [23,24,25]. Asymmetry in non-rotating brake components, such as hub bolts, can also contribute to frequency splitting [26]. One significant outcome of geometric asymmetry is the frequency split between doublet modes in symmetric-like structures. The frequency split effects in stationary brake discs have been widely studied, with previous models showing that mode-coupling instability increases as the frequency split between two adjacent modes decreases [9,10]. The frequency split of doublet mode pairs is of particular interest, as it is typically very small or even zero. In principle, this split exists only when axis-symmetry is broken and is always present in automotive brake discs due to geometric imperfections or bolt assemblies disrupting rotational symmetry [1]. However, the effect of slight frequency split on doublet modes in rotating discs remains underexplored.
To address this, the solution approach for rotating discs must consider the rotation of phase angles. For perfectly symmetric rotating discs with zero frequency split between doublet modes, stationary mode shape functions satisfying boundary conditions can describe compact solutions as the number of modes approaches infinity. However, for asymmetric rotating discs, frequency splitting between doublet modes necessitates incorporating the disc phase angle during rotation into the compact solution form. In this context, the moving mode shape function approach provides an accurate solution for mode discretisation. Recently, this approach has been developed using finite element and analytical methods [21,22]. Notably, periodic time-varying squeal phenomena can be captured using the moving mode shape approach in both linear and nonlinear models [21].
When the mode shape function rotates, the linearised system matrices become time-varying. Due to the periodic nature of rotation, these matrices exhibit time-periodicity. Consequently, the stability of squeal propensity is determined by solving the eigenvalues of the linear time-periodic system. Floquet theory is used to assess stability via characteristic multipliers [27,28,29,30,31,32,33].
In references [21,22], mathematical and finite element model developments using the moving mode shape function approach were introduced, and some insights into squeal propensity due to frequency splitting were discussed. However, the detailed effects of frequency splitting on squeal propensity have not been fully explored using the exact solution form of the moving mode shape functions.
The primary objective of this study is to formulate and investigate the modal instability of doublet mode pairs in rotating asymmetric discs. The frequency split between doublet modes is described analytically, and the friction-engaged system equations are reduced to a time-periodic doublet mode model using the moving mode shape function approach. The modal instability is then determined by the eigenvalues of the transition matrix via Floquet theory. Subsequently, the stability of various doublet mode pairs is numerically evaluated. This study focuses on the parametric stability analysis of frequency split effects, addressing a topic that has been rarely explored in the literature.
2. Materials and Methods
The stability of a time-varying annular disc under distributed frictional contact is investigated using a reduced-order model that considers a doublet mode pair of the disc. When the frequencies of two modes are closely spaced, the eigenvalues of the friction-coupled system are dominated by these two mode shapes. The influence of other mode shapes is found to be negligible, as demonstrated in Equations (38) and (39) of the eigenvalue perturbation method [10]. For a symmetric disc, the doublet mode pair has identical frequencies. Even in a slightly asymmetric disc, the frequency split between the doublet modes remains very small. Consequently, the reduced-order model, incorporating the closely spaced frequencies of the doublet mode pair, can effectively approximate the stability of the doublet mode pair in a full-order model with a sufficiently large number of mode shapes.
The annular disc is clamped at the inner radius and free at the outer radius. It rotates at a constant speed and is subjected to an annular sector-shaped frictional contact, as illustrated in Figure 1.
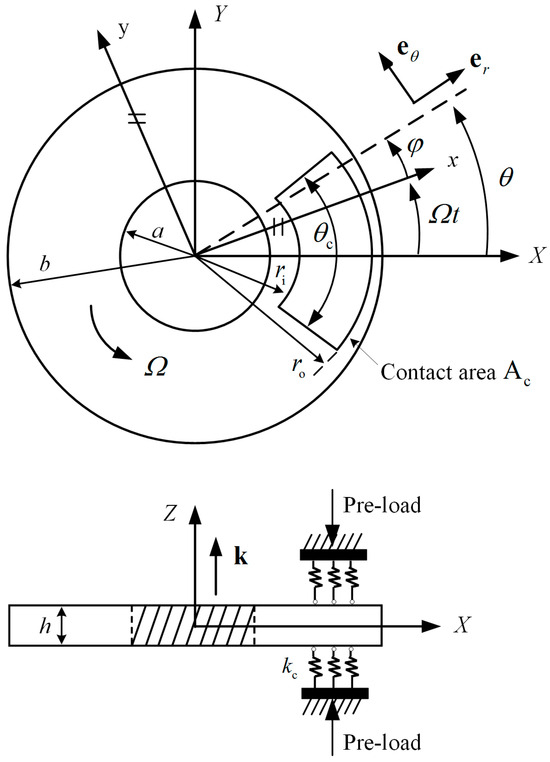
Figure 1.
Configuration of a rotating disc in contact with friction material of annular sector shape; , , and are the inner and outer radii and thickness of the disc, and , , and are the inner and outer radii and contact angle of the contact area, respectively.
In automotive brake applications, the disc doublet pair typically exhibits a slight frequency split due to axis asymmetry arising from factors such as bolt assembly or geometric imperfections. The accurate mode shapes of each doublet mode pair can be obtained through Fourier series analysis or finite element analysis. However, for simplification, the mode shape functions used in the slightly asymmetric disc problem are approximated by those of the axis-symmetric annular disc [23,24,25].
The trial functions used in the assumed mode method should be the basic functions satisfying the boundary conditions and the following equation of motion in the rotating axis-symmetric annular plate in the local -frame:
where is the flexural rigidity and the solution can be expressed in the modal expansion form of the basic function with nodal circles and nodal diameters satisfying Equation (1) as follows:
where is the linear combination of Bessel functions for the axis-symmetric plate. Superscript C and S denote the cosine and sine functions, respectively. Alternatively, Equation (1) can be written in the reference XYZ-frame as follows:
where
Here, the basic functions satisfying Equation (4) must take the form of
And
In the case of the slightly asymmetric disc, the mode shape functions and the corresponding eigenvalues for a rotating disc with a small imperfection can be written as follows:
where the eigenvalues of the mode pair are given by the following:
where is the eigenvalue of the axis-symmetric disc, and is the circular natural frequency. In the perfectly axis-symmetric disc, . Thus, in Equation (10) is related to the frequency split and included in the asymmetric disc model. But of the mode shape functions in Equation (8) is assumed to be negligible.
The mode shape functions obtained in Equations (8) and (9) are applied to the Hamilton principle of the friction-coupled system:
where
where and B stand for the contact area and the volume of the body, and and are the radial and tangential contact displacements, respectively. Here, , , and are the generalised force induced by the contact stresses in the , , and directions, respectively, to be derived as follows. It is noted that the in-plane stress distribution due to rotation is neglected by the assumption of the slow rotation of the brake disc application.
For the formulation of the contact kinematics, the position vector of the upper contact location is described on the un-deformed state of the disc surface as follows:
where is the contact displacement vector and
In the two-mode model with the th disc doublet mode, the displacement functions on the upper contact surface are reduced to the summation of the mode shape functions of the mode pair in Equation (8):
where the radial and tangential mode shape functions are obtained from the thin plate theory as follows:
It is noted that the mode shape functions are time-varying with respect to the stationary contact locations and they are referred to as the moving mode shape function [21,22]. At a contact location () fixed to the reference frame, the time-derivative of the moving mode shape functions can be taken as the reference [21,22]:
Therefore, the velocity vector at the contact location can be written in the form of two mode discretisation as follows:
The friction force vector at the contact location is expressed by the Coulomb’s friction law as follows:
where is the friction coefficient and the normal contact stress is obtained from the summation of the pre-stress and the normal load variation, such as
The contact stresses on the lower contact can be derived in a similar manner.
Therefore, the generalised force is obtained from the work performed by the friction and normal forces over both contact surfaces, such that
where is the inner vector product and denotes the lower contact.
By linearising Equation (11) at the equilibrium, taking the integration as and applying the two mode expansion form of Equations (17)–(19), the doublet-mode model can be written in the matrix form:
where the internal structural damping is not included in the model. is the circular natural frequency of the th disc doublet mode, is the slightly detuned frequency of as , and
It is noted that Equation (27) represents the analytical formulation for the two closely spaced frequency doublet mode pairs of the brake disc. This formulation significantly simplifies the stability analysis of the full vibration mode system presented in [22] while also providing valuable physical insights into the friction-engaged modal instability. The off-diagonal elements in the system matrices, specifically within the gyroscopic matrix and friction-coupled matrices, are known to contribute to system destabilisation in the eigenvalue analyses. Notably, the off-diagonal elements in S2 of the friction-coupled system matrices exhibit time-periodic behaviour. Consequently, this paper focuses on analysing the brake squeal propensity associated with the doublet mode pair in a brake disc with slightly asymmetric geometry.
It is also noteworthy that Equation (27) represents the homogeneous differential equations of motion for a self-excited vibration problem. When the pre-stress is not constant but oscillates with the brake cylinder, parametric excitation can be introduced into the brake system. This parametric excitation may induce dither, potentially affecting the system’s stability. However, the investigation of parametric excitation lies beyond the scope of this paper and is referenced in [34].
Here, the ratio of frequency split is set to be less than one percentile of the natural frequency as follows:
It is noted that the damping and stiffness matrices in EOM (27) are time-periodic with a period . But, the period of the system matrices is set to be a period per revolution as for any modes, which does not change the results. For determining the stability of the periodic time-varying system by the Floquet theory, EOM is written in the state-space form of of Equation (27) as follows:
where
The periodic time-varying system of Equation (35) is discretised by the time step (), and the transition matrix of each time step is calculated in the discretisation method [23,24,25,26], such that
The system is unstable if the largest modulus of the eigenvalues of the transition matrix in Equation (38) is larger than one and stable otherwise.
3. Results
The nominal values of the system parameters in the numerical calculation are brought from the automotive brake application. The geometry and material properties of the annular disc with a free boundary condition at the outer radius and clamped boundary condition at the inner radius used in the analysis are shown as Table 1. The operating condition is chosen to be 8 [bar] braking pressure and rotating speed. The natural frequencies of the freely stationary annular disc can be obtained by the boundary value analysis [9] as in Table 2, and the corresponding mode shapes are illustrated in Figure 2. From the assumption of the slightly asymmetric disc, the mode shape functions with small imperfections approximate those of the symmetric annular disc in Figure 2.

Table 2.
The natural frequencies of the transverse modes in the annular disc (Hz).
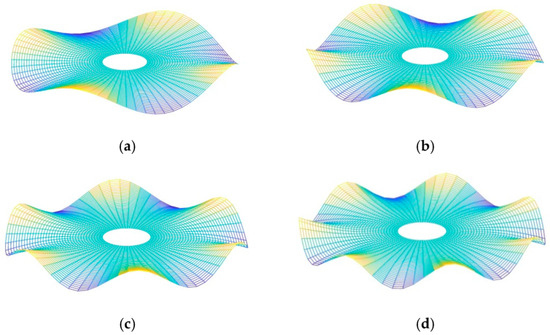
Figure 2.
Mode shapes, (a) , (b) , (c) , (d) .
For the numerical calculation of the transition matrix, the period over one revolution is discretised by the equally spacing time interval as . The number of the discretisation interval is chosen by the convergence check, as illustrated in Figure 3. For the unstable mode pairs, the modulus of critical eigenvalues is calculated with respect to . It is shown that the modulus converges to a fixed value as . Hereafter, is set to be 720 in the Floquet stability analysis.
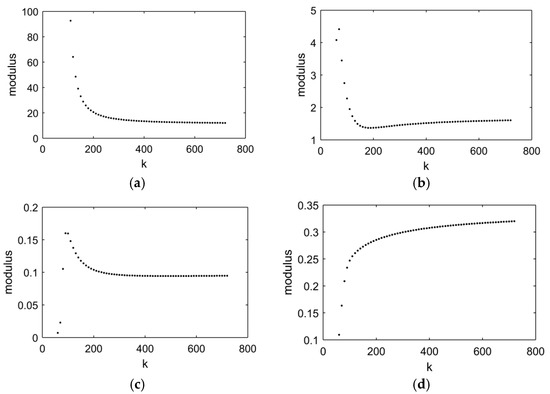
Figure 3.
Convergence at for (a) , (b) , (c) , (d) .
The analysis focuses on the effect of the mode splitting between the doublet mode pair on the stability of the time-periodic system. For this, the stability boundary is calculated with respect to the frequency split and one of the other important parameters such as the friction coefficient, the contact angle, and the contact stiffness. From the stability analysis, the mode pairs with are found to be stable at , so their results are excluded from this study.
Figure 4 illustrates the stability boundaries for the mode number in the and domain. For , 5, and 6, the minimum friction coefficient for the instability arises near , 0.3%, and 0.2%, respectively. For , the unstable region appears below . This reveals that the stability of the mode pair is highly dependent on the frequency split. Particularly, it is noted that the specific frequency split exists for the minimum friction coefficient generating the instability. It is interesting that zero frequency split does not maximise the squeal propensity. However, it is seen in Figure 4 that the mode pair under friction loading becomes more stable as the frequency split increases.
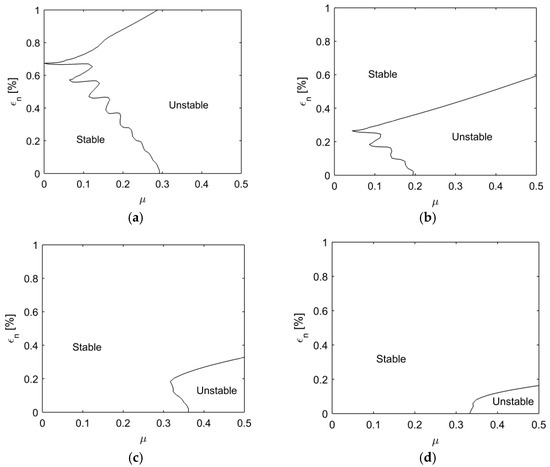
Figure 4.
Stability boundary of the doublet modes with respect to and for the unstable mode pair (a) , (b) , (c) , (d) .
Figure 5 shows the stability of the split mode pair () for the contact angle variation. In Figure 5a, the instability for occurs nearly above , but the stable region appears between and below . In Figure 5b for , the stability boundary lies near for , but the instability that occurs as is increased above . In Figure 4c,d, the instability arises for the smaller and the larger for and 7. It is notable that the critical contact span angle is much more susceptible as the mode number increases. For example, in , squeal occurs at 23 degrees for zero frequency split, but it disappears if a small amount of frequency split exists. In contrast, squeal does not disappear even if frequency split exists for .
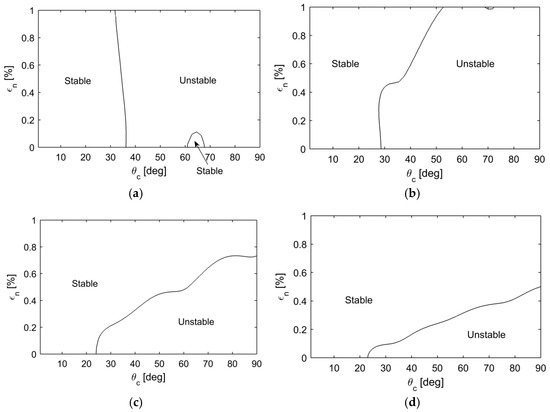
Figure 5.
Stability boundary of the doublet modes at with respect to and for the unstable mode pair (a) , (b) , (c) , (d) .
Similarly, Figure 6 demonstrates the instability of the split doublet mode with respect to the contact stiffness . The instability that occurs as increases and decreases for all of , 5, 6, and 7. This implies that the higher contact stiffness produces the higher propensity of the instability in the split mode pair under friction contact. The rate of change in critical contact stiffness over frequency split is increased as the mode number increases. Therefore, it is noted from Figure 4, Figure 5 and Figure 6 that the susceptibility of the frequency split on squeal is seen to increase as the mode number decreases.
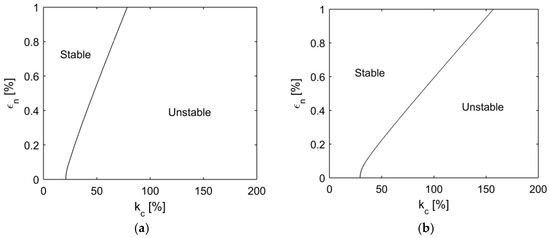
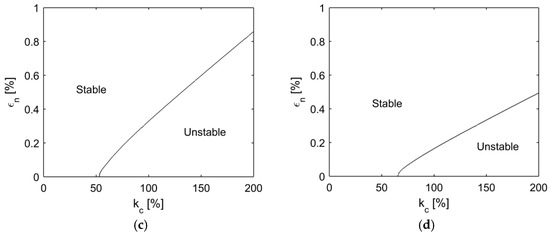
Figure 6.
Stability boundary of the doublet modes at with respect to and for the unstable mode pair (a) , (b) , (c) , (d) .
4. Conclusions
Based on the numerical results and Floquet stability analysis of the asymmetric disc subjected to friction contact, the following conclusions are drawn:
- Influence of Frequency Split on Modal Instability
- ○
- The frequency split significantly affects the modal instability of the doublet mode pair in the rotating disc brake system.
- ○
- For each mode number, there exists a specific frequency split that minimises the critical friction coefficient. This suggests that the highest squeal propensity occurs at a particular frequency split.
- Dependence on Mode Number
- ○
- The influence of frequency split on squeal propensity increases as the mode number decreases.
- ○
- Doublet modes with lower mode numbers are more susceptible to frequency split, making their squeal propensity more pronounced compared to those with higher mode numbers.
- Effect of Contact Parameters
- ○
- Variations in contact parameters, such as contact angle and stiffness, typically reduce the instability region as the frequency split increases.
- ○
- However, in certain ranges of contact angles, a decrease in frequency split can stabilise the system. This indicates that careful tuning of the frequency split between the doublet mode pair is crucial for mitigating friction-induced vibrations in slightly asymmetric discs.
By addressing these factors, the findings provide valuable insights for optimising the design of rotating disc systems to reduce squeal propensity and enhance stability.
Author Contributions
Conceptualization, J.K.; Methodology, D.S. and J.K.; Investigation, D.S.; Writing—original draft, D.S. and J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kinkaid, N.M.; O’Reilly, O.M.; Papadopoulos, P. Automotive disc brake squeal. J. Sound Vib. 2003, 267, 105–166. [Google Scholar] [CrossRef]
- Ouyang, H.; Nack, W.; Yuan, Y.; Chen, F. Numerical analysis of automotive disc brake squeal: A review. Int. J. Veh. Noise Vib. 2005, 1, 207–231. [Google Scholar] [CrossRef]
- Nack, W.V. Brake squeal analysis by finite elements. Int. J. Veh. Des. 2000, 23, 263–275. [Google Scholar] [CrossRef]
- Bajer, A.; Belsky, V.; Zeng, L. Combining a Nonlinear Static Analysis and Complex Eigenvalue Extraction in Brake Squeal Simulation; Technical Report. 2003-01-3349; SAE: Warrendale, PA, USA, 2003. [Google Scholar]
- Mo, J.; Wnag, Z.; Chen, G.; Shao, T.; Zhu, M.; Zhou, Z. The effect of groove-textured surface on friction and wear and friction-induced vibration and noise. Wear 2013, 301, 671–681. [Google Scholar] [CrossRef]
- Jibiki, T.; Shima, M.; Akita, H.; Tamura, M. A basic study of friction noise caused by fretting. Wear 2001, 251, 1492–1503. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, Z.; Leo, V. Effect of surface topography on formation of squeal under reciprocating sliding. Wear 2002, 253, 411–423. [Google Scholar]
- Flint, J.; Hulten, J. Lining-deformation-induced modal coupling as squeal generator in a distributed parameter disc brake model. J. Sound Vib. 2002, 254, 1–21. [Google Scholar] [CrossRef]
- Kang, J.; Krousgrill, C.M.; Sadeghi, F. Dynamic instability of a thin circular plate with friction interface and its application to disc brake squeal. J. Sound Vib. 2008, 316, 164–179. [Google Scholar] [CrossRef]
- Kang, J.; Krousgrill, C.M.; Sadeghi, F. Analytical formulation of mode-coupling instability in disc-pad coupled system. Int. J. Mech. Sci. 2009, 51, 52–63. [Google Scholar] [CrossRef]
- Kang, J.; Krousgrill, C.M.; Sadeghi, F. Comprehensive stability analysis of disc brake: Gyroscopic, negative slope and mode-coupling instability. J. Sound Vib. 2009, 324, 387–407. [Google Scholar] [CrossRef]
- Stender, M.; Tiedemann, M.; Hoffmann, N.; Oberst, S. Impact of an irregular friction formulation on dynamics of a minimal model for brake squeal. Mech. Syst. Signal Process. 2018, 107, 439–451. [Google Scholar] [CrossRef]
- Pugi, L.; Rosano, G.; Viviani, R.; Cabrucci, L.; Bocciolini, L. Modeling, testing and validation of the vibrational behavior of a dynamometric test rig for railway braking systems. World J. Eng. 2023, 21, 425–442. [Google Scholar] [CrossRef]
- Oberst, S.; Lai, J. Statistical analysis of brake squeal noise. J. Sound Vib. 2011, 330, 2978–2994. [Google Scholar] [CrossRef]
- Gilsovic, J.; Radonjic, R.; Miloradovic, D. Experimental method for analyzing friction phenomenon related to drum brake squeal. Tribol. Ind. 2010, 32, 28–35. [Google Scholar]
- Zainudin, M.; Baker, A. Preventing disc brake squeal using a thin plate shim. Int. J. Veh. Strc. Sys. 2012, 4, 23–27. [Google Scholar]
- Wu, Y.; Tang, B.; Xiang, Z.; Qian, H.; Mo, J.; Zhou, Z. Brake squeal of a high-speed train for different friction block configurations. Appl. Aoustics 2021, 171, 107540. [Google Scholar] [CrossRef]
- Renault, A.; Massa, F.; Lallemand, B.; Tison, T. Experimental investigations for uncertainty quantification in brake squeal analysis. J. Sound Vib. 2016, 367, 37–55. [Google Scholar] [CrossRef]
- Kang, J. Squeal analysis of gyroscopic disc brake system based on finite element method. Int. J. Mech. Sci. 2009, 51, 284–294. [Google Scholar] [CrossRef]
- Huang, J.; Krousgrill, C.M.; Bajaj, A.K. Modeling of automotive drum brake for squeal and parameter sensitivity analysis. J. Sound Vib. 2006, 289, 245–263. [Google Scholar] [CrossRef]
- Kang, J. Automotive brake squeal analysis with rotating finite elements of asymmetric disc in time. J. Sound Vib. 2017, 393, 388–400. [Google Scholar] [CrossRef]
- Kang, J. Moving mode shape function approach for spinning disk and asymmetric disc brake squeal. J. Sound Vib. 2018, 424, 48–63. [Google Scholar] [CrossRef]
- Chang, J.Y.; Wickert, J.A. Measurement and analysis of modulated doublet mode response in mock bladed disks. J. Sound Vib. 2002, 250, 379–400. [Google Scholar] [CrossRef]
- Yu, R.C.; Mote, C.D. Vibration and parametric excitation in asymmetric circular plates under moving loads. J. Sound Vib. 1987, 119, 409–427. [Google Scholar] [CrossRef]
- Touze, C.; Thomas, O.; Chaigne, A. Asymmetric non-linear forced vibrations of free-edge circular plates. Part 1: Theory. J. Sound Vib. 2002, 258, 649–676. [Google Scholar] [CrossRef]
- de Felice, A.; Sorrentino, S. Effects of anisotropic supports on the stability of parametrically excited slender rotors. Nonlinear Dyn. 2022, 109, 793–813. [Google Scholar] [CrossRef]
- Fakas, M. Periodic Motions; Springer: New York, NY, USA, 1994. [Google Scholar]
- Richards, J. Analysis of Periodic Time-Varying Systems; Springer: New York, NY, USA, 2011. [Google Scholar]
- Insperger, T.; Stepan, G. Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int. J. Numer. Methods Eng. 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. A full-discretization method for prediction of milling stability. Int. J. Mach. Tools Manuf. 2010, 50, 502–509. [Google Scholar] [CrossRef]
- Fan, S.; Hong, L.; Jiang, J. Model reduction of high-dimensional self-excited nonlinear system using Floquet theory based parameterization method. Nonlinear Dyn. 2025, 113, 1137–1161. [Google Scholar] [CrossRef]
- Hou, L.; Chen, H.; Chen, Y.; Lu, K.; Liu, Z. Bifurcation and stability analysis of a nonlinear rotor system subjected to constant excitation and rub-impact. Mech. Syst. Signal Process. 2019, 125, 65–78. [Google Scholar] [CrossRef]
- Frulla, G. Rigid rotor dynamic stability using Floquet theory. Eur. J. Mech.-A/Solids 2000, 19, 139–150. [Google Scholar] [CrossRef]
- Tentarelli, M.; Cantelli, S.; Sorrentino, S.; De Felice, A. Parametric excitation as a cause of clutch judder: Theoretical study and experimental validation. Mech. Syst. Signal Process. 2023, 193, 110256. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).