Friction in Cylindrical Joints
Abstract
1. Introduction
2. Materials and Methods
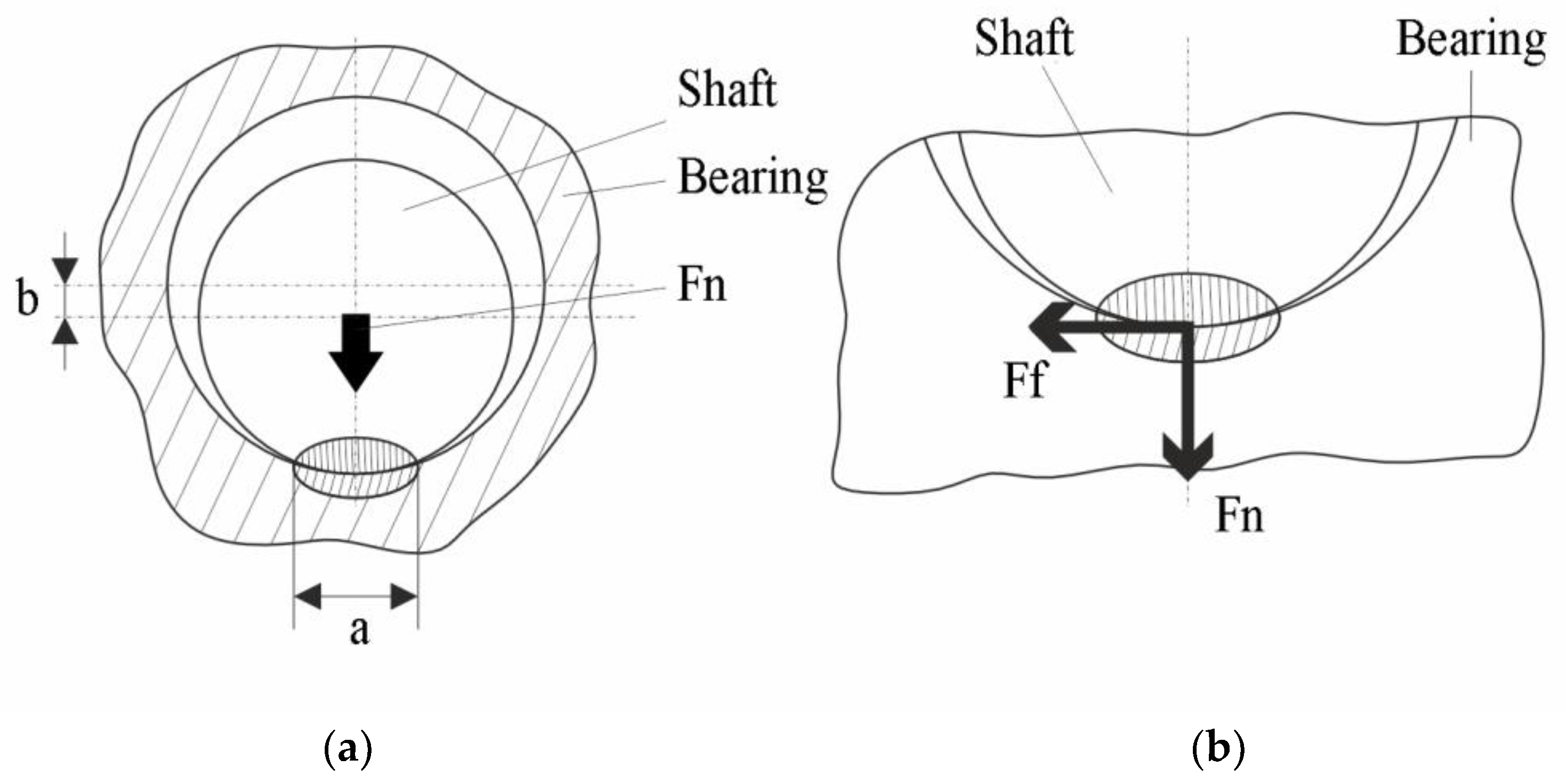
2.1. Friction Processes in Cylindrical Joints with Clearance
- −
- The magnitude of the normal force Fn;
- −
- The diameter d of the circular cross-section through the spindle and the diameter D of the circular section through the bore in which the spindle is located, along with the length of the contact area between the spindle and the bearing;
- −
- The nature and some physical-mechanical properties of the properties of the materials from which the spindle and the sliding bearing bushing are made;
- −
- The heights of the asperities on the surfaces in contact with the spindle and the shaft;
- −
- The presence and lubricating properties of the eventual lubricant are located between the spindle and the bearing.
2.2. Modeling by the Finite Element Method of Specific Aspects of the Functioning of a Cylindrical Joint
2.3. Conditions for Conducting Experimental Tests
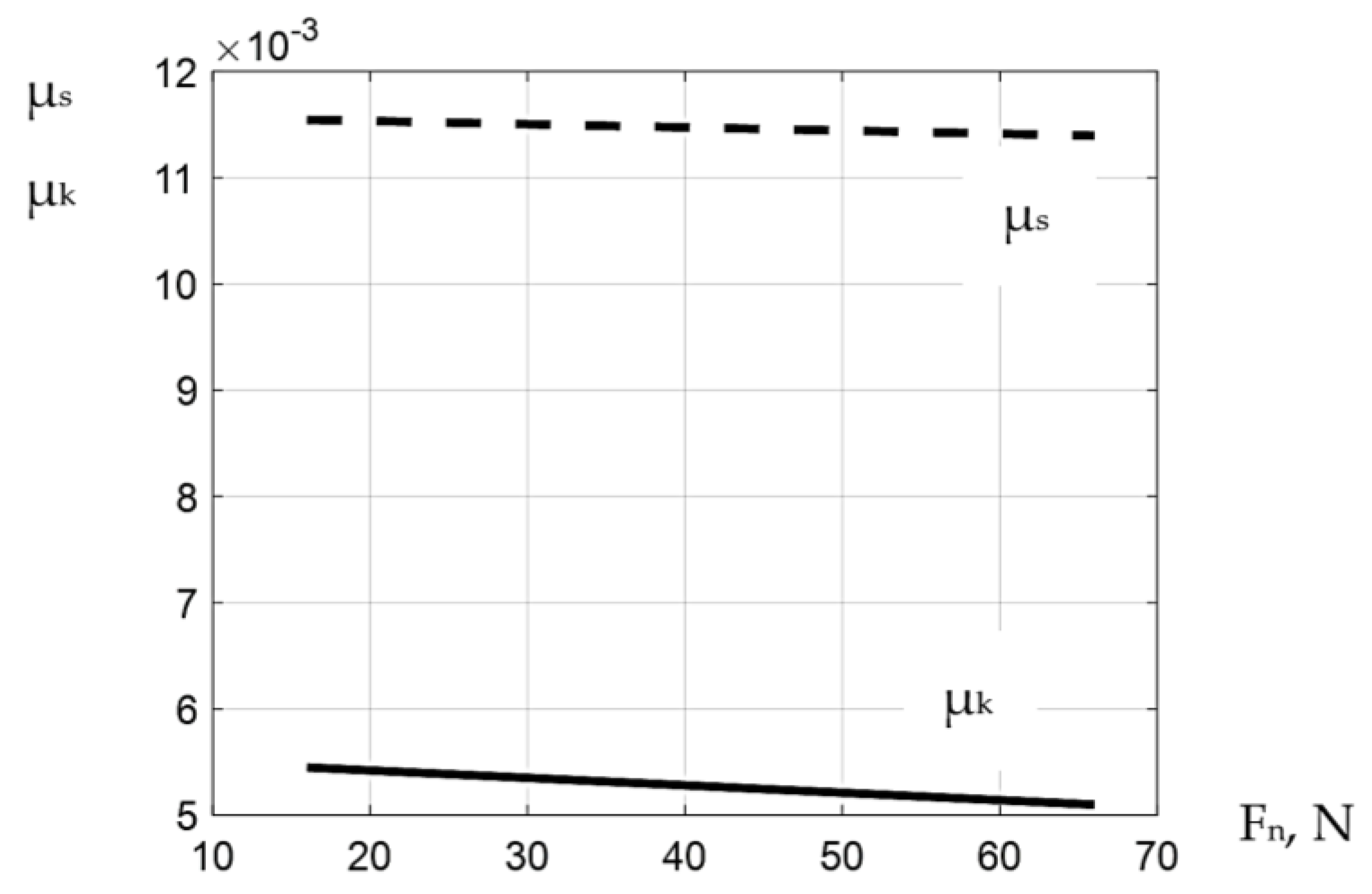
3. Results
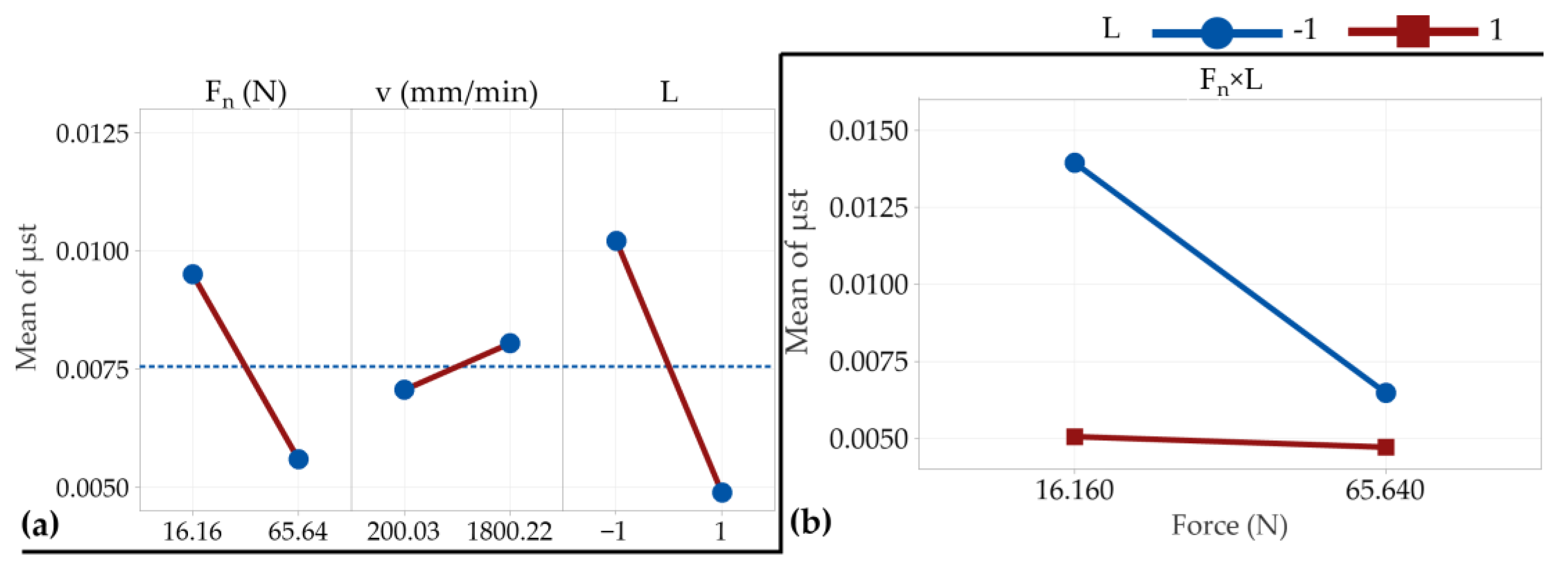
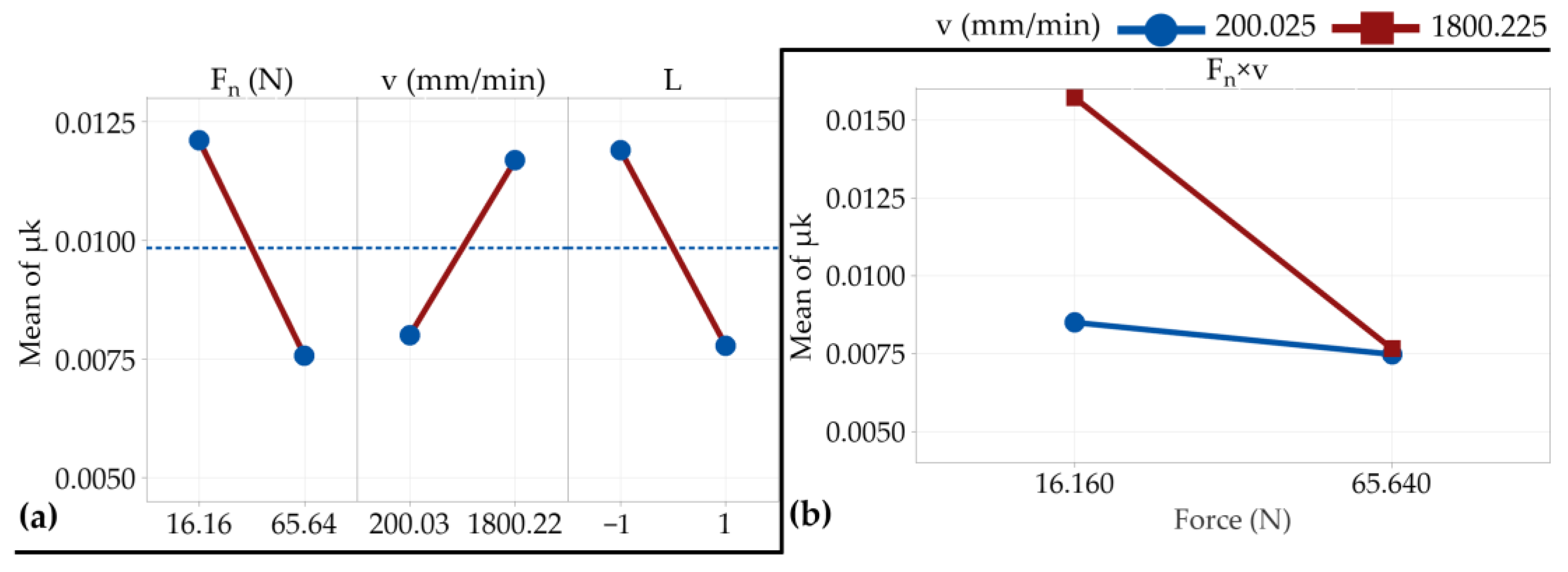
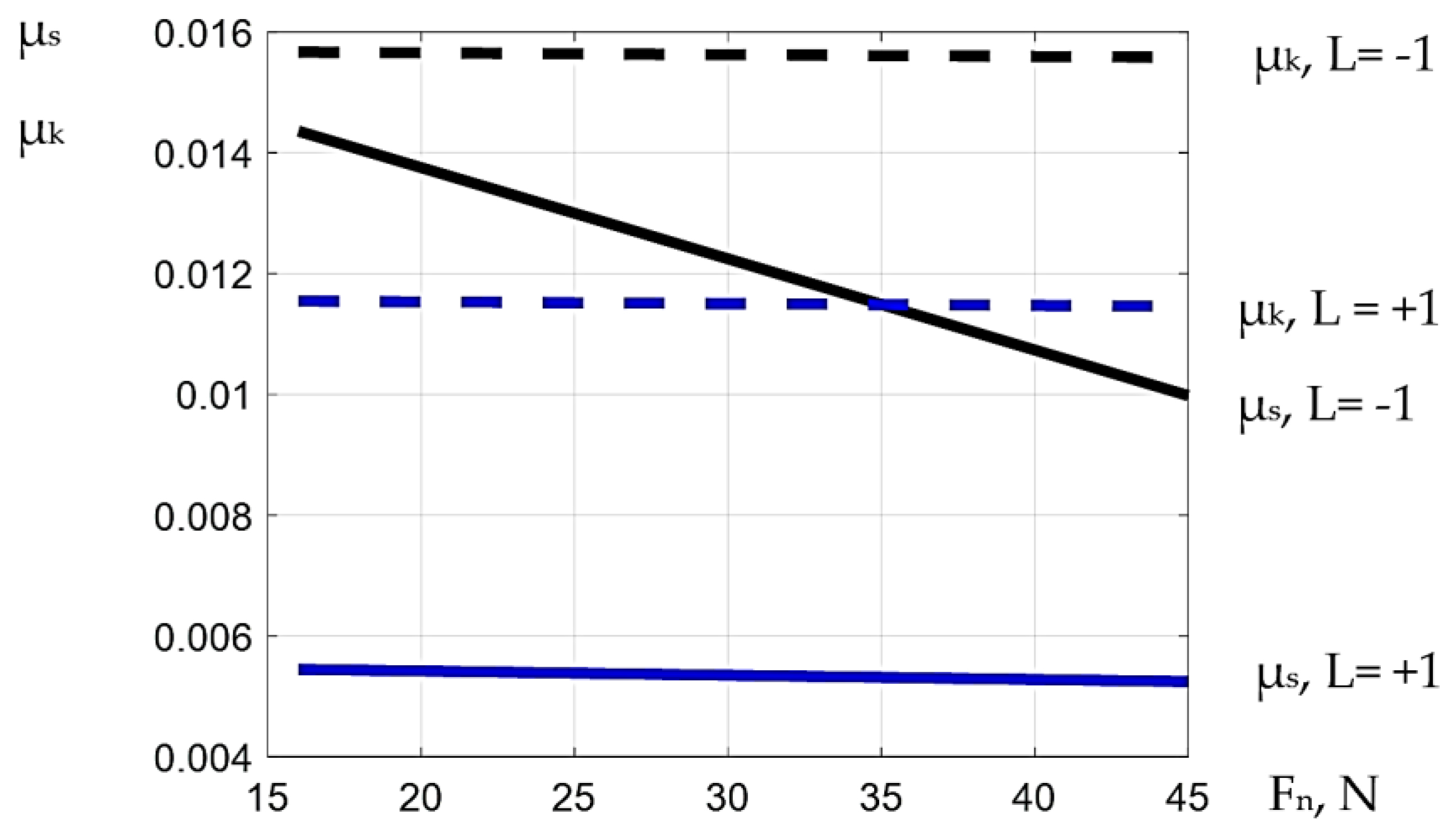
3.1. Variables Effects
3.2. Regression Analysis
4. Conclusions
- The finite element modeling of the friction processes in cylindrical clearance joints facilitated the evaluation of the equivalent stresses for different dimensions of the clearance between the shaft and the bore.
- An adaptable device was designed and adapted on a universal lathe to facilitate the measurement of the magnitudes of the friction force under controlled conditions, allowing the variation of the normal force, the relative velocity, and the lubrication.
- Experimental tests were carried out to evaluate the influence of key factors, such as the magnitude of the normal force, the relative velocity between the shaft and the bore, and the presence or absence of a lubricant, on the magnitude of the static and kinetic friction coefficients. The experiments were conducted using a full factorial experiment with three independent variables, each tested at two levels of variation.
- The experimental results were processed mathematically using specialized software. Empirical mathematical models of the first-degree polynomial type were determined. These empirical mathematical models quantify the influence of each input factor on the static and kinetic friction coefficients.
- Among the factors studied, the presence or absence of lubricant was identified as having the most significant impact on the magnitudes of both friction coefficients.
- Future research aims to investigate various other material pairs for cylindrical clearance joint components and to incorporate additional input factors into the experiments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, Q.; Liu, C.; Machado, M.; Flores, P. A new model for dry and lubricated cylindrical joints with clearance in spatial flexible multibody systems. Nonlinear Dyn. 2011, 64, 25–47. [Google Scholar] [CrossRef]
- Theory for Friction in Joints. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.mbd/mbd_ug_theory.4.20.html (accessed on 11 November 2024).
- Todi-Eftimie, A.; Bobancu, S.; Gavrila, C.; Eftimie, L. Static friction coefficient into cylindrical joints assemblies. Tribol. Ind. 2015, 37, 421–426. Available online: https://www.tribology.rs/journals/2015/2015-4/4.pdf (accessed on 14 September 2024).
- Liu, C.; Zhang, K.; Yang, L. Compliance contact model of cylindrical joints with clearances. Acta Mech. Sin. 2005, 21, 451–458. Available online: https://link.springer.com/article/10.1007/s10409-005-0061-7 (accessed on 17 September 2024). [CrossRef]
- Stamenkovic, D.; Milosevic, M.; Mijajlovic, M.; Banic, M. Estimation of the static friction coefficient for press fit joints. J. Balk. Tribol. Asso. 2011, 17, 341–355. Available online: https://www.researchgate.net/publication/241688933_Estimation_of_the_static_friction_coefficient_for_press_fit_joints (accessed on 17 September 2024).
- Tadić, B.; Kočović, V.; Matejić, M.; Brzaković, L.; Mijatović, M.; Vukelić, Đ. Static coefficient of rolling friction at high contact temperatures and various contact pressure. Tribol. Ind. 2016, 38, 83–89. Available online: https://www.researchgate.net/publication/301043681_Static_Coefficient_of_Rolling_Friction_at_High_Contact_Temperatures_and_Various_Contact_Pressure (accessed on 19 September 2024).
- Rung, S.; Bokan, K.; Kleinwort, F.; Schwarz, S.; Simon, P.; Klein-Wiele, J.-H.; Esen, C.; Hellmann, R. Possibilities of dry and lubricated friction modification enabled by different ultrashort laser-based surface structuring methods. Lubricants 2019, 7, 43. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Jamari, J.; Wicaksono, A.A.; Muchammad, M.; Susilowati, S.; Ngatilah, Y.; Pujiastuti, C. CFD analysis of journal bearing with a heterogeneous rough/smooth surface. Lubricants 2021, 9, 88. [Google Scholar] [CrossRef]
- Millan, P.; Pagaimo, J.; Magalhães, H.; Ambrósio, J. Clearance joints and friction models for the modelling of friction damped railway freight vehicles. Multibody Syst. Dyn. 2023, 58, 21–45. [Google Scholar] [CrossRef]
- Aleem, M.; Saad, A.A.; Sohail, A.; Siraj, S.M.; Reddy, M.R. Design and analysis of drum brakes. Int. J. Adv. Innov. Res. 2018, 10, 0348–0354. Available online: https://www.ijatir.org/uploads/541362IJATIR16691-64.pdf (accessed on 21 September 2024).
- Dinescu, I.; Bardocz, G. Experimental research on the variation of coefficient of friction in sliding bearings. Științe Teh. Și Mat. Apl. 2006, 7–14. Available online: https://www.afahc.ro/ro/revista/Nr_1_2006/1.pdf (accessed on 22 September 2024). (In Romanian).
- Leonov, O.A.; Shkaruba, N.Z.; Vergazova, Y.G. Calculation of the maximum functional clearance of a cylindrical joint between a steel shaft and a cast iron sprocke. CIS Iron Steel Rev. 2024, 27, 108–112. Available online: https://rudmet.net/media/articles/Article_CIS_2024_27_pp.108-112.pdf (accessed on 22 September 2024). [CrossRef]
- Qiu, T.; Yan, L.; Wang, F.; Xie, H.; Shui, Y.; Zhang, T.; Jiang, F. Research advances of Rehbinder effect in material removal process. China Surf. Eng. 2024, 37, 59–74. [Google Scholar] [CrossRef]
- Chaudhari, A.; Soh, Z.Y.; Wang, H.; Kumar, A. Senthil. Rehbinder effect in ultraprecision machining of ductile materials. Int. J. Mach. Tools Manuf. 2018, 133, 47–60. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Qin, L.; Guo, Z.; Lu, Z.; Zhao, X.; Dong, H.; Xiao, Q. Friction and wear properties of a novel interface of ordered microporous Ni-based coating combined with MoS2 under complex working conditions. Tribol. Int. 2023, 189, 108970. [Google Scholar] [CrossRef]
- Liu, X.; Guo, Z.; Lu, Z.; Qin, L. Tribological behavior of the wear-resistant and self-lubrication integrated interface structure with ordered micro-pits. Surf. Coat. Technol. 2023, 454, 129159. [Google Scholar] [CrossRef]
- Kamga, L.S.; Meffert, D.; Magyar, B.; Oehler, M.; Sauer, B. Simulative investigation of the influence of surface texturing on the elastohydrodynamic lubrication in chain joints. Tribol. Int. 2022, 171, 107564. [Google Scholar] [CrossRef]
- Pereira, C.; Ambrosio, J.; Ramalho, A. Contact mechanics in cylindrical clearance revolute joints. Appl. Mech. Mater. 2013, 365–366, 412–415. [Google Scholar] [CrossRef]
- Pereira, C.; Ramalho, A.; Ambrosio, J. Applicability domain of internal cylindrical contact force models. Mech. Mach. Theory 2014, 78, 141–157. [Google Scholar] [CrossRef]
- Liu, C.-S.; Zhang, K.; Yang, R. The FEM analysis and approximate model for cylindrical joints with clearances. Mech. Mach. Theory 2007, 42, 183–197. [Google Scholar] [CrossRef]
- Lookman, T.; Balachandran, P.V.; Xue, D.; Hogden, J.; Theiler, J. Statistical inference and adaptive design for materials discovery. Curr. Opin. Solid State Mater. Sci. 2017, 21, 121–128. [Google Scholar] [CrossRef]
- Sutton, A.P. Materials by design. In Concepts of Materials Science, Online ed.; Oxford Academic: Oxford, UK, 2021. [Google Scholar] [CrossRef]
- Hong, X.; Xu, H.; Xu, Y.; Huang, T.; Guo, Y.; Zhang, J.; Peng, Y. Study on spinning process parameters of the copper bushing by tribological properties and physical testing. In Proceedings of the 2021 2nd International Conference on Applied Physics and Computing (ICAPC 2021), Ottawa, Canada, 8–10 September 2021; Volume 2083, p. 022084. [Google Scholar] [CrossRef]
- Copper Bushing for Crawler Crane Track Roller. Available online: https://www.tradekorea.com/product/detail/P757318/Copper-bushing-for-crawler-crane-track-roller-.html (accessed on 20 January 2025).
- Automobile Copper Bushing. Available online: https://www.indiamart.com/proddetail/automobile-copper-bushing-1894301530.html?srsltid=AfmBOopsQbMRPvZF5_GzVWmXrQ2MW_uvva33BFLVSAiGqaazcetjqzOU (accessed on 20 January 2025).








| Input Factors | Static Friction Force | Kinetic Friction Force | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Run No. | Normal Force, Fn, N | Travel Speed, v, mm/min | Lubrication, L | Meas. | Avg. | St. Dev. | Ffs | μs | Meas. | Avg. | St. Dev. | Ffk | μk |
| 1.1 | 16.16 | 200.025 | −1 | 0.080 | 0.081 | 0.010 | 0.217 | 0.0135 | 0.165 | 0.162 | 0.026 | 0.435 | 0.0100 |
| 1.2 | 0.075 | 0.120 | |||||||||||
| 1.3 | 0.085 | 0.160 | |||||||||||
| 1.4 | 0.070 | 0.180 | |||||||||||
| 1.5 | 0.095 | 0.185 | |||||||||||
| 2.1 | 16.16 | 200.025 | 1 | 0.025 | 0.030 | 0.004 | 0.081 | 0.0050 | 0.090 | 0.113 | 0.018 | 0.303 | 0.0070 |
| 2.2 | 0.030 | 0.105 | |||||||||||
| 2.3 | 0.035 | 0.110 | |||||||||||
| 2.4 | 0.030 | 0.125 | |||||||||||
| 2.5 | 0.030 | 0.135 | |||||||||||
| 3.1 | 16.16 | 1800.225 | −1 | 0.080 | 0.087 | 0.007 | 0.234 | 0.0054 | 0.250 | 0.287 | 0.022 | 0.770 | 0.0178 |
| 3.2 | 0.090 | 0.295 | |||||||||||
| 3.3 | 0.095 | 0.285 | |||||||||||
| 3.4 | 0.080 | 0.300 | |||||||||||
| 3.5 | 0.090 | 0.305 | |||||||||||
| 4.1 | 16.16 | 1800.225 | 1 | 0.020 | 0.031 | 0.010 | 0.083 | 0.0019 | 0.180 | 0.221 | 0.024 | 0.593 | 0.0137 |
| 4.2 | 0.045 | 0.220 | |||||||||||
| 4.3 | 0.025 | 0.240 | |||||||||||
| 4.4 | 0.035 | 0.235 | |||||||||||
| 4.5 | 0.030 | 0.230 | |||||||||||
| 5.1 | 65.64 | 200.025 | −1 | 0.175 | 0.150 | 0.020 | 0.403 | 0.0023 | 0.680 | 0.635 | 0.067 | 1.704 | 0.0097 |
| 5.2 | 0.140 | 0.665 | |||||||||||
| 5.3 | 0.145 | 0.680 | |||||||||||
| 5.4 | 0.125 | 0.630 | |||||||||||
| 5.5 | 0.165 | 0.520 | |||||||||||
| 6.1 | 65.64 | 200.025 | 1 | 0.085 | 0.090 | 0.013 | 0.242 | 0.0014 | 0.250 | 0.348 | 0.077 | 0.934 | 0.0053 |
| 6.2 | 0.070 | 0.375 | |||||||||||
| 6.3 | 0.100 | 0.285 | |||||||||||
| 6.4 | 0.100 | 0.430 | |||||||||||
| 6.5 | 0.095 | 0.400 | |||||||||||
| 7.1 | 65.64 | 1800.225 | −1 | 0.205 | 0.167 | 0.025 | 0.448 | 0.0025 | 0.715 | 0.667 | 0.103 | 1.790 | 0.0102 |
| 7.2 | 0.165 | 0.640 | |||||||||||
| 7.3 | 0.145 | 0.500 | |||||||||||
| 7.4 | 0.175 | 0.715 | |||||||||||
| 7.5 | 0.145 | 0.765 | |||||||||||
| 8.1 | 65.64 | 1800.225 | 1 | 0.145 | 0.141 | 0.011 | 0.378 | 0.0021 | 0.335 | 0.339 | 0.016 | 0.910 | 0.0052 |
| 8.2 | 0.135 | 0.345 | |||||||||||
| 8.3 | 0.145 | 0.340 | |||||||||||
| 8.4 | 0.125 | 0.360 | |||||||||||
| 8.5 | 0.155 | 0.315 | |||||||||||
| Source | DF | Seq SS | Contrib. | Adj SS | Adj MS | F-Value | p-Value | VIF |
|---|---|---|---|---|---|---|---|---|
| Regression | 4 | 0.000573 | 93.40% | 0.000573 | 0.000143 | 123.86 | 0.000 | |
| Fn | 1 | 0.000153 | 24.90% | 0.000279 | 0.000279 | 241.44 | 0.000 | 2.00 |
| v | 1 | 0.000010 | 1.59% | 0.000010 | 0.000010 | 8.41 | 0.006 | 1.00 |
| L | 1 | 0.000283 | 46.20% | 0.000283 | 0.000283 | 245.08 | 0.000 | 1.00 |
| Fn L | 1 | 0.000127 | 20.72% | 0.000127 | 0.000127 | 109.89 | 0.000 | 2.00 |
| Error | 35 | 0.000040 | 6.60% | 0.000040 | 0.000001 | |||
| Lack-of-Fit | 3 | 0.000005 | 0.80% | 0.000005 | 0.000002 | 1.48 | 0.240 | |
| Pure Error | 32 | 0.000036 | 5.80% | 0.000036 | 0.000001 | |||
| Total | 39 | 0.000613 | 100.00% |
| S | R2 | R2(adj) | PRESS | R2(pred) | AICc | BIC |
|---|---|---|---|---|---|---|
| 0.0010750 | 93.40% | 92.65% | 0.0000528 | 91.38% | −424.11 | −416.52 |
| Source | DF | Seq SS | Contrib. | Adj SS | Adj MS | F-Value | p-Value | VIF |
|---|---|---|---|---|---|---|---|---|
| Regression | 4 | 0.000636 | 91.90% | 0.000636 | 0.000159 | 99.31 | 0.000 | |
| Fn | 1 | 0.000206 | 29.77% | 0.000206 | 0.000206 | 128.65 | 0.000 | 1.00 |
| v | 1 | 0.000136 | 19.71% | 0.000136 | 0.000136 | 85.17 | 0.000 | 1.00 |
| L | 1 | 0.000170 | 24.55% | 0.000170 | 0.000170 | 106.13 | 0.000 | 1.00 |
| Fn × v | 1 | 0.000124 | 17.88% | 0.000124 | 0.000124 | 77.28 | 0.000 | 1.00 |
| Error | 35 | 0.000056 | 8.10% | 0.000056 | 0.000002 | |||
| Lack-of-Fit | 3 | 0.000005 | 0.73% | 0.000005 | 0.000002 | 1.06 | 0.382 | |
| Pure Error | 32 | 0.000051 | 7.37% | 0.000051 | 0.000002 | |||
| Total | 39 | 0.000692 | 100.00% |
| S | R2 | R2(adj) | PRESS | R2(pred) | AIC | BIC |
|---|---|---|---|---|---|---|
| 0.0012651 | 91.90% | 90.98% | 0.0000732 | 89.42% | −411.09 | −403.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihalache, A.M.; Merticaru, V.; Ermolai, V.; Dodun, O.; Nagiț, G.; Hrițuc, A.; Rîpanu, M.I.; Slătineanu, L. Friction in Cylindrical Joints. Lubricants 2025, 13, 66. https://doi.org/10.3390/lubricants13020066
Mihalache AM, Merticaru V, Ermolai V, Dodun O, Nagiț G, Hrițuc A, Rîpanu MI, Slătineanu L. Friction in Cylindrical Joints. Lubricants. 2025; 13(2):66. https://doi.org/10.3390/lubricants13020066
Chicago/Turabian StyleMihalache, Andrei Marius, Vasile Merticaru, Vasile Ermolai, Oana Dodun, Gheorghe Nagiț, Adelina Hrițuc, Marius Ionuț Rîpanu, and Laurențiu Slătineanu. 2025. "Friction in Cylindrical Joints" Lubricants 13, no. 2: 66. https://doi.org/10.3390/lubricants13020066
APA StyleMihalache, A. M., Merticaru, V., Ermolai, V., Dodun, O., Nagiț, G., Hrițuc, A., Rîpanu, M. I., & Slătineanu, L. (2025). Friction in Cylindrical Joints. Lubricants, 13(2), 66. https://doi.org/10.3390/lubricants13020066








