The Influence of Initial Solution Estimate Method on Efficient Boundary Element Modeling of Rolling Contact
Abstract
1. Introduction
1.1. The Accurate Solution
1.2. The Simplified Solution
1.3. The Purpose of This Paper
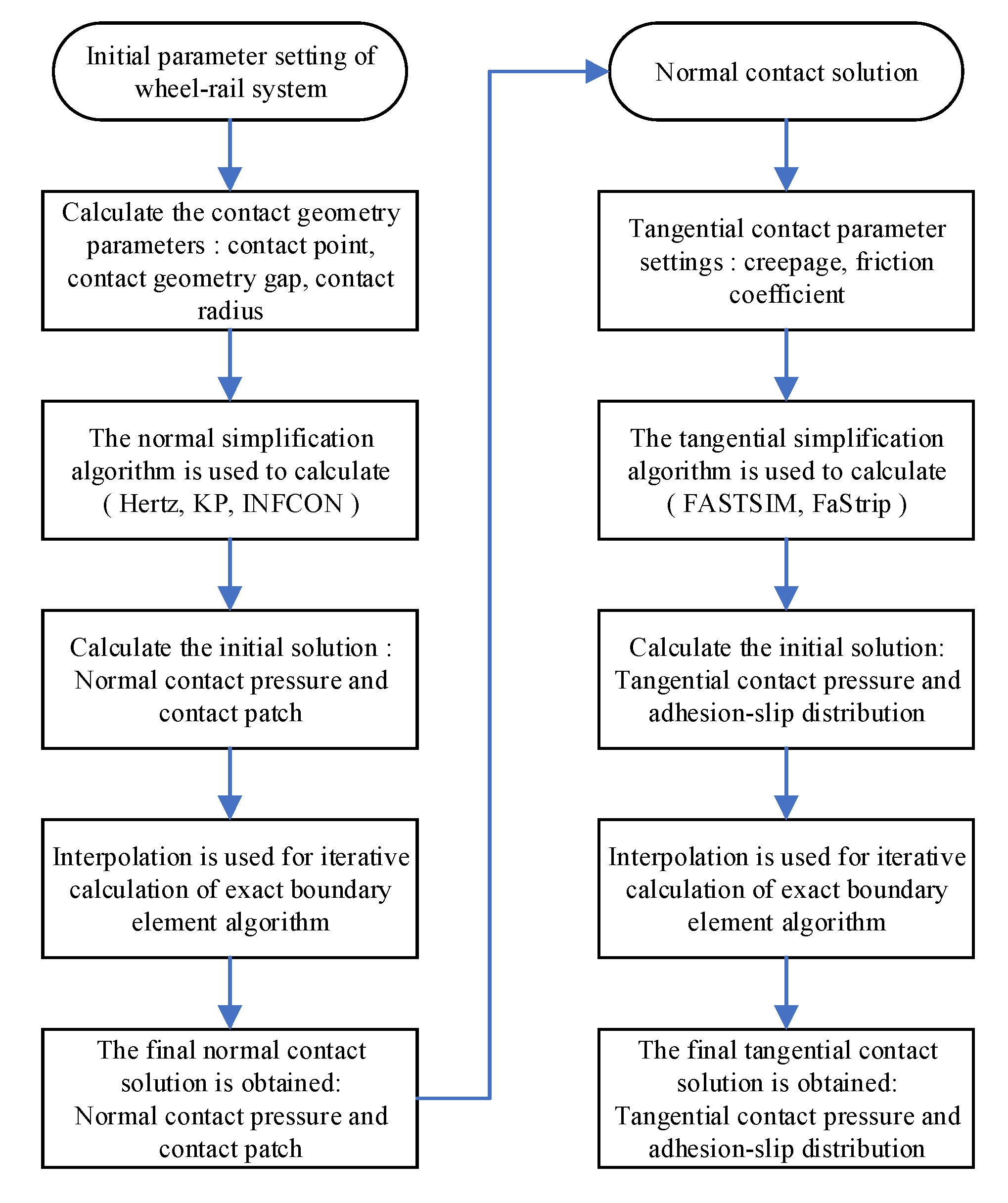
2. Methodology of Initial Estimate on Normal Contact
2.1. Iterative Calculation of Normal Contact Using BEM
2.2. Initial Estimate Using Simplified Normal Contact Models
2.2.1. Hertz Contact Theory
2.2.2. Kik–Piotrowski’s Approximate Method
2.2.3. An–Wang’s Model (INFCON)
3. Methodology of Initial Estimate on Tangential Contact
3.1. Iterative Calculation of Tangential Contact Using BEM
3.2. Initial Estimate Using Simplified Tangential Contact Models
3.2.1. Kalker’s Simplification Theory and Its Numerical Algorithm
3.2.2. Sichani–Enblom–Berg’s Numerical Algorithm
4. Results and Discussions
4.1. The Influence of Initial Estimate on Normal Contact
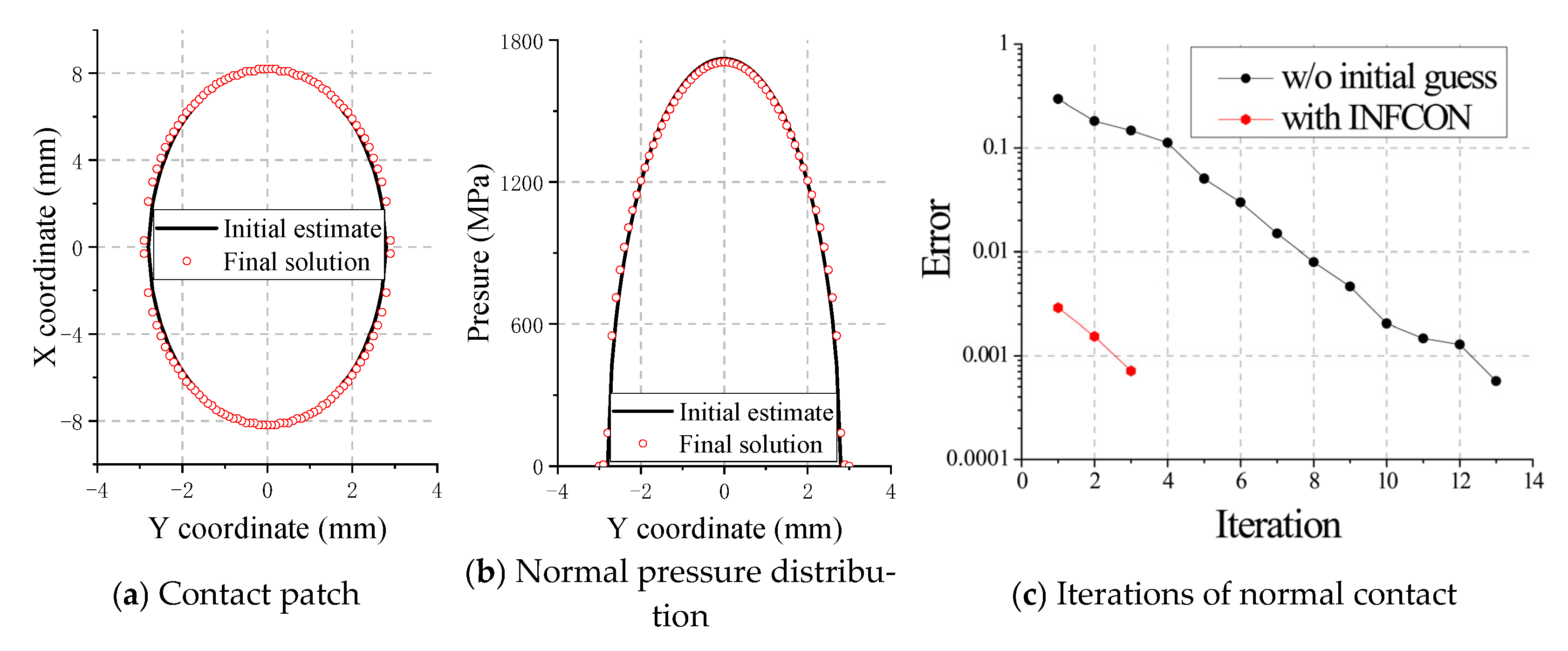
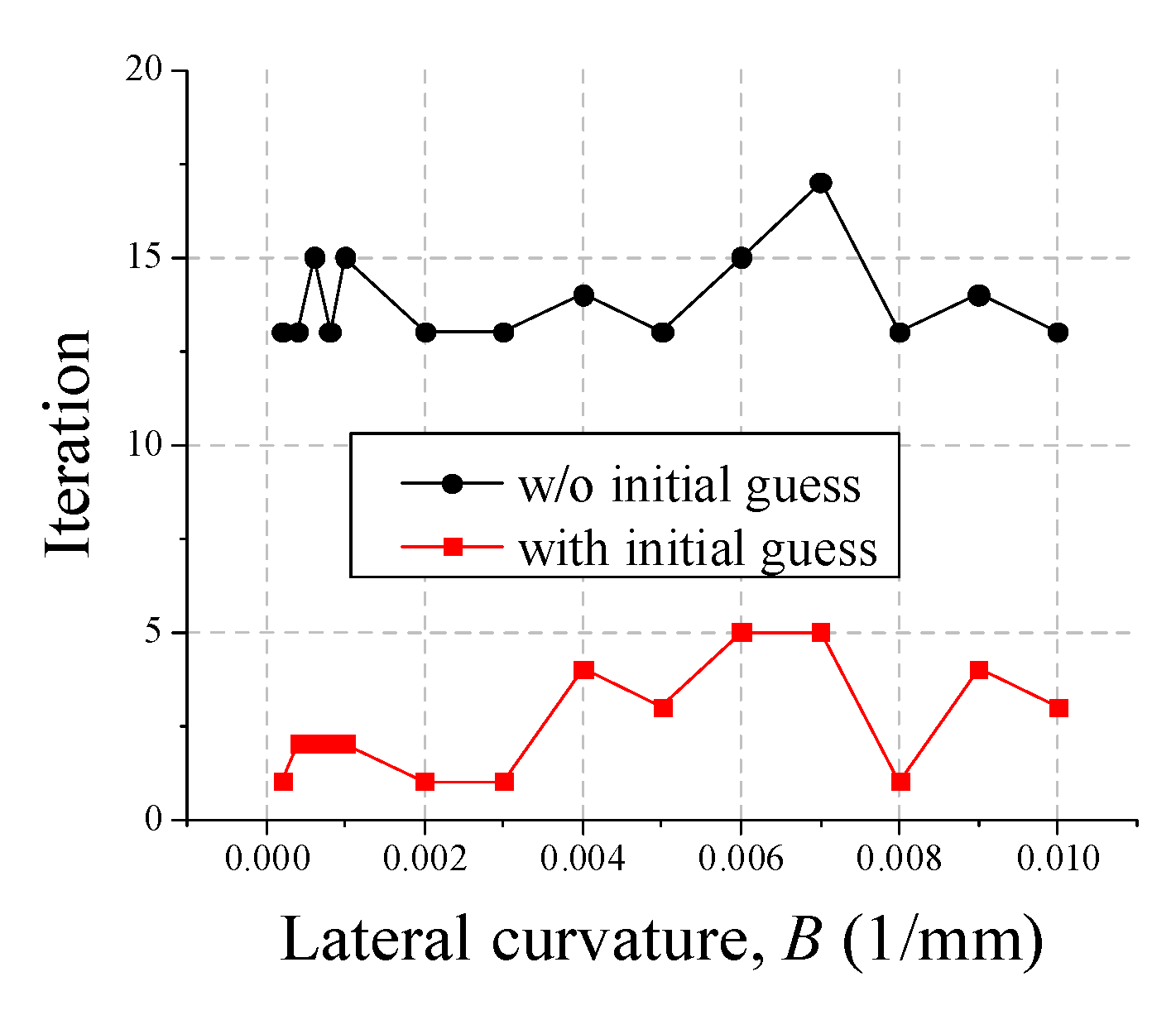
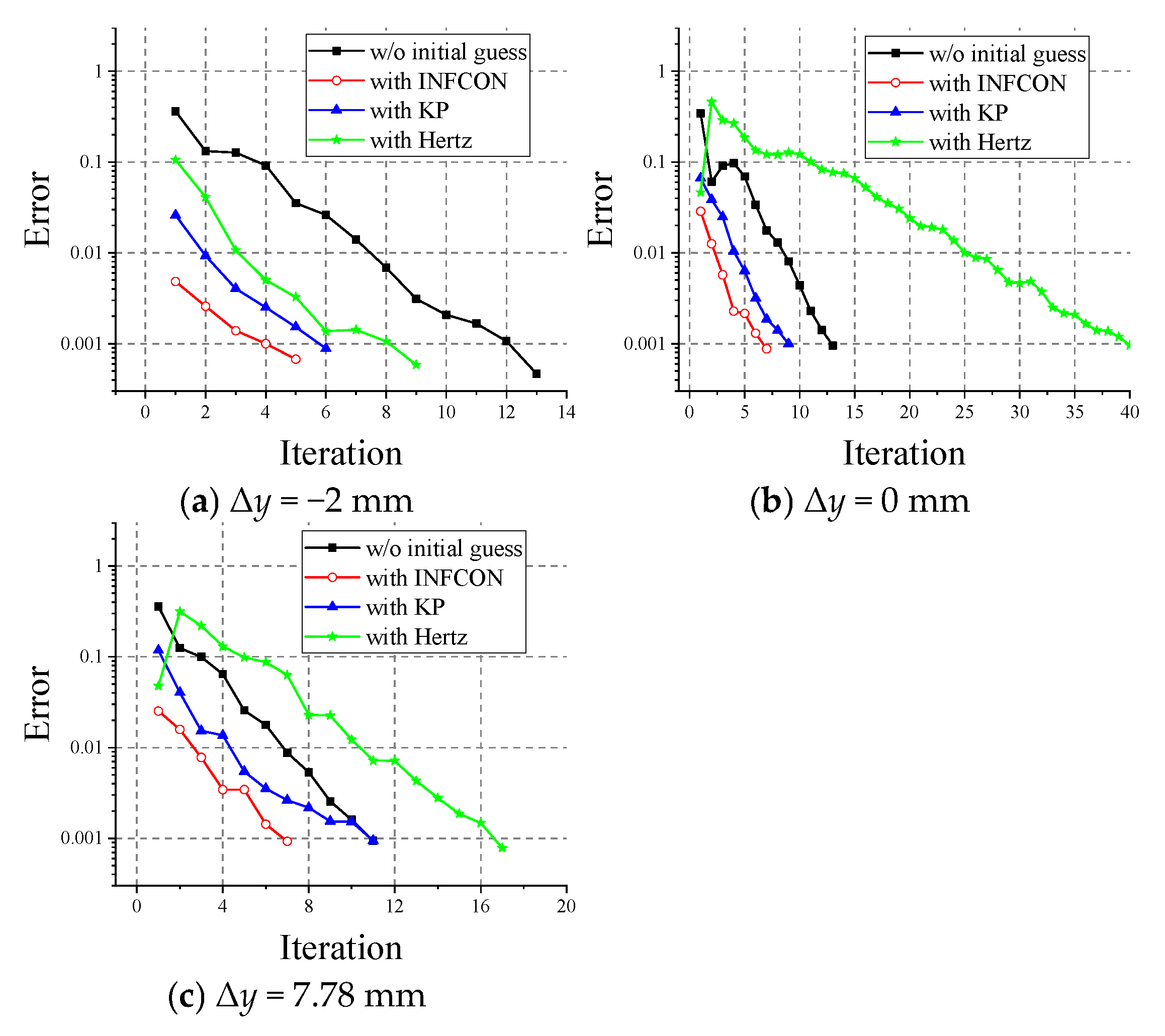
4.1.1. Performance for Hertz Contact
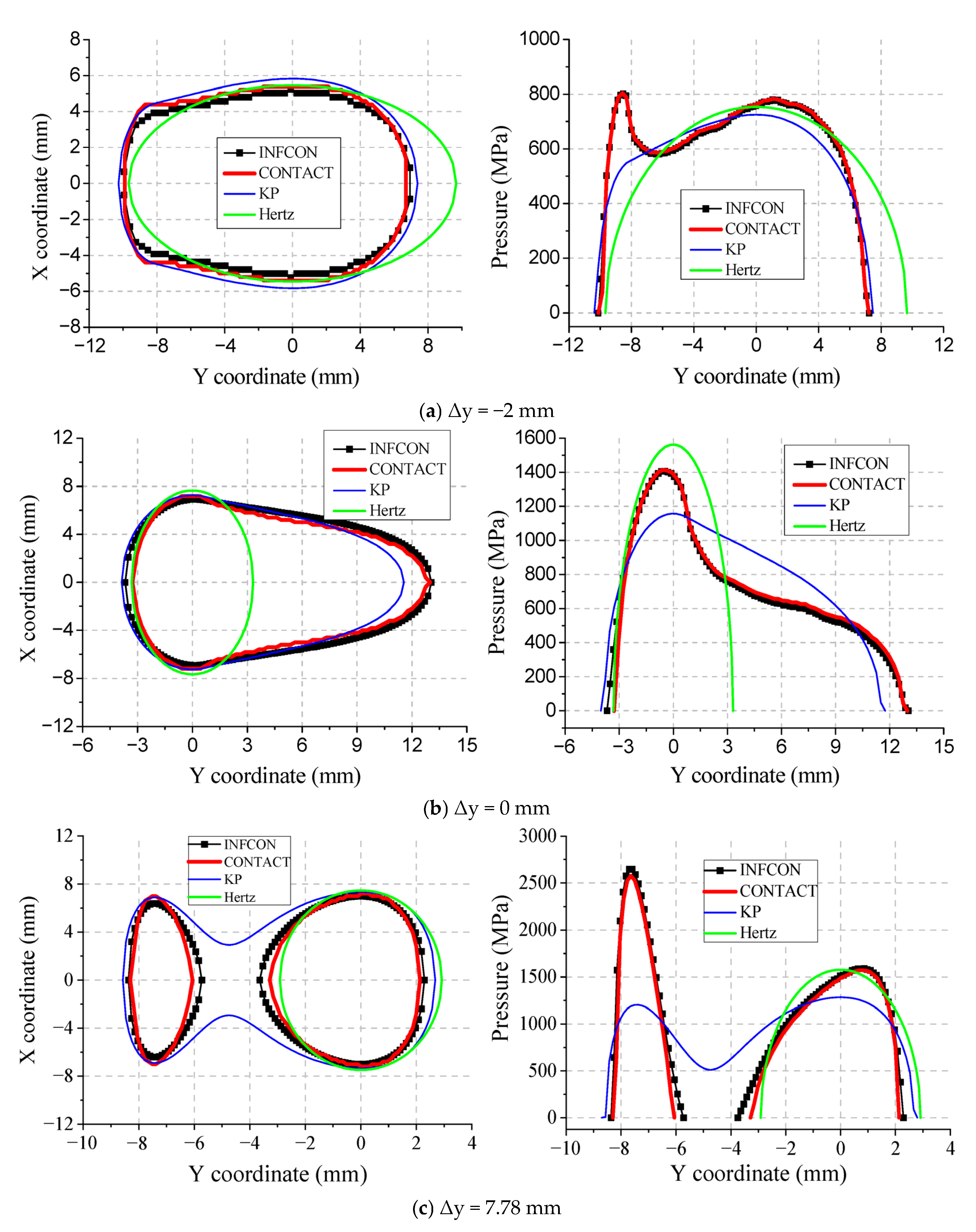
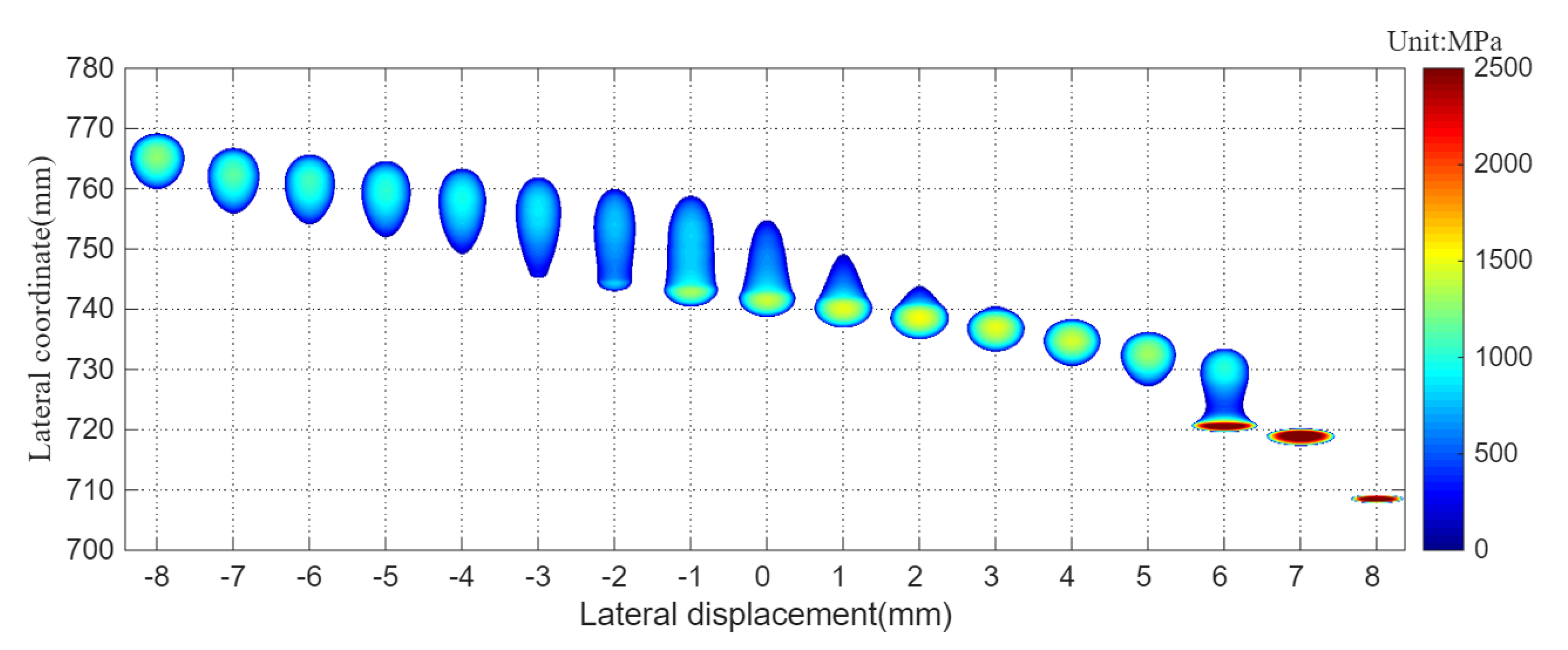
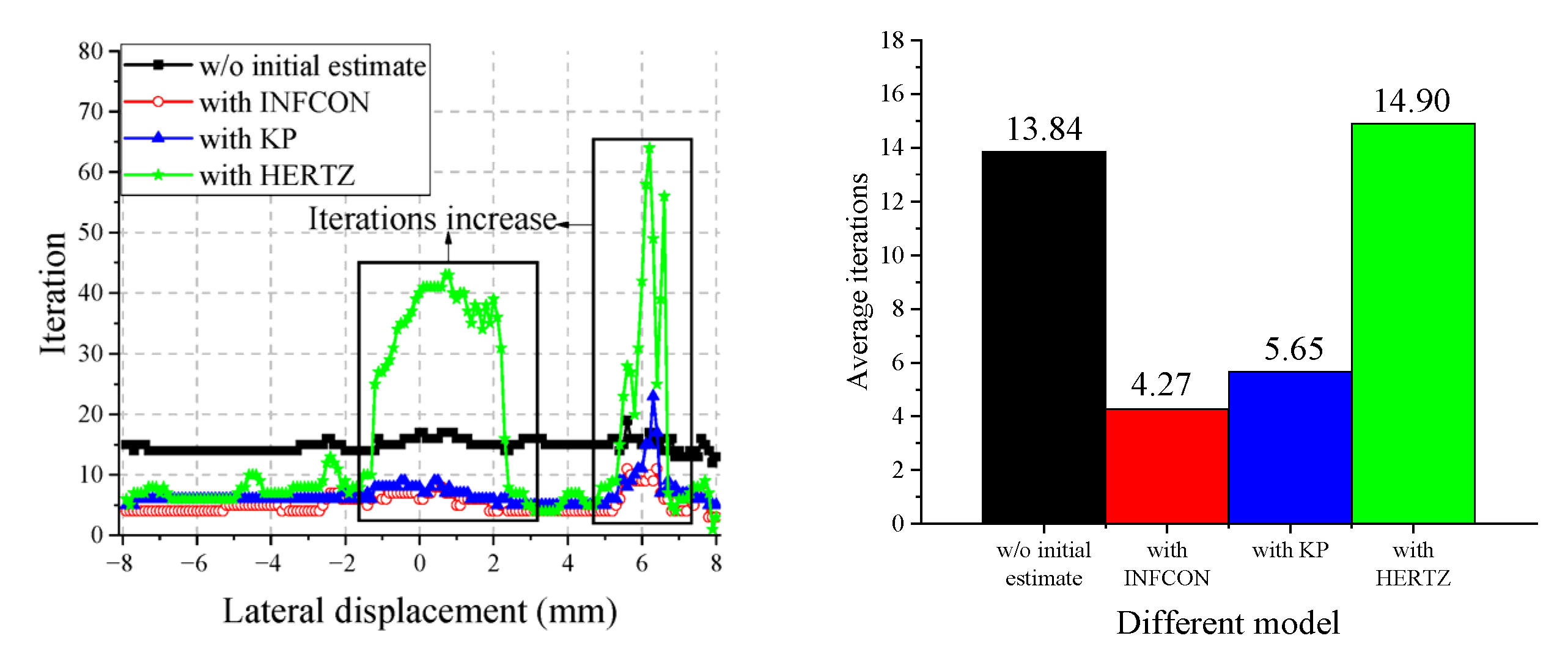
4.1.2. Performance for Non-Hertz Contact of Wheel and Rail
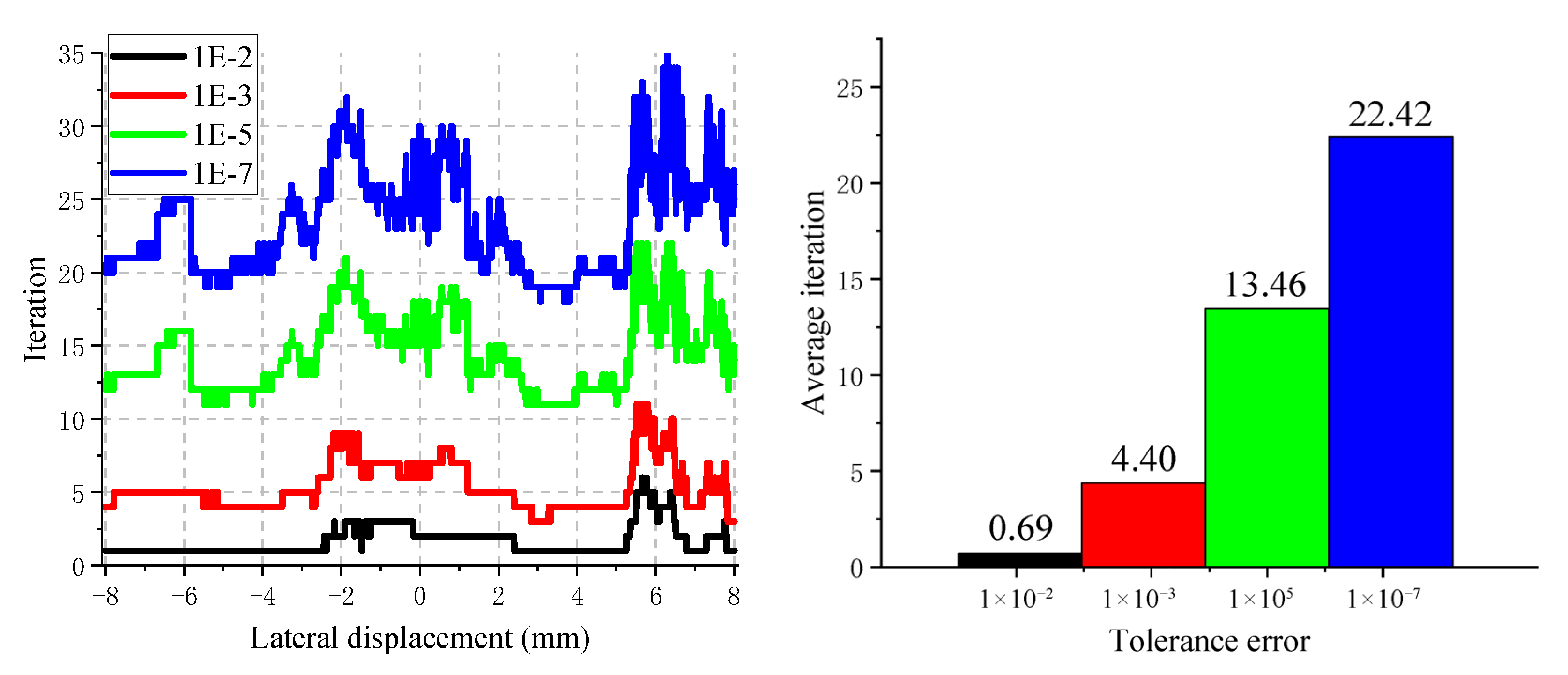
4.1.3. The Influence of Normal Tolerance Error on Computational Accuracy and Efficiency
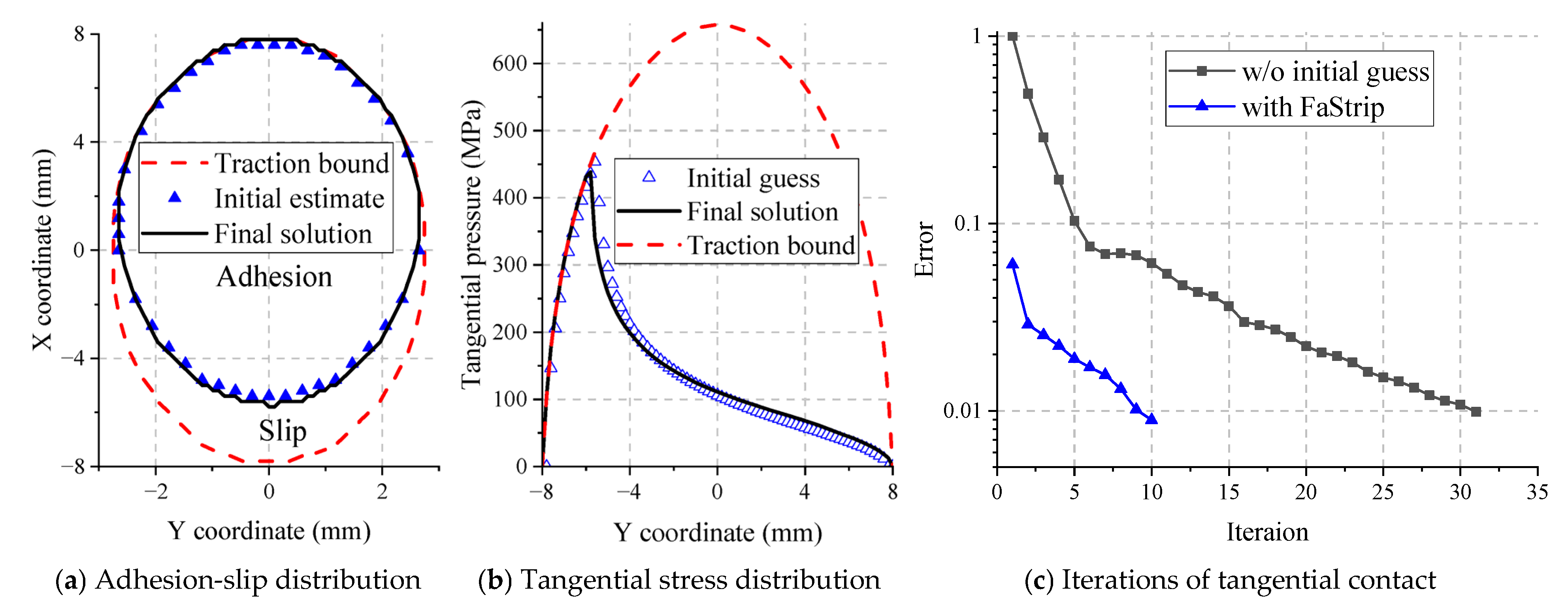
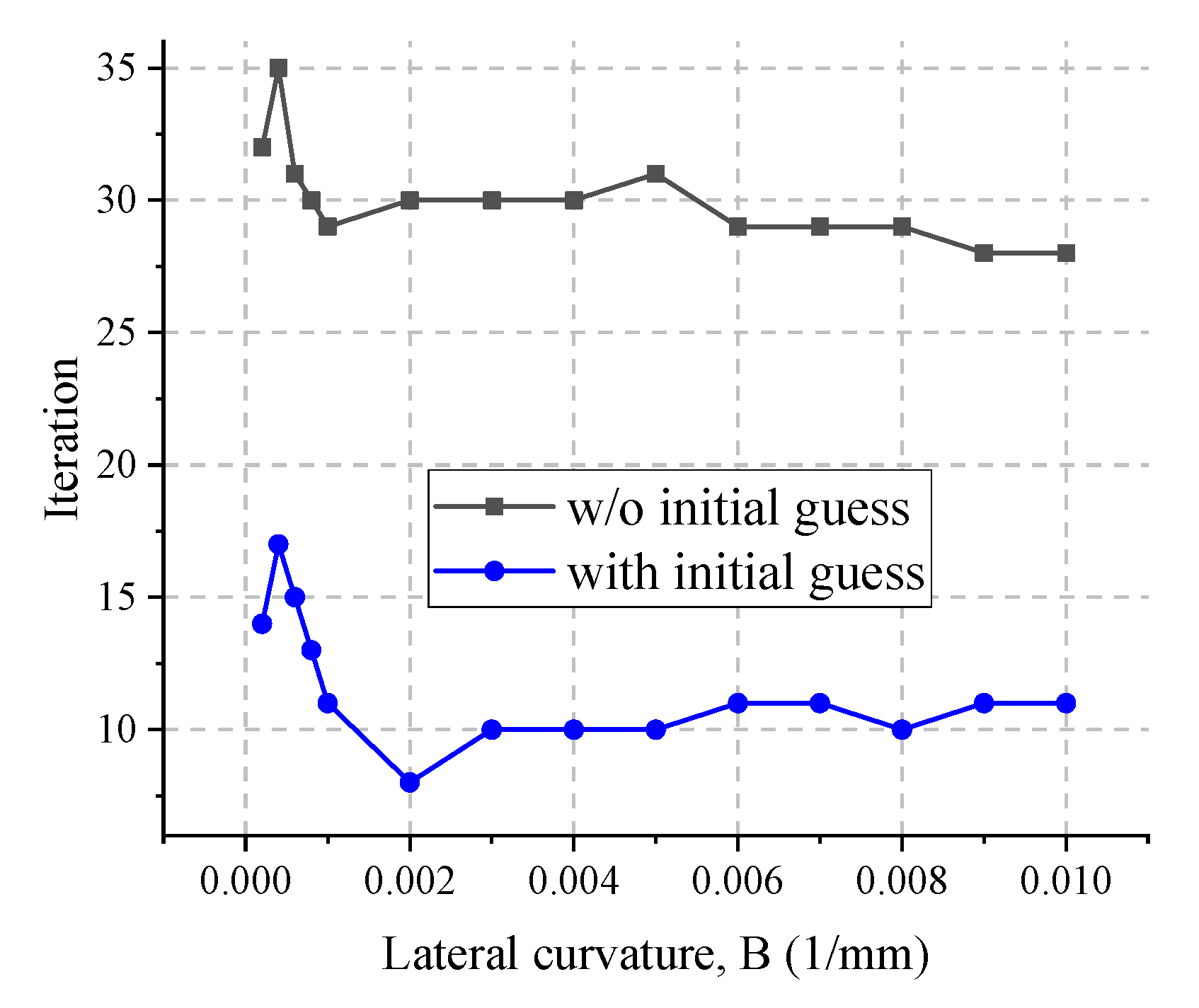
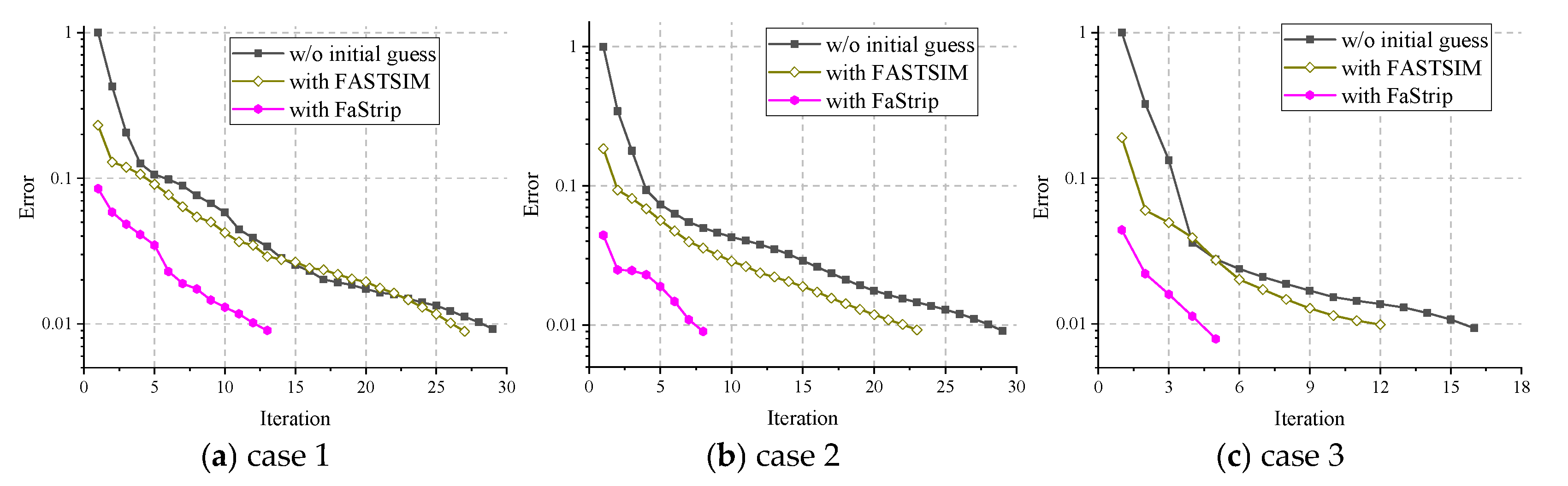
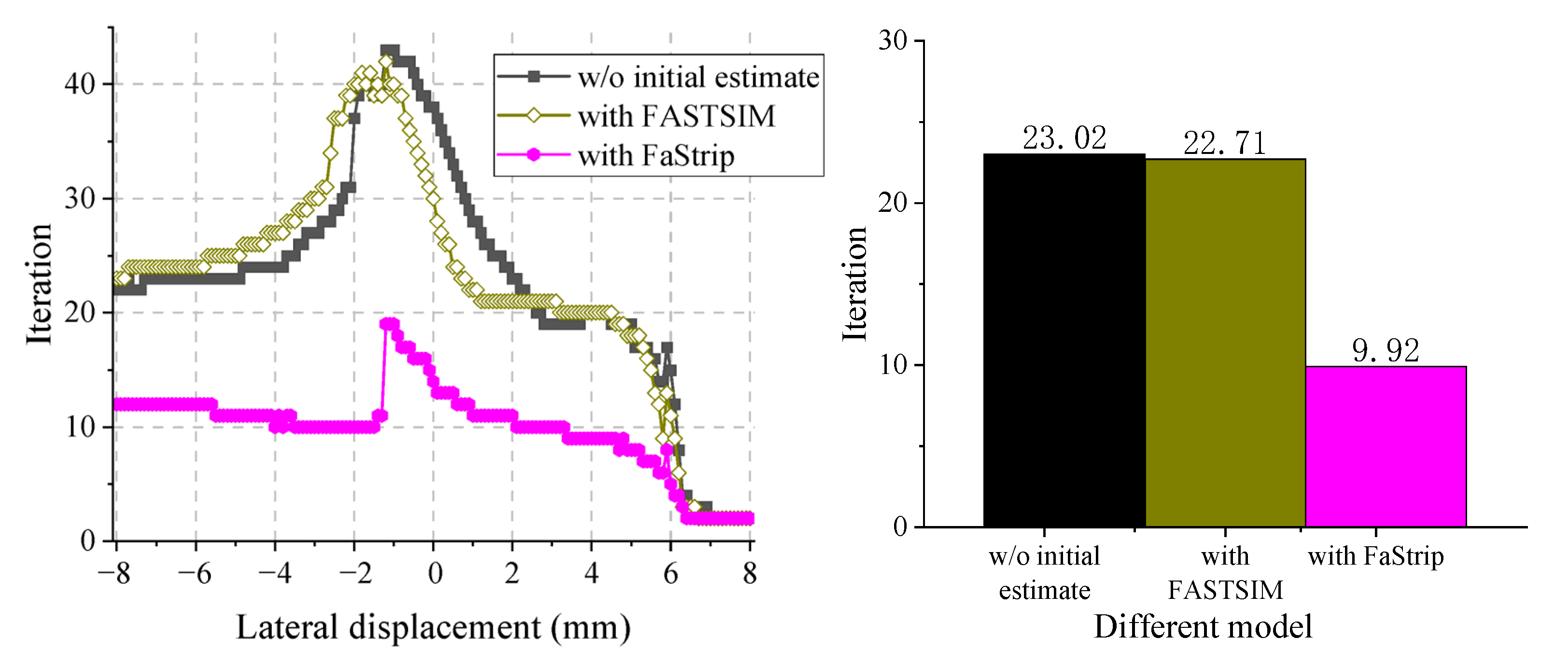
4.2. The Influence of Initial Estimate on Tangential Contact
4.2.1. Performance for Hertz Contact
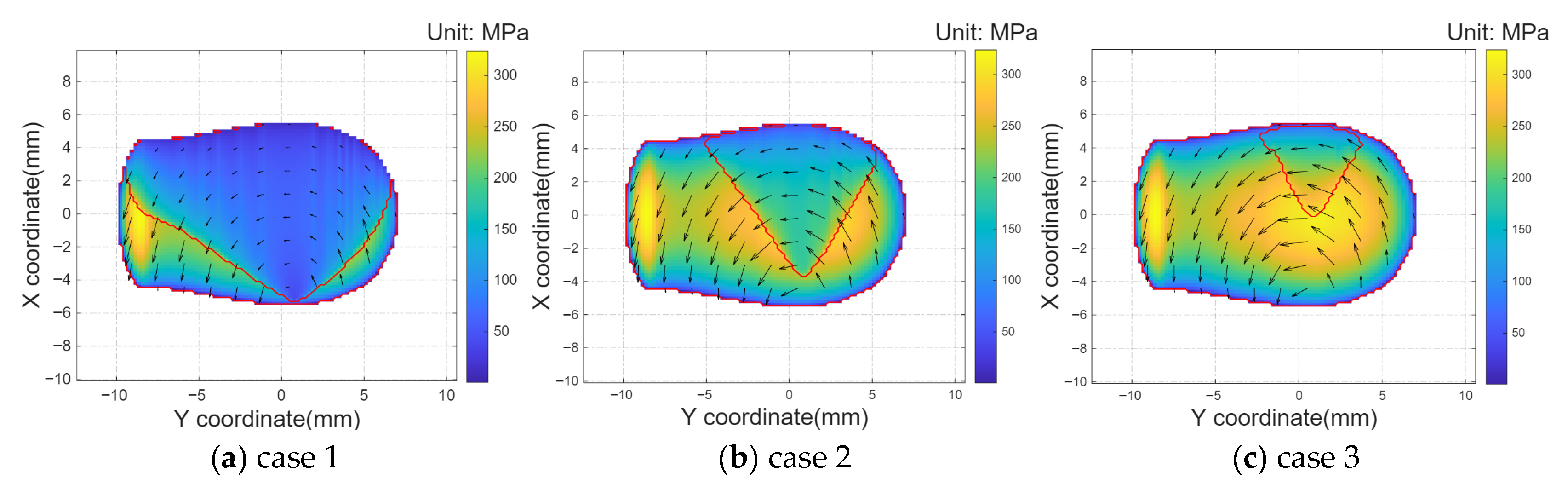
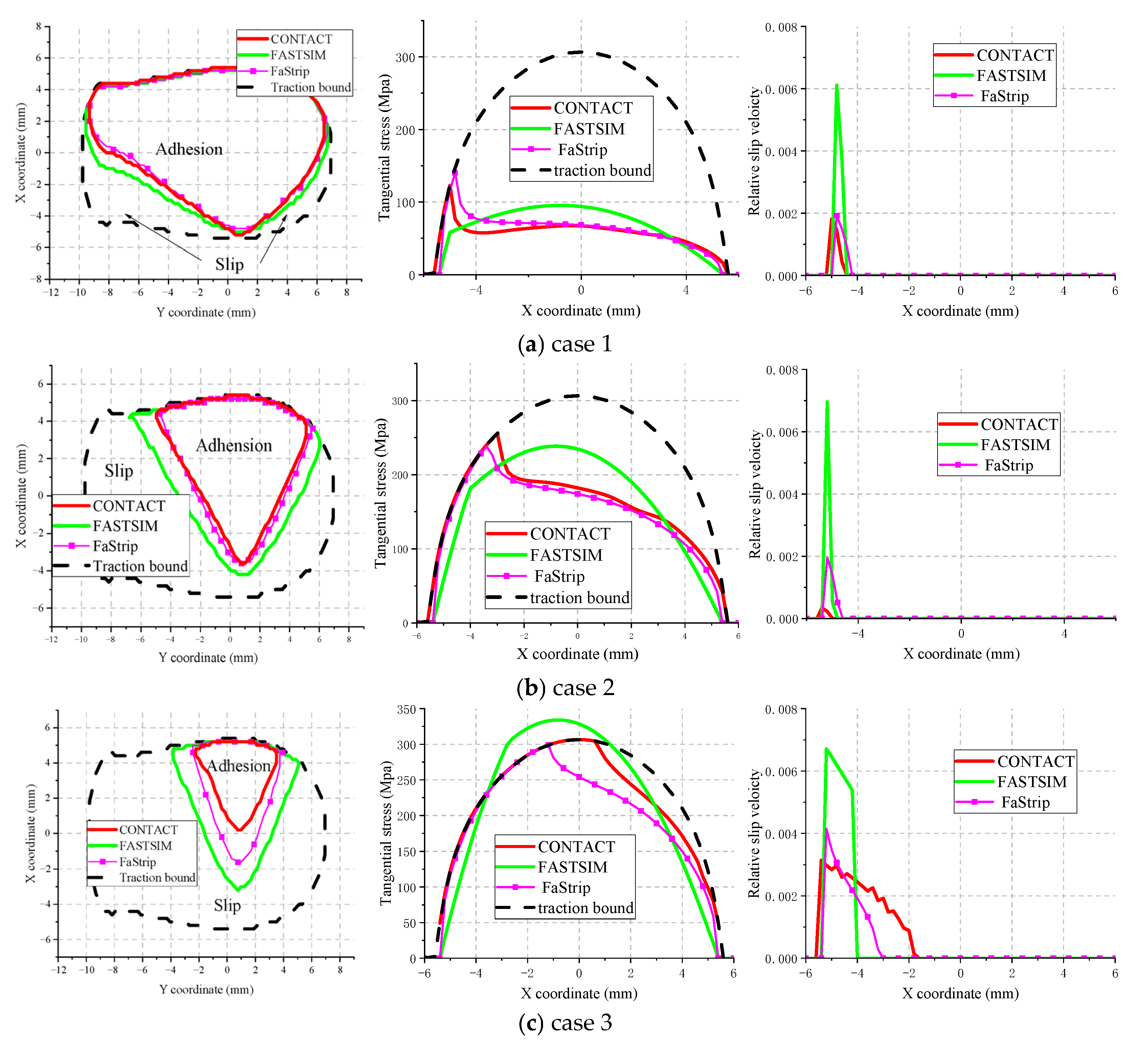
4.2.2. Performance for Non-Hertz Contact of Wheel and Rail
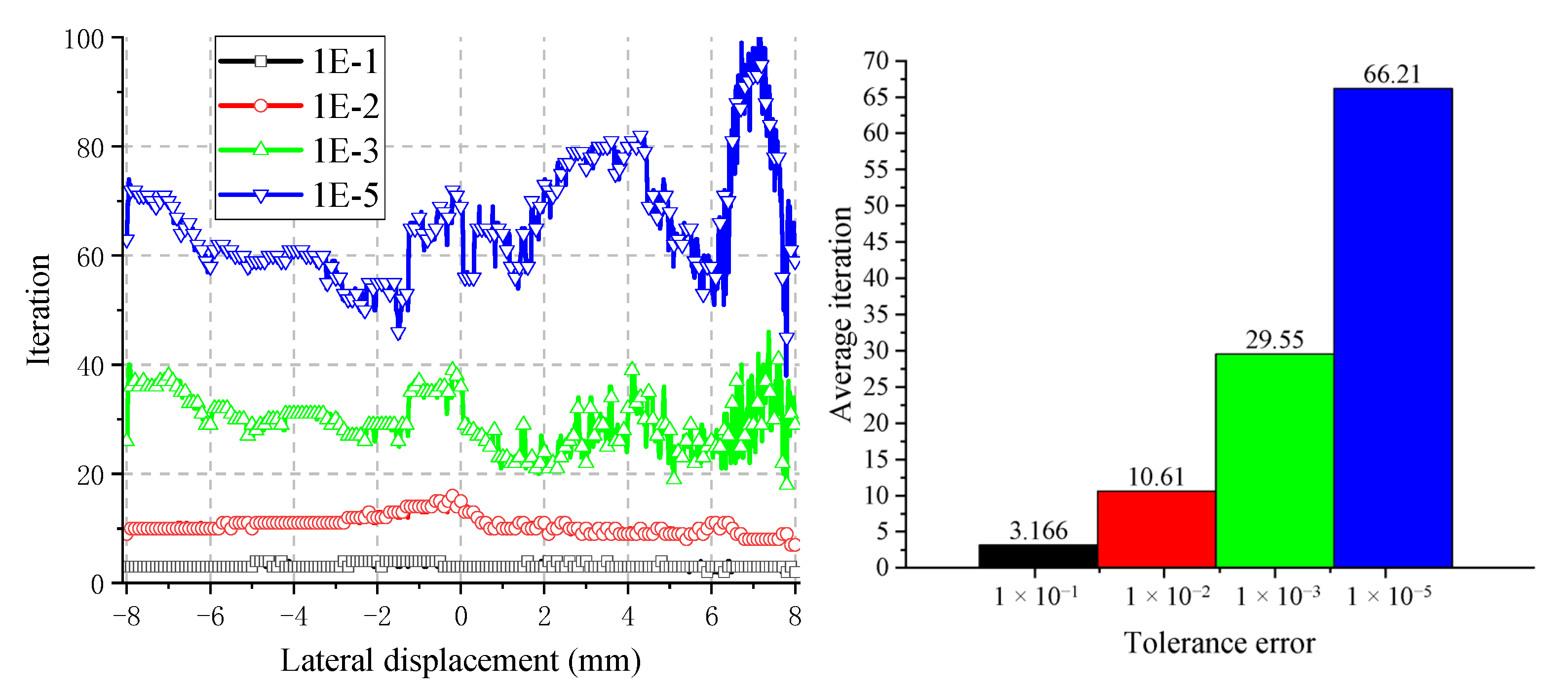
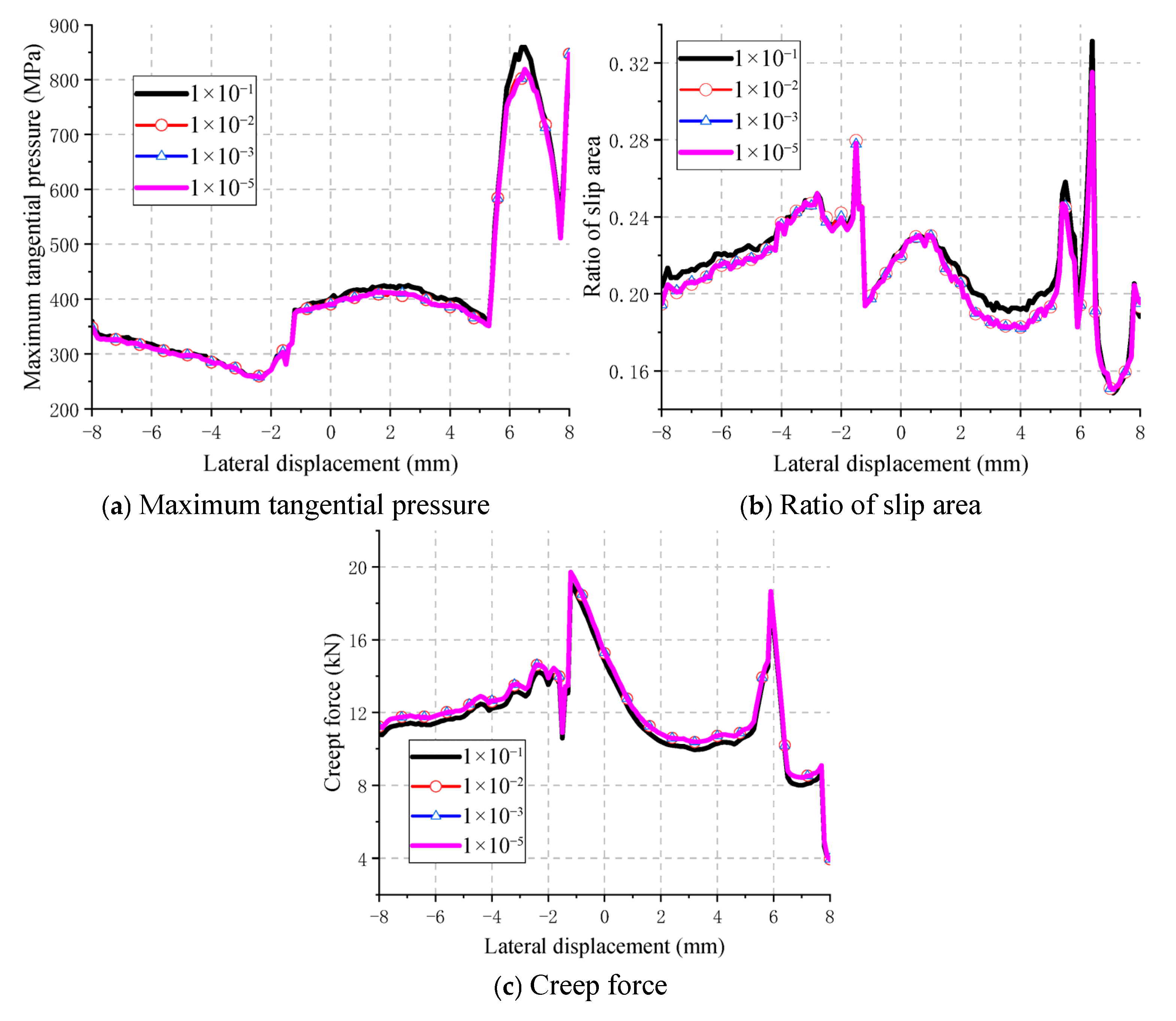
4.2.3. The Influence of Tangential Tolerance Error on Computational Accuracy and Efficiency
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- An, B. Numerical Study of Wheel-Rail Rolling Contact Behavior. Ph.D. Thesis, Southwest Jiaotong University, Sichuan, China, 2020. [Google Scholar]
- Yan, W.; Fischer, F.D. Applicability of the Hertz contact theory to rail-wheel contact problems. Arch. Appl. Mech. 2000, 70, 255–268. [Google Scholar] [CrossRef]
- Deng, X.; Qian, Z.; Li, Z.; Dollevoet, R. Applicability of half-space-based methods to non-conforming elastic normal contact problems. Int. J. Mech. Sci. 2017, 126, 229–234. [Google Scholar] [CrossRef]
- Deng, X.; Qian, Z.; Li, Z. Numerical modeling of dynamic frictional rolling contact with an explicit finite element method. Tribol. Int. 2019, 129, 214–231. [Google Scholar] [CrossRef]
- Pun, C.L.; Kan, Q.; Mutton, P.J.; Kang, G.; Yan, W. An efficient computational approach to evaluate the ratcheting performance of rail steels under cyclic rolling contact in service. Int. J. Mech. Sci. 2015, 101, 214–226. [Google Scholar] [CrossRef]
- Kalker, J.J. Rolling contact phenomena—Linear elasticity. In Rolling Contact Phenomena, CISM Courses and Lectures; Jacobson, B., Kalker, J., Eds.; Springer: New York, NY, USA, 2000; pp. 1–84. [Google Scholar]
- Knothe, K. A contribution to the calculation of the contact stress distribution between two elastic bodies of revolution with non-elliptical contact area. Comput. Struct. 1984, 18, 1025–1033. [Google Scholar] [CrossRef]
- Yu, C.; Yaoliang, S.; Wenhao, D.; Ping, W. Assessing the fast non-Hertzian methods for wheel-rail rolling contact integrated in the vehicle dynamics simulation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2023, 237, 371–384. [Google Scholar] [CrossRef]
- Triantafyllidis, T. 3-D time domain be using half-space green-functions. Eng. Anal. Bound. Elem. 1991, 8, 115–124. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, Z.; Wang, H.; Fan, Y.; An, B.; Chen, P.; Wang, P. Study on the Influence of Wheel-rail Conformal Contact Modeling on Vehicle-track Coupling Dynamics. Railw. Stand. Des. 2025, 69, 12–23. [Google Scholar] [CrossRef]
- Huang, S.; Zhao, X.; Cai, Y.; Wem, Z. Modeling of Wheel-Rail Adhesion Behavior at Large Creepages Based on Polach Adhesion Theory. J. Tribol. 2025, 69, 133–155, (In Chinese and English). [Google Scholar]
- Yang, Z.; Boogaard, A.; Chen, R.; Dollevoet, R.; Li, Z. Numerical and experimental study of wheel-rail impact vibration and noise generated at an insulated rail joint. Int. J. Impact Eng. 2018, 113, 29–39. [Google Scholar] [CrossRef]
- Yang, Z.; Boogaard, A.; Wei, Z.; Liu, J.; Dollevoet, R.; Li, Z. Numerical study of wheel-rail impact contact solutions at an insulated rail joint. Int. J. Mech. Sci. 2018, 138, 310–322. [Google Scholar] [CrossRef]
- Zhao, X.; An, B.; Zhao, X.; Wen, Z.; Jin, X. Local rolling contact fatigue and indentations on high-speed railway wheels: Observations and numerical simulations. Int. J. Fatigue 2017, 103, 5–16. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, S.; Yang, J.; Yang, Z.; Wen, Z. On Transient Wheel-Rail Rolling-Sliding-Jumping Contact and Critical Sizes of Short/Medium-wave Irregularities at Higher Speeds. Railw. J. 2024, 46, 21–32. [Google Scholar]
- Zhao, X.; Wen, Z.; Wang, H.; Jin, X.; Zhu, M. Modeling of high-speed wheel-rail rolling contact on a corrugated rail and corrugation development. J. Zhejiang Univ. Sci. A 2014, 15, 946–963. [Google Scholar] [CrossRef]
- An, B.; Wang, P. A novel local ellipse method for ellipse-based tangential contact model applied to wheel-rail contact. Int. J. Rail Transport. 2022, 12, 180–199. [Google Scholar] [CrossRef]
- Kalker, J.J. The computation of three-dimensional rolling contact with dry friction. Int. J. Numer. Methods Eng. 1979, 14, 1293–1307. [Google Scholar] [CrossRef]
- Kalker, J.J. Three-Dimensional Elastic Bodies in Rolling Contact; Kluwer Academis Publishers: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Vollebregt, E.A.H. A new solver for the elastic normal contact problem using conjugate gradients: Deflation, and an FFT-based preconditioner. J. Comput. Phys. 2014, 257, 333–351. [Google Scholar] [CrossRef]
- Zhao, J.; Vollebregt, E.A.H.; Oosterlee, C.W. A fast nonlinear conjugate gradient based method for 3D concentrated frictional contact problems. J. Comput. Phys. 2015, 288, 86–100. [Google Scholar] [CrossRef]
- Vollebregt, E.A.H. 100-fold speedup of the normal contact problem and other developments in CONTACT. In Proceedings of the CM 2012, Chengdu, China, 15 March 2012; Southwest Jiaotaong University: Chengdu, China, 2012; pp. 79–86. [Google Scholar]
- Polonsky, I.A.; Keer, L.M. A numerical method for solving rough contact problems based on the multi-level multi-summation and conjugate gradient techniques. Wear 1999, 231, 206–219. [Google Scholar] [CrossRef]
- Piotrowski, J.; Kik, W. A simplified model of wheel/rail contact mechanics for non-Hertzian problems and its application in rail vehicle dynamic simulations. Veh. Syst. Dyn. 2008, 46, 27–48. [Google Scholar] [CrossRef]
- Piotrowski, J.; Chollet, H. Wheel–rail contact models for vehicle system dynamics including multi-point contact. Veh. Syst. Dyn. 2005, 43, 455–483. [Google Scholar] [CrossRef]
- Ayasse, J.B.; Chollet, H. Determination of the wheel rail contact patch in semi-Hertzian conditions. Veh. Syst. Dyn. 2005, 43, 161–172. [Google Scholar] [CrossRef]
- Liu, B.; Bruni, S.; Vollebregt, E. A non-Hertzian method for solving wheel–rail normal contact problem taking into account the effect of yaw. Veh. Syst. Dyn. 2016, 54, 1226–1246. [Google Scholar] [CrossRef]
- Sun, Y.; Zhai, W.; Guo, Y. A robust non-Hertzian contact method for wheel–rail normal contact analysis. Veh. Syst. Dyn. 2018, 56, 1899–1921. [Google Scholar] [CrossRef]
- Zhu, B.; Zeng, J.; Wang, Q.; Wu, Y.; Qu, S. Modification of the semi-Hertz wheel–rail contact method based on recalculating the virtual penetration value. Veh. Syst. Dyn. 2018, 57, 1407–1420. [Google Scholar] [CrossRef]
- Kalker, J.J. A fast algorithm for the simplified theory of rolling contact. Veh. Syst. Dyn. 1982, 11, 1–13. [Google Scholar] [CrossRef]
- Vollebregt, E.A.H.; Wilders, P. FASTSIMsd a second-order accurate frictional rolling contact algorithm. Comput. Mech. 2011, 47, 105–116. [Google Scholar] [CrossRef]
- Sichani, M.S.; Enblom, R.; Berg, M. An alternative to FASTSIM for tangential solution of the wheel–rail contact. Veh. Syst. Dyn. 2016, 54, 748–764. [Google Scholar] [CrossRef]
- Kik, W.; Piotrowski, J. A fast, approximate method to calculate normal load at contact between wheel and rail and creep forces during rolling. In Proceedings of the Second Mini Conference on Contact Mechanics and Wear of Rail/Wheel Systems, TU Budapest, Budapest, Hungary, 29–31 July 1996. [Google Scholar]
- Wang, K. Calculation of wheel contact point trace and wheel/rail contact geometric parameters. J. Southwest Jiaotong Univ. 1984, 18, 89–99. [Google Scholar]
- Liu, S.; Wang, Q.; Liu, G. A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 2000, 243, 101–111. [Google Scholar] [CrossRef]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Und Angew. Math. 1882, 92, 156–171. [Google Scholar] [CrossRef]
- An, B.; Wang, P. A wheel-rail normal contact model using the combination of virtual penetration method and strip-like Boussinesq’s integral. Veh. Syst. Dyn. 2022, 61, 1583–1601. [Google Scholar] [CrossRef]
- Vollebregt, E.A.H. Improving the speed and accuracy of the frictional rolling contact model ‘CONTACT’. In Proceedings of the 10th International Conference on Computational Structures Technology, Valencia, Spain, 14–17 September 2010; Topping, B.H.V., Ed.; [Google Scholar]
- Vollebregt, E.A.H. A Gauss-Seidel type solver for special convex programs, with application to frictional contact mechanics. J. Optim. Theory Appl. 1995, 87, 47–67. [Google Scholar] [CrossRef]
- Goryacheva, I.G.; Tsukanov, I.Y. Modeling of normal contact of elastic bodies with surface relief taken into account. J. Phys. Conf. Ser. 2018, 991, 012028. [Google Scholar] [CrossRef]
- Huang, J.; Wu, B.; Li, D.; Wang, Z. Comparison of Results from Different Wheel-Rail Rolling Contact Models Considering Large Creepages. J. Railw. 2025, 47, 57–65. [Google Scholar]
- Alonso, A.; Giménez, J.G. A new method for the solution of the normal contact problem in the dynamic simulation of railway vehicles. Veh. Syst. Dyn. 2005, 43, 149–160. [Google Scholar] [CrossRef]
- Skipper, W.; Meierhofer, A.; Chalisey, A.; Six, K.; Lewis, R. Generation of Sanded Creep Curves Using the Extended Creep Force Model with High Pressure Torsion Data. Wear 2024, 542, 205278. [Google Scholar] [CrossRef]
- Majumdar, A.; Tien, C.L. Fractal Characterization and Simulation of Rough Surfaces. Wear 1990, 136, 313–327. [Google Scholar] [CrossRef]
- Zhou, S.; He, C.; Di, H. An efficient method for predicting train-induced vibrations from a tunnel in a poroelastic half-space. Eng. Anal. Bound. Elem. 2017, 85, 43–56. [Google Scholar] [CrossRef]

| Method | Characteristic | Advantage | Disadvantage | |
|---|---|---|---|---|
| The accurate solution | Finite Element Method | By dividing the wheel–rail system into physical units, contact is simulated using the penalty function method. | Simulation of real wheel–rail contact geometry and material nonlinearity. | Low computational efficiency. The finer the grid, the exponential higher growth of computing time. |
| Boundary Element Method | Only the contact surface is divided into grids. | High calculation precision. | The process requires iterative refinement until convergence is achieved, and its computational efficiency is suboptimal. | |
| The simplified solution | Virtual Penetration Method | Assuming the wheel/rail profiles can rigidly penetrate each other, the elastic deformation of the material can be equivalent to the reduction factor. | It has high computational efficiency, no iteration, and analytical solution. | The calculation’s precision is suboptimal, and significant calculation errors are observed when the transverse displacement and gauge angle are both large. |
| Method | Characteristic | Efficiency | Precision |
|---|---|---|---|
| Hertz | Based on the ellipse hypothesis, the contact patch and the contact pressure are elliptically distributed. | Highest | Low |
| KP | Based on the virtual penetration method, the calculation result is non-Hertz. | High | Rather high |
| INFCON | Based on virtual penetration method and Boussinesq integral. | Rather high | Highest |
| Method | Characteristic | Efficiency | Precision |
|---|---|---|---|
| FASTSIM | Based on Kalker’s simplified theory development, based on the ellipse hypothesis, several strips along the rolling direction are formed, and each strip is divided into several rectangular elements. | Highest | Low |
| FaStrip | Based on the ellipse hypothesis, several strips along the rolling direction are formed, but the rectangular grid is not further divided. | High | High |
| Average Iterations | Relative Error (%) | |||
|---|---|---|---|---|
| Max. Pressure | Contact Area | Contact Force | ||
| 1 × 10−2 | 0.69 | 1.56 | 3.73 | 0.63 |
| 1 × 10−3 | 4.40 | 0.40 | 2.05 | 0.10 |
| 1 × 10−5 | 13.46 | 0.34 | 1.58 | 0.04 |
| 1 × 10−7 | 22.42 | 0.14 | 0.60 | 0.01 |
| Creepage | Lateral | Longitudinal | Spin |
|---|---|---|---|
| Case1 | 0.5 × 10−4 | 0.5 × 10−4 | 0.5 × 10−4 |
| Case2 | 2 × 10−4 | 2 × 10−4 | 2 × 10−4 |
| Case3 | 5 × 10−4 | 5 × 10−4 | 5 × 10−4 |
| Average Iterations | Relative Error(%) | |||
|---|---|---|---|---|
| Max. Pressure | Contact Area | Contact Force | ||
| 1 × 10−1 | 3.17 | 1.23 | 1.67 | 3.38 |
| 1 × 10−2 | 10.61 | 0.14 | 0.27 | 7.87 × 10−2 |
| 1 × 10−3 | 29.55 | 5.9 × 10−2 | 7.98 × 10−2 | 6.51 × 10−3 |
| 1 × 10−5 | 66.21 | 5.58 × 10−4 | 3.34 × 10−4 | 1.26 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Lai, H.; An, B.; Liu, J. The Influence of Initial Solution Estimate Method on Efficient Boundary Element Modeling of Rolling Contact. Lubricants 2025, 13, 508. https://doi.org/10.3390/lubricants13110508
Chen S, Lai H, An B, Liu J. The Influence of Initial Solution Estimate Method on Efficient Boundary Element Modeling of Rolling Contact. Lubricants. 2025; 13(11):508. https://doi.org/10.3390/lubricants13110508
Chicago/Turabian StyleChen, Shuang, Hongxiang Lai, Boyang An, and Jiapeng Liu. 2025. "The Influence of Initial Solution Estimate Method on Efficient Boundary Element Modeling of Rolling Contact" Lubricants 13, no. 11: 508. https://doi.org/10.3390/lubricants13110508
APA StyleChen, S., Lai, H., An, B., & Liu, J. (2025). The Influence of Initial Solution Estimate Method on Efficient Boundary Element Modeling of Rolling Contact. Lubricants, 13(11), 508. https://doi.org/10.3390/lubricants13110508





