Abstract
This study presents a numerical investigation into the adhesion strength of micro fibrillar structures, incorporating statistical analysis and the effects of excessive pre–load leading to fibril buckling. Fibrils are modeled as soft cylinders using the Euler–Bernoulli beam theory, with buckling conditions described across three distinct states, each affecting the adhesive properties of the fibrils. Iterative simulations analyze how adhesion strength varies with pre–load, roughness, number of fibrils, and the work of adhesion. Roughness is modeled both in fibril heights and in the texture of a rigid counter surface, following a normal distribution with a single variance parameter. Results indicate that roughness and pre–load significantly influence adhesion strength, with excessive pre–load causing substantial buckling and a dramatic reduction in adhesion. This study also finds that adhesion strength decreases exponentially with increasing roughness, in line with theoretical expectations. The findings highlight the importance of buckling and roughness parameters in determining adhesion strength. This study offers valuable insights into the complex adhesive interactions of fibrillar structures, offering a scalable solution for rapid assessment of adhesion in various rough surface and loading scenarios.
1. Introduction
Recent research has increasingly focused on the contact mechanics of rough surfaces. Classical theories reveal that even small roughness amplitudes can significantly impact adhesion strength, particularly in materials with a low Young’s modulus, such as smooth rubber against rough rigid surfaces [1,2,3]. This complexity poses a challenge for accurately predicting adhesive strength when one of the contacting surfaces is textured. To address this, several formulations have been proposed, including statistical models like the Greenwood–Williamson model [4] and fractal models. For a comprehensive overview of these models, see [5].
In numerical and statistical models, surface roughness is typically described using a distribution function such as the Gaussian distribution [4]. Each asperity is generally represented as a geometry such as hemispherical geometry that deforms independently during contact between two surfaces. The Hertzian solution can be applied to describe this contact. When adhesion is considered, the Johnson–Kendall–Roberts (JKR) model [6] can be used to determine the adhesion of a single hemispherical asperity. This approach allows for the investigation of the adhesion of rough surfaces with a distribution function, assuming each asperity contacts independently without influencing others. This method is powerful for studying contact mechanics as it allows for the use of different asperity shapes [7].
It is well–known that roughness negatively influences adhesion [1]. One way to mitigate this negative impact is by splitting the contact into finer parts [8]. Generally, partitioning the contact into smaller or finer parts, a process known as contact splitting or the gecko effect [9,10], is accomplished using fibrillar structures. These structures are renowned for their exceptional adhesive properties, even on rough surfaces [11,12,13]. They are inspired by biological attachment systems, such as those found in geckos [14]. Gecko–like fibrillar structures are typically fabricated using elastic polymer fibrils through techniques like soft lithography or molding [15]. These fibrils texture surfaces and modify contact mechanics [16]. The creation of fibrils on a textured surface distributes contact forces among them, allowing for the adjustment of adhesive strength by varying fibril geometry or dimensions. Research in this area primarily explores the impact of different fibril geometries [17,18] and tip shapes [19] on adhesion. However, the influence of roughness on the adhesion strength of fibrillar structures requires further detailed investigation.
Several studies have investigated the adhesion strength of fibrillar structures exhibiting various types of roughness, either in the height distribution among the fibrils [20,21,22] or in the texture of the counter surface [23,24]. Porwal et al. examined the effect of counter surface roughness and fibril variability on adhesion strength in fibrillar systems [20]. They modeled fibril height and detachment strength using probability distributions and performed Monte Carlo simulations to analyze adhesion strength, with fibril heights following normal or uniform distributions and attachment strengths described by a power–law distribution. Their results indicated that roughness reduces adhesion. Li et al. investigated the adhesive contact between an elastic half–space and rigid fibrillar structures using the FFT–based boundary element method [21]. They found that roughness in the fibril height distribution decreases adhesion, with adhesion depending on the applied pre–load. He et al. conducted a similar study numerically, modeling the fibrils as soft cylinders with constant stiffness and normally distributed heights [22]. Using the adhesive strength of a flat–punch based on the Kendall’s solution [25], they examined adhesive strength under various applied pre–loads, roughness, and fibril stiffness. They concluded that adhesive strength diminishes as roughness increases, with the application of additional pre–load eventually causing the strength to level off at a plateau. These studies reveal that variations in fibril heights affect adhesive strength and that adhesion reduces to a limit at a certain roughness parameter. Additionally, increasing the pre–load on the fibril array enhances adhesion strength to some extent. However, the effect of excessive pre–load was not evaluated in these studies. Excessive pre–load can cause fibril buckling [26], which reduces adhesion [27]. Zhang et al. examined the effect of pre–load on the adhesion of fibril arrays in contact with a rough rigid surface [23]. The roughness of the rigid surface is modeled by steps following a normal distribution. Increasing the pre–load enhances adhesion up to a threshold value. In the numerical model, the adhesion is considered to be reversible despite the buckled fibrils, assuming the pre–load is not very large. However, even a small increase in pre–load beyond the buckling load can lead to irreversible adhesion, as shown in [28]. Hu et al. studied the effect of contact splitting on the adhesion strength of fibrillar structures in contact with a rough rigid surface using the finite–element method [24]. The fibrils buckled, and the adjacent fibrils can make contact. They concluded that at lower roughness parameters, splitting the contact into finer fibrils slightly affects the adhesion, whereas under higher roughness conditions, having fibrils enhances adhesion due to increased compliance. In their study, since all the fibrils are in contact and buckled, the resulting adhesion strength was almost the same for all the fibrils, which can be defined by a constant parameter of compliance. Under different pre–load (indentation displacement in this case), some of the fibrils can buckle while others do not. Buckling of a fibril results in lower adhesion compared to unbuckled states [26,28,29,30]. Therefore, a comprehensive investigation into the adhesion strength of fibrillar structures, considering differences in height or contact with a rough rigid surface, must account for the buckling failure of fibrils due to excessive pre–load while differentiating the unbuckled ones. Computational algorithms frequently overlook the effects of excessive pre–load, which can lead to fibril buckling and subsequently influence adhesion properties. Therefore, it is crucial to develop efficient algorithms capable of accurately addressing these factors.
This study employs a numerical and statistical approach to investigate the adhesive strength of fibrillar structures, differentiating between buckled and non–buckled fibrils and identifying non–contacted fibrils. Roughness is incorporated either into the fibril height distribution or the texture of the rigid surface. Adhesion strength is examined across various levels of roughness, pre–load, number of fibrils, and work of adhesion. The structure of the paper is as follows: Section 2 details the materials and methods, explaining the problem and the underlying theory. Section 3 presents the results. Section 4 offers a detailed discussion of the findings. Section 5 concludes the paper and suggests directions for future research.
2. Materials and Methods
2.1. Problem Statement and Theory
This section addresses the challenge of quantifying the adhesive strength between a fibril array and a rigid counter surface, incorporating fundamental equations from solid and contact mechanics. The rigid surface, which may exhibit either smooth or rough textures, interacts with an elastic fibril array characterized by varying heights across its fibrils. Consider a scenario where a rigid surface comes into contact with an elastic array composed of n fibrils, illustrated in Figure 1. The fibrils are supported by a fixed backing layer at their base. Contact initiation involves incremental movement of the rigid surface in the direction by a relative displacement . Upon reaching a certain relative displacement, contact is established, creating a pre–load between the rigid surface and the fibril array. This phase is referred to as the loading process.
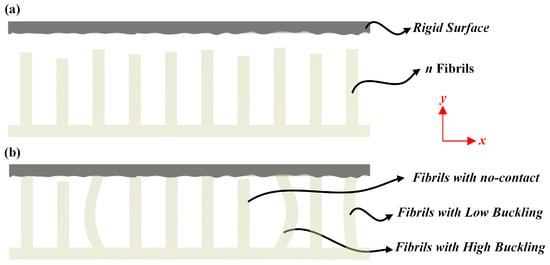
Figure 1.
The interested problem: (a) A rigid surface attempting to make contact with an elastic fibril array. (b) After the rigid surface indents the fibril array, a static contact occurs. Depending on the pre–load and the roughness of the elastic fibril array (variation in their height) or the roughness of the rigid surface, some fibrils establish contact, some fibrils become buckled, and the remaining fibrils have no contact at all.
After establishing initial static contact with a desired pre–load, the rigid surface proceeds to move incrementally in the opposite direction () by the displacement . At a specific displacement, the fibrils within the array undergo elongation, thereby generating adhesive forces or stresses due to their adhesive properties. As the displacement increases, these adhesive forces come into play. If the adhesive force exerted by a single fibril surpasses its intrinsic adhesive strength, contact between the fibril and the rigid surface is lost. This phase is known as the unloading stage. Further increases in the relative displacement lead to complete loss of contact.
Depending on the pre–load and the roughness of the contacting surfaces, some fibrils may maintain contact, while others may buckle or fail to establish contact altogether. Fibril buckling can manifest in two states: Low buckling and High buckling, triggered when the pre–load on a fibril exceeds its Euler buckling load [31]. Buckled fibrils typically exhibit reduced adhesion compared to their unbuckled counterparts [26,28,29,30], and the adhesion force varies accordingly between low and high buckling states.
2.1.1. The Loading Process
The loading process is governed by controlling the displacement of the counter relative to an individual fibril. During this phase, contact is initiated between the fibril and the counter surface. The load between the counter surface and the fibril can be calculated using the stiffness of the fibril and the compressive displacement, represented by the equation:
where represents the load between the counter surface and the fibril, denotes the axial stiffness of the fibril, and d signifies the compressive displacement of the counter surface at the onset of initial contact. The axial stiffness is typically determined by modeling the single fibril as an Euler–Bernoulli beam, a method known for its close agreement with experimental data [26,32,33]. Specifically, the axial stiffness of a single fibril is given by [31], where is the Young’s modulus of the fibril, is the cross–sectional area, and is the height of the fibril.
As the counter surface compresses the single fibril, a static load develops between the fibril and the counter surface. This load increases with further compressive displacement. Eventually, the load may reach a critical value where the fibril is susceptible to buckling, significantly impacting its adhesion strength. Excessive loads can diminish the adhesion of fibrils [26,28,29,30]. Therefore, precise control of the load between fibrils and a rigid counter surface is crucial. The critical load of a single fibril, which marks the onset of instability and potential buckling, is determined as follows [31]:
Here, represents the critical load, is the effective height factor depending on the boundary conditions, , and are the Young’s modulus, area moment of inertia and height of a fibril, respectively. In this study, is selected for a fixed–free boundary condition, that resembles a frictional contact. The effective height factor is based on experimentally observed results reported in [26]. However, it is important to note that for different aspect ratios (the ratio of fibril height to its diameter) of a fibril, a different effective height factor would need to be selected.
For a fibril array comprised of n fibrils, the total load is the sum of the individual loads of the fibrils. The total force of a fibril array contacting a smooth, rigid counter surface, can be easily computed by just multiplying the single fibril load by the number of fibrils. However, for either a rough rigid counter surface or a rough fibril array (where the height of the fibrils in the array may differ), the total load between the contacting surfaces can be obtained via the following equations:
where is the total load between a fibril array and a rigid counter surface, is the load of the ith fibril, and n is the number of the fibrils in the fibril array, respectively. The total load can be adjusted by regulating the compressive displacement of the counter surface (whether smooth or rough). This ensures that the total load can remain below the critical load (). Consequently, the adhesion strength of a single fibril might fully contribute to the total adhesion strength due to the unbuckled condition. It should be noted that even if the total load is regulated to remain below the critical load, the contact load of individual fibrils can exceed their critical buckling load. This can occur due to variations in the roughness of either the rough fibril array or the rough rigid counter surface.
2.1.2. The Unloading Process
The unloading process is similarly managed by controlling the displacement of the counter surface after contact. During the unloading phase, the objective is to separate the contact between the counter surface and a single fibril or fibril array. The load between the counter surface and the single fibril can be calculated again using the stiffness of the single fibril and the displacement, as expressed in Equation (1).
If the counter surface is moved above the initial height of a single fibril before contact, the single fibril undergoes elongation, resulting in an adhesion force between the single fibril and the counter surface. The adhesion force between a circular flat–ended fibril and a smooth rigid surface can be given as [34]:
where R is the radius of the fibril, is the effective work of adhesion, and represents the contact modulus given by:
and are Young’s moduli of the fibril and the surface, respectively, and and are Poisson’s ratios. represents the contacting area. Although Equation (4) is originally derived for a rigid punch indenting an elastic surface, it serves as a suitable approximation for the adhesive force of a circular fibril with a flat tip in contact with a rigid surface [35]. In a fibril array where each fibril exerts an adhesive force on a surface, the total adhesion force can be calculated by summing up the individual adhesive forces of the fibrils. This can be expressed as:
where n is the number of fibrils in the array, denotes the total adhesion force and is the adhesive force exerted by the ith fibril. In calculating the total adhesion force, it is assumed that each fibril makes full contact with the surface, irrespective of surface roughness, whether on the rough counter surface or within the fibril array. The adhesion force of a fibril is influenced by the applied pre–load of a single fibril (). Therefore, the total adhesion force should be calculated taking into account the pre–load of a single fibril.
2.1.3. Roughness
In the context of a fibril array contacting a rigid surface, surface roughness can manifest in either surface texture characteristics of a rigid counter surface or variations in the heights of the fibrils within the array. These roughness are often described using well–known distribution functions such as Weibull, Gaussian (normal), and non–Gaussian distributions [36]. In this study, the distribution of fibril heights and surface roughness of a rigid surface follows a normal distribution function given by:
where x is the mean value of the height of a single fibril or the mean value of the asperity height of a rigid counter surface, is the mean parameter (selected as 0 in this study), and is the variance. The variance governs the extent of roughness variation from an initial height of a single fibril or a rigid counter surface. The ratio determines the range of height variation across the fibril array or the counter surface. Hence, this approach facilitates a quantitative characterization of fibril array roughness, which is crucial for understanding its impact on adhesion properties when in contact with either a smooth or rough rigid surface.
2.2. Numerical Computation
This section focuses on the numerical computational method employed to analyze the adhesion of a fibril array consisting of n fibrils in contact with either a smooth or rough rigid counter surface. The numerical calculation is conducted in two phases: Loading and Unloading. During the loading phase, the pre–load is monitored with each iteration of the rigid counter surface’s motion. The calculation halts if the pre–load exceeds the desired load. This condition is governed by a pre–load coefficient expressed as follows:
Here, represents the total load during the loading phase, is the pre–load factor, n is the number of fibrils, and is the mean critical load of the fibril array. The mean critical load is calculated by the following:
Here, denotes the critical load of the ith fibril, and n is the number of fibrils. This approach ensures an accurate assessment of the adhesion behavior under varying pre–load conditions compared to the buckling load. The numerical computation during the loading phase follows the steps outlined in Algorithm 1 as detailed below:
| Algorithm 1 Loading Phase |
|
A typical loading procedure of a rough rigid counter surface indenting a rough fibril array is shown in Figure 2.
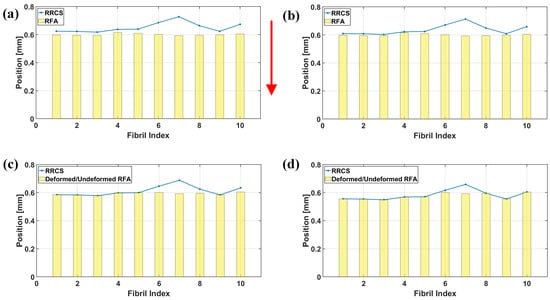
Figure 2.
Representative results in the numerical calculation of loading phase, where n is 10, is 600 m, R is 100 m, is 100, is 2.5. (a) Initial Contact Configuration: Initially, there is a gap between the rough fibril array and the rough counter surface, and the fibril array remains undeformed with no contact established. (b) Partial Contact Initiation: As the counter surface begins its compressive motion, partial contact is established between an asperity on the counter surface and some of the fibrils in the array. (c) Increasing Contact Area: With continued compressive motion of the counter surface, nearly all fibrils come into full contact with the surface. However, some fibrils, like the sixth, seventh and eighth fibril, may still not have made contact at this stage. (d) Contact with Higher pre–load: With a higher pre–load factor, either all fibrils make contact with the counter surface or some do not make contact. In this example, two fibrils do not make contact with the counter surface. The simulation concludes once the total pre–load condition is met, ensuring a comprehensive assessment of the fibril array’s adhesion behavior under varying pre–load conditions. The red arrow indicates the direction of the counter surface’s motion. RRCS stands for Rough Rigid Counter Surface, and RFA denotes Rough Fibril Array. Note that the radius of the fibrils is not scaled in the illustrations, and the buckled condition of the fibrils is not depicted in these figures.
In the unloading phase, the adhesion force of individual fibrils varies based on their buckling conditions, categorized into three distinct states: no buckling, low buckling and high buckling.
- No Buckling Condition: In this state, a fibril is not buckled. Under this condition, the adhesion force remains as described in Equation (4).
- Low Buckling Condition: In the low buckling state, the adhesion force of the ith fibril decreases to 75% of its value in the unbuckled state. This reduction is based on experimental observations of fibril adhesion forces [26].
- High Buckling Condition: In contrast, under high buckling conditions, the adhesion force of the fibril is reduced to 25% of its unbuckled value. This adjustment reflects experimental findings that indicate significant decreases in adhesion forces under severe buckling conditions, with values approximating 30% in some studies [28,29]. For the purposes of simulation, a conservative estimate lower than the observed value is used.
The boundary between the low and high buckling conditions is defined as occurring when the load on a single fibril is less than 150% of its critical load. This value is based on experimental observations in [26]. This categorization helps to more accurately model the adhesive behavior of fibrils during the unloading phase, taking into account the varying degrees of buckling and their impact on adhesion forces. The modified adhesion force of a single fibril due to the buckled condition can be described as follows:
When the counter surface moves beyond the initial height of a fibril in the elongation direction after contact, causing deformation of the fibrils, the contact must be released if the load between the fibril and the counter surface equals or exceeds the modified adhesion force. This condition is governed by the following inequality:
Here, denotes the absolute value of the load between the counter surface and the ith fibril in the unloading phase, and the represents the adhesion force of the ith fibril. The absolute value is used because the load during loading is positive, while in the unloading phase, the load becomes negative. The numerical computation during the loading phase follows the steps outlined in Algorithm 2, as detailed below:
| Algorithm 2 Unloading Phase |
|
A typical unloading procedure of a rough rigid surface indented a rough fibril array is shown in Figure 3.
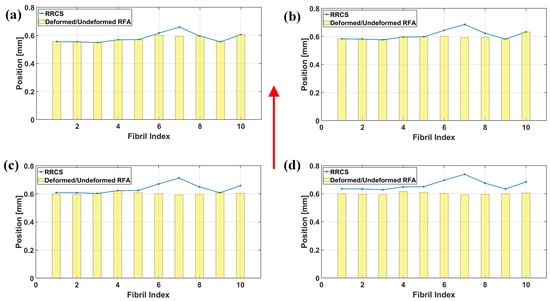
Figure 3.
Representative results in the numerical calculation of unloading phase, where n is 10, is 600 m, R is 100 m, is 100, is 2.5. (a) Final Contact Configuration: At the final stage, the rough fibril array and the counter surface achieve contact depending on the applied pre–load factor. (b) Partial Contact Configuration: As the counter surface begins to move in the opposite direction to compression, some fibrils start to lose contact with the asperities of the counter surface. (c) Loss of Contact: With further movement of the counter surface in the opposite direction, most fibrils begin to lose contact. However, certain fibrils, such as the ninth fibril, may still remain in contact, depending on the motion of the counter surface and individual adhesion forces. (d) Complete Loss of Contact: Depending on the adhesion forces and the loads on each fibril, contact is eventually lost entirely. This procedure captures the dynamic process of contact release between the fibril array and the counter surface during the unloading phase. The red arrow indicates the direction of the counter surface’s motion. RRCS stands for Rough Rigid Counter Surface, and RFA denotes Rough Fibril Array. Note that the radius of the fibrils is not scaled in the illustrations, and the buckled condition of the fibrils is not depicted in these figures.
Multiple Simulations and Normalization
Due to potential variations in fibril height or the surface roughness of the counter surface across different parameterizations, multiple simulations were conducted. For each set of parameters, simulations were iterated 200 times with a constant variance. Subsequently, the variance was changed, and the simulations were repeated 200 times for each new variance. The key metrics analyzed include the maximum adhesion force (), the number of fibrils in contact (), the number of buckled fibrils (), and the variance () in the normal distribution.
To facilitate comparison, the results are normalized as follows:
- Maximum Adhesion Force Normalization: The maximum adhesion force is normalized against the adhesion force of a fibril array with no variance in fibril height or surface roughness of the counter surface. This normalization is performed using the single fibril adhesion value given by Equation (4) () and the number of fibrils (n) in the array. This approach allows for a clear distinction of the effects of height variance in the fibril array or roughness in the rigid counter surface on the adhesion strength.
- Number of Fibrils in Contact () and Number of Buckled Fibrils () Normalization: These metrics are normalized to the total number of fibrils in the array (n). This normalization enables clear observation of the impact of the pre–load factor on the number of fibrils in contact and buckled fibrils.
- Relative Displacement Normalization: The relative displacement of the counter surface () is normalized to the maximum elongation of the fibril, which is calculated assuming no variation in fibril height or counter surface roughness before contact loss. This maximum elongation occurs during the unloading phase due to the adhesive interaction between the fibril and the counter surface. The maximum elongation is determined using Equation (4) and the stiffness of the fibril () under ideal conditions, where the pre–load is below the critical value and there are no height variations or surface roughness. This normalization procedure ensures that the elongation of a rough fibril array is accurately related to the maximum deformation experienced by a smooth fibril array in contact with a smooth, rigid surface.
The normalized quantities are expressed as follows:
Here, and represent the normalized adhesion force and the maximum absolute value of the normal load during the unloading phase shown in Figure 4, respectively. and denote the normalized numbers of fibrils in contact and the actual number of fibrils in contact. Similarly, and refer to the normalized and actual numbers of buckled fibrils, respectively. is the normalized displacement, while represents the incremental motion of the counter surface. These normalized quantities allow for a consistent comparison of the effects of height variance and surface roughness on adhesion performance. The representative results of these normalized values are shown in Figure 4a–c for a smooth fibril array in contact with a rigid, smooth surface. The black and blue lines represent the adhesion strength results when the pre–load is below the critical value, while the yellow and green lines illustrate the adhesion strength when the pre–load exceeds the critical threshold. In Figure 4a, the effect of excessive pre–load on adhesion strength is evident, as it leads to reduced adhesion due to the buckling of the smooth fibril array under high pre–load conditions (). Additionally, Figure 4c shows the status of fibrils in contact and those that are buckled. The blue and dark blue lines correspond to cases where the pre–load is below the critical value, and under these conditions, all the fibrils are in contact, as expected, since there is no roughness in either the fibril array or the counter surface. When the pre–load exceeds the critical value, the fibrils buckle, which is indicated by the orange dashed line in Figure 4c. Figure 4b–d present the normalized force–displacement curves for a rough fibril array in contact with a rough, rigid surface. The results indicate that the loading and unloading curves do not intersect, leading to adhesion hysteresis. Similar hysteresis is observed in simulations involving fibrils in contact with an elastic half–space [10]. This hysteresis can be attributed to the roughness of the two contacting surfaces, as demonstrated in another study [37]. Additionally, the loading–unloading procedure and corresponding results are demonstrated in Supplementary Video File S1: “video–loadunload” for a rough fibril array contacting a rough surface.
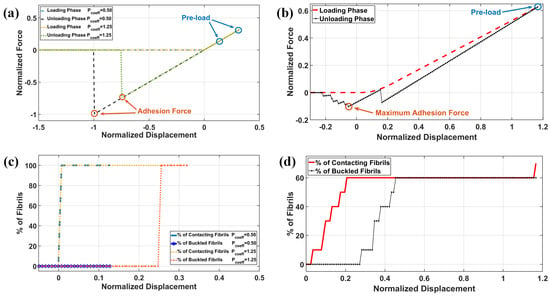
Figure 4.
The representative results include (a) Normalized force (pre–load and adhesion) and normalized displacement of the counter surface for a smooth fibril array in contact with a rigid, smooth surface, where the blue and black lines represent the adhesion strength below the critical pre–load, the green and yellow lines illustrate the adhesion strength when the pre–load exceeds the critical threshold, (b) Normalized force (pre–load and adhesion) and normalized displacement of the counter surface for a rough fibril array in contact with a rigid, rough surface, (c) The percentage of fibrils in contact and buckled fibrils during the loading phase for a smooth fibril array in contact with a rigid, smooth surface, and (d) The percentage of fibrils in contact and buckled fibrils during the loading phase for a rough fibril array in contact with a rigid, rough surface. The indicated values correspond to the pre–load and maximum adhesion force.
3. Results
This section presents the results of 200 iterated simulations, focusing exclusively on the mean and standard deviations of the normalized results unless otherwise specified. The mechanical parameters of the fibril array and the rigid surface, along with the related simulation parameters, are provided in Table 1.

Table 1.
Parameters used in the simulations.
3.1. Adhesion between a Rigid Surface and a Rough Fibril Array
Figure 5a illustrates the normalized adhesion of a rough fibril array in contact with a smooth, rigid surface, under varying roughness variances and low pre–load conditions (below the critical buckling load). The results show that the fibril array maintains consistent adhesion strength across different roughness variances, with maximum normalized adhesion close to 1 at lower variances. However, as the variance increases, the adhesion strength steadily decreases, likely due to the greater differences in fibril height caused by higher variance. During the unloading phase, this height disparity leads to a sequential loss of contact among fibrils, thereby reducing maximum adhesion. Furthermore, increasing the pre–load enhances the adhesion strength, which is expected since a higher pre–load causes more fibrils to be in contact, thus increasing adhesion strength. However, as the pre–load approaches the critical value, even slight increases in roughness significantly impact adhesion strength. This is because some fibrils buckle while others do not, leading to deviations from the typical exponential decay in adhesion strength due to varying buckling conditions among the fibrils. With further increases in variance, the adhesion strength returns to the typical exponential decay observed at these pre–load values.
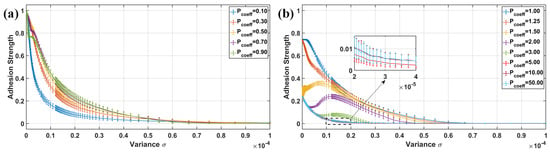
Figure 5.
The results of normalized adhesion with different variances () are shown in the following conditions (a) Low pre–load condition ( is less than 1.00), and (b) High pre–load condition () is greater than 1.00.
Figure 5b presents the adhesion strength under higher pre–load conditions. The results indicate that increasing the pre–load reduces the normalized adhesion, with a maximum of around 0.75 at the lowest variance. Additionally, a distinct adhesive characteristic is observed: up to a pre–load factor of 1.5, the normalized adhesion decreases with increasing variance. However, when the pre–load factor is between 1.5 and 5, there is an initial increase in adhesion followed by a decrease. This can be explained by the fact that some fibrils undergo low buckling while others become highly buckled. The increase occurs because fibrils in the low buckling condition retain about 75% of their unbuckled adhesive strength, whereas highly buckled fibrils retain only 25%. Despite these variations, the overall trend is that adhesion decreases as variance increases due to greater differentiation in fibril height.
Figure 6 shows the normalized number of fibrils in contact for a rough fibril array interacting with a smooth rigid surface, under various variances and pre–load conditions. The results demonstrate that, at low variances, almost all fibrils are in contact with the rigid surface. At lower variances, the fibrils can adhere to the rigid surface due to the nearly uniform height distribution among the fibrils, despite different pre–load conditions. However, as the variance increases, resulting in greater height differences among the fibrils, the percentage of fibrils in contact decreases. For a lower pre–load below the critical buckling load, between 15% and 25% of the fibrils in the array maintain contact. Under pre–loads higher than the critical buckling load, the normalized number of fibrils in contact approaches the theoretical maximum value of 1. To achieve a higher pre–load, a greater number of fibrils must be in contact. Ultimately, the higher the pre–load, the more fibrils are in contact.
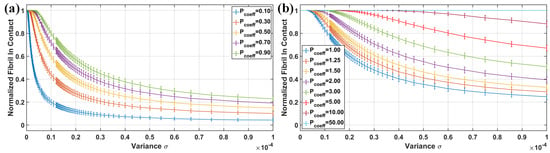
Figure 6.
The results of normalized fibrils in contact with different variances () are shown in the following conditions (a) Low pre–load condition ( is less than 1.00), and (b) High pre–load condition () is greater than 1.00.
Figure 7 illustrates the correlation between normalized adhesion and the normalized number of fibrils in contact for a rough fibril array interacting with a smooth rigid surface, under varying pre–load conditions. The results show that under low pre–load conditions, adhesion is linearly related to the number of fibrils in contact. This is expected, as the total adhesion is the sum of the individual fibrils’ adhesion strength, resulting in a slope of approximately 1 for the adhesion–fibril in contact relationship. At high pre–load conditions, almost all fibrils must be in contact to achieve the higher pre–load. However, as demonstrated in Figure 5, higher pre–load reduces adhesion. Consequently, as the pre–load approaches infinity, all fibrils would be in contact, but the adhesion would decrease.
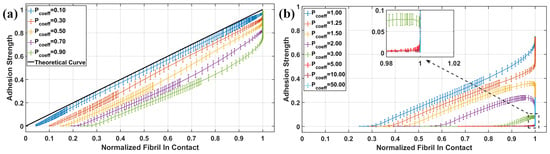
Figure 7.
The correlation between the normalized adhesion and the normalized fibrils in contact is shown under the following conditions: (a) Low pre–load condition ( is less than 1.00), and (b) High pre–load condition () is greater than 1.00.
Figure 8 and Figure 9 depict the normalized number of buckled fibrils with varying variances and the relationship between normalized adhesion and normalized buckled fibrils, respectively, for a rough fibril array in contact with a rigid surface. As the variance increases, the number of buckled fibrils exhibits a decremental characteristic. However, if the pre–load factor approaches a very high value, all fibrils are expected to buckle due to the excessive pre–load, as shown in Figure 8. When the pre–load is below the critical buckling load, the number of buckled fibrils initially increases with the variance up to a certain value (approximately . Beyond this point, the number of buckled fibrils decreases very slowly as the variance continues to rise. Additionally, at low variance values, higher pre–loads result in a greater number of buckled fibrils, as illustrated in Figure 8.
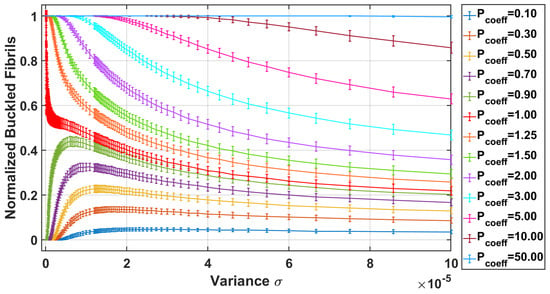
Figure 8.
The normalized buckled fibrils with different variances ().
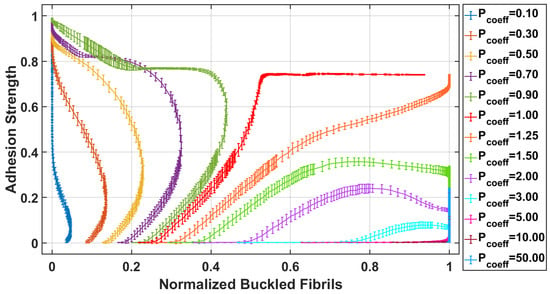
Figure 9.
The correlation between the normalized adhesion and the normalized buckled fibrils in different pre–load conditions.
Under varying pre–load conditions, the normalized adhesion varies with respect to the buckled fibrils. At lower pre–load conditions, the total adhesion is primarily contributed by the unbuckled fibrils. However, as demonstrated in Figure 9, as the pre–load increases, fibril buckling becomes more prevalent. Consequently, the adhesion contribution from the buckled fibrils increases, although it remains lower compared to the adhesion from unbuckled fibrils. At higher pre–loads, the adhesion is predominantly due to the buckled fibrils, as illustrated in Figure 9.
3.1.1. Effect of Number of Fibrils on the Adhesive Strength
Figure 10 shows the adhesive strength of rough fibril arrays with varying numbers of fibrils in contact with a smooth rigid surface under different pre–load conditions and variances. The results reveal no significant variation in adhesive strength based on the number of fibrils. Whether using a smaller or larger number of fibrils, the adhesive strength remains consistent. In the numerical computations, adhesive forces are normalized with respect to the maximum achievable adhesive force under conditions where there is no roughness in either the fibril heights or the counter surface. Therefore, it can be concluded that the number of fibrils in the array does not impact the maximum achievable normalized adhesive strength. However, it is noted that increasing the number of fibrils results in more absolute adhesive strength, but this does not translate to a change in normalized adhesion.
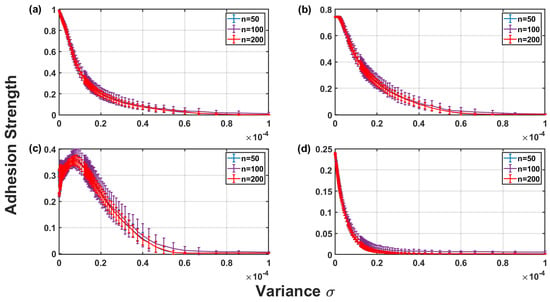
Figure 10.
The effect of number on the adhesive strength of fibrils under varying pre–load conditions (a) , (b) , (c) , (d) .
3.1.2. Effect of Work of Adhesion on the Adhesive Strength
Elastic fibrils may exhibit different work of adhesion due to alterations in their mechanical properties [39]. Figure 11 illustrates the adhesive strength of rough fibril arrays in contact with a smooth rigid surface, considering varying work of adhesion under different pre–load conditions and variances. The results show that fibrils with a lower work of adhesion demonstrate reduced adhesive strength. At both low and very high pre–load values relative to the buckling load, the difference in adhesive strength due to varying work of adhesion is less pronounced. However, this difference becomes more significant when the pre–load exceeds the threshold that distinguishes between low and high buckling states. This is because some fibrils are in a low buckling state while others are highly buckled. Given that the difference in work of adhesion affects the adhesive strength as a square root function, as stated in Equation (4), the maximum variation in adhesive strength can reach up to 3.625. At the transition between lower and higher buckling states, the adhesive strength reflects this maximum difference. Therefore, a reduced work of adhesion results in decreased adhesive strength, which is expected as it directly influences the adhesive properties.
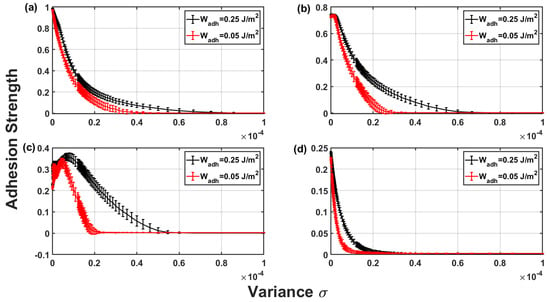
Figure 11.
The effect of work of adhesion on the adhesive strength of fibrils under varying pre–load conditions (a) , (b) , (c) , (d) .
3.1.3. Effect of Both Surfaces Being Rough on the Adhesive Strength
Figure 12 illustrates the normalized adhesion of rough fibril arrays under varying pre–load conditions and different variances when in contact with both a smooth and a rough rigid surface. The roughness of the rigid surface and the height distribution in the fibril array follow the same variance condition. The results reveal a consistent pattern across the same variance and pre–load conditions. However, the adhesive strength of a rough fibril array in contact with a rough rigid surface is lower compared to that with a smooth rigid surface. This reduction is expected, as surface roughness significantly diminishes adhesive strength. Thus, the observed decrease in adhesion when both contacting surfaces are rough, compared to when one surface is smooth and the other is rough, aligns with the anticipated results.
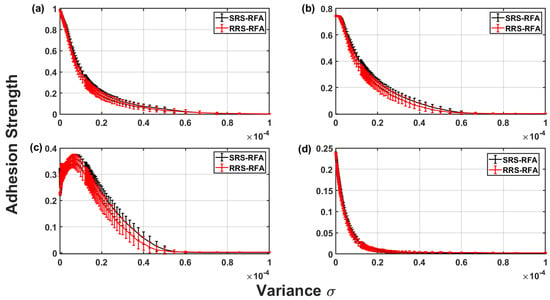
Figure 12.
Normalized adhesive strength of a rough fibril array in contact with both a smooth rigid surface and a rough rigid surface, where both surfaces have the same roughness variance, . The data is shown under varying pre–load conditions: (a) , (b) , (c) , (d) . SRS indicates a smooth rigid surface, while RRS refers to a rough rigid surface. RFA denotes rough fibril array.
4. Discussion
The variation in adhesion force with respect to the roughness parameter has been studied in this study. It has been observed that the variation exhibits an exponential decay. The ratio of maximum adhesion strength to adhesion strength with roughness has also been shown to follow an exponential relationship in other studies [36,40]. Additionally, it has been demonstrated that the adhesion strength in the contact of fibrillar structures with rough surfaces decreases similarly with respect to the roughness parameter and other loading conditions [22]. However, it should be noted that different results may emerge when considering a Weibull distribution as opposed to a Gaussian distribution, as shown in [36]. This highlights the necessity of considering different distributions, which can be adjusted by modifying Equation (7). Nevertheless, the main aim of this study is not to investigate the effect of different distributions on adhesion strength, but rather to demonstrate how the adhesion force changes in fibrillar structures, given that buckling effects are often neglected in theoretical models. This is achieved through a quick and simple algorithm, assuming that each fibril in the fibril array has an independent mechanical effect. Some studies also indicate that each fibril can be modeled discretely [27,41,42], and the same approach was applied here.
The contact mechanics of the fibril array are influenced by the distance between the fibrils [42]. As the distance between two fibrils changes, interactions occur between them on an elastic backing layer. This suggests that the adhesion force can be adjusted based on the interaction between the fibrils. Therefore, the interaction between two fibrils should also be considered in the adjustment of the adhesion force. Additionally, the aspect ratio (the ratio of fibril height to diameter) has a direct impact on the adhesion force [17]. For fibrils with a high aspect ratio, adjacent fibrils can collide with each other [43], leading to adhesion between the adjacent fibrils [44]. In this study, the aspect ratio is conservatively set to 3, which aligns with the values found in manufactured fibril arrays. The limit of the aspect ratio can generally be determined by considering various fibril parameters, as discussed in [44]. Naturally, changing the fibril height while keeping the diameter constant will also alter the buckling load. Consequently, the effects of both the aspect ratio and the spacing between adjacent fibrils can be incorporated into the adhesion force in Equation (4), taking into account the backing layer model as well [45,46]. This approach ensures that both the buckling condition and the structural interaction of adjacent fibrils are not overlooked. However, the primary aim of this study is to consider the buckling condition of the fibrils rather than the structural coupling in the fibril array. Therefore, it is assumed that all fibrils are on a rigid backing layer in a decoupled manner.
We demonstrated that the number of fibrils has a negligible effect on normalized adhesion when considering a normal distribution of fibril heights, which contrasts with the findings in [42]. The efficiency of using different numbers of fibrils in a fibril array decreases monotonically as the number of fibrils increases, impacting the load–sharing capacity of the array [42]. The discrepancy arises from the assumptions in the theoretical model. We neglected the effects of backing layer thickness [47,48], backing layer Young’s modulus [49], and the structural coupling of adjacent fibrils in the array [33] on the adhesion capacity of a fibril array. The load–sharing capacity in a fibril array is influenced by the elastic coupling due to interactions with the backing layer [42,47]. Considering an elastic backing layer with finite thickness would alter the load–sharing capacity of the array, making the number of fibrils in the array more significant. During the unloading phase, the total elastic deformation of a fibril is regarded as a combination of the fibril elongation and the deformation of the elastic backing layer [49], which can be calculated using a compliance matrix [50]. The compliance matrix includes non–diagonal terms due to structural coupling over the elastic backing layer [50]. For fibrils on an infinitesimally thin backing layer, the elongation of fibrils under load would be uniform, resulting in equal load sharing [47]. However, as the backing layer thickness increases, the elastic deformation at the backing layer interface of the ith fibril would induce deformation in adjacent fibrils (jth), influenced by the spacing between them [49]. This variation affects the adhesive force experienced by the fibril [47], consequently affecting its load capacity. If the Young’s modulus of the backing layer is significantly larger than that of the fibrils, the fibrils would undergo uniform deformation, leading to equal load sharing [49], rendering the number of fibrils in the array less significant. Similarly, in the case of a very thin backing layer, which can be considered rigid and with zero off–diagonal terms in the compliance matrix [51], the backing layer remains undeformed, resulting in equal load sharing within the fibril array [49]. The primary factor in the inconsistency regarding the effect of the number of fibrils on adhesion strength lies in the assumption of a rigid backing layer, which makes the number of fibrils inconsequential, as shown in Figure 10. However, the effects of backing layer interaction and structural coupling due to varying spacings could be incorporated into Equation (4).
The adhesion of flat–ended circular elastic fibrils is directly related to the work of adhesion, as demonstrated in Equation (4) [34]. A decrease in the work of adhesion consequently reduces the adhesion strength, as illustrated in Figure 11. However, other parameters besides the work of adhesion can be used to describe the adhesion behavior of flat–ended fibrils [52], such as the intrinsic adhesion strength, , and the adhesion range, . These parameters relate the adhesion strength of flat–ended fibrils to the detachment mode during unloading. The detachment mode, which determines how a fibril separates from the contacting surface, can be categorized into two distinct regimes [53]: (i) the JKR regime or energy–controlled adhesion regime, and (ii) the DMT–type adhesion or strength–limited regime. A single non–dimensional parameter, , governs the transition between these two regimes and defines the adhesion strength of an elastic fibril in contact with a rigid surface [54,55]:
where the intrinsic adhesion strength, R is the fibril radius, is the contact modulus determined by Equation (5), and is the work of adhesion. The value of indicates the detachment mode of the elastic fibril. When is less than 0.5, corresponding to the strength–limited regime, the fibril detaches uniformly from the counter surface, exhibiting strong adhesion strength. Conversely, when exceeds 0.5, the adhesion falls within the energy–controlled regime, leading to crack–propagated detachment with reduced adhesion strength. The adhesion strength in the energy–controlled regime is significantly lower than that in the strength–limited regime [56]. However, as the fibril radius is reduced, the adhesion strength in the energy–controlled regime can approach the value observed in the strength–limited regime. Thus, a critical radius for a single fibril, which delineates the adhesion regime, can be determined by .
Using the physical parameters outlined in Table 1, the non–dimensional parameter is calculated as 26.52 with a critical radius of m when assuming the intrinsic adhesion strength of Polydimethylsiloxane (PDMS) fibrils to be 1 MPa [55]. Consequently, Kendall’s solution, as stated in Equation (4), is applicable to the fibril arrays studied with the dimensions provided in Table 1. Conversely, assuming an intrinsic adhesion strength of 0.1 MPa for a typical PDMS fibril [57] results in being 0.26 and the critical radius increasing to m, indicating that the adhesion regime is strength–limited. Therefore, the adhesion force based on Kendall’s solution in Equation (4) would need to be adjusted to reflect higher values in the strength–limited adhesion regime.
However, when the work of adhesion is reduced to 0.05 J/m2, the detachment mode shifts to the energy–controlled regime, as exceeds 0.5, regardless of the intrinsic adhesion strength. In this scenario, the critical radius of the fibril decreases to approximately m and m for the intrinsic adhesion strength, which is smaller than the radii of the fibrils used in this study. The fibril radii thus fall within the energy–controlled regime, aligning with Kendall’s solution. This shift notably affects the adhesion force described by Equation (4).
Adhesion in both the strength–limited and energy–controlled regimes can be estimated using the non–dimensional parameter along with the constants and [57]. Thus, is crucial for determining the adhesion strength or the critical radius of the fibril. Although the primary focus of this study is on the buckling behavior of the fibrils rather than their detachment mode, recalculating the adhesion force using could offer additional insights, particularly when considering different fibril radii.
This study assumes that all fibrils achieve full contact with the surface, irrespective of roughness. However, in reality, a fibril’s contact behavior varies depending on its diameter and the surface roughness [13]. When the fibril diameter exceeds the spacing between adjacent roughness peaks, it establishes partial contact with multiple peaks, and the adhesion strength is primarily determined by this partial contact. Increasing the pre–load up to the critical value can enhance the contact area, thereby increasing adhesion strength without inducing significant bending or buckling. In contrast, when the fibril diameter is smaller than the spacing between peaks, the contact status depends on the pre–load, leading to either partial contact or full surface conformity. Partial contact can manifest either as a reduced contact area without noticeable bending or as a smaller contact area accompanied by significant bending, resulting in a contact angle that is influenced by surface roughness and fibril diameter [13]. This configuration can lead to potential shearing effects.
Shearing substantially impacts fibril adhesion [58], with shear adhesion being particularly dependent on the fibril’s aspect ratio [59]. Normal adhesion strength typically decreases due to bending induced by shearing [13,58]. Thus, the ratio of fibril diameter to spacing between peaks, along with the fibril’s aspect ratio, are critical factors in determining adhesive strength. Despite these complexities, this study employs a numerical and conservative approach to estimate the adhesion strength of fibrillar structures, accounting for non–contact and buckled fibrils, which are influenced by the pre–load. Buckling, leading to contact loss during loading, significantly impacts adhesion [26] and must be considered in numerical models. To more accurately capture potential shearing when the fibril diameter is smaller than the spacing between surface peaks, further discretizing the displacement field along the x–axis (perpendicular to the normal load in Figure 1) could be beneficial. Rather than modeling the fibril as a single discretized element, representing it as a series of discretized segments across its diameter could offer a more precise depiction of shearing effects and the resulting contact angles. This approach would better capture the nuances of partial contact during loading.
It is well known that polymers exhibit a rate–dependent mechanical response due to their viscoelastic nature. Fibrils are generally manufactured using polymers such as PDMS [33]. Consequently, fibrils also demonstrate a rate–dependent adhesion behavior, even when in contact with a smooth surface [60]. In unloading scenarios, the adhesion behavior can be considered in relation to the unloading velocity [61]. This can be achieved by considering the effective work of adhesion as a function of the unloading velocity. To account for this, the motion of the counter surface () can be modeled with a time–dependent behavior. The incremental motion can be converted into a time–related motion, allowing the rate–dependent adhesion to be incorporated into the algorithm. This can be represented as [62], where can be taken as the reference adhesion force in a quasi–static unloading scenario. Hence, this approach accounts for the velocity dependence of the adhesion in a fibril array.
This study investigated the adhesive strength of fibrillar structures, taking into account the buckling conditions under varying levels of surface roughness, including both fibril array height distribution and the texture of a rigid surface. It is well established that applying a high pre–load to achieve contact between fibril arrays and a rough surface enhances adhesion strength [20,21,22,23]. Our findings also confirm that increasing the pre–load improves adhesion strength, provided it does not surpass a critical threshold—namely, the critical buckling load. Fibrils, being elastic long cylinders, become unstable under excessive compressive forces, which reduces the contact area and, consequently, the adhesion [26,28,29,30]. Therefore, it is crucial to consider the pre–load condition to maximize the contact area while maintaining the stability of the fibrils.
Figure 13 illustrates the ratio of normalized adhesion forces to the adhesion force at the lowest pre–load () on a logarithmic scale against the variance in surface roughness. The results show that at low roughness variance and pre–loads below the critical buckling load, normalized adhesion remains consistent. This consistency is expected since the lower variance in fibril height distribution or an almost smooth surface results in adhesion values similar to those observed in fibril arrays in contact with a smooth surface. Notably, the change in adhesion strength remains nearly identical across different variance parameters, irrespective of pre–load. As both the pre–load and variance increase, so does the adhesion strength. The divergence in adhesion strength is closely tied to the buckling limit. The adhesion strength increases when the pre–load is below the critical value at the onset of a high buckling load. However, at higher roughness variance, the change in normalized adhesion remains nearly constant up to a pre–load value of 1.5. Beyond a pre–load value of 2, adhesion strength drops significantly as most fibrils buckle, as shown in Figure 8. The pre–load factor values of 1.5 and beyond, which signify the onset of low and high buckling conditions, respectively, align with experimentally observed buckling effects on the adhesion of fibril arrays [26,28,29]. These values can be adjusted in algorithms as conservative approximations. Consequently, it is imperative to account for the buckling effect in numerical calculations of adhesion.
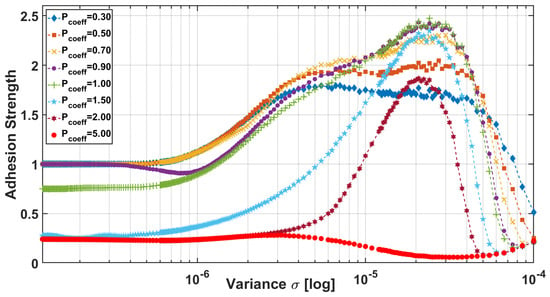
Figure 13.
Effect of pre–load on the adhesion strength normalized to the adhesion obtained at the lowest pre–load.
For fibril arrays in contact with rough surfaces, shape memory polymers (SMPs) can greatly improve adhesion strength under high pre–load conditions despite buckling failure of the fibrils [55,63,64]. SMPs can switch their modulus between glassy and rubbery states [53,65,66]. When heated above their phase transition temperature (Tg), SMPs become soft with a Young’s modulus of around 1 MPa, allowing them to easily conform to surfaces. Cooling below Tg makes them rigid with a Young’s modulus over 1 GPa, which locks their deformed shape in place, a process known as rubbery–to–glass (R2G) adhesion [55]. This combination of modulus change and shape–locking contributes to enhanced adhesion strength, with the adhesion being energy–controlled in the rubbery phase and strength–limited in the glassy phase. This transition is represented by a single non–dimensional parameter, with shape–locking being crucial for increased adhesion strength [53]. In applications with fibril arrays in contact with a rough surface, SMPs can help to minimize adhesion strength loss due to buckling under excessive pre–load, compared to traditional polymers. As fibril arrays buckle under high pre–load, side surfaces come into contact with the counter surface due to significant bending deformation, which increases the contact area [64]. Cooling below Tg can further enhance adhesion strength, even on rough surfaces, due to this increased contact area. Additionally, in the rubbery phase, SMPs provide adhesion switchability with buckling failure, allowing for detachment on demand [55]. Therefore, SMPs could be an effective material choice for a fibril array, particularly in managing excessive pre–load and surface roughness.
5. Conclusions
In this study, the adhesion strength of fibril arrays in contact with either a smooth or a rough rigid surface was investigated for various pre–loads, number of fibrils, and roughness parameters. The fibrils in the arrays were considered as soft cylinders modeled using Euler–Bernoulli beam theory. The adhesion model was incorporated into the numerical computational model by assuming that the influence of each fibril does not affect the other fibrils. The following conclusions were drawn from the results:
- Effect of Roughness on Adhesion: The adhesion strength exhibits an exponential decay with increasing roughness parameters. This relationship is consistent across various pre–loads. This finding aligns with existing studies which show that the adhesion strength decreases in a similar manner with respect to roughness. The numerical model effectively captured the influence of surface roughness on adhesion strength.
- Role of Fibril Number: The number of fibrils in the array has a negligible effect on normalized adhesion strength when considering a normal distribution of fibril heights. This finding contrasts with previous studies that incorporated backing layer effects and structural coupling [33,42,47], indicating the importance of model assumptions in predicting adhesion behavior.
- Impact of Pre–Load on Adhesion Strength: Increasing the pre–load enhances the adhesion strength up to a certain threshold, beyond which the fibrils begin to buckle. The critical pre–load is directly related to the onset of buckling, and exceeding this value significantly reduces adhesion due to the instability introduced by buckling.
Buckling is pivotal to the adhesion performance in fibrillar structures [26]. High compressive forces can cause these structures to buckle, leading to a reduction in contact area and, consequently, adhesion strength. The numerical model developed in this study accounts for buckling effects, underscoring the necessity of integrating this phenomenon into both theoretical and computational models. The results offer valuable insights into designing fibrillar adhesives by optimizing pre–load and surface roughness. Understanding critical buckling loads and roughness impacts will facilitate the development of effective fibrillar structures for practical use. Future research will include further discretization of individual fibrils, and exploring different tip shapes, such as mushroom–like [67].
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/lubricants12080294/s1, Video S1: Video-loadunload represents the typical loading-unloading results of a rough fibril array in contact with a rough surface.
Funding
This research received no external funding.
Data Availability Statement
Data generated during the current study are available from the author on reasonable request.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Persson, B.; Tosatti, E. The effect of surface roughness on the adhesion of elastic solids. J. Chem. Phys. 2001, 115, 5597–5610. [Google Scholar] [CrossRef]
- Persson, B. Adhesion between an elastic body and a randomly rough hard surface. Eur. Phys. J. E 2002, 8, 385–401. [Google Scholar] [CrossRef] [PubMed]
- Peressadko, A.; Hosoda, N.; Persson, B. Influence of surface roughness on adhesion between elastic bodies. Phys. Rev. Lett. 2005, 95, 124301. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Zhang, S.; Li, D.; Liu, Y. Friction behavior of rough surfaces on the basis of contact mechanics: A review and prospects. Micromachines 2022, 13, 1907. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 324, 301–313. [Google Scholar]
- Greenwood, J.A. Contact of Rough Surfaces: The Greenwood and Williamson/Tripp, Fuller and Tabor Theories. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.W., Eds.; Springer: Boston, MA, USA, 2013; pp. 517–522. [Google Scholar]
- Kim, J.K.; Varenberg, M. Contact splitting in dry adhesion and friction: Reducing the influence of roughness. Beilstein J. Nanotechnol. 2019, 10, 1–8. [Google Scholar] [CrossRef]
- Kamperman, M.; Kroner, E.; del Campo, A.; McMeeking, R.M.; Arzt, E. Functional adhesive surfaces with “gecko” effect: The concept of contact splitting. Adv. Eng. Mater. 2010, 12, 335–348. [Google Scholar] [CrossRef]
- He, X.; Li, Q.; Popov, V.L. Simulation of adhesive contact of soft microfibrils. Lubricants 2020, 8, 94. [Google Scholar] [CrossRef]
- Boesel, L.F.; Greiner, C.; Arzt, E.; Del Campo, A. Gecko-inspired surfaces: A path to strong and reversible dry adhesives. Adv. Mater. 2010, 22, 2125–2137. [Google Scholar] [CrossRef]
- Kasem, H.; Varenberg, M. Effect of counterface roughness on adhesion of mushroom-shaped microstructure. J. R. Soc. Interface 2013, 10, 20130620. [Google Scholar] [CrossRef] [PubMed]
- Barreau, V.; Hensel, R.; Guimard, N.K.; Ghatak, A.; McMeeking, R.M.; Arzt, E. Fibrillar elastomeric micropatterns create tunable adhesion even to rough surfaces. Adv. Funct. Mater. 2016, 26, 4687–4694. [Google Scholar] [CrossRef]
- Autumn, K.; Gravish, N. Gecko adhesion: Evolutionary nanotechnology. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 1575–1590. [Google Scholar] [CrossRef] [PubMed]
- Eisenhaure, J.; Kim, S. A review of the state of dry adhesives: Biomimetic structures and the alternative designs they inspire. Micromachines 2017, 8, 125. [Google Scholar] [CrossRef]
- He, B.; Chen, W.; Jane Wang, Q. Surface texture effect on friction of a microtextured poly(dimethylsiloxane) (PDMS). Tribol. Lett. 2008, 31, 187–197. [Google Scholar] [CrossRef]
- Greiner, C.; del Campo, A.; Arzt, E. Adhesion of bioinspired micropatterned surfaces: Effects of pillar radius, aspect ratio, and preload. Langmuir 2007, 23, 3495–3502. [Google Scholar] [CrossRef] [PubMed]
- Micciché, M.; Arzt, E.; Kroner, E. Single macroscopic pillars as model system for bioinspired adhesives: Influence of tip dimension, aspect ratio, and tilt angle. ACS Appl. Mater. Interfaces 2014, 6, 7076–7083. [Google Scholar] [CrossRef] [PubMed]
- Del Campo, A.; Greiner, C.; Arzt, E. Contact shape controls adhesion of bioinspired fibrillar surfaces. Langmuir 2007, 23, 10235–10243. [Google Scholar] [CrossRef] [PubMed]
- Porwal, P.K.; Hui, C.Y. Strength statistics of adhesive contact between a fibrillar structure and a rough substrate. J. R. Soc. Interface 2008, 5, 441–448. [Google Scholar] [CrossRef]
- Li, Q.; Popov, V.L. Adhesive contact of rough brushes. Beilstein J. Nanotechnol. 2018, 9, 2405–2412. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Li, Q.; Popov, V.L. Strength of adhesive contact between a rough fibrillar structure and an elastic body: Influence of fibrillar stiffness. J. Adhes. 2022, 98, 1820–1833. [Google Scholar] [CrossRef]
- Zhang, Y.; He, L. Preload-responsive adhesion of microfibre arrays to rough surfaces. Appl. Math. Mech. 2017, 38, 155–160. [Google Scholar] [CrossRef]
- Hu, H.; Tian, H.; Gao, Y.; Wan, Z.; Wang, L.; Xu, H.; Wang, C.; Shao, J.; Zheng, Z. Revisiting the contact splitting hypothesis: An effective route for enhancing adhesion on rough surface. J. Mech. Phys. Solids 2023, 170, 105121. [Google Scholar] [CrossRef]
- Kendall, K. The adhesion and surface energy of elastic solids. J. Phys. D Appl. Phys. 1971, 4, 1186. [Google Scholar] [CrossRef]
- Paretkar, D.R.; Bartlett, M.D.; McMeeking, R.; Crosby, A.J.; Arzt, E. Buckling of an adhesive polymeric micropillar. J. Adhes. 2013, 89, 140–158. [Google Scholar] [CrossRef]
- Long, R.; Hui, C.Y. The effect of preload on the pull-off force in indentation tests of microfibre arrays. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 961–981. [Google Scholar] [CrossRef]
- Purtov, J.; Frensemeier, M.; Kroner, E. Switchable adhesion in vacuum using bio-inspired dry adhesives. ACS Appl. Mater. Interfaces 2015, 7, 24127–24135. [Google Scholar] [CrossRef] [PubMed]
- Isla, P.Y.; Kroner, E. A novel bioinspired switchable adhesive with three distinct adhesive states. Adv. Funct. Mater. 2015, 25, 2444–2450. [Google Scholar] [CrossRef] [PubMed]
- Tinnemann, V.; Arzt, E.; Hensel, R. Switchable double-sided micropatterned adhesives for selective fixation and detachment. J. Mech. Phys. Solids 2019, 123, 20–27. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J.N. Theoy of Elasticity; McGraw Hill Education: New York, NY, USA, 1986. [Google Scholar]
- Eray, T.; Sümer, B.; Koc, I.M. Analytical and experimental analysis on frictional dynamics of a single elastomeric pillar. Tribol. Int. 2016, 100, 293–305. [Google Scholar] [CrossRef]
- Koç, I.M.; Eray, T. Modeling frictional dynamics of a visco-elastic pillar rubbed on a smooth surface. Tribol. Int. 2018, 127, 187–199. [Google Scholar] [CrossRef]
- Maugis, D. Contact, Adhesion and Rupture of Elastic Solids; Springer Science & Business Media: Berlin, Germany, 2013; Volume 130. [Google Scholar]
- Aksak, B.; Murphy, M.P.; Sitti, M. Adhesion of biologically inspired vertical and angled polymer microfiber arrays. Langmuir 2007, 23, 3322–3332. [Google Scholar] [CrossRef] [PubMed]
- Ciavarella, M.; Papangelo, A. On the sensitivity of adhesion between rough surfaces to asperity height distribution. Phys. Mesomech. 2018, 21, 59–66. [Google Scholar] [CrossRef]
- Wei, Z.; He, M.F.; Zhao, Y.P. The effects of roughness on adhesion hysteresis. J. Adhes. Sci. Technol. 2010, 24, 1045–1054. [Google Scholar] [CrossRef]
- Eray, T. Tunable adhesion of an elastic pillar by pressurizing inner cavity. Proc. Inst. Mech. Eng. Part J Eng. Tribol. 2022, 236, 541–551. [Google Scholar] [CrossRef]
- Yu, Y.; Sanchez, D.; Lu, N. Work of adhesion/separation between soft elastomers of different mixing ratios. J. Mater. Res. 2015, 30, 2702–2712. [Google Scholar] [CrossRef]
- Ciavarella, M.; Papangelo, A. A generalized Johnson parameter for pull-off decay in the adhesion of rough surfaces. Phys. Mesomech. 2018, 21, 67–75. [Google Scholar] [CrossRef]
- Guidoni, G.; Schillo, D.; Hangen, U.; Castellanos, G.; Arzt, E.; McMeeking, R.; Bennewitz, R. Discrete contact mechanics of a fibrillar surface with backing layer interactions. J. Mech. Phys. Solids 2010, 58, 1571–1581. [Google Scholar] [CrossRef]
- Bacca, M.; Booth, J.A.; Turner, K.L.; McMeeking, R.M. Load sharing in bioinspired fibrillar adhesives with backing layer interactions and interfacial misalignment. J. Mech. Phys. Solids 2016, 96, 428–444. [Google Scholar] [CrossRef]
- Amato, L.; Keller, S.S.; Heiskanen, A.; Dimaki, M.; Emnéus, J.; Boisen, A.; Tenje, M. Fabrication of high-aspect ratio SU-8 micropillar arrays. Microelectron. Eng. 2012, 98, 483–487. [Google Scholar] [CrossRef]
- Spolenak, R.; Gorb, S.; Arzt, E. Adhesion design maps for bio-inspired attachment systems. Acta Biomater. 2005, 1, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Long, R.; Hui, C.Y.; Kim, S.; Sitti, M. Modeling the soft backing layer thickness effect on adhesion of elastic microfiber arrays. J. Appl. Phys. 2008, 104. [Google Scholar] [CrossRef]
- Aksak, B.; Hui, C.Y.; Sitti, M. The effect of aspect ratio on adhesion and stiffness for soft elastic fibres. J. R. Soc. Interface 2011, 8, 1166–1175. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Sitti, M.; Hui, C.Y.; Long, R.; Jagota, A. Effect of backing layer thickness on adhesion of single-level elastomer fiber arrays. Appl. Phys. Lett. 2007, 91. [Google Scholar] [CrossRef]
- Greiner, C.; Buhl, S.; del Campo, A.; Arzt, E. Experimental parameters controlling adhesion of biomimetic fibrillar surfaces. J. Adhes. 2009, 85, 646–661. [Google Scholar] [CrossRef]
- Cheng, Y.; Peng, Z.; Chen, S. A Theoretical Model of Enhanced Adhesion of Bioinspired Micropillar Arrayed Surfaces. J. Mech. Phys. Solids 2024, 186, 105592. [Google Scholar] [CrossRef]
- Argatov, I.; Li, Q.; Popov, V.L. Cluster of the Kendall-type adhesive microcontacts as a simple model for load sharing in bioinspired fibrillar adhesives. Arch. Appl. Mech. 2019, 89, 1447–1472. [Google Scholar] [CrossRef]
- Booth, J.A.; Bacca, M.; McMeeking, R.M.; Foster, K.L. Benefit of backing-layer compliance in fibrillar adhesive patches—Resistance to peel propagation in the presence of interfacial misalignment. Adv. Mater. Interfaces 2018, 5, 1800272. [Google Scholar] [CrossRef]
- Jiang, Y.; Grierson, D.S.; Turner, K.T. Flat punch adhesion: Transition from fracture-based to strength-limited pull-off. J. Phys. D Appl. Phys. 2014, 47, 325301. [Google Scholar] [CrossRef]
- Linghu, C.; Yang, X.; Liu, Y.; Li, D.; Gao, H.; Hsia, K.J. Mechanics of shape-locking-governed R2G adhesion with shape memory polymers. J. Mech. Phys. Solids 2023, 170, 105091. [Google Scholar] [CrossRef]
- Hui, C.Y.; Glassmaker, N.; Tang, T.; Jagota, A. Design of biomimetic fibrillar interfaces: 2. Mechanics of enhanced adhesion. J. R. Soc. Interface 2004, 1, 35–48. [Google Scholar] [CrossRef]
- Linghu, C.; Liu, Y.; Yang, X.; Li, D.; Tan, Y.Y.; Mohamed Hafiz, M.H.B.; Rohani, M.F.B.; Du, Z.; Su, J.; Li, Y.; et al. Fibrillar adhesives with unprecedented adhesion strength, switchability and scalability. Natl. Sci. Rev. 2024, nwae106. [Google Scholar] [CrossRef]
- Yao, H.; Gao, H. Mechanics of robust and releasable adhesion in biology: Bottom–up designed hierarchical structures of gecko. J. Mech. Phys. Solids 2006, 54, 1120–1146. [Google Scholar] [CrossRef]
- Tang, T.; Hui, C.Y.; Glassmaker, N.J. Can a fibrillar interface be stronger and tougher than a non-fibrillar one? J. R. Soc. Interface 2005, 2, 505–516. [Google Scholar] [CrossRef]
- Varenberg, M.; Gorb, S. Shearing of fibrillar adhesive microstructure: Friction and shear-related changes in pull-off force. J. R. Soc. Interface 2007, 4, 721–725. [Google Scholar] [CrossRef]
- Linghu, C.; Du, Z.; Sun, Y.; Chen, W.; Hsia, K.J. On shear adhesion of adhesive fibrils. Extrem. Mech. Lett. 2023, 64, 102092. [Google Scholar] [CrossRef]
- Abusomwan, U.; Sitti, M. Effect of retracton speed on adhesion of elastomer fibrillar structures. Appl. Phys. Lett. 2012, 101, 211907. [Google Scholar] [CrossRef]
- Afferrante, L.; Violano, G.; Carbone, G. Exploring the dynamics of viscoelastic adhesion in rough line contacts. Sci. Rep. 2023, 13, 15060. [Google Scholar] [CrossRef] [PubMed]
- Papangelo, A.; Ciavarella, M. Detachment of a rigid flat punch from a viscoelastic material. Tribol. Lett. 2023, 71, 48. [Google Scholar] [CrossRef]
- Tan, D.; Wang, X.; Liu, Q.; Shi, K.; Yang, B.; Liu, S.; Wu, Z.S.; Xue, L. Switchable adhesion of micropillar adhesive on rough surfaces. Small 2019, 15, 1904248. [Google Scholar] [CrossRef]
- He, Q.; Zhao, Z.; Zhong, Q.; Liu, S.; Deng, K.; Liu, Y.; Zhang, N.; Zhao, Z.; Zhan, F.; Zhao, J. Switchable shape memory polymer bio-inspired adhesive and its application for unmanned aerial vehicle landing. Chin. J. Aeronaut. 2024, 37, 380–390. [Google Scholar] [CrossRef]
- Linghu, C.; Liu, Y.; Tan, Y.Y.; Sing, J.H.M.; Tang, Y.; Zhou, A.; Wang, X.; Li, D.; Gao, H.; Hsia, K.J. Overcoming the adhesion paradox and switchability conflict on rough surfaces with shape-memory polymers. Proc. Natl. Acad. Sci. USA 2023, 120, e2221049120. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Xia, N.; Zhang, L. A review of bioinspired dry adhesives: From achieving strong adhesion to realizing switchable adhesion. Bioinspir. Biomimetics 2024, 19, 051003. [Google Scholar] [CrossRef] [PubMed]
- Aksak, B.; Sahin, K.; Sitti, M. The optimal shape of elastomer mushroom-like fibers for high and robust adhesion. Beilstein J. Nanotechnol. 2014, 5, 630–638. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).