Braking Friction Coefficient Prediction Using PSO–GRU Algorithm Based on Braking Dynamometer Testing
Abstract
1. Introduction
2. Braking Dynamometer Testing and Typical Results
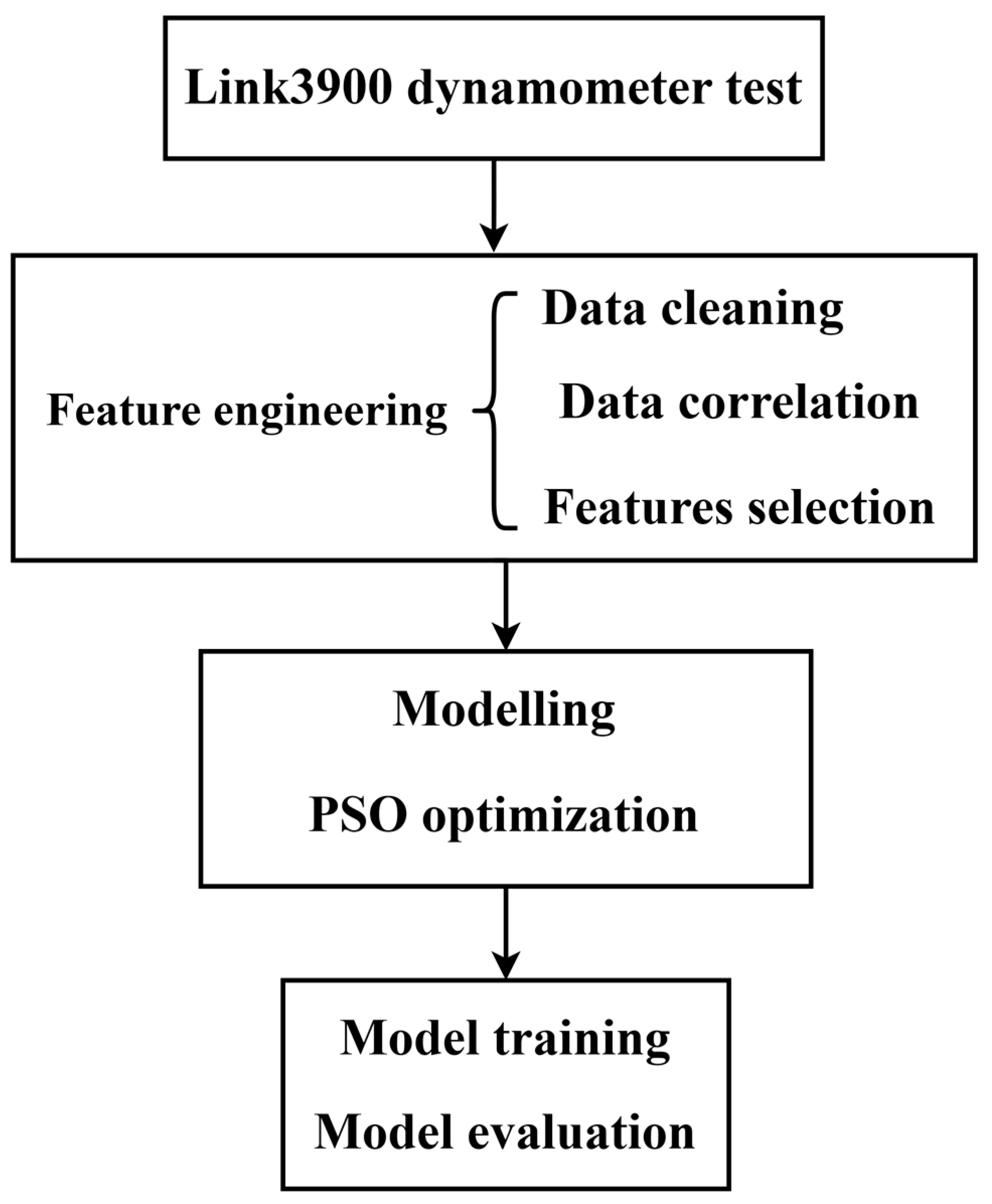
3. Feature Engineering
3.1. Data Cleaning
3.1.1. Min–Max Scaling
3.1.2. Z-Score Normalization
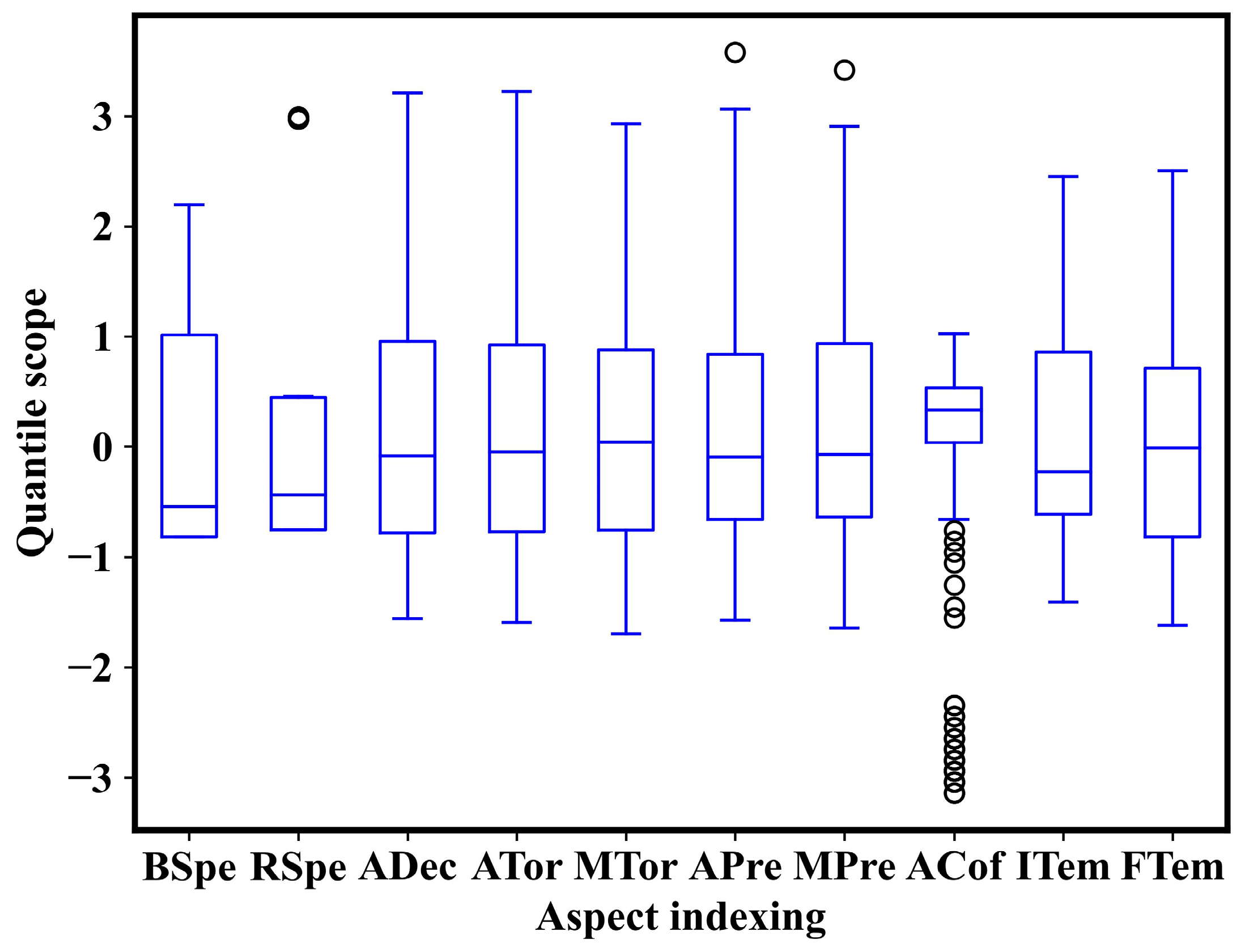
3.1.3. Outlier and Missing Value Treatment
3.2. Investigating the Relationships between Features
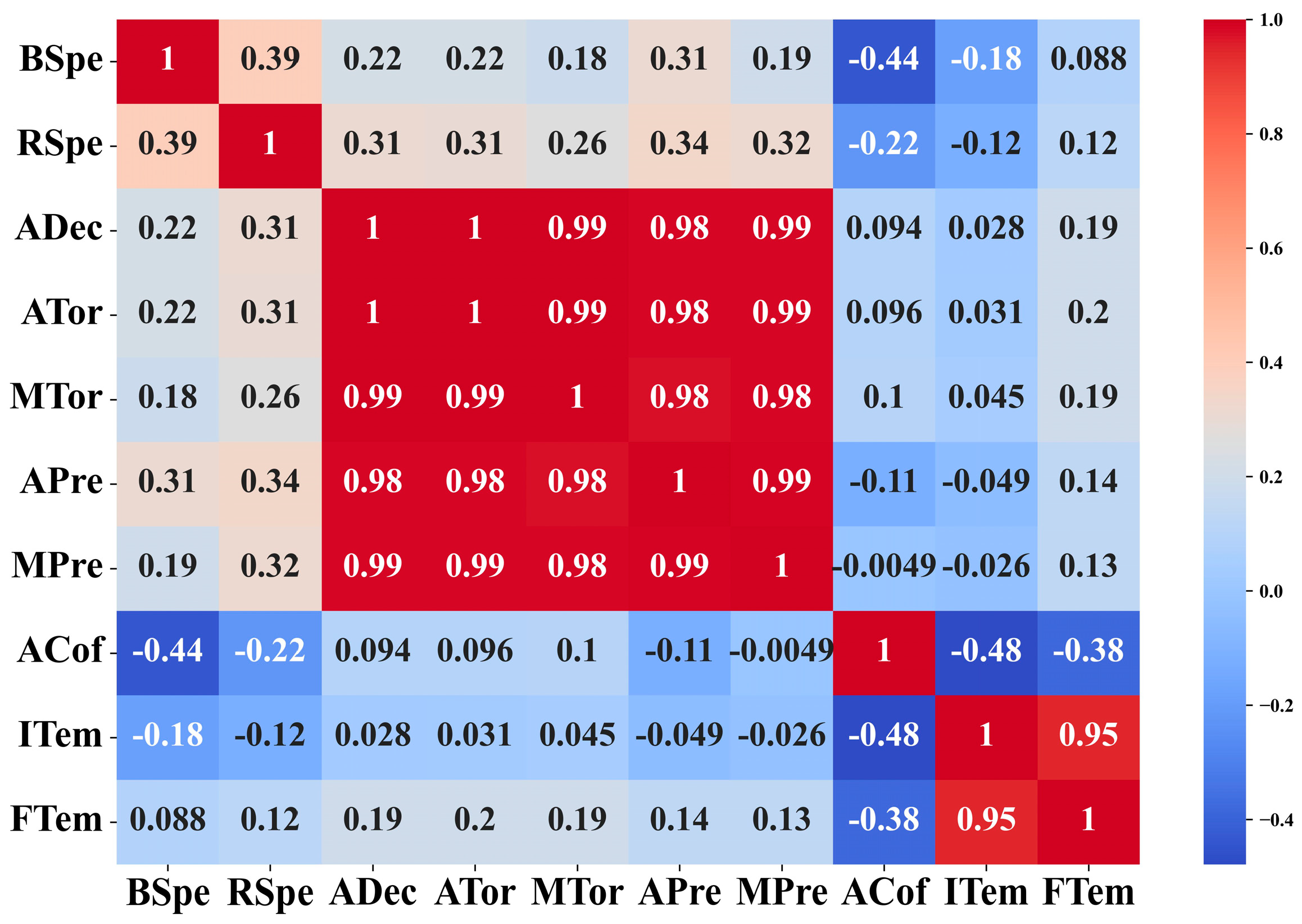
3.2.1. Pearson Correlation Coefficient
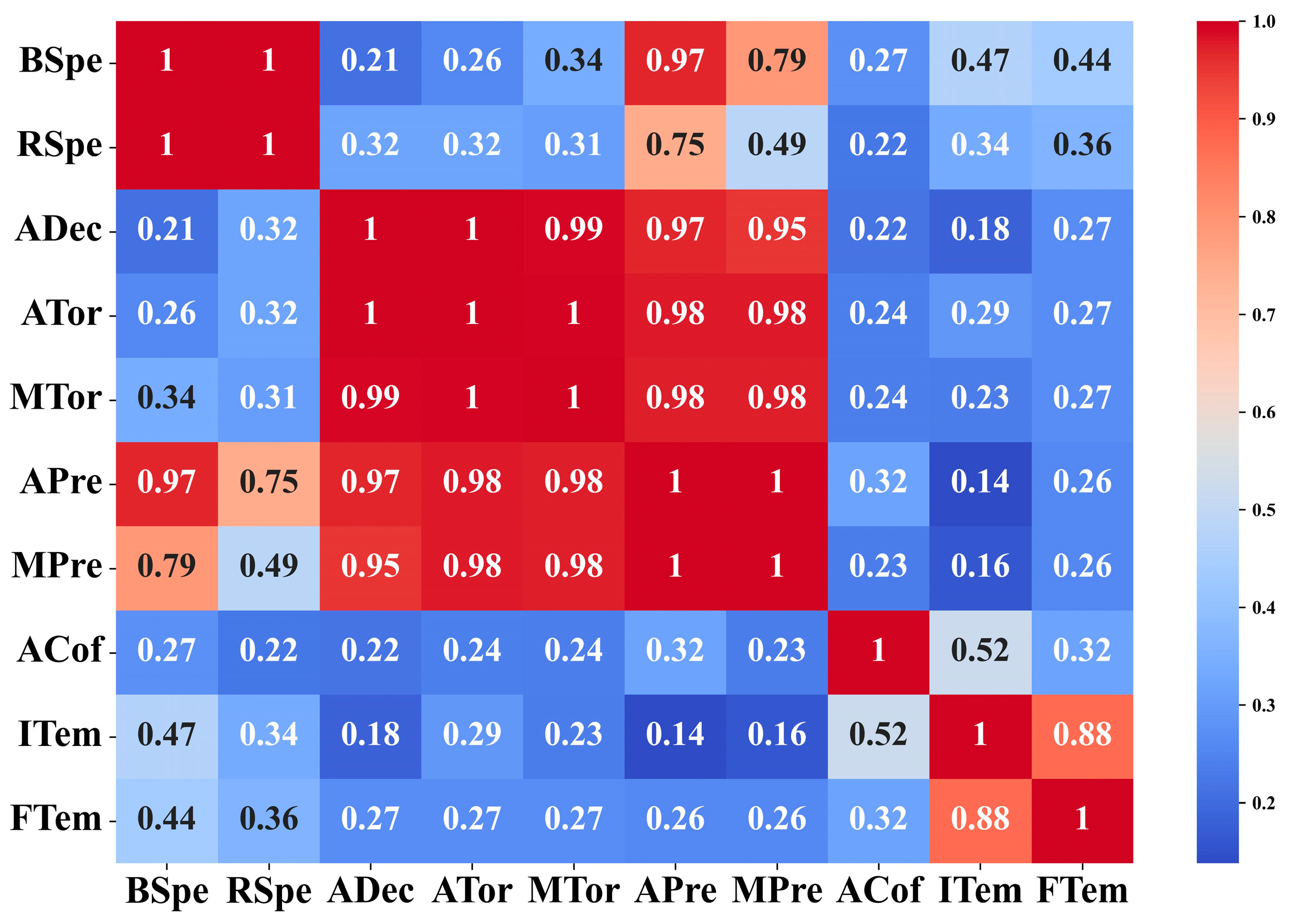
3.2.2. Maximal Information Coefficient
3.3. Selection of Features
4. Prediction Algorithms
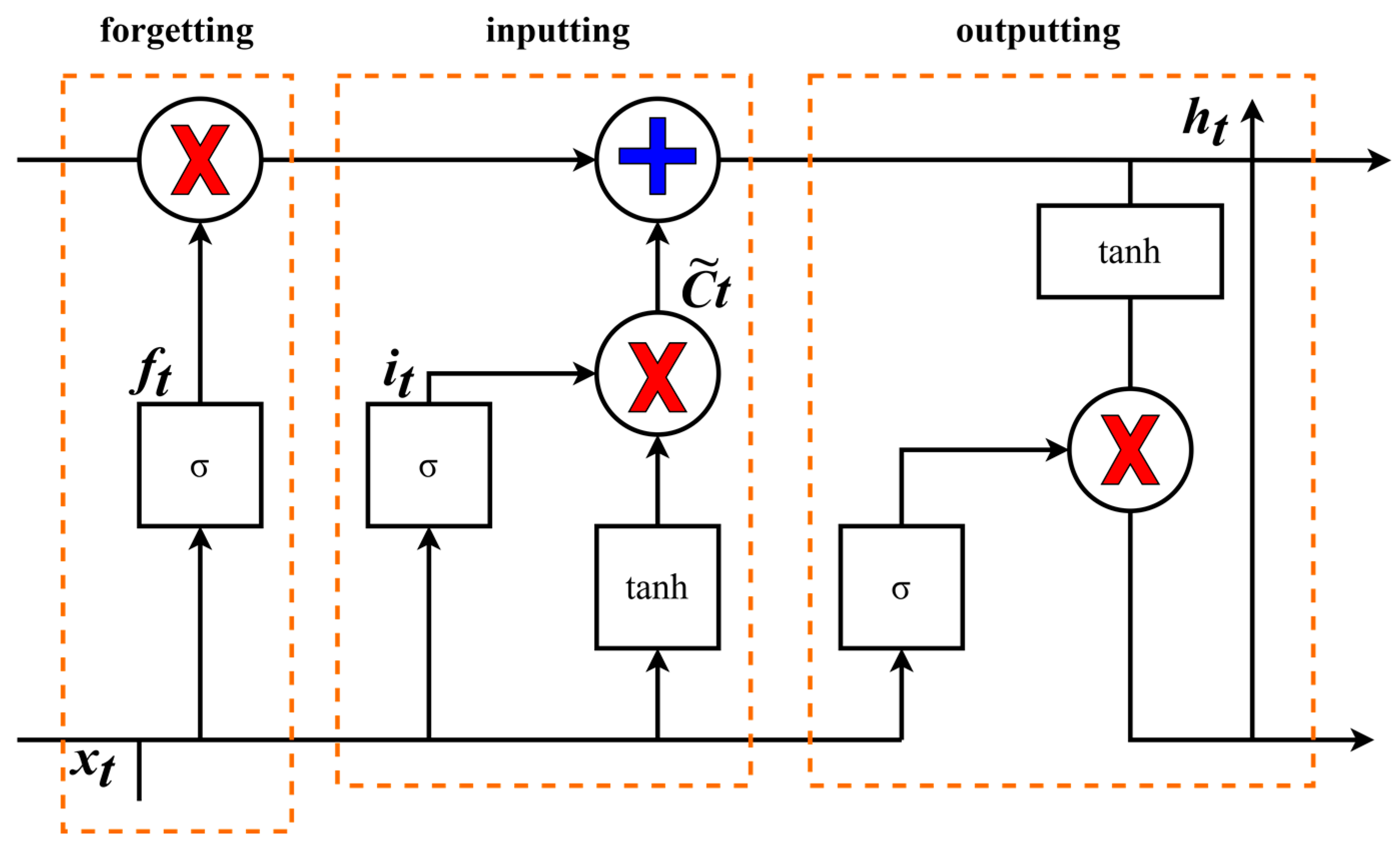
4.1. LSTM Method
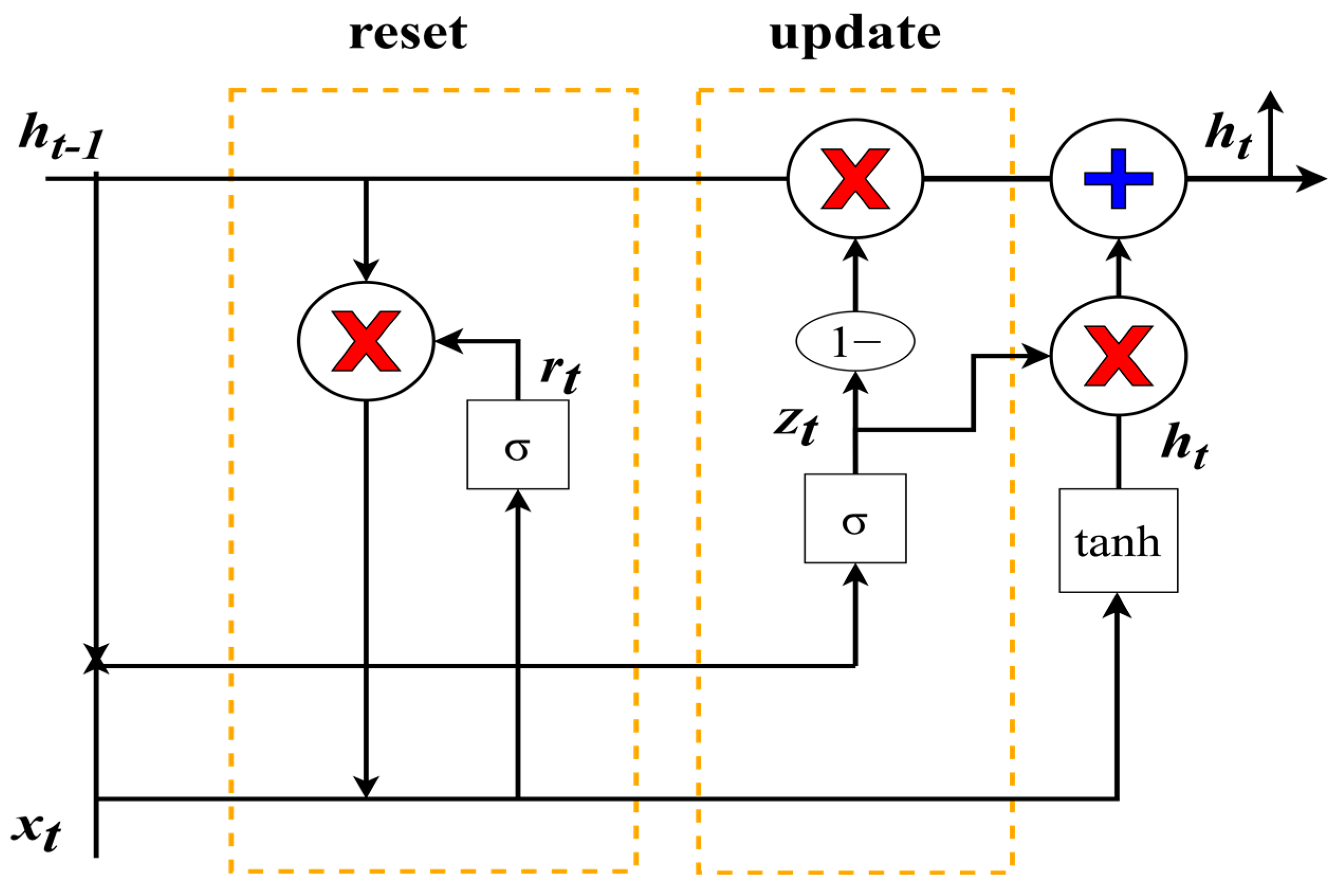
4.2. GRU Method
- (1)
- The reset gate determines how much previous information is forgotten and how new input information is combined with the previous memory, and it uses the current input information to make the hidden state forget any information that is found to be irrelevant to the prediction in the future. It also allows for the construction of more interdependent features. Essentially, the reset gate determines how much of the past data should be forgotten.
- (2)
- The update gate acts similarly to the forget gate and input gate in LSTM. It decides what information to forget and what new information needs to be added. Controlling how much information from previous hidden states gets passed to the current hidden state is very similar to the memory cells in LSTM networks. It helps RNNs to remember long-term information and decide whether to copy all information from the past to reduce the risk of vanishing gradients.
Gated Computation for GRU
- (1)
- Update gate.
- (2)
- Reset gate.
- (3)
- Current memory content.
- (4)
- The final memory of the current time step.
4.3. Model Evaluation Index
4.3.1. Correlation Index R2
4.3.2. MAE Index
5. Prediction Results
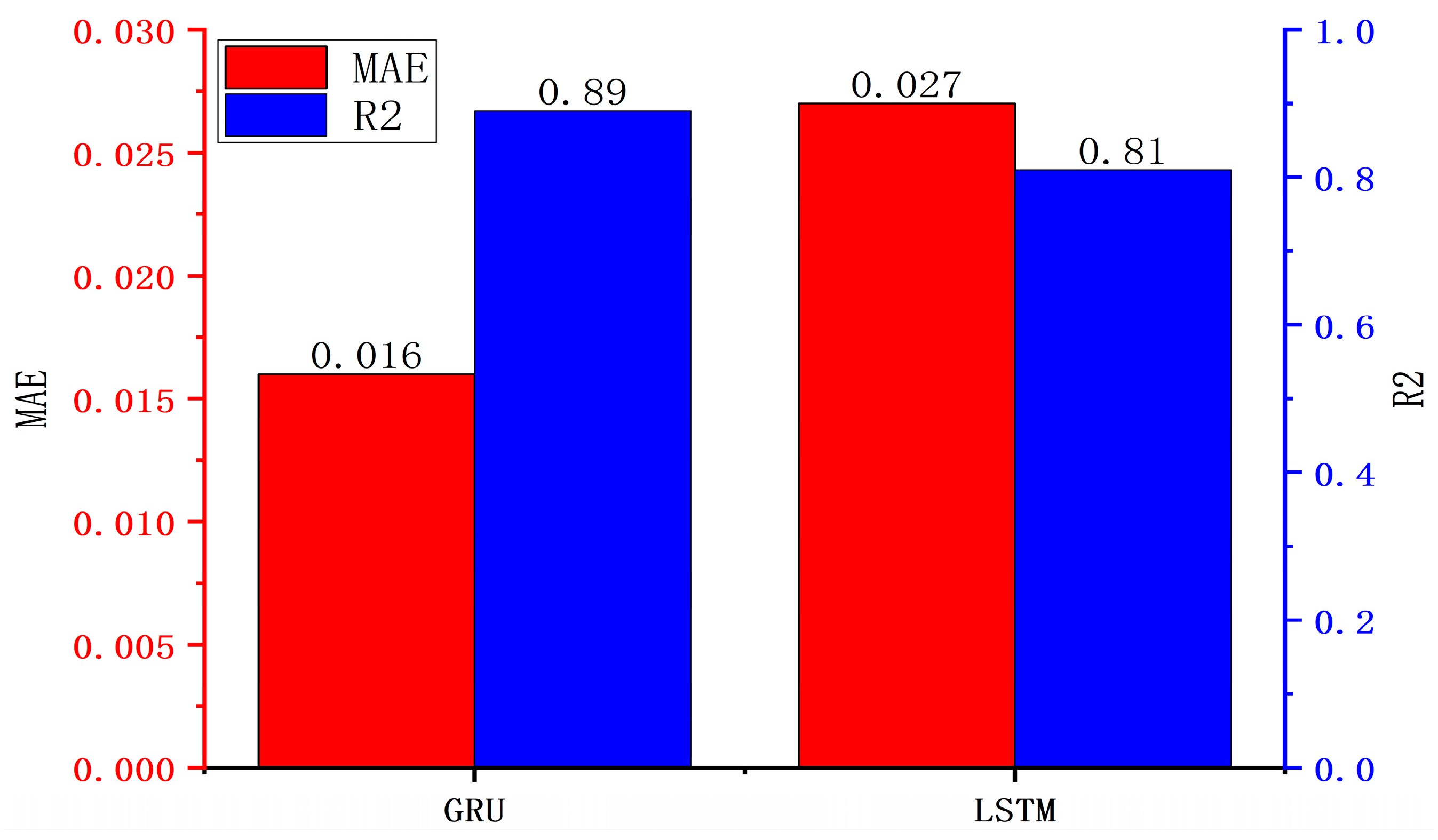
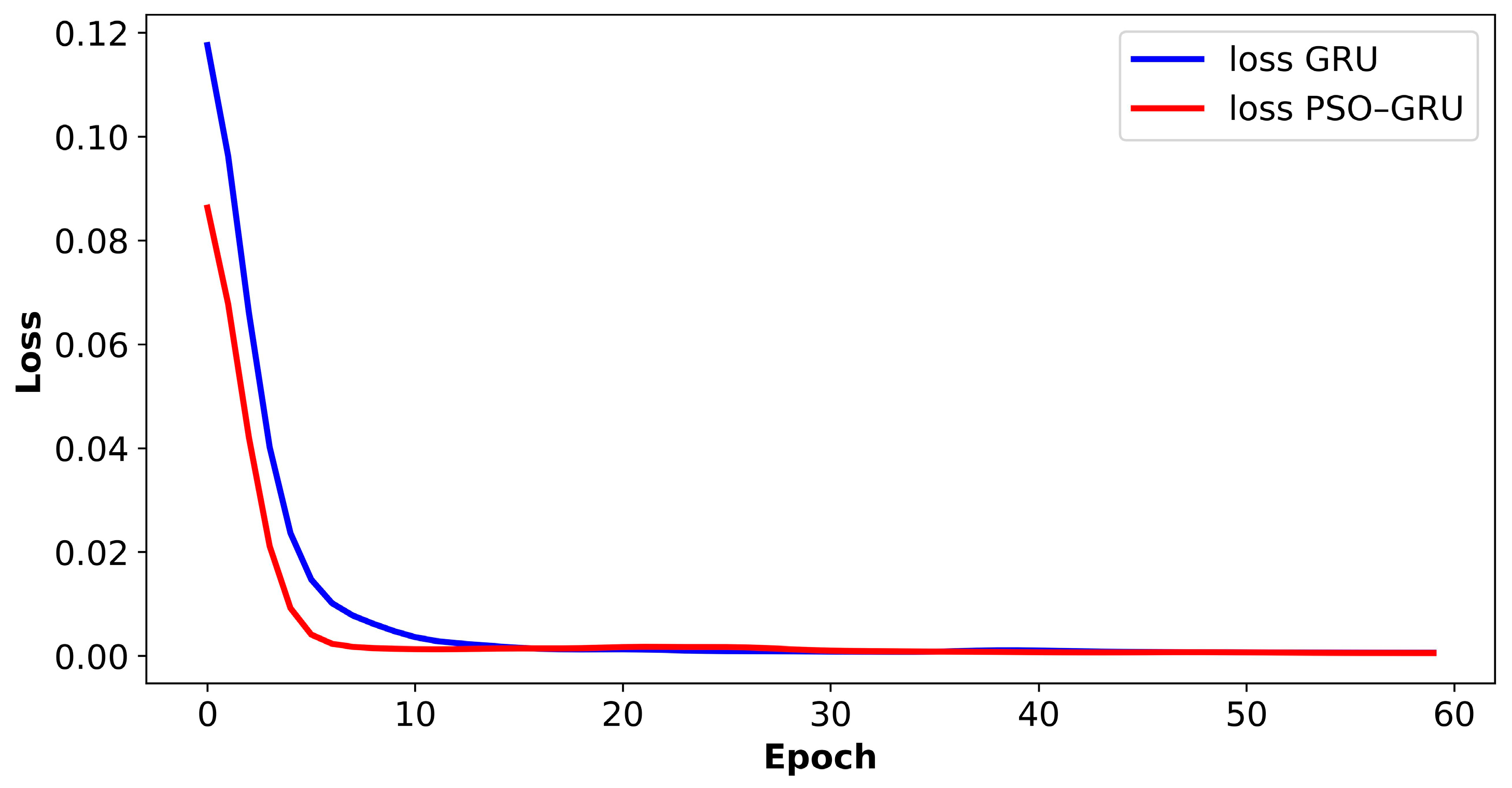
5.1. Model Comparison
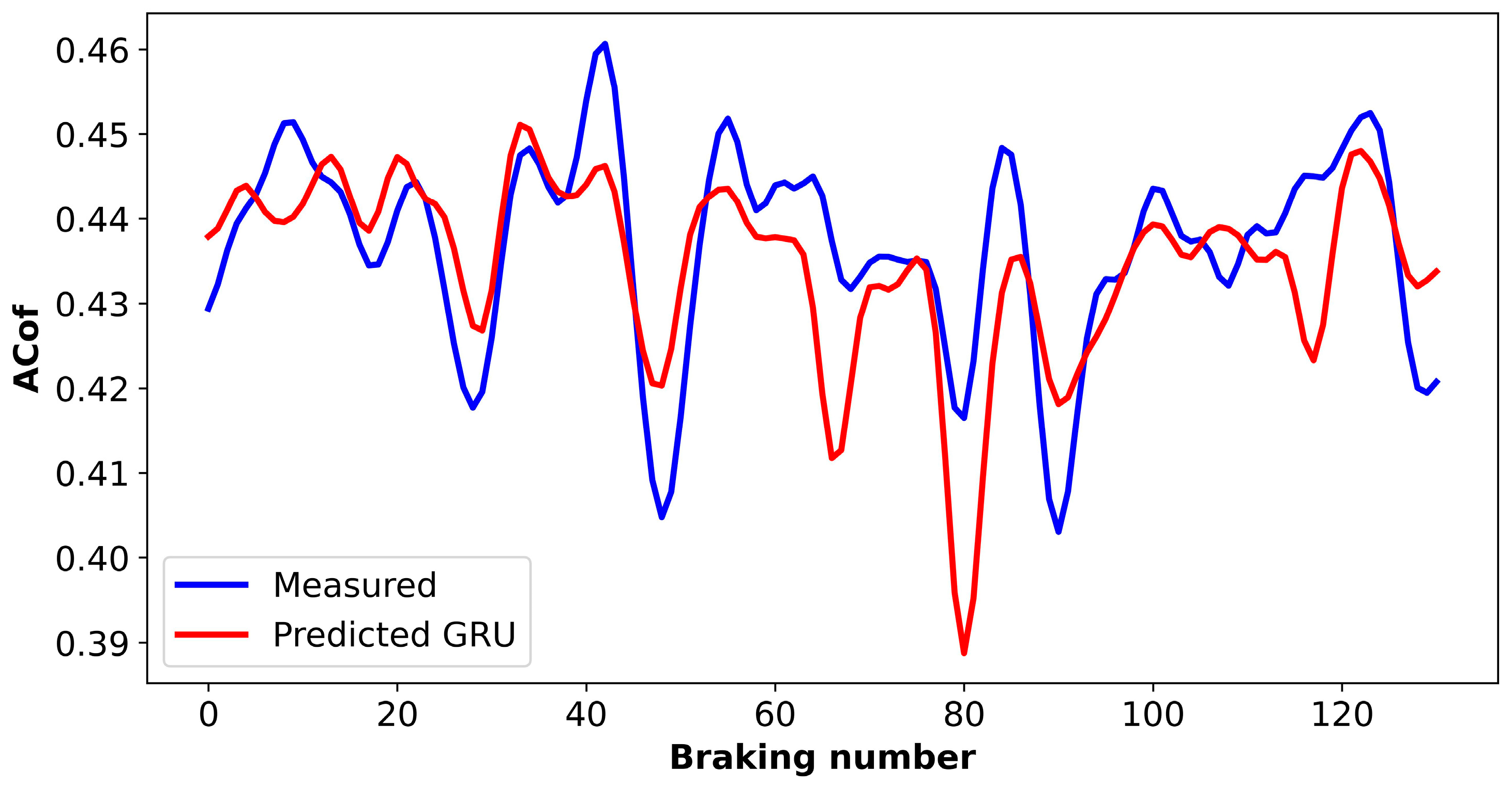
5.2. Predictions of the GRU Model
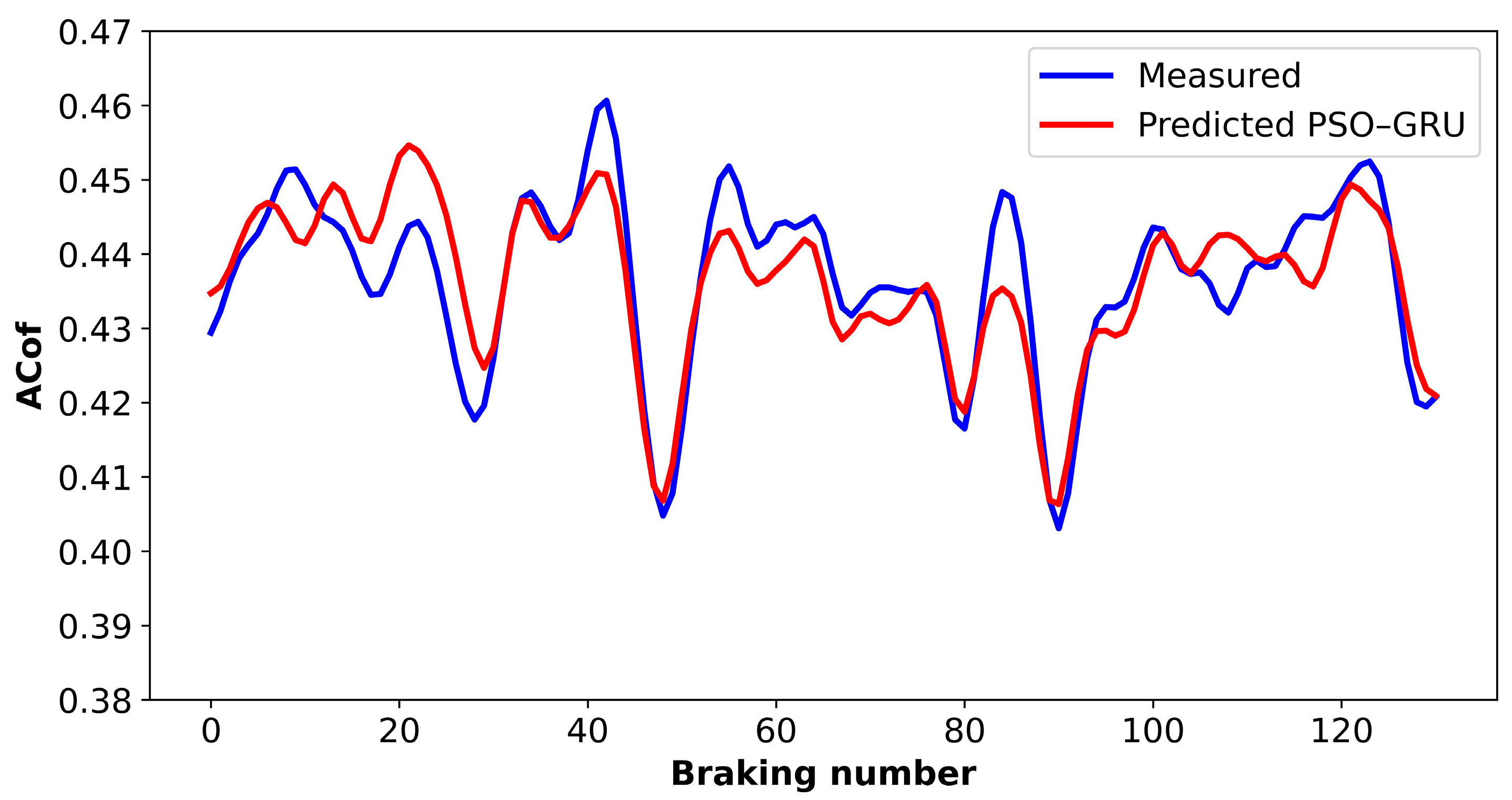
5.3. Predictions of the GRU Model Optimized with the PSO Algorithm
5.4. Model Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Definition | Unit |
| ACof | average COF | / |
| ADec | average deceleration | g |
| APre | average pressure | bar |
| ATor | average torque | Nm |
| B | monotone increasing function | / |
| BSpe | initial braking speed | kph |
| COF | coefficient of friction | / |
| COFs | coefficients of friction | / |
| FTem | final braking temperature | °C |
| GRU | gated recurrent unit | / |
| ht | hidden state at time step t | / |
| h(xi) | predicted value | / |
| I(D|G) | probability distribution | / |
| I*(D, x, y) | probability distribution under different grid division | |
| ITem | initial braking temperature | °C |
| LSTM | long short-term memory | / |
| MAE | mean absolute error | / |
| MIC | maximal information coefficient | / |
| MIC(D) | value of MIC | / |
| MPre | max pressure | bar |
| MTor | max torque | Nm |
| PPMCC | Pearson product moment correlation coefficient | / |
| PSO | particle swarm optimization | / |
| r | value of PPMCC | / |
| rt | activation vector of reset gate | / |
| R2 | evaluation of the model | / |
| RSpe | release speed | kph |
| RSS | the sum of residual squares | / |
| TSS | the sum of the squares of the total deviation | / |
| vparticle | particle velocity | / |
| maximum value of all samples | / | |
| minimum value of all samples | / | |
| xi | measured value of x | / |
| normalized result | / | |
| average value of x | / | |
| standardized value | / | |
| average value of y | / | |
| yi | measured value of y | / |
| Zt | activation vector of update gate | / |
| mean of all samples | / | |
| standard deviation of all samples | / | |
| weight matrix of the update gate | / | |
| weight matrix of the reset gate | / |
References
- Zhu, D.; Yu, X.; Sai, Q.; Wang, S.; Barton, D.; Fieldhouse, J.; Kosarieh, S. Noise and vibration performance of automotive disk brakes with laser-machined M-shaped grooves. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 237, 978–990. [Google Scholar] [CrossRef]
- Wang, S.; Guo, W.; Zeng, K.; Zhang, X. Characterization of automotive brake discs with laser-machined surfaces. Automot. Innov. 2019, 2, 190–200. [Google Scholar] [CrossRef]
- Khairnar, H.P.; Phalle, V.M.; Mantha, S.S. Estimation of automotive brake drum-shoe interface friction coefficient under varying conditions of longitudinal forces using Simulink. Friction 2015, 3, 214–227. [Google Scholar] [CrossRef]
- Riva, G.; Varriale, F.; Wahlström, J. A finite element analysis (FEA) approach to simulate the coefficient of friction of a brake system starting from material friction characterization. Friction 2021, 9, 191–200. [Google Scholar] [CrossRef]
- Meng, Y.; Xu, J.; Ma, L.; Jin, Z.; Prakash, B.; Ma, T.; Wang, W. A review of advances in tribology in 2020–2021. Friction 2022, 10, 1443–1595. [Google Scholar]
- Balaji, V.; Lenin, N.; Anand, P.; Rajesh, D.; Raja, V.B.; Palanikumar, K. Brake squeal analysis of disc brake. Mater. Today Proc. 2021, 46, 3824–3827. [Google Scholar] [CrossRef]
- Crolla, D.A.; Lang, A.M. Brake noise and vibration: The state of the art. Veh. Tribol. 1991, 18, 165–174. [Google Scholar]
- Oberst, S.; Lai, J. Chaos in brake squeal noise. J. Sound Vib. 2011, 330, 955–975. [Google Scholar] [CrossRef]
- Jarvis, R.P.; Member, B.M. Vibrations induced by dry friction. Proc. Inst. Mech. Eng. 1963, 178, 847–857. [Google Scholar] [CrossRef]
- Nishiwaki, M. Generalized theory of brake noise. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1993, 207, 195–202. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, W.; Liu, X.; Liu, Y.; Zhou, J.; Li, B.; Lu, Q.; Yang, S. LSTM-based analysis of industrial IoT equipment. IEEE Access 2018, 6, 23551–23560. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, N.; Xue, X.; Xu, Y.; Zhou, J.; Wang, X. Intelligent deep learning method for forecasting the health evolution trend of aero-engine with dispersion entropy-based multi-scale series aggregation and LSTM neural network. IEEE Access 2020, 8, 34350–34361. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.; Xiang, Z.; Mo, J. Research on diagnosis algorithm of mechanical equipment brake friction fault based on MCNN-SVM. Measurement 2021, 186, 110065. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, X.; Mo, J.; Xiang, Z.; Zheng, P. Brake uneven wear of high-speed train intelligent monitoring using an ensemble model based on multi-sensor feature fusion and deep learning. Eng. Fail. Anal. 2022, 137, 106219. [Google Scholar] [CrossRef]
- Yang, X.; Chen, L. Dynamic state estimation for the advanced brake system of electric vehicles by using deep recurrent neural networks. IEEE Trans. Ind. Electron. 2019, 99, 9536–9547. [Google Scholar]
- Šabanovič, E.; Žuraulis, V.; Prentkovskis, O.; Skrickij, V. Identification of road-surface type using deep neural networks for friction coefficient estimation. Sensors 2020, 20, 612. [Google Scholar] [CrossRef] [PubMed]
- Stender, M.; Tiedemann, M.; Spieler, D.; Schoepflin, D.; Hoffmann, N.; Oberst, S. Deep learning for brake squeal: Brake noise detection, characterization and prediction. Mech. Syst. Signal Process. 2021, 149, 107181. [Google Scholar] [CrossRef]
- Wang, S.; Zhong, L.; Niu, Y.; Liu, S.; Wang, S.; Li, K.; Wang, L.; Barton, D. Prediction of frictional braking noise based on brake dynamometer test and artificial intelligent algorithms. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 236, 2681–2695. [Google Scholar] [CrossRef]
- Alexsendric, D.; Barton, D.C. Neural network prediction of disc brake performance. Tribol. Int. 2009, 42, 1074–1080. [Google Scholar] [CrossRef]
- Alexsendric, D.; Barton, D.C.; Vasic, B. Prediction of brake friction materials recovery performance using artificial neural networks. Tribol. Int. 2010, 43, 2092–2099. [Google Scholar] [CrossRef]
- J2521_201304; Disc and Drum Brake Dynamometer Squeal Noise Test Procedure. SAE International: Warrendale, PA, USA, 2013.
- Shalabi, L.A.; Shaaban, Z.; Kasasbeh, B. Data mining: A preprocessing engine. J. Comput. Sci. 2006, 2, 735–739. [Google Scholar] [CrossRef]
- Curtis, A.E.; Smith, T.A.; Ziganshin, B.A.; Elefteriades, J.A. The mystery of the Z-score. Aorta 2016, 4, 124–130. [Google Scholar] [CrossRef] [PubMed]
- Benesty, J.; Chen, J.D.; Huang, Y. On the importance of the Pearson correlation coefficient in noise reduction. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 757–765. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]
- Zargar, S. Introduction to Sequence Learning Models: RNN, LSTM, GRU; Department of Mechanical and Aerospace Engineering: Colorado Springs, CO, USA, 2021. [Google Scholar]



| Stop | Brake Speed (kph) | Release Speed (kph) | Stop Time (s) | Avg Decel (g) | Avg Torq (Nm) | Max Torq (Nm) | Avg Press (bar) | Max Press (bar) | Avg μ Level | Initial Temp Rotor C | Final Temp Rotor C | Peak Level (dBA) | Frequency of Peak (Hz) | Above Threshold 70 dBA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 79.7 | 30.0 | 8.377 | 0.18 | 565 | 617 | 15.0 | 15.8 | 0.44 | 100 | 158 | 73.5 | 2800 | YES |
| 2 | 80.0 | 30.0 | 4.68 | 0.35 | 1087 | 1145 | 29.9 | 30.6 | 0.42 | 100 | 163 | 69.9 | 5900 | |
| 3 | 80.1 | 30.0 | 8.32 | 0.18 | 569 | 620 | 15.0 | 15.7 | 0.44 | 100 | 158 | 59.2 | 5950 | |
| 4 | 79.8 | 30.0 | 7.01 | 0.22 | 674 | 730 | 18.0 | 18.6 | 0.44 | 100 | 157 | 69.0 | 5975 | |
| 5 | 80.0 | 30.0 | 5.99 | 0.26 | 819 | 877 | 21.9 | 22.5 | 0.43 | 100 | 158 | 70.9 | 2800 | YES |
| 6 | 79.8 | 30.0 | 3.83 | 0.44 | 1357 | 1404 | 37.8 | 38.6 | 0.42 | 100 | 164 | 71.5 | 2800 | YES |
| 7 | 79.7 | 30.0 | 8.35 | 0.18 | 563 | 615 | 15.0 | 15.9 | 0.44 | 100 | 156 | 69.1 | 6200 | |
| 8 | 79.7 | 30.0 | 5.25 | 0.31 | 948 | 1010 | 25.9 | 26.5 | 0.43 | 100 | 160 | 69.9 | 5975 | |
| 9 | 80.1 | 30.0 | 7.06 | 0.22 | 670 | 726 | 18.0 | 18.5 | 0.43 | 100 | 157 | 67.6 | 6325 | |
| 10 | 80.0 | 30.0 | 4.19 | 0.40 | 1232 | 1288 | 33.9 | 34.6 | 0.42 | 100 | 160 | 71.4 | 2925 | YES |
| 11 | 80.0 | 30.0 | 8.36 | 0.18 | 564 | 621 | 15.0 | 15.8 | 0.44 | 100 | 155 | 68.6 | 6350 |
| Parameter | Parameter Interpretation | Default |
|---|---|---|
| input_size | Number of input features | 4 |
| output_size | Number of output features | 1 |
| rnn_unit | Hidden layers | 64 |
| lr | Learning rate | 0.001 |
| epoch | Iterations | 100 |
| Model | R2 | MAE | Training Time (ms) |
|---|---|---|---|
| GRU | 0.893 | 0.016 | 220 |
| PSO–GRU | 0.935 | 0.014 | 157 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Yu, Y.; Liu, S.; Barton, D. Braking Friction Coefficient Prediction Using PSO–GRU Algorithm Based on Braking Dynamometer Testing. Lubricants 2024, 12, 195. https://doi.org/10.3390/lubricants12060195
Wang S, Yu Y, Liu S, Barton D. Braking Friction Coefficient Prediction Using PSO–GRU Algorithm Based on Braking Dynamometer Testing. Lubricants. 2024; 12(6):195. https://doi.org/10.3390/lubricants12060195
Chicago/Turabian StyleWang, Shuwen, Yang Yu, Shuangxia Liu, and David Barton. 2024. "Braking Friction Coefficient Prediction Using PSO–GRU Algorithm Based on Braking Dynamometer Testing" Lubricants 12, no. 6: 195. https://doi.org/10.3390/lubricants12060195
APA StyleWang, S., Yu, Y., Liu, S., & Barton, D. (2024). Braking Friction Coefficient Prediction Using PSO–GRU Algorithm Based on Braking Dynamometer Testing. Lubricants, 12(6), 195. https://doi.org/10.3390/lubricants12060195






