Numerical Investigations of Static and Dynamic Characteristics of a Novel Staggered Labyrinth Seal with Semi-Elliptical Structure
Abstract
1. Introduction
2. The Novel Labyrinth Seal with SET Structure
2.1. Geometric Model
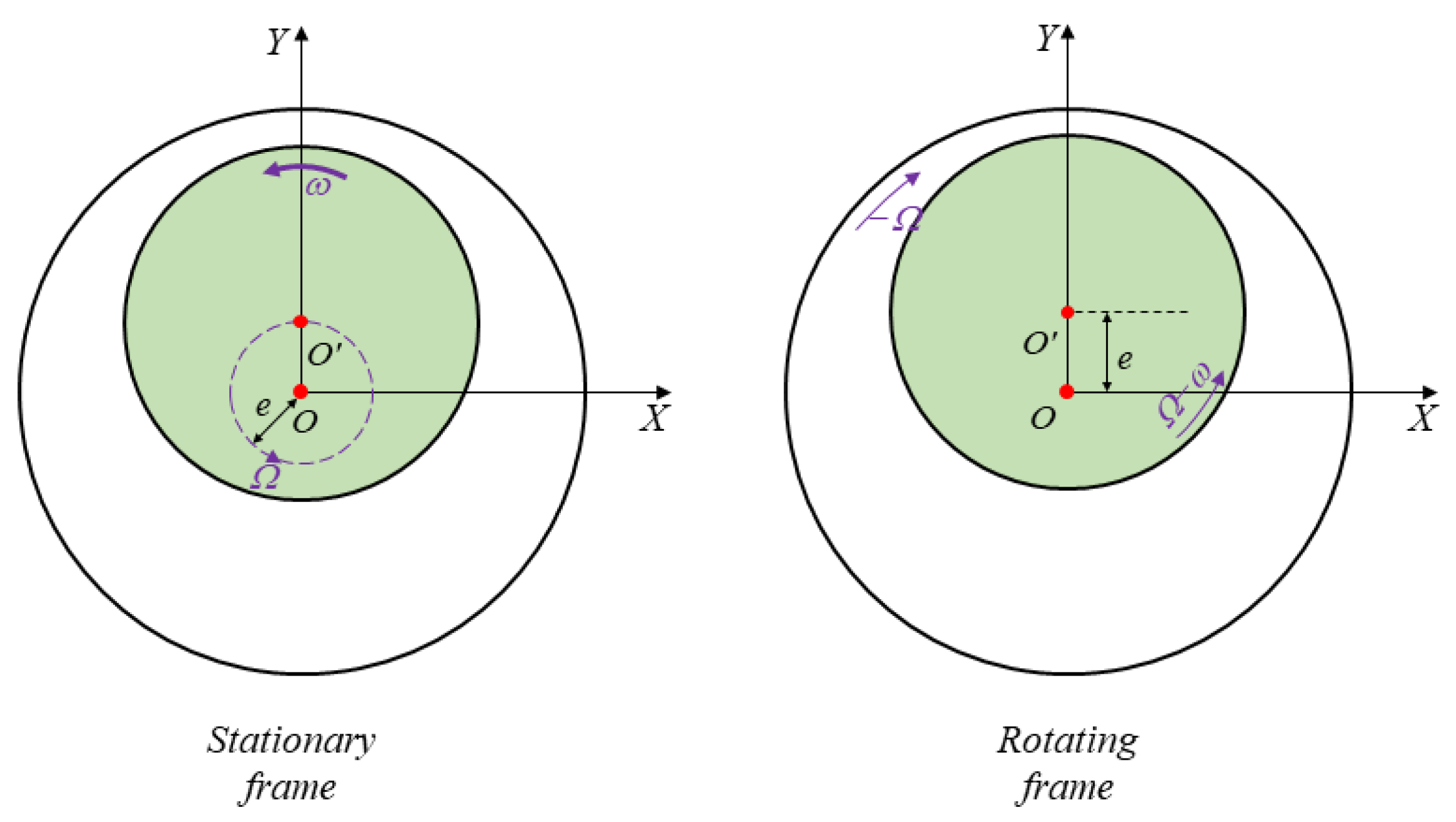
2.2. Numerical Simulation Method
3. Computational Model Validation
3.1. Grid Independence Verification
3.2. Validation of Numerical Method
4. Results and Discussion
4.1. The Static Characteristics of the SET Structure
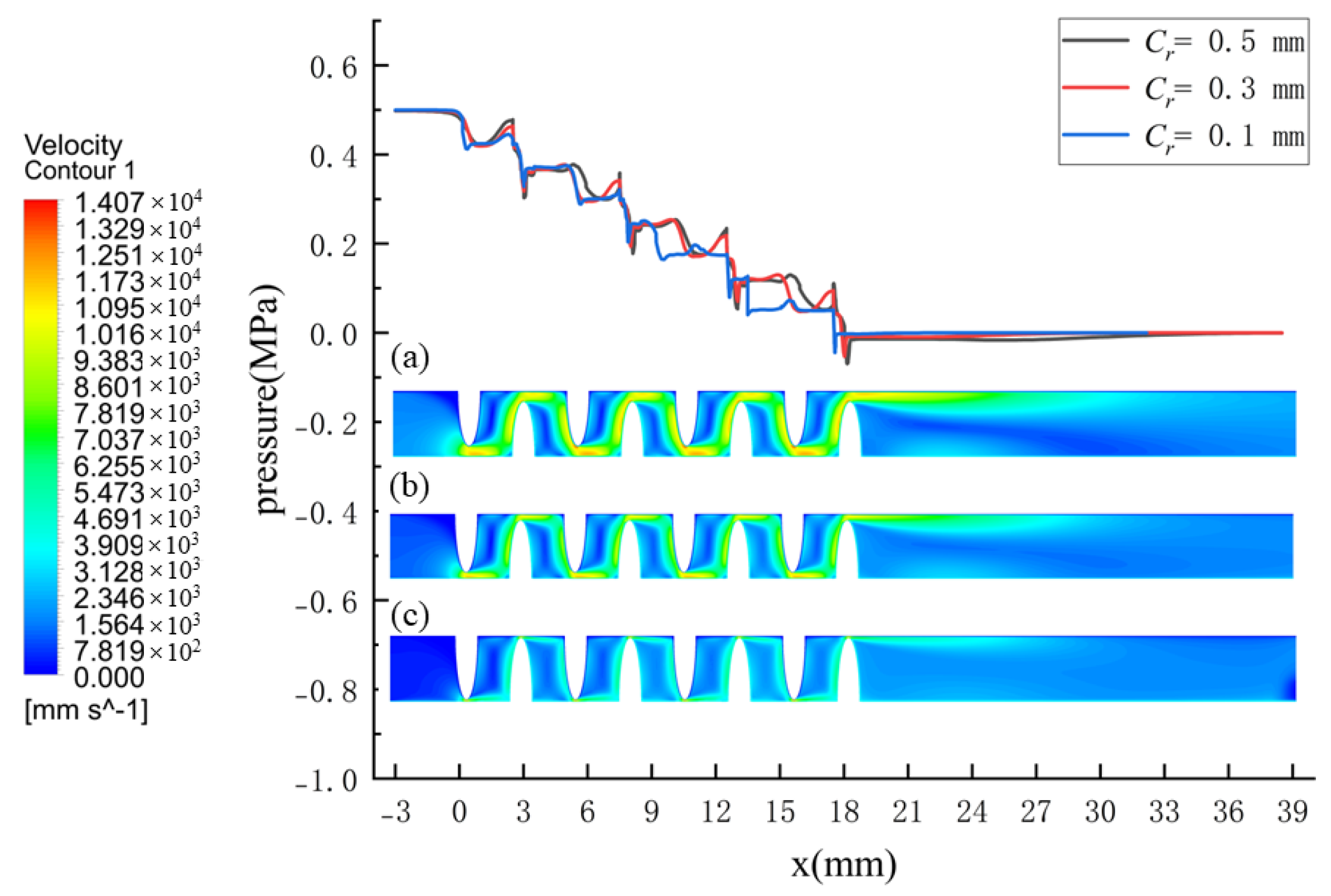
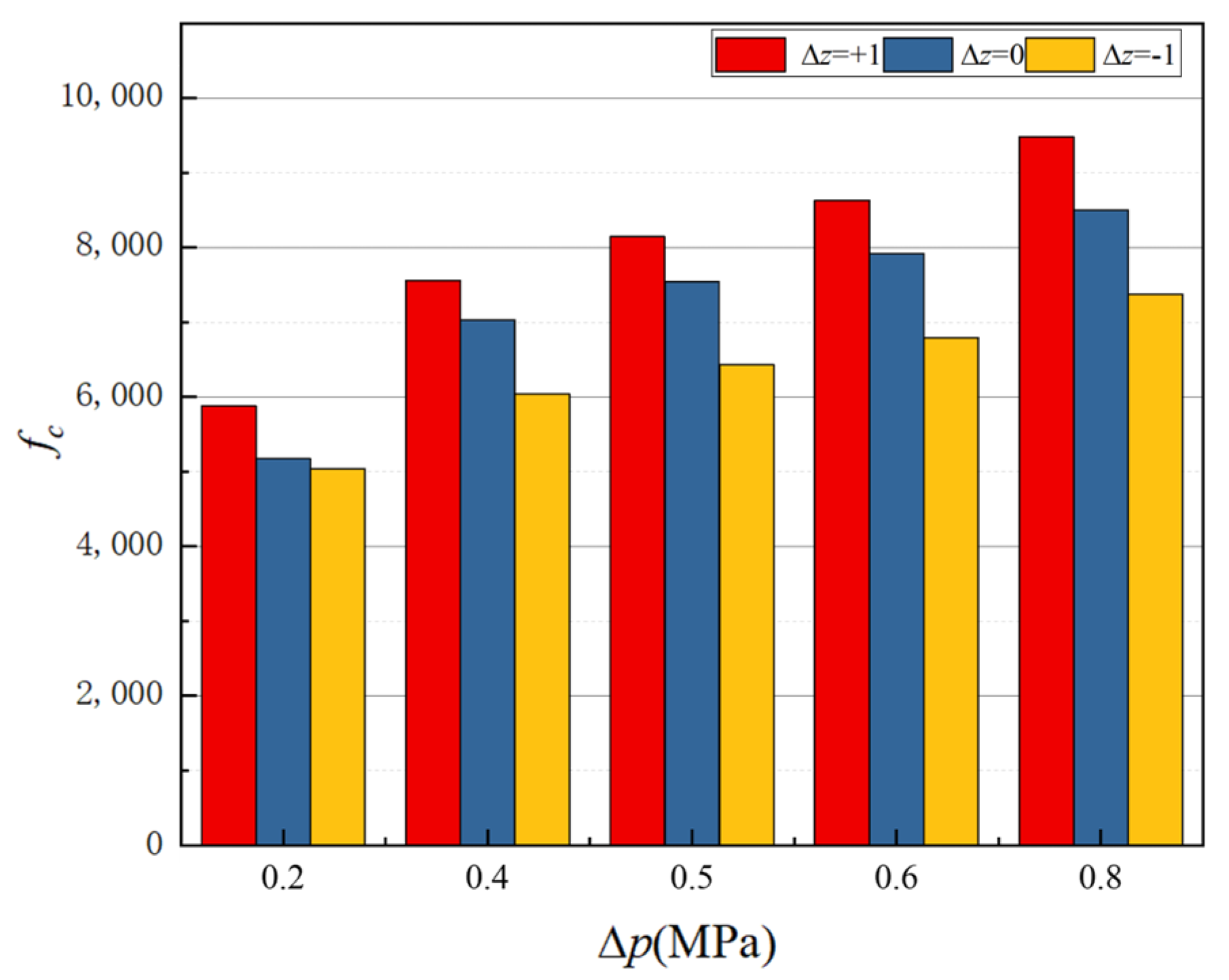
4.1.1. The Influences of Axial Offset and Pressure Drop on Leakage Performance
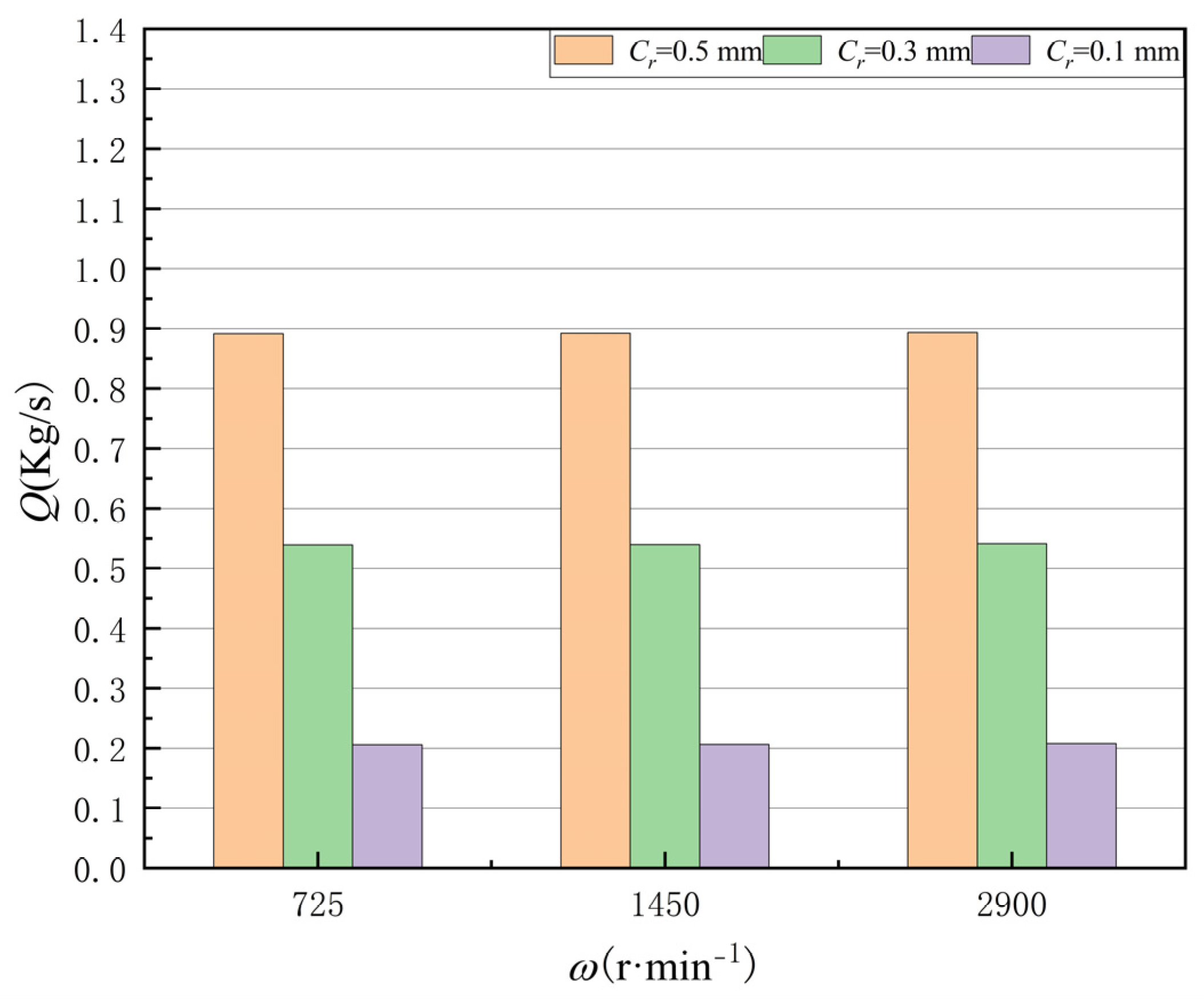
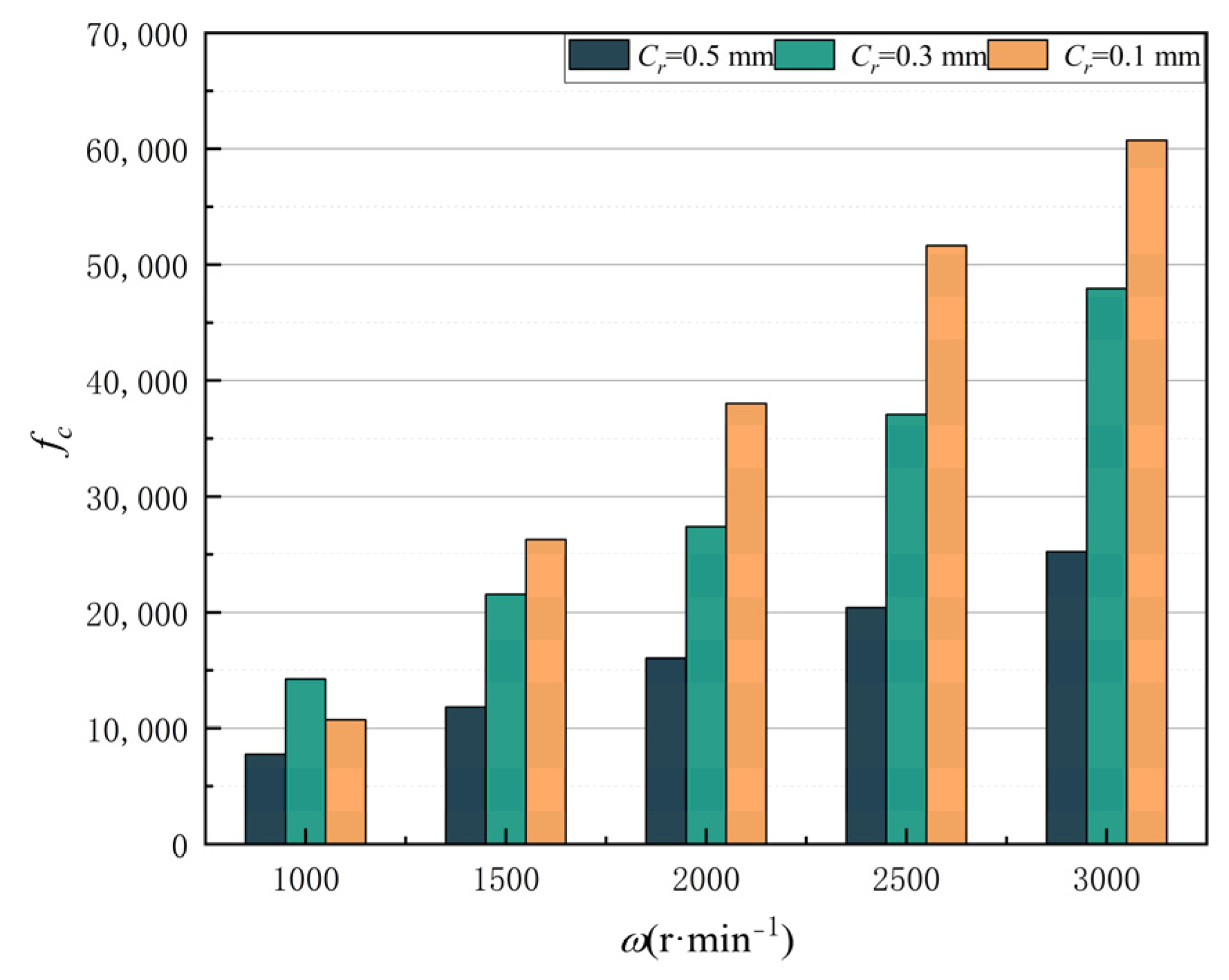
4.1.2. The Influences of Seal Clearance and Rotating Speed on Leakage Performance
4.2. The Dynamic Characteristics of the SET Structure
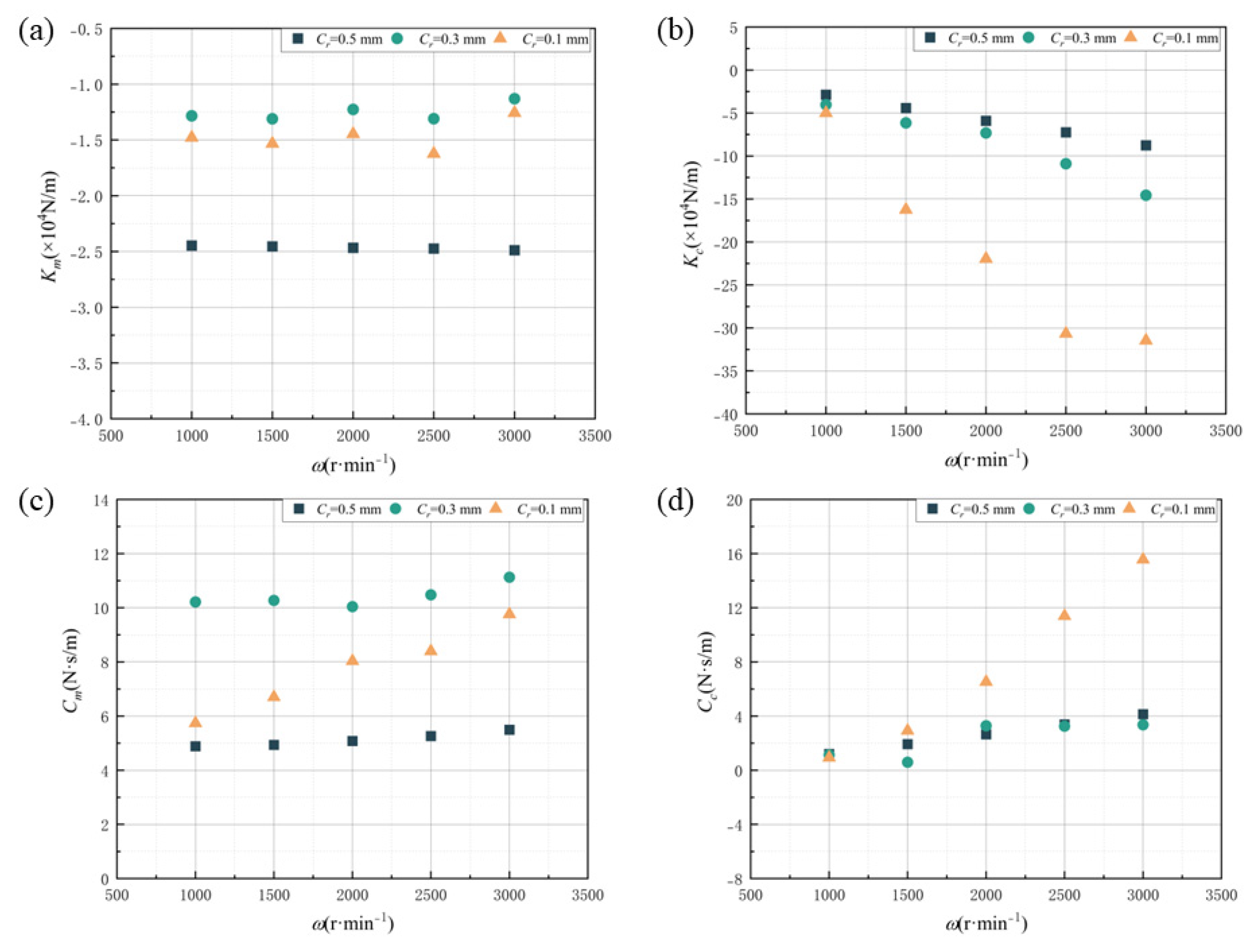
4.2.1. The Dynamic Characteristic Coefficients
4.2.2. The Stability Performance of the SET Structure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| L | Seal length (mm) |
| Cr | Clearance (mm) |
| H | Height of rotor tooth (mm) |
| B1 | Tooth width (mm) |
| B2 | Cavity width (mm) |
| Z | Tooth number |
| Lg | Pitch between rotor teeth and static teeth (mm) |
| D | Rotor diameter (mm) |
| Q | Leakage (kg/s) |
| Δp | Pressure drop (MPa) |
| Whirling speed (rpm) | |
| Rotating speed (rpm) | |
| Fx, Fy | Seal reaction force in x and y axis (N) |
| Fr, Fτ | Seal reaction force in radial and tangential direction (N) |
| Km | Direct stiffness coefficient (N/m) |
| Kc | Cross-coupled stiffness coefficient (N/m) |
| Cm | Direct damping coefficient (N·s/m) |
| Cc | Cross-coupled damping coefficient (N·s/m) |
| Mm | Direct added mass (kg) |
| Mc | Cross-coupled added mass (kg) |
| f | Whirl frequency ratio |
| fc | Quantized whirl-frequency ratio |
| Δz | Static tooth offset(mm) |
References
- Li, Q.; Li, S.; Wu, P.; Huang, B.; Wu, D. Investigation on Reduction of Pressure Fluctuation for a Double-Suction Centrifugal Pump. Chin. J. Mech. Eng. 2021, 34, 12. [Google Scholar] [CrossRef]
- Wu, C.; Li, Q.; Zheng, F.; Wu, P.; Yang, S.; Ye, H.; Huang, B.; Wu, D. Improve of Unsteady Pressure Pulsation Based on Jet–Wake Suppression for a Low Specific Centrifugal Pump. J. Fluids Eng. 2021, 143, 111202. [Google Scholar] [CrossRef]
- Zahorulko, A. Experimental and CFD Analysis of Static and Dynamic Rotor Stabilities in Three-Annular Seals. Tribol. Int. 2023, 185, 108566. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, D.; Wang, Y.; Shi, J.; Gan, B. Research on the Fluid-Induced Excitation Characteristics of the Centrifugal Pump Considering the Compound Whirl Effect. Facta Univ. Ser. Mech. Eng. 2023, 21, 223–238. [Google Scholar] [CrossRef]
- Chupp, R.E.; Hendricks, R.C.; Lattime, S.B.; Steinetz, B.M. Sealing in Turbomachinery. J. Propul. Power 2006, 22, 313–349. [Google Scholar] [CrossRef]
- Wang, L.; Huang, F.; Luo, Y.; Chen, C. Research on the Dynamic Characteristics of Crack Damage of a Seal-Rotor System. Nonlinear Dyn. 2022, 109, 1851–1876. [Google Scholar] [CrossRef]
- Kim, T.S.; Cha, K.S. Comparative Analysis of the Influence of Labyrinth Seal Configuration on Leakage Behavior. J. Mech. Sci. Technol. 2009, 23, 2830–2838. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, K.; Cao, H.; Wang, T.; Yang, J.; Li, C. The Static Instability Characteristics of Labyrinth Seals: Experiments and Computational Fluid Dynamics Verification. J. Vib. Acoust. 2020, 142, 041005. [Google Scholar] [CrossRef]
- Qin, H.; Lu, D.; Zhong, D.; Wang, Y.; Song, Y. Experimental and Numerical Investigation for the Geometrical Parameters Effect on the Labyrinth-Seal Flow Characteristics of Fast Reactor Fuel Assembly. Ann. Nucl. Energy 2020, 135, 106964. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, J.; Peng, X.; Zhao, W.; Li, J. Leakage Reduction by Optimization of Hole-Pattern Damping Seal with Inclined Hole Cavity. Int. J. Heat Mass Transf. 2021, 169, 120924. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, Z.; Wang, Y.; Shi, J.; Gan, B.; Li, B.; Qiu, N. Research on Leakage Performance and Dynamic Characteristics of a Novel Labyrinth Seal with Staggered Helical Teeth Structure. Alex. Eng. J. 2021, 60, 3177–3187. [Google Scholar] [CrossRef]
- Hirs, G.G. A Bulk-Flow Theory for Turbulence in Lubricant Films. J. Lubr. Technol. 1973, 95, 137–145. [Google Scholar] [CrossRef]
- Childs, D.W.; Scharrer, J.K. Theory Versus Experiment for the Rotordynamic Coefficient of Labyrinth Gas Seals: Part II—A Comparison to Experiment. J. Vib. Acoust. 1988, 110, 281–287. [Google Scholar] [CrossRef]
- Eser, D.; Kazakia, J.Y. Air Flow in Cavities of Labyrinth Seals. Int. J. Eng. Sci. 1995, 33, 2309–2326. [Google Scholar] [CrossRef]
- Nordmann, R.; Dietzen, F.J.; Weiser, H.P. Calculation of Rotordynamic Coefficients and Leakage for Annular Gas Seals by Means of Finite Difference Techniques. J. Tribol. 1989, 111, 545–552. [Google Scholar] [CrossRef]
- Saber, E.; Abdou, K.M.; Afify, R. Effect of Shaft Eccentricity on Dynamic Characteristics for Different Geometries of Stationary Labyrinth Seals. Alex. Eng. J. 2020, 59, 61–75. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Y.; Qu, X.; Zhou, J.; Zhao, Z. Rotordynamic Analysis and Leakage Performance Study of a Hole Diaphragm Labyrinth Seal Using the CFD Method. Alex. Eng. J. 2022, 61, 9921–9928. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Y.; Du, H.; Huo, G.; Xu, Y.; Che, R. Transient Investigations of Teeth on Rotor and Teeth on Stator Modified Labyrinth Seals. Tribol. Int. 2024, 192, 109296. [Google Scholar] [CrossRef]
- Sun, D.; Wang, S.; Ai, Y.; Zhou, H.; Wang, K. Experimental Investigation of Rotordynamic Coefficients for the Labyrinth Seals with and without Shunt Injection. J. Vibroeng. 2015, 17, 4289–4300. [Google Scholar]
- Zhai, L.; Zhu, Z.; Zhang, Z.; Guo, J.; Cui, B. Theoretical Solutions for Dynamic Characteristics of Spiral-Grooved Liquid Seals. Tribol. Trans. 2019, 62, 22–33. [Google Scholar] [CrossRef]
- Zhai, L.; Zhenjie, Z.; Zhonghuang, C.; Jia, G. Dynamic Analysis of Liquid Annular Seals with Herringbone Grooves on the Rotor Based on the Perturbation Method. R. Soc. Open Sci. 2018, 5, 180101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, J.; Li, Z.; Yan, X. Effect of Bristle Pack Position on the Rotordynamic Characteristics of Brush-Labyrinth Seals at Various Operating Conditions. Chin. J. Aeronaut. 2020, 33, 1192–1205. [Google Scholar] [CrossRef]
- Wu, T.; San Andrés, L. Leakage and Dynamic Force Coefficients for Two Labyrinth Gas Seals: Teeth-on-Stator and Interlocking Teeth Configurations. A Computational Fluid Dynamics Approach to Their Performance. J. Eng. Gas Turb. Power 2019, 141, 042501. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Feng, Z. Numerical Comparisons of Rotordynamic Characteristics for Three Types of Labyrinth Gas Seals with Inlet Preswirl. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 721–738. [Google Scholar] [CrossRef]
- Jia, X.; Zheng, Q.; Jiang, Y.; Zhang, H. Leakage and Rotordynamic Performance of T Type Labyrinth Seal. Aerosp. Sci. Technol. 2019, 88, 22–31. [Google Scholar] [CrossRef]
- Iwatsubo, T.; Sheng, B.C. Evaluation of Seal Effects on the Stability of Rotating Fluid Machinery. Int. J. Rotating Mach. 1995, 1, 145–152. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, D.; Wang, Z. Analysis of upper-end seal leakage of high-temperature molten salt pump based on VOF model. J. Drain. Irrig. Mach. Eng. 2020, 38, 1209–1214. (In Chinese) [Google Scholar]
- Zhang, X.; Xu, Y.; Zhang, S.; Che, R.; Chen, Z.; Jiao, Y. Improved Vibration Performance of a Nonlinear Rotor-Seal System with Modified Labyrinth Seals by an Interpolating Database Method. Tribol. Int. 2024, 191, 109170. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, J. Spiral Flow Induced Destabilizing Force Analysis and Its Reduction with a Novel Helix-Comb Gas Seal. Aerosp. Sci. Technol. 2020, 105, 105997. [Google Scholar] [CrossRef]
- Xue, W.; Fang, Z.; Wang, T.; Li, Z.; Li, J. Rotordynamic Characteristics of a Novel Labyrinth Seal with Partition Walls and Helical Groove Teeth. Proc. Inst. Mech. Eng. Part A J. Power Energy 2024, 238, 515–529. [Google Scholar] [CrossRef]
- Zhai, L.; Wu, G.; Wei, X.; Qin, D.; Wang, L. Theoretical and Experimental Analysis for Leakage Rate and Dynamic Characteristics of Herringbone-Grooved Liquid Seals. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 849–860. [Google Scholar] [CrossRef]
- Li, J.; Obi, S.; Feng, Z. The Effects of Clearance Sizes on Labyrinth Brush Seal Leakage Performance Using a Reynolds-Averaged Navier—Stokes Solver and Non-Darcian Porous Medium Model. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 953–964. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, X.; Yuan, X.; Shibukawa, N.; Noguchi, T. Investigation and Improvement of the Staggered Labyrinth Seal. Chin. J. Mech. Eng. 2015, 28, 402–408. [Google Scholar] [CrossRef]
- Gu, Q.; Zhang, W.; Chen, L.; Ma, K.; Li, C.; Yang, J. Study on the Critical Stable State of the Labyrinth Seal. J. Mech. Eng. 2020, 56, 144–151. (In Chinese) [Google Scholar]
- Pugachev, A.O. CFD Optimization of Liquid Annular Seals for Leakage and Rotordynamics Improvement. In Turbo Expo: Power for Land, Sea, and Air; ASME: Orlando, FL, USA, 2009. [Google Scholar]
- Iwatsubo, T.; Ishimaru, H. Consideration of Whirl Frequency Ratio and Effective Damping Coefficient of Seal. J. Syst. Des. Dyn. 2010, 4, 177–188. [Google Scholar] [CrossRef]

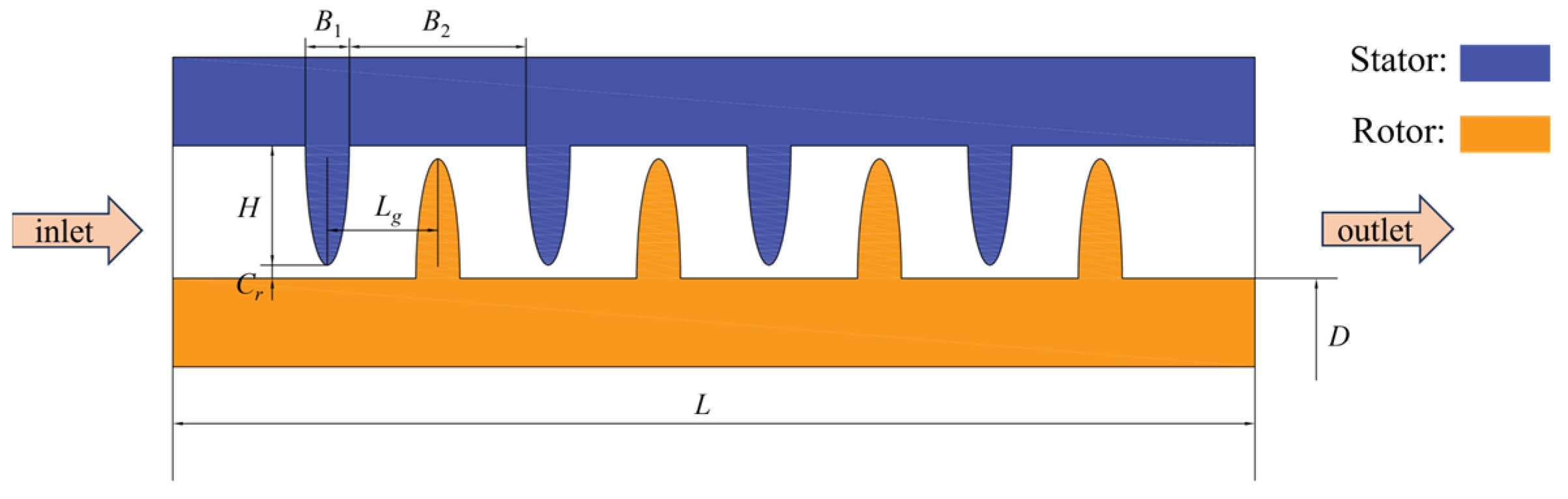
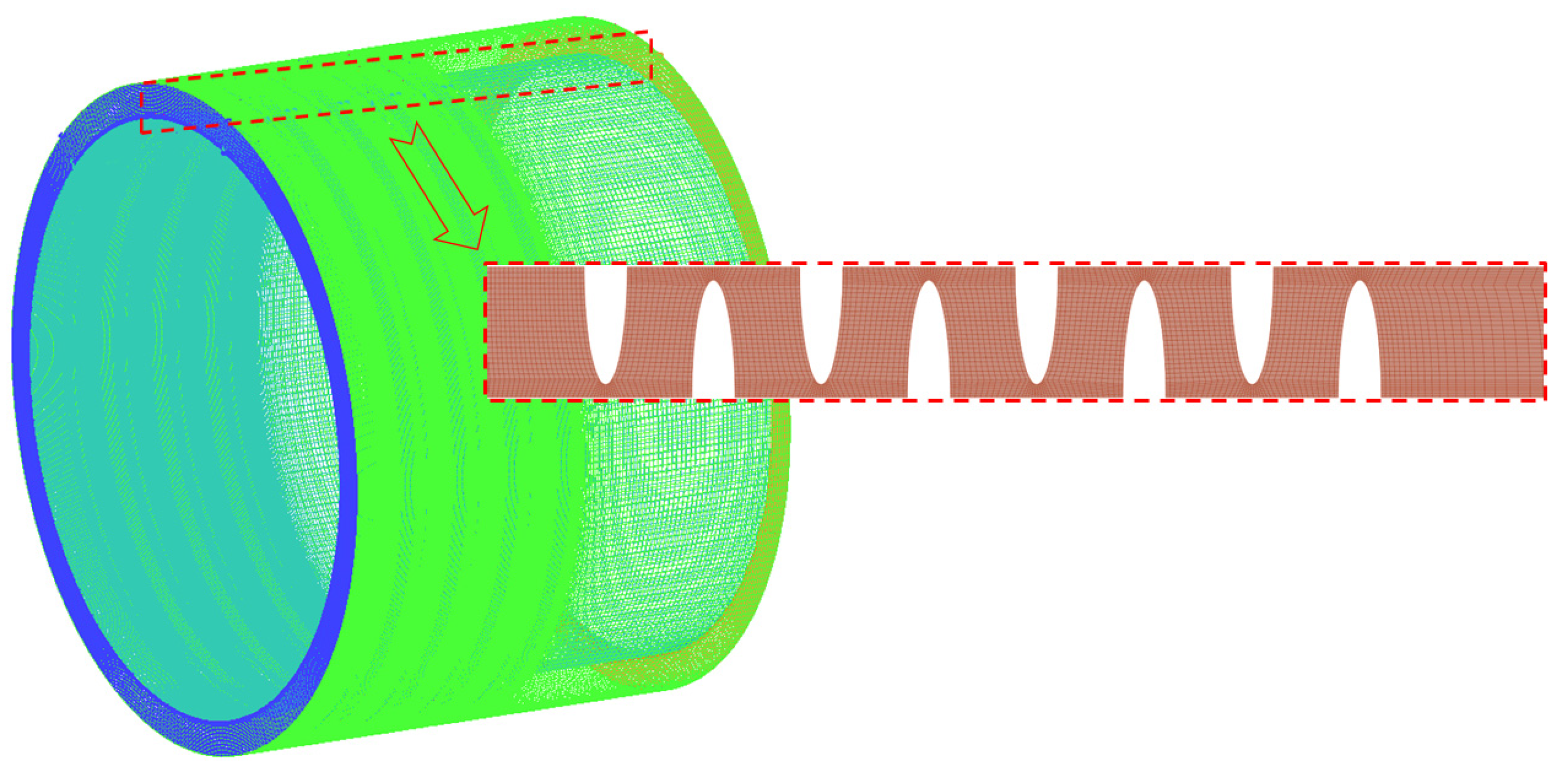
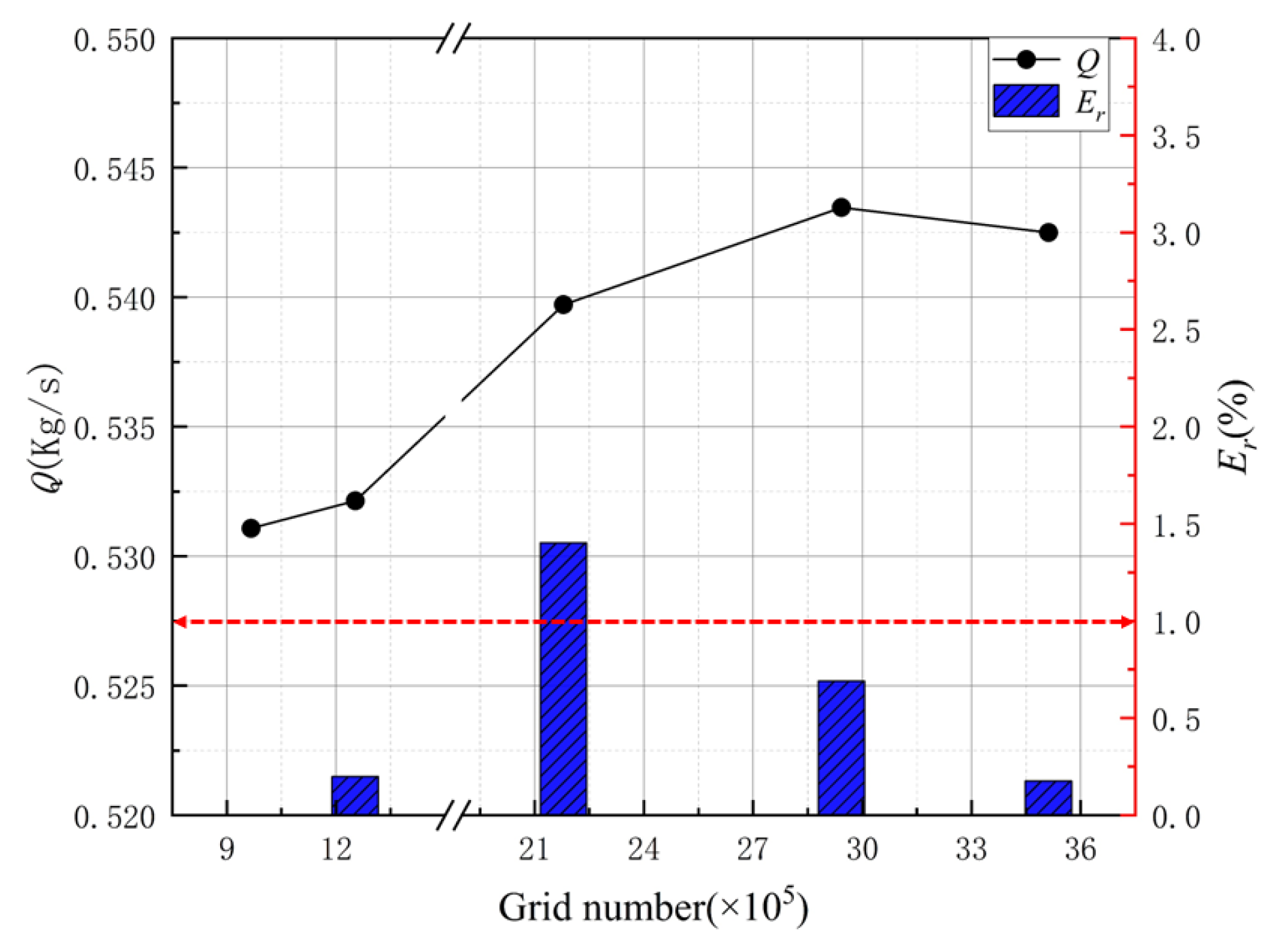
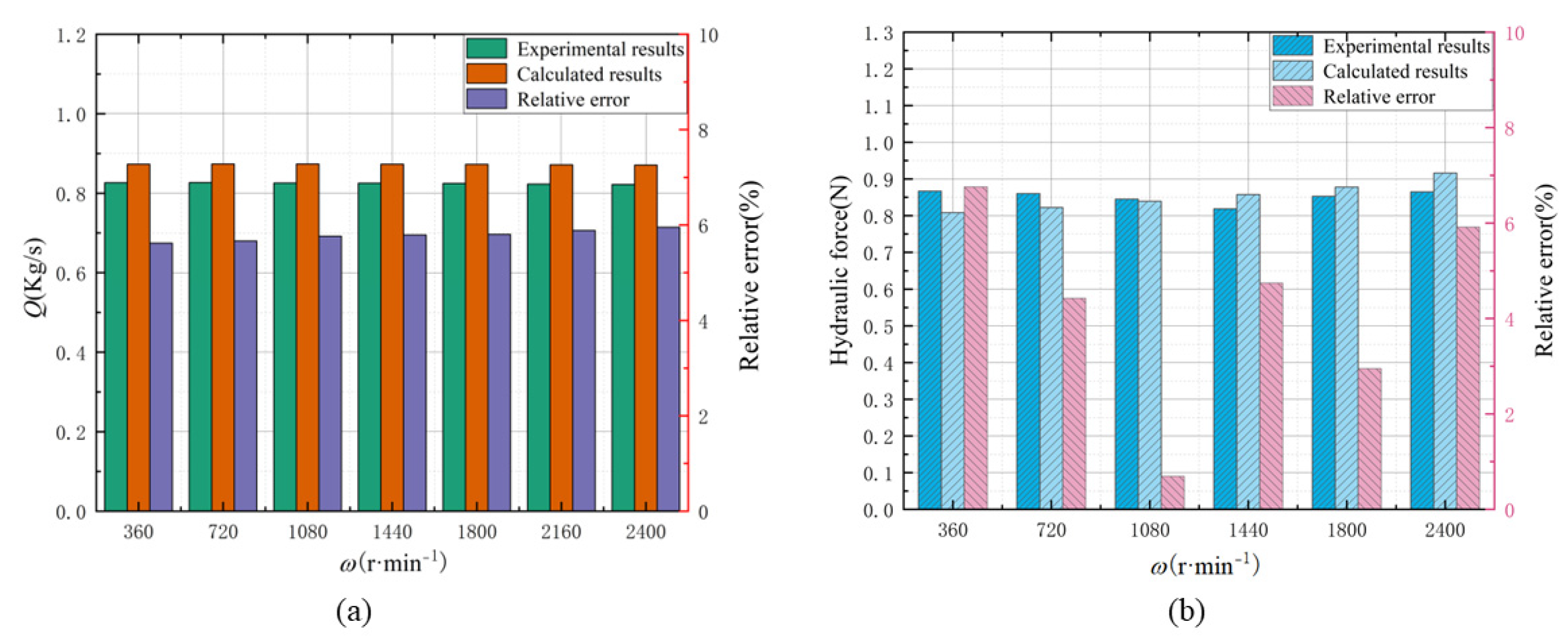




| Parameters | L/mm | Cr/mm | H/mm | B1/mm | B2/mm | Z | Lg/mm | D/mm |
|---|---|---|---|---|---|---|---|---|
| Value | 41.5 | 0.3 | 2.7 | 1 | 4 | 4 | 2.5 | 50 |
| Numerical Parameters | Specification |
|---|---|
| Inlet pressure | 0.2 MPa |
| Outlet pressure | 0 MPa |
| Turbulence model | Standard k-ε |
| Wall function | Scalable |
| Discretization | 2nd order upwind scheme |
| Rotation speed | 1450 rpm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, S.; Ye, Z.; Wang, D.; Su, H.; Zhou, W. Numerical Investigations of Static and Dynamic Characteristics of a Novel Staggered Labyrinth Seal with Semi-Elliptical Structure. Lubricants 2024, 12, 169. https://doi.org/10.3390/lubricants12050169
Yan S, Ye Z, Wang D, Su H, Zhou W. Numerical Investigations of Static and Dynamic Characteristics of a Novel Staggered Labyrinth Seal with Semi-Elliptical Structure. Lubricants. 2024; 12(5):169. https://doi.org/10.3390/lubricants12050169
Chicago/Turabian StyleYan, Shebin, Zhifeng Ye, Dezhao Wang, Huihao Su, and Wenjie Zhou. 2024. "Numerical Investigations of Static and Dynamic Characteristics of a Novel Staggered Labyrinth Seal with Semi-Elliptical Structure" Lubricants 12, no. 5: 169. https://doi.org/10.3390/lubricants12050169
APA StyleYan, S., Ye, Z., Wang, D., Su, H., & Zhou, W. (2024). Numerical Investigations of Static and Dynamic Characteristics of a Novel Staggered Labyrinth Seal with Semi-Elliptical Structure. Lubricants, 12(5), 169. https://doi.org/10.3390/lubricants12050169




