Experimental and Numerical Analysis of Torsional—Lateral Vibrations in Drive Lines Supported by Hydrodynamic Journal Bearings
Abstract
1. Introduction
1.1. Nature of the Issue
1.2. Aim of the Work
2. System Layout and Model
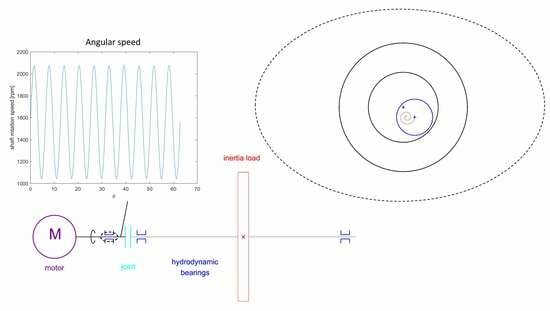
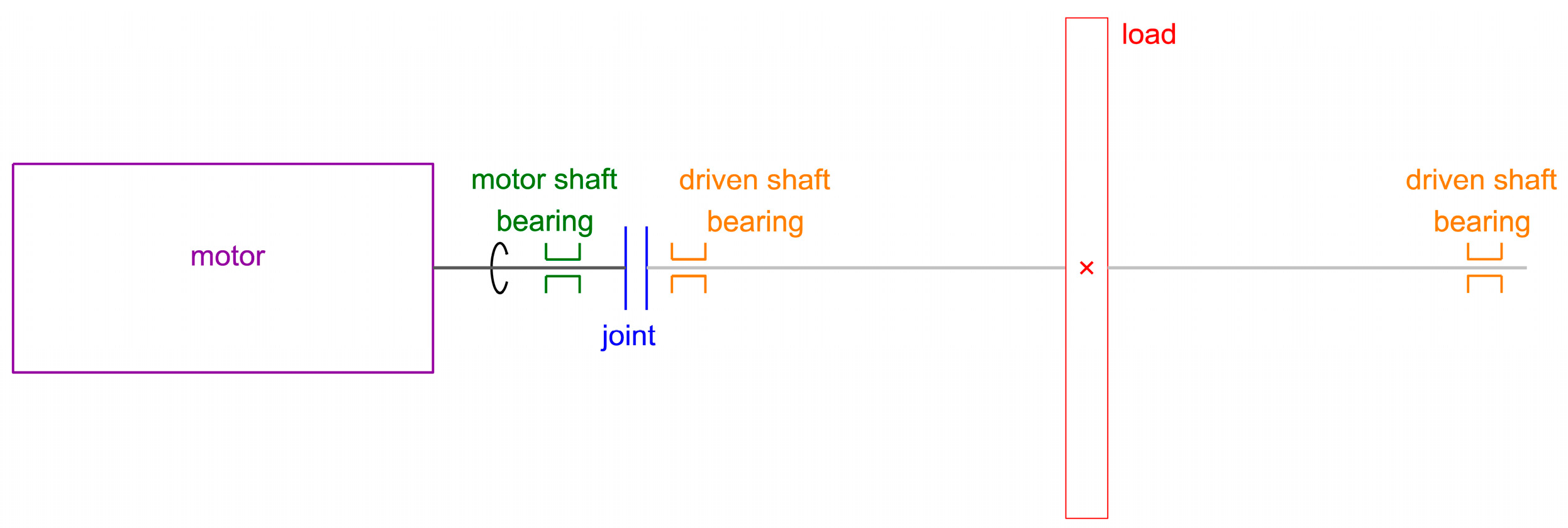
2.1. Layout of the Drive Lines
2.2. Lumped Parameter Model
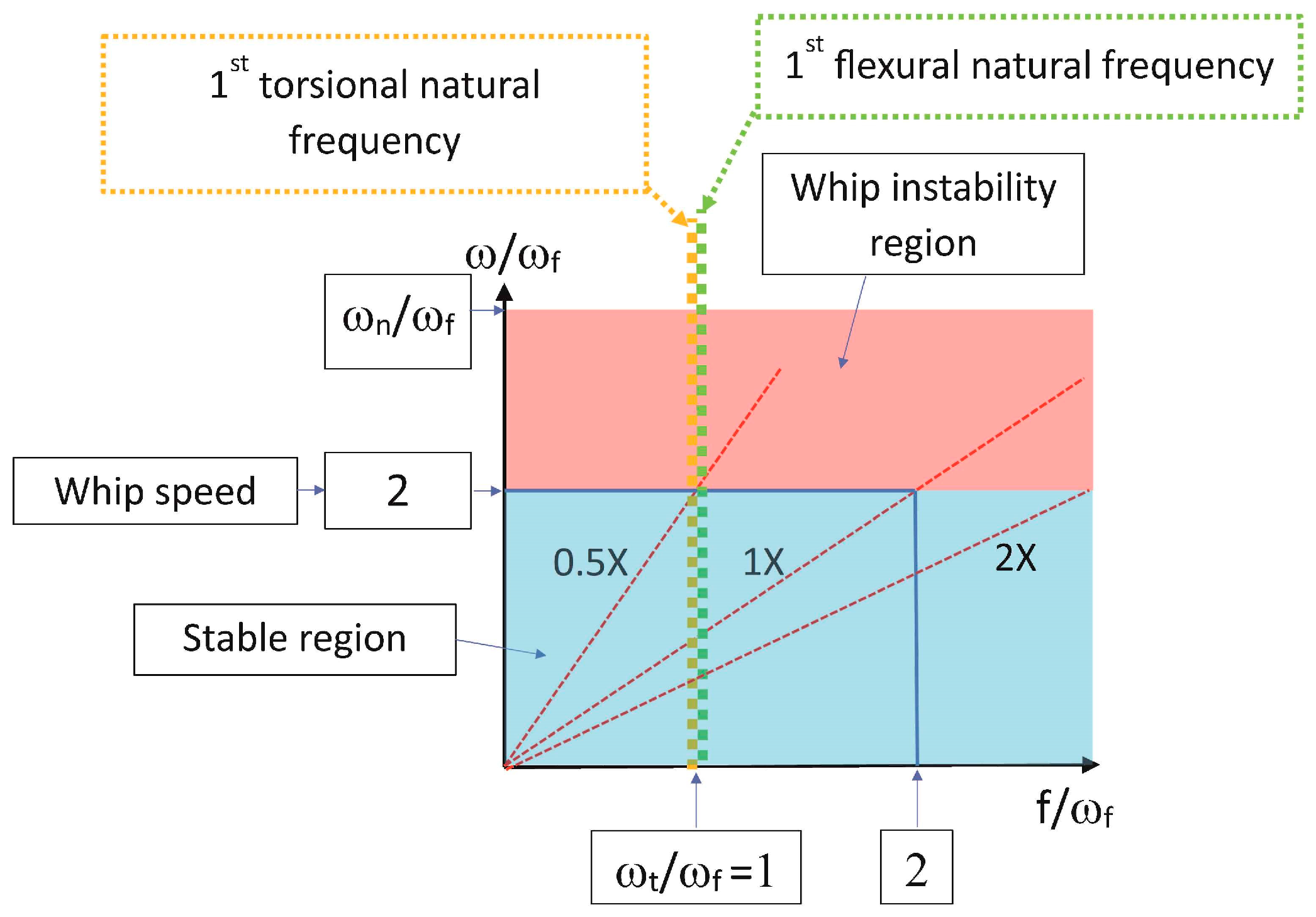
2.3. Critical Design for the Coupling of Torsional and Lateral Vibrations
3. Experimental Observations
3.1. Identification of the Vibrating System
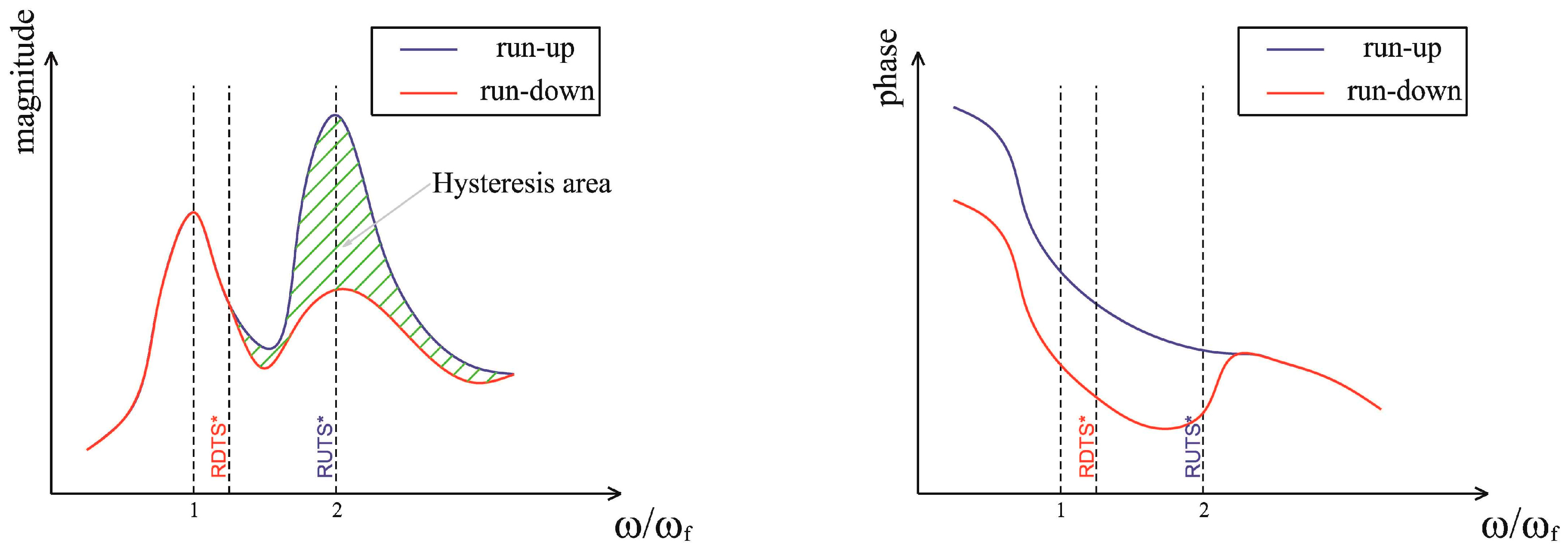
3.2. Hysteresis
3.3. Vibration Analysis
4. Bearing Instability and System Dynamics
4.1. Instability according HBT
4.2. Perturbation Mechanisms
4.3. Dynamic Perturbation
4.4. Kinematic Perturbation
4.5. Dynamic Model of the System
5. Numerical Analysis of Bearings
5.1. Lubrication Analysis Method
5.2. Effect of Kinematic Perturbation
5.3. Effect of Dynamic Perturbation
5.4. Bearing Lubrication Analysis
5.5. Causes of Instability and Hysteresis
6. Conclusions
- Oil-whip not preceded by oil-whirl can be detected in cascade plots of both lateral and torsional vibrations of journal bearings roughly at the same frequency.
- A perceivable degree of irregularity is measured in the rotation speed of the driven shaft, i.e., the part of the shaft directly driven by the electric motor, due to the large driving torque variations.
- Particularly, the threshold speeds RUTS and RDTS identified in cascade plots of the lateral vibrations can be different in the bearings of the driven shaft due to their rotation irregularity so that the cause of the hysteresis detected in the machine is identified according to HBT.
- A kinematic perturbation can modify the stability margin of a journal bearing; such phenomenon is identified as “torsional whirl”.
- The torsional whirl occurs at the same frequency as the excitation.
- The journal precession due to the dynamic perturbation usually develops at the same frequency of the excitation, when the static load is higher than the rotating load, but periodic motions at half the excitation frequency may occur, when the dynamic load component prevails.
- The maximum amplification of the journal precession whirling due to both kinematic and dynamic perturbation is found when the excitation frequency is half the rotation speed.
- Although its isolated contribution to the journal vibration is very small, torsional whirl is required to trigger the dynamic perturbation in the dynamic model and must also be simulated in lubrication analysis to achieve consistent results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c, cb | Nominal (assembled) radial clearance of the bearing |
| cp | Pad clearance |
| d | Shaft overhang |
| es | Misalignment between the parallel drive shafts |
| ex | Horizontal component of journal eccentricity |
| ey | Vertical component (weight direction) of journal eccentricity |
| f | Frequency |
| g | Acceleration of gravity |
| m | Journal lumped mass |
| md | Mass of the driven shaft |
| mm | Mass of the motor shaft |
| mp | Pad preload |
| p | Hydrodynamic pressure |
| ps | Supply pressure |
| t | Time |
| x | Horizontal coordinate, bearing reference frame |
| y | Vertical coordinate (weight direction), bearing reference frame |
| z | Axial coordinate, bearing reference frame |
| Amax | Whirling amplitude |
| D | Nominal diameter of the bearing |
| Fr | Dynamic (rotating) load of the bearing |
| H | Film thickness |
| Kt | Torsional stiffness |
| Ktm | Torsional stiffness of the motor shaft |
| Kj | Torsional stiffness of the joint |
| M | Dimensionless shaft mass |
| Md | Torque applied to the driven shaft |
| Mm | Torque applied to the motor shaft |
| Jd | Inertia of the driven shaft |
| Jm | Inertia of the motor shaft |
| L | Axial length of the bearing |
| R | Journal radius |
| S | Sommerfeld number |
| T | Period of the critical torsional vibration |
| U | Peripheral speed of the journal |
| W | Rotor weight supported by the bearing |
| X | Dimensionless horizontal coordinate, bearing reference frame |
| Y | Dimensionless vertical coordinate (weight direction), bearing reference frame |
| α | Shaft angular acceleration |
| αs | Relative angular acceleration of the drive shafts |
| θ | Shaft rotation angle |
| θd | Rotation angle of the driven shaft |
| θg | Circumferential span of the supply axial groove |
| θm | Rotation angle of the motor shaft |
| θs | Relative rotation angle of the drive shafts |
| ϑ | Circumferential coordinate of the bearing |
| μL | Lubricant dynamic viscosity |
| ρ | Fluid film density of the lubricant |
| ρL | Liquid phase density of the lubricant |
| φr | Phase of bearing dynamic perturbation |
| φU | Phase of bearing kinematic perturbation |
| ω | Shaft rotation speed |
| ωd | Rotation speed of the driven shaft |
| ωm | Rotation speed of the motor shaft |
| ωf | Critical flexural speed |
| ωs | Relative angular speed of the drive shafts |
| ωt | Critical torsional speed |
| Δ | Peak-to-peak amplitude |
| Ω | Developed bearing surface |
References
- Liu, W.; Bättig, P.; Wagner, P.H.; Schiffmann, J. Nonlinear Study on a Rigid Rotor Supported by Herringbone Grooved Gas Bearings: Theory and Validation. Mech. Syst. Signal Process. 2020, 146, 106983. [Google Scholar] [CrossRef]
- Guenat, E.; Schiffmann, J. Dynamic Force Coefficients Identification on Air-Lubricated Herringbone Grooved Journal Bearing. Mech. Syst. Signal Process. 2020, 136, 106498. [Google Scholar] [CrossRef]
- Niccolini Marmont Du Haut Champ, C.A. Analysis of Dynamic Responses and Instabilities in Rotating Machinery. Ph.D. Thesis, Polytechnic School, University of Genoa, Genoa, Italy, 2022. [Google Scholar]
- Niccolini Marmont du Haut Champ, C.A.; Stefani, F.; Silvestri, P. Experimental and Numerical Investigation about Small Clearance Journal Bearings under Static Load Conditions. Adv. Tribol. 2020, 2020, 8844879. [Google Scholar] [CrossRef]
- Childs, D. Turbomachinery Rotordynamics: Phenomena, Modeling, and Analysis; Wiley-Interscience: Hoboken, NJ, USA, 1993; ISBN 978-0-471-53840-0. [Google Scholar]
- Al-Bedoor, B.O. Modeling the Coupled Torsional and Lateral Vibrations of Unbalanced Rotors. Comput. Methods Appl. Mech. Eng. 2001, 190, 5999–6008. [Google Scholar] [CrossRef]
- Kita, M.; Hataya, T.; Tokimasa, Y. Study of a Rotordynamic Analysis Method That Considers Torsional and Lateral Coupled Vibrations in Compressor Trains with a Gearbox. In Proceedings of the 36th Turbomachinery Symposium, Texas A&M University, Houston, TX, USA, 11–13 September 2007. [Google Scholar]
- Chiu, Y.J.; Chen, D.Z. The Coupled Vibration in a Rotating Multi-Disk Rotor System. Int. J. Mech. Sci. 2011, 53, 1–10. [Google Scholar] [CrossRef]
- Gosiewski, Z. Analysis of Coupling Mechanism in Lateral/Torsional Rotor Vibrations. J. Theor. Appl. Mech. 2008, 46, 829–844. [Google Scholar]
- Sukkar, R.; Yigit, A.S. Analysis of Fully Coupled Torsional and Lateral Vibrations of Unbalanced Rotors Subject to Axial Loads. Kuwait J. Sci. Eng. 2008, 35, 143–170. [Google Scholar]
- Mohiuddin, M.A.; Khulief, Y.A. Coupled Bending Torsional Vibration of Rotors Using Finite Element. J. Sound Vib. 1999, 223, 297–316. [Google Scholar] [CrossRef]
- Yuan, Z.; Chu, F.; Lin, Y. External and Internal Coupling Effects of Rotor’s Bending and Torsional Vibrations under Unbalances. J. Sound Vib. 2007, 299, 339–347. [Google Scholar] [CrossRef]
- Rao, J.S.; Shiau, T.N.; Chang, J.R. Theoretical Analysis of Lateral Response Due to Torsional Excitation of Geared Rotors. Mech. Mach. Theory 1998, 33, 761–783. [Google Scholar] [CrossRef]
- Patel, T.H.; Darpe, A.K. Coupled Bending-Torsional Vibration Analysis of Rotor with Rub and Crack. J. Sound Vib. 2009, 326, 740–752. [Google Scholar] [CrossRef]
- Muszyńska, A.; Goldman, P.; Bently, D.E. Torsional/Lateral Vibration Cross-Coupled Response Due to Shaft Anisotropy: A New Tool in Shaft Crack Detection. In Proceedings of the 5th International Conference on Vibrations in Rotating Machinery (IMechE ’92), Bath, UK, 7–10 September 1992. [Google Scholar]
- Genta, G. Vibration of Structures and Machines. Springer-Verlag: New York, NY, USA, 1999; ISBN 978-1-4612-1450-2. [Google Scholar]
- Perera, I. Theoretical and Experimental Study of Coupled Torsional—Lateral Vibrations in Rotor Dynamics. Ph.D. Thesis, Department of Mechanical Engineering, University of Calgary, Calgary, AB, Canada, 1998. [Google Scholar]
- Mihajlović, N.; Van De Wouw, N.; Rosielle, P.C.J.N.; Nijmeijer, H. Interaction between Torsional and Lateral Vibrations in Flexible Rotor Systems with Discontinuous Friction. Nonlinear Dyn. 2007, 50, 679–699. [Google Scholar] [CrossRef][Green Version]
- Xiang, L.; Gao, N. Coupled Torsion–Bending Dynamic Analysis of Gear-Rotor-Bearing System with Eccentricity Fluctuation. Appl. Math. Model. 2017, 50, 569–584. [Google Scholar] [CrossRef]
- L’vov, M.M.; Gunter, E.J. Application of Rotor Dynamic Analysis for Evaluation of Syncronous Speed Instability and Amplitude Hysteresis at 2nd Mode for a Generator Rotor in a High-Speed Balancing Facility. In Proceedings of the ISCORMA-3, Cleveland, OH, USA, 19–23 September 2005; pp. 19–23. [Google Scholar]
- Mendes, R.U.; Cavalca, K.L. On the Instability Threshold of Journal Bearing Supported Rotors. Int. J. Rotating Mach. 2014, 2014, 351261. [Google Scholar] [CrossRef]
- Luneno, J. Coupled Vibrations in Horizontal and Vertical Rotor-Bearings Systems. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2010. [Google Scholar]
- Wang, J.K.; Khonsari, M.M. On the Hysteresis Phenomenon Associated with Instability of Rotor-Bearing Systems. J. Tribol. 2006, 128, 188–196. [Google Scholar] [CrossRef]
- Wang, J.K.; Khonsari, M.M. Thermohydrodynamic Instability in Fluid-Film Bearings; Wiley: Chichester, West Sussex, UK, 2016; ISBN 9780470057216. [Google Scholar]
- Cui, Y.; Wang, Y.; Zhong, J. Numerical Analysis on the Nonlinear Hysteresis Phenomenon Associated with Instability of a Steam Turbine Rotor-Bearing System. In Mechanisms and Machine Science, Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Milano, Italy, 22–25 September 2014; Pennacchi, P., Ed.; Springer: Cham, Switzerland, 2015; Volume 21, p. 21. [Google Scholar]
- Chouchane, M.; Sghir, R. Stability and Bifurcation Analysis of a Flexible Rotor-Bearing System by Numerical Continuation. In Proceedings of the 10th International Conference on Vibrations in Rotating Machineries, London, UK, 11–13 September 2012; IMechE: London, UK, 2012; pp. 647–656. [Google Scholar]
- Amamou, A.; Chouchane, M. Non-Linear Stability Analysis of Floating Ring Bearings Using Hopf Bifurcation Theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 2804–2818. [Google Scholar] [CrossRef]
- Wang, J.K.; Khonsari, M.M. Bifurcation Analysis of a Flexible Rotor Supported by Two Fluid-Film Journal Bearings. J. Tribol. 2006, 128, 594–603. [Google Scholar] [CrossRef]
- Newkirk, B.L.; Taylor, H.D. Shaft Whipping Due to Oil Action in Journal Bearings. Gen. Electr. Rev. 1925, 28, 559–568. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory and Practice; Wiley/SEM: Bethel, NY, USA, 2009; ISBN 978-0-863-80218-8. [Google Scholar]
- Niccolini Marmont Du Haut Champ, C.A.; Silvestri, P. Experimental and Numerical Vibro-Acoustic Investigation on a Trimmed Car Door to Analyze Slamming Event. Appl. Acoust. 2020, 166, 107380. [Google Scholar] [CrossRef]
- Hauptmann, E.G.; Eckert, W.F.; Howes, B.C. The Influence on Torsional Vibration Analysis of Electromagnetic Effects across an Induction Motor Air Gap. In Proceedings of the Gas Machinery Conference 2013, Albuquerque, NM, USA, 6–9 October 2013; pp. 1–11. [Google Scholar]
- Niccolini Marmont Du Haut Champ, C.A.; Stefani, F.; Silvestri, P. Development of a New Test Rig for the Analysis of Hydrodynamic Bearings for Rotors of MicroGT. E3S Web Conf. 2019, 113, 4–12. [Google Scholar] [CrossRef]
- ISO 20816-3; Mechanical vibration. Measurement and evaluation of machine vibration, International Standard. ISO: Vernier, Geneva, Switzerland, 2022.
- Campbell, B.J.; Lovet, P.I.; Martint, F.A. Bearings for Reciprocating Machinery: A Review of the Present State of Theoretical, Experimental and Service Knowledge. Proc. Inst. Mech. Eng. Conf. Proc. 1967, 182 Pt 3A, 51–74. [Google Scholar] [CrossRef]
- Stefani, F. FEM Applied to Hydrodynamic Bearing Design. In New Tribological Ways; InTech: London, UK, 2011. [Google Scholar] [CrossRef][Green Version]
- Brindley, J.; Savage, M.D.; Taylor, C.M. The Nonlinear Dynamics of Journal Bearings. Philos. Trans. Phys. Sci. Eng. 1990, 332, 107–119. [Google Scholar]
- Stefani, F. Computer-Aided Design of Pocket Elliptical Journal Bearings, Part 1: Theory. J. Adv. Mech. Des. Syst. Manuf. 2013, 7, 576–593. [Google Scholar] [CrossRef][Green Version]
- San Andreés, L. Hydrodynamic Fluid Film Bearings and Their Effect on the Stability of Rotating Machinery. In Design and Analysis of High Speed Pumps; Educational Notes RTO-EN-AVT-143; RTO: Neuilly-sur-Seine, France, 2006; pp. 10-1–10-36. [Google Scholar]
- Frêne, J.; Nicolas, D.; Degueurce, B.; Berthe, D.; Godet, M. Hydrodynamic Lubrication Bearings and Thrust Bearings; Elsevier: Amsterdam, The Netherlands, 1990; ISBN 978-0-444-82366-3. [Google Scholar]
- Betti, A.; Forte, P.; Ciulli, E. Turbulence Effects in Tilting Pad Journal Bearings: A Review. Lubricants 2022, 10, 171. [Google Scholar] [CrossRef]
- Selecting for Torsional Stiffness. Available online: https://www.huco.com/design-guide/selecting-for-torsional-stiffness# (accessed on 4 March 2024).
- Loewy, R.G.; Piarulli, V.J. Dynamics of Rotating Shafts; The Shock and Vibration Information Center, United States Department of Defense, Navai Research Laboratory: Washington, DC, USA, 1969. [Google Scholar]
- Ogrodnik, P.J.; Goodwin, M.J.; Penny, J.E.T. Influence of Design Parameters on Occurrence of Oil Whirl in Rotor-Bearing Systems; NASA RP-19860020699, NASA. Lewis Research Center Instability in Rotating Machinery: Cleveland, OH, USA, 1985.
- Holmes, R. Oil-Whirl Characteristics of a Rigid Rotor in 360° Journal Bearings. Proc. Inst. Mech. Eng. 1963, 177, 291–307. [Google Scholar] [CrossRef]
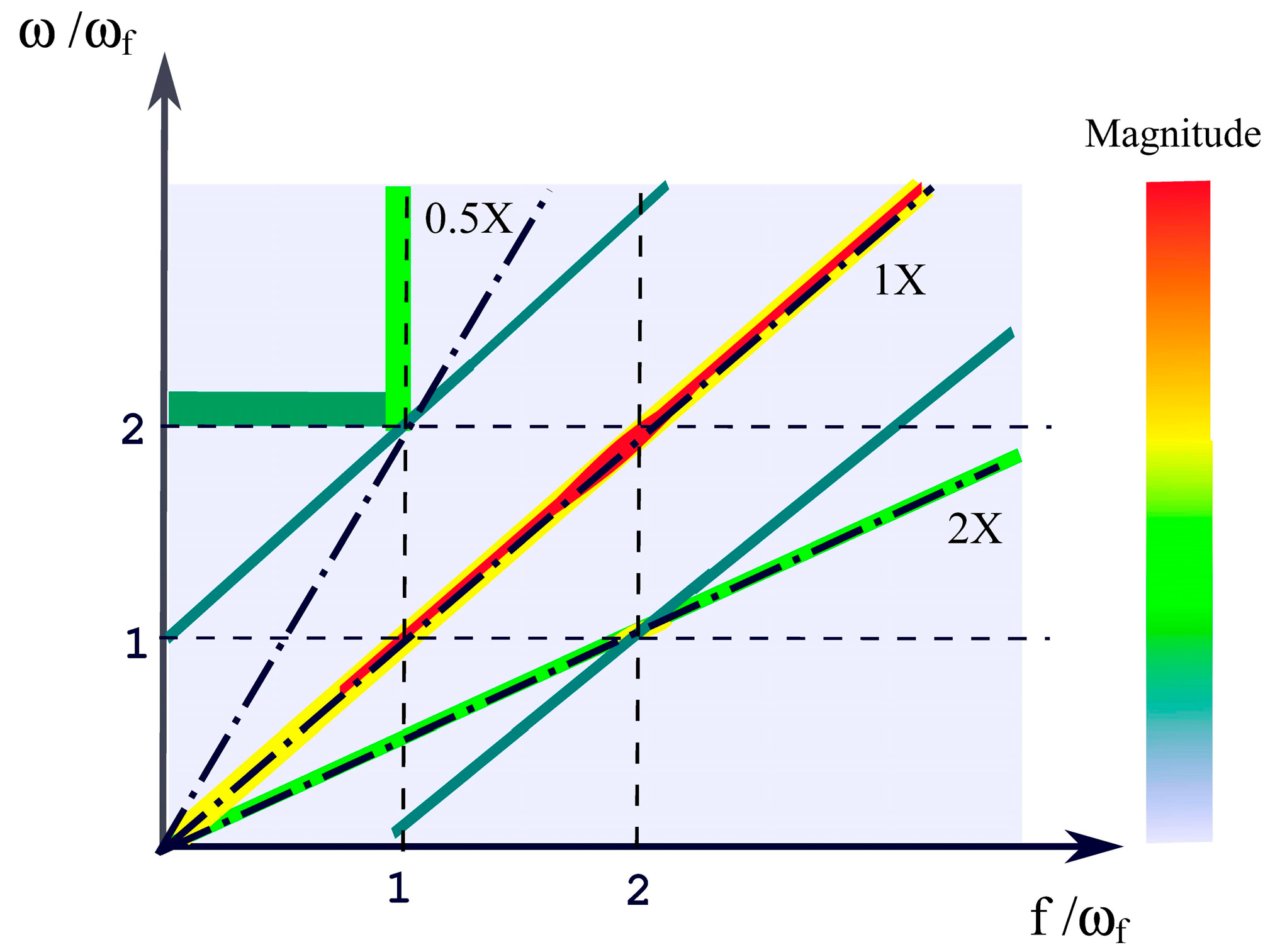

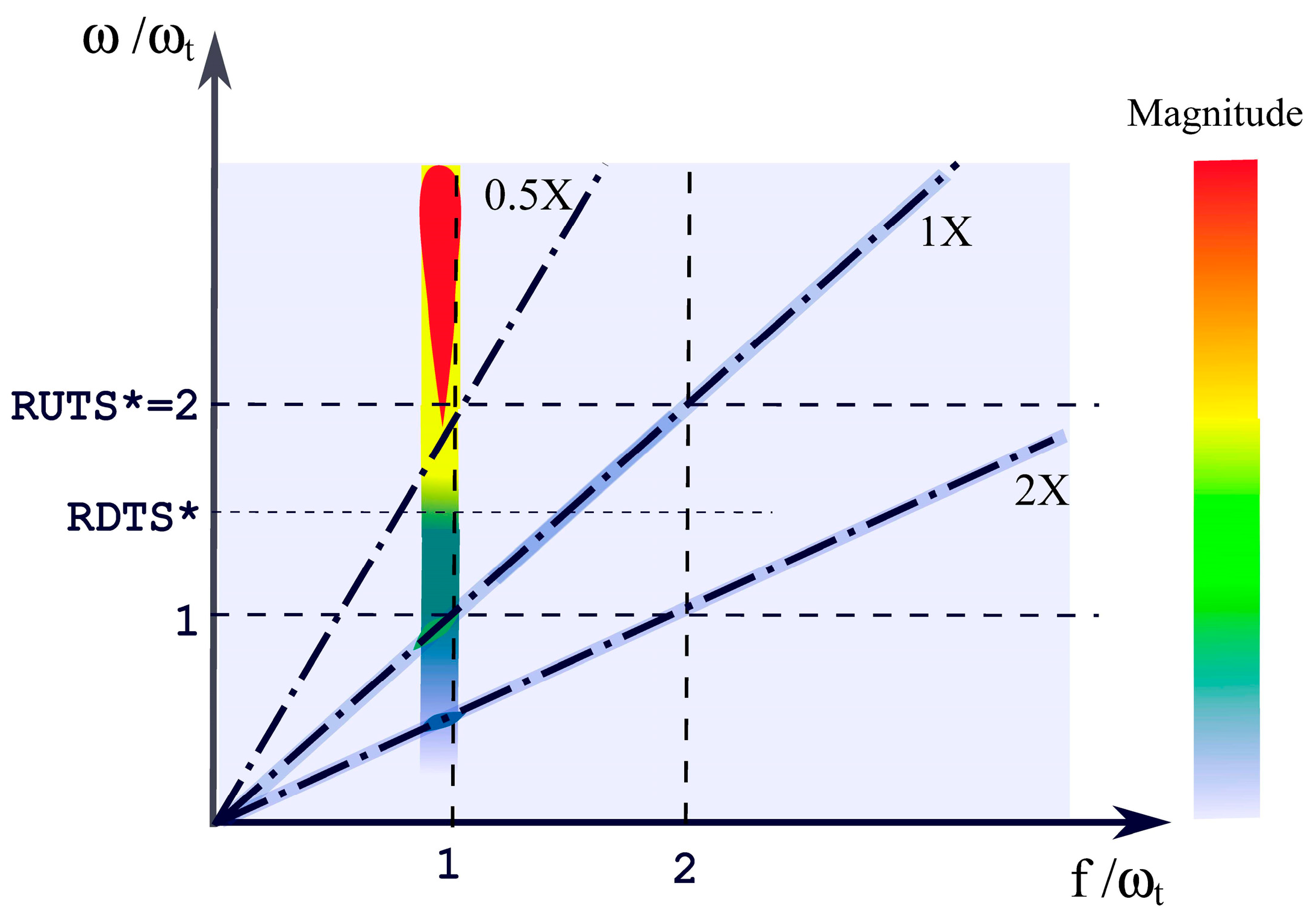

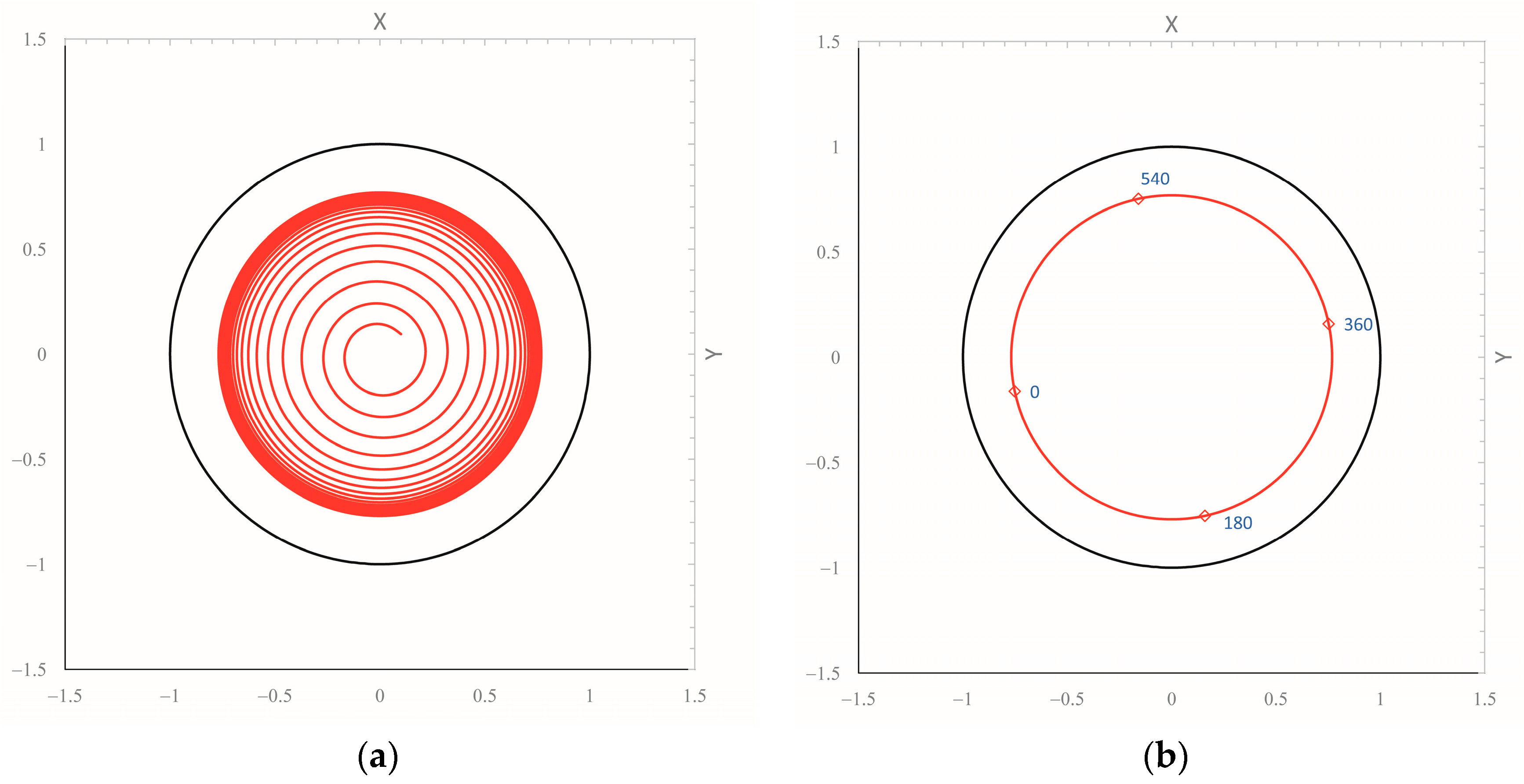


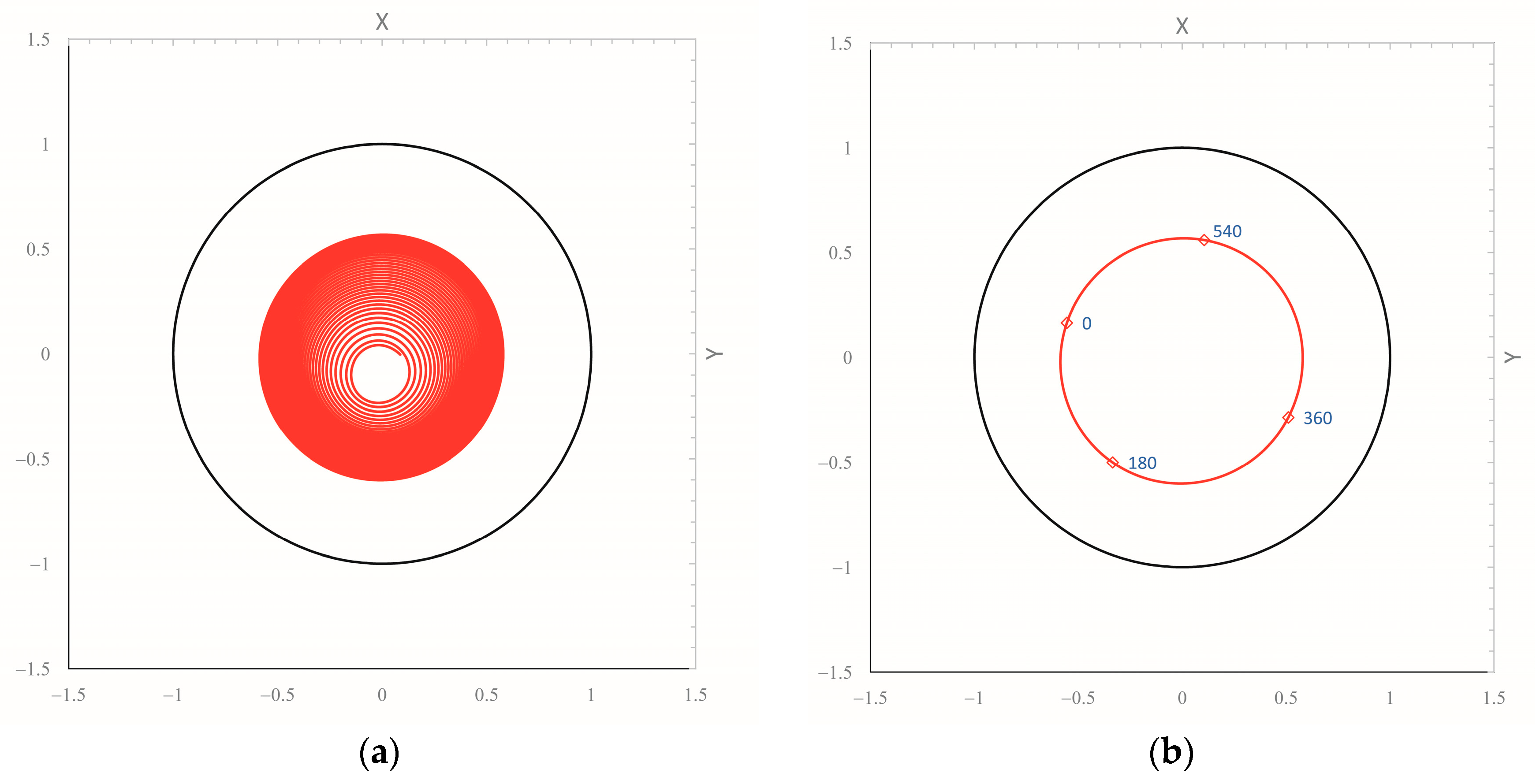
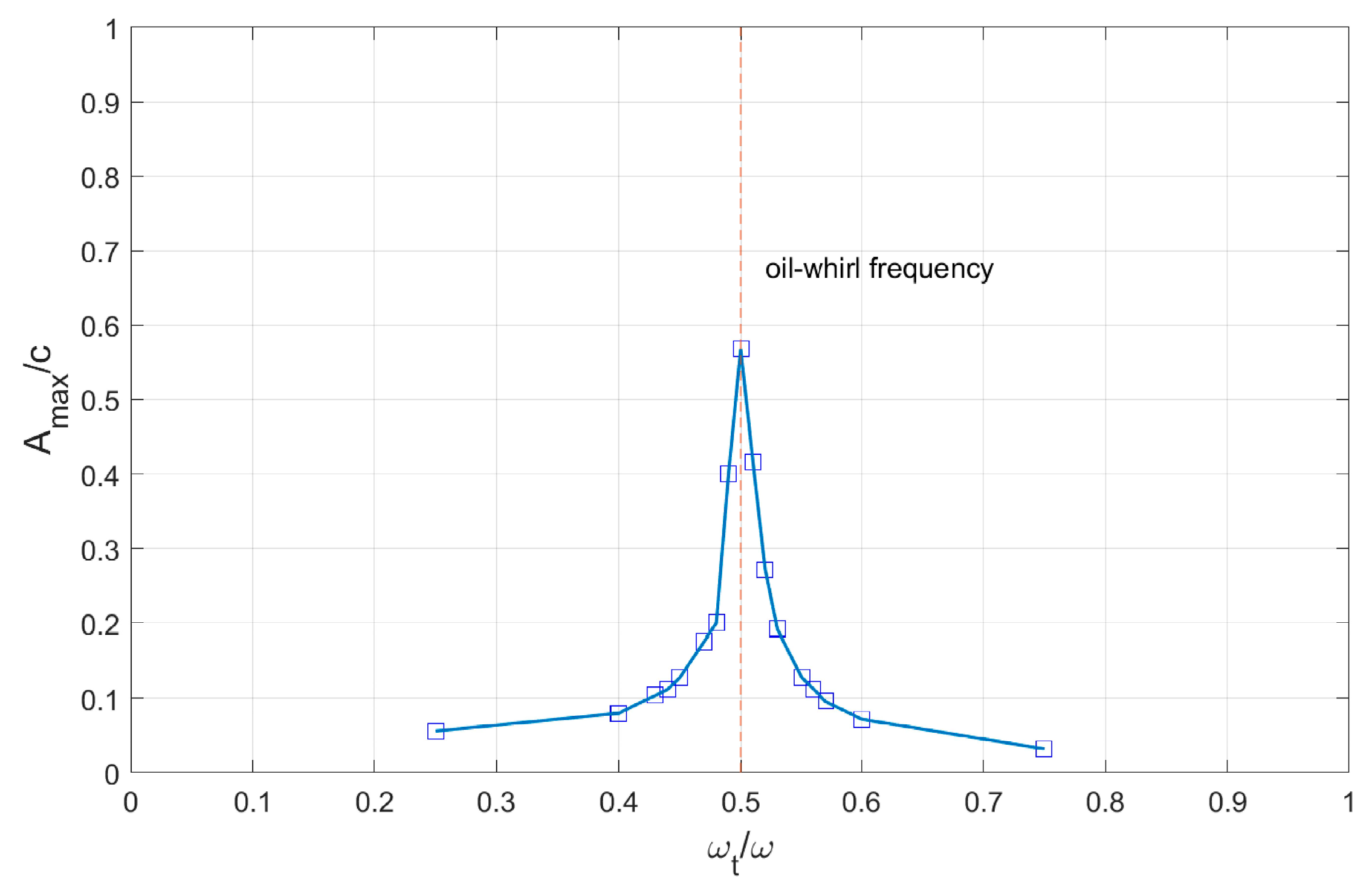
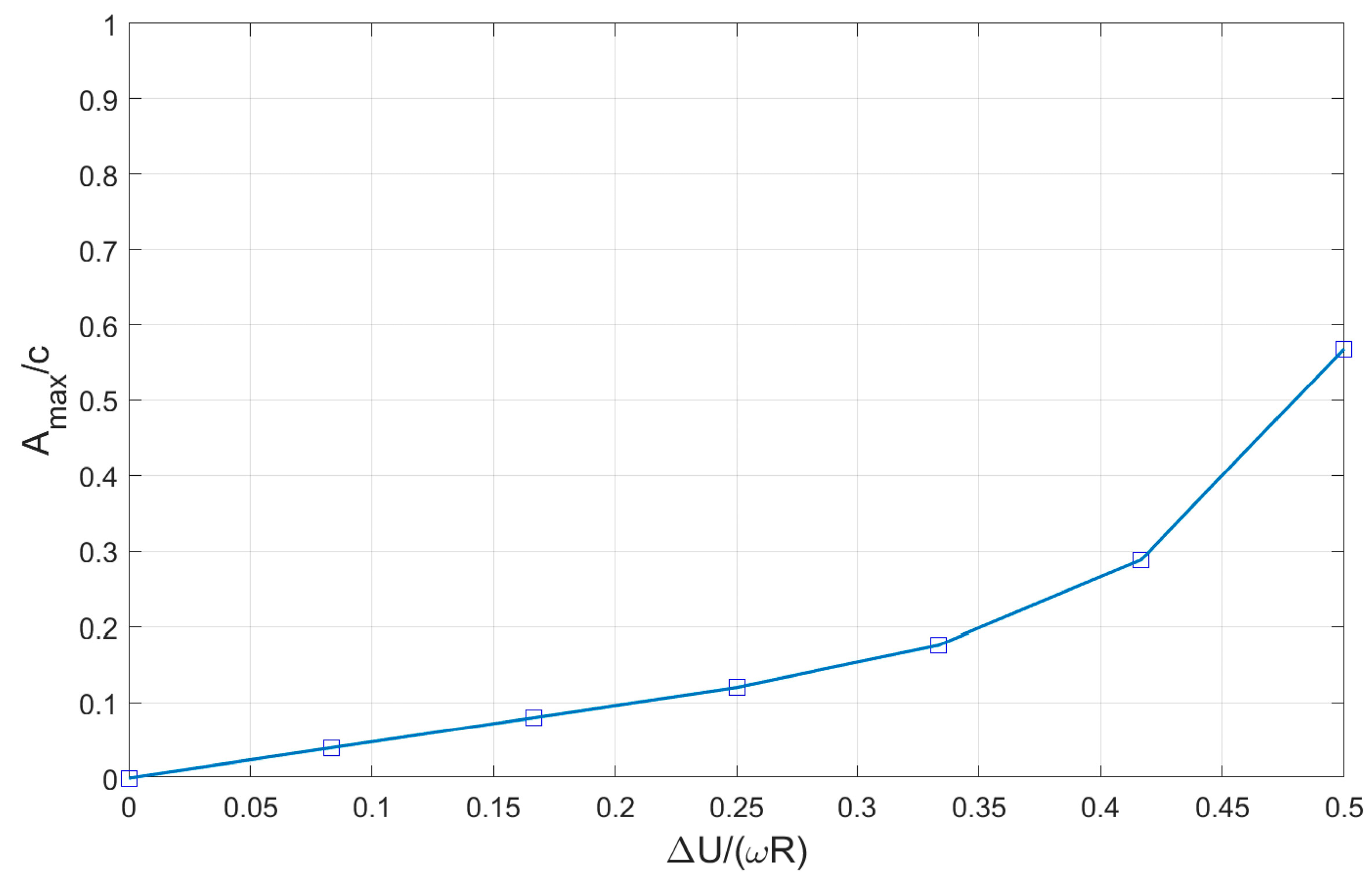
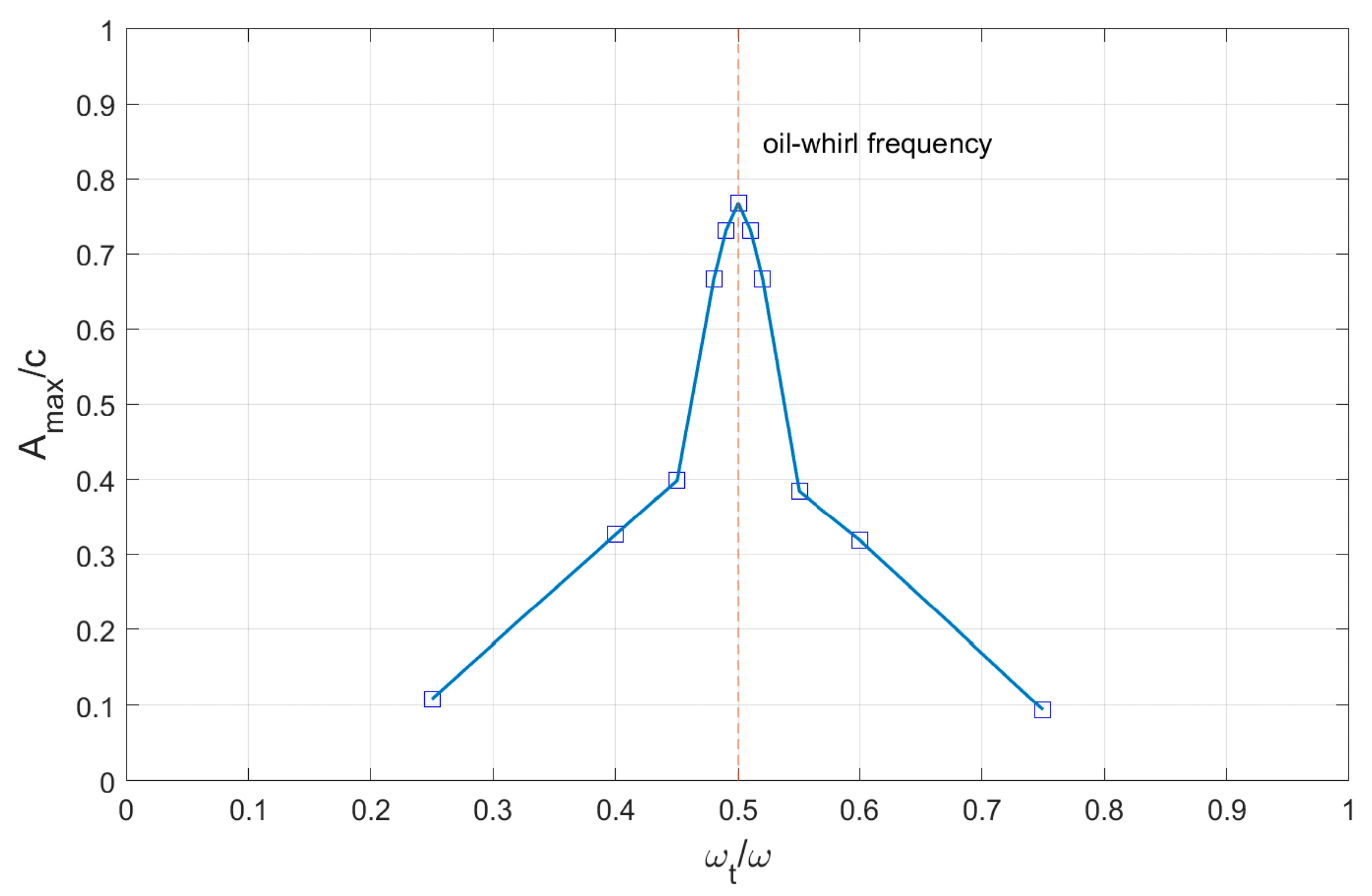

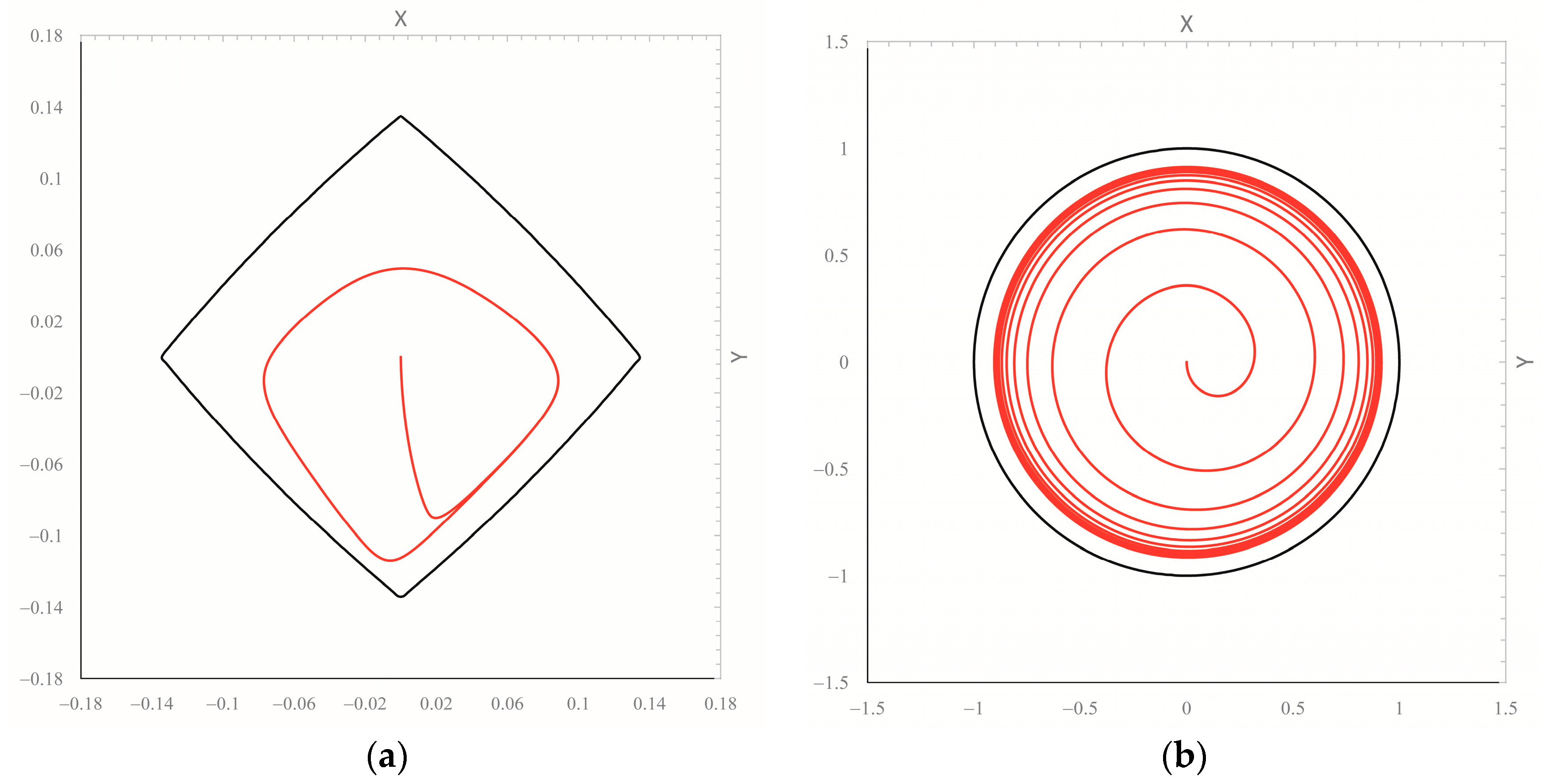
| Parameter Description | Symbol [unit] | Value |
|---|---|---|
| Joint stiffness | Kj [Nm/rad] | 7.41 |
| Moment of inertia of motor (or motor shaft) | Jm [kg m2] | 0.001125 |
| Moment of inertia of load (or driven shaft) | Jd [kg m2] | 0.1125 |
| Assumed motor torque ripple amplitude (peak to peak) at the simulation speed | ΔMm [N m] | 1 |
| Computed motor shaft angular speed oscillation amplitude (peak to peak) at the simulation speed | Δωm [rpm] | 515.46 |
| Computed critical (natural) torsional frequency (equal to bending frequency) | ωt [Hz] ([rpm]) | 12.98 (779.13) |
| Simulation speed equal to whip speed | ω [rpm] | 1558.3 |
| Shaft overhang (distance between motor bearing and motor shaft end) | d [mm] | 35 |
| Parameter Description | Symbol [unit] | Value |
|---|---|---|
| Bearing diameter | D [mm] | 25 |
| Bearing length | L [mm] | 35 |
| Aspect ratio | L/D | 1.4 |
| Nominal (assembled) radial clearance | cb [mm] | 0.1 |
| Relative clearance | 2 cb/D | 0.008 |
| Pad preload (four-lobe bearing) | mp | 0.9 |
| Pad preload (cylindrical bearing) | mp | 0.0 |
| Supply axial groove circumferential span | θg [deg] | 10 |
| Supply pressure | ps [Pa] | 10,000 |
| Oil viscosity | μL [Pa s] | 0.0251 |
| Rotation speed | ω [rpm] | 1558.3 |
| Rotor weight supported by the bearing | W [N] | 10.6 |
| Rotating load amplitude | ΔFr [N] | 16.49 |
| Speed variation amplitude | Δω [rpm] | 515.46 |
| Rotating load and speed variation frequency | ωt [Hz] ([rpm]) | 13.0 (779.15) |
| Bearing Type | Load Case | Frequency [Hz] | Relative x Amplitude | Relative y Amplitude |
|---|---|---|---|---|
| four-lobe | A (kinematic perturbation) | 13.0 | 0.14 | 0.016 |
| four-lobe | B (dynamic perturbation) | 13.0 | 1.61 | 1.70 |
| four-lobe | C (both perturbations) | 13.0 | 1.64 | 1.66 |
| cylindrical | A (kinematic perturbation) | 13.0 | 0.16 | 0.16 |
| cylindrical | B (dynamic perturbation) | 6.5 | 1.82 | 1.81 |
| cylindrical | C (both perturbations) | 13.0 | 1.83 | 1.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefani, F.A.; Niccolini Marmont Du Haut Champ, C.A.; Silvestri, P.; Massardo, A.F. Experimental and Numerical Analysis of Torsional—Lateral Vibrations in Drive Lines Supported by Hydrodynamic Journal Bearings. Lubricants 2024, 12, 82. https://doi.org/10.3390/lubricants12030082
Stefani FA, Niccolini Marmont Du Haut Champ CA, Silvestri P, Massardo AF. Experimental and Numerical Analysis of Torsional—Lateral Vibrations in Drive Lines Supported by Hydrodynamic Journal Bearings. Lubricants. 2024; 12(3):82. https://doi.org/10.3390/lubricants12030082
Chicago/Turabian StyleStefani, Fabrizio Antonio, Carlo Alberto Niccolini Marmont Du Haut Champ, Paolo Silvestri, and Aristide Fausto Massardo. 2024. "Experimental and Numerical Analysis of Torsional—Lateral Vibrations in Drive Lines Supported by Hydrodynamic Journal Bearings" Lubricants 12, no. 3: 82. https://doi.org/10.3390/lubricants12030082
APA StyleStefani, F. A., Niccolini Marmont Du Haut Champ, C. A., Silvestri, P., & Massardo, A. F. (2024). Experimental and Numerical Analysis of Torsional—Lateral Vibrations in Drive Lines Supported by Hydrodynamic Journal Bearings. Lubricants, 12(3), 82. https://doi.org/10.3390/lubricants12030082