Modeling and Dynamic Analysis of Double-Row Angular Contact Ball Bearing–Rotor–Disk System
Abstract
1. Introduction
2. Mathematical Model
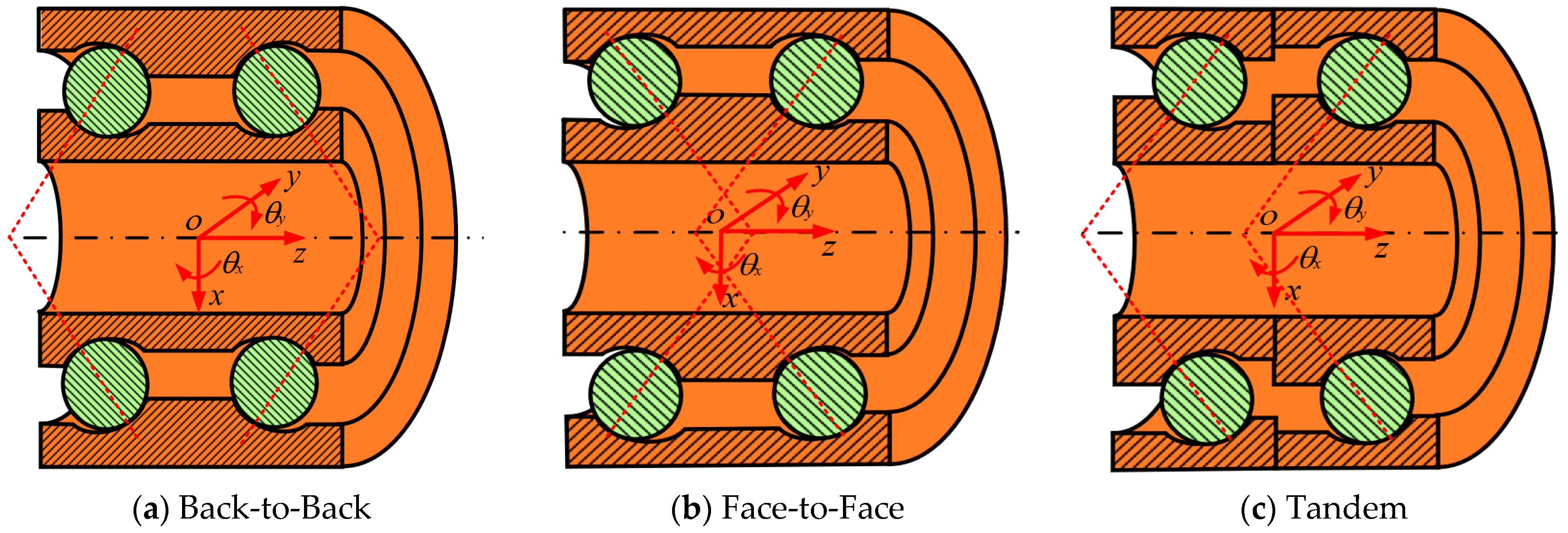
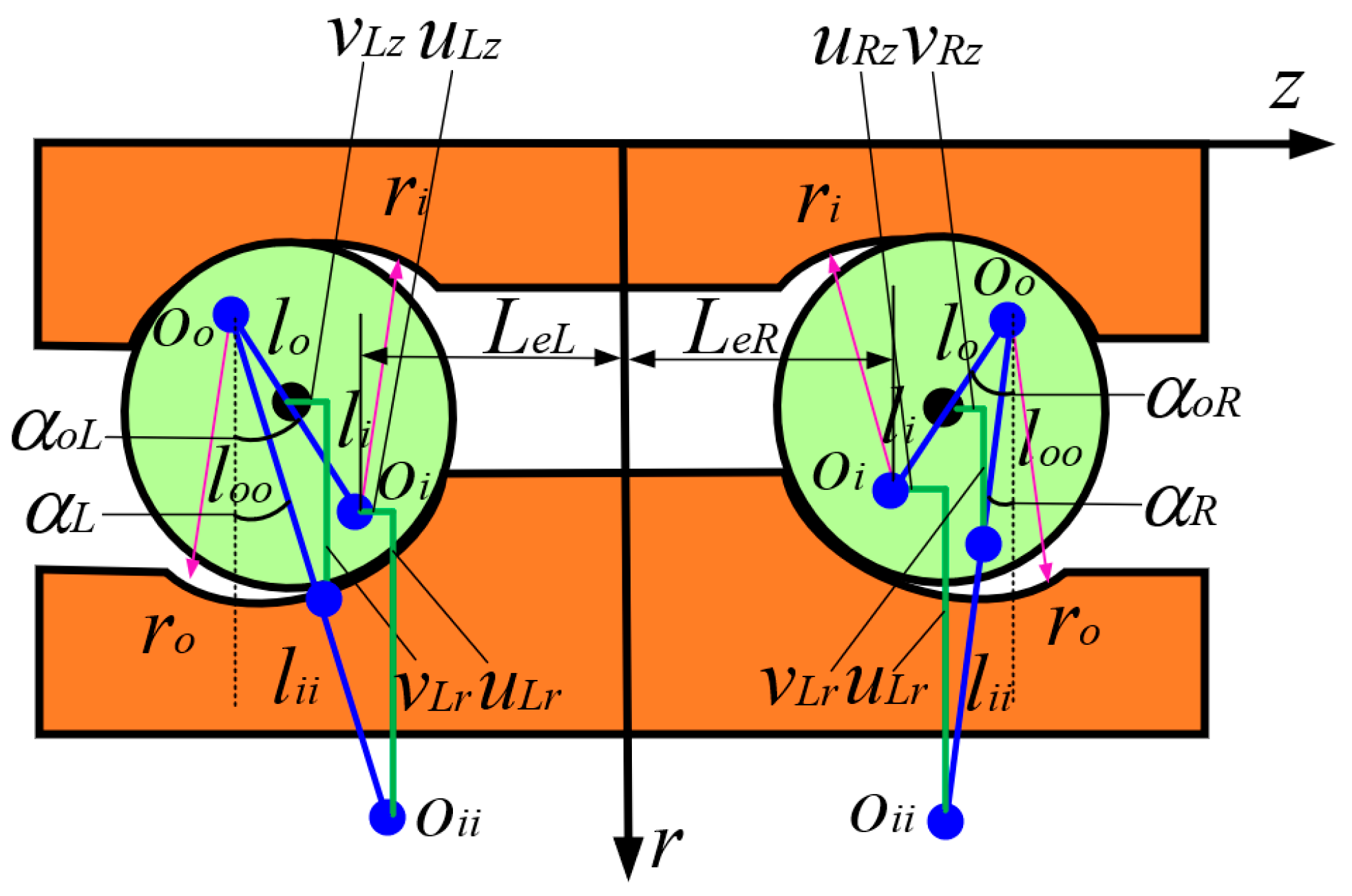
2.1. The Equations of Motion of the DRACBB
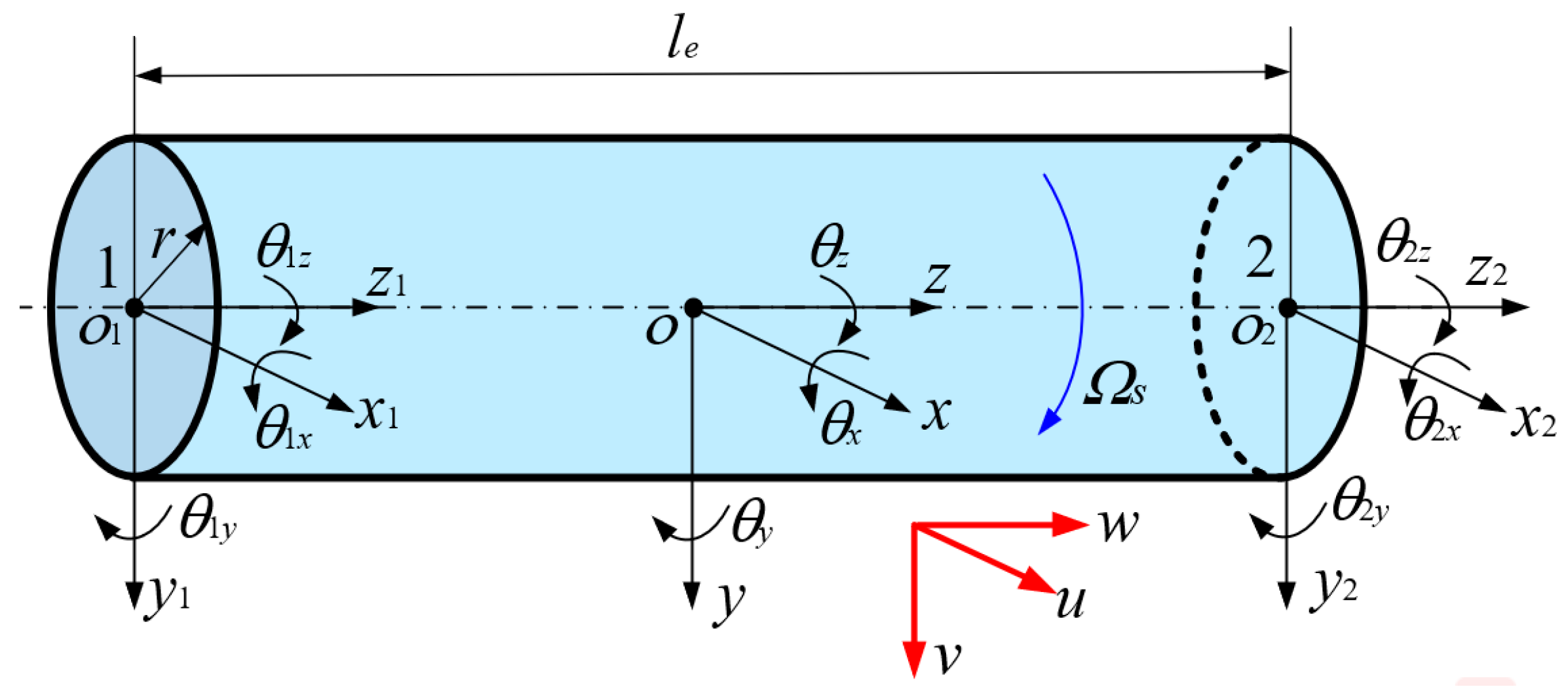
2.2. The Equations of Motion of the Rotor and Disk
2.3. The Equations of Motion of the Bearing–Rotor–Disk System
3. Results and Discussion
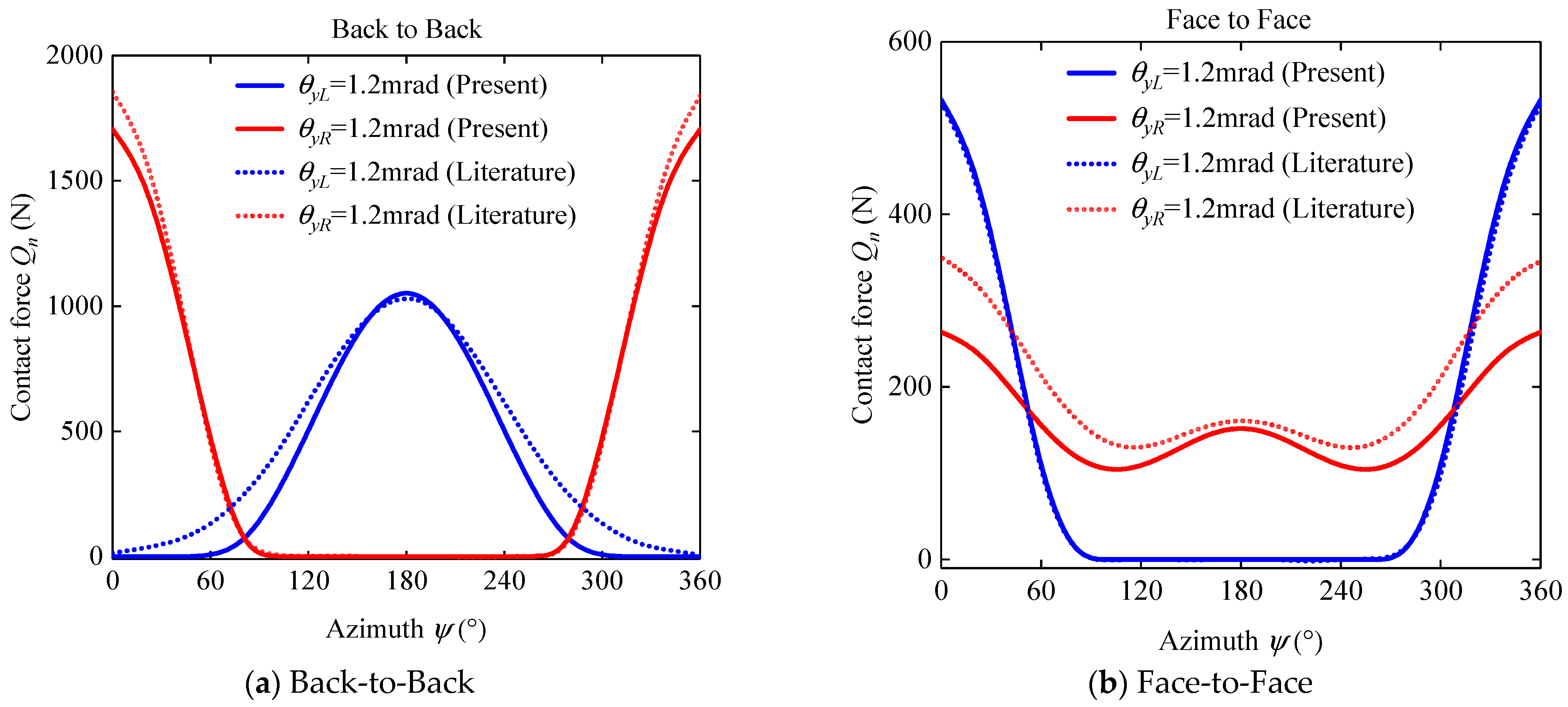
3.1. Mathematical Model Validation
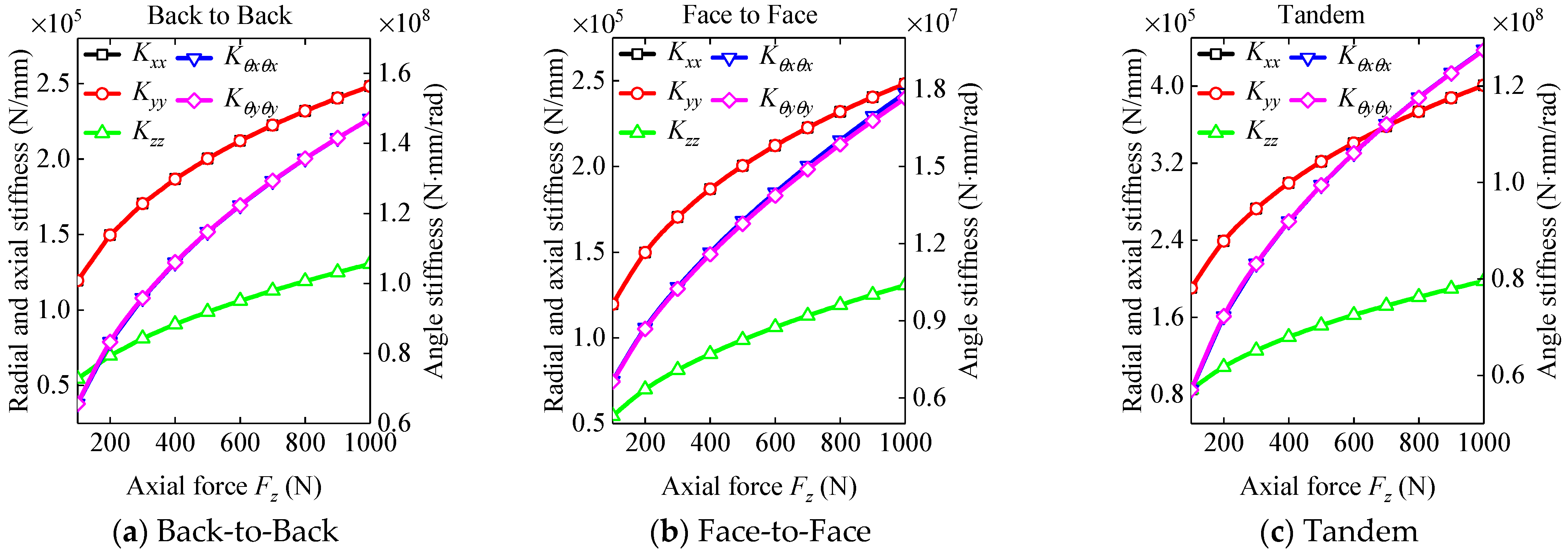
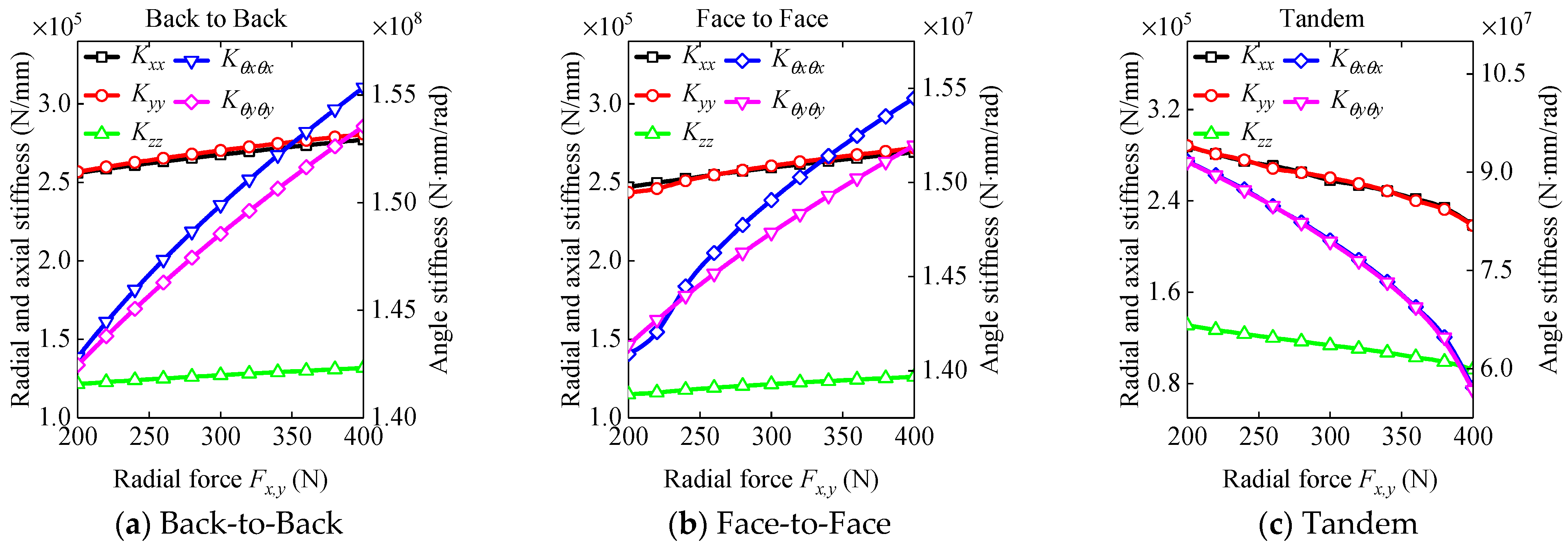
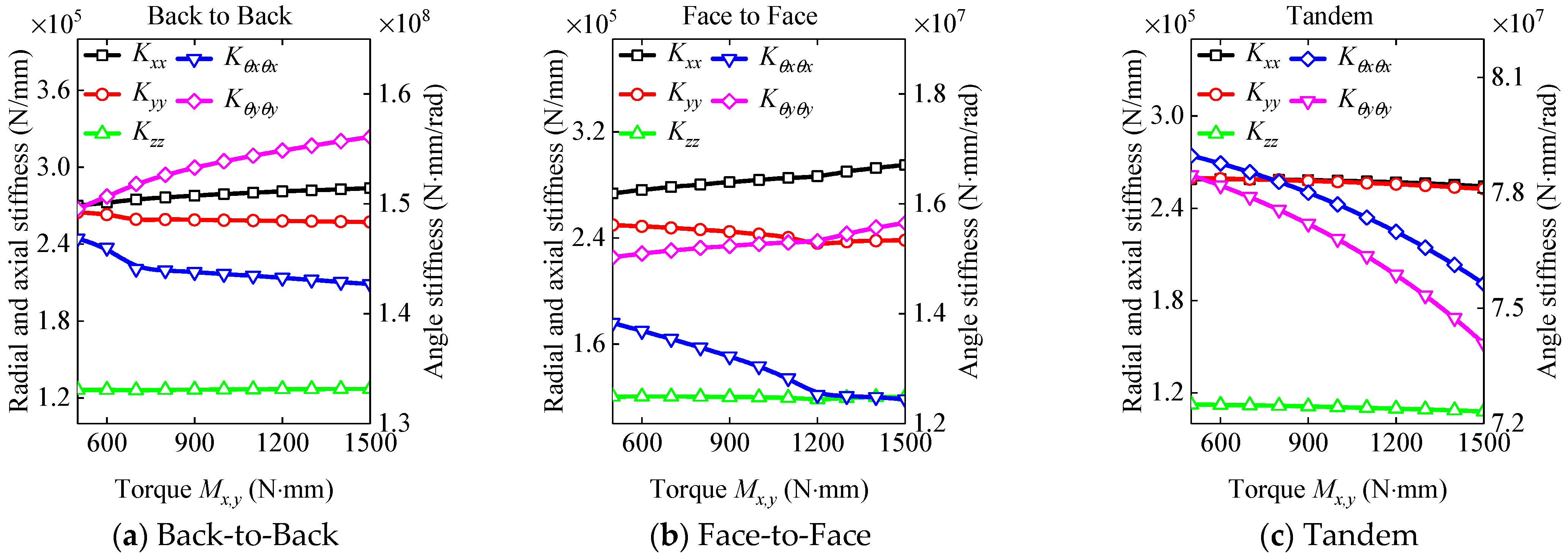
3.2. The Dynamic Characteristic Analysis of the DRACBB
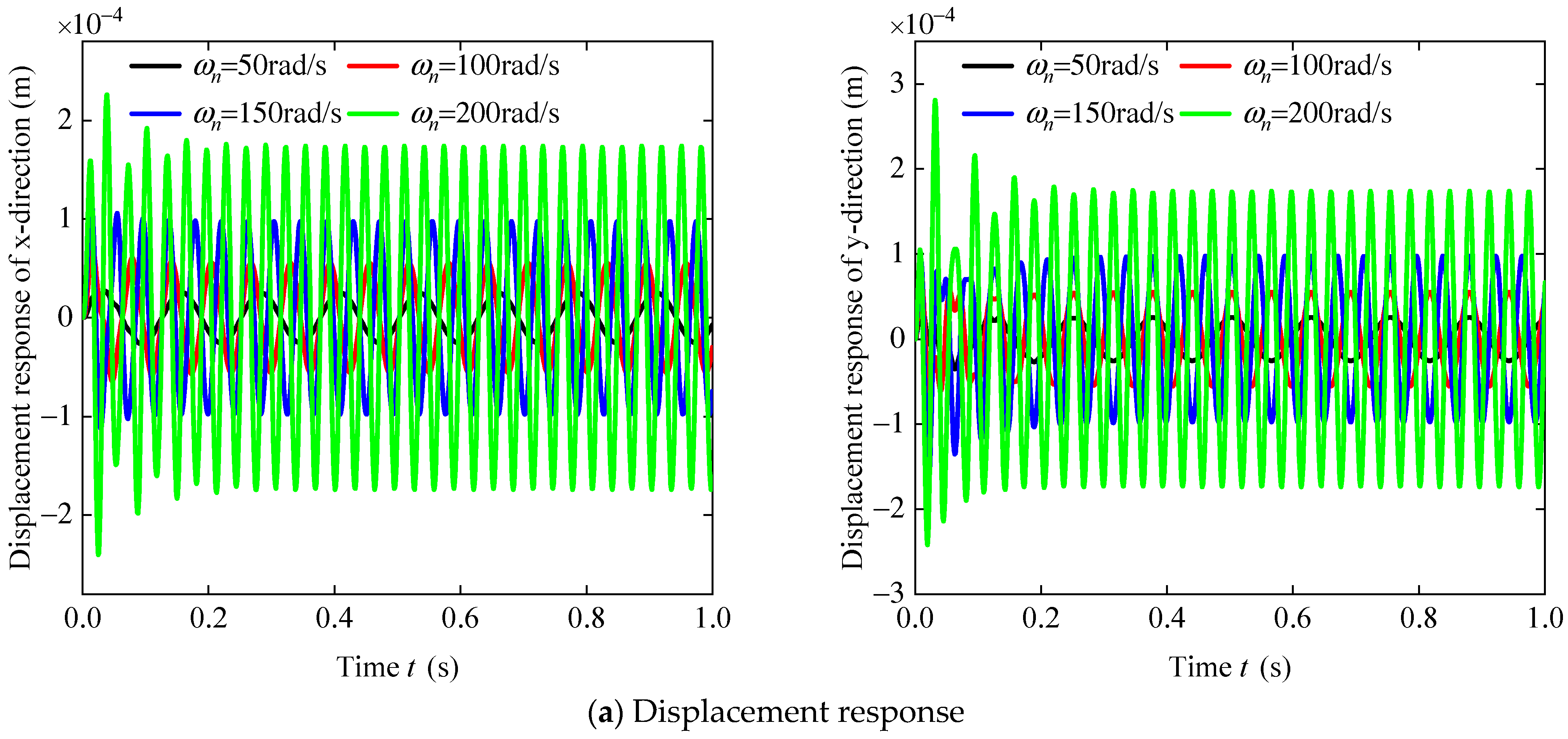
3.3. The Dynamic Response of the Bearing–Rotor–Disk System
4. Conclusions
- (1)
- Back-to-Back DRACBBs under complex external loads have greater dynamic performance when compared with the other structural forms of DRACBBs.
- (2)
- The dynamic response of the y-direction of the bearing–rotor–disk system is more significant than the dynamic response of the x-direction when the rotating speed of the bearing–rotor–disk system is increased.
- (3)
- There are two resonant peaks, which are caused by the rotor–disk system and the DRACBBs, respectively, and their variation tendencies are different. The above research can offer a theoretical basis for the design and manufacture of power systems in aero-engines.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description |
| αo | The free contact angle |
| N | The number of single rolling elements |
| ψj | The azimuth |
| D | The diameter of the ball |
| Dm | The pitch diameter of double-row angular contact ball bearings |
| ci, co | The clearances between the ball and the inner and outer raceways |
| c1 | The judgement coefficient of left and right rows of angular contact ball bearings |
| c2 | The judgement coefficient of the structural form |
| fi, fo | The inner and outer raceway curvature coefficients |
| ri, ro | The inner and outer raceway curvature radii |
| B | The width of double-row angular contact ball bearings |
| Ki, Ko | The contact stiffness coefficients of the inner and outer raceway |
| ωn | The angular velocity of the rotor |
Appendix A
Appendix B
References
- Parmar, V.; Saran, V.H.; Harsha, S. Effect of an unbalanced rotor on dynamic characteristics of double-row self-aligning ball bearing. Eur. J. Mech.-A/Solids 2020, 82, 104006. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Z.; Liu, J.; Ma, H.; Yang, D. Dynamic modeling and stability analysis of a rotor-bearing system with bolted-disk joint. Mech. Syst. Signal Process. 2021, 158, 107778. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Ghayour, M.; Khanlo, H.M. Nonlinear dynamic analysis and experimental verification of a magnetically supported flexible rotor system with auxiliary bearings. Mech. Mach. Theory 2018, 121, 545–562. [Google Scholar] [CrossRef]
- Singh, S.; Tiwari, R. Model based identification of crack and bearing dynamic parameters in flexible rotor systems supported with an auxiliary active magnetic bearing. Mech. Mach. Theory 2018, 122, 292–307. [Google Scholar] [CrossRef]
- Saeed, N.A.; Kandil, A. Lateral vibration control and stabilization of the quasiperiodic oscillations for rotor-active magnetic bearings system. Nonlinear Dyn. 2019, 98, 1191–1218. [Google Scholar] [CrossRef]
- Ma, H.; Li, H.; Zhao, X.; Niu, H.; Wen, B. Effects of eccentric phase difference between two discs on oil-film instability in a rotor–bearing system. Mech. Syst. Signal Process. 2013, 41, 526–545. [Google Scholar] [CrossRef]
- She, H.; Li, C.; Tang, Q.; Wen, B. The investigation of the coupled vibration in a flexible-disk blades system considering the influence of shaft bending vibration. Mech. Syst. Signal Process. 2018, 111, 545–569. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Chen, D.Z. The coupled vibration in a rotating multi-disk rotor system. Int. J. Mech. Sci. 2011, 53, 1–10. [Google Scholar] [CrossRef]
- Yang, C.H.; Huang, S.C. The influence of disk’s flexibility on coupling vibration of shaft–disk–blades systems. J. Sound Vib. 2007, 301, 1–17. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Yang, C.H. The coupled vibration in a rotating multi-disk rotor system with grouped blades. J. Mech. Sci. Technol. 2014, 28, 1653–1662. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Huang, S.C. The influence on coupling vibration of a rotor system due to a mistuned blade length. Int. J. Mech. Sci. 2007, 49, 522–532. [Google Scholar] [CrossRef]
- Ding, Q.; Leung, A.Y.T. Numerical and experimental investigations on flexible multi-bearing rotor dynamics. J. Vib. Acoust. 2005, 127, 408–415. [Google Scholar] [CrossRef]
- Li, C.; She, H.; Tang, Q.; Wen, B. The effect of blade vibration on the nonlinear characteristics of rotor–bearing system supported by nonlinear suspension. Nonlinear Dyn. 2017, 89, 987–1010. [Google Scholar] [CrossRef]
- Ma, H.; Lu, Y.; Wu, Z.; Tai, X.; Wen, B. Vibration response analysis of a rotational shaft–disk–blade system with blade-tip rubbing. Int. J. Mech. Sci. 2016, 107, 110–125. [Google Scholar] [CrossRef]
- Ma, H.; Li, H.; Niu, H.; Song, R.; Wen, B. Numerical and experimental analysis of the first-and second-mode instability in a rotor-bearing system. Arch. Appl. Mech. 2013, 84, 519–541. [Google Scholar] [CrossRef]
- Wang, L.; Cao, D.Q.; Huang, W. Nonlinear coupled dynamics of flexible blade–rotor–bearing systems. Tribol. Int. 2010, 43, 759–778. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, L.; Wang, X.; Ma, Y.; Chen, H. Dynamic modeling and bifurcation analysis of blade-disk rotor system supported by rolling bearing. Appl. Math. Model. 2022, 106, 524–548. [Google Scholar] [CrossRef]
- Zhou, S.T.; Chiu, Y.J.; Yu, G.F.; Yang, C.-H.; Huang, H.-W.; Jian, S.-R. An assumed mode method and finite element method investigation of the coupled vibration in a flexible-disk rotor system with lacing wires. J. Mech. Sci. Technol. 2017, 31, 577–586. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhu, R.; Han, Q.; Qin, Z.; Chu, F. Modeling approach for flexible shaft-disk-drum rotor systems with elastic connections and supports. Appl. Math. Model. 2022, 106, 402–425. [Google Scholar] [CrossRef]
- Tuzzi, G.; Schwingshackl, C.; Green, J. Cross-disc coupling in a flexible shaft–disc assembly in presence of asymmetric axial–radial bearing supports. J. Sound Vib. 2022, 527, 116826. [Google Scholar] [CrossRef]
- Mereles, A.; Cavalca, K.L. Modeling of multi-stepped rotor-bearing systems by the continuous segment method. Appl. Math. Model. 2021, 96, 402–430. [Google Scholar] [CrossRef]
- Mereles, A.; Cavalca, K.L. Mathematical modeling of continuous multi-stepped rotor-bearing systems. Appl. Math. Model. 2021, 90, 327–350. [Google Scholar] [CrossRef]
- Khorrami, H.; Rakheja, S.; Sedaghati, R. Vibration behavior of a two-crack shaft in a rotor disc-bearing system. Mech. Mach. Theory 2017, 113, 67–84. [Google Scholar] [CrossRef]
- Al-Solihat, M.K.; Behdinan, K. Force transmissibility and frequency response of a flexible shaft–disk rotor supported by a nonlinear suspension system. Int. J. Non-linear Mech. 2020, 124, 103501. [Google Scholar] [CrossRef]
- Xiang, L.; Hu, A.; Hou, L.; Xiong, Y.; Xing, J. Nonlinear coupled dynamics of an asymmetric double-disc rotor-bearing system under rub-impact and oil-film forces. Appl. Math. Model. 2016, 40, 4505–4523. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Q.; Qin, B.; Shao, W. Vibration characteristic analysis of flexible rotor-bearing system subjected to external combined loads. Eur. J. Mech.-A/Solids 2022, 96, 104688. [Google Scholar] [CrossRef]
- Wang, P.; Yang, Y.; Ma, H.; Xu, H.; Li, X.; Luo, Z.; Wen, B. Vibration characteristics of rotor-bearing system with angular misalignment and cage fracture: Simulation and experiment. Mech. Syst. Signal Process. 2022, 182, 109545. [Google Scholar] [CrossRef]
- Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Process. 2018, 102, 37–58. [Google Scholar] [CrossRef]
- Petersen, D.; Howard, C.; Sawalhi, N.; Ahmadi, A.M.; Singh, S. Analysis of bearing stiffness variations, contact forces and vibrations in radially loaded double row rolling element bearings with raceway defects. Mech. Syst. Signal Process. 2015, 50, 139–160. [Google Scholar] [CrossRef]
- Gunduz, A.; Singh, R. Stiffness matrix formulation for double row angular contact ball bearings: Analytical development and validation. J. Sound Vib. 2013, 332, 5898–5916. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, B.; Hong, J.; Wan, S.; Zhu, Y. A general model for preload calculation and stiffness analysis for combined angular contact ball bearings. J. Sound Vib. 2017, 411, 435–449. [Google Scholar] [CrossRef]
- Yang, L.; Xu, T.; Xu, H.; Wu, Y. Mechanical behavior of double-row tapered roller bearing under combined external loads and angular misalignment. Int. J. Mech. Sci. 2018, 142, 561–574. [Google Scholar] [CrossRef]
- Ai, S.; Wang, W.; Wang, Y.; Zhao, Z. Temperature rise of double-row tapered roller bearings analyzed with the thermal network method. Tribol. Int. 2015, 87, 11–22. [Google Scholar] [CrossRef]
- Gunduz, A.; Dreyer, J.T.; Singh, R. Effect of bearing preloads on the modal characteristics of a shaft-bearing assembly: Experiments on double row angular contact ball bearings. Mech. Syst. Signal Process. 2012, 31, 176–195. [Google Scholar] [CrossRef]
- Xu, T.; Yang, L.; Wu, W.; Han, Y.; Xu, E.; Wang, K. The stiffness characteristics analysis of the duplex angular contact ball bearings based on a comprehensive multi-degree-of-freedom mathematical model. Appl. Math. Model. 2022, 106, 601–626. [Google Scholar] [CrossRef]
- Xu, T.; Yang, L.; Wu, W.; Wang, K. Effect of angular misalignment of inner ring on the contact characteristics and stiffness coefficients of duplex angular contact ball bearings. Mech. Mach. Theory 2020, 157, 104178. [Google Scholar] [CrossRef]









| Structural Parameter | Parameter Unit | Value |
|---|---|---|
| D | mm | 9 |
| N (single row) | - | 18 |
| αo | ° | 25 |
| E | MPa | 2.06 × 105 |
| ν | - | 0.3 |
| ρ | kg/m3 | 7850 |
| ri | mm | 4.635 |
| ro | mm | 4.725 |
| ci | mm | 0 |
| co | mm | 0 |
| B | mm | 32 |
| Dm | mm | 65 |
| Order | F-F | S-S | C-C | |||
|---|---|---|---|---|---|---|
| Present | ANSYS | Present | ANSYS | Present | ANSYS | |
| 1 | 119.0 | 118.9 | 25.7 | 25.7 | 48.3 | 48.2 |
| 2 | 188.9 | 188.8 | 95.2 | 95.1 | 121.7 | 121.6 |
| 3 | 373.4 | 372.5 | 312.7 | 311.9 | 148.2 | 148.0 |
| 4 | 746.4 | 745.4 | 585.3 | 584.7 | 374.2 | 373.0 |
| 5 | 925.8 | 925.9 | 665.1 | 665.0 | 665.1 | 665.0 |
| 6 | 1220.2 | 1215.5 | 724.6 | 723.6 | 752.0 | 749.9 |
| 7 | 1371.8 | 1358.0 | 1098.2 | 1092.3 | 927.6 | 925.8 |
| 8 | 1475.5 | 1447.6 | 1371.8 | 1358.0 | 1216.4 | 1210.2 |
| 9 | 1744.9 | 1732.2 | 1475.5 | 1447.6 | 1610.6 | 1609.0 |
| 10 | 1829.5 | 1828.6 | 1592.1 | 1582.7 | 1737.1 | 1722.6 |
| Order | Natural Frequency | 50 rad/s | 100 rad/s | 150 rad/s | 200 rad/s | ||||
|---|---|---|---|---|---|---|---|---|---|
| Present | ANSYS | Present | ANSYS | Present | ANSYS | Present | ANSYS | ||
| 1 | Backward | 48.254 | 48.206 | 48.253 | 48.204 | 48.252 | 48.203 | 48.251 | 48.201 |
| Forward | 48.255 | 48.209 | 48.256 | 48.21 | 48.256 | 48.212 | 48.257 | 48.213 | |
| 2 | Backward | 121.725 | 121.64 | 121.725 | 121.64 | 121.725 | 121.64 | 121.725 | 121.64 |
| Forward | 121.725 | 121.64 | 121.725 | 121.64 | 121.725 | 121.64 | 121.725 | 121.64 | |
| 3 | Backward | 148.104 | 147.78 | 147.961 | 147.57 | 147.817 | 147.36 | 147.673 | 147.14 |
| Forward | 148.391 | 148.2 | 148.534 | 148.42 | 148.677 | 148.63 | 148.820 | 148.84 | |
| 4 | Backward | 374.095 | 372.9 | 374.031 | 372.8 | 373.968 | 372.69 | 373.904 | 372.59 |
| Forward | 374.222 | 373.11 | 374.286 | 373.21 | 374.349 | 373.32 | 374.413 | 373.42 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, Z.; Liu, H.; Liu, T.; Wang, Q. Modeling and Dynamic Analysis of Double-Row Angular Contact Ball Bearing–Rotor–Disk System. Lubricants 2024, 12, 441. https://doi.org/10.3390/lubricants12120441
Zhang H, Li Z, Liu H, Liu T, Wang Q. Modeling and Dynamic Analysis of Double-Row Angular Contact Ball Bearing–Rotor–Disk System. Lubricants. 2024; 12(12):441. https://doi.org/10.3390/lubricants12120441
Chicago/Turabian StyleZhang, Haibiao, Zhen Li, Haijian Liu, Tao Liu, and Qingshan Wang. 2024. "Modeling and Dynamic Analysis of Double-Row Angular Contact Ball Bearing–Rotor–Disk System" Lubricants 12, no. 12: 441. https://doi.org/10.3390/lubricants12120441
APA StyleZhang, H., Li, Z., Liu, H., Liu, T., & Wang, Q. (2024). Modeling and Dynamic Analysis of Double-Row Angular Contact Ball Bearing–Rotor–Disk System. Lubricants, 12(12), 441. https://doi.org/10.3390/lubricants12120441







