Machine Learning-Based Predictions of Metal and Non-Metal Elements in Engine Oil Using Electrical Properties
Abstract
1. Introduction
2. Materials and Methods
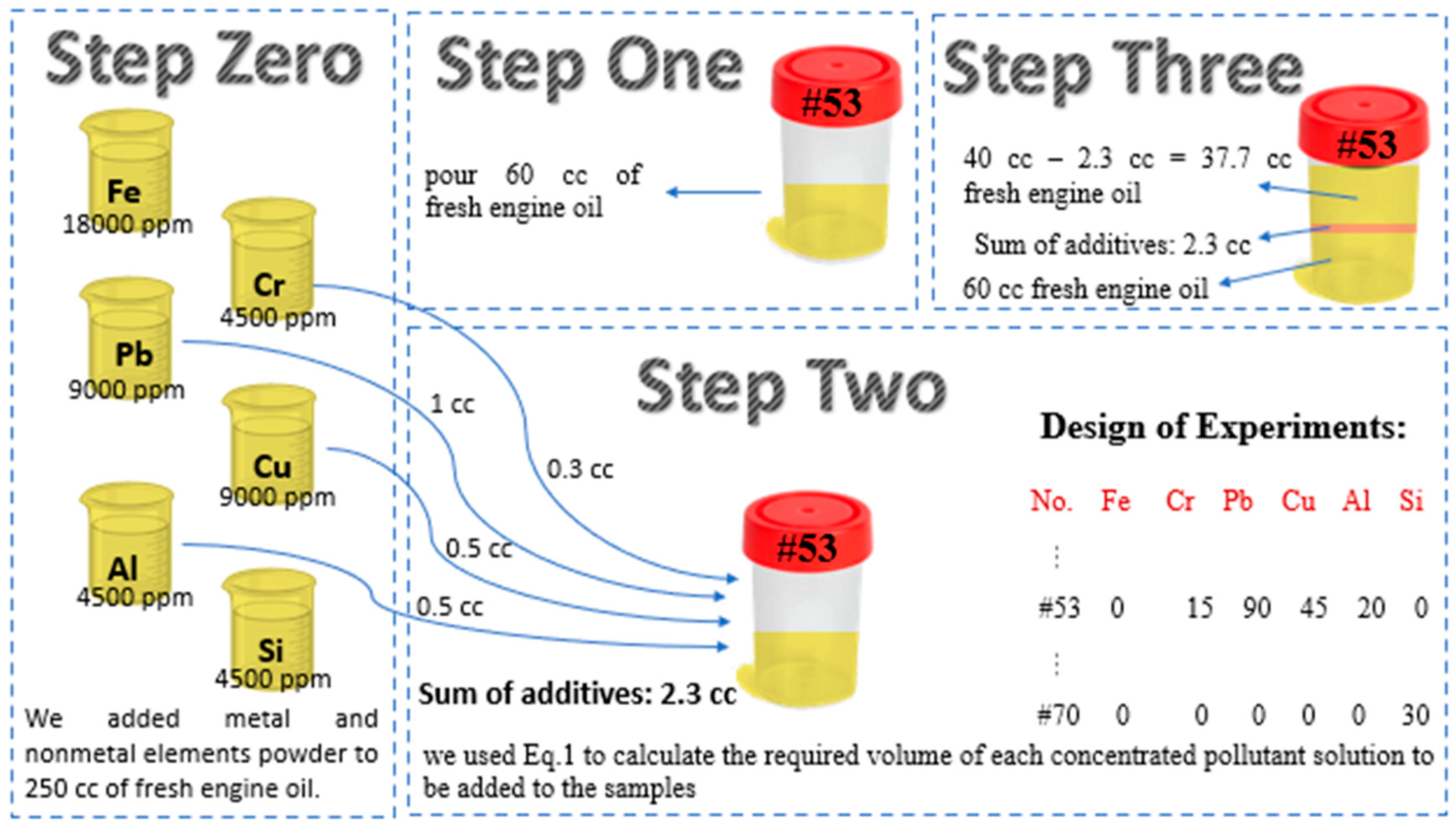
2.1. Sample Preparation
- Viscosity at 100 °C was equal to 19.5 cSt based on ASTM D445 test [55].
- Flash point was equal to 228 °C according to ASTM D92 test [56].
- Pour point was equal to −27 °C based on ASTM D97 test [57].
- Density was equal to 884 kg/m3 according to ASTM D4052 test [58].
- Total alkalinity was equal to 7.5 mg KOH/g based on ASTM D2896 test [59].
- High Fe concentration (approximately 18,000 ppm): We added 4 g of Fe powder to 250 cc of fresh engine oil.
- High Cr concentration (approximately 4500 ppm): We added 1 g of Cr powder to 250 cc of fresh engine oil.
- High Pb concentration (approximately 9000 ppm): We added 2 g of Pb powder to 250 cc of fresh engine oil.
- High Cu concentration (approximately 9000 ppm): We added 2 g of Cu powder to 250 cc of fresh engine oil.
- High Al concentration (approximately 4500 ppm): We added 1 g of Al powder to 250 cc of fresh engine oil.
- High Si concentration (approximately 4500 ppm): We added 1 g of Si powder to 250 cc of fresh engine oil.
2.2. Electrical Measurement
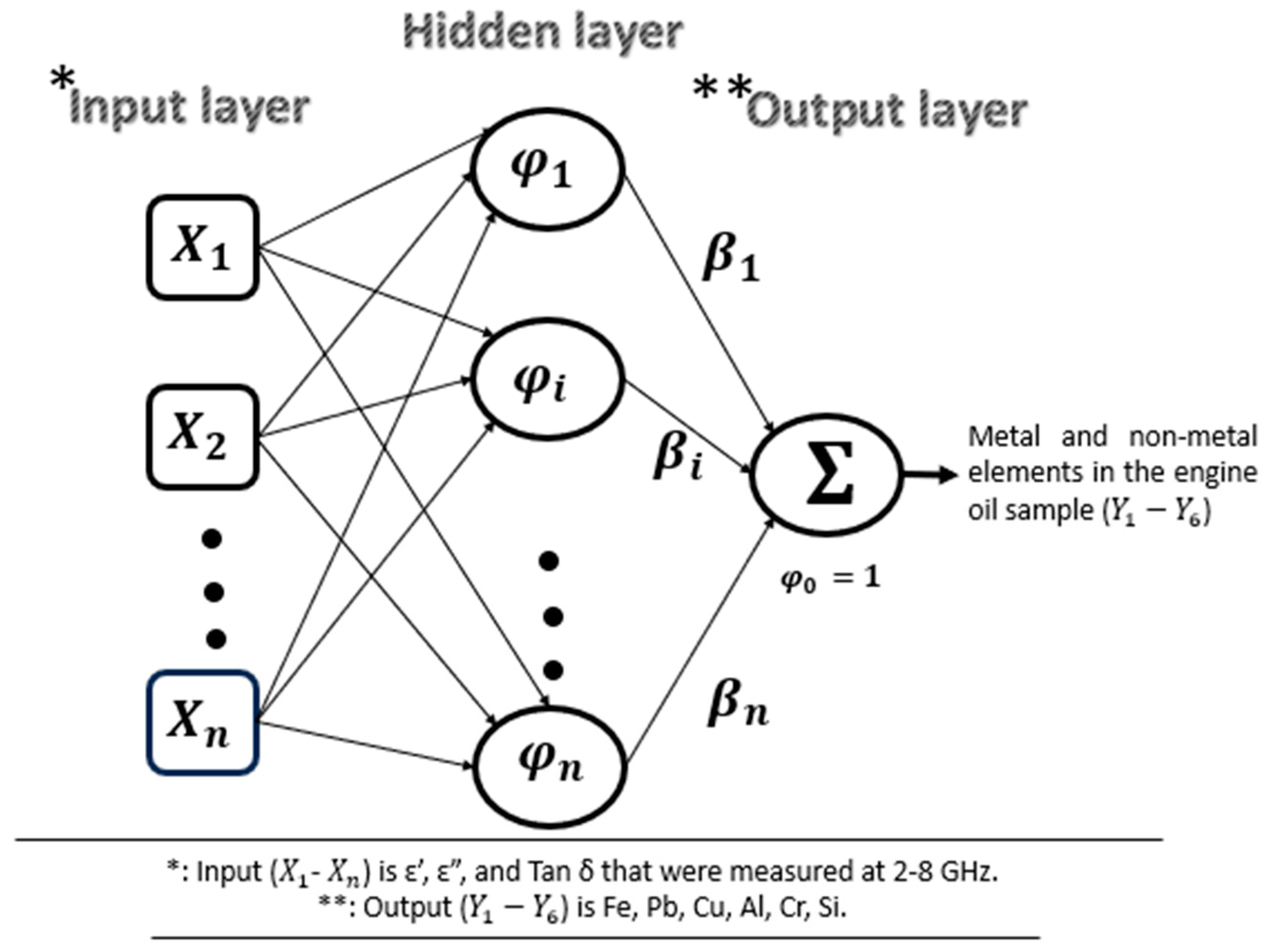
2.3. Soft Computing Modeling
3. Results and Discussion
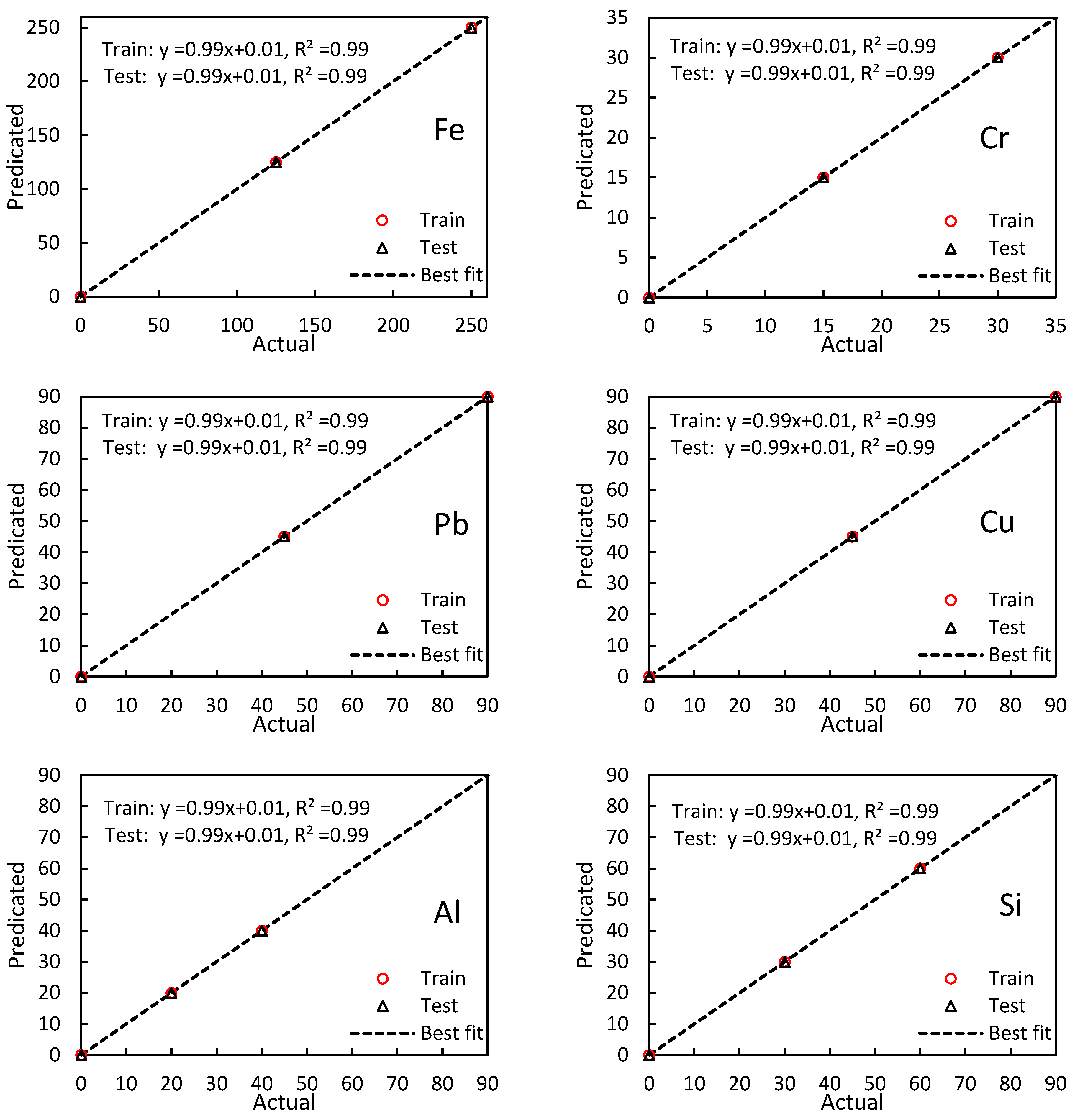
3.1. Performance Comparison of Models
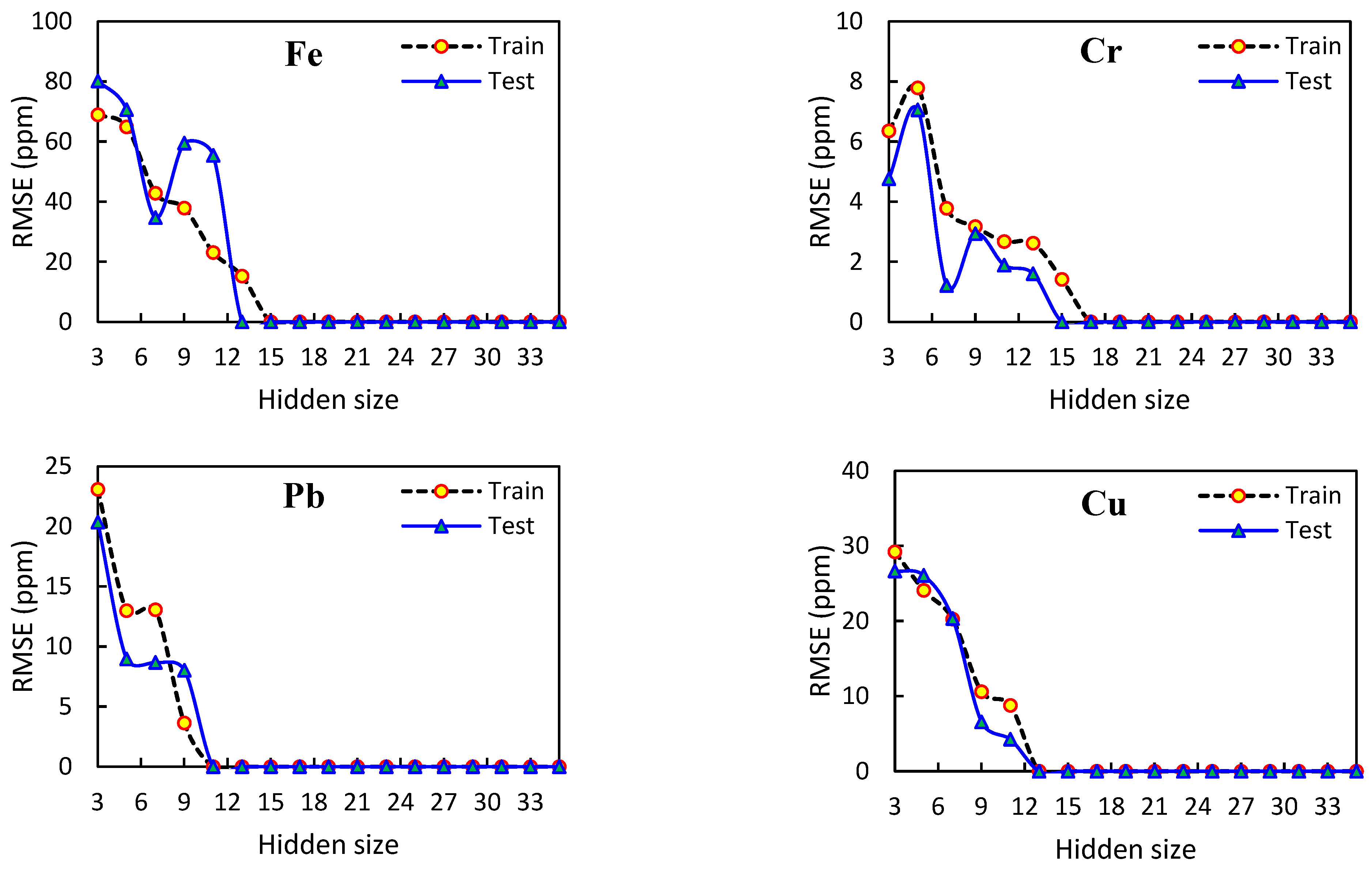
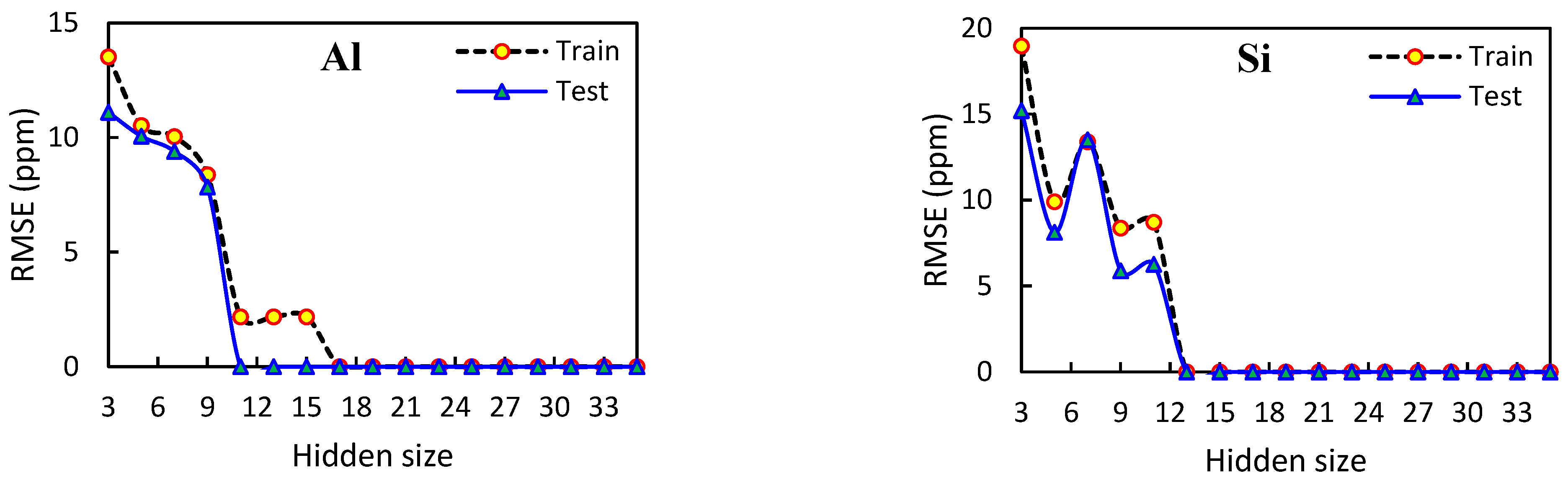
3.2. Optimizing Superior Model Parameters: Findings and Recommendations
3.3. Model Generalization Capability
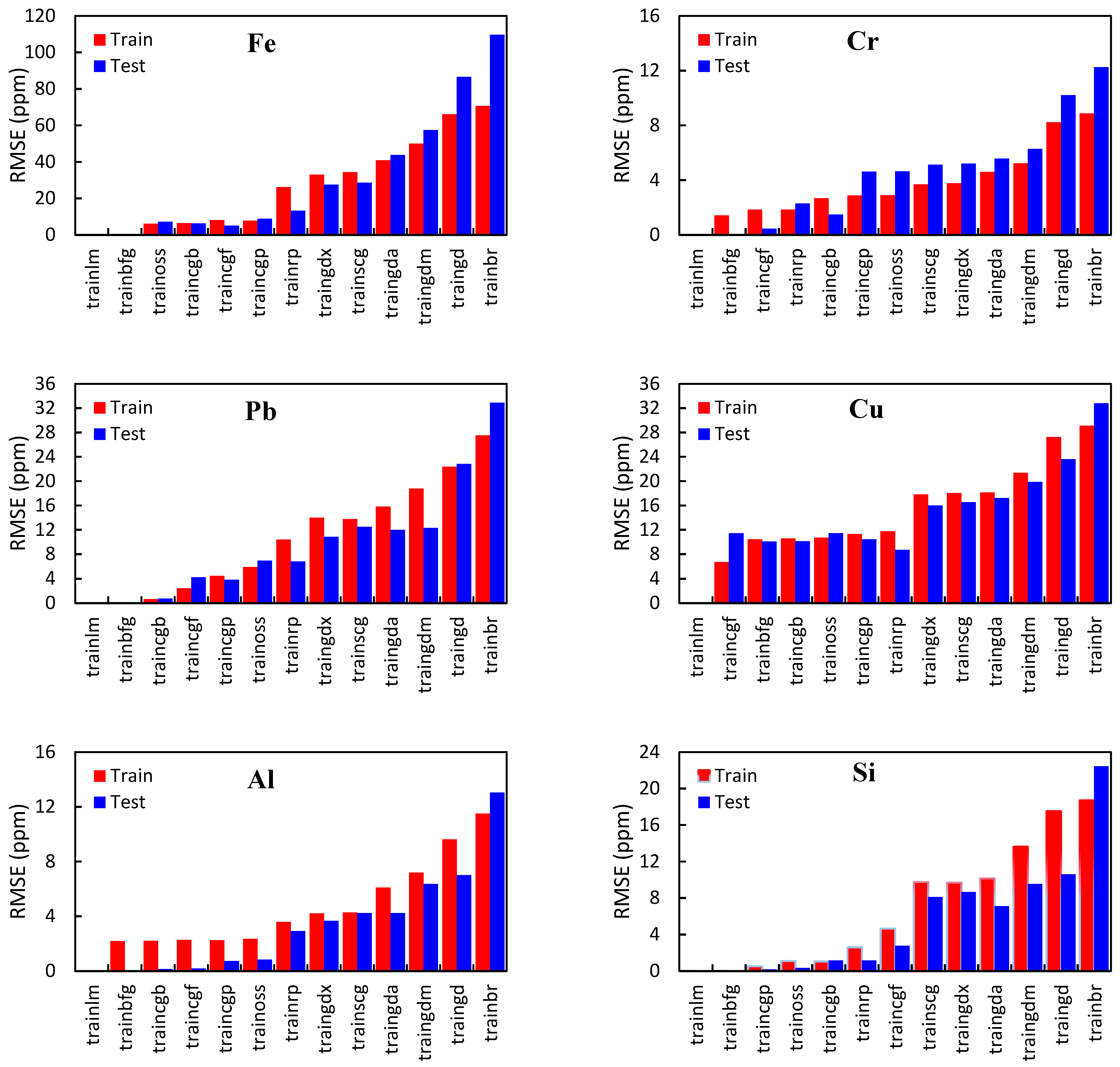
3.4. Comparison with Background
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Xin, Q. Diesel Engine System Design; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Ernst, R.J.; Pefley, R.K.; Wiens, F.J. Methanol Engine Durability; 0148-7191; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1983. [Google Scholar]
- Cyrus, J.D. Engine component life prediction methodology for conceptual design investigations. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 1986. [Google Scholar]
- Nieto, P.G.; García-Gonzalo, E.; Lasheras, F.S.; de Cos Juez, F.J. Hybrid PSO–SVM-based method for forecasting of the remaining useful life for aircraft engines and evaluation of its reliability. Reliab. Eng. Syst. Saf. 2015, 138, 219–231. [Google Scholar] [CrossRef]
- Piancastelli, L.; Frizziero, L.; Marcoppido, S.; Pezzuti, E. Methodology to evaluate aircraft piston engine durability. Int. J. Heat Technol. 2012, 30, 89–92. [Google Scholar]
- Deng, K.; Zhang, X.; Cheng, Y.; Zheng, Z.; Jiang, F.; Liu, W.; Peng, J. A remaining useful life prediction method with long-short term feature processing for aircraft engines. Appl. Soft Comput. 2020, 93, 106344. [Google Scholar] [CrossRef]
- Zaman, M.; Siswantoro, N.; Priyanta, D.; Pitana, T.; Prastowo, H.; Busse, W. The combination of reliability and predictive tools to determine ship engine performance based on condition monitoring. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Surakarta, Indonesia, 24–25 August 2021; p. 012015. [Google Scholar]
- Cao, D.; Bai, G. A study osn aeroengine conceptual design considering multi-mission performance reliability. Appl. Sci. 2020, 10, 4668. [Google Scholar] [CrossRef]
- Loiselle, R.; Xu, Z.; Voloh, I. Essential motor health monitoring: Making informed decisions about motor maintenance before a failure occurs. IEEE Ind. Appl. Mag. 2018, 24, 8–13. [Google Scholar] [CrossRef]
- Glavaš, H.; Kljajin, M.; Desnica, E. Essential Preventive Automobile Maintenance during a Pandemic. Teh. Vjesn. 2021, 28, 2190–2199. [Google Scholar]
- Hutchings, I.; Shipway, P. Tribology: Friction and Wear of Engineering Materials; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Lin, H.-H.; Heinze, J.; Croy, A.; Gutiérrez, R.; Cuniberti, G. Effect of lubricants on the rotational transmission between solid-state gears. Beilstein J. Nanotechnol. 2022, 13, 54–62. [Google Scholar] [CrossRef]
- Rahim, K.A.; Al-Humairi, S.N.S. Influence of Lubrication Technology on Internal Combustion Engine Performance: An Overview. In Proceedings of the 2020 IEEE 8th Conference on Systems, Process and Control (ICSPC), Melaka, Malaysia, 11–12 December 2020; pp. 184–189. [Google Scholar]
- Grassart, P. Monitoring of the Lubrication System of an Aircraft Engine through a Prognostic and Health Monitoring Approach. Master’s Thesis, KTH School of Industrial Engineering and Management, Stockholm, Sweden, 2015. [Google Scholar]
- Domínguez-García, S.; Béjar-Gómez, L.; López-Velázquez, A.; Maya-Yescas, R.; Nápoles-Rivera, F. Maximizing Lubricant Life for Internal Combustion Engines. Processes 2022, 10, 2070. [Google Scholar] [CrossRef]
- Bulgakov, N.; Kovalenko, V.; Gorbaneva, A.; Shalimov, S. Management of preventive maintenance of vehicles. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kazimierz Dolny, Poland, 21–23 November 2019; p. 012074. [Google Scholar]
- Figueredo, G.P.; Owa, K.; John, R. Multi-objective optimization for time-based preventive maintenance within the transport network: A review. Acad. Libr. Comput. 2020. [Google Scholar] [CrossRef]
- Ventikos, N.P.; Sotiralis, P.; Annetis, E. A combined risk-based and condition monitoring approach: Developing a dynamic model for the case of marine engine lubrication. Transp. Saf. Environ. 2022, 4, tdac020. [Google Scholar] [CrossRef]
- Vališ, D.; Žák, L.; Pokora, O. Failure prediction of diesel engine based on occurrence of selected wear particles in oil. Eng. Fail. Anal. 2015, 56, 501–511. [Google Scholar] [CrossRef]
- Kučera, M.; Kopčanová, S.; Sejkorová, M. Lubricant analysis as the most useful tool in the proactive maintenance philosophies of machinery and its components. Manag. Syst. Prod. Eng. 2020, 28, 196–201. [Google Scholar] [CrossRef]
- Ganiboyeva, E.; Khakimov, B.; Shermuxamedov, X.; Rakhimov, Y. Theoretical study of the accumulation of mechanical mixtures in the engine lubrication system. IOP Conf. Ser. Earth Environ. Sci. 2022, 1076, 012085. [Google Scholar] [CrossRef]
- Heredia-Cancino, J.; Ramezani, M.; Álvarez-Ramos, M. Effect of degradation on tribological performance of engine lubricants at elevated temperatures. Tribol. Int. 2018, 124, 230–237. [Google Scholar] [CrossRef]
- Srinivasan, U.; Muthuveerappan, N.; Sudhindra, K. Development of Data Prediction Model for the Lubrication System in a Developmental Gas Turbine Engine. J. Aerosp. Sci. Technol. 2020, 1–8. [Google Scholar] [CrossRef]
- Rahman, M.H.; Shahriar, S.; Menezes, P.L. Recent Progress of Machine Learning Algorithms for the Oil and Lubricant Industry. Lubricants 2023, 11, 289. [Google Scholar] [CrossRef]
- Zhu, J.; Yoon, J.M.; He, D.; Qu, Y.; Bechhoefer, E. Lubrication oil condition monitoring and remaining useful life prediction with particle filtering. Int. J. Progn. Health Manag. 2013, 4, 124–138. [Google Scholar] [CrossRef]
- He, M.; He, D.; Yoon, J.; Nostrand, T.J.; Zhu, J.; Bechhoefer, E. Wind turbine planetary gearbox feature extraction and fault diagnosis using a deep-learning-based approach. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2019, 233, 303–316. [Google Scholar] [CrossRef]
- Kornaeva, E.; Kornaev, A.; Kazakov, Y.N.; Polyakov, R. Application of artificial neural networks to diagnostics of fluid-film bearing lubrication. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Chennai, India, 16–17 September 2020; p. 012154. [Google Scholar]
- Afzal, A.B.; Jain, U.; Khan, N.A. Condition Monitoring of Dielectrics. In Proceedings of the 2018 3rd International Innovative Applications of Computational Intelligence on Power, Energy and Controls with their Impact on Humanity (CIPECH), Ghaziabad, India, 1–2 November 2018; pp. 221–226. [Google Scholar]
- Gogoi, N.; Chen, J.; Kirchner, J.; Fischer, G. Dependence of piezoelectric discs electrical impedance on mechanical loading condition. Sensors 2022, 22, 1710. [Google Scholar] [CrossRef]
- Palomino, L.V.; Steffen Jr, V.; de Moura, J.d.R.V.; Tsuruta, K.M.; Rade, D.A. Impedance-based health monitoring and mechanical testing of structures. Smart Struct. Syst. Int. J. 2011, 7, 15–25. [Google Scholar] [CrossRef]
- Fiorenza, P.; Greco, G.; Di Franco, S.; Giannazzo, F.; Monnoye, S.; Zielinski, M.; La Via, F.; Roccaforte, F. Electrical properties of thermal oxide on 3C-SiC layers grown on silicon. In Materials Science Forum; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2019; pp. 479–482. [Google Scholar]
- Torreblanca González, J.; García Ovejero, R.; Lozano Murciego, Á.; Villarrubia González, G.; De Paz, J.F. Effects of environmental conditions and composition on the electrical properties of textile fabrics. Sensors 2019, 19, 5145. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ding, Q.; Wang, H.; Wu, Z.; Gui, X.; Li, C.; Hu, N.; Tao, K.; Wu, J. Engineering Smart Composite Hydrogels for Wearable Disease Monitoring. Nano-Micro Lett. 2023, 15, 105. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, M.; Harvánek, L. Online Monitoring and Lifetime Estimations of Materials for Electrical Insulation. In Proceedings of the 2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Sydney, Australia, 19–22 July 2015; pp. 568–571. [Google Scholar]
- Kumar, S.; Mukherjee, P.; Mishra, N. Online condition monitoring of engine oil. Ind. Lubr. Tribol. 2005, 57, 260–267. [Google Scholar] [CrossRef]
- Chun, S.M. Analysis of Test Results for Small Dipstick-Gage-Type Engine-Oil-Deterioration-Detection Sensor. Tribol. Lubr. 2014, 30, 156–167. [Google Scholar]
- Turner, J.; Austin, L. Electrical techniques for monitoring the condition of lubrication oil. Meas. Sci. Technol. 2003, 14, 1794. [Google Scholar] [CrossRef]
- Vasanthan, B.; Devaradjane, G.; Shanmugam, V. Online condition monitoring of lubricating oil on test bench diesel engine & vehicle. J. Chem. Pharm. Sci. 2015, 9, 315–320. [Google Scholar]
- Mauntz, M.; Kuipers, U.; Gegner, J. New Electric Online Oil Condition Monitoring Sensor—An Innovation in Early Failure Detection of Industrial Gears. In Proceedings of the The 4th International Multi-Conference on Engineering and Technological Innovation, Orlando, FL, USA, 19–22 July 2011; pp. 238–242. [Google Scholar]
- Abellán-Martín, S.J.; Aguirre, M.Á.; Canals, A. Applicability of microwave induced plasma optical emission spectrometry for wear metal determination in lubricant oil using a multinebulizer. J. Anal. At. Spectrom. J. Anal. At. Spectrom. 2023, 38, 1379–1386. [Google Scholar] [CrossRef]
- Fernández-Feal, M.; Sánchez-Fernández, L.; Pérez-Prado, J. Study of Metal Concentration in Lubricating Oil with Predictive Purposes. Curr. J. Appl. Sci. Technol. 2018, 27, 1–12. [Google Scholar] [CrossRef]
- Han, W.; Mu, X.; Liu, Y.; Wang, X.; Li, W.; Bai, C.; Zhang, H. A Critical Review of On-Line Oil Wear Debris Particle Detection Sensors. J. Mar. Sci. Eng. 2023, 11, 2363. [Google Scholar] [CrossRef]
- Guan, L.; Feng, X.; Xiong, G.; Xie, J. Application of dielectric spectroscopy for engine lubricating oil degradation monitoring. Sens. Actuators A Phys. 2011, 168, 22–29. [Google Scholar] [CrossRef]
- Guan, L.; Feng, X.; Xiong, G. Engine lubricating oil classification by SAE grade and source based on dielectric spectroscopy data. Anal. Chim. Acta 2008, 628, 117–120. [Google Scholar] [CrossRef]
- Xiao, J.; Wu, Y.; Zhang, W.; Chen, J.; Zhang, C. Friction of metal-matrix self-lubricating composites: Relationships among lubricant content, lubricating film coverage, and friction coefficient. Friction 2020, 8, 517–530. [Google Scholar] [CrossRef]
- Ulrich, C.; Petersson, H.; Sundgren, H.; Björefors, F.; Krantz-Rülcker, C. Simultaneous estimation of soot and diesel contamination in engine oil using electrochemical impedance spectroscopy. Sens. Actuators B Chem. 2007, 127, 613–618. [Google Scholar] [CrossRef]
- Qiang, L.; Xiaowei, L.; Lili, C.; Jiang, W. Research on a Method for the Determination of Iron in Lubricating Oil. In Proceedings of the 1st International Conference on Mechanical Engineering and Material Science (MEMS 2012), Shanghai, China, 28–30 December 2012; Atlantis Press: Zhengzhou, China, 2012; pp. 180–182. [Google Scholar]
- Qiang, L.; Jiang, W.; Lili, C.; Xiaowei, L. A Study of Moisture Content of Lubricating Oil Based on Impedance Analysis. In Proceedings of the 1st International Conference on Mechanical Engineering and Material Science (MEMS 2012), Shanghai, China, 28–30 December 2012; Atlantis Press: Zhengzhou, China, 2012; pp. 183–186. [Google Scholar]
- Zhou, Y.; Hao, M.; Chen, G.; Wilson, G.; Jarman, P. Frequency-dependence of conductivity of new mineral oil studied by dielectric spectroscopy. In Proceedings of the 2012 International Conference on High Voltage Engineering and Application, Shanghai, China, 17–20 September 2012; pp. 634–637. [Google Scholar]
- Delgado, E.; Aperador, W.; Hernández, A. Impedance Spectroscopy as a Tool for the Diagnosis of the State of Vegetable Oils Used as Lubricants. Int. J. Electrochem. Sci. 2015, 10, 8190–8199. [Google Scholar] [CrossRef]
- Chowdhury, S.R.; Kumar, R.; Kaur, R.; Sharma, A.; Bhondekar, A.P. Quality assessment of engine oil: An impedance spectroscopy based approach. In Proceedings of the 2016 IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics Engineering (UPCON), Varanasi, India, 9–11 December 2016; pp. 608–612. [Google Scholar]
- Macioszek, Ł.; Włodarczak, S.; Rybski, R. Mineral oil moisture measurement with the use of impedance spectroscopy. IET Sci. Meas. Technol. 2019, 13, 1158–1162. [Google Scholar] [CrossRef]
- Altıntaş, O.; Aksoy, M.; Ünal, E.; Akgöl, O.; Karaaslan, M. Artificial neural network approach for locomotive maintenance by monitoring dielectric properties of engine lubricant. Measurement 2019, 145, 678–686. [Google Scholar] [CrossRef]
- Pourramezan, M.-R.; Rohani, A.; Abbaspour-Fard, M.H. Unlocking the Potential of Soft Computing for Predicting Lubricant Elemental Spectroscopy. Lubricants 2023, 11, 382. [Google Scholar] [CrossRef]
- Ruggiero, A.; D’Amato, R.; Merola, M.; Valášek, P.; Müller, M. On the tribological performance of vegetal lubricants: Experimental investigation on Jatropha Curcas L. oil. Procedia Eng. 2016, 149, 431–437. [Google Scholar] [CrossRef]
- Abdelkhalik, A.; Elsayed, H.; Hassan, M.; Nour, M.; Shehata, A.B.; Helmy, M. Using thermal analysis techniques for identifying the flash point temperatures of some lubricant and base oils. Egypt. J. Pet. 2018, 27, 131–136. [Google Scholar] [CrossRef]
- Oliveira, L.M.; Nunes, R.C.; Ribeiro, Y.L.; Coutinho, D.M.; Azevedo, D.A.; Dias, J.; Lucas, E.F. Wax behavior in crude oils by pour point analyses. J. Braz. Chem. Soc. 2018, 29, 2158–2168. [Google Scholar] [CrossRef]
- Abdurrojaq, N.; Devitasari, R.D.; Aisyah, L.; Faturrahman, N.A.; Bahtiar, S.; Sujarwati, W.; Wibowo, C.S.; Anggarani, R.; Maymuchar, M. Perbandingan Uji Densitas Menggunakan Metode ASTM D1298 dengan ASTM D4052 pada Biodiesel Berbasis Kelapa Sawit. Lembaran Publ. Miny. Gas Bumi 2021, 55, 49–57. [Google Scholar] [CrossRef]
- Dutta, M.; Pathiparampil, A.; Murella, J.; Villacarte, D.; Hamada, D.; Hernandez, J.; Lopez-Linares, F. Determination of base number in lubricants and additives by ASTM D2896: Substitution of chlorinated solvents and alternate electrolyte study. Fuel 2021, 297, 120701. [Google Scholar] [CrossRef]
- Li, L.; Chang, W.; Zhou, S.; Xiao, Y. An identification and prediction model of wear-out fault based on oil monitoring data using PSO-SVM method. In Proceedings of the 2017 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 23–26 January 2017; pp. 1–6. [Google Scholar]
- Zhou, P.; Liu, D. Research on marine diesel’s fault prognostic and health management based on oil monitoring. In Proceedings of the 2011 Prognostics and System Health Managment Conference, Shenzhen, China, 24–25 May 2011; pp. 1–4. [Google Scholar]
- Al-Nozili, M.S.; Abeed, F.A.; Ahmed, M.M. Studying the Changes of Some Heavy Metals Content in Lubricating Oil Caused by Using; Part I: Diagnostic Study. Int. J. Emerg. Technol. Adv. Eng. 2014, 4, 396. [Google Scholar]
- Wolak, A.; Zając, G.; Gołębiowski, W. Determination of the content of metals in used lubricating oils using AAS. Pet. Sci. Technol. 2019, 37, 93–102. [Google Scholar] [CrossRef]
- Pourramezan, M.-R.; Rohani, A.; Keramat Siavash, N.; Zarein, M. Evaluation of lubricant condition and engine health based on soft computing methods. Neural Comput. Appl. 2022, 35, 5465–5477. [Google Scholar] [CrossRef]
- Pourramezan, M.-R.; Rohani, A.; Abbaspour-Fard, M.H. Comparative Analysis of Soft Computing Models for Predicting Viscosity in Diesel Engine Lubricants: An Alternative Approach to Condition Monitoring. ACS Omega 2023, 9, 1398–1415. [Google Scholar] [CrossRef]
- Rawat, A.; Jhawat, V.; Dutt, R. DoE Enabled Development and In-Vitro Optimization of Curcumin-tagged Cilostazol Solid Nano Dispersion. Curr. Nanomed. Former. Recent Pat. Nanomed. 2023, 13, 113–131. [Google Scholar] [CrossRef]
- Palandurkar, K.; Bhandre, R.; Boddu, S.H.; Harde, M.; Lakade, S.; Kandekar, U.; Waghmare, P. Quality risk assessment and DoE–Practiced validated stability-indicating chromatographic method for quantification of Rivaroxaban in bulk and tablet dosage form. Acta Chromatogr. 2023, 35, 10–20. [Google Scholar] [CrossRef]
- Kamani, H.; Safari, G.H.; Asgari, G.; Ashrafi, S.D. Data on modeling of enzymatic elimination of direct red 81 using response surface methodology. Data Brief 2018, 18, 80–86. [Google Scholar] [CrossRef]
- Musa, M.A.; Chowdhury, S.; Biswas, S.; Alam, S.N.; Parvin, S.; Sattar, M.A. Removal of aqueous methylene blue dye over Vallisneria Natans biosorbent using artificial neural network and statistical response surface methodology analysis. J. Mol. Liq. 2024, 393, 123624. [Google Scholar] [CrossRef]
- Pourramezan, E.; Omidvar, M.; Motavalizadehkakhky, A.; Zhiani, R.; Darzi, H.H. Enhanced adsorptive removal of methylene blue using ternary nanometal oxides in an aqueous solution. Biomass Convers. Biorefinery 2024, 1–13. [Google Scholar] [CrossRef]
- An, D.; Guo, J.; Chang, X.; Wang, Z.; Jia, Y.; Liu, X.; Bondur, V.; Sun, H. High-precision 1′ × 1′ bathymetric model of Philippine Sea inversed from marine gravity anomalies. EGUsphere 2024, 17, 2039–2052. [Google Scholar] [CrossRef]
- Seyed Ahmad Soleymani, S.A.S.; Shidrokh Goudarzi, S.G.; Mohammad Hossein Anisi, M.H.A.; Wan Haslina Hassan, W.H.H.; Mohd Yamani, I.; Shahaboddin Shamshirband, S.S.; Noorzaily Mohamed Noor, N.M.N.; Ismail Ahmedy, I.A. A novel method to water level prediction using RBF and FFA. Water Res. Manag. 2016, 30, 3265–3283. [Google Scholar] [CrossRef]
- Szwajka, K.; Zielińska-Szwajka, J.; Trzepieciński, T. The use of a radial basis function neural network and fuzzy modelling in the assessment of surface roughness in the MDF milling process. Materials 2023, 16, 5292. [Google Scholar] [CrossRef] [PubMed]
- Stojčić, M.; Stjepanović, A.; Stjepanović, Đ. ANFIS model for the prediction of generated electricity of photovoltaic modules. Decis. Mak. Appl. Manag. Eng. 2019, 2, 35–48. [Google Scholar] [CrossRef]
- Borghi, P.H.; Zakordonets, O.; Teixeira, J.P. A COVID-19 time series forecasting model based on MLP ANN. Procedia Comput. Sci. 2021, 181, 940–947. [Google Scholar] [CrossRef]
- Thapa, S.; Zhao, Z.; Li, B.; Lu, L.; Fu, D.; Shi, X.; Tang, B.; Qi, H. Snowmelt-driven streamflow prediction using machine learning techniques (LSTM, NARX, GPR, and SVR). Water 2020, 12, 1734. [Google Scholar] [CrossRef]
- Otchere, D.A.; Ganat, T.O.A.; Gholami, R.; Ridha, S. Application of supervised machine learning paradigms in the prediction of petroleum reservoir properties: Comparative analysis of ANN and SVM models. J. Pet. Sci. Eng. 2021, 200, 108182. [Google Scholar] [CrossRef]
- Heidari, P.; Rezaei, M.; Rohani, A. Soft computing-based approach on prediction promising pistachio seedling base on leaf characteristics. Sci. Hortic. 2020, 274, 109647. [Google Scholar] [CrossRef]
- Masoudi, H.; Rohani, A. Citrus fruit grading based on the volume and mass estimation from their projected areas using ANFIS and GPR models. Fruits Int. J. Trop. Subtrop. Hortic. 2021, 76, 169–180. [Google Scholar] [CrossRef]
- Abbasnia, A.; Jafari, M.; Rohani, A. A novel method for estimation of stress concentration factor of central cutouts located in orthotropic plate. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 348. [Google Scholar] [CrossRef]
- Taki, M.; Mehdizadeh, S.A.; Rohani, A.; Rahnama, M.; Rahmati-Joneidabad, M. Applied machine learning in greenhouse simulation; new application and analysis. Inf. Process. Agric. 2018, 5, 253–268. [Google Scholar] [CrossRef]
- Siavash, N.K.; Ghobadian, B.; Najafi, G.; Rohani, A.; Tavakoli, T.; Mahmoodi, E.; Mamat, R. Prediction of power generation and rotor angular speed of a small wind turbine equipped to a controllable duct using artificial neural network and multiple linear regression. Environ. Res. 2021, 196, 110434. [Google Scholar] [CrossRef] [PubMed]


| Goal | Measured Parameter | Electrical Settings | Description | Ref. |
|---|---|---|---|---|
| Soot and diesel measurements | Impedance | 20 Hz–600 KHz | Electrochemical Impedance Spectroscopy (EIS) | [46] |
| Oxidation Duration (OD), Total Acid Number (TAN), and Insoluble Content (IC) | Dielectric | 50 KHz–16 MHz | Dielectric Spectroscopy (DS) compared with Fourier Transform Infrared Spectroscopy (FTIR) | [43] |
| Iron Content | Impedance | 40 Hz–10 KHz | liquid test fixture 16452 | [47] |
| Moisture Content | Impedance | 100 Hz–100 KHz | liquid test fixture 16452 | [48] |
| focused on the change in the dielectric at different temperatures with two different gaps between electrodes | Dielectric | 0.001 Hz–100 Hz | Dielectric Spectroscopy (DS) | [49] |
| Diagnosis of the State | Impedance | 200 Hz–2 MHz | - | [50] |
| Diagnosis of the State | Impedance | 0.1 Hz–10 KHz | Electrochemical Impedance Spectroscopy (EIS), constituted the input feature matrix for the classifiers. Classifiers, based on Support Vector Machine (SVM) and Artificial Neural Network applied separately. | [51] |
| Moisture measurement | electrochemical impedance spectroscopy (EIS) and dielectric constant calculation based on the measured impedance values. | 0.01 Hz–100 Hz | - | [52] |
| Dielectric (ε′, ε″, tan δ) | The metal and non-metal content Fe, Pb, Cu, Cr, Al, Si, Zn | 2.4 GHz, 5.8 GHz, 7.4 GHz, 9.6 GHz | The ANN method is used for monitoring the correlation between predicted and observed dielectric characteristics. | [53] |
| The metal and non-metal content Fe, Pb, Cu, Cr, Al, Si, Zn | Dielectric (ε′, ε″, tan δ) | 2.4 GHz, 5.8 GHz, 7.4 GHz | The soft computing models are used to predict the elemental spectroscopy of lubricants through their electrical properties. | [54] |
| Unit | Factors | Actual and Coded Values | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| ppm | Fe | 0 | 125 | 250 |
| Cr | 0 | 15 | 30 | |
| Pb | 0 | 45 | 90 | |
| Cu | 0 | 45 | 90 | |
| Al | 0 | 20 | 40 | |
| Si | 0 | 30 | 60 | |
| cc * | Fe | 0 | 0.7 | 1.4 |
| Cr | 0 | 0.3 | 0.6 | |
| Pb | 0 | 0.5 | 1.0 | |
| Cu | 0 | 0.5 | 1.0 | |
| Al | 0 | 0.5 | 1.0 | |
| Si | 0 | 0.7 | 1.4 | |
| No | Model | Input: X | Output: Y1–Y6 * | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.64 GHz | 4.76 GHz | 5.9 GHz | |||||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | |||
| 1 | RBF | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | Y1: Fe |
| 2 | ANFIS | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | Y1: Fe |
| 3 | MLP | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | Y1: Fe |
| 4 | GPR | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | Y1: Fe |
| 5 | SVM | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | Y1: Fe |
| Model | Train | Test | All | ||||
|---|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | ||
| Fe | RBF | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| ANFIS | 1.67 | 0.99 | 0.85 | 0.99 | 1.54 | 0.99 | |
| MLP | 78.15 | 0.22 | 92.85 | 0.14 | 81.3 | 0.20 | |
| GPR | 78.13 | 0.22 | 90.92 | 0.17 | 80.85 | 0.21 | |
| SVM | 69.39 | 0.38 | 109.07 | 0.19 | 78.94 | 0.25 | |
| Cr | RBF | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| ANFIS | 0.24 | 0.99 | 0.15 | 0.99 | 0.22 | 0.99 | |
| MLP | 9.13 | 0.33 | 11.06 | 0.20 | 9.54 | 0.24 | |
| GPR | 9.19 | 0.32 | 10.52 | 0.08 | 9.47 | 0.25 | |
| SVM | 7.56 | 0.54 | 14.71 | 0.12 | 9.43 | 0.26 | |
| Pb | RBF | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| ANFIS | 0.24 | 0.99 | 0.15 | 0.99 | 0.22 | 0.99 | |
| MLP | 24.88 | 0.46 | 27.83 | 0.06 | 25.50 | 0.40 | |
| GPR | 29.66 | 0.23 | 32.69 | 0.29 | 30.29 | 0.15 | |
| SVM | 23.20 | 0.53 | 27.38 | 0.09 | 24.10 | 0.46 | |
| Cu | RBF | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| ANFIS | 0.35 | 0.99 | 0.02 | 0.99 | 0.32 | 0.99 | |
| MLP | 30.14 | 0.17 | 30.92 | 0.04 | 30.30 | 0.15 | |
| GPR | 30.49 | 0.15 | 31.54 | 0.01 | 30.70 | 0.12 | |
| SVM | 25.01 | 0.43 | 50.18 | 0.54 | 31.68 | 0.07 | |
| Al | RBF | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| ANFIS | 0.11 | 0.99 | 0.01 | 0.99 | 0.10 | 0.99 | |
| MLP | 13.44 | 0.19 | 13.59 | 0.13 | 13.47 | 0.15 | |
| GPR | 13.02 | 0.24 | 16.01 | 0.57 | 13.67 | 0.12 | |
| SVM | 11.54 | 0.41 | 15.67 | 0.50 | 12.48 | 0.27 | |
| Si | RBF | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| ANFIS | 0.19 | 0.99 | 0.04 | 0.99 | 0.17 | 0.99 | |
| MLP | 17.98 | 0.39 | 17.17 | 0.05 | 17.82 | 0.34 | |
| GPR | 16.43 | 0.49 | 16.84 | 0.01 | 16.51 | 0.43 | |
| SVM | 17.56 | 0.42 | 28.70 | 0.05 | 20.28 | 0.14 | |
| Model | Train Size (%) | Train | Test | All | |||
|---|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | ||
| Fe | 80 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| 70 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 60 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 50 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| Cr | 80 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| 70 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 60 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 50 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| Pb | 80 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| 70 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 60 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 50 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| Cu | 80 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| 70 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 60 | 7.76 | 0.95 | 14.10 | 0.77 | 10.76 | 0.89 | |
| 50 | 9.22 | 0.93 | 14.00 | 0.78 | 11.85 | 0.87 | |
| Al | 80 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| 70 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 60 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 50 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| Si | 80 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 |
| 70 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 60 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
| 50 | 0.01 | 0.99 | 0.01 | 0.99 | 0.01 | 0.99 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourramezan, M.-R.; Rohani, A.; Abbaspour-Fard, M.H. Machine Learning-Based Predictions of Metal and Non-Metal Elements in Engine Oil Using Electrical Properties. Lubricants 2024, 12, 411. https://doi.org/10.3390/lubricants12120411
Pourramezan M-R, Rohani A, Abbaspour-Fard MH. Machine Learning-Based Predictions of Metal and Non-Metal Elements in Engine Oil Using Electrical Properties. Lubricants. 2024; 12(12):411. https://doi.org/10.3390/lubricants12120411
Chicago/Turabian StylePourramezan, Mohammad-Reza, Abbas Rohani, and Mohammad Hossein Abbaspour-Fard. 2024. "Machine Learning-Based Predictions of Metal and Non-Metal Elements in Engine Oil Using Electrical Properties" Lubricants 12, no. 12: 411. https://doi.org/10.3390/lubricants12120411
APA StylePourramezan, M.-R., Rohani, A., & Abbaspour-Fard, M. H. (2024). Machine Learning-Based Predictions of Metal and Non-Metal Elements in Engine Oil Using Electrical Properties. Lubricants, 12(12), 411. https://doi.org/10.3390/lubricants12120411






