Parametric Optimization of Surface Textures in Oil-Lubricated Long-Life Aircraft Valves

Abstract

The oil-lubricated long-life aircraft valve is one of the most important components to ensure the safety of the entire aircraft system, and it needs to operate millions of times during the whole service life, significantly necessitating techniques to enhance its tribological performance. To this end, five different surface textures, i.e., spherical cap, ellipsoidal cap, tree-frog, grass-lip and nepenthes textures were introduced to the pin’s surface of an aircraft valve to improve the valve’s tribological performance. By numerically solving the Reynolds equation with the Jakobsson–Floberg–Olsson cavitation boundary conditions, the effect of the five textures on the tribological performance was simulated. To optimize the geometric parameters of the five textures for a better tribological performance, the Analytic Hierarchy Process was introduced to derive a coupled tribological parameter, which accounts for three classical tribological parameters, including load bearing capacity, friction and friction coefficient. The five textures with optimal values of geometric parameters were also compared to one another using the Analytic Hierarchy Process, and this finally led to a suggestion of the best surface texture for the aircraft valve. The parametric optimization approach proposed in this work can be widely applied for the parametric optimization of surface textures in other applications.

1. Introduction

Oil-lubricated long-life aircraft valves are significant for the protection of hydraulic systems from overpressure. A long-life valve may need to open and close millions of times during its whole service life, and this may lead to a high risk of large friction and severe wear of the valve, causing energy loss and even the failure of the whole hydraulic system. Hence, many efforts have been made to optimize the tribological performance of oil-lubricated long-life aircraft valves, and surface texture is one of most favorable techniques. Manufacturing specifically designed features (i.e., textures), such as grooves and pockets on the lubricated surfaces [1,2], introduces additional changes in the gradient of the oil film thickness and, thus, enhances the hydrodynamic effect of lubrication and load bearing capacity [3,4]. Additionally, the surface texture also acts as a lubricant reservoir that can trap wear particles to minimize abrasion and even maintain a continuous oil film under heavy load [5]. Therefore, surface texture has been widely used to improve the load bearing capacity, wear resistance, and friction coefficient of tribomechanical components [6,7,8,9,10].

In the past decades, many studies of surface texture have been focused on reducing friction and wear between lubricated surfaces [11], which necessitates a good understanding of the effect of texture parameters on lubrication performance [12], and the outcomes have been widely applied in various mechanical systems for the improvement of lubrication status and tribological performance [13]. For instance, via a series of experimental tests, Kovalchenko et al. [14] concluded that the use of laser concave texture under boundary lubrication conditions is effective in reducing the friction coefficient. Pettersson et al. [15] observed that concave textures of specific dimensions can serve as tiny oil reservoirs and, thus, can effectively reduce the friction and wear, especially under boundary lubrication. Ryk et al. [16] investigated the effect of a partial laser surface texture (LST) on the friction of piston rings and found it was reduced by a quarter.

Subsequently, many researchers found that different types of textures may lead to different influences on the lubrication performance [17], and a good texture design can effectively reduce the friction coefficient and improve the load bearing capacity. For example, Qiu et al. [18] conducted a study on the performance of parallel sliding bearings with spherical, ellipsoidal, circular, elliptical, and triangular textures and found that the ellipsoidal texture results in the highest load bearing capacity. Yu et al. [19] investigated the effects of different texture shapes (circular, triangular, and elliptical) and their orientation on the pressure distribution between lubricated surfaces, with a particular focus on the effect of both the shape and the orientation of the spherical cap texture on the load bearing capacity. Costa and Hutchings [3] studied the effects of different geometries of grooves, circular or herringbone, on the dynamic compressive properties of sliding contacts, and the results show that the circular texture is optimal. Shen and Khonsari [20] investigated fully textured parallel slide bearings with optimal groove-shaped textures for one-way sliding and two-way sliding shapes, and also compared the performances of these optimized textures with those having normal geometrical textures (circular, elliptical, square, hexagonal, and rhombic shapes). These studies were focused on the influence of parameters of surface textures such as grooves and simple geometric polygons on the tribological properties of lubricated sliding surfaces. This implies the promising potential of using surface textures to enhance the tribological performance of aircraft valves, which are also formed by lubricated sliding surfaces. However, further in-depth investigations are still required to fully understand how textures can improve tribological performance in specific applications.

The tribological performances of lubricated surfaces with textures vary greatly with the texture’s geometric parameters. Hence, the optimization of textures is significant to further improve the tribological performance. In the past decades, optimization algorithms have been successfully applied in various engineering optimization problems, including the optimization of surface textures [21]. For instance, Zhang et al. [22] used a Genetic Algorithm (GA) to optimize the shapes of elliptical, cylindrical and spindle surface textures to achieve low friction in reciprocating motion and experimentally compared the tribological performance between the optimized textures and the cylindrical surface texture. The results showed that elliptical and spindle surface textures are effective in increasing the load bearing capacity and reducing the friction coefficient compared to cylindrical textures. Shen et al. [23] optimized the shapes of cylindrical, elliptical, trigonal, and herringbone groove surface textures using a Sequential Quadratic Programming (SQP)-based algorithm and compared the tribological performance with those of regular shapes. The results showed that the friction coefficient of the optimal texture is better than that of the regular shape. Chen et al. [24] optimized the geometric parameters of asymmetric herringbone groove texture for dynamic radial bearing based on Taguchi’s algorithm. Wang et al. [25] used a hybrid GA-SQP algorithm to optimize the parameters of straight, large-angle, and small-angle grooves to obtain the globally optimal shape of the surface texture. The groove texture optimized by the two hybrid methods can effectively reduce the friction coefficient of the specimen. Huang et al. [26] used the Analytic Hierarchy Process (AHP), a method proposed for addressing multifactorial and multidimensional problems [27,28,29], to optimize the effects of the tribological properties of AISI 4140 composites under different load, speed, and sliding distance conditions. The AHP method is particularly effective in quantifying opinions based on personal experience and knowledge and is a particularly useful way of quantifying and comparing subjective data [30].

The operational mechanism of a certain type of component involves the axial reciprocating motion of a ring on a pin. The wear generated during this process can be mitigated by adding surface textures to the pin. Xu et al. [31] machined rhomboid textures on the spool of a pilot valve, which effectively reduced friction and improved lubrication performance compared to a pilot valve without texture. Tao et al. [32] applied hemispherical textures to the valve core to address the issues of poor lubrication performance and severe wear in water hydraulic slide valves. Chen et al. [33] used rhombic and striped textures on the surface of a hydraulic cylinder, and found that under identical working conditions, the friction coefficient of the rhombic texture was only one-quarter of that of the striped texture, significantly enhancing the hydraulic cylinder’s frictional performance. Wang [34] conducted a study on the hydrodynamic lubrication characteristics of composite textures (cylindrical, trapezoid prism, and quadrangular prism) on the valve spool of a hydraulic safety valve. The results demonstrated that incorporating composite textures on the valve spool effectively reduces friction and wear.

In the literature, many efforts have been made on investigating the effects of textures on lubricated surfaces, as well as optimizing the dimensions of textures. However, there seems to be very limited work on finding the optimal textures for oil-lubricated long-life aircraft valves, which also need a long-life reciprocating motion. In this work, two classical textures, i.e., spherical and ellipsoidal caps, and three bionic textures, tree-frog, grass-lip, and nepenthes textures, were considered to improve the tribological performance of an oil-lubricated long-life aircraft valve. The Reynolds equation for hydrodynamic lubrication was used to obtain the oil film pressure and derive other tribological parameters, such as friction and load bearing capacity, which were then incorporated into the AHP method to optimize the textures’ geometric parameters.

2. Lubrication Model

The oil-lubricated long-life aircraft valve considered in this work is shown in Figure 1. Both the ring and the pin are made of 1Cr18Ni10Ti stainless steel, due to its excellent corrosion resistance, high strength, and suitability for high-stress and high-friction environments, and its mechanical properties are shown in Table 1. The ring and pin have an initial roughness of $Ra=0.1\mathsf{\mu }\mathrm{m}$, and were thus assumed to be smooth in this study. To turn the valve off or on, the ring needs to slide forward or backward on the pin, and this operation may need to repeat millions of times during the whole service life of the valve, making it important to improve the lubrication performance of the valve, although the radial load on the ring is small. As discussed above, introducing textures on the surface of the pin may reduce the friction and enhance the load bearing capacity, and this approach was thus adopted in this work. To calculate the oil film pressure between the pin’s surface and the ring’s inner surface, the Reynolds equation was used, whereby the deformation of surfaces is ignored because of the small radial load of the valve. This is detailed below.

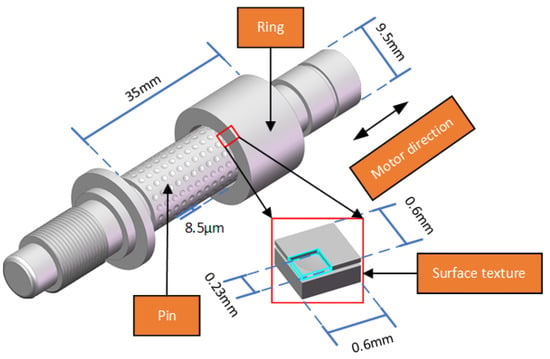
Figure 1. Illustration of an oil-lubricated long-life aircraft valve studied in this work.

Table 1. The mechanical properties of the ring and pin’s material 1Cr18Ni10Ti stainless steel.

Ring and Pin
Materials		1Cr18Ni10Ti Stainless Steel
Mechanical properties	$\mathrm{Tensile} \mathrm{strength} \left(\mathrm{M}\mathrm{P}\mathrm{a}\right)$	520
	$\mathrm{Yield} \mathrm{strength} \left(\mathrm{M}\mathrm{P}\mathrm{a}\right)$	206
	$\mathrm{Hardness} \left(\mathrm{H}\mathrm{B}\right)$	187

2.1. Reynolds Equation with JFO Boundary Condition

Since the radial load of the valve is small, the elastic deformation of the pin and ring’s surfaces is negligible, and the viscosity of the lubricant can be considered as constant. If only a small region of the textured surface is considered, the Reynolds equation can be expressed in the Cartesian coordinate system as [35]

$${\displaystyle \frac{\partial }{\partial x}}\left(h^3{\displaystyle \frac{\partial p}{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial y}}\left(h^3{\displaystyle \frac{\partial p}{\partial y}}\right)=6u\eta {\displaystyle \frac{\partial h}{\partial x}}$$

(1)

where $x$ is the sliding (or axial) direction between the pin and ring, $y$ corresponds to the circumferential direction, $h$ is the thickness of the oil film between the pin and ring, $p$ is the oil film pressure, $\eta$ is the dynamic viscosity of the lubricant, and $u$ is the relative sliding speed between the pin and ring. Relative rotation between the pin and ring is not allowed in this work.

Boundary conditions determining the rupture of oil film are important for solving the Reynolds equation, and the most common ones are Sommerfeld, Half–Sommerfeld, Reynolds, and Jakobsson–Floberg–Olsson (JFO) boundary conditions. The Sommerfeld and Half–Sommerfeld boundary conditions are easy to use, but their assumption of continuous oil film in the whole or half of fluid domain may lead to unacceptable errors. The Reynolds boundary condition accounts for cavitation by postulating that the oil film initiates at the point of maximum film thickness and ruptures at the location where both the film pressure and the pressure gradient normal to the $x$-direction reach zero. While this model provides a more reasonable explanation at the point where the oil film ruptures, it cannot accurately describe the reformation of the oil film. The JFO cavitation boundary condition not only provides an accurate prediction of the oil film rupture location, but also gives the boundary of oil film reformation, and was thus adopted in this paper. The Reynolds equation based on the JFO cavitation boundary conditions can be expressed as [36]

$${\displaystyle \frac{\partial }{\partial x}}\left(h^3{\displaystyle \frac{\partial p}{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial y}}\left(h^3{\displaystyle \frac{\partial p}{\partial y}}\right)=6u\eta {\displaystyle \frac{\partial h\theta }{\partial x}}$$

(2)

where $\theta$ is the lubricant density ratio, defined as $\theta =1+\left(1-S\right)\Phi$. Here, $S$ is a cavitation index defined as

$$S=\left\{\begin{array}{cc}1,& \Phi >0\\ 0,& \Phi \le 0\end{array}\right.$$

(3)

and $\Phi$ is a dimensionless parameter distinguishing the full film region (if $\Phi$ is positive) and cavitation region (if $\Phi$ is nonpositive), and usually defined by ${\displaystyle \frac{p}{p_0}}=S\Phi$, where $p_0$ is the reference (atmosphere) pressure.

For ease of numerical calculation, the Reynolds equation is usually nondimensionalized by defining the following dimensionless parameters:

$$H={\displaystyle \frac{h}{h_0}},P={\displaystyle \frac{p}{p_0}},Y={\displaystyle \frac{y}{L_y}},X={\displaystyle \frac{x}{L_x}},\Lambda ={\displaystyle \frac{6u\eta Lx}{h_0^2\left(p-p_0\right)}},\alpha ={\displaystyle \frac{L_x}{L_y}},P=S\Phi$$

(4)

where $H$ represents the dimensionless oil film thickness, $h_0$ is the referenced oil film thickness, $P$ is the dimensionless oil film pressure, $p_0$ denotes the atmospheric pressure, $X$ and $Y$ refer to the dimensionless coordinates in the $x$ and $y$ directions, respectively, and $L_x$ and $L_y$ denote the length and width of a unit cell of the texture, respectively. Substitution of these dimensionless parameters into the Reynolds equation (Equation (2)) enables it to be rewritten as

$${\displaystyle \frac{\partial }{\partial X}}\left(H^3{\displaystyle \frac{\partial \left(S\Phi \right)}{\partial X}}\right)+{\alpha }^2{\displaystyle \frac{\partial }{\partial Y}}\left(H^3{\displaystyle \frac{\partial \left(S\Phi \right)}{\partial Y}}\right)=\Lambda {\displaystyle \frac{\partial \left(\left(1+\left(1-S\right)\Phi \right)H\right)}{\partial X}}$$

(5)

For such an equation, it is very challenging to obtain its analytical solution and, thus, numerical methods for partial differential equation (PDE) are usually preferred. Among the numerical methods for solving Reynolds equation, the Finite Difference Method (FDM) is a straightforward and well-established numerical approach frequently employed in many references [37], and was also adopted in this work, whereby central differential scheme [36] was used to derive the first and second partial derivatives. Following the FDM [38], the discretized form of the dimensionless Reynolds equation (see Equation (5)), can be expressed as

$$A_{i,j}{\Phi }_{i,j}-B_{i,j}{\Phi }_{i-1,j}{S}_{i-1,j}-C_{i,j}{\Phi }_{i+1,j}{S}_{i+1,j}-{\mathrm{D}}_{i,j}{\Phi }_{i,j-1}{S}_{i,j-1}-E_{i,j}{\Phi }_{i,j+1}{S}_{i,j+1}=-F_{i,j}$$

(6)

where

$$\begin{array}{c}{B}_{i,j}={\displaystyle \frac{H_{i-1/2,j}^3}{\Delta X^2}}={\displaystyle \frac{(H_{i-1,j}+H_{i,j}{)}^3}{8\Delta X^2}}\\ C_{i,j}={\displaystyle \frac{H_{i+1/2,j}^3}{\Delta X^2}}={\displaystyle \frac{(H_{i+1,j}+H_{i,j}{)}^3}{8\Delta X^2}}\\ \begin{array}{c}{D}_{i,j}={\displaystyle \frac{H_{i,j-1/2}^3}{\Delta Y^2}}={\displaystyle \frac{(H_{i,j-1}+H_{i,j}{)}^3}{8\Delta Y^2}}{\alpha }^2\\ E_{i,j}={\displaystyle \frac{H_{i,j-1/2}^3}{\Delta Y^2}}={\displaystyle \frac{(H_{i,j-1}+H_{i,j}{)}^3}{8\Delta Y^2}}{\alpha }^2\\ \begin{array}{c}{A}_{i,j}=\left(B_{i,j}+C_{i,j}+D_{i,j}+E_{i,j}\right)S_{i,j}+{\displaystyle \frac{\Lambda \left(1-S_{i,j}\right)H_{i,j}}{\Delta X}}\\ F_{i,j}={\displaystyle \frac{\Lambda }{\Delta X}}(H_{i+1,j}-H_{i-1,j}-\left(1-S_{i-1,j}\right){\Phi }_{i-1,j}{H}_{i-1,j})\end{array}\end{array}\end{array}$$

(7)

where $A,B,C,D,E,F$ are coefficient matrices, subscripts $i,j$ refer to node $\left(i,j\right)$, and $\Delta X$ and $\Delta Y$ denote the distances in $x$ and $y$ directions between two neighboring nodes. The whole computational domain was discretized into an equally spaced grid, with $m$ nodes along the $x$-direction and $n$ nodes along the $y$-direction, resulting in a total of $m\times n$ nodes within the entire computational domain.

The discretized Reynolds equation (see Equation (6)), can then be solved iteratively:

$${\Phi }_{i,j}^{k+1}={\displaystyle \frac{-F_{i,j}+B_{i,j}{\Phi }_{i-1,j}^{k+1}{S}_{i-1,j}^{k+1}+D_{i,j}{\Phi }_{i,j-1}^{k+1}{S}_{i,j-1}^{k+1}+C_{i,j}{\Phi }_{i+1,j}^k{S}_{i+1,j}^k+E_{i,j}{\Phi }_{i,j+1}^k{S}_{i,j+1}^k}{A_{i,j}}}$$

(8)

where $k$ denotes the iteration step, and ${\left(·\right)}_{i,j}^k$ denotes the value of $\left(·\right)$ at the $k$-th iteration step at node $(i,j)$. For a faster convergence of iteration, one may use Successive Over-Relaxation (SOR), as follows:

$${\Phi }_{i,j}^{k+1}=\left(1-\beta \right){\Phi }_{i,j}^k+\beta {\displaystyle \frac{-F_{i,j}+B_{i,j}{\Phi }_{i-1,j}^{k+1}{S}_{i-1,j}^{k+1}+D_{i,j}{\Phi }_{i,j-1}^{k+1}{S}_{i,j-1}^{k+1}+C_{i,j}{\Phi }_{i+1,j}^k{S}_{i+1,j}^k+E_{i,j}{\Phi }_{i,j+1}^k{S}_{i,j+1}^k}{A_{i,j}}}$$

(9)

where $\beta$ is the super relaxation coefficient in the range (1, 2), and it was set to be $1.95$ in this work. The above iteration can be considered convergent when the following condition is satisfied:

$${\displaystyle \frac{{\sum }_{i=1}^m{\sum }_{j=1}^n\left|{\Phi }^{k+1}-{\Phi }^k\right|}{{\sum }_{i=1}^m{\sum }_{j=1}^n{\Phi }^{k+1}}}<1\times {10}^{-6}$$

(10)

Once the dimensionless parameter Φ is calculated, the cavitation index $S$ can be obtained from Equation (3), and the dimensionless film pressure $P$ can be obtained from Equation (4).

2.2. Parameters Evaluating Tribological Performance

Tribological performance of the aircraft valve can be evaluated using many parameters, while the load bearing capacity, friction and friction coefficient are of more interest during application [25,39,40,41]. Generally, a higher load bearing capacity implies a lower possibility of contact between the lubricated surfaces, while a lower friction and friction coefficient indicate a smaller energy loss and wear, respectively. Hence, these three parameters were used to evaluate the tribological performance in this work and defined as follows:

The load bearing capacity $W$ of the oil film can be obtained by integrating the oil film pressure $p(x,y)$ over the entire fluid domain

$$W=\iint p(x,y)dxdy$$

(11)

by noting that the oil film pressure can be derived from the dimensionless oil film pressure, i.e., $p=P{p}_0$.

The friction at the lubricated surface of the aircraft valve can be obtained by integrating the shear stress $\tau (x,y)$ over the entire fluid domain

$$f={\int }_0^{L_x}{\int }_0^{L_y}\tau (x,y)dxdy$$

(12)

where the shear stress can be obtained by $\tau (x,y)=-{\displaystyle \frac{h}{2}}{\displaystyle \frac{\partial p}{\partial x}}+{\displaystyle \frac{\eta }{h}}u$.

The friction coefficient $\mu$ can then be expressed as

$$\mu ={\displaystyle \frac{f}{W}}$$

(13)

2.3. Optimization Using AHP

All the three parameters defined above, i.e., load bearing capacity, friction and friction coefficient, are important tribological indices, and thus need to be considered in finding the optimal surface texture. To this end, the three parameters were coupled together using the Analytic Hierarchy Process (AHP) to describe the coupled tribological performances of surface textures.

The AHP optimization generally consists of the following four steps:

(1)

Definition of degrees of importance

• The to-be-optimized system is generally affected by more than one factor, while some factors may affect the system more severely compared to other factors. Hence, AHP requires definition of degrees of importance to characterize the significance of each factor in affecting the system.

(2)

Construction of judgement matrix

• The judgement matrix facilitates pairwise comparison between any two studied factors, and each value in it is calculated based on the degrees of importance and defines the relative importance between two factors.

(3)

Consistency check

• Consistency check is used to ensure logical consistency in the pairwise comparison between any two factors, by calculating the consistency index (CI) and consistency ratio (CR) based on the judgement matrix. If the CR is less than the commonly accepted threshold of 0.1, the judgment matrix is considered to have acceptable consistency, indicating that the pairwise comparisons are logically coherent.

(4)

Optimization using a coupled factor

• A coupled factor can then be defined using weighted sum of all factors, whereby the weight of each factor takes the corresponding value in the normalized eigen factor of the judgement matrix. Parametric optimization accounting for multiple factors is then transformed to be maximizing or minimizing the coupled factor.

Following the AHP optimization process, parametric optimization of the tribological performance of the valve was conducted as follows:

For many valves, load bearing capacity is usually significant, but it is less important for the one studied in this study because the radial load applied to this type of valve is very small, as mentioned above. Since the ring needs to slide back and forth along the pin millions of times during the service life of the valve, a small friction coefficient and frictional force will be more favorable. This is because a higher friction coefficient generally leads to severer wear [42], while a larger friction force means more energy loss when operating the valve. The ultimate goal of optimizing surface texture parameters for this aircraft valve is to minimize wear on the lubricated surface, thereby ensuring a long service life for the equipment. Thus, the friction coefficient seems to be more significant than the friction, while load bearing capacity is the least important for the aircraft valve learned in this work. The degrees of importance for the three tribological parameters, i.e., load bearing capacity, friction and friction coefficient, were finally defined as the following vector $\mathbf{Ħ}$:

$$\mathbf{Ħ}=[1,2,3]$$

(14)

while the degrees of importance may be defined differently depending on the actual needs in applications. Next, a judge matrix needs to be defined to facilitate pairwise comparison between any two of the three parameters.

In traditional AHP, the 1–9 scale method [43] is commonly used to establish the judgment matrix. Although this method provides excellent uniformity, it has certain drawbacks, such as poor consistency, which can lead to issues like rank reversal and a disconnect with logical consistency [43]. To this end, the exponential scale method was proposed in [43], and this method was adopted to construct the judgment matrix $\mathsf{\Psi }$.

$$\mathsf{\Psi }={\left[a_{ij}\right]}_{3\times 3}$$

(15)

The element $a_{ij}$ in the judgment matrix denotes the relative importance of factor $i$ to factor $j$.

$$a_{ij}=\mathit{exp}({\mathbf{Ħ}}^{*}\left(i\right)-{\mathbf{Ħ}}^{*}\left(j\right)\left)\right(1\le i\le 3,1\le j\le 3)$$

(16)

where ${\mathbf{Ħ}}^{*}$ is obtained by normalizing the vector $\mathbf{Ħ}$.

$${\mathbf{Ħ}}^{*}(\mathcal{l})={\displaystyle \frac{\mathbf{Ħ}\left(\mathcal{l}\right)}{\max (\mathbf{Ħ})}}(1\le \mathcal{l}\le 3)$$

(17)

where $\mathbf{Ħ}\left(\mathcal{l}\right)$ and ${\mathbf{Ħ}}^{*}\left(\mathcal{l}\right)$ refer to the $\mathcal{l}$-th element in $\mathbf{Ħ}$ and ${\mathbf{Ħ}}^{*}$, respectively. This enables the judgment matrix $\mathsf{\Psi }$ to be obtained as

$$\mathsf{\Psi }=\left[\begin{array}{cccc}& W& f& \mu \\ W& 1.0000& 0.7165& 0.5134\\ f& 1.3956& 1.0000& 0.7165\\ \mu & 1.9477& 1.3956& 1.0000\end{array}\right]$$

(18)

Next, the consistency of the judgment matrix must be checked, to avoid possible logical contradictions of pairwise comparisons. This is performed as follows:

The eigenvectors of the judgment matrix $\mathsf{\Psi }$ are

$$\mathsf{\omega }={\left({\displaystyle \frac{a_{11}\times a_{12}\times a_{13}}{3}},{\displaystyle \frac{a_{21}\times a_{22}\times a_{23}}{3}},{\displaystyle \frac{a_{31}\times a_{32}\times a_{33}}{3}}\right)}^{{\displaystyle \frac{1}{3}}}$$

(19)

The maximum eigenvalue ${\lambda }_{max}$ of the judgment matrix $\mathsf{\Psi }$ can be obtained by solving the following equation:

$$\mathsf{\Psi }\mathsf{\omega }={\lambda }_{max}\mathsf{\omega }$$

(20)

The CI is given by [43,44]:

$$CI={\displaystyle \frac{{\lambda }_{max}-\gamma }{\gamma -1}}$$

(21)

where $\gamma$ is the order of the judgment matrix, which is $3$ in this work. The CR is defined as

$$CR={\displaystyle \frac{CI}{RI}}$$

(22)

where $RI=0.36$ is the random consistency index [43]. For the judgement matrix $\mathsf{\Psi }$ in this work (see Equation (18)), its maximum eigenvalue ${\lambda }_{max}\approx 3$, leading to a consistency index $CI\approx -2.22\times {10}^{-16}$ and consistency ratio $CR\approx 3.83\times {10}^{-16}<0.1$. It is generally accepted that the judgment matrix has an acceptable consistency when $CR<0.1$ [43].

After checking the consistency of the judgement matrix $\mathsf{\Psi }$, the eigenvector $\mathsf{\omega }$ needs to be normalized to obtain the weights $\overline{\mathsf{\omega }}$ corresponding to the three parameters, i.e., load bearing capacity, friction and friction coefficient.

$$\overline{\mathsf{\omega }}=\left[0.2302,0.3213,0.4484\right]$$

(23)

When conducting parametric optimization of a certain type of surface texture, a series of numerical simulations are conducted by varying the geometric parameters of the texture. Next, the three tribological parameters, i.e., load bearing capacity, friction and friction coefficient, can be evaluated and denoted as vectors ${\mathsf{\Theta }}_1$, ${\mathsf{\Theta }}_2$ and ${\mathsf{\Theta }}_3$, respectively. It should be noted that a larger load bearing capacity combined with a smaller friction and friction coefficient indicates a better tribological performance for the valve studied in this work. Therefore, vectors of the three tribological parameters can be normalized as follows:

$${\overline{\mathsf{\Theta }}}_1,{\overline{\mathsf{\Theta }}}_2=\overline{\left({\displaystyle \frac{1}{{\mathsf{\Theta }}_2}}\right)},{\overline{\mathsf{\Theta }}}_3=\overline{\left({\displaystyle \frac{1}{{\mathsf{\Theta }}_3}}\right)}$$

(24)

where $\overline{\left(·\right)}$ is the normalization of $\left(·\right)$, $\overline{\left(·\right)}={\displaystyle \frac{\left(·\right)}{max\left(·\right)}}$. Next, a coupled tribological parameter accounting for load bearing capacity, friction and friction coefficient can be defined as

$$\mathfrak{R}=\mathsf{\Xi }·\overline{\mathsf{\omega }}$$

(25)

where

$$\mathsf{\Xi }=\left[{\overline{\mathsf{\Theta }}}_1,{\overline{\mathsf{\Theta }}}_2,{\overline{\mathsf{\Theta }}}_3\right]$$

(26)

Hence, the goal of the parametric optimization in this work is to find the maximum value in the results of the coupled tribological parameter $\mathfrak{R}$, and the corresponding values of geometric parameters of the texture are the optimal results.

3. Modeling of Surface Textures

In this work, five different surface textures, i.e., spherical cap, ellipsoidal cap, tree-frog, grass-lip and nepenthes, were considered to improve the tribological performance of the aircraft valve. Modelling of these surface textures is detailed below.

3.1. Geometric Models of Surface Textures

As shown in Figure 2, the surface textures are uniformly distributed both axially and circumferentially on the pin’s surface of the valve. For ease of explanation, only one unit cell of the texture is detailed below.

Figure 2. Optimization system for texture friction performance.

3.1.1. Spherical Cap

Figure 3 illustrates the geometric shape of the spherical cap texture on the valve surface. The lower part in Figure 3a represents a unit cell of the texture on the pin’s surface, while the upper part, i.e., a rectangular plate, represents the simplified ring. Figure 3b details the three views of the spherical cap texture, while Figure 3c is the corresponding 3D model. In the diagrams, $R$ and $d$ denote radius and depth of the spherical cap, respectively, $r$ represents the radius of the cap base, and $h_0$ is the clearance between the lubricated surface (which is also the referenced oil film thickness).

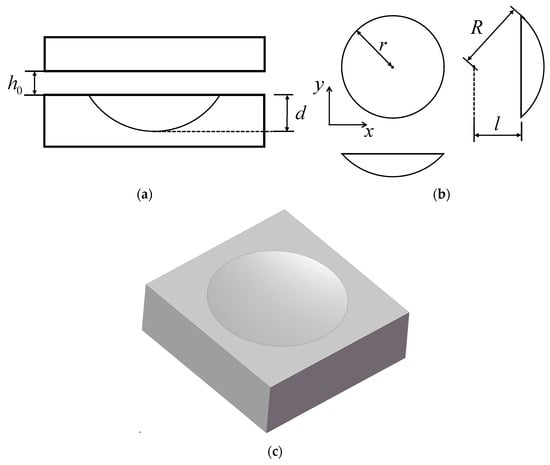
Figure 3. Modeling of spherical cap texture: (a) Section view; (b) three views; (c) 3D model.

For this texture, the oil film thickness $h$ can be expressed as

$$h=\left\{\begin{array}{cc}{h}_0+\left(\sqrt{R^2-\left((x-x_0{)}^2+(y-y_0{)}^2\right)}-l\right)& ,(x-x_0{)}^2+(y-y_0{)}^2\le r^2\\ h_0& ,otherwise\end{array}\right.$$

(27)

where $(x_0,y_0)$ denotes the coordinates of the cap base center.

3.1.2. Ellipsoidal Cap

Figure 4 illustrates the geometric shape of a unit cell of an ellipsoidal cap texture on the pin’s surface, in which Figure 4a–c displays the front view of the lubricated surfaces, three views of the texture’s unit cell and the corresponding 3D model, respectively.

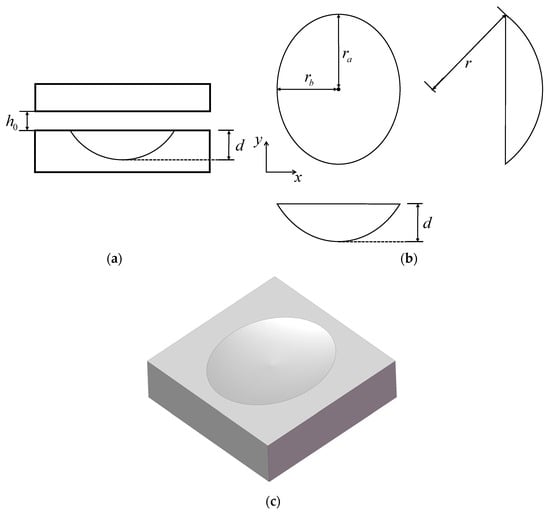
Figure 4. Modeling of ellipsoidal cap texture: (a) Section view; (b) three views; (c) 3D model.

The ellipsoidal cap can be mathematically expressed as

$${\displaystyle \frac{(x-x_0{)}^2}{a^2}}+{\displaystyle \frac{(y-y_0{)}^2}{b^2}}+{\displaystyle \frac{{\left(z+\sqrt{r^2-{r_a}^2}\right)}^2}{c^2}}=1$$

(28)

where $(x_0,y_0)$ is the center of the ellipsoidal cap base, and

$$\begin{array}{c}c=d+\sqrt{r^2-{r_a}^2}\\ a=r_a{\displaystyle \frac{c}{\sqrt{c^2-r^2+{r_b}^2}}}\\ b=r_b{\displaystyle \frac{c}{\sqrt{c^2-r^2+{r_b}^2}}}\end{array}$$

(29)

where $a,b,c$ are the long, middle and short semi-axes of the ellipsoid, respectively. $r_a$ and $r_b$ denote the half-lengths of the long and short axes of the ellipsoidal cap, respectively. d is the texture depth.

For this texture, the oil film thickness $h$ can be expressed as

$$h=\left\{\begin{array}{cc}{h}_0+\left(\sqrt{c^2\left(1-({\displaystyle \frac{x-x_0}{a}}{)}^2-({\displaystyle \frac{y-y_0}{b}}{)}^2\right)}-\sqrt{r^2-{r_a}^2}\right)& ,({\displaystyle \frac{x-x_0}{a}}{)}^2+({\displaystyle \frac{y-y_0}{b}}{)}^2\le r^2\\ h_0& ,otherwise\end{array}\right.$$

(30)

3.1.3. Tree-Frog

Figure 5 illustrates the geometric shape of a unit cell of a tree-frog texture on the pin’s surface, in which Figure 5a–c displays the front view of the lubricated surfaces, three views of the texture’s unit cell and the corresponding 3D model, respectively.

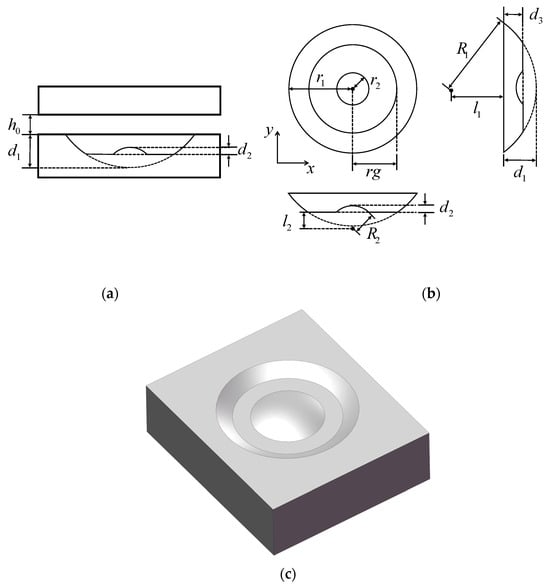
Figure 5. Modeling of tree-frog texture: (a) section view; (b) three views; (c) 3D model.

The tree-frog texture is a combination of a large spherical cap with a radius of $R_1$ and depth of $d_1$, a small spherical cap with a radius of R₂ and depth of $d_2$ and a flat platform with a radius of $rg$ and depth of $d_3$. The radius of the base of the large spherical cap is $r_1$, and that of the base of the small spherical cap is $r_2$.

Therefore, the oil film thickness h can be expressed as

$$h=\left\{\begin{array}{cc}{h}_0+\left(\begin{array}{c}{d}_3+l_2-\\ \sqrt{{R_2}^2-(x-x_0{)}^2-(y-y_0{)}^2}\end{array}\right)& ,(x-x_0{)}^2+(y-y_0{)}^2<{r_2}^2\\ h_0+d_3& ,{r_2}^2\le (x-x_0{)}^2+(y-y_0{)}^2<r{g}^2\\ h_0+\left(\begin{array}{c}\sqrt{{R_1}^2-(x-x_0{)}^2-(y-y_0{)}^2}\\ -l_1\end{array}\right)& ,r{g}^2\le (x-x_0{)}^2+(y-y_0{)}^2<{r_1}^2\\ h_0& ,otherwise\end{array}\right.$$

(31)

where $(x_0,y_0)$ denotes the coordinates of the center of the spherical cap base.

3.1.4. Grass-Lip

Figure 6 illustrates the geometric shape of the unit cell of a grass-lip texture on the pin’s surface, in which Figure 6a–c displays the front view of the lubricated surfaces, three views of the texture’s unit cell and the corresponding 3D model, respectively.

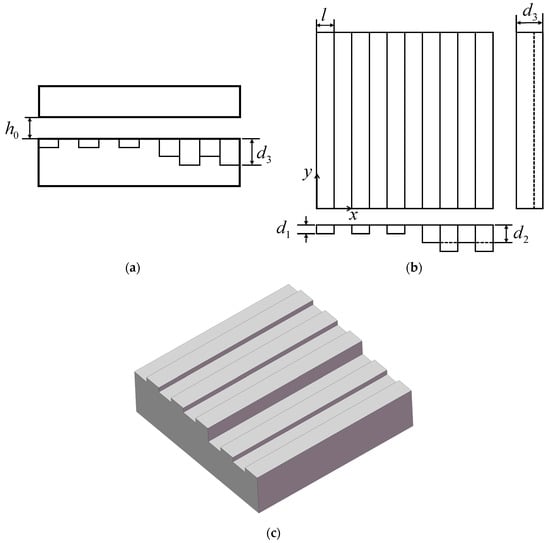
Figure 6. Modeling of grass-lip texture: (a) section view; (b) three views; (c) 3D model.

The grass-lip texture in this work consists of several straight grooves perpendicular to the $x$-direction (i.e., the direction of relative motion). These grooves have three different depths, as shown in Figure 6, where $d_1$, $d_2$ and $d_3$ denote the maximum, intermediate and minimum depths respectively, while $l$ denotes the width of the straight grooves.

Therefore, the oil film thickness $h$ for the grass-lip texture can be expressed as:

$$h=\left\{\begin{array}{cc}{h}_0+d_1& ,(0\le x<l)\cup (2l\le x<3l)\cup (4l\le x<5l)\\ h_0+d_2& ,(7l\le x<8l)\cup (9l\le x<10l)\\ h_0+d_3& ,(6l\le x<7l)\cup (8l\le x<9l)\\ h_0& ,otherwise\end{array}\right.$$

(32)

3.1.5. Nepenthes

Figure 7 illustrates the geometric shape of a unit cell of a nepenthes texture on the pin’s surface, in which Figure 7a–c displays the front view of the lubricated surfaces, three views of the texture’s unit cell and the corresponding 3D model, respectively.

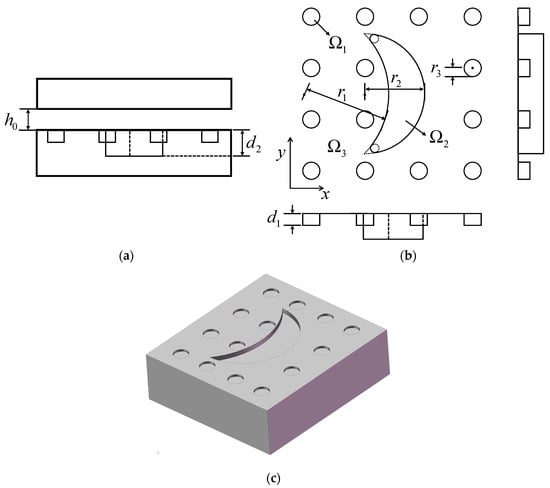
Figure 7. Modeling of nepenthes texture: (a) section view; (b) three views; (c) 3D model.

The nepenthes texture in this work consists of 4-by-4 small cylindrical textures with a radius of $r_3$ and depth of $d_2$, and a large crescent texture with radii of r₁ for the outer circle and $r_2$ for the inner circle and depth of $d_1$. For ease of mathematical expression, let ${\Omega }_1$, ${\Omega }_2$ and ${\Omega }_3$ be the regions of the cylindrical textures and crescent texture and the untextured region, respectively.

Therefore, the oil film thickness $h$ can be expressed as

$$h=\left\{\begin{array}{cc}{h}_0+d_1& ,\left(x,y\right)\in {\Omega }_1\\ h_0+d_2& ,\left(x,y\right)\in {\Omega }_2\\ h_0& ,\left(x,y\right)\in {\Omega }_3\end{array}\right.$$

(33)

3.2. Arrangements for Parametric Optimization

Since the texture’s unit cells are uniformly distributed on the pin’s surface in the valve and the radial load applied to the valve in this work is usually very small, it is reasonable to use the axial symmetry of the valve and simulate only a small region of the textured surface by assuming periodic boundary conditions in the circumferential direction of the pin, similar to the model in He’s study [45]. For instance, in this work, $3\times 1$ unit cells, i.e., $3$ unit cells uniformly distributed in the $x$-direction, were simulated to reduce the computational cost, as shown in Figure 8, which takes the spherical cap texture as an example. During the numerical simulation, the upper and lower boundaries (boundaries perpendicular to the circumferential direction of the pin) were prescribed with periodic boundary conditions, while the left and right boundaries (boundaries perpendicular to the pin’s axial direction) were given the atmospheric pressure $p_0$. In actual applications, more unit cells may be considered in x-direction (or pin’s axial direction), although this may significantly reduce the computational efficiency.

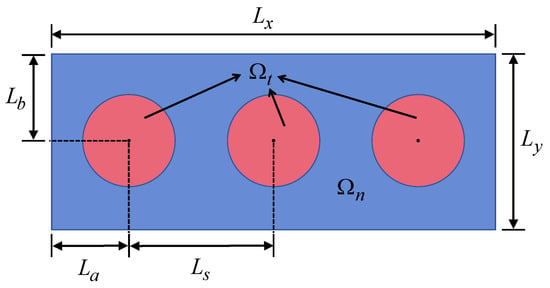
Figure 8. Optimization of geometric parameters of surface texture (illustrated by an example of spherical cap texture).

In Figure 8, ${\Omega }_t$ and ${\Omega }_n$ represent the textured and untextured regions, respectively. The distance $L_s$ between two unit cells can be expressed as

$$L_s={\displaystyle \frac{L_x}{N_n+1}}$$

(34)

where $N_n$ denotes the number of unit cells in the x-direction and $L_x$ is the length of the whole modeled region in the x-direction. Location of the left unit cell can thus be described using two distances, $L_a$ and $L_b$, as

$$\begin{array}{c}{L}_a={\displaystyle \frac{L_x}{n+1}}\\ L_b={\displaystyle \frac{L_y}{2}}\end{array}$$

(35)

where $L_y$ is the length of the whole modeled region in the y-direction.

The center ${(x}_0,y_0)$ of each unit cell is

$$\left\{\begin{array}{c}{x}_0=\left(N_i-{\displaystyle \frac{(N_n+1)}{2}}\right)\times {\displaystyle \frac{L_x}{N_n+1}}(1\le N_i\le n)\\ y_0=0\end{array}\right.$$

(36)

where $N_i$ denotes the $N_i$-th texture in the $x$-direction.

To optimize the geometric parameters, such as $r$ and $d$, for the spherical texture (see Figure 3), a series of different values was defined for the geometric parameters and the corresponding numerical simulations were conducted using the lubrication model detailed in Section 2.1. The optimal geometric parameters could then be found using the AHP introduced in Section 2.3. A detailed flowchart is depicted in Figure 9.

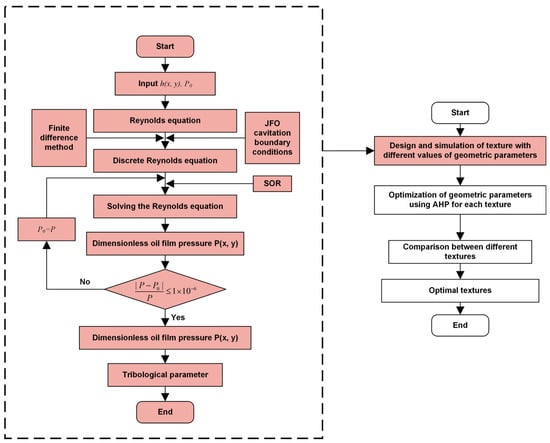
Figure 9. Flowchart of parametric optimization of surface textures.

4. Parametric Optimization of Surface Textures: Results and Discussion

4.1. Convergence of Numerical Simulation Results

To conduct the parametric optimization of surface textures, the convergence of numerical simulation results needs to be verified. To this end, a unit cell of the spherical cap texture was modeled (see Figure 10) and discretized using different numbers of grid nodes (from 50 to 350 nodes along the edge). All the boundaries of the modeled region were prescribed with periodic boundary conditions. By solving the Reynolds equation detailed in Section 2.1, the oil film pressure can be obtained and the three tribological parameters (i.e., load bearing capacity, friction and friction coefficient) can be calculated, as shown in Figure 11. The lubricant used in this study is a specific gearbox oil with excellent anti-wear properties and oxidation stability, and its density and viscosity are about 0.94 g/mm³ and 0.4 Pa∙s, respectively. The values of the other parameters needed in the Reynolds equation are listed in Table 2.

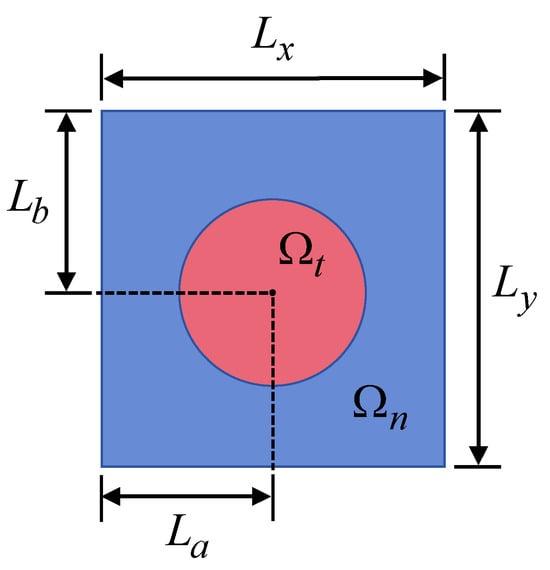
Figure 10. A unit cell model of spherical cap texture to validate convergence of numerical simulations.

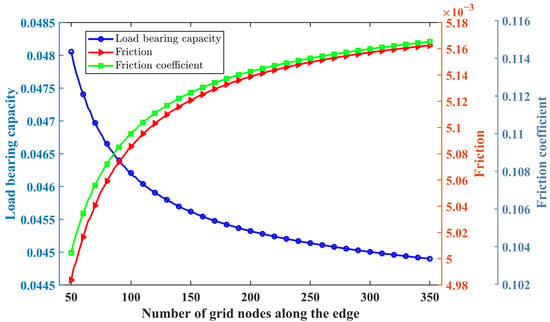
Figure 11. Convergence of numerical results with grid nodes number.

Table 2. Values of parameters needed for numerical simulations.

Texture Parameters	Unit	Parameter Value
$\mathrm{Relative} \mathrm{velocity} \mathrm{between} \mathrm{two} \mathrm{plates} u$	$\mathrm{m}/\mathrm{s}$	0.3
Lubricant viscosity η0	$\mathrm{P}\mathrm{a}·\mathrm{s}$	0.4
$\mathrm{Clearance} \mathrm{between} \mathrm{surfaces} h_0$	$\mathsf{\mu }\mathrm{m}$	8.5
$\mathrm{The} \mathrm{width} \mathrm{of} \mathrm{the} \mathrm{modeled} \mathrm{region} L_y$	$\mathsf{\mu }\mathrm{m}$	700
$\mathrm{The} \mathrm{length} \mathrm{of} \mathrm{the} \mathrm{modeled} \mathrm{region} L_x$	$\mathsf{\mu }\mathrm{m}$	700
$\mathrm{Spherical} \mathrm{cap} \mathrm{base} \mathrm{radius} r$	$\mathsf{\mu }\mathrm{m}$	230
$\mathrm{Spherical} \mathrm{cap} \mathrm{depth} d$	$\mathsf{\mu }\mathrm{m}$	20

Figure 11 shows a clear convergence of the results, i.e., when the edge node number is more than 200, the change of the three results becomes negligible, indicating that the numerical results are trustable. Hence, this edge node number was adopted for all the following numerical simulations.

4.2. Optimization of Geometric Parameters

In this work, the width $L_x$ and length $L_y$ of the modeled region (see Figure 8) were set to be $2000\mathsf{\mu }\mathrm{m}$ and $660\mathsf{\mu }\mathrm{m}$, respectively. The relative velocity $u$ and clearance $h_0$ between the two surfaces, as well as the lubricant viscosity η₀, assume the same values in Table 2.

The geometric parameters of each texture are presented in Table 3. For the spherical cap texture, five values were tried for each geometric parameter, leading to 25 numerical simulations. For textures with more geometric parameters, more numerical simulations are needed in general. In this work, 625 numerical simulations were conducted for the ellipsoidal cap texture, $324$ simulations for the tree-frog texture, $10$ for the grass-lip texture and 30 for the nepenthes texture (see details in Table 3). It may be noted that due to the geometric complexity of the grass-lip texture and nepenthes texture, only some of their geometric parameters were varied. One can also conduct a large number of numerical simulations to vary all the geometric parameters of these two textures and then optimize all the parameters using AHP.

Table 3. Texture geometric parameters.

Texture Type	$\mathbf{Geometric} \mathbf{Parameter} \left(\mathsf{\mu }\mathbf{m}\right)$	Value
Spherical cap	$r$	190, 200, 210, 220, 230
	$d$	9, 10, 11, 12, 13
Ellipsoidal cap	$r_a$	200, 220, 240, 260, 280
	$r_b$	190, 200, 210, 220, 230
	$r$	600, 700, 800, 900, 1000
	$d$	9, 10, 11, 12, 13
Tree-frog	$r_1$	220, 230, 240
	$r_2$	70, 80, 90
	$d_1$	11, 12, 13
	$d_2$	3, 4, 5
	$d_3$	6, 7, 8
Grass-lip	$d_1$	3, 6, 9, 12, 15, 18, 21, 24, 27, 30
	$d_2$	$2\times d_1$
	$d_3$	$3\times d_1$
	$l$	66
Nepenthes	$r_1$	300
	$r_2$	200
	$r_3$	30
	$r_4$	20
	$d_1$	6, 7, 8, 9, 10
	$d_2$	3, 4

4.2.1. Effects of Geometric Parameters on Tribological Performance

After conducting all the numerical simulations, the tribological performance of the valve using different textures can be evaluated using the three parameters, i.e., load bearing capacity, friction and friction coefficient, defined in Section 2.2. For instance, Figure 12 depicts the effects of the two geometric parameters $r$ and $d$ of the spherical cap texture on the tribological performance. It shows that when the cap base radius $r$ is constant, the load bearing capacity increases with the cap depth $d$, while the friction and friction coefficient decrease with $d$. When the texture depth $d$ is constant, the load bearing capacity increases with the cap base radius $r$, and the friction and friction coefficient decrease with $r$. This indicates that $r=230\mathsf{\mu }\mathrm{m}$ and $d=13\mathsf{\mu }\mathrm{m}$ are the optimal dimensions among the pre-defined values of the two geometric parameters.

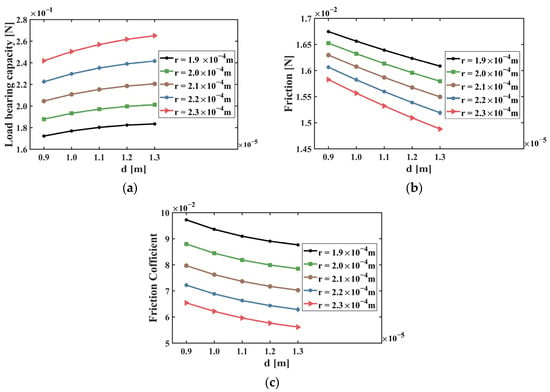
Figure 12. Effects of the geometric parameters $r$ and $d$ of spherical cap texture on the tribological performance: (a) load bearing capacity; (b) friction; (c) friction coefficient.

Figure 12 also shows that the absolute gradient of the three tribological parameters decreases with the texture depth $d$, implying that there may be an optimal value of $d$ larger than 13 $\mathsf{\mu }\mathrm{m}$. To this end, 27 more simulations were conducted using different values of the texture depth $d$ in the range of $\left[14,40\right]\mathsf{\mu }\mathrm{m}$ (see the last part of Table 4), while $r=230\mathsf{\mu }\mathrm{m}$. The simulation results are depicted in Figure 13, in which the peak load bearing capability was observed at $d=16\mathsf{\mu }\mathrm{m}$, the minimum friction coefficient was found at $d=20\mathsf{\mu }\mathrm{m}$, while the friction gradually decreased with $d$. A similar trend was also observed for the texture radius $r$ in the range of $190\mathsf{\mu }\mathrm{m}$ to $230\mathsf{\mu }\mathrm{m}$. However, due to the limited size of the texture model (see Figure 8), the distance between boundaries of two adjacent textures will be too small, making the texture not manufacturable if the r value increases beyond $230\mathsf{\mu }\mathrm{m}$, which is thus not considered in this work. Hence, the optimal values of the geometric parameters vary significantly, depending on which tribological parameter is considered. This is the main reason why the AHP method was introduced in this work to define a coupled tribological parameter. The parametric optimization of the five textures using AHP is detailed below.

Table 4. Values of tribological parameters corresponding to different values of geometric parameters for the spherical texture.

Tribological Results for Spherical Texture (Initial Designs Generated in Table 3)
Geometric Parameters		${\mathsf{\Theta }}_1$	${\mathsf{\Theta }}_2$	${\mathsf{\Theta }}_3$	${\overline{\mathsf{\Theta }}}_1$	${\overline{\mathsf{\Theta }}}_2$	${\overline{\mathsf{\Theta }}}_3$	$\mathfrak{R}$
$\mathit{r}\left(\mathsf{\mu }\mathbf{m}\right)$	$\mathit{d}\left(\mathsf{\mu }\mathbf{m}\right)$
190	9	0.17221	0.01675	0.09725	0.64607	0.73638	0.54172	0.62823
	10	0.17694	0.01656	0.09361	0.66381	0.74455	0.56277	0.64438
	11	0.18023	0.01639	0.09095	0.67618	0.75232	0.57923	0.65710
	12	0.18233	0.01623	0.08903	0.68404	0.75968	0.59170	0.66687
	13	0.18348	0.01609	0.08767	0.68836	0.76665	0.60090	0.67423
200	9	0.18782	0.01652	0.08798	0.70463	0.74626	0.59875	0.67046
	10	0.19325	0.01632	0.08446	0.72502	0.75552	0.62372	0.68932
	11	0.19711	0.01613	0.08185	0.73948	0.76436	0.64360	0.70441
	12	0.19968	0.01596	0.07992	0.74914	0.77276	0.65918	0.71632
	13	0.20119	0.01580	0.07851	0.75478	0.78074	0.67100	0.72548
210	9	0.20454	0.01630	0.07968	0.76736	0.75671	0.66118	0.71625
	10	0.21083	0.01607	0.07625	0.79095	0.76715	0.69090	0.73836
	11	0.21537	0.01587	0.07368	0.80799	0.77715	0.71499	0.75630
	12	0.21852	0.01568	0.07173	0.81982	0.78670	0.73438	0.77078
	13	0.22050	0.01550	0.07028	0.82724	0.79580	0.74959	0.78224
220	9	0.22245	0.01606	0.07221	0.83456	0.76768	0.72951	0.76588
	10	0.22976	0.01582	0.06886	0.86199	0.77940	0.76499	0.79187
	11	0.23518	0.01560	0.06632	0.88231	0.79067	0.79434	0.81333
	12	0.23905	0.01539	0.06436	0.89684	0.80148	0.81846	0.83096
	13	0.24160	0.01519	0.06288	0.90638	0.81181	0.83784	0.84517
230	9	0.24188	0.01583	0.06543	0.90744	0.77916	0.80508	0.82024
	10	0.25042	0.01557	0.06216	0.93950	0.79225	0.84752	0.85085
	11	0.25693	0.01532	0.05963	0.96392	0.80488	0.88342	0.87663
	12	0.26175	0.01509	0.05766	0.98200	0.81705	0.91359	0.89823
	13	0.26511	0.01488	0.05613	0.99461	0.82874	0.93856	0.91608
Tribological Results for Spherical Texture (Additional Designs Obtained by Expanding the Value Range of d)
Geometric parameters		${\mathsf{\Theta }}_1$	${\mathsf{\Theta }}_2$	${\mathsf{\Theta }}_3$	${\overline{\mathsf{\Theta }}}_1$	${\overline{\mathsf{\Theta }}}_2$	${\overline{\mathsf{\Theta }}}_3$	$\mathfrak{R}$
$\mathit{r}\left(\mathsf{\mu }\mathbf{m}\right)$	$\mathit{d}\left(\mathsf{\mu }\mathbf{m}\right)$
230	14	0.26545	0.01468	0.05531	0.99588	0.83987	0.95238	0.92615
	15	0.26643	0.01450	0.05442	0.99956	0.85057	0.96808	0.93747
	16	0.26655	0.01433	0.05375	1.00000	0.86079	0.98015	0.94627
	17	0.26593	0.01417	0.05327	0.99767	0.87054	0.98894	0.95281
	18	0.26473	0.01402	0.05294	0.99319	0.87983	0.99500	0.95748
	19	0.26305	0.01388	0.05275	0.98687	0.88868	0.99862	0.96049
	20	0.26094	0.01375	0.05268	0.97897	0.89709	1.00000	0.96200
	21	0.25849	0.01362	0.05271	0.96975	0.90509	0.99942	0.96218
	22	0.25574	0.01351	0.05283	0.95946	0.91270	0.99711	0.96122
	23	0.25281	0.01341	0.05303	0.94845	0.91992	0.99347	0.95938
	24	0.24971	0.01331	0.05329	0.93682	0.92678	0.98861	0.95672
	25	0.24648	0.01321	0.05361	0.92472	0.93330	0.98271	0.95339
	26	0.24314	0.01313	0.05399	0.91219	0.93949	0.97581	0.94940
	27	0.23971	0.01304	0.05442	0.89932	0.94537	0.96807	0.94485
	28	0.23621	0.01297	0.05490	0.88618	0.95095	0.95957	0.93981
	29	0.23267	0.01290	0.05542	0.87292	0.95626	0.95047	0.93438
	30	0.22911	0.01283	0.05599	0.85954	0.96130	0.94085	0.92861
	31	0.22556	0.01276	0.05659	0.84624	0.96609	0.93090	0.92262
	32	0.22202	0.01270	0.05722	0.83295	0.97065	0.92061	0.91641
	33	0.21849	0.01265	0.05789	0.81970	0.97498	0.91000	0.91000
	34	0.21497	0.01260	0.05859	0.80649	0.97910	0.89912	0.90340
	35	0.21149	0.01254	0.05932	0.79346	0.98302	0.88813	0.89674
	36	0.20805	0.01250	0.06007	0.78052	0.98675	0.87697	0.88995
	37	0.20463	0.01245	0.06085	0.76771	0.99031	0.86568	0.88308
	38	0.20125	0.01241	0.06166	0.75503	0.99370	0.85429	0.87615
	39	0.19791	0.01237	0.06250	0.74251	0.99692	0.84286	0.86917
	40	0.19461	0.01233	0.06337	0.73013	1.00000	0.83136	0.86216

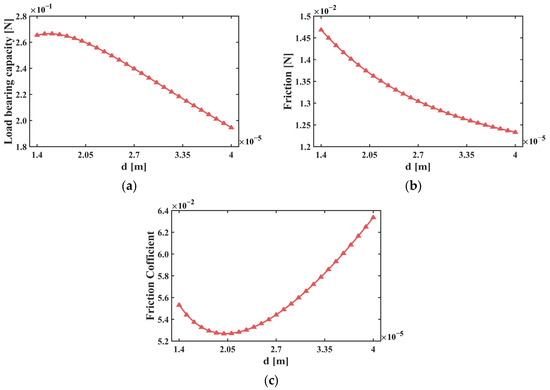
Figure 13. Effects of the spherical cap depth $d$ in range $\left[14,40\right]\mathsf{\mu }\mathrm{m}$ on the tribological performance: (a) load bearing capacity; (b) friction; (c) friction coefficient. The cap base radius $r=230$ $\mathsf{\mu }\mathrm{m}$.

4.2.2. Optimal Results of Geometric Parameters

For readers’ convenience of understanding, the parametric optimization of the spherical cap texture is detailed as follows:

As discussed above, 52 simulations were conducted for this type of texture. The values of the geometric parameters for these simulations are listed in Table 4, together with the load bearing capacity ${\mathsf{\Theta }}_1$, friction ${\mathsf{\Theta }}_2$ and friction coefficient ${\mathsf{\Theta }}_3$ derived from the simulation results based on Equations (11)–(13). Following the AHP method introduced in Section 2.3, normalized vectors of the three tribological parameters, i.e., ${\overline{\mathsf{\Theta }}}_1$, ${\overline{\mathsf{\Theta }}}_2$ and ${\overline{\mathsf{\Theta }}}_3$, could then be obtained to compute the coupled tribological parameter $\mathfrak{R}$, and their values are also listed in Table 4. This table is divided into two modules. The first module consists of results for the 25 parametric designs generated in Table 3 for spherical cap, and the second module includes the results for the 27 parametric designs generated by expanding the value range of d. Consequently, the optimal values of the geometric parameters can be determined by finding the maximum value of $\mathfrak{R}$.

The optimal values of the geometric parameters for all the five textures can be obtained similarly, and they are listed in Table 5, together with their tribological parameters.

Table 5. Optimal values of geometric parameters for the five textures and values of the corresponding tribological parameters.

Texture	Scheme		Tribological Parameter
	$\mathbf{Geometric} \mathbf{Parameters} \left(\mathsf{\mu }\mathbf{m}\right)$	Value	$\mathit{W}\left(\mathit{N}\right)$	$\mathit{f}\left(\mathit{N}\right)$	$\mathit{\mu }$
Spherical cap	$r$	230	0.25849	0.01362	0.05271
	$d$	21
Ellipsoidal cap	$r_a$	280	0.25530	0.01129	0.04423
	$r_b$	230
	$r$	600
	$d$	25
Tree-frog	$r_1$	240	0.29503	0.01501	0.05089
	$r_2$	70
	$d_1$	13
	$d_2$	3
	$d_3$	8
Grass-lip	$d_1$	9	0.12709	0.00584	0.04596
	$d_2$	18
	$d_3$	27
	$l$	66
Nepenthes	$r_1$	300	0.07877	0.01639	0.20802
	$r_2$	200
	$r_3$	30
	$r_4$	20
	$d_1$	7
	$d_2$	4

Figure 14 shows the oil film pressure of the five textures, with the optimal values of their geometric parameters. It clearly shows similar pressure profiles and peak values for the spherical cap, ellipsoidal cap and tree-frog textures, implying that the tribological performances of these three textures with optimized geometric parameters are similar to one another. The grass-lip and nepenthes textures result in a much smaller oil film pressure, and thus have a much lower load bearing capacity.

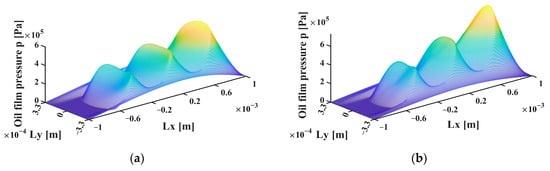
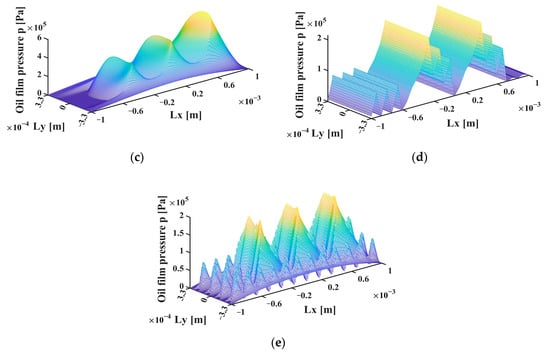
Figure 14. Oil film pressure of the five textures with optimal values of their geometric parameters: (a) spherical cap; (b) ellipsoidal cap; (c) tree-frog; (d) grass-lip; (e) nepenthes.

4.2.3. Comparison of Tribological Performances Between Different Textures

It should be noted that the optimization of geometric parameters in Section 4.2.2 aims at finding the optimal results for one type of surface texture, while the values of the coupled tribological parameter $\mathfrak{R}$ (such as those in Table 4) for one type of surface texture cannot be used for comparison to another type of texture. To compare the tribological performances of the five surface textures, one can simply start from the textures with optimal values of the geometric parameters listed in Table 5 and use the AHP detailed in Section 2.3, whereby the vectors ${\mathsf{\Theta }}_1$, ${\mathsf{\Theta }}_2$ and ${\mathsf{\Theta }}_3$ correspond to the last three columns in Table 5, respectively. Next, the coupled tribological parameters $\mathfrak{R}$ could be obtained using Equations (24)–(26), and they are listed in Table 6.

Table 6. Coupled tribological parameter $\mathfrak{R}$ for comparison of tribological performances between different textures.

Texture		$\mathbf{Coupled} \mathbf{Tribological} \mathbf{Parameter} \mathfrak{R}$
Conventional texture	Spherical cap	0.7096
	Ellipsoidal cap	0.8064
Biomimetic texture	Tree-frog	0.7555
	Grass-lip	0.8521
	Nepenthes	0.2736

Table 6 shows the coupled tribological parameters for different textures, including both conventional textures (spherical cap and ellipsoidal cap) and biomimetic textures (tree-frog, grass-lip, and nepenthes). It indicates that the grass-lip texture is the most favorable texture for the aircraft valve considered in this work. This is because this texture exhibits a very small friction and friction coefficient, although its load bearing capacity is smaller than those of the spherical cap and ellipsoidal cap textures, while the friction and friction coefficient were prescribed with higher degrees of importance compared to the load bearing capacity (see Section 2.3). The nepenthes texture has the lowest value for the coupled tribological parameter $\mathfrak{R}$, indicating that this texture is not a good choice for aircraft valves. For applications requiring a large load bearing capacity, the ellipsoidal cap texture may also be promising because of its high load bearing capacity and low friction and friction coefficient (see Table 5). The tree-frog may not be favorable due to its high friction and friction coefficient, although its load bearing capacity is the highest (see Table 5). A comparison between the conventional and biomimetic textures indicates that only proper biomimetic designs, such as the grass-lip texture, can lead to a favorable coupled tribological performance. A parametrically optimized conventional texture, such as the ellipsoidal cap, can also exhibit very good tribological performance, which is even better than those of some biomimetic textures. Hence, for surface texture design, parametric optimization is as important as the geometry (or shape) design.

It should be noted that users can vary the degree of importance for different parameters depending on the needs of their applications, and the final optimal results may also differ.

5. Conclusions

To improve the tribological performance of oil-lubricated long-life aircraft valves, five surface textures, namely, spherical cap, ellipsoidal cap, tree-frog, grass-lip,= and nepenthes, were introduced to the pin’s surface. Three classical tribological parameters, load bearing capacity, friction and friction coefficient, were obtained by solving the Reynolds equation based on the JFO cavitation boundary condition. Via using AHP, a coupled tribological parameter was defined to conduct parametric optimization of the five surface textures. The final optimization results indicate a ranking of grass-lip, ellipsoidal cap, tree-frog, spherical cap and nepenthes textures, from high to low tribological performance. This implies that for texture design, parametric optimization is as important as selecting a good geometry or shape. The AHP-based parametric optimization method proposed in this study can be widely used for surface textures in various applications, including bearings, shafts, gears and so on. It should also be noted that the degree of importance of tribological parameters in AHP is determined based on the demands of applications, and thus varies depending on the users and the problems studied.