Determination of the Friction Coefficient in the Ring Test for Selected Lubricants Dedicated to the Hot Forging Process of Precision Steel Products
Abstract
:1. Introduction
2. Review of Selected Experimental Methods of Determining the Friction Coefficient and the Tribological Conditions
- Analytical–experimental methods;
- Experimental methods.
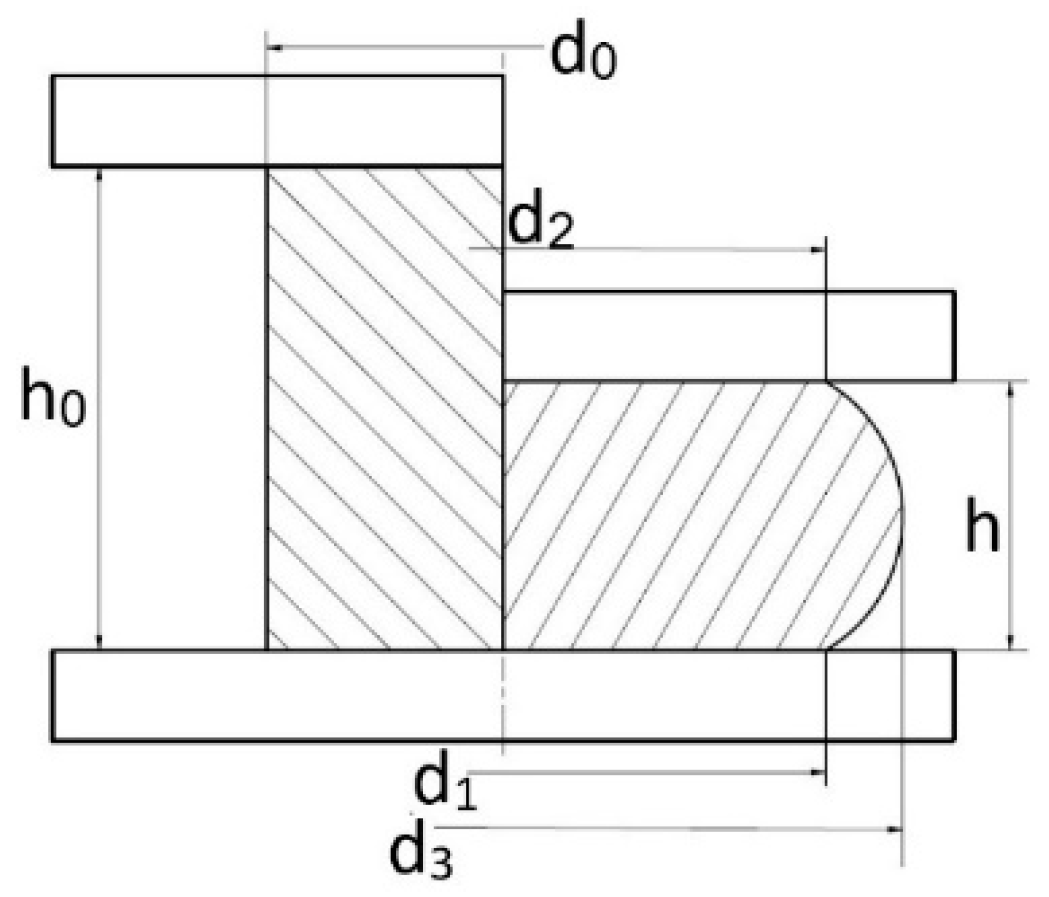
2.1. Method Based on Upsetting a Wedge Sample
2.2. Method of Upsetting with Conical Anvils
2.3. Cylinder Upsetting Method
2.4. Cigar Test
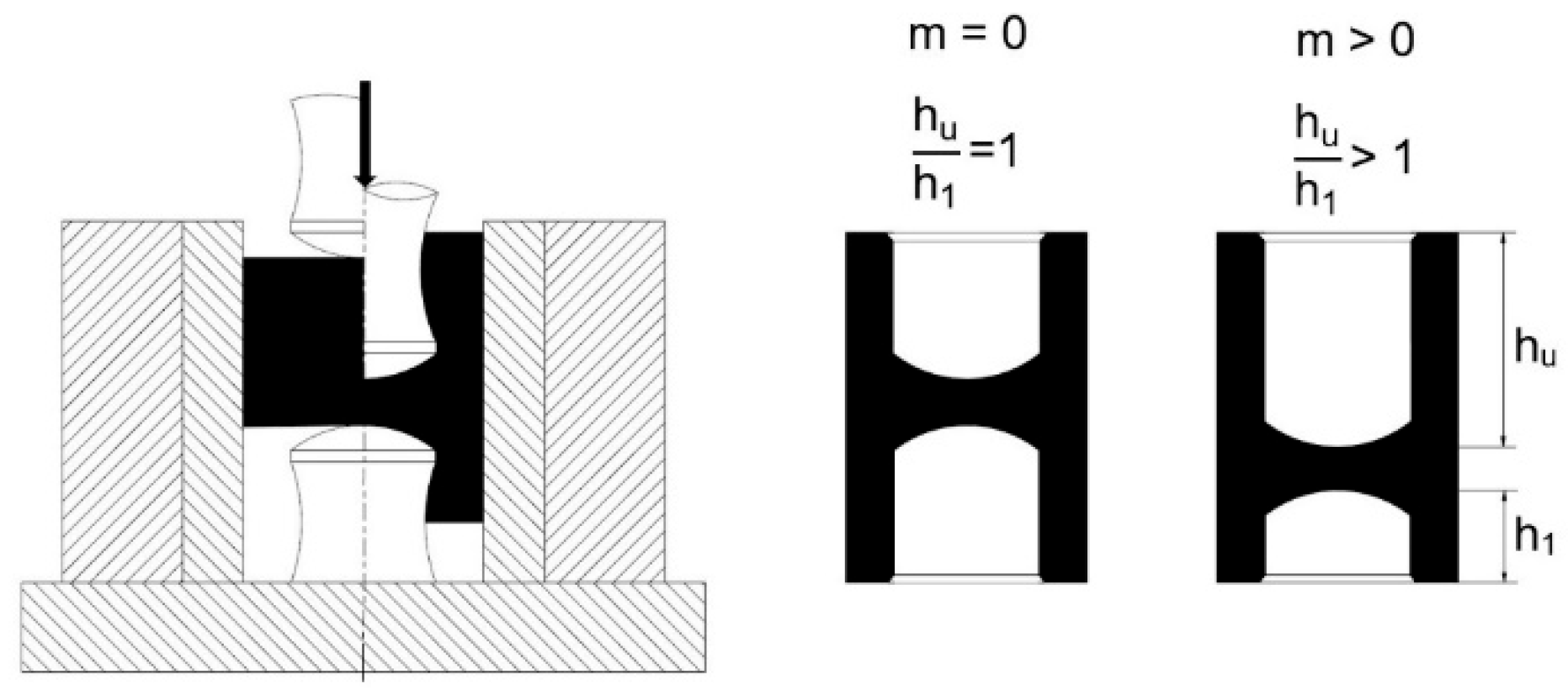
2.5. Test Method for the Process of Extruding Short Objects (Double Cup Extrusion)
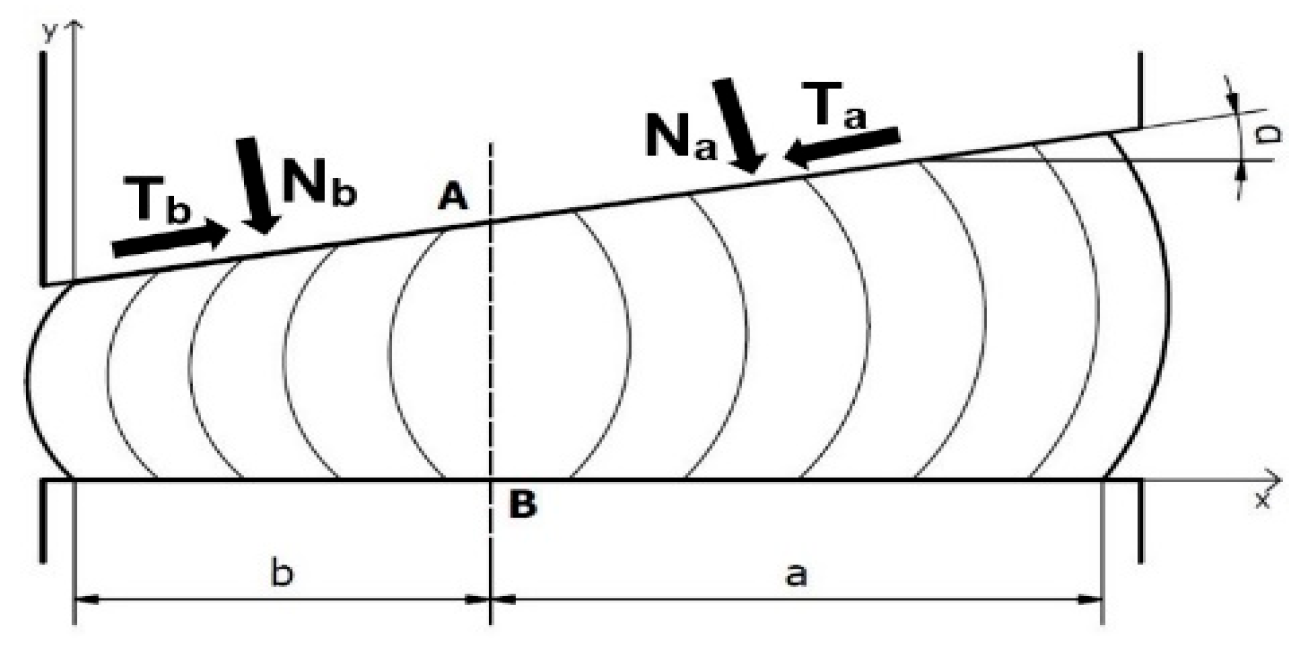
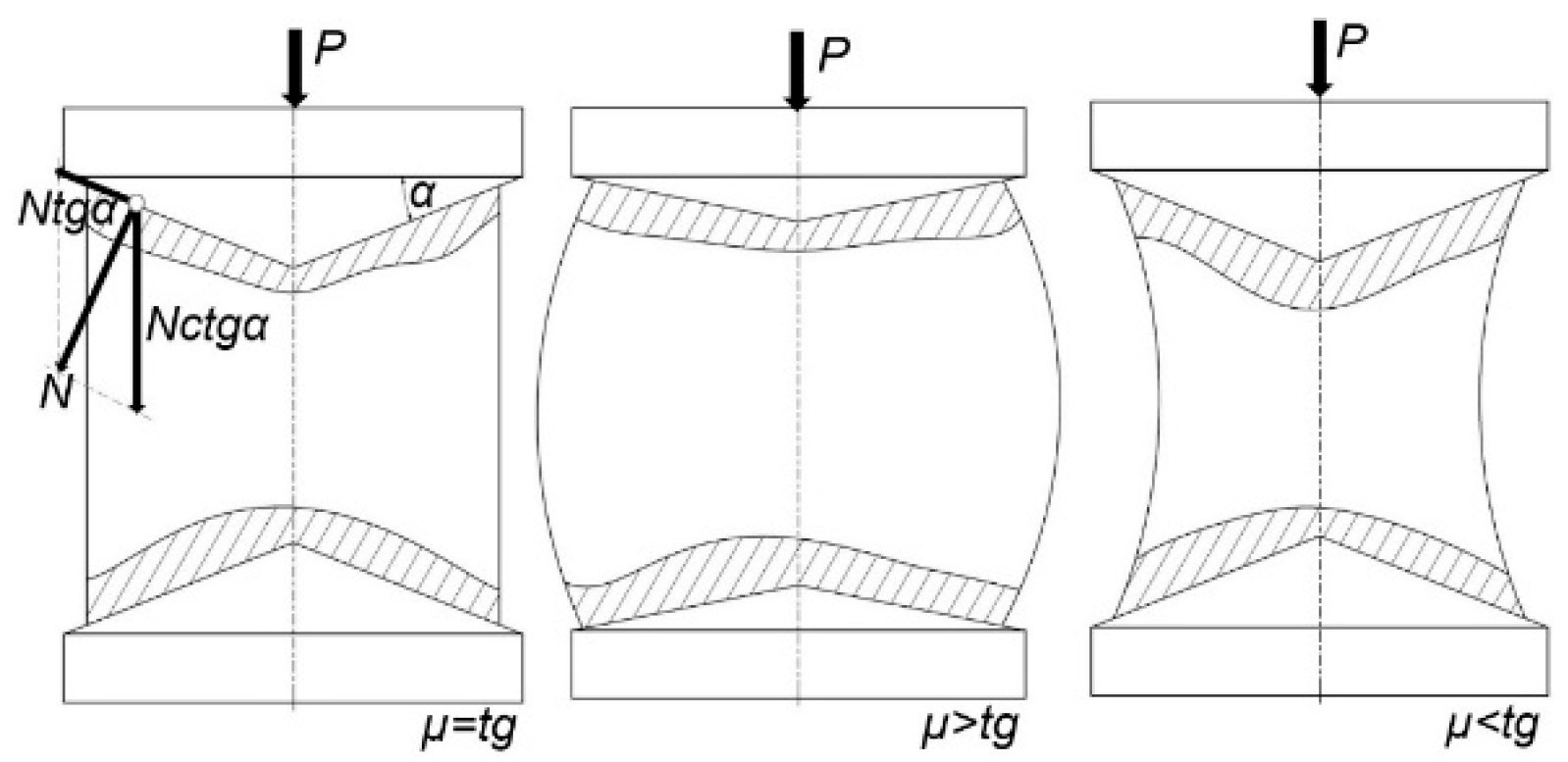
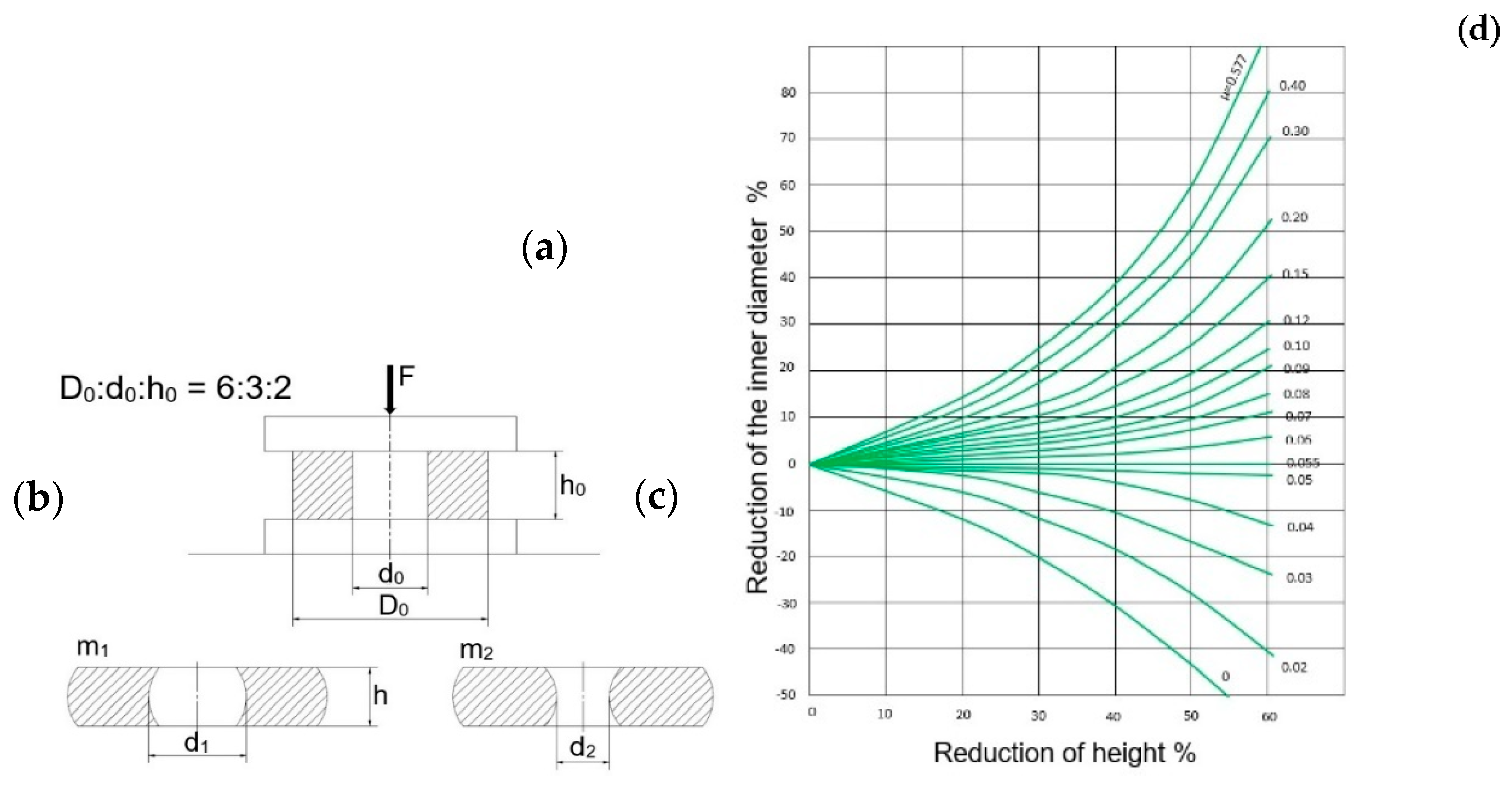
2.6. Ring Test Method
3. Test Subject and Methodology
- -
- Measurements of temperature changes with a thermal camera (FLIR T540 camera, FLIR Systems, Inc. Wilsonville, OR, USA) and a pyrometer with a type K thermocouple (Testo 850 pyrometer, Testo Poland, Pruszkow, Poland);
- -
- Scanning forging tools using the 3D scanner (ROMER Absolute ARM 7520si integrated with the scanner RS3 (Hexagon Manufacturing Intelligence, Aarau, Switzerland), together with the Polyworks software 2015);
- -
- Numerical modeling using Forge 3.0 NxT software (Transvalor, Biot, France);
- -
- CATIA software (V5R20 program by Dassault, Vélizy-Villacoublay, FRANCE) for designing and supporting engineering works;
- -
- Other classical measurement and research methods.
3.1. Test Materials
3.2. Characteristics of the Selected Lubricants
3.3. Description of the Ring Test Procedure
4. Results
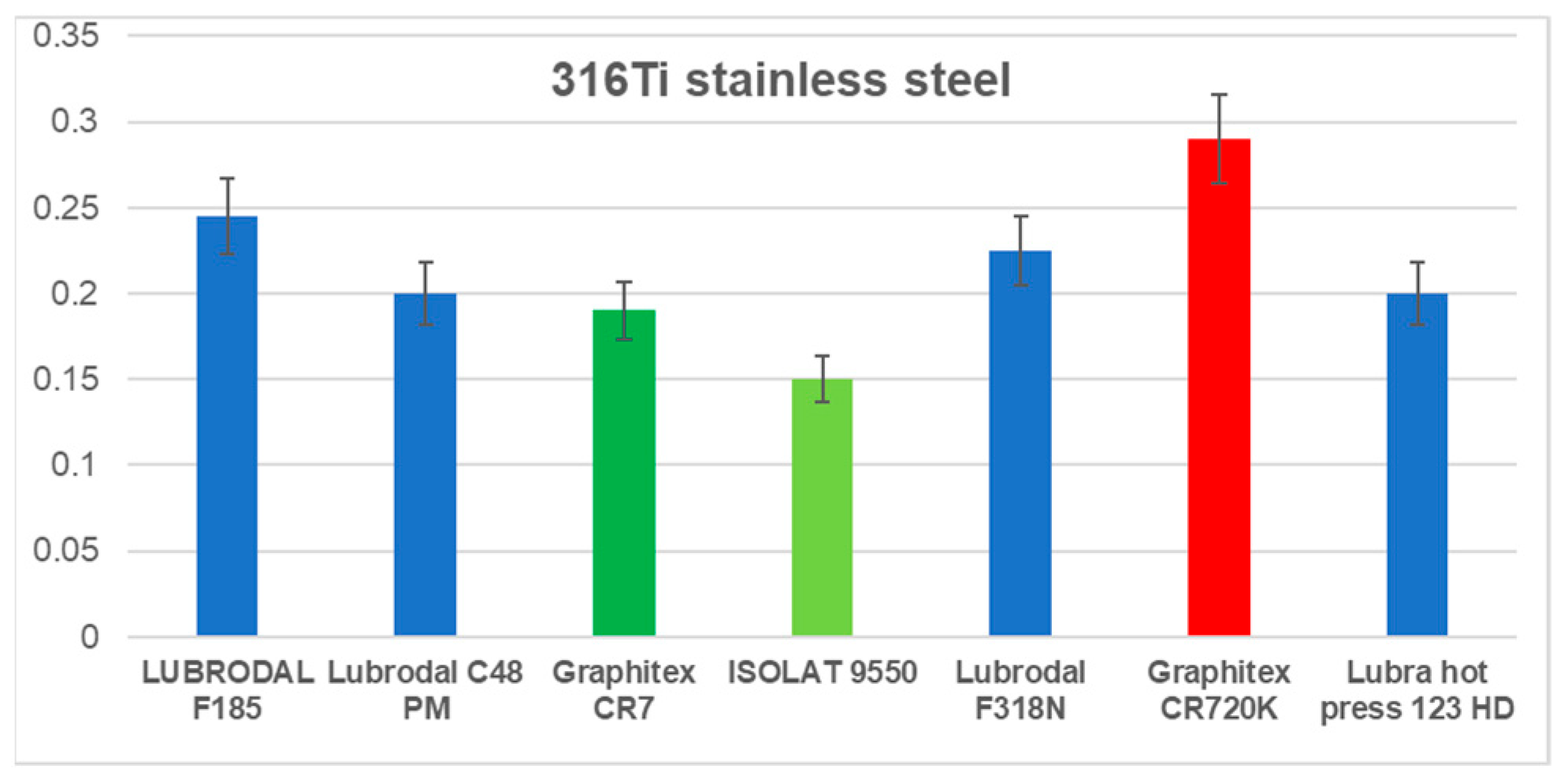
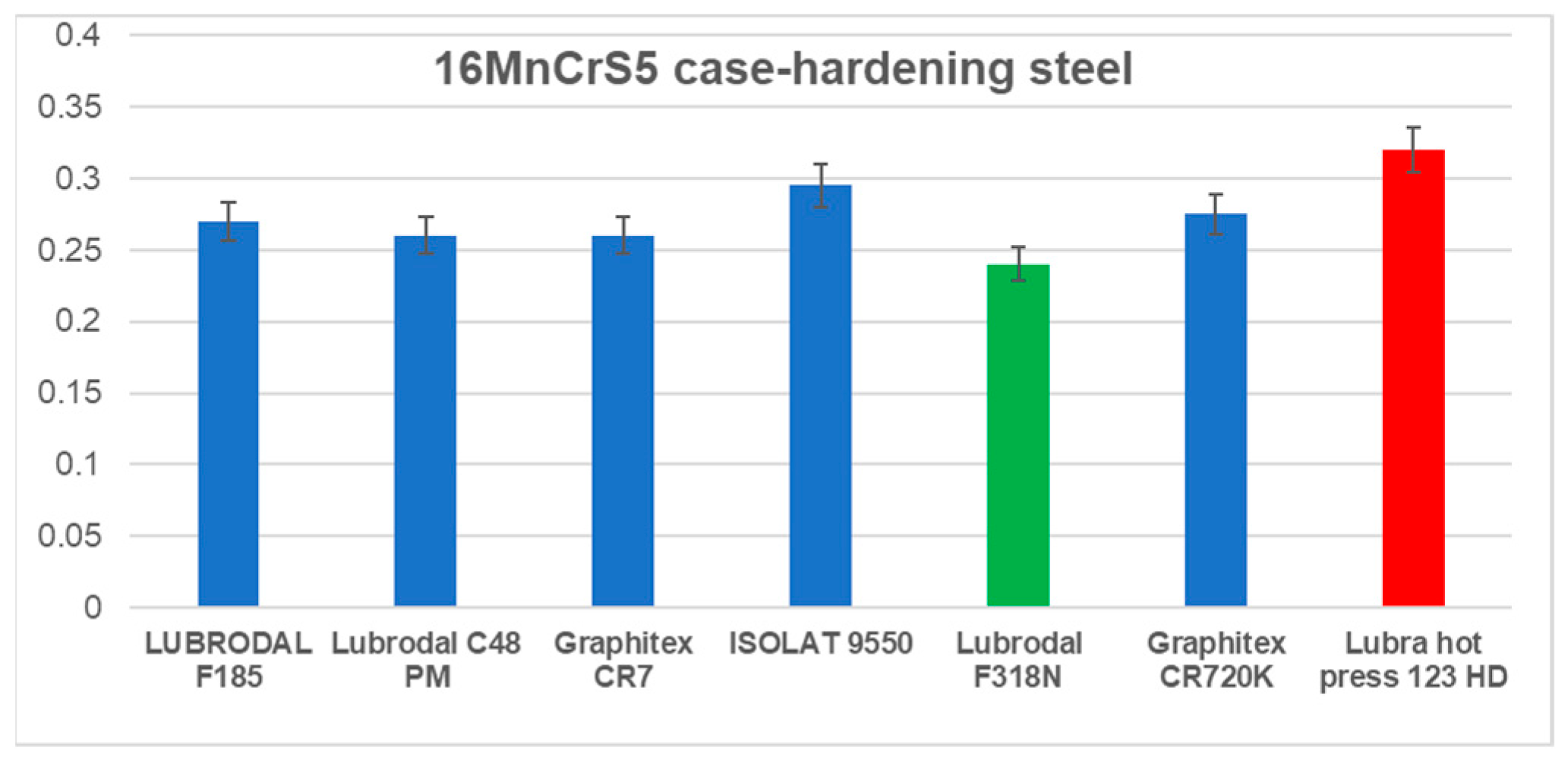
4.1. Results of Friction Coefficient Determination
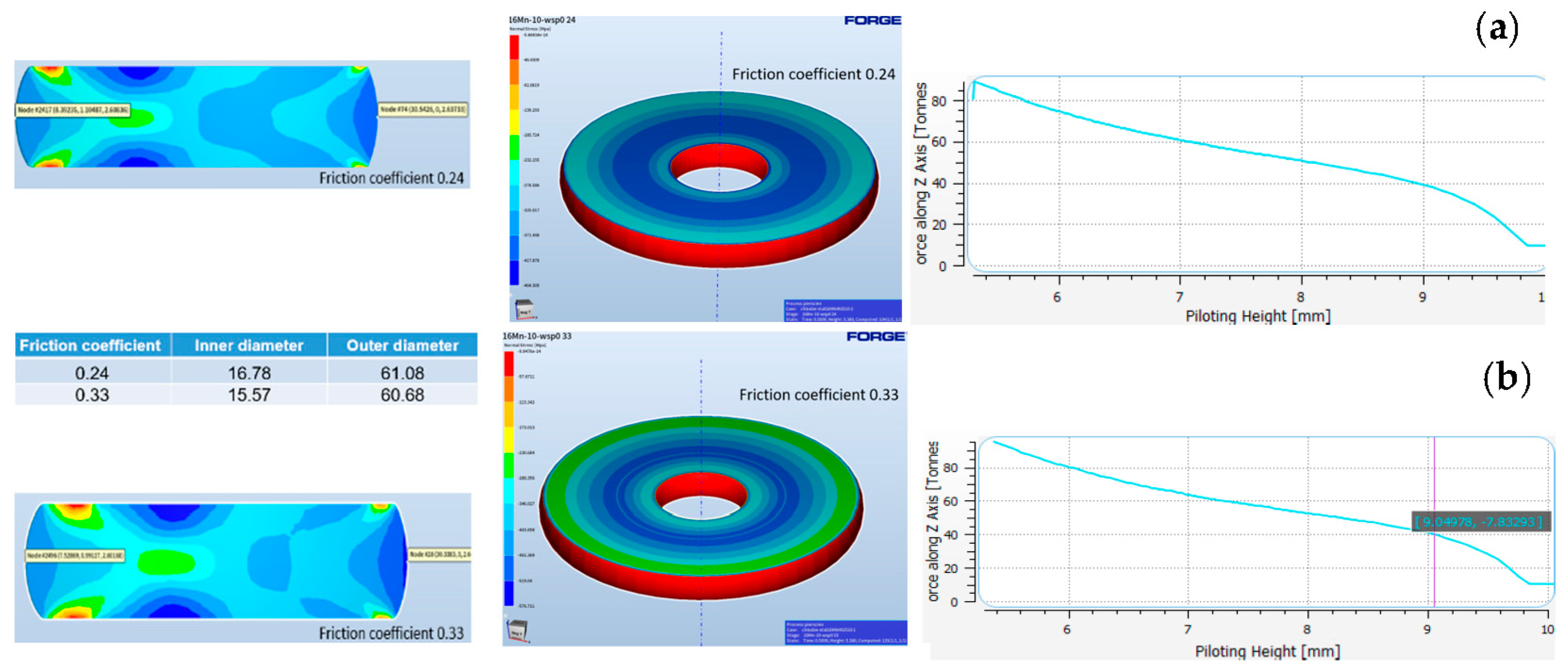
4.2. Results of 3D Scanning
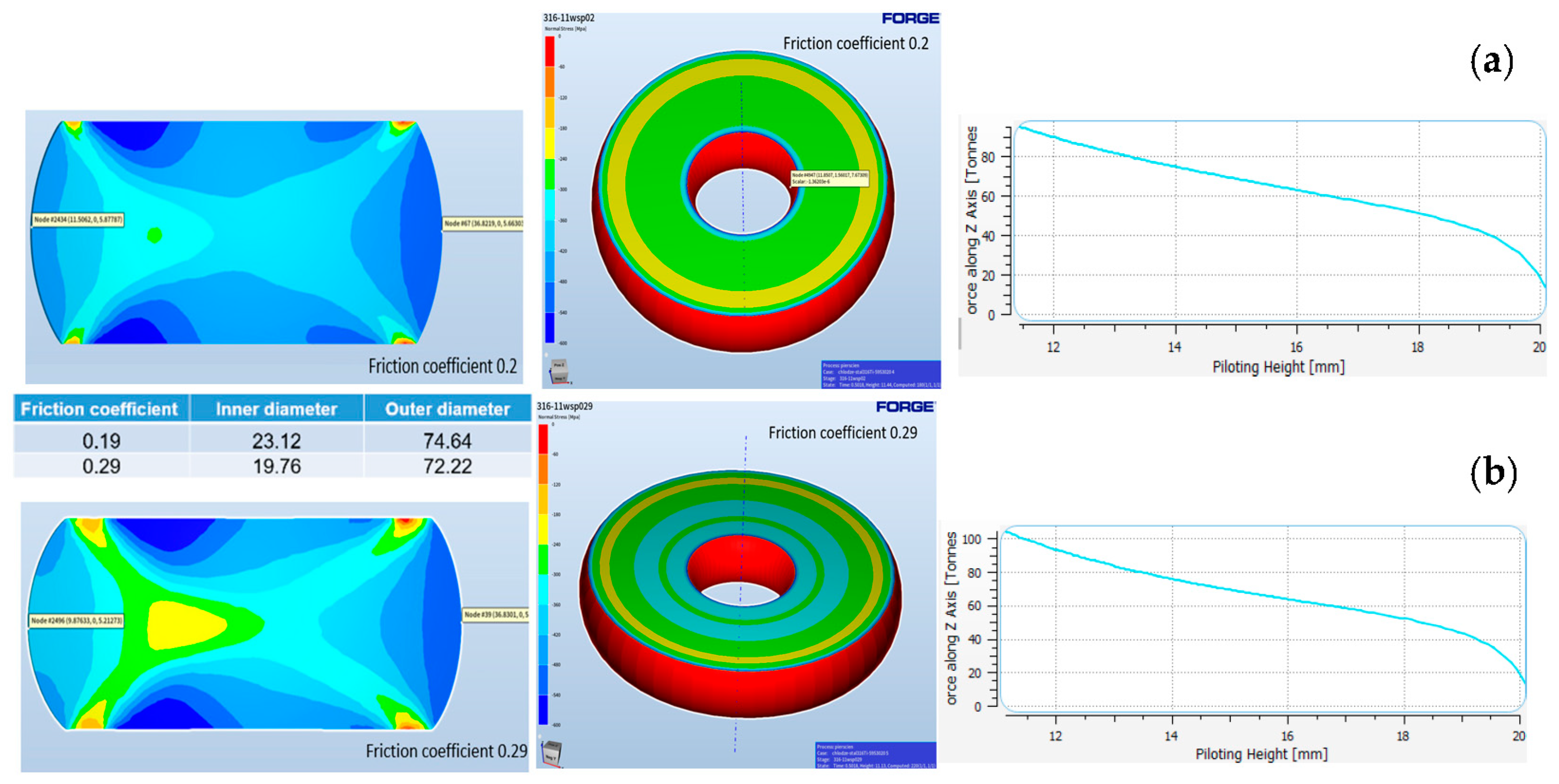
4.3. Results of Numerical Modeling of a Ring Upsetting Test
5. Summary and Conclusions
- -
- For carbon steel, the lowest value was achieved for the lubricant Lubrodal F185 (µ = 0.24) and the highest for Lubr_hot_press 123HD (µ = 0.32). Small differences were observed for this material in the value of friction in comparison to samples made from stainless steel (316Ti).
- -
- For stainless steel, the lowest value was obtained for Graphitex CR 7 (µ = 0.19). The highest friction coefficient was reached for the lubricant Graphitex CR720K (µ = 0.29).
- -
- It should be noted that the samples after the upsetting tests were not always symmetrical, and the internal and external diameters had a partially irregular shape, sometimes an elliptical one, and, so, in such cases, the average value of the internal diameter was determined. This can have an effect on the accuracy of the friction coefficient determination.
- -
- Measurements were made of the geometrical changes with the use of 3D scanning for the extreme friction coefficient values, and the obtained data confirmed the results achieved from the measurements by means of a digital slide caliper and thus also the correctness of the determined friction coefficient values.
- -
- The numerical simulations performed in the Forge 3.0 NxT program confirmed the possibility of obtaining a high agreement between the FEM and experimental tests, as modeling provides reliable information on the geometrical changes and plastic deformations and can constitute a support for the experiment through the use of IT tools, especially numerical modeling, for a more thorough analysis of the tribological conditions in industrial forging processes.
- -
- The key aspect of correct FE modeling is the proper determination of friction coefficients (test conditions very close to industrial) and also the right choice of the technological parameters and the heat transfer coefficients as well as others, along with knowledge and experience in the interpretation of the FEM results.
- -
- The directions of further research will be focused on a complex and long-term analysis of the lubricants selected in the conducted ring tests, which are used in the industrial processes of producing forgings from stainless steel and carbon steel, in the context of not only the lowest friction coefficient value but also other features and properties, which should be exhibited by the optimal lubricating agent.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Joun, M.S.; Moon, H.G.; Choi, I.S.; Lee, M.C.; Jun, B.Y. Effects of Friction Laws on Metal Forming Processes. Tribol. Int. 2009, 42, 311–319. [Google Scholar] [CrossRef]
- Bay, N.; Olsen, D.; Wibom, O.; Martins, P. Classification of Tribology Tests for Bulk Metal Forming; Personal Communications; Danish Technical University: Lyngby, Denmark, 2004. [Google Scholar]
- Male, A.T.; Cockcroft, M.G. A Method for the Determination of the Coefficient of Friction of Metals under Conditions of Bulk Plastic Deformation. Wear 1966, 9, 241. [Google Scholar] [CrossRef]
- Sigvant, M.; Pilthammar, J.; Hol, J.; Wiebenga, J.H.; Chezan, T.; Carleer, B.; van den Boogaard, T. Friction in sheet metal forming: Influence of surface roughness and strain rate on sheet metal forming simulation results. Procedia Manuf. 2019, 29, 512–519. [Google Scholar] [CrossRef]
- Stembalski, M.; Preś, P.; Skoczyński, W. Determination of the friction coefficient as a function of sliding speed and normal pressure for steel C45 and steel 40HM. Arch. Civ. Mech. Eng. 2013, 13, 444–448. [Google Scholar] [CrossRef]
- Ramaraj, T.C.; Shaw, M.C. A New Method of Evaluating Metal-Working Lubricants. J. Tribol. 1985, 107, 216–219. [Google Scholar] [CrossRef]
- Arentoft, M.; Bay, N.; Tang, P.T.; Jensen, J.D. A New Lubricant Carrier for Metal Forming. CIRP Ann. 2009, 58, 243–246. [Google Scholar] [CrossRef]
- Polcar, T.; Novák, R.; Široký, P. The Tribological Characteristics of TiCN Coating at Elevated Temperatures. Wear 2006, 260, 40–49. [Google Scholar] [CrossRef]
- Kubart, T.; Polcar, T.; Kopecký, L.; Novák, R.; Nováková, D. Temperature Dependence of Tribological Properties of MoS2 and MoSe2 Coatings. Surf. Coat. Technol. 2005, 193, 230–233. [Google Scholar] [CrossRef]
- Ludema, K.C. Mechanism-Based Modeling of Friction and Wear. Wear 1996, 200, 1–7. [Google Scholar] [CrossRef]
- Hawryluk, M.; Dudkiewicz, Ł.; Marzec, J.; Rychlik, M.; Tkocz, R. Selected aspects of lubrication in die forging processes at elevated temperatures—A review. Lubricants 2023, 11, 206. [Google Scholar] [CrossRef]
- Wu, Y.; Recklin, V.; Groche, P. Strain Induced Surface Change in Sheet Metal Forming: Numerical Prediction, Influence on Friction and Tool Wear. J. Manuf. Mater. Process. 2021, 5, 29. [Google Scholar] [CrossRef]
- Jeswiet, J.; Wild, P. Sensing friction: Methods and devices. J. Form. Process. 2001, 4, 125–134. [Google Scholar] [CrossRef]
- Sofuoglu, H.; Gedikli, H. Determination of Friction Coefficient Encountered in Large Deformation Processes. Tribol. Int. 2002, 35, 27–34. [Google Scholar] [CrossRef]
- Sofuoglu, H.; Gedikli, H.; Rasty, J. Determination of Friction Coefficient by Employing the Ring Compression Test. J. Eng. Mater. Technol. 2001, 123, 338–348. [Google Scholar] [CrossRef]
- Menezes, P.L.; Kumar, K.; Kishore; Kailas, S.V. Influence of Friction during Forming Processes—A Study Using a Numerical Simulation Technique. Int. J. Adv. Manuf. Technol. 2009, 40, 1067–1076. [Google Scholar] [CrossRef]
- Ramezani, M.; Ripin, Z.M. A Friction Model for Dry Contacts during Metal-Forming Processes. Int. J. Adv. Manuf. Technol. 2010, 51, 93–102. [Google Scholar] [CrossRef]
- Bucholz, E.W.; Kong, C.S.; Marchman, K.R.; Sawyer, W.G.; Phillpot, S.R.; Sinnott, S.B.; Rajan, K. Data-Driven Model for Estimation of Friction Coefficient Via Informatics Methods. Tribol. Lett. 2012, 47, 211–221. [Google Scholar] [CrossRef]
- Zhou, C.; Hu, B.; Qian, X.; Han, X. A Novel Prediction Method for Gear Friction Coefficients Based on a Computational Inverse Technique. Tribol. Int. 2018, 127, 200–208. [Google Scholar] [CrossRef]
- Weinmann, K.J.; Bhonsle, S.R.; Gerstenberger, J. On the Determination of the Coefficient of Friction and the Friction Factor by the Strip-Tension Friction Test. CIRP Ann. 1990, 39, 263–266. [Google Scholar] [CrossRef]
- Storchak, M.; Möhring, H.-C.; Stehle, T. Improving the Friction Model for the Simulation of Cutting Processes. Tribol. Int. 2022, 167, 107376. [Google Scholar] [CrossRef]
- Han, H. Determination of Mean Flow Stress and Friction Coefficient by the Modified Two-Specimen Method in Cold Rolling. J. Mater. Process. Technol. 2005, 159, 401–408. [Google Scholar] [CrossRef]
- Szarapin, E.F.; Maksimov, N.V. Primenenie Osadki Klinovidnych Obrazcov Dlja Opredelelenija Koefficenta Trenija. Izv. VUZ Cern. Metall. 1963. [Google Scholar]
- Dilmec, M.; Arap, M. Effect of Geometrical and Process Parameters on Coefficient of Friction in Deep Drawing Process at the Flange and the Radius Regions. Int. J. Adv. Manuf. Technol. 2016, 86, 747–759. [Google Scholar] [CrossRef]
- Halaunbrenner, M. Directional Effects in Friction. Wear 1960, 3, 421–425. [Google Scholar] [CrossRef]
- Fricker, D.C.; Wanheim, T. Low Friction Coefficient Estimation for Model Material Experiments. Wear 1974, 27, 303–317. [Google Scholar] [CrossRef]
- Siebel, E.; Pomp, A. Further Development of the Compression Test. Mitt. Kaiser–Wilhelm-Inst. Eisenforsch. 1928, 10, 55–62. (In German) [Google Scholar]
- Schrader, T.; Shirgaokar, M.; Altan, T. A Critical Evaluation of the Double Cup Extrusion Test for Selection of Cold Forging Lubricants. J. Mater. Process. Technol. 2007, 189, 36–44. [Google Scholar] [CrossRef]
- Bulzak, T.; Tomczak, J.; Pater, Z. A Comparative Analysis of Hot and Cold Flashless Forging of a Stepped Shaft Using Vertically-Parted Dies. Int. J. Adv. Manuf. Technol. 2021, 116, 2521–2530. [Google Scholar] [CrossRef]
- Gontarz, A.; Dziubińska, A.; Okoń, Ł. Determination of friction coefficients at elevated temperatures for some Al, Mg and Ti alloys. Arch. Metall. Mater. 2011, 56, 379–384. [Google Scholar] [CrossRef]
- Sánchez Egea, A.J.; Martynenko, V.; Abate, G.; Deferrari, N.; Martinez Krahmer, D.; López de Lacalle, L.N. Friction capabilities of graphite-based lubricants at room and over 1400 K temperatures. Int. J. Adv. Manuf. Technol. 2019, 102, 1623–1633. [Google Scholar] [CrossRef]





| C | Si | Mn | P | S | Cr | V | Ni | W | Mo | Ni | Ti | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 316 Ti | 0 | 0 | 0 | 0 | 0 | 16.5 | 2.0 | 10.5 | 0 | Min. | |||
| 0.08 | 1.0 | 2.0 | 0.045 | 0.015 | 18.5 | 2.5 | 13.5 | 0.70 | Max. | ||||
| 16MnCrS5 | 0.14 | 0.17 | 1.00 | 0 | 0 | 0.80 | 0 | 0 | 0 | Min. | |||
| 0.19 | 0.37 | 1.30 | 0.035 | 0.035 | 1.10 | <0.05 | 0.3 | 0.2 | Max. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudkiewicz, Ł.; Hawryluk, M.; Ziemba, J.; Miżejewski, A.; Polak, S.; Marzec, J.; Szymańska, T. Determination of the Friction Coefficient in the Ring Test for Selected Lubricants Dedicated to the Hot Forging Process of Precision Steel Products. Lubricants 2023, 11, 399. https://doi.org/10.3390/lubricants11090399
Dudkiewicz Ł, Hawryluk M, Ziemba J, Miżejewski A, Polak S, Marzec J, Szymańska T. Determination of the Friction Coefficient in the Ring Test for Selected Lubricants Dedicated to the Hot Forging Process of Precision Steel Products. Lubricants. 2023; 11(9):399. https://doi.org/10.3390/lubricants11090399
Chicago/Turabian StyleDudkiewicz, Łukasz, Marek Hawryluk, Jacek Ziemba, Adrian Miżejewski, Sławomir Polak, Jan Marzec, and Tatiana Szymańska. 2023. "Determination of the Friction Coefficient in the Ring Test for Selected Lubricants Dedicated to the Hot Forging Process of Precision Steel Products" Lubricants 11, no. 9: 399. https://doi.org/10.3390/lubricants11090399
APA StyleDudkiewicz, Ł., Hawryluk, M., Ziemba, J., Miżejewski, A., Polak, S., Marzec, J., & Szymańska, T. (2023). Determination of the Friction Coefficient in the Ring Test for Selected Lubricants Dedicated to the Hot Forging Process of Precision Steel Products. Lubricants, 11(9), 399. https://doi.org/10.3390/lubricants11090399





