Abstract
During curling sports, the movement of the stone is affected by the quality of the ice. Therefore, the delivery team led by the ice maker hopes that the quality of the ice surface will be stable and that the athletes will always ‘read the ice’ and pay attention to the small changes in the ice surface. This phenomenon is the charm of curling. Many friction models have been proposed to describe the regularity of the curling motion. In the curling competitions of the 2022 Beijing Winter Olympic Games, the 2021 World Wheelchair Curling Championships, and the warm-up competition before, the research team installed a video image capture system in the arena to capture and record the data of the curling motion by using the depth neural network and object tracking algorithm. Further motion data research verifies the relationship between the friction coefficient and the speed. The quality control parameter of ice rink α is proposed, which is related to the influencing factors of the ice surface temperature, the ice hardness, the size of the pebble point, and the width of the curling friction band. The quality of the curling ice rink can be evaluated accurately and comprehensively by using parameter α. Based on the relationship between the friction coefficient and the speed, a physical model of horizontal sliding of the curling stone is established, which agrees well with the results of data obtained from video acquisition. Therefore, the movement distance along the rink can be accurately predicted. This paper analyzes the relationship between the long-time (the time it takes for the curling stone to travel between the two hog lines) and the stop position and that between the long-time and the split-time (the time it takes for the curling stone to travel from the back line to the hog line). Based on this result, a ruler can be established to assist athletes in estimating the sliding distance of the stone before curling throwing. This research also studies the relationship between three factors (the sliding speed in the x-direction, the angular speed, and a tiny lateral deflection speed in the y-direction) and the deviation of the stone. At the same time, there are also some interesting phenomena of the lateral deflection of the stone, such as the relationship between the lateral deflection angle tanθ and the initial lateral speed. As a result, the prediction of the curling stone’s exact final location can be realized. In summary, this article proposes an indicator for evaluating the quality of ice rinks and a physical model of curling based on the curling friction model, which is validated by data obtained from a video capture system of the 2022 Beijing Winter Olympics. The results described above have been applied in the post-match operation of the National Aquatics Center to guide the production of Olympic-grade ice surfaces and to guide athletes to “read ice” accurately during training.
1. Introduction
Because of the success of the 2022 Beijing Winter Olympics in China, snow and ice sports have attracted wide attention [1]. Amongst these national winter sports is curling, which combines strategy and skill and needs a lot of concentration and precision [2,3,4].
In curling, the rotating stone follows a curled trajectory instead of continuing to follow a straight line. In the case of a stone sliding clockwise, a transverse motion component will develop on the right-hand side, and vice versa [5,6]. Scholars have made numerous attempts to explain curling motion in the past century. For example, many researchers have used forward–backward asymmetry friction over the running band of curling stones to predict the observed behavior of the stones. The forward–backward asymmetry friction models are divided into six categories based on different mechanisms explaining the asymmetry. There are five types of models: the pressure difference model, the water layer model, the snowplow model, the evaporation–abrasion model, the scratch-guiding model, and the edge model [3,7,8,9,10,11]. A pivot-slide-based model has recently been used to study how the stone follows a curved trajectory [12,13]. In short, despite several proposed models in the surveyed literature, the mechanism remains under scientific debate, primarily due to the complicated moving process and a lack of sufficient observational data [5,14].
The curling stone is specially made of about 20 kg of granite rock with a rough bottom. The bottom of the curling stone is in contact with the curling ice through a raised annulus named the running band/RB, whose width is approximately 6 mm; the diameter is approximately 120 mm. Many small protrusions on the curling ice, known as pebbles, reduce friction and increase the sliding distance. There are about 104 pebbles per square meter [15,16]. Pebbles are produced by spraying purified water droplets onto the initially flat surface of the ice. The size of the spray hole controls the pebble size, with an average height of 1–2 mm and a diameter of 1–5 mm. Approximately 10 to 100 pebbles are constantly in contact with the curling stone RB. As a result, the stone exerts considerable pressure on each pebble, from about 0.4 to 8.1 MPa [17]. This combination of features contributes to the stone’s comprehensive movement and enhances the game’s entertainment value. A study conducted by Kameda et al. [10] in 2020 found that the sliding distance of the curling stone was primarily influenced by the stone RB (surface roughness and area) rather than the surface conditions of the ice. The curl phenomenon can be regarded as the result of multiple physical mechanisms working together, whose influence can be expressed by the stone–ice friction coefficient [17].
There are two forms of study of the stone–ice friction coefficient, which are experiment-based and theory-based research. On the one hand, Penner [18] derived the coefficient of kinetic friction between a curling rock and an ice surface. The result was compared with an experiment using a curling rock dragged along the ice of a local curling rink at a constant velocity. However, the range of the coefficient of kinetic friction cannot be greater than approximately 1 m/s or less than 0.15 m/s. Furthermore, Nyberg et al. designed a special device to measure the friction force versus the sliding speed for a curling stone by connecting the motor-driven rotating cylinder and the stone through a thin wire [19]. All of the above experimental results show that the coefficient of friction is related to the sliding speed of the curling stone and the roughness of the stone’s RB (running band). On the other hand, many theoretical models with limitations have been proposed for kinetic friction on ice [20,21,22,23]. One of the limited models was presented by Penner [18], which calculated the coefficient of kinetic friction from the perspective of energy. In addition, based on the ice-skating friction derivation method [24], Lozowski et al. [25] developed a physical model of the stone–ice friction coefficient, which had good agreement with the experiment results.
In fact, many curling competitions have been held in the past. If the results of these competitions could be adequately collected, this would provide sufficient experimental data to support the study of curling. However, using traditional experimental methods to collect these curling data can have a negative impact on the sport. Fortunately, the rapid development of computer vision technology in recent years has provided new ideas for curling research, making it possible to make full use of curling competition data [26].
Recently, Murata [27] adopted a digital image analysis technique to perform precision kinematic measurements of a curling stone’s motion. He found that swinging around the discrete left–right asymmetric friction points was the dominant curling mechanism. Li et al. [28] measured the stone–ice friction coefficient on-site in a prefabricated ice rink based on computer vision technology. However, there are few studies of curling using computer vision technology, so the dataset is relatively small. The 2022 Beijing Winter Olympics provided a large amount of high-level video recognition data using the CurlingHunter system. If these data can be utilized, they will provide more accurate results for the study of curling.
The remainder of the paper is organized as follows. The second part introduces the curling rules, prefabricated assembly ice rinks, and the CurlingHunter systems used in live curling competitions. The third part explains the terminology used in the text. The fourth part cites the model of the friction coefficient between the stone and the ice surface. It proposes a model of the x-direction (the direction along the rink) movement of the stone based on this friction model. At the same time, the relational equation of the y-direction (the direction perpendicular to the rink) deflection of the stone is obtained, which can realize the prediction of the exact position of the stone’s landing point. The fourth part also analyzes the relationship between the long-time (the time it takes for the curling stone to travel between the two hog lines) and the stop position, as well as the relationship between the long-time and the split-time (the time it takes for the curling stone to travel from the back line to the hog line). Finally, conclusions are drawn from the video recognition results and analyses.
2. Methods
The ‘Ice Cube’, transformed from the ‘Water Cube’, was used to measure curling stone motion on location for the Beijing Winter Olympics. The following section presents a brief overview of the information on the researched curling ice rink and measuring methods.
2.1. Curling Competition
As a combination of bowling and chess, curling, which requires a lot of concentration and precision, is a turn-based game played alternately by two teams on the ice [2,3,4]. The two teams consist of eight athletes, and the competition usually consists of ten rounds. The curling ice rink consists of four ice tracks, as shown in Figure 1. Each ice track consists of a side line, a house region, a hack, a tee line, and a hog line. The movement of the stone is affected by the quality of the ice. Unlike the ice surface of figure skating or short-track speed skating, the ice surface of curling is not entirely flat. Instead, its top layer is covered with specially made tiny particles, so the ice is also called pebbled ice. The pebbled ice creates the main friction between the stone and the ice. The interaction between the stone and the ice affects the direction and speed of the stone. The pebbled ice slows down the stone and also affects its bending trajectory. At the same time, the curling stones are not symmetrical; they are designed to bend or rotate as they slide. The curling stones have a concave base on one side and a convex shape on the other. The curling stones will naturally bend towards the concave side. Players use this design to control the path of the stone’s movement. Scrubbing is also an essential element of curling. Players use a broom to wipe the ice in front of the stone. This action heats the ice slightly and temporarily reduces the friction between the stone and the ice. Scrubbing can help the stone travel farther and straighter or affect its curving trajectory. The timing and strength of the scrub are key tactical elements. In summary, the movement of curling stones is primarily influenced by the interaction between the stone and the pebble texture on the ice surface, as well as the delivery technique used by the players.
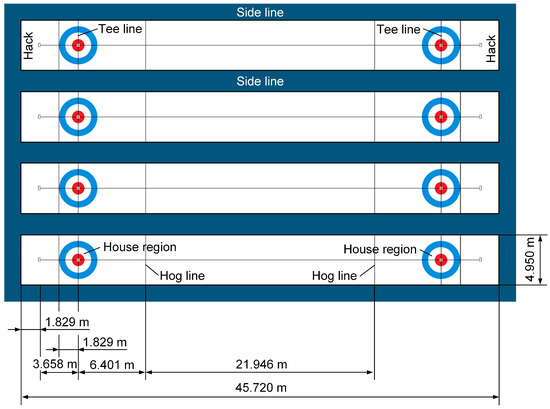
Figure 1.
The layout of the curling ice rink.
2.2. Curling Ice Rink
Figure 2 illustrates the prefabricated ice rink in the Notational Aquatics Center in Beijing, China, which was constructed in preparation for the Beijing Winter Olympics in 2022. Unlike traditional ice rinks, which are constructed directly on rigid concrete bases, the prefabricated rink was constructed on a steel frame and concrete slab supporting system based on a swimming pool. The ice sheets were 60–70 mm thick and embedded with a network of cooling pipes and the honeycombed pipe support.

Figure 2.
The prefabricated curling ice rink under construction.
Curling rinks in international competitions need to meet a number of high-quality requirements to ensure the fairness of the game and the safety of the athletes, such as a level ice surface, appropriate pebbled ice, correct temperature control, correct humidity control, etc. In order to meet the high-quality requirements for ice rinks at international competitive events, pebbled ice is prepared by experts in the field. The temperature of the ice surface, the air closest to the ice sheet, and the air 1500 mm above the ice sheet are maintained, respectively, at −6 °C, 7~9 °C, and 12~14 °C. The humidity ratio of the air (the mass of moisture contained in a unit mass of air) closest to the ice sheet and the air above the ice sheet 1500 mm are 2~3 g/kg and 3~3.5 g/kg. This distribution of temperature and humidity helps create the right conditions during a curling match. The cooler air in proximity to the ice surface aids in maintaining a lower temperature on the ice sheet, ensuring that the curling stone can glide smoothly on a solid ice surface. Simultaneously, the relatively warmer air at higher altitudes contributes to the formation of pebble ice, thereby enhancing the curling stone’s sliding conditions. This distribution of humidity and temperature is orchestrated to uphold the optimal competitive conditions for curling matches.
2.3. Methods of Measurement
The curling game has strict regulations that prohibit adding auxiliary equipment on the curling stones. As a result, an AI-based curling game system named CurlingHunter, which utilizes non-contact measurements based on machine vision, is used [29].
As shown in Figure 3a–c, the CurlingHunter comprises forty-two cameras arranged in the Ice Cube to ensure that at least three cameras capture all parts of the ice track from different perspectives. There are three main modules in CurlingHunter (Figure 3d): single-camera tracking and visual positioning, multi-camera data association and trajectory generation, and motion analysis and trajectory prediction. During curling games, it can display the actual trajectory, the predicted trajectory, and the house regions of curling on giant screens in curling stadiums and through live streaming media platforms online in real time to assist the game. It not only can increase the attraction of the game to the spectators, but it also can assist the athletes in routine training.
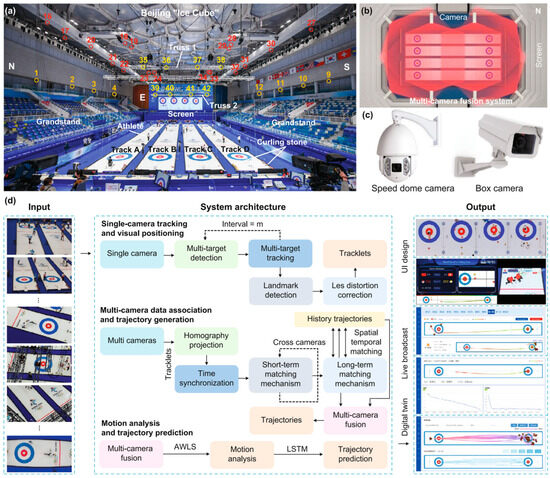
Figure 3.
Equipment and system architecture of the CurlingHunter. (a) Forty-two cameras were arranged in “Ice Cube” and divided into three heights, i.e., 2nd floor of grandstand (F2), Cat walk (CW), and Truss, where three colors of orange, red, and yellow were used to represent different heights. (b) Schematic diagram of multicamera fusion system with eight cameras. (c) Two types of cameras, i.e., speed dome camera and box camera. Speed dome camera can adjust its angle through its cradle head while box camera cannot move when it is fixed, but its resolution is higher. (d) System architecture. CurlingHunter consists of three main modules: single-camera tracking and visual positioning, multicamera data association and trajectory generation, and motion analysis and trajectory prediction. The input is images taken by each camera, and the output is actual trajectories, predicted trajectories, house regions, motion analysis of curling stones, etc. Adapted from [29].
The management system of the CurlingHunter consists of three subsystems: the trajectory management system, the motion management system, and the ice-surface-path management system. The trajectory of the curling stone can be dynamically displayed by the trajectory management system. The velocity, acceleration, and rotation angle of the curling stone can be dynamically displayed by the motion management system. The smoothness expressed by the friction coefficient of the ice surface during the curling movement can be dynamically displayed by the ice-surface-path management system. Therefore, this study uses the actual motion data collected from curling competitions based on the management system for a mechanical analysis study of curling. In this paper, we are focusing on the trajectory of the curling stone, and we have developed a physical model of the curling process.
It has been demonstrated that the CurlingHunter possesses remarkable real-time performance (~9.005 ms), high accuracy (30 ± 3 cm under measurement distance > 20 m), and good stability. The high accuracy of curling video capture can ensure position and time deviation. It has been successfully applied in actual curling games, including the 2021 Wheelchair Curling World Championships from 23 October 2021 to 30 October 2021; the 2022 Beijing Winter Olympic Games of curling from 10 February 2022 to 17 February 2022; the 2022 Beijing Winter Paralympic Games of curling from 5 March 2022 to 15 March 2022; and the 2022 Junior Curling Tournament from 1 April 2022 to 10 April 2022, and it achieved excellent results.
The research team deployed structural performance detection sensors under the ice, temperature sensors inside the ice, and air temperature and humidity sensors above the ice. During the above competitions, the temperature and humidity of the ice rink and the environment were completely recorded to ensure that the ice surface would not crack or frost. The acquisition of data in curling is heavily reliant on video capture systems, while the role of sensors lies in monitoring the deformation of the entire prefabricated field, as well as site factors, such as ice temperature and air temperature. Through real-time sensor monitoring, the integrity and safety of the venue are ensured, meeting the environmental prerequisites for curling matches, and enabling prompt adjustments based on sensor-derived data.
3. Basic Concepts of Curling
For a more comprehensive understanding, this section presents some basic concepts of curling used in this study. Figure 4 presents a diagrammatic sketch of the curling ice track.
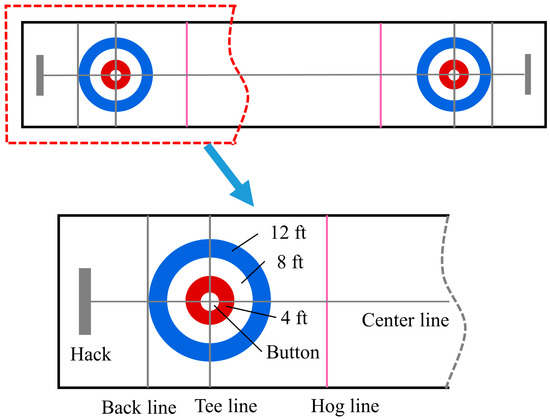
Figure 4.
A diagrammatic sketch of the curling ice track.
The “hack” is a specific area on the curling rink, typically situated at both ends of the curling sheet. It consists of a marker (commonly referred to as the “hack”) and a rubber foothold known as the “hack foot”. In a match, athletes position themselves within the “hack” area and initiate their slide from here to propel the curling stone towards the center of the sheet, which is the target area (the house).
The “house” is the target area on a curling rink, typically located at both ends of the curling sheet, corresponding to the hack area. The house is a rectangular region, typically comprising a circular center and a series of concentric circles, which is 1 foot (0.31 m), 4 feet (1.22 m), 8 feet (2.44 m), and 12 feet (3.66 m) in diameter. Curling aims to deliver the curling stone into the house area, aiming to place it as close to the center of the concentric circle as possible to score points. Different circles within the house have varying point values, with shots closer to the center generally earning higher scores.
The “hog line” is a line on the curling rink, located at each end of the rink, some distance from the house area. In official matches, a curling stone must cross the hog line during the delivery process; otherwise, it is deemed an invalid throw, and the stone is removed from the game. The presence of the hog line ensures that curling stones are not released too early or too late, maintaining fairness in the game. The “back line” is a line on the curling rink, usually at each end of the rink, opposite the hog line. The back line is used to determine whether the curling stone is completely clear of the rink for scoring purposes. When a curling stone crosses the back line, it is considered to have fully entered the rink.
During the process from the back line to the first hog line, the athletes give the stone a sliding speed. At the first hog line, the athlete gives the stone an angular velocity of rotation, and the stone breaks away from the athlete’s control and slides freely. Therefore, the position of the stone at the first hog line is defined as the initial position of the analysis. On this basis, the concept of initial velocity is proposed as the speed of the curling stone on the first hog line, and the initial acceleration is proposed as the acceleration of the curling stone on the first hog line.
The last stone draw (LSD) is used in competitive play and international competitions. The entire team executes LSDs before the game starts, and each skip will throw a draw to the button. The team with the smaller stone distance from the center of the button will win the advantage of the first hand.
4. Results and Discussion
4.1. Relationship between the Friction Coefficient and Speed
Figure 5 presents the influence of the sliding velocity on the friction coefficient between the ice and the curling stone. An extensive database containing 110,000 data points was plotted in this figure. Most of the measurement results fluctuate in the dark area, showing that local non-uniform factors strongly influence the coefficient of friction. The ice surface quality is determined by the ice maker, the ice surface wearing is caused by the overlapped curling trajectory, and the tracking error on the coordinates described in the CurlingHunter system all affect the local, instantaneous coefficient of friction. The friction coefficient and acceleration are extremely sensitive to error because they result from differentiating twice over time. It is more practical to use average friction coefficients for sub-regions.
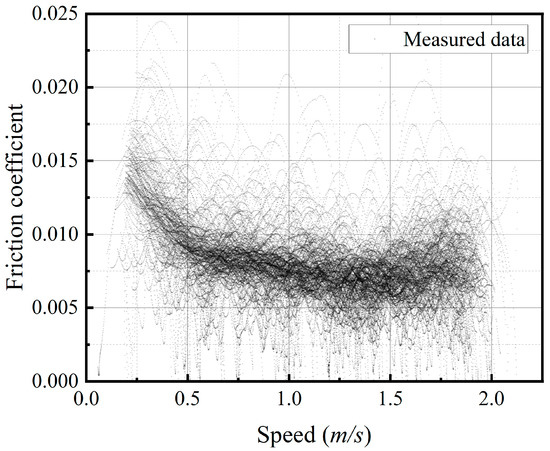
Figure 5.
The relationship between the friction coefficient and speed.
Therefore, statistical methods were adopted to present video recognition results better, as shown in Figure 6. The speed range was divided into 20 groups (0.2~0.3 m/s, 0.3~0.4 m/s, …, 2.1~2.2 m/s), and the average value and corresponding standard deviation of the friction coefficient in each interval were calculated. It can be seen from Figure 6 that the curling stone on the ice had a low coefficient of friction, ranging from 0.007 to 0.012. The friction coefficient, belonging to a mixed lubrication regime, showed descent as the curling stone sliding velocity increased. This is consistent with the law of the effect of speed on the friction coefficient as described by Li [28], indicating the reliability of the measurement method based on artificial intelligence.
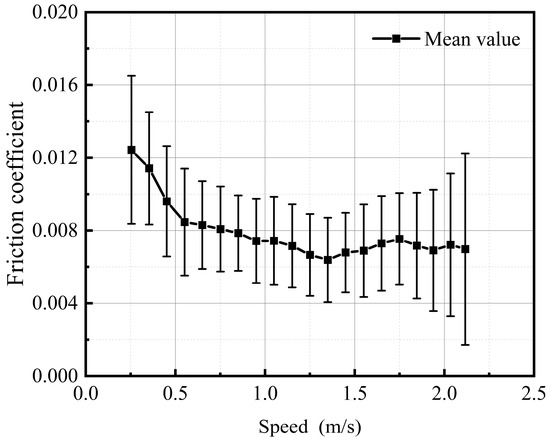
Figure 6.
Video recognition results adopted by statistical methods.
As presented in Figure 7, this research obtained the relationship data from the World Championship. It can be noticed that the data from the World Championship and those from the Beijing Winter Olympics show the same trend of variation. Because the ice rink quality of the Beijing Winter Olympics is better than that of the World Championship (proved in Section 4.4), the relationship curve of the Beijing Winter Olympics is lower than that of the World Championship. In addition, publicly available friction data of curling stones based on experimental measurements were also collected to compare with our obtained values. It can be noted that the friction coefficient in our work was mainly measured at speeds of 0.25 m/s to 3.25 m/s, whereas the literature data were primarily obtained at speeds of less than 1.0 m/s. Regarding the speed dependency of friction, the literature data agreed with our measured results. This research obtained a large amount of data on the relationship between the friction coefficient and speed, which provides an abundant reference for future relevant research.
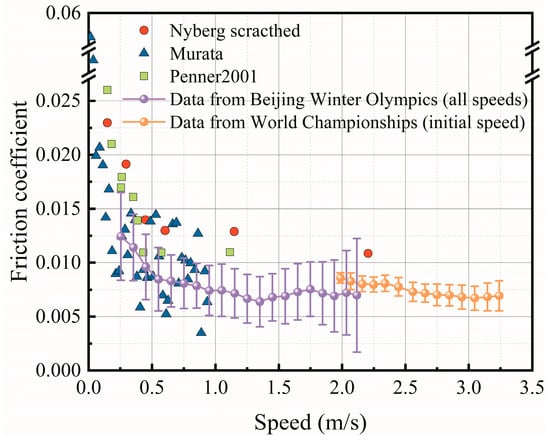
Figure 7.
The comparison of stone–ice friction coefficient.
4.2. Quality Assessment Indicator of the Curling Ice Rink—α
Lozowski et al. [25] derived a friction coefficient function based on thermodynamic equilibrium without considering the details of dry and wet friction. Based on the assumption that the total friction force exerted on the curling stone is composed of the shear stress force and the plowing force, the numerical model of the stone–ice friction coefficient is expressed as Equation (1). Although this model bypasses the role of periodic roughness of the running band, which is an essential aspect of the actual game, it is still enough to model the sliding process of the curling stone in the case of only translation without rotation.
with
where the variables and parameters are defined in Table 1. Units, ranges, and standard values are indicated in square brackets.

Table 1.
Variables and parameters of Equation (1) to Equation (7).
According to the research results of Barnes and Tabor [30], at temperatures lower than about −1.2 °C, the indentation hardness (H) of the ice obtained with a spherical indenter is approximately linearly correlated with the temperature. As a result, the hardness of the ice can be expressed as Equation (8), a relationship only related to the temperature. It is convenient to use this relationship because the temperature can be directly obtained from the monitoring data of Olympic games and post-Olympic games.
where H is the hardness of the ice in MPa, Ti is the temperature of the ice in °C, and C1 = −3.43 and C2 = 16.34 (by linear fitting) with a minimum contact time of 10 s [30].
Figure 8 presents the obtained results from on-site measurement (the same as Section 4.1) and the values calculated by the Lozowski model [25]. It can be noticed that when the stone’s speed is slow, the measured data are close to the lower limit, and when the stone’s speed is high, the measured data are close to the upper limit. Most of the video recognition results in this study are within the range of the upper and lower limits predicted by the Lozowski model, demonstrating that the model can quantitatively describe the relationship between the friction coefficient of the ice rink surface and the speed of the curling movement. However, the Lozowski model still deserves further improvement.
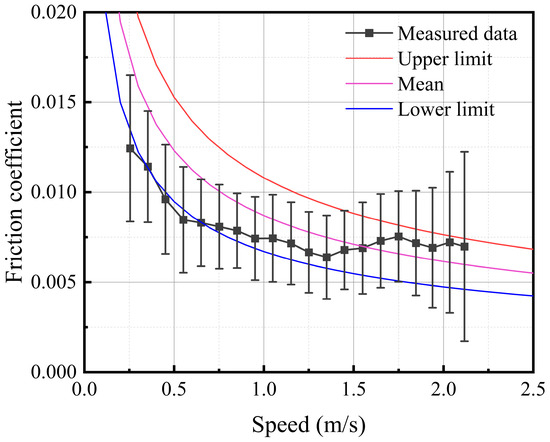
Figure 8.
Friction coefficient predicted by the Lozowski model [25].
It can be noticed from Equation (5) that the calculation result of tb is a range of values. As a result, the calculation result of μ is also a range of values, and it is inconvenient to assess the value of the friction coefficient on different curling rinks. In this case, the average of the upper and lower limits during the μ calculation is taken as the representative value of the friction coefficient for curling rinks. By substituting Equations (2)–(8) into Equation (1), the expression for the coefficient of friction can be obtained as Equation (9).
With
where α is defined as the quality evaluation indicator of the curling ice rink. It can be used to comprehensively assess the ice quality of a curling rink and reflects the effect of all aspects on the friction coefficient, other than the speed of the curling stone.
α is calculated based on a number of important factors, including the temperature of the ice surface, the radius of the top contact of a pebble, the width of the curling stone RB, the inner radius of the curling stone RB, and some constants related to heat conduction. This indicator is essential because it can be used as a critical assessment of the quality of different curling ice rinks, and it provides a standardized method of assessing ice quality for the sport of curling, ensuring fairness and consistency of play.
According to Equations (9) and (10), it can be noticed that the higher ice surface temperature, the softer ice, the bigger pebble size, as well as the wider curling stone RB, all result in a smaller α. The smaller the value α is, the lower the friction coefficient μ at the same speed, and the higher the manufacturing quality of the curling ice rink. The calculation of specific α will be based on actual field measurements, but, in practice, it can help curling venue managers to monitor and improve the ice quality to ensure consistent playing conditions. This parameter will play an important role in curling.
According to the descriptions of the national team athletes, the factors affecting the quality of the curling rink were ranked from most significant to most minor, among which the most influential was temperature. Therefore, it was necessary to study the relationship between the quality evaluation indicator α and the ice temperature, as shown in Figure 9. As the temperature T increases, the quality evaluation indicator α decreases, and the rate of decrease continues to increase. When the temperature is high, the hardness of the ice is low, and the ice rink is slippery, the quality evaluation indicator is small. However, when the temperature exceeds −4 °C, it involves the issue of whether there is frost. If there is less frost, the ice rink will be very slippery; on the contrary, if there is more frost, the ice rink will not be slippery at all. The situation will become very complicated, and it is beyond the normal temperature of curling competitions. This part is out of the research scope of this paper.
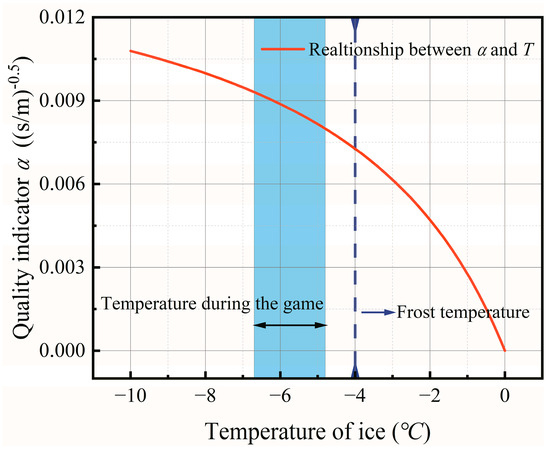
Figure 9.
Relationship between the quality evaluation indicator and the temperature.
By substituting the variables and parameters mentioned above into Equations (9) and (10), the quality evaluation indicator α range can be found to be from 0.0083 to 0.0158, which is consistent with the value of α (0.0087 for the Winter Olympics, 0.0119 for the World Championships) obtained by database fitting in Section 4.4. It can also be found here that the quality evaluation indicator α for the 2022 Beijing Winter Olympics is close to the lower limit of the theoretical calculation, indicating that smoother ice is produced at a specific temperature, which is close to the perfect ice surface expected by ice makers.
4.3. A Simplified Physical Model of the Stone-Sliding Process
Generally speaking, the motion of a curling stone on an ice rink is under the combined action of the translational and angular velocities. The translational motion of the stone is considered here, and it can be described as follows:
with
where is the frictional force exerted on the stone; m is the mass of the stone; a is the acceleration of the stone; is the friction coefficient between the stone and the pebbled ice; g is the gravitational acceleration; and L is the sliding distance until time t.
Assuming that the friction coefficient is related to the sliding speed in the form of μ = α v−0.5, we can rewrite Equation (11) as Equation (14)
in consideration of the initial physical condition of the stone sliding process in the actual situation (that is, first, at t = 0, the sliding distance L is 0; and, second, the speed at t = 0 is v0), which can be expressed as Equation (15):
By solving Equation (14), the sliding distance L, the sliding time t, the sliding velocity v, and the sliding acceleration a can be expressed as Equations (16)–(19), respectively.
4.4. Validation of the Physical Model
The diagram of the sliding process of the stone is shown in Figure 10. The process corresponding to the long-time (the time it takes for the curling stone to travel between the two hog lines) is the stone sliding from point F to point S. Based on the previous simplified physical model, the relationship between the long-time and the initial speed and the relationship between the initial acceleration and the initial speed can be expressed as Equations (20) and (21), respectively.
where tL is the long-time, LL is the distance corresponding to tL, v0 is the initial velocity of the stone at the first hog line (point F), αL is the quality evaluation indicator of the curling ice rink, and a0 is the initial acceleration.

Figure 10.
The diagram of the sliding process of the stone.
The results of 13,862 curling competitions from the database of the Beijing Winter Olympics and the World Championships are taken as examples. Figure 11 shows the relationship between the long-time and the initial speed, and Figure 12 shows the relationship between the initial acceleration and the initial speed (the same data with Figure 7). On the one hand, it can be found that when αL is 0.0119, the results of Equations (20) and (21) can stay in good agreement with measured data from the World Championships simultaneously, which proves that the physical model can be used to describe the movement process. On the other hand, in Figure 11, the two curves represent the Equation (20) calculation results corresponding to different coefficients α. The αL of the Beijing Winter Olympics is 0.0087, which is smaller than that of the World Championships, indicating that the level of craftsmanship of the ice rink of the Beijing Winter Olympics is better.
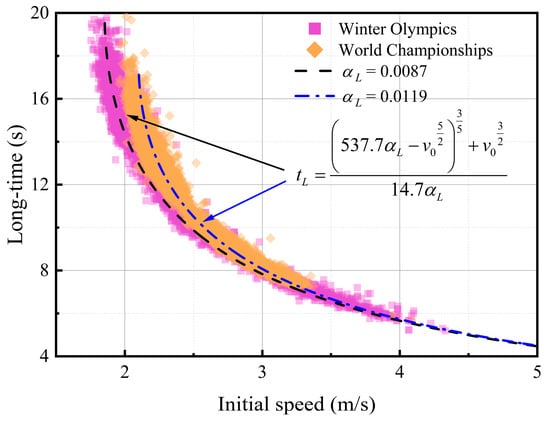
Figure 11.
Relationship between the long-time and the initial speed.
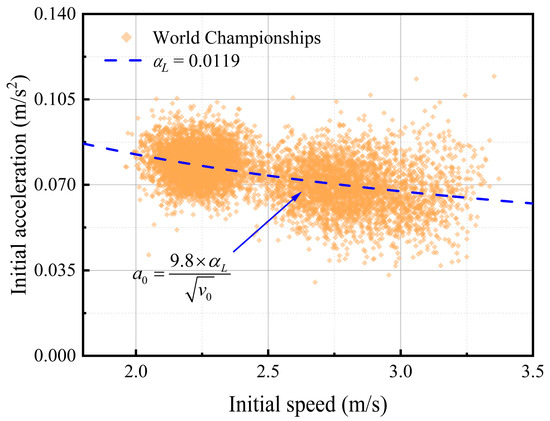
Figure 12.
Relationship between the initial acceleration and the initial speed.
4.5. Relationship between the Long-Time and the Stop Location
From 1 April to 10 April 2021, the curling venue held a youth curling competition, and 130 LSDs’ (the abbreviation of last stone draws) curling data were obtained during the competition. During the LSD throwing, the curling stone slides without athletes sweeping the ice, representing fewer anthropic factors in the stone’s motion. As a result, the LSD database can be used to study the average friction coefficient and other laws.
Figure 13 presents the relationship between the long-time and the stop location of the curling stone during the LSD throw. It can be found that the long-time decreased with the increase of the slipping distance. Those stones with a longer long-time tend to fall within the tee line and run shorter; those with a shorter long-time tend to fall outside the tee line and run longer. In Equation (18), if we let v = 0, then we can obtain the relationship between the total sliding distance (from start to stop) and the initial speed, which can be expressed as . By substituting the relationship into Equation (20), the relationship between the long-time and the sliding distance can be expressed as Equation (22), which can be used to predict the stop location, provided that the long-time is measured. For the time at about 13.71 s, the stone will stop at the center of the button; for the time shorter than the critical value, the stone will stop behind the button; for the times higher than the critical value, the stone will stop earlier.
where L is the sliding distance from the first hog line to the stop location.
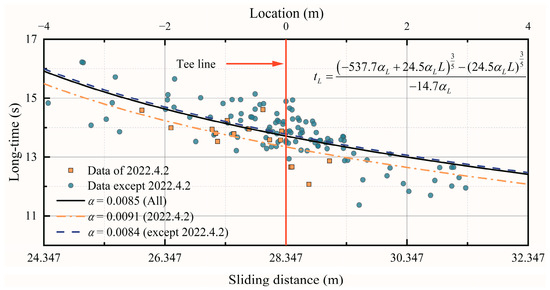
Figure 13.
Relationship between the long-time and the sliding distance (as well as the stop location).
It should be noted that the air humidity was high due to the rain on 2 April 2021, resulting in frosting on the individual tracks. The ice condition on that day was different from other days. Therefore, the relationship between the stop position and the long-time between 2 April and other dates of the same schedule is compared, as shown in Figure 13. It can be found that the α on 2 April 2021 is 0.0091, which is distinctively larger than that of other dates of the same schedule, while the relationships on other dates of the same schedule stay in good agreement with all data. The stones at 2 April 2021 slid a shorter distance in the same long-time interval, which reflected a stronger kinetic resistance and a higher friction coefficient. The quality of the ice rink can be compared directly with the value of the ice rink quality evaluation indicator α.
4.6. Relationship between the Split-Time and the Long-Time
Although the long-time can be related to the position where the stone will end up, it is not a suitable ice assessment tool for sweeping judgment because the remaining distance after the last hog line is too small. As a result, it is not long enough for sweepers to adjust the stone motion. The relationship between the split-time and the long-time is explored to help the athletes assess the sliding distance before throwing stones in this section.
During the split-time (the time it takes for the curling stone to travel from the back line to the hog line), the main body sliding on the ice rink is the athlete plus the stone, but after throwing the stone at the first hog line, the main body sliding is only the stone. The soles of curlers’ shoes are made of professional plastic with a slippery surface and a minimal coefficient of friction. Therefore, the coefficients of friction for these two parts may be different, and they need to be considered in segments. The diagram of the sliding process of the stone is shown in Figure 10. The split-time and long-time intervals can be expressed as Equations (23) and (24), respectively. At the same time, the velocity at point B and point F satisfies the relationship in Equation (25). As a result, the relationship between the split-time and the long-time can be expressed as Equation (26), which is a parametric equation about v0.
where ts is the split-time, Ls is the sliding distance during the split-time, and αs is the quality evaluation indicator during the split-time, which is a mean value in consideration of the stone and the slippery soles of the curlers’ shoes.
Taking 9 February 2022 and 10 February 2022 during Beijing Winter Olympics as examples, Figure 14 presents the extracted split-time and long-time. Because αL is already known as 0.087 through the relationship between the long-time and the initial speed, αs can be obtained by data fitting as 0.04, which is smaller than αL. This indicates that the combination of the athlete and the stone has a smaller friction coefficient than the stone alone, because the sole of the shoe is made of special plastic and has a smaller friction coefficient. It can be found from Figure 14 that there is a clear relationship between the split-time and the long-time, which means that the long-time can be accurately converted to the split-time. In this way, the split-time provides the earliest information for sweepers, who can react immediately with this number.
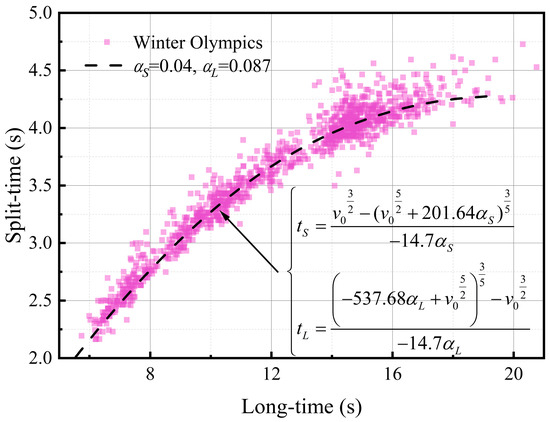
Figure 14.
Relationship between the split-time and the long-time.
Skip, the fourth base player of the Chinese national curling men’s team, proposed the idea of making a sliding calculating ruler to record the size table time of the ice rink, as shown in Figure 15. When athletes are training in different ice rinks, or training at different times, this ruler can record the correspondence of the split-time and the long-time, which makes it easier for athletes to observe the change of the correspondence and adjust the strength of the curling throw. The findings of this section prove that this idea is correct. The change in the split-time and the long-time correspondence reflects the change in the ice rink quality, and the understanding of this law is called the “ice reading ability” of the athletes. In the future, ice rink quality control can also be realized by recording the split-time and the long-time through video capture or magnetic induction to form a curve. By observing the change of the curve at different times, the change in ice quality can be evaluated.

Figure 15.
The sliding calculating ruler.
4.7. A Practical Method to Evaluate the Quality of the Ice Rink
Section 4.2 and Section 4.3 established a physical model of the stone sliding process by introducing the curling quality evaluation indicator α. In Section 4.4, Section 4.5 and Section 4.6, this model can describe the state of the curling stone in each stage of the sliding process and agrees well with the measured data. Although the quality of different ice rinks can be assessed by comparing the quality evaluation indicator α, it is inconvenient, because its implementation relies on a large amount of pre-measurement data.
In this section, a practical method for assessing the quality of the ice rink is used. Athletes are asked to throw the curling stone, and the total time it takes for the curling stone from starting at the back line to stopping at the center of the last button (that is, in Figure 5, from point B to point E) is used as the measurement indicator. Under the same sliding distance, a longer time means the smaller the friction coefficient of the ice rink and the higher the quality of the ice rink. Therefore, the quality of the ice rink can be assessed by directly comparing this special total time for different ice rinks.
Based on Equation (18), if we let v = 0 and eliminate v0, the relationship between the sliding time and the sliding distance after the first hog line can be deduced as Equation (27). As a result, the time from point F to point S (the long-time) and the time from point F to point E can be calculated as 13.52 s and 22.90 s. By substituting the long-time into Equation (26), the split-time can be calculated as 3.88 s. Thus, the total sliding time can be summed as 26.78 s. Nowadays, for most curling ice rinks, the total time ranges from 24 s to 26 s, which proves that the curling ice rink of the 2022 Beijing Winter Olympics is better than the vast majority and close to the perfect ice rink; the same conclusion was reached in Section 4.2.
4.8. Relationship between Deviation and the Initial Speed
According to the study above, it is possible to help players estimate the sliding distance of the stone in the x-direction. However, the final position of the curling stone is also closely related to the deviation in the y-direction, as shown in Figure 16. Taking the results of curling competitions from the database of the World Wheelchair Curling Championships as an example, this section explores the relationship between deviation and the initial speed. The green scattered dots represent the stop locations of the stones, and the solid black lines represent the trajectory of some curling sliding. It can be noticed that some stones have sudden y-direction deviation due to the collision with the stones that already stopped at the end position, so these results are not considered in the analysis.
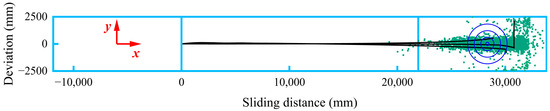
Figure 16.
The schematic diagram of curling stone drop points and sliding trajectory.
During the World Wheelchair Curling Championships, there are no athletes sweeping the ice, so the only control athletes have is what happens before the stone leaves their hand. Once the stone leaves the hand, then the motion of the stone is only influenced by the rink factors. The moment the stone leaves the hand, the stone is affected by the sliding speed in the x-direction, the angular speed, and a tiny lateral deflection speed (which is ignored by the athletes) in the y-direction, as shown in Figure 17. The deviation is defined as the distance of the actual lateral deflection minus the distance at which the stone maintains its initial lateral speed. The relationship between these three factors and the deviation of the stone is studied in turn.
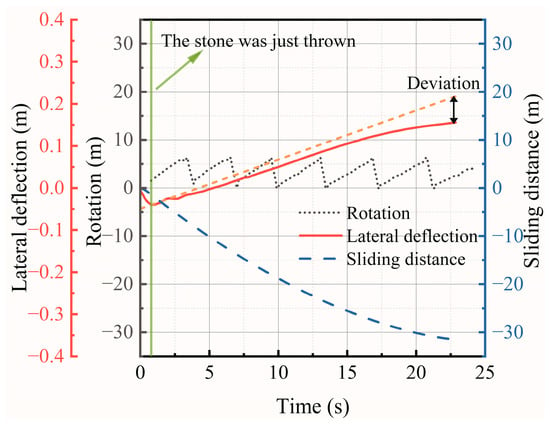
Figure 17.
Changes in the three factors during stone sliding.
As shown in Figure 18, Figure 19 and Figure 20, here are the video recognition data of the first track of the first race. Because two adjacent games required adjustment of the direction of the stone throw, data were extracted for each of the two directions. It can be noticed from Figure 18 that the deviation is approximately symmetric at about 0. When the sliding speed in the x-direction is slow, the deviation is scattered, but when the sliding speed is fast, the deviation is relatively concentrated, indicating that the faster the sliding speed, the smaller the deviation.
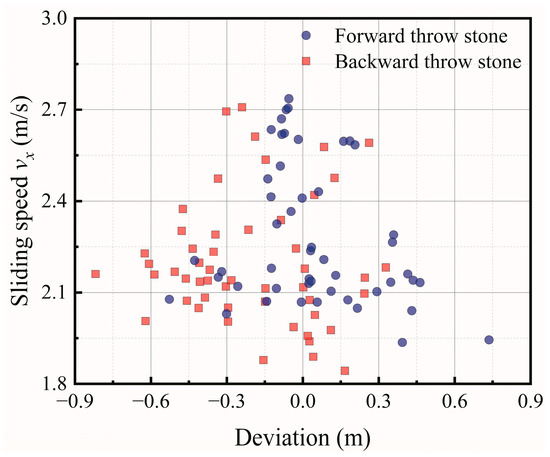
Figure 18.
Relationship between the sliding speed and deviation.
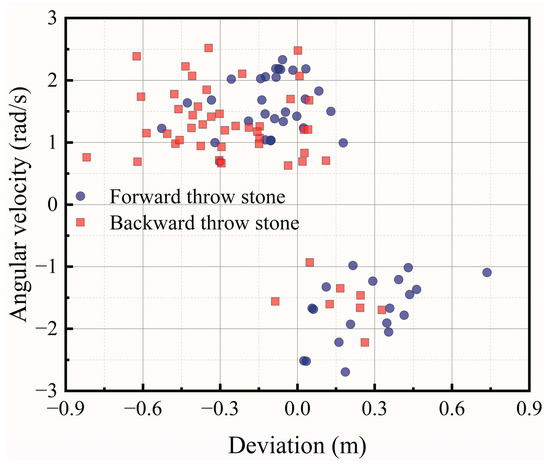
Figure 19.
The relationship between the angular speed and deviation.
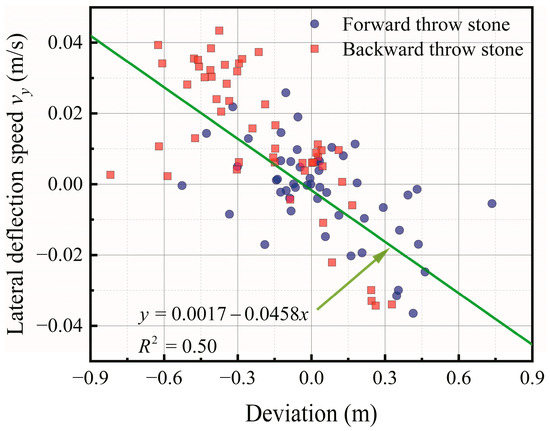
Figure 20.
Relationship between the lateral deflection speed and deviation.
As shown in Figure 19, there is a strong correlation between the direction of rotation and the direction of the deviation. If the stone rotates clockwise, then it will deflect to the right of the forward direction; but if the stone rotates counterclockwise, then it will deflect to the left of the forward direction [5,6]. However, there is no clear numerical relationship between the magnitude of the rotation speed and the magnitude of the deviation. Some literature [5,14] suggests that stone deviation is related to its angular rotation speed and the direction of rotation, but there is serious disagreement about the relationship between the value of deviation and the angular speed of rotation. Some literature suggests that there is no direct correspondence between deviation and the value of the rotation speed, and that the direction of rotation affects the direction of deviation. The deviation is due to incidental factors, such as asymmetric friction between the bottom surface of the curler and the ice point. This research proves this argument.
The initial lateral deflection speed provides an alternative way of thinking for determining the stone’s deviation. It can be noticed from Figure 20 that the lateral deflection speed in the y-direction and the deviation are linearly related with R2 = 0.50, indicating that the higher the lateral deflection speed of the stone in the y-direction when thrown, the greater its deviation in the opposite direction. Therefore, it is crucial for the athletes to control the lateral deflection speed of the stone.
4.9. Relationship between Lateral Deflection and the Initial Speed
In order to help athletes determine the stop location of the stone, this section studies the relationship between lateral deflection, which is a more practical parameter compared to the deviation, and the initial speed.
According to Section 4.7, the lateral deflection of the curling stone in the y-direction between its final stop position and the initial position at the first hog line should be related to the initial lateral deflection speed vy. In addition, according to Figure 16, the lateral deflection in the y-direction of the curling stone increases as the sliding distance increases. Therefore, the relationship between tanθ (the tangent of the lateral deflection angle, that is, the ratio of the y-direction lateral deflection of the curling stone to the x-direction sliding distance) and the initial speed in the y-direction vy is analyzed to assist athletes in determining the final stop position. The relationship, similar to the power function, can be expressed as Equation (28).
where tanθ is the tangent of the lateral deflection angle, vy is the initial speed in the y-direction at the first hog line, and A and B are constants to be determined.
When A = 5.7 and B = 1.5, the calculation results of Equation (28) can fit well with the World Championships’ measured data, as shown in Figure 21. It can be noticed that the lateral deflection angle ranges in [−0.04, 0.04] increase as the initial speed vy increases. The greater the absolute value of the initial speed in the y-direction, the greater the rate of increase of the lateral deflection angle.
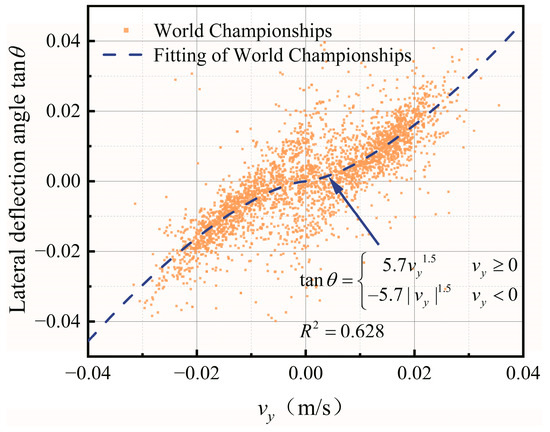
Figure 21.
Relationship between the lateral deflection angle tanθ and the initial speed in the y-direction.
For the four tracks of the curling rink, the fitting results of lateral deflection at the same speed are not the same. This is shown in Figure 22, with track A and track D having more significant lateral deflections, and track B and track C having more minor lateral deflections. Considering the proximity of the two outside tracks to the dehumidification ventilation ducts, as shown in Figure 3, the results agree with the ice maker’s expectations.
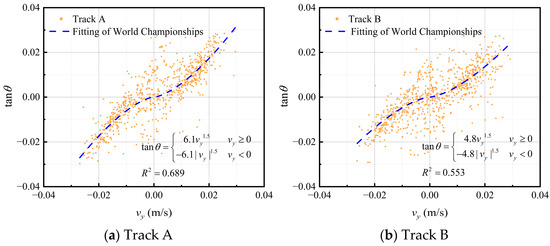
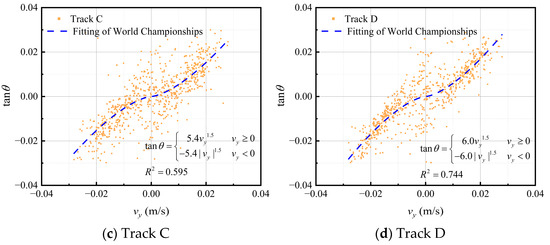
Figure 22.
The comparison of different tracks.
Although the fitting results of Equation (28) agree with the measured data, this method still has an obvious drawback. The initial lateral speed in the y-direction is minimal, and the video recognition error dramatically impacts the results, which puts forward very high requirements for the precision and accuracy of video recognition.
4.10. Application
The results described above have been applied in the post-match operation of the National Aquatics Center to guide the production of Olympic-grade ice surfaces and to guide athletes to “read ice” accurately during training. Our research goes beyond theoretical analysis and has had a positive impact on practical applications. It has already changed the way curling venues are managed, enhancing athlete performance and the overall curling game experience.
For ice fabrication, curling venue operators and facility managers utilize our findings to fine-tune ice surfaces. By keeping the ice in the optimal temperature range, controlling the level of hardness, and adjusting the bump texture size to meet specific requirements, they provide curlers with consistently ideal playing conditions. This increases athlete satisfaction and enhances the quality of play. For athlete training, curling coaches and trainers incorporate our research into their training programs. They use the α parameter to assess ice conditions during training. Athletes received targeted coaching based on the specific ice conditions they encountered, resulting in improved overall performance levels.
These results highlight the importance of considering subtle differences in ice quality in curling and demonstrate the broader implications for sustainability and competitive excellence.
5. Conclusions
Using the curling motion data of the 2022 Beijing Winter Olympics acquired through a video recognition method, quality evaluation indicator α to measure the quality of ice rinks is proposed, and the patterns of curling motion are analyzed. The conclusions are drawn as follows:
- The relationship between the friction coefficient and the speed was studied using extensive data from the 2022 Beijing Winter Olympics. This study obtained friction coefficients in a more extensive speed range than previous research because of the convenience of the image recognition method. The results show that the friction coefficient decreases when the stone speed increases, ranging from 0.007 to 0.012.
- The quality control indicator α of the curling ice rink is proposed based on the existing friction model, which is used to measure the quality of different curling rinks instead of the friction coefficient. The smaller the α is, the more perfect the curling rink is. The α range can be obtained theoretically from 0.0083 to 0.0158. The α of the curling rink in the 2022 Beijing Winter Olympics is 0.0087, proving that this curling rink is close to the ideal perfect ice rink.
- A simplified physical model of the curling sliding process equation was developed, and its reliability was verified by video recognition data.
- The relationship between the long-time and the stop location and the split-time and the long-time were analyzed in turn. The split-time can be used to determine the long-time and the stopping position of the curling stone. As a result, a time ruler can be used to help athletes estimate the stopping position of the stone when throwing.
- The total time it takes for the curling stone from starting at the back line to stopping at the center of the button is 26.78 s, which is greater than most of the curling ice rinks, proving that the curling ice rink of the 2022 Beijing Winter Olympics had a smoother ice surface.
- The relationship between three factors (the sliding speed in the x-direction, the angular speed, and a tiny lateral deflection speed in the y-direction) and the deviation (which refers to the lateral deflection in the y-direction) of the stone was studied. The deviation and the initial lateral deflection speed are linearly correlated. The faster the sliding speed, the less time that is required for the same sliding distance, and the smaller the deviation. The angular speed only affects the deflection direction. The lateral deflection speed is linearly related to the deflection.
- The relationship between the lateral deflection angle of the stone and the initial lateral deflection velocity vy is proposed, which is expressed as a power function, to aid the athletes in determining the exact point of the final stone location.
Author Contributions
Conceptualization, Q.Y., W.Z. and S.L.; methodology, S.L., J.L., Q.W. and X.M.; investigation: Q.Y., W.Z. and S.L.; writing—original draft preparation, S.L. and J.L.; writing—review and editing, W.Z. and S.L.; project administration, Q.Y. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by the National Key Research and Development Project of China (No. 2020YFF0304300) and the Science and Technology R&D plan of CSCEC (No. CSCEC-2019-Z-7).
Data Availability Statement
Not applicable.
Acknowledgments
This work was financially supported by the National Key Research and Development Project of China (2020YFF0304300) and the science and technology R&D plan of CSCEC (CSCEC-2019-Z-7). The authors gratefully acknowledge Toyo Ogawa (Board Director of the World Curling Federation) for the valuable suggestions provided for this study.
Conflicts of Interest
The authors have no conflict of interest to declare.
References
- Zhang, W.; Li, J.; Yang, Q.; Mu, L. Practical Application of a Novel Prefabricated Curling Ice Rink Supported by Steel–Concrete Composite Floors: In Situ Measurements of Static and Dynamic Response. Structures 2021, 32, 1888–1906. [Google Scholar] [CrossRef]
- Kim, T.-W.; Lee, S.-C.; Kil, S.-K.; Choi, S.-H.; Song, Y.-G. A Case Study on Curling Stone and Sweeping Effect According to Sweeping Conditions. Int. J. Environ. Res. Public Health 2021, 18, 833. [Google Scholar] [CrossRef] [PubMed]
- Maeno, N. Dynamics and Curl Ratio of a Curling Stone. Sport. Eng. 2014, 17, 33–41. [Google Scholar] [CrossRef]
- Gwon, J.; Kim, H.; Bae, H.; Lee, S. Path Planning of a Sweeping Robot Based on Path Estimation of a Curling Stone Using Sensor Fusion. Electronics 2020, 9, 457. [Google Scholar] [CrossRef]
- Maeno, N. Assignments and Progress of Curling Stone Dynamics. Proc. IMechE 2016, 237, 175433711664724. [Google Scholar] [CrossRef]
- Bradley, J.L. The Sports Science of Curling: A Practical Review. J. Sport. Sci. Med. 2009, 8, 495–500. [Google Scholar]
- Denny, M. Curling Rock Dynamics: Towards a Realistic Model. Can. J. Phys. 2002, 80, 1005–1014. [Google Scholar] [CrossRef]
- Jensen, E.T.; Shegelski, M.R. The Motion of Curling Rocks: Experimental Investigation and Semi-Phenomenological Description. Can. J. Phys. 2004, 82, 791–809. [Google Scholar] [CrossRef]
- Nyberg, H.; Hogmark, S.; Jacobson, S. Calculated Trajectories of Curling Stones Sliding Under Asymmetrical Friction: Validation of Published Models. Tribol. Lett. 2013, 50, 379–385. [Google Scholar] [CrossRef]
- Kameda, T.; Shikano, D.; Harada, Y.; Yanagi, S.; Sado, K. The Importance of the Surface Roughness and Running Band Area on the Bottom of a Stone for the Curling Phenomenon. Sci. Rep. 2020, 10, 20637. [Google Scholar] [CrossRef]
- MAENO, N. Curl Mechanism of a Curling Stone on Ice Pebbles. Bull. Glaciol. Res. 2010, 28, 1–6. [Google Scholar] [CrossRef]
- Shegelski, M.R.A.; Lozowski, E. First Principles Pivot-Slide Model of the Motion of a Curling Rock: Qualitative and Quantitative Predictions. Cold Reg. Sci. Technol. 2018, 146, 182–186. [Google Scholar] [CrossRef]
- Shegelski, M.R.A.; Lozowski, E. Pivot–Slide Model of the Motion of a Curling Rock. Can. J. Phys. 2016, 94, 1305–1309. [Google Scholar] [CrossRef]
- Hattori, K.; Tokumoto, M.; Kashiwazaki, K.; Maeno, N. High-Precision Measurements of Curling Stone Dynamics: Curl Distance by Digital Image Analysis. Proc. IMechE 2016, 237, 175433711667906. [Google Scholar] [CrossRef]
- Denny, M. Ice Deformation Explains Curling Stone Trajectories. Tribol. Lett. 2022, 70, 1–13. [Google Scholar] [CrossRef]
- Denny, M. A First-Principles Model of Curling Stone Dynamics. Tribol. Lett. 2022, 70, 84. [Google Scholar] [CrossRef]
- Braghin, F.; Cheli, F.; Maldifassi, S.; Melzi, S.; Sabbioni, E. (Eds.) The Engineering Approach to Winter Sports; Springer: New York, NY, USA, 2016; ISBN 978-1-4939-3019-7. [Google Scholar]
- Penner, A.R. The Physics of Sliding Cylinders and Curling Rocks. Am. J. Phys. 2001, 69, 332–339. [Google Scholar] [CrossRef]
- Nyberg, H.; Alfredson, S.; Hogmark, S.; Jacobson, S. The Asymmetrical Friction Mechanism That Puts the Curl in the Curling Stone. Wear 2013, 301, 583–589. [Google Scholar] [CrossRef]
- Scherge, M.; Böttcher, R.; Spagni, A.; Marchetto, D. High-Speed Measurements of Steel–Ice Friction: Experiment vs. Calculation. Lubricants 2018, 6, 26. [Google Scholar] [CrossRef]
- Makkonen, L.; Tikanmäki, M. Modeling the Friction of Ice. Cold Reg. Sci. Technol. 2014, 102, 84–93. [Google Scholar] [CrossRef]
- Kietzig, A.-M.; Hatzikiriakos, S.G.; Englezos, P. Physics of Ice Friction. J. Appl. Phys. 2010, 107, 081101. [Google Scholar] [CrossRef]
- Spagni, A.; Berardo, A.; Marchetto, D.; Gualtieri, E.; Pugno, N.M.; Valeri, S. Friction of Rough Surfaces on Ice: Experiments and Modeling. Wear 2016, 368–369, 258–266. [Google Scholar] [CrossRef]
- Evans, D.C.B.; Nye, J.F.; Cheeseman, K.J. The Kinetic Friction of Ice. Proc. R. Soc. Lond. 1976, A347, 493–512. [Google Scholar] [CrossRef]
- Lozowski, E.P.; Szilder, K.; Maw, S.; Morris, A.; Poirier, L.; Kleiner, B. Towards a First Principles Model of Curling Ice Friction and Curling Stone Dynamics. In Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015; pp. 1730–1738. [Google Scholar]
- Marian, M.; Tremmel, S. Current Trends and Applications of Machine Learning in Tribology—A Review. Lubricants 2021, 9, 86. [Google Scholar] [CrossRef]
- Murata, J. Study of Curling Mechanism by Precision Kinematic Measurements of Curling Stone’s Motion. Sci. Rep. 2022, 12, 15047. [Google Scholar] [CrossRef]
- Li, J.; Li, S.; Zhang, W.; Wei, B.; Yang, Q. Experimental Measurement of Ice-Curling Stone Friction Coefficient Based on Computer Vision Technology: A Case Study of “Ice Cube” for 2022 Beijing Winter Olympics. Lubricants 2022, 10, 265. [Google Scholar] [CrossRef]
- Shi, X.; Wang, Q.; Wang, C.; Wang, R.; Zheng, L.; Qian, C.; Tang, W. An AI-Based Curling Game System for Winter Olympics. Research 2022, 2022, 9805054. [Google Scholar] [CrossRef]
- Barnes, P.; Tabor, D. Plastic Flow and Pressure Melting in the Deformation of Ice I. Nature 1966, 210, 878–882. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).