Abstract
To increase the power density of the electromechanical drive train of wind turbines, journal bearings can be used as planetary gear bearings instead of rolling bearings. This technological change presents new challenges. For example, wind turbine drive systems are subject to dynamic and low-speed operating conditions, which can lead to accelerated abrasive wear of the journal bearings. In addition, oil supply failure or peak loads due to wind gusts and grid and power converter faults could potentially result in catastrophic failure due to adhesive wear in a very short time. Such operating characteristics are, therefore, critical regarding the journal bearing wear lifetime and must be considered in the design. The successful implementation of journal bearings in wind turbines depends on a reliable estimation of adhesive and abrasive wear. In this paper, five different models for the wear calculation of journal bearings are evaluated regarding their suitability for the wear calculation of planetary gear bearings in wind turbines. For this purpose, the following evaluation criteria were defined: parameter uncertainty, parametrization effort, in particular number of parameters, parameterization method, load case dependency of parameters and calculation effort. In order to be able to evaluate the wear models, the wear models are numerically implemented, and the wear of a test journal bearing is exemplarily calculated under load conditions, which are comparable to load conditions in a wind turbine. Relevant influences from the wind turbine system, such as lubricant, material and manufacturing-dependent surface influences, such as roughness and hardness, are considered. The wear models are evaluated with respect to their fulfillment of the defined criteria. The resulting evaluation allows the selection of a wear model that can be used to calculate the wear of planetary gear journal bearings in wind turbines, considering the available input variables.
1. Introduction
Wind energy is a mainstay of electricity generation from renewable sources and plays a central role in the EU Commission’s Green Deal. New generations of wind turbines with high power classes and low electricity production costs are desired in order to be able to realize further expansion and a higher share of renewable energies overall. To further increase the power density of wind turbines, even more compact designs of drive trains are needed. Therefore, the substitution of rolling bearings with journal bearings in planetary gearboxes is an obvious solution since journal bearings require less installation space and thus allow more planetary gears in smaller gearboxes. Journal bearings as planetary gear bearings for wind turbines are already available on the market. However, there is currently no standardized approach for the wear prediction of planetary gear bearings. In addition, experience regarding the use of journal bearings in wind turbines over the 30-year operational life of a wind turbine has been limited so far. Furthermore, wind turbines must increasingly generate electricity reliably even under difficult operating conditions, e.g., less steady wind conditions. This means that the wind turbines must not be damaged by start-up processes or by operation at low speeds. Such operating points are of particular relevance for journal bearings in terms of wear and, therefore, must be considered in the design process of the bearing. In order to ensure the reliable operation of planetary gears with journal bearings in wind turbines, a calculation method is needed that predicts the wear and, thus, durability of the journal bearing over the lifetime of the turbine.
Wear is the progressive loss of material from the surface of a body caused by tribological stress [1]. Depending on the structure of the tribological system and the kinematics of the tribological stress, a distinction is made between different types of wear. Due to dynamic and slow-speed operating conditions, journal bearings in wind turbines are generally subject to sliding wear. According to Czichos [1], the four wear mechanisms for journal bearings are adhesion, abrasion, micro fatigue and tribochemical reaction. In order to be able to predict the bearing wear analytically, different approaches have been developed in the past, which are based on different wear mechanisms. Holm [2] developed a wear approach by assuming the contact between atoms of opposing surfaces as the cause of wear. Archard [3] developed this approach further and considered not the contact of atoms but the contact and the resulting plastic deformation of asperity peaks of the surfaces. Rowe [4] extended the model developed by Archard to include the influence of the lubricant used in the wear calculation. Chun [5] used the model created by Rowe to simulatively predict the wear of journal bearings in the starting and stopping operations of a reciprocating engine. Besides Archard, the most widely used model for wear calculation is the energetic approach developed by Fleischer [6]. In this approach, it is assumed that friction energy is generated during the sliding process, which is accumulated in the material. If the accumulated energy has reached a critical limit, the lattice energy of the material is overcome, and wear occurs.
The wear models of Archard and Rowe assume a linear wear process in their calculation. However, when observing real wear processes in journal bearings, a deviation from this prediction can be observed. It can be seen that the rate of wear is initially higher than the one predicted by the linear wear calculations and only approaches the wear behavior of the linear forecasts after a run-in phase has been completed [7]. Simultaneously with the change in the rate of wear, the coefficient of friction also changes. In lubricated friction contacts, the friction process usually starts with increased coefficients of friction until wear leads to a smoothing of the surfaces, and the value of the coefficient of friction decreases [8].
In the recent past, attempts have been made to take the running-in phase of a journal bearing into account in the wear calculation and thus to be able to predict the entire course of wear more accurately. In Fleischer’s wear approach, the behavior of the friction coefficient is not specified in more detail. Therefore, Fleischer’s wear approach can be implemented both linearly, with a time-constant friction coefficient, and with transient behavior, using a time-varying friction coefficient. König [8], using Fleischer’s approach, developed a numerical method for wear prediction of journal bearings under start-stop conditions, iteratively considering both the journal bearing wear at the macroscopic level and at the roughness level. In this way, a simulative prediction of run-in wear became possible using the Fleischer approach. By means of the developed method, agreements between simulation and experiment regarding journal bearing wear during the running-in process could be shown. Nevertheless, the approach by König requires an iterative adjustment of the friction coefficient of Fleischer’s wear approach, which changes continuously during the running-in process. Additionally, the input parameters of the model were based on roughness measurements, some of which were subject to large scatter. Another approach that enables transient wear calculation was developed by Xiang et al. In this approach, two mechanisms are assumed to contribute to wear [9]. On the one hand, wear is considered to be caused by the plastic deformation of asperity peaks in contact; this affects the material above the contact surface. On the other hand, it is assumed that fatigue cracks develop below the contact surface and lead to the breakout of material after a certain accumulation. In further publications, Xiang et al. have shown that the developed wear approach can also be applied to water-lubricated journal bearings [10,11]. As an alternative to these mechanical approaches, the wear approach of Lijesh [12], based on the work of Bryant [13], takes a thermodynamic approach to describe wear. The free enthalpy is assumed to decrease in proportion to the degradation of the tribological system until an equilibrium state is reached at the minimum free enthalpy. Since the decrease in free enthalpy is coupled to the generation of entropy, the increase of entropy is regarded as the driving variable of wear in the model. The wear behavior is described with the aid of a degradation coefficient, which sets the wear volume created in relation to the entropy produced. Independently of the previous approaches, Cao et al. [14] developed a method for calculating adhesive wear, which is based on the assumption that a wear particle is formed during the wear process, which detaches from the surface and thus leads to material loss at the surface. The size of the wear particle and the time of detachment are subject to a statistical distribution. To map the statistical distribution, Cao et al. introduced a numerical criterion that calculates the probability that a wear particle will form and be detached. A major uncertainty in the approach of Cao et al. is the determination of the mean surface energy of the contact partners and its standard deviation, as well as the determination of the material-specific maximum work of adhesion. A summary of the wear approaches for journal bearing wear calculation is shown in Table 1.

Table 1.
Wear approaches for journal bearing wear calculation and basic wear mechanism.
As shown in Table 1, the presented wear approaches consider different damage mechanisms responsible for the wear. In addition, only some models allow the consideration of a transient wear rate. Furthermore, the approaches use partly physically based parameters and partly empirical parameters to describe the wear of the system. As a result, different wear approaches are expected to be suitable for different applications or varying tribological systems. So far, it is not known which of the wear approaches is best suited for describing the wear in planetary gears of wind turbines. Therefore, in this paper, the different wear approaches are screened, implemented and evaluated regarding their suitability for the wear calculation of planetary gear bearings in wind turbines. In this study, only the slow-progressing wear process is addressed. However, the frictional heat generated by severe adhesion events can also lead to critical operating conditions and even to spontaneous failure of the plain bearings. This damage mechanism will be considered in subsequent studies.
2. Approach
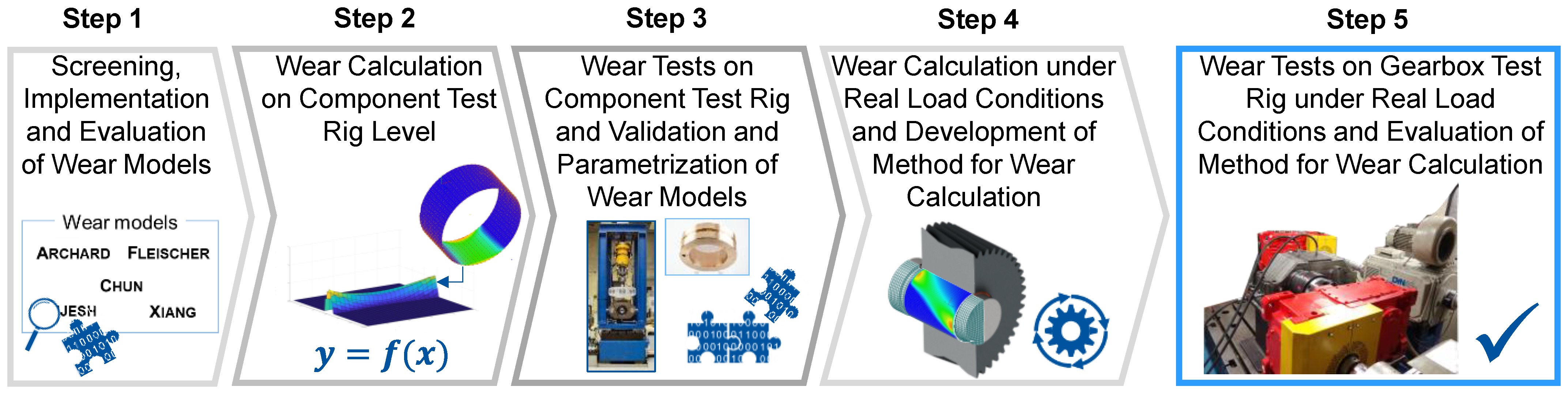
In order to identify the best-suited approach for describing the wear in planetary gears of wind turbines, the different wear approaches presented in Section 1 are tested at the Institute for Machine Elements and Systems Engineering with the aim of selecting a suitable approach for the wear calculation and subsequently to be able to reliably predict the wear of planetary gear bearings in wind turbines. The procedure is divided into five steps and shown in Figure 1. First, the wear approaches are screened, implemented and evaluated (Step 1). Then, calculations of the wear progress are performed from a radially loaded journal bearing using the different wear approaches (Step 2). The results are then compared with experimental results generated on a component test rig (Step 3). The component test rig allows several bearings to be tested in a short time and under defined conditions. In this way, sufficient test data is collected to parameterize and validate the wear approaches. On the component test rig, wear conditions are also considered, which leads to the fretting of the bearing. Materials and lubricants used in real wind turbines are used for the experimental tests on the component test rig. Steps 1 to 3 result in a wear approach and a methodology with which the wear behavior of the test bearing can be reliably predicted, initially under radial load. Subsequently, the methodology is applied to a model of a gearbox test rig (Step 4). The gearbox test rig reproduces real load conditions in wind turbines. In order to consider the real load conditions in the simulative wear prediction, it is extended for the locally resolved wear calculation of planetary gear bearings. The results of the simulative wear prediction are then compared with test data from the gearbox test rig (Step 5). In this way, it can be evaluated whether the selected wear approach and the developed method are suitable for the wear calculation of planetary gear bearings under real load conditions or whether further development is necessary. In combination with the published work Simulation methodology for the identification of critical operating conditions of planetary journal bearings in wind turbines [15], both studies represent the first steps towards the development of a framework for the use of planetary journal bearings in wind turbines.
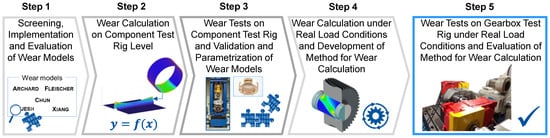
Figure 1.
Procedure for establishing a reliable prediction of the wear of planetary gear bearings in wind turbines.
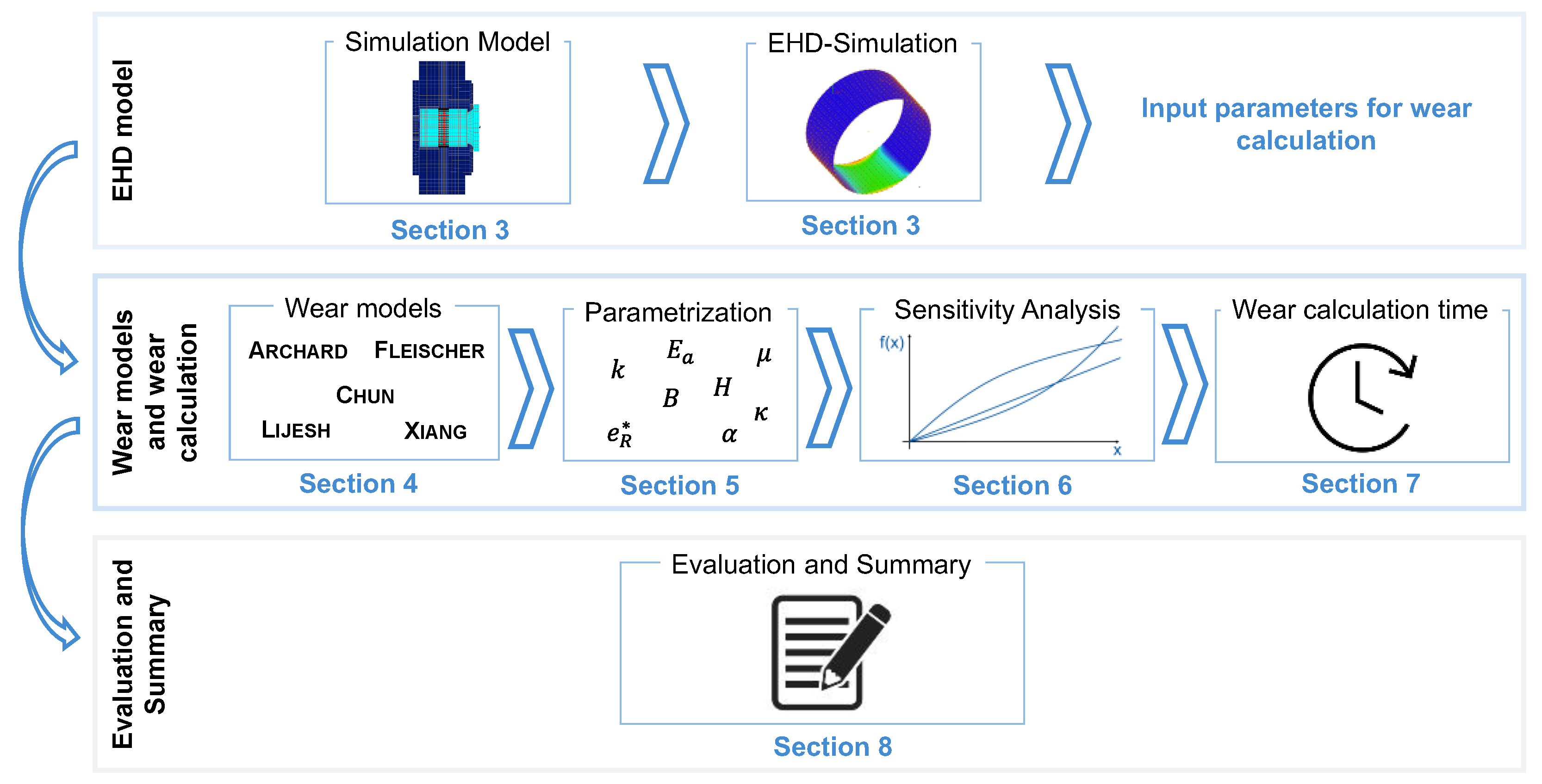
This study addresses the screening, implementation and evaluation of the wear approaches (Step 1) and wear calculations of the component test rig bearing (Step 2) considering materials and lubricants used in wind turbines. The approach of the study is shown in Figure 2. First, EHD simulations of the component test rig are performed to simulatively determine the contact conditions in the journal bearing, which provide the input parameters for the wear calculations (Section 3). Subsequently, the wear models and the procedures for their parameterization are presented in detail (Section 4 and Section 5). This is followed by sensitivity analyses to evaluate the parameter uncertainties and analyses of the calculation time of the different wear approaches (Section 6 and Section 7). Finally, the wear approaches are evaluated with respect to their suitability for wear calculation (Section 8).
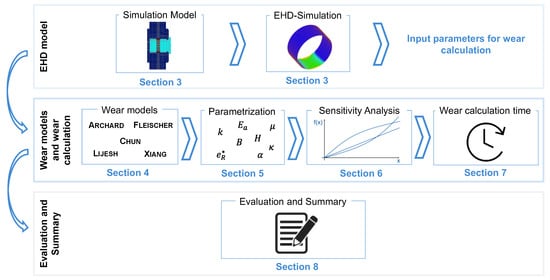
Figure 2.
Procedure for the evaluation of the wear models.
3. Journal Bearing Test Rig and EHD Simulation Model
In addition to material and lubricant properties, the resulting contact conditions within the journal bearing, such as asperity contact pressure and lubricant film height at a defined load condition, are input variables for the wear calculation. In order to determine the contact conditions of a test bearing, an EHD/MBS model was built. The EHD/MBS model reproduces an existing component test rig at the Institute for Machine Elements and Systems Engineering of the RWTH Aachen University (Figure 3a). The shaft is supported by two supporting bearings. The test bearing (Figure 3c) is mounted torsionally rigid in the bearing support. The bearing support is designed as a friction balance in order to be able to record frictional torques acting in the journal bearing. The test bearing is pulled against the shaft by the load unit. A 250 kN servo-hydraulic cylinder is used as the load unit. During the tests, the following quantities can be recorded:
- -
- Radial force;
- -
- Shaft speed;
- -
- Bearing temperature;
- -
- Friction torque.
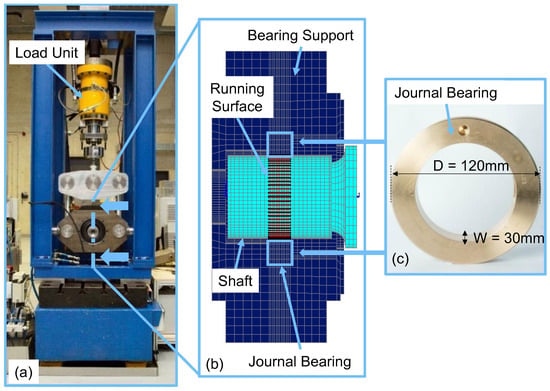
Figure 3.
(a) Test rig. (b) Modeled part of the test rig (bearing support). (c) Journal bearing.
Figure 3.
(a) Test rig. (b) Modeled part of the test rig (bearing support). (c) Journal bearing.
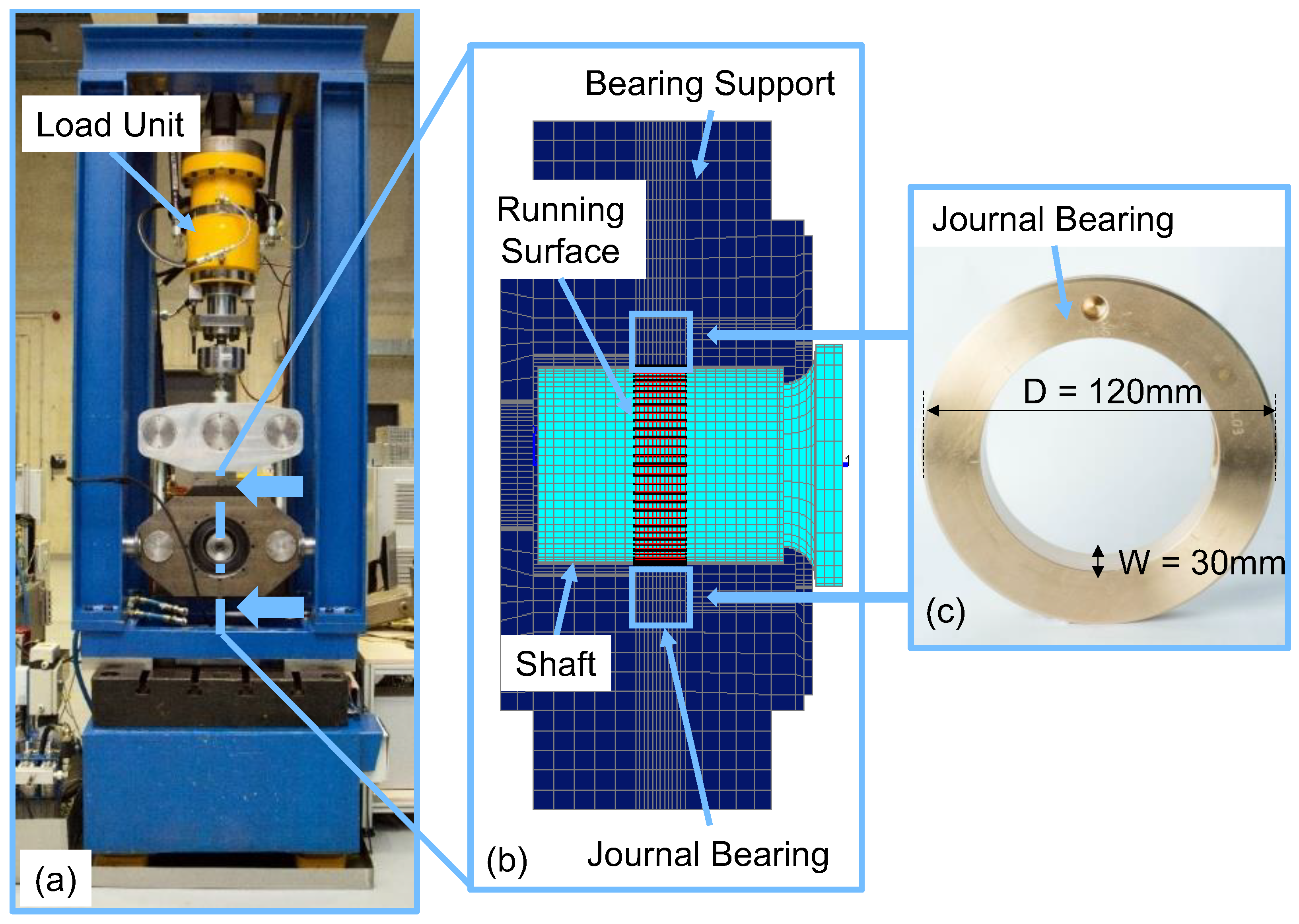
The built EHD/MBS simulation model comprises the test bearing, the shaft and the surrounding structure for bearing support (Figure 3b). The geometrical and material-specific data of the test bearing and the shaft, as well as data on the oil used, are given in Table 2. The materials and oil correspond to those used in wind turbines, whereas additivation of the oil cannot be considered in the simulation model.

Table 2.
Geometrical and material-specific data of the test bearing.
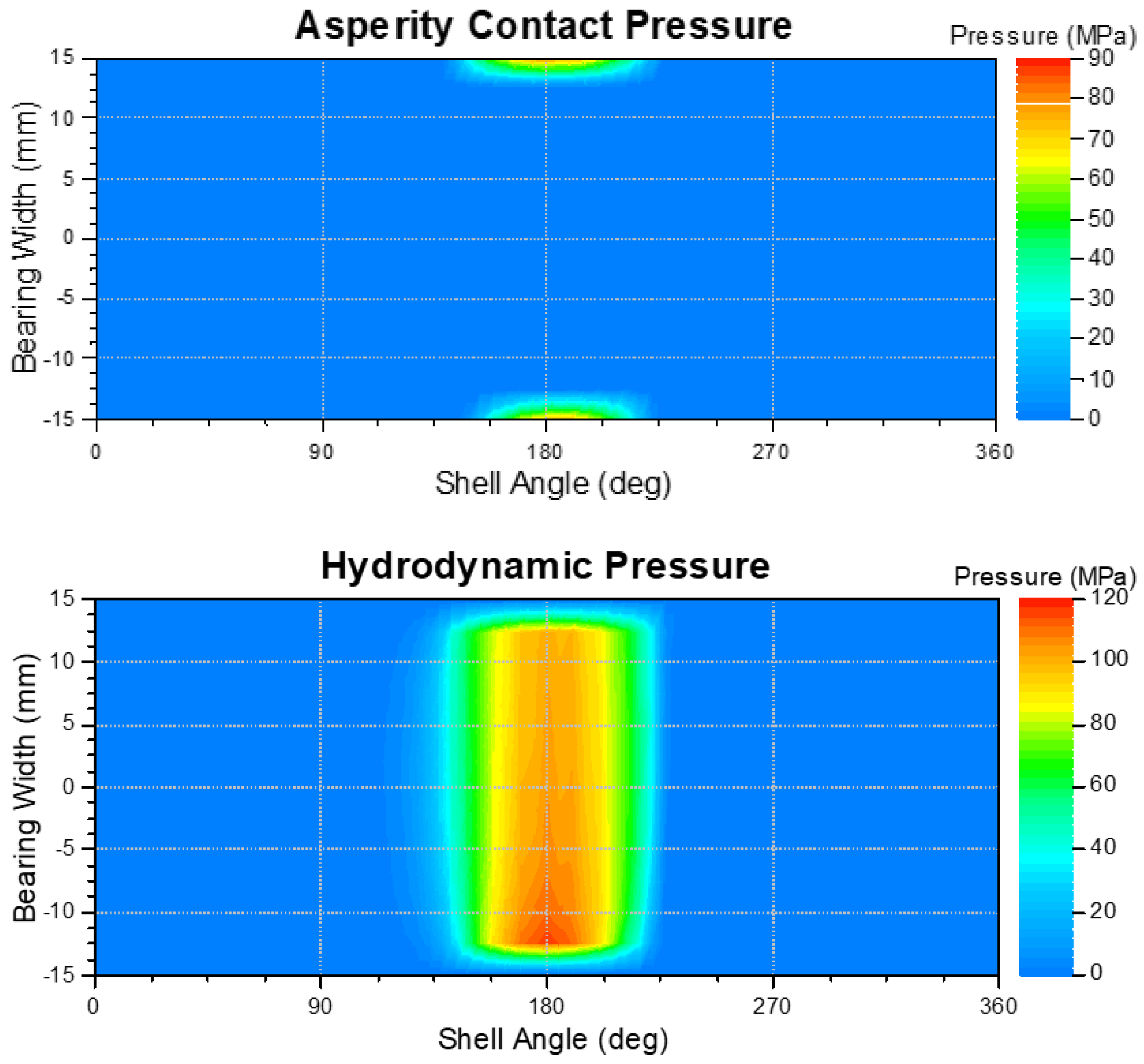
In order to be able to calculate wear occurring in planetary gear journal bearings, wear-critical conditions must be generated at circumferential speeds, which occur in wind turbines today. Therefore, in the EHD/MBS simulation, a constant normal force of 200 kN at a speed of 100 rpm (specific pressure of 55 MPa and a circumferential speed of 0.628 m/s) was applied as the load. The result of the EHD/MBS simulation is the asperity contact pressure occurring in the bearing, the asperity contact ratio and the height of the lubricant film, which are used as input variables for the wear calculation. The distribution and height of the asperity contact pressure over the bearing surface for the given load condition are shown in Figure 4 (top). In addition, the hydrodynamic pressure is shown in Figure 4 (bottom). The asperity contact pressure initially occurs at the bearing edges. Due to the radially acting load, the areas of maximum asperity and hydrodynamic contact pressure are at a 180° shell angle. Although edge bearing loading with high asperity contact pressures also occurs in planetary gear bearings, the maximum loaded zones are not directly opposite each other. Therefore, the load condition shown in Figure 4 is only an approximation of real load conditions occurring in planetary journal bearings.
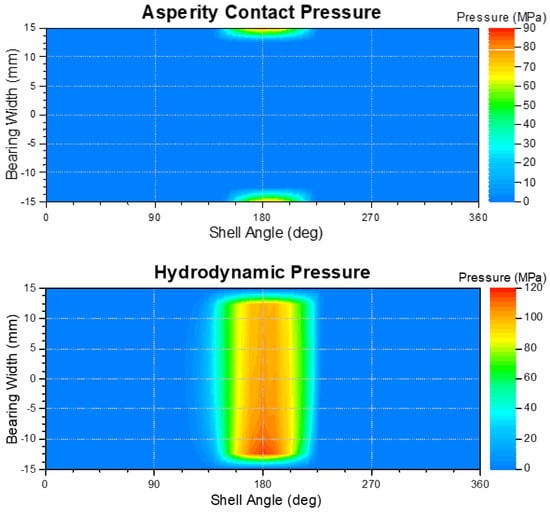
Figure 4.
Asperity contact pressure (top) and hydrodynamic pressure (bottom) for a specific pressure of 55 MPa and a rotational speed of 100 rpm.
4. Implementation of the Wear Models
The wear approaches of Arachard, Fleischer, Chun, Lijesh and Xiang were implemented and coupled with the EHD/MBS simulation of the test bearing (see Section 3). Since the approaches of Holm, Rowe and Bryant only represent preliminary development stages of the previously mentioned approaches, they are not considered further. In addition, the model of Cao et al. is not considered since it requires a complex initial three-dimensional surface microanalysis and has so far only been applied for point contacts. In the following, the underlying equations and the parameters of the wear approaches mentioned and implemented at the beginning will be discussed.
In the Archard approach [16], the wear volume is related to the contact force acting on a body , the sliding distance , the reciprocal of the hardness and a proportionality factor . The proportionality factor describes the probability of material removal due to plastic deformation of the asperity peaks. Assuming the wear mechanism remains unchanged, assumes time-constant values for constant load cases. The wear volume is calculated as:
Chun’s wear approach [5] is based on the approach of Rowe [4], who introduces the parameter , which describes the ratio of real contact area to nominal contact area. The difference between these areas is caused by lubricant molecules adsorbed on the surface, which prevent direct metallic contact. Rowe developed this approach by examining wear behavior using n-hexadecane as a lubricant, allowing to include the influence of the lubricant in the wear calculation. is calculated by:
The values used for calculation are derived from the chemical properties of the lubricant and describe how many of the molecules adsorbed on the rough metal surface are displaced by oncoming asperity peaks. is the diameter that is affected by a molecule adsorbed on the surface, is the period of vibration of a lubricant molecule adsorbed on the surface, is the molar gas constant and is the adsorption energy. is the relative sliding velocity between the two surfaces and is the temperature of the lubricating film. Integrating into the Equation previously defined by Archard for calculating wear results in:
Fleischer [6] assumes in his approach that frictional energy is generated during the sliding process, which is accumulated in the material until a critical limit is reached. This is described by the friction energy density , which represents the ratio of wear volume created and the frictional energy responsible. Following this approach, the wear volume can be represented considering the friction coefficient as follows:
As previously described, Xiang’s approach considers two wear mechanisms [9]. The fraction of wear due to plastic deformation of asperity peaks in contact (this concerns the material which experiences deformation) is calculated with:
represents the asperity radius and is the plastic deformation of the asperity peaks in contact, which is determined by the Hertzian contact theory considering the average force affecting a single asperity (cf. Equation (2)).
In order to calculate the proportion of fatigue cracks developing below the contact surface, which propagate along the angle and lead to material breaking out after a certain accumulation, the following Equation is used:
In order to be able to map the transient wear progression during the running-in phase, the wear is calculated for a previously defined sliding cycle, the relevant parameters of the wear calculation are updated, and the calculation is performed again. This is performed until the end of a pre-defined wear period is reached. The wear within cycle i is calculated by:
is the number of contact cycles between asperity peaks necessary for material removal due to fatigue (cf. Equation (9)).
The asperity contact force and the real contact area are calculated with the help of the statistical model of Greenwood and Williamson [17] for the description of rough surfaces. Here, a statistically normal distribution of asperities is assumed in order to be able to describe the asperity contact as a function of the lubricant film thickness. As the lubricant film height changes due to wear and as a result of roughness smoothing, the asperity contact force and the real contact area change in each sliding cycle. The parameters of tensile strength , coefficient of friction and fatigue exponent are nevertheless assumed by Xiang to be constant throughout the wear process. The fatigue coefficient was established by Tan [18] and is an empirical exponent to describe fatigue behavior. At this time, the availability of values for is very limited. Only some experiments for nonmetallic materials and 1045 steel were conducted. is used to describe the number of asperity contacts that occur within the i-th sliding cycle. For the calculation of , the contact model according to Greenwood and Tripp [19] is used (cf. Equation (10)).
depends on the current lubricant film height and changes with each sliding cycle. is the nominal contact area, is the asperity density on the surface, is the sliding distance in one cycle, and is a Gaussian normal distribution. Through these calculations, the Xiang approach aims to establish a wear model based on realistic physical mechanisms rather than empirical wear factors being the predominant factor of the wear prognosis. It should, however, be mentioned that this represents only a preliminary attempt and will likely be subject to future research expanding and refining the underlying wear approach.
The degradation coefficient presented by Lijesh [20] puts the wear rate in relation to the rate of entropy production and is calculated according to the following Equation:
By using a time-dependent degradation coefficient, it is possible to map the transient behavior of the tribosystem during the run-in phase. The change in temperature is caused by the frictional heat generated, so the time-dependent temperature profile is dependent on the friction coefficient.
When the wear calculation approaches developed by Fleischer and Lijesh were used, the Coefficient of Friction was calculated using the following Equation by Offner and Knaus [21] describing the friction in mixed lubrication regimes:
The required values were chosen according to König [7].
5. Parameterization of the Wear Models
All of the wear approaches presented here follow a physical approach but contain empirical parameters that require prior determination. The methods and, consequently, the effort of parameter determination differ between the wear approaches. In the following, the necessary steps to determine the parameters of each wear approach are examined to allow for an assessment of the overall effort for complete parameterization. All parameters of the considered wear approaches and their respective methods for determination are presented in Table 3.

Table 3.
Parameters of the wear approaches and their methods for determination.
Common to all the approaches mentioned is that an experimental trial is required to determine at least one parameter. Pin-on-disc experiments are a commonly used method. In pin-on-disc experiments, both the wear and the coefficient of friction can be measured [26]. Based on the experiment results, the wear coefficient for Archard and Chun and the wear-specific friction work according to Fleischer can be determined. However, it was shown that these parameters are dependent on the applied load, which is why a measurement for each load case, which is to be considered, is necessary for an accurate prediction of the wear [12,23].
Lijesh developed the approach of a time-varying degradation coefficient in order to be able to map the transient running-in wear [20]. To determine this coefficient, it is necessary to experimentally determine the wear rate and the coefficient of friction with regard to their time dependency. One way to continuously measure wear is to incorporate a differential transformer into pin-on-disc experiments [27]. It has been shown that the wear of different load cases can be determined sufficiently accurately by a constant degradation coefficient as long as the acting friction force is known for the load cases [12]. Thus, the one-time determination of the degradation coefficient B applying a constant load is sufficient.
Since Xiang’s work uses the Greenwood and Williamson contact model as the basis of the wear calculation, this wear approach requires the parameters of asperity density and asperity radius to describe the rough surface. Although these parameters change in the course of the wear process, constant values are assumed in the calculation, which is why a measurement of the surface on a journal bearing in new condition is sufficient [9]. In this case, a two-dimensional profile is sufficient to form the average values required for the calculation. The propagation angle of the fatigue fracture cannot be determined before the wear occurs, so a value between 15° and 30° must be estimated [9]. To determine the fatigue coefficient, an experimental determination of the wear, e.g., by a pin-on-disc test, is necessary. As with the degradation coefficient B, it has been shown that the variations in the wear results at different load cases are sufficiently small that a single determination of the fatigue coefficient at constant load is sufficient. [18]
The Chun wear approach requires, in addition to the wear coefficient known from Archard, information about the lubricant used. The vibration time of a lubricant film molecule in the adsorbed state can be calculated under the assumption that this vibration time is equal to the lattice vibration time of the adsorbing metal surface [28]. The vibration time can be calculated using the Lindemann Equation [29]:
For this purpose, the molar mass M, the molar volume and the absolute melting point of the metal surface are required. For most materials, these values can be assumed to be known. Assuming that the molecular chains of the lubricant are arranged horizontally in all directions relative to the direction of movement of the asperity peaks, a circular area can be assumed to be affected by one molecule [4]. The diameter can be derived from the cross-sectional area affected by a lubricant molecule considering its length, 1.27n + 2 Å for alkanes, with n being the number of carbon atoms [25] and the distance between adjacent lubricant chains. The value of the adsorption energy can be derived from the friction value of pin-on-disc experiments at a constant temperature [24]. Due to the dependence of the coefficient of friction on the acting load, the adsorption heat is also load-dependent.
In summary, all approaches require a pin-on-disc experiment, although it could be argued that the parameters of the long-standing approaches of Archard, Fleischer and Rowe are well-known and should be seen as parameters found in the literature. However, since the parameters are highly dependent on the circumstances considered, e.g., applied load, lubrication regime, material pairing, etc., a prior experimental determination is recommended for accurate prediction of wear. Considering the effort of the necessary experiments alone, the parameter determination of the Lijesh wear approach shows the greatest complexity. The determination of the degradation coefficient requires a temporal resolution of the wear, while for the remaining wear approaches, the wear state at the end of the experiment is sufficient. In return, the degradation coefficient is independent of the applied load case, which is why a single experiment is sufficient to determine for several load cases [12]. The Xiang wear approach requires the largest number of parameters, which contributes to the overall parameterization effort. Analog to Lijesh, these parameters are, however, independent of the load case [18]. In order to determine the total effort necessary for complete parameterization of the wear approaches, the wear approaches can be rated in the categories “number of parameters”, “load dependency of parameters” and “complexity of parameter determination” using the overview provided in this chapter.
6. Sensitivity Analysis of the Wear Parameters
In the following, the sensitivity of the approaches to possible measurement deviations during the experiments for parameter determination or other parameter uncertainties will be evaluated. For this purpose, a local quantitative sensitivity analysis is performed according to the one-at-a-time principle. Here, one parameter is varied between limits obtained by literature research, while constant reference values are assumed for the remaining parameters. The selected number of variance points per parameter is . Due to the lack of experimental data needed to determine all relevant parameters, the reference parameters were chosen within the researched limits such that the same maximum wear depth resulted from the different approaches. The reference wear depth was determined based on the Fleischer wear approach, utilizing the friction energy density determined by König [7]. The chosen limits, as well as the reference values, can be found in Table 4. The asperity contact pressure and the height of the lubricant film required for the wear calculation are taken from the EHD simulation in Section 3.

Table 4.
Limits and reference values of the considered wear approaches.
The magnitude and units of the wear parameters differ significantly. Therefore, a comparison by simple local derivation is not possible since a large sensitivity would follow from parameters of small magnitude and a very low sensitivity from parameters of large magnitude. Instead, the sensitivity of the wear calculation is compared using a dimensionless value that represents the relative change of the parameters. The following methodology, described by Hamby [33], was used: The difference in wear depth between two adjacent variance points was formed and divided by the reference wear depth. In addition, the difference between the associated parameter values was formed and was also divided by the associated reference parameter. This allows a comparison of the sensitivities despite different magnitudes. The sensitivity values were thus calculated as follows:
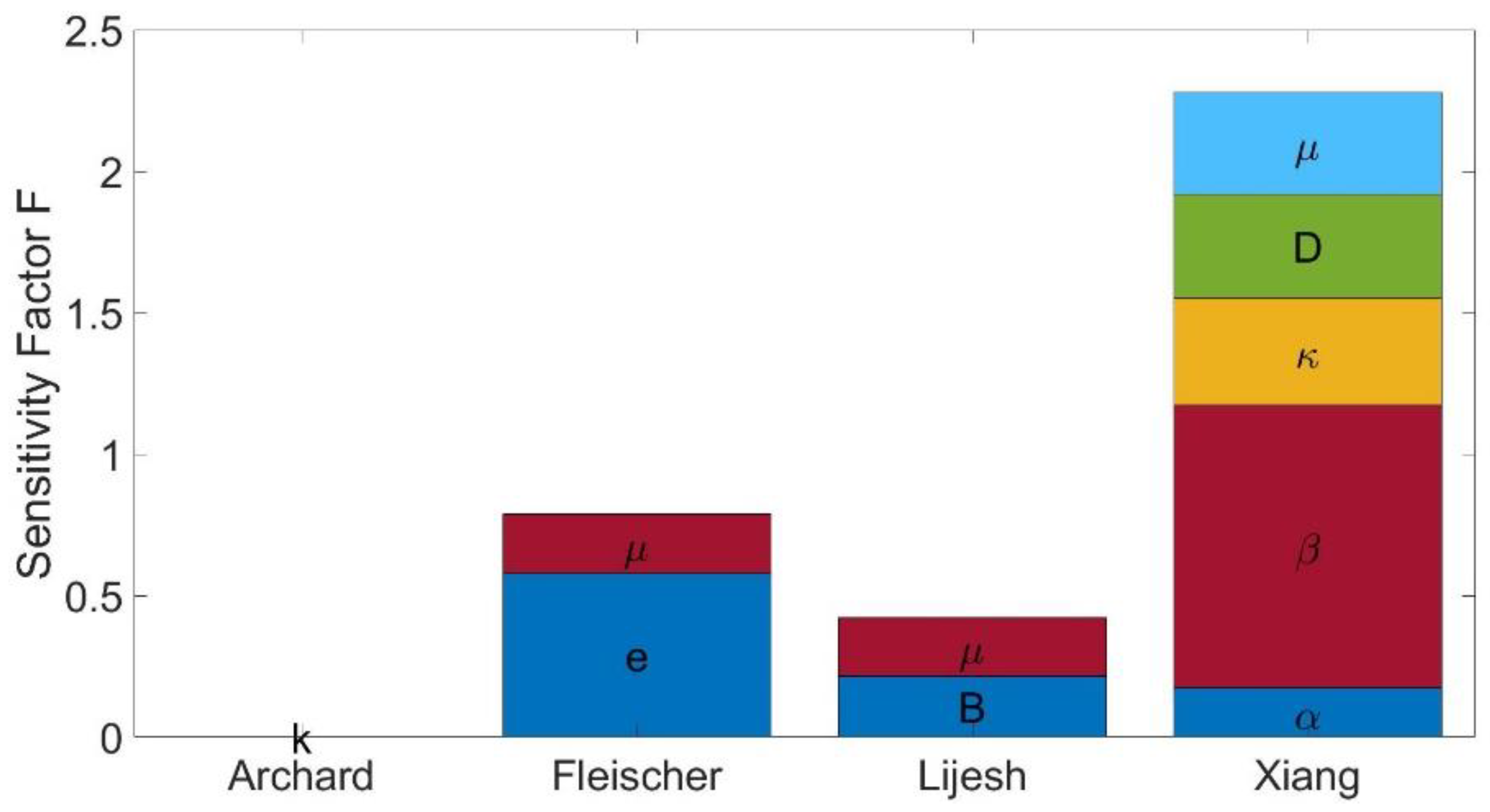
For further comparison, the maximum value of was determined for each parameter and used to compare the sensitivity of the calculated wear depth due to parameter deviations. The maximum values of were then scaled to values between 0 and 1 using the min–max normalization [34]. Then, the values of the parameters of each model were added to determine the total sensitivity. Going forward, the resulting sum will be called the sensitivity factor. The sensitivity factors of the wear approaches are shown in Figure 5. The sensitivities of the individual wear approaches as a function of their input parameters are shown in Figure 6, Figure 7, Figure 8 and Figure 9.
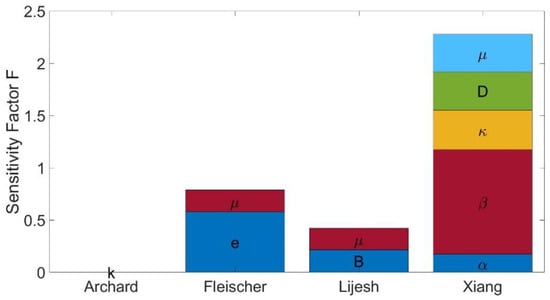
Figure 5.
Sensitivity factors of the wear approaches.
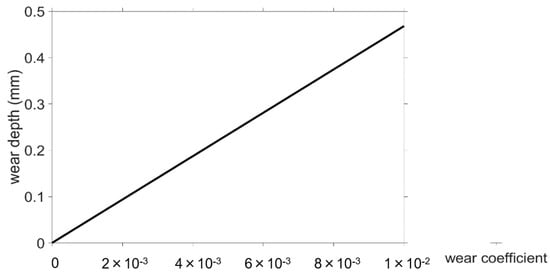
Figure 6.
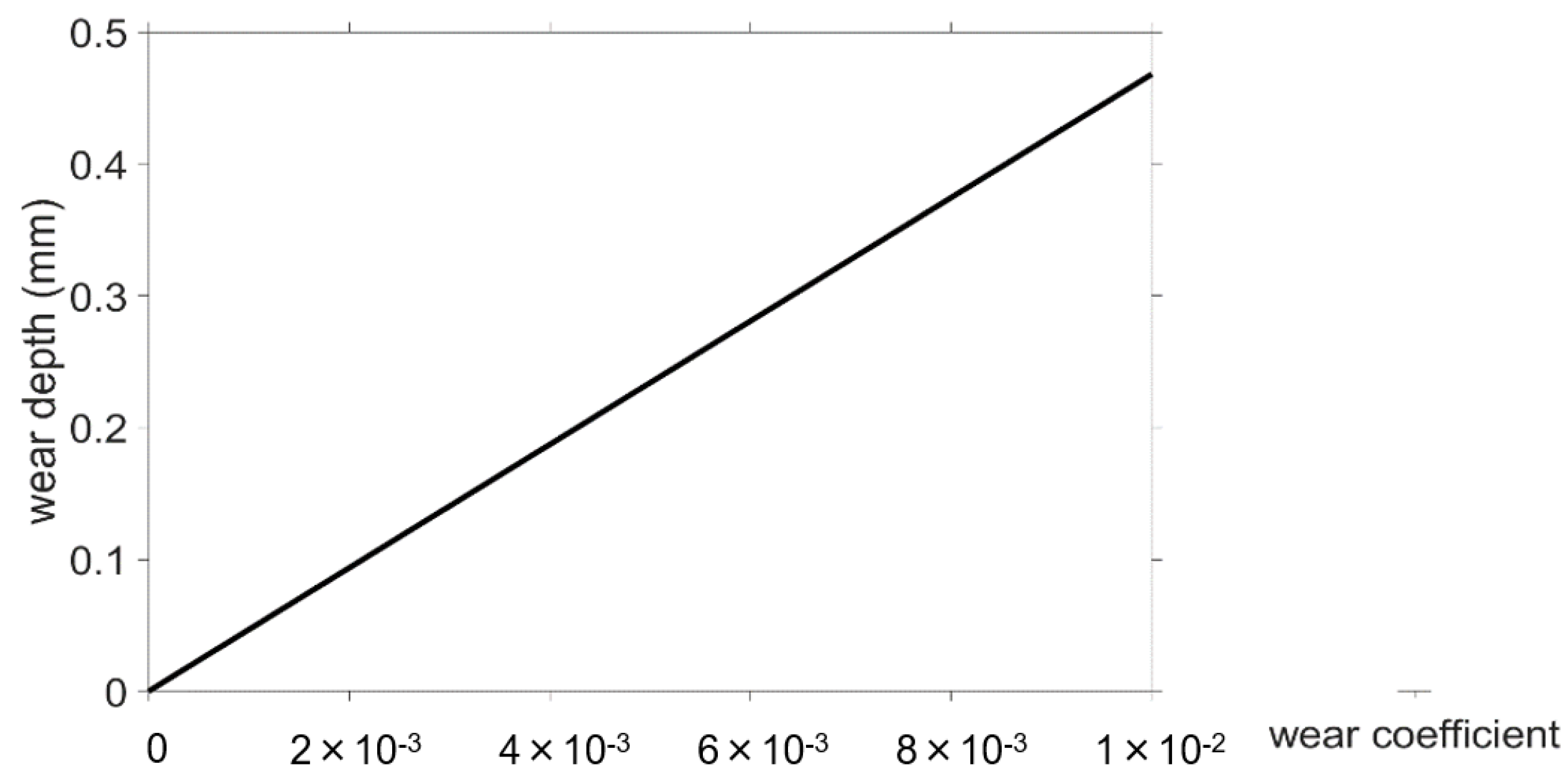
Sensitivities of the Archard wear approach as a function of the input parameter.
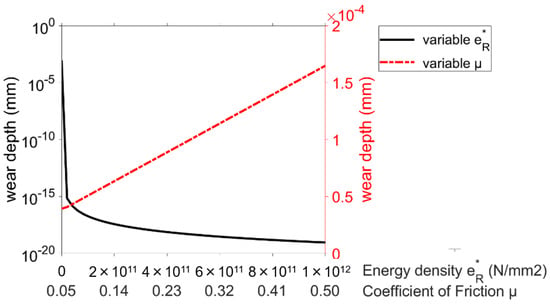
Figure 7.
Sensitivities of the Fleischer wear approach as a function of the input parameters.
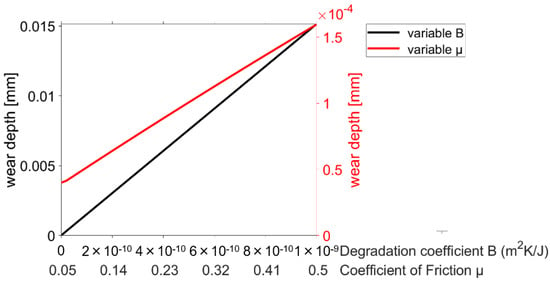
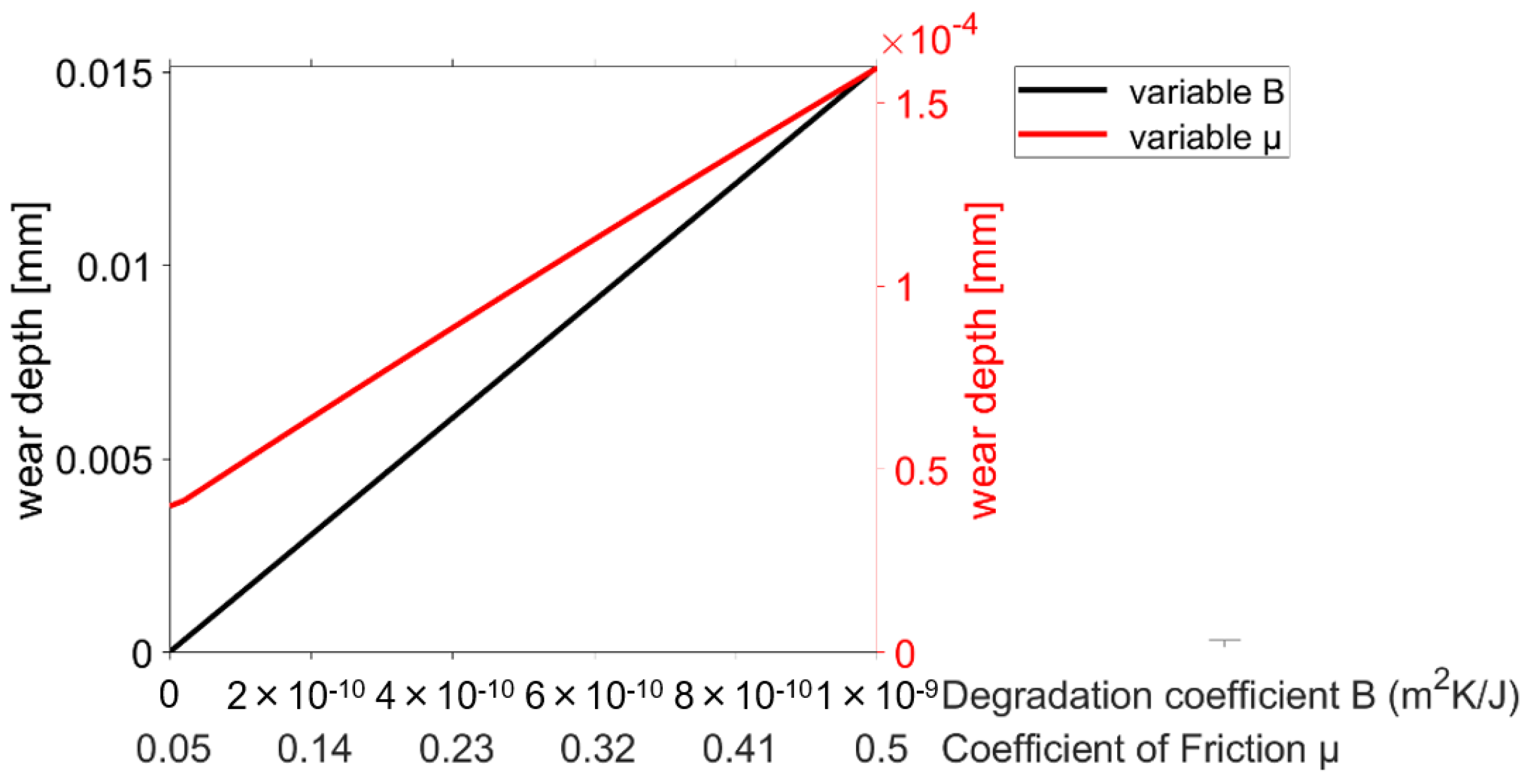
Figure 8.
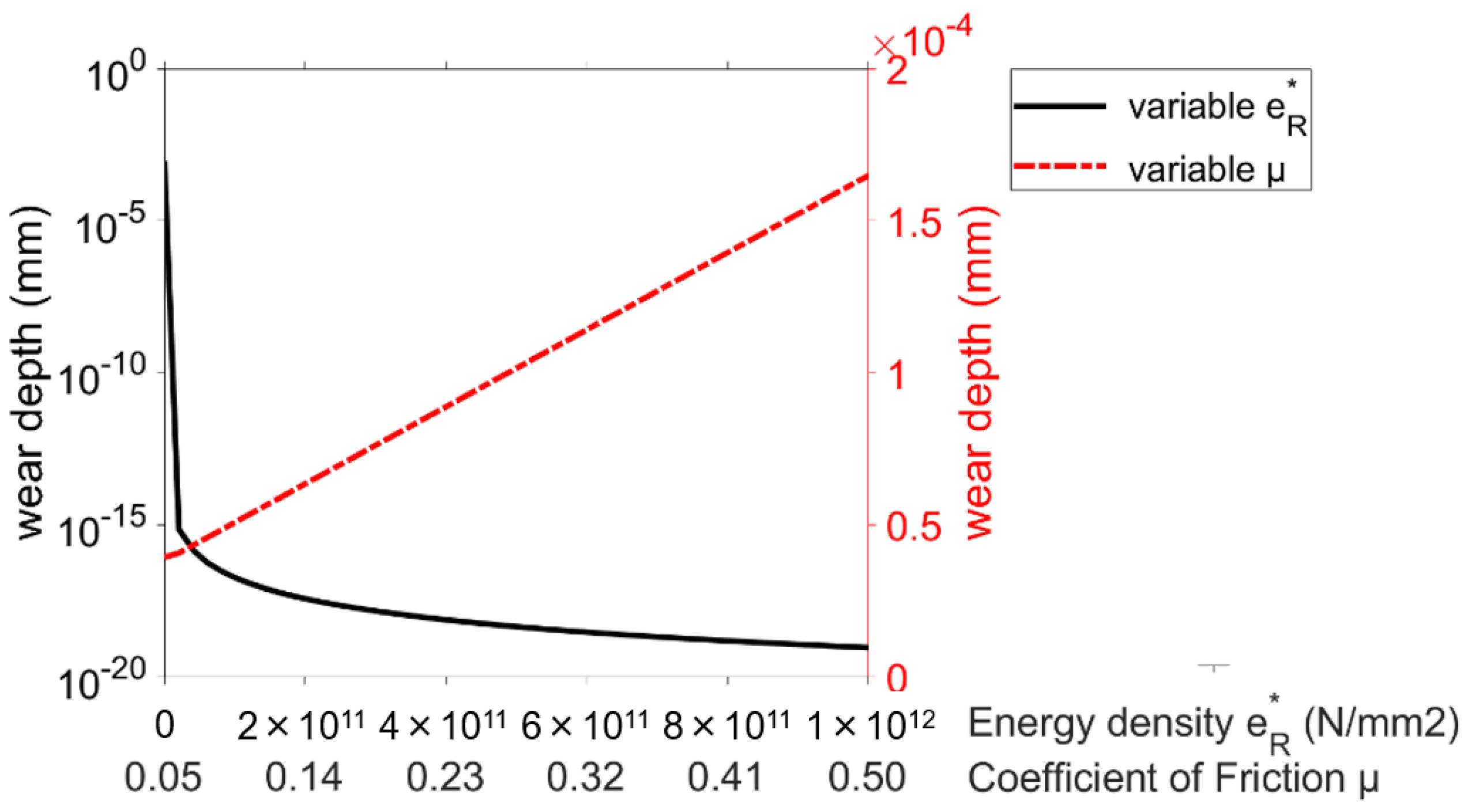
Sensitivities of the Lijesh wear approach as a function of the input parameters.
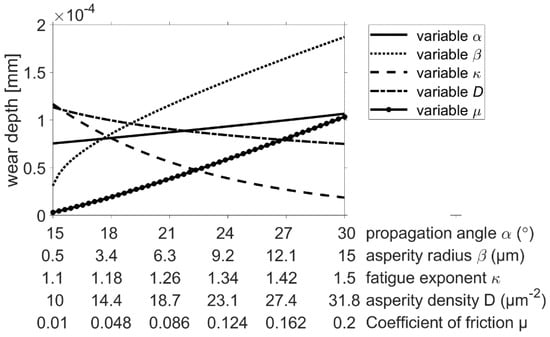
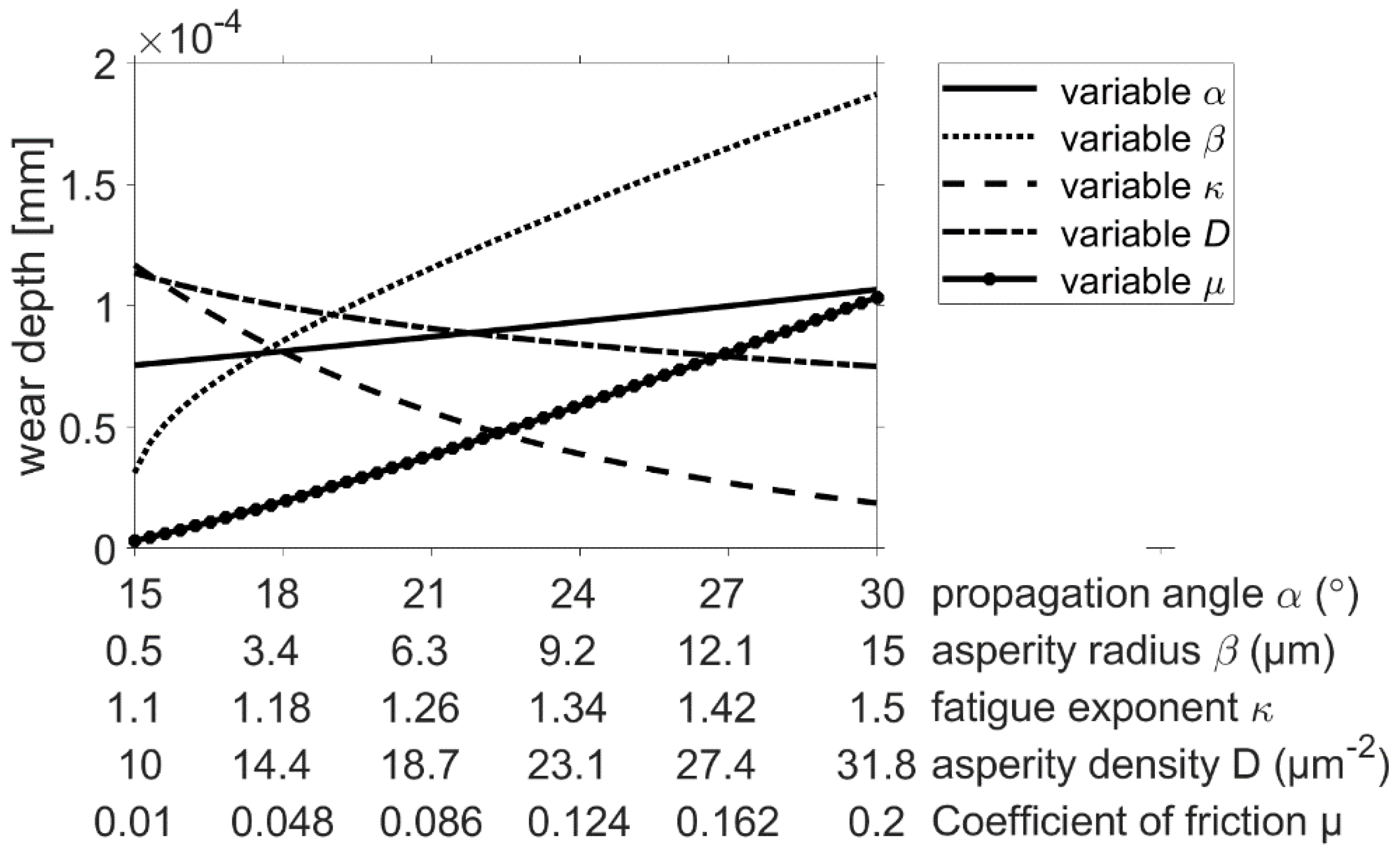
Figure 9.
Sensitivities of the Xiang wear approach as a function of the input parameters.
To increase the readability of the graphs depicting the sensitivity of the Lijesh and Fleischer wear approach, a second axis with a deviating scaling has been introduced to allow the clear representation of all parameter influences, although the resulting wear depth differs in its order of magnitude.
Since k is only included as a constant factor in the Archard wear calculation, a linear increase in the wear height proportional to k follows. Lijesh also shows a relatively low sensitivity to a change in the parameters B and μ, as the relationship between the wear height and the calculation parameters also follows a linear course. The wear approach of Fleischer shows a slightly greater sensitivity. The wear is proportional to the reciprocal of the friction energy density, so a regressive decrease in the maximum wear height is seen with increasing . The overall sensitivity of the wear approach, according to Xiang, is considerably greater than that of the approaches mentioned so far (see Figure 5). This is partly due to the high number of parameters required. However, the asperity radius β, in particular, shows a slightly greater sensitivity than the other parameters.
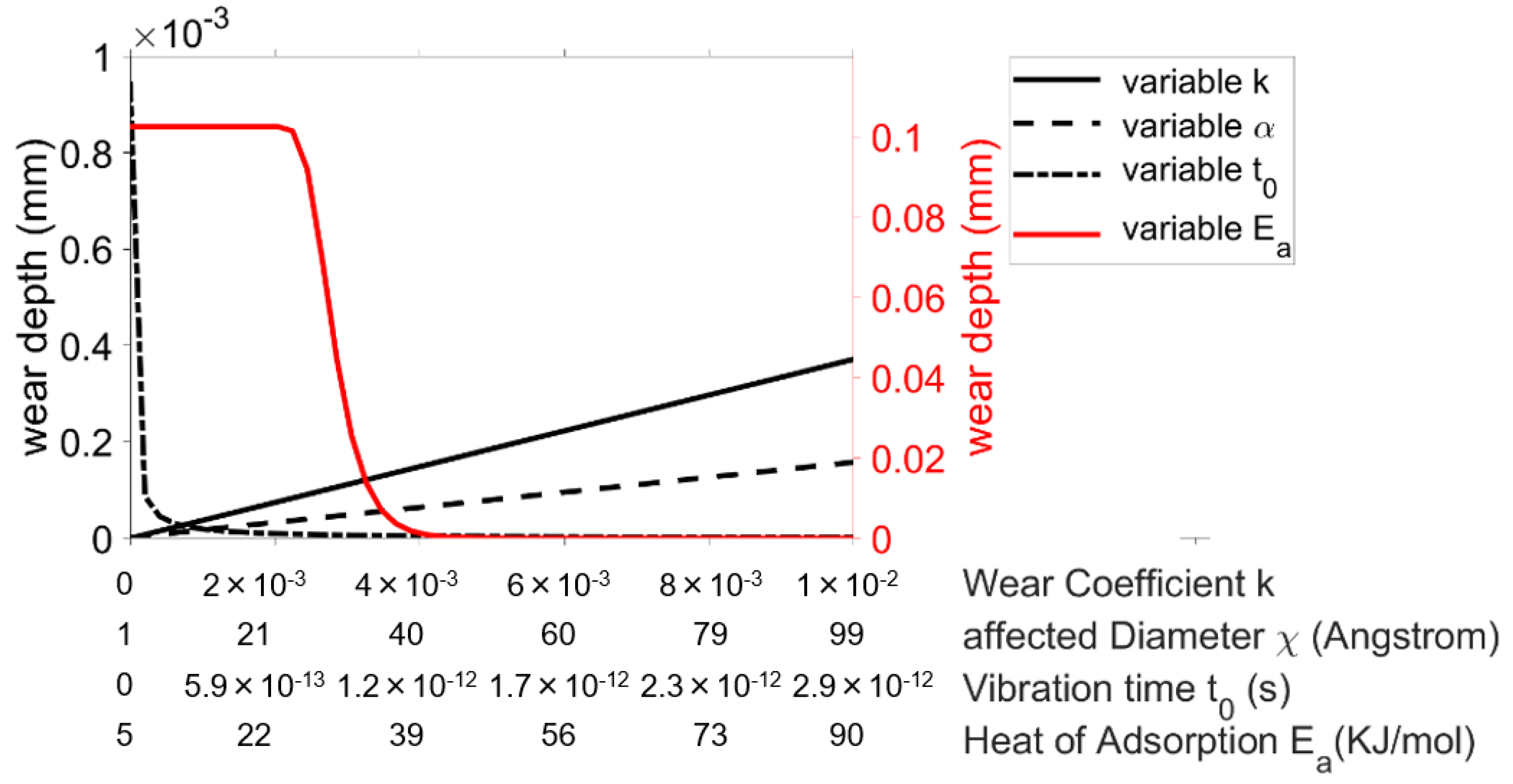
The Chun wear approach was not included in the previous analysis. This is due to the fact that this approach has a sensitivity whose difference from the remaining wear approaches is so large that a comparison with the previously mentioned methodology using the sensitivity factor will lead to negligible sensitivities of the other wear approaches due to the used min–max normalization. Figure 10 shows the curves of the wear depth as a function of the parameters for the Chun approach. The parameters wear coefficient k and diameter influenced by the adsorbed lubricant film molecule follow a linear course and exhibit relatively low sensitivity. The vibration time is included in the denominator of the relevant equation, resulting in a high sensitivity at values close to the researched lower limit. However, the largest contribution to the sensitivity of Chun’s model is made by the adsorption energy of the lubricant. As can be seen, there is a range for this parameter in which even very small changes cause a very large fluctuation in the wear level. When considering the curve of the wear depth, it should be noted that the graph for the adsorption energy refers to the right axis of the diagram. The right axis was scaled up by a factor of approximately 100 to be able to map the sensitivity in the graph. The reason for the massive sensitivity of is the double exponential influence on the calculated wear.
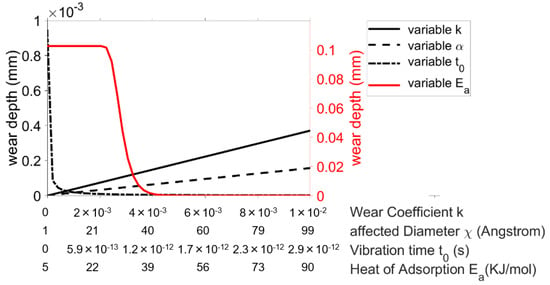
Figure 10.
Curves of the wear depth as a function of the parameters for the Chun approach.
7. Calculation Time
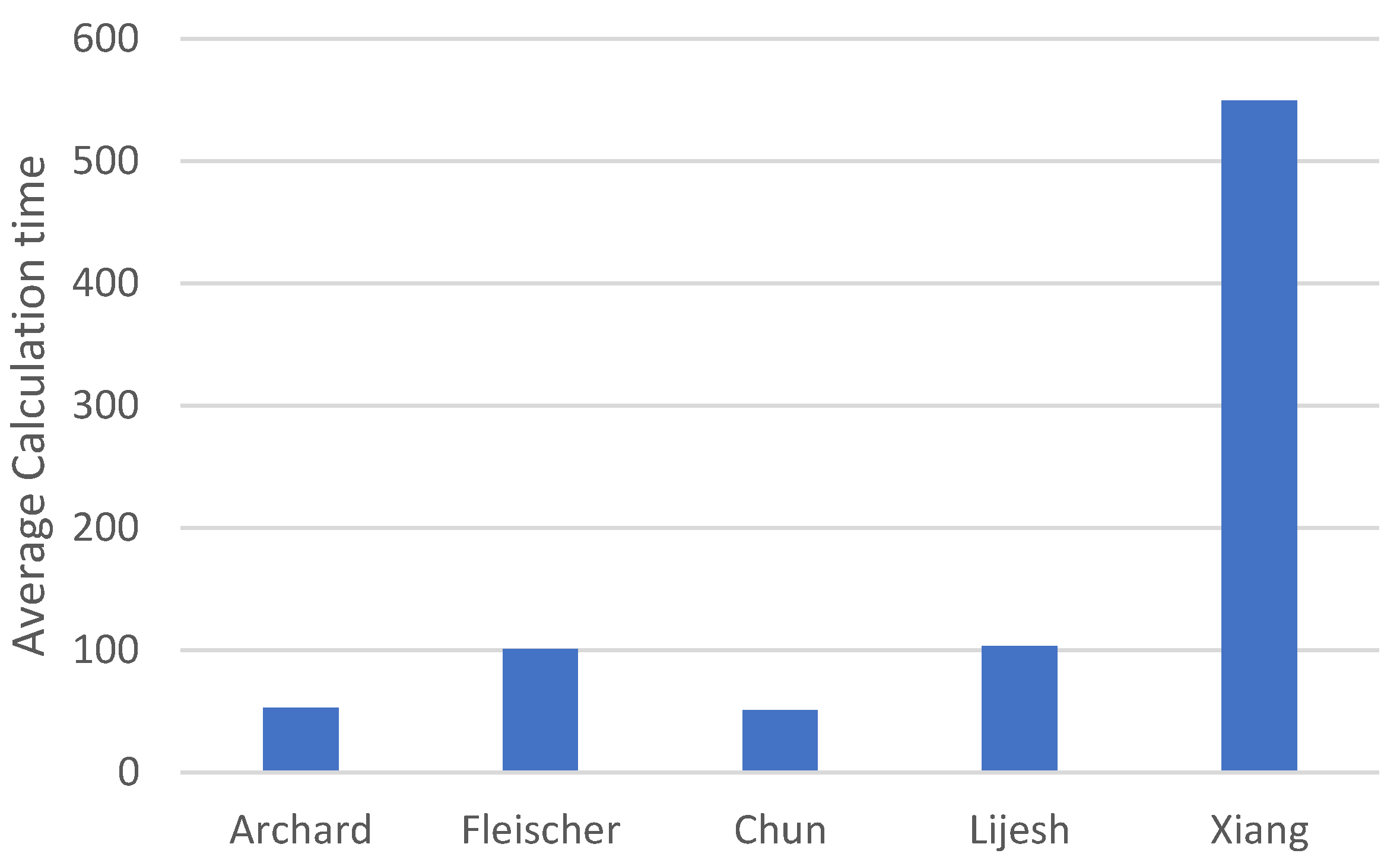
With regard to a fast provision of results, it is necessary to evaluate the duration of the wear calculation. This gains particular importance when several iterative calculations are conducted. To compare the calculation time, three calculations were performed for each wear approach, and the time required was measured. The basis for these calculations was the results of the EHD simulation (see Section 3). The FE mesh used consists of 38 points in the circumferential direction of the bearing and 13 points across the width of the bearing. This results in 719 × 38 × 13 = 355,186 data points considering a total rotation angle of 719° and a time increment of 1° rotation angle. The calculation was performed by an Intel Core i5-7600 3.5 GHz quad-core CPU using Matlab R2018b. The exact results are shown in Table 5. Additionally, for a visual comparison, the mean values of the results are shown in Figure 11.

Table 5.
Duration of the wear calculation of the different wear approaches.

Figure 11.
Comparison of mean values of the wear calculation time of the different wear approaches.
The lowest time needed for calculation can be obtained using the approaches of Archard and Chun. The reason for this is the simplicity of the equations used and the need for only the asperity contact pressure as an input for the calculation. Most of the calculation time is due to the processing of result files. In the calculations of Lijesh and Fleischer, the lubrication gap height is required in addition to the asperity contact pressure in order to calculate the coefficient of friction using the equation of Offner and Knaus. Accordingly, the number of required files is doubled, and the data processing consequently takes about twice as long. The computation time of the Xiang approach is considerably larger in comparison to the other approaches. This is due to the integrals contained in the equations used, which require considerably more computing time than the simple algebraic equations of the remaining models.
8. Summary and Outlook
The aim of this study was a screening, implementation and evaluation of different wear approaches regarding their suitability for the wear calculation of planetary gear bearings in wind turbines. Five different wear approaches (according to Archard, Fleischer, Chun, Lijesh and Xiang) were evaluated with respect to their suitability for the wear calculation of planetary gear bearings in wind turbines. For this purpose, an MBS/EHD simulation model was set up, which calculates the wear-relevant variables, such as asperity contact pressure, fluid contact pressure, shear rate and lubricant film height. Bearing materials and lubricating oils, which are commonly used in wind turbines, were considered. Subsequently, the five wear approaches were implemented. All of the wear approaches follow a physical approach but contain empirical parameters that require prior determination. Therefore, all parameters of the considered wear approaches, their respective methods for determination and additionally their limit values were presented in tables. Subsequently, sensitivity analyses were performed. The inputs of the sensitivity analysis were the results of the MBS/EHD calculation. The results of the sensitivity analysis allow a conclusion on the parameter uncertainty, which is a criterion for the evaluation of the wear approaches. In addition, the methods for parameter determination, the number of parameters, the load case dependency and the calculation time are further criteria for the evaluation of the wear approaches.
The results show that regarding parameter uncertainty, Archard, Fleischer, and Lijesh present good approaches. Xiang’s approach, on the other hand, has a higher parameter uncertainty and can, therefore, lead to strong deviations in the wear calculation. Therefore, Xiang’s approach is, at the moment, not recommended for predicting the wear in journal bearings of wind turbines. However, basing the wear model on realistic physical mechanisms enables the consideration of multiple, genuine system factors influencing the wear progress. In this way, the dependency on wear experiments, whose results allow only for limited transferability to deviating conditions and show significant fluctuations, can be reduced. This approach to wear calculation can be important in order to deepen the understanding of wear mechanisms, but it has to be further researched and analyzed before it should be considered for practical applications. In the Chun approach, the adsorption energy parameter has an extreme sensitivity and, therefore, leads to the highest parameter uncertainty. The Lijesh approach is the overall best approach for wear calculation according to the previously mentioned evaluation criteria. This is due to the fact that this approach achieves good results in almost all areas considered. Its calculation time is adequately low, and the sensitivity of the parameters is lower than that of most other approaches. Its biggest disadvantage is the relatively elaborate experiment necessary for the parameterization, requiring a continuous measurement of the wear volume, which can be achieved by integrating a linear variable differential transducer. This disadvantage is, however, compensated by the load case independence of the determined parameters, giving the approach a huge advantage when examining multiple occurring conditions leading to wear.
In the near future, the further steps mentioned in Figure 1 will be tackled. Currently, calculations of the local contour change and roughness change of the component test rig journal bearing are performed using the presented wear approaches. This has the aim of evaluating the wear approaches with respect to their agreement with experimental data (Step 3). The agreement with experimental data will then represent a further criterion for the evaluation of wear models. Furthermore, real load situations will be considered for the wear calculation in the future (Step 4). A method for wear calculation under real load conditions will be developed, and the method will then be validated using experimental data from a gearbox test rig (Step 5).
Author Contributions
Conceptualization, methodology, writing—review and editing, B.L.; conceptualization, methodology, writing—original draft preparation, P.T.; writing—review and editing, F.G.G.; supervision, G.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Federal Ministry for Economic Affairs and Climate Action of Germany. Funding Number: 03EE3054A.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank our project partners, who provided equipment, insight and expertise that greatly assisted the research.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| EHD | Elastohydrodynamic |
| MBS | Multibody Simulation |
References
- Czichos, H. 3. überarbeitete und erweiterte Auflage. In Tribologie-Handbuch: Tribometrie, Tribomaterialien, Tribotechnik; Springer eBook Collection Computer Science & Engineering; Vieweg + Teubner: Wiesbaden, Germany, 2010. [Google Scholar]
- Holm, R. Electric contacts. In Alquvist & Wiksells Akademisk Handböker; Gebers: Stockholm, Sweden, 1946. [Google Scholar]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Rowe, C.N. Some Aspects of the Heat of Adsorption in the Function of a Boundary Lubricant. ASLE Trans. 1966, 9, 101–111. [Google Scholar] [CrossRef]
- Chun, S.M.; Khonsari, M.M. Wear simulation for the journal bearings operating under aligned shaft and steady load during start-up and coast-down conditions. Tribol. Int. 2016, 97, 440–466. [Google Scholar] [CrossRef]
- Fleischer, G. Verschleiß und Zuverlässigkeit, 1st ed.; Verlag Technik: Berlin, Germany, 1980. [Google Scholar]
- König, F. Prognose des Verschleißverhaltens Ölgeschmierter Gleitlager: Wear Prediction of Plain Bearings under Mixed Friction Conditions. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2020. [Google Scholar]
- König, F.; Chaib, A.O.; Jacobs, G.; Sous, C. A multiscale-approach for wear prediction in journal bearing systems—From wearing-in towards steady-state wear. Wear 2019, 426–427, 1203–1211. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; Wang, J.; Wang, J.; Ni, X. Coupling transient mixed lubrication and wear for journal bearing modeling. Tribol. Int. 2019, 138, 1–15. [Google Scholar] [CrossRef]
- Xiang, G.; Yang, T.; Guo, J.; Wang, J.; Liu, B.; Chen, S. Optimization transient wear and contact performances of water-lubricated bearings under fluid-solid-thermal coupling condition using profile modification. Wear 2022, 502, 204379. [Google Scholar] [CrossRef]
- Chen, S.; Xiang, G.; Fillon, M.; Guo, J.; Wang, J.; Cai, J. On the tribo-dynamic behaviors during start-up of water lubricated bearing considering imperfect journal. Tribol. Int. 2022, 174, 107685. [Google Scholar] [CrossRef]
- Lijesh, K.P.; Khonsari, M.M. On the Modeling of Adhesive Wear with Consideration of Loading Sequence. Tribol. Lett. 2018, 66, 105. [Google Scholar] [CrossRef]
- Bryant, M.; Khonsari, M.; Ling, F. On the thermodynamics of degradation. Proc. R. Soc. Lond. Ser. A 2008, 464, 2001–2014. [Google Scholar] [CrossRef]
- Cao, H.; Tian, Y.; Meng, Y. A Fracture-Induced Adhesive Wear Criterion and its Application to the Simulation of Wear Process of the Point Contacts under Mixed Lubrication Condition. Facta Univ. Mech. Eng. 2021, 19, 23. [Google Scholar] [CrossRef]
- Lucassen, M.; Decker, T.; Guzmán, F.G.; Lehmann, B.; Bosse, D.; Jacobs, G. Simulation methodology for the identification of critical operating conditions of planetary journal bearings in wind turbines. Forsch. Ing. 2023, 87, 147–157. [Google Scholar] [CrossRef]
- Archard, J.F. The wear of metals under unlubricated conditions. Proc. R. Soc. Lond. Ser. A 1956, 236, 397–410. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, L.; Hu, Y. A Wear Model of Plane Sliding Pairs Based on Fatigue Contact Analysis of Asperities. Tribol. Trans. 2014, 58, 148–157. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Lijesh, K.; Khonsari, M.; Kailas, S.V. On the integrated degradation coefficient for adhesive wear: A thermodynamic approach. Wear 2018, 408–409, 138–150. [Google Scholar] [CrossRef]
- Offner, G.; Knaus, O. A Generic Friction Model for Radial Slider Bearing Simulation Considering Elastic and Plastic Deformation. Lubricants 2015, 3, 522–538. [Google Scholar] [CrossRef]
- Yuqin, W.; Jinyuan, T.; Wei, Z. Influence of distribution parameters of rough surface asperities on the contact fatigue life of gears. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 234, 821–832. [Google Scholar] [CrossRef]
- Meier, V.; Illner, T. Gleitlagerverschleißgrenzen—Einsatzgrenzen von Hydrodynamischen Weißmetallgleitlagern Infolge von Verschleiß: Abschlussbericht; Lehrstuhl und Institut für Maschinenelemente und Maschinengestaltung, RWTH Aachen University: Aachen, Germany, 2013. [Google Scholar]
- Kingsbury, E.P. Some Aspects of the Thermal Desorption of a Boundary Lubricant. J. Appl. Phys. 1958, 29, 888–891. [Google Scholar] [CrossRef]
- Kurtz, S.S., Jr.; Brooks, B.T.; Boord, C.E.; Schmerling, L. The Chemistry of Petroleum Hydrocarbons 1; Reinhold: New York, NY, USA, 1954. [Google Scholar]
- Sedlaček, M.; Podgornik, B.; Vižintin, J. Influence of surface preparation on roughness parameters, friction and wear. Wear 2009, 266, 482–487. [Google Scholar] [CrossRef]
- Pottirayil, A.; Kailas, S.V. Dry Sliding Wear Behavior of Ti-6Al-4V Pin Against SS316L Disk at Constant Contact Pressure. J. Tribol. 2017, 139, 021603. [Google Scholar] [CrossRef]
- de Boer, J.H. The Dynamical Character of Adsorption, 2nd ed.; Clarendon P: Oxford, UK, 1968. [Google Scholar]
- Lindemann, F.A. The calculation of molecular vibration frequencies. Phys. Z. 1910, 11, 609–612. [Google Scholar]
- AVL List GmbH. AVL Excite User Manual; AVL List GmbH: Graz, Austria, 2020. [Google Scholar]
- Leighton, M.; Morris, N.; Gore, M.; Rahmani, R.; Rahnejat, H.; King, P. Boundary interactions of rough non-Gaussian surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 1359–1370. [Google Scholar] [CrossRef]
- Kingsbury, E.P. The Heat of Adsorption of a Boundary Lubricant. ASLE Trans. 1960, 3, 30–33. [Google Scholar] [CrossRef]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- Akanbi, O.A.; Amiri, I.S.; Fazeldehkordi, E. Chapter 4—Feature Extraction. In A Machine-Learning Approach to Phishing Detection and Defense; Akanbi, O.A., Fazeldehkordi, E., Amiri, I.S., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 45–54. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).