Numerical Calculation Method of Multi-Lip Seal Wear under Mixed Thermal Elastohydrodynamic Lubrication
Abstract
1. Introduction
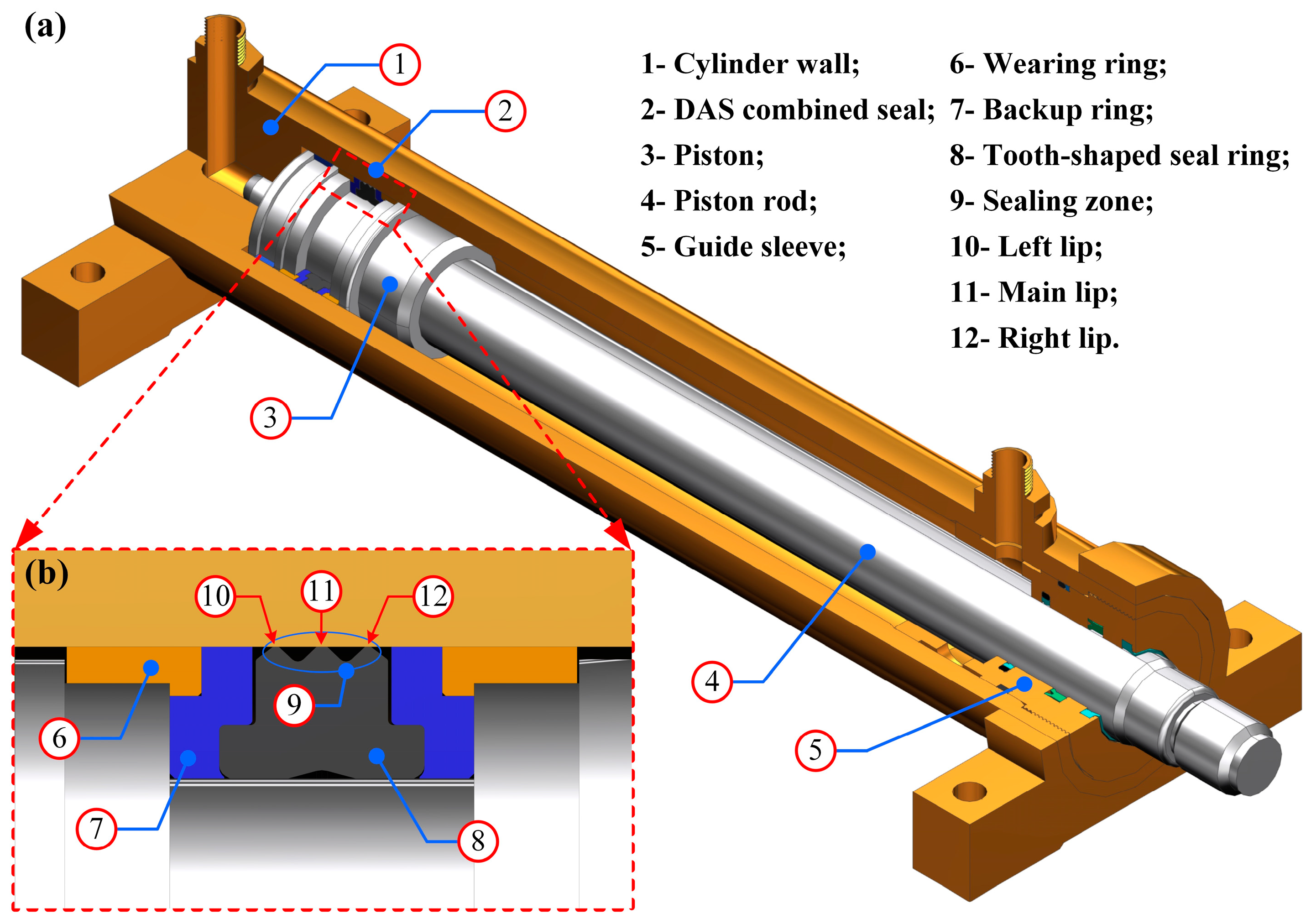
2. Geometric Structure
3. Theoretical Analysis
3.1. Hydrodynamics
3.2. Contact Mechanics
3.3. Deformation Mechanics
3.4. Thermal Mechanics
3.5. Coupling Mechanics
3.6. Wear Mechanics
3.7. Numerical Calculation Procedure
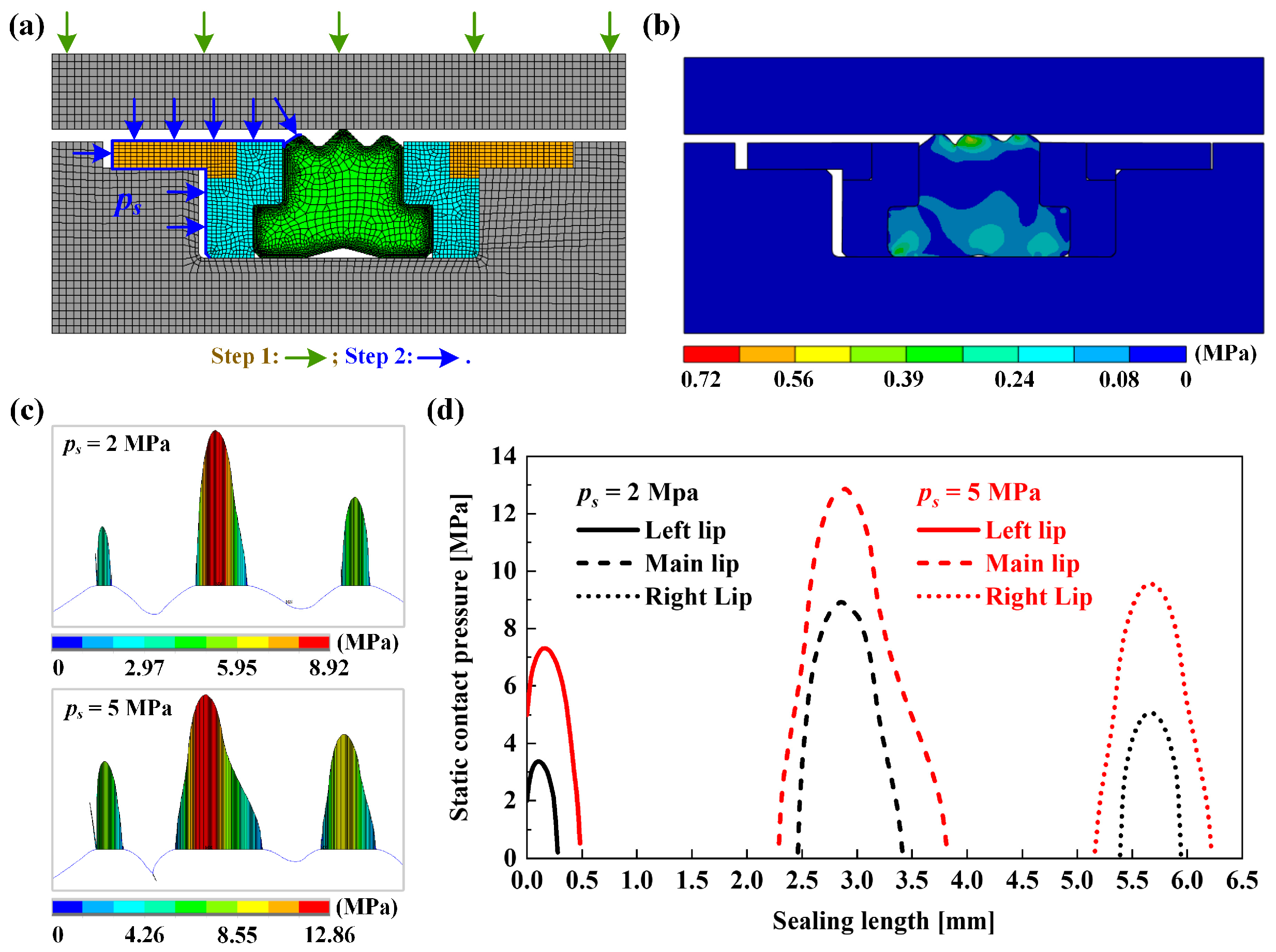
- In ANSYS software, the finite element analysis (FEA) of seal static solid mechanics is performed based on the characteristics of the seal, fluid and operating conditions.
- The static contact pressure Psc, Lx, K obtained via FEA and the static initial film thickness Hs calculated by Psc are input into the MATLAB program and initialized.
- The film fluid pressure Pf and the asperity contact pressure Pc are calculated using the fluid mechanics model and the contact mechanics model, respectively. Then, compare the sum of Pf and Pc with Psc to obtain the pressure difference under dynamic conditions; the pressure difference is applied to calculate the new film thickness.
- If the film thickness converges, the film temperature can be determined with the thermal mechanics model, which can also determine the fluid viscosity at this temperature convergence via the coupling mechanics model.
- If the fluid viscosity converges, compare whether the fluid flow rate of the three seal lips is equal. If not equal, the pressure in the first and second inter-lip zone is adjusted until the fluid flow rate is balanced.
- If the flow rate is equal, judge whether the stroke is reached. If not, carry on simulating the subsequent time step. The wear mechanics model is used to output the results once all the time steps have been performed.
4. Results and Discussion
4.1. Static Sealing Performance
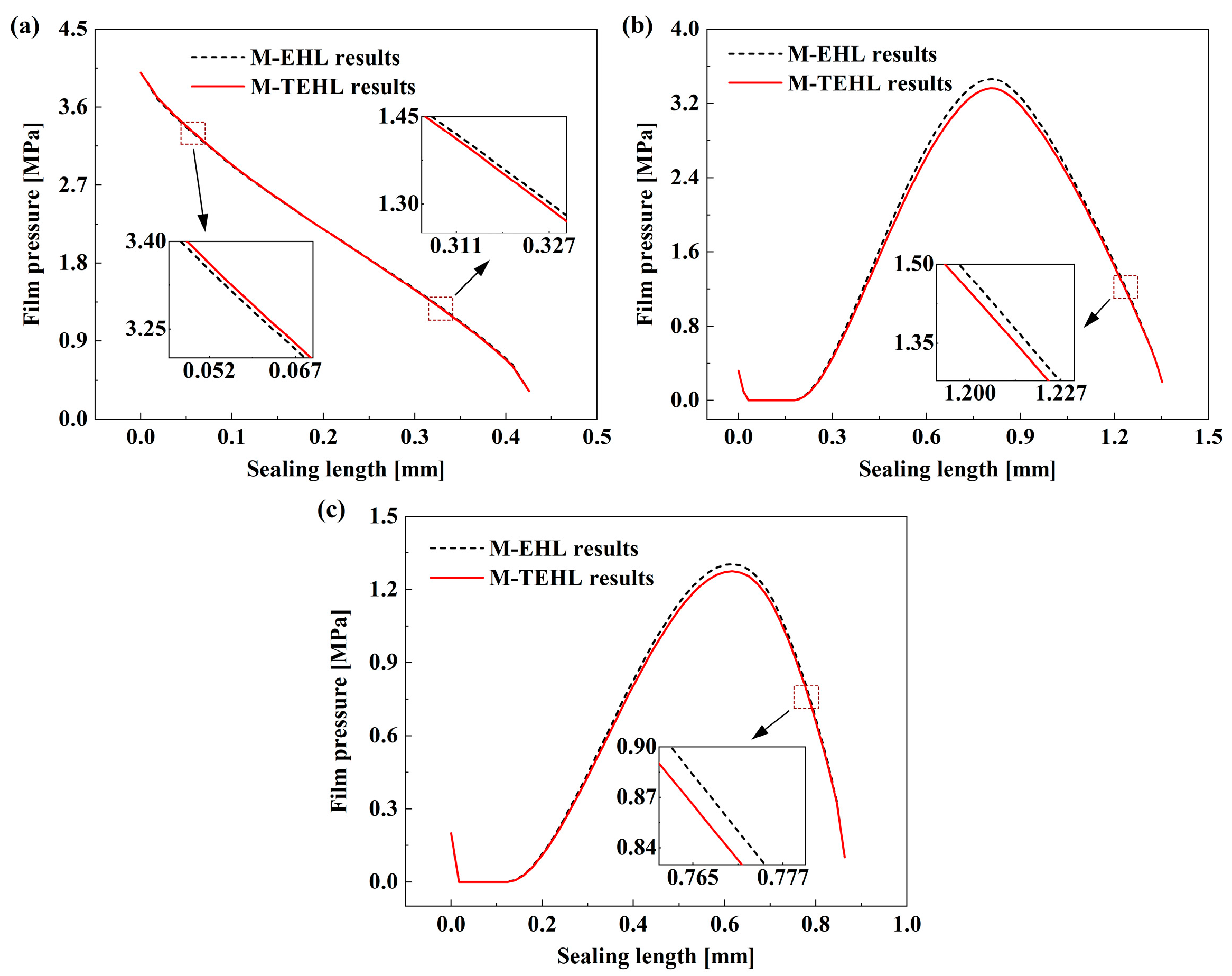
4.2. Model Validation
4.3. Dynamic Sealing Performance
4.3.1. Effect of Sealed Pressure
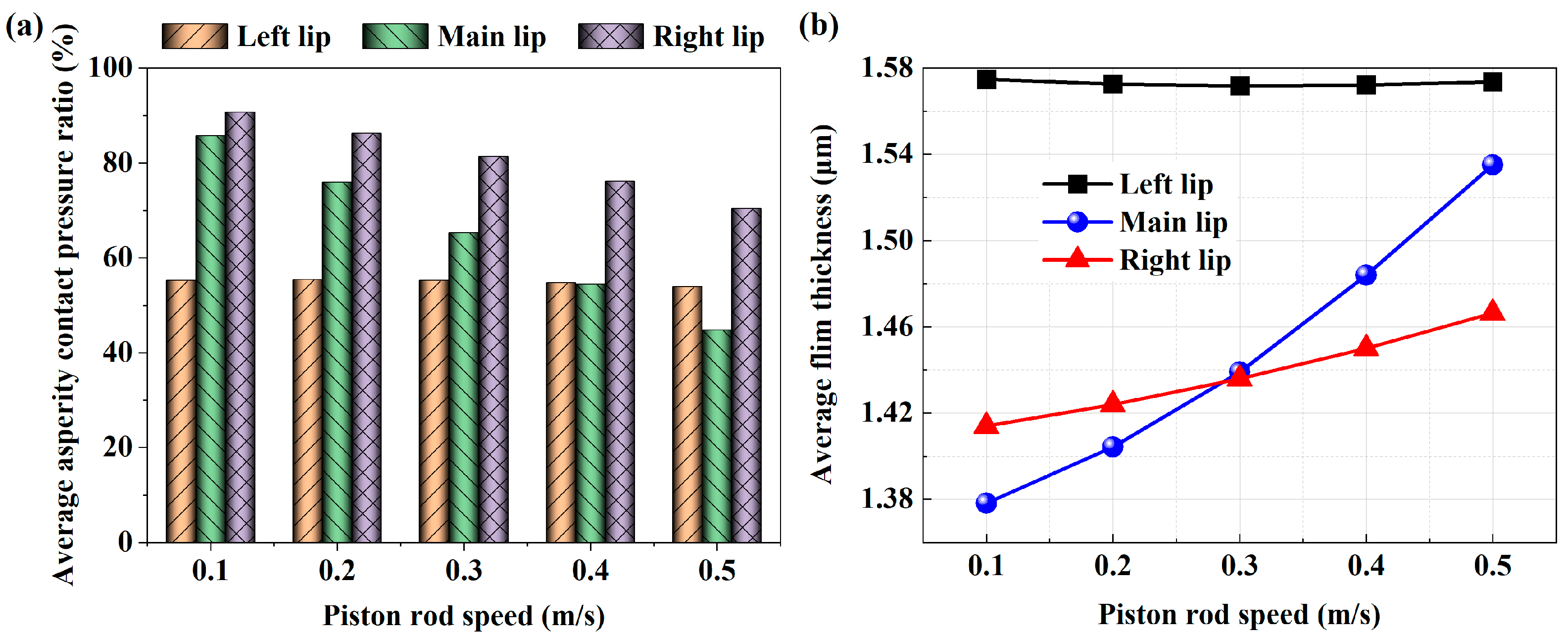
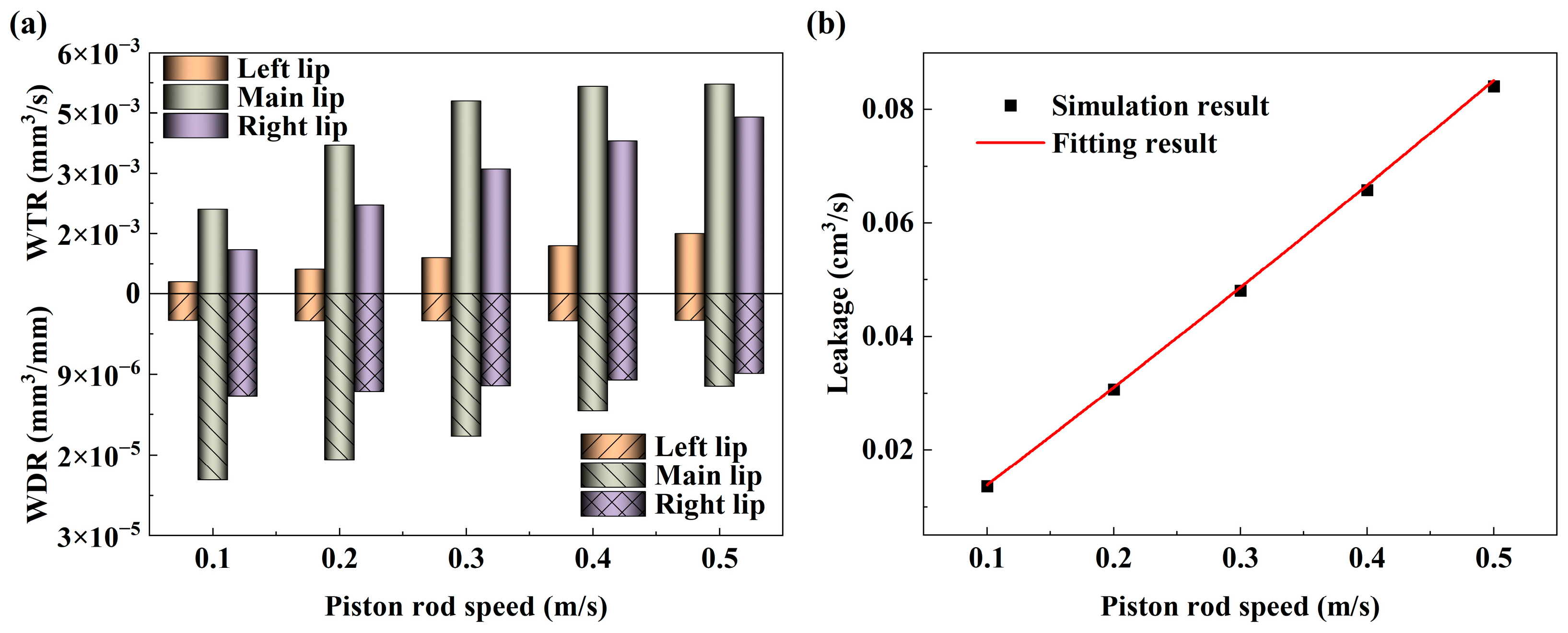
4.3.2. Effect of Piston Rod Speed
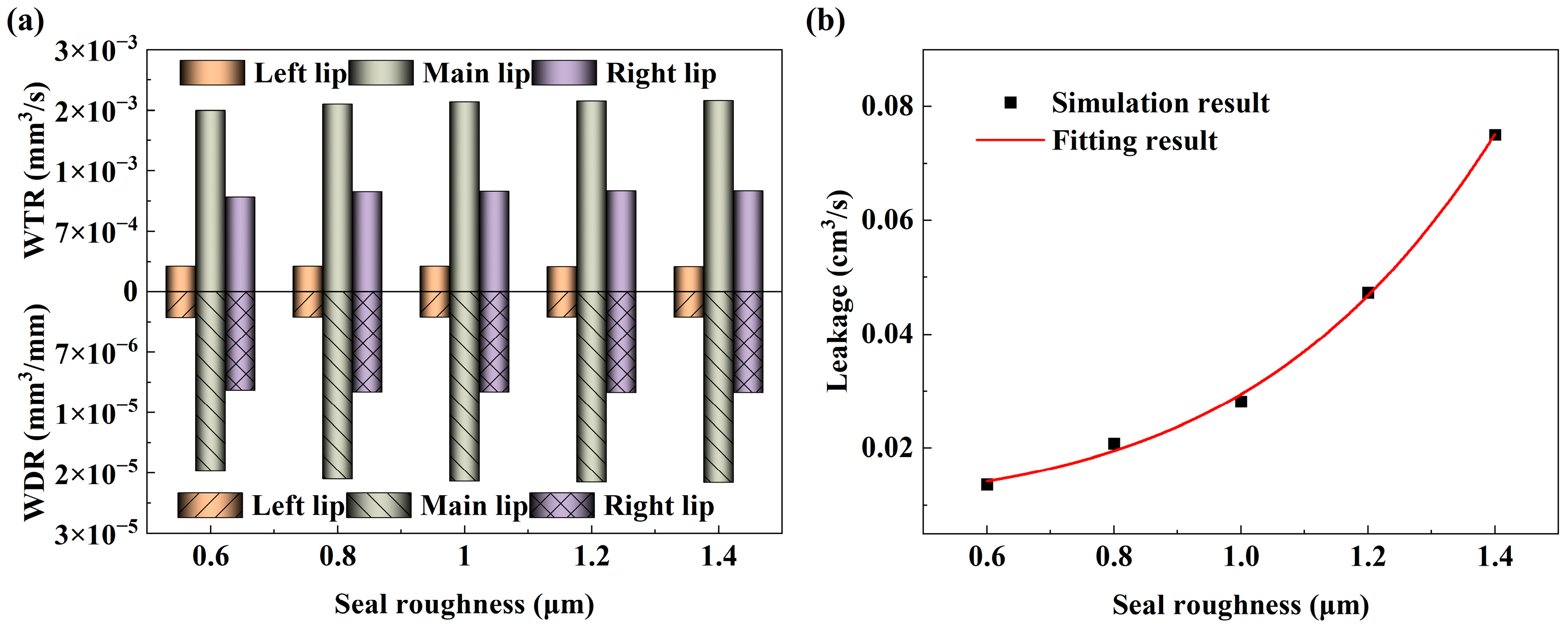
4.3.3. Effect of Seal Roughness
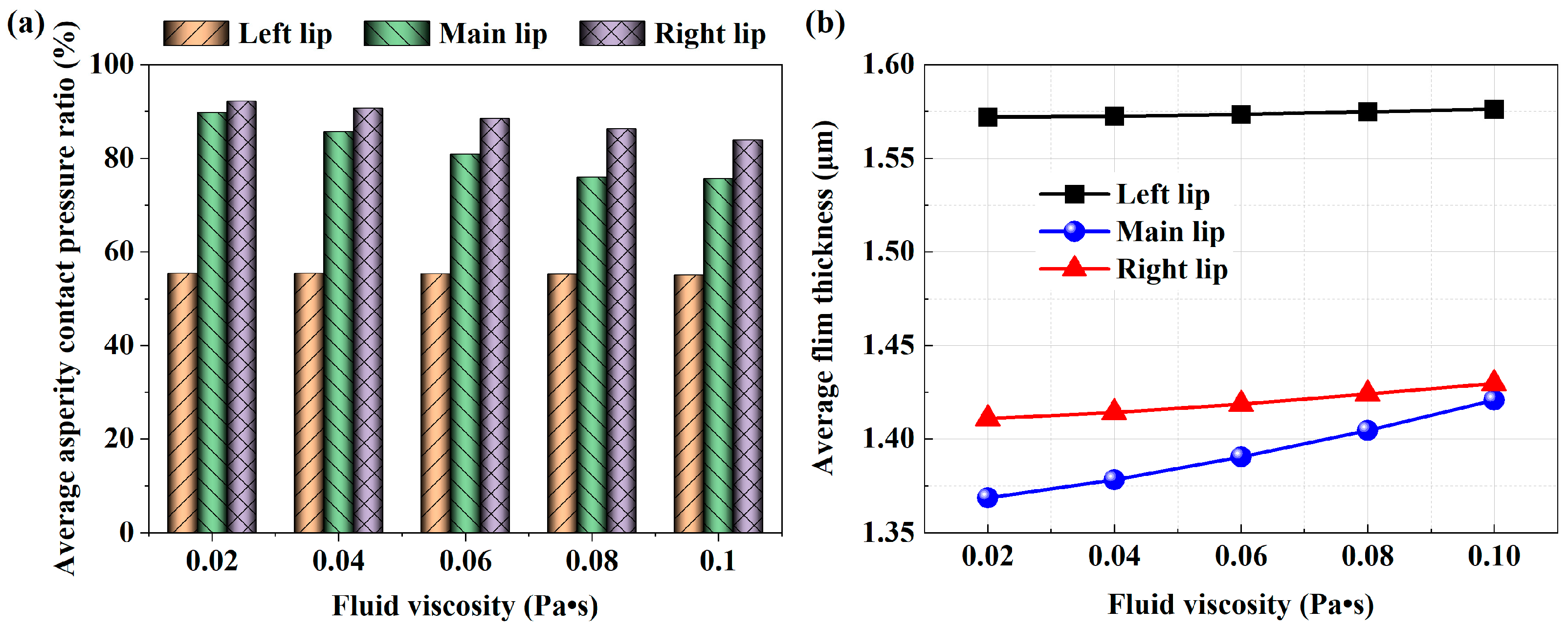
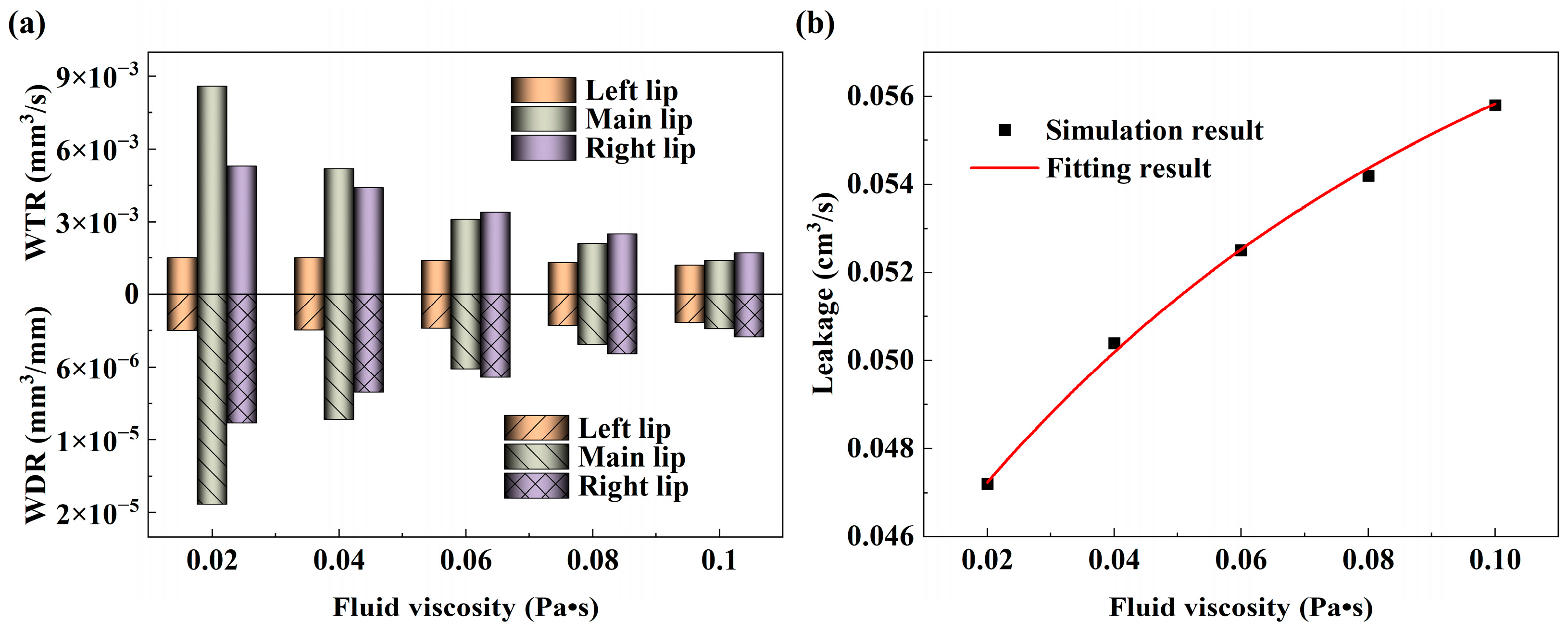
4.3.4. Effect of Fluid Viscosity
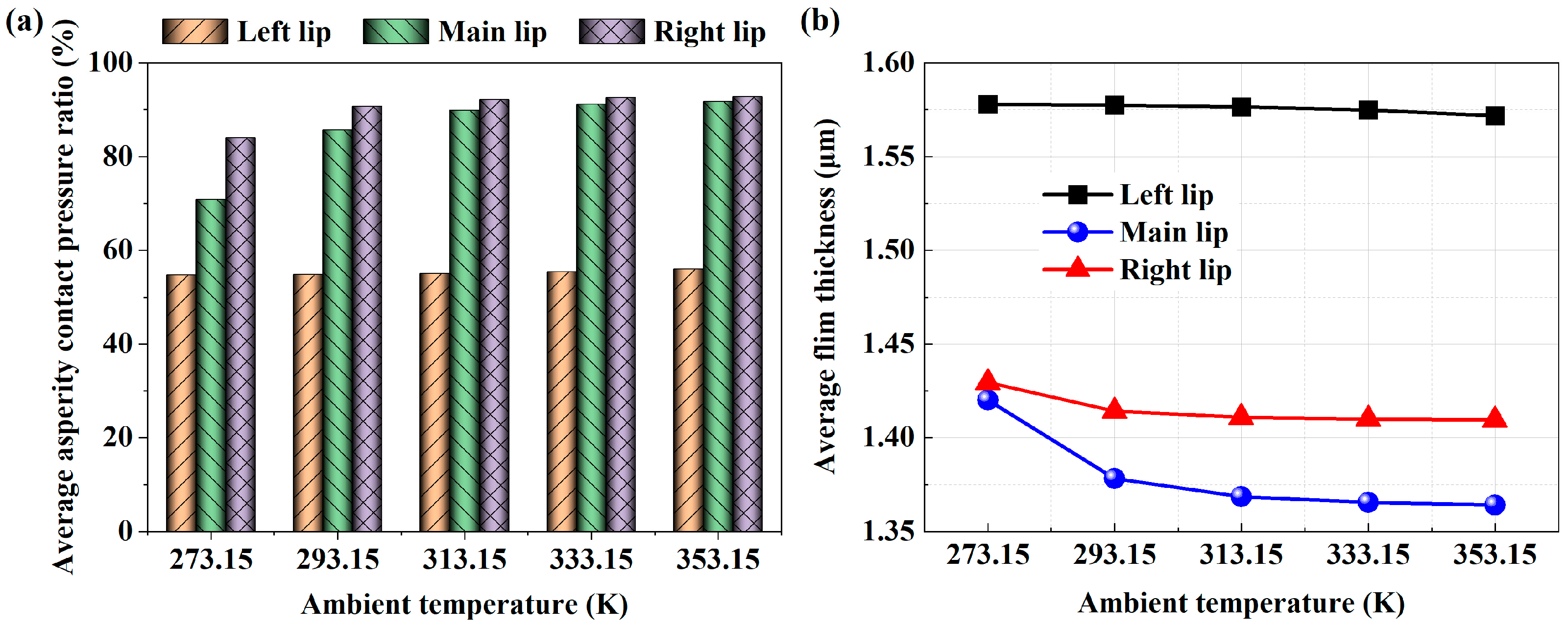
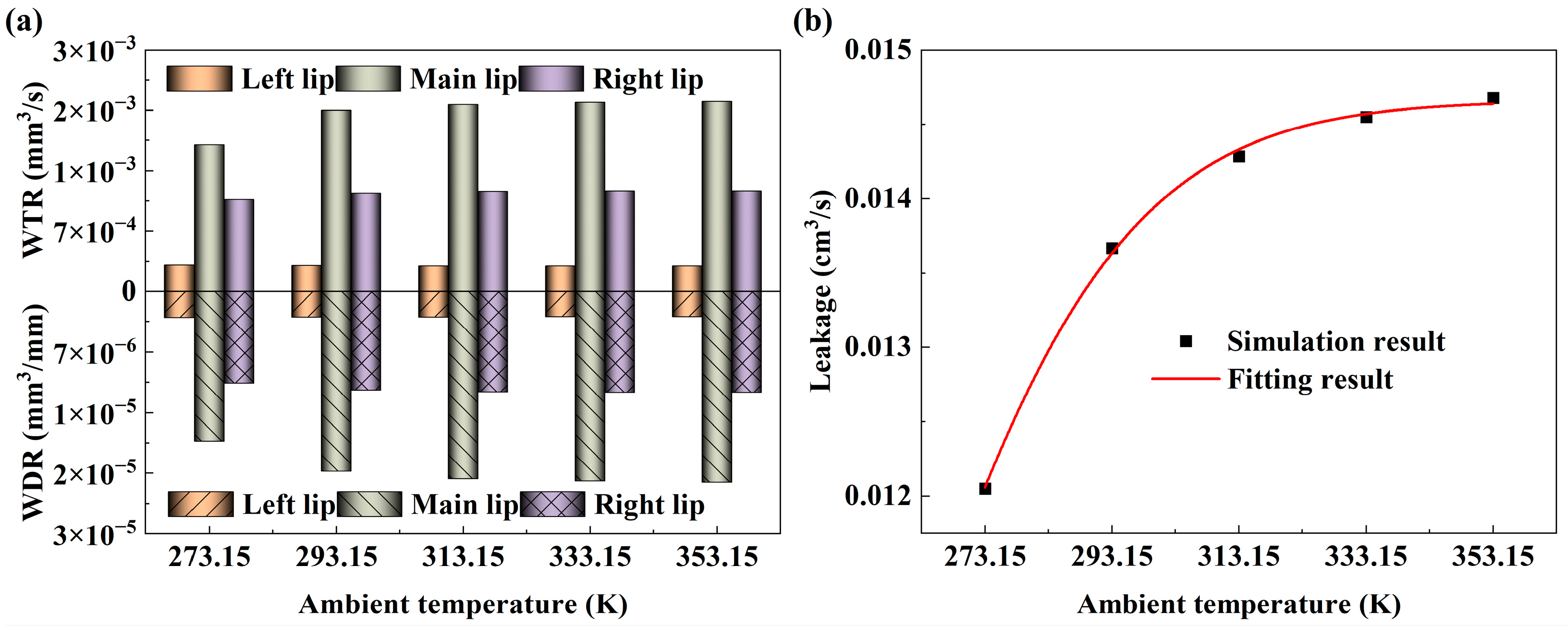
4.3.5. Effect of Ambient Temperature
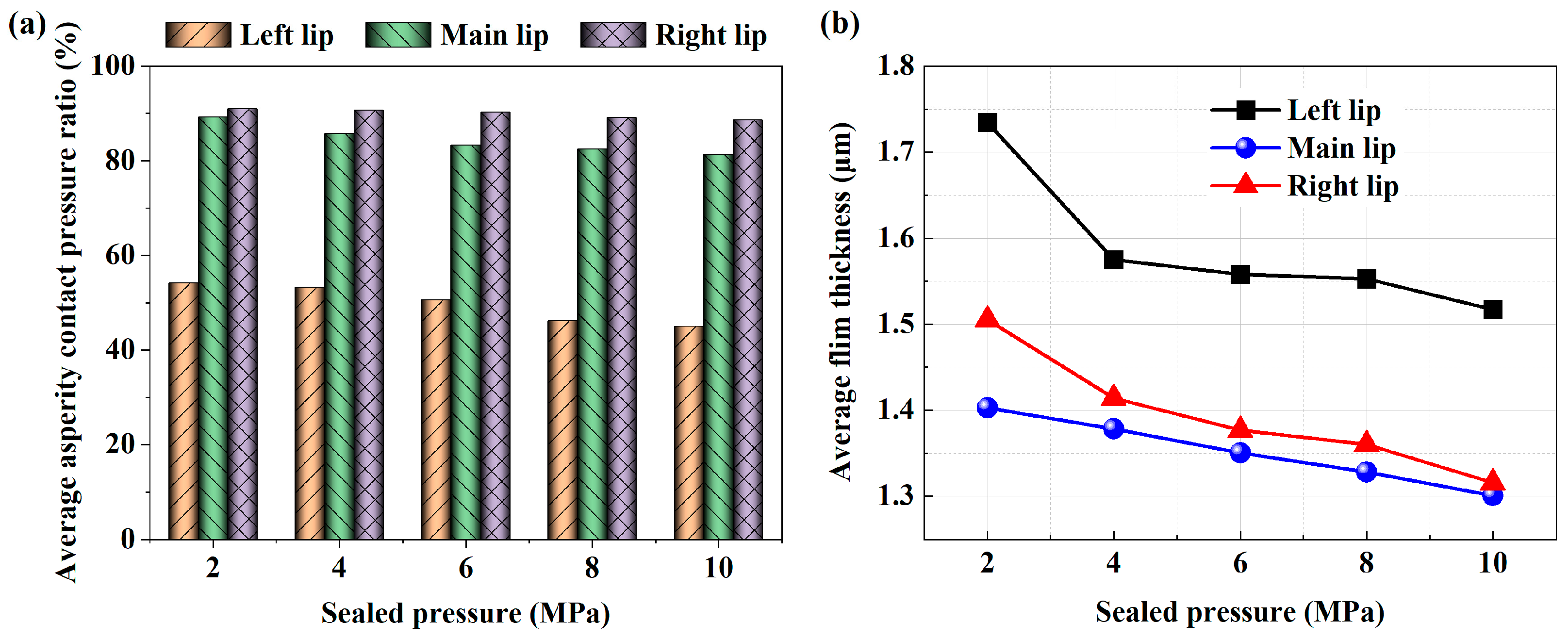
4.4. Analysis of Seal Wear Characteristics
4.4.1. Effects of Sealed Pressure
4.4.2. Effects of Piston Rod Speed
4.4.3. Effects of Seal Roughness
4.4.4. Effects of Fluid Viscosity
4.4.5. Effects of Ambient Temperature
5. Conclusions
- Some characteristics of the single-lip seal are also reflected in the DAS multi-lip combined seal. The increase in sealed pressure decreases the sealed performance and increases the seal wear rate. When the piston rod speed is increased, the WTR also increases. The high-temperature environment leads to the deterioration of the lubrication characteristics in the sealing zone and increases the seal wear. Therefore, it is not difficult to find that high pressure, high speed and high temperature are still great challenges for the lip seal.
- The load on the sealing zone under mixed lubrication is mainly shared by asperity contact, and the asperity contact load is as high as 50%. When the roughness is greater than 0.6 μm, the seal wear rate clearly increases. Therefore, smaller surface roughness is more conducive in reducing the seal wear and fluid leakage.
- The lubrication characteristics of each seal lip in a DAS multi-lip combined seal largely depend on the working conditions. In the piston rod extension motion, the sealing behavior of each seal lip is not identical due to the existence of critical speed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| cc | Specific heat capacity of the cylinder wall |
| Dc | Insider diameter of cylinder |
| E | Elastic modulus |
| F | Cavitation index |
| Fn | Normal force |
| fc | Friction coefficient for asperity contact |
| H | Dimensionless average film thickness, h/σ |
| HB | Hardness of the seal material |
| Hs | Dimensionless static film thickness, hs/σ |
| HT | Dimensionless average truncated film thickness, hT/σ |
| ∆hw | Seal wear depth |
| K | Deformation coefficient matrix |
| kc | Thermal conductivity of the cylinder wall |
| kn | Seal material wear coefficient, Kn/HB |
| L | Contact length of sealing zone |
| Lstroke | Cylinder stroke length |
| ∆L | Relative sliding distance |
| Pc | Dimensionless asperity contact pressure, pc/E |
| Pf | Dimensionless fluid film pressure, pf/pa |
| Pi1, Pi2 | Pressure in the first and second inter-lip region |
| Pl | Dimensionless pressure in low-pressure side, pl/pa |
| Ps | Dimensionless sealed pressure, ps/pa |
| Psc | Dimensionless static contact pressure, psc/E |
| pa | Ambient pressure |
| pn | Normal contact pressure |
| Q | Heat production rate of the cylinder wall, |
| Dimensionless flow rate, | |
| R | Radius of asperities |
| T | Fluid film temperature |
| T0 | Ambient temperature |
| U | Dimensionless piston rod speed, |
| ∆Vw | Seal wear volume |
| Dimensionless coordinate parallel to the fluid film thickness, x/L | |
| z | Dimensionless coordinate normal to the fluid film thickness |
| α | Viscosity-pressure coefficient |
| Dimensionless pressure-viscosity coefficient, αpa | |
| β | Viscosity-temperature coefficient |
| ξ | |
| Φ | Fluid pressure/density function |
| ϕf, ϕfs, ϕfp | Shear stress factors |
| ϕs.c.x, ϕxx | Flow factor |
| η | Asperity density |
| μ0 | Fluid viscosity at atmospheric pressure |
| ρc | Density of the cylinder wall |
| v | Poisson’s ratio |
| ρf | Fluid density |
| Dimensionless density, ρ/ρf | |
| Dimensionless RMS roughness of the seal, σR1/3η2/3 | |
| Dimensionless viscous shear stress, | |
| Dimensionless asperity shear stress, |
Abbreviations
| DAS | Double-acting seal |
| FEA | Finite element analysis |
| FEM | Finite element method |
| M-EHL | Mixed elastohydrodynamic lubrication |
| M-TEHL | Mixed thermal elastohydrodynamic lubrication |
| NBR | Nitrile rubber |
| PTFE | Polytetrafluoroethylene |
| POM | Polyformaldehyde |
| RMS | Root mean square |
| TPE | Thermoplastic polyester elastomer |
| WTR | Wear time rate |
| WDR | Wear distance rate |
Appendix A
References
- Guo, F.; Jia, X.H.; Wang, L.K.; Salant, R.F.; Wang, Y.M. The Effect of Wear on t Performance of a Rotary Lip Seal. J. Tribol. 2014, 136, 0417031–0417038. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.X.; He, X.Y.; Wang, L.T.; Chen, P. Research on pressure compensation and friction characteristics of piston rod seals with different degrees of wear. Tribol. Int. 2020, 142, 105999. [Google Scholar] [CrossRef]
- Paige, J.; Stephens, L.S. Surface Characterization and Experimental Design for Testing of a Radial Lip Seal. Tribol. Trans. 2004, 47, 341–355. [Google Scholar] [CrossRef]
- Hao, L.C.; Meng, Y.G. Numerical Prediction of Wear Process of an Initial Line Contact in Mixed Lubrication Conditions. Tribol. Lett. 2015, 60, 31. [Google Scholar] [CrossRef]
- Ridgway, N.; Colby, C.B.; O’Neill, B.K. Slurry pump gland seal wear. Tribol. Int. 2009, 42, 1715–1721. [Google Scholar] [CrossRef]
- Yang, X.B.; Jin, X.Q.; Du, Z.M.; Cui, T.S.; Yang, S.K. Frictional behavior investigation on three types of PTFE composites under oil-free sliding conditions. Ind. Lubr. Tribol. 2009, 61, 254–260. [Google Scholar] [CrossRef]
- Lee, S.H.; Yoo, S.S.; Kim, D.E.; Kang, B.S.; Kim, H.E. Accelerated wear test of FKM elastomer for life prediction of seals. Polym. Test. 2012, 31, 993–1000. [Google Scholar] [CrossRef]
- Wang, J.L.; Jia, Q.; Yuan, X.Y.; Wang, S.P. Experimental study on friction and wear behaviour of amorphous carbon coatings for mechanical seals in cryogenic environment. Appl. Surf. Sci. 2012, 258, 9531–9535. [Google Scholar] [CrossRef]
- Liu, Y.L.; Tang, D.; Liu, J.; John, L. Wear behaviour of piston seals in flow meter of fuel dispenser under different pressure conditions. Flow Meas. Instrum. 2012, 28, 45–49. [Google Scholar] [CrossRef]
- Gao, S.Y.; Xue, W.H.; Duan, D.L.; Li, S.; Zheng, H.L. Effect of thermal-physical properties on the abradability of seal coating under high-speed rubbing condition. Wear 2018, 394, 20–29. [Google Scholar] [CrossRef]
- Kozuch, E.; Nomikos, P.; Rahmani, R.; Morris, N.; Rahnejat, H. Effect of Shaft Surface Roughness on the Performance of Radial Lip Seals. Lubricants 2018, 6, 99. [Google Scholar] [CrossRef]
- Nomikos, P.; Rahmani, R.; Morris, N.; Rahnejat, H. An investigation of oil leakage from automotive driveshaft radial lip seals. Proc. Inst. Mech. Eng. Part D J. Aut. Eng. 2022, 1–17. [Google Scholar] [CrossRef]
- Yang, L.M.; Moan, T. Numerical Modeling of Wear Damage in Seals of a Wave Energy Converter with Hydraulic Power Take-Off under Random Loads. Tribol. Trans. 2010, 54, 44–56. [Google Scholar] [CrossRef]
- Békési, N.; Váradi, K.; Felhős, D. Wear Simulation of a Reciprocating Seal. J. Tribol. 2011, 133, 031601. [Google Scholar] [CrossRef]
- Frölich, D.; Magyar, B.; Sauer, B. A comprehensive model of wear, friction and contact temperature in radial shaft seals. Wear 2014, 311, 71–80. [Google Scholar] [CrossRef]
- Li, X.; Peng, G.L.; Li, Z. Prediction of seal wear with thermal–structural coupled finite element method. Finite Elem. Anal. Des. 2014, 83, 10–21. [Google Scholar] [CrossRef]
- Xiang, C.; Guo, F.; Jia, X.H.; Wang, Y.M.; Huang, X. Thermo-elastohydrodynamic mixed-lubrication model for reciprocating rod seals. Tribol. Int. 2019, 140, 105894. [Google Scholar] [CrossRef]
- Salant, R.F.; Flaherty, A.L. Elastohydrodynamics of lip seals. Lubr. Sci. 1995, 8, 15–26. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, S.Y.; Zhong, S.P.; Xiong, Z.J.; Yang, Q. Solution and analysis of VL combined seal lubrication model under the effect of wear. J. Mech. Sci. Technol. 2022, 36, 5599–5609. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.P.; Zhang, C. A multiscale wear simulation method for rotary lip seal under mixed lubricating conditions. Tribol. Int. 2018, 121, 190–203. [Google Scholar] [CrossRef]
- Ran, H.L.; Wang, S.P.; Liu, D. A multiscale wear model for reciprocating rod stepseal under mixed lubricating conditions based on linear elasticity. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 235, 161–180. [Google Scholar] [CrossRef]
- Cheng, D.H.; Gu, L.C.; Sun, Y. Mixed Lubrication Modeling of Multi-Lip Reciprocating Seals Based on Elastohydrodynamic Lubrication Theory. Machines 2022, 10, 483. [Google Scholar] [CrossRef]
- Salant, R.F.; Yang, B.; Thatte, A. Simulation of hydraulic seals. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 865–876. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. A. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Gadari, M.E.; Fatu, A.; Hajjam, M. Shaft roughness effect on elasto-hydrodynamic lubrication of rotary lip seals: Experimentation and numerical simulation. Tribol. Int. 2015, 88, 218–227. [Google Scholar] [CrossRef]
- Yang, B.; Salant, R.F. Elastohydrodynamic lubrication simulation of O-ring and U-cup hydraulic seals. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2011, 225, 603–610. [Google Scholar] [CrossRef]
- Roelands, C.J.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. Ph.D. Thesis, Deft University of Technology, Delft, Netherlands, 1966. [Google Scholar]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Ran, H.L.; Liu, D.; Wang, S.P. A Numerical Wear Simulation Method of Reciprocating Seals with a Textured Rod. Materials 2020, 13, 4458. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, J. Investigation of static and dynamic seal performances of a rubber O-ring. J. Tribol. 2018, 140, 042202. [Google Scholar] [CrossRef]
- Xiang, C.; Guo, F.; Jia, X.H.; Wang, Y.M. Numerical simulation model of reciprocating rod seal systems with axial wear texture on rod surface. Lubr. Sci. 2023, 1–19. [Google Scholar] [CrossRef]
- Wang, B.Q.; Peng, X.D.; Meng, X.K. Simulation of the effects of non-Newtonian fluid on the behavior of a step hydraulic rod seal based on a power law fluid model. J. Zhejiang Univ. Sci. A 2018, 19, 824–842. [Google Scholar] [CrossRef]



| Parameter Type | Value |
|---|---|
| Ambient temperature, T0 | 273.15~313.15 K |
| Ambient pressure, p0 | 0.1 MPa |
| Fluid viscosity, μ0 | 0.02~0.10 Pa·s |
| Viscosity-pressure coefficient, α | 2 × 10−8 Pa−1 |
| Viscosity-temperature coefficient, β | 3.17908 × 10−2 K−1 |
| Sealed pressure, ps | 2~10 MPa |
| Wear coefficient, kn | 1.2 × 10−5 mm3/Nm [31] |
| Stroke length, Lstroke | 300 mm |
| Insider diameter of cylinder, Dc | 63 mm |
| Piston rod extension speed, u | 0.1~0.5 m/s |
| Seal RMS roughness, σ | 0.6~1.4 μm |
| Friction coefficient, fc | 0.1 [32,33] |
| Thermal conductivity of cylinder wall, kc | 46 W/(m·K) |
| Density of cylinder wall, ρc | 7850 kg/m3 |
| Specific heat capacity of cylinder wall, cc | 460 J/(kg·K) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, D.; Gu, L.; Sun, Y.; Shi, Y. Numerical Calculation Method of Multi-Lip Seal Wear under Mixed Thermal Elastohydrodynamic Lubrication. Lubricants 2023, 11, 248. https://doi.org/10.3390/lubricants11060248
Cheng D, Gu L, Sun Y, Shi Y. Numerical Calculation Method of Multi-Lip Seal Wear under Mixed Thermal Elastohydrodynamic Lubrication. Lubricants. 2023; 11(6):248. https://doi.org/10.3390/lubricants11060248
Chicago/Turabian StyleCheng, Donghong, Lichen Gu, Yu Sun, and Yuan Shi. 2023. "Numerical Calculation Method of Multi-Lip Seal Wear under Mixed Thermal Elastohydrodynamic Lubrication" Lubricants 11, no. 6: 248. https://doi.org/10.3390/lubricants11060248
APA StyleCheng, D., Gu, L., Sun, Y., & Shi, Y. (2023). Numerical Calculation Method of Multi-Lip Seal Wear under Mixed Thermal Elastohydrodynamic Lubrication. Lubricants, 11(6), 248. https://doi.org/10.3390/lubricants11060248





