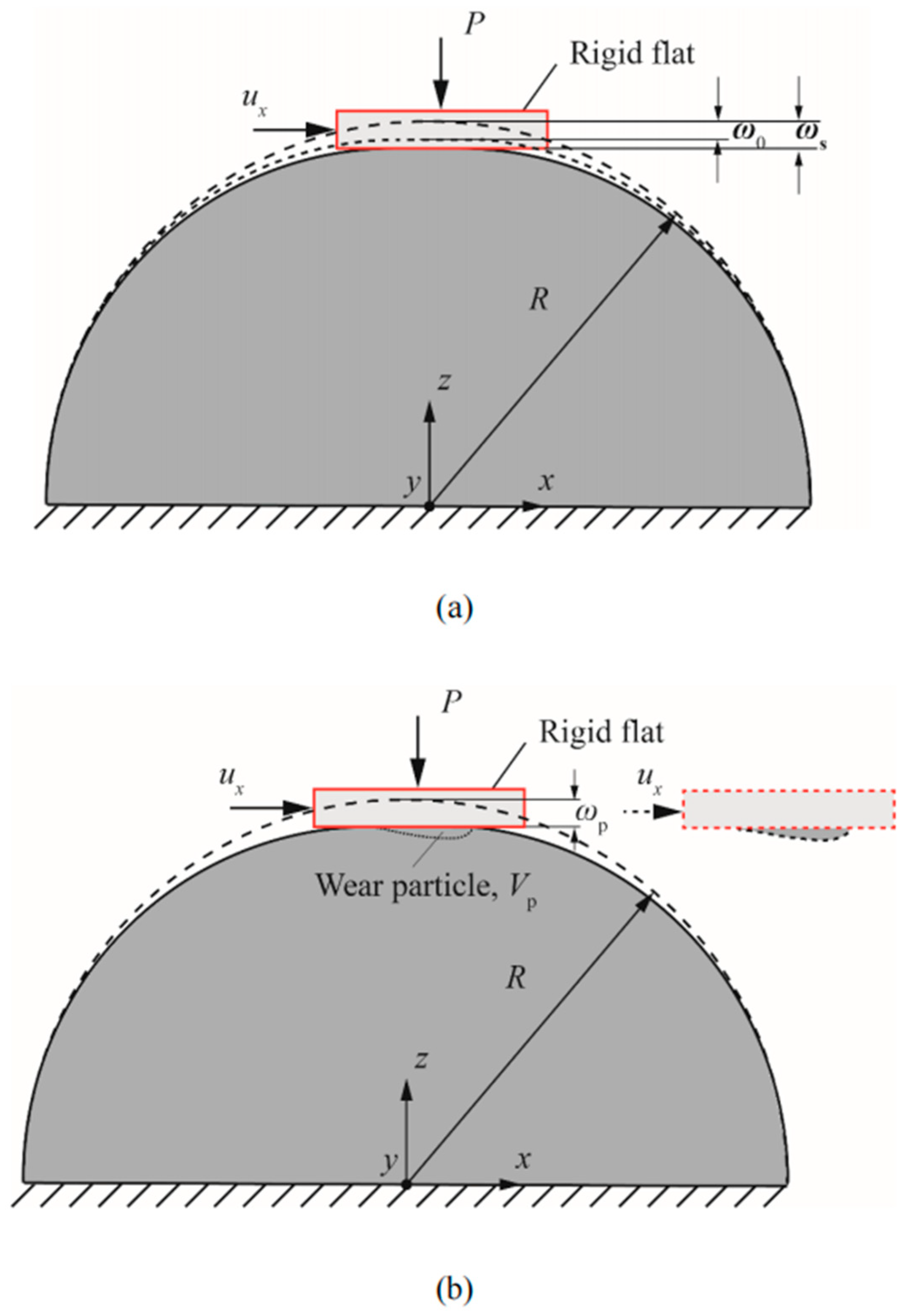
The adhesive wear and friction behaviors of the spherical contact under combined loading were studied by carrying out wear simulations using the improved sub-model for the sphere radius ranging from 5 [mm] to 50 [mm], with dimensionless normal loads
ranging from 15 to 150. It was found in the current model that the tangential displacement
was sufficient to achieve a wear particle for all the different simulations. It was also observed in [
13] with the global model. Hence, to ensure the full formation of the wear particle, a value of
was used for all the simulations. Similarly, in Refs. [
13,
15], the sphere material was aluminum 2024 T351, as this particular material was thoroughly studied both numerically and experimentally [
25,
26,
27,
28]. The material properties of aluminum 2024 T351 are:
and a density of
. The JC criterion coefficients of the damage initiation for aluminum 2024 T351 are (Ref. [
28]):
. For the damage evolution, the fracture energy was
[
28].
In the following, the verification of the improved sub-model is presented, followed by the investigation of the tangential mechanical response and the wear particle morphology for the different normal loads and sphere radii. The effect of changing the different mechanical properties () on the obtained results is also discussed.
4.1. Verification of the Improved Sub-Model
The results from Ref. [
13] were used to verify the adequacy of the present model.
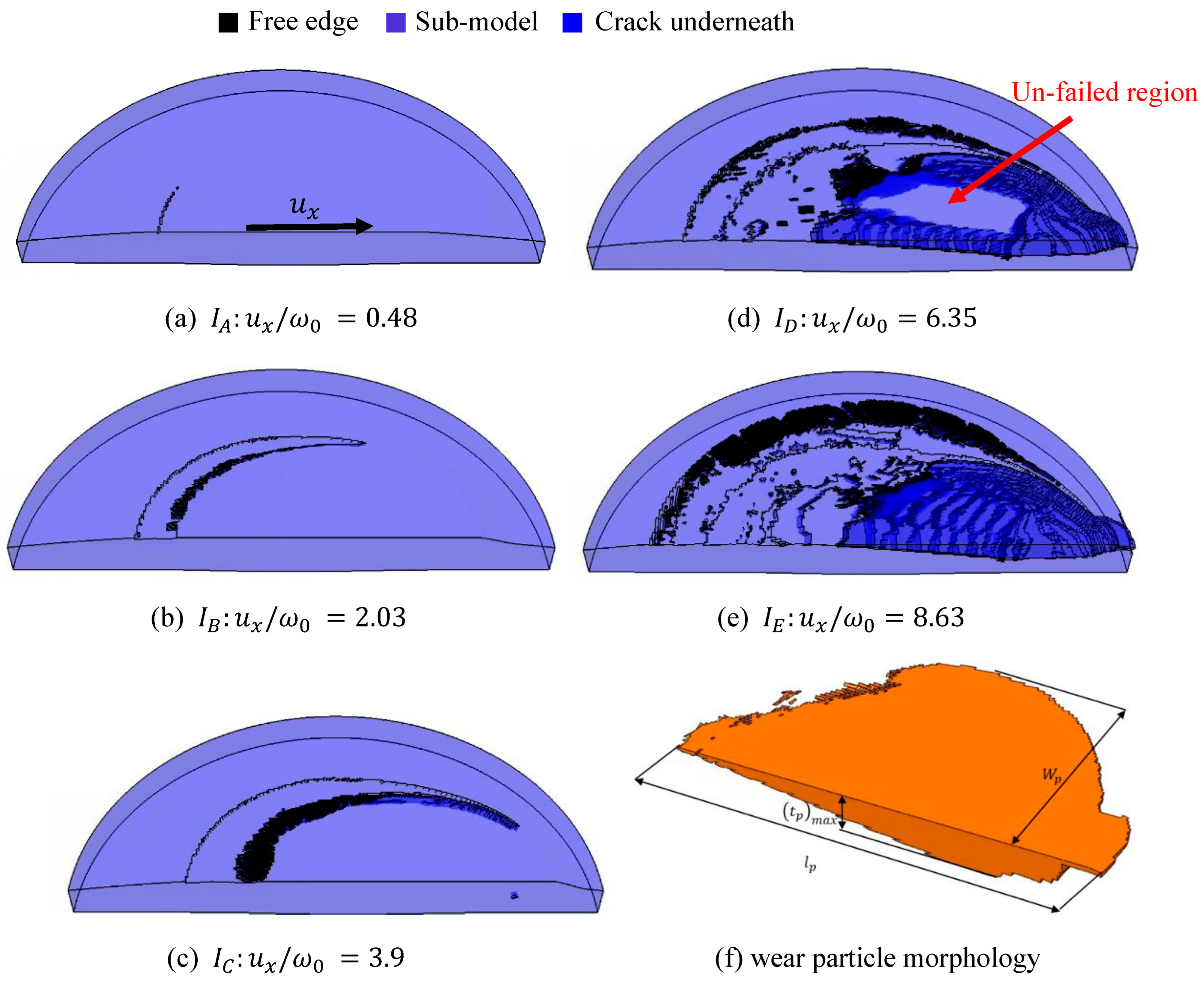
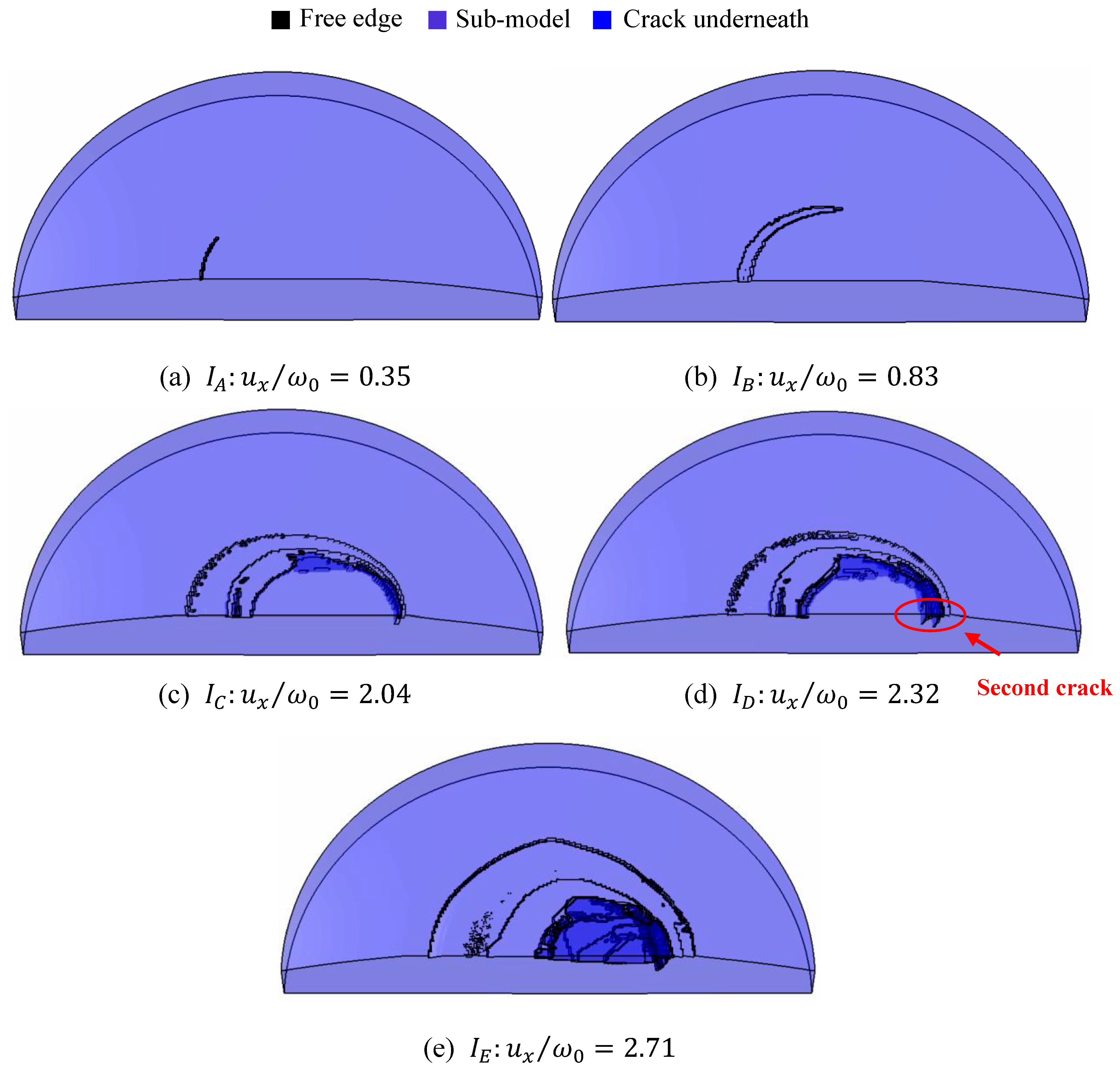
Figure 3 shows the five instants for the fracture evolution obtained by the improved sub-model, corresponding to the five instants obtained in Ref. [
13] for the
and
case with the definition of the wear particle parameters. The black color represents the free edge formed during the fracture evolution process; the deeper blue color represents the crack formed below the contact surface.
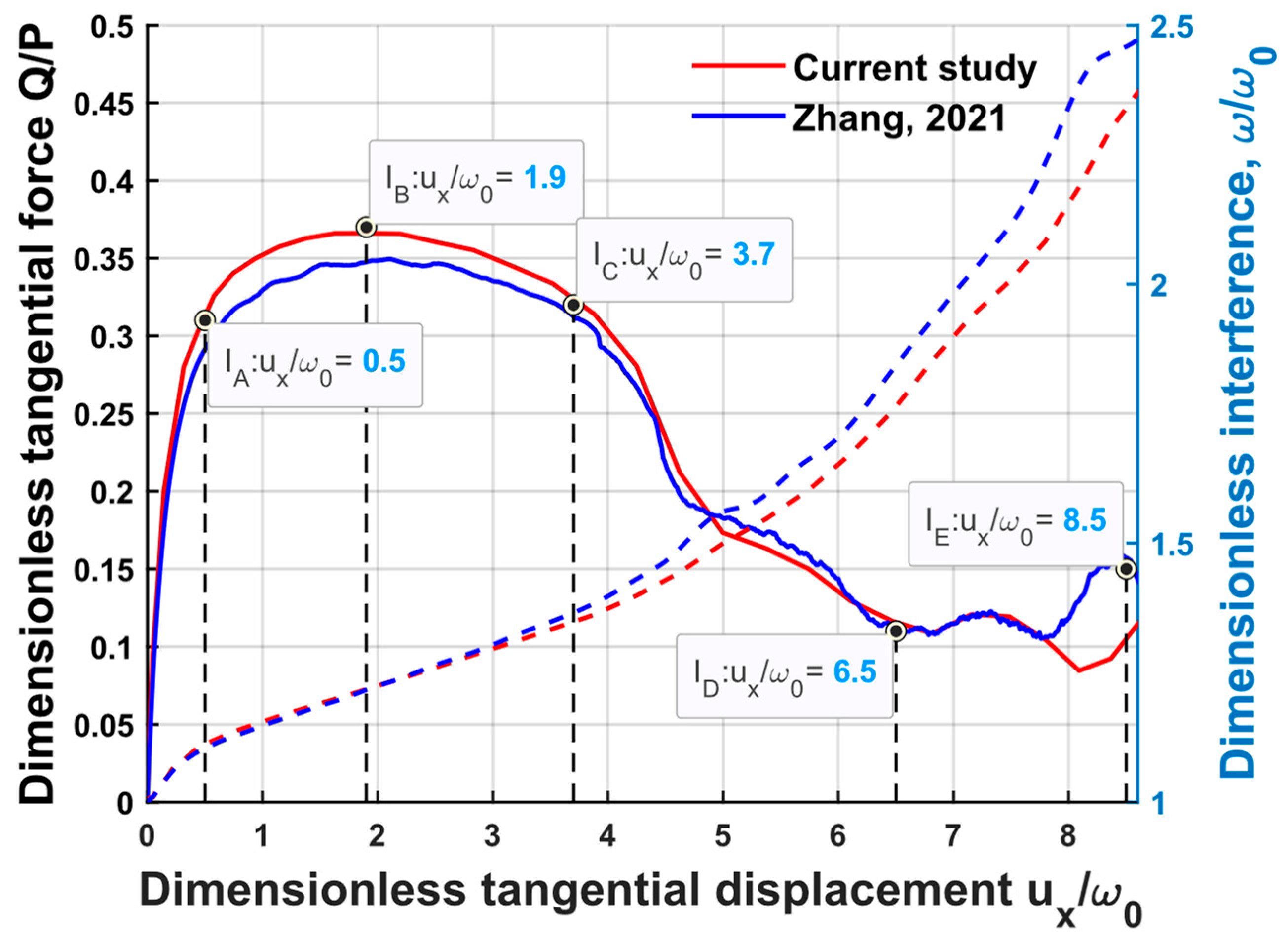
Figure 4 shows the friction behavior and the interference for the same case, as shown in
Figure 3. Both the dimensionless tangential force
and the dimensionless interference
are plotted with respect to the dimensionless tangential displacement
. The five instants of the fracture evolution are marked in vertical dash line.
For instant
, the crack initially appeared on the trailing edge of the contact surface. The term ‘trailing edge’ refers to the edge located in the direction opposite to the tangential displacement
, as indicated by the arrow shown in
Figure 3a pointing in the
direction. With an increasing tangential displacement, the crack spread along the edge of the growing contact interface, and at instant
, the tangential force reached its maximum, resulting in a sliding inception. At instant
, the first crack at the leading edge under the contact surface appeared. With the fracture extending below the contact surface, the fracture from the trailing edge linked with the one from the leading edge at instant
, as shown in
Figure 3d. A region of un-failed elements that were not deleted according to the JC and fracture energy criteria was surrounded by the linked cracks. Eventually, at instant
the un-failed region vanished leading to the wear particle creation. These five stages for the fracture evolution using the improved sub-model matched well with the results given in [
13]. The differences in the corresponding tangential displacement for the five instants, as shown in
Figure 4, were 4%, 6.8%, 5.4%, 2.3% and 1.5%, respectively.
Along with the crack initiation and propagation, the tangential force behavior of the improved sub-model corresponded well to the results from [
13]. The tangential stiffness reduced with the increasing tangential displacement
until instant
, at which the tangential stiffness completely vanished. The static friction coefficient represented by
was 0.36 for the improved sub-model and 0.35 in [
13]. The relative error of the static friction coefficient between these two models was less than 5%.
Regarding the comparison between the dimensionless interference shown in
Figure 4, the difference between [
13] and the current result increased with the dimensionless displacement, which was due to the element deletion, as the element size used in the improved sub-model was larger than in [
13]. However, the largest difference was less than 7%.
The wear particles formed in [
13] and the one formed using the improved sub-model were similar in shape, having the shape shown in
Figure 3f. The maximum thickness and length of the wear particle in [
13] were
and
, with a particle volume of
. The corresponding value using the improved sub-model were
and
. The differences between these three parameters were less than 10%, especially for the wear particle volume having a 2% difference. An additional parameter was also denoted in
Figure 3f, which was the wear particle half width
, being
for this case.
To conclude, the results predicted by the improved sub-model were in a good agreement with the predictions made in [
13], validating the improved sub-model for predicting the tangential behavior wear particle geometry. These results verified that the new sub-model can provide a reliable prediction for the wear morphology and the mechanical response, thereby validating the effectiveness of the present model.
The computation time was reduced from 90 h to 30 h, compared to the model used in [
13]. A further reduction in the computation time can be achieved by reasonably increasing the loading rate of the simulation, both in the normal and tangential directions. Moreover, as shown in
Figure 3, it can be observed that some non-contact and non-wear regions existed, which had no effect on the wear predictions when the tangential loading was terminated, indicating that the current sub-model simulating area can be further reduced for the purpose of a parametric study. Therefore, using a smaller sub-model simulating region compared to the present one, which fully covers the potential wear and contact regions and reasonably increases the loading rate, can further reduce the simulating time. For
R = 10 [mm] and
P* = 100, using the above accelerating techniques reduced the computing time from 30 h to 15 h, and the relative errors of the wear particle volume and the static friction coefficient compared to the current improved sub-model were less than 3%.
4.2. The Effect of the Normal Load
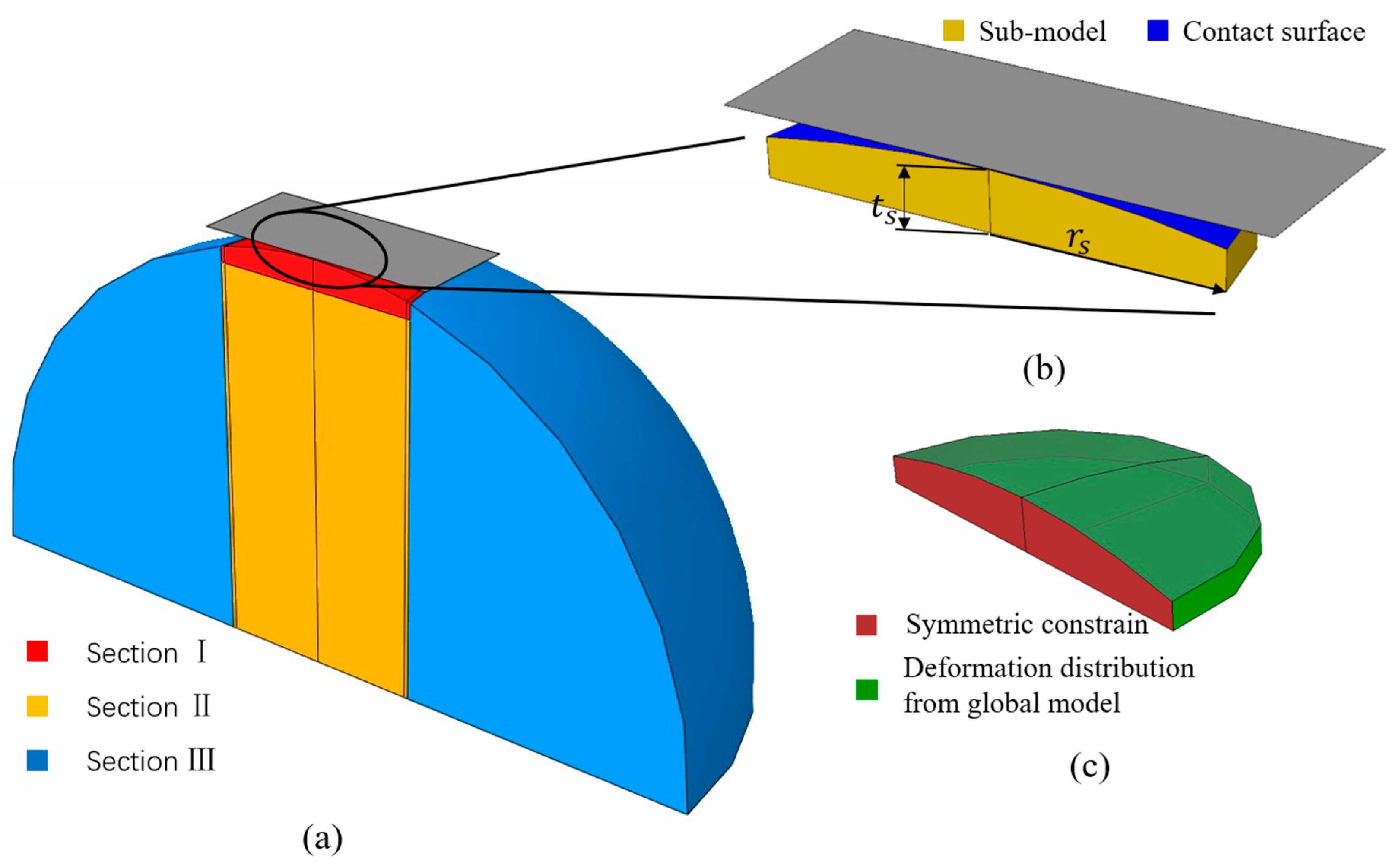
Table 1 summarizes the parameters used in the sub-model to study the effect of the normal load on the wear volume and the tangential load. The elements
and
are the radius and thickness of section I in the global model (
Figure 2a), respectively. The elements
and
are the mesh sizes of section I in the global model and in the improved sub-model, respectively. Superscript
is used to indicate the dimensionless parameter, normalized by the sphere radius
.
For accuracy, the mesh size should be decreased as the applied normal load decreases. On the other hand, in order to reduce the number of elements and the computation time, the radius and thickness of section I in the global model were reduced as well since decreasing the normal load resulted in a smaller potential region for the wear particle.
The parameters used in the sub-model were adjusted according to the stress field in the global model. As the simulations were conducted for the different radii, ranging from 5 to 50 mm, the parameters were normalized using the sphere radius R.
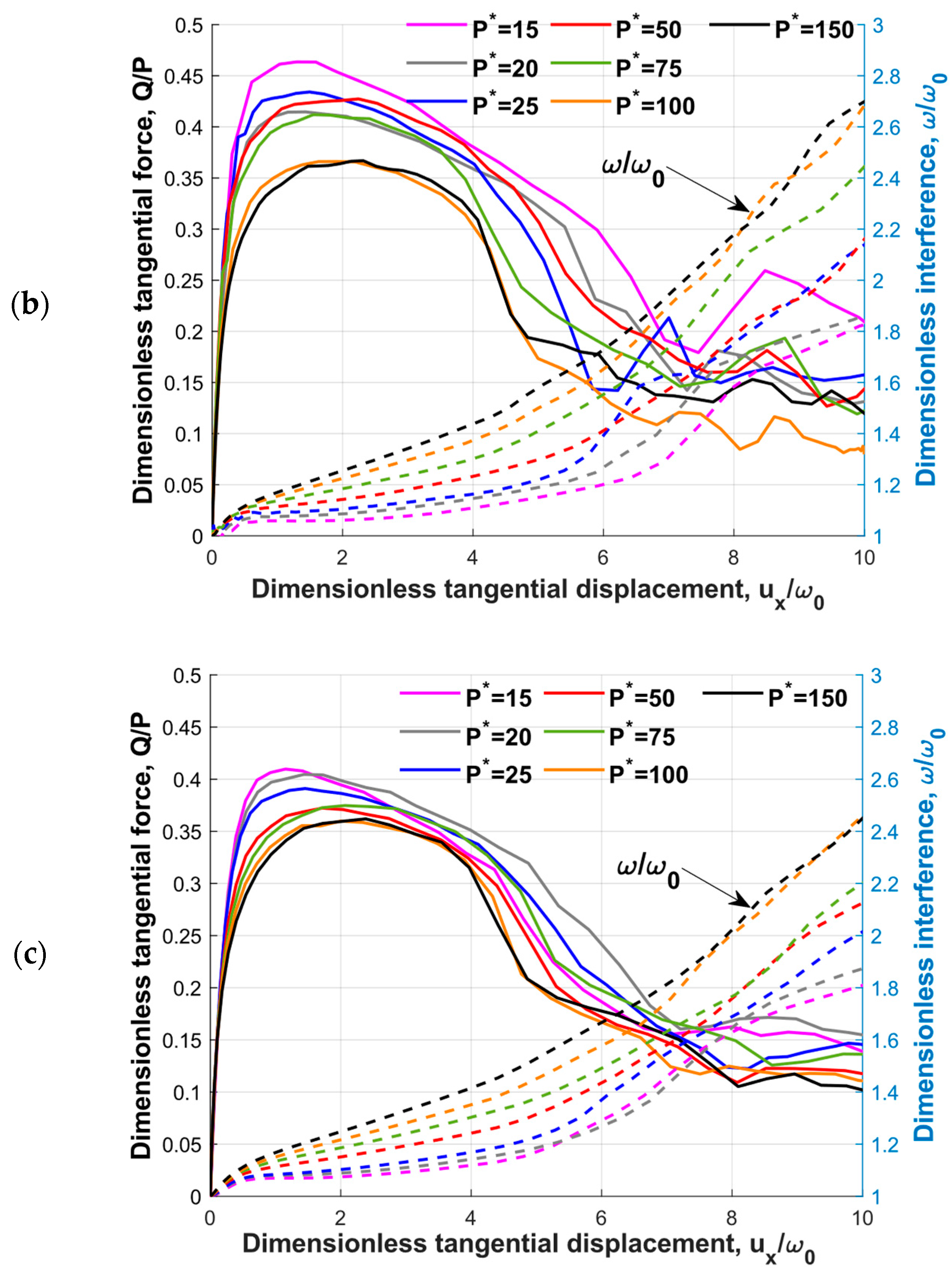
Figure 5 presents the results for the dimensionless tangential load
and the dimensionless interference
vs. the dimensionless tangential displacement
for different dimensionless normal loads
P* and different radii
R.
Figure 5 demonstrates that the transient dimensionless tangential forces and interferences exhibited a similar trend for the given material properties under different sphere radii and normal loads.
The dimensionless tangential force curves exhibited a certain non-monotonic behavior, particularly following the formation of the wear particles. These non-monotonic fluctuations were caused by the inherent numerical error. More specifically, the deletion and recontacting of the elements on the newly generated surface during the tangential loading led to the observed non-monotonic fluctuations. While it was impossible to entirely eliminate these fluctuations, they were reduced by implementing a more refined mesh. Similar fluctuations were also reported in Ref. [
13].
Figure 4 provides a comparison that demonstrates that the fluctuation levels were within an acceptable range when compared to the previously published results.
As shown in
Figure 5, the curves for the larger sphere radius were more consolidated. This behavior was caused by the dimensionless sub-model parameters (
,
). Although these two parameters allowed for the wear particle formation, the sub-model geometry might not have been large enough to exclude the influence of the applied boundary conditions. A few simulations of
R = 5 [mm] were carried out using larger geometry, and the friction behavior was close to the friction behavior of
R = 50 [mm]. It should be noted that the wear volume and wear particle parameters had a slight difference, below 10%. Since, as will be shown, the dimensionless results were independent of the radius, it was more beneficial to look at the larger radii as long as the adhesion, which was associated with nano and micron scale, was not considered.
Furthermore, it can be observed that the dimensionless interference during tangential loading increased with the increase in the dimensionless normal load. This can be explained by the junction growth under the combined loading [
29].
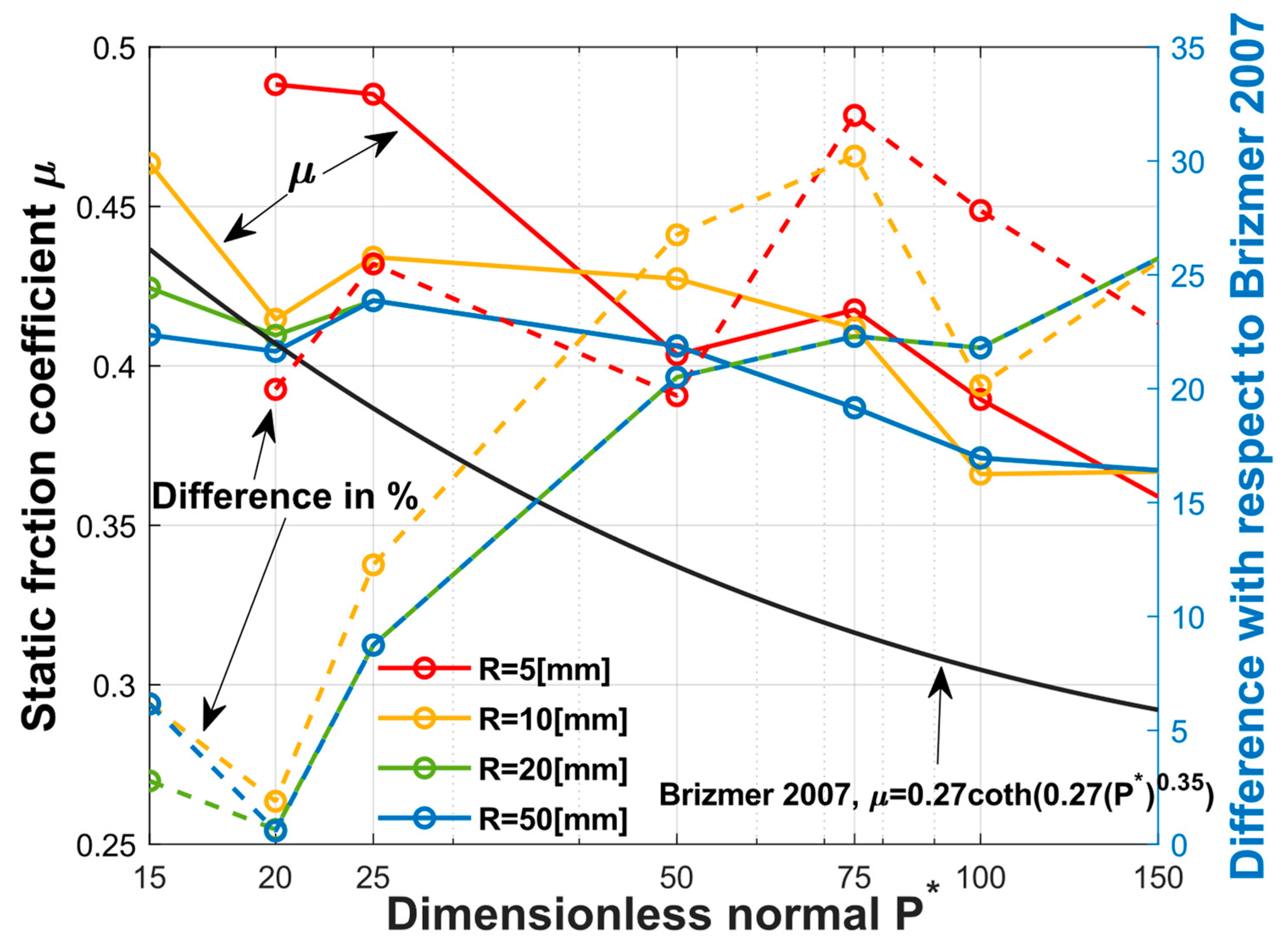
Figure 6 illustrates the maximum dimensionless tangential forces, which indicate the static friction coefficient corresponding to the different sphere radii plotted against the dimensionless normal load. In general, the static friction coefficient decreased with the increasing dimensionless normal load, which showed a consistent result with [
17]. A comparison between the results presented in [
17] is also shown in percentages by the dashed lines. The differences for the small normal load,
, were lower than 10%; however, for the larger normal loads,
, the differences became larger, but were no more than 35% with respect to [
17].
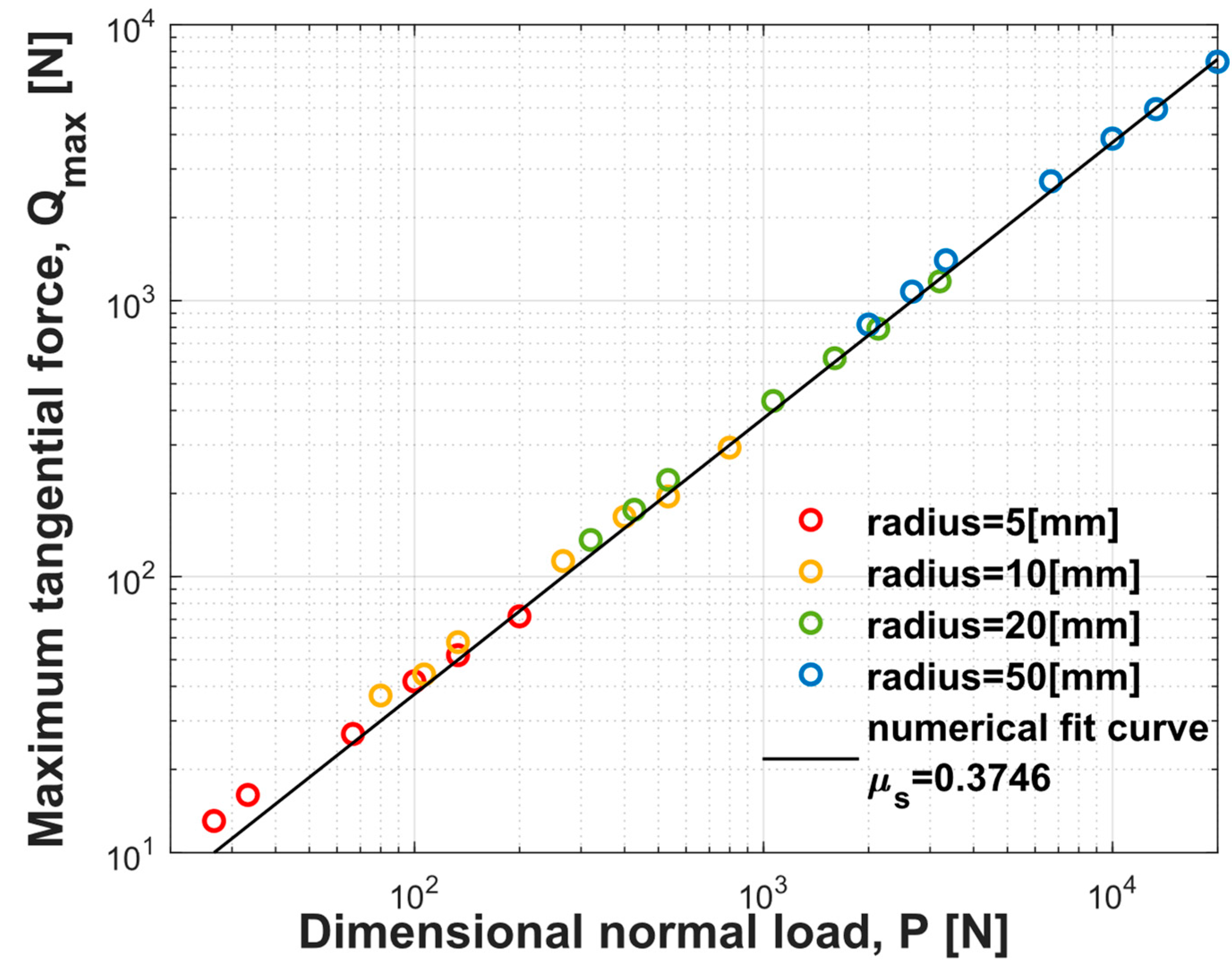
As shown in
Figure 7, the maximum tangential force and the corresponding normal load are shown for the different sphere radii, where the different colors represent the different sphere radii.
A numerical fitted curve, in the black solid line, with
resulted in
= 0.37 for all the simulations conducted in the current study, regardless of the sphere radius. Interestingly, in Rabinowicz [
30], for 50 separate experiments with different material combinations, a lower limit for the friction coefficient, approx. 0.37, was reported.
4.3. Wear Characteristics
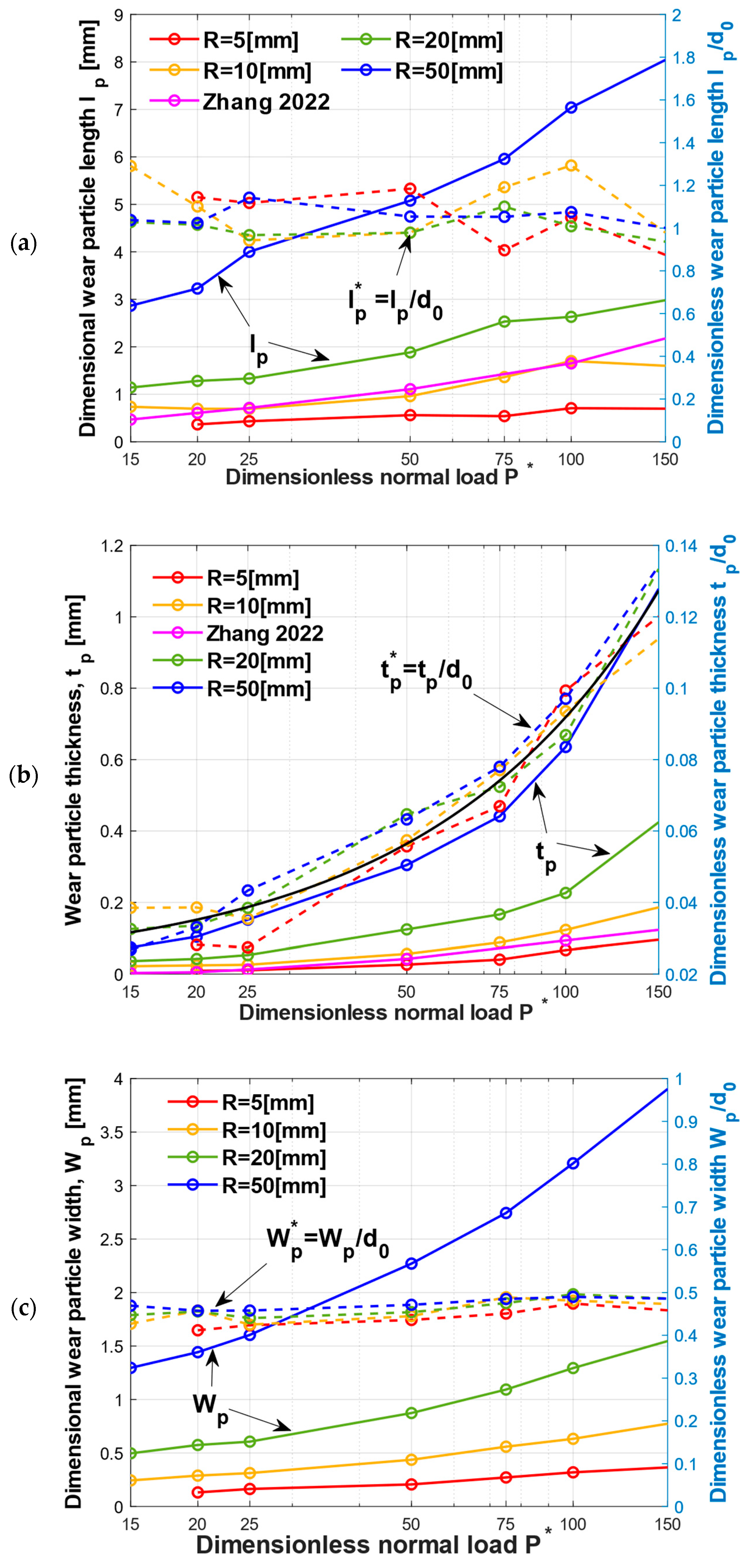
The effects of the normal load intensity and the sphere radius on the wear particle morphology and wear rate were also analyzed. The geometry of a typical wear particle is presented in
Figure 3f and the obtained results for the wear particle length
, thickness
and half width
are shown in
Figure 8, in both dimensional and dimensionless manners. As shown in
Figure 8, the dimensional and dimensionless parameters are indicated by the solid and the dashed lines, respectively. The same normalization as in [
15] was adopted in the current study. All three wear particle parameters were normalized using the diameter of the contact area after the normal loading,
, which is a function of the radius and the interference in the following formula [
16].
It can be seen in
Figure 8 that all the dimensional parameters of the wear particle increased as
increased, indicating that increasing the normal load led to an increase in the wear particle size.
A consolidation of the dimensionless results can be observed. With the increases in the dimensionless normal load, the dimensionless wear particle length remained constant at a value of one. The behavior of the dimensionless wear particle length in this study was in contrast to that reported in [
15], where
was observed to increase with the dimensionless normal load caused by the junction growth. This difference can be attributed to the deletion of elements on the trailing edge of the contact surface in the current sub-model. Following the initiation of the crack, the element adjacent to the crack, as shown in
Figure 3a, continued to be deleted from the wear particle. This deletion of the adjacent element ultimately resulted in a reduction in the wear particle length. Although some deletion occurred due to the small thickness at the trailing edge, it didn’t affect the prediction of the wear volume.
As shown in
Figure 8b, the dimensionless wear particle thickness increased with the dimensionless normal load, and this behavior corelates well with [
15]. The numerical curve fitting shown in the black solid line provided a function
with respect to the
with a goodness of
.
It can be observed that the predicted thickness was slightly higher compared to the results in Ref. [
15]. The differences in
were caused by the differences in the obtained interferences in both sub-models. Including the rigid flat in the sub-model resulted in a slightly increased interference. As the interference increased, so did the size of the plastic region [
31], forcing the crack to propagate more in the vertical direction and resulting in a thicker wear particle.
As shown in
Figure 8c, the dimensionless wear particle half width was almost constant with a value of
, meaning half of the contact diameter
. This was due to the growth of the junctions primarily affecting the contact area in the tangential loading direction, which was perpendicular to the width direction of the wear particle. As a result, the wear particle width remained unchanged.
The wear volume is defined as the volume of the wear particle. The wear rate represents the wear volume per unit of tangential displacement, and it could be used for surface wear evaluation.
The wear rate is given by the following equation.
where
is the sliding distance when the wear particle is fully detached from the sphere and is calculated as the following.
where
is the tangential displacement of the rigid flat when the wear particle is formed. It is noteworthy that the simulation ran until the tangential displacement of
and not
s was achieved. With this method, the computational time can be reduced while ensuring a more realistic result. Obtaining a complete detachment of the wear particles by defining the sliding distance for the simulation required an extensive computational time and led to an unphysical wear volume. This was because the element deletion driven by the JC criterion and fracture energy continued after the wear particle was fully formed (at tangential displacement
). This led to an additional element removal from the wear particle during the detachment. Consequently, the wear volume for the complete detachment was smaller than the wear particle volume
when it was just formed. The previous studies on the adhesive wear also utilized the same concept [
13,
15,
32].
Figure 9 presents the results of the wear volume
and the wear rate
for the various dimensionless normal loads
and different sphere radii
R. The wear volume was normalized by the hemisphere volume,
, where
. The wear rate was normalized term by term, where the nominator was normalized by the hemisphere volume and the denominator was normalized by
.
This normalization led to a general relation between the dimensionless wear rate
and the dimensionless normal load
, allowing for the prediction of the wear rate and the wear volume independent of the radius for aluminum 2024 T351. The only parameter required to obtain the dimensionless wear rate was
, which can be calculated by following equation [
33].
where
is the linear function of Poisson’s ratio,
, and
is normalized by the critical interference
for the stick contact condition, given by [
33].
where
is the critical interference at the yield inception for a slip contact condition [
33].
Figure 9a shows that the wear volume increased as
and
R increased. The dimensionless wear volume curves were consolidated. In order to demonstrate the relation between
and
, a numerical curve fitting with a goodness of
was given as following equation.
By using Equation (15) and the normalization
, the dimensional wear volume can be calculated. The obtained result corelated well with the result in [
15], with a difference less than 9%.
Figure 9b shows a similar behavior for the wear volume. The relation between
and
were given by a numerical fitted curve with a goodness of
= 0.989.
By substituting Equations (12)–(14) into Equation (16), the dimensional wear rate can be calculated. The presented model deals with the creation of a wear particle from a well-defined spherical asperity. The other shapes of the contacting asperities or post-abrasive asperities were not examined in the present study.
Since there is an exchange of asperities in in the contact between rough surfaces in relative motion during the tangential displacement, and assuming that all these asperities are spherical, the wear rate for the entire rough surface was derived from the uniformed dimensionless result of one asperity obtained in this study.
The power-law dependency on the dimensionless normal load for the wear rate reported in [
15] is given by the following equation.
The dimensionless relation obtained in the current study had the power of 2.5 in term. The reason for this difference was the normalization used for the dimensionless wear rate. The normalization used for the dimensionless wear rate was . The denominator was normalized by , which was affected by the dimensionless normal load, as shown in Equation (12). The numerator was normalized by , which was a constant. Hence, in Equation (16), a higher power on term was obtained.
To verify the expression obtained above, a simulation using the sphere radius, , was carried out for a dimensionless normal . The dimensionless wear rate was 10−7, and the relative difference between the simulation result and the predicted results from Equation (16) was approx. 2.5%.
In Ref. [
15], a transition region was observed for the wear rates. Three regimes of the wear rate with different exponents of
were identified, which were
,
and
, representing the mild wear, transition region and severe wear, respectively. However, with the improved sub-model, this transition region was not observed. The power-law dependency on the dimensionless normal load for the wear rate
in the current study is given by following equation.
The change in the power of
was not as significant between the two regions compared to what was reported in [
15]. This difference was due to the different boundary condition at the contact surface of the sub-model. The deformation distribution used on the contact surface in [
15] did not include the crack initiation and propagation, resulting in a smaller interference for the same normal load in the transition region. For instance, for
R = 10 [mm] with
, the dimensionless interference when the wear particle was formed
was 1.2 in [
15], while in the current study
.
4.4. Parametric Study for the Material Properties
The results presented above were limited to a specific material, aluminum 2024 T351. To obtain a more general understanding of how the material properties affected the wear particle formation and mechanical behavior, a parametric study was utilized. The initiation and propagation of a crack was influenced by the three coefficients in the JC failure model and by the fracture energy .
The range of the studied coefficients
and
was from 0.05 to 0.2, and
ranging from −1 to −2. These ranges covered the changes of approx. 50% of the original values for the aluminum analyzed in the current study. However, different materials can have values outside this range, for example FeCoNiCr high entropy alloy [
34] had values of
,
, and
and free-cutting steel 50SiB8 [
35] had values of
,
, and
.
The effect of on the friction behavior and wear volume was very small, and the maximum difference of the static friction coefficient and wear volume was less than 5% and 6%, respectively, for the range of the tested values. had a relatively large influence on the wear volume. The maximum change in the wear volume was 30% for the smallest value of .
For and , the most affected result was the wear particle thickness . As these two parameters decreased, increased. As shown in Equation (3), and influenced the equivalent plastic strain in the same way. As and decreased, decreased. For the spherical contact under normal loading, the stress triaxiality had a negative value as the element was being compressed, and it increased with the distance from the contact surface. This implies that the equivalent plastic strain for the crack generation decreased with an increasing distance from the contact surface. By reducing , the crack propagation in the vertical direction became higher. Hence, the wear particle thickness increased as and decreased.
For the influence of , the most affected values were and . A maximum increases in about 60% was observed, compared to the original values of and for the smallest value of . As decreased, the equivalent plastic strain increased for the negative value of , meaning that a larger strain is need for the element deletion, which explains the increase in . The wear volume change was caused by an additional element deletion during the larger tangential displacement., which may have resulted in fewer physical results.
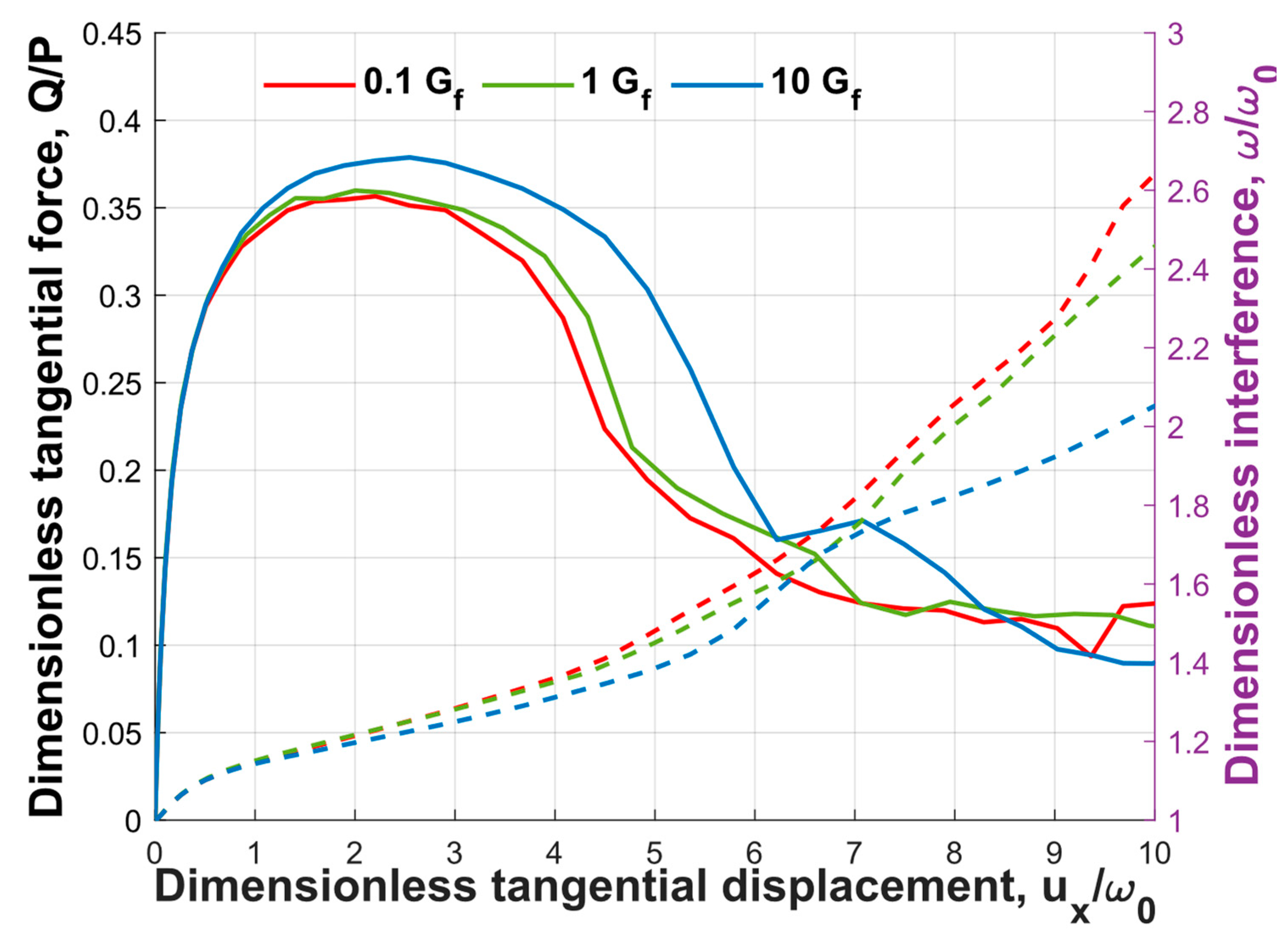
Figure 10 displays the friction behavior and dimensionless interference for various values of the fracture energy. While the JC parameters were more available in the literature, the same was not observed for the fracture energy. Hence, for the current parametric study on
, a range spanning two orders of magnitude around the fracture energy of aluminum was used. It is important to note that the fracture energy values shown in
Figure 10 were normalized by the fracture energy of aluminum 2024 T351.
It can be observed from
Figure 10 that the static friction coefficient increased with the fracture energy. As shown in
Figure 3, the maximum value of the dimensionless tangential force, or the static friction coefficient, was achieved after the crack initiation. This suggests that the fracture energy had an impact on the static friction coefficient. Since the force required to open a crack increased with the fracture energy, the static friction increased as well. However, it should be noted that the influence of the fracture energy was relatively small, with a maximum difference of only 6.2% observed between the two orders of magnitude of the fracture energy.
In contrast, the dimensionless interference decreased with the fracture energy. The change in the interference consisted of two contributors, namely the junction growth and element deletion. With an increase in the fracture energy, the number of elements deleted decreased, leading to a reduction in the dimensionless interference.
While changing
,
,
and
caused some changes to the wear particle morphology, the wear particle formation process for the different parameters was similar to those presented in
Figure 3.
However, for a different material, Ti-6Al-4V, a difference in the crack propagation behavior was observed, as presented in
Figure 11. The material properties were [
36]:
,
,
and a density of
. The JC criterion [
36] and the fracture energy [
37] were:
,
,
and
.
As shown in
Figure 11, at instant
, a crack was generated on the trailing edge of the contact surface. At instant
, the tangential force reached its maximum. These two stages are similar to
Figure 3. However, at instant
, instead of a crack generated below the leading edge of the contact surface, the crack propagated along the edge of the contact surface and reached the leading edge. Interestingly, at
, a second crack was generated within the contact surface surrounded by the first crack. As the tangential displacement increased, the second crack linked with the crack at the trailing edge of the contact surface and led to the formation of a wear particle at instant
.
Since it was not observed that changing the JC coefficients or fracture energy led to such changes in the wear particle formation process, it was assumed that this new crack propagation may have been caused by the change in . For aluminum 2024 T351 and for Ti-6Al-4V, this value was .