Mixed Lubrication Analysis of Tapered Roller Bearings and Crowning Profile Optimization Based on Numerical Running-In Method
Abstract
1. Introduction
2. Mathematic Models
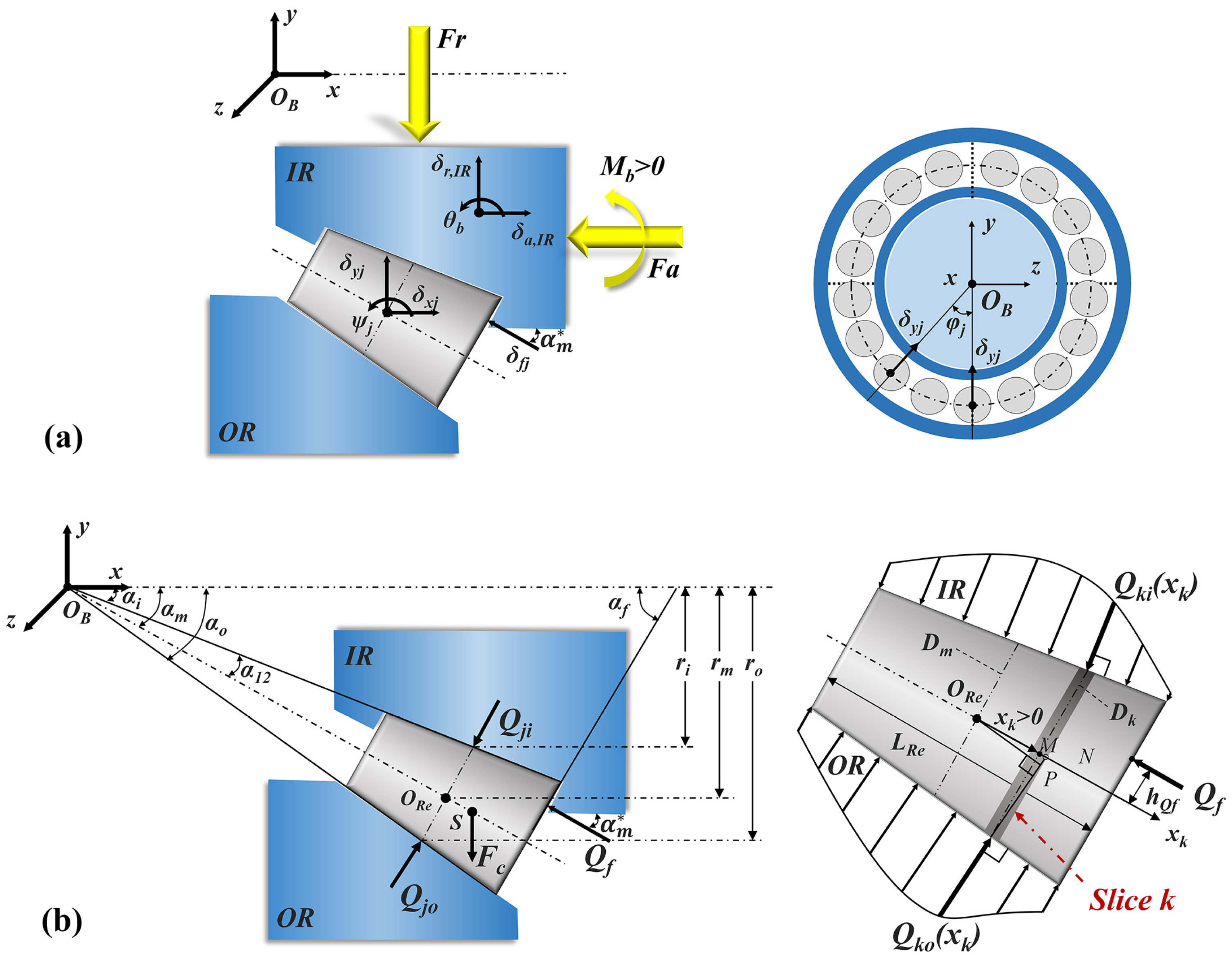
2.1. Quasi-Static Model of a Tapered Roller Bearing
2.2. Mixed Lubrication Model of Finite Line Contacts
2.2.1. Velocity Relationship
2.2.2. Reynolds Equation
2.2.3. Film Thickness Equation
2.2.4. Viscosity and Density Relationships
2.2.5. Asperity Contact Model
2.2.6. Thermal Effect
2.2.7. Load Balance
2.3. Numerical Running-In Method
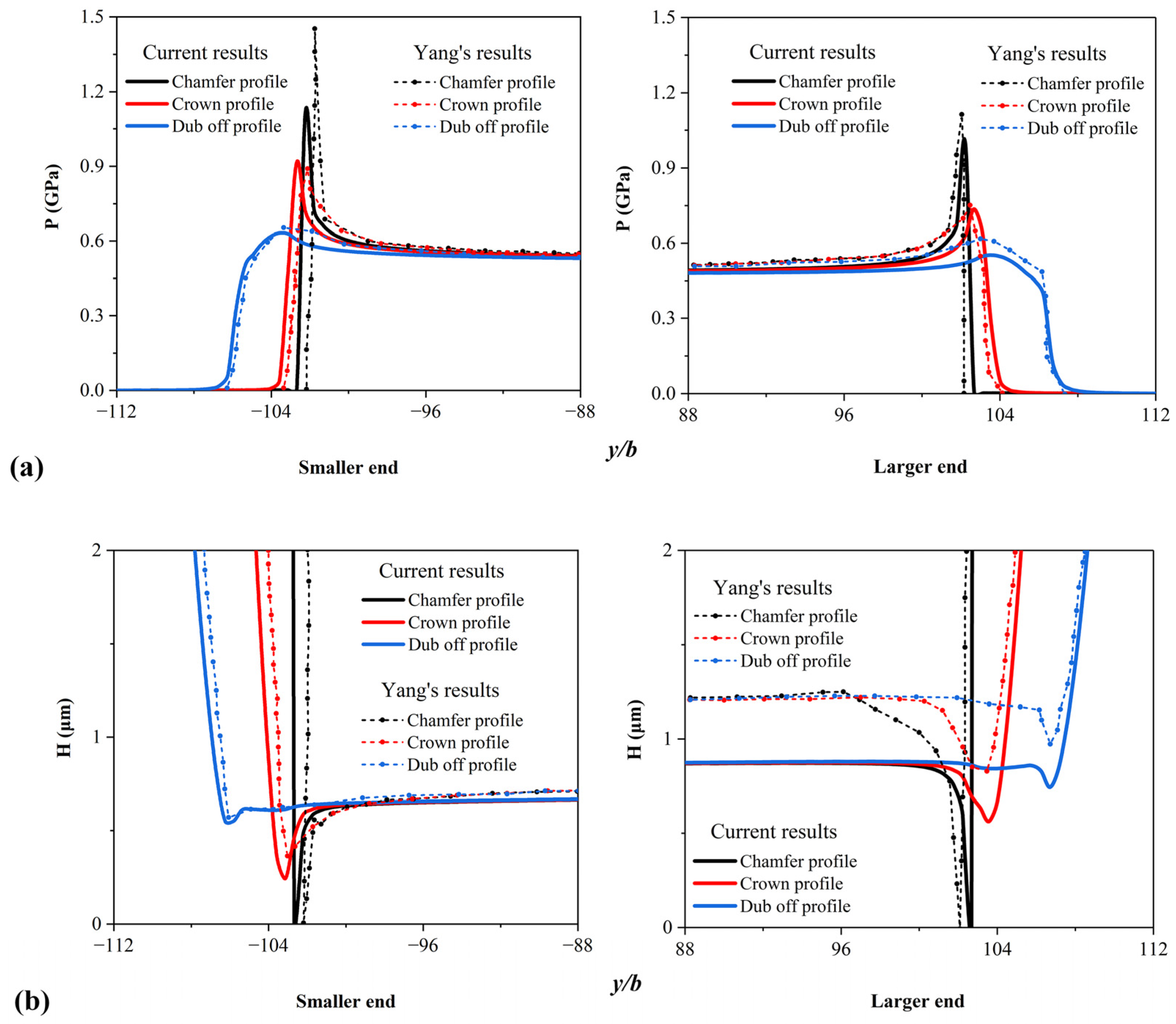
3. Numerical Model Validation
4. Results and Discussion
4.1. Calculation Parameters of the Axial Box TRBs
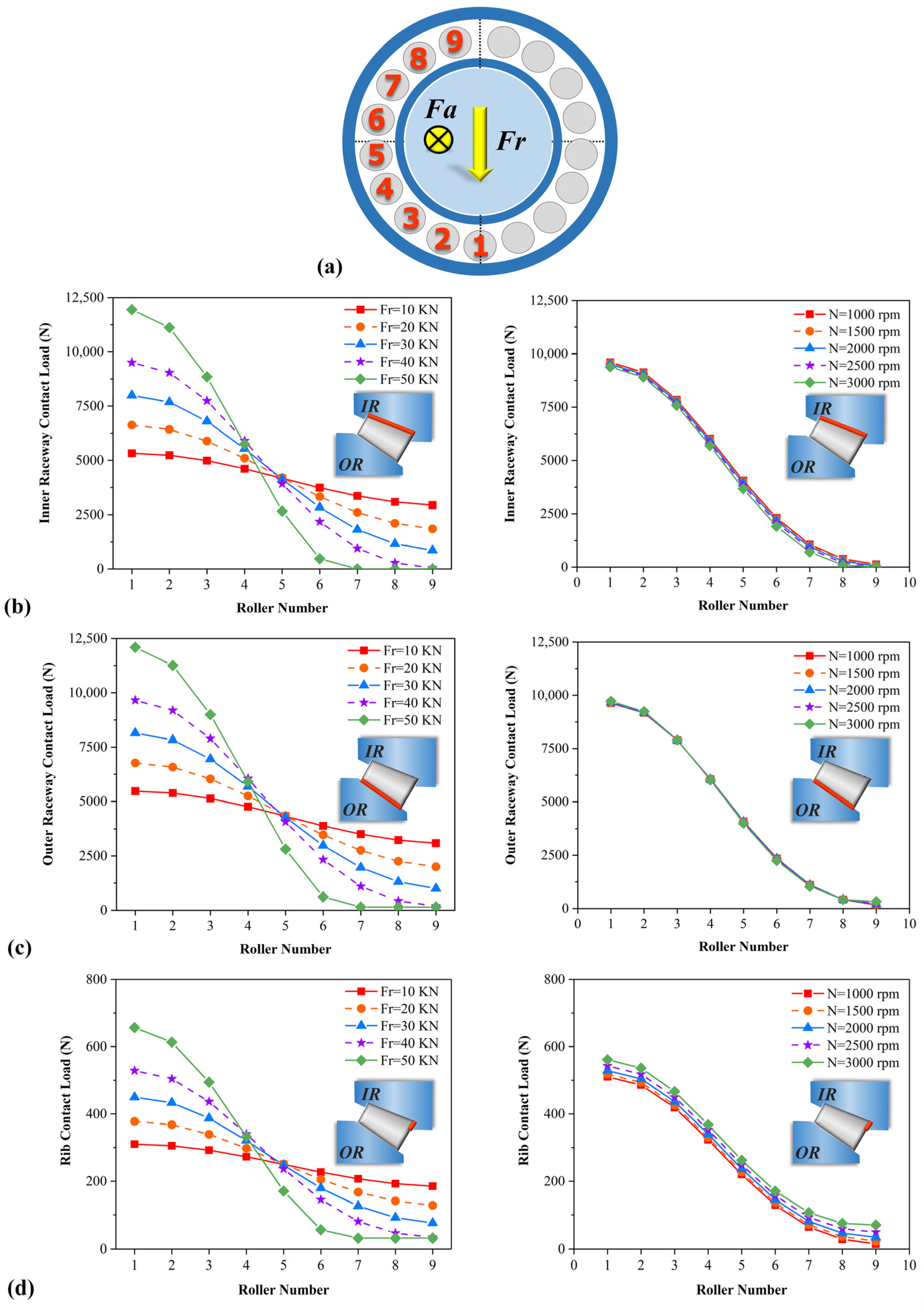
4.2. Internal Load Distributions
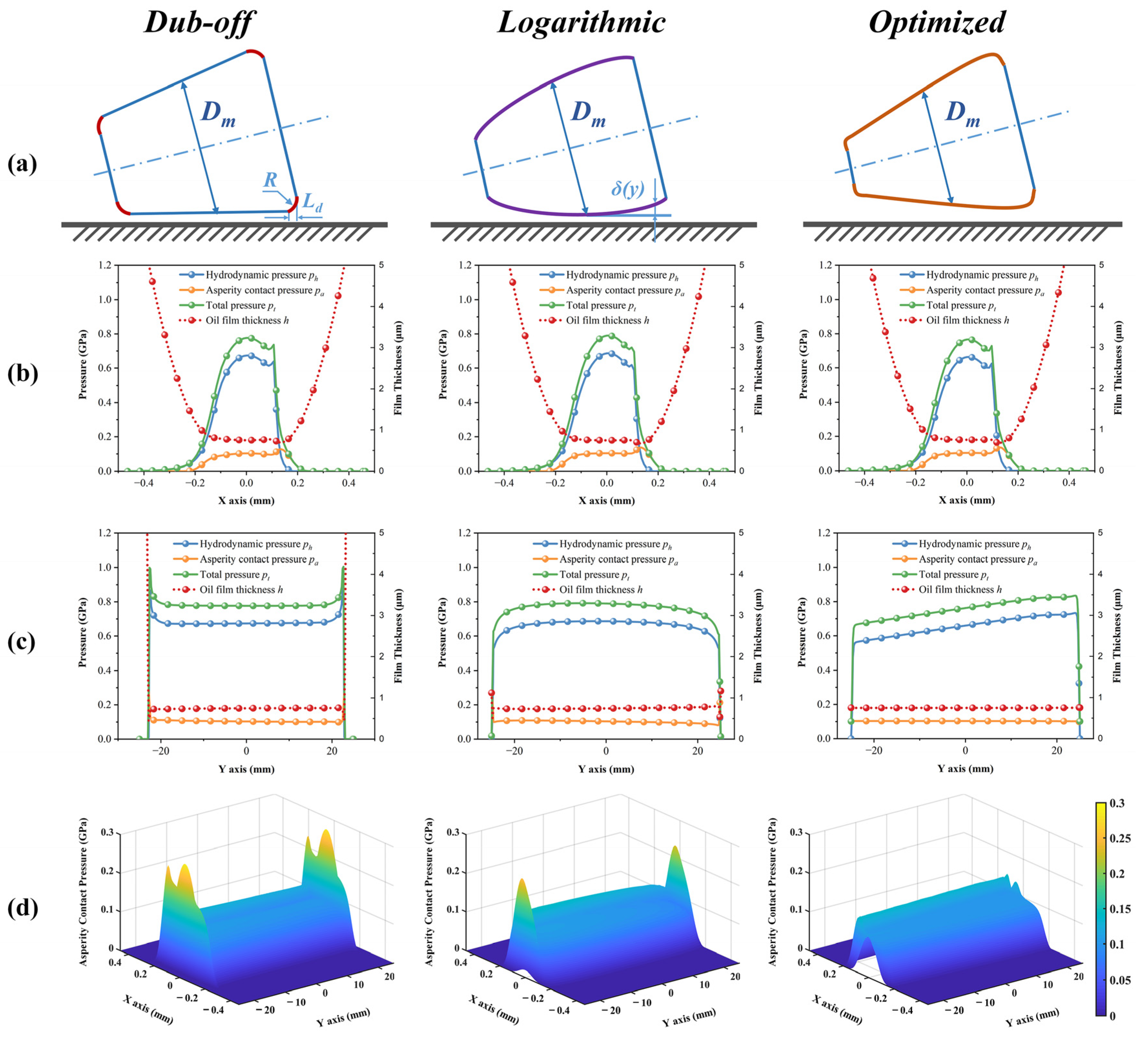
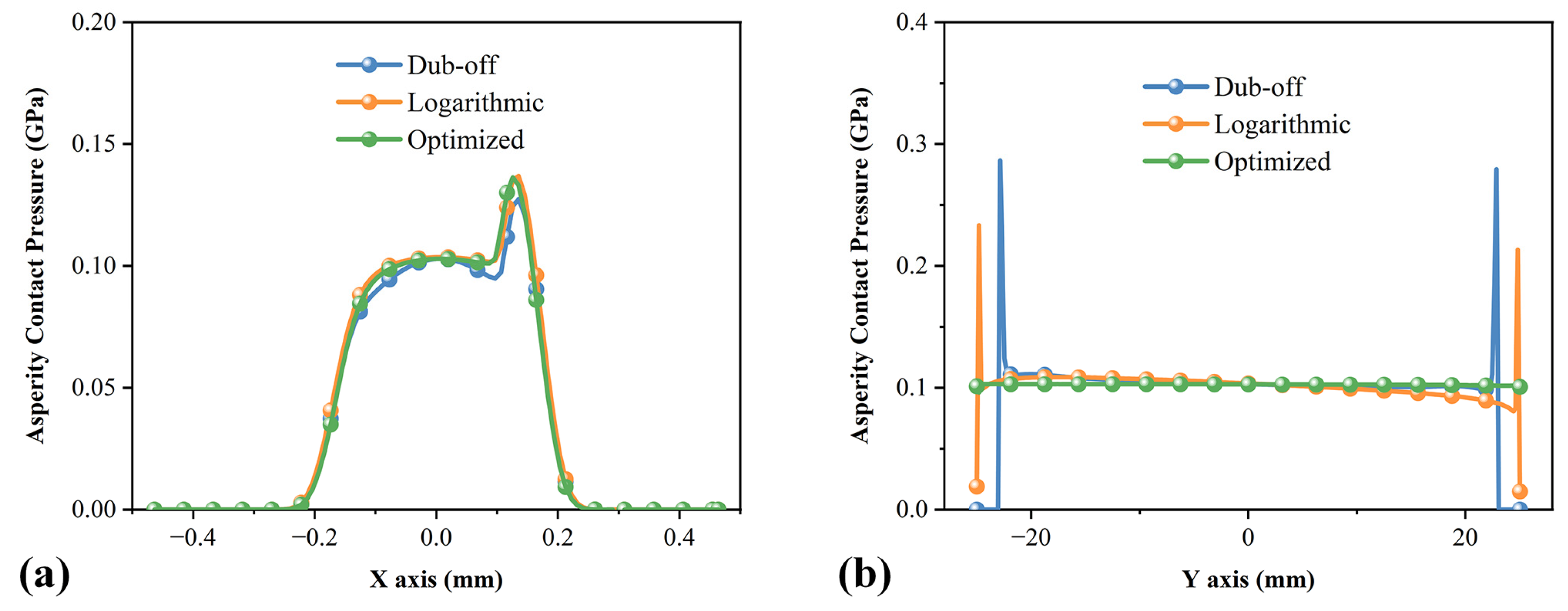
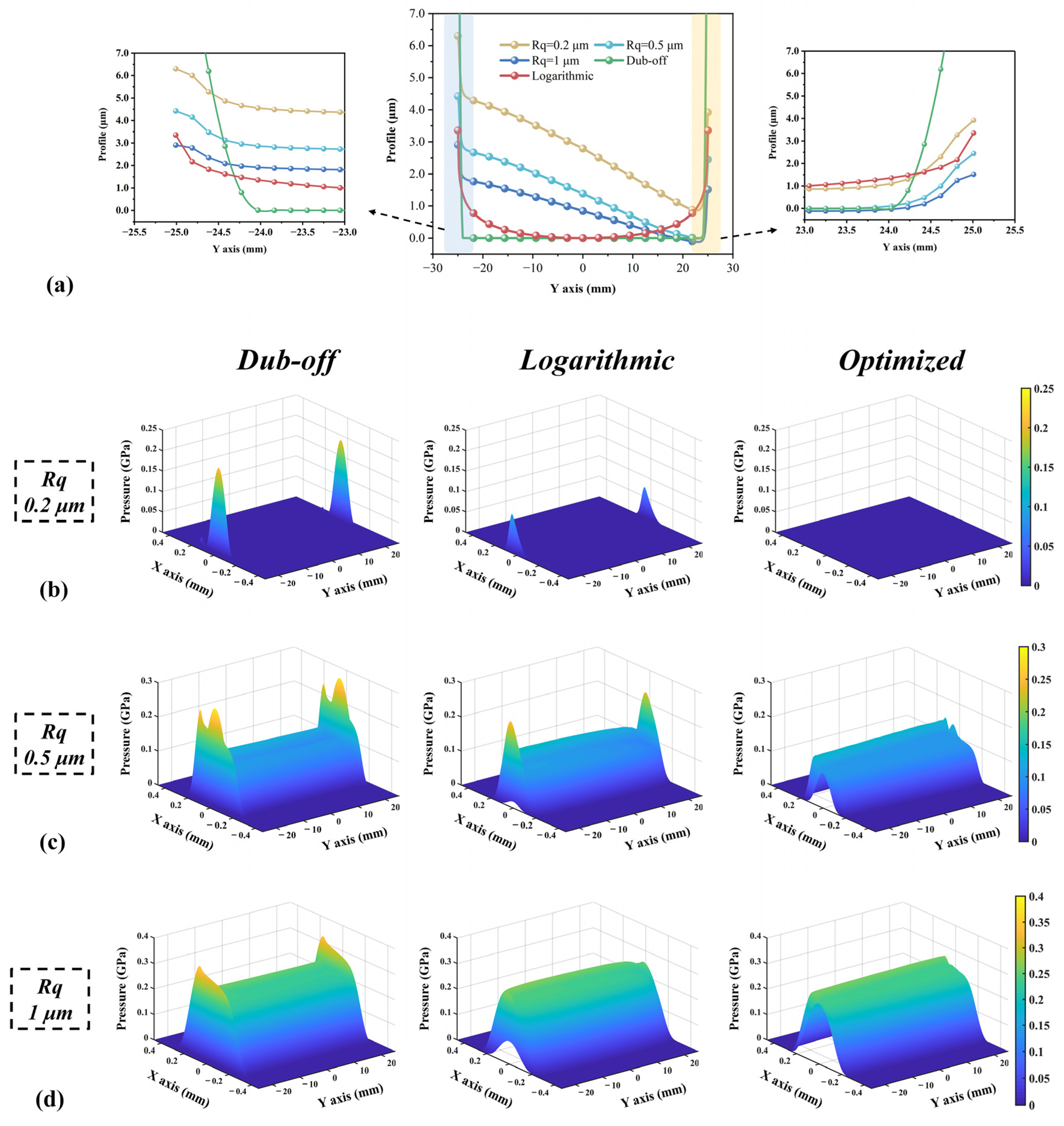
4.3. Effect of Different Axial Roller Profiles
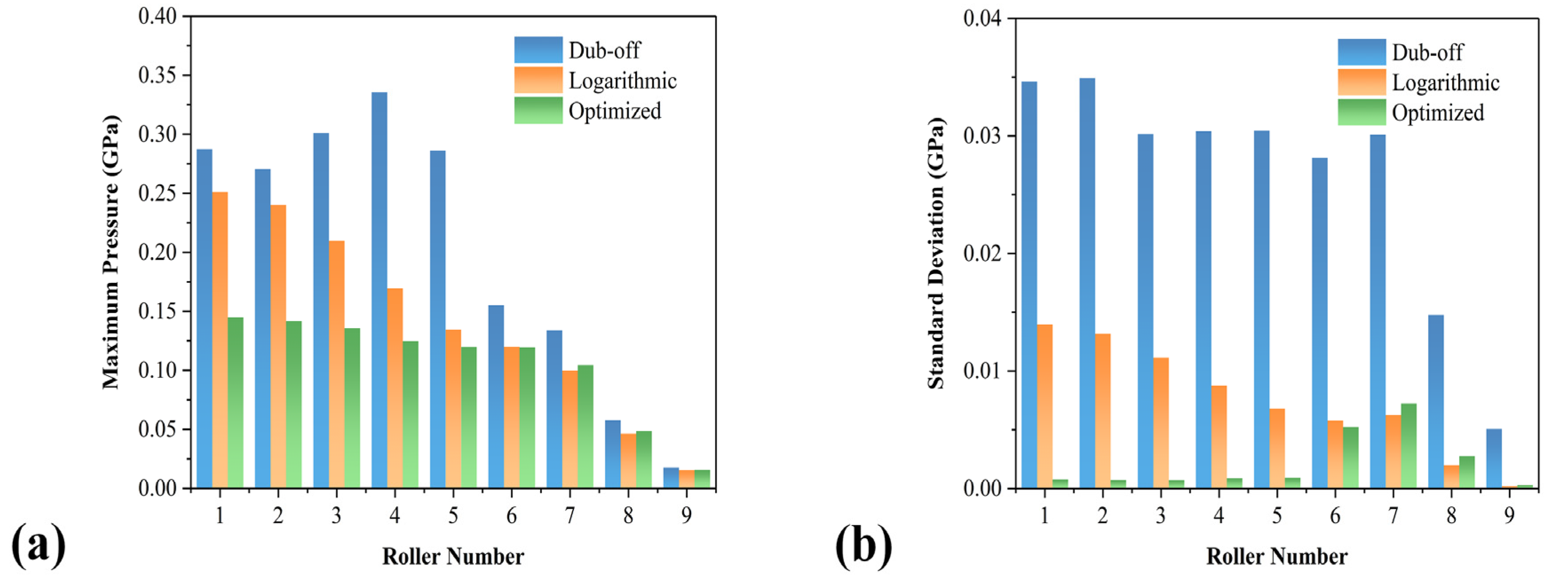
4.4. Influences on Bearing Performance
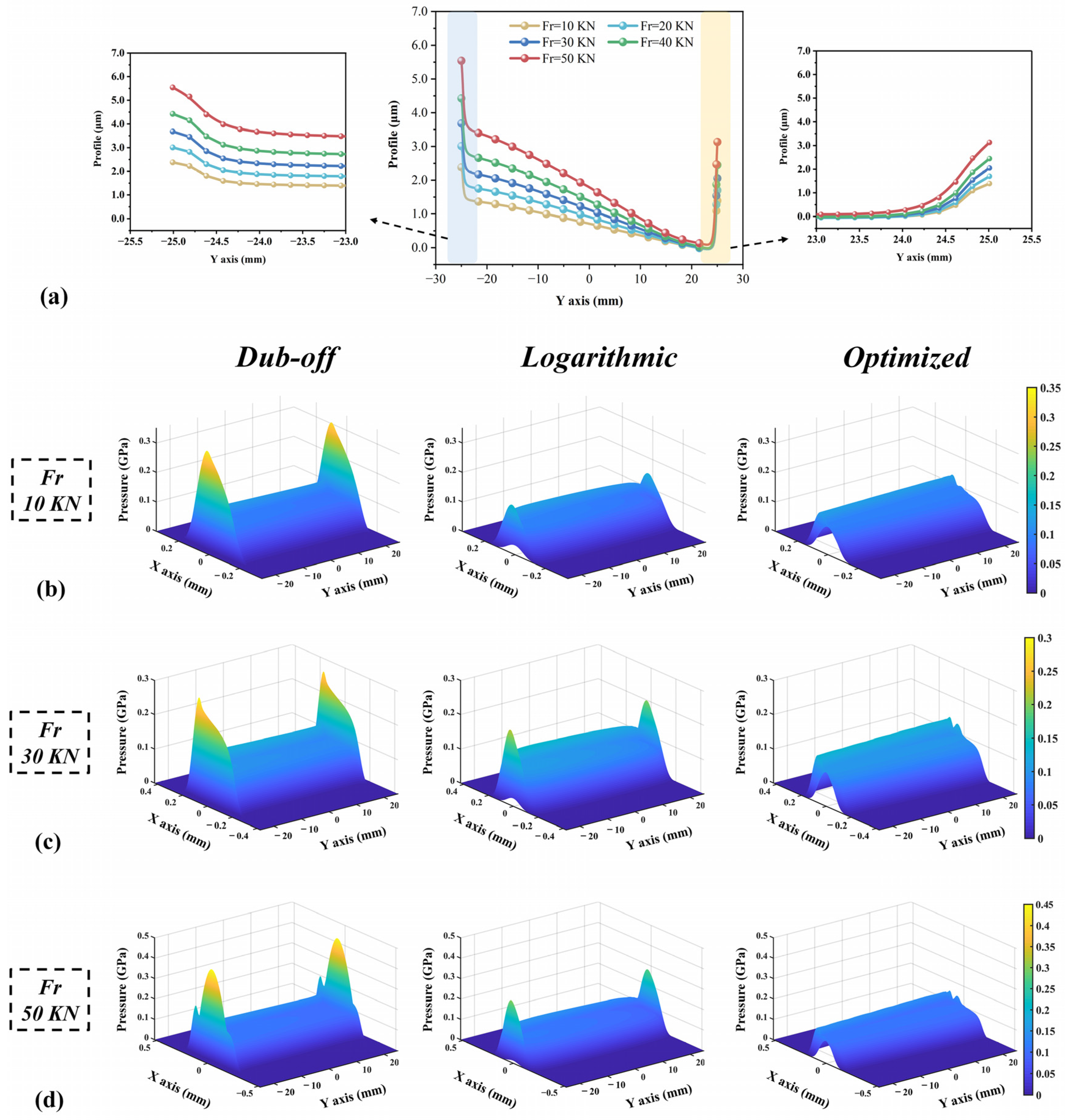
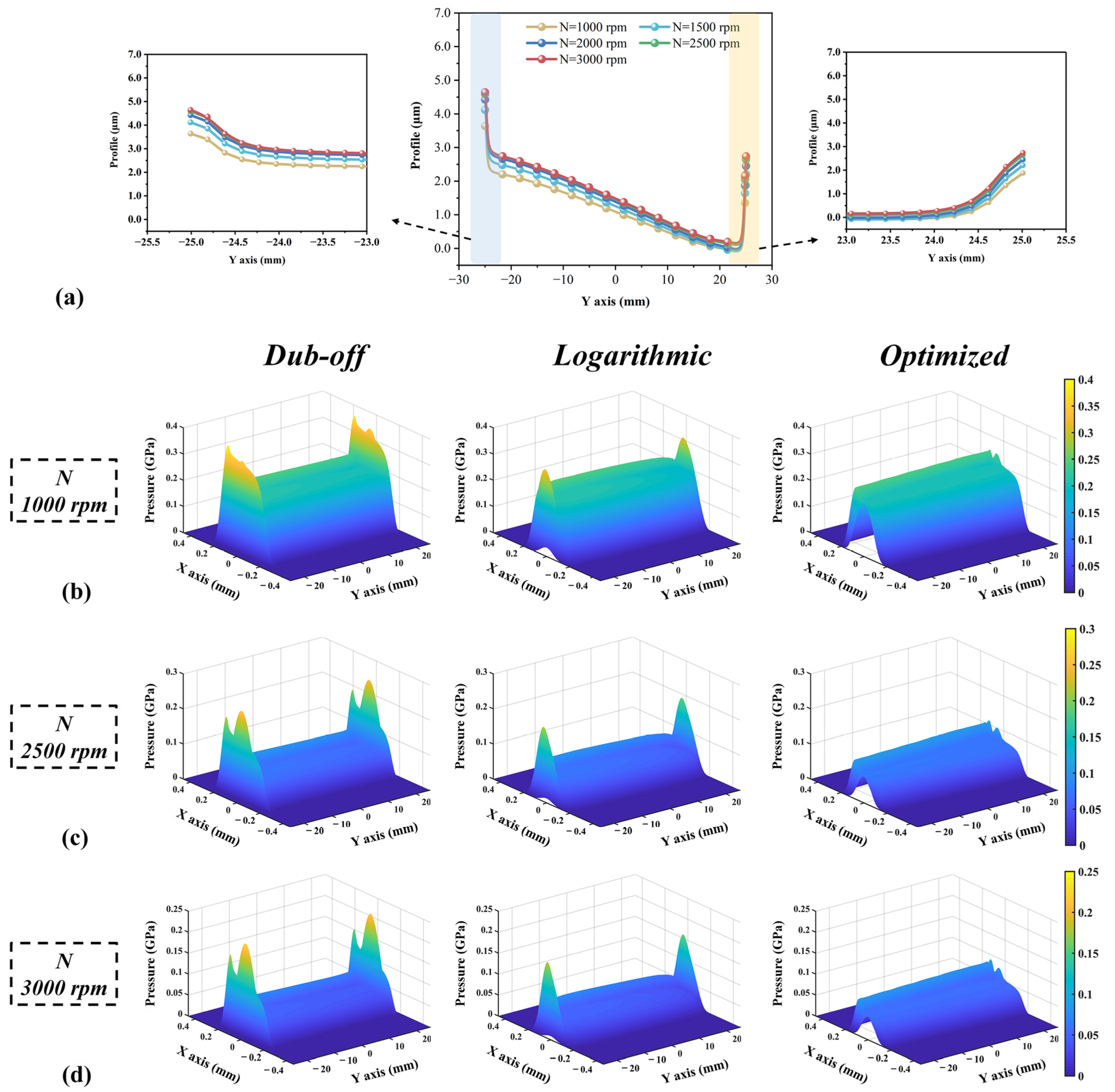
4.5. Effects of Other Factors on Asperity Contact Pressure Distributions
4.5.1. Radial Load (Fr) Effect
4.5.2. Rotation Speed (N) Effect
4.5.3. Standard Deviation of Roughness (Rq) Effect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| half width, m | , , | rolling speed, m/s | |
| , , | specific heat of lubricant, upper solid and lower solid, J/(kg·K) | entrainment velocities of roller–inner raceway, m/s | |
| , | contact stiffness coefficient, N/m10/9 | dimensionless velocity parameter | |
| dimensionless asperity separation | elastic deformation, m | ||
| pitch diameter, m | applied load, N | ||
| effective elastic modulus, Pa | dimensionless load parameter | ||
| Reusner’s correction factor | dimensionless asperity height | ||
| axial load, N | number of rollers | ||
| centrifugal force, N | , | race contact angle, (°) | |
| radial load, N | rib contact angle, (°) | ||
| original geometry profile, m | thermos–viscosity index | ||
| dimensionless material parameter | temperature coefficient | ||
| nominal film thickness, m | surface roughness parameter | ||
| approach between the two bodies, m | shear rate, s−1 | ||
| hardness of the softer material, Pa | pressure coefficient | ||
| , , | thermal conductivity of lubricant, upper solid and lower solid, W/(m·K) | sliding distance interval, m | |
| hardness coefficient, 0.454 + 0.41 | wear depth interval, m | ||
| wear coefficient | crown drop, m | ||
| , | moment arm, m | bending deformation, m | |
| contact length, m | , , | DOF of IR | |
| rounding width, m | ,, | DOF of roller #j | |
| length of roller, m | , | modified deformation on the slice k, m | |
| bending moment, N·m | viscosity of lubricant, Pa·s | ||
| circular slices | ambient viscosity of lubricant, Pa·s | ||
| bearing rotation speed, rpm | coefficient of asperity contact | ||
| center of bearing | Poisson’s ratio | ||
| asperity contact pressure, Pa | density of lubricant, kg/m3 | ||
| hydrodynamic pressure, Pa | shear stress, Pa | ||
| total pressure, Pa | shear stress of asperity contact, Pa | ||
| bearing diametric clearance, m | limiting shear stress, Pa | ||
| nominal maximum Hertzian pressure, Pa | initial limiting shear stress, Pa | ||
| , | normal load between roller and race, N | position angle of the roller, (°) | |
| , | radius of roller and inner race, m | shear flow factor | |
| rounding radius, m | , | flow factors | |
| mean radius of asperity, m | , , | angular velocities, rad/s | |
| , | composite standard deviation of roughness, m | dimensionless critical interference | |
| equivalent radius, m | correction factor | ||
| slide–roll ratio | contact regime | ||
| ambient temperature, K |
References
- Hong, S.-W.; Tong, V.-C. Rolling-element bearing modeling: A review. Int. J. Precis. Eng. Manuf. 2016, 17, 1729–1749. [Google Scholar] [CrossRef]
- Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Process. 2018, 102, 37–58. [Google Scholar] [CrossRef]
- Stacke, L.-E.; Fritzson, D.; Nordling, P. BEAST—A rolling bearing simulation tool. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 1999, 213, 63–71. [Google Scholar] [CrossRef]
- Rahnejat, H.; Gohar, R. Design of profiled taper roller bearings. Tribol. Int. 1979, 12, 269–275. [Google Scholar] [CrossRef]
- Creju, S.; Bercea, I.; Mitu, N. A dynamic analysis of tapered roller bearing under fully flooded conditions part 1: Theoretical formulation. Wear 1995, 188, 1–10. [Google Scholar] [CrossRef]
- Creţu, S.; Mitu, N.; Bercea, I. A dynamic analysis of tapered roller bearings under fully flooded conditions part 2: Results. Wear 1995, 188, 11–18. [Google Scholar] [CrossRef]
- Yamashita, R.; Dowson, D.; Taylor, C.M. An Analysis of Elastohydrodynamic Film Thickness in Tapered Roller Bearings. Tribol. Ser. 1997, 32, 617–637. [Google Scholar] [CrossRef]
- Zheng, J.; Ji, J.; Yin, S.; Tong, V.-C. Internal loads and contact pressure distributions on the main shaft bearing in a modern gearless wind turbine. Tribol. Int. 2020, 141, 105960. [Google Scholar] [CrossRef]
- Zhang, C.; Gu, L.; Mao, Y.; Wang, L. Modeling the frictional torque of a dry-lubricated tapered roller bearing considering the roller skewing. Friction 2019, 7, 551–563. [Google Scholar] [CrossRef]
- Nguyen-Schäfer, H. Computational Tapered and Cylinder Roller Bearings; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Petrusevich, A.I. Fundamental conclusions from the contact-hydrodynamic theory of lubrication. Izv. Akad. Nauk SSSR 1951, 2, 209–233. [Google Scholar]
- Dowson, D.; Higginson, G.R. A Numerical Solution to the Elasto-Hydrodynamic Problem. J. Mech. Eng. Sci. 1959, 1, 6–15. [Google Scholar] [CrossRef]
- Gohar, R.; Cameron, A. The Mapping of Elastohydrodynamic Contacts. A S L E Trans. 1967, 10, 215–225. [Google Scholar] [CrossRef]
- Wymer, D.G.; Cameron, A. Elastohydrodynamic lubrication of a line contact. Proc. Inst. Mech. Eng. 1974, 188, 221–238. [Google Scholar] [CrossRef]
- Bahadoran, H.; Gohar, R. Oil Film Thickness in Lightly-Loaded Roller Bearings. J. Mech. Eng. Sci. 1974, 16, 386–390. [Google Scholar] [CrossRef]
- Kushwaha, M.; Rahnejat, H.; Gohar, R. Aligned and misaligned contacts of rollers to races in elastohydrodynamic finite line conjunctions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 1051–1070. [Google Scholar] [CrossRef]
- Kushwaha, M.; Rahnejat, H. Transient concentrated finite line roller-to-race contact under combined entraining, tilting and squeeze film motions. J. Phys. D: Appl. Phys. 2004, 37, 2018–2034. [Google Scholar] [CrossRef]
- Liu, X.; Yang, P. Analysis of the thermal elastohydrodynamic lubrication of a finite line contact. Tribol. Int. 2002, 35, 137–144. [Google Scholar] [CrossRef]
- Yang, P.; Yang, P. Analysis on the thermal elastohydrodynamic lubrication of tapered rollers in opposite orientation. Tribol. Int. 2007, 40, 1627–1637. [Google Scholar] [CrossRef]
- Zhu, N.; Wang, J.; Ren, N.; Wang, Q.J. Mixed Elastohydrodynamic Lubrication in Finite Roller Contacts Involving Realistic Geometry and Surface Roughness. J. Tribol. 2012, 134, 011504. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Static Friction Model for Elastic-Plastic Contacting Rough Surfaces. J. Tribol. 2004, 126, 34–40. [Google Scholar] [CrossRef]
- Lundberg, G. Elastische Berührung zweier Halbräume. Forsch. Im Ingenieurwesen 1939, 10, 201–211. [Google Scholar] [CrossRef]
- Johns, P.; Gohar, R. Roller bearings under radial and eccentric loads. Tribol. Int. 1981, 14, 131–136. [Google Scholar] [CrossRef]
- Fujiwara, H.; Kawase, T. Logarithmic Profile of Rollers in Roller Bearing and Optimization of the Profile. Trans. Jpn. Soc. Mech. Eng. Ser. C 2006, 72, 3022–3029. [Google Scholar] [CrossRef]
- Fujiwara, H.; Kobayashi, T.; Kawase, T.; Yamauchi, K. Optimized Logarithmic Roller Crowning Design of Cylindrical Roller Bearings and Its Experimental Demonstration. Tribol. Trans. 2010, 53, 909–916. [Google Scholar] [CrossRef]
- Cui, L.; He, Y. A new logarithmic profile model and optimization design of cylindrical roller bearing. Ind. Lubr. Tribol. 2015, 67, 498–508. [Google Scholar] [CrossRef]
- Poplawski, J.V.; Peters, S.M.; Zaretsky, E.V. Effect of Roller Profile On Cylindrical Roller Bearing Life Prediction—Part II Comparison of Roller Profiles. Tribol. Trans. 2001, 44, 417–427. [Google Scholar] [CrossRef]
- Najjari, M.; Guilbault, R. Edge contact effect on thermal elastohydrodynamic lubrication of finite contact lines. Tribol. Int. 2014, 71, 50–61. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, H.; Kovalev, A.; Meng, Y. Numerical Running-In Method for Modifying Cylindrical Roller Profile Under Mixed Lubrication of Finite Line Contacts. J. Tribol. 2019, 141, 041401. [Google Scholar] [CrossRef]
- Yang, P.; Yang, P.; Liu, X. Numerical Analysis of Isothermal EHL for Tapered Roller. Tribology 2005, 25, 456–460. [Google Scholar]
- Chen, F.; Wang, J.; Zhang, G. Elastohydrodynamic lubrication of tapered roller with logarithmic profile. Chin. J. Mech. Eng. 2011, 47, 143–148. [Google Scholar] [CrossRef]
- Guilbault, R. A Fast Correction for Elastic Quarter-Space Applied to 3D Modeling of Edge Contact Problems. J. Tribol. 2011, 133, 031402. [Google Scholar] [CrossRef]
- Cen, H.; Lugt, P.; Morales-Espejel, G.E. On the Film Thickness of Grease-Lubricated Contacts at Low Speeds. Tribol. Trans. 2014, 57, 668–678. [Google Scholar] [CrossRef]
- Roelands, C.J.A.; Winer, W.O.; Wright, W.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils (Dr In dissertation at Technical University of Delft, 1966). J. Lubr. Technol. 1971, 93, 209–210. [Google Scholar] [CrossRef]
- Zhu, N.; Wen, S.-Z. A Full Numerical Solution for the Thermoelastohydrodynamic Problem in Elliptical Contacts. J. Tribol. 1984, 106, 246–254. [Google Scholar] [CrossRef]
- Peiran, Y.; Shizhu, W. A Generalized Reynolds Equation for Non-Newtonian Thermal Elastohydrodynamic Lubrication. J. Tribol. 1990, 112, 631–636. [Google Scholar] [CrossRef]
- Bair, S.; Winer, W.O. A rheological model for elastohydrodynamic contacts based on primary laboratory data. J. Lubr. Technol. 1979, 101, 258–265. [Google Scholar] [CrossRef]
- Houpert, L.; Flamand, L.; Berthe, D. Rheological and Thermal Effects in Lubricated E.H.D. Contacts. J. Lubr. Technol. 1981, 103, 526–532. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M.M. Film Thickness and Asperity Load Formulas for Line-Contact Elastohydrodynamic Lubrication with Provision for Surface Roughness. J. Tribol. 2012, 134, 011503. [Google Scholar] [CrossRef]
- Chang, W.-R.; Etsion, I.; Bogy, D.B. Static Friction Coefficient Model for Metallic Rough Surfaces. J. Tribol. 1988, 110, 57–63. [Google Scholar] [CrossRef]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Half length of rollers, l, mm | 20 | Effective elastic modulus, , GPa | 228 |
| Radius of rollers on the section y = 0, r, m | 0.02 | Material parameter, G, dimensionless | 5000 |
| Deflective angles of tapered rollers, , (°) | 10 | Nominal maximum Hertzian pressure, , GPa | 0.5 |
| Ambient viscosity of lubricant, , Ns/m2 | 0.08 | Angular velocities of rollers, , rad/s | 9.86 |
| Ambient density of lubricant, , kg/m3 | 870 | Angular velocities of plane, , rad/s | 56.4 |
| Parameter | Value |
|---|---|
| Ambient temperature, , K | 313 |
| Specific heat of lubricant, c, J/kg K | 1880 |
| Specific heat of solids, c1 and c2, J/kg K | 460 |
| Thermal conductivity of lubricant, k, W/m K | 0.145 |
| Thermal conductivity of solids, k1 and k2, W/m K | 46 |
| Density of the solids, and , kg/m3 | 7850 |
| Thermos-viscosity index, , K−1 | 0.0585 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Constant axial load, , KN | 15 | Length of rollers, , mm | 50 |
| Varying radial load, , KN | 10–50 | Radius of rollers on the section y = 0, r, mm | 13 |
| Bearing rotation speed, N, 103 rpm | 1–3 | Mean pitch radius of bearing, , mm | 92.5 |
| Bending moment, , Nm | 50 | Outer race contact angle, , (°) | 12 |
| Number of bearing rollers, | 17 | Inner race contact angle, , (°) | 9 |
| Bearing diametric clearance, , | 30 | Ambient temperature, , K | 353 |
| Effective elastic modulus, , GPa | 226 | Ambient viscosity of lubricant, , Ns/m2 | 0.014 |
| Poisson’s ratio, | 0.3 | Composite standard deviation of roughness, Rq, | 0.5 |
| Slide–roll ratio, s | 0.05 | Hardness of the softer material, Hd, GPa | 4.04 |
| Material parameter, G, dimensionless | 4241 | Mean radius of asperity, Ras, | 10 |
| The Bearing Rotation Speed | The High-Speed Railway Speed |
|---|---|
| 1000 rpm | 152 km/h |
| 1500 rpm | 228 km/h |
| 2000 rpm | 304 km/h |
| 2500 rpm | 380 km/h |
| 3000 rpm | 456 km/h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, R.; Bai, H.; Cao, H.; Zhang, Y.; Meng, Y. Mixed Lubrication Analysis of Tapered Roller Bearings and Crowning Profile Optimization Based on Numerical Running-In Method. Lubricants 2023, 11, 97. https://doi.org/10.3390/lubricants11030097
Cao R, Bai H, Cao H, Zhang Y, Meng Y. Mixed Lubrication Analysis of Tapered Roller Bearings and Crowning Profile Optimization Based on Numerical Running-In Method. Lubricants. 2023; 11(3):97. https://doi.org/10.3390/lubricants11030097
Chicago/Turabian StyleCao, Renshui, Hang Bai, Hui Cao, Yazhao Zhang, and Yonggang Meng. 2023. "Mixed Lubrication Analysis of Tapered Roller Bearings and Crowning Profile Optimization Based on Numerical Running-In Method" Lubricants 11, no. 3: 97. https://doi.org/10.3390/lubricants11030097
APA StyleCao, R., Bai, H., Cao, H., Zhang, Y., & Meng, Y. (2023). Mixed Lubrication Analysis of Tapered Roller Bearings and Crowning Profile Optimization Based on Numerical Running-In Method. Lubricants, 11(3), 97. https://doi.org/10.3390/lubricants11030097






