Theoretical Investigations on Tribological Properties of Air Foil Thrust Bearings during Start-Up Process
Abstract
1. Introduction
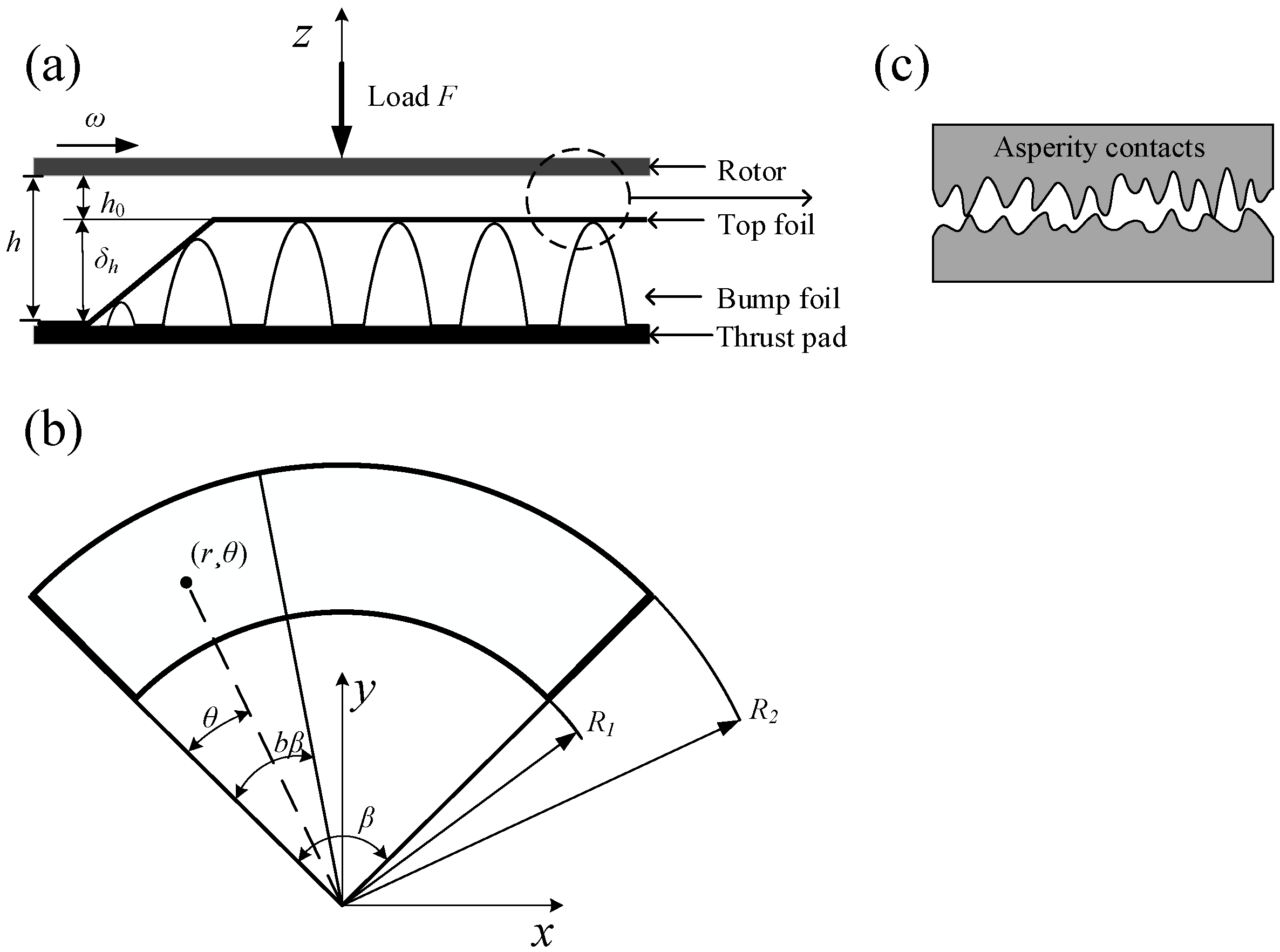
2. Theoretical Model
2.1. Lubrication Model
- (1)
- The air film thickness h is extremely small compared to the radial dimension, so the air pressure change along the thickness direction can be ignored and the velocity of the gas film along the direction can also be zeroed;
- (2)
- The dynamic pressure lubricating air is treated as an ideal gas, and an isothermal process is followed;
- (3)
- No relative sliding exists on the bearing surface.
2.2. Contact Model
2.3. Dynamic Model of the Start-Up Process
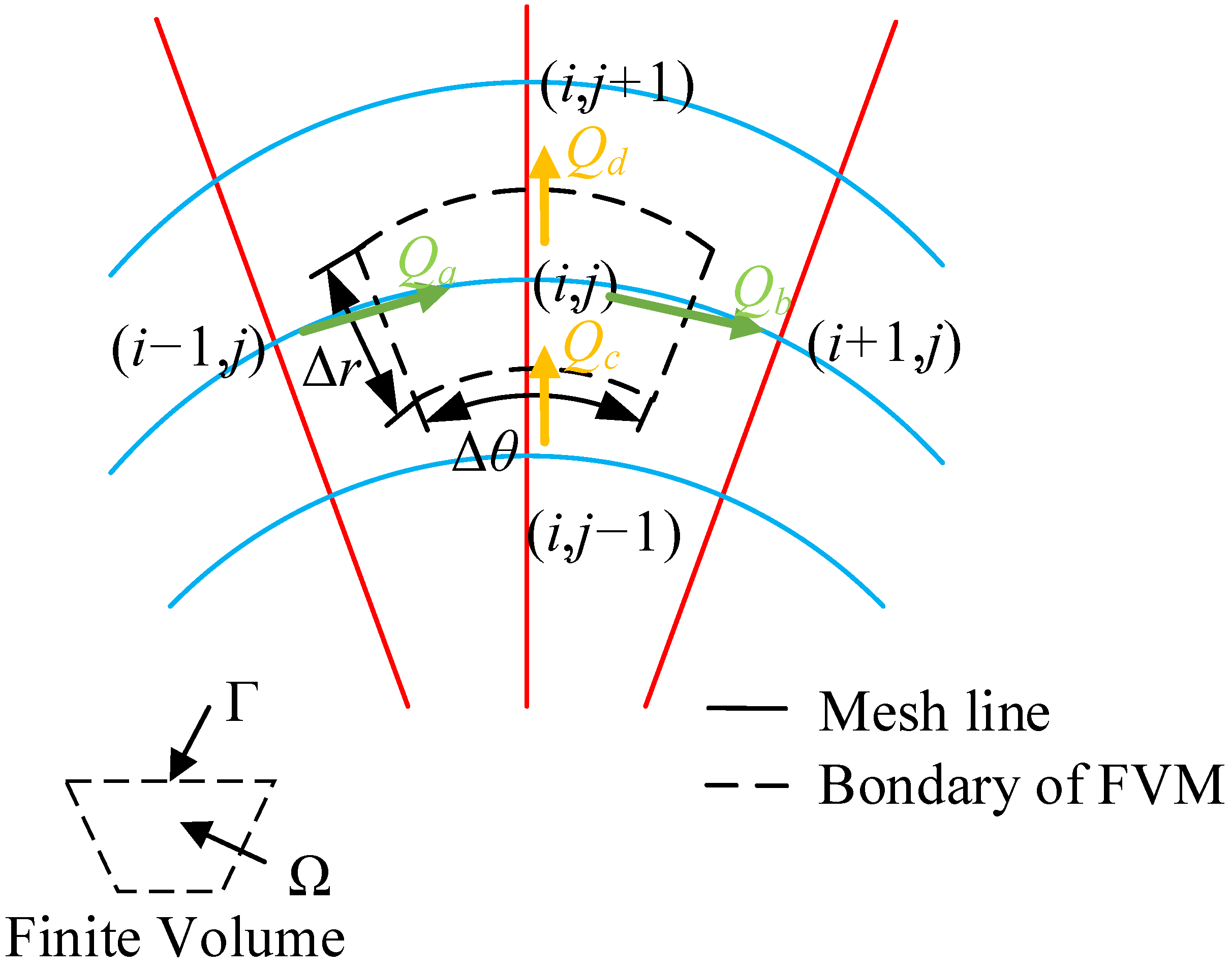
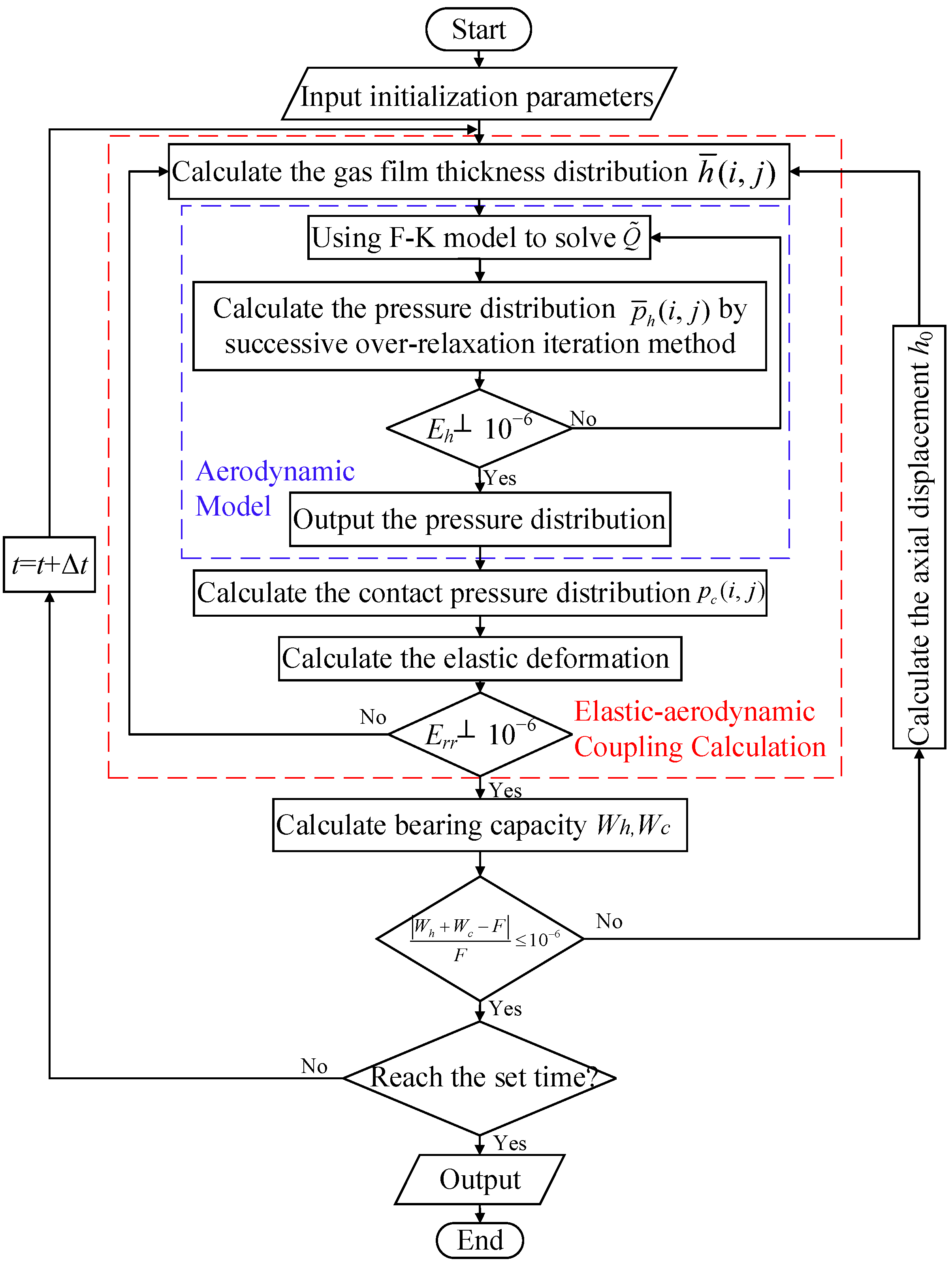
3. Numerical Solution
4. Results and Discussions
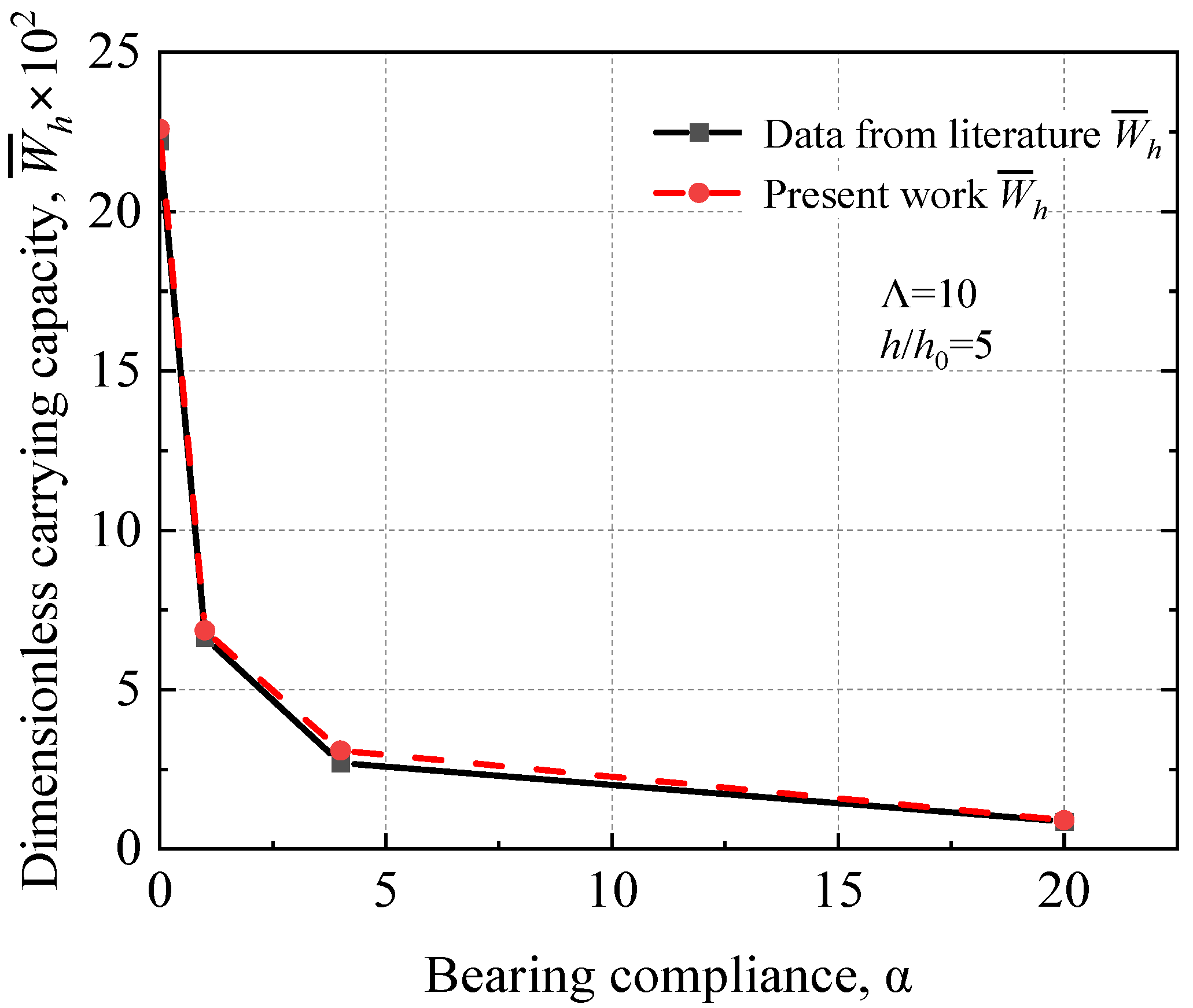
4.1. Model Validation
4.2. Start-Up Behavior
4.3. Effects of the Air Rarefaction on the Tribological Properties during Start-Up Process
4.4. Effects of Bearing Compliance on Start-Up Process
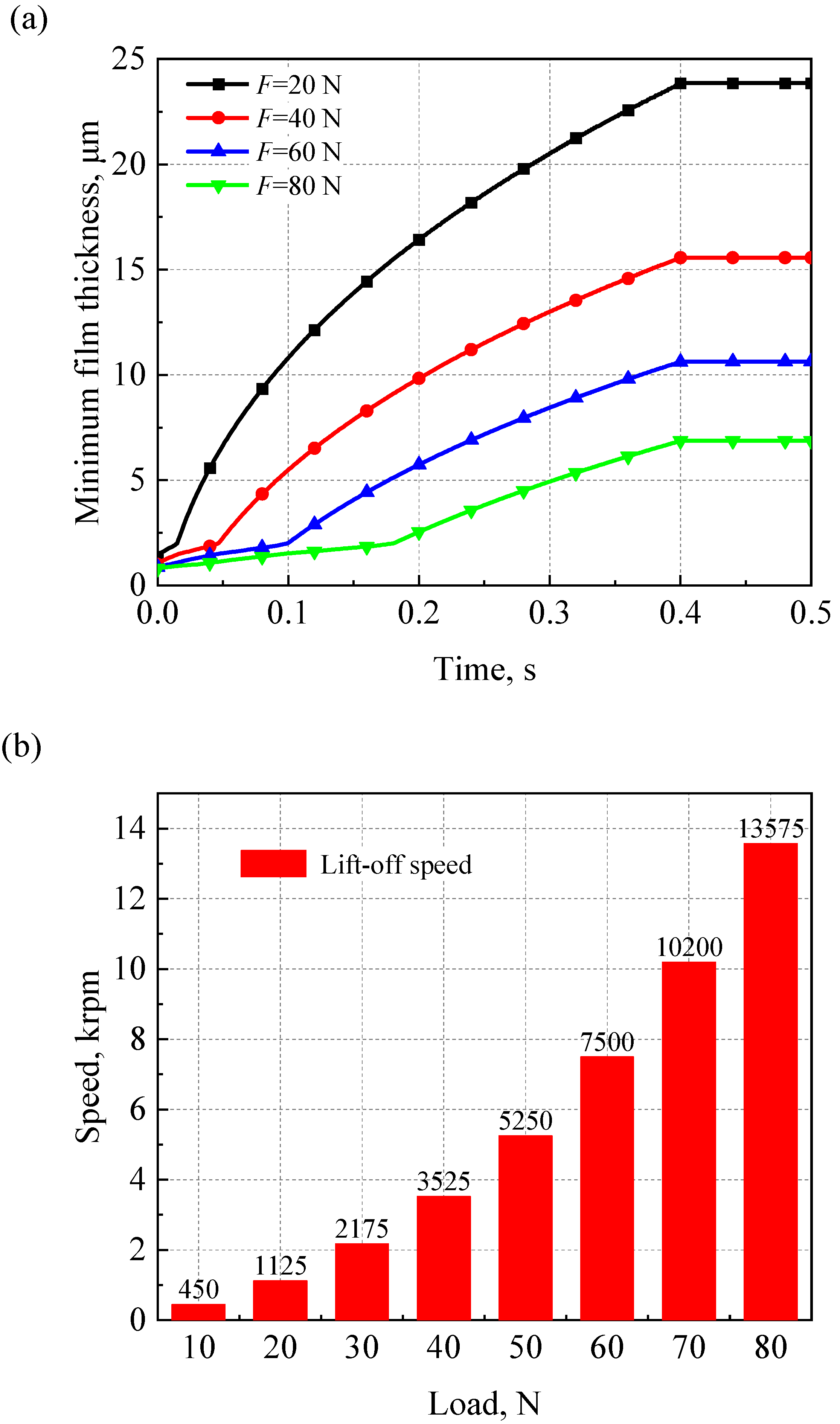
4.5. Changes in Lift-Off Characteristics under Various Loads
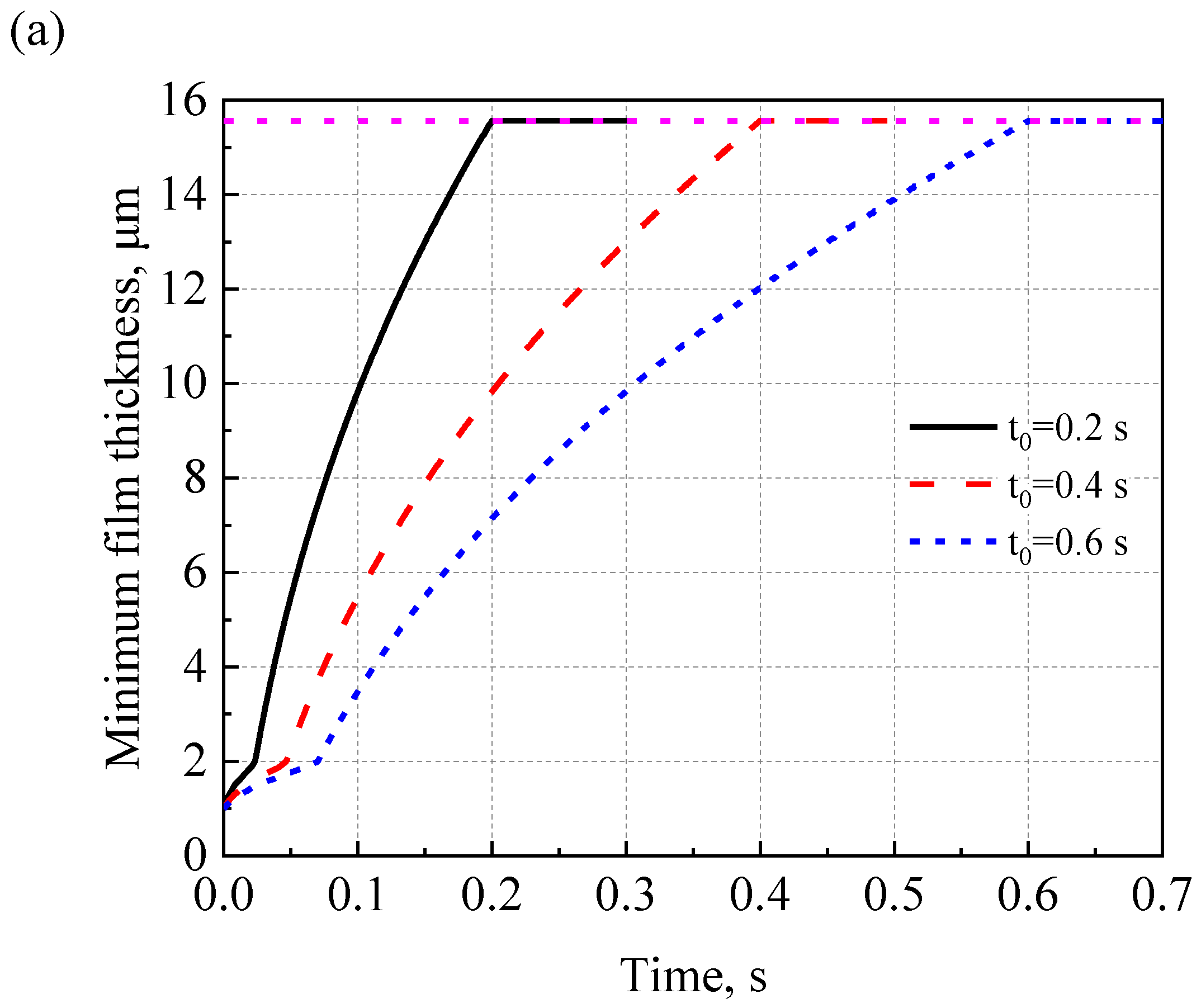
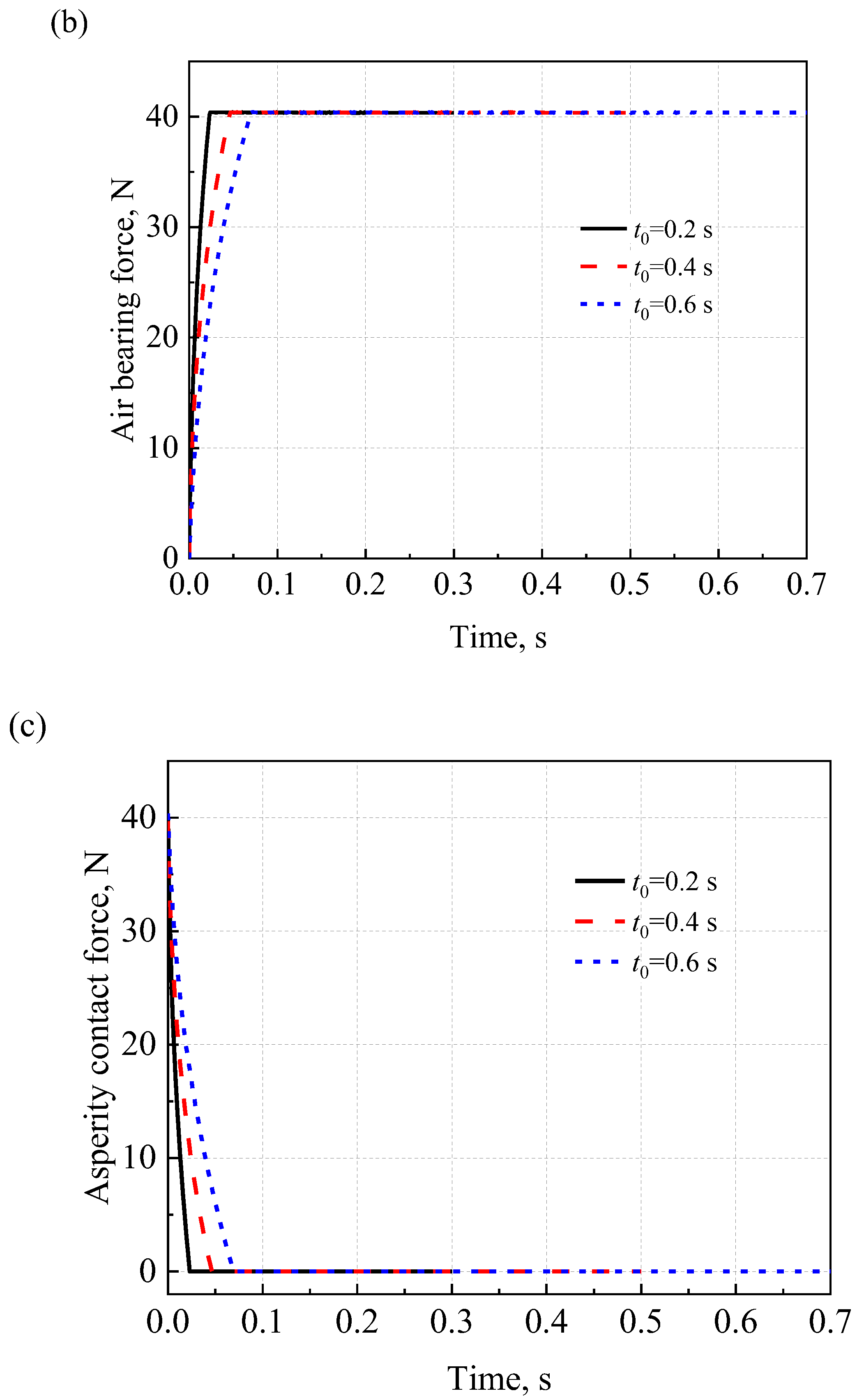
4.6. Effects of Acceleration Time on the Start-Up Process
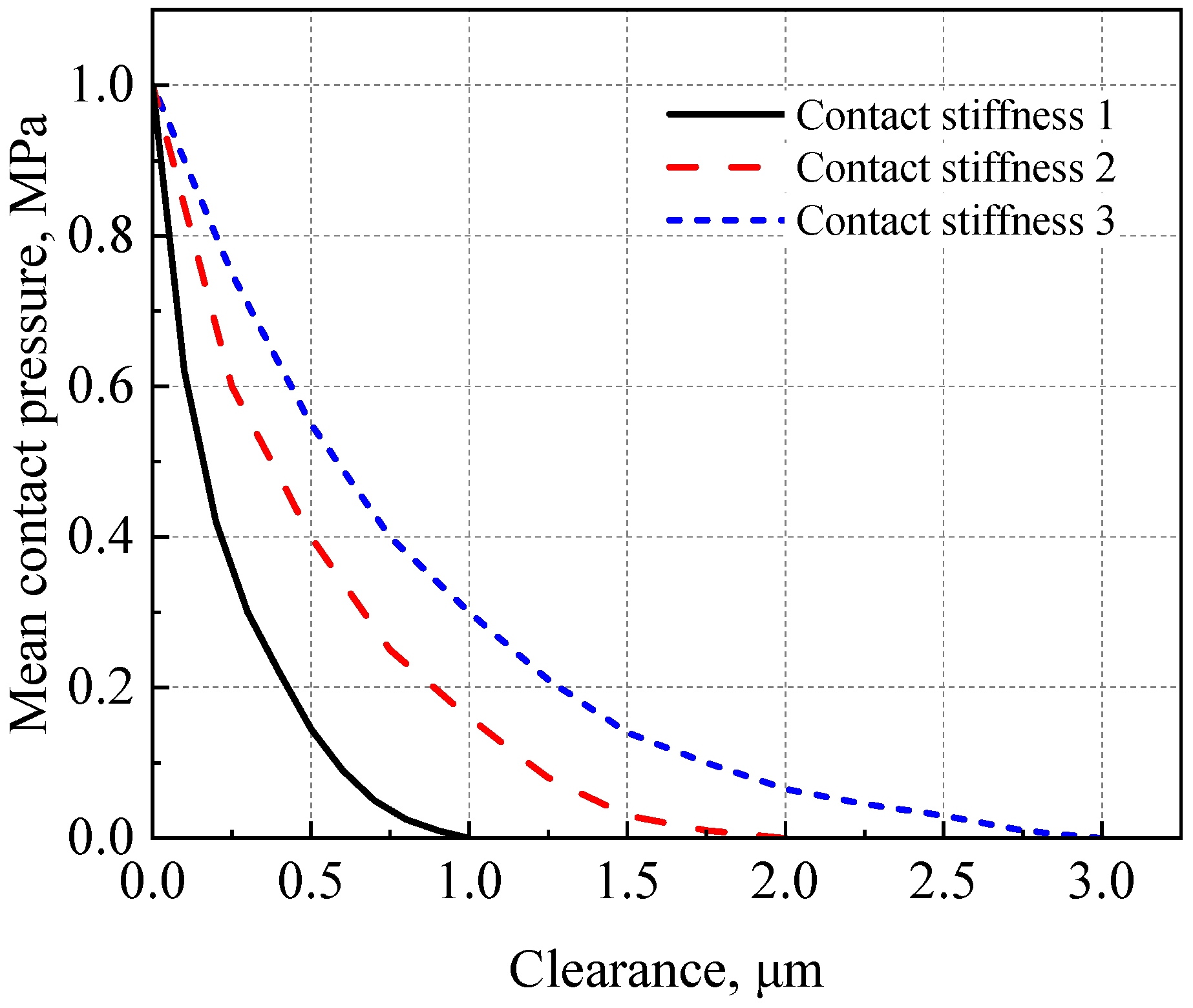
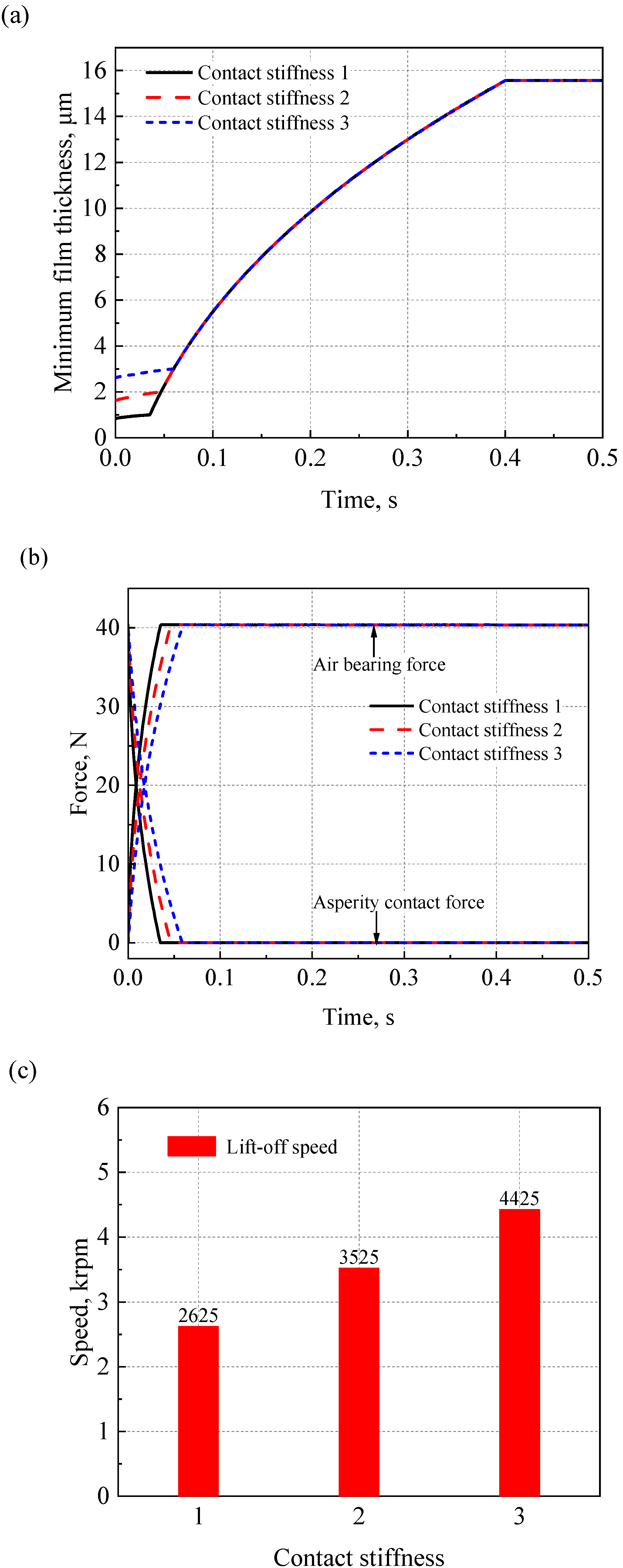
4.7. Effect of Contact Stiffness on Start-Up Performance
5. Conclusions
- (1)
- Compared to the continuum flow, the minimum air film thickness and air bearing force of the AFTB, considering the rarefied flow effect, are lower. However, the lift-off speed and the asperity contact pressure of the AFTB are higher during the start-up process.
- (2)
- As the bearing compliance of the AFTB increases, the lift-off speed increases. When the external load of the AFTB increases, the minimum air film thickness decreases and the lift-off speed increases significantly. When the acceleration time of the rotor is shorter, the lift-off time of the bearing decreases. However, the air bearing force rises sharply and the asperity contact force drops sharply.
- (3)
- The effects of various contact stiffnesses on the start-up performance were explored. It was found that with the increase of the surface roughness, the lift-off speed increases and the contact time of the AFTB becomes longer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| M | mass of the rotor, kg | ||
| b | pitch ratio of inclined plane | F | external load, N |
| D | inverse Knudsen number | W | bearing capacity, N |
| E* | equivalent elasticity modulus, Pa | Wh | air bearing force, N |
| h | air film thickness, m | Wc | asperity contact force, N |
| h0 | minimum film thickness, m | T | total friction torque, N·m |
| δh | the slope height, m | Th | aerodynamic friction torque, N·m |
| RS | rotational speed, rpm | Tc | asperity contact torque, N·m |
| Δt | the time step of quasi-static computation, s | h | dimensionless air bearing force, =Wh/(PaR22) |
| h | dimensionless air film thickness, =h/δh | c | dimensionless asperity contact force, =Wc/(PaR22) |
| 0 | dimensionless minimum film thickness, =h0/δh | dimensionless aerodynamic friction torque, =Th/(PaR22δh) | |
| Pa | ambient pressure, Pa | c | dimensionless asperity contact torque, =Tc/(PaR23) |
| p | air bearing pressure, Pa | Np | number of pads |
| dimensionless air bearing pressure, =p/Pa | μ | viscosity of air, N·s/m2 | |
| pcl | the asperity contact pressure on the local scale, N/mm2 | α | bearing compliance |
| pc | the asperity contact pressure on a global scale, N/mm2 | Λ | number of bearings |
| c | dimensionless asperity contact pressure, = pc/Pa | ν | whirl frequency, rad/s |
| R1 | inner radius, m | Ω | domain |
| R2 | outer radius, m | δ | gap between the two undeformed surfaces, m |
| r, θ | axis of the polar coordinate | β | angular extension of pad, =45° |
| dimensionless radius, =r/R2 | ω | angular velocity, rad/s | |
| t | time, s | u | the normal displacement, m |
| t0 | start-up period, s | x, y | the local scale coordinate |
| μ0 | friction coefficient between the top surface and rotor surface | lx, ly | the evaluation length and width of the surface roughness |
References
- Samanta, P.; Murmu, N.; Khonsari, M. The evolution of foil bearing technology. Tribol. Int. 2019, 135, 305–323. [Google Scholar] [CrossRef]
- DellaCorte, C. Oil-Free shaft support system rotordynamics: Past, present and future challenges and opportunities. Mech. Syst. Signal Process. 2012, 29, 67–76. [Google Scholar] [CrossRef]
- Branagan, M.; Griffin, D.; Goyne, C.; Untaroiu, A. Compliant Gas Foil Bearings and Analysis Tools. J. Eng. Gas Turbines Power 2015, 138, 054001. [Google Scholar] [CrossRef]
- Walowit, J.A.; Anno, J.N.; Hamrock, B.J. Modern Developments in Lubrication Mechanics. J. Lubr. Technol. 1977, 99, 304–305. [Google Scholar] [CrossRef]
- Kim, T.H.; Andrés, L.S. Heavily Loaded Gas Foil Bearings: A Model Anchored to Test Data. J. Eng. Gas Turbines Power 2008, 130, 012504. [Google Scholar] [CrossRef]
- Iordanoff, I. Analysis of an Aerodynamic Compliant Foil Thrust Bearing: Method for a Rapid Design. J. Tribol. 1999, 121, 816–822. [Google Scholar] [CrossRef]
- Iordanoff, I. Maximum Load Capacity Profiles for Gas Thrust Bearings Working Under High Compressibility Number Conditions. J. Tribol. 1998, 120, 571–576. [Google Scholar] [CrossRef]
- Yan, J.J.; Liu, Z.S.; Zhang, G.W.; Wei, J.Q. Static characteristics analysis of foil thrust bearing considering the rarefied gas effect. JASP 2016, 31, 1521–1529. [Google Scholar]
- Samanta, P.; Khonsari, M. The limiting load-carrying capacity of foil thrust bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 232, 1046–1052. [Google Scholar] [CrossRef]
- Xie, Z.; Jiao, J.; Yang, K. Experimental and numerical exploration on the nonlinear dynamic behaviors of a novel bearing lubricated by low viscosity lubricant. Mech. Syst. Signal Process. 2023, 182, 109349. [Google Scholar] [CrossRef]
- Xu, F.; Chu, J.; Sha, L. Air foil thrust bearings with top foil sagging: Theoretical predictions and experiments. Tribol. Int. 2023, 177, 107995. [Google Scholar] [CrossRef]
- Agrawal, G.L. Foil air/gas bearing technology—An overview. Turbo Expo Power Land Sea Air 1997, 78682, V001T04A006. [Google Scholar]
- Heshmat, H.; Walowit, J.A.; Pinkus, O. Analysis of Gas-Lubricated Foil Journal Bearings. ASME J. Lubr. Technol. 1983, 105, 647–655. [Google Scholar] [CrossRef]
- Heshmat, H.; Walowit, J.A.; Pinkus, O. Analysis of Gas Lubricated Compliant Thrust Bearings. J. Lubr. Technol. 1983, 105, 638–646. [Google Scholar] [CrossRef]
- Peng, J.-P.; Carpino, M. Calculation of Stiffness and Damping Coefficients for Elastically Supported Gas Foil Bearings. ASME Trans. J. Tribol. 1993, 115, 20–27. [Google Scholar] [CrossRef]
- Peng, J.-P.; Carpino, M. Coulomb Friction Damping Effects in Elastically Supported Gas Foil Bearings. Tribol. Trans. 1994, 37, 91–98. [Google Scholar] [CrossRef]
- Peng, J.-P.; Carpino, M. Finite Element Approach to the Prediction of Foil Bearing Rotor Dynamic Coefficients. J. Tribol. 1997, 119, 85–90. [Google Scholar] [CrossRef]
- Carpino, M.; Talmage, G. A Fully Coupled Finite Element Formulation for Elastically Supported Foil Journal Bearings. Tribol. Trans. 2003, 46, 560–565. [Google Scholar] [CrossRef]
- Liu, J.; Du, F.R. Simulation of Compliant Bump Foil Journal Bearing Using Coupled Reynolds Equation and Finite Element Model Method. Adv. Mater. Res. 2012, 479–481, 2499–2503. [Google Scholar] [CrossRef]
- Dunfee, J.D.; Shapiro, W. Start-Stop Testing of Two Self-Acting Air-Lubricated Micro Spiral Grooved Thrust Bearing Coating. NASA-CR-134673 1 April 1974. [Google Scholar]
- Jahanmir, S.; Heshmat, H.; Heshmat, C. Assessment of Tribological Coatings for Foil Bearing Applications. Tribol. Trans. 2009, 52, 231–242. [Google Scholar] [CrossRef]
- Kim, J.-H.; Blanchet, T.A.; Calabrese, S.J. High Velocity Oxyfuel Deposition for Low Surface Roughness PS304 Self-Lubricating Composite Coatings. Tribol. Trans. 2004, 47, 157–169. [Google Scholar] [CrossRef]
- Zhang, C.; Ao, H.; Jiang, H.; Zhou, N. Investigations on start-up performances of novel hybrid metal rubber-bump foil bearings. Tribol. Int. 2020, 154, 106751. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Hu, Y. Investigation on start-up performance of gas foil bearing considering wear topography evolution of non-Gaussian surface. Tribol. Int. 2023, 177, 108003. [Google Scholar] [CrossRef]
- Meybodi, R.R.; Mohammadi, A.K.; Bakhtiari-Nejad, F. Numerical analysis of a rigid rotor supported by aerodynamic four-lobe journal bearing system with mass unbalance. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 454–471. [Google Scholar] [CrossRef]
- Fukui, S.; Kaneko, R. A Database for Interpolation of Poiseuille Flow Rates for High Knudsen Number Lubrication Problems. J. Tribol. 1990, 112, 78–83. [Google Scholar] [CrossRef]
- Fukui, S.; Kaneko, R. Analysis of flying characteristics of magnetic heads with ultra-thin spacings based on the Boltzmann equation. IEEE Trans. Magn. 1988, 24, 2751–2753. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. London. Ser. A 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Hu, Y.; Meng, X.; Xie, Y. A computationally efficient mass-conservation-based, two-scale approach to modeling cylinder liner topography changes during running-in. Wear 2017, 386, 139–156. [Google Scholar] [CrossRef]
- Hu, Y.; Meng, Y. Theoretical and Experimental Study of Transient Behavior of Spiral-Groove Thrust Bearings during Start-Up. Tribol. Trans. 2019, 63, 154–172. [Google Scholar] [CrossRef]

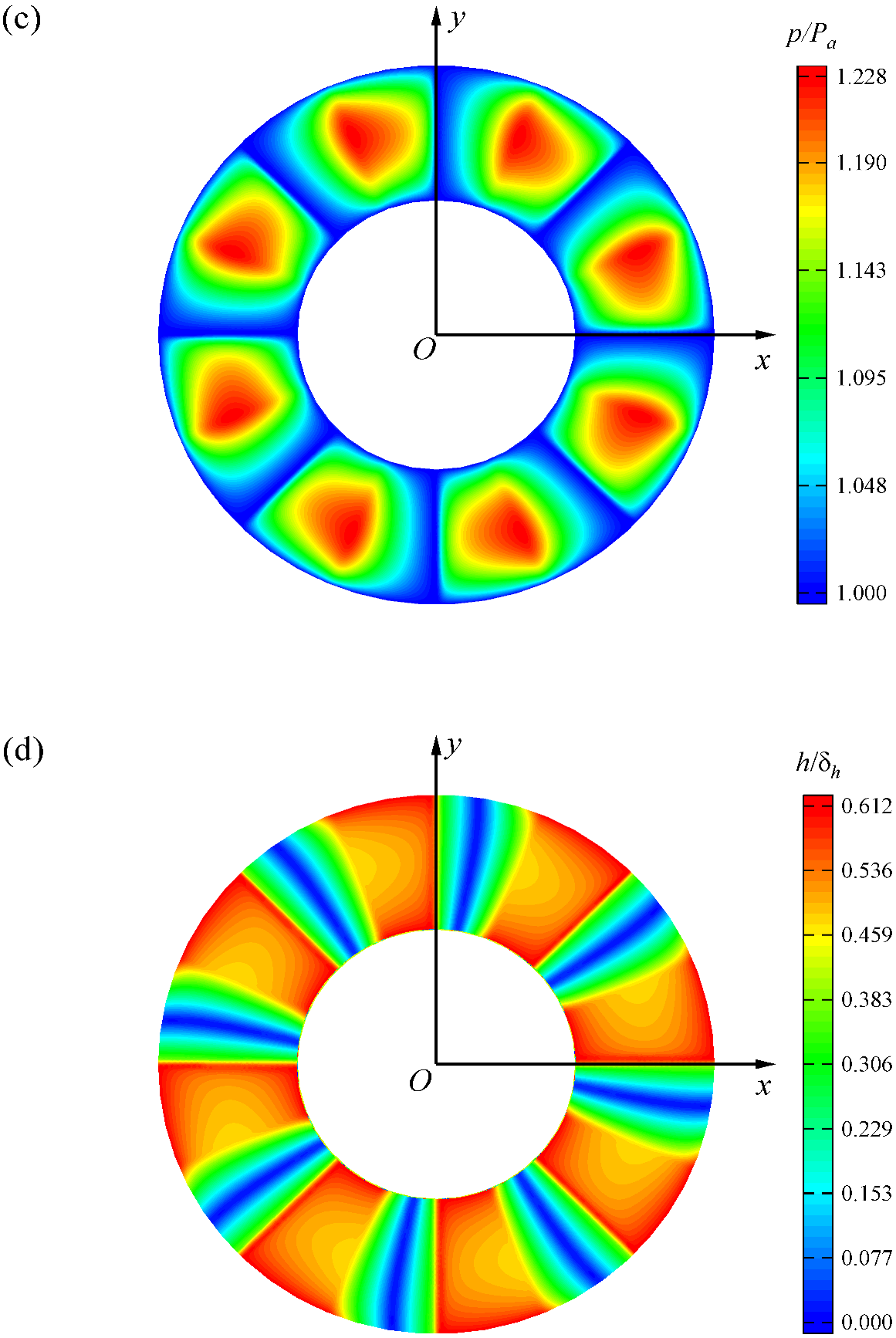
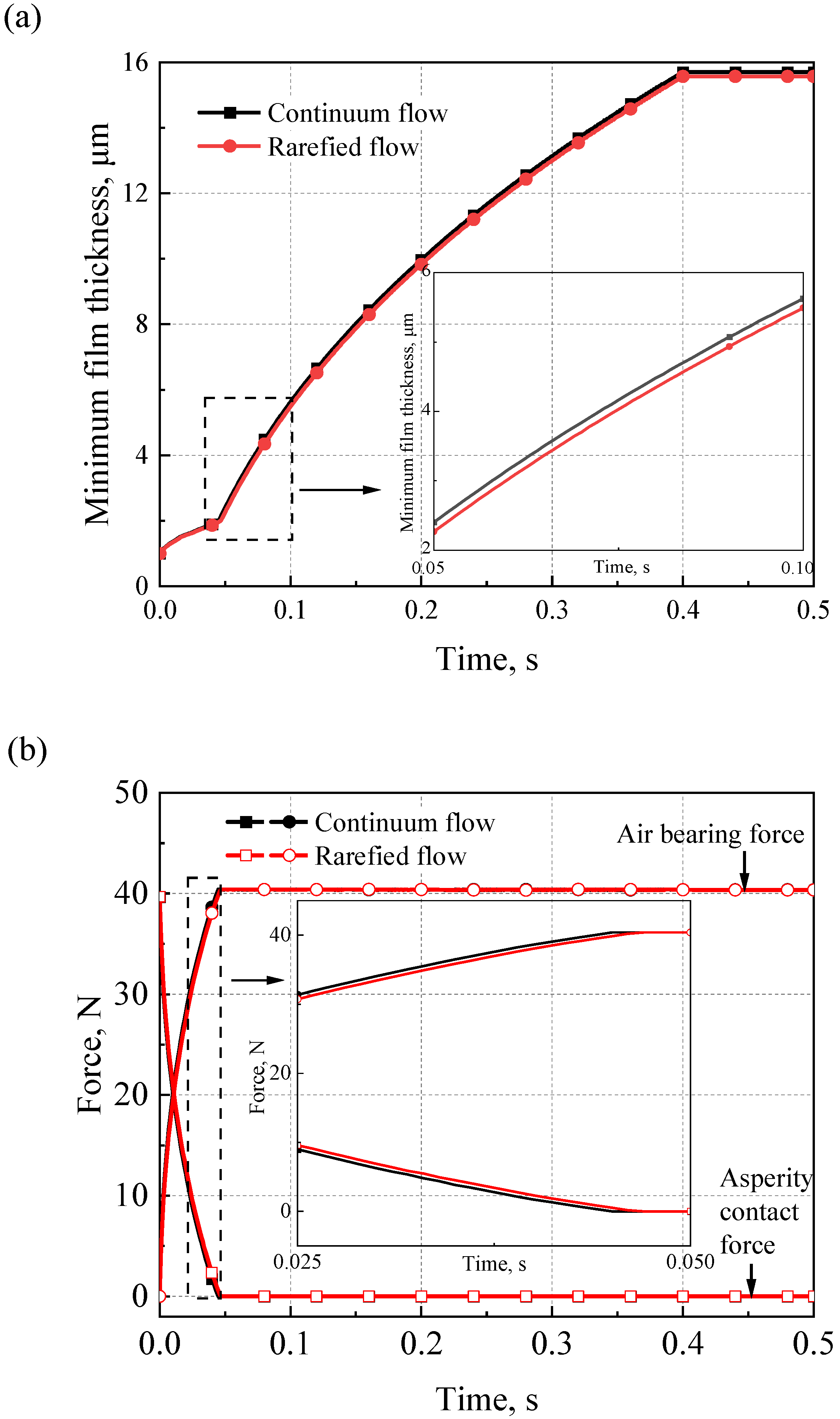
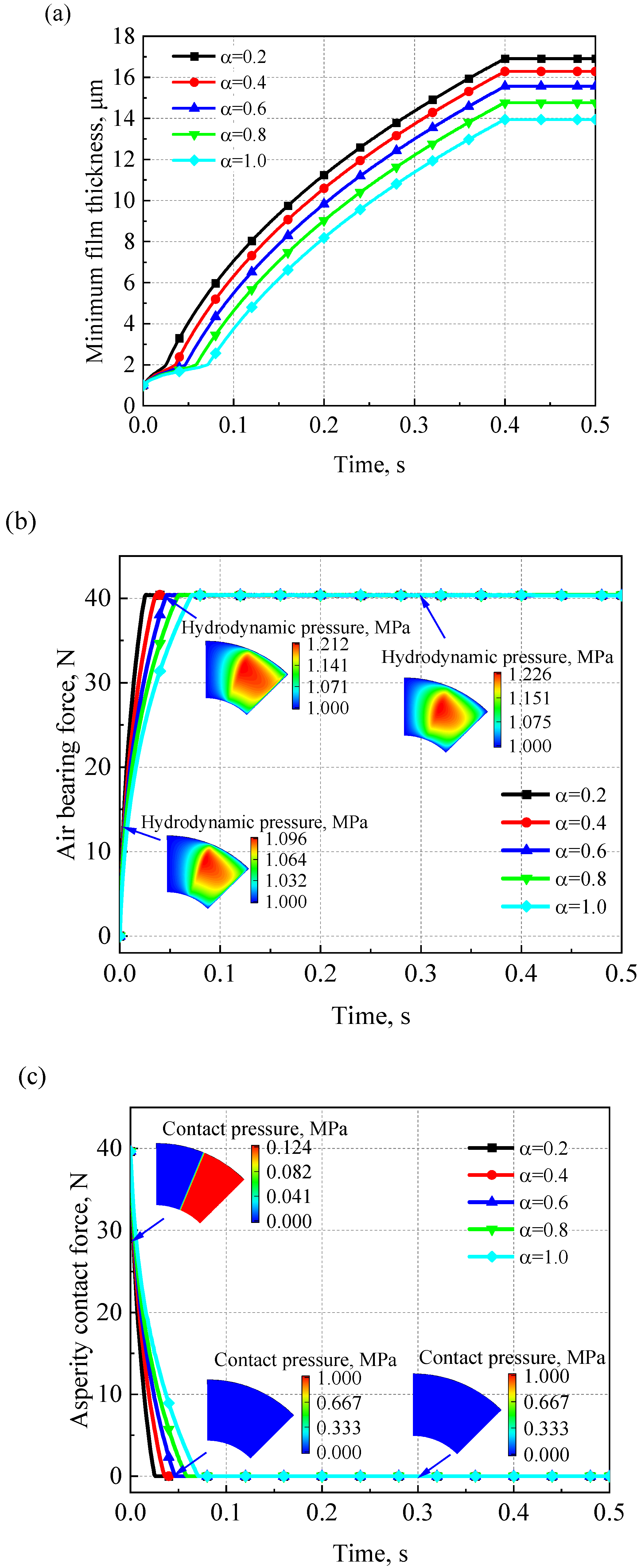
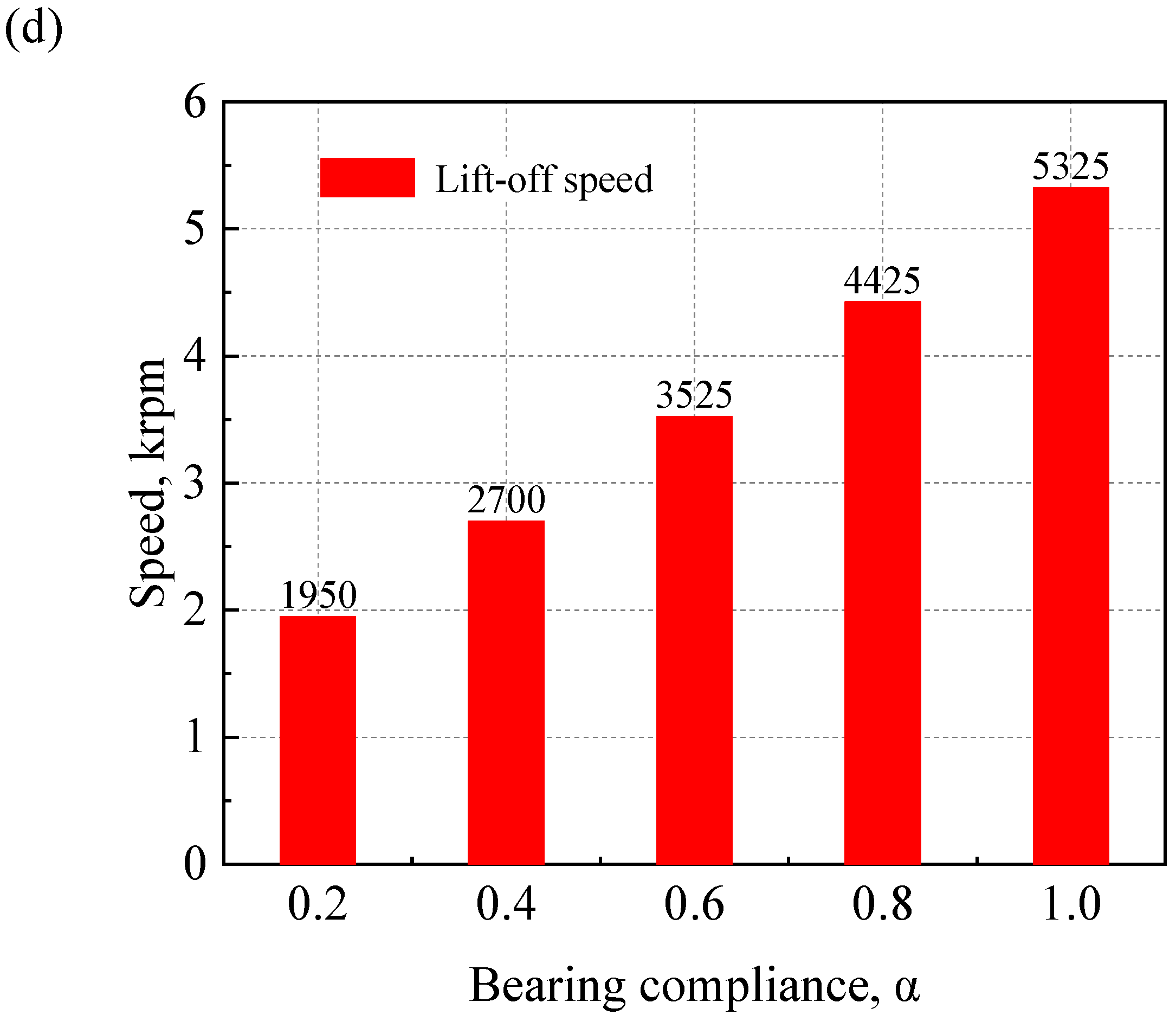
| Parameters | Values |
|---|---|
| Outer radius (R2) | 40 mm |
| Inner radius (R1) | 20 mm |
| Equivalent elasticity modulus | 214 GPa |
| Pitch ratio of inclined plane (b) | 0.5 |
| Angular extension of pad (β) | 45° |
| Number of pads (Np) | 8 |
| Gas film inlet/outlet thickness ratio (h/h0) | 5 |
| Bearing numbers(Λ) | 10 |
| Bearing compliance (α) | 0, 1, 4, 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Hu, Y. Theoretical Investigations on Tribological Properties of Air Foil Thrust Bearings during Start-Up Process. Lubricants 2023, 11, 94. https://doi.org/10.3390/lubricants11030094
Wu F, Hu Y. Theoretical Investigations on Tribological Properties of Air Foil Thrust Bearings during Start-Up Process. Lubricants. 2023; 11(3):94. https://doi.org/10.3390/lubricants11030094
Chicago/Turabian StyleWu, Fangling, and Yang Hu. 2023. "Theoretical Investigations on Tribological Properties of Air Foil Thrust Bearings during Start-Up Process" Lubricants 11, no. 3: 94. https://doi.org/10.3390/lubricants11030094
APA StyleWu, F., & Hu, Y. (2023). Theoretical Investigations on Tribological Properties of Air Foil Thrust Bearings during Start-Up Process. Lubricants, 11(3), 94. https://doi.org/10.3390/lubricants11030094





