Investigation of the Material Elasto-Plastic Response under Contact Indentation: The Effect of Indenter Material
Abstract
:1. Introduction
2. Indentation Analysis: Materials and Method
2.1. General Approach
2.2. Geometry and Boundary Conditions
- ASP 2060 PM is a tungsten-molybdenum-vanadium-cobalt speed steel made according to powder metallurgy;
- 100Cr6 is a common low-alloyed chromium steel;
- 440C is a martensitic stainless steel;
- Marval X12 is a precipitation-hardening martensitic stainless steel;
- Z15 CN17-03 is a ferritic-martensitic stainless steel, subjected to a carburising heat treatment.
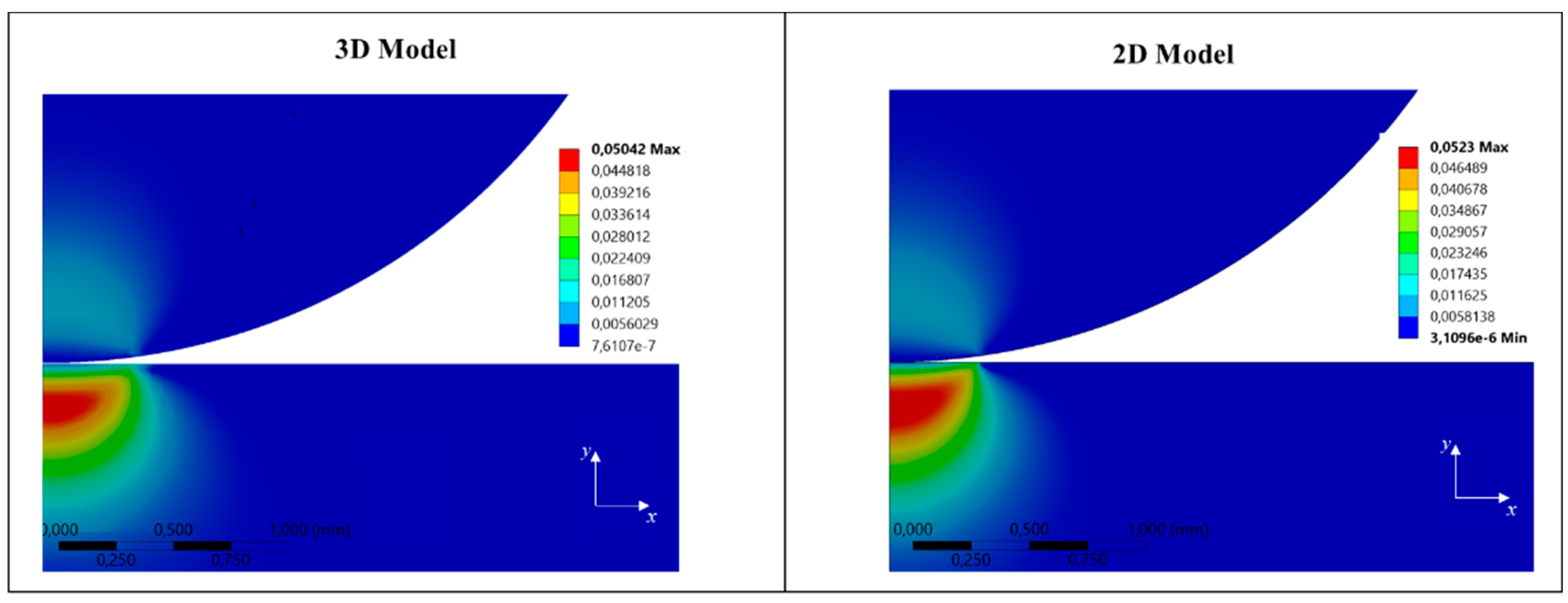
2.3. Validation of the 2D Model
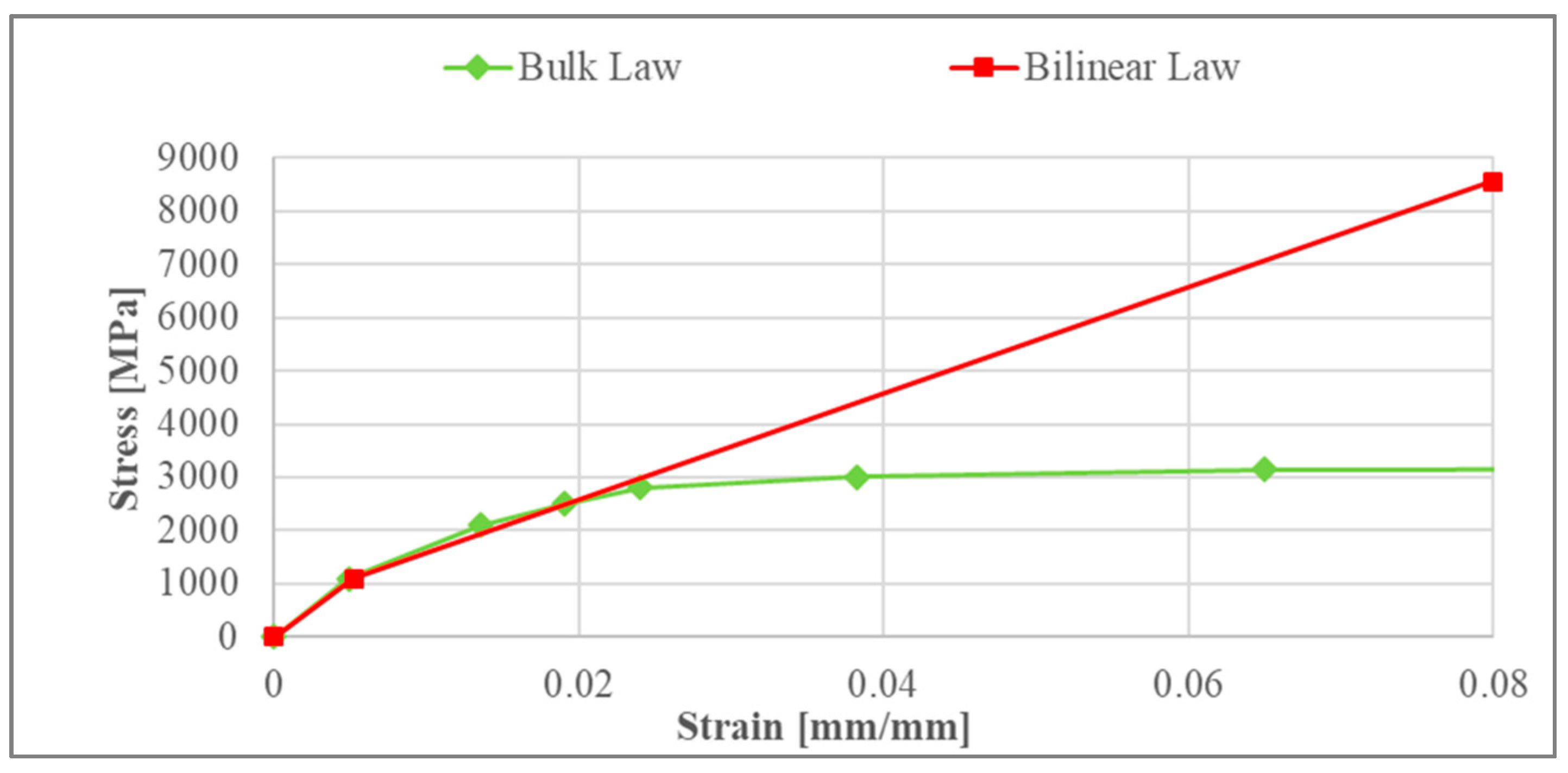
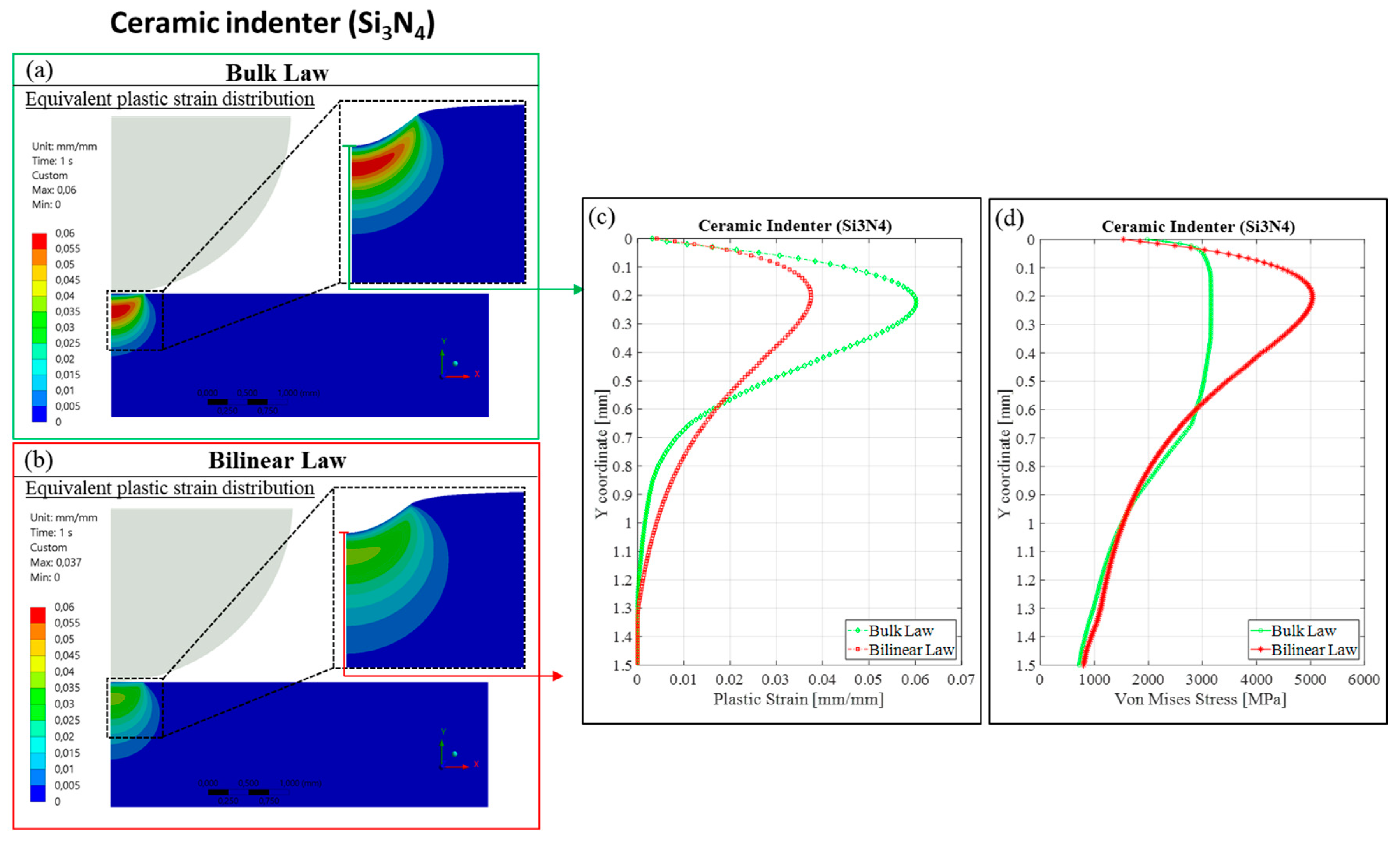
2.4. Elasto-Plastic Bulk Law vs. Experimental Indentation with Ceramic Indenter
3. Bilinear Material Law for Ceramic on Steel Indentation
3.1. Parametrical Analysis
3.1.1. Influence of the Elastic Modulus
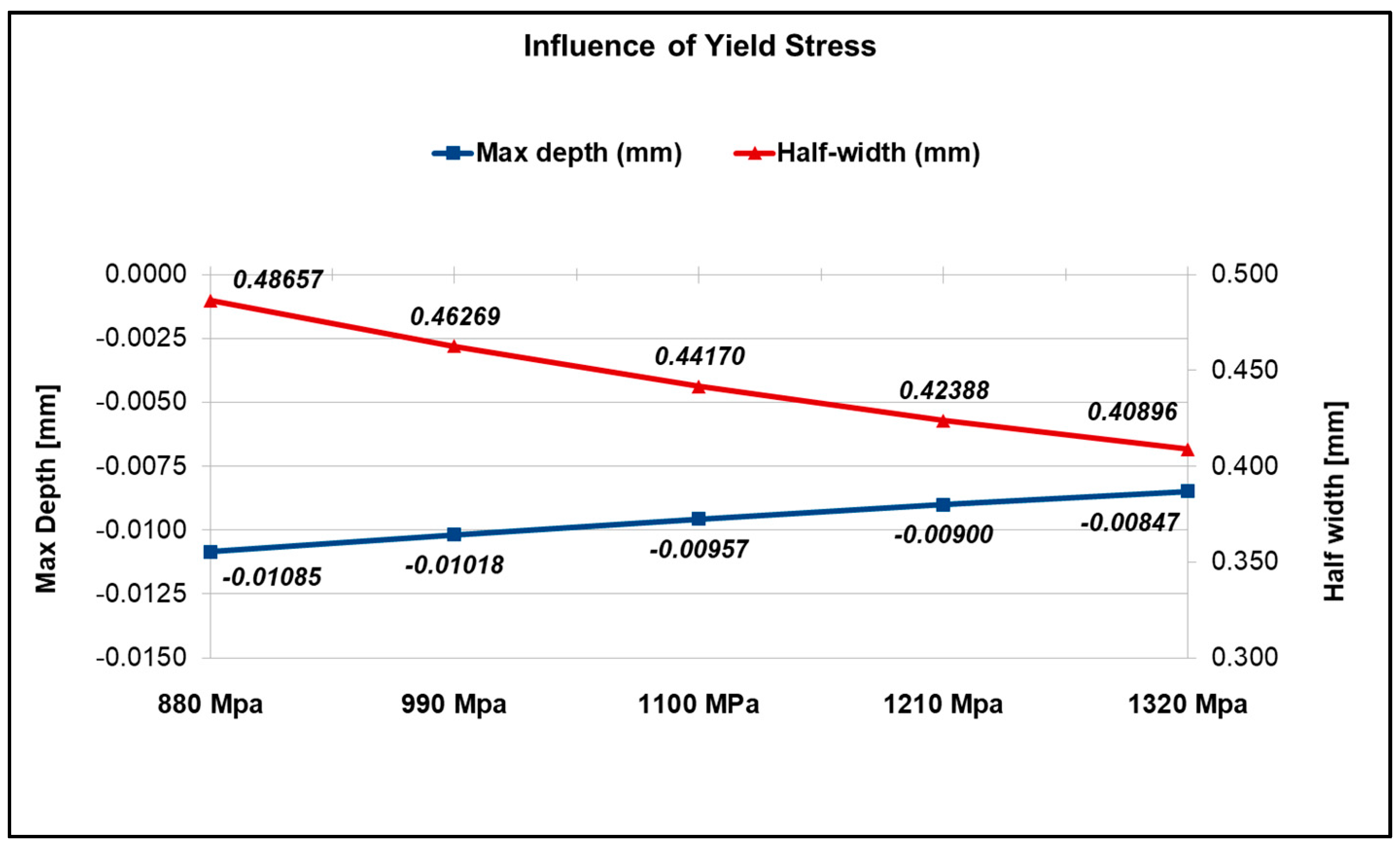
3.1.2. Influence of the Yield Stress
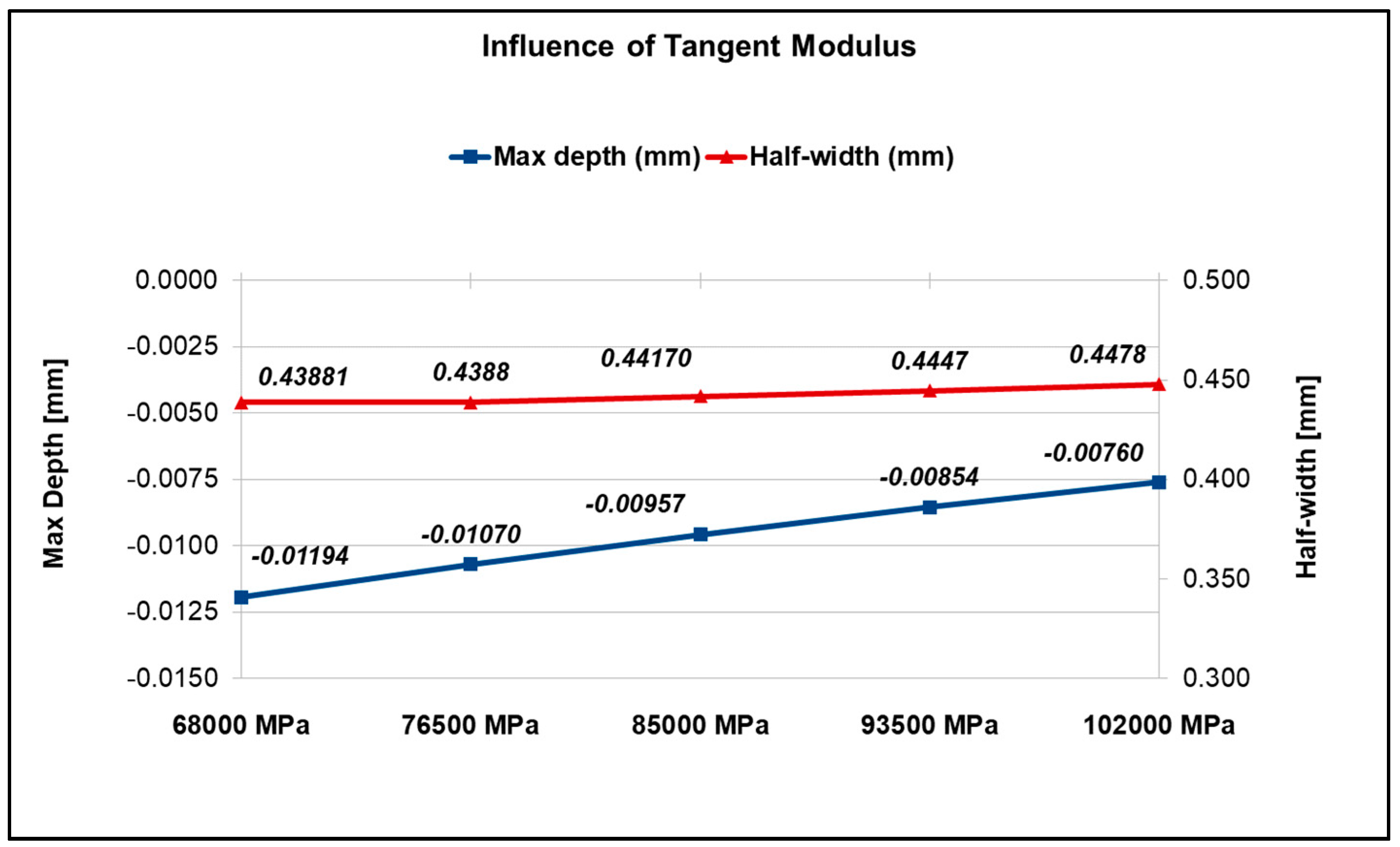
3.1.3. Influence of the Tangent Modulus
3.2. Bilinear Material Laws Identification
4. Effect of the Indenter Material
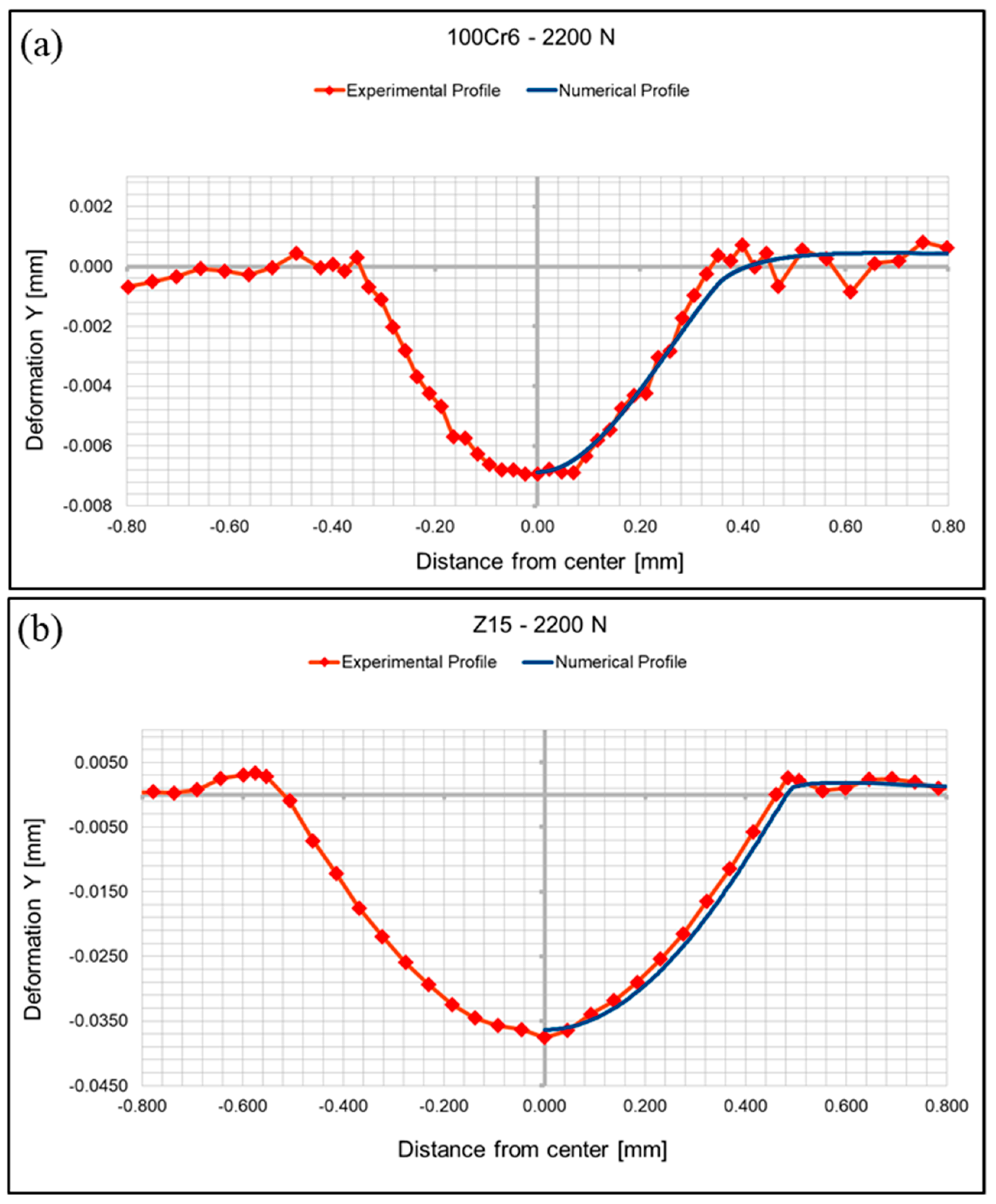
4.1. Ceramic on Steel Indentation Tests
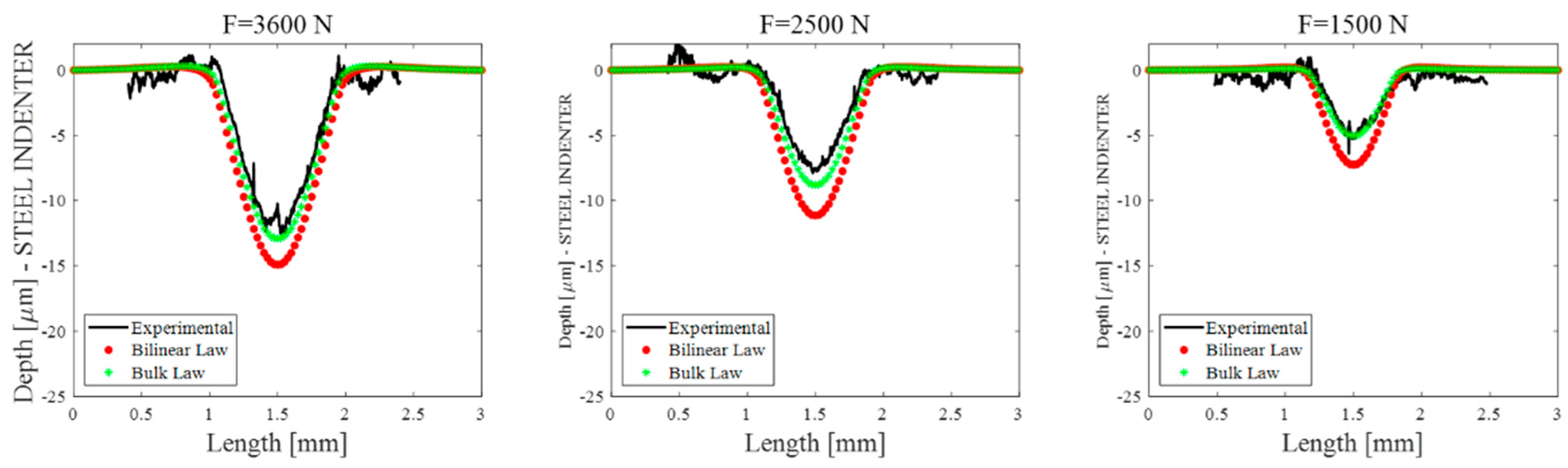
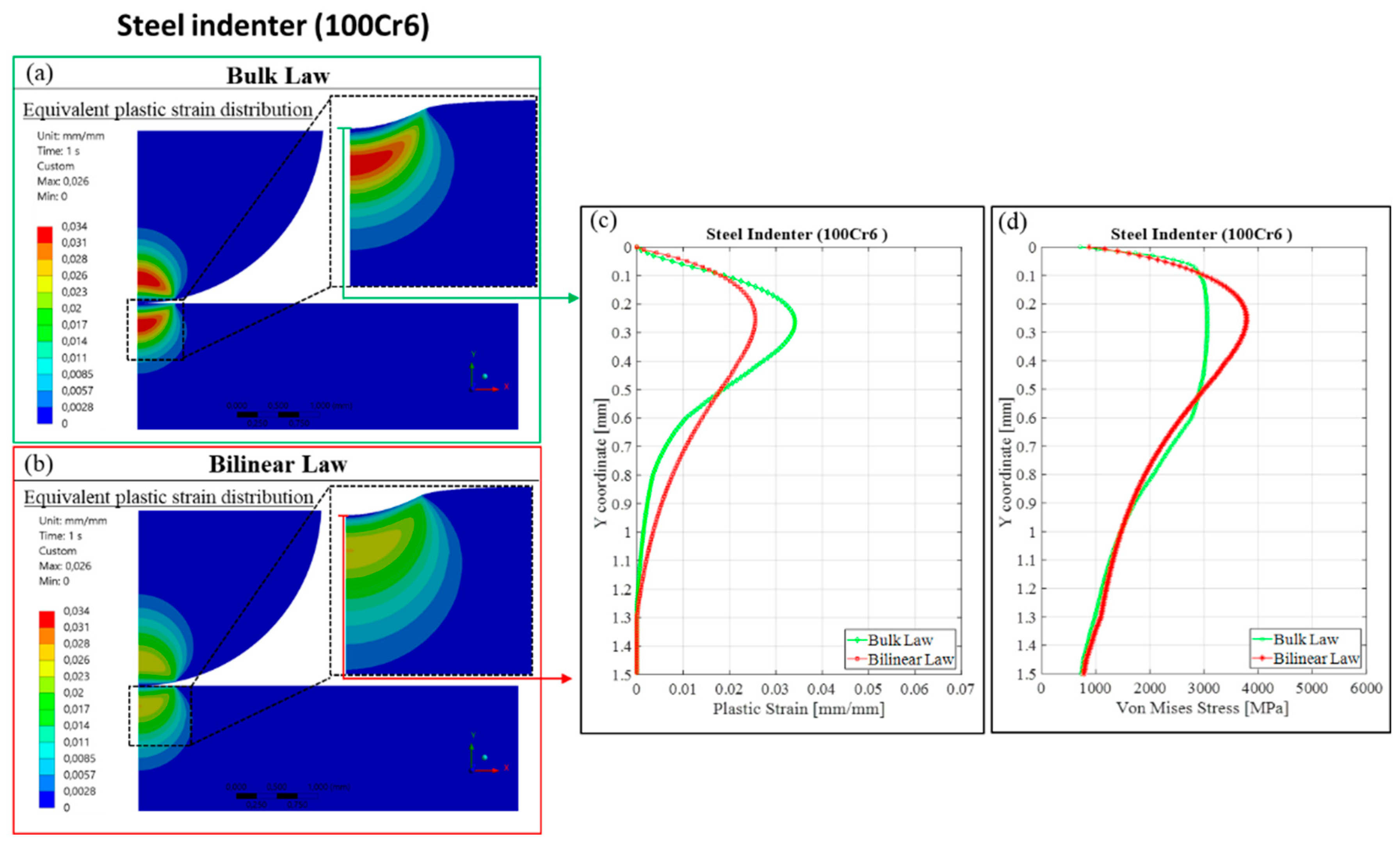
4.2. Steel-on-Steel Indentation Tests
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nejad, R.M.; Shariati, M.; Farhangdoost, K. Effect of wear on rolling contact fatigue crack growth in rails. Tribol. Int. 2016, 94, 118–125. [Google Scholar] [CrossRef]
- Daves, W.; Kubin, W.; Scheriau, S.; Pletz, M. A finite element model to simulate the physical mechanisms of wear and crack initiation in wheel/rail contact. Wear 2016, 366, 78–83. [Google Scholar] [CrossRef]
- Piotrowski, J.; Kik, W. A simplified model of wheel/rail contact mechanics for non-Hertzian problems and its application in rail vehicle dynamic simulations. Veh. Syst. Dyn. 2008, 46, 27–48. [Google Scholar] [CrossRef]
- Duan, F.; Pozzolini, C.; Saulot, A.; Berthier, Y. An improved 2D fem model for straight track corrugation using the mass redistribution method. Mech. Ind. 2017, 18, 310. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Mo, J.; Zhang, L. Nonlinear behaviors of the disc brake system under the effect of wheel−rail adhesion. Tribol. Int. 2021, 165, 107263. [Google Scholar] [CrossRef]
- Mann, R.; Magnier, V.; Brunel, J.; Dufrénoy, P.; Henrion, M.; Guillet-Revol, E. Thermomechanical characterization of high-speed train braking materials to improve models: Numerical validation via a comparison with an experimental braking test. Tribol. Int. 2020, 156, 106818. [Google Scholar] [CrossRef]
- Muflikhun, M.A.; Adyudya, M.; Rahman, N.F.; Sentanuhady, J.; Raghu, S.N.V. Comprehensive analysis and economic study of railway brake failure from metal-based and composites-based materials. Forces Mech. 2023, 12, 100223. [Google Scholar] [CrossRef]
- Hou, X.; Fang, Z.; Zhang, X. Static contact analysis of spiral bevel gear based on modified VFIFE (vector form intrinsic finite element) method. Appl. Math. Model. 2018, 60, 192–207. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, H.; Bai, H.; Zhu, C.; Wu, W. Ratchetting–multiaxial fatigue damage analysis in gear rolling contact considering tooth surface roughness. Wear 2019, 428, 137–146. [Google Scholar] [CrossRef]
- Bai, Z.; Ning, Z. Dynamic Responses of the Planetary Gear Mechanism Considering Dynamic Wear Effects. Lubricants 2023, 11, 255. [Google Scholar] [CrossRef]
- Hu, R.; Zhang, M.; Xiang, Z.; Mo, J. Guided deep subdomain adaptation network for fault diagnosis of different types of rolling bearings. J. Intell. Manuf. 2023, 34, 2225–2240. [Google Scholar] [CrossRef]
- Cavacece, F.; Frache, L.; Tonazzi, D.; Bouscharain, N.; Philippon, D.; Le Jeune, G.; Maheo, Y.; Massi, F. Roller bearing under high loaded oscillations: Life evolution and accommodation mechanisms. Tribol. Int. 2020, 147, 106278. [Google Scholar] [CrossRef]
- Ghezzi, I.; Komba, E.W.H.; Tonazzi, D.; Bouscharain, N.; Le Jeune, G.; Coudert, J.-B.; Massi, F. Damage evolution and contact surfaces analysis of high-loaded oscillating hybrid bearings. Wear 2018, 406, 1–12. [Google Scholar] [CrossRef]
- Strubel, V.; Fillot, N.; Ville, F.; Cavoret, J.; Vergne, P.; Mondelin, A.; Maheo, Y. Particle Entrapment in Rolling Element Bearings: The Effect of Ellipticity, Nature of Materials, and Sliding. Tribol. Trans. 2017, 60, 373–382. [Google Scholar] [CrossRef]
- Kerrigan, A.; Mondelin, A.; Coudert, J.B.; Sherif, M.Y.; Mahéo, Y. Temperature-resistant, corrosion-tolerant carburizing bearing steel for aero-engine applications. In Proceedings of the 12th Symposium on Bearing Steel Technologies: Progress in Bearing Steel Metallurgical Testing and Quality Assurance, Denver, CO, USA, 15–17 May 2019; ASTM Special Technical Publication: West Conshohocken, PA, USA, 2020; Volume STP 1623, pp. 403–420. [Google Scholar] [CrossRef]
- Warhadpande, A.; Sadeghi, F.; Kotzalas, M.N.; Doll, G. Effects of plasticity on subsurface initiated spalling in rolling contact fatigue. Int. J. Fatigue 2012, 36, 80–95. [Google Scholar] [CrossRef]
- Tonazzi, D.; Komba, E.H.; Massi, F.; Le Jeune, G.; Coudert, J.; Maheo, Y.; Berthier, Y. Numerical analysis of contact stress and strain distributions for greased and ungreased high loaded oscillating bearings. Wear 2017, 376, 1164–1175. [Google Scholar] [CrossRef]
- Chaise, T.; Nélias, D. Contact Pressure and Residual Strain in 3D Elasto-Plastic Rolling Contact for a Circular or Elliptical Point Contact. J. Tribol. 2011, 133, 041402. [Google Scholar] [CrossRef]
- Komba, E.H.; Massi, F.; Bouscharain, N.; Le Jeune, G.; Berthier, Y.; Maheo, Y. Experimental damage analysis in high loaded oscillating bearings. Tribol. Int. 2016, 102, 507–515. [Google Scholar] [CrossRef]
- Jacobs, W.; Van Hooreweder, B.; Boonen, R.; Sas, P.; Moens, D. The influence of external dynamic loads on the lifetime of rolling element bearings: Experimental analysis of the lubricant film and surface wear. Mech. Syst. Signal Process. 2016, 74, 144–164. [Google Scholar] [CrossRef]
- Raje, N.; Sadeghi, F.; Rateick, R.G. A Statistical Damage Mechanics Model for Subsurface Initiated Spalling in Rolling Contacts. J. Tribol. 2008, 130, 042201. [Google Scholar] [CrossRef]
- Wang, D.; de Boer, G.; Neville, A.; Ghanbarzadeh, A. A Review on Modelling of Viscoelastic Contact Problems. Lubricants 2022, 10, 358. [Google Scholar] [CrossRef]
- Zhao, J.; Fu, P.; Zhang, X.; Zhou, L.; Wang, P.; Kan, Q. An effective method for calculating elasto-plastic contact pressure and contact patch size under elliptical, circular and line contact conditions. Appl. Math. Model. 2021, 95, 541–574. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Li, L.-Y.; Thornton, C. Rebound behaviour of spheres for plastic impacts. Int. J. Impact Eng. 2003, 28, 929–946. [Google Scholar] [CrossRef]
- Albahrani, S.M.B.; Alves, J.T.; Duval, A.; Chaise, T.; De Vaujany, J.-P.; Guingand, M. Modelling of elastoplastic, multi-scale and multi-contact problems: Application to worm gears. Mech. Ind. 2022, 23, 6. [Google Scholar] [CrossRef]
- Pei, L.; Hyun, S.; Molinari, J.; Robbins, M.O. Finite element modeling of elasto-plastic contact between rough surfaces. J. Mech. Phys. Solids 2005, 53, 2385–2409. [Google Scholar] [CrossRef]
- Eumelen, G.; Suiker, A.; Bosco, E.; Fleck, N. Analytical model for elasto-plastic indentation of a hemispherical surface inclusion. Int. J. Mech. Sci. 2022, 224, 107267. [Google Scholar] [CrossRef]
- Jacq, C.; Ne´lias, D.; Lormand, G.; Girodin, D. Development of a Three-Dimensional Semi-Analytical Elastic-Plastic Contact Code. J. Tribol. 2002, 124, 653–667. [Google Scholar] [CrossRef]
- Papangelo, A.M. Ciavarella, Viscoelastic dissipation in repeated normal indentation of an Hertzian profile. Int. J. Solids Struct. 2022, 236, 111362. [Google Scholar] [CrossRef]
- Lyashenko, I.A.; Popov, V.L.; Borysiuk, V. Experimental Verification of the Boundary Element Method for Adhesive Contacts of a Coated Elastic Half-Space. Lubricants 2023, 11, 84. [Google Scholar] [CrossRef]
- Lacroix, S.; Nélias, D.; Leblanc, A. Experimental Study of Four-Point Contact Ball Bearing with Deformable Rings. Tribol. Trans. 2015, 58, 963–970. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Brizmer, V.; Kligerman, Y.; Etsion, I. Elastic–plastic spherical contact under combined normal and tangential loading in full stick. Tribol. Lett. 2007, 25, 61–70. [Google Scholar] [CrossRef]
- Tonazzi, D.; Passafiume, M.; Papangelo, A.; Hoffmann, N.; Massi, F. Numerical and experimental analysis of the bi-stable state for frictional continuous system. Nonlinear Dyn. 2020, 102, 1361–1374. [Google Scholar] [CrossRef]
- Meyer, K.A.; Skrypnyk, R.; Pletz, M. Efficient 3d finite element modeling of cyclic elasto-plastic rolling contact. Tribol. Int. 2021, 161, 107053. [Google Scholar] [CrossRef]
- Lai, V.V.; Anciant, M.; Chiello, O.; Brunel, J.F.; Dufrenoy, P. Dufrénoy, A nonlinear FE model for wheel/rail curve squeal in the time-domain including acoustic predictions. Appl. Acoust. 2021, 179, 108031. [Google Scholar] [CrossRef]
- Li, Y.P.; Onodera, E.; Matsumoto, H.; Chiba, A. Correcting the Stress-Strain Curve in Hot Compression Process to High Strain Level. Met. Mater. Trans. A 2009, 40, 982–990. [Google Scholar] [CrossRef]
- Juliá, J.M.; Rodríguez-Tembleque, L. Wear and Subsurface Stress Evolution in a Half-Space under Cyclic Flat-Punch Indentation. Lubricants 2023, 11, 265. [Google Scholar] [CrossRef]
- Bonfanti, A.; Fouchard, J.; Khalilgharibi, N.; Charras, G.; Kabla, A. A unified rheological model for cells and cellularised materials. R. Soc. Open Sci. 2020, 7, 190920. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, M.; Huang, J.; Sun, M.; Zhao, X.; Zhao, Q. Robotic Micropipette Aspiration for Multiple Cells. Micromachines 2019, 10, 348. [Google Scholar] [CrossRef]
- Magazzù, A.; Marcuello, C. Investigation of Soft Matter Nanomechanics by Atomic Force Microscopy and Optical Tweezers: A Comprehensive Review. Nanomaterials 2023, 13, 963. [Google Scholar] [CrossRef]
- Lostao, A.; Lim, K.; Pallarés, M.C.; Ptak, A.; Marcuello, C. Recent advances in sensing the inter-biomolecular interactions at the nanoscale—A comprehensive review of AFM-based force spectroscopy. Int. J. Biol. Macromol. 2023, 238, 124089. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, M.U.; A Khan, Z.; Kruhoeffer, W.; Blass, T. A 3D Finite Element Model of Rolling Contact Fatigue for Evolved Material Response and Residual Stress Estimation. Tribol. Lett. 2020, 68, 122. [Google Scholar] [CrossRef]





| ASP 2060 | 100Cr6 | 440C | Marval X12 | Z15 | |
|---|---|---|---|---|---|
| Elastic Modulus [GPa] | 250 | 210 | 200 | 195 | 215 |
| Ultimate Tensile Stress [MPa] | 4300 | 3100 | 1965 | 1430 | 1410 |
| Yield Tensile Stress [MPa] | 3800 | 1034 | 1865 | 1385 | 1200 |
| Elongation [%] | - | 5 | 4 | 10.5 | 16 |
| Hardness [HRC] | 67 | 60–66 | 58 | 31 | 46 |
| Experimental Depth (SD) [μm] | Numerical Depth [μm] | Relative Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2200 N | 500 N | 150 N | 2200 N | 500 N | 150 N | 2200 N | 500 N | 150 N | |
| 100Cr6 | 7.34 (1.93) | 1.97 (0.27) | 7.34 (1.93) | 11.40 | 1.92 | - | 35 | 2.5 | - |
| 440C | 14.23 (0.52) | 3.90 (0.50) | 14.23 (0.52) | 17.24 | 2.70 | 0.29 | 21 | −30 | −89 |
| Marval | 28.55 (0.58) | 7.88 (1.79) | 28.55 (0.58) | 25.25 | 4.29 | 0.95 | −12 | −37 | −75 |
| Z15 | 38.00 (1.17) | 8.86 (0.34) | 38.00 (1.17) | 27.49 | 5.71 | 1.30 | −28 | −36 | −70 |
| ASP2060 | 100Cr6 | 400C | MarvalX12 | Z15 | |
|---|---|---|---|---|---|
| E (GPa) | 250 | 210 | 200 | 195 | 215 |
| σy (MPa) | 1922 | 1100 | 955 | 810 | 797 |
| Et (GPa) | 91.4 | 99.4 | 57.4 | 16.5 | 7.1 |
| Experimental Depth (SD) [μm] | Numerical Depth [μm] | Relative Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2200 N | 500 N | 150 N | 2200 N | 500 N | 150 N | 2200 N | 500 N | 150 N | |
| ASP 2060 | 6.29 (0.85) | 1.23 (0.47) | 0.95 (0.04) | 6.41 | 1.20 | 0.17 | 2 | −2 | −82 |
| 100Cr6 | 7.34 (1.93) | 1.97 (0.27) | ----- | 7.65 | 1.92 | ----- | 4 | −2 | ----- |
| 440C | 14.23 (0.52) | 3.90 (0.50) | 2.73 (0.15) | 14.68 | 3.77 | 1.06 | 3 | −3 | −61 |
| Marval | 28.55 (0.58) | 7.88 (1.79) | 4.12 (0.58) | 29.88 | 7.55 | 2.18 | 4.6 | −4 | −47 |
| Z15 | 38.00 (1.17) | 8.86 (0.34) | 4.40 (1.97) | 36.37 | 8.88 | 2.56 | −4 | 0.2 | −58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tonazzi, D.; Piva, F.; Mondelin, A.; Le Jeune, G.; Mahéo, Y.; Massi, F. Investigation of the Material Elasto-Plastic Response under Contact Indentation: The Effect of Indenter Material. Lubricants 2023, 11, 438. https://doi.org/10.3390/lubricants11100438
Tonazzi D, Piva F, Mondelin A, Le Jeune G, Mahéo Y, Massi F. Investigation of the Material Elasto-Plastic Response under Contact Indentation: The Effect of Indenter Material. Lubricants. 2023; 11(10):438. https://doi.org/10.3390/lubricants11100438
Chicago/Turabian StyleTonazzi, Davide, Francesco Piva, Alexandre Mondelin, Gwenolè Le Jeune, Yves Mahéo, and Francesco Massi. 2023. "Investigation of the Material Elasto-Plastic Response under Contact Indentation: The Effect of Indenter Material" Lubricants 11, no. 10: 438. https://doi.org/10.3390/lubricants11100438
APA StyleTonazzi, D., Piva, F., Mondelin, A., Le Jeune, G., Mahéo, Y., & Massi, F. (2023). Investigation of the Material Elasto-Plastic Response under Contact Indentation: The Effect of Indenter Material. Lubricants, 11(10), 438. https://doi.org/10.3390/lubricants11100438






