Research on the Effect of Spindle Speed on the Softening and Hardening Characteristics of the Axial Operating Stiffness of Machine Tool Spindle
Abstract
:1. Introduction
2. Axial Operating Stiffness Model of Spindle
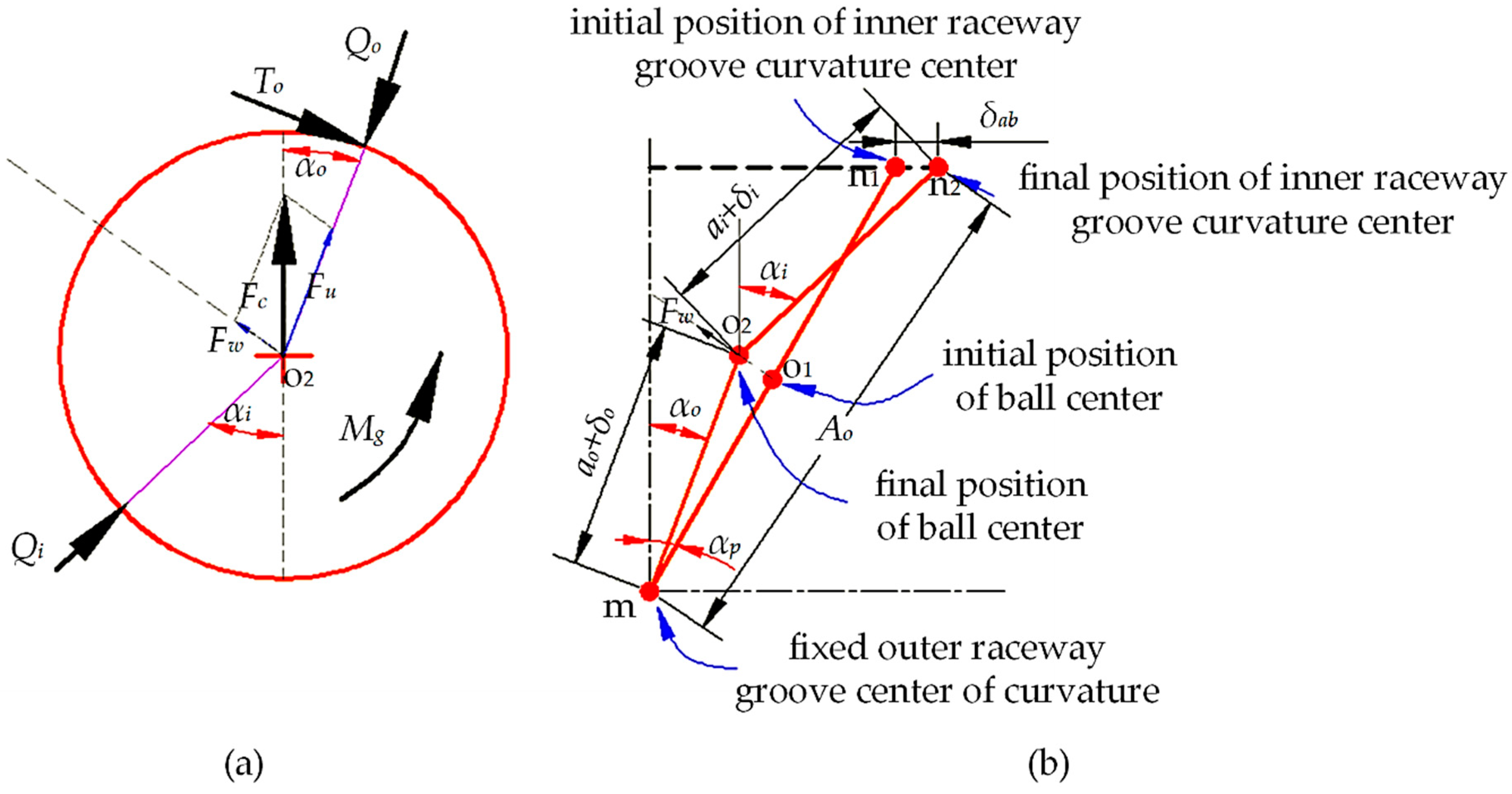
2.1. Bearing Mechanics Model
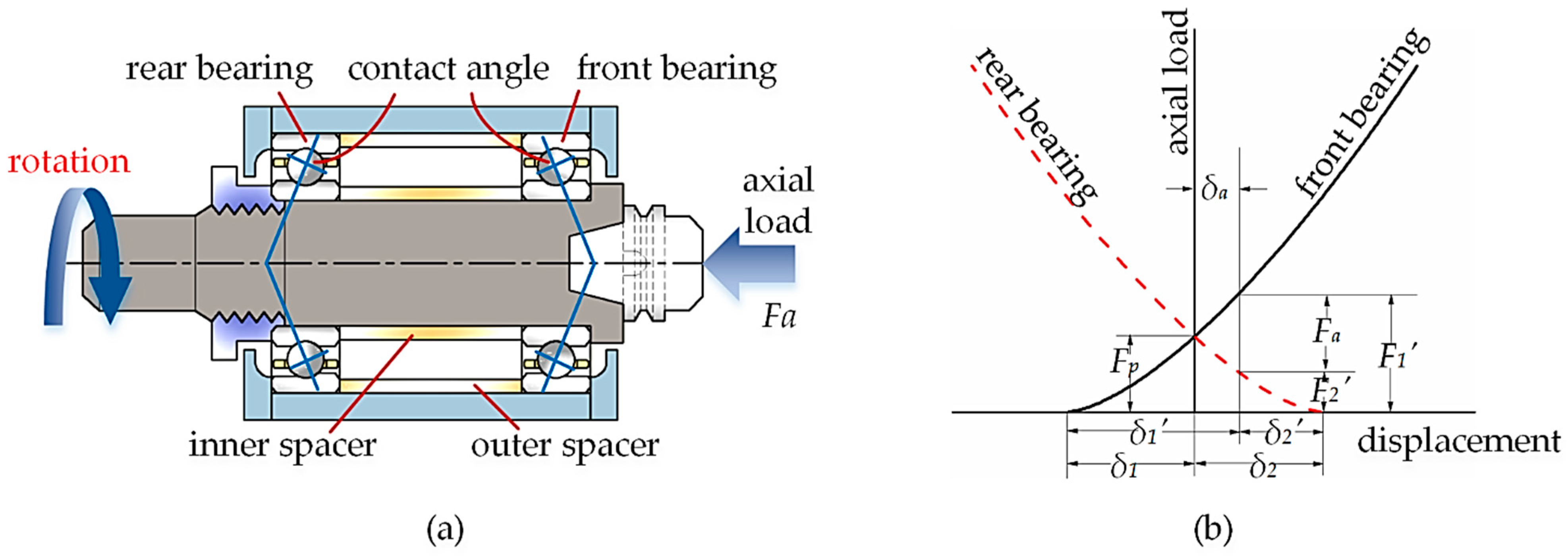
2.2. Spindle Axial Operating Stiffness Model
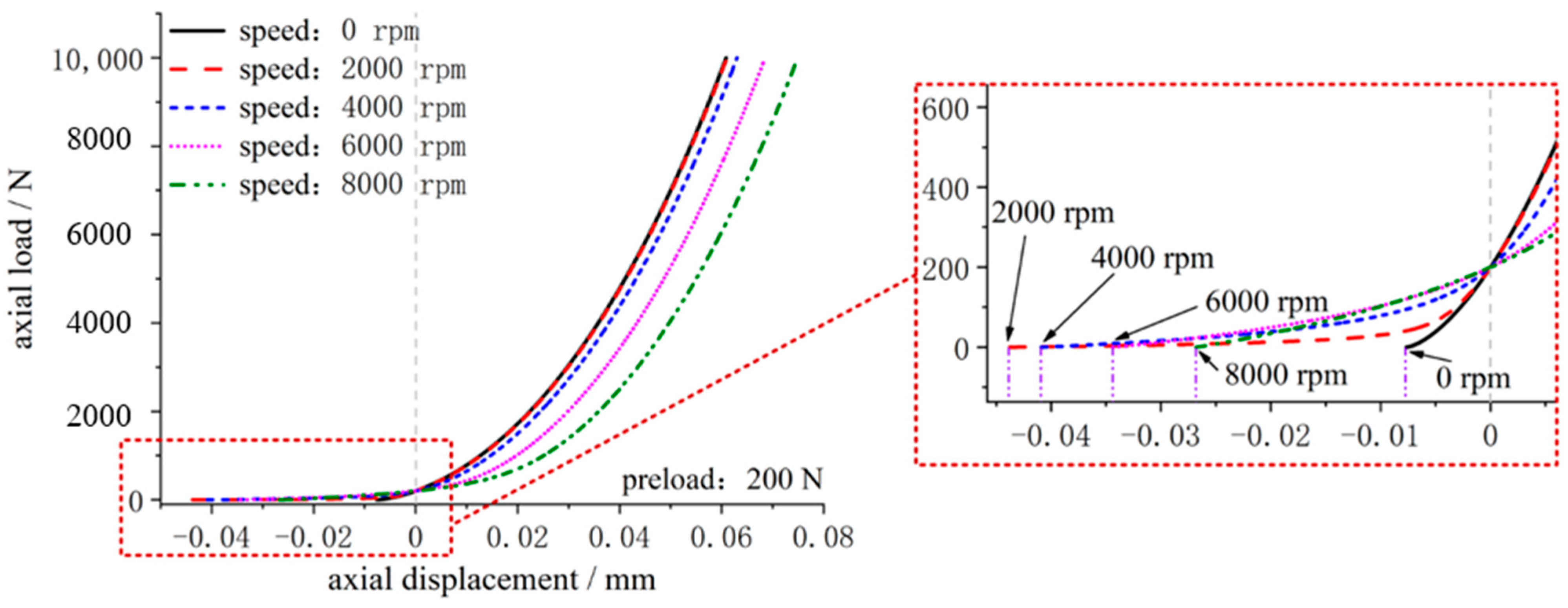
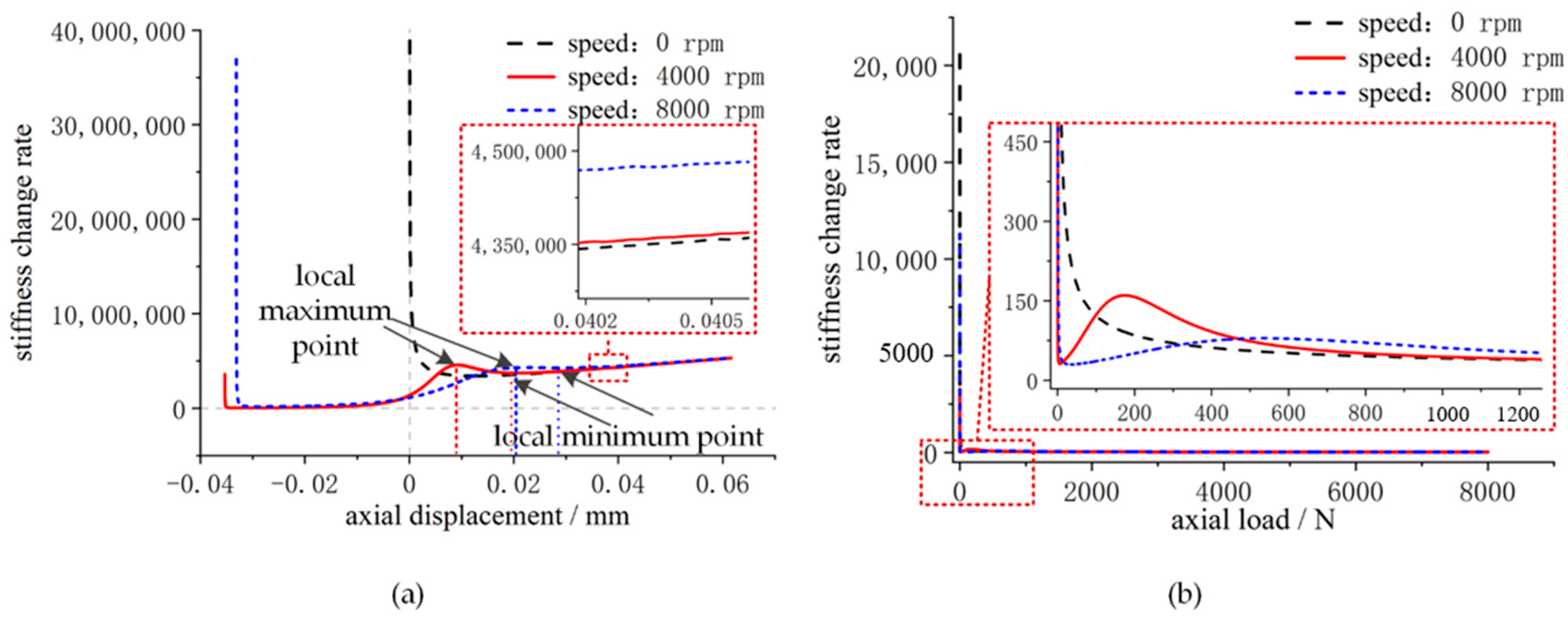
3. Effect of Spindle Speed on Spindle Axial Operating Stiffness
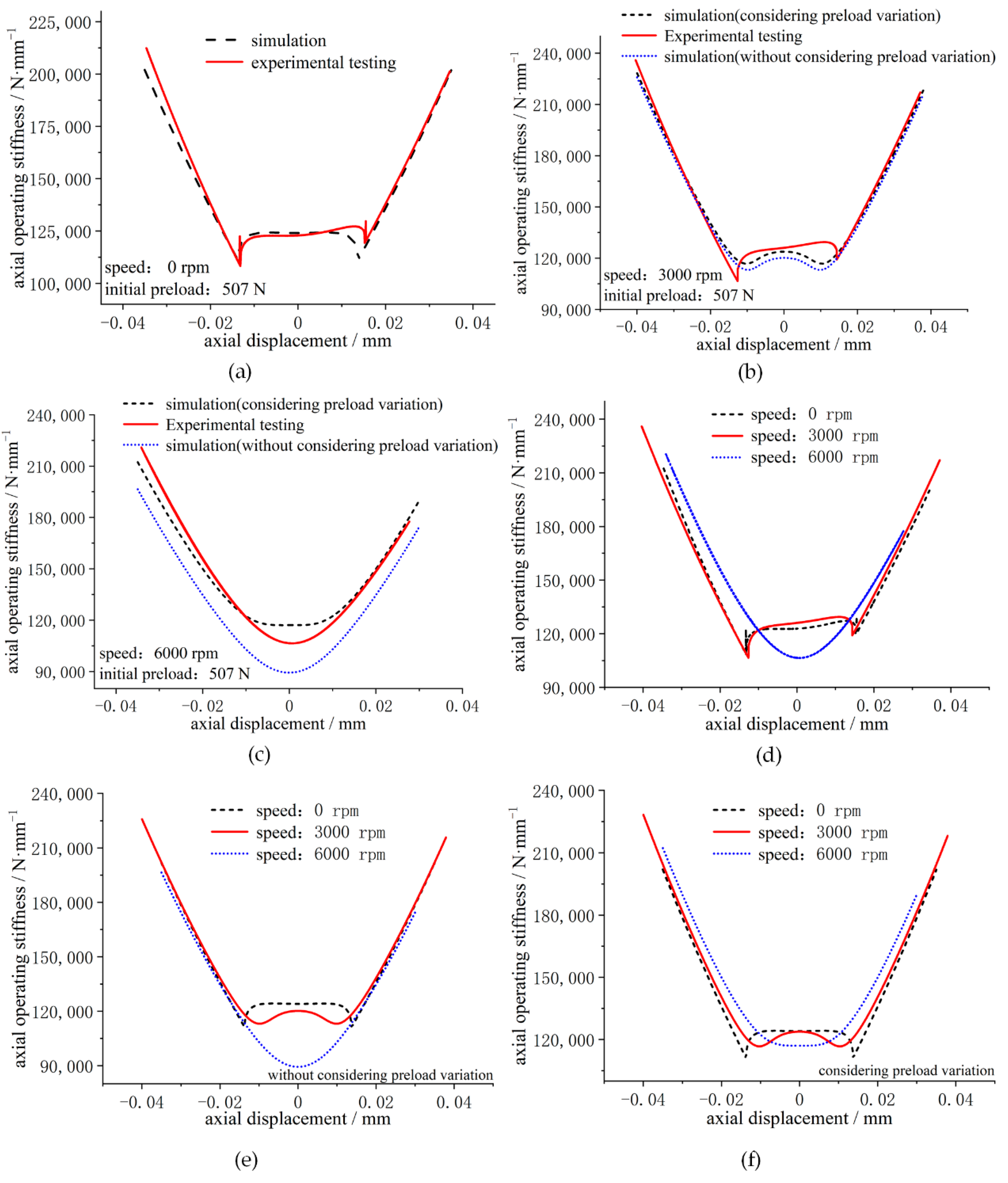
4. Experimental Verification
5. Conclusions
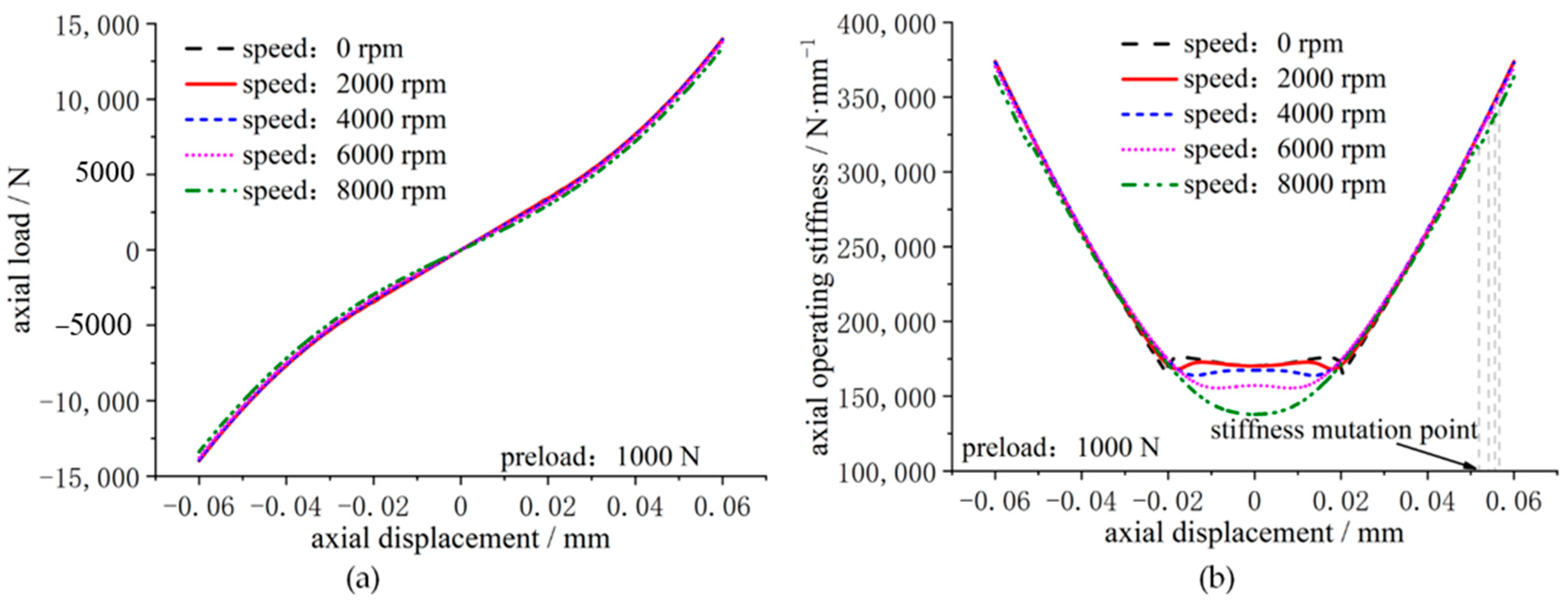
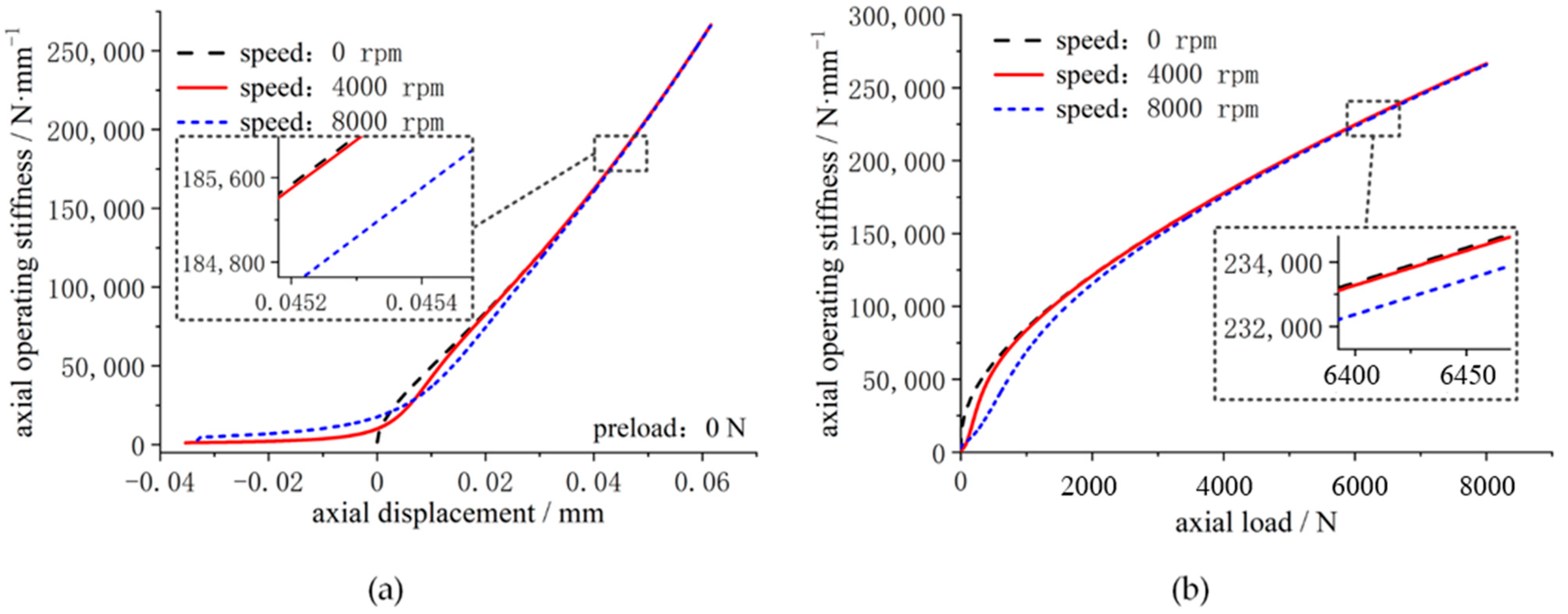
- For the fixed-position preload spindle with a smaller initial preload, the rotational speed has a greater influence on the load–displacement relationship and axial operating stiffness. However, the spindle speed has less effect on the load–displacement relationship and axial operating stiffness when the spindle’s initial preload is greater.
- When the spindle is rotated, the axial displacement at the stiffness mutation point is greater than the axial displacement at zero speed. In the meantime, when the rotational speed increases, the axial displacement of the spindle’s axial operating stiffness mutation point decreases.
- When the spindle is rotating slowly, the axial stiffness of the spindle fluctuates in the phase with small displacement increments. However, as the spindle speeds up, the stiffness fluctuation is gradually suppressed. When the spindle is operating at high speeds, the spindle axial stiffness displays a clear “sag” phenomenon, which shows the “stiffness hardening” characteristic.
- During the experimental test of the axial operating stiffness of the spindle, the change in spindle preload due to the speed factor has a large impact on test results and is also an important factor causing the change in spindle axial operating stiffness.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Capital Letters | |
| Fa | Axial load applied to spindle |
| Fab | Axial load applied to bearing |
| Fc | Centrifugal force |
| Fp | Preload applied to bearing |
| Z | Number of balls |
| Lowercase Letters | |
| a | Distance between the raceway groove curvature center and the ball center |
| dm | Diameter of bearing pitch circle |
| mb | Ball mass |
| n | Spindle bearing speed |
| Greek Letters | |
| αf | Initial contact angle of bearing |
| αp | Bearing contact angle with preload applied |
| αi | The ball-inner contact angle |
| αo | The ball-outer contact angle |
| δ | Ball-race deformation |
| δa | Spindle axial displacement |
| δab | Bearing axial displacement |
| δ1 | Pre-deflection of front bearing |
| δ2 | Pre-deflection of rear bearing |
| ωc | Bearing cage speed |
| Subscripts | |
| o | Outer ring |
| i | Inner ring |
References
- De Lacalle, L.L.; Lamikiz, A.; Sánchez, J.; De Bustos, I.F. Recording of Real Cutting Forces along the Milling of Complex Parts. Mechatronics 2006, 16, 21–32. [Google Scholar] [CrossRef]
- Van Luttervelt, C.; Childs, T.; Jawahir, I.; Klocke, F.; Venuvinod, P.; Altintas, Y.; Armarego, E.; Dornfeld, D.; Grabec, I.; Leopold, J.; et al. Present Situation and Future Trends in Modelling of Machining Operations Progress Report of the CIRP Working Group ‘Modelling of Machining Operations’. CIRP Ann. 1998, 47, 587–626. [Google Scholar] [CrossRef]
- Ehmann, K.; Kapoor, S.; DeVor, R.; Lazoglu, I. Machining Process Modeling: A Review. J. Manuf. Sci. Eng. Trans. ASME 1997, 119, 655–663. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Y.; Yan, K.; Yan, X.; Liu, Y.; Hong, J. Research on the Axial Stiffness Softening and Hardening Characteristics of Machine Tool Spindle System. Int. J. Adv. Manuf. Technol. 2018, 99, 951–963. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Hong, J.; Zhao, H.; Li, H. Experiment Analysis of Spindle Performance with Rolling Bearing under Non-Uniform Preload. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 3135–3146. [Google Scholar] [CrossRef]
- Hwang, Y.-K.; Lee, C.-M. A Review on the Preload Technology of the Rolling Bearing for the Spindle of Machine Tools. Int. J. Precis. Eng. Manuf. 2010, 11, 491–498. [Google Scholar] [CrossRef]
- Uriarte, L.; Herrero, A.; Zatarain, M.; Santiso, G.; de Lacalle, L.L.; Lamikiz, A.; Albizuri, J. Error Budget and Stiffness Chain Assessment in a Micromilling Machine Equipped with Tools Less than 0.3 Mm in Diameter. Precis. Eng. 2007, 31, 1–12. [Google Scholar] [CrossRef]
- Hsu, W.-Y.; Chen, J.-S. Error Analysis and Auto-Calibration for a Cartesian-Guided Tripod Machine Tool. Int. J. Adv. Manuf. Technol. 2004, 24, 899–909. [Google Scholar] [CrossRef]
- Kim, B.-S.; Ro, S.-K.; Park, J.-K. Development of a 3-Axis Desktop Milling Machine and a CNC System Using Advanced Modern Control Algorithms. Int. J. Precis. Eng. Manuf. 2010, 11, 39–47. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, B.; Wu, J.; Zhao, Q.; Wang, J. Stiffness Modeling, Identification, and Measuring of a Rotating Spindle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1239–1252. [Google Scholar] [CrossRef]
- Yan, K.; Yan, B.; Wang, Y.; Hong, J.; Zhang, J. Study on Thermal Induced Preload of Ball Bearing with Temperature Compensation Based on State Observer Approach. Int. J. Adv. Manuf. Technol. 2018, 94, 3029–3040. [Google Scholar] [CrossRef]
- Mahfoudi, F.; Boulanouar, L.; List, G. Experimental Study of the Influence of the Static Stiffness of Lathes on the Tool Wear Behaviour. Int. Rev. Mech. Eng. 2007, 1, 495–501. [Google Scholar]
- Ma, S.; Zhang, X.; Yan, K.; Zhu, Y.; Hong, J. A Study on Bearing Dynamic Features under the Condition of Multiball—Cage Collision. Lubricants 2022, 10, 9. [Google Scholar] [CrossRef]
- Cao, H.; Li, B.; Chen, X.; He, Z. Centrifugal Expansion of High-Speed Spindle and Its Influences on Bearing Dynamic Characteristics. J. Mech. Eng. 2012, 48, 59–64. [Google Scholar] [CrossRef]
- Qianjian, G.; Jianguo, Y. Application of Projection Pursuit Regression to Thermal Error Modeling of a CNC Machine Tool. Int. J. Adv. Manuf. Technol. 2011, 55, 623–629. [Google Scholar] [CrossRef]
- Matsubara, A.; Tsujimoto, S.; Kono, D. Evaluation of Dynamic Stiffness of Machine Tool Spindle by Non-Contact Excitation Tests. CIRP Ann. 2015, 64, 365–368. [Google Scholar] [CrossRef]
- Slocum, A.H. Precision Machine Design; Society of Manufacturing Engineers: Michigan, MI, USA, 1992. [Google Scholar]
- Olvera, D.; de Lacalle, L.; Compeán, F.; Fz-Valdivielso, A.; Lamikiz, A.; Campa, F. Analysis of the Tool Tip Radial Stiffness of Turn-Milling Centers. Int. J. Adv. Manuf. Technol. 2012, 60, 883–891. [Google Scholar] [CrossRef]
- Laspas, T.; Theissen, N.; Archenti, A. Novel Methodology for the Measurement and Identification for Quasi-Static Stiffness of Five-Axis Machine Tools. Precis. Eng. 2020, 65, 164–170. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Y.; Yan, K.; Hong, J.; Yan, X. An Improved Thermo-Mechanical Model for Spindle Transient Preload Analysis. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 1698–1711. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Y.; Yan, K.; Yan, X.; Hong, J. A Novel Approach for Preload Measurement and Analysis of Fixed Position Preload Spindle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 3619–3632. [Google Scholar] [CrossRef]
- Matsubara, A.; Yamazaki, T.; Ikenaga, S. Non-Contact Measurement of Spindle Stiffness by Using Magnetic Loading Device. Int. J. Mach. Tools Manuf. 2013, 71, 20–25. [Google Scholar] [CrossRef]
- Tsuneyoshi, T. Spindle Preload Measurement and Analysis. In Proceedings of the ASPE Summer Topical Meeting, State College, PA, USA, 11–12 June 2007; pp. 35–38. [Google Scholar]
- Zivkovic, A.; Zeljkovic, M.; Tabakovic, S.; Milojevic, Z. Mathematical Modeling and Experimental Testing of High-Speed Spindle Behavior. Int. J. Adv. Manuf. Technol. 2015, 77, 1071–1086. [Google Scholar] [CrossRef]
- Rabréau, C.; Noël, D.; Loch, S.L.; Ritou, M.; Furet, B. Phenomenological Model of Preloaded Spindle Behavior at High Speed. Int. J. Adv. Manuf. Technol. 2017, 90, 3643–3654. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology: Rolling Bearing Analysis, 5th ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Rolling Bearing Analysis: Essential Concepts of Bearing Technology; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Antoine, J.-F.; Abba, G.; Molinari, A. A New Proposal for Explicit Angle Calculation in Angular Contact Ball Bearing. J. Mech. Des. 2006, 128, 468–478. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, B.; Hong, J.; Zhu, Y. Effect of Preload on Ball-Raceway Contact State and Fatigue Life of Angular Contact Ball Bearing. Tribol. Int. 2017, 114, 365–372. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, B.; Zhu, Y.; Hong, J. A Comparative Study and Stiffness Analysis of Angular Contact Ball Bearings under Different Preload Mechanisms. Mech. Mach. Theory 2017, 115, 1–17. [Google Scholar] [CrossRef]




| Parameters | Values |
|---|---|
| Number of balls | 20 |
| Ball diameter | 11.906 mm |
| Bearing pitch diameter | 90 mm |
| Inner raceway groove curvature radius | 6.19112 mm |
| Outer raceway groove curvature radius | 6.19112 mm |
| Initial contact angle of bearing | 15° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, Q.; Sun, X.; Qu, J.; Qiu, A.; Kang, W.; Ma, S. Research on the Effect of Spindle Speed on the Softening and Hardening Characteristics of the Axial Operating Stiffness of Machine Tool Spindle. Lubricants 2022, 10, 132. https://doi.org/10.3390/lubricants10070132
Li J, Wang Q, Sun X, Qu J, Qiu A, Kang W, Ma S. Research on the Effect of Spindle Speed on the Softening and Hardening Characteristics of the Axial Operating Stiffness of Machine Tool Spindle. Lubricants. 2022; 10(7):132. https://doi.org/10.3390/lubricants10070132
Chicago/Turabian StyleLi, Jiandong, Qiang Wang, Xurui Sun, Jue Qu, Ang Qiu, Wei Kang, and Shuaijun Ma. 2022. "Research on the Effect of Spindle Speed on the Softening and Hardening Characteristics of the Axial Operating Stiffness of Machine Tool Spindle" Lubricants 10, no. 7: 132. https://doi.org/10.3390/lubricants10070132
APA StyleLi, J., Wang, Q., Sun, X., Qu, J., Qiu, A., Kang, W., & Ma, S. (2022). Research on the Effect of Spindle Speed on the Softening and Hardening Characteristics of the Axial Operating Stiffness of Machine Tool Spindle. Lubricants, 10(7), 132. https://doi.org/10.3390/lubricants10070132





