Abstract
The initiation of erosion and the coupled damage of erosion and corrosion on the surface of X65 pipeline steel with varying applied anodic currents were online monitored using the electrical resistance (ER) method. Results show that ER method in conjunction with anodic polarization was a highly effective approach for the investigation of the interaction effect between erosion and corrosion, which can be used to quickly and conveniently obtain the synchronously changed erosion and corrosion rates. The critical impact energy is a key parameter of sand particles to induce erosion damage on the steel surface, which can remove the flaky cementite at the edge of the pits. The threshold anodic current density that can cause a synergic effect between erosion and corrosion of X65 pipeline steel can be quantitatively fitted based on the erosion rates under varying anodic currents.
1. Introduction
The oil and gas media transported in subsea pipelines usually contain formation water, seawater and sand particles. In the presence of coexisting corrosive fluid and abrasive particles, pipeline steel suffers from coupled damage of erosion and corrosion [1,2,3,4,5,6]. According to the various material damage mechanisms, the metal loss induced by erosion–corrosion comprises a corrosion component and an erosion component, which are caused by corrosive fluid and abrasive particles, respectively [7,8,9,10]:
where is the erosion–corrosion rate, is the corrosion rate, is the erosion rate, is the pure corrosion rate, is the erosion-enhanced corrosion rate, is the pure erosion rate and is the corrosion-enhanced erosion rate. Because the corrosion current causes the generation of vacancies on the subsurface of the steel and induces hardness degradation of the surface layer, the mechanical damage caused by the impact of sand is significantly aggravated when interacting with the active dissolution process [11,12]. Moreover, both the flowing electrolyte and the solid particle impact can enhance the mass transfer process of the reactants and resultants and remove the corrosion product, leading to an increase in the corrosion rate [13,14,15]. As a result, the metal loss caused by the interaction between erosion and corrosion is much higher than the sum of the pure erosion and pure corrosion [16,17,18,19,20] rates. After erosion–corrosion occurs, the inner wall of the energy pipeline is soon consumed. Therefore, the erosion and corrosion rates are key parameters necessary to understand the synergic effect between the erosion and corrosion processes.
A combination of gravimetric measurements and electrochemical tests is normally used to decouple the erosion and the corrosion components of erosion–corrosion metal loss [3,17,21,22,23,24]. Because the erosion–corrosion rate, as well as the corrosion rate, can be measured gravimetrically and using electrochemical methods, respectively, the erosion rate can be easily calculated according to the difference between the erosion–corrosion rate and the corrosion rate [11,25]. When conducting a weight loss measurement on a coupon, only the accumulated erosion–corrosion metal loss can be obtained. However, the study of the synergy of erosion–corrosion should be based on a number of synchronously varied erosion and corrosion rate results [2,11]. As a result, exploration of the dynamic progression of erosion–corrosion under varied flow conditions requires considerable coupon consumption. The electrical resistance (ER) method is a suitable substitute for gravimetric measurements, as the thickness loss rate induced by erosion–corrosion can be sensitively probed on the basis of the change in ERs [16,26,27,28,29,30]. Recently, a novel erosion–corrosion sensor was proposed, combining the electrical resistance method (ER) and electrochemical measurements for online monitoring of erosion–corrosion of pipeline steel [16,26]. With the application of the ER method in conjunction with linear polarization resistance (LPR) or electrochemical impedance spectroscopy (EIS), both the erosion rate and the in situ corrosion rate can be online decoupled from the erosion–corrosion rate [16,26,30]. Thereafter, the interaction of erosion and corrosion can be dynamically investigated by decoupling the erosion and corrosion components.
In this work, a new method combining microelectrical resistance measurement and anodic polarization tests was adopted to study the dynamic progression of erosion–corrosion of pipeline steel with varying applied anodic currents under various flow velocities. Both the erosion rate and corrosion rate can be online monitored using ER and electrochemical methods. Combined with surface morphology observations, both the critical impact energy, which can induce the initiation of erosion, and the threshold anodic current density, which can have a chemomechanical effect on erosion–corrosion, are analyzed herein.
2. Materials and Methods
2.1. The Sensor System and Measurement Principle
An erosion–corrosion sensor that integrates the functions of ER measurement and an electrochemical test was established as shown in Figure 1. The erosion–corrosion sensor consists of two identical electronic coupons with dimensions of 80 mm × 5 mm × 3 mm, as plotted in Figure 1a, which act as the temperature compensation element and the sensitive element, respectively. The temperature compensation element is completely covered by an epoxy resin layer (Caster, Shenzhen Huasheng Tongchuang Technology Co., Ltd., Shenzhen, China) comprising C2H3O-[C18H20O3]C15H14O2-C2H3 with R-C2H3O as a dilution agent, whereas the sensitive element is partially covered so that a 30 mm long bare area can be left in the middle of the working surface. The measurement circuit of the erosion–corrosion sensor is plotted in Figure 1b. The measurement system is composed of an erosion–corrosion sensor, a reference 600 + electrochemical workstation (Gamry, Warminster, PA, USA), a micro-resistance meter (RM 3545, Hioki), a reference electrode (RE), a counter electrode (CE) and two auto switches (Switch 1 and Switch 2).
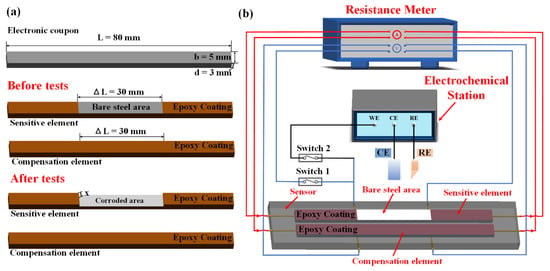
Figure 1.
Schematic diagram of the erosion–corrosion sensor: (a) three-dimensional diagram of the sensitive element and the compensation element, and (b) the measurement circuit.
When switch 1 is on and switch 2 is off, the ERs of the sensitive element and the temperature element can be online probed by the micro-resistance meter. During the erosion–corrosion experiments, the bare steel area was immersed into the test solution and suffered erosion–corrosion damage. Thereafter, the erosion–corrosion depth (x) of the sensitive element can be expressed as Equation (2):
where d is the thickness of the sensitive element, and and are the online measured resistances of the temperature compensation element and sensitive element, respectively. The erosion–corrosion rate () can be calculated using Equation (3):
When switch 1 is off and switch 2 is on, the sensitive element can be connected to the electrochemical workstation. A three-electrode system comprising a sensitive element, RE and CE can be established. Therefore, galvanostatic polarization can be conducted on the sensitive element. In order to investigate the erosion–corrosion of X65 steel under varying anodic currents, anodic currents in the range of 1~6 mA/cm2 were applied to the sensitive element. Accordingly, the corrosion rate ( of the sensitive element was approximately evaluated according to the applied current density:
where is the corrosion rate (mm/y), i is the applied current density, M is the molecular weight of iron, m is the number of transferred electrons, F is the Faradic constant and ρ is the steel density (7.8 g/cm3). Thereafter, the erosion rate () can be obtained online based on the difference between and .
2.2. Test Setup and Materials
A cylindrical stirring electrolytic cell as shown in Figure 2a was employed for erosion–corrosion tests in this study. The diameter and height of the test cell were 100 mm and 200 mm, respectively. A four-blade propeller was used to stir the solution with a diameter of 70 mm and a thickness of 20 mm. The distance between the bottom of the electrolytic cell and the propeller was 30 mm. The rotation speed of the propeller could be adjusted from 0–3000 rpm through a frequency conversion motor. A detailed schematic representation of the erosion–corrosion sensor is shown in Figure 2b. When conducting erosion–corrosion experiment, the erosion–corrosion sensor was fixed on the wall of the electrolytic cell with the bare steel area at the same height as the propeller. The surface of the bare steel area was flush with the wall of the cell. The gap between the erosion–corrosion sensor and the wall of the cell was sealed by hot melt glue. The sensitive element and the temperature compensation element were both made of X65 pipeline steel, the chemical compositions of which is (mass%): 0.12 C, 1.27 Mn, 0.18 Si, 0.008 P, 0.002 S, 0.17 Mo, 0.11 Cr, 0.12 Cu, 0.07 Ni, 0.022 Al and Fe balance. Copper wires were soldered on the back sides of the electrodes using copper foil tape to keep electrical connection with the resistance meter and the electrochemical workstation. The surfaces of the sensitive element and the temperature compensation element were successively grounded using 400–1000 abrasive papers before the tests. Then, the polished surfaces were washed with acetone and rinsed with distilled water. An Ag/AgCl electrode and a titanium mesh were used as RE and CE, respectively. The 3.5% NaCl solution entraining 10% silica sand particles by weight was used as test medium. The shape of the sand particles is shown in Figure 2c, with an average diameter of 600 μm.
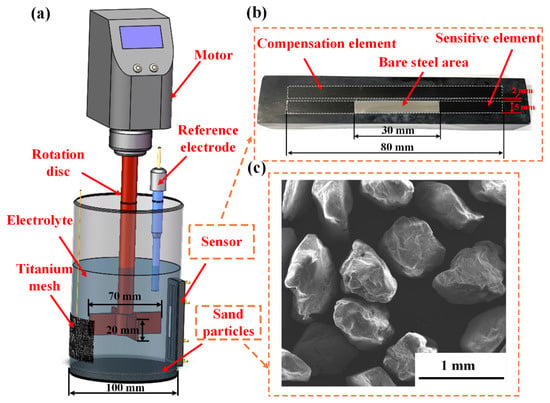
Figure 2.
The test setup for erosion-corrosion, (a) schematic illustration of the cylindrical stirring electrolytic cell, (b) photo of the erosion–corrosion sensor and (c) SEM image of the sand particles.
2.3. Test Procedure
The erosion–corrosion tests were conducted under four rotation speeds (200 rpm, 500 rpm, 1000 rpm and 2000 rpm). At each rotation speed, varied current densities (1 mA/cm2, 2 mA/cm2, 3 mA/cm2, 4 mA/cm2, 5 mA/cm2 and 6 mA/cm2) were sequentially applied on the surface of the sensitive element, with each applied current lasting for 2 h. The ERs of the sensitive and compensation elements were measured every 10 min. After the erosion–corrosion tests, the sensitive elements were immediately taken out of the cylindrical stirring electrolytic cell and cleaned by the pickling agent suggested in ASTM G1-03. The depth profiles and the local 3D profiles of the steel surface were observed with an OLS 5000 infinite microscope (Olympus, Tokyo, Japan). Moreover, the local morphologies of the surface of the sensitive element were further observed using an EM-20AX Plus scanning electron microscope (SEM, Coxem, Korean). The erosion–corrosion test was repeated three times at each rotation speed to ensure the repeatability of the results. In addition, the polarization curves of the sensitive element were measured at each rotation speed with a scanning rate of 1 mV/s, which was used to calculate the compensated cathodic current of the sensitive element.
2.4. CFD Simulation
Because the erosion–corrosion tests were performed under anodic polarization conditions, the erosion–corrosion rate of X65 steel was mainly determined by the mechanical factor, which is induced by the impact of sand particles. Therefore, the motion parameters of sand particles, such as the impact angles and the velocities, are significant for the analysis of erosion–corrosion behaviour under varied flowing conditions. In order to obtain the moving trajectories and the impact velocities of the sand particles around the steel surface, the commercial CFD code ANSYS-FLUENT 19.0 was used to conduct flow field simulation and particle trajectory prediction in the stirred electrolytic cell. A geometric model of the stirred electrolytic cell was established and meshed in ICEM preprocessing software, as shown in Figure 3. The model was divided into a dynamic region and a static region using the multiple reference frame method. The unstructured tetrahedral grid was used to mesh the geometric model. Moreover, the grid near the wall was refined to ensure accurate simulation results. After the gird sensitivity analysis and the grid refinement study, a mesh with a total cell number of 946,230 was employed. In this study, the fluid is assumed as an incompressible, steady-state and isoviscous liquid. The RNG k-ε turbulence model and Euler two-phase model were adopted to determine the flow field of the test solution. The density and viscosity of solution used in the simulation were 1.025 × 103 kg/m3 and 1.003 × 10−3 kg/(m·s), respectively. The density of the sand was set as 2.65 × 103 kg/m3, with a mass fraction of 10%.
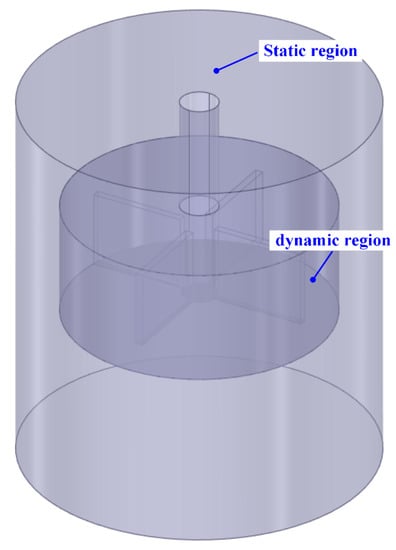
Figure 3.
Geometric model of the stirred electrolytic cell.
3. Results
3.1. CFD Simulation Results
The velocity, magnitude and trajectory distributions of the sand particles in the stirred electrolytic cell at various rotation speeds are shown in Figure 4. When the sand particles impact the steel surface, the velocities of the particles are 0.4 m/s, 0.83 m/s, 1.78 m/s and 3.3 m/s, respectively. Moreover, as indicated in the longitudinal sectional view, although the length of the bare steel area is longer than the blade height, the impact velocity distribution of the sand particles is uniform around the whole area of the bare steel length. Additionally, the sand particles always impact the steel surface from the tangential direction at all rotation speeds. Therefore, the impact velocity is the key parameter that determines the erosion metal loss, as the impact angles are identical when the rotation speed increases from 200 rpm to 2000 rpm.
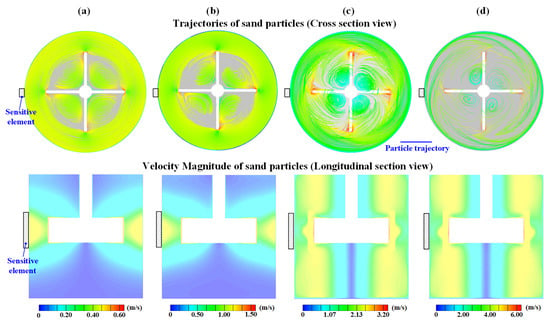
Figure 4.
Velocity distributions and trajectories of sand particles in the stirred electrolytic cell at various rotation speeds: (a) 200 rpm, (b) 500 rpm, (c) 1000 rpm and (d) 2000 rpm.
3.2. The Erosion–Corrosion Depth and Total Metal Loss Rate Measured by ER Method
The erosion–corrosion depths measured by the erosion–corrosion sensor at various rotation speeds are presented in Figure 5. The error bars represent the standard deviations of the three repeated tests. As the rotation speed increases, the total erosion–corrosion depth increases significantly. Moreover, the erosion–corrosion depth curves become steeper with increased applied anodic current density, indicating that the erosion–corrosion damage becomes increasingly severe.
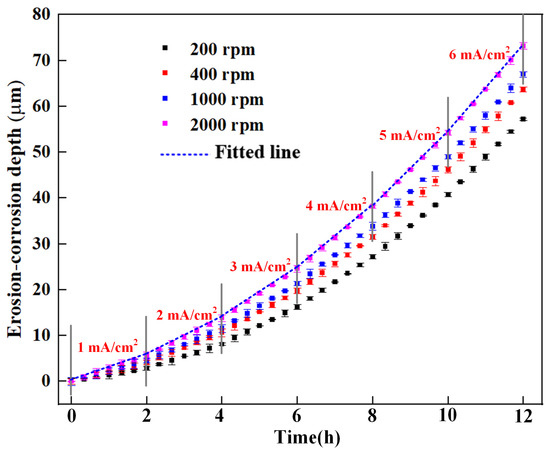
Figure 5.
The time dependence of the instantaneous erosion–corrosion depth of the sensitive element measured by resistance method under galvanostatic conditions at various rotation speeds.
Photos and three-dimensional topographies of the sensitive elements after the 12 h erosion–corrosion tests under various flow conditions are shown in Figure 6. The sensitive elements present with uniform corrosion pattern under all test conditions. The depth profile curves show that the erosion–corrosion depths of sensitive elements reach 56.9 μm, 63.8 μm, 66.9 μm and 73.3 μm at various rotation speeds. A comparison with the monitoring results of the erosion–corrosion sensor shows that the erosion–corrosion depths measured by ER method are in agreement with the three-dimensional topographic results, suggesting that the ER method is highly accurate in probing erosion–corrosion damage.
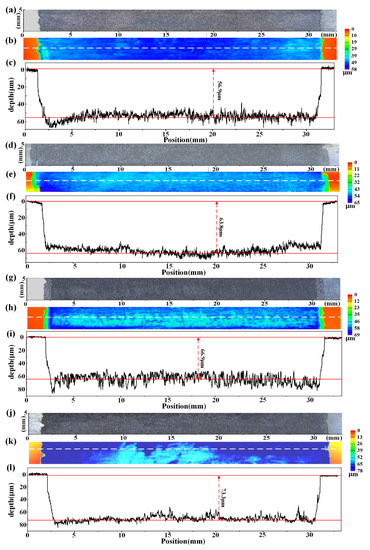
Figure 6.
Photos (a,d,g,j), 3D topographies (b,e,h,k) and depth profile curves (c,f,i,l) of sensitive element after 12 h erosion–corrosion tests under varied flow conditions: (a–c) 200 rpm, (d–f) 500 rpm, (g–i) 1000 rpm and (j–l) 2000 rpm.
The erosion–corrosion rate can be further fitted according to the time dependence of the erosion–corrosion depths using the least squares method, as shown in Figure 5. The erosion–corrosion rates with varying applied current densities are plotted in Figure 7. The error bars represent the results of the three repeated tests. Figure 7 shows that the erosion–corrosion rate dramatically increases with increased applied anodic current densities under varied flow conditions. When the applied anodic current density changes from 1 mA/cm2 to 6 mA/cm2, the erosion–corrosion rate is almost quadrupled for each flow rate, indicating that erosion–corrosion can be aggravated by the corrosion current. With the increased rotation speed, the erosion–corrosion rate also increases significantly, as both the impact velocity and the impact frequency of the sand particles are increased.
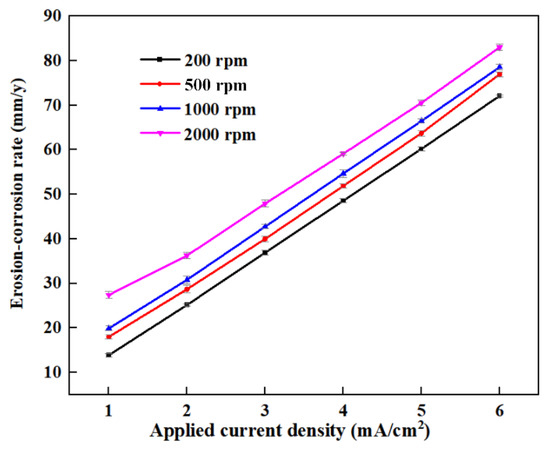
Figure 7.
The applied current density dependence of the erosion–corrosion rate of the sensitive element at various rotation speeds.
3.3. Dynamically Changed Erosion and Corrosion Rates Measured by the Erosion–Corrosion Sensor
If an anodic current is applied to the sensitive element, cathodic reaction still occurs on the steel surface, which could result in error in the calculation of the corrosion rate based on the applied anodic current density [25]. Therefore, the Tafel extrapolation method was used to estimate the cathodic current in order to obtain an accurate anodic current density. The polarization curves that were used to compensate for the cathodic current at various rotation speeds were measured, as shown in Figure 8a. The calculation method of the cathodic current under anodic polarization at 200 rpm is presented in Figure 8b. The polarization potential corresponds to the applied current density of 1 mA/cm2 is –392 mV at a rotation speed of 200 rpm, which is 31 mV higher than the corrosion potential (−432 mV). The current corresponding to the intersection of the cathodic linear fitting line and the applied anodic potential can be used to compensate for the cathodic current. The applied anodic current density (i) on the sensitive element surface can be expressed as:
where and are the anodic and cathodic current densities of the sensitive element, respectively. Then, the true anodic current density () can be calculated:
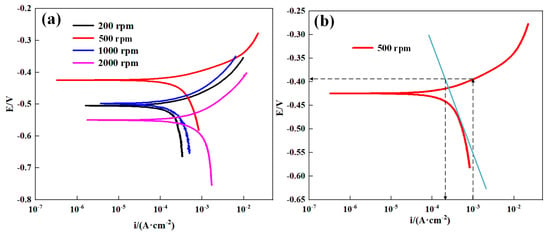
Figure 8.
The polarization curves of sensitive element tested in sand-entraining solution at various rotation speeds (a) and an example of the Tafel extrapolation method for estimation of the cathodic current (b). The blue straight line represents the cathodic linear fitting line.
Thereafter, the corrosion rate can be further calculated by Equation (4). Using a similar method, the true anodic current densities and the corrosion rates of the sensitive elements at four flow conditions are calculated, as listed in Table 1.

Table 1.
The true anodic current densities and corrosion rates of sensitive elements calculated by applied current densities after cathodic current compensation.
Based on the erosion–corrosion rate measured by the ER method and the corrosion rate calculated by the true anodic current density, the erosion rate can be calculated using Equation (5); the results are shown in Figure 9. The error bars represent the standard deviations of three repeated tests. As shown in Figure 9, the erosion rate of the sensitive element is close to zero at 200 rpm, which suggests that the impact effect of sand particles at 200 rpm cannot cause erosion damage on the steel surface. As the rotation speed increases to 500 rpm, the erosion rate is remains low when the applied current density is lower than 2 mA/cm2. The erosion rate increases gradually from 0.2 to 3.2 mm/y with an increase in the applied current density from 3 to 6 mA/cm2, suggesting that erosion damage can be considerably enhanced by the anodic current. With increased rotation speed, the erosion significantly increases. Moreover, the dependence of the erosion rate on the applied anodic current density shows a similar trend at 500 rpm, 1000 rpm and 2000 rpm.
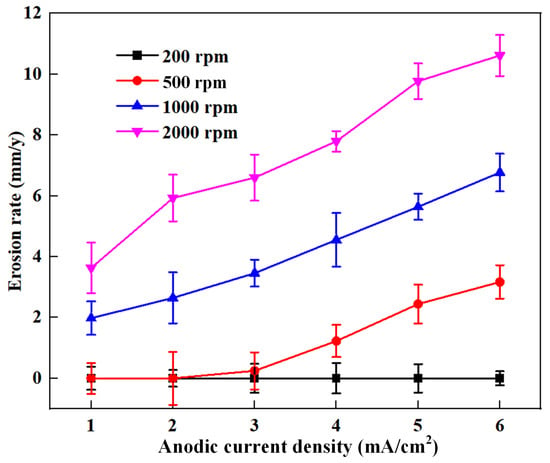
Figure 9.
The erosion rate of the sensitive element
with under various applied currents at varied rotation speeds.
3.4. The Surface Morphologies under Different Test Conditions
Local SEM images of the sensitive element after the erosion–corrosion test are presented in Figure 10. Corrosion pits are visible on the steel surface of all the sensitive elements. Moreover, the steel surfaces become increasingly rough with increased rotation speeds. As shown in Figure 10a, a number of flaky cementite skeletons are present at the edge of the corrosion pits (Figure 10(a-1)) at 200 rpm. However, the flaky cementite skeletons are only observed inside the pits when the rotation speed is higher than 200 rpm (Figure 10(b-1,c-1,d-1)), indicating that the cementite skeletons at the edge of the pit are removed by sand particle impacts at high rotation speeds. Furthermore, no evidence of sand impacts can be found in the steel surface at 200 rpm (Figure 10(a-2)), whereas slight micro-cutting grooves are visible in Figure 10(b-2) when the rotation speed is 500 rpm, indicating the initiation of erosion damage. When the rotation speed is 1000 rpm, material peeling at the edge of the pits is visible Figure 10(c-2). As the rotation speed increases to 2000 rpm, additional cutting grooves and peeling lips are become visible (Figure 10(d-2)), suggesting enhanced mechanical erosion damage.

Figure 10.
SEM images of the sensitive element after 12 h erosion–corrosion tests at rotation speeds of (a) 200 rpm, (b) 500 rpm, (c) 1000 rpm and (d) 2000 rpm.
4. Discussion
4.1. The Critical Impact Energy Required to Induce Initiation of Erosion
According to the CFD simulation results, sand particles always impact the steel surface in a tangential direction, independent of the flow velocity. Therefore, the impact velocity is the crucial index for the evaluation of the erosion rate.
In neutral NaCl solution, the cathodic and anodic reactions of X65 steel can be expressed as Equations (8) and (9):
As indicated by the polarization curves (Figure 8), the corrosion potential increases as the rotation speed changes from 200 rpm to 500 rpm. When the rotation speed increases to more than 1000 rpm, the corrosion potential decreases with increased rotation speed. It is known that both anodic and cathodic reactions are enhanced by flowing solution [31]. The impacts of sand particles can also induce plastic deformation on the steel surface, which can lead to a potential reduction in corrosion potential. As the literature indicates [31], the influence of flowing solution on the cathodic reaction is stronger than that on the anodic reaction. Therefore, the increase in corrosion potential when the rotation speed is less than 500 rpm is ascribed to the acceleration of the mass transfer process of oxygen, as the sand impact effect is minimal at a relatively low rotation speed. The reduction in the corrosion potential at high rotation speed is induced by the more intense impact effect of sand particles. Furthermore, a number of cutting grooves and peeling lips occur on the steel surface when the rotation speed is higher than 1000 rpm (Figure 10), suggesting an enhanced impact effect on the steel surface. The variation of corrosion potentials suggests that the steel surface underwent more and more serious mechanical erosion damage.
A comparison of the erosion rates at various rotation speeds shows that the erosion rate was almost 0 at 200 rpm, even when the anodic polarization current reached 6 mA/cm2, indicating that electrochemical corrosion was the only factor to induce metal loss under these conditions. To further verify that the impact of sand particles would cause no erosion damage on the steel surface, another erosion–corrosion test was performed using the erosion–corrosion sensor at 200 rpm in the test solution without sand particles. The time dependence of erosion–corrosion depths in the test solution with and without sand particles are shown in Figure 11. The erosion–corrosion depth measured in the solution with sand is close to that measured in the solution without sand. Because erosion damage would not occur without the impact of sand particles at a low flow velocity, the flowing slurry at 200 rpm cannot cause mechanical erosion on the steel surface.
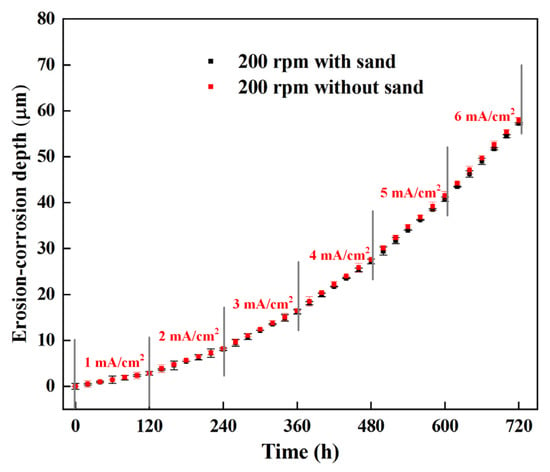
Figure 11.
The time dependence of erosion–corrosion depths measured by ER method under galvanostatic conditions at 200 rpm in the test solution with and without sand particles.
When the rotation speed reaches 500 rpm, the erosion rate can increase to as high as 2.7 mm/y, suggesting the initiation of erosion and the synergy of erosion–corrosion. The surface morphologies show that as the rotation speed increases from 200 rpm to 500 rpm, the presence of flaky cementite skeletons is significantly reduced. Moreover, less cementite is attached at the edge of the pit with increased rotation speed. The flow field simulation results show that the impact velocities of sand particles drastically increase from 0.4 m/s to 3.3 m/s with increased rotation speed.
According to the literature [32,33], the microstructure of X65 pipeline steel is normally made of pearlite and ferrite. Pearlite is a eutectoid phase that consists of alternate lamellae of cementite and ferrite. Flaky cementite occurs when ferrite lamellae is selectively corroded as a result of galvanic effects [34,35]. A decrease in cementite on the outer surface of the steel at a rotation speed higher than 500 rpm indicates that the sand particles have sufficient kinetic energy to impact the steel surface and remove the flaky cementite located at the edge of the pits, causing mechanical erosion on the steel surface. Therefore, the kinetic energy of sand particles at 500 rpm is a critical value with respect to the induction of erosion damage on steel. The impact energy (Ek) can be calculated using Equation (10):
where Vp is the impact velocity of sand particles, and mp is the mass of a particle. The average mass of a sand particle is approximately 7.67 × 10−5 g. Based on the impact velocity of a sand particle at 500 rpm, the critical impact energy that can induce the initiation of erosion is approximately 0.026 μJ.
4.2. Interaction of Mechanical and Electrochemical Factors in Erosion–Corrosion of X65 Steel
When corrosion and erosion occur on the steel surface simultaneously, both the electrochemical and the mechanical damages are aggravated, owing to the synergy of the anodic dissolution and slurry erosion processes. Because the erosion–corrosion tests were conducted in flowing slurry with varied applied anodic current densities, the chemomechanical effect was induced by the corrosion-enhanced erosion. Based on the monitoring results of the erosion–corrosion sensor with varied applied anodic currents, the dynamic changes of the erosion rate and the anodic current density were conveniently obtained online, which provided an efficient approach to quantitatively study the coupling mechanisms of mechanical erosion and electrochemical corrosion.
According to Guo and Luo’s work [11,12], the surface hardness degradation induced by the anodic current density is the main factor that causes waste of corrosion-enhanced erosion. The relationship between the corrosion-enhanced erosion rate and hardness can be expressed as Equation (11):
where n (n > 0) is the experimental constant, Hv is the hardness of the steel and ΔHv is the decrease in the hardness due to the anodic current. Moreover, the decrease in hardness can be formulated as Equation (12) [11]:
where ia is the anodic current density, ith is the threshold anodic current density required to induce hardness degradation on the surface layer and B (B > 0) is the experimental constant. Therefore, the relationship between the erosion rate () and the anodic current (ia) can be calculated by the combination of Equations (11) and (12):
The dependence of the erosion rate on various anodic current densities at various rotation speeds is shown in Figure 12. The pure erosion rates at various rotation speeds (, , ) (Figure 12) are based on a previously study [2]. Based on the erosion rate monitored by the erosion–corrosion sensor under various anodic currents, the threshold anodic current density ith, and the experimental constant (n) and B can be fitted at different rotation speeds. The fitting line and the fitting parameters are presented in Figure 12 and Table 2, respectively. When anodic current density is lower than the threshold anodic current density, the erosion rate is equal to the pure erosion rate, whereas the erosion rate dramatically increases when the anodic current density increases beyond the threshold anodic current density. In order to verify the validity of the fitting results, as shown in Table 3, the experimental results reported in [2] were used to compare with the predicted results calculated by Equation (13). Table 3 shows that the erosion rates predicted using Equation (13) are close to the results reported in the literature [2], indicating that erosion rates can be reliably calculated based on the fitting results presented in Table 2. Noted the pure erosion rate and anodic current density in the flowing slurry can be predicted based on the multiphysics approach when the synergy of erosion and corrosion is not considered. On the basis of the quantitative relation between the erosion rate and anodic current density shown in Figure 12, the erosion damage can be further predicted, even when the mechanical and electrochemical factors interact.
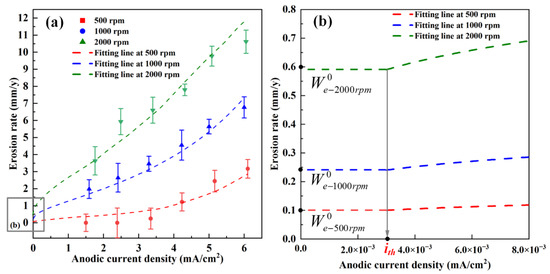
Figure 12.
The fitting results of the relationship between the erosion rate and the anodic current density at various rotation speeds (a), the detailed illustration diagram of ith (b).

Table 2.
The fitting parameters at various rotation speeds.

Table 3.
Comparison of the results reported in the literature with those predicted using Equation (13).
5. Conclusions
Based on the study of electrochemical and mechanical characteristics of erosion–corrosion of X65 pipeline steel using an erosion–corrosion sensor under varied flow conditions, the following conclusions can be drawn:
- The combination of microelectrical resistance measurement and anodic polarization tests is a highly effective approach to study the interactive effects of mechanical and electrochemical factors on erosion–corrosion of X65 pipeline steel. The synchronously changed erosion and corrosion rates at various rotation speeds can be probed online using a small number of test samples.
- There is a critical impact energy at which particles begin to induce erosion damage on the surface of X65 pipeline steel in flowing slurry. When the kinetic energy of sand particles is higher than the critical impact energy, the impact of sand particles can remove the flaky cementite skeletons at the edge of the pits and cause the initiation of erosion.
- The threshold anodic current density that can induce a chemomechanical effect on erosion–corrosion of X65 steel can be quickly fitted based on the probing results of the erosion–corrosion sensor. The quantitative relationship between erosion and corrosion components, which can be used for erosion–corrosion simulation by numerical method, is established.
Author Contributions
Conceptualization, K.L., L.L. and Y.X.; software, W.C.; validation, W.J. and L.L.; formal analysis, L.L.; investigation, L.L.; resources, K.L.; data curation, Y.X.; writing—original draft preparation, K.L. and L.L.; writing—review and editing, L.L.; visualization, Y.H.; supervision, Y.H.; project administration, Y.H.; funding acquisition, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was sponsored by National Natural Science Foundation of China (no. 52001055).
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the funders of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- El-Sherik, A. Trends in Oil and Gas Corrosion Research and Technologies; Woodhead Publishing: Sawston, UK, 2017. [Google Scholar]
- Xu, Y.; Liu, L.; Xu, C.; Wang, X.; Huang, Y. Electrochemical characteristics of the dynamic progression of erosion-corrosion under different flow conditions and their effects on corrosion rate calculation. J. Solid State Electrochem. 2020, 24, 2511–2524. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, L.; Zhou, Q.; Wang, X.; Huang, Y. An Overview of Major Experimental Methods and Apparatus for Measuring and Investigating Erosion-Corrosion of Ferrous-Based Steels. Metals 2020, 10, 180. [Google Scholar] [CrossRef]
- Maher, M.; Iraola-Arregui, I.; Ben, Y.; Rhouta, B.; Trabadelo, V. The synergistic effect of wear-corrosion in stainless steels: A review. Mater. Today Proc. 2022, 51, 1975–1990. [Google Scholar] [CrossRef]
- Chung, R.J.; Jiang, J.; Pang, C.; Yu, B.; Eadie, R.; Li, D. Erosion-corrosion behaviour of steels used in slurry pipelines. Wear 2021, 477, 203771. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.; Yao, J. Synergistic erosion–corrosion behavior of X80 pipeline steel at various impingement angles in two-phase flow impingement. Wear 2021, 466–467, 203572. [Google Scholar] [CrossRef]
- Lu, B.; Xia, D.; Luo, J. Mechanism of Corrosion-Enhanced Erosion of Steel in Oil and Gas Production; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Lu, B.; Luo, J. Correlation between surface-hardness degradation and erosion resistance of carbon steel-Effects of slurry chemistry. Tribol. Int. 2015, 83, 146–155. [Google Scholar] [CrossRef]
- Stack, M.; Stott, F.H. An approach to modeling erosion-corrosion of alloys using erosion-corrosion maps. Corros. Sci. 1993, 35, 1027–1034. [Google Scholar] [CrossRef]
- Malka, R.; Nešić, S.; Gulino, D. Erosion-corrosion and synergistic effects in disturbed liquid-particle flow. Wear 2007, 262, 791–799. [Google Scholar] [CrossRef]
- Guo, H.; Lu, B.; Luo, J. Interaction of mechanical and electrochemical factors in erosion-corrosion of carbon steel. Electrochim. Acta 2005, 51, 315–323. [Google Scholar] [CrossRef]
- Guo, H.; Lu, B.; Luo, J. Response of surface mechanical properties to electrochemical dissolution determined by in situ nano-indentation technique. Electrochem. Commun. 2006, 8, 1092–1098. [Google Scholar] [CrossRef]
- Liu, L.; Xu, Y.; Zhu, Y.; Wang, X.; Huang, Y. The Roles of Fluid Hydrodynamics, Mass Transfer, Rust Layer and Macro-Cell Current on Flow Accelerated Corrosion of Carbon Steel in Oxygen Containing Electrolyte. J. Electrochem. Soc. 2020, 167, 141510. [Google Scholar] [CrossRef]
- Fujiwara, K.; Domae, M.; Yoneda, K.; Inada, F.; Ohira, T.; Hisamune, K. Correlation of flow accelerated corrosion rate with iron solubility. Nucl. Eng. Des. 2011, 241, 4482–4486. [Google Scholar] [CrossRef]
- Uchida, S.; Naitoh, M.; Okada, H.; Uehara, Y.; Koshizuka, S. Evaluation of flow accelerated corrosion by coupled analysis of corrosion and flow dynamics. Relationship of oxide film thickness, hematite/magnetite ratio, ECP and wall thinning rate. Nucl. Eng. Des. 2011, 241, 4585–4593. [Google Scholar] [CrossRef]
- Liu, L.; Xu, Y.; Xu, C.; Wang, X.; Huang, Y. Detecting and monitoring erosion-corrosion using ring pair electrical resistance sensor in conjunction with electrochemical measurements. Wear 2019, 428–429, 328–339. [Google Scholar] [CrossRef]
- Zeng, L.; Zhang, G.; Guo, X. Erosion–corrosion at different locations of X65 carbon steel elbow. Corros. Sci. 2014, 85, 318–330. [Google Scholar] [CrossRef]
- Owen, J.; Ramsey, C.; Barker, R.; Neville, A. Erosion-corrosion interactions of X65 carbon steel in aqueous CO2 environments. Wear 2018, 414–415, 376–389.
- Wood, R. Erosion–corrosion interactions and their effect on marine and offshore materials. Wear 2006, 261, 1012–1023. [Google Scholar] [CrossRef]
- Barik, R.; Wharton, J.; Wood, R.; Stokes, K. Electro-mechanical interactions during erosion–corrosion. Wear 2009, 267, 1900–1908. [Google Scholar] [CrossRef]
- Zeng, L.; Shuang, S.; Guo, X.; Zhang, G. Erosion-corrosion of stainless steel at different locations of a 90° elbow. Corros. Sci. 2016, 111, 72–83. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, L.; Zhou, Q.; Wang, X.; Huang, Y. Understanding the influences of pre-corrosion on the erosion-corrosion performance of pipeline steel. Wear 2020, 442–443, 203151. [Google Scholar] [CrossRef]
- Xu, Y.; Tan, M.Y. Probing the initiation and propagation processes of flow accelerated corrosion and erosion corrosion under simulated turbulent flow conditions. Corros. Sci. 2019, 151, 163–174. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Q.; Gao, S.; Wang, X.; Huang, Y. Exploring the effects of sand impacts and anodic dissolution on localized erosion-corrosion in sand entraining electrolyte. Wear 2021, 478–479, 203907. [Google Scholar] [CrossRef]
- Guo, H.; Lu, B.; Luo, J. Non-Faraday material loss in flowing corrosive solution. Electrochim. Acta 2006, 51, 5341–5348. [Google Scholar] [CrossRef]
- Liu, L.; Xu, Y.; Wang, Z.; Wang, X.; Huang, Y. Probing and separating corrosion and erosion of pipeline steel using electrical resistance method in conjunction with electrochemical measurements. Measurement 2021, 183, 109797. [Google Scholar] [CrossRef]
- Vieira, R.; Parsi, M.; Zahedi, P.; McLaury, B.; Shirazi, S. Electrical resistance probe measurements of solid particle erosion in multiphase annular flow. Wear 2017, 382–383, 15–28. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, Y.; Wang, X.; Lin, X. Experimental study on pipeline internal corrosion based on a new kind of electrical resistance sensor. Sens. Actuators B Chem. 2016, 224, 37–47. [Google Scholar] [CrossRef]
- Orlikowski, J.; Darowicki, K.; Mikołajski, S. Multi-sensor monitoring of the corrosion rate and the assessment of the efficiency of a corrosion inhibitor in utility water installations. Sens. Actuators B Chem. 2013, 181, 22–28. [Google Scholar] [CrossRef]
- Xia, D.; Deng, C.; Macdnald, D.; Jamali, S.; Mills, D.; Luo, J.L.; Strebl, M.G.; Amiri, M.; Jin, W.; Song, S.; et al. Electrochemical measurements used for assessment of corrosion and protection of metallic materials in the field: A critical review. J. Mater. Sci. Technol. 2022, 112, 151–183. [Google Scholar] [CrossRef]
- Zheng, Z.B.; Zheng, Y.G. Erosion-enhanced corrosion of stainless steel and carbon steel. Corros. Sci. 2016, 102, 259–268. [Google Scholar] [CrossRef]
- Maria, D.; Bruce, B.; Srdjan, N.; Marc, S. Effect of Flow and Steel Microstructure on the Formation of Iron Carbonate. Corros. J. Sci. Eng. 2019, 10, 75. [Google Scholar]
- Md. Aminul, I.; Zoheir, N. Mechanical and Electrochemical Synergism of API X42 Pipeline Steel during Erosion-Corrosion. J. Bio Tribo Corros. 2015, 1, 26. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, Y.; Wang, M.; Wang, X.; Liu, G.; Huang, Y. Understanding the influences of temperature and microstructure on localized corrosion of subsea pipeline weldment using an integrated multi-electrode array. Ocean. Eng. 2019, 189, 106351. [Google Scholar] [CrossRef]
- Farelas, F.; Galicia, M.; Brown, B.; Nesic, S.; Castaneda, H. Evolution of dissolution processes at the interface of carbon steel corroding in a CO2 environment studied by EIS. Corros. Sci. 2010, 52, 509–517. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).