Message in a Bottle: Unveiling the Magneto-Ionic Complexity of AGNs through the Stokes QU-Fitting Technique
Abstract
1. Introduction
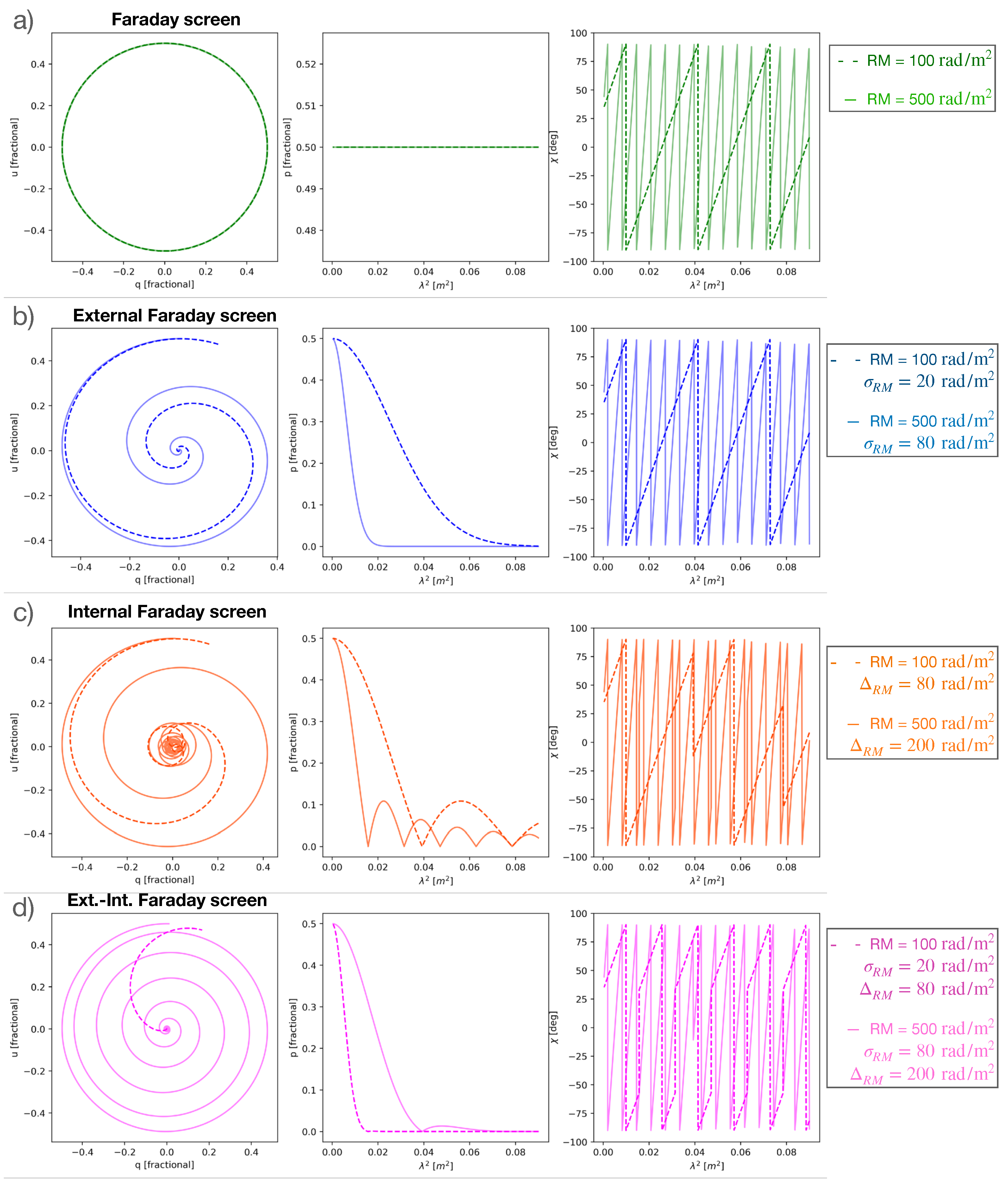
2. Polarization Models
3. Observational Broad-Band Spectropolarimetry Works
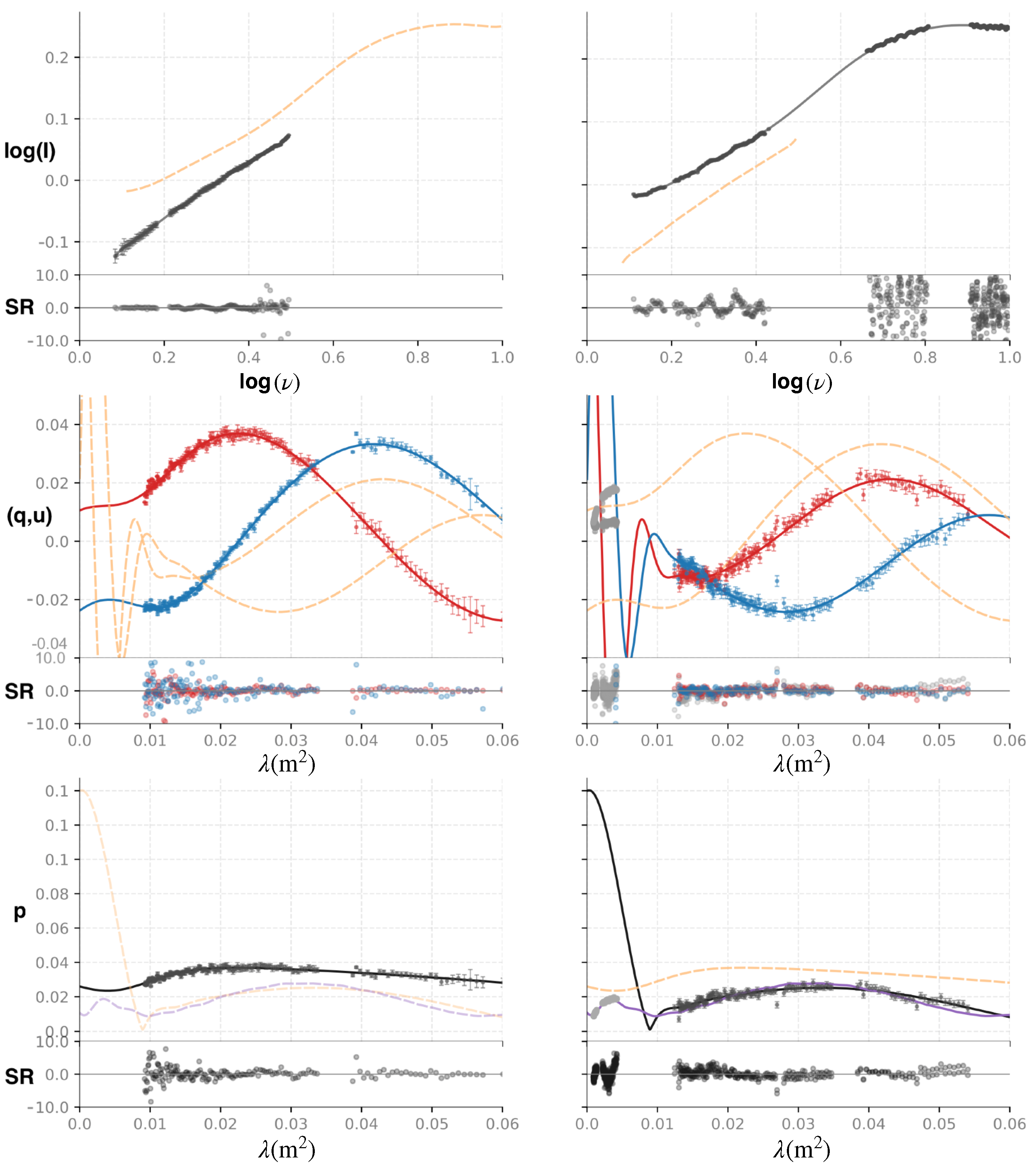
3.1. Unresolved Sources
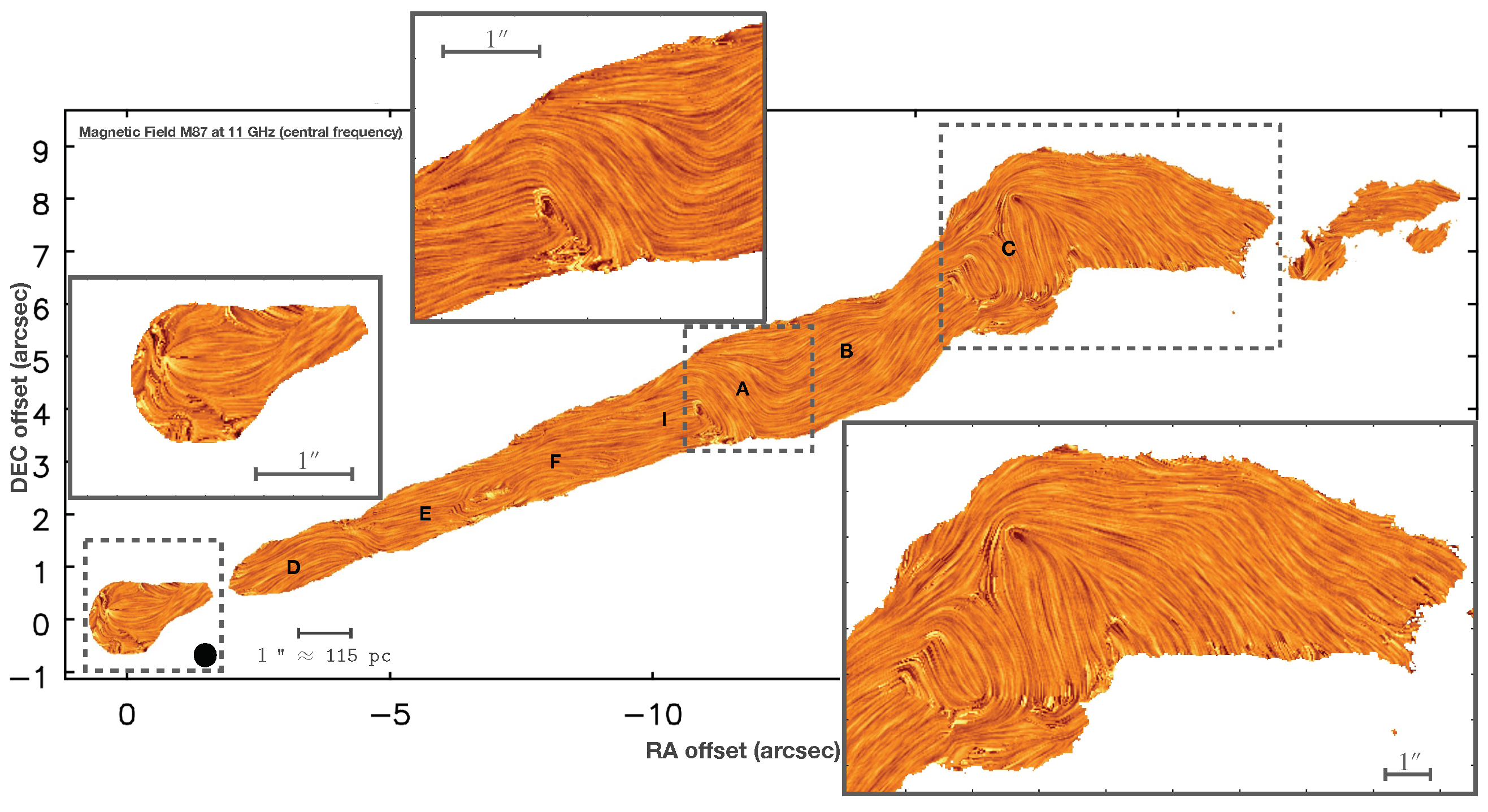
3.2. Resolved Sources
3.3. Future Spectropolarimetric Surveys
4. Summary and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vikhlinin, A.; Markevitch, M.; Murray, S.S. Chandra Estimate of the Magnetic Field Strength near the Cold Front in A3667. Astrophys. J. Lett. 2001, 549, L47–L50. [Google Scholar] [CrossRef]
- Cotton, W.D.; Geldzahler, B.J.; Marcaide, J.M.; Shapiro, I.I.; Sanroma, M.; Rius, A. VLBI observations of the polarized radio emission from the quasar 3C 454.3. Astrophys. J. 1984, 286, 503–508. [Google Scholar] [CrossRef]
- Dreher, J.W.; Carilli, C.L.; Perley, R.A. The Faraday Rotation of Cygnus A: Magnetic Fields in Cluster Gas. Astrophys. J. 1987, 316, 611. [Google Scholar] [CrossRef]
- Attridge, J.M.; Roberts, D.H.; Wardle, J.F.C. Radio Jet-Ambient Medium Interactions on Parsec Scales in the Blazar 1055+018. Astrophys. J. Lett. 1999, 518, L87–L90. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Beck, R.; Hoernes, P. The polarized disk in M 31 at lambda 6 cm. Astron. Astrophys. 2003, 398, 937–948. [Google Scholar] [CrossRef]
- Zavala, R.T.; Taylor, G.B. A View through Faraday’s Fog: Parsec-Scale Rotation Measures in Active Galactic Nuclei. Astrophys. J. 2003, 589, 126–146. [Google Scholar] [CrossRef]
- Wardle, J. An Unofficial Account of the Beginnings of VLBI Polarimetry: From Jodrell Bank to the Event Horizon Telescope. Galaxies 2021, 9, 52. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H. Relativistic jet models for two low-luminosity radio galaxies: Evidence for backflow? Mon. Not. R. Astron. Soc. 2012, 424, 1149–1169. [Google Scholar] [CrossRef][Green Version]
- Laing, R.A.; Bridle, A.H. Systematic properties of decelerating relativistic jets in low-luminosity radio galaxies. Mon. Not. R. Astron. Soc. 2014, 437, 3405–3441. [Google Scholar] [CrossRef]
- Katz-Stone, D.M.; Rudnick, L. An Analysis of the Synchrotron Spectrum in the Fanaroff-Riley Type I Galaxy 3C 449. Astrophys. J. 1997, 488, 146–154. [Google Scholar] [CrossRef]
- Katz-Stone, D.M.; Rudnick, L.; Butenhoff, C.; O’Donoghue, A.A. Coaxial Jets and Sheaths in Wide-Angle-tailed Radio Galaxies. Astrophys. J. 1999, 516, 716–728. [Google Scholar] [CrossRef]
- Hardcastle, M.J. The complex radio spectrum of 3C 130. Astron. Astrophys. 1999, 349, 381–388. [Google Scholar]
- van Haarlem, M.P.; Wise, M.W.; Gunst, A.W.; Heald, G.; McKean, J.P.; Hessels, J.W.T.; de Bruyn, A.G.; Nijboer, R.; Swinbank, J.; Fallows, R.; et al. LOFAR: The LOw-Frequency ARray. Astron. Astrophys. 2013, 556, A2. [Google Scholar] [CrossRef]
- Tingay, S.J.; Goeke, R.; Bowman, J.D.; Emrich, D.; Ord, S.M.; Mitchell, D.A.; Morales, M.F.; Booler, T.; Crosse, B.; Wayth, R.B.; et al. The Murchison Widefield Array: The Square Kilometre Array Precursor at Low Radio Frequencies. Publ. Astron. Soc. Aust 2013, 30, e007. [Google Scholar] [CrossRef]
- McConnell, D.; Allison, J.R.; Bannister, K.; Bell, M.E.; Bignall, H.E.; Chippendale, A.P.; Edwards, P.G.; Harvey-Smith, L.; Hegarty, S.; Heywood, I.; et al. The Australian Square Kilometre Array Pathfinder: Performance of the Boolardy Engineering Test Array. Publ. Astron. Soc. Aust 2016, 33, e042. [Google Scholar] [CrossRef]
- Brentjens, M.A.; de Bruyn, A.G. Faraday rotation measure synthesis. Astron. Astrophys 2005, 441, 1217–1228. [Google Scholar] [CrossRef]
- Farnsworth, D.; Rudnick, L.; Brown, S. Integrated Polarization of Sources at λ˜1 m and New Rotation Measure Ambiguities. Astro J. 2011, 141, 191. [Google Scholar] [CrossRef]
- O’Sullivan, S.P.; Brown, S.; Robishaw, T.; Schnitzeler, D.H.F.M.; McClure-Griffiths, N.M.; Feain, I.J.; Taylor, A.R.; Gaensler, B.M.; Landecker, T.L.; Harvey-Smith, L.; et al. Complex Faraday depth structure of active galactic nuclei as revealed by broad-band radio polarimetry. Mon. Not. R. Astron. Soc. 2012, 421, 3300–3315. [Google Scholar] [CrossRef]
- Loi, F.; Murgia, M.; Govoni, F.; Vacca, V.; Bonafede, A.; Ferrari, C.; Prandoni, I.; Feretti, L.; Giovannini, G.; Li, H. Rotation measure synthesis applied to synthetic SKA images of galaxy clusters. Mon. Not. R. Astron. Soc. 2019, 490, 4841–4857. [Google Scholar] [CrossRef]
- Krause, M.; Irwin, J.; Schmidt, P.; Stein, Y.; Miskolczi, A.; Carolina Mora-Partiarroyo, S.; Wiegert, T.; Beck, R.; Stil, J.M.; Heald, G.; et al. CHANG-ES. XXII. Coherent magnetic fields in the halos of spiral galaxies. Astron. Astrophys. 2020, 639, A112. [Google Scholar] [CrossRef]
- Stuardi, C.; O’Sullivan, S.P.; Bonafede, A.; Brüggen, M.; Dabhade, P.; Horellou, C.; Morganti, R.; Carretti, E.; Heald, G.; Iacobelli, M.; et al. The LOFAR view of intergalactic magnetic fields with giant radio galaxies. Astron. Astrophys. 2020, 638, A48. [Google Scholar] [CrossRef]
- Sun, X.H.; Rudnick, L.; Akahori, T.; Anderson, C.S.; Bell, M.R.; Bray, J.D.; Farnes, J.S.; Ideguchi, S.; Kumazaki, K.; O’Brien, T.; et al. Comparison of Algorithms for Determination of Rotation Measure and Faraday Structure. I. 1100–1400 MHz. Astro J. 2015, 149, 60. [Google Scholar] [CrossRef]
- Burn, B.J. On the depolarization of discrete radio sources by Faraday dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67. [Google Scholar] [CrossRef]
- Tribble, P.C. Depolarization of extended radio sources by a foreground Faraday screen. Mon. Not. R. Astron. Soc. 1991, 250, 726. [Google Scholar] [CrossRef]
- Sokoloff, D.D.; Bykov, A.A.; Shukurov, A.; Berkhuijsen, E.M.; Beck, R.; Poezd, A.D. Depolarization and Faraday effects in galaxies. Mon. Not. R. Astron. Soc. 1998, 299, 189–206. [Google Scholar] [CrossRef]
- Rossetti, A.; Dallacasa, D.; Fanti, C.; Fanti, R.; Mack, K.H. The B3-VLA CSS sample. VII. WSRT polarisation observations and the ambient Faraday medium properties revisited. Astron. Astrophys 2008, 487, 865–883. [Google Scholar] [CrossRef]
- Saikia, D.J.; Salter, C.J. Polarization properties of extragalactic radio sources. Annu. Rev. Astron. Astrophys. 1988, 26, 93–144. [Google Scholar] [CrossRef]
- Simard-Normandin, M.; Kronberg, P.P.; Button, S. The Faraday rotation measures of extragalactic radio sources. Astrophys. J. Suppl. 1981, 45, 97–111. [Google Scholar] [CrossRef]
- Law, C.J.; Gaensler, B.M.; Bower, G.C.; Backer, D.C.; Bauermeister, A.; Croft, S.; Forster, R.; Gutierrez-Kraybill, C.; Harvey-Smith, L.; Heiles, C.; et al. Spectropolarimetry with the Allen Telescope Array: Faraday Rotation Toward Bright Polarized Radio Galaxies. Astrophys. J. 2011, 728, 57. [Google Scholar] [CrossRef]
- Anderson, C.S.; Gaensler, B.M.; Feain, I.J.; Franzen, T.M.O. Broadband Radio Polarimetry and Faraday Rotation of 563 Extragalactic Radio Sources. Astrophys. J. 2015, 815, 49. [Google Scholar] [CrossRef]
- Anderson, C.S.; Gaensler, B.M.; Feain, I.J. A Study of Broadband Faraday Rotation and Polarization Behavior over 1.3–10 GHz in 36 Discrete Radio Sources. Astrophys. J. 2016, 825, 59. [Google Scholar] [CrossRef]
- Pasetto, A.; Kraus, A.; Mack, K.H.; Bruni, G.; Carrasco-González, C. A study of a sample of high rotation-measure AGNs through multifrequency single-dish observations. Astron. Astrophys 2016, 586, A117. [Google Scholar] [CrossRef]
- Pasetto, A.; Carrasco-González, C.; O’Sullivan, S.; Basu, A.; Bruni, G.; Kraus, A.; Curiel, S.; Mack, K.H. Broadband radio spectro-polarimetric observations of high-Faraday-rotation-measure AGN. Astron. Astrophys 2018, 613, A74. [Google Scholar] [CrossRef]
- Farnes, J.S.; Gaensler, B.M.; Carretti, E. A Broadband Polarization Catalog of Extragalactic Radio Sources. Astrophys. J. Suppl. 2014, 212, 15. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Beck, R. What Mechanism Depolarizes the Emission from the Southwest Arm of M31. In Galactic and Intergalactic Magnetic Fields; Beck, R., Kronberg, P.P., Wielebinski, R., Eds.; Springer: Berlin, Germany, 1990; Volume 140, p. 201. [Google Scholar]
- Schnitzeler, D.H.F.M.; Banfield, J.K.; Lee, K.J. Polarization signatures of unresolved radio sources. Mon. Not. R. Astron. Soc. 2015, 450, 3579–3596. [Google Scholar] [CrossRef][Green Version]
- Laing, R.A. Magnetic fields in extragalactic radio sources. Astrophys. J. 1981, 248, 87–104. [Google Scholar] [CrossRef]
- Blandford, R.D. Astrophysical Jets; Burgarella, D., Livio, M., O’Dea, C.P., Eds.; Cambridge University Press: Cambridge, UK, 1993; p. 15. [Google Scholar]
- Laing, R.A.; Bridle, A.H. Rotation measure variation across M 84. Mon. Not. R. Astron. Soc. 1987, 228, 557–571. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H.; Parma, P.; Murgia, M. Structures of the magnetoionic media around the Fanaroff-Riley Class I radio galaxies 3C31 and Hydra A. Mon. Not. R. Astron. Soc. 2008, 391, 521–549. [Google Scholar] [CrossRef]
- Guidetti, D.; Laing, R.A.; Murgia, M.; Govoni, F.; Gregorini, L.; Parma, P. Structure of the magnetoionic medium around the Fanaroff-Riley Class I radio galaxy 3C 449. Astron. Astrophys. 2010, 514, A50. [Google Scholar] [CrossRef]
- O’Sullivan, S.P.; Purcell, C.R.; Anderson, C.S.; Farnes, J.S.; Sun, X.H.; Gaensler, B.M. Broad-band, radio spectro-polarimetric study of 100 radiative-mode and jet-mode AGN. Mon. Not. R. Astron. Soc. 2017, 469, 4034–4062. [Google Scholar] [CrossRef]
- Anderson, C.S.; O’Sullivan, S.P.; Heald, G.H.; Hodgson, T.; Pasetto, A.; Gaensler, B.M. Blazar jet evolution revealed by multi-epoch broad-band radio polarimetry. Mon. Not. R. Astron. Soc. 2019, 485, 3600–3622. [Google Scholar] [CrossRef]
- Owen, F.N.; Eilek, J.A.; Keel, W.C. Detection of Large Faraday Rotation in the Inner 2 Kiloparsecs of M87. Astrophys. J. 1990, 362, 449. [Google Scholar] [CrossRef]
- Banfield, J.K.; O’Sullivan, S.P.; Wieringa, M.H.; Emonts, B.H.C. Faraday rotation study of NGC 612 (PKS 0131-36): A hybrid radio source and its magnetized circumgalactic environment. Mon. Not. R. Astron. Soc. 2019, 482, 5250–5258. [Google Scholar] [CrossRef]
- Anderson, C.S.; Gaensler, B.M.; Heald, G.H.; O’Sullivan, S.P.; Kaczmarek, J.F.; Feain, I.J. Broadband Radio Polarimetry of Fornax A. I. Depolarized Patches Generated by Advected Thermal Material from NGC 1316. Astrophys. J. 2018, 855, 41. [Google Scholar] [CrossRef]
- Pasetto, A.; Carrasco-González, C.; Gómez, J.L.; Martí, J.M.; Perucho, M.; O’Sullivan, S.; Fuentes, A.; Wardle, J.; Anderson, C. Reading M87’s DNA: A Double Helix tracing a Helical Magnetic Field at kpc scales. Astrophys. J. 2021. submitted. [Google Scholar]
- Owen, F.N.; Hardee, P.E.; Bignell, R.C. VLA observations of the M87 jet at 6 and 2 cm. Astrophys. J. Lett. 1980, 239, L11–L15. [Google Scholar] [CrossRef]
- Owen, F.N.; Hardee, P.E.; Cornwell, T.J. High-Resolution, High Dynamic Range VLA Images of the M87 Jet at 2 Centimeters. Astrophys. J. 1989, 340, 698. [Google Scholar] [CrossRef]
- Capetti, A.; Macchetto, F.D.; Sparks, W.B.; Biretta, J.A. HST polarization observations of the jet of M87. Astron. Astrophys. 1997, 317, 637–645. [Google Scholar]
- Heinz, S.; Begelman, M.C. Analysis of the Synchrotron Emission from the M87 Jet. Astrophys. J. 1997, 490, 653–663. [Google Scholar] [CrossRef]
- Perlman, E.S.; Biretta, J.A.; Zhou, F.; Sparks, W.B.; Macchetto, F.D. Optical and Radio Polarimetry of the M87 Jet at 0.2′′ Resolution. Astro J. 1999, 117, 2185–2198. [Google Scholar] [CrossRef]
- Avachat, S.S.; Perlman, E.S.; Adams, S.C.; Cara, M.; Owen, F.; Sparks, W.B.; Georganopoulos, M. Multi-wavelength Polarimetry and Spectral Study of the M87 Jet during 2002–2008. Astrophys. J. 2016, 832, 3. [Google Scholar] [CrossRef]
- Chen, Y.J.; Zhao, G.Y.; Shen, Z.Q. The core-like nature of HST-1 in the M87 jet. Mon. Not. R. Astron. Soc. 2011, 416, L109–L113. [Google Scholar] [CrossRef]
- Algaba, J.C.; Asada, K.; Nakamura, M. Resolving the Rotation Measure of the M87 Jet on Kiloparsec Scales. Astrophys. J. 2016, 823, 86. [Google Scholar] [CrossRef]
- Park, J.; Hada, K.; Kino, M.; Nakamura, M.; Ro, H.; Trippe, S. Faraday Rotation in the Jet of M87 inside the Bondi Radius: Indication of Winds from Hot Accretion Flows Confining the Relativistic Jet. Astrophys. J. 2019, 871, 257. [Google Scholar] [CrossRef]
- Kravchenko, E.; Giroletti, M.; Hada, K.; Meier, D.L.; Nakamura, M.; Park, J.; Walker, R.C. Linear polarization in the nucleus of M87 at 7 mm and 1.3 cm. Astron. Astrophys. 2020, 637, L6. [Google Scholar] [CrossRef]
- Lyutikov, M.; Pariev, V.I.; Gabuzda, D.C. Polarization and structure of relativistic parsec-scale AGN jets. Mon. Not. R. Astron. Soc. 2005, 360, 869–891. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Horellou, C.; Krause, M.; Neininger, N.; Poezd, A.D.; Shukurov, A.; Sokoloff, D.D. Magnetic fields in the disk and halo of M 51. Astron. Astrophys. 1997, 318, 700–720. [Google Scholar]
- Basu, A.; Mao, S.A.; Kepley, A.A.; Robishaw, T.; Zweibel, E.G.; Gallagher, J.S.I. Detection of an ∼20 kpc coherent magnetic field in the outskirt of merging spirals: The Antennae galaxies. Mon. Not. R. Astron. Soc. 2017, 464, 1003–1017. [Google Scholar] [CrossRef]
- Mao, S.A.; Carilli, C.; Gaensler, B.M.; Wucknitz, O.; Keeton, C.; Basu, A.; Beck, R.; Kronberg, P.P.; Zweibel, E. Detection of microgauss coherent magnetic fields in a galaxy five billion years ago. Nat. Astron. 2017, 1, 621–626. [Google Scholar] [CrossRef]
- Ozawa, T.; Nakanishi, H.; Akahori, T.; Anraku, K.; Takizawa, M.; Takahashi, I.; Onodera, S.; Tsuda, Y.; Sofue, Y. JVLA S- and X-band polarimetry of the merging cluster Abell 2256. Publ. Astron. Soc. Jpn 2015, 67, 110. [Google Scholar] [CrossRef]
- Mizener, A.; Williams, A. Probing Magnetic Fields in Cosmic Web Filaments. American Astronomical Society Meeting Abstracts #235. In American Astronomical Society Meeting Abstracts; AAS: Washington, DC, WA, USA, 2020; Volume 235, p. 205.01. [Google Scholar]
- Di Gennaro, G.; van Weeren, R.J.; Rudnick, L.; Hoeft, M.; Brüggen, M.; Ryu, D.; Röttgering, H.J.A.; Forman, W.; Stroe, A.; Shimwell, T.W.; et al. Downstream Depolarization in the Sausage Relic: A 1-4 GHz Very Large Array Study. Astrophys. J. 2021, 911, 3. [Google Scholar] [CrossRef]
- Gaensler, B.M.; Landecker, T.L.; Taylor, A.R.; POSSUM Collaboration. Survey Science with ASKAP: Polarization Sky Survey of the Universe’s Magnetism (POSSUM). In American Astronomical Society Meeting Abstracts #215; AAS: Washington, DC, USA, 2010; Volume 215, p. 470.13, AAS: Washington, DC, USA, 2010. [Google Scholar]
- Anderson, C.S.; Heald, G.H.; Eilek, J.A.; Lenc, E.; Gaensler, B.M.; Rudnick, L.; Van Eck, C.L.; O’Sullivan, S.P.; Stil, J.M.; Chippendale, A.; et al. Early Science from POSSUM: Shocks, turbulence, and a massive new reservoir of ionised gas in the Fornax cluster. arXiv 2021, arXiv:2102.01702. [Google Scholar]
- Johnston-Hollitt, M.; Govoni, F.; Beck, R.; Dehghan, S.; Pratley, L.; Akahori, T.; Heald, G.; Agudo, I.; Bonafede, A.; Carretti, E.; et al. Using SKA Rotation Measures to Reveal the Mysteries of the Magnetised Universe. Adv. Astrophys. Sq. Km. Array 2015, arXiv:1506.00808. [Google Scholar]
- Gaensler, B.; Agudo, I.; Akahori, T.; Banfield, J.; Beck, R.; Carretti, E.; Farnes, J.; Haverkorn, M.; Heald, G.; Jones, D.; et al. Broadband Polarimetry with the Square Kilometre Array: A Unique Astrophysical Probe. Adv. Astrophys. Sq. Km. Array 2015, arXiv:astro-ph.CO/1501.00626. [Google Scholar]
- Beck, R.; Gaensler, B.M. Observations of magnetic fields in the Milky Way and in nearby galaxies with a Square Kilometre Array. NewAR 2004, 48, 1289–1304. [Google Scholar] [CrossRef]


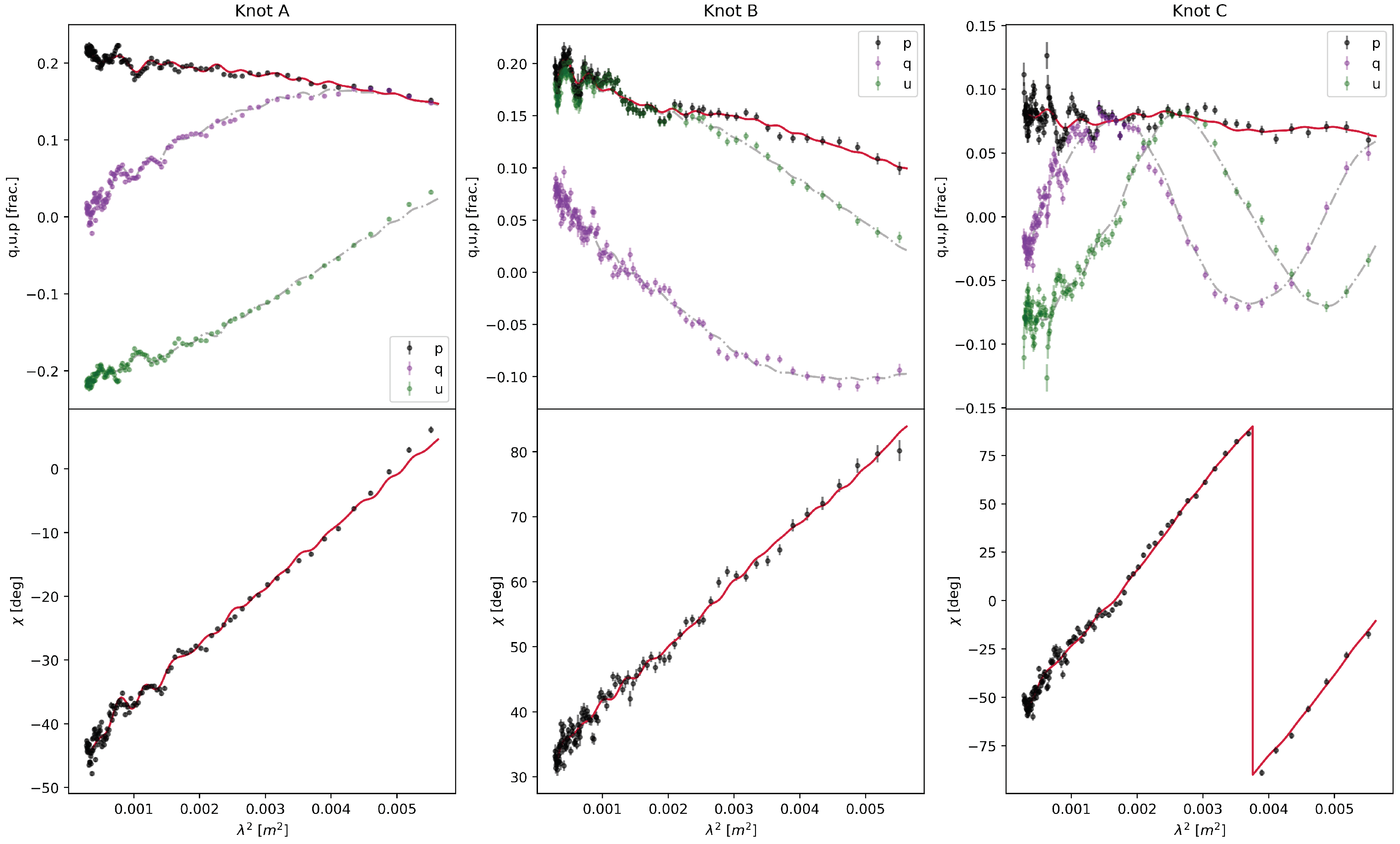
| Knot | p | p | p | RM | RM | RM | RM | RM | RM | Std | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [deg] | [rad/m] | ||||||||||||
| A | 0.20 | 0.11 | 0.11 | −45 | 49 | 34 | 155 | −1420 | −573 | −240 | 10,420 | 17,160 | 0.005 |
| B | 0.17 | 0.03 | 0.09 | 32 | 21 | −133 | 160 | 355 | −850 | −300 | 2270 | −17,460 | 0.007 |
| C | 0.01 | 0.08 | 0.06 | 120 | 113 | −0.1 | 1945 | 730 | −520 | −300 | −210 | 12,200 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasetto, A. Message in a Bottle: Unveiling the Magneto-Ionic Complexity of AGNs through the Stokes QU-Fitting Technique. Galaxies 2021, 9, 56. https://doi.org/10.3390/galaxies9030056
Pasetto A. Message in a Bottle: Unveiling the Magneto-Ionic Complexity of AGNs through the Stokes QU-Fitting Technique. Galaxies. 2021; 9(3):56. https://doi.org/10.3390/galaxies9030056
Chicago/Turabian StylePasetto, Alice. 2021. "Message in a Bottle: Unveiling the Magneto-Ionic Complexity of AGNs through the Stokes QU-Fitting Technique" Galaxies 9, no. 3: 56. https://doi.org/10.3390/galaxies9030056
APA StylePasetto, A. (2021). Message in a Bottle: Unveiling the Magneto-Ionic Complexity of AGNs through the Stokes QU-Fitting Technique. Galaxies, 9(3), 56. https://doi.org/10.3390/galaxies9030056






