The Radiative Newtonian 1 < γ ≤ 1.66 and the Paczyński–Wiita γ = 5/3 Regime of Non-Isothermal Bondi Accretion onto a Massive Black Hole with an Accretion Disc
Abstract
1. Introduction
2. Non-Isothermal Radial Bondi Accretion
3. Results
4. Catalogue of Pure Absorption Spectral Line Shapes for
5. Estimated Bondi Radius and Mass Accretion with Respect to Conditions at Infinity
6. Conclusions
- Mass inflows with occur at lower Mach numbers everywhere compared with pure isothermal () inflows, while isothermal outflows take place at much lower Mach numbers than their non-isothermal counterparts. In addition, for the isothermal accretion the sonic radius occurs at larger distances from the centre compared to the non-isothermal inflows, implying that in the former case the supersonic flow occupies a much larger central volume.
- When the UV flux dominates over the X-ray heating in models with spectral line driving, the inflow for given becomes faster everywhere. In particular, at radial distances as close as from the central source the inflow is always supersonic regardless of , where is the Bondi radius. However, as the adiabatic index is increased from to , the inflow of matter occurs at lower Mach numbers.
- The position of the sonic point depends on both the radiation field and the adiabatic index. In particular, when line driving is allowed and is increased from 1.1 to 1.66 the sonic point is at smaller radial distances from the centre. Hence, the central volume occupied by the supersonic inflow decreases in radius with increasing . For given , as the UV emission dominates over the X-ray heating the sonic point is shifted towards larger radii and, as a consequence, the supersonic inflow will occupy larger volumes.
- As long as the fraction of X-ray heating is comparable to that of UV emission from the accretion disc, the outflow at large radii from the central source becomes more supersonic than the inflow close to the black hole. Independently of the radiation field, the faster outflows always occur when .
- With no line driving, the inflow becomes less supersonic as the UV emission dominates over the X-ray heating and the values of increases. In fact, as the UV radiation becomes stronger, the central volume occupied by the supersonic inflow becomes larger as the sonic points are shifted towards larger radii from the gravitational source. In contrast, the outflows become more supersonic as the UV emission becomes stronger and is increased.
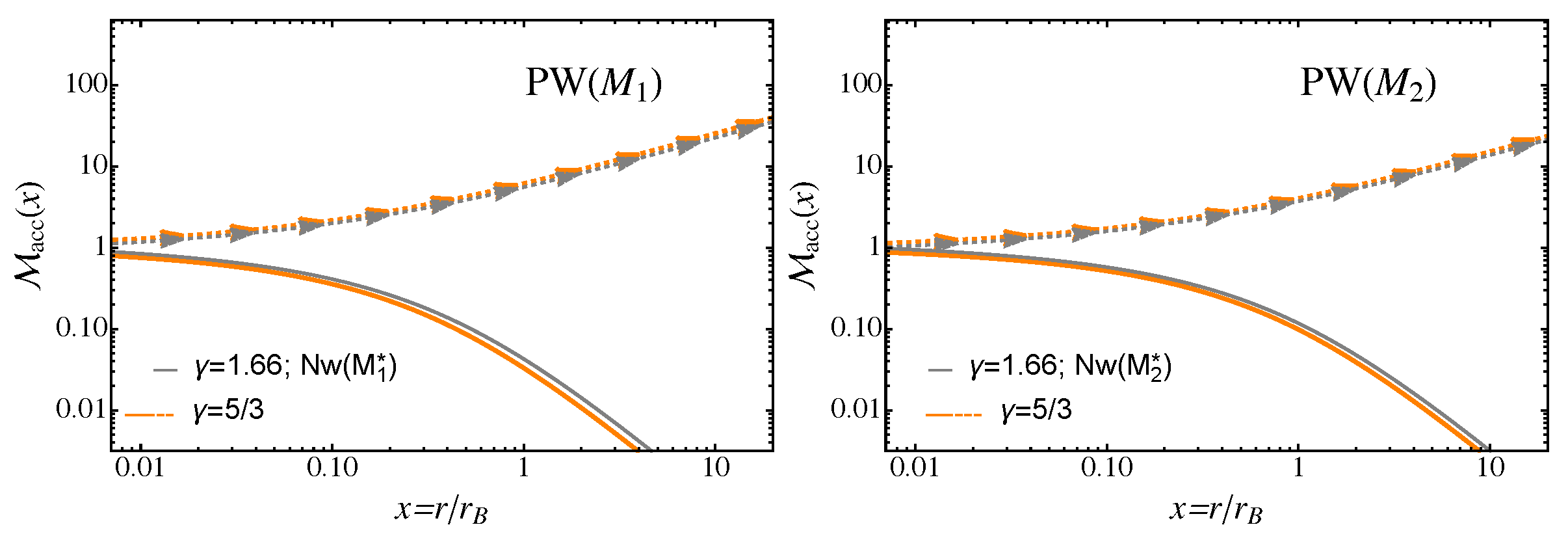
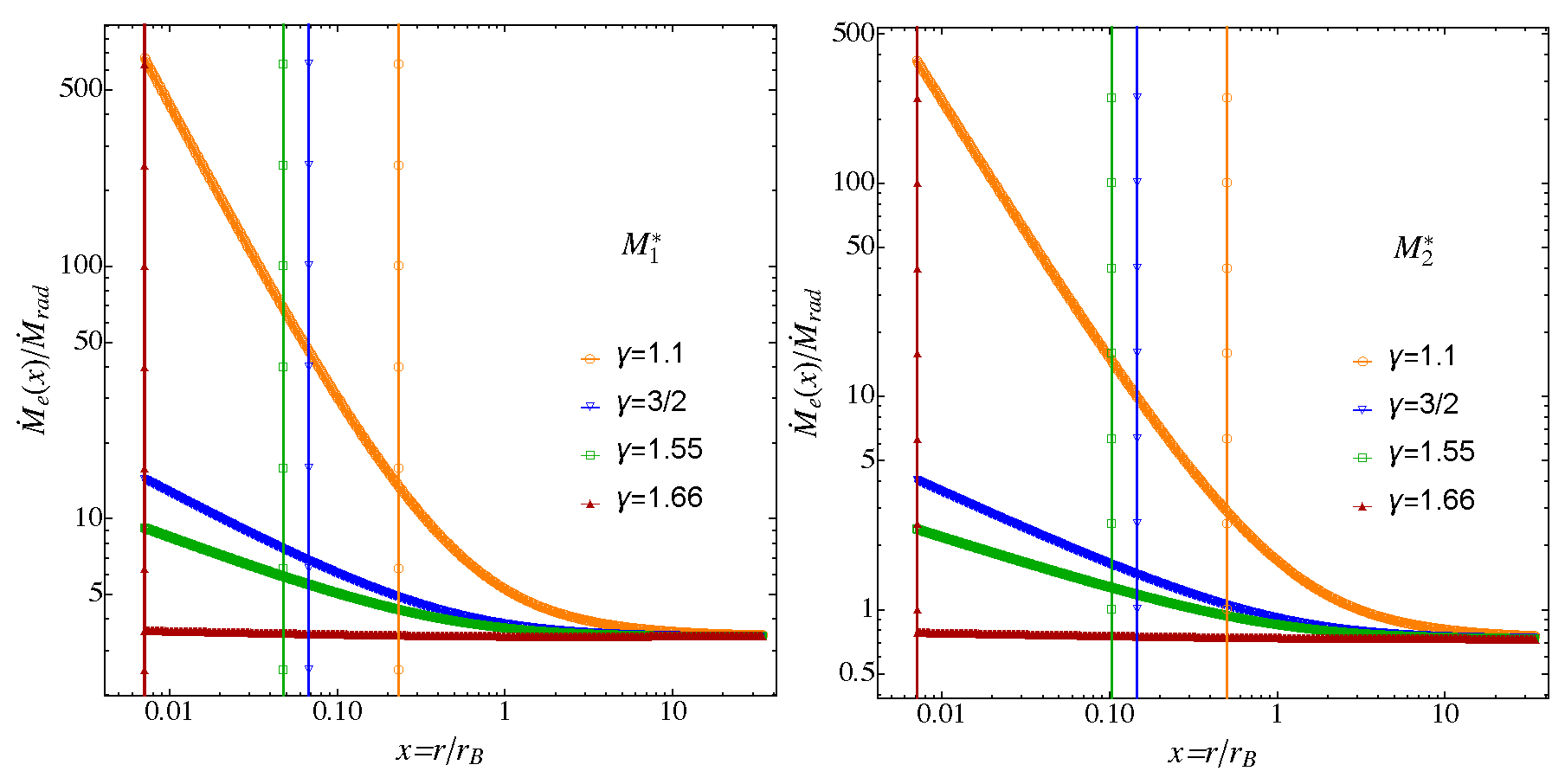
- At distances of from the central source, the ratio of the estimated to the true Bondi radius is always below one. Independently of the dominant type of radiation, the deviations between the estimated and true Bondi radius increase with increasing . For given between and , this ratio drops faster as the radiation field is dominated by the UV emission.
- Under the effects of line driving, the radiative effects lead to an overestimation of the accretion rates close to the centre. The deviation between the estimated and the true accretion rate increases with decreasing . For given , the deviation decreases as the UV emission becomes stronger.
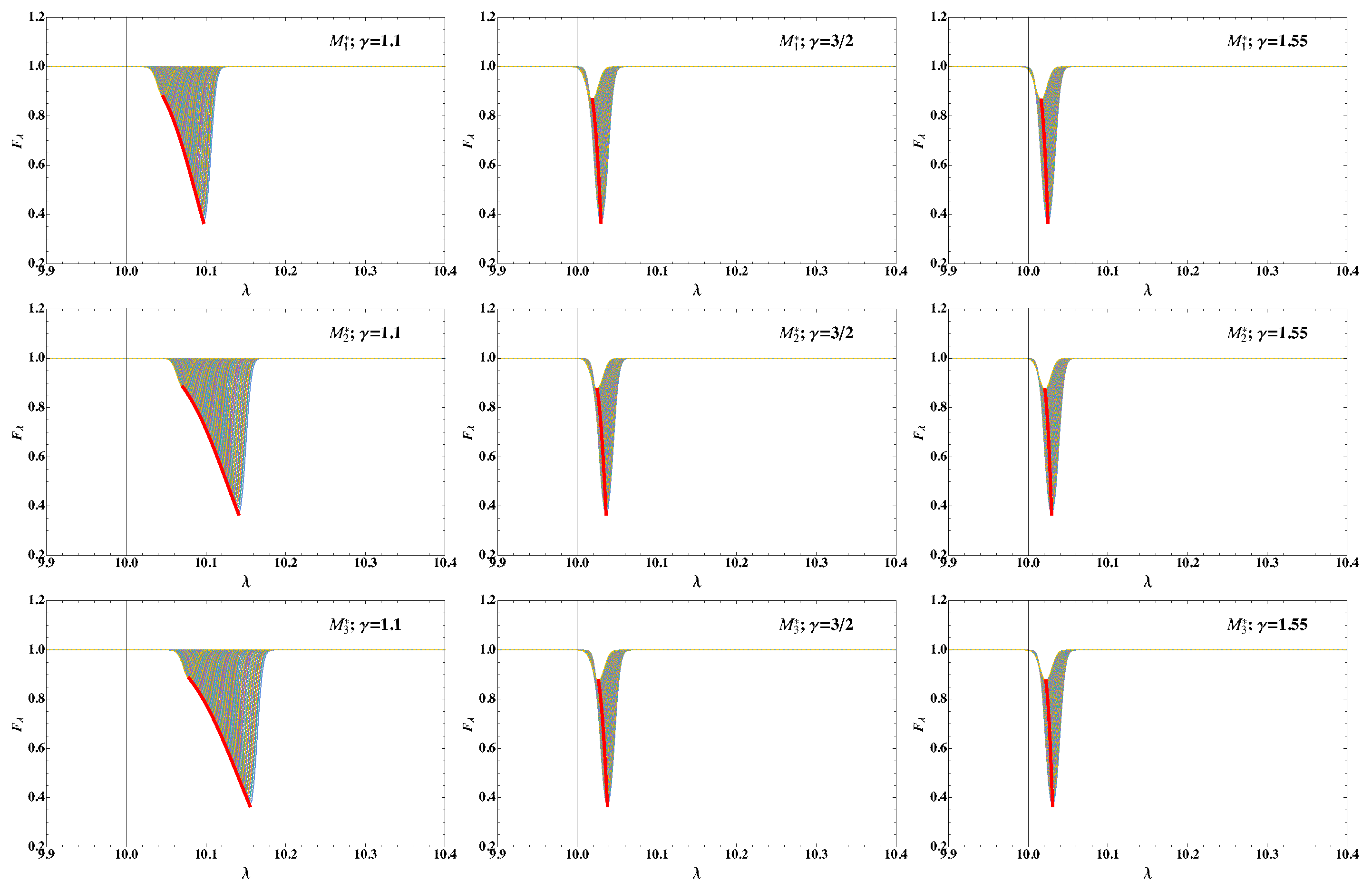
- The models predict broader absorption lines when the UV emission dominates over the high-energy (X-ray) heating, when going from , which in turn become narrower as the value of is increased. For low the lines are so asymmetric, e.g., [52,53], that they can be used to infer which source of radiation is dominant with resolutions of ≈3000 km s. As is increased and the lines become narrower, their shape can no longer be used to distinguish the dominant source of heating.
- Compared to the Newtonian case, the PW model with and no spectral line driving exhibits almost identical inflow Mach numbers everywhere. As the UV emission dominates over the X-ray heating, i.e., when increases from 0.5 to 0.8, both the inflow and outflow become slightly faster for the Newtonian case.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | The structure of our solutions is in X, in the same terms as in [48]. Types 5 and 6 solutions are doubled valued in for a given position x, and we exclude them as physical solutions. |
| 2 | With K and . |
References
- Kormendy, J.; Richstone, D. Inward bound—The search for supermassive black holes in galactic nuclei. Annu. Rev. Astron. Astrophys. 1995, 33, 581–624. [Google Scholar] [CrossRef]
- Ferrarese, L.; Ford, H. Supermassive black holes in galactic nuclei: Past, present and future research. Space Sci. Rev. 2005, 116, 523–624. [Google Scholar] [CrossRef]
- Contreras, E.; Rincón, Á.; Ramírez-Velásquez, J.M. Relativistic dust accretion onto a scale-dependent polytropic black hole. Eur. Phys. J. C 2019, 79, 53. [Google Scholar] [CrossRef]
- Bondi, H. On spherically symmetrical accretion. Mon. Not. R. Astron. Soc. 1952, 112, 195–204. [Google Scholar] [CrossRef]
- Salpeter, E.E. Accretion of interstellar matter by massive objects. Astrophys. J. 1964, 140, 796–800. [Google Scholar] [CrossRef]
- Fabian, A.C. The obscured growth of massive black holes. Mon. Not. R. Astron. Soc. 1999, 308, L39–L43. [Google Scholar] [CrossRef]
- Barai, P. Large-scale impact of the cosmological population of expanding radio galaxies. Astrophys. J. Lett. 2008, 682, L17–L20. [Google Scholar] [CrossRef]
- Germain, J.; Barai, P.; Martel, H. Anisotropic active galactic nucleus outflows and enrichment of the intergalactic medium. I. Metal disribution. Astrophys. J. 2009, 704, 1002–1020. [Google Scholar] [CrossRef]
- Croston, J.H.; Hardcastle, M.J.; Birkinshaw, M.; Worrall, D.M.; Laing, R.A. An XMM-Newton study of the environments, particle content and impact of low-power radio galaxies. Mon. Not. R. Astron. Soc. 2008, 386, 1709–1728. [Google Scholar] [CrossRef][Green Version]
- DiMatteo, T.; Springel, V.; Hernquist, L. Energy input from quasars regulates the growth and activity of black holes and their host galaxies. Nature 2005, 433, 604–607. [Google Scholar] [CrossRef]
- Sincell, M.W.; Krolik, J.H. The vertical structure and ultraviolet spectrum of X-ray-irradiated accretion disks in active galactic nuclei. Astrophys. J. 1997, 476, 605–619. [Google Scholar] [CrossRef]
- Proga, D. Winds from accretion disks driven by radiation and magnetocentrifugal force. Astrophys. J. 2000, 538, 684–690. [Google Scholar] [CrossRef]
- Proga, D. Dynamics of accretion flows irradiated by a quasar. Astrophys. J. 2007, 661, 693–702. [Google Scholar] [CrossRef]
- Proga, D.; Waters, T. Cloud formation and acceleration in a radiative environment. Astrophys. J. 2015, 804, 137. [Google Scholar] [CrossRef]
- Ramírez-Velasquez, J.M.; Klapp, J.; Gabbasov, R.; Cruz, F.; Sigalotti, L.D. Impetus: New cloudy’s radiative tables for accretion onto a galaxy black hole. Astrophys. J. Suppl. Ser. 2016, 226, 22. [Google Scholar] [CrossRef]
- Dyda, S.; Dannen, R.; Waters, T.; Proga, D. Irradiation of astrophysical objects—SED and flux effects on thermally driven winds. Mon. Not. R. Astron. Soc. 2017, 467, 4161–4173. [Google Scholar] [CrossRef]
- Ramírez-Velasquez, J.M.; Klapp, J.; Gabbasov, R.; Cruz, F.; Sigalotti, L.D. The IMPETUS project: Using ABACUS for the high performance computation of radiative tables for accretion onto a galaxy black hole. In Recent Developments in High Performance Computing; Barrios Hernández, C.J., Gitler, I., Klapp, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 697, pp. 374–386. [Google Scholar]
- Silk, J.; Rees, M.J. Quasars and galaxy formation. Astron. Astrophys. 1998, 331, L1–L4. [Google Scholar]
- Furlanetto, S.R.; Loeb, A. Metal absorption lines as probes of the intergalactic medium prior to the reionization epoch. Astrophys. J. 2003, 588, 18–34. [Google Scholar] [CrossRef]
- Haiman, Z.; Bryan, G.L. Was star formation suppressed in high-redshift minihalos? Astrophys. J. 2006, 65, 7–11. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Hernquist, L.; Cox, T.J.; Robertson, B.; Springel, V. Determining the properties and evolution of red galaxies from the quasar luminosity function. Astrophys. J. Suppl. Ser. 2006, 163, 50–79. [Google Scholar] [CrossRef]
- Ciotti, L.; Ostriker, J.P.; Proga, D. Feedback from central black holes in elliptical galaxies. III. Models with both radiative and mechanical feedback. Astrophys. J. 2010, 717, 708–723. [Google Scholar] [CrossRef]
- McCarthy, I.G.; Schaye, J.; Ponman, T.J.; Bower, R.G.; Booth, C.M.; DallaVecchia, C.; Crain, R.A.; Springel, V.; Theuns, T.; Wiersma, R.P.C. The case for AGN feedback in galaxy groups. Mon. Not. R. Astron. Soc. 2010, 406, 822–839. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Choi, E.; Ciotti, L.; Novak, G.S.; Proga, D. Momentum driving: Which physical processes dominate active galactic nucleus feedback? Astrophys. J. 2010, 722, 642–652. [Google Scholar] [CrossRef]
- Fabian, A.C. Observational evidence of active galactic nuclei feefback. Annu. Rev. Astron. Astrophys. 2012, 50, 455–489. [Google Scholar] [CrossRef]
- Faucher-Giguère, C.-A.; Quataert, E.; Murray, N. A physical model of FeLoBALs: Implications for quasar feedback. Mon. Not. R. Astron. Soc. 2012, 420, 1347–1353. [Google Scholar] [CrossRef]
- Choi, E.; Naab, T.; Ostriker, J.P.; Johansson, P.H.; Moster, B.P. Consequences of mechaical and radiative feedback from black holes in disc galaxy mergers. Mon. Not. R. Astron. Soc. 2014, 442, 440–453. [Google Scholar] [CrossRef]
- Dannen, R.C.; Proga, D.; Kallman, T.R.; Waters, T. Photoionization calculations of the radiation force due to spectral lines in AGNs. arXiv 2019, arXiv:1812.01773v2. [Google Scholar] [CrossRef]
- Palit, I.; Janiuk, A.; Sukova, P. Effects of adiabatic index on the sonic surface and time variability of low angular momentum accretion flows. Mon. Not. R. Astron. Soc. 2019, 487, 755–768. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Das, S. Model dependence of transonic properties of accretion flows around black holes. Mon. Not. R. Astron. Soc. 2001, 327, 808–812. [Google Scholar] [CrossRef]
- Das, T.K. On some transonic aspects of general relativistic spherical accretion on to Schwarzschild black holes. Mon. Not. R. Astron. Soc. 2002, 330, 563–566. [Google Scholar] [CrossRef][Green Version]
- Meliani, Z.; Sauty, C.; Tsinganos, K.; Vlahakis, N. Relativistic Parker winds with variable effective polytropic index. Astron. Astrophys. 2004, 425, 773–781. [Google Scholar] [CrossRef]
- Fukue, J. Transonic disk accretion revisited. Publ. Astron. Soc. Jpn. 1987, 39, 309–327. [Google Scholar]
- Chattopadhyay, I.; Ryu, D. Effects of fluid composition on spherical flows around black holes. Astrophys. J. 2009, 694, 492. [Google Scholar] [CrossRef]
- Sarkar, S.; Chattopadhyay, I.; Laurent, P. Two-temperature solutions and emergent spectra from relativistic accretion discs around black holes. Astron. Astrophys. 2020, 642, A209. [Google Scholar] [CrossRef]
- Fabian, A.C.; Rees, M.J. The accretion luminosity of a massive black hole in an elliptical galaxy. Mon. Not. R. Astron. Soc. 1995, 277, L55–L58. [Google Scholar] [CrossRef]
- Volonteri, M.; Rees, M.J. Rapid growth of high-redshift black holes. Astrophys. J. 2005, 633, 624–629. [Google Scholar] [CrossRef]
- Ramírez-Velasquez, J.M.; Sigalotti, L.D.; Gabbasov, R.; Klapp, J.; Contreras, E. Bondi accretion for adiabatic flows onto a massive black hole with an accretion disc. The one dimensional problem. Astron. Astrophys. 2019, 631, A13. [Google Scholar] [CrossRef]
- Ciotti, L.; Pellegrini, S. Isothermal Bondi accretion in Jaffe and Hernquist galaxies with a central black hole: Fully analytical solutions. Astrophys. J. 2017, 848, 29. [Google Scholar] [CrossRef]
- Ciotti, L.; ZiaeeLorzad, A. Two-component Jaffe models with a central black hole—I. The spherical case. Mon. Not. R. Astron. Soc. 2018, 473, 5476–5491. [Google Scholar] [CrossRef]
- Korol, V.; Ciotti, L.; Pellegrini, S. Bondi accretion in early-type galaxies. Mon. Not. R. Astron. Soc. 2016, 460, 1188–1200. [Google Scholar] [CrossRef]
- Ramírez-Velasquez, J.M.; Sigalotti, L.D.; Gabbasov, R.; Cruz, F.; Klapp, J. IMPETUS: Consistent SPH calculations of 3D spherical Bondi accretion on to a black hole. Mon. Not. R. Astron. Soc. 2018, 477, 4308–4329. [Google Scholar] [CrossRef]
- Castor, J.I.; Abbott, D.C.; Klein, R.I. Radiation-driven winds of of stars. Astrophys. J. 1975, 195, 157–174. [Google Scholar] [CrossRef]
- Stevens, I.R.; Kallman, T.R. X-ray illuminated stellar winds: Ionization effects in the radiative driving of stellar winds in massive X-ray binary systems. Astrophys. J. 1990, 365, 321–331. [Google Scholar] [CrossRef]
- Paczyński, B.; Wiita, P.J. Thick accretion disks and supercritical luminosities. Astron. Astrophys. 1980, 88, 23–31. [Google Scholar]
- Abramowicz, M.A. The Paczyński-Wiita potential. A step-by-step derivation. Astron. Astrophys. 2009, 500, 213–214. [Google Scholar] [CrossRef]
- Proga, D.; Begelman, M.C. Accretion of low angular momentum material onto black holes: Two-dimensional hydrodynamical inviscid case. Astrophys. J. 2003, 582, 69–81. [Google Scholar] [CrossRef]
- Frank, J.; King, A.; Raine, D.J. Accretion Power in Astrophysics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Laor, A.; Fiore, F.; Elvis, M.; Wilkes, B.J.; McDowell, J.C. The soft X-ray properties of a complete sample of optically selected quasars. II. Final results. Astrophys. J. 1997, 477, 93–113. [Google Scholar] [CrossRef]
- Zheng, W.; Kriss, G.A.; Telfer, R.C.; Grimes, J.P.; Davidsen, A.F. A composite HST spectrum of quasars. Astrophys. J. 1997, 475, 469–478. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wiley-Interscience: New York, NY, USA, 1979. [Google Scholar]
- Ramírez, J.M.; Bautista, M.; Kallman, T. Line asymmetry in the Seyfert galaxy NGC 3783. Astrophys. J. 2005, 627, 166–176. [Google Scholar] [CrossRef]
- Ramírez, J.M. Kinematics from spectral lines for AGN outflows based on time-independent radiation-driven wind theory. Rev. Mex. Astron. Astrofísica 2011, 47, 385–399. [Google Scholar]




| Run | Lines | |||||
|---|---|---|---|---|---|---|
| (rad) | (rad) | |||||
| M | yes | 0.50 | 0.50 | - | 1.1 | |
| M | yes | 0.20 | 0.80 | - | 1.6 | |
| M | yes | 0.05 | 0.95 | - | 1.7 | |
| M | no | 0.50 | 0.50 | - | 1 | |
| M | no | 0.20 | 0.80 | - | 1.5 | |
| M | no | 0.05 | 0.95 | - | 1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Velásquez, J.M.; Sigalotti, L.D.G.; Gabbasov, R.; Klapp, J.; Contreras, E. The Radiative Newtonian 1 < γ ≤ 1.66 and the Paczyński–Wiita γ = 5/3 Regime of Non-Isothermal Bondi Accretion onto a Massive Black Hole with an Accretion Disc. Galaxies 2021, 9, 55. https://doi.org/10.3390/galaxies9030055
Ramírez-Velásquez JM, Sigalotti LDG, Gabbasov R, Klapp J, Contreras E. The Radiative Newtonian 1 < γ ≤ 1.66 and the Paczyński–Wiita γ = 5/3 Regime of Non-Isothermal Bondi Accretion onto a Massive Black Hole with an Accretion Disc. Galaxies. 2021; 9(3):55. https://doi.org/10.3390/galaxies9030055
Chicago/Turabian StyleRamírez-Velásquez, Jose M., Leonardo Di G. Sigalotti, Ruslan Gabbasov, Jaime Klapp, and Ernesto Contreras. 2021. "The Radiative Newtonian 1 < γ ≤ 1.66 and the Paczyński–Wiita γ = 5/3 Regime of Non-Isothermal Bondi Accretion onto a Massive Black Hole with an Accretion Disc" Galaxies 9, no. 3: 55. https://doi.org/10.3390/galaxies9030055
APA StyleRamírez-Velásquez, J. M., Sigalotti, L. D. G., Gabbasov, R., Klapp, J., & Contreras, E. (2021). The Radiative Newtonian 1 < γ ≤ 1.66 and the Paczyński–Wiita γ = 5/3 Regime of Non-Isothermal Bondi Accretion onto a Massive Black Hole with an Accretion Disc. Galaxies, 9(3), 55. https://doi.org/10.3390/galaxies9030055






