Particle Motion and Plasma Effects on Gravitational Weak Lensing in Lorentzian Wormhole Spacetime

Abstract

Here we study particle motion in the specific Lorentzian wormhole spacetime characterized, in addition to the total mass M, with the dimensionless parameter $\mathsf{\lambda }$. In particular we calculate the radius of the innermost stable circular orbit (ISCO) for test particles and the photonsphere for massless particles. We show that the effect of the dimensionless wormhole parameter decreases the ISCO radius and the radius of the photon orbit. Then, we study plasma effects on gravitational weak lensing in wormhole spacetime and obtain the deflection angle of the light. We show that the effect of $\mathsf{\lambda }$ decreases the deflection angle. We study the effects of uniform and non-uniform plasma on the light deflection angle separately, and show that the uniform plasma causes the deflection angle to be smaller in contrast to the non-uniform plasma.

1. Introduction

In general relativity (GR), black holes are very exciting and fascinating objects, with geometric properties that pertain to the occurrence of singularity. Recent experiments related to VLBI [1,2], BlackHoleCam, and EHT [3,4] have provided strong evidence for presence of black holes and opened a qualitatively new stage to study remarkable properties of astrophysical black holes regardless of fundamental problems of GR that pertain to the occurrence of singularity, spacetime quantization, etc. Furthermore, the Sagittarius A${}^{🟉}$ (Sgr* A${}^{🟉}$) at the center of the Milky Way galaxy has also provided excellent tests in probing black hole accretion disk, jet formation, magnetic field structure, etc. [5,6,7,8].

Although the abovementioned experiments and observations play a decisive role in probing unknown aspects of astrophysical compact objects in the Universe, there are still no departures from the expected behavior of general relativistic compact objects. Among exciting and fascinating objects the occurrence of wormholes in the Universe is extremely important to connect two or more points in the spacetime. However, the geometry of wormholes can be found as a generic result of finding an exact analytical solution of Einstein field equations, and thus they are well supported by Einstein’s general theory of relativity (e.g., [9,10,11,12,13]) regardless of the fact that there is still no any evidence in favour of the existence of wormholes endowed with such exotic properties in the Universe. There is a vast body of literature in the context of different wormhole models, starting from Einstein and Rosen (1935) (e.g., [9,10,11,14,15,16,17,18,19]). Later, the above wormhole model was extended to the context of axially symmetric wormholes [20,21], Einstein–Gauss–Bonnet gravity [22,23], higher-dimensional wormholes [24], cosmological wormholes in $f\left(R\right)$ gravity [25], scalar–tensor field [26], 4D Einstein–Gauss–Bonnet and Einstein–Maxwell–Dirac theories of gravity [27,28], as well as braneworld gravity [29]. There are also investigations suggesting that supermassive black hole candidates could be regarded like the abovementioned wormholes (e.g., [30,31,32,33]). However, this would not be the case for wormholes in nature. Very recently, epicyclic frequencies have been studied in static and spherically symmetric wormhole geometries to infer information about the related gravity background [34]. The optical properties of wormholes in the presence of a plasma medium were studied in [35], and particle motion around a static axially symmetric wormhole has also been considered [36]. Interestingly, the authors in [37] constrained the wormhole geometries using the motion of the S2 star orbiting the Sgr* A${}^{🟉}$ at the center of the Milky Way galaxy.

Recent analyses suggest that the wormholes are intriguing objects in GR, similarly to astrophysical black holes. The investigation of their remarkable properties (e.g., optical properties) is very important, as it is possible to analyze the recent image of the detected M87 galaxy to distinguish between two geometries (i.e., wormholes and black holes). In fact, the image of the supermassive black hole at the center of the elliptical M87 galaxy has been used to test various forms of wormholes [38,39]. Additionally, its geometry and structure have been tested by the gravitational lensing effects using compact gravitational objects [40,41,42] and the motion of test particles [43,44,45,46,47,48]. With this motivation, we wish to study particle motion and gravitational lensing in the wormhole spacetime. We also consider plasma effects on the gravitational lensing by wormhole since there is plasma medium in the nearby environment in the astrophysical scenario. Extensive analysis has already been done along these lines to study gravitational weak lensing [49,50,51,52] by different gravity models in the weak-field regime in the presence of plasma medium [53,54,55,56,57,58,59,60,61].

This paper is organized as follows. We briefly introduce the wormhole spacetime metric, which is followed by the main discussion of the geodesic equations and particle orbits in Section 2. In Section 3, we study the plasma effect on gravitational lensing in the weak-field regime in wormhole geometry. We end with conclusions in Section 4.

Throughout, we use a system of units in which $G=c=1$ and choose the sign conventions $(-,+,+,+)$.

2. Wormhole Spacetime Metric and Geodesic Equation

The metric describing spherically symmetric wormhole spacetime in the Boyer–Lindquist coordinates $(t,r,\theta ,\phi )$ is given by [62]

$$d{s}^2=-\left(f\left(r\right)+{\mathsf{\lambda }}^2\right)d{t}^2+\frac{1}{f\left(r\right)}d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2),$$

(1)

with $\mathsf{\lambda }$ being a dimensionless parameter and $f\left(r\right)=1-2M/r$, where M is the wormhole mass. Note that in the limit $\mathsf{\lambda }\to 0$ the above metric recovers the standard Schwarzschild metric.

Let us evaluate the Kretschmann scalar to understand the property of Lorentzian wormhole singularity and compare it with the Schwarzschild case. The Kretschmann scalar for Lorentzian wormhole geometry reads as follows:

$$\begin{array}{ccc}\hfill \mathcal{K}& =& R_{\alpha \beta \mu \nu }{R}^{\alpha \beta \mu \nu }=\frac{48M^2{(r-2M)}^4}{r^6{\left(r-2M+{\mathsf{\lambda }}^{2}r\right)}^4}\hfill \\ & +& \frac{4M^2\left. [4(9r-19M){(r-2M)}^{2}r{\mathsf{\lambda }}^2+\left(42r^2-172Mr+177M^2\right)r^2{\mathsf{\lambda }}^4+24(r-2M)r^3{\mathsf{\lambda }}^6+6r^4{\mathsf{\lambda }}^8\right]}{r^6{\left(r-2M+{\mathsf{\lambda }}^{2}r\right)}^4},\hfill \end{array}$$

(2)

which recovers the Schwarzschild case when $\mathsf{\lambda }=0$. This clearly shows that the Kretschmann scalar considered here is quite distinct from the Schwarzschild case, for which the real singularity exists only at $r=0$.

We further study particle motion around Lorentzian wormhole, described by the line element given by Equation (1). For particle dynamics treatment one can use geodesic equations [63] rewritten with the following components of the equations of motion:

$$\begin{array}{ccc}\hfill \dot{t}& =& \frac{E}{f\left(r\right)+{\mathsf{\lambda }}^2},\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \dot{\varphi }& =& \frac{L}{r^2},\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \dot{r}& =& E^2\frac{f\left(r\right)}{f\left(r\right)+{\mathsf{\lambda }}^2}-f\left(r\right)\left(\frac{L^2}{r^2}+m^2\right),\hfill \end{array}$$

(5)

where $\dot{t}$, $\dot{\varphi }$, $\dot{r}$ are three velocity components (i.e., the first derivative with respect to the affine parameter) and $m=1$ refers to the mass of the test particle ($m=0$ for the massless particle). Now we obtain the effective potential using the usual conception of radial motion $\dot{r}$:

$$\begin{array}{ccc}\hfill V_{eff}\left(r\right)& =& \left(1-\frac{2M}{r}+{\mathsf{\lambda }}^2\right)\left(m^2+\frac{L^2}{r^2}\right).\hfill \end{array}$$

(6)

The radial profile of the effective potential is shown in Figure 1 for different values of $\mathsf{\lambda }$ for massive and massless particle cases. As can bee seen from the radial profile of $V_{eff}$, the curves shift toward the left to smaller r in both cases. However, one can observe that the strength of effective potential becomes stronger with as the dimensionless parameter $\mathsf{\lambda }$ increases for massive particle and photon motion.

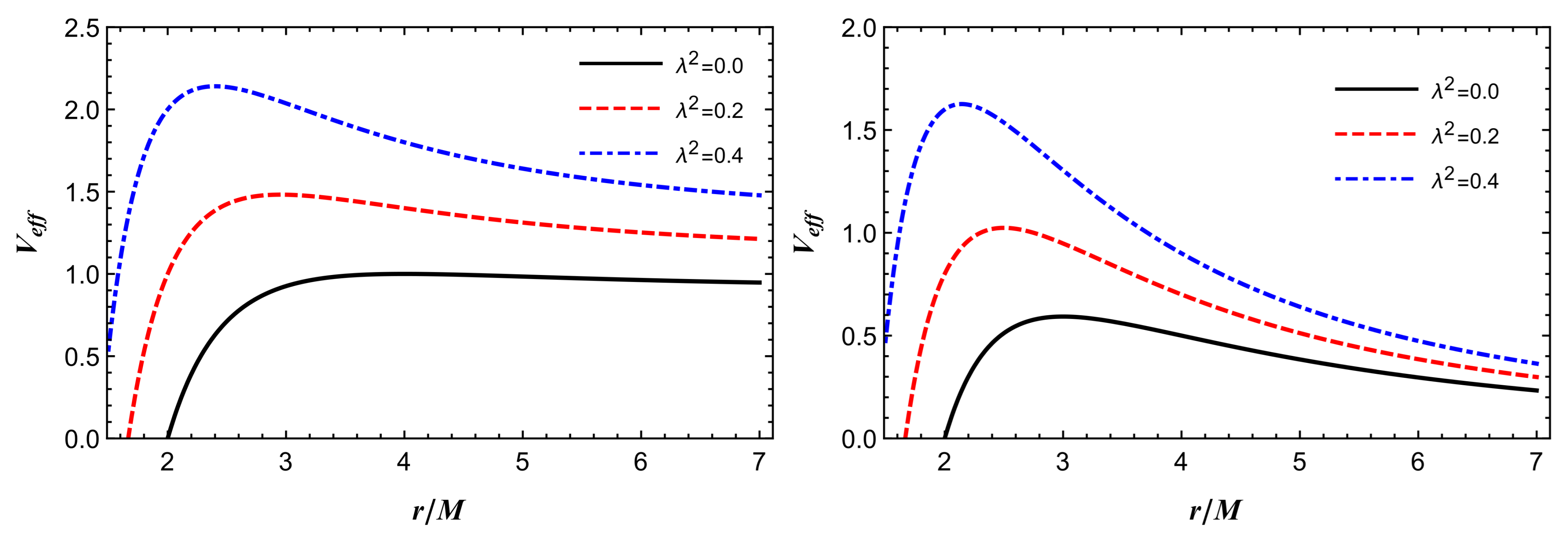
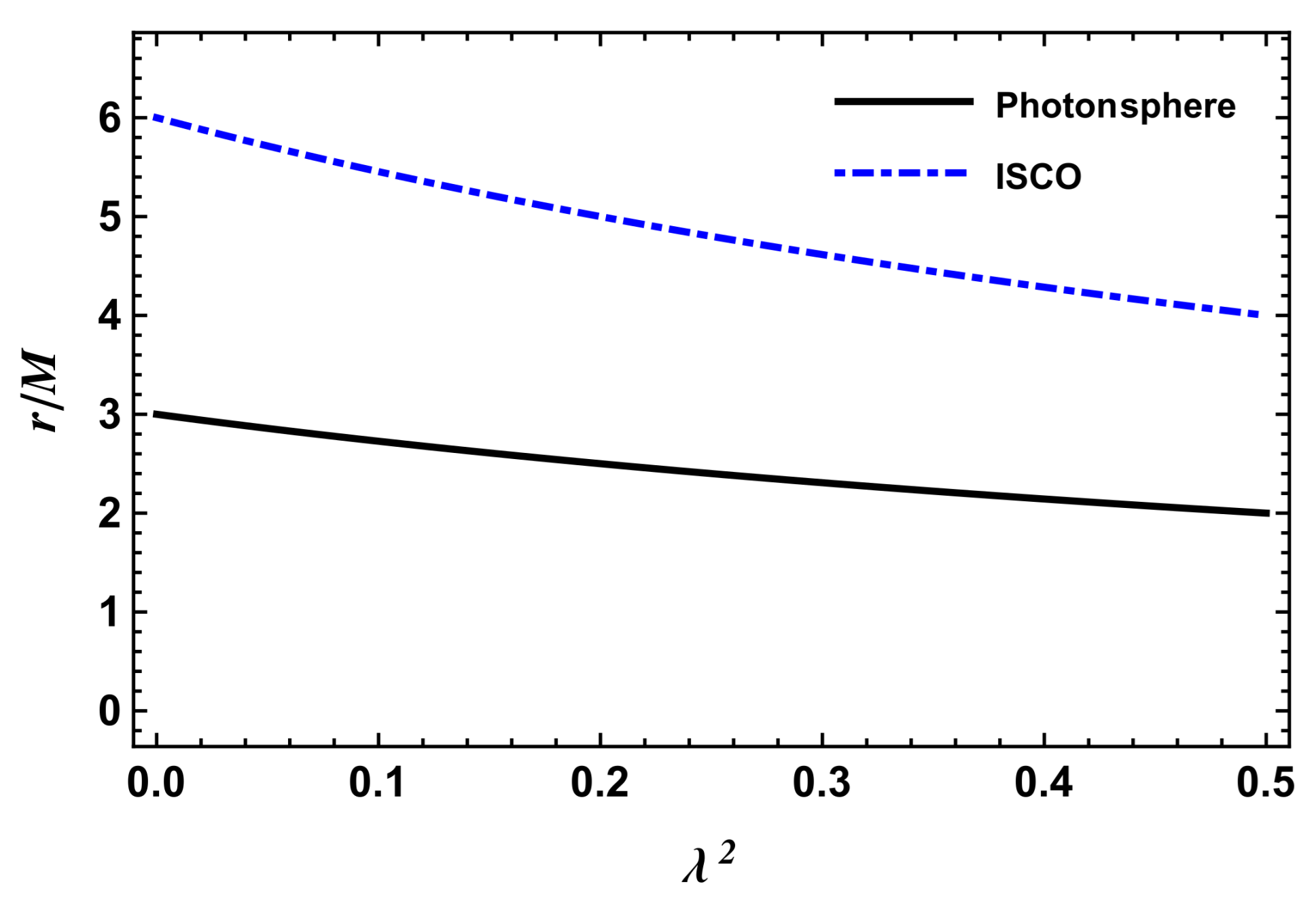
Stable Circular Orbits

We then turn to the the effective potential to study circular orbits around wormhole geometry, solving $V_{eff}(r,\mathcal{L})=0$ and ${\partial }_r{V}_{eff}(r,\mathcal{L})=0$ simultaneously to give the radii of circular orbits. The radial dependence of specific angular momentum $\mathcal{L}$ and energy $\mathcal{E}$ at the circular orbits are given by

$$\begin{array}{c}\hfill {\mathcal{E}}^2=\frac{\left(-6M+{\mathsf{\lambda }}^{2}r+r\right){\left(-2M+{\mathsf{\lambda }}^{2}r+r\right)}^3}{{\mathsf{\lambda }}^2{r}^2\left(24M^2-12\left({\mathsf{\lambda }}^2+1\right)Mr+{\left({\mathsf{\lambda }}^2+1\right)}^2{r}^2\right)}\end{array}$$

(7)

and

$$\begin{array}{c}\hfill {\mathcal{L}}^2=-\frac{4M^2{r}^2}{24M^2-12{\mathsf{\lambda }}^{2}Mr-12Mr+{\mathsf{\lambda }}^4{r}^2+2{\mathsf{\lambda }}^2{r}^2+r^2}.\end{array}$$

(8)

Note that we have used the specific constants of motion per unit particle mass, that is, $\mathcal{E}=E/m$$\mathcal{L}=L/m$. To find the radii of the innermost stable circular orbit (ISCO) one needs to impose the following condition ${\partial }_{rr}{V}_{eff}\left(r\right)=0$ that solves to give the analytical expression

$$\begin{array}{c}\hfill r_{ISCO}=\frac{6M}{1+{\mathsf{\lambda }}^2}.\end{array}$$

(9)

This clearly shows that the ISCO decreases as the dimensionless wormhole parameter $\mathsf{\lambda }$ increases. The behavior of this result is also demonstrated in Figure 2. One can infer from Figure 2 that the dimensionless wormhole parameter $\mathsf{\lambda }$ exhibits a repulsive gravitational charge, thus reducing the radii of circular orbits for massive test particles to be closer to the central object.

Now we explore photon orbits which determine the existence of threshold for circular orbits which would not exist $r<r_{ph}$. For unstable circular orbits of photons one needs to solve ${\tilde{V}}_{eff}\left(r\right)=0={\partial }_r{\tilde{V}}_{eff}\left(r\right)$ simultaneously, so that the radius of the photon orbit takes

$$\begin{array}{c}\hfill r_{ph}=\frac{3M}{1+{\mathsf{\lambda }}^2}.\end{array}$$

(10)

From the above analytical expression, it is obvious that the radius of the photon orbit $r_{ph}$ decreases with increasing dimensionless parameter $\mathsf{\lambda }$, similarly to what is observed in the ISCO case. Now we wish to show the resulting plot of the radius of the photon orbit. As a consequence of the presence of $\mathsf{\lambda }$ the radius of the photon orbit slightly decreases as compared to the curve of ISCO, as seen in Figure 2.

3. Weak-Field Lensing

In this section, we study plasma effects on the gravitational lensing around wormhole in the weak-field regime for simplicity. Thus, the line element given by Equation (1) for the weak-field regime can be approximated by the following expression:

$$\begin{array}{c}\hfill g_{\alpha \beta }={\eta }_{\alpha \beta }+h_{\alpha \beta },\end{array}$$

(11)

where ${\eta }_{\alpha \beta }$ and $h_{\alpha \beta }$ respectively refer to the Minkowski spacetime metric and perturbation of the gravity field regime for the GR part. Thus, Equation (11) can be rewritten as [49,64]

$$\begin{array}{cc}\hfill {\eta }_{\alpha \beta }& =\mathrm{diag}(-1,1,1,1),\hfill \\ \hfill h_{\alpha \beta }& \ll 1,h_{\alpha \beta }\to 0\mathrm{under}{x}^{\alpha }\to \infty ,\hfill \\ \hfill g^{\alpha \beta }& ={\eta }^{\alpha \beta }-h^{\alpha \beta },h^{\alpha \beta }=h_{\alpha \beta }.\hfill \end{array}$$

(12)

From the above approximation we then consider the weak-field regime and plasma medium to obtain the gravitational deflection angle for the light propagating along the z axis [49,64]. It is then defined by

$$\begin{array}{cc}\hfill {\widehat{\alpha }}_i& =\frac{1}{2}{\int }_{-\infty }^{\infty }\left(h_{{33}_{,}i}+\frac{{\omega }^2}{{\omega }^2-{\omega }_e^2}{h}_{{00}_{,}i}-\frac{K_e}{{\omega }^2-{\omega }_e^2}N{}_{,}i\right)dz,\hfill \end{array}$$

(13)

where ${\widehat{\alpha }}_i$ takes negative and positive values, that is, it depends on the light which moves either towards or away from the central object considered here. We note that $\omega$ can be fixed $\omega (\infty )=\omega$ at infinity as a limitation. For the weak-field regime, the wormhole spacetime metric considered here can be defined by [64]

$$\begin{array}{c}\hfill d{s}^2=d{s}_0^2+\left(\frac{R_g}{r}+{\mathsf{\lambda }}^2\right)d{t}^2+\left(\frac{R_g}{r}\right)d{r}^2,\end{array}$$

(14)

where the first part $d{s}_0^2=-d{t}^2+d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2)$ describes Minkowski spacetime. The second part of Equation (10), $h_{\alpha \beta }$, can be rewritten in the Cartesian coordinate system as follows:

$$\begin{array}{cc}\hfill h_{00}=& \left(\frac{R_g}{r}+{\mathsf{\lambda }}^2\right),\hfill \\ \hfill h_{33}=& h_{00}{cos}^{2}x,\hfill \end{array}$$

(15)

where we have used $cosx=z/\sqrt{b^2+z^2}$ and $r=\sqrt{b^2+z^2}$ [64].

From the new notation given in Equation (15) we can write the deflection in terms of the impact parameter b for the wormhole spacetime metric in the presence of plasma medium. Thus, we have

$$\begin{array}{c}\hfill {\widehat{\alpha }}_b={\int }_{-\infty }^{\infty }\frac{b}{2r}\left({\partial }_r\left(\left(\frac{R_g}{r}+{\mathsf{\lambda }}^2\right)\frac{z^2}{r^2}\right)+{\partial }_r\left(\frac{R_g}{r}\right)\frac{{\omega }^2}{{\omega }^2-{\omega }_e^2}-\frac{K_e}{{\omega }^2-{\omega }_e^2}{\partial }_{r}N\right)dz.\end{array}$$

(16)

In the following, we analyze the deflection angle for uniform and non-uniform cases with more details.

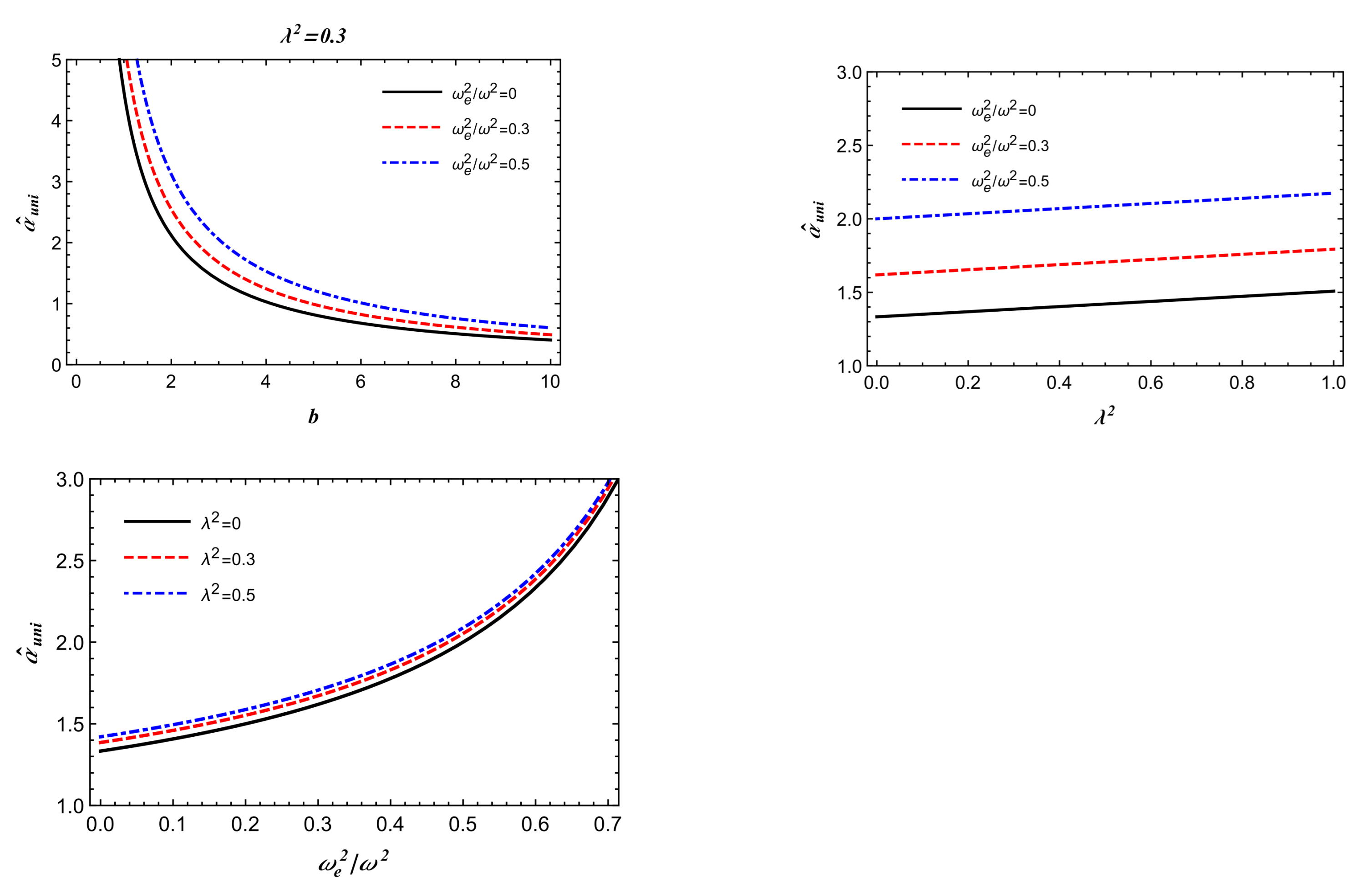
3.1. Uniform Plasma

We now consider the light deflection angle with uniform plasma medium. Hence, Equation (16) yields

$$\begin{array}{c}\hfill {\widehat{\alpha }}_{\mathrm{uni}}=-\frac{R_g}{b}(1+\frac{1}{1-\frac{w_e^2}{w^2}})-\frac{\pi {\mathsf{\lambda }}^2}{2b^2}.\end{array}$$

(17)

For the uniform plasma, ${\partial }_{r}N=0$ is always satisfied. We then analyse the impact of plasma parameter $\frac{{\omega }_e^2}{{\omega }^2}$ and wormhole parameter $\mathsf{\lambda }$ on the deflection angle for various possible cases. We used Equation (17) to obtain Figure 3. As can be seen from Figure 3, the deflection angle increases with an increase in the values of both the dimensionless wormhole parameter $\mathsf{\lambda }$ and the plasma medium parameter $\frac{{\omega }_e^2}{{\omega }^2}$. The circular orbits of the propagating light shift toward the central object due to the impact of the wormhole parameter $\mathsf{\lambda }$, as seen in Figure 3. However, as a consequence of the plasma medium parameter $\frac{{\omega }_e^2}{{\omega }^2}$ the deflection angle of light increases irrespective of the value of $\mathsf{\lambda }$. From an observational point of view, a far away observer could only observe an image being larger than its original one as a consequence of the plasma effect and $\mathsf{\lambda }$.

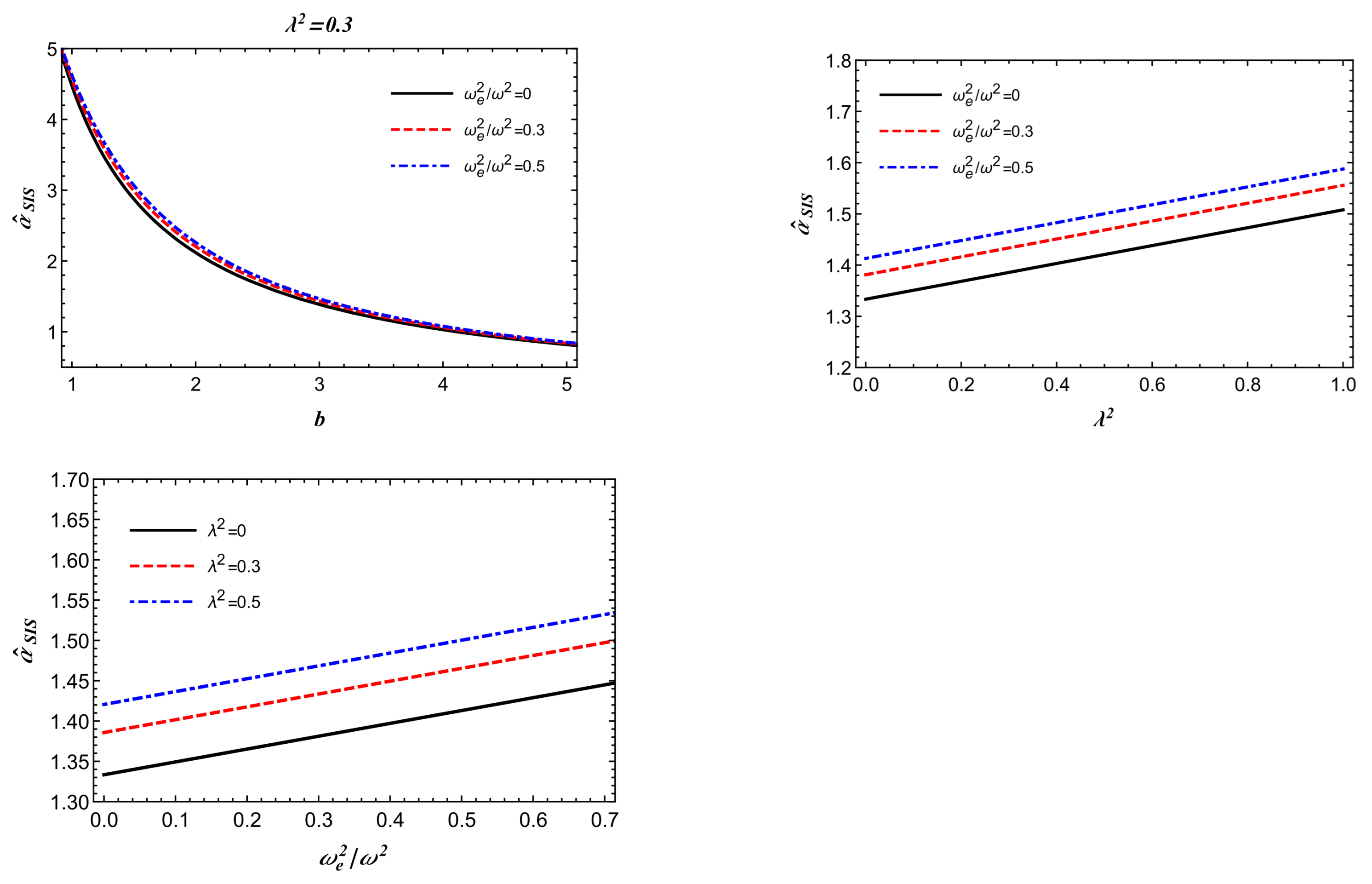
3.2. Non-Uniform Plasma

Next we study the deflection angle as a result of the wormhole gravity in the presence of a singular isothermal sphere (SIS) plasma, which would play the crucial determining role to explain the properties of galaxies and clusters [49] through gravitational weak lensing.

Following [49,64], the configuration of density and the plasma concentration respectively read as follows:

$$\begin{array}{c}\hfill \rho \left(r\right)=\frac{{\sigma }_v^2}{2\pi r^2},\end{array}$$

(18)

where ${\sigma }_v^2$ is a 1D velocity dispersion and

$$\begin{array}{c}\hfill N\left(r\right)=\frac{\rho \left(r\right)}{\kappa m_p},\end{array}$$

(19)

where $m_p$ is the mass of a proton and $\kappa$ is a 1D coefficient corresponding to the dark matter contribution.

From Equation (16) the deflection angle for the non-uniform plasma medium (SIS) can be defined by [49]

$$\begin{array}{c}\hfill {\widehat{\alpha }}_{\mathrm{SIS}}=-\frac{2R_g}{b}+\frac{2R_g^3{w}_c^2}{3\pi b^3{w}^2}-\frac{w_c^2{R}_g^2}{2b^2{w}^2}-\frac{\pi {\mathsf{\lambda }}^2}{2b^2},\end{array}$$

(20)

where we define ${\omega }_c^2$ to represent another plasma constant for simplification, that is, it has the form [64,65]

$$\begin{array}{c}\hfill {\omega }_c^2=\frac{{\sigma }_v^2{K}_e}{2\kappa m_p{R}_g^2}.\end{array}$$

(21)

On the basis of Equation (21), we provide plots reflecting the impact of non-uniform plasma and the dimensionless parameter $\mathsf{\lambda }$ on gravitational lensing properties in the weak-field regime. The dependence of the deflection angle on the impact parameter b of orbits is shown in Figure 4. For large values of the impact parameter b the deflection angle becomes close to zero in the case where $\mathsf{\lambda }$ and $\frac{{\omega }_e^2}{{\omega }^2}$ are taken into consideration (Figure 4). In Figure 4 we show the deflection angle as a function of $\mathsf{\lambda }$ and the plasma parameter $\frac{{\omega }_e^2}{{\omega }^2}$. The bottom panel shows the deflection angle as a function of plasma parameter $\frac{{\omega }_e^2}{{\omega }^2}$ for different values of $\mathsf{\lambda }$, while the left (top) and right (top) panels respectively show the deflection angle as a function of $\mathsf{\lambda }$ for different values of $\frac{{\omega }_e^2}{{\omega }^2}$. From Figure 4 we observe that the parameter $\mathsf{\lambda }$ has similar effect that increases the deflection angle. However, the deflection angle increases in the presence of a non-uniform plasma medium surrounding wormhole geometry—see Figure 4 (top left panel). From the results we infer that the deflection angle in the non-uniform plasma case is smaller than the one for uniform plasma medium.

4. Conclusions

In this work we studied the motion of test massive and massless particles and the effect of plasma on gravitational weak lensing by Lorentzian wormhole. As a consequence of the treatment performed and the results obtained we can summarize the following main conclusions:

• The radii of photon orbit and ISCO were obtained in Lorentzian wormhole spacetime. We found that with increasing dimensionless wormhole parameter $\mathsf{\lambda }$ the radii of ISCO and photon sphere decreased, and consequently approached the central wormhole object.
• We analysed the behaviour of the effective potential, and clearly showed that as a consequence of the effect of $\mathsf{\lambda }$, circular orbits shifted towards the central wormhole object.
• It is well-known that the optical properties of compact objects are very important in testing general relativity versus alternate theories of gravity. In fact, gravitational lensing effect plays the crucial determining role for astrophysical observations. With this motivation, we studied the deflection angle of the light propagation under the gravitational field of Lorentzian wormhole. Uniform and non-uniform (SIS) plasma cases were considered for gravitational weak lensing. We found that the influence of the plasma and $\mathsf{\lambda }$ on the gravitational lensing was noticeable. Namely, with increasing $\mathsf{\lambda }$ the deflection angle also increased, and this was also true when the plasma medium effect was taken into account. We found that the deflection angle for wormhole geometry was either as large as or slightly larger than the value for the Schwarzschild black hole case.