Abstract
To explain the X-ray spectra of active galactic nuclei (AGN), non-thermal activity in AGN coronae such as pair cascade models has been extensively discussed in the past literature. Although X-ray and gamma-ray observations in the 1990s disfavored such pair cascade models, recent millimeter-wave observations of nearby Seyferts have established the existence of weak non-thermal coronal activity. In addition, the IceCube collaboration reported NGC 1068, a nearby Seyfert, as the hottest spot in their 10 year survey. These pieces of evidence are enough to investigate the non-thermal perspective of AGN coronae in depth again. This article summarizes our current observational understanding of AGN coronae and describes how AGN coronae generate high-energy particles. We also provide ways to test the AGN corona model with radio, X-ray, MeV gamma ray, and high-energy neutrino observations.
1. Introduction
Back in 2013, the IceCube collaboration reported evidence of astrophysical neutrinos with energies in the 30 TeV–1 PeV range [1]. The detected neutrinos show an isotropic distribution with a flux level of ≈10 [2]. This discovery indicates that TeV–PeV neutrinos travel to the Earth from the distant Universe. Although various theoretical models have attempted to explain the cosmic TeV–PeV neutrino fluxes even before the operation of IceCube (see, e.g., [3,4] for reviews), the lack of clear source identification hampers our understanding of the origin of the TeV–PeV neutrinos.
In 2018, the IceCube collaboration, together with the other electromagnetic wave observatories, reported a possible spatial and temporal coincidence of a neutrino event with a blazar flare TXS 0506+056 [5,6]. This observation provided the first evidence of a blazar as a cosmic neutrino factory. However, stacking analysis of blazars shows that they can afford only up to ∼30% of the measured cosmic TeV–PeV neutrino background flux [7]. Therefore, even after the first possible source identification, the origin of the cosmic neutrino background flux was still veiled in mystery.
Very recently, the accumulation of 10 year IceCube survey data revealed the existence of a neutrino hot spot toward the direction of NGC 1068 with a confidence level [8]. NGC 1068 is one of the nearest (∼14 Mpc; [9]) and the best-studied Seyfert 2 galaxies in the broadband [10,11,12]. A Seyfert 2 galaxy is a type of active galactic nucleus (AGN) population, where the central engine is supposed to be blocked by the dusty torus. The surface density of Seyferts is ≈ [13], which is about four orders of magnitude higher than that of blazars [14]. This possible neutrino signal from NGC 1068 may indicate that Seyferts dominate the cosmic neutrino sky. An immediate question is how Seyferts generate neutrinos.
Connecting gamma ray and neutrino measurements would allow us to understand the neutrino production mechanism. Indeed, gamma-ray observatories such as Fermi and MAGIC have detected GeV–TeV gamma-ray photons from NGC 1068 [15,16]. However, it turns out that the neutrino flux is brighter than the gamma-ray flux, which simple hadronuclear () or photomeson () interpretation processes cannot accommodate.
Several theoretical models have already been proposed to explain the neutrino excess seen in NGC 1068, such as an accretion disk corona [17,18,19,20], the interaction of broad-line-region clouds with an accretion disk [21], and a galactic cosmic-ray halo [22]. However, as always, for theoretical models, model uncertainties in all of these models are still non-negligible.
Non-thermal activity in AGN coronae has been studied in the literature for several decades (e.g., [18,23,24,25,26,27,28,29,30,31,32,33,34]). The diffuse neutrino flux predicted by one of the pioneering works was at the level of ∼ [35]. Although this is significantly higher than the measured values, we note that it was more than 20 years before the first measurement. When those models were proposed, the lack of various observational information led to such a huge model uncertainty. These results highlight that a better understanding of AGN coronae properties is critical for understanding the neutrino production in AGN coronae.
The recent development of radio and X-ray telescopes now allows us to determine various physical parameters of AGN coronae, such as electron density, temperature, size, and magnetic field strength [36,37]. ALMA observations also show evidence of weak non-thermal coronal activity, which establishes the existence of high-energy particles in AGN coronae [17].
In this Review, we aim to summarize our current understanding of AGN coronae and describe how high-energy signals arise from AGN coronae following Inoue et al. [34]. In Section 2, we briefly look back at the research history of the highenergy aspect of AGN coronae and summarize our current observational understandings of AGN coronae. In Section 3, we describe the generation process of high-energy particles in AGN coronae. In Section 4, we show the expected gamma-ray and neutrino signals and discuss the corona scenario interpretation of the neutrino signals from NGC 1068. In Section 5, the expected cosmic gamma-ray and neutrino background fluxes are described. In Section 6, we compare available models and discuss the ways to test the coronal hypothesis. In Section 7, we summarize this review.
2. Research History of Non-Thermal Activity in AGN Coronae
2.1. Failure of Pair Cascade Model
In this section, we briefly review the research history of non-thermal coronal activity in Seyferts. Scenarios involving the acceleration of high-energy particles in the nuclei of Seyferts have been discussed for a long time.
In the 1980s, about 20 years after the dawn of X-ray astronomy, the production mechanism of X-ray emission in Seyferts was still under debate. One possibility was pair cascades induced by high-energy particles (e.g., [23,24,29]). In the pair cascade model, particles are thought to be accelerated by shock dissipation in accretion flows (e.g., [23,24,25,26,38,39]). These investigations tossed a coin towards Seyferts as cosmic-ray factories [25,26,27,35]. Stecker et al. [27,35] made the first quantitative estimate of the expected neutrino fluxes from Seyferts at the level of ∼3 at 1 PeV. However, in the 1990s, the detection of the X-ray spectral cutoffs (e.g., [40,41]) and non-detection of Seyfert AGNs in the gamma-ray band (e.g., [42]) ruled out the pair cascade scenario as a dominant source for X-ray emission of Seyferts, lowering the expected neutrino fluxes from Seyferts significantly. Therefore, high-energy signals from AGN coronae were not extensively investigated in the community in the late 1990s and 2000s.
2.2. Properties of AGN Coronae Revealed by X-ray Observations
Today, it is widely believed that the AGN X-ray emission is primarily from the Comptonized accretion disk photons from moderately thick thermal plasma, namely coronae, above an accretion disk [43,44,45,46,47,48]. This Comptonized emission appears together with emission reprocessed by the surrounding cold materials, a so-called Compton reflection component (e.g., [49,50,51]). Figure 1 shows a current schematic representation of the AGN spectral energy distribution (SED) without obscuration (see [52,53] for details). We note that the origin of soft X-ray excess is still under debate [54,55].
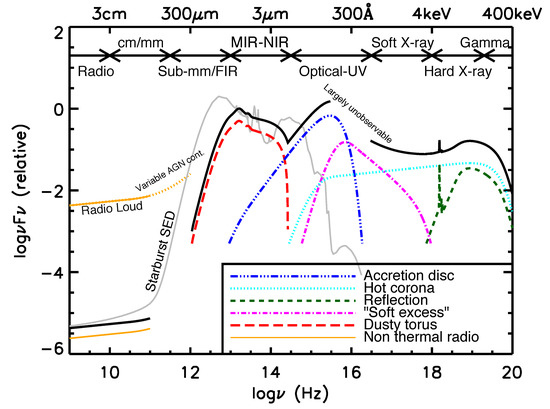
Figure 1.
Schematic representation of the AGN SED (black curve), separated into the main physical components, as indicated by the colored curves. For comparison, the SED of a star-forming galaxy (light gray curve) is also shown. Taken from Harrison [52], Hickox and Alexander [53].
X-ray spectral studies allow us to determine some of the coronal parameters such as the coronal electron temperature, , and the Thomson scattering optical depth (e.g., [56]). Here is the electron number density, is the Thomson scattering cross section, and is the coronal size. Dadina [57] reported that local bright Seyferts typically have their spectral cutoff at keV (Figure 2). This cutoff corresponds to the electron temperature of keV (here k is the Boltzmann constant). The process of Comptonization by thermal plasma is described by the Kompaneets equation [58]. The photon index of the primary X-ray emission of Seyferts is typically [59] (Figure 3). This corresponds to based on the solution to the Kompaneets equation [60] as , where the dimensionless electron temperature . It should be also mentioned that simultaneous optical–X-ray spectral fitting studies [61] and microlensing observation [62] have suggested a corona size , where is the Schwarzschild radius.
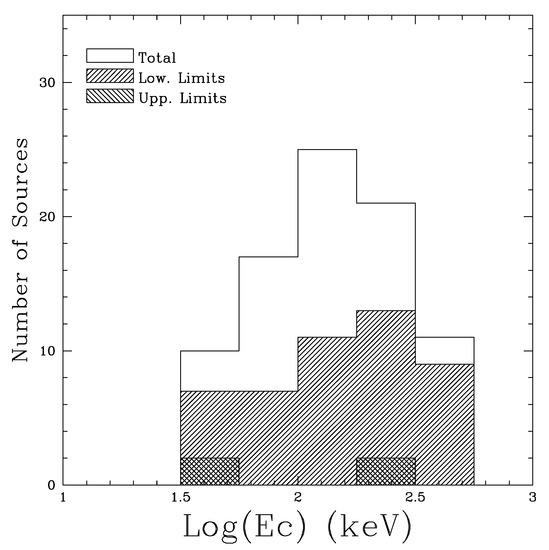
Figure 2.
Distribution of of local Seyferts determined from the BeppoSAX observations. Taken from Dadina [57].
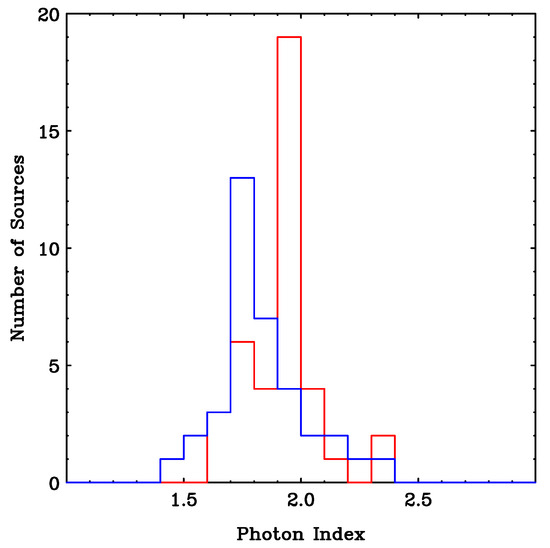
Figure 3.
Distribution of of local Seyferts determined from the Swift/BAT survey. Red and blue correspond to type 1 and type 2 AGNs, respectively. Taken from Ueda et al. [59].
Hard X-ray observations of Seyferts allow us to investigate the AGN coronae further. These have constrained the amount of non-thermal particles in the AGN coronae from the non-detection of the non-thermal features. In order not to violate the NuSTAR observations, the latest constraint on the non-thermal electron energy fraction is obtained as [63].
Together with the success of the Comptonized corona model, population studies of Seyferts have revealed that Seyferts dominate the cosmic X-ray background radiation up to ∼300 keV (e.g., [64,65]). Here, as shown in Figure 4, the cosmic MeV gamma-ray background radiation spectrum smoothly extends from the cosmic X-ray background spectrum [66,67,68]. Because of a spectral cutoff in individual Seyferts, integrated Seyfert X-ray photons would not explain the cosmic MeV gamma-ray background radiation. Several theoretical models have proposed that a small fraction of non-thermal electrons in AGN coronae may be enough to explain the MeV background radiation as well [69,70]. The required fraction was . This amount indicated the possible existence of weak non-thermal activity in AGN coronae. However, this was an ad hoc way to have a simultaneous explanation of the X-ray and MeV backgrounds 1.
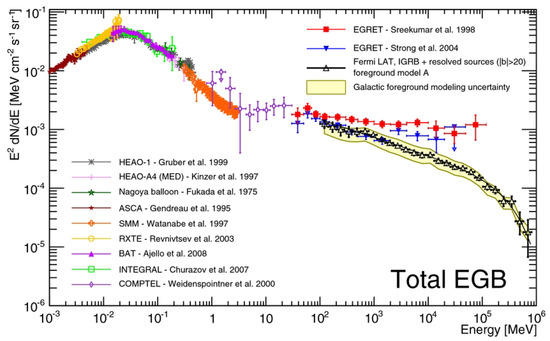
Figure 4.
Cosmic X-ray, MeV gamma-ray, and GeV gamma-ray background radiation spectrum. Taken from Ackermann et al. [73].
2.3. Properties of AGN Coronae Revealed by Millimeter Observations
Theoretically, it is natural to expect that AGN coronae are magnetized [74,75]. Then, coronal non-thermal electrons, as expected for the MeV background radiation, inevitably generate coronal synchrotron emission [76,77,78], which should appear as an excess in the millimeter (mm) band. Inconclusive signs of such a new component in the radio spectra of several Seyfert galaxies have been reported in the literature [79,80,81,82]. However, a paucity of multi-band data and the contamination of extended dust emission hamper the investigation.
Recently, Inoue and Doi [37] reported the detection of power-law coronal radio synchrotron emission from two nearby Seyferts, IC 4329A and NGC 985, utilizing ALMA (See Figure 5), which enabled multi-band observations with high enough angular resolution to exclude the galactic contamination. These observations provided the first determination of the fundamental physical parameters of the AGN coronae: magnetic field strength and its size. The inferred coronal magnetic field strength was ∼10 G with a size of for both Seyferts with a central black hole mass of ∼.
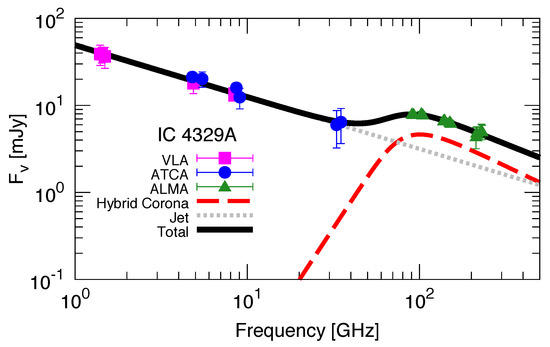
Figure 5.
The cm–mm spectrum of IC 4329A after subtracting extended emission due to galactic star formation activity. The square, circle, and triangle points show the VLA, ATCA, and ALMA data, respectively. The error bars correspond to 1- uncertainties. The dashed and dotted lines show the fitted hybrid corona and jet components, respectively. The solid line shows the sum of these two components. Taken from Inoue and Doi [37].
Coronal synchrotron emission is also reported for NGC 1068 in Inoue et al. [17]. Figure 6 shows the cm–mm spectrum of NGC 1068, which shows a mm excess similar to IC 4329A and NGC 985. The coronal synchrotron emission can reproduce the mm excess of NGC 1068 with parameters of G, , and the spectral index of non-thermal electrons .
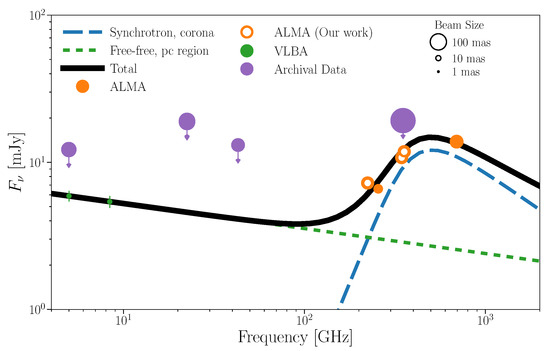
Figure 6.
The cm–mm spectrum of NGC 1068. The data points from VLBA [83] and ALMA [84,85,86] are shown in green and orange, respectively. The open points represent the newly analyzed ALMA data. The size of circles corresponds to the beam sizes as indicated in the figure. We also show the archival mm–cm data having large beam sizes as upper limits in purple [12,87,88]. The error bars correspond to 1- uncertainties. The blue dashed and green dotted lines show the coronal synchrotron and pc-scale free–free components, respectively. The solid black line shows the sum of these two components. Taken from Inoue et al. [17].
Power-law coronal synchrotron emission also suggests that AGN coronae contain both thermal and non-thermal electrons, i.e., hybrid coronae. Therefore, acceleration of high-energy particles should happen in AGN coronae. However, the exact cannot be determined by the current measurements because of degeneracy among , , and . Here, significantly low requires a relatively large based on the radio spectral fitting, which contradicts optical–X-ray spectral fitting studies [61] and microlensing observations [62]. Thus, we may have weak but non-negligible non-thermal coronal activity at the level of .
Inoue and Doi [37] also suggested that the coronae are likely to be advection-heated hot accretion flows [89,90] rather than magnetically heated coronae [74,75] because the measured magnetic field strength (i) is too weak to keep the coronae hot and (ii) is consistent with the value based on the self-similar solutions of hot accretion flows. Thus, we may assume that coronal magnetic field strength scales as [90], where we ignore its dependence on the accretion rate and other parameters for simplicity.
3. Generation of High-Energy Particles in AGN Coronae
Previous non-thermal coronal models have overestimated the non-thermal activity strength since various coronal parameters are not well determined. As described above, current X-ray and radio observations now allow us to determine the corona size , the electron density , the magnetic field , non-thermal electron spectral index p, and even the non-thermal electron energy fraction . With that knowledge, we can again investigate the high-energy particle production processes in AGN coronae. This section provides an overview of the energy loss and acceleration processes of high-energy particles in AGN coronae.
The geometry of black hole coronae is still under debate. A recent polarization study revealed an extended coronal structure in a nearby black hole binary [91]. Such extended coronal geometry is also naturally expected in AGNs. The detailed structure of extended coronae can be a spherical, slab, or patchy. For simplicity, in this review, coronae are assumed to be spherical with a radius of , where is the dimensionless corona size.
Coronae are also set to be in a steady state. The proton number density is set to be equal to , which gives the maximum number of protons in coronae. is defined through as
For simplicity, the gas is assumed to be accreted onto the SMBH with free-fall velocity . The free-fall timescale from the coronal region is estimated to be
3.1. Energy Loss Processes
High-energy particles lose their energies through radiative cooling processes. In AGN coronae, high-energy electrons mainly lose their energies via synchrotron and inverse Compton (IC) radiation. The synchrotron cooling rate for an electron with a Lorentz factor of is
where is the electron rest mass and is the magnetic field energy density of magnetic field strength B.
The inverse Compton cooling rate including the Klein–Nishina cross section [92,93,94] is
where and [93]. The photon energy density, , is given as , where is the AGN core (disk + corona) luminosity and is the photon energy.
Relativistic protons are predominately cooled through inelastic interactions and reactions. Proton synchrotron and IC cooling channels are inefficient as compared to the hardronic mechanisms. Hereinafter, we do not consider proton IC/synchrotron coolings. The cooling time can be expressed as
where is the proton inelasticity of the process and we adopt and . Below we follow the formalism developed by Kelner et al. [95].
The cooling time via photomeson interactions is
where is the proton Lorentz factor, and are the photon energies in the proton rest frame and the black hole frame, respectively, is the energy density of the photon target, and MeV [96].
The interaction also generates secondary leptons and enables pair production via the so-called Bethe–Heitler process. The cooling timescale for the Bethe–Heitler process is approximated as [97]
where is the proton rest mass and is the fine-structure constant.
3.2. Acceleration
Various acceleration mechanisms can take place in the coronae such as the diffusive shock acceleration (DSA) mechanism (e.g., [98,99]), turbulent acceleration (e.g., [100]), magnetosphere acceleration (e.g., [101,102]), and magnetic reconnection (e.g., [103]. In this section, we consider these processes given our current observational knowledge (Section 2).
3.2.1. Diffusive Shock Acceleration
In the framework of DSA (e.g., [98,99]), the acceleration timescale can be approximated as
where D is the diffusion coefficient, is the particle energy, and is the shock speed. is a numerical factor that depends on the shock compression ratio and the spatial dependence of D [98]. We set . Assuming a Bohm-like diffusion,
where e is the electric charge and is the gyrofactor, which is the mean free path of a particle in units of the gyroradius. characterizes the efficiency of the acceleration. corresponds to the Bohm limit case. The DSA time can be written as
where is the gyro radius. is set as . Thus, appears in Equation (10). varies in different astrophysical environments. is possibly seen in a Galactic supernova remnant [104] and a microquasar jet [105], while is seen in the case of blazars in the framework of one-zone leptonic models (e.g., [106,107,108]).
3.2.2. Stochastic Acceleration
Stochastic (turbulent) acceleration has been considered for low accretion rate objects such as low-luminosity AGN (e.g., [100,109,110,111]). In this scenario, particles are accelerated stochastically by turbulence and magnetic reconnection in accretion disks or coronae. We briefly follow the stochastic acceleration in the AGN coronae case. According to the quasi-linear theory, the diffusion coefficient in the momentum space is (e.g., [112])
where is the minimum wave number of the turbulence spectrum (corresponding to the size of the corona), is the Alfvén speed, is the gyro radius, is the ratio of the strength of turbulence fields against the background, and q describes the spectrum of the turbulence. Then, the acceleration timescale is estimated to be
Assuming the Kolomogorov spectrum for the turbulence () and , the timescale becomes
Thus, stochastic acceleration appears to be inefficient compared to the typical cooling rates because of the measured weak magnetic fields, which results in a slow Alfvén speed.
3.2.3. Magnetosphere Acceleration
Magnetosphere acceleration can also accelerate particles in the vicinity of SMBH (e.g., [101,102,113,114,115]). At low accretion rates, the injection of charges into the BH magnetosphere is not sufficient for a full screening of the electric field induced by the rotation of the compact object. The regions with the unscreened electric field, so-called gaps, can accelerate charged particles effectively.
In order to have gaps, the maximum allowed accretion rate is [114,116,117]
where is the accretion rate in Eddington units. Since we are considering the standard accretion disk regime , particle acceleration by gaps does not operate in our case.
3.2.4. Reconnection Acceleration
Magnetic reconnection would accelerate particles (see e.g., [103] for reviews). Reconnection would naturally happen in magnetized coronae, and radiative magnetic reconnection is also suggested as a possible origin of the X-ray emission seen in accreting black hole systems [118]. However, even in the case of solar flares, particle acceleration mechanisms in magnetic reconnection are still uncertain (e.g., [119,120]). Therefore, a quantitative discussion is not straightforward.
Here, given the magnetic field measurements, we can estimate the available energy injection power by global magnetic activity as
This power seems insufficient for providing non-thermal particle energies under one-zone estimates. However, highly non-homogeneous configurations of magnetic field, such as by a local magneto-rotational instability [121], may provide enough energy to produce non-thermal particles.
3.3. Comparison of Timescales
Given the observed properties of AGN core regions, one can estimate the radiative cooling and acceleration timescales of high-energy particles in the coronae. Here, we take the DSA as a fiducial acceleration process.
The left panel of Figure 7 shows the timescales of high-energy electrons for (see [34] for details). With , electron acceleration up to ( GeV) is feasible in AGN coronae. Because of the intense radiation field, Compton cooling dominates the cooling. However, at higher energy regions, the main cooling channel is replaced by synchrotron cooling due to the Klein–Nishina effect. We note that the dominance of photon fields over the magnetic field does not necessarily prevent particle acceleration as such conditions are met in some efficient non-thermal sources, e.g., in gamma-ray binary systems [122,123]. Moreover, the high density of target photons can enable the converter acceleration mechanism if a relativistic velocity jump is present in the system [124].
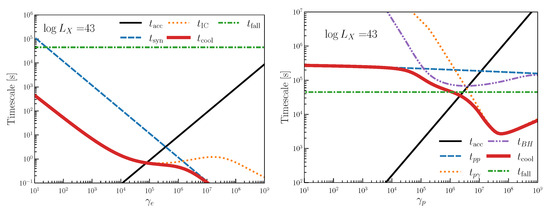
Figure 7.
(Left) Electron energy losses in AGN coronae together with acceleration and dynamical timescales for . Thin solid line shows the acceleration timescale assuming DSA. Dashed, dotted, and thick solid curves correspond to synchrotron cooling, IC cooling, and total cooling timescales, respectively. The dot-dashed curve shows the free-fall timescale. (Right) Same as in the (Left) panel, but for protons. Dashed, dotted, double-dot-dashed, and thick solid curves correspond to cooling, cooling, Bethe–Heitler cooling, and total cooling timescales, respectively. For both panels, different luminosity cases are shown in Inoue et al. [34].
The right panel of Figure 7 shows the timescales for protons (see [34] for details). Protons can be accelerated up to ( PeV) in AGN coronae. The maximum attainable energy is controlled by different processes for AGNs with different luminosities. For low-luminosity Seyferts (), acceleration is limited by the dynamical timescale rather than radiative cooling, while it becomes limited by Bethe–Heitler cooling for higher luminosity objects.
3.4. Particle Spectrum
The steady-state particle distributions can be derived from the solution of the transport equation [125]
where is the total cooling rate and is the injection function, which describes phenomenologically some acceleration process. is set as . Here, is the maximum Lorentz factor determined by balancing the acceleration and cooling timescales. The corresponding solution is
where
By solving Equation (17), we can obtain a steady-state spectrum of the non-thermal particles. Figure 8 shows the steady-state non-thermal electron spectrum obtained for the injection spectral index of together with the observationally determined electron spectral distribution for IC 4329A [37]. The synthetic electron distribution obtained for nicely reproduces the observationally determined electron spectrum in the energy range constrained by the observations. This injection index is naturally expected in a simple DSA scenario for a strong shock.
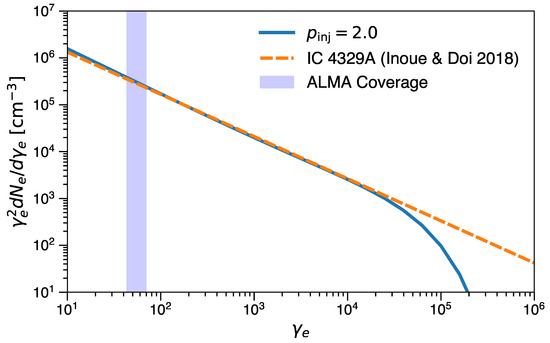
Figure 8.
The steady-state electron spectral distribution in AGN coronae. Solid curve corresponds to the model with . Dashed curve corresponds to the observationally determined electron distribution for IC 4329A [37]. The shaded region shows the Lorentz factors responsible for the observed radio spectrum.
3.5. Energy Injection
The total shock power can be estimated as
corresponds to ∼5% of the shock power being injected into the acceleration of electrons. Moreover, to explain the observed IceCube neutrino fluxes, the same energy injection rate is achieved for protons [34]. This high value implies that if DSA is responsible for particle acceleration in AGN coronae, then processes regulating the injection of electrons into DSA are very efficient. For example, in the case of DSA in supernovae remnants, non-thermal electrons obtain only ∼1% of the energy transferred to non-thermal protons [126]. Detailed consideration needs to be given to the reasons for this unusually high efficiency of electron acceleration in the future. However, recent particle-in-cell simulations of proton–electron plasma considering radiatively inefficient accretion flows have shown that the energy ratio depends on the proton temperature. Higher proton temperature will result in a higher electron energy fraction [100]. A further detailed investigation in the corona cases is required.
4. Gamma Rays and Neutrinos from AGN Coronae
4.1. Internal Gamma-ray Attenuation in Coronae
Accelerated electrons and protons in AGN coronae generate gamma-ray and neutrino emission through IC scattering, interaction, and interaction. Those high-energy gamma-ray photons are attenuated by photon–photon pair production interactions () with low-energy photons [127,128,129]. We can compute the optical depth for high-energy gamma rays to pair production interactions from the SED of AGN core regions. Figure 9 shows the internal gamma-ray optical depth () in the core region. The core region is expected to be optically thick against gamma-ray photons above 10–100 MeV depending on disk luminosities. Such high optical thicknesses against pair production in AGN coronae are well known (e.g., [36,130,131]) based on the compactness parameter argument [132].
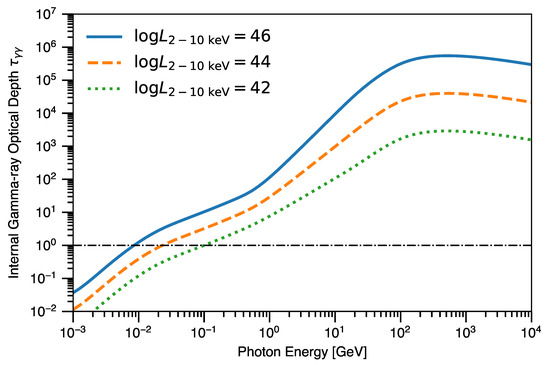
Figure 9.
Internal gamma-ray optical depth in the core region of AGNs. From top to bottom, each curve corresponds to 2–10 keV luminosity of , , , respectively. The horizontal dot-dashed line represents .
For the gamma-ray attenuation in AGNs, we can consider two cases. One is the “uniform” emissivity case, while the other is the “screened” case. In the uniform emissivity case, gamma rays and target photons are uniformly distributed. Gamma rays are attenuated by a factor of , where (see Section 7.8 in [133]). In the screened case, gamma-rays are assumed to be generated in the inner part of the corona, and the dominant attenuating photon field surrounds it. Since the disk and corona temperature depends on the disk radius [134], such configuration can be realized. Then, gamma rays are attenuated by a factor of .
4.2. General SED Pictures
Figure 10 shows the resulting steady-state gamma-ray and neutrino spectra from AGN coronae for the case assuming IC 4329A ( at a distance of 69 Mpc). The neutrino flux is shown in the form of per flavor. In this figure, the injection spectral index is , and the gyrofactor is for both electrons and protons. We also set the same power injected in protons and electrons. For the gamma-ray attenuation, the uniform emissivity model is adopted.
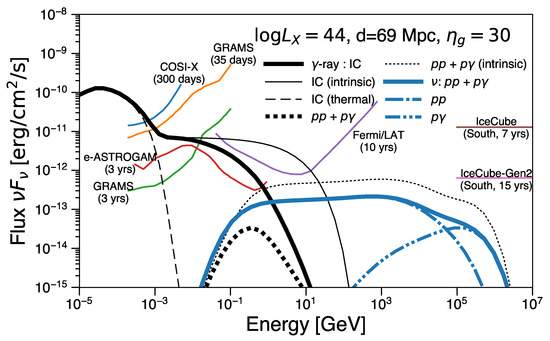
Figure 10.
Gamma-ray and neutrino spectra per flavor from AGN coronae with and . We set 2–10 keV luminosity of at a distance of 69 Mpc (IC 4329A). The thick black solid and thick dot curves show gamma rays from IC interaction and interaction including the attenuation effect. Each thin curve shows the spectrum before the attenuation. Taken from Inoue et al. [34].
Since the spectral index of electrons becomes ∼3 after radiative cooling, the resulting non-thermal gamma-ray spectrum is flat in in the MeV band after the thermal cutoff at ≳1 MeV. Due to the internal gamma-ray attenuation effect, the spectra will have a cutoff of around 100 MeV.
Gamma rays and neutrinos induced by hadronic interactions carry and of those interacted hadron energies. In addition, the and production efficiency are given by the ratio between the dynamical timescale and the interaction timescales. The production efficiency is analytically given as . Therefore, hadronic gamma-ray and neutrino luminosity is expected to be ∼5% and ∼3% of the intrinsic proton luminosity. Since we assume the same energy injection to electrons and protons, hadronic gamma-ray and neutrino fluxes are ∼5% and ∼3% of the IC gamma-ray flux.
Contrary to gamma rays, neutrinos induced by hadronic interactions can escape from the system without attenuation. Since we adopt the same for protons as for electrons, we expect a flat spectrum for neutrinos, to which makes the dominant contribution. The exact position of the cutoff energy depends on the assumed . Here, as described later, we set in order to be consistent with the IceCube background flux measurements. This gyrofactor results in a neutrino spectral cutoff around 100 TeV.
4.3. Application to NGC 1068
A nearby Seyfert galaxy NGC 1068 was reported as the hottest neutrino spot with a 2.9- confidence level in 10-year all-sky survey observations of IceCube [8]. As we have described above, the hybrid corona model is one possible solution. Thus, understanding the required physical parameters to explain the neutrinos in NGC 1068 is crucial for the coronal model test.
Figure 11 shows the expected gamma-ray and neutrino signals from NGC 1068 together with the observed gamma-ray data [16,135,136] and the IceCube data [8]. We follow the assumptions on the coronal parameters as described above except for the gyrofactor and parameters determined by the coronal synchrotron model explaining the mm-excess (see Section 2 and Figure 6). Considering the neutrino measurement uncertainty, in the figure, we plotted the model curve region in the range of for each curve. The darker region corresponds to lower , in which models extend to higher energies. Further detailed neutrino spectra will narrow down the range of allowed .
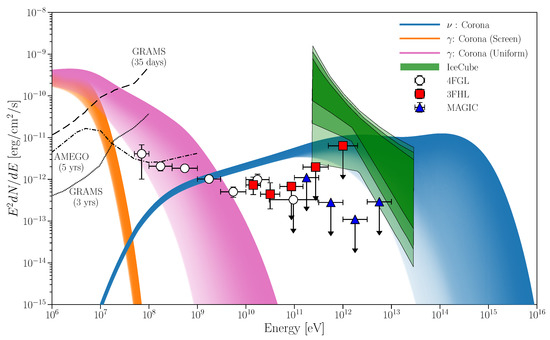
Figure 11.
The gamma-ray and neutrino spectra of NGC 1068. The circle, square, and triangle data points are from The Fermi-LAT collaboration [135], Ajello et al. [136], and Acciari et al. [16], respectively. The green shaded regions represent the 1, 2, and regions on the spectrum measured by IceCube [8]. The expected gamma-ray and neutrino spectra from the corona are shown for . The darker region corresponds to lower . The blue region shows the expected neutrino spectrum. The orange and magenta shaded region shows the gamma-ray spectra for the uniform case and the screened case, respectively. Taken from Inoue et al. [17].
Regarding the gamma-ray measurements, in the screened gamma-ray attenuation case, the model can explain the preliminary neutrino signals above several TeV without violating the gamma-ray data. However, the uniform emissivity model violates the low-energy gamma-ray data. This implies that a further detailed study of coronal geometry is necessary. In either case, it is not easy for the corona model to explain the entire observed gamma-ray flux data up to 20 GeV, requiring another mechanism to explain gamma-rays above 100 MeV, such as star formation activity [15], jet [137], or disk wind [138]. Therefore, the coronal model can explain the IceCube neutrino signal without violating the gamma-ray data.
An important question is what differentiates NGC 1068 from other nearby Seyfert galaxies. NGC 1068 is not the brightest X-ray Seyfert [139]. Its observed hard X-ray flux is a factor of ∼16 fainter than that of the brightest Seyfert, NGC 4151. NGC 1068 is a type 2 Seyfert galaxy and is obscured by materials up to the neutral hydrogen column density of [10,11]. If we correct this attenuation effect to understand the intrinsic X-ray radiation power, NGC 1068 appears to be the intrinsically brightest Seyfert. For example, intrinsically, it would be by a factor of ∼3.6 brighter than NGC 4151 in the X-ray band. As the dusty torus does not obscure coronal neutrino emission, which can scale with accretion power, NGC 1068 might be the brightest source in the neutrino sky. This could be why NGC 1068 appears as the hottest spot in the IceCube map rather than other Seyfert galaxies.
In NGC 1068, the jets are prominent and extend for several kpcs in both directions. In the central ∼14–70 pc region, the downstream jet emission dominates in the centimeter regime [83,87]. These jets can also be the production site of the reported neutrinos. However, gamma-ray attenuation is not significant in these far-side regions from the nucleus. Therefore, these jets may not be the dominant neutrino production sites.
5. Cosmic Gamma-ray and Neutrino Background Radiation
In this section, we consider the cosmic gamma-ray and neutrino background spectra from AGN coronae. For the details of the calculation, readers may refer to Inoue et al. [34]. Figure 12 shows the cosmic X-ray/gamma-ray and neutrino background spectra from AGN coronae assuming the case of and together with the observed background spectrum data by HEAO-1 A2 [140], INTEGRAL [141], HEAO-1 A4 [142], Swift-BAT [143], SMM [67], Nagoya–Balloon [66], COMPTEL [144], Fermi-LAT [73], and IceCube [145].
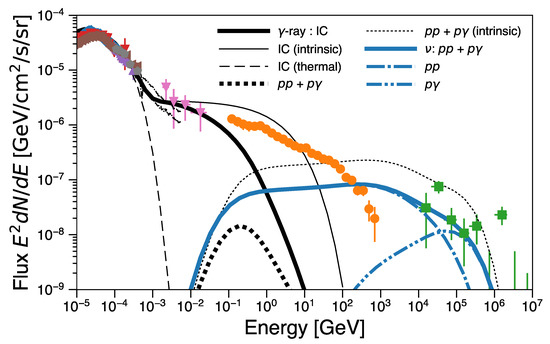
Figure 12.
The cosmic gamma-ray and neutrino background spectra from AGN coronae with and . Each component is labeled as in the figure. Thin curves show the spectra before the attenuation. The circle-orange and square-green data points correspond to the total cosmic gamma-ray background spectrum measured by Fermi/LAT [73] and the cosmic neutrino background spectrum by IceCube [145], respectively. The cosmic X-ray and MeV gamma-ray background spectrum data of HEAO-1 A2 (triangle-brown; [140]), INTEGRAL (triangle-red; [141]), HEAO-1 A4 (triangle-purple; [142]), Swift-BAT (diamond-blue [143]), SMM (black-thin-dot-dashed [67]), Nagoya–Ballon (pentagon-gray; [66]), COMPTEL (pink-triangle; [144]) are also shown in the figure. Taken from Inoue et al. [34].
By setting , AGN coronae can nicely explain the cosmic MeV gamma-ray background in an extension from the cosmic X-ray background radiation. Since the spectral index of non-thermal electrons in the coronae is ∼3, the resulting MeV gamma-ray background spectrum becomes flat in . Since the dominant IC contributors switch from thermal electrons to non-thermal electrons at around 1 MeV, the MeV background spectrum may have a spectral hardening feature at ∼1 MeV.
In Figure 12, we set . The result for the MeV background does not significantly change as far as . If , we may require lower . Here, IC emission due to non-thermal electrons also contributes to the X-ray band. Their contribution is about ∼5% at 30 keV of the observed cosmic X-ray background flux, which may reduce the required number of the Compton-thick population of AGNs. Due to the internal gamma-ray attenuation effect, these non-thermal gamma rays cannot contribute to the emission above GeV, where blazars, radio galaxies, and star-forming galaxies dominate (see, e.g., [146]).
For neutrinos, the combination of and interactions can nicely reproduce the IceCube fluxes below 100–300 TeV. interactions dominate the flux at ≲10 TeV, while interactions prevail above this energy. Because of the target photon field SED, is subdominant in the GeV–TeV band. If we inject more power into protons, this inevitably overproduces the IceCube background fluxes.
Figure 13 shows the cosmic neutrino background spectra from AGN cores with various gyro factors ranging from 1 (Bohm limit) to . It is clear that if , the resulting neutrino fluxes overproduce the measured fluxes. On the contrary, if , AGN coronae cannot significantly contribute to the observed neutrino background fluxes. Thus, to explain the IceCube neutrino background fluxes by AGN cores, is required.
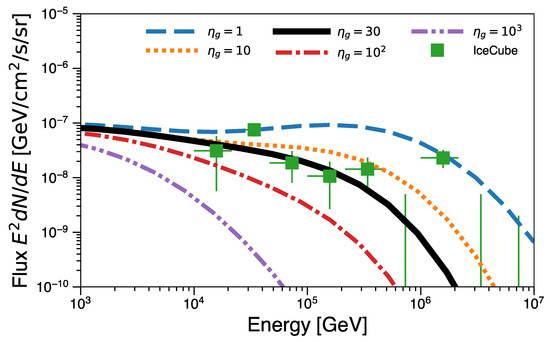
Figure 13.
The cosmic neutrino background spectra per flavor from AGN coronae. The dashed, dotted, solid, dot-dashed, and double-dot-dashed curves show the contributions with 1 (Bohm limit), 10, 30, , and , respectively. The square data points correspond to the cosmic neutrino background spectrum by IceCube [145]. Taken from Inoue et al. [34].
6. Discussion
6.1. Role of Secondary Particles
Secondary particles can be injected in the corona by hadronic processes and by pair creation. Even if these secondary particles are negligible by the number density, they still can be energetically important. Hadronic gamma-ray fluxes before the pair creation are about a factor of 10 less than that by primary electrons (see Figure 10) because of radiative efficiency differences between protons and electrons. Therefore, hadronically induced secondary pairs should not be energetically important.
Pairs generated through annihilation of primary leptonic fluxes may also contribute such as to the MeV gamma-ray spectrum. However, considering the intrinsic photon index and acceleration limit, the resulting pair contribution will not be higher than primaries. Thus, the secondary particle component would not significantly alter the resulting spectra.
Here, hadronic power can be much higher than we assume. Then, secondary leptons can energetically dominate the primary leptons. However, as seen in Figure 12, such models cannot explain the cosmic MeV gamma ray and TeV–PeV neutrino background fluxes.
6.2. Comparison of Current Available Models
In the literature, it has been argued that high-energy particles in the AGN coronae generate intense neutrino emission (e.g., [26,35,147]). These originally predicted fluxes have been ruled out by the IceCube observations [148]. However, recent studies have revisited the estimated fluxes [18,33,34,149]. In this section, we clarify the differences in recent AGN corona models for high-energy neutrinos. Figure 14 shows the resulting cosmic neutrino background spectra from those papers. These corona models predict different neutrino spectra, although they consider the same neutrino production region. This section briefly describes the differences among those models.
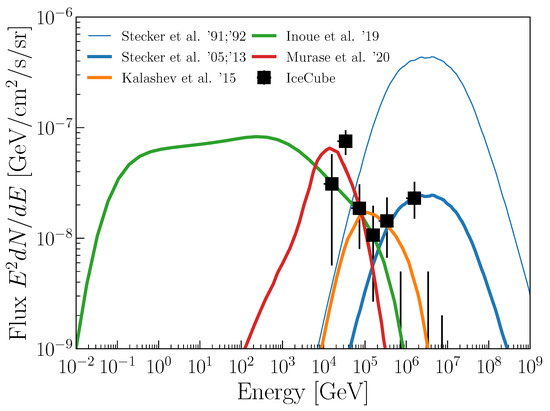
Figure 14.
The cosmic neutrino background spectra per flavor from AGN coronae, showing the currently available models [18,33,34,149]. The original prediction by Stecker et al. [27,35] is also shown.
Stecker [149] considered a similar model to the one originally proposed [35], but the background flux is assumed to be lower by a factor of 20 to match the IceCube flux. The shock radius and the magnetic field strength were assumed to be and G in the model by Stecker et al. [35]. The particle spectral index was also assumed to be 2 in the framework of the DSA.
Kalashev et al. [33] followed the treatment in Stecker et al. [35], Stecker [149], but accounting for the radial emission profile in the standard accretion disk in their consideration of the cooling processes. The particle spectra in Kalashev et al. [33] are normalized to match with the IceCube data. Given the observationally determined corona size , the dominant photon target is likely to be generated in the inner region of the coronae.
Inoue et al. [34] took into account both X-ray and radio measurements, which allowed us to derive and G [37]. In addition, to explain the cosmic MeV background by Seyferts, is set as . The proton spectral index is assumed to be the same as that of electrons, determined through the radio measurement. However, the non-thermal electron/proton energy ratio is set to be , and are assumed to reproduce the cosmic neutrino background fluxes. We note that it can be for the explanation of NGC 1068. , , p, and are, for the first time, observationally determined, while and are still assumed to reproduce the IceCube measurements. However, the exact acceleration processes are not well determined, as they follow the radio observation results.
Murase et al. [18] consider stochastic acceleration motivated by recent numerical simulations for low-luminosity AGNs [150]. The required cosmic ray pressure to explain the IceCube data is about 1–10% of thermal pressure, which is similar to Inoue et al. [34]. Their model assumed and G. This high magnetic field contradicts the radio measurements. As discussed above, the measured magnetic field may not be high enough to accelerate particles in the stochastic acceleration scheme efficiently.
Very recently, Gutiérrez et al. [19] also modeled high energy signals from AGN coronae taking into account X-ray and radio observations. They basically followed Inoue et al. [34]. However, they considered lower than in Inoue et al. [34]. This assumption is more consistent with seen in nearby supernova remnants. Because of this low , secondary leptons make the dominant contribution in the MeV band. Although they have not estimated the integrated MeV gamma-ray and TeV–PeV neutrino background fluxes in their paper yet, such a study based on their model will be helpful for future comparison.
6.3. Future Testing of Models
Although non-thermal AGN coronal models have failed to explain the X-ray data in the 1990s, millimeter radio observations found weak coronal activity in nearby Seyferts in 2018, and then the possible detection of NGC 1068 in 2020 shed light again on the AGN corona model. However, as described above, the models still have profound ambiguity. We require multi-messenger tests on that. Below we list possible ways to test the AGN corona scenario.
6.3.1. Radio Synchrotron Emission
As non-thermal particles are accelerated in the magnetized coronae, we should expect coronal synchrotron emission. ALMA observations have already grasped the evidence of the coronal synchrotron emission. Therefore, we need to consider the expected radio synchrotron emission for each model and compare it with the ALMA measurements. As the ALMA data are already available for nearby Seyferts, this test can easily be performed.
6.3.2. Nuclear Spallation Effect Appearing in X-ray
High-energy protons can be traced by future high-resolution calorimeter spectroscopy in the X-ray band such as XRISM [151] and Athena [152]. As narrow-line features are seen in AGN X-ray disk spectra, there are abundant metal elements in AGN cores. Accelerated protons interact with those nuclei and induce nuclear spallation. The nuclear spallation in AGN disks will enhance emission lines from Mn, Cr, V, and Ti [153]. Those signatures will be another clue for the testing of the corona model.
6.3.3. MeV Power-Law Tail
In the hybrid AGN corona model, the non-thermal gamma-rays should appear after the thermal cutoff (∼300 keV). The expected MeV gamma-ray flux is about 5% of the intrinsic X-ray flux. Due to the strong internal gamma-ray attenuation effect, the spectra will have a cutoff around 10–100 MeV depending on the photon distribution. These MeV gamma-ray photons should be seen by future MeV gamma-ray observatories. If not, this means that the amount of non-thermal population is much less than required for the MeV gamma-ray background radiation, which means the corona model cannot explain the neutrino background.
6.3.4. Further Neutrino Observations
The neutrino measurement can provide a critical test of AGN corona scenarios and robustly constrain the acceleration of protons. Currently, only NGC 1068 is reported as a possible neutrino production site. Further neutrino observations should see more nearby Seyferts following the AGN corona model [19,34,154]. Additionally, neutrino observations may pin down the acceleration mechanism in the AGN corona by taking the neutrino spectra from individual objects.
7. Summary
In this review, we have given an overview of our current understanding of AGN coronae from X-ray and mm radio observations. We have shown that these measurements contain critical information for constraining particle acceleration in AGN coronae. AGN coronae are feasible sites for particle acceleration. If the energy injection rate is adequate, AGN coronae can explain the neutrino signals from NGC 1068 and a part of the diffuse neutrino fluxes. Future radio, X-ray, MeV gamma ray, and TeV neutrino observations will be able to test this scenario by observations of nearby bright Seyferts.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
Y.I. is supported by JSPS KAKENHI Grant Numbers JP16K13813, JP18H05458, and JP19K14772, and the Leading Initiative for Excellent Young Researchers, MEXT, Japan, and RIKEN iTHEMS programs. D.K. is supported by JSPS KAKENHI Grant Numbers JP18H03722, JP18H05463, and JP20H00153.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aartsen, M.G.; Abbasi, R.; Abdou, Y.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Auffenberg, J.; Bai, X.; et al. First Observation of PeV-Energy Neutrinos with IceCube. Phys. Rev. Lett. 2013, 111, 021103. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Arguelles, C.; Arlen, T.C.; et al. Observation of High-Energy Astrophysical Neutrinos in Three Years of IceCube Data. Phys. Rev. Lett. 2014, 113, 101101. [Google Scholar] [CrossRef] [PubMed]
- Murase, K. Active Galactic Nuclei as High-Energy Neutrino Sources. In Neutrino Astronomy: Current Status, Future Prospects; Gaisser, T., Karle, A., Eds.; World Scientific: Singapore, 2017; pp. 15–31. [Google Scholar] [CrossRef]
- Ahlers, M.; Halzen, F. Opening a new window onto the universe with IceCube. Prog. Part. Nucl. Phys. 2018, 102, 73–88. [Google Scholar] [CrossRef]
- IceCube Collaboration; Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K.; et al. Neutrino emission from the direction of the blazar TXS 0506+056 prior to the IceCube-170922A alert. Science 2018, 361, 147–151. [Google Scholar] [CrossRef]
- IceCube Collaboration; Aartsen, M.G.; Ackermann, M.; Adams, J. Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science 2018, 361, eaat1378. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Andeen, K.; Anderson, T.; et al. The Contribution of Fermi-2LAC Blazars to Diffuse TeV-PeV Neutrino Flux. Astrophys. J. 2017, 835, 45. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Andeen, K.; Anderson, T.; Ansseau, I.; et al. Time-Integrated Neutrino Source Searches with 10 Years of IceCube Data. Phys. Rev. Lett. 2020, 124, 051103. [Google Scholar] [CrossRef] [PubMed]
- Tully, R.B. Nearby Galaxies Catalog; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Bauer, F.E.; Arévalo, P.; Walton, D.J.; Koss, M.J.; Puccetti, S.; Gandhi, P.; Stern, D.; Alexander, D.M.; Baloković, M.; Boggs, S.E.; et al. NuSTAR Spectroscopy of Multi-component X-ray Reflection from NGC 1068. Astrophys. J. 2015, 812, 116. [Google Scholar] [CrossRef]
- Marinucci, A.; Bianchi, S.; Matt, G.; Alexander, D.M.; Baloković, M.; Bauer, F.E.; Brandt, W.N.; Gand hi, P.; Guainazzi, M.; Harrison, F.A.; et al. NuSTAR catches the unveiling nucleus of NGC 1068. Mon. Not. R. Astron. Soc. 2016, 456, L94–L98. [Google Scholar] [CrossRef]
- Pasetto, A.; González-Martín, O.; Esparza-Arredondo, D.; Osorio-Clavijo, N.; Victoria-Ceballos, C.I.; Martínez-Paredes, M. AGN Torus Detectability at Submillimeter Wavelengths: What to Expect from ALMA Continuum Data. Astrophys. J. 2019, 872, 69. [Google Scholar] [CrossRef]
- Luo, B.; Brandt, W.N.; Xue, Y.Q.; Lehmer, B.; Alexander, D.M.; Bauer, F.E.; Vito, F.; Yang, G.; Basu-Zych, A.R.; Comastri, A.; et al. The Chandra Deep Field-South Survey: 7 Ms Source Catalogs. Astrophys. J. Suppl. 2017, 228, 2. [Google Scholar] [CrossRef]
- Marcotulli, L.; Di Mauro, M.; Ajello, M. Source-count Distribution of Gamma-ray Blazars. Astrophys. J. 2020, 896, 6. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Berenji, B.; Bloom, E.D.; et al. GeV Observations of Star-forming Galaxies with the Fermi Large Area Telescope. Astrophys. J. 2012, 755, 164. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Constraints on Gamma-ray and Neutrino Emission from NGC 1068 with the MAGIC Telescopes. Astrophys. J. 2019, 883, 135. [Google Scholar] [CrossRef]
- Inoue, Y.; Khangulyan, D.; Doi, A. On the Origin of High-energy Neutrinos from NGC 1068: The Role of Nonthermal Coronal Activity. Astrophys. J. 2020, 891, L33. [Google Scholar] [CrossRef]
- Murase, K.; Kimura, S.S.; Mészáros, P. Hidden Cores of Active Galactic Nuclei as the Origin of Medium-Energy Neutrinos: Critical Tests with the MeV Gamma-ray Connection. Phys. Rev. Lett. 2020, 125, 011101. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, E.M.; Vieyro, F.L.; Romero, G.E. Nonthermal processes in hot accretion flows onto supermassive black holes: An inhomogeneous model. arXiv 2021, arXiv:2102.11921. [Google Scholar]
- Anchordoqui, L.A.; Krizmanic, J.F.; Stecker, F.W. High-Energy Neutrinos from NGC 1068. arXiv 2021, arXiv:2102.12409. [Google Scholar]
- Müller, A.L.; Romero, G.E. Radiation from the impact of broad-line region clouds onto AGN accretion disks. Astron. Astrophys. 2020, 636, A92. [Google Scholar] [CrossRef]
- Recchia, S.; Gabici, S.; Aharonian, F.A.; Niro, V. Giant cosmic ray halos around M31 and the Milky Way. arXiv 2021, arXiv:2101.05016. [Google Scholar]
- Zdziarski, A.A. On the origin of the infrared and X-ray continua of active galactic nuclei. Astrophys. J. 1986, 305, 45–56. [Google Scholar] [CrossRef]
- Kazanas, D.; Ellison, D.C. The central engine of quasars and active galactic nuclei Hadronic interactions of shock-accelerated relativistic protons. Astrophys. J. 1986, 304, 178–187. [Google Scholar] [CrossRef]
- Sikora, M.; Kirk, J.G.; Begelman, M.C.; Schneider, P. Electron injection by relativistic protons in active galactic nuclei. Astrophys. J. Lett. 1987, 320, L81–L85. [Google Scholar] [CrossRef]
- Begelman, M.C.; Rudak, B.; Sikora, M. Consequences of relativistic proton injection in active galactic nuclei. Astrophys. J. 1990, 362, 38–51. [Google Scholar] [CrossRef]
- Stecker, F.W.; Done, C.; Salamon, M.H.; Sommers, P. High-energy neutrinos from active galactic nuclei. Phys. Rev. Lett. 1991, 66, 2697–2700. [Google Scholar] [CrossRef] [PubMed]
- Coppi, P.S. Time-dependent models of magnetized pair plasmas. Mon. Not. R. Astron. Soc. 1992, 258, 657–683. [Google Scholar] [CrossRef][Green Version]
- Ghisellini, G.; Haardt, F.; Matt, G. Aborted jets and the X-ray emission of radio-quiet AGNs. Astron. Astrophys. 2004, 413, 535–545. [Google Scholar] [CrossRef]
- Mastichiadis, A.; Protheroe, R.J.; Kirk, J.G. Spectral and temporal signatures of ultrarelativistic protons in compact sources. I. Effects of Bethe-Heitler pair production. Astron. Astrophys. 2005, 433, 765–776. [Google Scholar] [CrossRef]
- Belmont, R.; Malzac, J.; Marcowith, A. Simulating radiation and kinetic processes in relativistic plasmas. Astron. Astrophys. 2008, 491, 617–631. [Google Scholar] [CrossRef]
- Poutanen, J.; Vurm, I. On the Origin of Spectral States in Accreting Black Holes. Astrophys. J. Lett. 2009, 690, L97–L100. [Google Scholar] [CrossRef]
- Kalashev, O.; Semikoz, D.; Tkachev, I. Neutrinos in IceCube from active galactic nuclei. Sov. J. Exp. Theor. Phys. 2015, 120, 541–548. [Google Scholar] [CrossRef]
- Inoue, Y.; Khangulyan, D.; Inoue, S.; Doi, A. On High-energy Particles in Accretion Disk Coronae of Supermassive Black Holes: Implications for MeV Gamma-rays and High-energy Neutrinos from AGN Cores. Astrophys. J. 2019, 880, 40. [Google Scholar] [CrossRef]
- Stecker, F.W.; Done, C.; Salamon, M.H.; Sommers, P. Erratum: “High-energy neutrinos from active galactic nuclei” [Phys. Rev. Lett. 66, 2697 (1991)]. Phys. Rev. Lett. 1992, 69, 2738. [Google Scholar] [CrossRef]
- Fabian, A.C.; Lohfink, A.; Kara, E.; Parker, M.L.; Vasudevan, R.; Reynolds, C.S. Properties of AGN coronae in the NuSTAR era. Mon. Not. R. Astron. Soc. 2015, 451, 4375–4383. [Google Scholar] [CrossRef]
- Inoue, Y.; Doi, A. Detection of Coronal Magnetic Activity in nearby Active Supermassive Black Holes. Astrophys. J. 2018, 869, 114. [Google Scholar] [CrossRef]
- Cowsik, R.; Lee, M.A. Transport of neutrinos, radiation and energetic particles in accretion flows. Proc. R. Soc. Lond. Ser. A 1982, 383, 409–437. [Google Scholar] [CrossRef]
- Protheroe, R.J.; Kazanas, D. On the origin of relativistic particles and gamma-rays in quasars. Astrophys. J. 1983, 265, 620–624. [Google Scholar] [CrossRef]
- Madejski, G.M.; Zdziarski, A.A.; Turner, T.J.; Done, C.; Mushotzky, R.F.; Hartman, R.C.; Gehrels, N.; Connors, A.; Fabian, A.C.; Nandra, K.; et al. Joint ROSAT-Compton GRO observations of the X-ray bright Seyfert galaxy IC 4329A. Astrophys. J. 1995, 438, 672–679. [Google Scholar] [CrossRef]
- Zdziarski, A.A.; Poutanen, J.; Johnson, W.N. Observations of Seyfert Galaxies by OSSE and Parameters of Their X-ray/Gamma-ray Sources. Astrophys. J. 2000, 542, 703–709. [Google Scholar] [CrossRef]
- Lin, Y.C.; Bertsch, D.L.; Dingus, B.L.; Fichtel, C.E.; Hartman, R.C.; Hunter, S.D.; Kanbach, G.; Kniffen, D.A.; Mattox, J.R.; Mayer-Hasselwander, H.A.; et al. EGRET Limits on High-Energy Gamma-ray Emission from X-ray- and Low-Energy Gamma-ray–selected Seyfert Galaxies. Astrophys. J. Lett. 1993, 416, L53. [Google Scholar] [CrossRef]
- Katz, J.I. Nonrelativistic Compton scattering and models of quasars. Astrophys. J. 1976, 206, 910–916. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Blinnikov, S.I. Disk accretion onto a black hole at subcritical luminosity. Astron. Astrophys. 1977, 59, 111–125. [Google Scholar]
- Pozdniakov, L.A.; Sobol, I.M.; Siuniaev, R.A. Effect of the multiple Compton scatterings on an X-ray emission spectrum. Calculation by the Monte Carlo method. Soviet Ast. 1977, 21, 708–714. [Google Scholar]
- Galeev, A.A.; Rosner, R.; Vaiana, G.S. Structured coronae of accretion disks. Astrophys. J. 1979, 229, 318–326. [Google Scholar] [CrossRef]
- Takahara, F. Magnetic Flare Model of Quasars and Active Galactic Nuclei—Magnetized Accretion Disk around a Massive Black Hole. Prog. Theor. Phys. 1979, 62, 629–643. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Titarchuk, L.G. Comptonization of X-rays in plasma clouds. Typical radiation spectra. Astron. Astrophys. 1980, 500, 167–184. [Google Scholar]
- Lightman, A.P.; White, T.R. Effects of cold matter in active galactic nuclei—A broad hump in the X-ray spectra. Astrophys. J. 1988, 335, 57–66. [Google Scholar] [CrossRef]
- Magdziarz, P.; Zdziarski, A.A. Angle-dependent Compton reflection of X-rays and gamma-rays. Mon. Not. R. Astron. Soc. 1995, 273, 837–848. [Google Scholar] [CrossRef]
- Ricci, C.; Walter, R.; Courvoisier, T.J.L.; Paltani, S. Reflection in Seyfert galaxies and the unified model of AGN. Astron. Astrophys. 2011, 532, A102. [Google Scholar] [CrossRef]
- Harrison, C. Observational Constraints on the Influence of Active Galactic Nuclei on the Evolution of Galaxies. Ph.D. Thesis, Durham University, Durham, UK, 2014. [Google Scholar]
- Hickox, R.C.; Alexander, D.M. Obscured Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2018, 56, 625–671. [Google Scholar] [CrossRef]
- Done, C.; Nayakshin, S. Can the soft excess in AGN originate from disc reflection? Mon. Not. R. Astron. Soc. 2007, 377, L59–L63. [Google Scholar] [CrossRef]
- Boissay, R.; Ricci, C.; Paltani, S. A hard X-ray view of the soft excess in AGN. Astron. Astrophys. 2016, 588, A70. [Google Scholar] [CrossRef]
- Brenneman, L.W.; Madejski, G.; Fuerst, F.; Matt, G.; Elvis, M.; Harrison, F.A.; Ballantyne, D.R.; Boggs, S.E.; Christensen, F.E.; Craig, W.W.; et al. The Broad-band X-ray Spectrum of IC 4329A from a Joint NuSTAR/Suzaku Observation. Astrophys. J. 2014, 788, 61. [Google Scholar] [CrossRef]
- Dadina, M. Seyfert galaxies in the local Universe (z ≤ 0.1): The average X-ray spectrum as seen by BeppoSAX. Astron. Astrophys. 2008, 485, 417–424. [Google Scholar] [CrossRef]
- Kompaneets, A. The establishment of thermal equilibrium between quanta and electrons. Sov. Phys. JETP 1957, 4, 730–737. [Google Scholar]
- Ueda, Y.; Akiyama, M.; Hasinger, G.; Miyaji, T.; Watson, M.G. Toward the Standard Population Synthesis Model of the X-ray Background: Evolution of X-ray Luminosity and Absorption Functions of Active Galactic Nuclei Including Compton-thick Populations. Astrophys. J. 2014, 786, 104. [Google Scholar] [CrossRef]
- Zdziarski, A.A.; Johnson, W.N.; Magdziarz, P. Broad-band γ-ray and X-ray spectra of NGC 4151 and their implications for physical processes and geometry. Mon. Not. R. Astron. Soc. 1996, 283, 193–206. [Google Scholar] [CrossRef]
- Jin, C.; Ward, M.; Done, C.; Gelbord, J. A combined optical and X-ray study of unobscured type 1 active galactic nuclei-I. Optical spectra and spectral energy distribution modelling. Mon. Not. R. Astron. Soc. 2012, 420, 1825–1847. [Google Scholar] [CrossRef]
- Morgan, C.W.; Hainline, L.J.; Chen, B.; Tewes, M.; Kochanek, C.S.; Dai, X.; Kozlowski, S.; Blackburne, J.A.; Mosquera, A.M.; Chartas, G.; et al. Further Evidence that Quasar X-ray Emitting Regions are Compact: X-Ray and Optical Microlensing in the Lensed Quasar Q J0158-4325. Astrophys. J. 2012, 756, 52. [Google Scholar] [CrossRef]
- Fabian, A.C.; Lohfink, A.; Belmont, R.; Malzac, J.; Coppi, P. Properties of AGN coronae in the NuSTAR era-II. Hybrid plasma. Mon. Not. R. Astron. Soc. 2017, 467, 2566–2570. [Google Scholar] [CrossRef]
- Ueda, Y.; Akiyama, M.; Ohta, K.; Miyaji, T. Cosmological Evolution of the Hard X-ray Active Galactic Nucleus Luminosity Function and the Origin of the Hard X-ray Background. Astrophys. J. 2003, 598, 886–908. [Google Scholar] [CrossRef]
- Hasinger, G.; Miyaji, T.; Schmidt, M. Luminosity-dependent evolution of soft X-ray selected AGN. New Chandra and XMM-Newton surveys. Astron. Astrophys. 2005, 441, 417–434. [Google Scholar] [CrossRef]
- Fukada, Y.; Hayakawa, S.; Kasahara, I.; Makino, F.; Tanaka, Y.; Sreekantan, B.V. Energy spectrum of diffuse component of cosmic soft gamma rays. Nature 1975, 254, 398. [Google Scholar] [CrossRef]
- Watanabe, K.; Hartmann, D.H.; Leising, M.D.; The, L.S.; Share, G.H.; Kinzer, R.L. The Cosmic γ-ray Background from supernovae. In Proceedings of the Fourth Compton Symposium, American Institute of Physics Conference Series, Williamsburg, VA, USA, 27–30 April 1997; Dermer, C.D., Strickman, M.S., Kurfess, J.D., Eds.; Volume 410, pp. 1223–1227. [Google Scholar] [CrossRef]
- Weidenspointner, G.; Varendorff, M.; Kappadath, S.C.; Bennett, K.; Bloemen, H.; Diehl, R.; Hermsen, W.; Lichti, G.G.; Ryan, J.; Schönfelder, V. The cosmic diffuse gamma-ray background measured with COMPTEL. In Proceedings of the Fifth Compton Symposium, American Institute of Physics Conference Series, Portsmouth, NH, USA, 1 April 2000; McConnell, M.L., Ryan, J.M., Eds.; Volume 510, pp. 467–470. [Google Scholar] [CrossRef]
- Stecker, F.W.; Salamon, M.H.; Done, C. On the Origin of the MeV Gamma-ray Background. arXiv 1999, arXiv:astro-ph/9912106. [Google Scholar]
- Inoue, Y.; Totani, T.; Ueda, Y. The Cosmic MeV Gamma-ray Background and Hard X-ray Spectra of Active Galactic Nuclei: Implications for the Origin of Hot AGN Coronae. Astrophys. J. 2008, 672, L5. [Google Scholar] [CrossRef]
- Ajello, M.; Costamante, L.; Sambruna, R.M.; Gehrels, N.; Chiang, J.; Rau, A.; Escala, A.; Greiner, J.; Tueller, J.; Wall, J.V.; et al. The Evolution of Swift/BAT Blazars and the Origin of the MeV Background. Astrophys. J. 2009, 699, 603–625. [Google Scholar] [CrossRef]
- Toda, K.; Fukazawa, Y.; Inoue, Y. Cosmological Evolution of Flat-spectrum Radio Quasars Based on the Swift/BAT 105 Month Catalog and Their Contribution to the Cosmic MeV Gamma-ray Background Radiation. Astrophys. J. 2020, 896, 172. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. The Spectrum of Isotropic Diffuse Gamma-ray Emission between 100 MeV and 820 GeV. Astrophys. J. 2015, 799, 86. [Google Scholar] [CrossRef]
- Haardt, F.; Maraschi, L. A two-phase model for the X-ray emission from Seyfert galaxies. Astrophys. J. Lett. 1991, 380, L51–L54. [Google Scholar] [CrossRef]
- Liu, B.F.; Mineshige, S.; Shibata, K. A Simple Model for a Magnetic Reconnection-heated Corona. Astrophys. J. 2002, 572, L173–L176. [Google Scholar] [CrossRef]
- Di Matteo, T.; Celotti, A.; Fabian, A.C. Cyclo-synchrotron emission from magnetically dominated active regions above accretion discs. Mon. Not. R. Astron. Soc. 1997, 291, 805–810. [Google Scholar] [CrossRef]
- Inoue, Y.; Doi, A. Unveiling the nature of coronae in active galactic nuclei through submillimeter observations. Publ. Astron. Soc. Jpn. 2014, 66, L8. [Google Scholar] [CrossRef]
- Raginski, I.; Laor, A. AGN coronal emission models-I. The predicted radio emission. Mon. Not. R. Astron. Soc. 2016, 459, 2082–2096. [Google Scholar] [CrossRef]
- Antonucci, R.; Barvainis, R. Excess 2 Centimeter Emission: A New Continuum Component in the Spectra of Radio-quiet Quasars. Astrophys. J. Lett. 1988, 332, L13. [Google Scholar] [CrossRef]
- Barvainis, R.; Lonsdale, C.; Antonucci, R. Radio Spectra of Radio Quiet Quasars. Astron. J. 1996, 111, 1431. [Google Scholar] [CrossRef]
- Doi, A.; Inoue, Y. High-frequency excess in the radio continuum spectrum of the type-1 Seyfert galaxy NGC 985. Publ. Astron. Soc. Jpn. 2016, 68, 56. [Google Scholar] [CrossRef]
- Behar, E.; Vogel, S.; Baldi, R.D.; Smith, K.L.; Mushotzky, R.F. The mm-wave compact component of an AGN. Mon. Not. R. Astron. Soc. 2018, 478, 399–406. [Google Scholar] [CrossRef]
- Gallimore, J.F.; Baum, S.A.; O’Dea, C.P. The Parsec-Scale Radio Structure of NGC 1068 and the Nature of the Nuclear Radio Source. Astrophys. J. 2004, 613, 794–810. [Google Scholar] [CrossRef]
- García-Burillo, S.; Combes, F.; Ramos Almeida, C.; Usero, A.; Krips, M.; Alonso-Herrero, A.; Aalto, S.; Casasola, V.; Hunt, L.K.; Martín, S.; et al. ALMA Resolves the Torus of NGC 1068: Continuum and Molecular Line Emission. Astrophys. J. Lett. 2016, 823, L12. [Google Scholar] [CrossRef]
- Impellizzeri, C.M.V.; Gallimore, J.F.; Baum, S.A.; Elitzur, M.; Davies, R.; Lutz, D.; Maiolino, R.; Marconi, A.; Nikutta, R.; O’Dea, C.P.; et al. Counter-Rotation and High Velocity Outflow in the Parsec-Scale Molecular Torus of NGC 1068. arXiv 2019, arXiv:1908.07981. [Google Scholar] [CrossRef]
- García-Burillo, S.; Combes, F.; Ramos Almeida, C.; Usero, A.; Alonso-Herrero, A.; Hunt, L.K.; Rouan, D.; Aalto, S.; Querejeta, M.; Viti, S.; et al. ALMA images the many faces of the <ASTROBJ>NGC 1068</ASTROBJ> torus and its surroundings. Astron. Astrophys. 2019, 632, A61. [Google Scholar] [CrossRef]
- Gallimore, J.F.; Baum, S.A.; O’Dea, C.P.; Pedlar, A. The Subarcsecond Radio Structure in NGC 1068. I. Observations and Results. Astrophys. J. 1996, 458, 136. [Google Scholar] [CrossRef]
- Cotton, W.D.; Jaffe, W.; Perrin, G.; Woillez, J. Observations of the inner jet in NGC 1068 at 43 GHz. Astron. Astrophys. 2008, 477, 517–520. [Google Scholar] [CrossRef]
- Kato, S.; Fukue, J.; Mineshige, S. Black-Hole Accretion Disks—Towards a New Paradigm; Kyoto University Press: Kyoto, Japan, 2008. [Google Scholar]
- Yuan, F.; Narayan, R. Hot Accretion Flows Around Black Holes. Annu. Rev. Astron. Astrophys. 2014, 52, 529–588. [Google Scholar] [CrossRef]
- Chauvin, M.; Florén, H.G.; Friis, M.; Jackson, M.; Kamae, T.; Kataoka, J.; Kawano, T.; Kiss, M.; Mikhalev, V.; Mizuno, T.; et al. Accretion geometry of the black-hole binary Cygnus X-1 from X-ray polarimetry. Nat. Astron. 2018, 2, 652–655. [Google Scholar] [CrossRef]
- Jones, F.C. Calculated Spectrum of Inverse-Compton-Scattered Photons. Phys. Rev. 1968, 167, 1159–1169. [Google Scholar] [CrossRef]
- Moderski, R.; Sikora, M.; Coppi, P.S.; Aharonian, F. Klein-Nishina effects in the spectra of non-thermal sources immersed in external radiation fields. Mon. Not. R. Astron. Soc. 2005, 363, 954–966. [Google Scholar] [CrossRef]
- Khangulyan, D.; Aharonian, F.A.; Kelner, S.R. Simple Analytical Approximations for Treatment of Inverse Compton Scattering of Relativistic Electrons in the Blackbody Radiation Field. Astrophys. J. 2014, 783, 100. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma rays, electrons, and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 034018. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A. Energy spectra of gamma rays, electrons, and neutrinos produced at interactions of relativistic protons with low energy radiation. Phys. Rev. D 2008, 78, 034013. [Google Scholar] [CrossRef]
- Gao, S.; Asano, K.; Mészáros, P. High energy neutrinos from dissipative photospheric models of gamma ray bursts. J. Cosmol. Astro-Part. Phys. 2012, 2012, 058. [Google Scholar] [CrossRef][Green Version]
- Drury, L.O. An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 1983, 46, 973–1027. [Google Scholar] [CrossRef]
- Blandford, R.; Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 1987, 154, 1–75. [Google Scholar] [CrossRef]
- Zhdankin, V.; Uzdensky, D.A.; Werner, G.R.; Begelman, M.C. Electron and ion energization in relativistic plasma turbulence. arXiv 2018, arXiv:astro-ph.HE/1809.01966. [Google Scholar] [CrossRef]
- Beskin, V.S.; Istomin, Y.N.; Parev, V.I. Filling the Magnetosphere of a Supermassive Black-Hole with Plasma. Soviet Ast. 1992, 36, 642. [Google Scholar]
- Levinson, A. Particle Acceleration and Curvature TeV Emission by Rotating, Supermassive Black Holes. Phys. Rev. Lett. 2000, 85, 912–915. [Google Scholar] [CrossRef]
- Hoshino, M.; Lyubarsky, Y. Relativistic Reconnection and Particle Acceleration. Space Sci. Rev. 2012, 173, 521–533. [Google Scholar] [CrossRef]
- Uchiyama, Y.; Aharonian, F.A.; Tanaka, T.; Takahashi, T.; Maeda, Y. Extremely fast acceleration of cosmic rays in a supernova remnant. Nature 2007, 449, 576–578. [Google Scholar] [CrossRef]
- Sudoh, T.; Inoue, Y.; Khangulyan, D. Multiwavelength Emission from Galactic Jets: The Case of the Microquasar SS433. Astrophys. J. 2020, 889, 146. [Google Scholar] [CrossRef]
- Inoue, S.; Takahara, F. Electron Acceleration and Gamma-ray Emission from Blazars. Astrophys. J. 1996, 463, 555. [Google Scholar] [CrossRef]
- Finke, J.D.; Dermer, C.D.; Böttcher, M. Synchrotron Self-Compton Analysis of TeV X-ray-Selected BL Lacertae Objects. Astrophys. J. 2008, 686, 181–194. [Google Scholar] [CrossRef]
- Inoue, Y.; Tanaka, Y.T. Baryon Loading Efficiency and Particle Acceleration Efficiency of Relativistic Jets: Cases for Low Luminosity BL Lacs. Astrophys. J. 2016, 828, 13. [Google Scholar] [CrossRef]
- Kimura, S.S.; Murase, K.; Toma, K. Neutrino and Cosmic-Ray Emission and Cumulative Background from Radiatively Inefficient Accretion Flows in Low-luminosity Active Galactic Nuclei. Astrophys. J. 2015, 806, 159. [Google Scholar] [CrossRef]
- Zhdankin, V.; Werner, G.R.; Uzdensky, D.A.; Begelman, M.C. Kinetic Turbulence in Relativistic Plasma: From Thermal Bath to Nonthermal Continuum. Phys. Rev. Lett. 2017, 118, 055103. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.; Zhdankin, V.; Uzdensky, D.A.; Werner, G.R.; Begelman, M.C. First-principles demonstration of diffusive particle acceleration in kinetic simulations of relativistic plasma turbulence. arXiv 2019, arXiv:astro-ph.HE/1901.03439. [Google Scholar]
- Dermer, C.D.; Miller, J.A.; Li, H. Stochastic Particle Acceleration near Accreting Black Holes. Astrophys. J. 1996, 456, 106. [Google Scholar] [CrossRef]
- Neronov, A.; Aharonian, F.A. Production of TeV Gamma Radiation in the Vicinity of the Supermassive Black Hole in the Giant Radio Galaxy M87. Astrophys. J. 2007, 671, 85–96. [Google Scholar] [CrossRef]
- Levinson, A.; Rieger, F. Variable TeV Emission as a Manifestation of Jet Formation in M87? Astrophys. J. 2011, 730, 123. [Google Scholar] [CrossRef]
- Rieger, F.M. Nonthermal Processes in Black Hole-Jet Magnetospheres. Int. J. Mod. Phys. D 2011, 20, 1547–1596. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barrio, J.A.; González, J.B.; Bednarek, W.; Bernardini, E.; et al. Black hole lightning due to particle acceleration at subhorizon scales. Science 2014, 346, 1080–1084. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Barkov, M.V.; Khangulyan, D. Scenarios for Ultrafast Gamma-ray Variability in AGN. Astrophys. J. 2017, 841, 61. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Radiative Magnetic Reconnection Near Accreting Black Holes. Astrophys. J. 2017, 850, 141. [Google Scholar] [CrossRef]
- Liu, W.; Petrosian, V.; Dennis, B.R.; Jiang, Y.W. Double Coronal Hard and Soft X-ray Source Observed by RHESSI: Evidence for Magnetic Reconnection and Particle Acceleration in Solar Flares. Astrophys. J. 2008, 676, 704–716. [Google Scholar] [CrossRef]
- Nishizuka, N.; Shibata, K. Fermi Acceleration in Plasmoids Interacting with Fast Shocks of Reconnection via Fractal Reconnection. Phys. Rev. Lett. 2013, 110, 051101. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A Powerful Local Shear Instability in Weakly Magnetized Disks. I. Linear Analysis. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- Aharonian, F.; Anchordoqui, L.; Khangulyan, D.; Montaruli, T. Microquasar LS 5039: A TeV gamma-ray emitter and a potential TeV neutrino source. J. Phys. Conf. Ser. 2006, 39, 408–415. [Google Scholar] [CrossRef]
- Khangulyan, D.; Aharonian, F.; Bosch-Ramon, V. On the formation of TeV radiation in LS 5039. Mon. Not. R. Astron. Soc. 2008, 383, 467–478. [Google Scholar] [CrossRef]
- Derishev, E.V.; Aharonian, F.A.; Kocharovsky, V.V.; Kocharovsky, V.V. Particle acceleration through multiple conversions from a charged into a neutral state and back. Phys. Rev. D 2003, 68, 043003. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Syrovatskii, S.I. The Origin of Cosmic Rays; Macmillan: New York, NY, USA, 1964. [Google Scholar]
- Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Detection of the Characteristic Pion-Decay Signature in Supernova Remnants. Science 2013, 339, 807–811. [Google Scholar] [CrossRef]
- Breit, G.; Wheeler, J.A. Collision of Two Light Quanta. Phys. Rev. 1934, 46, 1087–1091. [Google Scholar] [CrossRef]
- Heitler, W. Quantum Theory of Radiation; Clarendon: Oxford, UK, 1954. [Google Scholar]
- Aharonian, F.A. Very High Energy Cosmic Gamma Radiation: A Crucial Window on the Extreme Universe; World Scientific Publishing Co.: Singapore, 2004. [Google Scholar] [CrossRef]
- Bonometto, S.; Rees, M.J. On possible observable effects of electron pair-production in QSOs. Mon. Not. R. Astron. Soc. 1971, 152, 21. [Google Scholar] [CrossRef]
- Done, C.; Fabian, A.C. The behaviour of compact non-thermal sources with pair production. Mon. Not. R. Astron. Soc. 1989, 240, 81–102. [Google Scholar] [CrossRef][Green Version]
- Guilbert, P.W.; Fabian, A.C.; Rees, M.J. Spectral and variability constraints on compact sources. Mon. Not. R. Astron. Soc. 1983, 205, 593–603. [Google Scholar] [CrossRef]
- Dermer, C.D.; Menon, G. High Energy Radiation from Black Holes: Gamma Rays, Cosmic Rays, and Neutrinos; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Kawanaka, N.; Kato, Y.; Mineshige, S. X-ray Emissions from Three-Dimensional Magnetohydrodynamic Coronal Accretion Flows. Publ. Astron. Soc. Jpn. 2008, 60, 399. [Google Scholar] [CrossRef]
- The Fermi-LAT collaboration. Fermi Large Area Telescope Fourth Source Catalog. arXiv 2019, arXiv:1902.10045. [Google Scholar]
- Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; et al. 3FHL: The Third Catalog of Hard Fermi-LAT Sources. Astrophys. J. 2017, 232, 18. [Google Scholar] [CrossRef]
- Lenain, J.P.; Ricci, C.; Türler, M.; Dorner, D.; Walter, R. Seyfert 2 galaxies in the GeV band: Jets and starburst. Astron. Astrophys. 2010, 524, A72. [Google Scholar] [CrossRef]
- Lamastra, A.; Fiore, F.; Guetta, D.; Antonelli, L.A.; Colafrancesco, S.; Menci, N.; Puccetti, S.; Stamerra, A.; Zappacosta, L. Galactic outflow driven by the active nucleus and the origin of the gamma-ray emission in NGC 1068. Astron. Astrophys. 2016, 596, A68. [Google Scholar] [CrossRef]
- Oh, K.; Koss, M.; Markwardt, C.B.; Schawinski, K.; Baumgartner, W.H.; Barthelmy, S.D.; Cenko, S.B.; Gehrels, N.; Mushotzky, R.; Petulante, A.; et al. The 105-Month Swift-BAT All-sky Hard X-ray Survey. Astrophys. J. Suppl. Ser. 2018, 235, 4. [Google Scholar] [CrossRef]
- Gruber, D.E.; Matteson, J.L.; Peterson, L.E.; Jung, G.V. The Spectrum of Diffuse Cosmic Hard X-rays Measured with HEAO 1. Astrophys. J. 1999, 520, 124–129. [Google Scholar] [CrossRef]
- Churazov, E.; Sunyaev, R.; Revnivtsev, M.; Sazonov, S.; Molkov, S.; Grebenev, S.; Winkler, C.; Parmar, A.; Bazzano, A.; Falanga, M.; et al. INTEGRAL observations of the cosmic X-ray background in the 5–100 keV range via occultation by the Earth. Astron. Astrophys. 2007, 467, 529–540. [Google Scholar] [CrossRef]
- Kinzer, R.L.; Jung, G.V.; Gruber, D.E.; Matteson, J.L.; Peterson, L.E. Diffuse Cosmic Gamma Radiation Measured by HEAO 1. Astrophys. J. 1997, 475, 361. [Google Scholar] [CrossRef]
- Ajello, M.; Greiner, J.; Sato, G.; Willis, D.R.; Kanbach, G.; Strong, A.W.; Diehl, R.; Hasinger, G.; Gehrels, N.; Markwardt, C.B.; et al. Cosmic X-ray Background and Earth Albedo Spectra with Swift BAT. Astrophys. J. 2008, 689, 666–677. [Google Scholar] [CrossRef]
- Weidenspointner, G.; Varendorff, M.; Kappadath, S.C.; Bennett, K.; Bloemen, H.; Diehl, R.; Hermsen, W.; Lichti, G.G.; Ryan, J.; Schönfelder, V. The cosmic diffuse gamma-ray background measured with COMPTEL. Am. Inst. Phys. Conf. Ser. 2000, 510, 467–470. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Archinger, M.; et al. A Combined Maximum-likelihood Analysis of the High-energy Astrophysical Neutrino Flux Measured with IceCube. Astrophys. J. 2015, 809, 98. [Google Scholar] [CrossRef]
- Ajello, M.; Gasparrini, D.; Sánchez-Conde, M.; Zaharijas, G.; Gustafsson, M.; Cohen-Tanugi, J.; Dermer, C.D.; Inoue, Y.; Hartmann, D.; Ackermann, M.; et al. The Origin of the Extragalactic Gamma-ray Background and Implications for Dark Matter Annihilation. Astrophys. J. Lett. 2015, 800, L27. [Google Scholar] [CrossRef]
- Eichler, D. High-energy neutrino astronomy: A probe of galactic nuclei? Astrophys. J 1979, 232, 106–112. [Google Scholar] [CrossRef]
- The IceCube Collaboration. The IceCube Collaboration: Contributions to the 29th International Cosmic Ray Conference (ICRC 2005), Pune, India, Aug. 2005. arXiv 2005, arXiv:astro-ph/astro-ph/0509330. [Google Scholar]
- Stecker, F.W. PeV neutrinos observed by IceCube from cores of active galactic nuclei. Phys. Rev. D 2013, 88, 047301. [Google Scholar] [CrossRef]
- Kimura, S.S.; Tomida, K.; Murase, K. Acceleration and escape processes of high-energy particles in turbulence inside hot accretion flows. Mon. Not. R. Astron. Soc. 2019, 485, 163–178. [Google Scholar] [CrossRef]
- Tashiro, M.; Maejima, H.; Toda, K.; Kelley, R.; Reichenthal, L.; Lobell, J.; Petre, R.; Guainazzi, M.; Costantini, E.; Edison, M.; et al. Concept of the X-ray Astronomy Recovery Mission. In Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Austin, TX, USA, 6 July 2018; Volume 10699, p. 1069922. [Google Scholar] [CrossRef]
- Nandra, K.; Barret, D.; Barcons, X.; Fabian, A.; Herder, J.W.D.; Piro, L.; Watson, M.; Adami, C.; Aird, J.; Afonso, J.M.; et al. The Hot and Energetic Universe: A White Paper presenting the science theme motivating the Athena+ mission. arXiv 2013, arXiv:1306.2307. [Google Scholar]
- Gallo, L.C.; Randhawa, J.S.; Waddell, S.G.H.; Hani, M.H.; García, J.A.; Reynolds, C.S. Nuclear spallation in active galaxies. Mon. Not. R. Astron. Soc. 2019, 484, 3036–3041. [Google Scholar] [CrossRef]
- Kheirandish, A.; Murase, K.; Kimura, S.S. High-Energy Neutrinos from Magnetized Coronae of Active Galactic Nuclei and Prospects for Identification of Seyfert Galaxies and Quasars in Neutrino Telescopes. arXiv 2021, arXiv:2102.04475. [Google Scholar]
| 1 | Blazars are another possible origin of the cosmic MeV gamma-ray background radiation [71]. However, recent studies suggest that blazars can explain only ∼3% of the cosmic MeV gamma-ray background radiation [72]. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).