Abstract
THESEUS is an ESA space based project, which aims to explore the early universe by unveiling a complete census of Gamma-ray Burst (GRB) population in the first billion years. This goal is expected to be realized by the combined observations of its three instruments on board: the Soft X-ray Imager (SXI), the X and Gamma Imaging Spectrometer (XGIS), and the InfraRed Telescope (IRT). This last one will identify, localise, and study the afterglow of the GRBs detected by SXI and XGIS, and about 40% of its time will be devoted to an all-sky photometric survey, which will certainly detect a relevant number of extragalactic sources, including Quasars. In this paper, we focus on the capability of IRT-THESEUS Telescope to observe Quasars and, in particular, Quasars lensed by foreground galaxies. In our analysis we consider the recent results for the Quasar Luminosity Function (QLF) in the infrared band based on the Spitzer Space Telescope imaging survey. In order to estimate the number of lensed Quasars, we develop Monte Carlo simulations using the mass-luminosity distribution function of galaxies and the galaxy and Quasar redshift distributions. We predict about 2.14 × 105 Quasars to be observed during IRT-Theseus sky survey, and approximately 140 of them lensed by foreground galaxies. Detailed studies of these events would provide a powerful probe of the physical properties of Quasars and the mass distribution models of the galaxies.
1. Introduction
THESEUS is an ESA space based project. Its specific scientific objective is to explore the physical conditions of the Early Universe by unveiling a complete census of the GRB population in the first billion years since the Big Bang, and it can also perform an unprecedented deep monitoring of the X-ray transient Universe. THESEUS will observe several hundreds of GRBs per year [1].
During the time of waiting for any GRB alert, THESEUS will be able to create a rich database about objects at high z, due to its three instruments on board, which is dedicated to , X, and bands [2].
In this paper, in particular we aim to consider the information about Quasars gathered by the instruments on-board THESEUS. Quasars are very energetic and distant galaxies with an active galactic nucleus (AGN). Being distant and with extremely high luminosity, Quasars are considered to be important instruments for discovering the content and the history of Universe. In this respect, one of the source of information is related to Quasars lensed by foreground galaxies.
Quasars were discovered in the 1960s and Barnothy [3] was the first to connect them with the gravitational lens effect. However, Quasar lensing received a real boost only in 1979, when Walsh et al. [4] discovered the first double Quasar. Concerning the gravitational lensing, General Relativity predicts the value of the deflection angle of a light ray by a spherically symmetric mass M. If the impact parameter (the smaller distance of the light ray with respect to the deflecting body) is much larger than the Schwarzschild radius of the lens mass (), then the deflection angle is given by
This is exactly twice the value that was obtained in Newtonian gravity. The deflection angle of an ensemble of mass points is the sum of the deflections due to individual mass components, which, in the case of the geometrical thin lens (the extent of the deflecting mass along the line of sight is much smaller than both its distances to the observer and the source), is given by [5]:
Here, is the mass density that was projected onto a plane perpendicular to the incoming light ray from the source and arriving to the observer (line of sight).
From here, the so-called lens equation is found to be [6]
where is the angular position of the source, are the angular positions of the source images, and is the Einstein ring radius, the angular radius of the image when the lens and the source are perfectly aligned. It is given by
where is the lens galaxy mass inside the Einstein radius and , , are the angular diameter distances observer-source, observer-lens, and lens-source, respectively.
In cosmology, the angular diameter distance of a source at redshift seen by an observer at redshift is given by [7],
with
Here, is Hubble constant and , , are the dimensionless density parameters for the matter (i.e., the sum of the cold dark matter and baryonic matter, the space-curvature, and the dark energy, respectively). There are three different scales in gravitational lensing: strong gravitational lensing (when the lens images are separated by more than a few tenths of arcsecs and they can be observed as distinct images); weak lensing (when the involved light deflection angles are much smaller and galaxy distortion can only be observed statistically over a large number of galaxies); and, microlensing (in the case of star-on-star lensing, where the angular separation between images is of the order of arcsec) (see, e.g., [6] for a review on the subject).
Gravitationally lensed Quasars by foreground galaxies belong to the strong lensing scale. They come in a variety of classes: double, triple, and quadruple systems, observed up to now by several space- and ground-based telescopes (Hubble Space Telescope (HST) [8], Sloan Digital Sky Survey (SDSS) [9], Chandra [10], Spitzer [11], etc.). Their study provides a lot of precious information regarding the lens (foreground galaxies), the source (Quasars), and allows for a better understanding of galactic and Quasar populations in the Universe, their distribution in distance (or redshift), and mass.
Recently, these studies even lead to the discovery of exoplanets in faraway galaxies [12]. Indeed, strongly lensed Quasars may also be affected by microlensing (Quasars might also sometime be microlensed by e.g., a star in the Quasar hosting galaxy, as possibly happened recently in the event towards J1249 + 3449. These kind of events would give rise to an X-ray flare, analogous to the optical flare that is associated to that event [13,14]), since light bundles from the lensed Quasar may go through the lensing galaxy and/or its galactic halo. Galaxies consist at least partly of stars, and galactic halos consist possibly of compact objects in the mass range , as well. Each of these stars (or other compact objects, like black holes, brown dwarfs, or planets) may act as a “compact lens” or “microlens” and produces new images of the source. However, because the image splitting is proportional to the square root of the lens mass, these microimages are only of the order a arcsec apart and cannot be directly resolved by any of the up to date available techniques. Instead, a characteristic light-curve is observed. Recent studies focused on microlensing examination show that, sometimes, the variation in the Quasar light could be a source of information for the presence of compact objects in the lensing galaxy or in the galaxy hosting the Quasar [14].
In this work, we aim to examine the capacities of IRT-THESEUS to observe Quasars and, in particular, Quasars that are lensed by foreground galaxies. The structure of this paper is as follows: in Section 2, we predict and the number of Quasar observed in a IR band close to the band of IRT-THESEUS. In Section 3, we describe the algorithm that we established and used to estimate the number of lensed Quasars by foreground galaxies, as observed by any telescope, and explain how we find the estimated number of lensed Quasars, observed by IRT-THESEUS. In this section, we show the test of this algorithm on the data of the SDSS and of the Chandra X-ray telescope. Our conclusions are drawn in Section 4.
In our calculations we use the following cosmological parameters: , , , and km s Mpc.
2. Quasars as Expected to Be Observed by IRT-THESEUS
In this section, we examine the possibility of the IR instrument on board of THESEUS to observe Quasars. IRT-THESEUS is designed to be a 0.7 m class telescope with arcmin FOV, with both imaging and spectroscopy capabilities in the 0.7–1.8 m band [1], designed to operate in three observation modes: the photometric mode, the low-resolution (LR) mode, and the high-resolution (HR) mode. When a gamma-ray burst is identified, the IRT instrument will execute the following observational sequence: it will observe in imaging mode within 1 arcsec of the GRB error box and by frames in ZJH photometric bands, so that the source colour can be determined; then, IRT will enter the spectroscopy mode to define the redshift value and the position of the source. In the case of a bright source, it can go back to imaging mode (H-band) for at least another 1800 s. When the source is faint, IRT takes data in imaging mode for a 3600 s time interval to establish the GRB photometric light curve [2]. The rest of the time, IRT-THESEUS will be able to perform an all-sky photometric survey and detect a number of extragalactic sources, including Quasars. Here, we estimate the number of Quasars expected to be detected and recorded on the IRT-THESEUS database, based on the instrument’s sensitivity.
2.1. Number of Quasars Observed in IR Band
Quasars are luminous in almost all accessible bands. The Quasar luminosity function (QLF), the comoving number density of Quasars as a function of luminosity, is perhaps the most important observational signature of Quasar populations. Lacy et al. [15], based on the Spitzer Space Telescope imaging surveys, derived the luminosity functions of active galactic nuclei (AGNs) in the IR band as a double power-law function of the following form:
where is the comoving space density of the AGN, is the characteristic space density, both in units of comoving Mpc, L is the rest-frame luminosity at m, and is the break luminosity at m, both in units of erg s Hz. The evolution in is a cubic expression (e.g., [16])
where , is a free parameter in the fit, which corresponds to the break luminosity at redshift zero, is the faint-end slope, is the bright-end slope and is fixed at . The coefficients , , , , , , and are given in the Table 1 of Lacy et al. [15].
In order to determine the number of Quasars in the redshift range –, we calculate the integral
where is the comoving volume element in the solid angle and redshift interval , is the Hubble distance, is the angular diameter distance at redshift z, and is defined through the Equation (6).
2.1.1. A Test on Spitzer Space Telescope
Spitzer Space Telescope observed the Universe in several bands in mid-infrared wavelengths. Based on its capability, we consider the case of the band 3.6 m (the closest to the IRT-THESEUS band of observation), with an apparent magnitude 18 [11] and calculate the number that is given by Equation (9) to be tested. For this magnitude, we find the minimum luminosity to be, , where erg s is the solar luminosity and is the luminosity distance of the source. When considering erg s in Equation (9), we estimate the number of Quasars observed by Spitzer in the whole sky survey to be . At the same time, Equation (9) limits Spitzer observation of Quasars up to . In order to check the number , we find, in Lacy and Sajina [17], that over 20,000 AGN candidates exist in the Spitzer archive, which is close to the theoretical value found above.
2.1.2. Results on IRT-THESEUS
In the case of IRT-THESEUS, we are based on the instrument description [1]: the AB mag (300 s) is designed to be 20.6 for H band. Using the Vega - AB Magnitude Conversion, we convert this value to the value 19.21 of the apparent magnitude. In such conditions, we find , where is the luminosity distance of the source. When considering erg s in Equation (9), we calculate the number of Quasars to be observed by the IRT-THESEUS (in the overall field of view): . At the same time, Equation (9) leads to a limit for the redshift of the Quasars observed by this instrument.
With THESEUS Field of Regards (FoR) (the fraction of the sky to be monitored) [2], the number of Quasars to be observed by THESEUS reduces to . We note that this high number provides an opportunity to also detect lensing effects on Quasars. For this reason, we devoted a thorough analysis in order to estimate the number of lensed Quasars by foreground galaxies in the IRT-THESEUS database, which is shown in the next section.
3. Quasar Lensing with IRT-THESEUS
Gravitational lensing of Quasars is a powerful tool for different kinds of investigations in astrophysics and cosmology. It occurs whenever the source (Quasar), the lens (foreground galaxy), and the observer are so well aligned that the observer-source direction lies inside the so-called Einstein radius of the lens [5]. Approximately one out of 500 Quasars has multiple images as a result of lensing by a foreground galaxy [18]. Below, we describe an algorithm to estimate the number of these lensed Quasars to be observed by IRT-THESEUS telescope.
3.1. The Algorithm Generating Quasars and Galaxies
We assume that a strong lensing event is detectable by the telescope if the image separation, which is of the order of the Einstein angle, is higher than the accuracy of the telescope. For investigating the possibility to observe such events, we establish a method that is based on Monte Carlo numerical simulations. For each generated event, we extract, via the procedure detailed below, all of the needed parameters. In particular:
1—We generate the redshift of the Quasar, following the Quasar distribution that was obtained by Schneider et al. [19] (see Section 3.1.1, below).
2—We generate the redshift of the galaxy following the distribution that was obtained by Appenzeller et al. [20] (see Section 3.1.2 below), provided that the galactic redshift is lower than the Quasar redshift. The number of galaxies fulfilling this condition for each Quasar is found by the cumulative number of galaxies.
3—For each generated galaxy, we extract its mass by the stellar mass function [21] (see Section 3.1.3 below) and, based on the relation between the stellar mass of the galaxy and stellar velocity distribution obtained by Zahid et al. [22] (see Section 3.1.4 below), we find its velocity dispersion.
4—Based on the Singular Isothermal Sphere model for the galaxies (see Section 3.1.5 below), and making use of the galaxy and Quasar redshifts generated above, we define the Einstein angle for the couple Quasar/galaxy [18].
Is the galaxy inside the Einstein angle? For an isolated galaxy, its probability to be inside this Einstein angle has the tiny value of . However, when considering 200 billions of galaxies in the observable Universe, this probability raises to ≃10.
We take a sample of 7000 galaxies into consideration, so we repeat the procedure of galaxy’s parameter generation 7000 times [20]. In such conditions, the probability for each synthetic galaxy to be inside the Einstein angle turns out to be .
The code extracts a uniformly distributed number n in the interval . It keeps the case when (aligned couple Quasar/galaxy); otherwise, it rejects it (nonaligned couple Quasar/galaxy).
This procedure is repeated as many times as the number of galaxies with a redshift lower than the Quasar redshift.
In the case of any aligned couple Quasar-galaxy, the Einstein angle is then compared with the angular accuracy of the instrument.
The procedure must be repeated as many times as the number of Quasars observed by the instrument.
Below, we explain the distributions mentioned above and find the expression of the Einstein angular radius when considering a singular isothermal sphere (SIS) model for the galaxy. Afterwards, we follow with estimating the number of lensed Quasars in the case of three instruments: SDSS, Chandra and IRT-THESEUS.
3.1.1. Quasar Redshift Distribution
In [19], Schneider et al. found a Quasar redshift distribution based on the SDSS Data Catalog (Third Data Release). This catalogue contains 46,420 Quasars with spectroscopic redshifts from to . The area covered by the catalog is 4188 deg. A clear majority of Quasars have redshifts below , the median redshift is , (the mode is ). There are 520 Quasars at redshifts greater than four, of which 17 are at redshifts greater than five. The catalog contains 69 Quasars with redshifts below .
3.1.2. Galaxy Redshift Distribution
Appenzeller et al. [20] found a photometric redshift distribution of 7000 galaxies. They analyzed distant galaxies that were observed near the South Galactic Pole by the FORS Deep Field (ESO VLT), in a sky area of about arcmin. Davison et al. also confirmed this distribution [21].
3.1.3. Galaxy Mass Distribution
Davidzon et al. [21], based on the COSMOS2015 catalogue, provided a comprehensive view of the galaxy stellar mass assembly between and 6. They fitted measurements with double (up to ) and a single (beyond that bin) Schechter function, as given by
Schechter parameters of the COSMOS2015 galaxy stellar mass function (SMF) are found in the Table 1 of the [21].
3.1.4. Galactic Velocity Dispersion
Based on an analysis of the SDSS and SHELS data, Zahid et al. [22] proposed a relation between the central stellar velocity dispersion and the stellar mass M of the galaxies, which is a power law with a break point
The central stellar velocity dispersion is a measure of the stellar kinematics and it is directly related to the gravitational potential of the system. The fit parameters are: , , and . The two indices and define the power law below and above the break point, respectively.
3.1.5. The Singular Isothermal Distribution
For the lensing properties of galaxies, we assume a singular isothermal sphere (SIS) distribution. This spherical mass distribution yields flat rotation curves, such as that observed for spiral galaxies. Their density distribution is described by [5]
Physically, this model corresponds to a distribution of self-gravitating particles, where the velocity distribution at all radii is a Maxwellian with one-dimensional velocity dispersion . The mass distribution (12) has two limitations: the central density diverges as (hence, the name ‘singular’) and the total mass of this distribution diverges as . However, these do not dismiss our assumption. First, although real galaxies have nonzero core radii, they are generally too small (as compared to the critical impact parameter) to make much difference. Second, because we are restricting our attention to lenses that produce multiple images, our results will be very insensitive to the mass distribution outside of the critical impact parameter, and the calculation does not depend on the existence or nature of extended massive halos, but only on the well determined (by rotation curves) mass distribution in the inner regions of galaxies.
By projecting the three-dimensional density along the line of sight, we obtain the corresponding surface density
The mass of the lens inside a radius R from the galactic center in the galactic plane is given by
and, by replacing in the lens Equation (4), we have
Because the central stellar velocity dispersion in Equation (11) is a measure of the stellar kinematics related to the gravitational potential of the system, we have considered it to be the same to in Equation (15).
Anyway, we have to remark that Ofek et al. [23] predicted a not exactly equal to the observed stellar velocity dispersion , for the reason of the dark matter halos, which are shown to be dynamically hotter than luminous stars. This conclusion is based on X-ray observations. Furthermore, they propose , where .
3.2. Test on SDSS and Chandra
We tested the numbers found through our algorithm with the results of the observations that were conducted by the SDSS and Chandra X-ray telescope.
In the case of SDSS, we are based on a final statistical sample of lensed Quasars [9] for this instrument, which consists of 26 lensed Quasars brighter than , in the redshift range of , selected from the 50,836 spectroscopically confirmed Quasars in the SDSS Data. The image separation range is restricted to arcsec.
We generate the same conditions in our code and obtain 33 synthetic lensed Quasars. In Figure 1, we show the histogram of redshift distributions for our 33 synthetic lensed Quasars (dashed line) and, for comparison, the redshift distribution for 26 lensed Quasars that were observed by the SDSS (continuous line). Overall, the two distributions appear in agreement, even if there appear to be a small excess, in the simulated sample, at low reshifts.
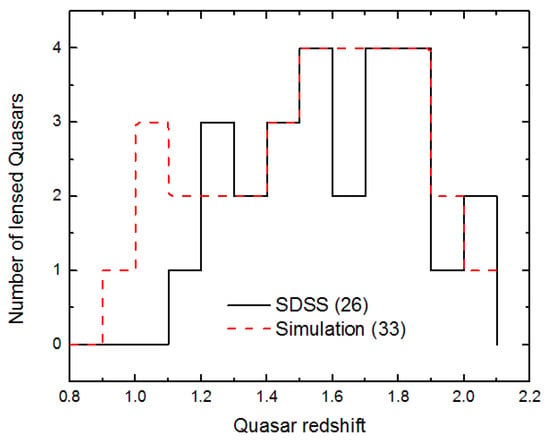
Figure 1.
Histogram of the redshift distributions for 26 lensed Quasars observed by the SDSS (continuous line) and for 33 synthetic lensed Quasars (dashed line).
In the case of Chandra telescope, we are based on Walton et al. [10], who analysed 27 lensed Quasars observed by this instrument, with redshift . In order to find the overall number of Quasars in its fied of view, we make use of Evans et al. [24], who show that Chandra observed in 320 deg of the sky up to a limit flux erg/s/cm; 135 deg up to a flux erg/s/cm and 6 deg up to a flux erg/s/cm. Using the results obtained in [25] about the cumulative number counts N(>S) versus flux limit, we estimate the total number of Quasars observed by Chandra telescope to be 12,725. The Chandra resolution angle is arcsec.
We simulate the same conditions inside our code and find 24 synthetic lensed Quasars with the image separation higher than arcsec. In Figure 2, we show the histogram of redshift distributions for 27 Lensed Quasars that were observed by Chandra and 24 synthetic lensed Quasars simulated numerically. One can remark a good match in all bins of the Quasar redshift.
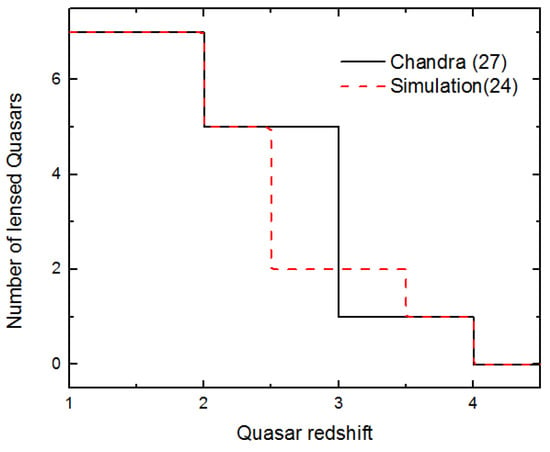
Figure 2.
Histogram of the redshift distributions for 24 synthetic lensed Quasars (dashed line) and 27 lensed Quasars observed by Chandra (continuous line).
3.3. Prediction on IRT-THESEUS
Based on the number of Quasars (≃) expected to be detectable by IRT-THESEUS (see Section 2) and requiring the angular separation between images to be above the IRT-THESEUS angular resolution (≃1 arcsec) [2], our algorithm produces approximately 140 strongly lensed Quasars by foreground galaxies.
In Figure 3, the obtained redshift distribution of the lensed Quasars is shown. As one can see, the redshift distribution peaks for redshift values in the range 1.5–2 and becomes almost flat for Quasar redshifts larger than about 2.5.
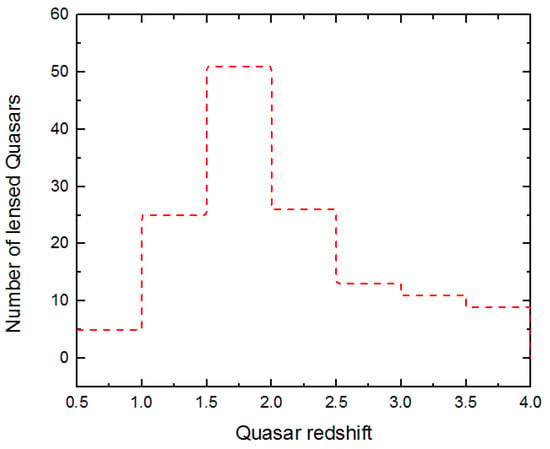
Figure 3.
Histogram of the redshift distribution for the 140 expected Quasars, lensed by foreground galaxies, and detectable by IRT-THESEUS.
4. Concluding Remarks
THESEUS is an ESA space based project. Its specific scientific objective is to create a complete census of the GRB population in the first billion years since the Big Bang. During the time of waiting for any GRB alert, its three instruments will be able to create a rich database on objects at high z. One of them is IRT-THESEUS, a 0.7 m class telescope with arcmin FOV, observing in the 0.7–1.8 m band.
In this work, we estimated the number of Quasars that IRT-THESEUS will be able to detect during the waiting time between GRB alerts, and found that approximately Quasars should be detected by the IRT instrument. Our calculation is based on the Quasar luminosity function (QLF) that was obtained by Lacy et al. [15] from the Spitzer Space Telescope imaging survey. A parallel calculation for Spitzer gives a lower number, ≃, which is, in fact, close to the number 20,000 of AGN candidates existing in the Spitzer archive [17].
Here, we have to remark that we used the same QLF for both instruments, even if there is some discrepancy in their band observation, 0.7–1.8 m for IRT-THESEUS and m for Spitzer, whereas the QLF is established for the waveband of 5 m. The collection of data by IRT-THESEUS could help in recognizing and studying in more details the Quasar population. An important phenomenon that is related to Quasars is their gravitational lensing by foreground galaxies.
Nowadays, gravitational lensing is a powerful method of investigation in both astrophysics and cosmology for the study of Quasars, the distribution of stars in galaxies, in evaluating the amount of the dark matter component in galaxies and even in discovering extragalactic planets.
Lensed Quasars are currently detected by several facilities, like Hubble Space Telescope (HST), SDSS, Chandra, Spitzer, etc. Their observation in different bands give a great help in understanding the physical processes that take place in Quasars. Inspired by the great number of Quasars predicted to be observed by IRT-THESEUS, we considered the possibility of observation of strongly lensed Quasars. For this reason, we establish Monte Carlo numerical simulations in order to estimate the expected number of lensed Quasars that are detectable by IRT-THESEUS.
In our calculations, we used the redshift distributions of both Quasars and galaxies, as well as the galactic mass distribution and stellar velocity dispersion (see Section 3).
First of all, we compare the results of our numerical code on two existing databases: SDSS and Chandra X-ray Telescope and find a close compatibility. Secondly, based on the estimated number of Quasars detectable by IRT-THESEUS (≃) and requiring the angular separation between the lensed images to be above the IRT-THESEUS angular resolution (≃1 arcsec), we find that approximately 140 strongly lensed Quasars by foreground galaxies would be detectable by IRT-THESEUS.
Another instrument that we were interested in is eROSITA European X-ray instrument, which observes in (0.5–2.0 keV band), with an angular accuracy of arcsec [26], being designed to observe about three0million AGN in the extragalactic sky (|b| > 10) [27]. We checked this number by using a similar calculation, as in the case of Chandra, and found a very close value, . Although this number is high, our algorithm does not produce any single lensed AGN by foreground galaxies in the case of eROSITA, due to relatively large angular accuracy.
We would like to remark that finding strongly lensed Quasars is of great importance in astrophysics and cosmology, since it allows for increasing our knowledge not only of Quasars, but also of the structure, dark matter content, dynamics and evolution, of the lens galaxies. It may even allow further test the theory of general relativity, constrain the parameters of alternative gravity theories, and gather information on the cosmological parameters.
Author Contributions
All authors have contributed to the article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to the anonymous referee for his/her comments which significantly help to improve the manuscript. FDP and AAN acknowledge the TAsP and Euclid INFN Projects.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Götz, D.; Boulade, O.; Cordier, B.; Floc’h, E.L.; Pinsard, F.; Amiaux, J.; Tourrette, T.; Basa, S.; Vergani, S.; Atteia, J.; et al. The Infra-Red Telescope on board the THESEUS mission. arXiv 2018, arXiv:1802.01676. [Google Scholar]
- Amati, L.; O’Brien, P.; Götz, D.; Bozzo, E.; Tenzer, C.; Frontera, F.; Ghirlanda, G.; Labanti, C.; Osborne, J.; Stratta, G.; et al. The THESEUS space mission concept: Science case, design and expected performances. Adv. Space Res. 2018, 62, 191–244. [Google Scholar] [CrossRef]
- Barnothy, J. Quasars and the Gravitational Image Intensifier. Astron. J. 1965, 70, 666. [Google Scholar] [CrossRef]
- Walsh, D.; Carswell, R.F.; Weymann, R.J. 0957 + 561 A, B: Twin quasistellar objects or gravitational lens? Nature 1979, 279, 381–384. [Google Scholar] [CrossRef]
- Schneider, P.; Kochanek, C.; Wambsganss, J. Gravitational Lensing: Strong, Weak and Micro: Saas-Fee Advanced Course 33; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 33. [Google Scholar]
- De Paolis, F.; Giordano, M.; Ingrosso, G.; Manni, L.; Nucita, A.; Strafella, F. The Scales of Gravitational Lensing. Universe 2016, 2, 6. [Google Scholar] [CrossRef]
- Krawczynski, H.; Chartas, G.; Kislat, F. The Effect of Microlensing on the Observed X-ray Energy Spectra of Gravitationally Lensed Quasars. Astrophys. J. 2019, 870, 125. [Google Scholar] [CrossRef]
- Keeton, C.; Falco, E.; Impey, C.D.; Kochanek, C.; Lehár, J.; McLeod, B.; Rix, H.W.; Munoz, J.; Peng, C. The host galaxy of the lensed quasar Q0957 + 561. Astrophys. J. 2000, 542, 74. [Google Scholar] [CrossRef]
- Inada, N.; Oguri, M.; Shin, M.S.; Kayo, I.; Strauss, M.A.; Morokuma, T.; Rusu, C.E.; Fukugita, M.; Kochanek, C.S.; Richards, G.T.; et al. The Sloan Digital Sky Survey quasar lens search. V. Final catalog from the seventh data release. Astron. J. 2012, 143, 119. [Google Scholar] [CrossRef]
- Walton, D.; Reynolds, M.; Miller, J.; Reis, R.; Stern, D.; Harrison, F. Broad Iron Emission from Gravitationally Lensed Quasars Observed by Chandra. Astrophys. J. 2015, 805, 161. [Google Scholar] [CrossRef]
- Williams, S.; Bonanos, A. Spitzer mid-infrared point sources in the fields of nearby galaxies. Astron. Astrophys. 2016, 587, A121. [Google Scholar] [CrossRef]
- Dai, X.; Guerras, E. Probing extragalactic planets using quasar microlensing. Astrophys. J. Lett. 2018, 853, L27. [Google Scholar] [CrossRef]
- Graham, M.J.; Ford, K.E.S.; McKernan, B.; Ross, N.P.; Stern, D.; Burdge, K.; Coughlin, M.; Djorgovski, S.G.; Drake, A.J.; Duev, D.; et al. Candidate Electromagnetic Counterpart to the Binary Black Hole Merger Gravitational-Wave Event S190521g*. Phys. Rev. Lett. 2020, 124, 251102. [Google Scholar] [CrossRef]
- De Paolis, F.; Nucita, A.; Strafella, F.; Licchelli, D.; Ingrosso, G. A quasar microlensing event towards J1249 + 3449? Mon. Not. R. Astron. Soc. Lett. 2020, 499, L87–L90. [Google Scholar] [CrossRef]
- Lacy, M.; Ridgway, S.E.; Sajina, A.; Petric, A.O.; Gates, E.L.; Urrutia, T.; Storrie-Lombardi, L.J. The Spitzer mid-infrared AGN Survey. II. The demographics and cosmic evolution of the AGN population. Astrophys. J. 2015, 802, 102. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Richards, G.T.; Hernquist, L. An observational determination of the bolometric quasar luminosity function. Astrophys. J. 2007, 654, 731. [Google Scholar] [CrossRef]
- Lacy, M.; Sajina, A. Active galactic nuclei as seen by the Spitzer Space Telescope. Nat. Astron. 2020, 4, 352–363. [Google Scholar] [CrossRef]
- Schmidt, R.; Wambsganss, J. Quasar microlensing. Gen. Relat. Gravit. 2010, 42, 2127–2150. [Google Scholar] [CrossRef]
- Schneider, D.P.; Hall, P.B.; Richards, G.T.; Berk, D.E.V.; Anderson, S.F.; Fan, X.; Jester, S.; Stoughton, C.; Strauss, M.A.; SubbaRao, M.; et al. The sloan digital sky survey quasar catalog. III. Third data release. Astron. J. 2005, 130, 367. [Google Scholar] [CrossRef]
- Appenzeller, I.; Bender, R.; Böhm, A.; Frank, S.; Fricke, K.; Gabasch, A.; Heidt, J.; Hopp, U.; Jäger, K.; Mehlert, D.; et al. Exploring Cosmic Evolution with the FORS Deep Field. Messenger 2004, 116, 18. [Google Scholar]
- Davidzon, I.; Ilbert, O.; Laigle, C.; Coupon, J.; McCracken, H.; Delvecchio, I.; Masters, D.; Capak, P.; Hsieh, B.; Le Fèvre, O.; et al. The COSMOS2015 galaxy stellar mass function-Thirteen billion years of stellar mass assembly in ten snapshots. Astron. Astrophys. 2017, 605, A70. [Google Scholar] [CrossRef]
- Zahid, H.J.; Geller, M.J.; Fabricant, D.G.; Hwang, H.S. The scaling of stellar mass and central stellar velocity dispersion for quiescent galaxies at z < 0.7. Astrophys. J. 2016, 832, 203. [Google Scholar]
- Ofek, E.O.; Rix, H.W.; Maoz, D. The redshift distribution of gravitational lenses revisited: Constraints on galaxy mass evolution. Mon. Not. R. Astron. Soc. 2003, 343, 639–652. [Google Scholar] [CrossRef][Green Version]
- Evans, I.N.; Primini, F.A.; Glotfelty, K.J.; Anderson, C.S.; Bonaventura, N.R.; Chen, J.C.; Davis, J.E.; Doe, S.M.; Evans, J.D.; Fabbiano, G.; et al. The Chandra source catalog. Astrophys. J. Suppl. Ser. 2010, 189, 37. [Google Scholar] [CrossRef]
- Hasinger, G.; Miyaji, T.; Schmidt, M. Luminosity-dependent evolution of soft X-ray selected AGN-New Chandra and XMM-Newton surveys. Astron. Astrophys. 2005, 441, 417–434. [Google Scholar] [CrossRef]
- Merloni, A.; Predehl, P.; Becker, W.; Böhringer, H.; Boller, T.; Brunner, H.; Brusa, M.; Dennerl, K.; Freyberg, M.; Friedrich, P.; et al. eROSITA science book: Mapping the structure of the energetic universe. arXiv 2012, arXiv:1209.3114. [Google Scholar]
- Kolodzig, A.; Gilfanov, M.; Sunyaev, R.; Sazonov, S.; Brusa, M. AGN and QSOs in the eROSITA all-sky survey-I. Statistical properties. Astron. Astrophys. 2013, 558, A89. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).