1. Introduction
The mean-field approach was one of the first methods for studying the dynamo. This approach assumes averaging of the magnetic induction equation over uniform and isotropic random velocity field. Averaged equations describing the magnetic energy generation in helical rotated streams were developed by Steenbeck, Krause and Rädler in the 60 s, see bibliography in [
1]. Since then, these models were used in various analytical and numerical investigations of large-scale magnetic fields generation in stars and galaxies [
2]. Now the situation has changed: powerful parallel simulations allow us to avoid equation averaging and study small details of magnetic field evolution in real-time [
3]. However mean-field models are still widely used, see, e.g., [
4,
5,
6]. The reason for their use is our ignorance of initial and boundary information needed for statements of numerical problems. The possibility of detailed magnetic field reconstruction leads to the requirement of much more explicit input astrophysical data, e.g., [
7], while for the mean-field approach, we need only two averaged moments of the isotropic velocity field which can be obtained from modern observations or from general physical ideas. Despite the fact that simplicity is the main virtue of the mean-field approach, in this paper we consider its unusual complication and refuse from one of the basic mean-field assumption—isotropy condition, considering anisotropic effects in the frame of the well-known dynamo model.
Usually, dynamo anisotropy or inhomogeneity are studied for the standard mean-field equation:
where
is the averaged magnetic field
and the averaged velocity parameters—hydrodynamical helicity
and turbulent diffusivity
—are anisotropically or nonuniformly distributed in the space. However, this start point seems a bit controversial, because Equation (
1) itself is obtained under isotropic and uniform assumption, so it should be used for nonuniform
and
, if only the scale of inhomogenity of anisotropy/diffusivity is much larger than the scales of magnetic field perturbations. To consider problem more correctly we should start a little earlier and re-obtain mean-field Equation (
1) for anisotropic and nonuniform turbulence.
There are various methods of mean-field model derivation from the induction equation
here and further we use notations
and
for cross and dot products respectively. In their pioneer works, Steenbeck and Krause used the timeseries in respect to the small magnetic Reynolds number
, though astrophysical applications usually presume that
is very high (here
V and
L are typical velocity and length scales of the flow, and
is the magnetic diffusivity, more details can be found, e.g., in [
8]). Other works were based on the two-scale assumption, that looks quite reasonable at first sight, but can demand a delicate application for astrophysical non-spherical objects, which have at least two large scales, such as spiral galaxies with diameters much larger than thicknesses. More recent methods were based on less sophisticated hypotheses however each of them failed to reproduce all properties of interstellar medium. We base our analysis on the path integral approach to get the mean-field equations for a short-correlated flow. This method was firstly suggested in [
9], and then developed and generalized in many works, see details, e.g., in [
10,
11]. More recent applications of the method can be found, e.g., in [
12]. Here we demonstrate that this approach, working in a field with memory time much smaller than a typical time of vortices rotations, is applied also in anisotropic and nonuniform turbulence, see, e.g., [
13]. Untying the averaging process for the magnetic and velocity field, it defines the anisotropic mean-field dynamo by helicity and diffusivity tensors and, what is not less important, in the statistically homogeneous and isotropic situation it restores the classical Equation (
1).
However, we apply the path integral method not to Equation (
2) as usual, but to the induction equation, written in terms of vector potential,
:
Our intention here is motivated by two reasons: first of all, Equation (
3) has a gradient uncertainty, which helps to rewrite it in multiplication form (see the explanation after transformation (4)), and, secondly, such form allows after averaging move anisotropic and nonuniform effects under the
. Indeed, one can present the induction Equation (
2) for the microscopic magnetic field
in two forms: writing it in the form
or writing it like
. Both forms are equivalent due to the additional equations
and
. Note that incompressible assumption for velocity field, which is usually used in mean-field models with constant averaged velocity characteristics, looks reasonable for our approach, however it is well-known that compressible effects can play a very important role in astrophysical magnetic field formation, see, e.g., [
14,
15,
16,
17]. The second form is more practical to get the mean-field equation and is widely used. The corresponding shortcoming is that it is not obvious how to write the mean-field equation in the form with a
, which provides the implementation of a solenoidal condition for the averaged field
. Using the vector potential we avoid this technical problem, getting the equation for evolution of the averaged potential, and then getting the
from its both sides.
Basing on the obtained model, we find its isotropic/anisotropic solutions in an uniform field and analyze the dynamo growth rate depending on helicity and diffusivity tensors. Moreover we apply it to two more specific problems. We confirm that for a statistically anisotropic situation dynamo excitation is possible for near-zero helical component and even if the trace
vanishes at all (a similarly test was in [
9] ). Another obtained effect is connected with the very early stage of dynamo self-excitation. We demonstrate that for a statistically anisotropic (or isotropic) flow and suitable initial localized conditions a superexponential growth is possible. This result can be important for the galactic magnetic field evolution because the mean-field dynamo time scale in galaxies is smaller however comparable with the age of galaxies, see, e.g., [
18].
2. Functional Integral as a Solution of the Magnetic Induction Equation
Let us begin from the ideal induction Equation (
3) with zero conductivity
. Assume that the problem is defined in a random velocity field with very short correlation time. In this case, the magnetic field is totally frozen in moving plasma and its evolution can be described by known velocities of fluid particles, see, e.g., [
19]. Find the changing of the vector potential by rewriting the ideal Equation (
3) in the form of the full time derivative:
Here, the full Euler derivative is combined in the left side, while in the right side the last term can be removed due to the gradient uncertainty. In other words, we remove the last term, defining the potential gauge and using not Equation (
3), but Equation (
3) minus
. Note further, that this gauge would not play a fundamental role, because the final mean-field equation would be written not for potential
, but for magnetic field
, see Equation (
22).The obtained expression
allows us to write the vector potential shift for a particle moved from the point
into the point
:
That means that the potential evolution in two near-time moments for the ideal case can be defined by the multiplier
and, consequently, for an arbitrary time
—by the product integral, see, e.g., [
20]:
The velocities
in this integral are calculated in consecutive time steps and the vector potential in the right side
is taken in the initial time moment
t. Of course, it will be more correct to go to the limit for
, however, for convenience, we save notation below without the limit symbol, assuming that
is much smaller than
(here
is the interval twice large than velocity field memory time, that guarantees velocity independence beyond
). Note that using the theory of path integrals, we can present this solution by Taylor asymptotic representation (see, e.g., [
21]) in the form
The obtained solution (
7) satisfies Equation (
3) only for ideal flow
, however diffusivity can be included in it by the standard stochastic way, which is usually used in quantum mechanics [
22]. We can re-change the uniquely defined trajectory on Wiener random set of trajectories and then average the solution in form (
6) over this set by analogy with the Feynman approach. Note that functional integral (
6) averaged over Wiener trajectories but on a defined nonstochastic velocity field should be the solution of induction Equation (
3). We start with a demonstration of this fact, because, for a stochastic velocity field, the algorithm will be the same as for the nonstochastic case, except for random field it leads not to the induction equation, but to the mean-field anisotropic model.
Change the defined fluid particle trajectory to the stochastic one:
Wiener noise
here has first zero moment,
, and second moment proportional to time interval,
. If time-shifting
is small, then space-shifting
is also small, so for the vector potential
in the right side of (
7) we can use asymptotic decomposition:
where shifts
are defined by velocity field
, see (
8), in the following asymptotic way:
Note that velocities and their derivatives here are defined in the initial point
and redefine them in the arbitrary point
x by a Taylor series:
Substituting (
10) in the shift
, we obtain its asymptotic form
as well as asymptotic decomposition for the vector potential:
Combining the asymptotics (
12) with the functional integral (
7) and saving terms until to the first order of time
, we obtain the following expression for the vector potential evolution:
Averaging Equation (
13) over Wiener trajectories and moving the term
from the right side to the left, we obtain the equality:
Dividing it on
and using the finite-increment formula for small time shifting
, we expectedly obtain the classical induction Equation (
3), written for each component of the vector potential. Absolutely analogous the functional solution (
7) can be considered on a random velocity field, that expectedly should give us the classical mean-field equation, after velocity averaging.
3. Anisotropic Mean-Field Equation
Consider now the functional integral (
6), defined on the random velocity field
. Let us average solution over this field, using the idea of short time-correlated turbulence [
9]. We proceed in three steps: first of all, average vector potential
over the main time interval
, where it does not depend on short-correlated velocity; then average the velocity field
on the interval
, assuming that vector potential does not change for the short time
, at last, average Wiener noise independent on the first two processes to take into account a nonzero plasma diffusivity
.
After magnetic potential averaging we can rewrite solution (
7), saving the old denotation for averaged potential and substituting its decomposition (
12):
For random short-correlated velocity fields with zero mean value it seems reasonable that averaged velocity moments should decrease with time-shift increasing, because if we take large time-shifting, then the correlation between short-correlated velocity components should be negligible. Suppose that this behavior of averaged velocity moments is proportional to
. We do not consider this assumption in detail, but it is easily verified that for faster decreasing we obtain singularity near
, while for smaller decreasing we always get the standard induction equation after averaging. This assumption
makes immediately clear our decomposition in the form (
12), where we save only terms decreasing slower than
for
. By the same reason in Formula (
15) we should save double sum in addition to a single sum.
Using an asymptotic representation for these sums:
and multiplying terms in (
15), we obtain the equality similar to (
13):
We already make averaging here over Wiener trajectories, thus the first four terms in the right side totally correspond to induction Equation (
14) and for random velocity with zero mean value, two of them disappear after velocity averaging. Dividing (
18) on
, regrouping terms and averaging over velocity field, we obtain the following system of differential equations:
For averaged terms we introduce helicity and turbulent diffusivity notations for velocity tensors:
and substitute them into (
19) to rewrite mean-field system:
Here we use the gradient uncertainty for vector potential, but taking the curl operator over left and right side we obtain the mean-field system for the magnetic field:
We emphasize that the obtained Equation (
22) in uniform and isotropic case completely match the standard mean field Equation (
1). Indeed, averaged values (
20) are two- and three-indexes tensors, for isotropic random field they should be proportional to
- and
-tensors only [
1]. It means that symmetric
and antisymmetric
transforms in scalar functions
and the Equation (
22) transforms in the standard mean-field model (
1). Note that the time
used here is the time interval, beyond which the velocities does not correlate. It is usually assumed that
is twice large than memory time
from one point to another where the correlation disappears. It is a standard suggestion
, particularly used in the first path-integral dynamo investigations, see, e.g., [
9].
In general anisotropic flow tensors (
20) can not be presented in such scalar forms. However we can distinguish them on symmetric and antisymmetric parts, and choose the coordinate system, where the symmetrical parts will be diagonal due to Jacobi’s theorem:
Note that the vector
defines helicity antisymmetry and describes turbulence transport in a nonuniform stream. For a uniform velocity field it disappears, thus only symmetrical tensors
and
remain and the anisotropy mean-field equation can be reduced to
4. Solutions in Uniform Streams
To solve mean-field model (
25) in uniform stream we can apply Fourier transformation. It transforms the partial differential system to the following system of ordinary equations
where
and
are the diagonal components of diffusivity and helicity tensors. This system has easily calculated eigenvalues for solutions proportional to
:
Solving system (
26), it is possible to find problem eigenvectors and by initial conditions
obtain the following Fourier image of averaged magnetic field:
In an isotropic stream (
29) this solution can be reduced to more common expression:
These imagines of mean-field solutions (
29) and (
30) allow us to make reverse transformations, which we consider on particular examples below, and analyze the mean magnetic field evolution at small and large times.
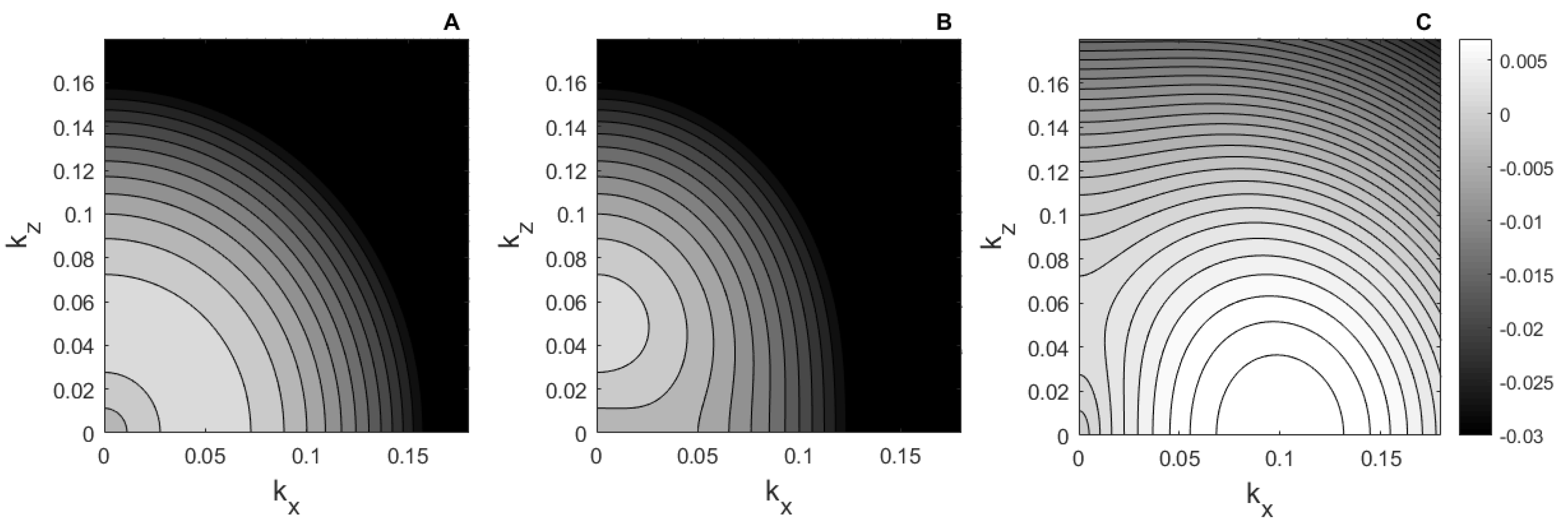
(1) For large
t the hyperbolic functions in (
29) and (
30) grow like exponentials, thus these solutions allow us to find maximal dynamo growth rates. For example, in isotropic streams (
29) the fastest harmonic
grows with classical velocity
, while in anisotropic flows the maximal growth is defined by function
, compare with [
23]. The distributions of growth rate for isotropic and anisotropic cases are presented on
Figure 1. It shows that anisotropy leads to different evolution for various harmonics, for instance, the harmonic along z-axis
can grow with rate
, which depends only on the helicity
-tensor components. It can be a reason for an interesting situation, when decrease of helicity components does not change the generation speed. Indeed, for the situation with anisotropy only along z-direction
the maximum of the function
gives two possible extrema:
The first one is maximum for cases with , the second for . It follows that for very small and for near-zero ,-harmonics mean-field growth rate remains proportional and does not depend on . On the other hand, the growth rate for large and for harmonics in -plane becomes proportional to the first, not to the second power of as usual. Moreover, there can exist harmonics , when the generation will be observed if helicity components , and would have different signs, even with zero trace
(2) For small
the functions in (
29) and (
30) can be expanded in a time-Taylor series [
24]:
and after reverse Fourier transformation, the evolution of magnetic field will be described by
for an anisotropic field, and for an isotropic field it will be defined by
It is clearly seen that the first terms in (
32) and (
33) characterize an initial field, terms with
describe diffusion and terms with
define changing of the magnetic field along the current density for an isotropic case (
33) and along
in anisotropic stream. Therefore, at small times in an isotropic random field force-free plasma saves its property, while anisotropy leads to effective growth of Lorentze forces, because the magnetic field generates in inclined direction to initial current density, and thus to the pressure gradient growth in the stationary case and to the Lorentz force back reaction.
5. Particular Examples
Consider now two initial magnetic field configurations: force-free distribution with single
x-harmonic and a magnetic field localized in the
-plane with a current density along
z-axis
For the first force-free distribution, using formulas (
29) and (
30) we can obtain for isotropic and anisotropic flows the following solutions
It is well seen that in isotropic flow (
35) the harmonic grows along the initial field parallel to the current density. The growth rate is defined by the power
and force-free structure
saves its configuration. The anisotropic case (
36) shows that for the considered harmonic the growth rate
does not depend on the
x-helicity component and the initial force-free magnetic field structure break down due to the exponentially increasing Lorenz force:
This formula, written for large t, demonstrates that the Lorentz-forcing grows with double rate along or opposite to the magnetic field depending on helicity components. Apparently, it means that anisotropy can lead to velocity field transformation, that can not be studied in the frame of this simple approach but can be proved in numerical and astrophysical experiments.
The second case (
34) defines the initial magnetic field image in the form
For such a function, the original field can be calculated only for the isotropic case
where we use functions
and
, defining azimuthal and axial components of magnetic field:
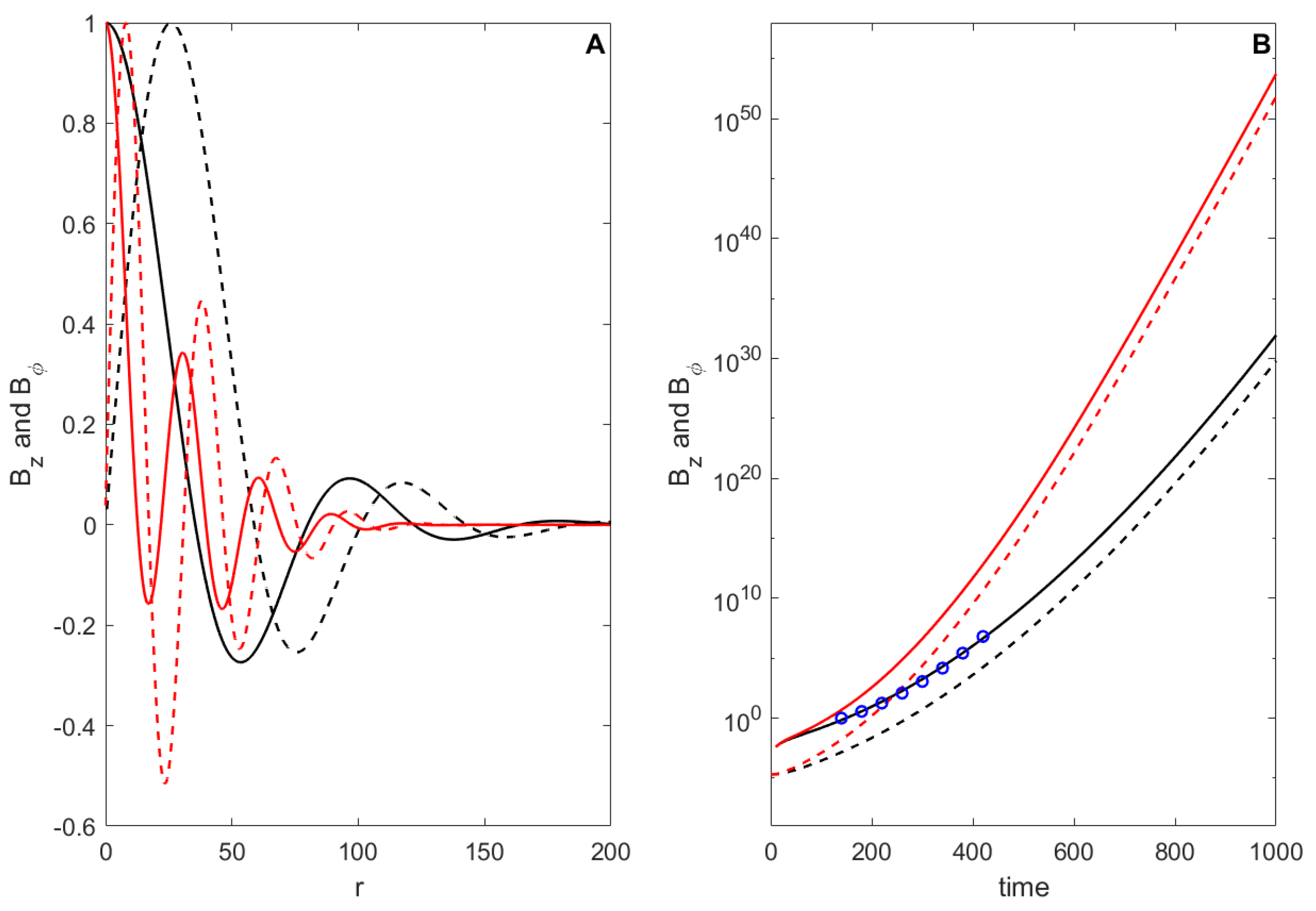
For an anisotropic flow the evolution of magnetic field components can be restored numerically. We realize it in the
-cube
with
cells, using Formula (
29). The results of the calculation are presented in
Figure 2 both for isotropic and anisotropic cases. The left panel shows the behavior of azimuthal and axial magnetic field components for the
r-dependency and the right panel for the time-dependency. The first one demonstrates periodical structures of the averaged magnetic field, the second shows exponential growth in the log–log scale. It is very interesting that at the initial moment the axial components for both cases increase much faster than their exponential growth rate. This super-exponential growth is not connected with anisotropy and is easily explained by Formula (
38). It is well seen that at small times during magnetic field redistribution the exponent power is proportional to
:
The special interest of this result follows from the obtained exact solution, because neither analysis at small times by Taylor expansion, when the only power behavior can be obtained, see (
32) and (
33), nor analysis at large times, when only exponential growth can be observed, can not demonstrate the
growth of initially localized solutions. However Formula (
39) clearly shows that in a fixed point
r for
and
the growth is superexponential and the same picture is demonstrated on
Figure 2. Note that for considered on
Figure 2 case the superexponential growth begins from
(blue circles correspond to the curve proportional to
) and after
it gradually transforms into exponential
, linear in log-scale used on the figure (the pure exponential growth begins from
).
In the first example, we saw that the anisotropy leads to the transforming of force-free structure, and the sign of Lorentz force depended on anisotropy components. For the second example, we also calculate the anisotropy forces and present the time-dependence of their absolute values in
Figure 3. It shows that due to the
-field being not force-free, Lorentz force always increases. However, for
(red) it grows faster than in the isotropic case (black), and for
(blue) it initially decreases, that possibly connects with changing of Lorentz force sign or initial magnetic field redistribution, and than grows like isotropic case, that corresponds to
.
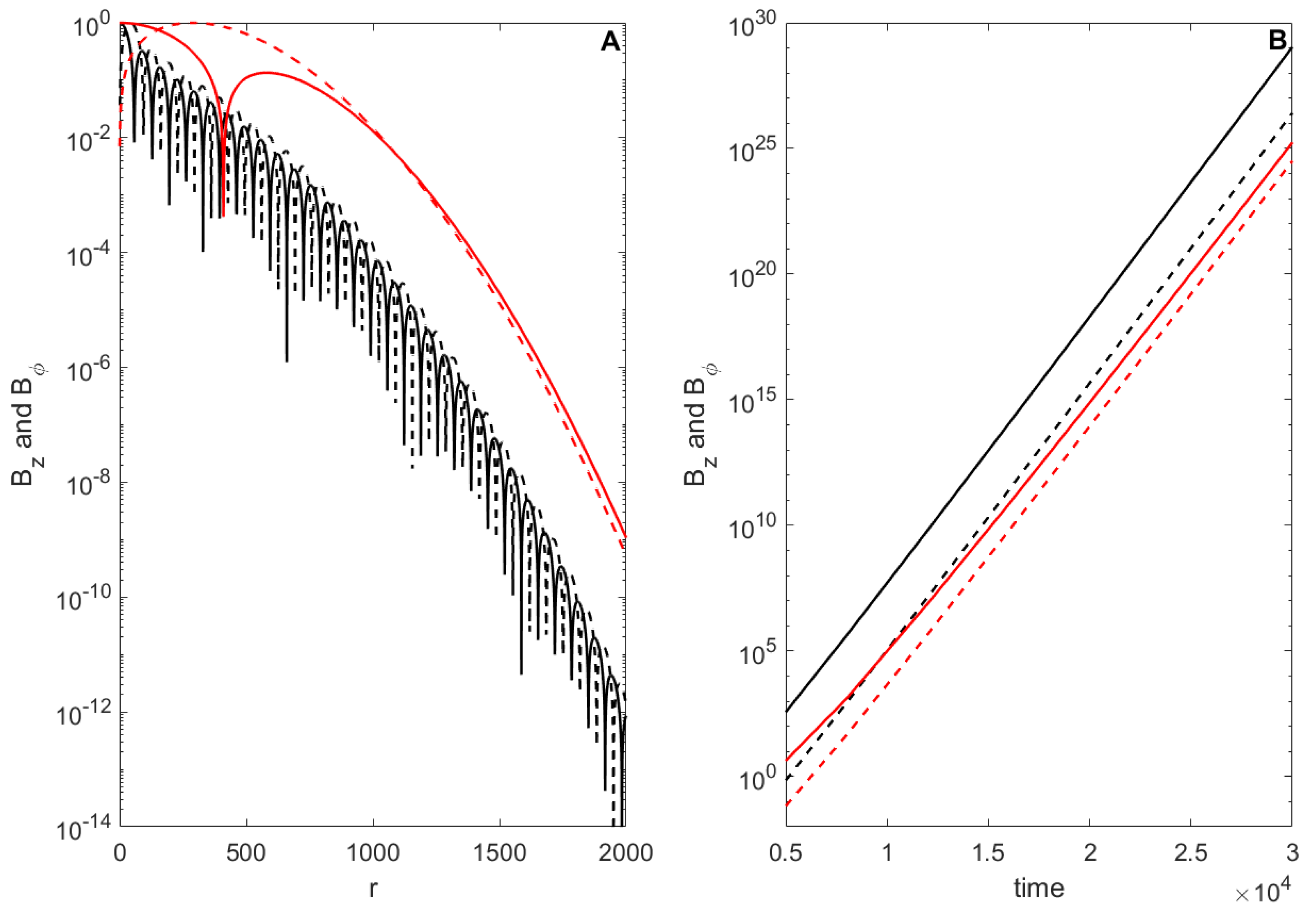
At last, for
we numerically check the idea mentioned above.
Figure 4 shows the time- and
r-dependencies in log-log scale for very small
(red). Comparing it with the isotropic case (black) we see the same growth rate. Therefore the dynamo successfully works even for near-zero tensor helicity component, thought its decreasing leads to the growth of
-periodic structure, presented on the right panel. If we take into account that helicity components can not only be near-zero but also change signs we come to the conclusion that in anisotropic turbulent flows dynamo can work in a more wide range of external conditions and can be a key condition of mean-field generation.
6. Discussion and Conclusions
The method of path integrals is one of the powerful approaches, which allows us to obtain mean-field equations without additional assumptions about spatial separation of turbulence scales or about small Reynolds number, which is usually assumed in traditional Krause–Radler approaches. The method is based on the assumption about short-correlated velocity field, but this assumption looks reasonable for astrophysical objects with rotational intervals larger than typical memory time. That is why we use it in this work to get the well-known dynamo model skipping two other common conditions—flow isotropy and uniformity. We derive the system (
25), describing the mean-field dynamo generation, controlled by helicity and diffusivity diagonal tensors (
20), which in uniform flows look like
The obtained model (
25) is more general than the classical Equation (
1), thought in a statistically homogeneous and isotropic situation it reduces to the classical case. However, one of the main advantage of the obtained equation is the saving of solenoidal conditions for the averaged magnetic field, due to the curl in the right side of the equation. To combine such a form of the equation we start from the microscopic induction equation, written not for the total magnetic field
, but for the magnetic potential
. From the technical point of view, the problem was that the governing equation for
has a form of transport equation along a fluid particle trajectory while the governing equation for
has a more complicated and less comfortable form for the path integral method form, but has the advantage in gradient uncertainty.
Here we do not consider nonuniform effects, solving the anisotropic model by standard Fourier transformation. That method gives us imagines of magnetic field components both in isotropic and anisotropic situations. We obtain that isotropic generation is commonly defined by exponential power, proportional to
, while the growth of the anisotropic dynamo is defined by function:
Therefore, in anisotropic cases harmonics grow in particular directions and the dependence on helicity components becomes more complex: for example, anisotropic generation can be observed for zero helicity component, or for components with different signs, as well as for tensors with zero trace . That means, that we can observe, e.g., pure anisotropic dynamos or dynamos, where velocity field anisotropy plays the key role.
Using the obtained solution we study two cases of initial magnetic field distributions. The first one is a force-free harmonic, by the example of which we consider a magnetic field with fixed wave vector; the second one is a solution localized in
-sphere, which allows us to descry initial averaged magnetic field transformation. These examples show that for an isotropic flow initially, force-free structure does not change with time, because the magnetic field generates along the current density, so the Lorentz force is zero and there is no Lorentz back-reaction (note that for not force-free initial structure the Lorentz force, of course, increases exponentially.). However, obtained results show that velocity anisotropy can lead to much faster growth of Lorentz forces, and more effective back-reaction, because in an anisotropic flow the magnetic field generates inclined to the current density. We suppose that this effect can be a reason of turbulence properties changing but in the frame of the simplest linear mean-field model that can not be checked. Another interesting observed effect connects with the redistribution of the initially
-localized field. The obtained analytical and numerical solutions show that the averaged magnetic field grows super-exponentially at times
. The growth rate is proportional to
, which can explain why in some galaxies estimates of dynamo time scale is comparable with the ages of galaxies. However we should note that this effect can sufficiently depend on the velocity field parameters and the initial averaged field, moreover, it can be only temporary, because at large times this increasing should transform in exponential growth or slow down by nonlinear effects, lying out of the mean-field model bounds [
25].
Finally note that the obtained system is general for anisotropic turbulence and we do not associate here the particular conditions of the velocity field, initial data, spatial or time scales with astrophysical systems. However it can be used for calculating the anisotropic mean-field dynamo for comparison with numerical, analytical or observational data, see, e.g., the review paper [
3]. We hope that our results will be useful for investigations of galaxies and stars dynamo, where heterogeneity and anisotropy are strongly marked.