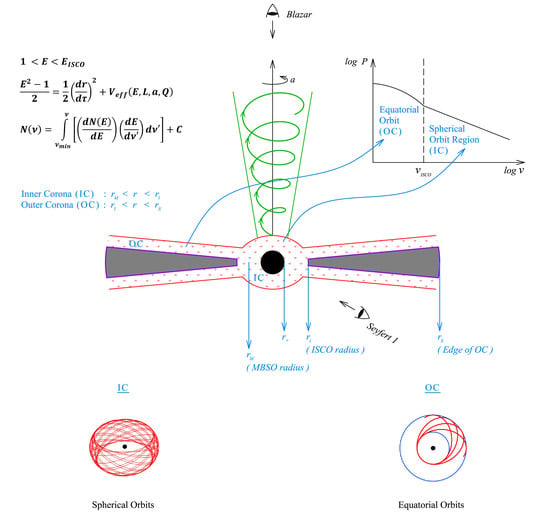
A Relativistic Orbit Model for Temporal Properties of AGN
Abstract
1. Introduction
2. Relativistic Circular and Spherical Orbits as Solutions to X-Ray QPOs
2.1. Method for the Error Estimation
- 1.
- We assume that the frequencies, and , of QPOs are Gaussian distributed with their mean values at the centroid of observed QPO frequencies, and (with ). The joint probability density distribution of these frequencies is given bywhere represents the Gaussian distribution of ith QPO frequency, given bywhere is the observed standard dispersion (error) of the ith QPO.
- 2.
- We find the Jacobian, , of the transformation from frequency to orbital parameter space using the formulae of fundamental frequencies, which is given bywhere and represent the orbital parameters. For the equatorial circular trajectories (), we have {, }{r, a}; whereas for the spherical trajectories (), we have {, }{, a}. The Jacobian is completely expressible in an analytic form and can be easily evaluated from Equation (3), and using the frequency formulae. We utilize Equation (7) for circular orbits in Section 2.2, and Equation (8) for spherical orbits in Section 2.3, to evaluate (Equation (3)), where and according to the RPM and GRPM.
- 3.
- Next, we write the probability density distribution in the parameter space given bywhere represents the set of parameters {, } and is given by Equation (3); and {, } are substituted in terms of parameters using the analytic formulae, Equation (7) for the circular orbits and Equation (8) for the spherical orbits.
- 4.
- We calculate the exact solutions for parameters by solving and using Equation (7) for circular trajectories {, }, and Equation (8) for spherical trajectories {, } for fixed Q. We fix to the previously known values. We find 1 errors in the parameters by taking an appropriate parameter volume around the exact solution, and generate sets of parameter combinations with resolution in this volume. The chosen parameter range, exact solutions, and corresponding resolutions are summarized in Table 3 and Table 4. We then calculate the probability density using Equation (4), for all the generated parameter combinations and normalize the probability density by the normalization factorwhere k varies from 1 to the number of total parameter combinations taken in the parameter volume; is the kth combination of the parameters in the parameter volume. Hence, the normalized probability density is given byThe normalization of the probability density in the parameter space, discussed above, is done because only a sub-volume in the parameter space is astrophysically allowed for bound orbits, which is discussed below.
- 5.
- The allowed parameter combinations for the bound orbits is governed by the condition given by [54]where e is the eccentricity and is the inverse latus-rectum of the general non-equatorial trajectory. We have for spherical orbits; hence, we ensure that the parameters (, a, Q) for spherical trajectories follow the above bound orbit condition. If any parameter combination does not obey the bound orbit condition, then is taken to be zero at that point in the parameter volume.
- 6.
- For the circular orbit case, there are two parameters to estimate {r, a} using two QPO frequencies. For the case of spherical orbits, there are three unknown parameters {, a, Q}; hence, we first take {1, 4, 8, 12} for the spherical trajectory solutions, where the extrema of coordinate deviates away from the equatorial plane with an increase in Q. For each fixed value of Q, we find the normalized probability density distribution in the parameter space using Equation (5b). Later, using the calculated spin values and their errors for each fixed Q, we estimate the distribution of spin and the most probable spin. Using this distribution and the most probable value of the spin, we then determine the probability distribution in the parameter space.
- 7.
- Next, we integrate the normalized probability density, , Equation (5b), in one dimension to obtain the profile in the other dimension. Thus, we finally obtain the one dimensional distributions {, } for circular orbits, and {, } for spherical orbits.
- 8.
- Finally, we fit the normalized probability density profiles in each of the parameter dimensions to find the corresponding mean values and quoted errors are obtained such that it contains a probability of 68.2% about the peak value of the probability density. The results of these fit are given in Table 3 and Table 4.
2.2. Circular Orbits
- 1.
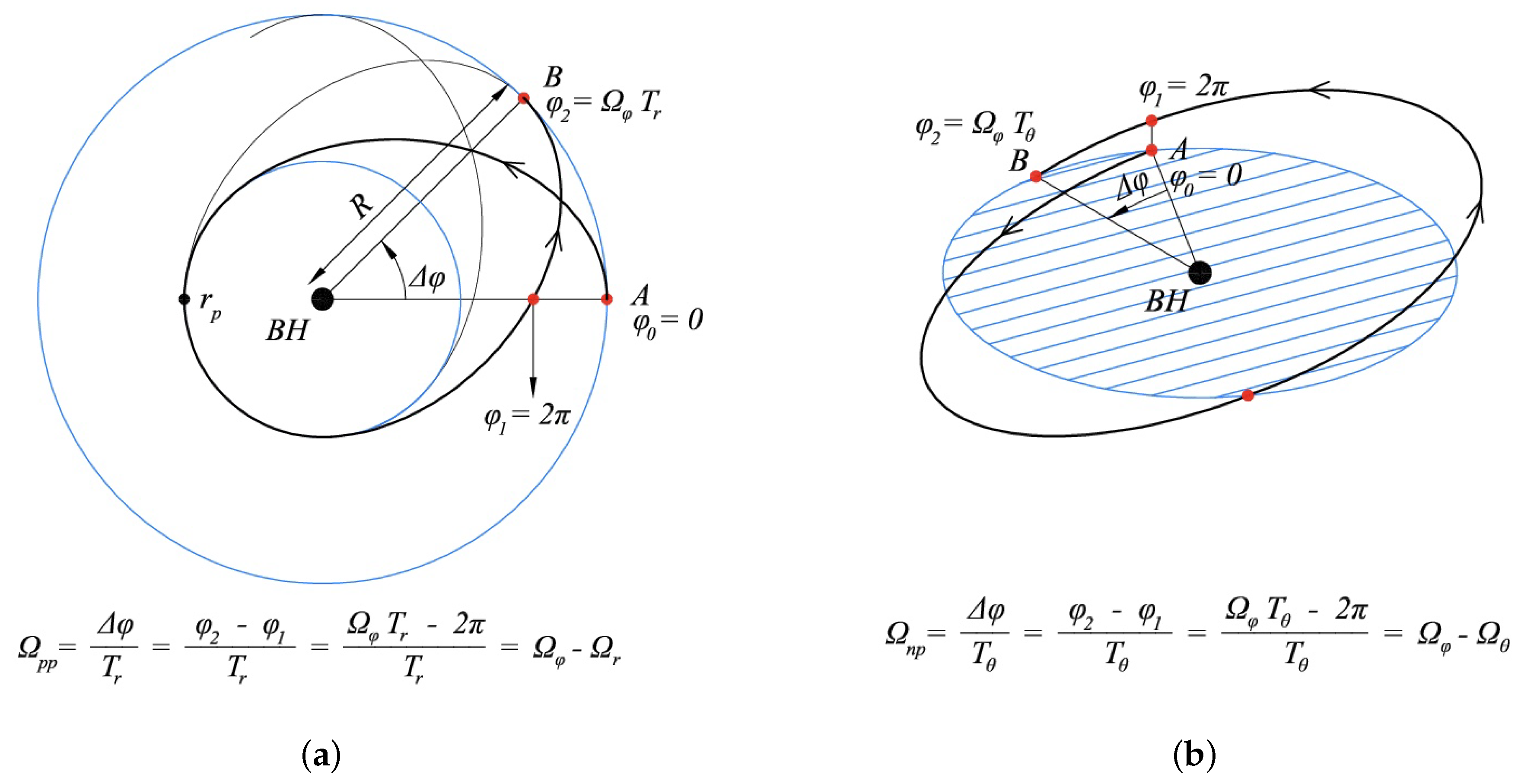
- We have computed the contours of , using Equation (7a), for the QPO frequencies (given in Table 2) of RE J1034+396 (blue), MS 2254.9-3712 (red), and MCG-06-30-15 (magenta), shown in the plane in Figure 3a. The masses of these black holes were assumed from the previous estimations (see Table 2). We see that the QPO emission originates from a very narrow region of the accretion disk, where (9.4–9.9) for RE J1034+396, r∼(10.4–11.4) for MS 2254.9-3712, and for MCG-06-30-15 even though a ranges from 0 to 1. This implies that the QPO emission region is very close to the black hole, and this emission region remains very narrow and nearly independent of the spin of the black hole.
- 2.
- For the case of Mrk 766, two QPO frequencies were detected (see Table 2), but at different epochs. We have shown contours for both these frequencies in Figure 3a, where Hz (orange) and Hz (green). The mass of the black hole was fixed to [58]. The QPO origin range is for and (12.6−14) for , which is again found to be in a narrow range and very close to the black hole. Although these QPOs were not detected simultaneously, we tried to estimate a simultaneous solution for by equating and as per GRPM. We show them as curves in the plane in Figure 3b, and we see that these contours do not cross each other, implying that there is no simultaneous solution for .
- 3.
- For the Type-2 AGN 2XMM J123103.2+110648, the detected QPO (see Table 2) was suggested as an LFQPO type because of its large rms value [9]. If this QPO frequency is equated to the high-frequency component, , of the GRPM, we found that , which is far from the black hole to emit X-rays. Hence, the GRPM predicts that this should be an LFQPO. We show the contours of the LFQPO component of the GRPM, , in the plane for the QPO frequency of 2XMM J123103.2+110648 in Figure 3c, where we fixed [56]. We see that the emission region for this LFQPO is r∼(6–20), for the whole range of a. Hence, the detected QPO of 2XMM J123103.2+110648 is an LFQPO that originated very close to the black hole.
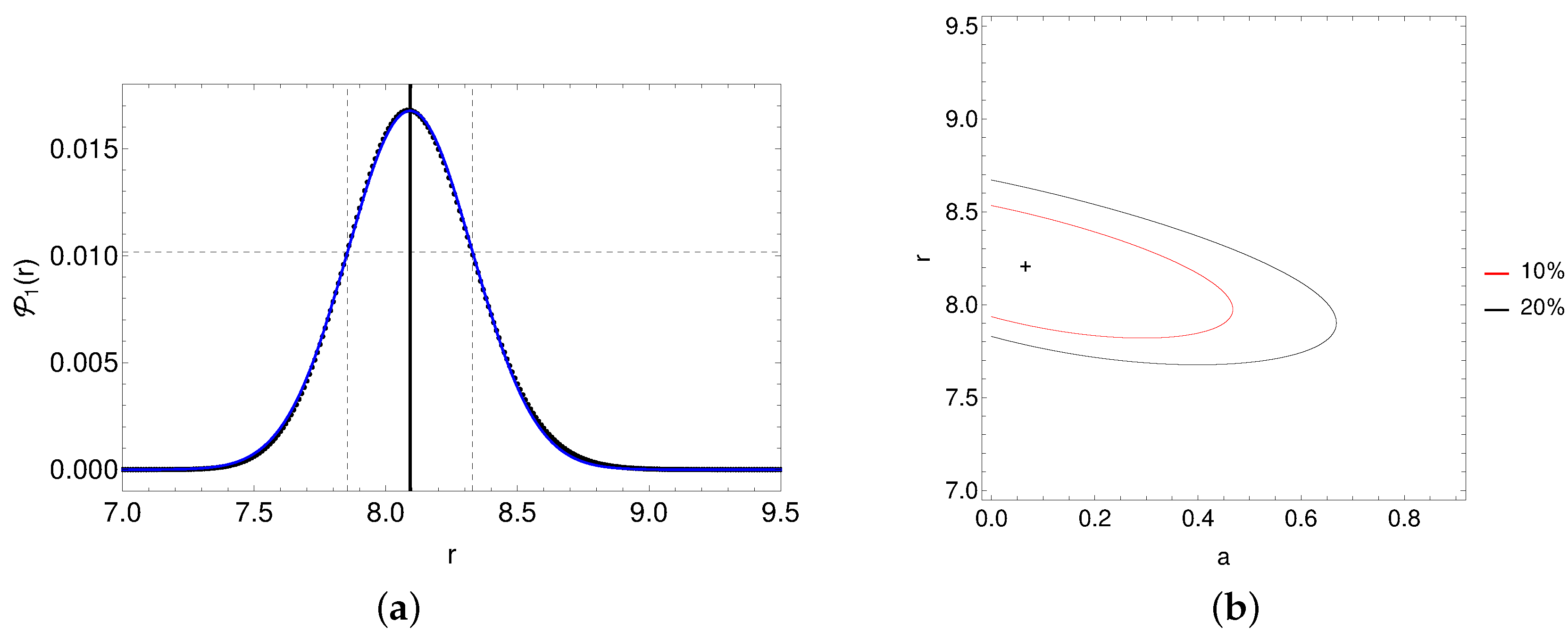
- 4.
- For the case having two simultaneous X-ray QPOs, 1H 0707-495 (see Table 2), we first solve the equations {, } (using Equation (7a,b)), assuming [36], as per GRPM to estimate the exact solution for (r, a), which is found to be (, ). We then apply the method, described in Section 2.1, to estimate the errors in the parameters (r, a) implied due to the errors of the QPO frequencies. The range of (r, a) and corresponding resolutions used for our simulations are summarized in Table 3. Finally, we generate the probability density profiles in each parameter dimension {, }, shown in Figure 4, where we have also shown the probability contours in the parameter space. The results of the model fits to the probability density profiles are summarized in Table 3. The errors in the parameters are quoted with respect to the exact solution (, ), whereas the simulated {, } profiles peak at (, ), which slightly differs from the exact solution. Hence, our analysis assuming the circular orbit frequencies as the origin of QPOs, using the GRPM, in NLSy1 1H 0707-495, suggests that it harbors a slowly rotating black hole () at the center, and that the X-ray QPOs originate in the inner region of the accretion disk and very close to the black hole ().
2.3. Spherical Orbits
- 1.
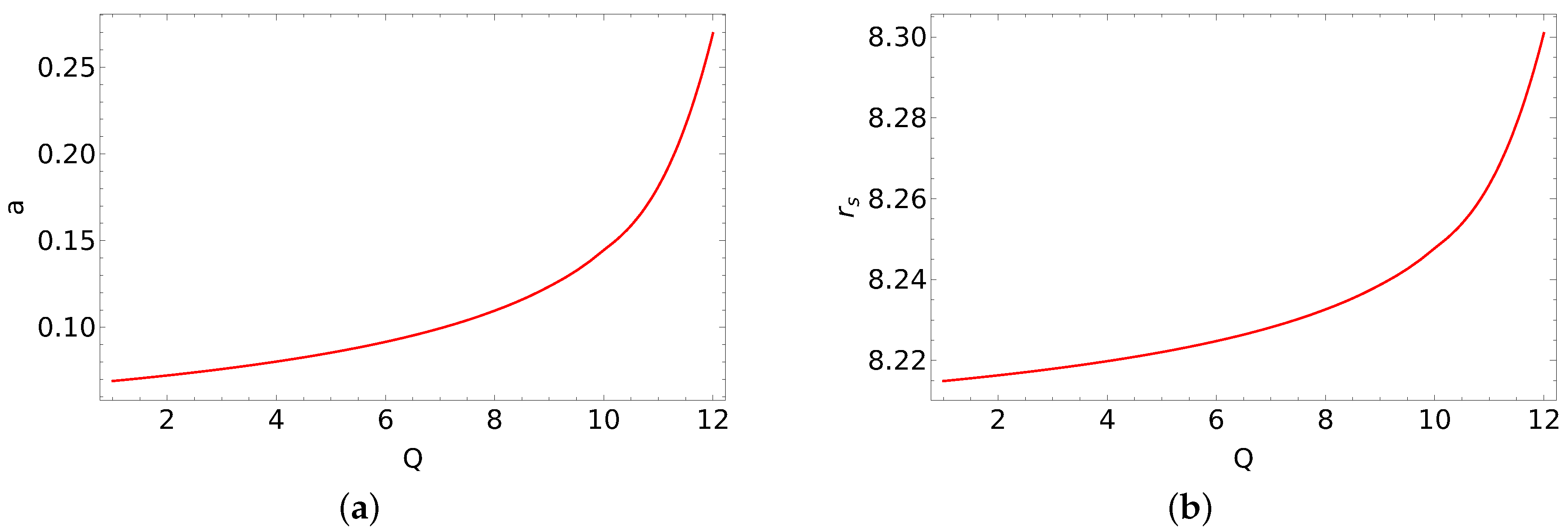
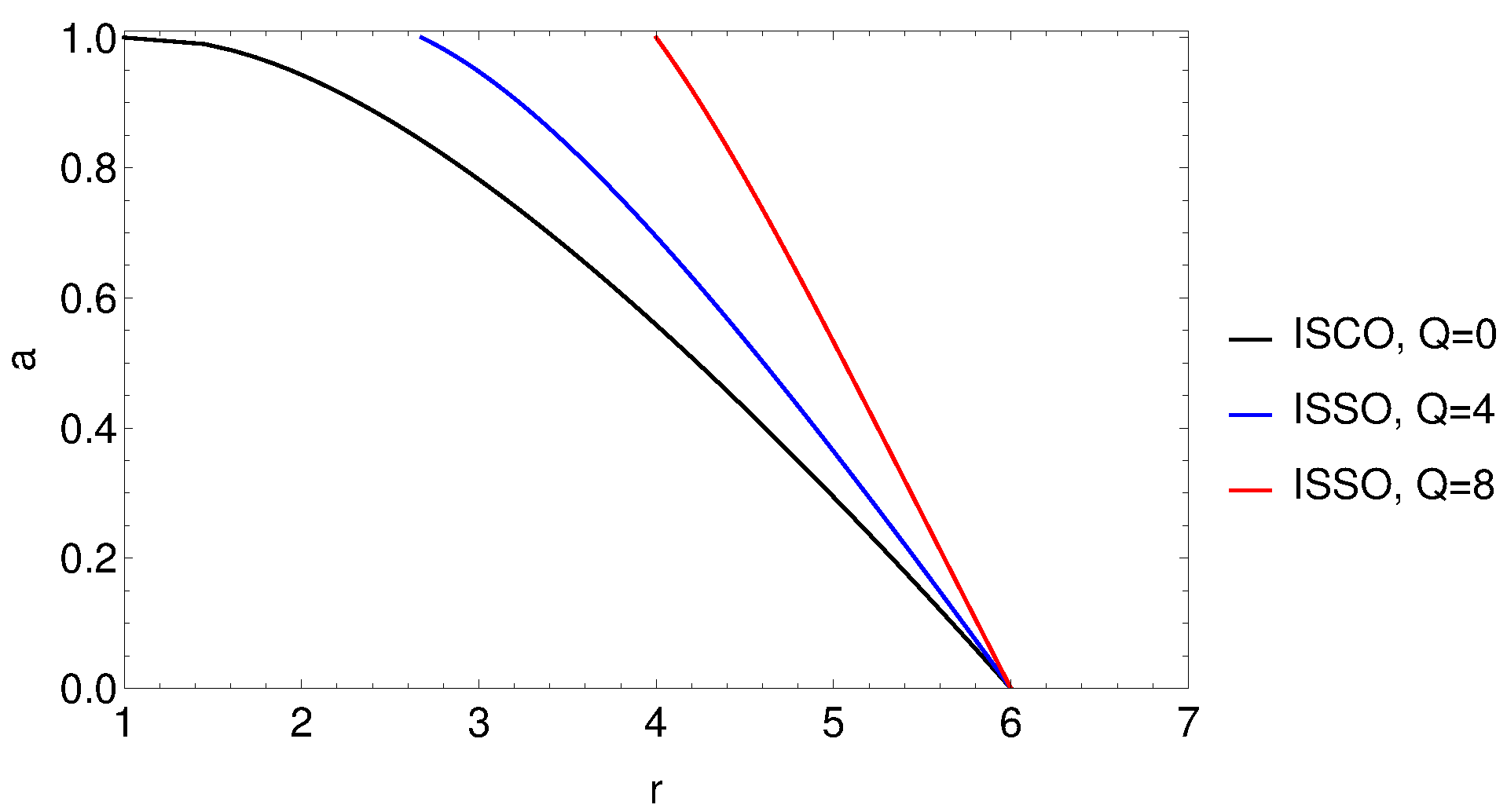
- We explore the parameter space (, a, Q) for the spherical orbits. Since there are two input QPO frequencies, we first vary the Q value to find various solutions of {, a} by solving equations {, } as per GRPM. is at the limit of astrophysically allowed bound orbits, Equation (6); in the case of 1H 0707-495. The orbit is an unstable orbit very close to the separation of bound and unbound (called a separatrix orbit), and such an unstable orbit is not relevant to our study; hence, we fix our parameter exploration between Q= 1 and 12. In Figure 5, we have shown these solutions in the (Q, a) and (Q, ) planes.
- 2.
- Next, we fix and find the errors in the {, a} parameters using the method described in Section 2.1. The range of {, a}, resolution taken in the simulations, along with the exact solutions and their errors obtained by fitting and are summarized in Table 4.
- 3.
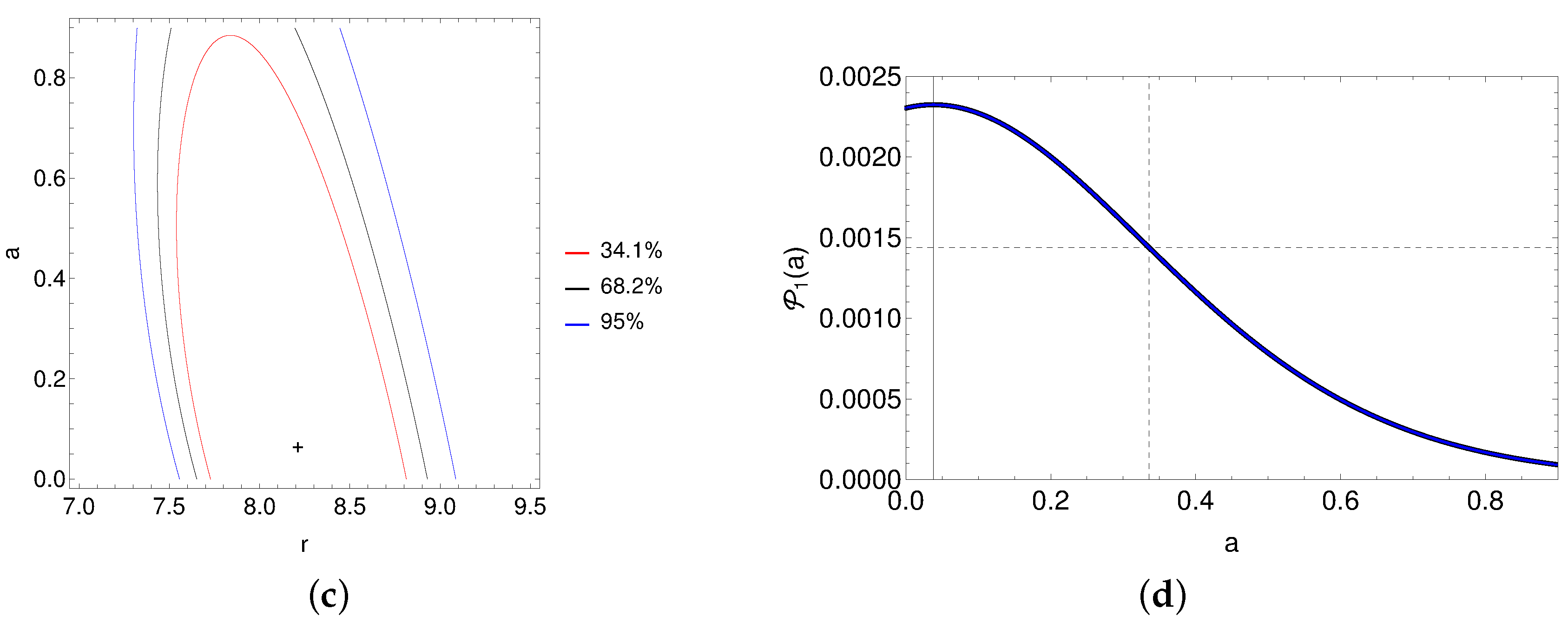
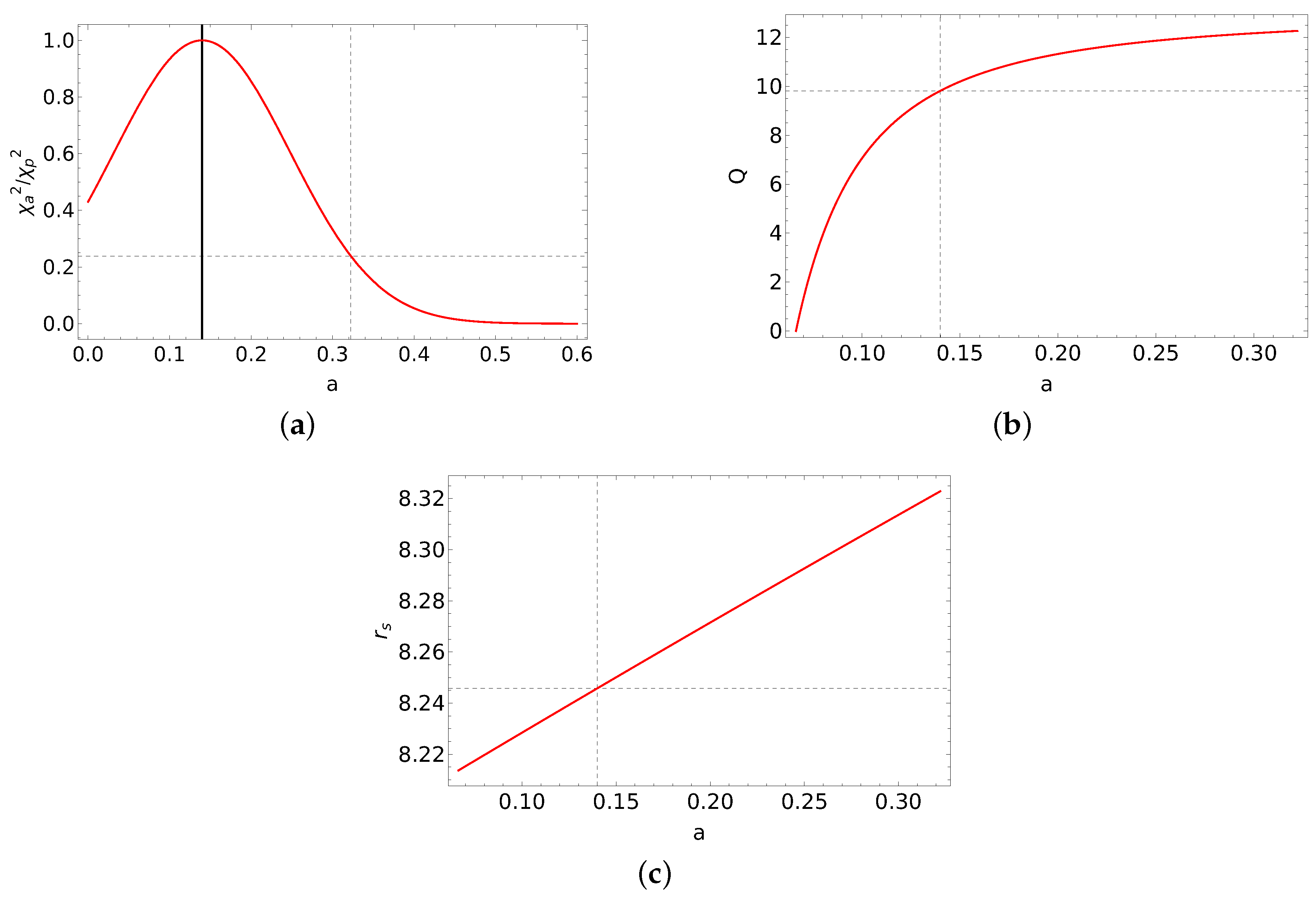
- The ranges of {a, , Q}, shown in Table 4 and Figure 5, span the complete parameter volume for QPO frequencies of 1H 0707-495. As the spin of the black hole does not change in the timescale of a few months or years, we need to find the most probable value of spin. We first find the variance of with respect to the exact solution of a for each Q, given in Table 4, which is given bywhere is the probability density ditribution in a parameter space for each value of Q. We have summarized the values of for each Q in Table 4. We then minimize the likelihood functionto obtain the most probable value of the spin given byWe find the peak value to be for 1H 0707-495, and corresponding solution of {, Q} for the QPO frequencies is {, }.
- 4.
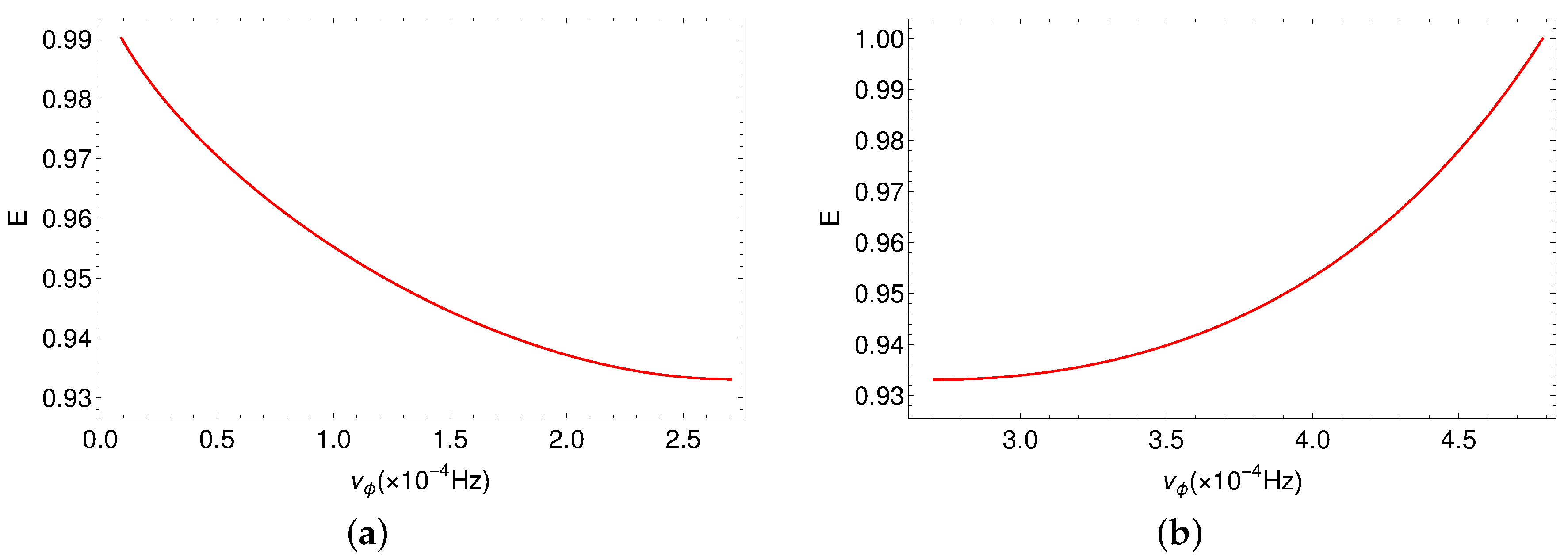
- Next, we obtain the distribution function of a given byA plot of is shown in Figure 6a, where . We obtain the errors with respect to by normalizing the function and obtain , where the region of 95% probability is indicated by the vertical dashed line in Figure 6a. We also show the range of and Q in Figure 6b,c within the region of a, as seen in Figure 6a, where the parameter ranges are (8.214–8.323) and (0.0001–12.264).
- 5.
- Hence, we conclude that the spherical orbits, close to the black hole in the region, (8.214–8.323) with Q values between (0.0001–12.264), are possible sources of the QPO frequencies observed in 1H 0707-495, while the most probable spin value to be with confidence.
3. Relativistic Jet Model for the Optical and Ray QPOs
4. Relativistic Orbit Model (ROM) and PSD Shape
The ROM
- 1.
- We associate the temporal frequency, , in the observed power spectral density with the fundamental azimuthal frequency of the particles orbiting in the circular orbits in the accretion disk outside ISCO, , and both circular and spherical trajectories between and marginally bound spherical orbit (MBSO) radius, . These frequencies are functions of the orbital radius, r or , (Equations (7a) and (8a)), and hence they are also fundamentally related to the mechanical energy of the orbit through Equations (14) and (15).
- 2.
- We assume a prior distribution of the energy of particles (or electrons) given by a power-lawwhere represents the number of particles having energy E, and are the power-law indices inside and outside respectively, is the particle energy at , and A is the normalization constant. The energy distribution, (Equation (16), is constructed so that it is continous at . Assuming that the total number of particles are (however, the PSD solution is independent of this), we have the normalization condition given bywhere the first and the second terms contribute for the regions inside and outside respectively, and corresponds to the energy of the particles at the outer radius of the equatorial circular accretion disk, . Subsequently, we obtainWe redefine such thatwhere
- 3.
- We assume that the break frequency of the PSD corresponds to the temporal frequency at the ISCO radius.
- 4.
- We also assume that the particle distrbution in the temporal frequency space, , directly translates to the observed intensity for a given temporal frequency, so that the power density is given by .
- 1.
- If is the average slope of the observed PSD after the break frequency, , given bywhere represents the difference of values at the end points defined by MBSO and ISCO in our model: the end point of the PSD for (where ) is at the MBSO radius (), so thatwherewhere can be substituted using Equation (24), which yieldsHence, for a given combination of {a, Q}, we obtain a relation, given by Equation (25f), where {, } are unknowns.
- 2.
- Similarly, if is the average slope of the observed PSD before the break frequency, , we haveThe lower extreme of the PSD at , for , is given by , so thatwhere
- 3.
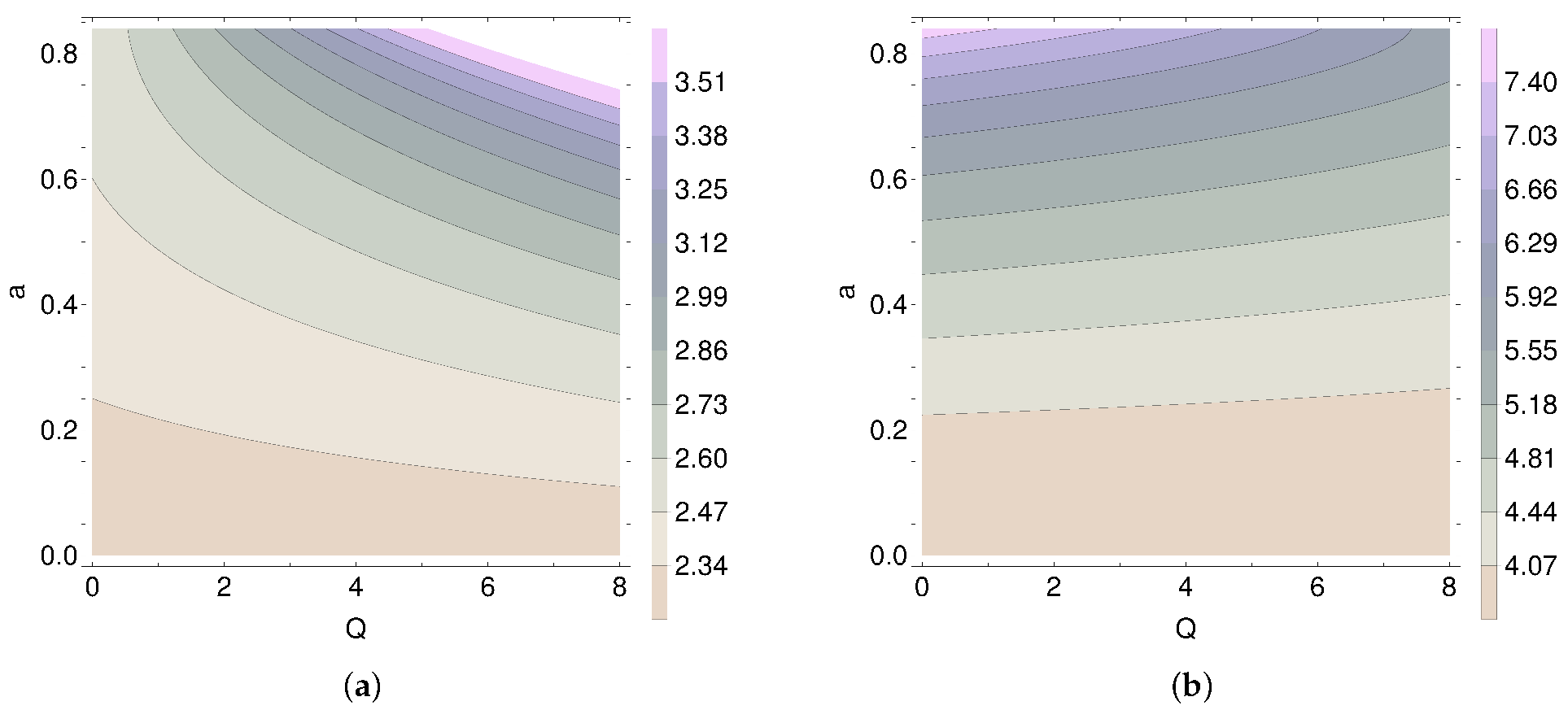
- We compute the slopes {, } by the above mentioned criteria for different combinations of (a, Q), which are shown in Table 6. We find that ranges between ∼[2.3–4] and is in the range ∼[3.7–8.9], indicating that a power-law model for the intrinsic mechanical energy of the orbiting matter describes the shape of the observed PSD reasonably well. Additionally, if we reverse the analysis to estimate {, } by fixing {, } for (, ), we find {, } which are in good agreement with observations. We also show contours of and in the (Q, a) plane in Figure 10, where the values of and increase with a. We also see that contours are independent of Q for small a, which is expected because the non-equatorial orbits do not exist in Schwarzschild spacetime.
- 4.
- The examples of PSD profile obtained in the scaled frequency space, , are shown in Figure 11. We see that the PSD profiles for given parameter combinations in Table 6 show good fits to the expected bending power-law model, Equation (13). The PSD represents a general power spectrum obtained independent of the mass of the black hole; hence, it applies to the stellar-mass black holes also. This validates the ROM as a plausible model for PSD observed in black holes.
5. Summary
- In Section 2, we motivated the creation of (G)RPM models for X-ray QPOs and extracted the spins and radii for the sources, listed in Table 2, based on the model given in [48,49,50]. The GRPM model confirms that the detected QPO in Type-2 AGN 2XMM J123103.2+110648 is an LFQPO, as it was also suggested by [9]. In a statistical analysis, we were able to determine these parameters and their errors for 1H 0707-495, the case of two simultaneous QPOs, based on the observed QPO frequencies and their errors. The results are presented in Table 3 for circular orbits and in Table 4 for spherical orbits. We found non-planar orbits, with (1–12), which are very close to a Kerr black hole, that ( (8.2–8.3); ) are the possible solutions for QPO frequencies of 1H 0707-495.
- Next, in Section 3, we applied the relativistic kinematic jet model to check its validity by comparing the basic frequency with the observed QPO periods in BL Lac objects, given in Table 5. The ratio is typically in the range , which is reasonable, given the range of footpoint radii of the field lines and typical location of the Alfvén point up to which the field line is rigid [52]. It motivates detailed relativistic MHD models along with polarization profile predictions (as given in [51]) to compare with observations.
- In Section 4, we built a relativistic orbit model consisting of circular and spherical orbits that have a power-law distribution, and its mechanical energy is split into two parts (above and below the energy at ISCO). This formulation leads to unique results relating to the PSD slopes (before () and after () the break) with those of the energy spectrum for the given spin and mass of the black hole (Figure 10 and Figure 11). We plan to test this model against observations to extract {a, }.
6. Discussion and Conclusions
- 1.
- The periastron and nodal precession of the particle orbits is an intrinsic phenomenon in Kerr geometry, which is a consequence of strong gravity and axisymmetry of the spacetime. We propose in the GRPM [50] that the precession frequencies of matter blobs orbiting in these trajectories, very close to the Kerr black hole, modulate the X-ray flux, from the thin accretion disk where the flow is hot. The origin of these non-equatorial orbits of blobs in a slim torus region having a single radius is motivated in [50], where a model of fluid flow in the general relativistic thin accretion disk [73] is studied. In this study, we suggest that the edge region, defined in [73], is a launchpad for plasma instabilities, where blobs orbit with fundamental frequencies of the geodesics near the edge and in the geodesic region (defined in [73]), in which Hamiltonian dynamics is applicable. We also show in the GRPM that these geodesics span a torus region, which overlaps with the edge and geodesic region of [73].
- 2.
- The QPOs in NLSy1s are usually observed when is very high; for example, in the case of RE J1034+396 [8] implies a high accretion rate, but the association of with the QPO frequencies is not clear. Moreover, even if one assumes that the accretion process in AGN and BHXRB is the same and that both show similar characteristic shape in the hardness-intensity diagram [6], over a timescale, T, this would be − times more than BHXRB timescales, as .
- 3.
- Our relativistic orbit model (ROM) is built on the formulation of the intrinsic mechanical energy distribution of the plasma in motion, where three frequencies correspond to the low-frequency end, break frequency, and the high-frequency end of the PSD. However, there is a noise component to be added at higher frequencies of the PSD to obtain a more realistic PSD shape to the intrinsic energy distribution related to the frequencies of the unstable orbits inside MBSO. A more generalized approach will be to incorporate frequencies of the more general eccentric and non-planar orbits (, ) contributing to the PSD shape. This is planned as future work.
- 4.
- The fundamental frequencies of the spherical geodesics in the Kerr geometry seem to explain the PSD in the Inner Corona (IC) region, where ; whereas the frequencies of the Outer Corona (OC) region are associated with the circular orbits, where . The results of this toy statistical model, ROM, seem promising. A detailed physical model is required to predict the power law indices in the energy spectrum. Furthermore, including a more ellaborate transfer function taking into account the GR effects like light bending and Doppler boosting, is in order for further study.
- 5.
- The paradigm of the ROM can be tested against observations by extracting {, a} from observed {}, and by exploring the parameter space {, } which is the basis of the PSD for the ROM model. In the future, we plan to apply and test this model against several observed PSD of various AGN sources.
- 6.
- The total power of a PSD having a power-law profile is given bywhere , is the power-law index, and is the upper frequency cut-off of the PSD. On the other hand, from the Wiener–Khinchin theorem, , where gives a measure of the time signal variance above the noise and is the variance in the noise measurable from observations. This gives the relation between the measured quantity and as, , where the cutoff provides a measure of the spin and mass of the black hole if the disk cuts off at the ISCO or MBSO radius; this implies . Using a more complicated PSD distribution expected from the ROM and using , we can give better estimates for and hence extract {, a}, using , and study statistical trends from a sample of sources with known {, a}.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AGN | Active Galactic Nuclei |
| BHXRB | Black Hole X-ray Binaries |
| ULX | Ultra-Luminous X-ray source |
| QPO | Quasi-Periodic Oscillation |
| IC | Inner Corona |
| OC | Outer Corona |
| ISCO | Innermost Stable Circular Orbit |
| MBCO | Marginally Bound Circular Orbit |
| MBSO | Marginally Bound Spherical Orbit |
| NLSy1 | Narrow-Line Seyfert 1 |
| GRPM | General Relativistic Precession Model |
| ROM | Relativistic Orbit Model |
| PSD | Power Spectral Density |
References
- Rees, M.J. Black Hole Models for Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 1984, 22, 471–506. [Google Scholar] [CrossRef]
- Blandford, R.D.; Rees, M.J. The standard model and some new directions. In American Institute of Physics Conference Series; Holt, S.S., Neff, S.G., Urry, C.M., Eds.; AIP: College Park, MD, USA, 1992; Volume 254, pp. 3–19. [Google Scholar]
- Antonucci, R. Unified models for active galactic nuclei and quasars. Annu. Rev. Astron. Astrophys. 1993, 31, 473–521. [Google Scholar] [CrossRef]
- McHardy, I. X-ray Variability of AGN and Relationship to Galactic Black Hole Binary Systems. In Lecture Notes in Physics; Belloni, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 794, p. 203. [Google Scholar]
- McHardy, I.M.; Koerding, E.; Knigge, C.; Uttley, P.; Fender, R.P. Active galactic nuclei as scaled-up Galactic black holes. Nature 2006, 444, 730–732. [Google Scholar] [CrossRef]
- Remillard, R.A.; McClintock, J.E. X-ray Properties of Black-Hole Binaries. Annu. Rev. Astron. Astrophys. 2006, 44, 49–92. [Google Scholar] [CrossRef]
- Belloni, T.M.; Stella, L. Fast Variability from Black-Hole Binaries. Space Sci. Rev. 2014, 183, 43–60. [Google Scholar] [CrossRef]
- Gierliński, M.; Middleton, M.; Ward, M.; Done, C. A periodicity of 1hour in X-ray emission from the active galaxy RE J1034+396. Nature 2008, 455, 369–371. [Google Scholar] [CrossRef]
- Lin, D.; Irwin, J.A.; Godet, O.; Webb, N.A.; Barret, D. A∼3.8 hr Periodicity from an Ultrasoft Active Galactic Nucleus Candidate. Astrophys. J. Lett. 2013, 776, L10. [Google Scholar] [CrossRef]
- Alston, W.N.; Parker, M.L.; Markevičiūtė, J.; Fabian, A.C.; Middleton, M.; Lohfink, A.; Kara, E.; Pinto, C. Discovery of an ∼2-h high-frequency X-ray QPO and iron Kα reverberation in the active galaxy MS 2254.9-3712. Mon. Not. R. Astron. Soc. Lett. 2015, 449, 467–476. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Treves, A. Quasi-periodicities of the BL Lacertae Object PKS 2155-304. Astrophys. J. Lett. 2014, 793, L1. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Dotti, M.; Treves, A. Quasi-periodicities at Year-like Timescales in Blazars. Astron. J. 2016, 151, 54. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.U.C.A.; Ballet, J.; Bissaldi, E. Multiwavelength Evidence for Quasi-periodic Modulation in the Gamma-Ray Blazar PG 1553+113. Astrophys. J. Lett. 2015, 813, L41. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Treves, A.; Holgado, A.M.; Sesana, A.; Lindfors, E.; Ramazani, V.F. Quasi-periodicities of BL Lacertae objects. Astron. Astrophys. 2018, 615, A118. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Treves, A. Gamma-Ray and Optical Oscillations in PKS 0537-441. Astrophys. J. 2016, 820, 20. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Treves, A.; Lindfors, E.; Raiteri, C.M.; Nilsson, K.; Takalo, L.O.; Reinthal, R.; Berdyugin, A.; Fallah Ramazani, V.; et al. Gamma-ray and optical oscillations of 0716+714, MRK 421, and BL Lacertae. Astron. Astrophys. 2017, 600, A132. [Google Scholar] [CrossRef]
- Gupta, A.C.; Srivastava, A.K.; Wiita, P.J. Periodic Oscillations in the Intra-Day Optical Light Curves of the Blazar S5 0716+714. Astrophys. J. 2009, 690, 216–223. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Stern, D.; Glikman, E.; Drake, A.J.; Mahabal, A.A.; Donalek, C.; Larson, S.; Christensen, E. A possible close supermassive black-hole binary in a quasar with optical periodicity. Nature 2015, 518, 74–76. [Google Scholar] [CrossRef]
- King, O.G.; Hovatta, T.; Max-Moerbeck, W.; Meier, D.L.; Pearson, T.J.; Readhead, A.C.S.; Reeves, R.; Richards, J.L.; Shepherd, M.C. A quasi-periodic oscillation in the blazar J1359+4011. Mon. Not. R. Astron. Soc. Lett. 2013, 436, L114–L117. [Google Scholar] [CrossRef]
- Fan, J.H.; Kurtanidze, O.; Liu, Y.; Richter, G.M.; Chanishvili, R.; Yuan, Y.H. Optical Monitoring of Two Brightest Nearby Quasars, PHL 1811 and 3C 273. Astrophys. J. Suppl. Ser. 2014, 213, 26. [Google Scholar] [CrossRef]
- Smith, K.L.; Mushotzky, R.F.; Boyd, P.T.; Wagoner, R.V. Evidence for an Optical Low-frequency Quasi-periodic Oscillation in the Kepler Light Curve of an Active Galaxy. Astrophys. J. Lett. 2018, 860, L10. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Zola, S.; Ciprini, S.; Gopakumar, A.; Matsumoto, K.; Sadakane, K.; Piirola, V. Primary Black Hole Spin in OJ 287 as Determined by the General Relativity Centenary Flare. Astrophys. J. Lett. 2016, 819, L37. [Google Scholar] [CrossRef]
- Britzen, S.; Fendt, C.; Witzel, G.; Qian, S.-J.; Pashchenko, I.N.; Kurtanidze, O.; Zajacek, M.; Martinez, G.; Karas, V.; Aller, M.; et al. OJ287: Deciphering the ‘Rosetta stone of blazars. Mon. Not. R. Astron. Soc. Lett. 2018, 478, 3199–3219. [Google Scholar] [CrossRef]
- Dey, L.; Valtonen, M.J.; Gopakumar, A.; Zola, S.; Hudec, R.; Pihajoki, P.; Nilsson, K. Authenticating the Presence of a Relativistic Massive Black Hole Binary in OJ 287 Using Its General Relativity Centenary Flare: Improved Orbital Parameters. Astrophys. J. 2018, 866, 11. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Zola, S.; Pihajoki, P.; Enestam, S.; Lehto, H.J.; Dey, L.; Gopakumar, A.; Drozdz, M.; Ogloza, W.; Zejmo, M.; et al. Accretion Disk Parameters Determined from the Great 2015 Flare of OJ 287. Astrophys. J. 2019, 882, 88. [Google Scholar] [CrossRef]
- Dey, L.; Gopakumar, A.; Valtonen, M.; Zola, S.; Susobhanan, A.; Hudec, R.; Pihajoki, P.; Pursimo, T.; Berdyugin, A.; Piirola, V.; et al. The Unique Blazar OJ 287 and Its Massive Binary Black Hole Central Engine. Universe 2019, 5, 108. [Google Scholar] [CrossRef]
- Komossa, S.; Grupe, D.; Parker, M.L.; Valtonen, M.J.; Gómez, J.L.; Gopakumar, A.; Dey, L. The 2020 April-June super-outburst of OJ 287 and its long-term multiwavelength light curve with Swift: Binary supermassive black hole and jet activity. Mon. Not. R. Astron. Soc. Lett. 2020, 498, L35–L39. [Google Scholar] [CrossRef]
- McHardy, I.M.; Papadakis, I.E.; Uttley, P.; Page, M.J.; Mason, K.O. Combined long and short time-scale X-ray variability of NGC 4051 with RXTE and XMM-Newton. Mon. Not. R. Astron. Soc. Lett. 2004, 348, 783–801. [Google Scholar] [CrossRef]
- Papadakis, I.E.; Brinkmann, W.; Gliozzi, M.; Raeth, C.; Nicastro, F.; Conciatore, M.L. XMM-Newton long-look observation of the narrow-line Seyfert 1 galaxy PKS 0558-504. II. Timing analysis. Astron. Astrophys. 2010, 518, A28. [Google Scholar] [CrossRef]
- Mangalam, A.V.; Wiita, P.J. Accretion Disk Models for Optical and Ultraviolet Microvariability in Active Galactic Nuclei. Astrophys. J. 1993, 406, 420. [Google Scholar] [CrossRef]
- Gonzalez-Martin, O.; Vaughan, S. X-ray variability of 104 active galactic nuclei. XMM-Newton power-spectrum density profiles. Astron. Astrophys. 2012, 544, A80. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, S.N.; Focke, W.; Swank, J.H. Temporal Properties of Cygnus X-1 during the Spectral Transitions. Astrophys. J. 1997, 484, 383–393. [Google Scholar] [CrossRef]
- Osterbrock, D.E.; Pogge, R.W. The spectra of narrow-line Seyfert 1 galaxies. Astrophys. J. 1985, 297, 66–76. [Google Scholar] [CrossRef]
- Goodrich, R.W. Spectropolarimetry of “Narrow-Line” Seyfert 1 Galaxies. Astrophys. J. 1989, 342, 224. [Google Scholar] [CrossRef]
- Komossa, S. Narrow-line Seyfert 1 Galaxies. Revista Mexicana de Astronomía y Astrofísica (Serie de Conferencias) 2008, 32, 86–92. [Google Scholar]
- Pan, H.W.; Yuan, W.; Yao, S.; Zhou, X.L.; Liu, B.; Zhou, H.; Zhang, S.N. Detection of a Possible X-ray Quasi-periodic Oscillation in the Active Galactic Nucleus 1H 0707-495. Astrophys. J. Lett. 2016, 819, L19. [Google Scholar] [CrossRef]
- Zhang, P.F.; Zhang, P.; Liao, N.H.; Yan, J.Z.; Fan, Y.Z.; Liu, Q.Z. Two Transient X-ray Quasi-periodic Oscillations Separated by an Intermediate State in 1H 0707-495. Astrophys. J. 2018, 853, 193. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, P.F.; Yan, J.Z.; Fan, Y.Z.; Liu, Q.Z. An X-ray Periodicity of 1.8 hr in Narrow-line Seyfert 1 Galaxy Mrk 766. Astrophys. J. 2017, 849, 9. [Google Scholar] [CrossRef]
- Boller, T.; Keil, R.; Trümper, J.; O’Brien, P.T.; Reeves, J.; Page, M. Detection of an X-ray periodicity in the Narrow-line Seyfert 1 Galaxy Mrk 766 with XMM-Newton. Astron. Astrophys. 2001, 365, L146–L151. [Google Scholar] [CrossRef][Green Version]
- Gupta, A.C.; Tripathi, A.; Wiita, P.J.; Gu, M.; Bambi, C.; Ho, L.C. Possible 1 hour quasi-periodic oscillation in narrow-line Seyfert 1 galaxy MCG-06-30-15. Astron. Astrophys. 2018, 616, L6. [Google Scholar] [CrossRef]
- Peng, Z.; Jing-Zhi, Y.; Qing-Zhong, L. Two Quasi-periodic Oscillations in ESO 113-G010. Chin. Astron. Astrophys. 2020, 44, 32–40. [Google Scholar] [CrossRef]
- Zhou, X.L.; Yuan, W.; Pan, H.W.; Liu, Z. Universal Scaling of the 3:2 Twin-peak Quasi-periodic Oscillation Frequencies With Black Hole Mass and Spin Revisited. Astrophys. J. Lett. 2015, 798, L5. [Google Scholar] [CrossRef]
- Falomo, R.; Pian, E.; Treves, A. An optical view of BL Lacertae objects. Astron. Astrophys. Rev. 2014, 22, 73. [Google Scholar] [CrossRef]
- Padovani, P.; Alexander, D.M.; Assef, R.J.; De Marco, B.; Giommi, P.; Hickox, R.C.; Richards, G.T.; Smolčić, V.; Hatziminaoglou, E.; Mainieri, V.; et al. Active galactic nuclei: What’s in a name? Astron. Astrophys. Rev. 2017, 25, 2. [Google Scholar] [CrossRef]
- Zhang, B.K.; Zhao, X.Y.; Wang, C.X.; Dai, B.Z. Optical quasi-periodic oscillation and color behavior of blazar PKS 2155-304. Res. Astron. Astrophys. 2014, 14, 933–941. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Z.; Chen, L.; Wiita, P.J.; Vadakkumthani, J.; Morrell, N.; Zhang, P.; Zhang, J. A 34.5 day quasi-periodic oscillation in γ-ray emission from the blazar PKS 2247-131. Nat. Commun. 2018, 9, 4599. [Google Scholar] [CrossRef]
- Tarnopolski, M.; Żywucka, N.; Marchenko, V.; Pascual-Granado, J. A comprehensive power spectral density analysis of astronomical time series I: The Fermi-LAT gamma-ray light curves of selected blazars. arXiv 2020, arXiv:2006.03991. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. kHz Quasiperiodic Oscillations in Low-Mass X-ray Binaries as Probes of General Relativity in the Strong-Field Regime. Phys. Rev. Lett. 1999, 82, 17–20. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M.; Morsink, S.M. Correlations in the Quasi-periodic Oscillation Frequencies of Low-Mass X-Ray Binaries and the Relativistic Precession Model. Astrophys. J. Lett. 1999, 524, L63–L66. [Google Scholar] [CrossRef]
- Rana, P.; Mangalam, A. A geometric origin for quasi-periodic oscillations in black hole X-ray binaries. arXiv 2020, arXiv:2009.01832. [Google Scholar]
- Mangalam, A. Polarization and QPOs from jets in black hole systems. J. Astrophys. Astron. 2018, 39, 68. [Google Scholar] [CrossRef]
- Mohan, P.; Mangalam, A. Kinematics of and Emission from Helically Orbiting Blobs in a Relativistic Magnetized Jet. Astrophys. J. 2015, 805, 91. [Google Scholar] [CrossRef]
- Carter, B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev. D 1968, 174, 1559–1571. [Google Scholar] [CrossRef]
- Rana, P.; Mangalam, A. Astrophysically relevant bound trajectories around a Kerr black hole. Class. Quantum Gravity 2019, 36, 045009. [Google Scholar] [CrossRef]
- Zhou, X.L.; Zhang, S.N.; Wang, D.X.; Zhu, L. Calibrating the Correlation Between Black Hole Mass and X-ray Variability Amplitude: X-ray Only Black Hole Mass Estimates for Active Galactic Nuclei and Ultra-luminous X-ray Sources. Astrophys. J. 2010, 710, 16–23. [Google Scholar] [CrossRef]
- Ho, L.C.; Kim, M.; Terashima, Y. The Low-mass, Highly Accreting Black Hole Associated with the Active Galactic Nucleus 2XMM J123103.2+110648. Astrophys. J. Lett. 2012, 759, L16. [Google Scholar] [CrossRef][Green Version]
- Grupe, D.; Wills, B.J.; Leighly, K.M.; Meusinger, H. A Complete Sample of Soft X-Ray-Selected AGNs. I. The Data. Astron. J. 2004, 127, 156–179. [Google Scholar] [CrossRef]
- Wang, T.; Lu, Y. Black hole mass and velocity dispersion of narrow line region in active galactic nuclei and narrow line Seyfert 1 galaxies. Astron. Astrophys. 2001, 377, 52–59. [Google Scholar] [CrossRef]
- Hu, C.; Wang, J.M.; Ho, L.C.; Bai, J.M.; Li, Y.R.; Du, P.; Lu, K.X. Improving the Flux Calibration in Reverberation Mapping by Spectral Fitting:Application to the Seyfert Galaxy MCG-6-30-15. Astrophys. J. 2016, 832, 197. [Google Scholar] [CrossRef]
- Motta, S.E.; Munoz-Darias, T.; Sanna, A.; Fender, R.; Belloni, T.; Stella, L. Black hole spin measurements through the relativistic precession model: XTE J1550-564. Mon. Not. R. Astron. Soc. Lett. 2014, 439, L65–L69. [Google Scholar] [CrossRef]
- Motta, S.E.; Belloni, T.M.; Stella, L.; Muñoz-Darias, T.; Fender, R. Precise mass and spin measurements for a stellar-mass black hole through X-ray timing: The case of GRO J1655-40. Mon. Not. R. Astron. Soc. Lett. 2014, 437, 2554–2565. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Wilkins, D.C. Bound Geodesics in the Kerr Metric. Phys. Rev. D 1972, 5, 814–822. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Elsevier/Academic Press: Amsterdam, The Netherlands, 2007; pp. xlviii+1171. [Google Scholar]
- Camenzind, M.; Krockenberger, M. The lighthouse effect of relativistic jets in blazars. A geometric originof intraday variability. Astron. Astrophys. 1992, 255, 59–62. [Google Scholar]
- Gupta, A.C.; Tripathi, A.; Wiita, P.J.; Kushwaha, P.; Zhang, Z.; Bambi, C. Detection of a quasi-periodic oscillation in γ-ray light curve of the high-redshift blazar B2 1520+31. Mon. Not. R. Astron. Soc. Lett. 2019, 484, 5785–5790. [Google Scholar] [CrossRef]
- Bhatta, G. Blazar Mrk 501 shows rhythmic oscillations in its γ-ray emission. Mon. Not. R. Astron. Soc. Lett. 2019, 487, 3990–3997. [Google Scholar] [CrossRef]
- Mohan, P.; Gupta, A.C.; Bachev, R.; Strigachev, A. Kepler light-curve analysis of the blazar W2R 1926+42. Mon. Not. R. Astron. Soc. Lett. 2016, 456, 654–664. [Google Scholar] [CrossRef]
- An, T.; Mohan, P.; Zhang, Y.; Frey, S.; Yang, J.; Gabányi, K.É.; Gurvits, L.I.; Paragi, Z.; Perger, K.; Zheng, Z. Evolving parsec-scale radio structure in the most distant blazar known. Nat. Commun. 2020, 11, 143. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Blandford, R.D. The Third Catalog of Active Galactic Nuclei Detected by the Fermi Large Area Telescope. Astrophys. J. 2015, 810, 14. [Google Scholar] [CrossRef]
- Chen, L. On the Jet Properties of γ-Ray-loud Active Galactic Nuclei. Astrophys. J. Suppl. Ser. 2018, 235, 39. [Google Scholar] [CrossRef]
- Tavani, M.; Cavaliere, A.; Munar-Adrover, P.; Argan, A. The Blazar PG 1553+113 as a Binary System of Supermassive Black Holes. Astrophys. J. 2018, 854, 11. [Google Scholar] [CrossRef]
- Penna, R.F.; Sądowski, A.; McKinney, J.C. Thin-disc theory with a non-zero-torque boundary condition and comparisons with simulations. Mon. Not. R. Astron. Soc. Lett. 2012, 420, 684–698. [Google Scholar] [CrossRef]
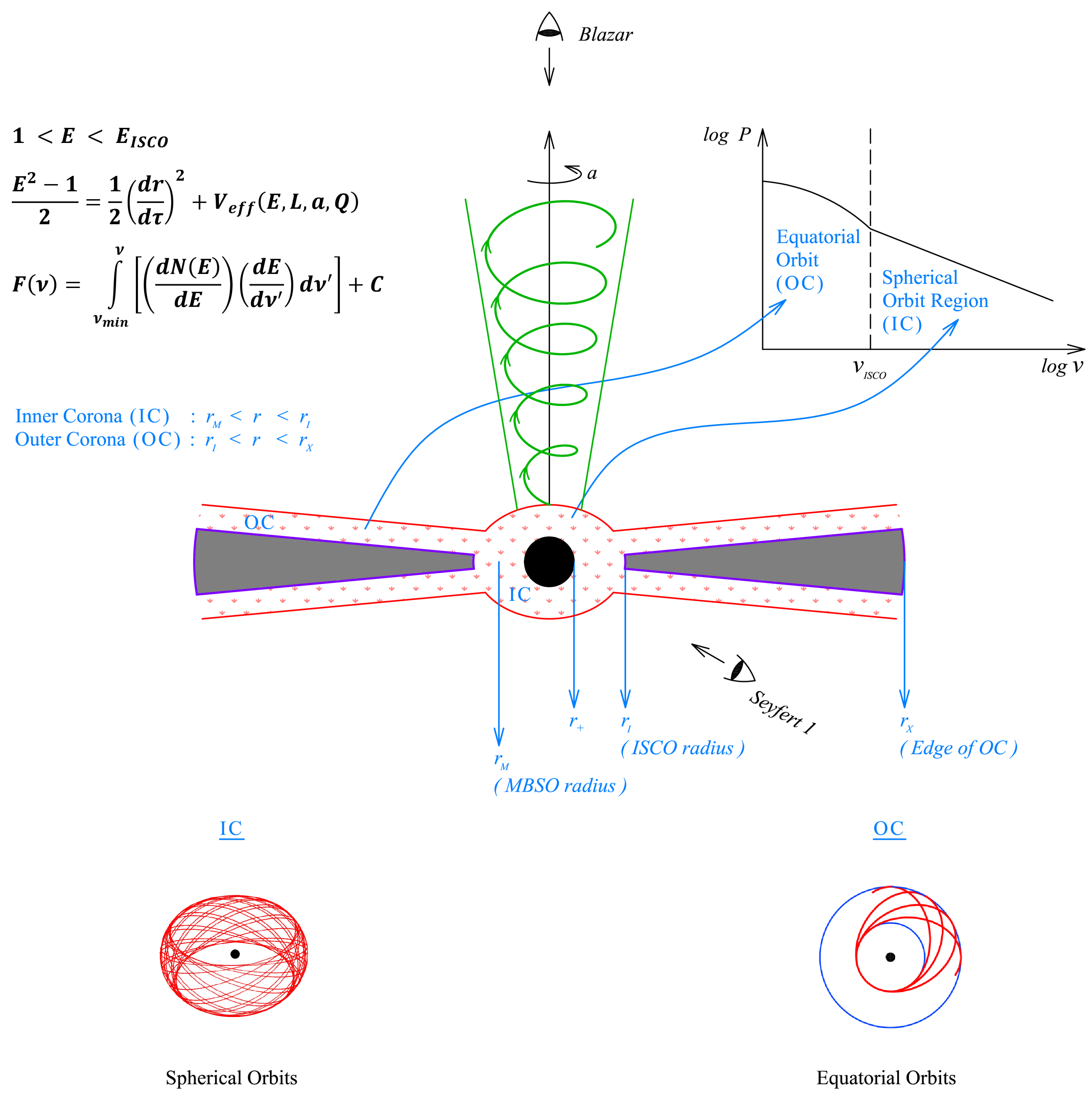
| 1 | stands for the periastron precession. |
| 2 | stands for the nodal precession. |

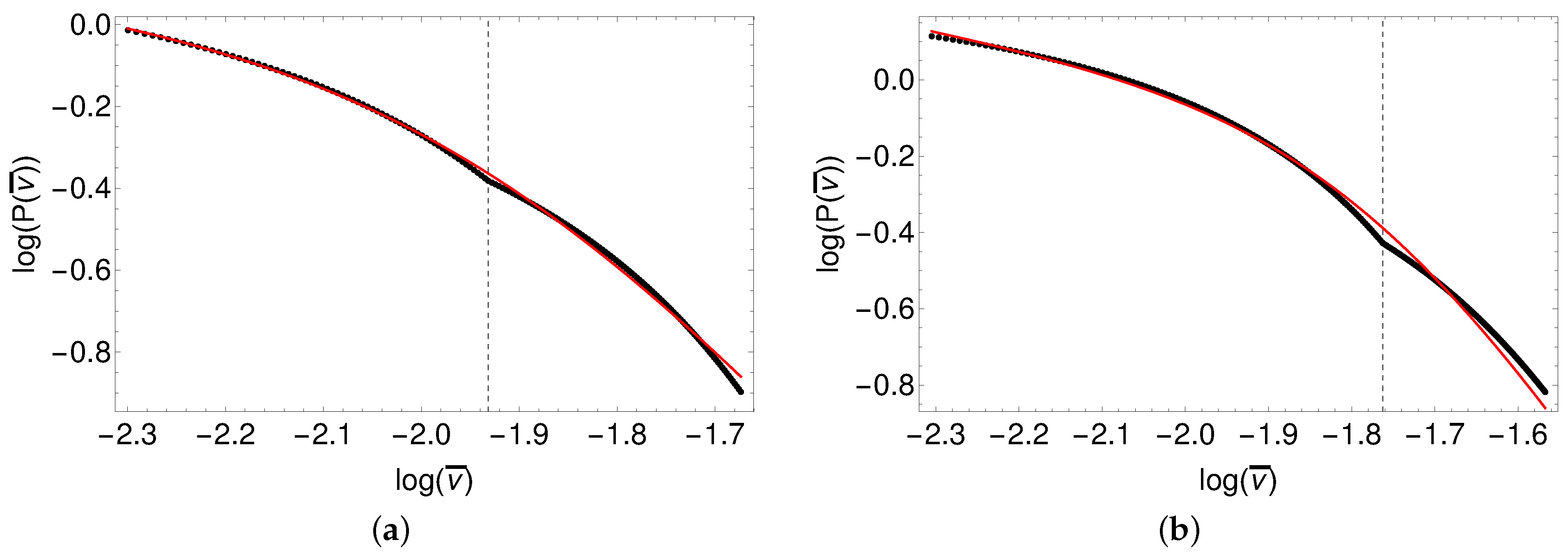
| Symbol | Explanation | Symbol | Explanation |
|---|---|---|---|
| c | speed of light | one-dimensional and normalized probability | |
| G | gravitational constant | density in parameter space | |
| mass of the black hole | liklihood function for spin | ||
| mass of the sun | most probable value of spin | ||
| a | spin of the black hole | distribution function of spin | |
| Q | Carter’s constant | variance of spin | |
| e | eccentricity of the orbit | QPO period | |
| inverse-latus rectum of the orbit | theoretical timescale for jet-based QPOs | ||
| frequency in Hz | radial footpoint of the magnetic field | ||
| frequency scaled by () | light cylinder radius | ||
| scaled azimuthal frequency | bending power-law profile for PSD | ||
| scaled radial frequency | break-frequency of PSD | ||
| scaled vertical oscillation frequency | & | PSD slopes for & | |
| r | radius of a circular orbit | distribution function for energy | |
| radius of a spherical orbit | distribution function for frequency | ||
| conjugate momentum of coordinate | power-law index of inside ISCO | ||
| E | energy per unit rest mass of a test particle | power-law index of outside ISCO | |
| z-component of the angular momentum | ISCO radius | ||
| per unit rest mass of a test particle | MBSO radius | ||
| proper time | outer edge of the accretion disk | ||
| radial effective potential in Kerr geometry | scaled azimuthal frequency at ISCO | ||
| probability density in frequency space | scaled azimuthal frequency at MBSO | ||
| jacobian of transformation from frequency | scaled azimuthal frequency at outer edge | ||
| to parameter space | of the accretion disk | ||
| observed centroid frequency of the ith QPO | average slope of PSD for | ||
| observed standard dispersion of the ith QPO | average slope of PSD for | ||
| normalized probability density in parameter | upper cut off frequency of PSD | ||
| space | total integrated power of PSD |
| # | Source | Class of AGN | () | QPO Period ks | QPO Frequency Hz | References |
|---|---|---|---|---|---|---|
| 1. | RE J1034+396 | NLSy1 | 4 | 2.681 ± 0.093 | [55] , [8] | |
| 2. | 2XMM J123103.2+110648 | Type-2 AGN | 0.1 | 0.729 | [56] , [9] | |
| 3. | MS 2254.9-3712 | NLSy1 | 4 e | [57] e, [10] | ||
| 4. | 1H 0707-495 | NLSy1 | 5.2 | [36] , [37] | ||
| 5. | Mrk 766 | NLSy1 | 4.3 | [58] , [38] | ||
| 2.38 | [39] | |||||
| 6. | MCG-06-30-15 | NLSy1 | 3.26 | 2.778 ± 0.177 | [59] , [40] |
| Source | r Range | Resolution | Exact Solution | Model Fit | a Range | Resolution | Exact Solution | Model Fit |
|---|---|---|---|---|---|---|---|---|
| 1H 0707-495 | 7–9.5 | 0.01 | 8.214 | 8.214 | 0–0.9 | 0.001 | 0.0662 | 0.0662 |
| Q | Range | Resolution | Exact Solution | Model Fit | a Range | Resolution | Exact Solution | Model Fit | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.5–9.5 | 0.01 | 8.215 | 0–0.9 | 0.001 | 0.069 | 0.290 | ||
| 4 | 6.5–9.5 | 0.01 | 8.219 | 0–0.9 | 0.001 | 0.080 | 0.317 | ||
| 8 | 6.5–10 | 0.01 | 8.233 | 0–0.9 | 0.001 | 0.109 | 0.348 | ||
| 12 | 6.5–10 | 0.01 | 8.301 | 0–0.9 | 0.001 | 0.269 | 0.277 |
| # | Source | z | Log | Energy Band | QPO Period (Days) | (Days) | References |
|---|---|---|---|---|---|---|---|
| 1. | PKS 2155-304 | 0.116 | 8.7 | 100 MeV–300 GeV | 620 ± 41 | 33–143 | [70] ,[71] ,[11,12,14] |
| 100 MeV–300 GeV | 612 ± 42 | [47] | |||||
| R (optical) | 315 ± 25 | ||||||
| 2. | PG 1553+113 | 0.36 e | ∼8 | 100 MeV–300 GeV | 780 ± 63 | 8–35 | [71] e,[72] ,[13,14] |
| R (optical) | 810 ± 52 | ||||||
| 3. | PKS 0537-441 | 0.892 | 8.56 | 100 MeV–300 GeV | 280 ± 39 | 40–176 | [70] ,[71] ,[15] |
| R (optical) | 148 ± 17 | ||||||
| 4. | BL Lac | 0.0686 | 8.21 | 100 MeV–300 GeV | 680 ± 35 | 10–44 | [70] ,[71] ,[14,16] |
| R (optical) | 670 ± 40 |
| # | (a, Q) | |||||
|---|---|---|---|---|---|---|
| 1 | () | 0.282 | 2.74 | 0.866 | ||
| 2 | () | 0.413 | 3.453 | 0.818 | ||
| 3 | () | 0.488 | 5.561 | 1.112 | ||
| 4 | () | 0.497 | 5.328 | 0.925 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rana, P.; Mangalam, A. A Relativistic Orbit Model for Temporal Properties of AGN. Galaxies 2020, 8, 67. https://doi.org/10.3390/galaxies8030067
Rana P, Mangalam A. A Relativistic Orbit Model for Temporal Properties of AGN. Galaxies. 2020; 8(3):67. https://doi.org/10.3390/galaxies8030067
Chicago/Turabian StyleRana, Prerna, and A. Mangalam. 2020. "A Relativistic Orbit Model for Temporal Properties of AGN" Galaxies 8, no. 3: 67. https://doi.org/10.3390/galaxies8030067
APA StyleRana, P., & Mangalam, A. (2020). A Relativistic Orbit Model for Temporal Properties of AGN. Galaxies, 8(3), 67. https://doi.org/10.3390/galaxies8030067