Constraints to Dark Matter Annihilation from High-Latitude HAWC Unidentified Sources
Abstract
1. Introduction
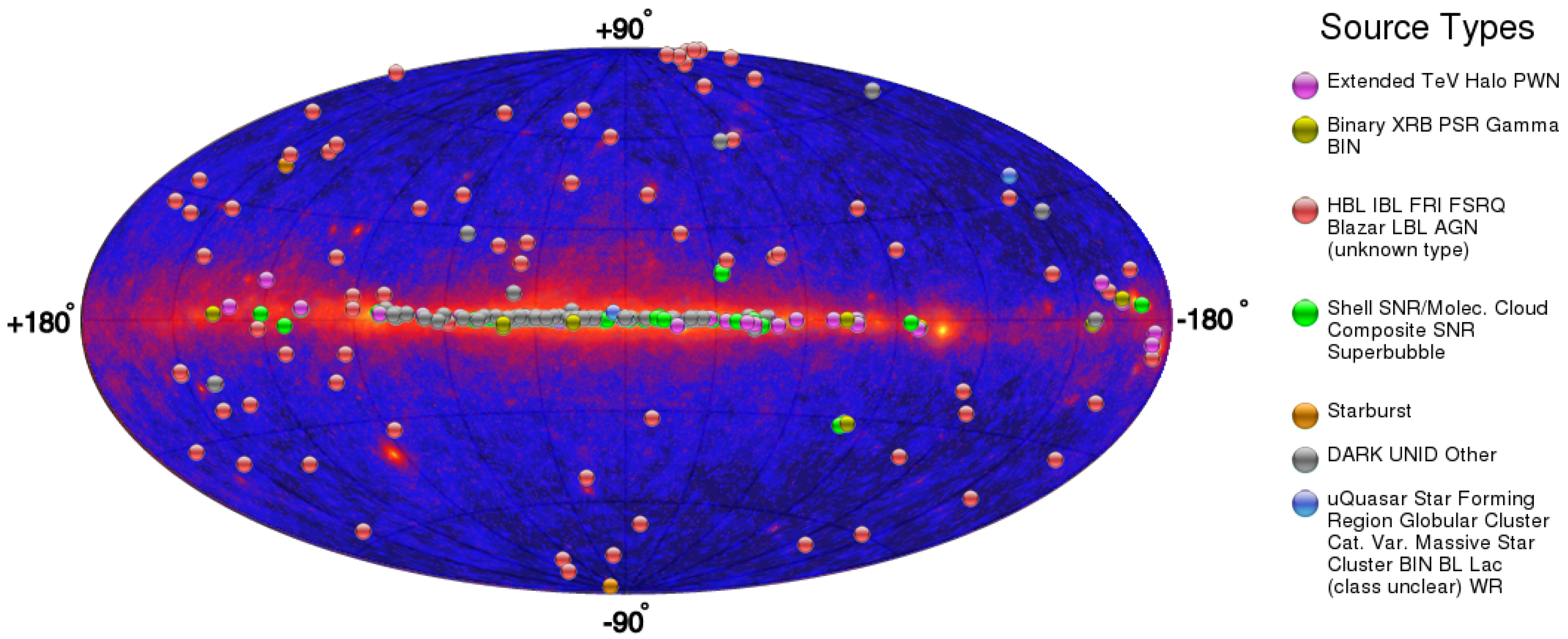
2. HAWC Unidentified Sources
2.1. HAWC and the TeV Sky
2.2. Target Selection
- Why HAWC?—HAWC is currently the only VHE observatory able to survey a significant fraction of the whole sky. Indeed, the combination of its 1.5 sr FoV, Earth rotation and location in Mexican soil, above the Equator, makes it possible to observe 2/3 of the sky every day.2 In contrast, IACTs are pointing telescopes, i.e., they need to know the location of the sources in advance and, thus, just point towards specific targets. For the purposes of this work, it becomes critical to have observations of a large fraction of the sky. This is so because we adopt the methodology introduced in [23] to set constraints on the DM annihilation parameter space using unIDs. The method is based on a comparison between the number of catalogued unID sources and subhalo predictions derived from N-body cosmological simulations. Large fractions of the sky, observed with a nearly uniform exposure, will allow for a more accurate comparison to N-body simulations, as we can derive a more robust statistical determination of the subhalo annihilation fluxes for significantly large sky areas. We remind that these fluxes are proportional to the so-called J-factor:where the first integral is performed over the solid angle of observation (), the second one along the line of sight (l.o.s, ), and is the dark matter density profile of a given subhalo.
- Why high latitude?CDM predicts the existence of DM subhalos at all Galactic latitudes distributed nearly isotropically from the Sun’s position in the Galaxy. On the other hand, the majority of Galactic VHE astrophysical sources, such as pulsars, binaries, supernova remnants and pulsar wind nebulae, are expected to cluster heavily along the Galactic plane, where most of the stars and gas reside. Since many of these objects are expected to also be hidden among the pool of unIDs awaiting for a proper classification, we expect the distribution of unIDs to peak around zero Galactic latitude as well (as already discussed in Figure 1). For our purposes, these low-latitude sources only add contamination to our sample of potential DM subhalo candidates. Therefore, we apply a cut in our analysis at Galactic latitudes . For consistency, this cut will also need to be done on our predicted subhalo distribution. On average, our Galactic cut removes only ∼11% of the simulated subhalos, while 87% of 2HWC unIDs are left out. Actually, in practice we cut a larger region in the N-body simulation in order to match the 2/3 sky coverage of HAWC, and in this way we have a totally fair one-to-one comparison among observed and simulated sky.
2.3. 2HWC J1040+308 as a DM Subhalo Candidate
- Spatial extension—Spatial extension has been hailed as a “smoking gun” for DM annihilation [24,25,26,47]. Indeed, low-mass yet sufficiently close DM subhalos may be expected to appear as extended unID sources. 2HWC J1040+308 is found to be spatially extended in HAWC data with a radius of [46]. This fact is even more notable for the case of very high latitude sources like this one (), as sources at high latitudes are typically extragalactic and thus the majority of them are expected to be point-like. Indeed, it would be hard to explain all these features with a single astrophysical source – AGNs would appear as point-like sources, while Galactic sources could appear as extended, yet this source’s high latitude would imply a small distance and thus it would be surprising not to have a detection in any other wavelengths. On the other hand, as these unIDs correspond to very faint sources near the detection threshold, it is currently unclear whether they would appear as extended, even if being actual DM subhalos, as the DM annihilation flux profile decreases very rapidly with distance to the subhalo center.
- Multi-wavelength search—As already mentioned, dark satellites are not massive enough to retain baryons and, as a result, they are not expected to shine at any wavelengths due to astrophysical processes. However, gamma-ray emission is expected to happen should these objects be composed of WIMP DM.3 A dedicated search at different wavelengths was performed for 2HWC J1040+308, with null results. In particular, a combined search in less energetic gamma rays with Fermi-LAT and VERITAS was performed in [52], with no detection. An additional search can be performed with the SSDC online tool,4 where no significant emission at lower energies is found.
- Heavy WIMP mass—It is interesting to note that a joint analysis of Fermi LAT [53], VERITAS [54] and HAWC data was recently done in [52] and no gamma-ray emission was reported for 2HWC J1040+308 in the comparatively lower energy range covered by the LAT and VERITAS. This is so despite the fact that 2HWC J1040+308 exhibits a hard spectrum with a photon spectral index of in the HAWC energy range [46], which would in principle make a detection at low energies easier to realize. If interpreted in a DM scenario, these results suggest heavy, TeV WIMP masses as we would not expect a detection by Fermi LAT or VERITAS only in case of significantly high values of the WIMP mass, for which a DM spectrum beyond the range of sensitivity of these two instruments would be generated. Also, interestingly, this unID slightly prefers a fit to a “Cutoff Power Law” instead of a “Simple Power Law” [35], which is a parametric form that better reproduces a typical DM annihilation spectrum [22,23]. Heavy WIMPs are well motivated [55,56,57] and, probably, favoured in the light of current DM constraints in the usual (velocity-averaged annihilation cross section) vs. (WIMP mass) parameter space: IACTs are still far from being able to probe the thermal relic cross section values [58] for large, TeV WIMP masses, while for much lighter, (GeV) masses there are already robust and strong constraints, e.g., [23,59].
3. DM Constraints
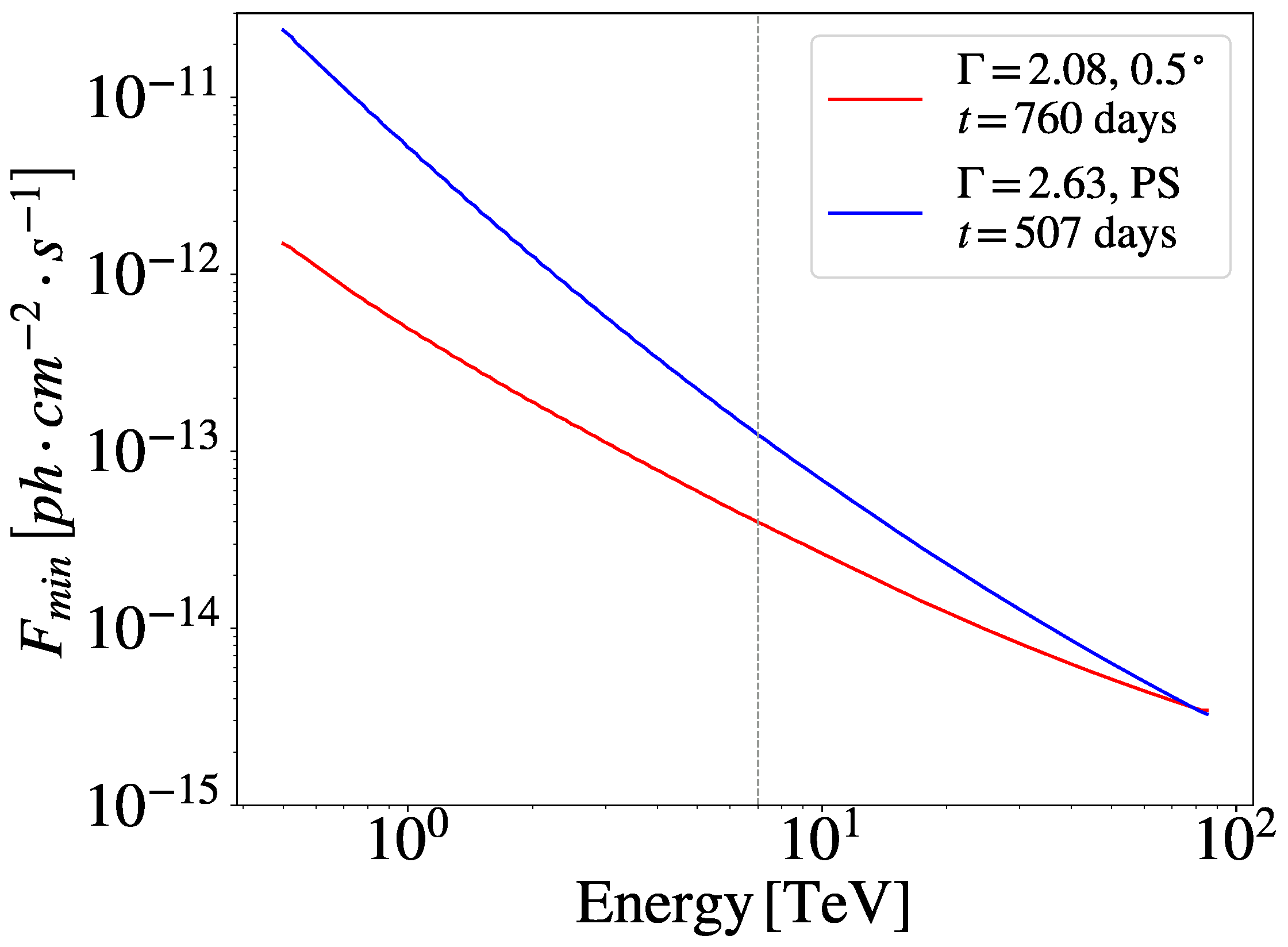
3.1. Minimum Detection Flux
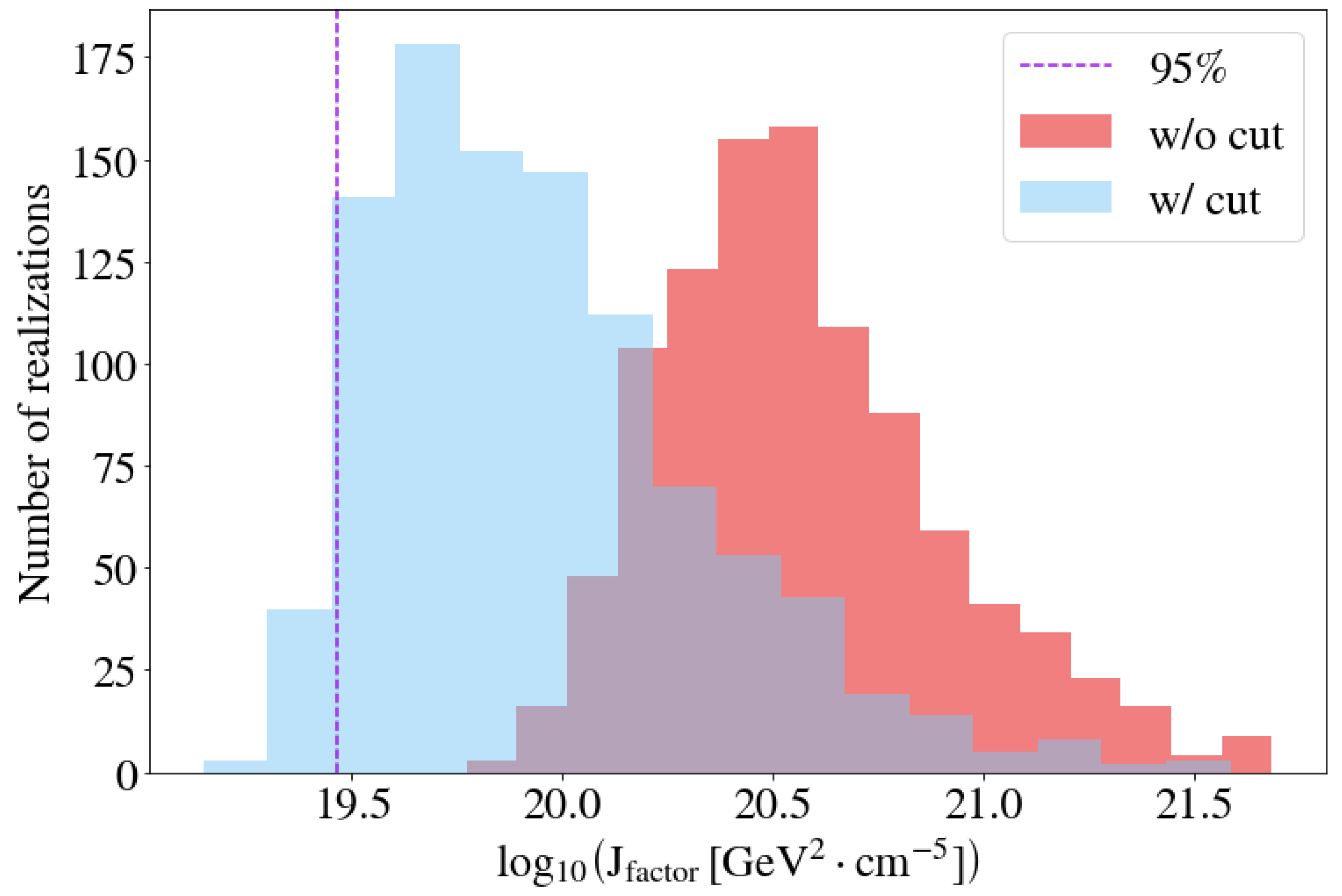
3.2. J-Factor
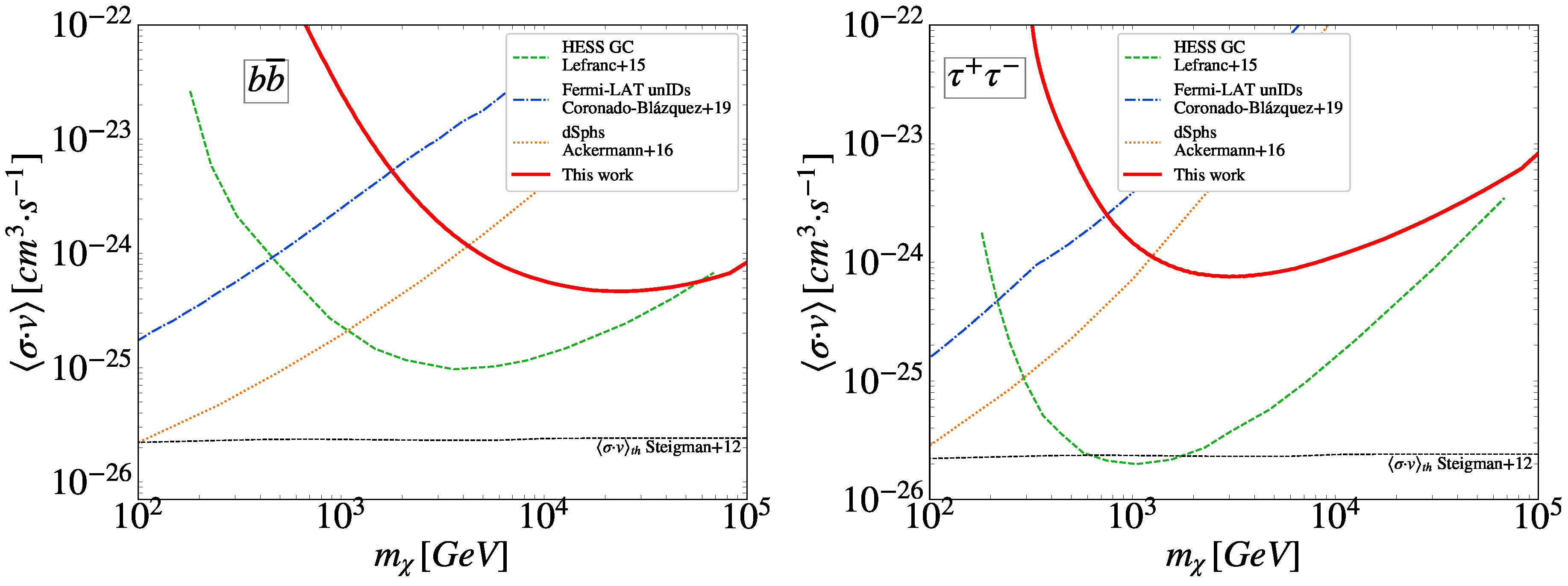
3.3. Results
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- The Planck Collaboration. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016. [Google Scholar] [CrossRef]
- Garrett, K.; Duda, G. Dark Matter: A Primer. Adv. Astron. 2010. [Google Scholar] [CrossRef]
- Freese, K. Review of Observational Evidence for Dark Matter in the Universe and in Upcoming Searches for Dark Stars; EAS Publications Series; EAS: Frascati, Italy, 2009; Volume 36, pp. 113–126. [Google Scholar] [CrossRef]
- Madau, P.; Diemand, J.; Kuhlen, M. Dark Matter Subhalos and the Dwarf Satellites of the Milky Way. Astrophys. J. 2008, 679, 1260–1271. [Google Scholar] [CrossRef]
- Zavala, J.; Frenk, C.S. Dark Matter Haloes and Subhaloes. Galaxies 2019, 7, 81. [Google Scholar] [CrossRef]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric dark matter. Phys. Rep. 1996, 267, 195–373. [Google Scholar] [CrossRef]
- Bertschinger, E. Effects of cold dark matter decoupling and pair annihilation on cosmological perturbations. Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
- Profumo, S.; Sigurdson, K.; Kamionkowski, M. What Mass Are the Smallest Protohalos? Phys. Rev. Lett. 2006, 97. [Google Scholar] [CrossRef]
- Bringmann, T. Particle Models and the Small-Scale Structure of Dark Matter. New J. Phys. 2009. [Google Scholar] [CrossRef]
- Gao, L.; White, S.D.M.; Jenkins, A.; Stoehr, F.; Springel, V. The subhalo populations of ΛCDM dark haloes. Mon. Not. R. Astron. Soc. 2004, 355, 819–834. [Google Scholar] [CrossRef]
- Ocvirk, P.; Gillet, N.; Shapiro, P.R.; Aubert, D.; Iliev, I.T.; Teyssier, R.; Yepes, G.; Choi, J.H.; Sullivan, D.; Knebe, A.; et al. Cosmic Dawn (CoDa): The first radiation-hydrodynamics simulation of reionization and galaxy formation in the Local Universe. Mon. Not. R. Astron. Soc. 2016, 463, 1462–1485. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.S.; Fattahi, A.; Navarro, J.F.; Theuns, T.; Bower, R.G.; Crain, R.A.; Furlong, M.; Jenkins, A.; Schaller, M.; et al. The chosen few: The low-mass haloes that host faint galaxies. Mon. Not. R. Astron. Soc. 2015, 456, 85–97. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.S.; Fattahi, A.; Navarro, J.F.; Bower, R.G.; Crain, R.A.; Vecchia, C.D.; Furlong, M.; Jenkins, A.; McCarthy, I.G.; et al. Bent by baryons: The low-mass galaxy-halo relation. Mon. Not. R. Astron. Soc. 2015, 448, 2941–2947. [Google Scholar] [CrossRef]
- Fitts, A.; Boylan-Kolchin, M.; Bullock, J.S.; Weisz, D.R.; El-Badry, K.; Wheeler, C.; Faucher-Giguère, C.A.; Quataert, E.; Hopkins, P.F.; Kereš, D.; et al. No assembly required: Mergers are mostly irrelevant for the growth of low-mass dwarf galaxies. Mon. Not. R. Astron. Soc. 2018, 479, 319–331. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P.; Zemp, M.; Moore, B.; Potter, D.; Stadel, J. Clumps and streams in the local dark matter distribution. Nature 2008. [Google Scholar] [CrossRef] [PubMed]
- Springel, V.; Wang, J.; Vogelsberger, M.; Ludlow, A.; Jenkins, A.; Helmi, A.; Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Aquarius Project: The subhaloes of galactic haloes. Mon. Not. R. Astron. Soc. 2008, 391, 1685–1711. [Google Scholar] [CrossRef]
- Roszkowski, L.; Sessolo, E.M.; Trojanowski, S. WIMP dark matter candidates and searches - current issues and future prospects. arXiv 2017, arXiv:1707.06277v1. [Google Scholar]
- Bertone, G. The moment of truth for WIMP Dark Matter. Nature 2010, 468, 389–393. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Bertone, G. (Ed.) Particle Dark Matter; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Anderson, B.; Kuhlen, M.; Diemand, J.; Johnson, R.P.; Madau, P. Fermi-LAT Sensitivity to Dark Matter Annihilation in VIA Lactea II Substructure. Astrophys. J. 2010, 718, 899–904. [Google Scholar] [CrossRef]
- Calore, F.; Romeri, V.D.; Mauro, M.D.; Donato, F.; Marinacci, F. Realistic estimation for the detectability of dark matter sub-halos with Fermi-LAT. Phys. Rev. D 2016. [Google Scholar] [CrossRef]
- Coronado-Blázquez, J.; Sánchez-Conde, M.A.; Domínguez, A.; Aguirre-Santaella, A.; Mauro, M.D.; Mirabal, N.; Nieto, D.; Charles, E. Unidentified gamma-ray sources as targets for indirect dark matter detection with the Fermi-Large Area Telescope. J. Cosmol. Astropart. Phys. 2019, 2019, 20. [Google Scholar] [CrossRef]
- Aguirre-Santaella, A.; Sánchez-Conde, M.; Moliné, A.; Coronado-Blázquez, J. TBD 2020. in preparation.
- Bertoni, B.; Hooper, D.; Linden, T. Examining The Fermi-LAT Third Source Catalog In Search Of Dark Matter Subhalos. J. Cosmol. Astropart. Phys. 2015, 12, 35. [Google Scholar] [CrossRef]
- Bertoni, B.; Hooper, D.; Linden, T. Is The Gamma-Ray Source 3FGL J2212.5+0703 A Dark Matter Subhalo? J. Cosmol. Astropart. Phys. 2016, 5, 49. [Google Scholar] [CrossRef]
- Buckley, M.R.; Hooper, D. Dark Matter Subhalos In the Fermi First Source Catalog. Phys. Rev. D 2010. [Google Scholar] [CrossRef]
- The Fermi LAT Collaboration. Search for Dark Matter Satellites using the FERMI-LAT. Astrophys. J. 2012. [Google Scholar] [CrossRef]
- Hooper, D.; Witte, S.J. Gamma Rays From Dark Matter Subhalos Revisited: Refining the Predictions and Constraints. J. Cosmol. Astropart. Phys. 2017, 4, 18. [Google Scholar] [CrossRef]
- Egorov, A.E.; Galper, A.M.; Topchiev, N.P.; Leonov, A.A.; Suchkov, S.I.; Kheymits, M.D.; Yurkin, Y.T. Detactability of Dark Matter Subhalos by Means of the GAMMA-400 Telescope. Phys. At. Nucl. 2018, 81, 373–378. [Google Scholar] [CrossRef]
- De Angelis, A.; Tatischeff, V.; Grenier, I.A.; McEnery, J.; Mallamaci, M.; Tavani, M.; Oberlack, U.; Hanlon, L.; Walter, R.; Argan, A.; et al. Science with e-ASTROGAM. J. High Energy Astrophys. 2018, 19, 1–106. [Google Scholar] [CrossRef]
- Zechlin, H.S.; Fernandes, M.V.; Elsaesser, D.; Horns, D. Dark matter subhaloes as gamma-ray sources and candidates in the first Fermi-LAT catalogue. Astron. Astrophys. 2011. [Google Scholar] [CrossRef]
- Zechlin, H.S.; Horns, D. Unidentified sources in the Fermi-LAT second source catalog: The case for DM subhalos. J. Cosmol. Astropart. Phys. 2012. [Google Scholar] [CrossRef]
- The HAWC Collaboration. Sensitivity of the high altitude water Cherenkov detector to sources of multi-TeV gamma rays. Astropart. Phys. 2013, 50–52, 26–32. [Google Scholar] [CrossRef]
- The HAWC Collaboration. Searching for dark matter sub-structure with HAWC. J. Cosmol. Astropart. Phys. 2019, 2019, 22. [Google Scholar] [CrossRef]
- Moliné, Á.; Sánchez-Conde, M.A.; Palomares-Ruiz, S.; Prada, F. Characterization of subhalo structural properties and implications for dark matter annihilation signals. Mon. Not. R. Astron. Soc. 2017, 466, 4974–4990. [Google Scholar] [CrossRef]
- The H.E.S.S. Collaboration. Calibration of cameras of the H.E.S.S. detector. Astropart. Phys. 2004, 22, 109–125. [Google Scholar] [CrossRef]
- The MAGIC Collaboration. The major upgrade of the MAGIC telescopes, Part II: A performance study using observations of the Crab Nebula. Astropart. Phys. 2016, 72, 76–94. [Google Scholar] [CrossRef]
- The VERITAS Collaboration. The first VERITAS telescope. Astropart. Phys. 2006, 25, 391–401. [Google Scholar] [CrossRef]
- Andrew J. Smith for the HAWC Collaboration. HAWC: A next generation all-sky gamma-ray telescope. J. Phys. Conf. Ser. 2007, 60, 131–134. [Google Scholar] [CrossRef]
- Andrew J. Smith for the HAWC Collaboration. HAWC: Design, Operation, Reconstruction and Analysis. arXiv 2015, arXiv:1508.05826. [Google Scholar]
- Dingus, B.L. HAWC (High Altitude Water Cherenkov) Observatory for Surveying the TeV Sky. In AIP Conference Proceedings; AIP: College Park, MD, USA, 2007. [Google Scholar] [CrossRef]
- The HAWC Collaboration. The HAWC Gamma-Ray Observatory: Design, Calibration, and Operation. arXiv 2013, arXiv:1310.0074v1. [Google Scholar]
- Wakely, S.P.; Horan, D. TeVCat: An online catalog for Very High Energy Gamma-Ray Astronomy. Proc. ICRC 2008 2008, 3, 1341–1344. [Google Scholar]
- The H.E.S.S. Collaboration. The H.E.S.S. Galactic plane survey. Astron. Astrophys. 2018, 612, A1. [Google Scholar] [CrossRef]
- The HAWC Collaboration. The 2HWC HAWC Observatory Gamma-Ray Catalog. Astrophys. J. 2017, 843, 40. [Google Scholar] [CrossRef]
- Coronado-Blázquez, J.; Sánchez-Conde, M.A.; Mauro, M.D.; Aguirre-Santaella, A.; Ciucă, I.; Domínguez, A.; Kawata, D.; Mirabal, N. Spectral and spatial analysis of the dark matter subhalo candidates among Fermi Large Area Telescope unidentified sources. J. Cosmol. Astropart. Phys. 2019, 2019, 45. [Google Scholar] [CrossRef]
- Colafrancesco, S.; Profumo, S.; Ullio, P. Multi-frequency analysis of neutralino dark matter annihilations in the Coma cluster. Astron. Astrophys. 2006, 455, 21–43. [Google Scholar] [CrossRef]
- Colafrancesco, S.; Profumo, S.; Ullio, P. Detecting dark matter WIMPs in the Draco dwarf: A multiwavelength perspective. Phys. Rev. D 2007, 75. [Google Scholar] [CrossRef]
- Marchegiani, P.; Colafrancesco, S.; Khanye, N.F. The role of dark matter annihilation in the radio emission of the galaxy cluster A520. Mon. Not. R. Astron. Soc. 2018, 483, 2795–2800. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; de la Cruz-Dombriz, A.; Gammaldi, V.; Mendez-Isla, M. SKA-Phase 1 sensitivity for synchrotron radio emission from multi-TeV Dark Matter candidates. arXiv 2019, arXiv:1905.11154v1. [Google Scholar]
- The Fermi-LAT, HAWC and VERITAS Collaborations. VERITAS and Fermi-LAT Observations of TeV Gamma-Ray Sources Discovered by HAWC in the 2HWC Catalog. Astrophys. J. 2018, 866, 24. [Google Scholar] [CrossRef]
- The Fermi-LAT Collaboration; Atwood, W.B. The Large Area Telescope on the Fermi Gamma-ray Space Telescope Mission. Astrophys. J. 2009. [Google Scholar] [CrossRef]
- Nahee Park for the VERITAS Collaboration. Performance of the VERITAS experiment. arXiv 2015, arXiv:1508.07070v2. [Google Scholar]
- Gammaldi, V. Multimessenger Multi-TeV Dark Matter. Front. Astron. Space Sci. 2019, 6. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Dobado, A.; Maroto, A.L. Brane-World Dark Matter. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef] [PubMed]
- Cembranos, J.A.R.; de la Cruz-Dombriz, A.; Gammaldi, V.; Maroto, A.L. Detection of branon dark matter with gamma ray telescopes. Phys. Rev. D 2012, 85. [Google Scholar] [CrossRef]
- Steigman, G.; Dasgupta, B.; Beacom, J.F. Precise Relic WIMP Abundance and its Impact on Searches for Dark Matter Annihilation. Phys. Rev. D 2012. [Google Scholar] [CrossRef]
- The Fermi-LAT Collaboration. Searching for Dark Matter Annihilation from Milky Way Dwarf Spheroidal Galaxies with Six Years of Fermi-LAT Data. Phys. Rev. Lett. 2015. [Google Scholar] [CrossRef]
- Cirelli, M.; Corcella, G.; Hektor, A.; Hütsi, G.; Kadastik, M.; Panci, P.; Raidal, M.; Sala, F.; Strumia, A. PPPC 4 DM ID: A Poor Particle Physicist Cookbook for Dark Matter Indirect Detection. J. Cosmol. Astropart. Phys. 2010. [Google Scholar] [CrossRef]
- The Fermi-LAT Collaboration. Fermi-LAT Observations of the Diffuse Gamma-Ray Emission: Implications for Cosmic Rays and the Interstellar Medium. Astrophys. J. 2012. [Google Scholar] [CrossRef]
- The HAWC Collaboration. Observation of the Crab Nebula with the HAWC Gamma-Ray Observatory. Astrophys. J. 2017, 843, 39. [Google Scholar] [CrossRef]
- The Fermi-LAT Collaboration. Searching for Dark Matter Annihilation in Recently Discovered Milky Way Satellites with Fermi-Lat. Astrophys. J. 2017, 834, 110. [Google Scholar] [CrossRef]
- The Fermi-LAT Collaboration. Limits on dark matter annihilation signals from the Fermi LAT 4-year measurement of the isotropic gamma-ray background. J. Cosmol. Astropart. Phys. 2015, 2015, 8. [Google Scholar] [CrossRef]
- Lefranc, V.; Moulin, E.; for the H. E. S. S. Collaboration. Dark matter search in the inner Galactic halo with H.E.S.S. I and H.E.S.S. II. arXiv 2015, arXiv:1509.04123v2. [Google Scholar]
- Sánchez-Conde, M.A.; Prada, F. The flattening of the concentration-mass relation towards low halo masses and its implications for the annihilation signal boost. Mon. Not. R. Astron. Soc. 2014, 442, 2271–2277. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Ogiya, G.; Hahn, O.; Burkert, A. Disruption of dark matter substructure: Fact or fiction? Mon. Not. R. Astron. Soc. 2017, 474, 3043–3066. [Google Scholar] [CrossRef]
- Garrison-Kimmel, S.; Wetzel, A.; Bullock, J.S.; Hopkins, P.F.; Boylan-Kolchin, M.; Faucher-Giguère, C.A.; Kereš, D.; Quataert, E.; Sanderson, R.E.; Graus, A.S.; et al. Not so lumpy after all: Modelling the depletion of dark matter subhaloes by Milky Way-like galaxies. Mon. Not. R. Astron. Soc. 2017, 471, 1709–1727. [Google Scholar] [CrossRef]
- Errani, R.; Peñarrubia, J. Can tides disrupt cold dark matter subhaloes? arXiv 2019, arXiv:1906.01642v1. [Google Scholar] [CrossRef]
- Kelley, T.; Bullock, J.S.; Garrison-Kimmel, S.; Boylan-Kolchin, M.; Pawlowski, M.S.; Graus, A.S. Phat ELVIS: The inevitable effect of the Milky Way’s disc on its dark matter subhaloes. Mon. Not. R. Astron. Soc. 2019, 487, 4409–4423. [Google Scholar] [CrossRef]
- Sawala, T.; Pihajoki, P.; Johansson, P.H.; Frenk, C.S.; Navarro, J.F.; Oman, K.A.; White, S.D.M. Shaken and stirred: The Milky Way’s dark substructures. Mon. Not. R. Astron. Soc. 2017, 467, 4383–4400. [Google Scholar] [CrossRef]
- The Cherenkov Telescope Array Consortium. Science with the Cherenkov Telescope Array. arXiv 2017, arXiv:1709.07997. [Google Scholar]
| 1. | |
| 2. | In fact, HAWC applies a zenith cut of , which for a daily exposure translates in 8.4sr, corresponding exactly to 66.85% of the sky. |
| 3. | |
| 4. | |
| 5. | This is so because, by default, this quantity is computed for a source spectrum with a power law index , while the DM is better parametrized by a “Power Law with SuperExponential Cutoff” [23], where the index and cutoff energy vary over the annihilation channel and WIMP mass. |
| 6. | This sensitivity is computed for the Crab, which is located at DEC, while our source is at instead. Fortunately, the HAWC sensitivity for both locations is expected to be very similar [34]. |
| 7. | We note that, should we have had more than one unID, we would have computed a mean value after averaging the corresponding differential sensitivities for each source’s declination. |
| 8. | The spectral index is reported to have an uncertainty . We checked that this uncertainty translates into a factor ∼4 uncertainty in at most (factor 2 when compared to the benchmark ). |
| 9. | The J-factor of our brightest subhalo is comparable to the one typically quoted for dwarf spheroidal satellite galaxies (see e.g., [63]), which are expected to be well above the extragalactic isotropic DM-induced gamma ray background. On the other hand, the value of the DM-induced Galactic diffuse emission is comparable to the isotropic contribution at high latitudes [64], and therefore also negligible compared to the brightest subhalo J-factor. Finally, the boost due to Galactic unresolved substructure contributing to the diffuse emission in the line of sight of this unID is expected to be at the level of a few percent and, thus, not relevant here. The boost due to substructures is only particularly important when integrating the subhalo signal for the whole host halo; see e.g., the discussions and results in [36]. |
| 10. | Namely the lack of both the HAWC IRFs and a Galactic diffuse TeV emission model. |
| 11. | We note that tidal stripping is implicitly included in our simulations. Yet, we note that the mentioned works claim that the disruption of a large fraction of low-mass subhalos in simulations may be artificial and numerical in origin—if this was indeed the case, the distribution of J-factors of the entire subhalo population would surely reach larger values, as we would expect more and closer-to-Earth subhalos. Therefore, our results are conservative, as the DM limits would become even more stringent for resilient subhalos. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronado-Blázquez, J.; Sánchez-Conde, M.A. Constraints to Dark Matter Annihilation from High-Latitude HAWC Unidentified Sources. Galaxies 2020, 8, 5. https://doi.org/10.3390/galaxies8010005
Coronado-Blázquez J, Sánchez-Conde MA. Constraints to Dark Matter Annihilation from High-Latitude HAWC Unidentified Sources. Galaxies. 2020; 8(1):5. https://doi.org/10.3390/galaxies8010005
Chicago/Turabian StyleCoronado-Blázquez, Javier, and Miguel A. Sánchez-Conde. 2020. "Constraints to Dark Matter Annihilation from High-Latitude HAWC Unidentified Sources" Galaxies 8, no. 1: 5. https://doi.org/10.3390/galaxies8010005
APA StyleCoronado-Blázquez, J., & Sánchez-Conde, M. A. (2020). Constraints to Dark Matter Annihilation from High-Latitude HAWC Unidentified Sources. Galaxies, 8(1), 5. https://doi.org/10.3390/galaxies8010005





