Synthesizing Observations and Theory to Understand Galactic Magnetic Fields: Progress and Challenges
Abstract
1. Introduction
1.1. Radio Observations
1.2. Galactic Dynamo Theory and Simulations
1.3. Outline
2. Definitions of Magnetic Field Components
2.1. Observations
2.2. Theory
3. Geometry of the Large-Scale Field
3.1. Sign of the Field
3.2. Parity of the Field
3.3. Reversals of the Large-Scale Field
3.4. Helicity of the Field
3.5. Boundary Conditions in Mean-Field Models
4. Strength of the Magnetic Field
4.1. Total Field Strength
4.2. Ordered Field Strength
4.3. Regular Field Strength
4.4. Mean-Field Strength from Dynamo Models
5. Seed Fields and Small-Scale Fields in Mean-Field Dynamos
5.1. Seed Fields
5.2. Small-Scale Magnetic Fields
6. Magnetic Pitch Angle
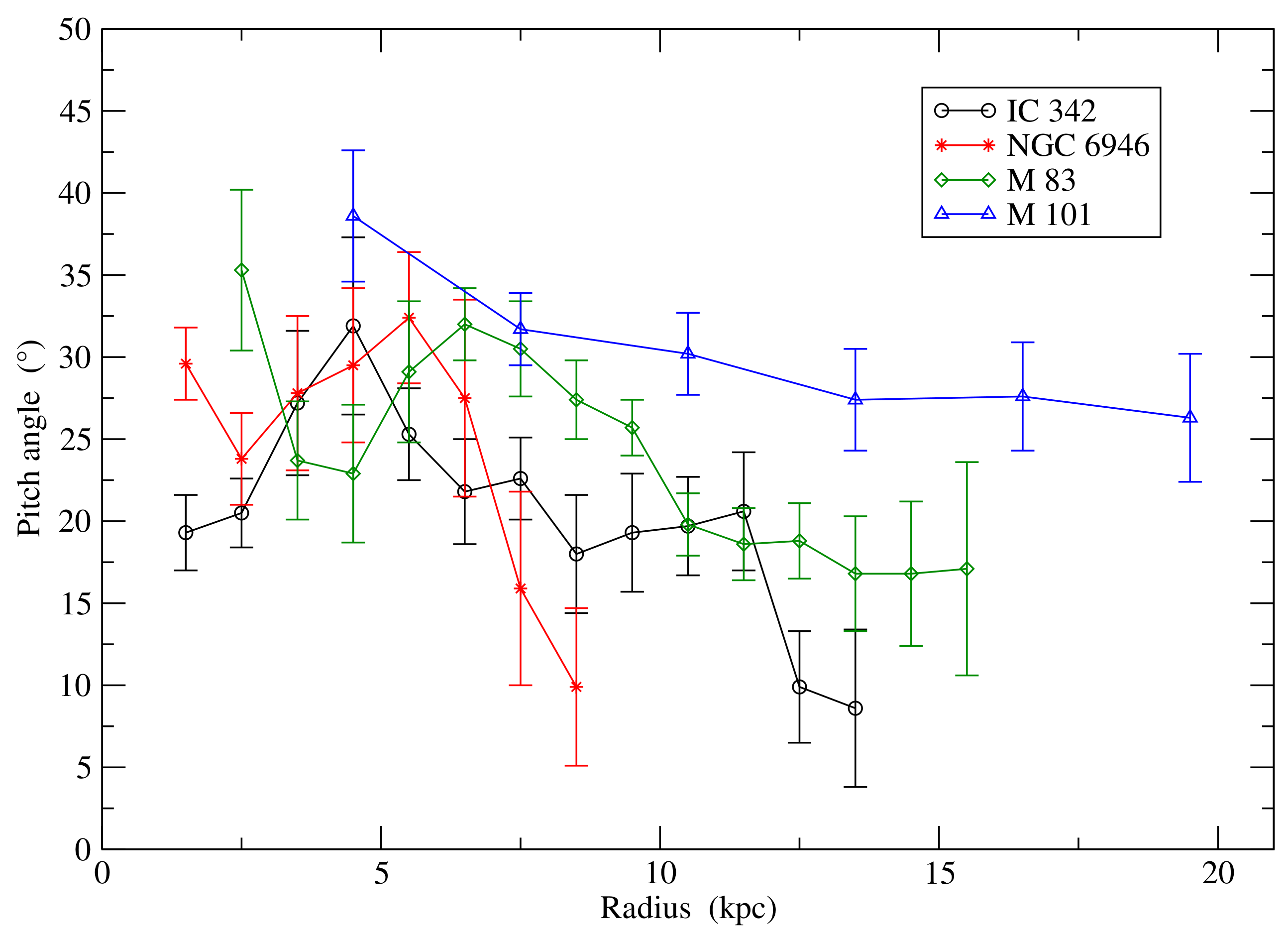
6.1. Observations
6.2. Magnetic Pitch Angle from Dynamo Models
7. Statistical Correlations
8. Halo Magnetic Fields
8.1. Observations
8.2. Dynamo Models
9. Non-Axisymmetric Large-Scale Fields
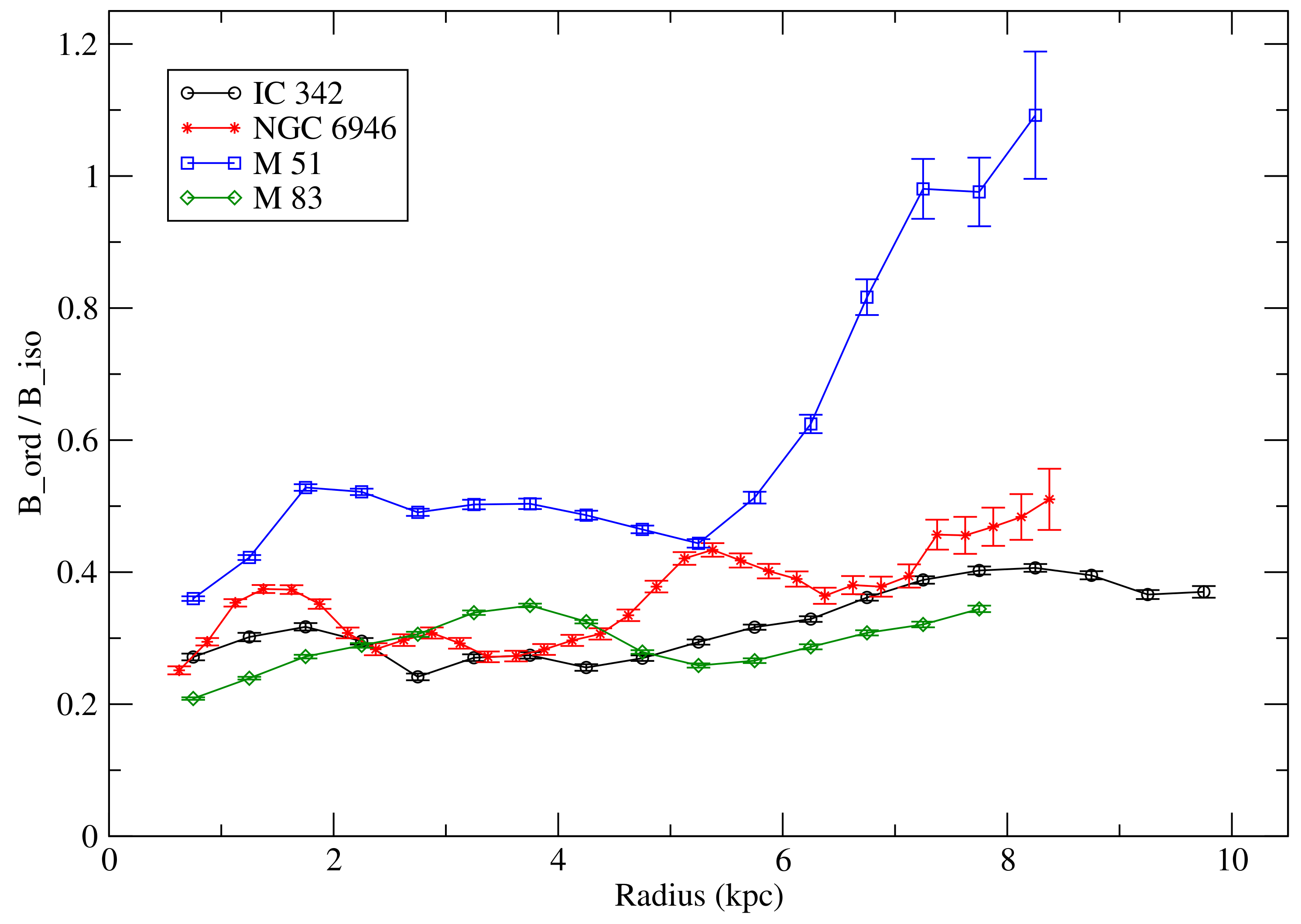
9.1. Magnetic Spiral Arms
9.2. Drivers of Non-Axisymmetry
9.3. Multiplicity of Magnetic Arms in Dynamo Models
9.4. Pitch Angles and Radial Extents of Magnetic Arm Structures in Dynamo Models
9.5. Localization of Magnetic Arms vis-à-vis Spiral Arms in Dynamo Models
9.6. Constraints on Non-Axisymmetric Dynamo Models Using Non-Magnetic Galaxy Data
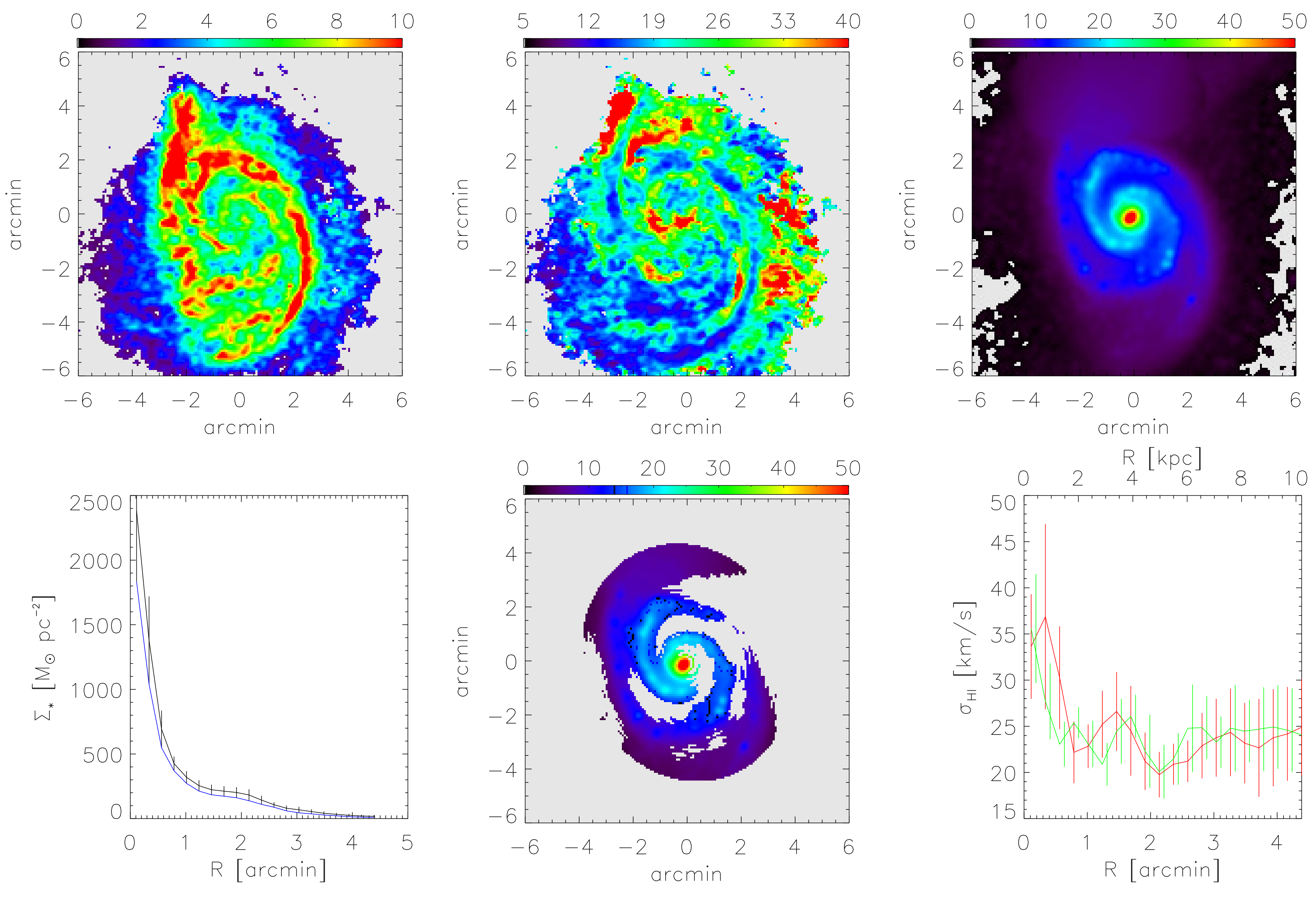
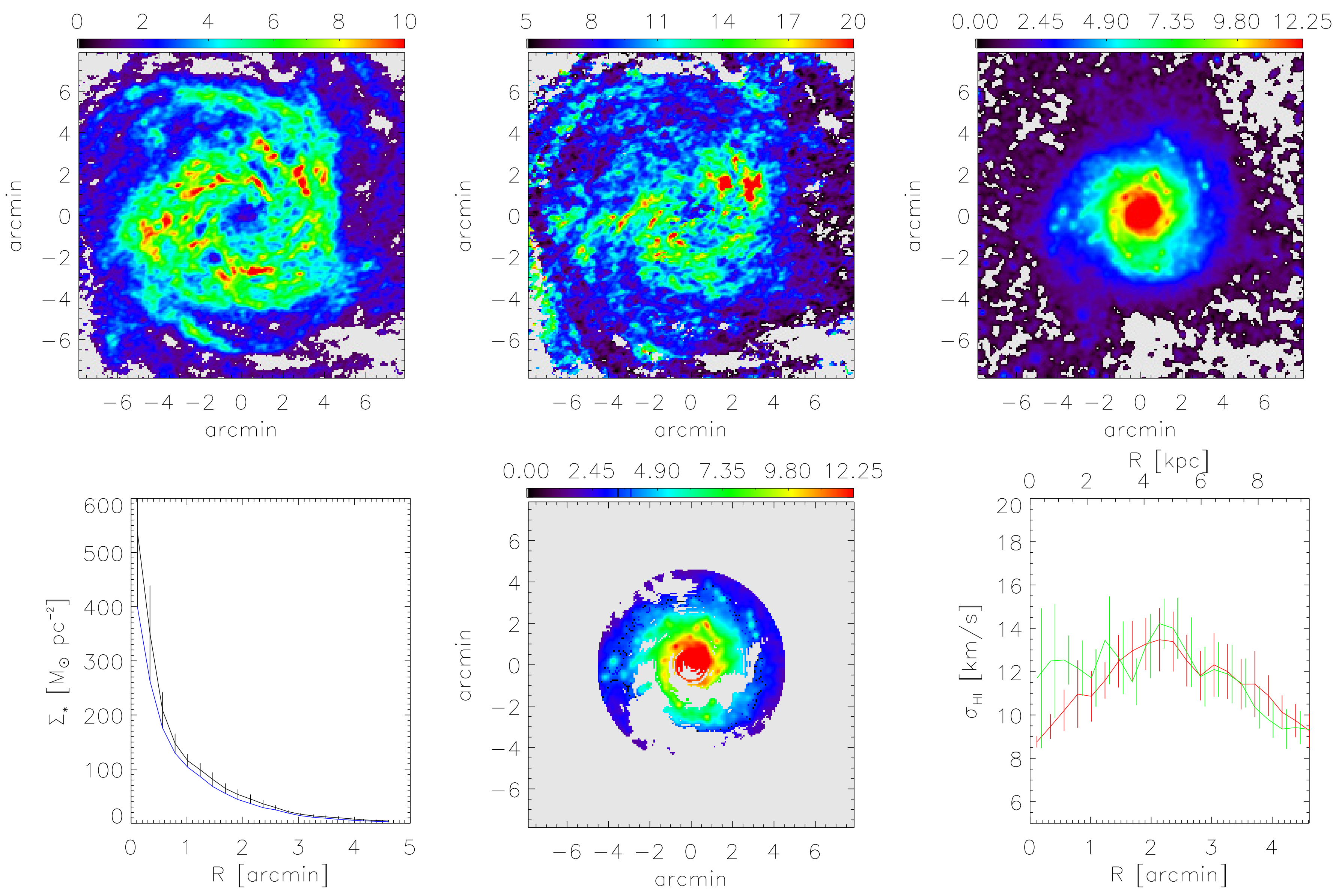
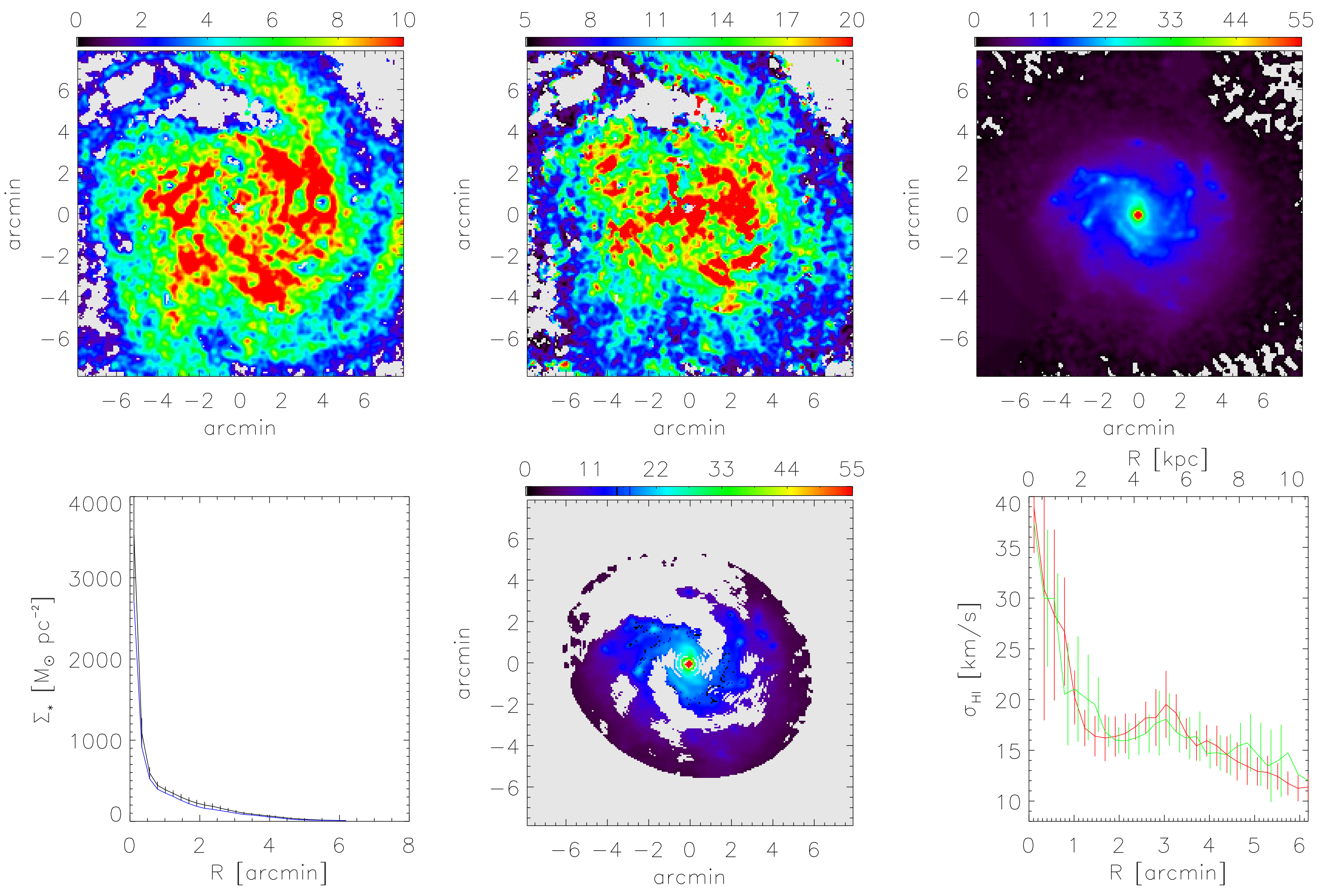
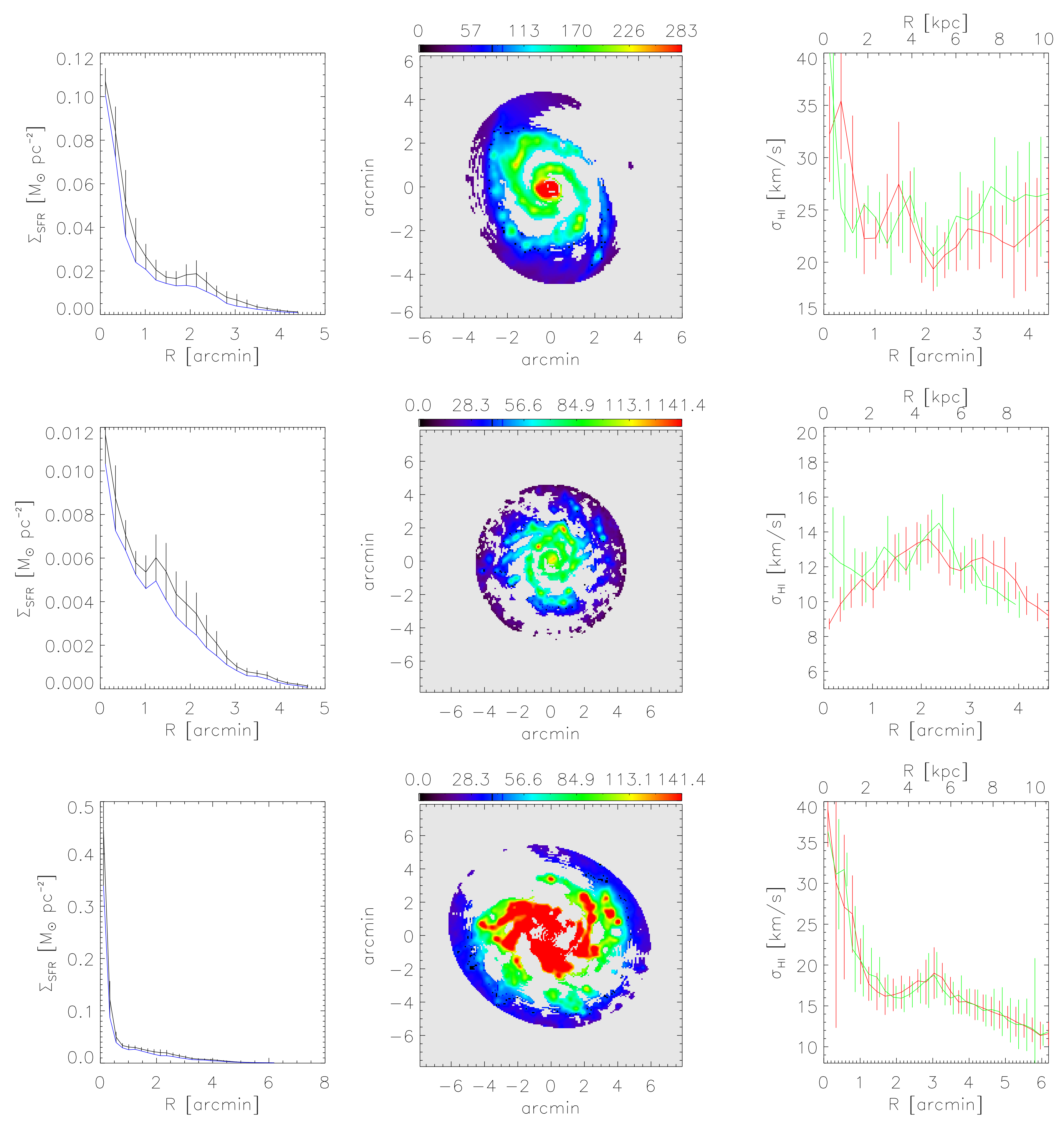
9.6.1. H i Data Products
- (i)
- A Gaussian kernel was used to smooth the cube to a spatial resolution of 13.5′′ × 13.5′′.
- (ii)
- The smoothed cube was spatially re-gridded to have pixels of size 4.5′′ × 4.5′′.
- (iii)
- The mean, , and standard deviation, , of the noise in a line-free channel of the smoothed, re-gridded cube was measured.
- (iv)
- All line profiles in the RA-Dec plane of this cube were fit with a Gaussian.
- (v)
- Fitted line profiles with less than 20% of their flux above a level of were discarded.
- (vi)
- The fitted Gaussian parameters of the remaining profiles were used to generate the H i maps.
9.6.2. Stellar Surface Density Maps
9.6.3. Arm/Inter-Arm H i Velocity Dispersions
9.6.4. Radial Variation of the Velocity Dispersion
9.6.5. Preliminary Theoretical Interpretation
9.7. Overall Level of Correspondence with Mean-Field Dynamo Models
10. Conclusions and Outlook
- making averaging in models consistent with averaging in observations or simulations to enable direct comparison;
- modeling parameters of interstellar turbulence as functions of observables using analytical theory and turbulent ISM/galaxy simulations [236], to better constrain dynamo models;
- including better models of small-scale magnetic field from the fluctuation dynamo, turbulent tangling, and helicity conservation, to explain observed isotropic and anisotropic turbulent fields;
- accounting self-consistently for all the effects of this small-scale magnetic field on the mean electromotive force to obtain more realistic dynamo solutions;
- extending mean-field models to include magnetic feedback onto the mean velocity field to better understand phenomena like magnetized outflows and spiral arms;
- quantifying the dependence of the dynamo on the ionization fraction by including partial ionization and ambipolar diffusion to enable more direct comparison with observation;
- including cosmic rays in dynamo models both for their possible role in magnetic field evolution, and to better constrain their properties to enable improved observational estimates of magnetic field properties;
- using global galaxy and local ISM DNS as a complementary laboratory both for testing the theory and synthesizing observations.
- resolving the structure of tangled/twisted/bent fields and the mysterious anisotropic turbulent fields;
- distinguishing regular from anisotropic turbulent fields with the help of high-quality data;
- measuring thermal gas densities from extinction-corrected H emission data (or other emission lines), to compute the strength of regular fields from data;
- identifying high-order azimuthal modes of regular fields in galaxy discs;
- searching for field reversals in galaxy discs and halos;
- measuring field parities in galaxy discs and halos;
- measuring velocity dispersions in arm and inter-arm regions from H i emission data;
- measuring scale heights of ionized gas discs from H emission data;
- studying the evolution of large-scale regular fields in galaxies at various redshifts.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MHD | magnetohydrodynamics |
| DNS | direct numerical simulation |
| ISM | interstellar medium |
| SN | supernova |
| CR | cosmic ray |
| SFR | star-formation rate |
| RM | Faraday rotation measures |
Appendix A. Rotation Measures in M 83
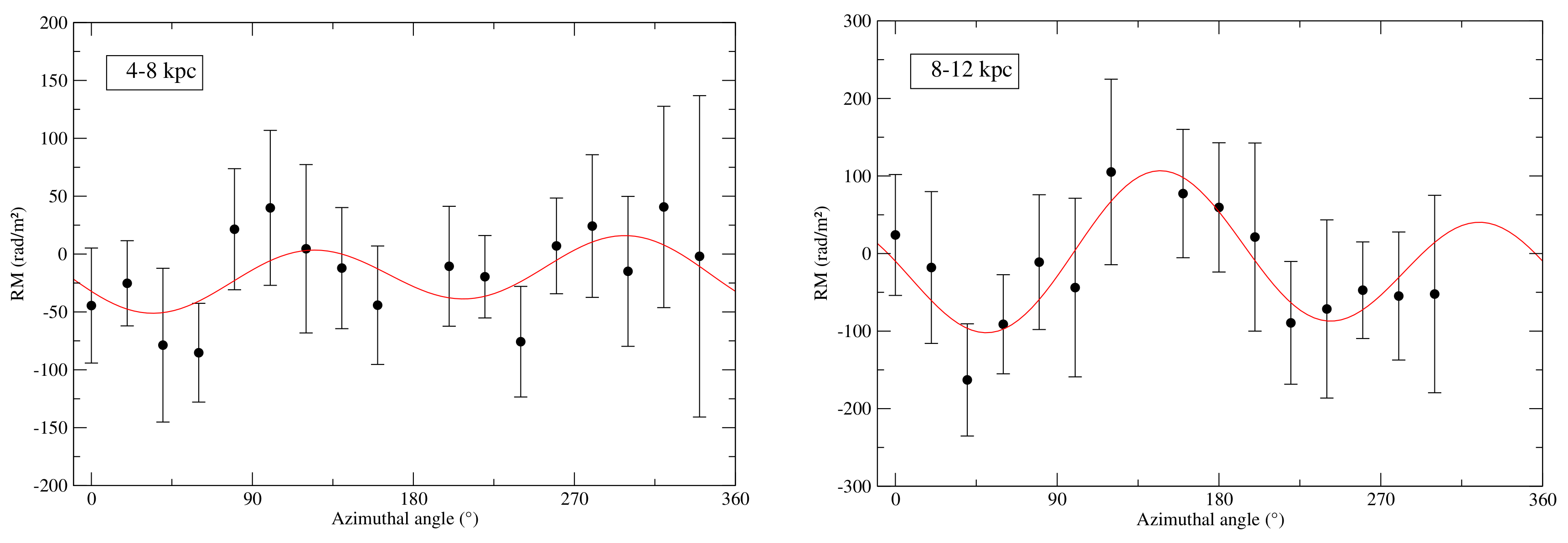
| Radial Range | RMfg [kpc] | RM0 [rad/m2] | p0 [°] | RM1 [rad/m2] | p1 [°] | Reduced |
|---|---|---|---|---|---|---|
| 4–8 | 0.46 | |||||
| 8–12 | 0.26 |
References
- Chamandy, L.; Shukurov, A.; Subramanian, K.; Stoker, K. Nonlinear galactic dynamos: A toolbox. Mon. Not. R. Astron. Soc. 2014, 443, 1867–1880. [Google Scholar] [CrossRef]
- Brown, R.H.; Hazard, C. Radio emission from the Andromeda nebula. Mon. Not. R. Astron. Soc. 1951, 111, 357. [Google Scholar] [CrossRef][Green Version]
- Westerhout, G.; Seeger, C.L.; Brouw, W.N.; Tinbergen, J. Polarization of the galactic 75-cm radiation. Bull. Astron. Inst. Neth. 1962, 16, 187. [Google Scholar]
- Wielebinski, R.; Shakeshaft, J.R. Faraday Rotation of Polarized Galactic Radio Emission. Nature 1962, 195, 982–983. [Google Scholar] [CrossRef]
- Mathewson, D.S.; van der Kruit, P.C.; Brouw, W.N. A High Resolution Radio Continuum Survey of M51 and NGC 5195 at 1415 MHz. Astron. Astrophys. 1972, 17, 468. [Google Scholar]
- Beck, R.; Berkhuijsen, E.M.; Wielebinski, R. Detection of polarised radio emission of M31. Astron. Astrophys. 1978, 68, L27–L29. [Google Scholar]
- Beck, R. The magnetic field in M31. Astron. Astrophys. 1982, 106, 121–132. [Google Scholar]
- Fletcher, A.; Beck, R.; Shukurov, A.; Berkhuijsen, E.M.; Horellou, C. Magnetic fields and spiral arms in the galaxy M51. Mon. Not. R. Astron. Soc. 2011, 412, 2396–2416. [Google Scholar] [CrossRef]
- Burn, B.J. On the depolarization of discrete radio sources by Faraday dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67. [Google Scholar] [CrossRef]
- Brentjens, M.A.; de Bruyn, A.G. Faraday rotation measure synthesis. Astron. Astrophys. 2005, 441, 1217–1228. [Google Scholar] [CrossRef]
- Beck, R.; Wielebinski, R. Magnetic Fields in Galaxies. In Planets, Stars and Stellar Systems. Volume 5: Galactic Structure and Stellar Populations; Oswalt, T.D., Gilmore, G., Eds.; Springer: Basel, Switzerland, 2013; p. 641. [Google Scholar] [CrossRef]
- Van Eck, C.L.; Brown, J.C.; Shukurov, A.; Fletcher, A. Magnetic Fields in a Sample of Nearby Spiral Galaxies. Astrophys. J. 2015, 799, 35. [Google Scholar] [CrossRef]
- Fletcher, A. Magnetic Fields in Nearby Galaxies. In The Dynamic Interstellar Medium: A Celebration of the Canadian Galactic Plane Survey; Kothes, R., Landecker, T.L., Willis, A.G., Eds.; Astronomical Society of the Pacific Conference Series: San Francisco, CA, USA, 2010; Volume 438, p. 197. [Google Scholar]
- Beck, R. Magnetic fields in spiral galaxies. Annu. Rev. Astron. Astrophys. 2016, 24, 4. [Google Scholar] [CrossRef]
- Moffatt, H.K. Magnetic Field Generation in Electrically Conducting Fluids; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Krause, F.; Rädler, K.H. Mean-Field Magnetohydrodynamics and Dynamo Theory; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2005, 417, 1–209. [Google Scholar] [CrossRef]
- Parker, E.N. Hydromagnetic Dynamo Models. Astrophys. J. 1955, 122, 293. [Google Scholar] [CrossRef]
- Ruzmaikin, A.A.; Shukurov, A.M.; Sokoloff, D.D. Magnetic Fields of Galaxies; Kluwer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Brandenburg, A.; Gressel, O.; Käpylä, P.J.; Kleeorin, N.; Mantere, M.J.; Rogachevskii, I. New Scaling for the Alpha Effect in Slowly Rotating Turbulence. Astrophys. J. 2013, 762, 127. [Google Scholar] [CrossRef][Green Version]
- Chamandy, L. An analytical dynamo solution for large-scale magnetic fields of galaxies. Mon. Not. R. Astron. Soc. 2016, 462, 4402–4415. [Google Scholar] [CrossRef]
- Parker, E.N. Fast Dynamos, Cosmic Rays, and the Galactic Magnetic Field. Astrophys. J. 1992, 401, 137. [Google Scholar] [CrossRef]
- Hanasz, M.; Lesch, H. Magnetic buoyancy and the galactic dynamo. Astron. Astrophys. 1993, 278, 561–568. [Google Scholar]
- Hanasz, M.; Lesch, H. The galactic dynamo effect due to Parker-shearing instability of magnetic flux tubes. III. The fast dynamo model. Astron. Astrophys. 1998, 332, 77–87. [Google Scholar]
- Moss, D.; Shukurov, A.; Sokoloff, D. Galactic dynamos driven by magnetic buoyancy. Astron. Astrophys. 1999, 343, 120–131. [Google Scholar]
- Kulsrud, R.M. The galactic dynamo and superbubbles. J. Plasma Phys. 2015, 81, 395810603. [Google Scholar] [CrossRef][Green Version]
- Hanasz, M.; Kowal, G.; Otmianowska-Mazur, K.; Lesch, H. Amplification of Galactic Magnetic Fields by the Cosmic-Ray-driven Dynamo. Astrophys. J. Lett. 2004, 605, L33–L36. [Google Scholar] [CrossRef]
- Hanasz, M.; Wóltański, D.; Kowalik, K. Global Galactic Dynamo Driven by Cosmic Rays and Exploding Magnetized Stars. Astrophys. J. Lett. 2009, 706, L155–L159. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Sarson, G.R.; Shukurov, A.; Bushby, P.J.; Fletcher, A. The Parker Instability in Disk Galaxies. Astrophys. J. 2016, 816, 2. [Google Scholar] [CrossRef]
- Pouquet, A.; Frisch, U.; Leorat, J. Strong MHD helical turbulence and the nonlinear dynamo effect. J. Fluid Mech. 1976, 77, 321–354. [Google Scholar] [CrossRef]
- Kleeorin, N.; Ruzmaikin, A.A. Dynamics of the average turbulent helicity in a magnetic field. Magnetohydrodynamics 1982, 18, 116. [Google Scholar]
- Blackman, E.G.; Field, G.B. New Dynamical Mean-Field Dynamo Theory and Closure Approach. Phys. Rev. Lett. 2002, 89, 265007. [Google Scholar] [CrossRef]
- Blackman, E.G.; Brandenburg, A. Dynamic Nonlinearity in Large-Scale Dynamos with Shear. Astrophys. J. 2002, 579, 359–373. [Google Scholar] [CrossRef]
- Subramanian, K.; Brandenburg, A. Magnetic Helicity Density and Its Flux in Weakly Inhomogeneous Turbulence. Astrophys. J. Lett. 2006, 648, L71–L74. [Google Scholar] [CrossRef]
- Kleeorin, N.; Rogachevskii, I. Magnetic helicity tensor for an anisotropic turbulence. Phys. Rev. E 1999, 59, 6724–6729. [Google Scholar] [CrossRef]
- Blackman, E.G.; Field, G.B. Constraints on the Magnitude of α in Dynamo Theory. Astrophys. J. 2000, 534, 984–988. [Google Scholar] [CrossRef]
- Vishniac, E.T.; Cho, J. Magnetic Helicity Conservation and Astrophysical Dynamos. Astrophys. J. 2001, 550, 752–760. [Google Scholar] [CrossRef]
- Field, G.B.; Blackman, E.G. Dynamical Quenching of the α2 Dynamo. Astrophys. J. 2002, 572, 685–692. [Google Scholar] [CrossRef]
- Beck, R.; Brandenburg, A.; Moss, D.; Shukurov, A.; Sokoloff, D. Galactic Magnetism: Recent Developments and Perspectives. Annu. Rev. Astron. Astrophys. 1996, 34, 155–206. [Google Scholar] [CrossRef]
- Shukurov, A. Mesoscale Magnetic Structures in Spiral Galaxies. In Cosmic Magnetic Fields; Wielebinski, R., Beck, R., Eds.; Lecture Notes in Physics; Springer: Berlin, Germany, 2005; Volume 664, p. 113. [Google Scholar] [CrossRef]
- Shukurov, A. Galactic dynamos. In Mathematical Aspects of Natural Dynamos; Dormy, E., Soward, A.M., Eds.; CRC Press: Boca Raton, FL, USA, 2007; pp. 313–359. [Google Scholar]
- Kulsrud, R.M.; Zweibel, E.G. On the origin of cosmic magnetic fields. Rep. Prog. Phys. 2008, 71, 046901. [Google Scholar] [CrossRef]
- Schaye, J. Star Formation Thresholds and Galaxy Edges: Why and Where. Astrophys. J. 2004, 609, 667–682. [Google Scholar] [CrossRef]
- Brandenburg, A. Simulations of Galactic Dynamos. In Magnetic Fields in Diffuse Media; Lazarian, A., de Gouveia Dal Pino, E.M., Melioli, C., Eds.; Springer: Basel, Switzerland, 2015; Volume 407, p. 529. [Google Scholar] [CrossRef]
- Moss, D.; Sokoloff, D. Magnetic Fields Around Galactic Discs. Galaxies 2019, 7, 36. [Google Scholar] [CrossRef]
- Subramanian, K. From Primordial Seed Magnetic Fields to the Galactic Dynamo. Galaxies 2019, 7, 47. [Google Scholar] [CrossRef]
- Jaffe, T.R. Practical Modeling of Large-Scale Galactic Magnetic Fields: Status and Prospects. Galaxies 2019, 7, 52. [Google Scholar] [CrossRef]
- Zhou, H.; Blackman, E.G.; Chamandy, L. Derivation and precision of mean field electrodynamics with mesoscale fluctuations. J. Plasma Phys. 2018, 84, 735840302. [Google Scholar] [CrossRef]
- Shapovalov, D.S.; Vishniac, E.T. Simulations of Turbulent Dynamos Driven by the Magnetic Helicity Flux. Astrophys. J. 2011, 738, 66. [Google Scholar] [CrossRef]
- Gent, F.A.; Shukurov, A.; Sarson, G.R.; Fletcher, A.; Mantere, M.J. The supernova-regulated ISM—II. The mean magnetic field. Mon. Not. R. Astron. Soc. 2013, 430, L40–L44. [Google Scholar] [CrossRef]
- Germano, M. Turbulence—The filtering approach. J. Fluid Mech. 1992, 238, 325–336. [Google Scholar] [CrossRef]
- Krause, F.; Beck, R. Symmetry and direction of seed magnetic fields in galaxies. Astron. Astrophys. 1998, 335, 789–796. [Google Scholar]
- Tabatabaei, F.S.; Krause, M.; Fletcher, A.; Beck, R. High-resolution radio continuum survey of M 33. III. Magnetic fields. Astron. Astrophys. 2008, 490, 1005–1017. [Google Scholar] [CrossRef]
- Heesen, V.; Krause, M.; Beck, R.; Dettmar, R.J. Cosmic rays and the magnetic field in the nearby starburst galaxy NGC 253. II. The magnetic field structure. Astron. Astrophys. 2009, 506, 1123–1135. [Google Scholar] [CrossRef]
- Beck, R. Magnetism in the spiral galaxy NGC 6946: magnetic arms, depolarization rings, dynamo modes, and helical fields. Astron. Astrophys. 2007, 470, 539–556. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Horellou, C.; Krause, M.; Neininger, N.; Poezd, A.D.; Shukurov, A.; Sokoloff, D.D. Magnetic fields in the disk and halo of M51. Astron. Astrophys. 1997, 318, 700–720. [Google Scholar]
- Gießübel, R.; Beck, R. The magnetic field structure of the central region in M 31. Astron. Astrophys. 2014, 571, A61. [Google Scholar] [CrossRef]
- Han, J.L.; Beck, R.; Ehle, M.; Haynes, R.F.; Wielebinski, R. Magnetic fields in the spiral galaxy NGC 2997. Astron. Astrophys. 1999, 348, 405–417. [Google Scholar]
- Beck, R. Magnetic fields in the nearby spiral galaxy IC 342: A multi-frequency radio polarization study. Astron. Astrophys. 2015, 578, A93. [Google Scholar] [CrossRef]
- Heald, G.; de Blok, W.J.G.; Lucero, D.; Carignan, C.; Jarrett, T.; Elson, E.; Oozeer, N.; Randriamampandry, T.H.; van Zee, L. Neutral hydrogen and magnetic fields in M83 observed with the SKA Pathfinder KAT-7. Mon. Not. R. Astron. Soc. 2016, 462, 1238–1255. [Google Scholar] [CrossRef]
- Krause, M. Large-scale magnetic field in spiral galaxies. Mem. Soc. Astron. Ital. 2007, 78, 314. [Google Scholar]
- Stein, Y.; Dettmar, R.J.; Weżgowiec, M.; Irwin, J.; Beck, R.; Wiegert, T.; Krause, M.; Li, J.T.; Heesen, V.; Miskolczi, A.; et al. CHANG-ES. XIX. Galaxy NGC 4013: A diffusion-dominated radio halo with plane-parallel disk and vertical halo magnetic fields. Astron. Astrophys. 2019, 632, A13. [Google Scholar] [CrossRef]
- Chyży, K.T. Magnetic fields and gas in the cluster-influenced spiral galaxy NGC 4254. II. Structures of magnetic fields. Astron. Astrophys. 2008, 482, 755–769. [Google Scholar] [CrossRef]
- Soida, M.; Beck, R.; Urbanik, M.; Braine, J. Magnetic fields in the absence of spiral density waves—NGC 4414. Astron. Astrophys. 2002, 394, 47–57. [Google Scholar] [CrossRef]
- Chyży, K.T.; Beck, R.; Kohle, S.; Klein, U.; Urbanik, M. Regular magnetic fields in the dwarf irregular galaxy NGC 4449. Astron. Astrophys. 2000, 355, 128–137. [Google Scholar]
- Chyży, K.T.; Buta, R.J. Discovery of a Strong Spiral Magnetic Field Crossing the Inner Pseudoring of NGC 4736. Astrophys. J. Lett. 2008, 677, L17–L20. [Google Scholar] [CrossRef]
- Soida, M.; Krause, M.; Dettmar, R.J.; Urbanik, M. The large scale magnetic field structure of the spiral galaxy NGC 5775. Astron. Astrophys. 2011, 531, A127. [Google Scholar] [CrossRef]
- Stein, Y.; Dettmar, R.J.; Irwin, J.; Beck, R.; Weżgowiec, M.; Miskolczi, A.; Krause, M.; Heesen, V.; Wiegert, T.; Heald, G.; et al. CHANG-ES. XIII. Transport processes and the magnetic fields of NGC 4666: Indication of a reversing disk magnetic field. Astron. Astrophys. 2019, 623, A33. [Google Scholar] [CrossRef]
- Brown, J.C.; Haverkorn, M.; Gaensler, B.M.; Taylor, A.R.; Bizunok, N.S.; McClure-Griffiths, N.M.; Dickey, J.M.; Green, A.J. Rotation Measures of Extragalactic Sources behind the Southern Galactic Plane: New Insights into the Large-Scale Magnetic Field of the Inner Milky Way. Astrophys. J. 2007, 663, 258–266. [Google Scholar] [CrossRef]
- Sokoloff, D.; Shukurov, A. Regular magnetic fields in coronae of spiral galaxies. Nature 1990, 347, 51–53. [Google Scholar] [CrossRef]
- Moss, D.; Sokoloff, D. The coexistence of odd and even parity magnetic fields in disc galaxies. Astron. Astrophys. 2008, 487, 197–203. [Google Scholar] [CrossRef]
- Moss, D.; Sokoloff, D.; Beck, R.; Krause, M. Galactic winds and the symmetry properties of galactic magnetic fields. Astron. Astrophys. 2010, 512, A61. [Google Scholar] [CrossRef]
- Gressel, O.; Elstner, D.; Ziegler, U. Towards a hybrid dynamo model for the Milky Way. Astron. Astrophys. 2013, 560, A93. [Google Scholar] [CrossRef]
- Poezd, A.; Shukurov, A.; Sokoloff, D. Global Magnetic Patterns in the Milky-Way and the Andromeda Nebula. Mon. Not. R. Astron. Soc. 1993, 264, 285. [Google Scholar] [CrossRef]
- Vasil’Eva, A.; Nikitin, A.; Petrov, A. Stability of contrasting solutions of nonlinear hydromagnetic dynamo equations and magnetic fields reversals in galaxies. Geophys. Astrophys. Fluid Dyn. 1994, 78, 261–279. [Google Scholar] [CrossRef]
- Belyanin, M.P.; Sokoloff, D.D.; Shukurov, A.M. Asymptotic steady-state solutions to the nonlinear hydromagnetic dynamo equations. Russ. J. Math. Phys. 1994, 2, 149. [Google Scholar]
- Moss, D.; Stepanov, R.; Arshakian, T.G.; Beck, R.; Krause, M.; Sokoloff, D. Multiscale magnetic fields in spiral galaxies: evolution and reversals. Astron. Astrophys. 2012, 537, A68. [Google Scholar] [CrossRef]
- Chamandy, L.; Subramanian, K.; Shukurov, A. Galactic spiral patterns and dynamo action—I. A new twist on magnetic arms. Mon. Not. R. Astron. Soc. 2013, 428, 3569–3589. [Google Scholar] [CrossRef]
- Moss, D.; Sokoloff, D. Magnetic field reversals and galactic dynamos. Geophys. Astrophys. Fluid Dyn. 2013, 107, 497–505. [Google Scholar] [CrossRef][Green Version]
- Moss, D.; Beck, R.; Sokoloff, D.; Stepanov, R.; Krause, M.; Arshakian, T.G. The relation between magnetic and material arms in models for spiral galaxies. Astron. Astrophys. 2013, 556, A147. [Google Scholar] [CrossRef]
- Krause, M. Magnetic Fields and Star Formation in Spiral Galaxies. In Magnetic Fields in the Universe II; Revista Mexicana de Astronomia y Astrofisica Conference Series; Instituto de Astronomía: Ciudad de México, Mexico, 2009; Volume 36, pp. 25–29. [Google Scholar]
- Mora, S.C.; Krause, M. Magnetic field structure and halo in NGC 4631. Astron. Astrophys. 2013, 560, A42. [Google Scholar] [CrossRef][Green Version]
- Mora-Partiarroyo, S.C.; Krause, M.; Basu, A.; Beck, R.; Wiegert, T.; Irwin, J.; Henriksen, R.; Stein, Y.; Vargas, C.J.; Heesen, V.; et al. CHANG-ES. XV. Large-scale magnetic field reversals in the radio halo of NGC 4631. Astron. Astrophys. 2019, 632, A11. [Google Scholar] [CrossRef]
- Mao, S.A.; McClure-Griffiths, N.M.; Gaensler, B.M.; Brown, J.C.; van Eck, C.L.; Haverkorn, M.; Kronberg, P.P.; Stil, J.M.; Shukurov, A.; Taylor, A.R. New Constraints on the Galactic Halo Magnetic Field Using Rotation Measures of Extragalactic Sources toward the Outer Galaxy. Astrophys. J. 2012, 755, 21. [Google Scholar] [CrossRef]
- Schnitzeler, D.H.F.M.; Carretti, E.; Wieringa, M.H.; Gaensler, B.M.; Haverkorn, M.; Poppi, S. S-PASS/ATCA: A window on the magnetic universe in the Southern hemisphere. Mon. Not. R. Astron. Soc. 2019, 485, 1293–1309. [Google Scholar] [CrossRef]
- Dobbs, C.L.; Price, D.J.; Pettitt, A.R.; Bate, M.R.; Tricco, T.S. Magnetic field evolution and reversals in spiral galaxies. Mon. Not. R. Astron. Soc. 2016, 461, 4482–4495. [Google Scholar] [CrossRef]
- Pakmor, R.; Guillet, T.; Pfrommer, C.; Gómez, F.A.; Grand, R.J.J.; Marinacci, F.; Simpson, C.M.; Springel, V. Faraday rotation maps of disc galaxies. Mon. Not. R. Astron. Soc. 2018, 481, 4410–4418. [Google Scholar] [CrossRef]
- Kulpa-Dybeł, K.; Otmianowska-Mazur, K.; Kulesza-Żydzik, B.; Hanasz, M.; Kowal, G.; Wóltański, D.; Kowalik, K. Global Simulations of the Magnetic Field Evolution in Barred Galaxies Under the Influence of the Cosmic-ray-driven Dynamo. Astrophys. J. Lett. 2011, 733, L18. [Google Scholar] [CrossRef]
- Machida, M.; Nakamura, K.E.; Kudoh, T.; Akahori, T.; Sofue, Y.; Matsumoto, R. Dynamo Activities Driven by Magnetorotational Instability and the Parker Instability in Galactic Gaseous Disks. Astrophys. J. 2013, 764, 81. [Google Scholar] [CrossRef]
- Sokoloff, D.D.; Bykov, A.A.; Shukurov, A.; Berkhuijsen, E.M.; Beck, R.; Poezd, A.D. Depolarization and Faraday effects in galaxies. Mon. Not. R. Astron. Soc. 1998, 299, 189–206. [Google Scholar] [CrossRef]
- Volegova, A.A.; Stepanov, R.A. Helicity detection of astrophysical magnetic fields from radio emission statistics. Sov. J. Exp. Theor. Phys. Lett. 2010, 90, 637–641. [Google Scholar] [CrossRef]
- Brandenburg, A.; Stepanov, R. Faraday Signature of Magnetic Helicity from Reduced Depolarization. Astrophys. J. 2014, 786, 91. [Google Scholar] [CrossRef]
- Horellou, C.; Fletcher, A. Magnetic field tomography, helical magnetic fields and Faraday depolarization. Mon. Not. R. Astron. Soc. 2014, 441, 2049–2057. [Google Scholar] [CrossRef][Green Version]
- Evirgen, C.C.; Gent, F.A.; Shukurov, A.; Fletcher, A.; Bushby, P. The distribution of mean and fluctuating magnetic fields in the multiphase interstellar medium. Mon. Not. R. Astron. Soc. 2017, 464, L105–L109. [Google Scholar] [CrossRef]
- Kulkarni, S.R.; Heiles, C. The Atomic Component. In Interstellar Processes; Hollenbach, D.J., Thronson, H.A., Jr., Eds.; Springer: Basel, Switzerland, 1987; Volume 134, p. 87. [Google Scholar] [CrossRef]
- Jenkins, E.B. The Fractional Ionization of the Warm Neutral Interstellar Medium. Astrophys. J. 2013, 764, 25. [Google Scholar] [CrossRef][Green Version]
- Blaes, O.M.; Balbus, S.A. Local Shear Instabilities in Weakly Ionized, Weakly Magnetized Disks. Astrophys. J. 1994, 421, 163. [Google Scholar] [CrossRef]
- Brandenburg, A. Ambipolar diffusion in large Prandtl number turbulence. Mon. Not. R. Astron. Soc. 2019, 487, 2673–2684. [Google Scholar] [CrossRef]
- Beck, R.; Krause, M. Revised equipartition and minimum energy formula for magnetic field strength estimates from radio synchrotron observations. Astron. Nachr. 2005, 326, 414–427. [Google Scholar] [CrossRef]
- Seta, A.; Beck, R. Revisiting the Equipartition Assumption in Star-Forming Galaxies. Galaxies 2019, 7, 45. [Google Scholar] [CrossRef]
- Pakmor, R.; Pfrommer, C.; Simpson, C.M.; Springel, V. Galactic Winds Driven by Isotropic and Anisotropic Cosmic-Ray Diffusion in Disk Galaxies. Astrophys. J. Lett. 2016, 824, L30. [Google Scholar] [CrossRef]
- Snodin, A.P.; Shukurov, A.; Sarson, G.R.; Bushby, P.J.; Rodrigues, L.F.S. Global diffusion of cosmic rays in random magnetic fields. Mon. Not. R. Astron. Soc. 2016, 457, 3975–3987. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Snodin, A.P.; Sarson, G.R.; Shukurov, A. Fickian and non-Fickian diffusion of cosmic rays. Mon. Not. R. Astron. Soc. 2019, 487, 975–980. [Google Scholar] [CrossRef]
- Beck, R. Magnetic Fields in Galaxies. In Magnetic Fields in Diffuse Media; Lazarian, A., de Gouveia Dal Pino, E.M., Melioli, C., Eds.; Springer: Basel, Switzerland, 2015; Volume 407, p. 507. [Google Scholar] [CrossRef]
- Hill, A.S.; Benjamin, R.A.; Kowal, G.; Reynolds, R.J.; Haffner, L.M.; Lazarian, A. The Turbulent Warm Ionized Medium: Emission Measure Distribution and MHD Simulations. Astrophys. J. 2008, 686, 363–378. [Google Scholar] [CrossRef]
- Gaensler, B.M.; Haverkorn, M.; Burkhart, B.; Newton-McGee, K.J.; Ekers, R.D.; Lazarian, A.; McClure-Griffiths, N.M.; Robishaw, T.; Dickey, J.M.; Green, A.J. Low-Mach-number turbulence in interstellar gas revealed by radio polarization gradients. Nature 2011, 478, 214–217. [Google Scholar] [CrossRef] [PubMed]
- Iacobelli, M.; Burkhart, B.; Haverkorn, M.; Lazarian, A.; Carretti, E.; Staveley-Smith, L.; Gaensler, B.M.; Bernardi, G.; Kesteven, M.J.; Poppi, S. Galactic interstellar turbulence across the southern sky seen through spatial gradients of the polarization vector. Astron. Astrophys. 2014, 566, A5. [Google Scholar] [CrossRef]
- Federrath, C.; Chabrier, G.; Schober, J.; Banerjee, R.; Klessen, R.S.; Schleicher, D.R.G. Mach Number Dependence of Turbulent Magnetic Field Amplification: Solenoidal versus Compressive Flows. Phys. Rev. Lett. 2011, 107, 114504. [Google Scholar] [CrossRef]
- Kim, C.G.; Ostriker, E.C. Vertical Equilibrium, Energetics, and Star Formation Rates in Magnetized Galactic Disks Regulated by Momentum Feedback from Supernovae. Astrophys. J. 2015, 815, 67. [Google Scholar] [CrossRef]
- Tabatabaei, F.S.; Schinnerer, E.; Krause, M.; Dumas, G.; Meidt, S.; Damas-Segovia, A.; Beck, R.; Murphy, E.J.; Mulcahy, D.D.; Groves, B.; et al. The Radio Spectral Energy Distribution and Star-formation Rate Calibration in Galaxies. Astrophys. J. 2017, 836, 185. [Google Scholar] [CrossRef]
- Fletcher, A.; Berkhuijsen, E.M.; Beck, R.; Shukurov, A. The magnetic field of M31 from multi-wavelength radio polarization observations. Astron. Astrophys. 2004, 414, 53–67. [Google Scholar] [CrossRef]
- Krause, M.; Beck, R.; Hummel, E. The magnetic field structures in two nearby spiral galaxies. II. The bisymmetric spiral magnetic field in M 81. Astron. Astrophys. 1989, 217, 17–30. [Google Scholar]
- Beck, R.; Fletcher, A.; Shukurov, A.; Snodin, A.; Sokoloff, D.D.; Ehle, M.; Moss, D.; Shoutenkov, V. Magnetic fields in barred galaxies. IV. NGC 1097 and NGC 1365. Astron. Astrophys. 2005, 444, 739–765. [Google Scholar] [CrossRef]
- Ehle, M.; Beck, R. Ionized Gas and Intrinsic Magnetic Fields in the Spiral Galaxy NGC6946. Astron. Astrophys. 1993, 273, 45. [Google Scholar]
- Walterbos, R.A.M.; Braun, R. Diffused ionized gas in the spiral galaxy M31. Astrophys. J. 1994, 431, 156–171. [Google Scholar] [CrossRef]
- Beck, R.; Klein, U.; Krause, M. M81 at high radio frequencies. Astron. Astrophys. 1985, 152, 237–249. [Google Scholar]
- Han, J.L.; Manchester, R.N.; Lyne, A.G.; Qiao, G.J.; van Straten, W. Pulsar Rotation Measures and the Large-Scale Structure of the Galactic Magnetic Field. Astrophys. J. 2006, 642, 868–881. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Müller, P. Densities and filling factors of the diffuse ionized gas in the Solar neighbourhood. Astron. Astrophys. 2008, 490, 179–187. [Google Scholar] [CrossRef]
- Savage, B.D.; Wakker, B.P. The Extension of the Transition Temperature Plasma into the Lower Galactic Halo. Astrophys. J. 2009, 702, 1472–1489. [Google Scholar] [CrossRef]
- Yao, J.M.; Manchester, R.N.; Wang, N. A New Electron-density Model for Estimation of Pulsar and FRB Distances. Astrophys. J. 2017, 835, 29. [Google Scholar] [CrossRef]
- Peters, S.P.C.; van der Kruit, P.C.; Allen, R.J.; Freeman, K.C. The shape of dark matter haloes—III. Kinematics and structure of the H I disc. Mon. Not. R. Astron. Soc. 2017, 464, 32–47. [Google Scholar] [CrossRef]
- Tabatabaei, F.S.; Berkhuijsen, E.M. Relating dust, gas, and the rate of star formation in M 31. Astron. Astrophys. 2010, 517, A77. [Google Scholar] [CrossRef]
- Schleicher, D.R.G.; Beck, R. A new interpretation of the far-infrared—Radio correlation and the expected breakdown at high redshift. Astron. Astrophys. 2013, 556, A142. [Google Scholar] [CrossRef]
- Schober, J.; Schleicher, D.R.G.; Klessen, R.S. Galactic Synchrotron Emission and the Far-infrared-Radio Correlation at High Redshift. Astrophys. J. 2016, 827, 109. [Google Scholar] [CrossRef]
- Rand, R.J.; Kulkarni, S.R. The local Galactic magnetic field. Astrophys. J. 1989, 343, 760–772. [Google Scholar] [CrossRef]
- Han, J.L.; Qiao, G.J. The magnetic field in the disk of our Galaxy. Astron. Astrophys. 1994, 288, 759–772. [Google Scholar]
- Men, H.; Ferrière, K.; Han, J.L. Observational constraints on models for the interstellar magnetic field in the Galactic disk. Astron. Astrophys. 2008, 486, 819–828. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Shukurov, A.; Fletcher, A.; Baugh, C.M. Galactic magnetic fields and hierarchical galaxy formation. Mon. Not. R. Astron. Soc. 2015, 450, 3472–3489. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Chamandy, L.; Shukurov, A.; Baugh, C.M.; Taylor, A.R. Evolution of galactic magnetic fields. Mon. Not. R. Astron. Soc. 2019, 483, 2424–2440. [Google Scholar] [CrossRef]
- Subramanian, K.; Mestel, L. Galactic Dynamos and Density Wave Theory—Part Two—An Alternative Treatment for Strong Non-Axisymmetry. Mon. Not. R. Astron. Soc. 1993, 265, 649. [Google Scholar] [CrossRef][Green Version]
- Moss, D. On the generation of bisymmetric magnetic field structures in spiral galaxies by tidal interactions. Mon. Not. R. Astron. Soc. 1995, 275, 191–194. [Google Scholar] [CrossRef]
- Phillips, A. A comparison of the asymptotic and no-z approximations for galactic dynamos. Geophys. Astrophys. Fluid Dyn. 2001, 94, 135–150. [Google Scholar] [CrossRef]
- Sur, S.; Shukurov, A.; Subramanian, K. Galactic dynamos supported by magnetic helicity fluxes. Mon. Not. R. Astron. Soc. 2007, 377, 874–882. [Google Scholar] [CrossRef]
- Chamandy, L.; Shukurov, A.; Taylor, A.R. Statistical Tests of Galactic Dynamo Theory. Astrophys. J. 2016, 833, 43. [Google Scholar] [CrossRef]
- Zhou, H.; Blackman, E.G. Some consequences of shear on galactic dynamos with helicity fluxes. Mon. Not. R. Astron. Soc. 2017, 469, 1466–1475. [Google Scholar] [CrossRef]
- Kleeorin, N.; Moss, D.; Rogachevskii, I.; Sokoloff, D. The role of magnetic helicity transport in nonlinear galactic dynamos. Astron. Astrophys. 2002, 387, 453–462. [Google Scholar] [CrossRef][Green Version]
- Mitra, D.; Candelaresi, S.; Chatterjee, P.; Tavakol, R.; Brandenburg, A. Equatorial magnetic helicity flux in simulations with different gauges. Astron. Nachr. 2010, 331, 130. [Google Scholar] [CrossRef]
- Subramanian, K. The origin, evolution and signatures of primordial magnetic fields. Rep. Prog. Phys. 2016, 79, 076901. [Google Scholar] [CrossRef]
- Beck, R.; Poezd, A.D.; Shukurov, A.; Sokoloff, D.D. Dynamos in evolving galaxies. Astron. Astrophys. 1994, 289, 94–100. [Google Scholar]
- Subramanian, K.; Brandenburg, A. Traces of large-scale dynamo action in the kinematic stage. Mon. Not. R. Astron. Soc. 2014, 445, 2930–2940. [Google Scholar] [CrossRef]
- Mao, S.A.; Carilli, C.; Gaensler, B.M.; Wucknitz, O.; Keeton, C.; Basu, A.; Beck, R.; Kronberg, P.P.; Zweibel, E. Detection of microgauss coherent magnetic fields in a galaxy five billion years ago. Nat. Astron. 2017, 1, 621–626. [Google Scholar] [CrossRef]
- Arshakian, T.G.; Beck, R.; Krause, M.; Sokoloff, D. Evolution of magnetic fields in galaxies and future observational tests with the Square Kilometre Array. Astron. Astrophys. 2009, 494, 21–32. [Google Scholar] [CrossRef]
- Biermann, L.; Schlüter, A. Cosmic Radiation and Cosmic Magnetic Fields. II. Origin of Cosmic Magnetic Fields. Phys. Rev. 1951, 82, 863–868. [Google Scholar] [CrossRef]
- Kraichnan, R.H.; Nagarajan, S. Growth of Turbulent Magnetic Fields. Phys. Fluids 1967, 10, 859–870. [Google Scholar] [CrossRef]
- Kazantsev, A.P. Enhancement of a Magnetic Field by a Conducting Fluid. Sov. J. Exp. Theor. Phys. 1968, 26, 1031. [Google Scholar]
- Meneguzzi, M.; Frisch, U.; Pouquet, A. Helical and nonhelical turbulent dynamos. Phys. Rev. Lett. 1981, 47, 1060–1064. [Google Scholar] [CrossRef]
- Kulsrud, R.M.; Anderson, S.W. The spectrum of random magnetic fields in the mean field dynamo theory of the Galactic magnetic field. Astrophys. J. 1992, 396, 606–630. [Google Scholar] [CrossRef]
- Brandenburg, A.; Sokoloff, D.; Subramanian, K. Current Status of Turbulent Dynamo Theory. From Large-Scale to Small-Scale Dynamos. Space Sci. Rev. 2012, 169, 123–157. [Google Scholar] [CrossRef]
- Käpylä, P.J.; Korpi, M.J.; Brandenburg, A. Large-scale dynamos in turbulent convection with shear. Astron. Astrophys. 2008, 491, 353–362. [Google Scholar] [CrossRef]
- Pietarila Graham, J.; Blackman, E.G.; Mininni, P.D.; Pouquet, A. Not much helicity is needed to drive large-scale dynamos. Phys. Rev. E 2012, 85, 066406. [Google Scholar] [CrossRef]
- Bhat, P.; Subramanian, K.; Brandenburg, A. Efficient quasi-kinematic large-scale dynamo as the small-scale dynamo saturates. arXiv 2019, arXiv:1905.08278. [Google Scholar]
- Schober, J.; Schleicher, D.R.G.; Federrath, C.; Bovino, S.; Klessen, R.S. Saturation of the turbulent dynamo. Phys. Rev. E 2015, 92, 023010. [Google Scholar] [CrossRef] [PubMed]
- Moss, D.; Stepanov, R.; Krause, M.; Beck, R.; Sokoloff, D. The formation of regular interarm magnetic fields in spiral galaxies. Astron. Astrophys. 2015, 578, A94. [Google Scholar] [CrossRef][Green Version]
- Chamandy, L.; Singh, N.K. A new constraint on mean-field galactic dynamo theory. Mon. Not. R. Astron. Soc. 2017, 468, 3657–3662. [Google Scholar] [CrossRef][Green Version]
- Chamandy, L.; Singh, N.K. Nonlinear galactic dynamos and the magnetic Rädler effect. Mon. Not. R. Astron. Soc. 2018, 481, 1300–1319. [Google Scholar] [CrossRef]
- Rädler, K.H.; Kleeorin, N.; Rogachevskii, I. The Mean Electromotive Force for MHD Turbulence: The Case of a Weak Mean Magnetic Field and Slow Rotation. Geophys. Astrophys. Fluid Dyn. 2003, 97, 249–274. [Google Scholar] [CrossRef]
- Rogachevskii, I.; Kleeorin, N. Magnetic fluctuations and formation of large-scale inhomogeneous magnetic structures in a turbulent convection. Phys. Rev. E 2007, 76, 056307. [Google Scholar] [CrossRef]
- Subramanian, K. Unified Treatment of Small- and Large-Scale Dynamos in Helical Turbulence. Phys. Rev. Lett. 1999, 83, 2957–2960. [Google Scholar] [CrossRef]
- Bhat, P.; Subramanian, K.; Brandenburg, A. A unified large/small-scale dynamo in helical turbulence. Mon. Not. R. Astron. Soc. 2016, 461, 240–247. [Google Scholar] [CrossRef]
- Shebalin, J.V.; Matthaeus, W.H.; Montgomery, D. Anisotropy in MHD turbulence due to a mean magnetic field. J. Plasma Phys. 1983, 29, 525–547. [Google Scholar] [CrossRef]
- Sridhar, S.; Goldreich, P. Toward a theory of interstellar turbulence. 1: Weak Alfvenic turbulence. Astrophys. J. 1994, 432, 612–621. [Google Scholar] [CrossRef]
- Blackman, E.G. In Situ Origin of Large-Scale Galactic Magnetic Fields without Kinetic Helicity? Astrophys. J. Lett. 1998, 496, L17–L20. [Google Scholar] [CrossRef][Green Version]
- Bhat, P.; Subramanian, K. Fluctuation dynamos and their Faraday rotation signatures. Mon. Not. R. Astron. Soc. 2013, 429, 2469–2481. [Google Scholar] [CrossRef]
- Sur, S.; Bhat, P.; Subramanian, K. Faraday rotation signatures of fluctuation dynamos in young galaxies. Mon. Not. R. Astron. Soc. 2018, 475, L72–L76. [Google Scholar] [CrossRef]
- Puerari, I.; Dottori, H.A. Fourier analysis of structure in spiral galaxies. Astrophys. J. Suppl. Ser. 1992, 93, 469–493. [Google Scholar]
- Oppermann, N.; Junklewitz, H.; Greiner, M.; Enßlin, T.A.; Akahori, T.; Carretti, E.; Gaensler, B.M.; Goobar, A.; Harvey-Smith, L.; Johnston-Hollitt, M.; et al. Estimating extragalactic Faraday rotation. Astron. Astrophys. 2015, 575, A118. [Google Scholar] [CrossRef]
- Nieten, C.; Neininger, N.; Guélin, M.; Ungerechts, H.; Lucas, R.; Berkhuijsen, E.M.; Beck, R.; Wielebinski, R. Molecular gas in the Andromeda galaxy. Astron. Astrophys. 2006, 453, 459–475. [Google Scholar] [CrossRef]
- Beck, R.; Berkhuijsen, E.M.; Gießübel, R.; Mulcahy, D.D. Magnetic fields and cosmic rays in M 31. I. Spectral indices, scale lengths, Faraday rotation & magnetic field pattern. Astron. Astrophys. 2020, 633, A5. [Google Scholar]
- Sandage, A.; Humphreys, R.M. On the warped optical plane of M33. Astrophys. J. Lett. 1980, 236, L1–L5. [Google Scholar] [CrossRef]
- Patrikeev, I.; Fletcher, A.; Stepanov, R.; Beck, R.; Berkhuijsen, E.M.; Frick, P.; Horellou, C. Analysis of spiral arms using anisotropic wavelets: gas, dust and magnetic fields in M51. Astron. Astrophys. 2006, 458, 441–452. [Google Scholar] [CrossRef]
- Mulcahy, D.D.; Beck, R.; Heald, G.H. Resolved magnetic structures in the disk-halo interface of NGC 628. Astron. Astrophys. 2017, 600, A6. [Google Scholar] [CrossRef]
- Sokoloff, D.; Shukurov, A.; Krause, M. Pattern recognition of the regular magnetic field in disks of spiral galaxies. Astron. Astrophys. 1992, 264, 396–405. [Google Scholar]
- Frick, P.; Stepanov, R.; Beck, R.; Sokoloff, D.; Shukurov, A.; Ehle, M.; Lundgren, A. Magnetic and gaseous spiral arms in M83. Astron. Astrophys. 2016, 585, A21. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Urbanik, M.; Beck, R.; Han, J.L. Radio polarization and magnetic field structure in M 101. Astron. Astrophys. 2016, 588, A114. [Google Scholar] [CrossRef][Green Version]
- Yu, S.Y.; Ho, L.C. Dependence of the Spiral Arms Pitch Angle on Wavelength as a Test of the Density Wave Theory. Astrophys. J. 2018, 869, 29. [Google Scholar] [CrossRef]
- Ehle, M.; Beck, R.; Haynes, R.F.; Vogler, A.; Pietsch, W.; Elmouttie, M.; Ryder, S. Magnetic fields and hot gas in the spiral galaxy NGC 1566 as derived from ATCA radio polarization and ROSAT X-ray observations. Astron. Astrophys. 1996, 306, 73. [Google Scholar]
- Soida, M.; Urbanik, M.; Beck, R.; Wielebinski, R.; Balkowski, C. Unusual magnetic fields in the interacting spiral NGC 3627. Astron. Astrophys. 2001, 378, 40–50. [Google Scholar] [CrossRef]
- Iye, M.; Okamura, S.; Hamabe, M.; Watanabe, M. Spectral analysis of the asymmetric spiral pattern of NGC 4254. Astrophys. J. 1982, 256, 103–111. [Google Scholar] [CrossRef]
- Thornley, M.D.; Mundy, L.G. Dynamic and Stochastic Influences on Spiral Structure in the Flocculent Spiral NGC 4414. Astrophys. J. 1997, 490, 682–697. [Google Scholar] [CrossRef]
- Gräve, R.; Beck, R. The axisymmetric spiral magnetic field in the galaxy IC 342. Astron. Astrophys. 1988, 192, 66–76. [Google Scholar]
- Crosthwaite, L.P.; Turner, J.L.; Ho, P.T.P. Structure in the Neutral Hydrogen Disk of the Spiral Galaxy IC 342. Astron. J. 2000, 119, 1720–1736. [Google Scholar] [CrossRef]
- Krause, M.; Hummel, E.; Beck, R. The magnetic field structures in two nearby spiral galaxies. I. The axisymmetric spiral magnetic field in IC 342. Astron. Astrophys. 1989, 217, 4–16. [Google Scholar]
- Mao, S.A.; McClure-Griffiths, N.M.; Gaensler, B.M.; Haverkorn, M.; Beck, R.; McConnell, D.; Wolleben, M.; Stanimirović, S.; Dickey, J.M.; Staveley-Smith, L. Magnetic Field Structure of the Large Magellanic Cloud from Faraday Rotation Measures of Diffuse Polarized Emission. Astrophys. J. 2012, 759, 25. [Google Scholar] [CrossRef]
- Beck, R. Magnetic Fields in Galaxies. In Cosmic Magnetic Fields; Wielebinski, R., Beck, R., Eds.; Lecture Notes in Physics; Springer: Berlin, Germany, 2005; Volume 664, p. 41. [Google Scholar] [CrossRef]
- Banerjee, A.; Jog, C.J.; Brinks, E.; Bagetakos, I. Theoretical determination of H I vertical scale heights in the dwarf galaxies DDO 154, Ho II, IC 2574 and NGC 2366. Mon. Not. R. Astron. Soc. 2011, 415, 687–694. [Google Scholar] [CrossRef][Green Version]
- Bacchini, C.; Fraternali, F.; Iorio, G.; Pezzulli, G. Volumetric star formation laws of disc galaxies. Astron. Astrophys. 2019, 622, A64. [Google Scholar] [CrossRef]
- Kalberla, P.M.W.; Kerp, J. The HI Distribution of the Milky Way. Annu. Rev. Astron. Astrophys. 2009, 47, 27–61. [Google Scholar] [CrossRef]
- Yim, K.; Wong, T.; Howk, J.C.; van der Hulst, J.M. The Interstellar Medium and Star Formation in Edge-on Galaxies. I. NGC 891. Astron. J. 2011, 141, 48. [Google Scholar] [CrossRef]
- Yim, K.; Wong, T.; Xue, R.; Rand, R.J.; Rosolowsky, E.; van der Hulst, J.M.; Benjamin, R.; Murphy, E.J. The Interstellar Medium and Star Formation in Edge-On Galaxies. II. NGC 4157, 4565, and 5907. Astron. J. 2014, 148, 127. [Google Scholar] [CrossRef]
- Tamburro, D.; Rix, H.W.; Leroy, A.K.; Mac Low, M.M.; Walter, F.; Kennicutt, R.C.; Brinks, E.; de Blok, W.J.G. What is Driving the H I Velocity Dispersion? Astron. J. 2009, 137, 4424–4435. [Google Scholar] [CrossRef]
- Ianjamasimanana, R.; de Blok, W.J.G.; Walter, F.; Heald, G.H.; Caldú-Primo, A.; Jarrett, T.H. The Radial Variation of H I Velocity Dispersions in Dwarfs and Spirals. Astron. J. 2015, 150, 47. [Google Scholar] [CrossRef]
- Blackman, E.G.; Nauman, F. Motivation and challenge to capture both large-scale and local transport in next generation accretion theory. J. Plasma Phys. 2015, 81, 395810505. [Google Scholar] [CrossRef][Green Version]
- Rohde, R.; Beck, R.; Elstner, D. Magnetic arms in NGC 6946 generated by a turbulent dynamo. Astron. Astrophys. 1999, 350, 423–433. [Google Scholar]
- Seigar, M.S.; Block, D.L.; Puerari, I.; Chorney, N.E.; James, P.A. Dust-penetrated arm classes: insights from rising and falling rotation curves. Mon. Not. R. Astron. Soc. 2005, 359, 1065–1076. [Google Scholar] [CrossRef][Green Version]
- Seigar, M.S.; Bullock, J.S.; Barth, A.J.; Ho, L.C. Constraining Dark Matter Halo Profiles and Galaxy Formation Models Using Spiral Arm Morphology. I. Method Outline. Astrophys. J. 2006, 645, 1012–1023. [Google Scholar] [CrossRef][Green Version]
- Grand, R.J.J.; Kawata, D.; Cropper, M. Spiral arm pitch angle and galactic shear rate in N-body simulations of disc galaxies. Astron. Astrophys. 2013, 553, A77. [Google Scholar] [CrossRef]
- Chyży, K.T.; Weżgowiec, M.; Beck, R.; Bomans, D.J. Magnetic fields in Local Group dwarf irregulars. Astron. Astrophys. 2011, 529, A94. [Google Scholar] [CrossRef]
- Chyży, K.T.; Sridhar, S.S.; Jurusik, W. What drives galactic magnetism? Astron. Astrophys. 2017, 603, A121. [Google Scholar] [CrossRef]
- Tabatabaei, F.S.; Martinsson, T.P.K.; Knapen, J.H.; Beckman, J.E.; Koribalski, B.; Elmegreen, B.G. An Empirical Relation between the Large-scale Magnetic Field and the Dynamical Mass in Galaxies. Astrophys. J. Lett. 2016, 818, L10. [Google Scholar] [CrossRef]
- Heesen, V.; Krause, M.; Beck, R.; Adebahr, B.; Bomans, D.J.; Carretti, E.; Dumke, M.; Heald, G.; Irwin, J.; Koribalski, B.S.; et al. Radio haloes in nearby galaxies modelled with 1D cosmic ray transport using SPINNAKER. Mon. Not. R. Astron. Soc. 2018, 476, 158–183. [Google Scholar] [CrossRef]
- Krause, M.; Irwin, J.; Wiegert, T.; Miskolczi, A.; Damas-Segovia, A.; Beck, R.; Li, J.T.; Heald, G.; Müller, P.; Stein, Y.; et al. CHANG-ES. IX. Radio scale heights and scale lengths of a consistent sample of 13 spiral galaxies seen edge-on and their correlations. Astron. Astrophys. 2018, 611, A72. [Google Scholar] [CrossRef]
- Rieder, M.; Teyssier, R. A small-scale dynamo in feedback-dominated galaxies—II. The saturation phase and the final magnetic configuration. Mon. Not. R. Astron. Soc. 2017, 471, 2674–2686. [Google Scholar] [CrossRef]
- Brandenburg, A.; Donner, K.J.; Moss, D.; Shukurov, A.; Sokoloff, D.D.; Tuominen, I. Vertical Magnetic Fields above the Discs of Spiral Galaxies. Astron. Astrophys. 1993, 271, 36. [Google Scholar]
- Moss, D.; Tuominen, I. Nonlinear galactic dynamos. Geophys. Astrophys. Fluid Dyn. 1990, 50, 113–120. [Google Scholar] [CrossRef]
- Brandenburg, A.; Donner, K.J.; Moss, D.; Shukurov, A.; Sokolov, D.D.; Tuominen, I. Dynamos in discs and halos of galaxies. Astron. Astrophys. 1992, 259, 453–461. [Google Scholar]
- Prasad, A.; Mangalam, A. A Global Galactic Dynamo with a Corona Constrained by Relative Helicity. Astrophys. J. 2016, 817, 12. [Google Scholar] [CrossRef]
- Evirgen, C.C.; Gent, F.A.; Shukurov, A.; Fletcher, A.; Bushby, P.J. The supernova-regulated ISM—VI. Magnetic effects on the structure of the interstellar medium. Mon. Not. R. Astron. Soc. 2019, 488, 5065–5074. [Google Scholar] [CrossRef]
- Moss, D.; Shukurov, A.; Sokoloff, D.; Beck, R.; Fletcher, A. Magnetic fields in barred galaxies. II. Dynamo models. Astron. Astrophys. 2001, 380, 55–71. [Google Scholar] [CrossRef]
- Beck, R.; Shoutenkov, V.; Ehle, M.; Harnett, J.I.; Haynes, R.F.; Shukurov, A.; Sokoloff, D.D.; Thierbach, M. Magnetic fields in barred galaxies. I. The atlas. Astron. Astrophys. 2002, 391, 83–102. [Google Scholar] [CrossRef]
- Henriksen, R.N. Magnetic spiral arms in galaxy haloes. Mon. Not. R. Astron. Soc. 2017, 469, 4806–4830. [Google Scholar] [CrossRef]
- Sokoloff, D.; Moss, D. What can we say about seed fields for galactic dynamos? Geophys. Astrophys. Fluid Dyn. 2013, 107, 3–10. [Google Scholar] [CrossRef][Green Version]
- Beck, R.; Hoernes, P. Magnetic spiral arms in the galaxy NGC6946. Nature 1996, 379, 47–49. [Google Scholar] [CrossRef]
- Elmegreen, D.M. A near-infrared atlas of spiral galaxies. Astrophys. J. Suppl. Ser. 1981, 47, 229–233. [Google Scholar] [CrossRef]
- Kendall, S.; Kennicutt, R.C.; Clarke, C. Spiral structure in nearby galaxies—I. Sample, data analysis and overview of results. Mon. Not. R. Astron. Soc. 2011, 414, 538–564. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G.; Yau, A.; Athanassoula, E.; Bosma, A.; Buta, R.J.; Helou, G.; Ho, L.C.; Gadotti, D.A.; Knapen, J.H.; et al. Grand Design and Flocculent Spirals in the Spitzer Survey of Stellar Structure in Galaxies (S4G). Astrophys. J. 2011, 737, 32. [Google Scholar] [CrossRef]
- Tabatabaei, F.S.; Krause, M.; Beck, R. High-resolution radio continuum survey of M 33. I. The radio maps. Astron. Astrophys. 2007, 472, 785–796. [Google Scholar] [CrossRef]
- Mao, S.A.; Zweibel, E.; Fletcher, A.; Ott, J.; Tabatabaei, F. Properties of the Magneto-ionic Medium in the Halo of M51 Revealed by Wide-band Polarimetry. Astrophys. J. 2015, 800, 92. [Google Scholar] [CrossRef]
- Chyży, K.T.; Ehle, M.; Beck, R. Magnetic fields and gas in the cluster-influenced spiral galaxy NGC 4254. I. Radio and X-rays observations. Astron. Astrophys. 2007, 474, 415–429. [Google Scholar] [CrossRef]
- Krause, M. High resolution observations of the magnetic field in IC 342. In The Cosmic Dynamo; Krause, F., Rädler, K.H., Rudiger, G., Eds.; IAU Symposium; Cambridge University Press: Cambridge, UK, 1993; Volume 157, pp. 305–310. [Google Scholar]
- Moss, D. The relation between magnetic and gas arms in spiral galaxies. Mon. Not. R. Astron. Soc. 1998, 297, 860–866. [Google Scholar] [CrossRef][Green Version]
- Mestel, L.; Subramanian, K. Galactic dynamos and density wave theory. Mon. Not. R. Astron. Soc. 1991, 248, 677–687. [Google Scholar] [CrossRef][Green Version]
- Chamandy, L.; Subramanian, K.; Shukurov, A. Galactic spiral patterns and dynamo action—II. Asymptotic solutions. Mon. Not. R. Astron. Soc. 2013, 433, 3274–3289. [Google Scholar] [CrossRef][Green Version]
- Chamandy, L.; Shukurov, A.; Subramanian, K. Magnetic spiral arms and galactic outflows. Mon. Not. R. Astron. Soc. 2015, 446, L6–L10. [Google Scholar] [CrossRef]
- Chamandy, L.; Subramanian, K.; Quillen, A. Magnetic arms generated by multiple interfering galactic spiral patterns. Mon. Not. R. Astron. Soc. 2014, 437, 562–574. [Google Scholar] [CrossRef]
- Dobbs, C.; Baba, J. Dawes Review 4: Spiral Structures in Disc Galaxies. Astron. Soc. Aust. 2014, 31, e035. [Google Scholar] [CrossRef]
- Masters, K.L.; Lintott, C.J.; Hart, R.E.; Kruk, S.J.; Smethurst, R.J.; Casteels, K.V.; Keel, W.C.; Simmons, B.D.; Stanescu, D.O.; Tate, J.; et al. Galaxy Zoo: Unwinding the Winding Problem—Observations of Spiral Bulge Prominence and Arm Pitch Angles Suggest Local Spiral Galaxies are Winding. Mon. Not. R. Astron. Soc. 2019. [Google Scholar] [CrossRef]
- Frick, P.; Beck, R.; Shukurov, A.; Sokoloff, D.; Ehle, M.; Kamphuis, J. Magnetic and optical spiral arms in the galaxy NGC 6946. Mon. Not. R. Astron. Soc. 2000, 318, 925–937. [Google Scholar] [CrossRef]
- Shukurov, A. Magnetic spiral arms in galaxies. Mon. Not. R. Astron. Soc. 1998, 299, L21. [Google Scholar] [CrossRef][Green Version]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Walter, F.; Brinks, E.; de Blok, W.J.G.; Bigiel, F.; Kennicutt, R.C., Jr.; Thornley, M.D.; Leroy, A. THINGS: The H I Nearby Galaxy Survey. Astron. J. 2008, 136, 2563–2647. [Google Scholar] [CrossRef]
- Wright, E.L.; Eisenhardt, P.R.M.; Mainzer, A.K.; Ressler, M.E.; Cutri, R.M.; Jarrett, T.; Kirkpatrick, J.D.; Padgett, D.; McMillan, R.S.; Skrutskie, M.; et al. The Wide-field Infrared Survey Explorer (WISE): Mission Description and Initial On-orbit Performance. Astron. J. 2010, 140, 1868–1881. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- Elson, E.C.; Kam, S.Z.; Chemin, L.; Carignan, C.; Jarrett, T.H. A multiscale study of star formation in Messier 33. Mon. Not. R. Astron. Soc. 2019, 483, 931–946. [Google Scholar] [CrossRef]
- Mogotsi, K.M.; de Blok, W.J.G.; Caldú-Primo, A.; Walter, F.; Ianjamasimanana, R.; Leroy, A.K. Hi and CO Velocity Dispersions in Nearby Galaxies. Astron. J. 2016, 151, 15. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Balbus, S.A. Differential Rotation and Turbulence in Extended H I Disks. Astrophys. J. 1999, 511, 660–665. [Google Scholar] [CrossRef]
- Hollins, J.F.; Sarson, G.R.; Shukurov, A.; Fletcher, A.; Gent, F.A. Supernova-regulated ISM. V. Space and Time Correlations. Astrophys. J. 2017, 850, 4. [Google Scholar] [CrossRef]
- Neininger, N.; Klein, U.; Beck, R.; Wielebinski, R. Correlation of magnetic and optical structure in the barred spiral galaxy M83. Nature 1991, 352, 781–783. [Google Scholar] [CrossRef]
- Neininger, N.; Beck, R.; Sukumar, S.; Allen, R.J. Magnetic Fields and Thermal Gas in M83. Astron. Astrophys. 1993, 274, 687. [Google Scholar]
| 1. | Other definitions of “ordered field” are used in the literature, e.g., in [47]. |
| 2. | A gauge independent formulation of the magnetic helicity density exists for the small-scale random component of the field [34]. |
| 3. | and was measured for just one pulsar in the Large Magellanic Cloud; many more are needed to estimate in this galaxy. |
| 4. | Yao et al. [120] described the Milky Way’s “thick disc” of thermal gas by a function with a scale height of kpc. The exponential tail of this function has an exponential scale height of 1.0 kpc. |
| 5. | Models of the disc of warm neutral gas, based on H i data of edge-on galaxies, indicate that the full thickness to half maximum increases beyond about 5 kpc radius (“flaring”) [121], while the radial dependence of the disc thickness of ionized gas has not been investigated so far. |
| 6. | The thermal gas in M 31 is distributed in an ellipsoidal ring in the plane of the sky with a Gaussian profile of about 6 kpc full width to half maximum (Berkhuijsen, priv. comm.) and 200–500 pc exponential scale height [115], corresponding to about 500 pc full thickness, which yield a pathlength of kpc for 75 inclination. |
| 7. | |
| 8. | Other helicity flux terms might also play a role [34]. |
| 9. | NGC 253 and IC 342 are excluded because of their exceptionally weak regular fields. |
| 10. | The term “mode” has a slightly different meaning in observation and theory. In theory, it usually refers to eigen modes in the kinematic regime of dynamo action. |
| 11. | Zhou et al. [48] explored the general case of comparing models and observations which employ different methods of averaging and highlighted the precision error caused when they are different. By using, as far as possible, the same averaging method in models as used in observations, their mutual comparison would become more straightforward. |

| Direction | Galaxies | References |
|---|---|---|
| Inward (disc) | M 33, NGC 253, NGC 6946 | [53,54,55] |
| Outward (central region) & inward (disc) | M 31, NGC 2997, IC 342 | [56,57,58,59] |
| Outward (disc) | M 51, M 83, | [8,60] and Figure A1 |
| NGC 891, NGC 4013, | [61,62] | |
| NGC 4254, NGC 4414, | [63,64] | |
| NGC 4449 | [65] (re-analyzed) | |
| NGC 4736, NGC 5775 | [66,67] | |
| Inward (central region) & outward (disc) | – | – |
| Inward (inner disc) & outward (outer disc) | NGC 4666 | [68] |
| Outward (inner disc) & inward (outer disc) | Milky Way | [69] |
| Galaxy | Parity & Remarks | References |
|---|---|---|
| NGC 253 | even | [54] |
| NGC 891 | even | [81] |
| NGC 4013 | even (disc) + odd (central region) | [62] |
| NGC 4631 | even (disc) + varying (halo) | [82,83] |
| NGC 4666 | even | [68] |
| NGC 5775 | even | [67] |
| Milky Way | even (outer disc) + odd (central region) | [84,85] |
| Galaxy | Radial Range [kpc] | [rad/m2] | i [°] | [μG] | [cm−3] | [μG] | [μG] | Btot | Breg | Reference |
|---|---|---|---|---|---|---|---|---|---|---|
| M 31 | 6.8–9.0 | 75 | 7.3 | 0.032 | 1.8 | 4.9 | 0.25 | 2.7 | [111] | |
| 9.0–11.3 | 7.5 | 0.033 | 2.1 | 5.2 | 0.28 | 2.5 | ||||
| 11.3–13.6 | 7.1 | 0.031 | 2.6 | 4.9 | 0.37 | 1.9 | ||||
| 13.6–15.8 | 6.3 | 0.026 | 2.7 | 4.6 | 0.43 | 1.7 | ||||
| M 33 | 1.0–3.0 | 56 | 8.7 | 0.031 | 1.3 | 3.1 | 0.15 | 2.4 | [53] | |
| 3.0–5.0 | 7.6 | 0.026 | 2.4 | 3.1 | 0.32 | 1.3 | ||||
| M 51 | 2.4–3.6 | 20 | 17 | 0.086 | 1.3 | 8.6 | 0.08 | 6.6 | [8] | |
| 3.6–4.8 | 16 | 0.078 | 1.8 | 7.6 | 0.11 | 4.2 | ||||
| 4.8–6.0 | 15 | 0.071 | 2.6 | 7.6 | 0.17 | 2.9 | ||||
| 6.0–7.2 | 13 | 0.057 | 3.2 | 7.8 | 0.25 | 2.4 | ||||
| M 81 | 6.0–9.0 | 59 | 8.0 | 0.028 | 0.4 e | 4.1 | – | – | [112] | |
| 9.0–12.0 | 6.4 | 0.020 | 0.5 e | 3.8 | – | – | ||||
| M 83 | 4–8 | 24 | 19 | 0.101 | 0.5 | 5.9 | 0.03 | 12 | Table A1 | |
| 8–12 | 16 | 0.078 | 2.1 | 6.5 | 0.13 | 3.1 | ||||
| NGC 253 | 1.4–6.7 | 78.5 | 15 | 0.071 | 0.30 | 4.3 | 0.02 | 14 | [54] | |
| NGC 1097 | 3.75–5.0 | 45 | 13 | 0.057 | 2.4 | 7.9 | 0.18 | 3.3 | [113] | |
| NGC 1365 | 2.625–4.375 | 40 | 15 | 0.071 | 0.8 | 4.8 | 0.05 | 6.0 | [113] | |
| 4.375–6.125 | 11 | 0.045 | 1.5 | 5.7 | 0.14 | 3.8 | ||||
| 6.125–7.875 | 12 | 0.051 | 1.1 | 4.7 | 0.09 | 4.3 | ||||
| 7.875–9.625 | 13 | 0.057 | 1.8 | 4.0 | 0.14 | 2.2 | ||||
| 9.625–11.375 | 12 | 0.051 | 1.8 | 3.8 | 0.15 | 2.1 | ||||
| 11.375–13.125 | 10 | 0.039 | 1.5 | 3.4 | 0.15 | 2.3 | ||||
| 13.125–14.875 | 8.4 | 0.030 | 1.1 | 2.9 | 0.13 | 2.6 | ||||
| NGC 4254 | 4.8–6.0 | 42 | 18 | 0.094 | 0.7 | 7.8 | 0.04 | 11 | [63] | |
| 6.0–7.2 | 17 | 0.086 | 1.0 | 8.7 | 0.06 | 8.7 | ||||
| NGC 4449 | 1.0–2.0 | 43 | 16 | 0.078 | 0.7 | 4.1 | 0.04 | 5.9 | [65] | |
| 2.0–3.0 | 11 | 0.045 | 1.4 | 4.8 | 0.13 | 3.4 | ||||
| NGC 6946 | 0–4.7 | 30 | 19 | 0.101 | 1.2 | 5.1 | 0.06 | 4.3 | [114] | |
| 4.7–9.4 | 13 | 0.057 | 1.9 | 5.1 | 0.15 | 2.7 | ||||
| IC 342 | 7.5–12.5 | 31 | 14 | 0.064 | 0.18 | 3.3 | 0.013 | 18 | [59] | |
| 12.5–17.5 | 12 | 0.051 | 0.17 | 2.9 | 0.014 | 17 |
| Galaxy | Distance [Mpc] | [] and Reference | Radial Range [kpc] | [°] | [°] | Method | Reference |
|---|---|---|---|---|---|---|---|
| M 31 | 0.78 | 7–8 | 6.8–9.0 | – | M | [111] | |
| (NGC 224) | [167] | 9.0–11.3 | – | M | |||
| 11.3–13.6 | – | M | |||||
| 13.6–15.8 | – | M | |||||
| 7.0–8.0 | RM | [168] | |||||
| 8.0–9.0 | RM | ||||||
| 9.0–10.0 | RM | ||||||
| 10.0–11.0 | RM | ||||||
| 11.0–12.0 | RM | ||||||
| M 33 | 0.84 | 29–50 | 1.0–3.0 | M | [53] | ||
| (NGC 598) | [169] | 3.0–5.0 | M | ||||
| 5.0–7.0 | – | – | |||||
| 7.0–9.0 | – | – | |||||
| M 51 | 7.6 | 15–25 | 1.2–2.4 | – | – | [8] | |
| (NGC 5194) | [170] | 2.4–3.6 | M | ||||
| 3.6–4.8 | – e | M | |||||
| 4.8–6.0 | – | M | |||||
| 6.0–7.2 | – | M | |||||
| 7.2–8.4 | e | – | – | ||||
| M 74 | 7.3 | 13–41 | 4.0–5.0 west | – | – | [171] | |
| (NGC 628) | [165] | 8.0–9.0 west | – | – | |||
| 4.0–5.0 east | – | – | |||||
| 8.0–9.0 east | – | – | |||||
| M 81 | 3.25 | 14–24 | 6.0–9.0 | RM | [112] | ||
| (NGC 3031) | [165] | 9.0–12.0 | RM | ||||
| 6.0–9.0 | – | M | [172] | ||||
| 9.0–12.0 | – | M | |||||
| M 83 | 8.9 | 14–17, ≈10 | 2.0–3.0 | – | – | Figure 3 | |
| (NGC 5236) | [165,173] | 4.0–5.0 | – | – | |||
| 6.0–7.0 | – | – | |||||
| 10.0–11.0 | – | – | |||||
| M 101 | 7.4 | 10–30 | 3.0–6.0 | – | – | Figure 3 | |
| (NGC 5457) | [174] | 9.0–12.0 | – | – | |||
| 15.0–18.0 | – | – | |||||
| NGC 253 | 3.94 | ? | ≈2–12 | e | RM | [54] | |
| NGC 1097 | 17.0 | 27–35 | 1.25–2.5 | – | M | [113] | |
| [175] | 2.5–3.75 | – | M | ||||
| 3.75–5.0 | – | M | |||||
| NGC 1365 | 18.6 | ? | 2.625–4.375 | – | M | [113] | |
| 4.375–6.125 | – | M | |||||
| 6.125–7.875 | – | M | |||||
| 7.875–9.625 | – | M | |||||
| 9.625–11.375 | – | M | |||||
| 11.375–13.125 | – | M | |||||
| 13.125–14.875 | – | M | |||||
| NGC 1566 | 17.4 | 19–21 | 2.0–4.0 | – | – | [176] | |
| [175] | 4.0–6.0 | – | – | ||||
| 6.0–8.0 | – | – | |||||
| NGC 3627 | 11.9 | 10–50 | ≈2–5 west | – | – | [177] | |
| [177] | ≈2–5 east | – | – | ||||
| 4.0–7.0 east | – | – | |||||
| NGC 4254 | 16.8 | 6–72 | 1.2–2.4 | – | – | ||
| [178] | 2.4–3.6 | – | – | ||||
| 3.6–4.8 | – | – | |||||
| 4.8–6.0 | e | RM | [63] | ||||
| 6.0–7.2 | e | RM | |||||
| 7.2–8.4 | e | RM | |||||
| NGC 4414 | 19.2 | 20–40 | ≈4–7 | – | ≈22 | M | [64] |
| [179] | 1.5–3.0 | – | – | ||||
| 3.0–4.5 | – | – | |||||
| 4.5–6.0 | – | – | |||||
| 6.0–7.5 | – | – | |||||
| NGC 4449 | 3.7 | – | 1.0–2.0 | – | e | RM | [65] |
| 2.0–3.0 | e | RM | |||||
| NGC 4736 | 4.66 | ? | ≈0.3–3.0 | – | – | [66] | |
| NGC 6946 | 7.0 | 20–28 | 0.0–6.0 | – | – | [114] | |
| [165] | 6.0–12.0 | – | – | ||||
| 12.0–18.0 | – | – | |||||
| 1.0–2.0 | – | – | Figure 3 | ||||
| 5.0–6.0 | – | – | |||||
| 8.0–9.0 | – | – | |||||
| IC 342 | 3.4 | 10–25 | 5.5–9.9 | RM | [180] | ||
| [181] | 9.9–14.3 | RM | |||||
| 5.5–9.9 | RM | [182] | |||||
| 9.9–14.3 | RM | ||||||
| 5.5–9.9 | – | M | [172] | ||||
| 9.9–14.3 | – | M | |||||
| 7.5–12.5 | RM | [59] | |||||
| 12.5–17.5 | RM | ||||||
| 1.0–2.0 | – | – | Figure 3 | ||||
| 5.0–6.0 | – | – | |||||
| 8.0–9.0 | – | – | |||||
| 12.0–13.0 | – | – | |||||
| LMC | 0.05 | ? | 0–3 | – | RM | [183] |
| Galaxy | Radial Range [kpc] | References | |||
|---|---|---|---|---|---|
| M 31 | 6.8–9.0 | 1 | ≈0 | [111] | |
| 9.0–15.8 | 1 | ≈0 | ≈0 | [111] | |
| M 31 | 9.0–11.0 | 1 | ? | [168] | |
| M 33 | 1–5 | 1 | ≈0 | [53] | |
| M 51 (disc) | 2.4–3.6 | 1 | ≈0 | [8] | |
| 3.6–7.2 | 1 | ≈0 | [8] | ||
| M 51 (halo) | 2.4–3.6 | 1 | ≈0 | [8] | |
| 3.6–7.2 | ≈0 | 1 | ≈0 | [8] | |
| M 81 | 9–12 | 1 | ? | [172] | |
| M 83 | 4–12 | 1 | ? | Table A1 | |
| NGC 253 | 1.4–6.7 | 1 | ? | ? | [54] |
| NGC 1097 | 3.75–5.0 | 1 | [113] | ||
| NGC 1365 | 2.625–14.875 | 1 | [113] | ||
| NGC 4254 | 4.8–7.2 | 1 | ? | [63] | |
| NGC 4414 | ≈2–7 | 1 | ≈0.6 | ≈0.4 | [64] |
| NGC 4449 | 1–3 | 1 | ? | ? | [65] (re-analyzed) |
| NGC 6946 | 0–18 | ≈1 | ? | ≈1 | [114,193] |
| IC 342 | 5.5–17.5 | 1 | ? | ? | [59,172,180,182] |
| LMC | 0–3 | 1 | ? | ? | [183] |
| Galaxy | Class (NED) | No.opt. arms | No.magn. arms | Length [kpc] | Width [kpc] | Offset to opt.arms | Freq. [GHz] | References |
|---|---|---|---|---|---|---|---|---|
| M 33 | SA(s)cd | 3 | 3–7 | 1 | y/n | 8.35 | [216] | |
| M 51 | SA(s)bc | 2 | 4 | 7–15 | 0.5–1 | y | 4.86, 8.46 | [8] |
| M 51 | 2 | 4 | 10–20 | 1 | y | 1.5 | [217] | |
| M 74 | SA(s)c | 5 | 6–30 | 0.5–3 | y/n | 3.1 | [171] | |
| M 81 | SA(s)ab | 2 | 2 | 6–8 | 1.5 | y | 1.4 | [112] |
| M 83 | SAB(s)c | 6 | 12–25 | 1–2.5 | y/n | 2.37, 4.86 | [173] | |
| M 101 | SAB(rs)cd | 2 | 30–40 | y/n | 2.70, 4.85 | [174] | ||
| NGC 1097 | SB(s)b | 2 | 2 | 4–9 | 1.5–2.5 | y | 4.86 | [113] |
| NGC 1365 | SB(s)b | 2 | 2 | 9–17 | 2–4 | y | 4.86 | [113] |
| NGC 1566 | SAB(s)bc | 2 | 5–7 | y | 4.80 | [176] | ||
| NGC 2997 | SAB(rs)c | 3 | 4 | 7–20 | 0.5–1 | y/n | 4.86 | [58] |
| NGC 3627 | SAB(s)b | 2 | 4 | 5–10 | 1.5–2 | y/n | 8.46 | [177] |
| NGC 4254 | SA(s)c | 3 | 2 | 13–15 | 1–1.5 | y/n | 4.86, 8.46 | [218] |
| NGC 4414 | SA(rs)c | 4 | 3–10 | 1–1.5 | y | 8.44 | [64] | |
| NGC 4736 | (R)SA(r)ab | 0 | 0 | – | – | – | 4.86, 8.46 | [66] |
| NGC 6946 | SAB(rs)cd | 5 | 4 | 6–12 | 0.5–1 | y | 4.86, 8.46 | [55] |
| NGC 6946 | 5 | 5 | 7–14 | 0.5–2 | y | 1.46 | [55] | |
| IC 342 | SAB(rs)cd | 4 | 6–15 | 0.5–1 | y/n | 4.86 | [59,219] | |
| IC 342 | 6 | 8–30 | 1–3 | y/n | 1.49 | [59,182] |
| Galaxy | [′′] | [′′] | Noise [mJy/beam] | Pixel Scale [′′] | Channel Width [km s−1] |
|---|---|---|---|---|---|
| M 51 (NGC 5194) | 11.92 | 10.01 | 0.39 | 1.5 | 5.2 |
| M 74 (NGC 628) | 11.88 | 9.30 | 0.60 | 1.5 | 2.6 |
| NGC 6946 | 6.04 | 5.61 | 0.55 | 1.5 | 2.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beck, R.; Chamandy, L.; Elson, E.; Blackman, E.G. Synthesizing Observations and Theory to Understand Galactic Magnetic Fields: Progress and Challenges. Galaxies 2020, 8, 4. https://doi.org/10.3390/galaxies8010004
Beck R, Chamandy L, Elson E, Blackman EG. Synthesizing Observations and Theory to Understand Galactic Magnetic Fields: Progress and Challenges. Galaxies. 2020; 8(1):4. https://doi.org/10.3390/galaxies8010004
Chicago/Turabian StyleBeck, Rainer, Luke Chamandy, Ed Elson, and Eric G. Blackman. 2020. "Synthesizing Observations and Theory to Understand Galactic Magnetic Fields: Progress and Challenges" Galaxies 8, no. 1: 4. https://doi.org/10.3390/galaxies8010004
APA StyleBeck, R., Chamandy, L., Elson, E., & Blackman, E. G. (2020). Synthesizing Observations and Theory to Understand Galactic Magnetic Fields: Progress and Challenges. Galaxies, 8(1), 4. https://doi.org/10.3390/galaxies8010004





