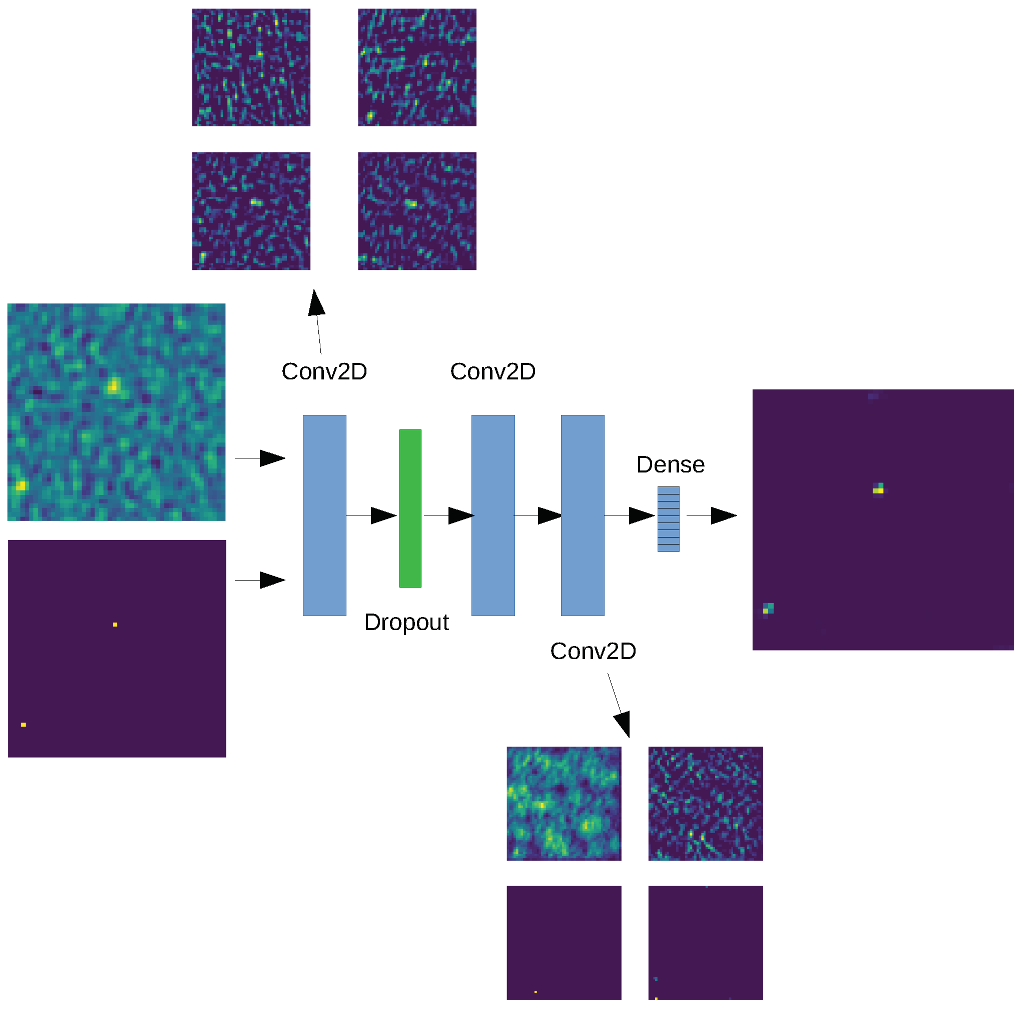
Figure 1.
ConvoSource architecture and examples of inputs when training (real maps and solution maps), features detected at the output of the first and third convolutional layer, as well as the resulting reconstructed image of the solution map. During testing, only the real maps are input into the network, and the predictions are given using the weights from the trained network.
Figure 1.
ConvoSource architecture and examples of inputs when training (real maps and solution maps), features detected at the output of the first and third convolutional layer, as well as the resulting reconstructed image of the solution map. During testing, only the real maps are input into the network, and the predictions are given using the weights from the trained network.
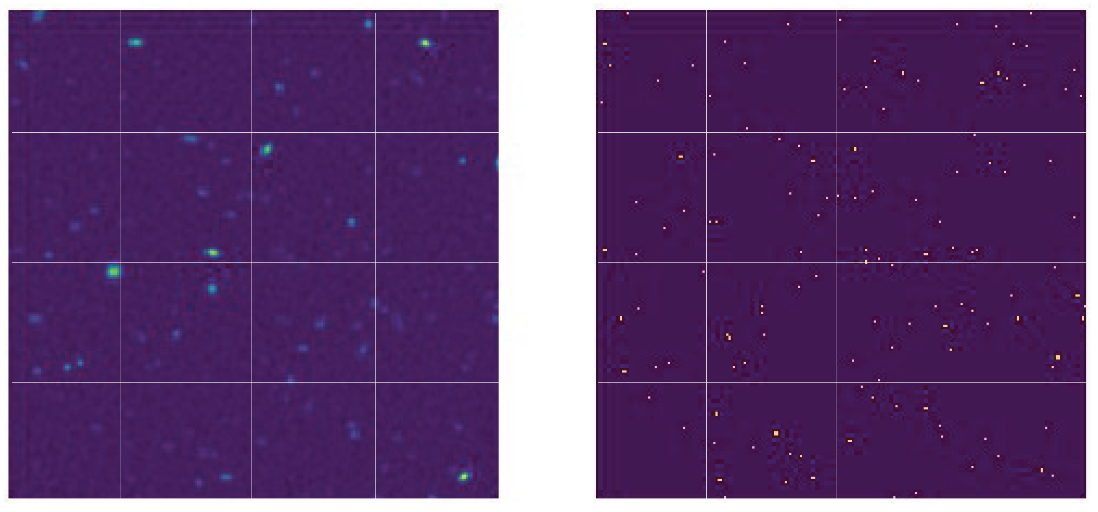
Figure 2.
(Left panel) Real map of a panel containing a combination of SFGs, SS, and FS sources at B1 at 1000 h. (Middle panel) True source locations at SNR = 2. (Right panel) True source locations at SNR = 5. The yellow, blue, and green pixels indicate SFGs, SS, and FS sources, respectively. In this particular case, both the SS and FS sources are very close together and very faint, which presents a challenge for both source-finders. The panels have a side length of 50 × 50 pixels.
Figure 2.
(Left panel) Real map of a panel containing a combination of SFGs, SS, and FS sources at B1 at 1000 h. (Middle panel) True source locations at SNR = 2. (Right panel) True source locations at SNR = 5. The yellow, blue, and green pixels indicate SFGs, SS, and FS sources, respectively. In this particular case, both the SS and FS sources are very close together and very faint, which presents a challenge for both source-finders. The panels have a side length of 50 × 50 pixels.
Figure 3.
(Left panel) Real map of a panel containing a combination of SFGs, SS, and FS sources at B2 at 8 h. (Middle panel) True source locations at SNR = 2. There are two SFGs and one each of SS and FS galaxies. (Right panel) True source locations at SNR = 5. At this SNR, only one SFG and one SS source remain. The other SFG and FS sources had a total flux that was lower than the cut-off threshold at that SNR. The yellow, blue, and green pixels indicate SFGs, SS, and FS sources, respectively. The panels have a side-length of 50 × 50 pixels.
Figure 3.
(Left panel) Real map of a panel containing a combination of SFGs, SS, and FS sources at B2 at 8 h. (Middle panel) True source locations at SNR = 2. There are two SFGs and one each of SS and FS galaxies. (Right panel) True source locations at SNR = 5. At this SNR, only one SFG and one SS source remain. The other SFG and FS sources had a total flux that was lower than the cut-off threshold at that SNR. The yellow, blue, and green pixels indicate SFGs, SS, and FS sources, respectively. The panels have a side-length of 50 × 50 pixels.
Figure 4.
(Left) Segmentation of a portion of the primary beam corrected images in the training set area. (Right) Segmentation of the solution map in the same area. These images are generated from the B1 1000 h dataset, using an SNR = 5 to determine the threshold of flux for injecting the solutions. Each block formed a single 50 × 50 pixel image that was input into the ConvoSource algorithm. The blocks on the left make up the training set images (train_X), and the blocks on the right make up the solution set images (train_Y).
Figure 4.
(Left) Segmentation of a portion of the primary beam corrected images in the training set area. (Right) Segmentation of the solution map in the same area. These images are generated from the B1 1000 h dataset, using an SNR = 5 to determine the threshold of flux for injecting the solutions. Each block formed a single 50 × 50 pixel image that was input into the ConvoSource algorithm. The blocks on the left make up the training set images (train_X), and the blocks on the right make up the solution set images (train_Y).
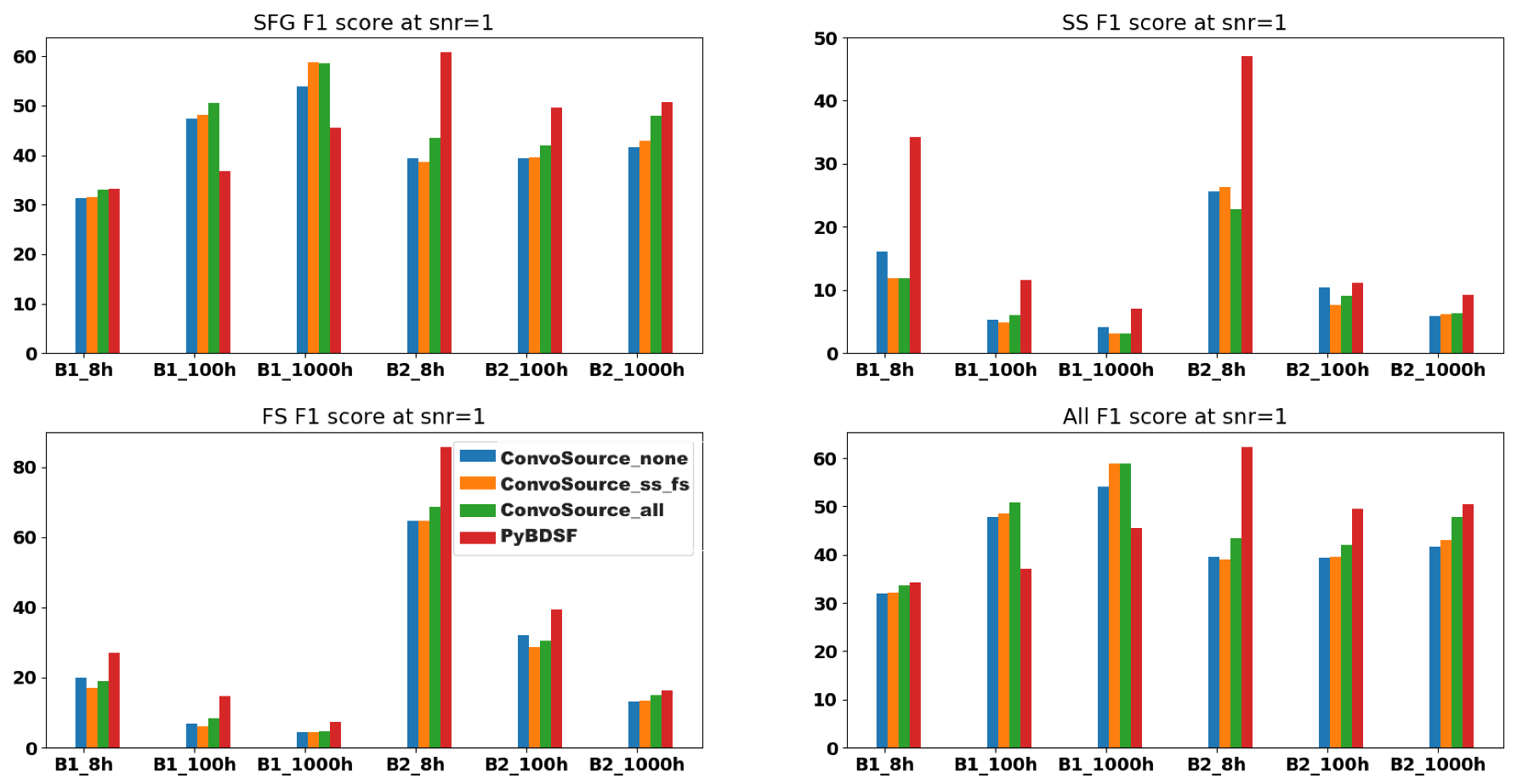
Figure 5.
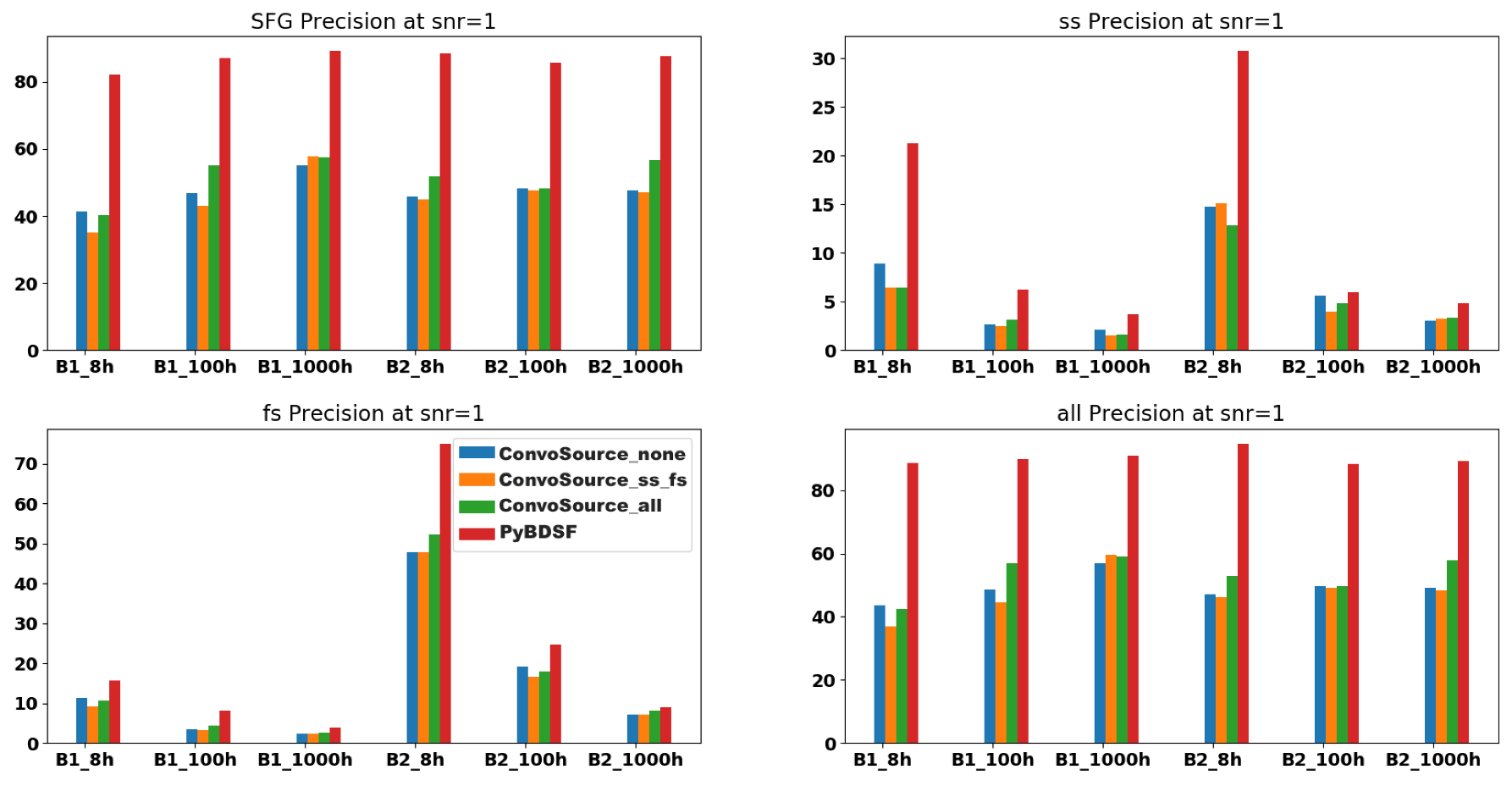
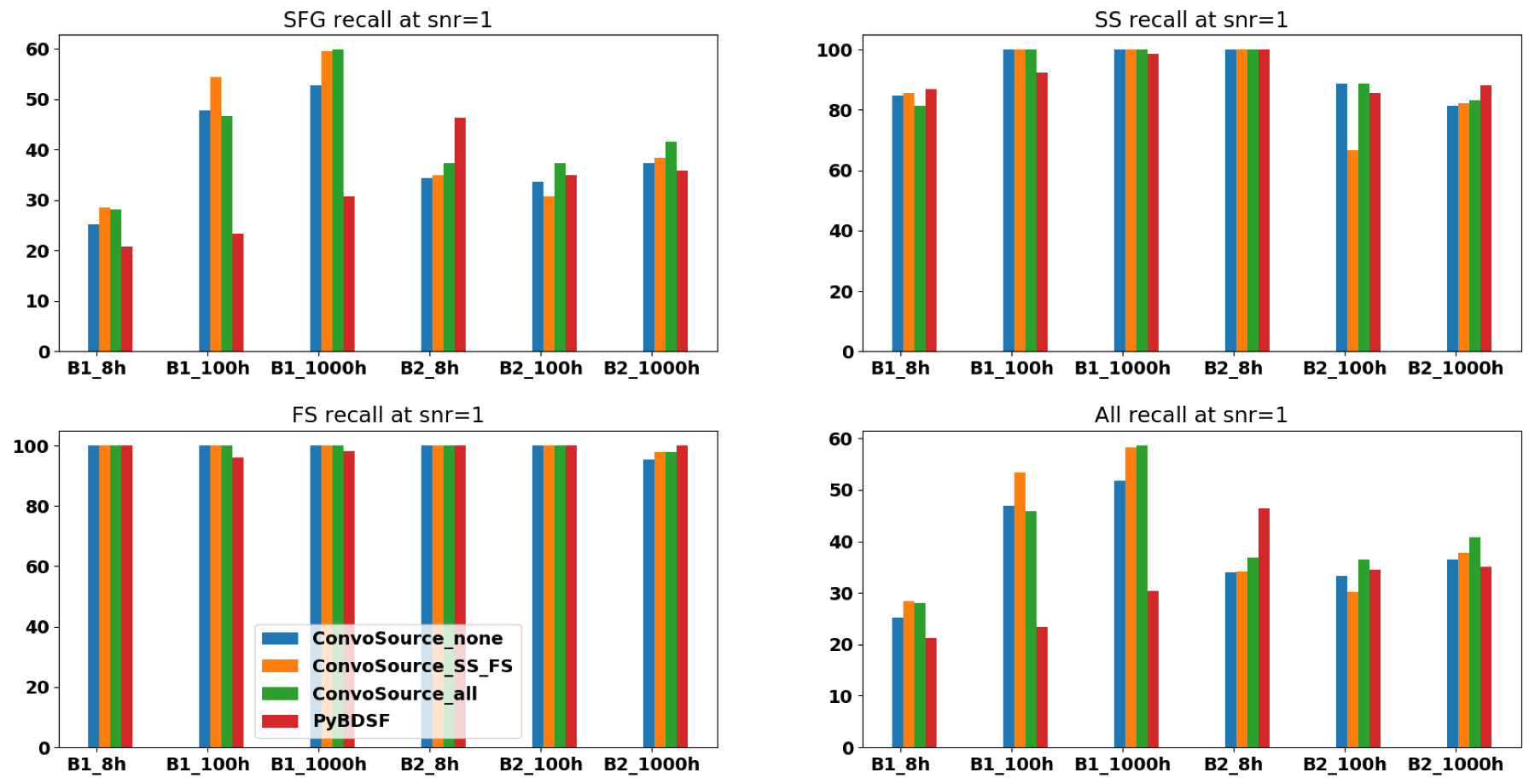
F1 scores at SNR = 1, across the two frequencies B1 (560 MHz) and B2 (1400 MHz) and the three integration times. There are three results given from ConvoSource, depending on the augmentation used when training. The blue bar represents no augmentation; orange represents augmenting the SS and FS sources; and the green bar represents augmenting all sources. The graphs show that PyBDSF usually performed better compared to ConvoSource at this SNR. Although it appeared that ConvoSource performed better across the SFGs and all sources in the B1 dataset, for all integration times, the better performance appeared to be explained by the increased proportion of chance matches at this SNR, as shown in
Figure 6. However, it should be noted that these sources had very low significance given the SNR.
Figure 5.
F1 scores at SNR = 1, across the two frequencies B1 (560 MHz) and B2 (1400 MHz) and the three integration times. There are three results given from ConvoSource, depending on the augmentation used when training. The blue bar represents no augmentation; orange represents augmenting the SS and FS sources; and the green bar represents augmenting all sources. The graphs show that PyBDSF usually performed better compared to ConvoSource at this SNR. Although it appeared that ConvoSource performed better across the SFGs and all sources in the B1 dataset, for all integration times, the better performance appeared to be explained by the increased proportion of chance matches at this SNR, as shown in
Figure 6. However, it should be noted that these sources had very low significance given the SNR.
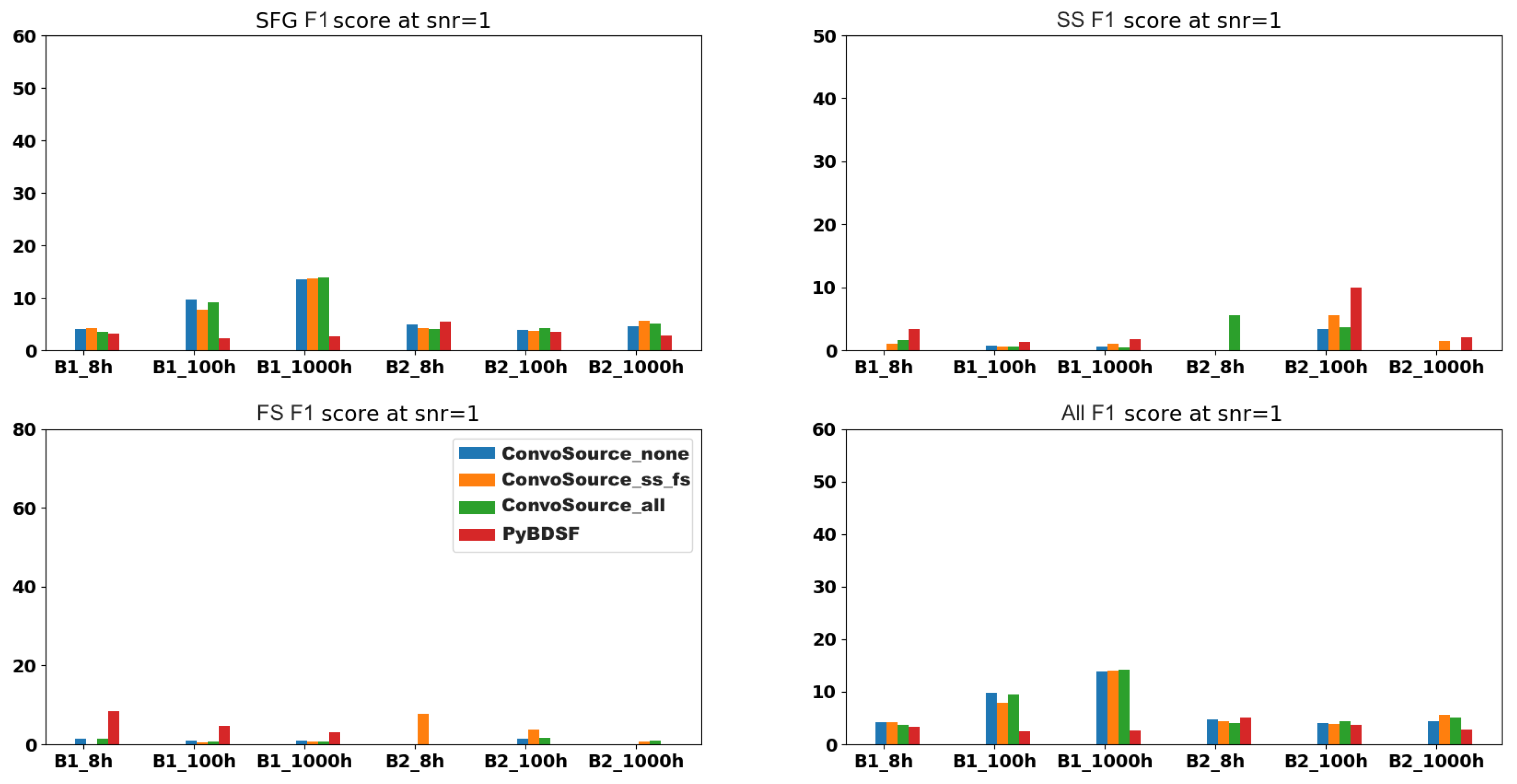
Figure 6.
Showing the effect of randomly rotating the reconstructed matrix of source locations to investigate the proportion of chance findings.
Figure 6.
Showing the effect of randomly rotating the reconstructed matrix of source locations to investigate the proportion of chance findings.
Figure 7.
The top and bottom rows show a couple of examples of a real map for B1 at 8 h (first column), the solutions when injected into the map given the SNR = 1 threshold (second column), the predicted locations by ConvoSource after training on the original images only (third column), and the predicted locations by PyBDSF (fourth column).
Figure 7.
The top and bottom rows show a couple of examples of a real map for B1 at 8 h (first column), the solutions when injected into the map given the SNR = 1 threshold (second column), the predicted locations by ConvoSource after training on the original images only (third column), and the predicted locations by PyBDSF (fourth column).
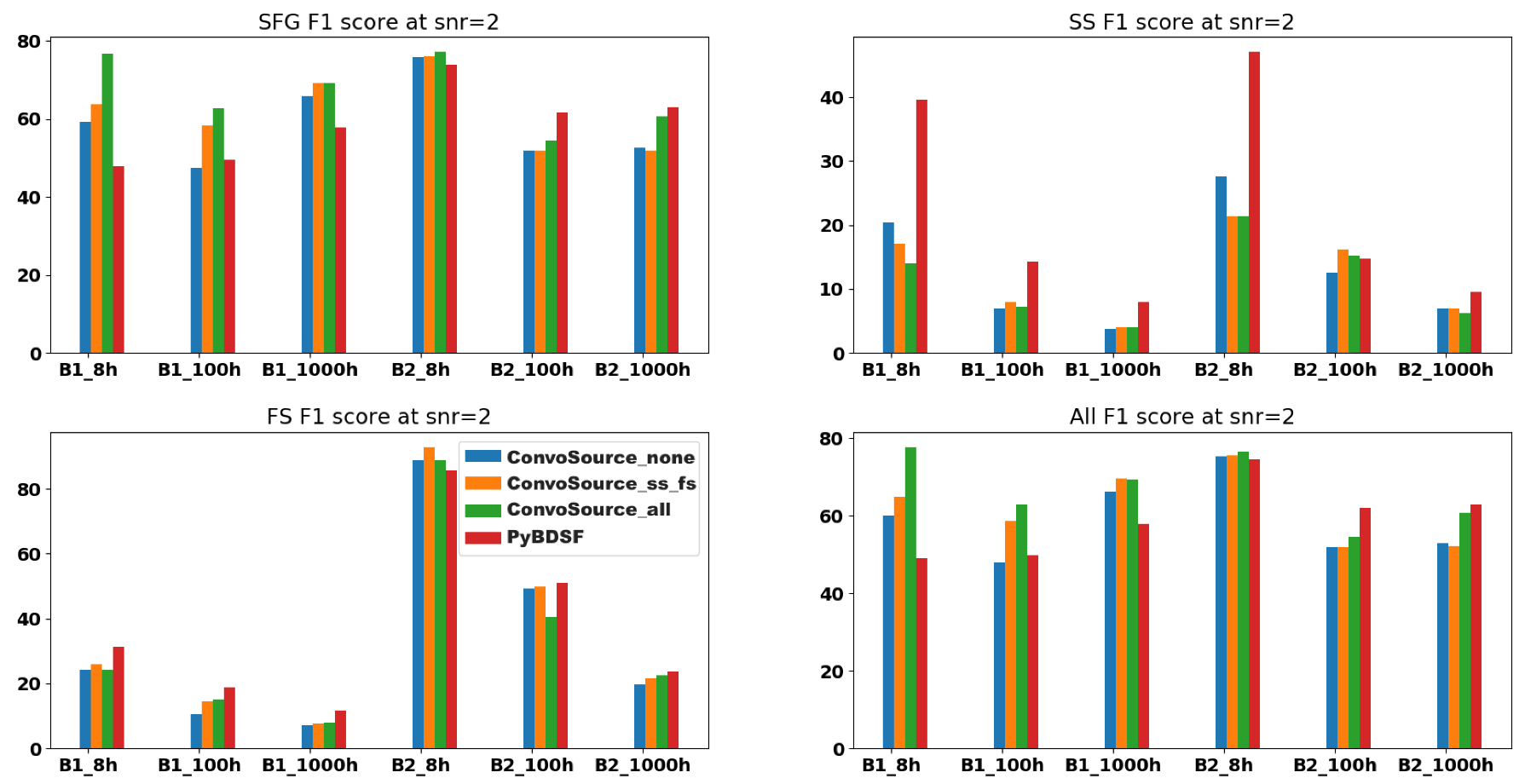
Figure 8.
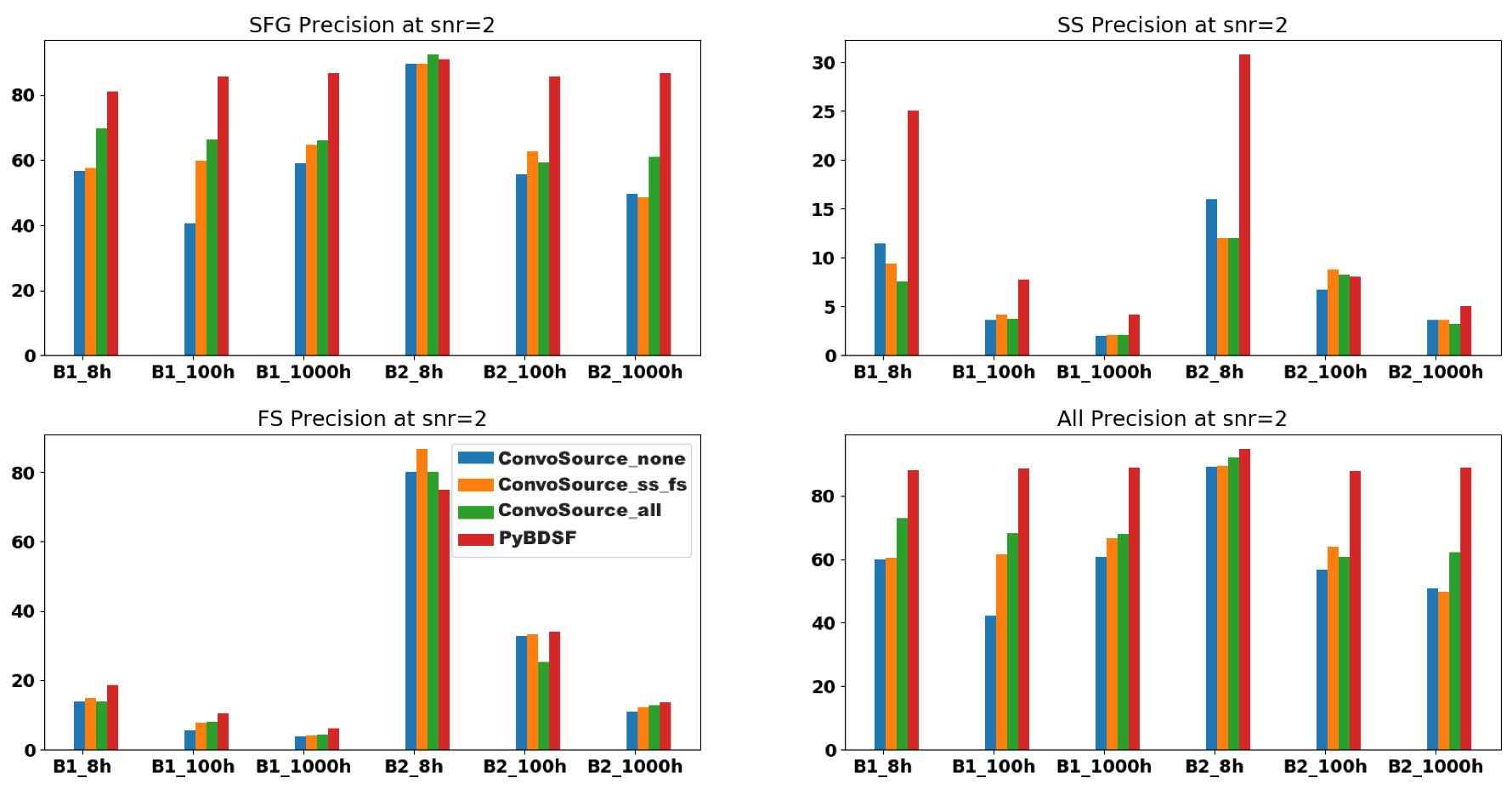
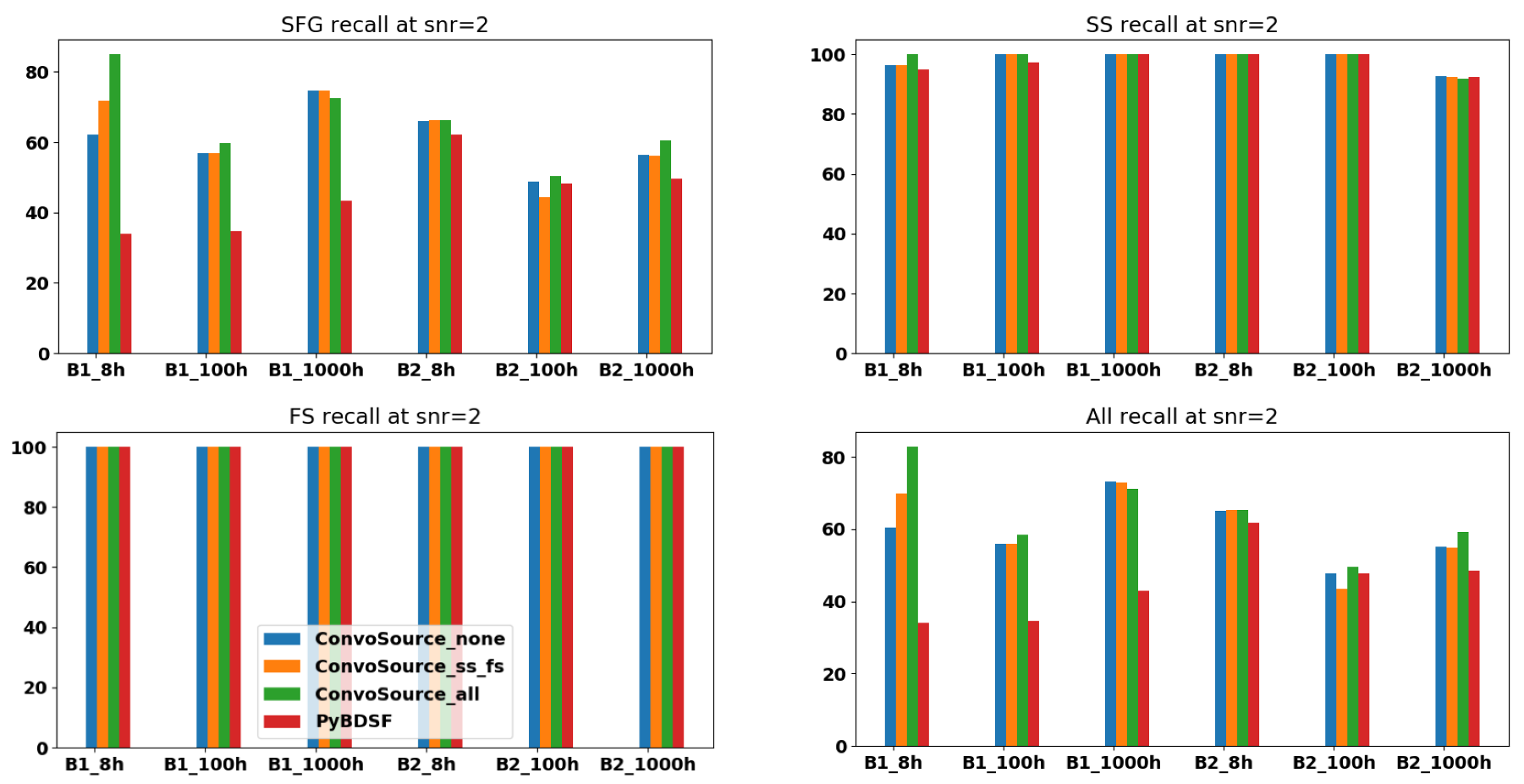
F1 scores at SNR = 2, across the two frequencies B1 (560 MHz) and B2 (1400 MHz) and the three integration times. There are three results given from ConvoSource, depending on the augmentation used when training. The blue bar represents no augmentation; orange represents augmenting the SS and FS sources; and the green bar represents augmenting all sources.
Figure 8.
F1 scores at SNR = 2, across the two frequencies B1 (560 MHz) and B2 (1400 MHz) and the three integration times. There are three results given from ConvoSource, depending on the augmentation used when training. The blue bar represents no augmentation; orange represents augmenting the SS and FS sources; and the green bar represents augmenting all sources.
Figure 9.
The top and bottom rows show a couple of examples of a real map for B2 at 8 h (first column), the solutions when injected into the map given the SNR = 2 threshold (second column), the predicted locations by ConvoSource after training on the original images only (third column), and the predicted locations by PyBDSF (fourth column).
Figure 9.
The top and bottom rows show a couple of examples of a real map for B2 at 8 h (first column), the solutions when injected into the map given the SNR = 2 threshold (second column), the predicted locations by ConvoSource after training on the original images only (third column), and the predicted locations by PyBDSF (fourth column).
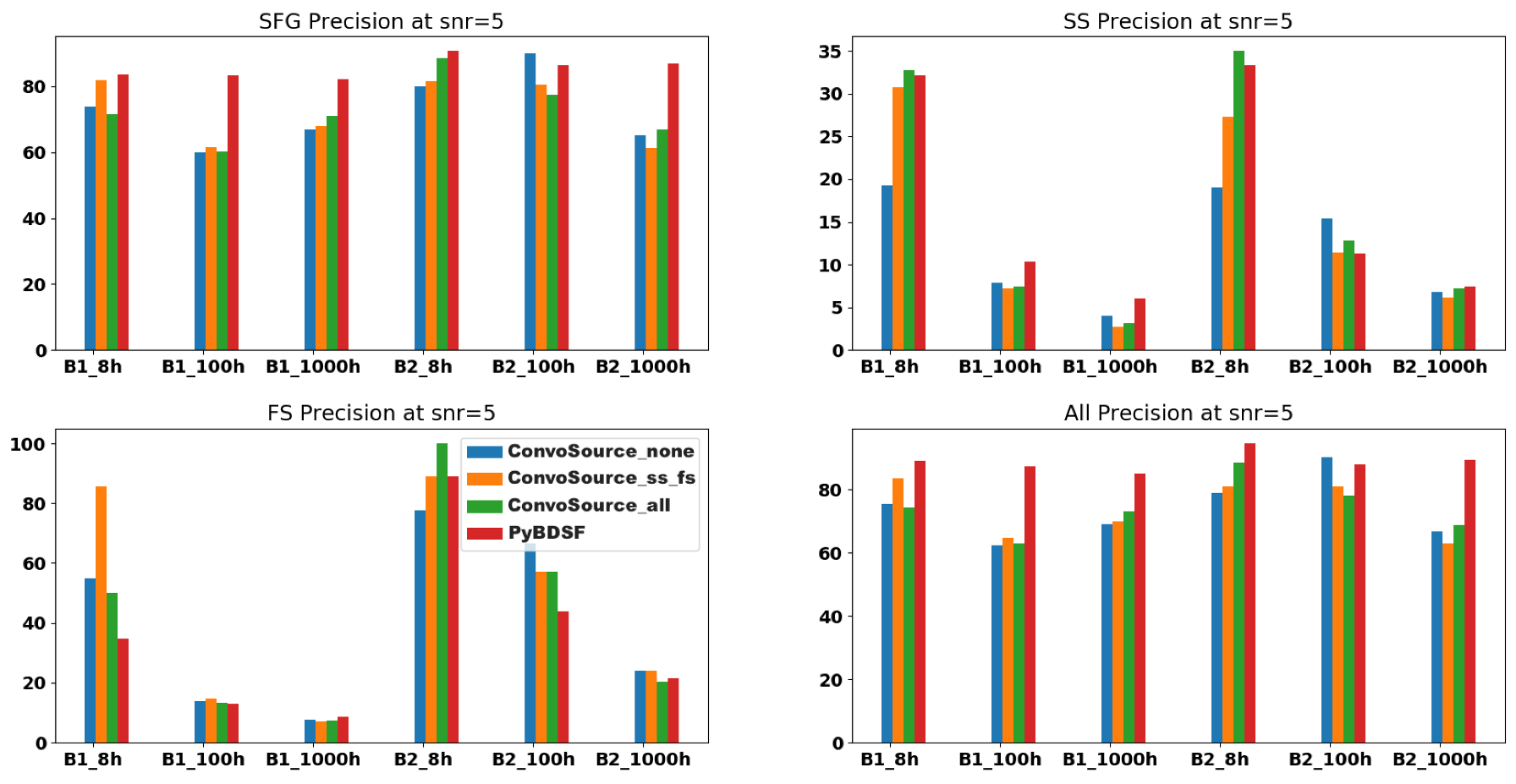
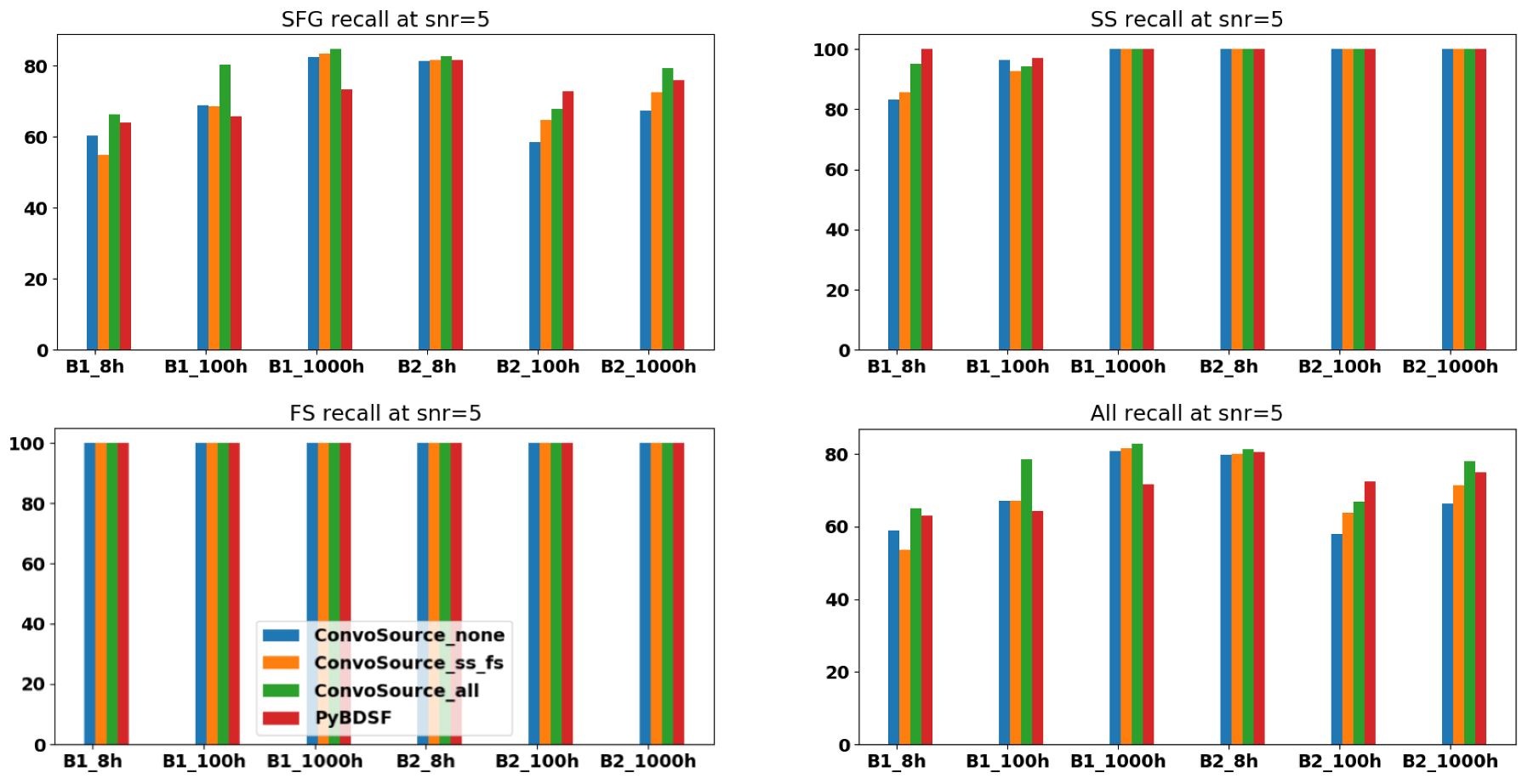
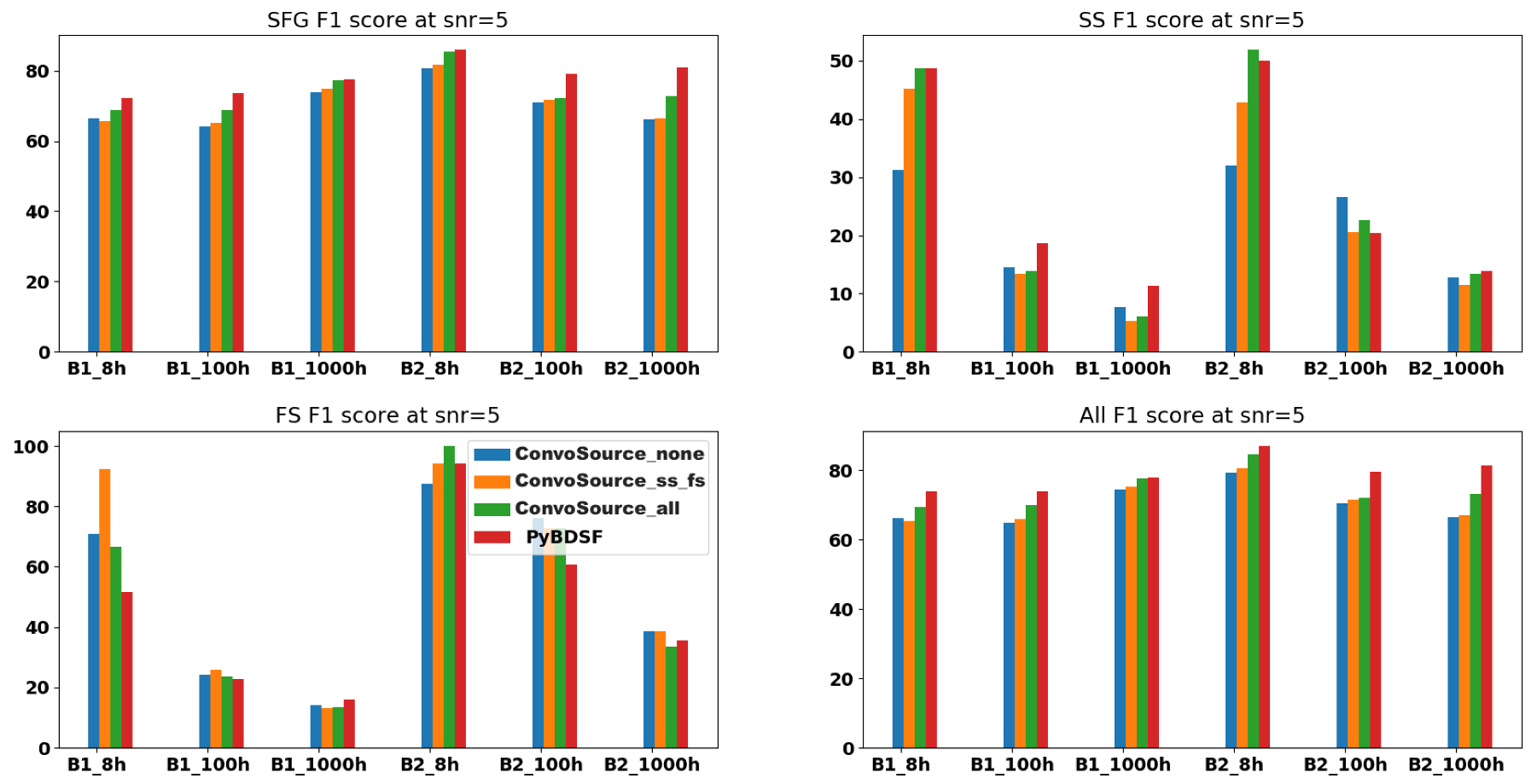
Figure 10.
F1 scores at SNR = 5, across the two frequencies B1 (560 MHz) and B2 (1400 MHz) and the three integration times. There are three results given from ConvoSource, depending on the augmentation used when training. The blue bar represents no augmentation; orange represents augmenting the SS and FS sources; and the green bar represents augmenting all sources.
Figure 10.
F1 scores at SNR = 5, across the two frequencies B1 (560 MHz) and B2 (1400 MHz) and the three integration times. There are three results given from ConvoSource, depending on the augmentation used when training. The blue bar represents no augmentation; orange represents augmenting the SS and FS sources; and the green bar represents augmenting all sources.
Figure 11.
The top and bottom rows show a couple of examples of a real map for B2 at 8 h (first column), the solutions when injected into the map given the SNR = 5 threshold (second column), the predicted locations by ConvoSource after training on the original images only (third column), and the predicted locations by PyBDSF (fourth column).
Figure 11.
The top and bottom rows show a couple of examples of a real map for B2 at 8 h (first column), the solutions when injected into the map given the SNR = 5 threshold (second column), the predicted locations by ConvoSource after training on the original images only (third column), and the predicted locations by PyBDSF (fourth column).
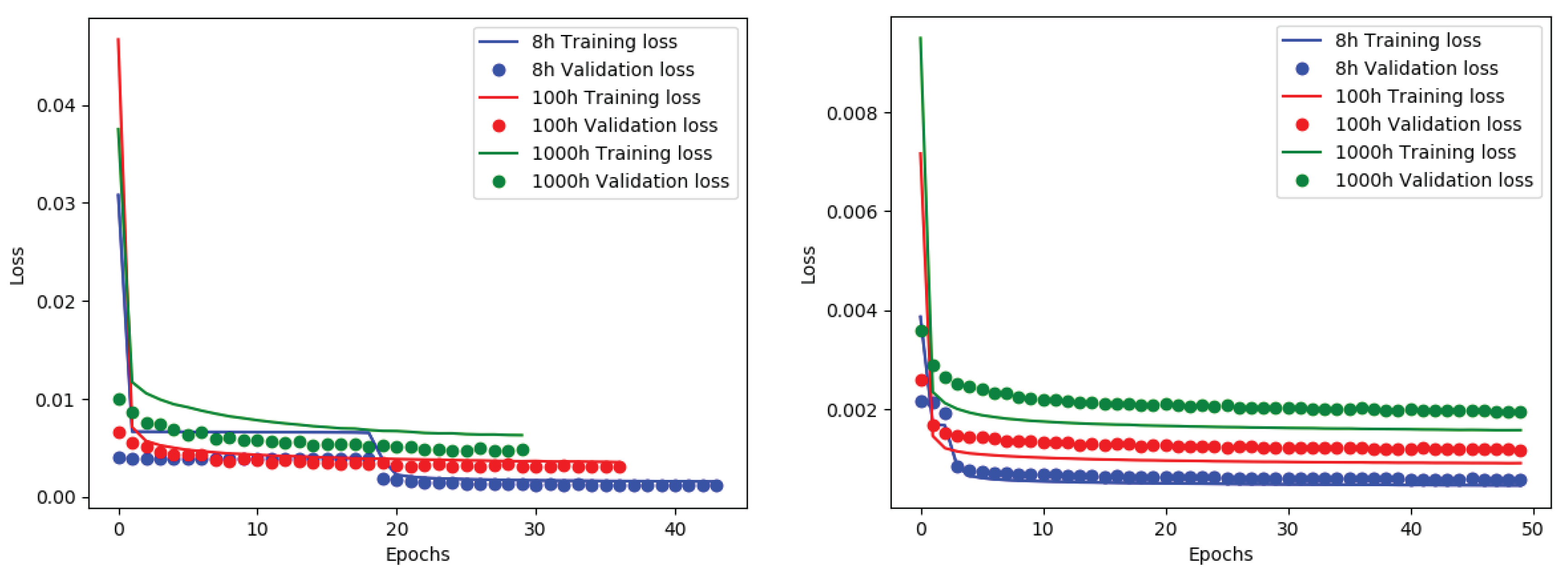
Figure 12.
Training and validation losses across the three integration times at SNR = 5 across B1 and B2 datasets in the left and rights panels, respectively.
Figure 12.
Training and validation losses across the three integration times at SNR = 5 across B1 and B2 datasets in the left and rights panels, respectively.
Table 1.
Architecture of the ConvoSource model.
Table 1.
Architecture of the ConvoSource model.
| Layer | Output Shape | # Params |
|---|
| Input_1 | (None, 50, 50, 1) | 0 |
| conv2d_1 | (None, 50, 50, 16) | 800 |
| dropout_1 | (None, 50, 50, 16) | 0 |
| conv2d_2 | (None, 50, 50, 32) | 12,832 |
| conv2d_3 | (None, 50, 50, 64) | 18,496 |
| dense_1 | (None, 50, 50, 1) | 65 |
| Total | | 32,193 |
Table 2.
The total number of steep-spectrum (SS) AGN, flat-spectrum (FS) AGN, and SFGs across each integration time across all frequencies, when using SNR = 2 and SNR = 5.
Table 2.
The total number of steep-spectrum (SS) AGN, flat-spectrum (FS) AGN, and SFGs across each integration time across all frequencies, when using SNR = 2 and SNR = 5.
| Dataset | # SS-AGN | # FS-AGN | # SFG |
|---|
| SNR = 2 | | | |
| B1 | | | |
| 8 h | 342 | 117 | 13,920 |
| 100 h | 644 | 386 | 34,158 |
| 1000 h | 957 | 682 | 57,797 |
| B2 | | | |
| 8 h | 91 | 64 | 4028 |
| 100 h | 166 | 151 | 9423 |
| 1000 h | 278 | 294 | 17,283 |
| B5 | | | |
| 8 h | 3 | 1 | 26 |
| 100 h | 4 | 2 | 103 |
| 1000 h | 6 | 6 | 223 |
| SNR = 5 | | | |
| B1 | | | |
| 8 h | 213 | 94 | 5717 |
| 100 h | 395 | 208 | 16,885 |
| 1000 h | 605 | 366 | 31,597 |
| B2 | | | |
| 8 h | 59 | 25 | 1877 |
| 100 h | 101 | 73 | 5096 |
| 1000 h | 178 | 155 | 10,251 |
| B5 | | | |
| 8 h | 3 | 1 | 7 |
| 100 h | 4 | 1 | 43 |
| 1000 h | 4 | 3 | 114 |
Table 3.
Percentage difference in the number of sources depending on whether the quartile threshold from the training set was taken versus using the threshold obtained from the training set as a whole, at an SNR = 5.
Table 3.
Percentage difference in the number of sources depending on whether the quartile threshold from the training set was taken versus using the threshold obtained from the training set as a whole, at an SNR = 5.
| Frequency | 8 h | 100 h | 1000 h |
|---|
| B1 | 4.4 | 3.7 | 2.6 |
| B2 | 4.5 | 3.6 | 2.8 |
Table 4.
The x and y ranges of the training area, according to the locations within the whole map.
Table 4.
The x and y ranges of the training area, according to the locations within the whole map.
| Frequency | x Range | y Range | Area |
|---|
| B1 | 16,300–20,300 | 16,300–20,300 | 4000 pixels sq. |
| B2 | 16,300–20,500 | 16,300–20,500 | 4200 pixels sq. |
Table 5.
Exploring different block sizes, pixel increments, and number of images produced, using the B1 frequency as an example.
Table 5.
Exploring different block sizes, pixel increments, and number of images produced, using the B1 frequency as an example.
| Block Size | Increment Size | # Images Produced |
|---|
| No overlap | | |
| 20 × 20 | 20 | 200 × 200 = 40,000 |
| 50 × 50 | 50 | 80 × 80 = 6400 |
| 80 × 80 | 80 | 50 × 50 = 2500 |
| 100 × 100 | 100 | 40 × 40 = 1600 |
| 200 × 200 | 200 | 20 × 20 = 400 |
| Overlap | | |
| 20 × 20 | 10 | 398 × 398 = 158,404 |
| 50 × 50 | 20 | 198 × 198 = 39,204 |
| 50 × 50 | 40 | 99 × 99 = 9801 |
| 80 × 80 | 40 | 98 × 98 = 9604 |
| 80 × 80 | 50 | 79 × 79 = 6241 |
Table 6.
The Kappa statistics as measured using the correlation of the predictions between all runs of ConvoSource against PyBDSF, across all frequencies and exposure times at SNR = 1.
Table 6.
The Kappa statistics as measured using the correlation of the predictions between all runs of ConvoSource against PyBDSF, across all frequencies and exposure times at SNR = 1.
| | B1_8 h | B1_100 h | B1_1000 h | B2_8 h | B2_100 h | B2_1000 h |
|---|
| ConvoSource_None | 0.30 | 0.56 | 0.55 | 0.0 | 0.0 | 0.32 |
| ConvoSource_Extended | 0.52 | 0.58 | 0.51 | 0.0 | 0.0 | 0.50 |
| ConvoSource_All | 0.33 | 0.61 | 0.53 | 0.0 | 0.0 | 0.41 |
Table 7.
Showing all of the TP, FP, and FN across (3) ConvoSource augment all and (4) PyBDSF, at B1 8 h, B1 1000 h, B2 8 h and B2 1000 h, at an SNR = 2. The symbols in the first row (e.g., SFG_tp, _fp and _fn) represent the SFG true positives, false positives, and false negatives, respectively. The same pattern applies to the SS, FS, and all sources combined in the following 9 columns. The final two columns refer to the ratio of false positives to true positives and the ratio of false negatives to true positives.
Table 7.
Showing all of the TP, FP, and FN across (3) ConvoSource augment all and (4) PyBDSF, at B1 8 h, B1 1000 h, B2 8 h and B2 1000 h, at an SNR = 2. The symbols in the first row (e.g., SFG_tp, _fp and _fn) represent the SFG true positives, false positives, and false negatives, respectively. The same pattern applies to the SS, FS, and all sources combined in the following 9 columns. The final two columns refer to the ratio of false positives to true positives and the ratio of false negatives to true positives.
| Method | SFG_tp | _fp | _fn | SS_tp | _fp | _fn | FS_tp | _fp | _fn | All_tp | _fp | _fn | #fp/#tp | #fn/#tp |
|---|
| B1_8 h |
| (3) | 1473 | 635 | 261 | 23 | 282 | 0 | 26 | 163 | 0 | 1522 | 561 | 316 | 0.37 | 0.21 |
| (4) | 314 | 73 | 611 | 19 | 57 | 1 | 8 | 35 | 0 | 341 | 46 | 663 | 0.14 | 1.94 |
| B1_1000 h |
| (3) | 5351 | 2735 | 2026 | 58 | 2722 | 0 | 68 | 1551 | 0 | 5477 | 2592 | 2235 | 0.47 | 0.41 |
| (4) | 3326 | 506 | 4333 | 57 | 1306 | 0 | 50 | 765 | 0 | 3433 | 429 | 4555 | 0.13 | 1.33 |
| B2_8 h |
| (3) | 628 | 52 | 319 | 3 | 22 | 0 | 12 | 3 | 0 | 643 | 56 | 340 | 0.09 | 0.53 |
| (4) | 130 | 13 | 79 | 4 | 9 | 0 | 9 | 3 | 0 | 143 | 8 | 89 | 0.06 | 0.62 |
| B2_1000 h |
| (3) | 2476 | 1593 | 1608 | 11 | 330 | 1 | 42 | 289 | 0 | 2529 | 1531 | 1734 | 0.61 | 0.69 |
| (4) | 1897 | 290 | 1932 | 12 | 226 | 1 | 31 | 199 | 0 | 1940 | 245 | 2050 | 0.13 | 1.06 |
Table 8.
The Kappa statistics as measured using the correlation of the predictions between all runs of ConvoSource against PyBDSF, across all frequencies and exposure times at SNR = 2.
Table 8.
The Kappa statistics as measured using the correlation of the predictions between all runs of ConvoSource against PyBDSF, across all frequencies and exposure times at SNR = 2.
| | B1_8 h | B1_100 h | B1_1000 h | B2_8 h | B2_100 h | B2_1000 h |
|---|
| ConvoSource_None | 0.30 | 0.53 | 0.60 | 0.0 | 0.0 | 0.33 |
| ConvoSource_Extended | 0.30 | 0.62 | 0.57 | 0.0 | 0.0 | 0.29 |
| ConvoSource_All | 0.24 | 0.62 | 0.62 | 0.0 | 0.0 | 0.52 |
Table 9.
Showing all of the TP, FP, and FN across (3) ConvoSource augment all and (4) PyBDSF, at B1 8 h, B1 1000 h, B2 8 h, and B2 1000 h, at an SNR = 5. The symbols in the first row (e.g., SFG_tp, _fp and _fn) represent the SFG true positives, false positives, and false negatives, respectively. The same pattern applies to the SS, FS, and all sources combined in the following 9 columns. The final two columns refer to the ratio of false positives to true positives and the ratio of false negatives to true positives.
Table 9.
Showing all of the TP, FP, and FN across (3) ConvoSource augment all and (4) PyBDSF, at B1 8 h, B1 1000 h, B2 8 h, and B2 1000 h, at an SNR = 5. The symbols in the first row (e.g., SFG_tp, _fp and _fn) represent the SFG true positives, false positives, and false negatives, respectively. The same pattern applies to the SS, FS, and all sources combined in the following 9 columns. The final two columns refer to the ratio of false positives to true positives and the ratio of false negatives to true positives.
| Method | SFG_tp | _fp | _fn | SS_tp | _fp | _fn | FS_tp | _fp | _fn | All_tp | _fp | _fn | #fp/#tp | #fn/#tp |
|---|
| B1_8 h |
| (3) | 444 | 175 | 225 | 20 | 41 | 1 | 11 | 11 | 0 | 475 | 164 | 256 | 0.35 | 0.54 |
| (4) | 304 | 60 | 172 | 18 | 38 | 0 | 8 | 15 | 0 | 330 | 40 | 193 | 0.12 | 0.58 |
| B1_1000 h |
| (3) | 3478 | 1422 | 629 | 35 | 1075 | 0 | 45 | 573 | 0 | 3558 | 1311 | 738 | 0.37 | 0.21 |
| (4) | 3070 | 663 | 1124 | 57 | 892 | 0 | 45 | 473 | 0 | 3172 | 554 | 1247 | 0.18 | 0.39 |
| B2_8 h |
| (3) | 332 | 44 | 70 | 7 | 13 | 0 | 8 | 0 | 0 | 347 | 47 | 80 | 0.14 | 0.23 |
| (4) | 128 | 13 | 29 | 4 | 8 | 0 | 8 | 1 | 0 | 140 | 8 | 34 | 0.06 | 0.24 |
| B2_1000 h |
| (3) | 1980 | 974 | 514 | 13 | 168 | 0 | 29 | 115 | 0 | 2022 | 923 | 567 | 0.46 | 0.28 |
| (4) | 1857 | 280 | 587 | 12 | 149 | 0 | 28 | 102 | 0 | 1897 | 224 | 637 | 0.12 | 0.34 |
Table 10.
The Kappa statistics as measured using the correlation of the predictions between all runs of ConvoSource against PyBDSF, across all frequencies and exposure times at SNR = 5.
Table 10.
The Kappa statistics as measured using the correlation of the predictions between all runs of ConvoSource against PyBDSF, across all frequencies and exposure times at SNR = 5.
| | B1_8 h | B1_100 h | B1_1000 h | B2_8 h | B2_100 h | B2_1000 h |
|---|
| ConvoSource_None | 0.0 | 0.52 | 0.67 | 0.0 | 0.0 | 0.1 |
| ConvoSource_Extended | 0.0 | 0.53 | 0.73 | 0.0 | 0.0 | 0.37 |
| ConvoSource_All | 0.1 | 0.46 | 0.73 | 0.0 | 0.0 | 0.1 |
Table 11.
Time required (in min) to generate segmented versions of the real and source location (solution) maps. For the different runs of ConvoSource, the time required to augment different sets of sources (SS and FS images, and all images) is given, as well as the corresponding times required for training and testing. We also show the amount of time needed to predict the source locations for PyBDSF. The number after the underscore in the first row of the table refers to the SNR at the given exposure time.
Table 11.
Time required (in min) to generate segmented versions of the real and source location (solution) maps. For the different runs of ConvoSource, the time required to augment different sets of sources (SS and FS images, and all images) is given, as well as the corresponding times required for training and testing. We also show the amount of time needed to predict the source locations for PyBDSF. The number after the underscore in the first row of the table refers to the SNR at the given exposure time.
| | 8 h_1 | 8 h_2 | 8 h_5 | 100 h_1 | 100 h_2 | 100 h_5 | 1000 h_1 | 1000 h_2 | 1000 h_5 |
|---|
| B1 |
| Generate solutions | 2.9 | 2.5 | 3.3 | 2.9 | 2.7 | 2.5 | 3.2 | 4.5 | 2.6 |
| Generate real data | 2.5 | 4.5 | 2.4 | 3.8 | 2.9 | 2.6 | 3.0 | 4.7 | 5.0 |
| Augment SS + FS | 0.2 | 0.2 | 0.1 | 0.6 | 0.4 | 0.1 | 1.8 | 1.1 | 0.3 |
| Augment all | 21.2 | 16.0 | 21.2 | 21.5 | 28.5 | 21.3 | 21.3 | 17.1 | 17.0 |
| Train none | 38.0 | 23.1 | 18.0 | 15.6 | 42.7 | 26.4 | 13.2 | 24.7 | 8.0 |
| Train SS + FS | 39.6 | 26.7 | 20.6 | 15.3 | 24.4 | 32.6 | 37.7 | 25.2 | 35.1 |
| Train all | 109.9 | 126.3 | 120.7 | 79.5 | 111.1 | 145.1 | 69.1 | 81.1 | 99.6 |
| Test none | 0.7 | 0.5 | 0.4 | 0.5 | 1.2 | 0.5 | 0.6 | 0.5 | 0.5 |
| Test SS + FS | 1.1 | 0.5 | 0.4 | 0.5 | 0.5 | 0.5 | 0.7 | 0.5 | 0.5 |
| Test all | 0.5 | 0.5 | 0.4 | 0.5 | 0.7 | 0.5 | 0.5 | 0.6 | 0.5 |
| PyBDSF | 5.2 | 5.7 | 5.7 | 6.2 | 6.3 | 5.2 | 19.1 | 18.4 | 20.1 |
| B2 |
| Generate solutions | 3.6 | 3.2 | 4.0 | 4.6 | 3.1 | 3.4 | 3.2 | 6.4 | 3.5 |
| Generate real data | 3.0 | 5.1 | 3.8 | 3.3 | 3.3 | 3.1 | 3.1 | 4.1 | 6.2 |
| Augment SS + FS | 0.1 | 0.1 | 0.0 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2 | 0.1 |
| Augment all | 26.1 | 26.0 | 35.8 | 26.0 | 26.0 | 20.6 | 22.7 | 25.8 | 20.6 |
| Train none | 35.2 | 31.9 | 29.1 | 75.4 | 32.5 | 29.2 | 52.4 | 28.9 | 29.1 |
| Train SS + FS | 38.3 | 32.4 | 30.7 | 59.2 | 35.7 | 32.9 | 27.2 | 40.6 | 35.9 |
| Train all | 190.5 | 148.6 | 281.6 | 148.6 | 152.8 | 231.8 | 263.8 | 129.1 | 446.8 |
| Test none | 0.7 | 0.7 | 0.4 | 1.9 | 0.7 | 0.6 | 1.3 | 0.7 | 0.7 |
| Test SS + FS | 0.7 | 0.5 | 0.4 | 1.6 | 0.6 | 0.5 | 0.7 | 0.7 | 0.7 |
| Test all | 0.6 | 0.7 | 0.6 | 0.7 | 0.6 | 0.6 | 1.3 | 0.7 | 1.2 |
| PyBDSF | 8.6 | 6.8 | 5.9 | 23.2 | 21.5 | 22.2 | 21.2 | 22.1 | 21.4 |