1. Introduction
Large-scale magnetic fields are a prominent and widespread in disc galaxies [
1,
2,
3]. Their origin is most likely due to the mean-field dynamo action that relies on random (turbulent) motions of the partially ionised interstellar gas, galactic differential rotation, and stratification of the gas distribution in the galactic gravity field. The mean-field dynamo theory (for a review, see [
4]) explains many salient properties of galactic magnetic fields [
5] (for a compendium of basic results, see [
6]). Galactic dynamo theory has been applied, with a significant success, to a number of specific spiral galaxies, including the Milky Way, M31, M33, M51 [
7], and a sample of barred galaxies ([
8] and references therein). Statistical comparisons of theory and observations of galactic magnetic fields can be found in Van Eck et al. [
9] and Chamandy et al. [
10]. Rodrigues et al. [
11,
12] discuss galactic mean-field dynamos in the context of galaxy formation theory.
Applications of the mean-field dynamo theory to galaxies are facilitated by the fact that the discs of spiral galaxies are thin (beyond a few hundred parsecs from the rotational axis) as the ratio of their scale height to radius is much less than unity, . Near the Sun, this ratio is about 0.06 for the warm interstellar gas () and the galactocentric distance . Asymptotic expansion in reduces the mean-field dynamo equations to tractable forms that can be efficiently analysed using both analytical and numerical methods.
Dynamo action is a threshold phenomenon: for a magnetic field to be sustained by plasma motions, the strength of magnetic induction effects due to large-scale and turbulent flows has to exceed the intensity of dissipation. In the case of a mean (large-scale) magnetic field, the main dissipation mechanism is the turbulent magnetic diffusion. The intensity of the mean-field dynamo action is measured by the dynamo number
D that can be expressed (in a simplified form) in terms of observable quantities as (for details, see [
1])
where
is a measure of the mean helicity of the turbulent motions;
is the angular velocity of galactic rotation;
is the shear rate of the rotation (
r is the galactocentric distance);
h is the scale height of the gas disc,
is the turbulent magnetic diffusivity; and
and
are the turbulent scale and root-mean-square speed. (We note that
D is negative in the main parts of galaxies since
, so
.) A central result of the theory of mean-field dynamo in a thin disc is the marginal value of the dynamo number required for the dynamo action,
: the magnetic field can grow and be maintained by interstellar turbulence and rotation when the magnitude of the dynamo number is large enough,
, and it decays otherwise. We stress—this will be essential later—that this value of
only applies to a
thin disc,
.
Despite successes of the galactic dynamo theory, there is a class of galaxies whose large-scale magnetic fields were hitherto unexplainable; namely, the low-mass (dwarf and irregular) galaxies. In some but not all nearby dwarf galaxies, radio observations of synchrotron polarisation and Faraday rotation have revealed magnetic fields ordered on scales comparable to the galaxy size and exceeding the turbulent scales. Their strength is similar to, albeit often weaker than, that in normal galaxies, e.g., in NGC 4449 [
13], the Large and Small Magellanic Clouds [
14,
15,
16] and NGC 1569 [
17]. Chyzy et al. [
18] detected synchrotron emission indicating random magnetic fields in three (IC 10, NGC 6822, and IC 1613) out of twelve Local Group irregular and dwarf irregular galaxies, with the upper limits of 3–5
G for the total magnetic fields in the remaining cases. Hindson et al. [
19] detected radio emission at
from 22 out of 40 nearby dwarf galaxies to find the average strength of the total magnetic field of 5–8
G (comprised of both random and possible large-scale parts) assuming energy equipartition between cosmic rays and magnetic fields. Rodrigues et al. [
12] found that 20%–50% of low-mass galaxies might host detectable large-scale magnetic fields, in agreement with (see arXiv:1302.5663 for an up-to-date list of galaxies) Beck and Wielebinski [
20].
In comparison with large spiral galaxies, dwarf and irregular galaxies have lower masses and correspondingly shallower gravitational potential wells. As a result, they have lower rotation speeds of the order of 50–100
or less, but a similarly intense turbulence (see, e.g., Table 3 in [
18] and references therein). For example, the maximum rotation speeds of IC 2574 and IC 10 are about
and
, respectively [
21,
22]. Rotation is often closer to solid-body than in spiral galaxies [
23,
24]; as an extreme example, the maximum rotation speed in IC 2574 is reached at the galactocentric distance of about
[
21,
25], suggesting a typical angular velocity
. Typical mean circular velocities in a sample of 17 dwarf irregular galaxies [
24] range from 16 to
; their H
i velocity dispersion is 8–
; and the radius of the observable H
i disc is 0.4–
. The 26 dwarf galaxies observed in H
i by Oh et al. [
23] have maximum rotational velocities of 12–
reached at galactocentric distances 0.3–
.
Residing in a shallower gravitational potential, the gas discs of dwarf galaxies are 3–4 times thicker than in massive spirals. In IC 2574, the H
i scale height is estimated as
(and the H
i volume density of
), whereas the one-dimensional velocity dispersion is
. Similarly,
in Ho II, and
in NGC 5023 [
21]. The aspect ratio of the neutral hydrogen discs of dwarf galaxies is about 10:1 as opposed to 100:1 in massive disc galaxies [
21]. The mean H
i axial ratio among 36 low surface brightness and blue compact galaxies is 0.58 [
26]—these are not flat objects. Roychowdhury et al. [
27] estimated the axial ratio to be about
for the faintest dwarf galaxies. As in spiral galaxies, their gas discs are flared at galactocentric distances exceeding (3–4)
, where
is the radial scale length of the stellar disc:
1.2, 2.1, and
in the four dwarf galaxies modelled by Banerjee et al. [
28], DDO 154, Ho II, IC 2574 and NGC 2366, respectively.
Because of the slow rotation, the typical magnitude of the dynamo number (
1) in the low-mass galaxies is of order unity,
significantly smaller by magnitude than
required for the mean-field dynamo action in a thin gas layer. This has prompted suggestions that magnetic fields observed in dwarf and irregular galaxies are due to the fluctuation dynamo action that does not require any overall rotation and generates random magnetic fields with vanishing mean [
4,
7,
29]. To explain the polarisation of observed radio emission, it is further suggested that differential rotation makes the random field anisotropic. However, the rotational velocity shear
S is also weak in low-mass galaxies, and such an option does not appear appealing. Moss and Sokoloff [
30] suggest that random magnetic fields generated by the fluctuation dynamo in the disc of a dwarf galaxy can be transported by a galactic outflow to the halo where their scale increases as the gas expands. As the random magnetic fields decay, those of a larger scale survive for longer, and the scale of the magnetic field increases as it decays. However, the scale of the random magnetic field in the halo remains much smaller than the size of the galaxy (especially at smaller distances from the disc where the advected random magnetic field has not yet decayed significantly) and this process can hardly explain the polarisation patterns observed to be ordered over several kiloparsecs. Such patterns occur in low-mass galaxies observed
both face-on and edge-on, suggesting that the polarised emission also originates in the disc rather than in the halo alone. There is little doubt that at least some low-mass galaxies host genuine mean magnetic fields that produce significant Faraday rotation. As in other galaxies, primordial magnetic fields are not a viable option because of the high intensity of turbulent motions.
The dominant dissipation mechanism of the large-scale magnetic field in a thin layer is turbulent diffusion
across it,
, where
is the turbulent magnetic diffusivity,
is the turbulent scale, and
h is the half-thickness (scale height) of the warm ionised gas layer. In spiral galaxies with
and
, we have
. This time scale is larger in a thick disc compared to a thin disk, which reduces the relative importance of dissipation compared to the magnetic induction effects, and the mean-fled dynamo is easier to excite in a thick layer than in a thin one. The radial diffusion also becomes more important in a thick disk, and then the magnitude of the critical dynamo number
increases with the layer thickness. However, the dynamo number increases even faster, so that the ratio
, a measure of the dynamo efficiency, is higher in a thicker disc (with all other parameters being the same). Similarly to this tendency, the dynamo efficiency in spheroids increases along the sequence from a flattened spheroid to the sphere [
31]. Stix [
32], Brandenburg et al. [
33], and Elstner et al. [
34] also show that mean-field dynamos are more efficient in thicker discs and oblate spheroids, and that magnetic fields of the quadrupolar symmetry are generated at smaller dynamo numbers than the dipolar fields.
Siejkowski et al. [
35] (see also [
36,
37]) present numerical simulations of the mean-field dynamo action in low-mass galaxies but adopt turbulent magnetic diffusivity of
, three times lower than the more plausible value of
. The spatial resolution of the simulations, 47 or
, is close to the turbulent scale, so that turbulent motions are not resolved and the adopted value of
is likely to be close to the effective one in the simulations. As shown in Equation (
1), the dynamo number in those simulations can, thus, be overestimated by a factor
and the efficiency of the dynamo action appears to be exaggerated, which makes the significance of these results questionable.
In this paper, we discuss solutions of the mean-field dynamo equation in thick discs to demonstrate that it can explain the amplification and maintenance of large-scale magnetic fields in low-mass galaxies. Having presented basic equations in
Section 2, we discuss dynamo action in a thick disc in
Section 3 where the value of
is estimated and the corresponding minimum rotational speed required for the dynamo action in a thick disc is derived. Numerical solutions of the dynamo equation are presented in
Section 4 and explored in
Section 5 with emphasis on the dependence of
and the corresponding critical rotational speed on the disc aspect ratio; the accuracy of the estimates of
Section 3 is confirmed. The results are discussed and summarised in
Section 6.
2. Basic Equations
The generation of a mean (large-scale) magnetic field
by a random velocity field is governed by the mean-field dynamo equation [
38,
39,
40,
41]
where
is the large-scale velocity dominated by rotation with the angular velocity
and the effects of galactic random flows (turbulence) are represented by the turbulent transport coefficients
(where
is the turbulent scale and
h is the density scale height), which depends on the mean helicity of the turbulence
, and turbulent diffusivity
(assumed to be much larger than the Ohmic magnetic diffusivity), with
the turbulent velocity field,
, its correlation time and angular brackets denote an appropriate average over the turbulent fluctuations.
We model a galaxy as an axisymmetric disc with a Brandt rotation curve
,
in terms of cylindrical polar coordinates
, with
, where
and
are the characteristic velocity and radial scale length. The corresponding velocity shear rate is defined as
. The half-thickness (or scale height) of the ionised gas disc is denoted
h. For the interstellar turbulence, we assume that the correlation scale,
and speed
, are both similar to those in spiral galaxies.
We consider the simplest axisymmetric solutions to the mean-field equation, and so the mean magnetic field can be written as
where
and
are the azimuthal components of the magnetic field and the vector potential, respectively, and
is the unit azimuthal vector. The assumption of axial symmetry may be rather crude when applied to low-mass galaxies but it is sufficient to assess the possibility of the mean-field dynamo action, our main goal in this paper. More realistic non-axisymmetric solutions and non-axisymmetric galaxies will be discussed elsewhere.
We use dimensionless variables, here denoted with tilde, defined in terms of the characteristic values denoted with subscript zero:
where
and we drop tilde at the dimensionless variables unless specified otherwise or obvious from the context. Since we here only consider kinematic dynamo solutions that vary exponentially in time, the characteristic magnetic field
can be chosen arbitrarily and can be used to normalise the results as convenient.
We consider a flat gas layer with
. Disc flaring can easily be included [
1] but it does not change our conclusions regarding the possibility of dynamo action at relatively small galactocentric distances although the radial distribution of magnetic field can be affected (e.g., [
42]). The coefficient
is assumed to be factorisable:
since
, where we adopt
for numerical solutions; this choice affects the results only weakly.
In terms of the dimensionless variables, the cylindrical components of the dynamo equation reduce to
where
and we note that
and
are functions of position. Magnetic induction effects are quantified by dimensionless dynamo numbers
for the differential rotation and
for the helical turbulence. The dynamo system is controlled by three dimensionless parameters,
,
, and
via
An advantage of selecting (the radial scale of the rotation curve) as the unit radial length is that the estimates and numerical results presented below are insensitive to the specific value of , as this parameter enters the results only via the disc aspect ratio .
When the term with
in Equation (
8) is neglected, the dynamo system is called the
-dynamo and its efficiency is fully characterised by the single dimensionless number, the dynamo number
This approximation is appropriate when the differential rotation is sufficiently strong to have . Otherwise, the dynamo is known as the -dynamo, characterised by two dimensionless numbers, and , or, equivalently, and D. For parameter values typical of low-mass galaxies, , 5–10 and , we get 1.5–3 and 30–70.
3. Mean-Field Dynamo in a Thick Disc
As any other dynamo mechanism, the mean-field dynamo is a threshold phenomenon: the mean magnetic field can be amplified and then maintained against turbulent diffusion only if the induction effects are strong enough. When differential rotation is strong (the -dynamo approximation), the mean magnetic field grows and then reaches a steady state if for a certain and decays if .
In galaxies with significant differential rotation, it dominates over the
-effect in Equation (
8) and the term with
can be neglected in this equation. To obtain an estimate of the dynamo threshold in a thick disc of a dwarf galaxy, we note that, in terms of dimensionless variables, spatial derivatives in Equations (
8) and (9) are of order unity in
. In the spirit of the no-
z approximation introduced by Subramanian and Mestel [
43] and refined by Phillips [
44] (details and further justification can be found in [
45]), we get the following estimates:
,
and
, and similar ones for the derivatives of
. The negative sign in the second derivatives follows from the properties of the diffusion operator and
k is a constant of order unity.
The dynamo is called marginal when
; this state corresponds to the marginal value of the dynamo number
, where
and
are the values of
and
S in the radius, averaged (note that
; hence,
, and both
and
are dimensionless, so of order unity). For the marginal state, Equations (
8) and (9) reduce, by the order of magnitude in
, to
leading to an order of magnitude estimate
where we adopt
. Combining the estimate of
with Equation (
12), we obtain a measure of the local dynamo efficiency as
confirming that the mean-field dynamo is more efficient in a thicker disc: this ratio increases with
for
, with the right-had side smaller than unity for
.
This estimate can also be rewritten in terms of the rotational velocity: magnetic field can be maintained when the characteristic rotation speed
exceeds a critical value
given by
and
decreases with
for
. This confirms again that the mean-field dynamo is easier to excite in a thicker disc.
It is convenient to introduce the local dynamo number
a function of galactocentric radius that quantifies the dynamo efficiency at a given
r. For a magnetic field growing at an exponential growth rate
, i.e.,
and
, estimates similar to those presented above yield
, or in dimensional variables, the local dynamo amplification (e-folding) time is estimated, for
, as
where the numerical value is obtained for
,
,
,
,
and
.
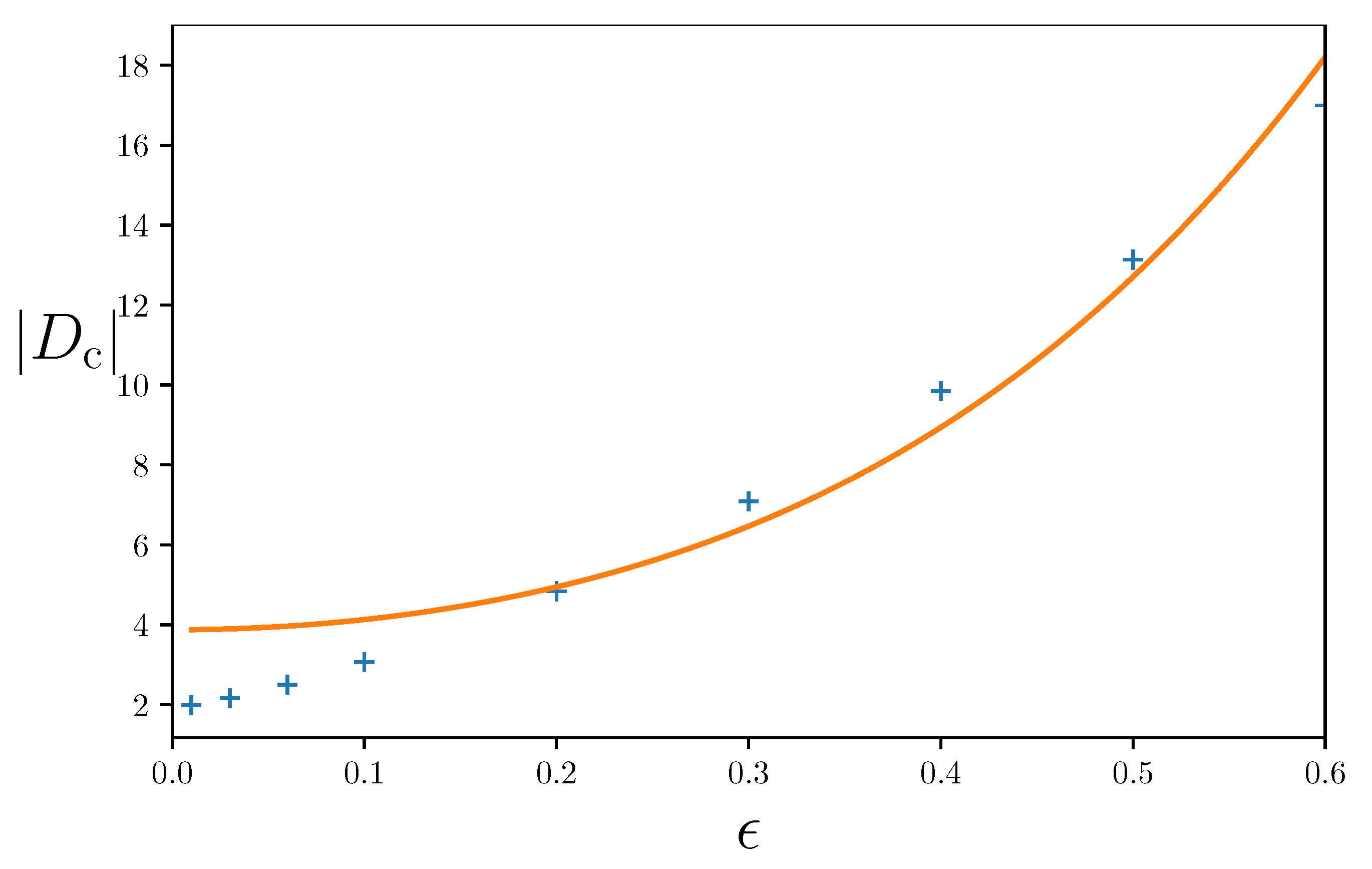
The ratio and are maximal, whereas is the minimum, for the mode with the radial wave number . For this leading mode, we obtain and , with the numerical value obtained for .
These estimates implicitly assume the quadrupolar parity of the large-scale magnetic field since the relations like
,
and
only apply in this case. The asymptotic solution for
[
46] (not presented here) shows that dipolar modes have much higher values of
and
and are oscillatory.
4. Numerical Solutions
We confirmed those estimates using numerical solutions of the dynamo equation in a thick disc. Equations (
8) and (9) were solved within a rectangle
in the
-plane. We adopted
and verified that the results were not sensitive to the position of the outer radial boundary when
3–10. The boundary conditions adopted in radius,
at
correspond to vanishing diffusive flux of magnetic field. The boundary conditions on the disc surface,
at
, apply when large-scale electric currents outside the disc are much weaker than those within the disc (the vacuum boundary conditions). The boundary condition for
at
is an approximation to
, and its accuracy reduces as
increases ([
5] and references therein). Boundary conditions at the disc mid-plane control the symmetry (either quadrupolar/even or dipolar/odd parity) of the magnetic field across the disc (see [
1] for details)
and we are free to consider the range
because of the symmetry of the solutions. The initial magnetic field is of a large scale, with sinusoidal variation in both
r and
z to satisfy the boundary conditions and has the average strength
in dimensionless units (its magnitude does not, in fact, matter as long as kinematic dynamo solutions are considered).
The solutions were obtained for the rotation curve (
4) and
in dimensionless units. Forward time stepping was performed using the fourth-order Runge–Kutta scheme and central finite differences were used for the spatial derivatives. The consistency of the results was verified by increasing the grid resolution. Here, we present results for
and
grids, with a uniform spacing in both radial and vertical directions (in terms of dimensionless variables).
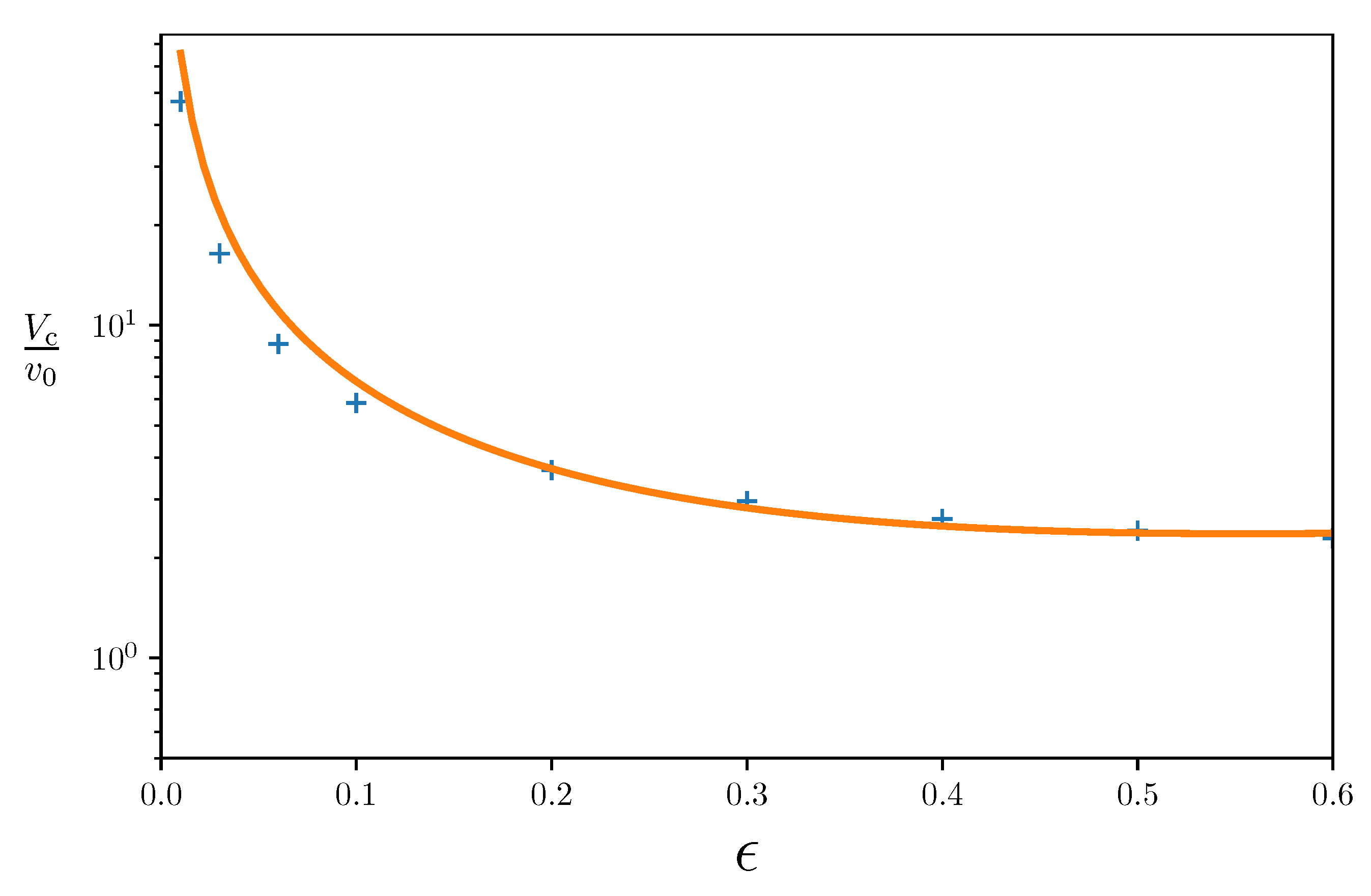
An efficient technique [
47] to find the critical value of the dynamo number,
, for a given
is to solve the dynamo equations for a sufficiently large (supercritical)
with a modified form of the coefficient,
, that depends on
(so that the field is eventually driven to a steady state) but has the same spatial form as
at all times:
where
is the volume of the computational domain, and we used dimensional variables. The value of
in the steady state (when
no longer varies with
t) for
in Equations (
10) and (
12) yields
.