Properties of Subhalos in the Interacting Dark Matter Scenario
Abstract
1. Introduction
2. Interacting Dark Matter
3. Simulations
4. Results
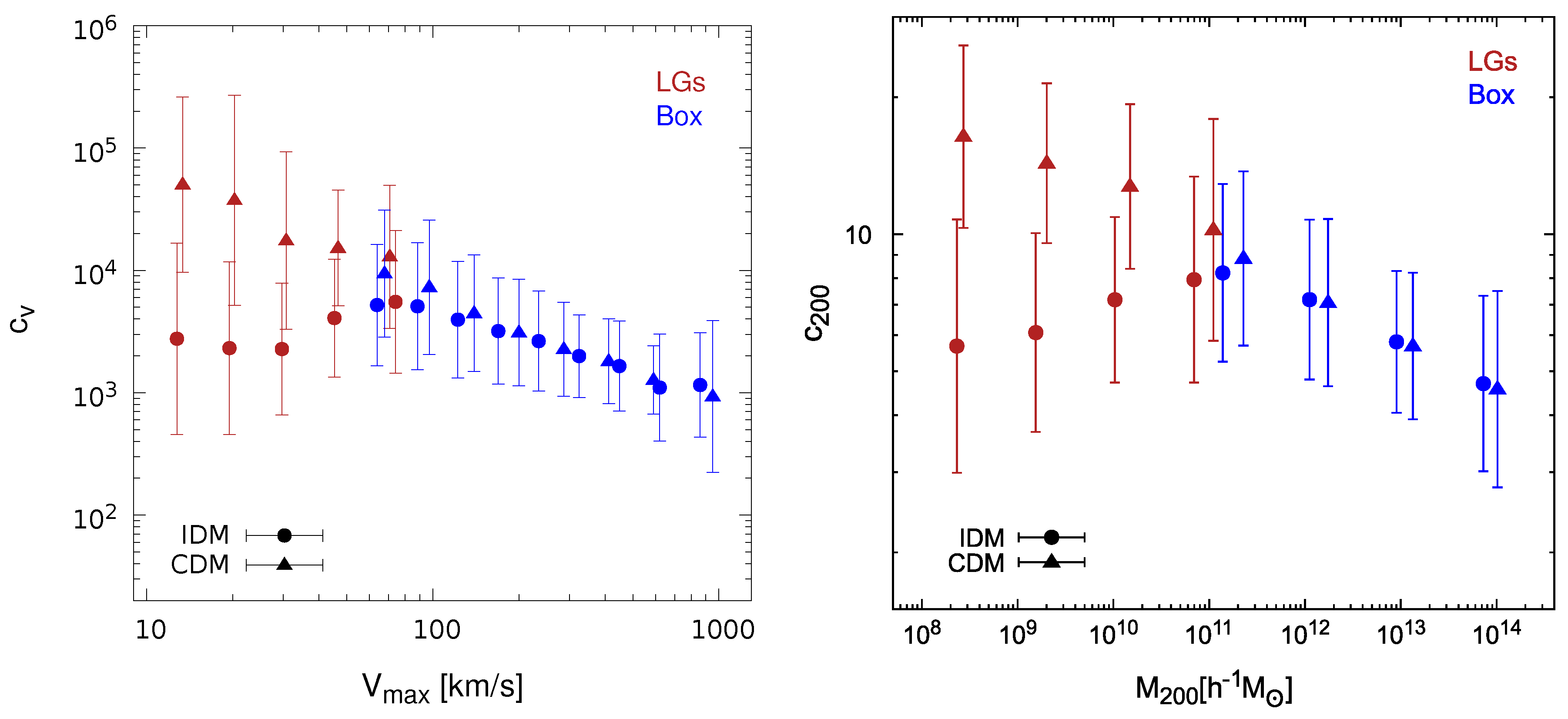
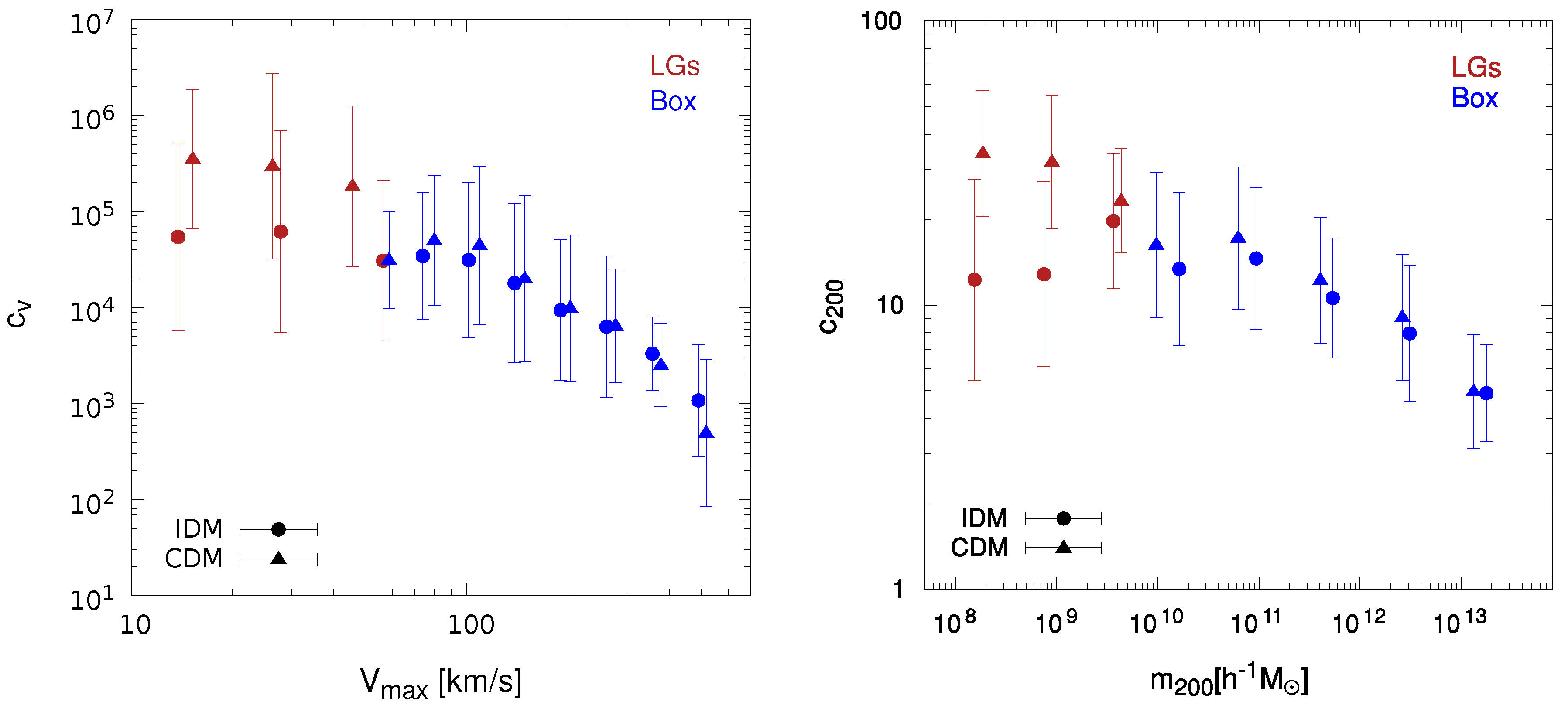
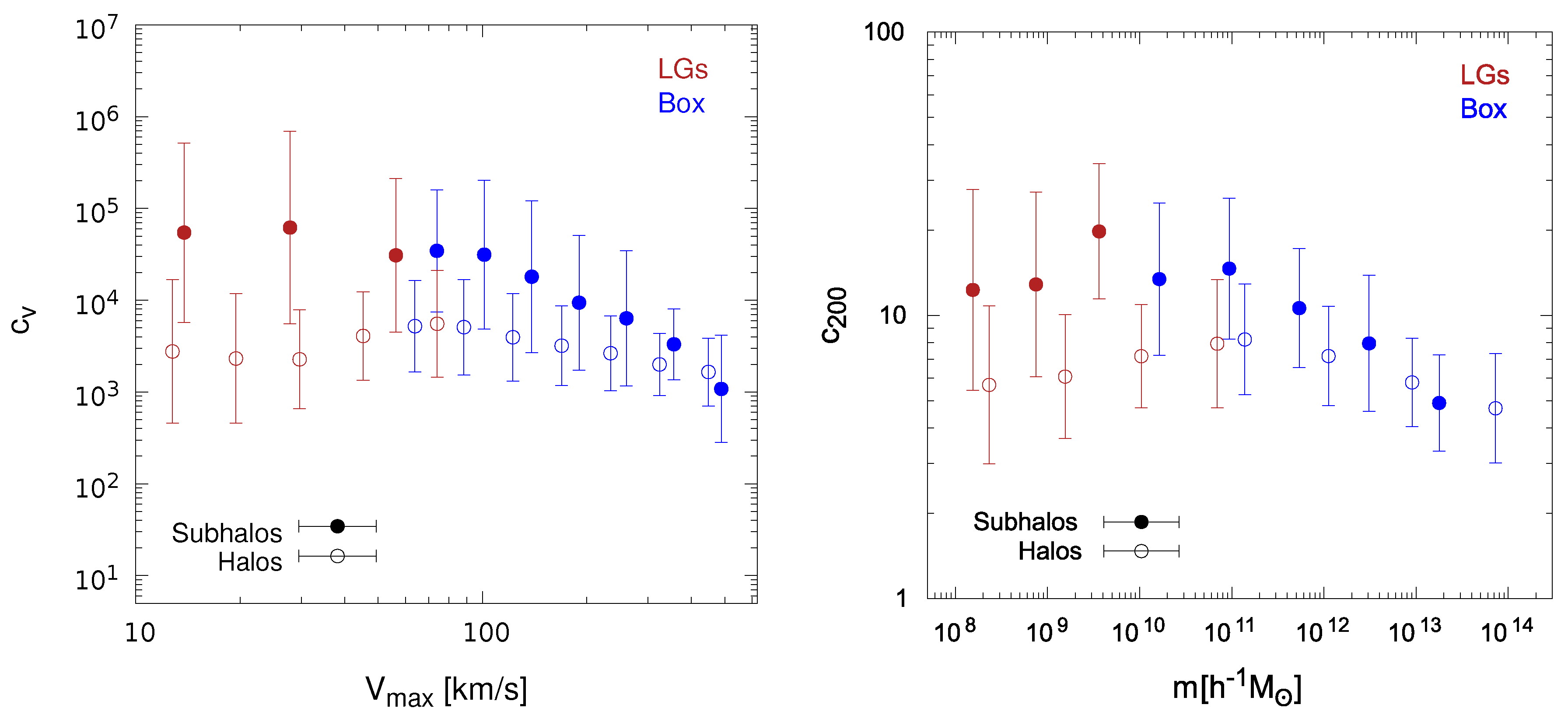
4.1. Halo Concentrations
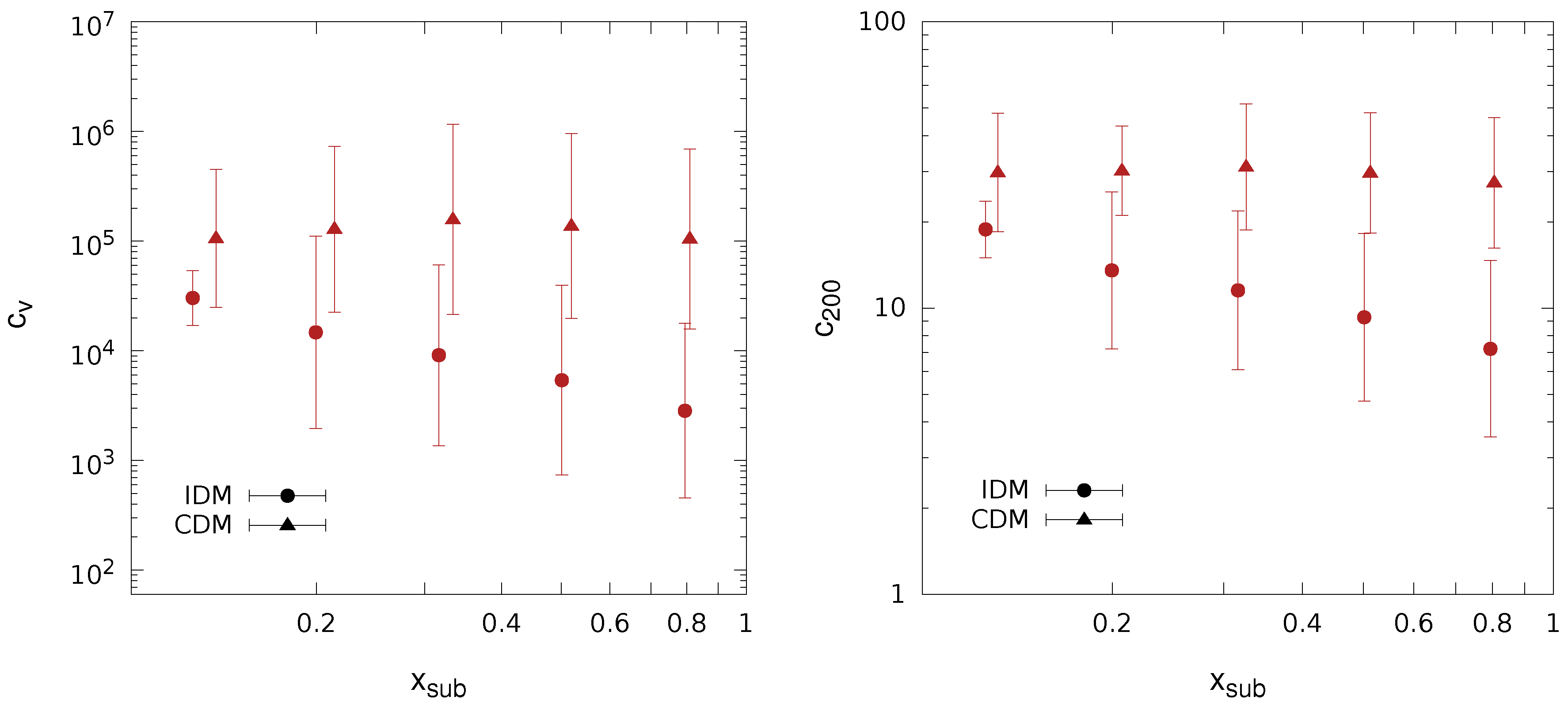
4.2. Subhalo Concentrations
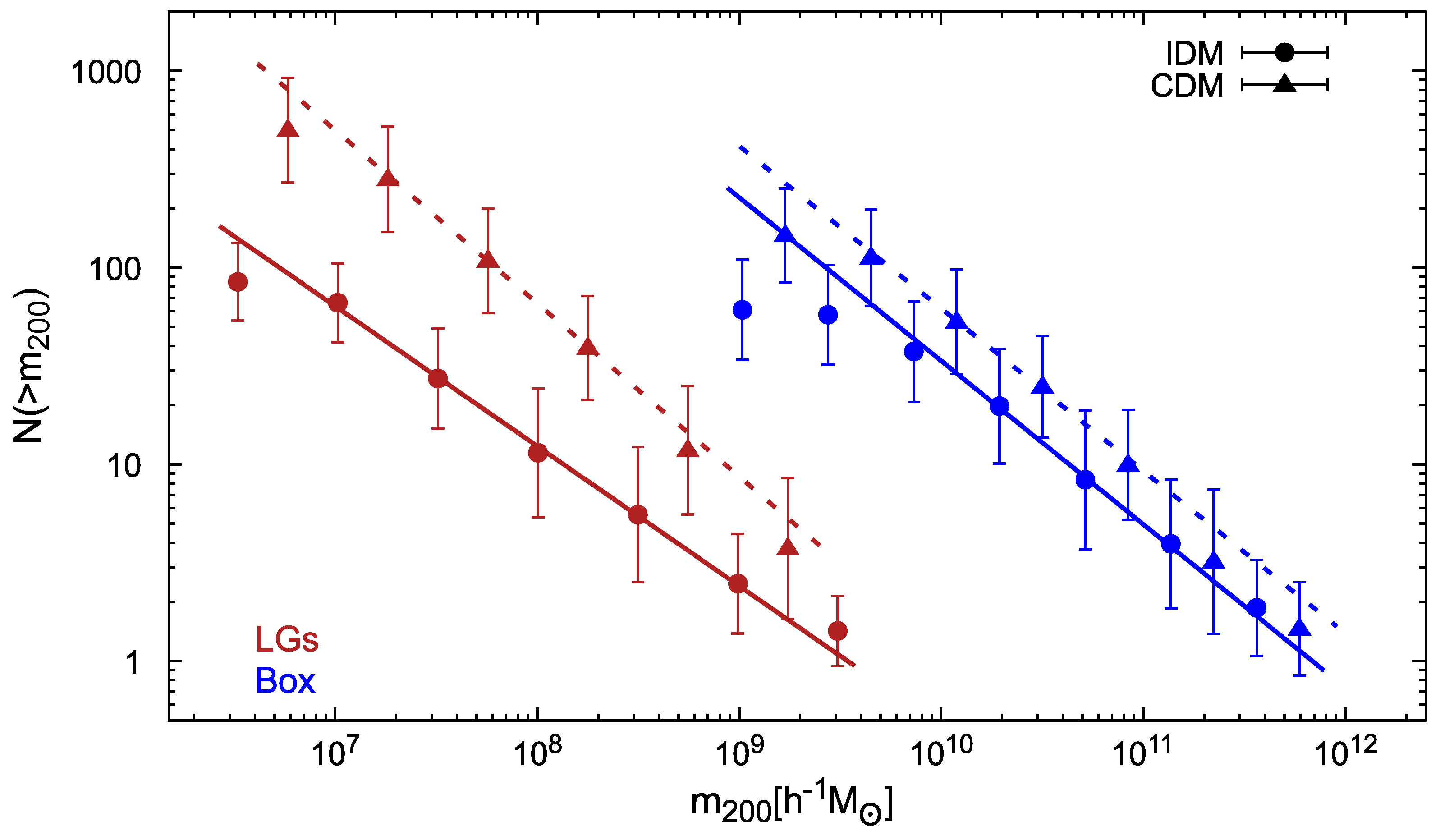
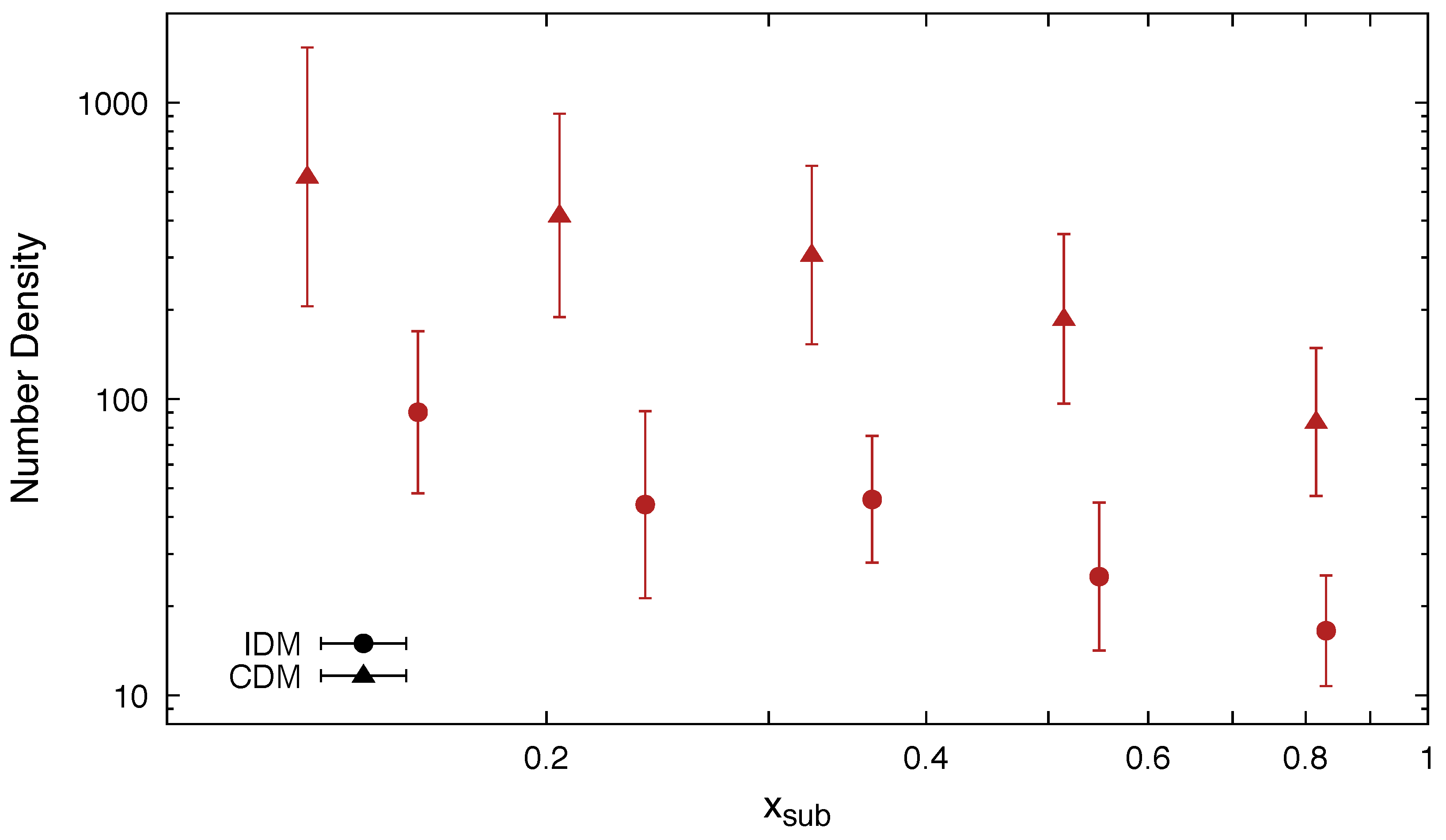
4.3. Subhalo Abundances
5. Summary and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:astro-ph.CO/1807.06209. [Google Scholar]
- Frenk, C.S.; White, S.D.M. Dark matter and cosmic structure. Ann. Phys. 2012, 524, 507–534. [Google Scholar] [CrossRef]
- Netterfield, C.B.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Contaldi, C.R.; Crill, B.P.; de Bernardis, P. A measurement by Boomerang of multiple peaks in the angular power spectrum of the cosmic microwave background. Astrophys. J. 2002, 571, 604–614. [Google Scholar] [CrossRef]
- Hinshaw, G.; Barnes, C.; Bennett, C.L.; Greason, M.R.; Halpern, M.; Hill, R.S.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Data processing methods and systematic errors limits. Astrophys. J. Suppl. 2003, 148, 63. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Davis, T.M.; Mörtsell, E.; Sollerman, J.; Becker, A.C.; Blondin, S.; Challis, P.; Clocchiatti, A.; Filippenko, A.V.; Foley, R.J.; Garnavich, P.M.; et al. Scrutinizing Exotic Cosmological Models Using ESSENCE Supernova Data Combined with Other Cosmological Probes. Astrophys. J. 2007, 666, 716–725. [Google Scholar] [CrossRef]
- Hamuy, M. The acceleration of the Universe in the light of supernovae - The key role of the Cerro Tololo Inter-American Observatory. arXiv 2013, arXiv:astro-ph.CO/1311.5099. [Google Scholar]
- Klypin, A.A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where are the missing Galactic satellites? Astrophys. J. 1999, 522, 82–92. [Google Scholar] [CrossRef]
- Moore, B.; Ghigna, S.; Governato, F.; Lake, G.; Quinn, T.; Stadel, J.; Tozzi, P. Dark matter substructure within galactic halos. Astrophys. J. 1999, 524, L19–L22. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. Too big to fail? The puzzling darkness of massive Milky Way subhaloes. Mon. Not. R. Astron. Soc. 2011, 415, L40–L44. [Google Scholar] [CrossRef]
- Dubinski, J.; Carlberg, R.G. The structure of cold dark matter halos. Astrophys.J. 1991, 378, 496–503. [Google Scholar] [CrossRef]
- Goetz, M.; Sommer-Larsen, J. Galaxy formation: Warm dark matter, missing satellites, and the angular momentum problem. Astrophys. Space Sci. 2003, 284, 341–344. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Loeb, A. Subhaloes in Self-Interacting Galactic Dark Matter Haloes. Mon. Not. R. Astron. Soc. 2012, 423, 3740. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.S.; Fattahi, A.; Navarro, J.F.; Bower, R.G.; Crain, R.A.; Vecchia, C.D.; Furlong, M.; Helly, J.C.; Jenkins, A.; et al. The APOSTLE simulations: Solutions to the Local Group’s cosmic puzzles. arXiv 2015, arXiv:1511.01098. [Google Scholar] [CrossRef]
- Kim, S.Y.; Peter, A.H.G.; Hargis, J.R. Missing Satellites Problem: Completeness Corrections to the Number of Satellite Galaxies in the Milky Way are Consistent with Cold Dark Matter Predictions. Phys. Rev. Lett. 2018, 121, 211302. [Google Scholar] [CrossRef]
- Renaud, F.; Bournaud, F.; Emsellem, E.; Elmegreen, B.; Teyssier, R.; Alves, J.; Chapon, D.; Combes, F.; Dekel, A.; Gabor, J.; et al. A sub-parsec resolution simulation of the Milky Way: Global structure of the interstellar medium and properties of molecular clouds. Mon. Not. R. Astron. Soc. 2013, 436, 1836–1851. [Google Scholar] [CrossRef]
- Rosdahl, J.; Schaye, J.; Dubois, Y.; Kimm, T.; Teyssier, R. Snap, crackle, pop: Sub-grid supernova feedback in AMR simulations of disc galaxies. Mon. Not. R. Astron. Soc. 2016, 466, 11–33. [Google Scholar] [CrossRef]
- Pillepich, A.; Springel, V.; Nelson, D.; Genel, S.; Naiman, J.; Pakmor, R.; Hernquist, L.; Torrey, P.; Vogelsberger, M.; Weinberger, R.; et al. Simulating galaxy formation with the IllustrisTNG model. Mon. Not. R. Astron. Soc. 2017, 473, 4077–4106. [Google Scholar] [CrossRef]
- Springel, V.; Pakmor, R.; Pillepich, A.; Weinberger, R.; Nelson, D.; Hernquist, L.; Vogelsberger, M.; Genel, S.; Torrey, P.; Marinacci, F.; et al. First results from the IllustrisTNG simulations: Matter and galaxy clustering. Mon. Not. R. Astron. Soc. 2017, 475, 676–698. [Google Scholar] [CrossRef]
- Read, J.I.; Gilmore, G. Mass loss from dwarf spheroidal galaxies: The origins of shallow dark matter cores and exponential surface brightness profiles. Mon. Not. R. Astron. Soc. 2005, 356, 107–124. [Google Scholar] [CrossRef]
- Navarro, J.F.; Eke, V.R.; Frenk, C.S. The cores of dwarf galaxy haloes. Mon. Not. R. Astron. Soc. 1996, 283, L72–L78. [Google Scholar] [CrossRef]
- Bode, P.; Ostriker, J.P.; Turok, N. Halo formation in warm dark matter models. Astrophys. J. 2001, 556, 93–107. [Google Scholar] [CrossRef]
- Bose, S.; Hellwing, W.A.; Frenk, C.S.; Jenkins, A.; Lovell, M.R.; Helly, J.C.; Li, B.; Gonzalez-Perez, V.; Gao, L. Substructure and galaxy formation in the Copernicus Complexio warm dark matter simulations. Mon. Not. R. Astron. Soc. 2016, 464, 4520–4533. [Google Scholar] [CrossRef]
- Rocha, M.; Peter, A.H.; Bullock, J.S.; Kaplinghat, M.; Garrison-Kimmel, S.; Onorbe, J.; Moustakas, L.A. Cosmological simulations with self-interacting dark matter—I. Constant-density cores and substructure. Mon. Not. R. Astron. Soc. 2013, 430, 81–104. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Simpson, C.; Jenkins, A. Dwarf galaxies in CDM and SIDM with baryons: Observational probes of the nature of dark matter. Mon. Not. R. Astron. Soc. 2014, 444, 3684–3698. [Google Scholar] [CrossRef]
- Bernal, N.; Cosme, C.; Tenkanen, T. Phenomenology of self-interacting dark matter in a matter-dominated universe. Eur. Phys. J. C 2019, 79, 99. [Google Scholar] [CrossRef]
- Boehm, C.; Fayet, P.; Schaeffer, R. Constraining dark matter candidates from structure formation. Phys. Lett. B 2001, 518, 8–14. [Google Scholar] [CrossRef]
- Boehm, C.; Riazuelo, A.; Hansen, S.H.; Schaeffer, R. Interacting dark matter disguised as warm dark matter. Phys. Rev. D 2002, 66, 083505. [Google Scholar] [CrossRef]
- Boehm, C.; Schaeffer, R. Constraints on dark matter interactions from structure formation: Damping lengths. Astron. Astrophys. 2005, 438, 419–442. [Google Scholar] [CrossRef]
- Chung, D.; Everett, L.; Kane, G.; King, S.; Lykken, J.; Wang, L.T. The soft supersymmetry-breaking Lagrangian: Theory and applications. Phys. Rep. 2005, 407, 1–203. [Google Scholar] [CrossRef]
- Servant, G.; Tait, T.M. Is the lightest Kaluza–Klein particle a viable dark matter candidate? Nucl. Phys. B 2003, 650, 391–419. [Google Scholar] [CrossRef]
- Fox, P.J.; Poppitz, E. Leptophilic dark matter. Phys. Rev. D 2009, 79, 083528. [Google Scholar] [CrossRef]
- Fox, P.J.; Harnik, R.; Kopp, J.; Tsai, Y. LEP shines light on dark matter. Phys. Rev. D 2011, 84, 014028. [Google Scholar] [CrossRef]
- Schewtschenko, J.A.; Wilkinson, R.J.; Baugh, C.M.; Bœhm, C.; Pascoli, S. Dark matter–radiation interactions: The impact on dark matter haloes. Mon. Not. R. Astron. Soc. 2015, 449, 3587–3596. [Google Scholar] [CrossRef]
- Sigurdson, K.; Doran, M.; Kurylov, A.; Caldwell, R.R.; Kamionkowski, M. Dark-matter electric and magnetic dipole moments. Phys. Rev. D 2004, 70, 083501. [Google Scholar] [CrossRef]
- Mangano, G.; Melchiorri, A.; Serra, P.; Cooray, A.; Kamionkowski, M. Cosmological bounds on dark matter-neutrino interactions. Phys. Rev. D 2006, 74, 043517. [Google Scholar] [CrossRef]
- Serra, P.; Zalamea, F.; Cooray, A.; Mangano, G.; Melchiorri, A. Constraints on neutrino—Dark matter interactions from cosmic microwave background and large scale structure data. Phys. Rev. D 2010, 81, 043507. [Google Scholar] [CrossRef]
- Wilkinson, R.J.; Lesgourgues, J.; Boehm, C. Using the CMB angular power spectrum to study Dark Matter-photon interactions. J. Cosmol. Astropart. Phys. 2014, 1404, 026. [Google Scholar] [CrossRef]
- Wilkinson, R.J.; Boehm, C.; Lesgourgues, J. Constraining Dark Matter-Neutrino Interactions using the CMB and Large-Scale Structure. J. Cosmol. Astropart. Phys. 2014, 1405, 011. [Google Scholar] [CrossRef]
- Cyr-Racine, F.Y.; de Putter, R.; Raccanelli, A.; Sigurdson, K. Constraints on Large-Scale Dark Acoustic Oscillations from Cosmology. Phys. Rev. 2014, D89, 063517. [Google Scholar] [CrossRef]
- Collett, T.E.; Buckley-Geer, E.; Lin, H.; Bacon, D.; Nichol, R.C.; Nord, B.; Morice-Atkinson, X.; Amara, A.; Birrer, S.; Kuropatkin, N.; et al. Core or Cusps: The Central Dark Matter Profile of a Strong Lensing Cluster with a Bright Central Image at Redshift 1. Astrophys. J. 2017, 843, 148. [Google Scholar] [CrossRef]
- Neyman, J.; Scott, E.L. A Theory of the Spatial Distribution of Galaxies. Astrophys. J. 1952, 116, 144. [Google Scholar] [CrossRef]
- Scherrer, R.J.; Bertschinger, E. Statistics of primordial density perturbations from discrete seed masses. Astrophys. J. 1991, 381, 349–360. [Google Scholar] [CrossRef]
- Cooray, A.; Sheth, R. Halo models of large scale structure. Phys. Rep. 2002, 372, 1–129. [Google Scholar] [CrossRef]
- Ullio, P.; Bergström, L.; Edsjö, J.; Lacey, C. Cosmological dark matter annihilations into γ rays: A closer look. Phys. Rev. D 2002, 66, 123502. [Google Scholar] [CrossRef]
- Moliné, Á.; Ibarra, A.; Palomares-Ruiz, S. Future sensitivity of neutrino telescopes to dark matter annihilations from the cosmic diffuse neutrino signal. J. Cosmol. Astropart. Phys. 2015, 2015, 005. [Google Scholar] [CrossRef]
- Sánchez-Conde, M.A.; Prada, F. The flattening of the concentration–mass relation towards low halo masses and its implications for the annihilation signal boost. Mon. Not. R. Astron. Soc. 2014, 442, 2271–2277. [Google Scholar] [CrossRef]
- Fermi LAT Collaboration. Limits on dark matter annihilation signals from the Fermi LAT 4-year measurement of the isotropic gamma-ray background. J. Cosmol. Astropart. Phys. 2015, 2015, 008. [Google Scholar] [CrossRef]
- Moliné, A.; Sánchez-Conde, M.A.; Palomares-Ruiz, S.; Prada, F. Characterization of subhalo structural properties and implications for dark matter annihilation signals. Mon. Not. R. Astron. Soc. 2017, 466, 4974–4990. [Google Scholar] [CrossRef]
- Moliné, Á.; Schewtschenko, J.A.; Palomares-Ruiz, S.; Bœhm, C.; Baugh, C.M. Isotropic extragalactic flux from dark matter annihilations: Lessons from interacting dark matter scenarios. J. Cosmol. Astropart. Phys. 2016, 2016, 069. [Google Scholar] [CrossRef]
- Boehm, C.; Schewtschenko, J.A.; Wilkinson, R.J.; Baugh, C.M.; Pascoli, S. Using the Milky Way satellites to study interactions between cold dark matter and radiation. Mon. Not. R. Astron. Soc. Lett. 2014, 445, L31–L35. [Google Scholar] [CrossRef]
- Ma, C.P.; Bertschinger, E. Cosmological Perturbation Theory in the Synchronous and Conformal Newtonian Gauges. Astrophys.J. 1995, 455, 7. [Google Scholar] [CrossRef]
- Springel, V. The Cosmological simulation code GADGET-2. Mon. Not. R. Astron. Soc. 2005, 364, 1105–1134. [Google Scholar] [CrossRef]
- Escudero, M.; Lopez-Honorez, L.; Mena, O.; Palomares-Ruiz, S.; Villanueva-Domingo, P. A fresh look into the interacting dark matter scenario. J. Cosmol. Astropart. Phys. 2018, 2018, 007. [Google Scholar] [CrossRef]
- Jenkins, A. Second-order Lagrangian perturbation theory initial conditions for resimulations. Mon. Not. R. Astron. Soc. 2010, 403, 1859–1872. [Google Scholar] [CrossRef]
- Navarro, J.F.; Oman, K.A.; Fattahi, A.; Sawala, T.; Jenkins, A.; Frenk, C.S.; Schaller, M.; Furlong, M.; Theuns, T.; Crain, R.A.; et al. The APOSTLE project: Local Group kinematic mass constraints and simulation candidate selection. Mon. Not. R. Astron. Soc. 2016, 457, 844–856. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Wechsler, R.H.; Wu, H.Y. The Rockstar Phase-Space Temporal Halo Finder and the Velocity Offsets of Cluster Cores. Astrophys. J. 2012, 762, 109. [Google Scholar] [CrossRef]
- Oñorbe, J.; Garrison-Kimmel, S.; Maller, A.H.; Bullock, J.S.; Rocha, M.; Hahn, O. How to zoom: Bias, contamination and Lagrange volumes in multimass cosmological simulations. Mon. Not. R. Astron. Soc. 2014, 437, 1894–1908. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P. Formation and evolution of galaxy dark matter halos and their substructure. Astrophys. J. 2007, 667, 859–877. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P.; Zemp, M.; Moore, B.; Potter, D.; Stadel, J. Clumps and streams in the local dark matter distribution. Nature 2008, 454, 735–738. [Google Scholar] [CrossRef]
- Springel, V.; Wang, J.; Vogelsberger, M.; Ludlow, A.; Jenkins, A.; Helmi, A.; Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Aquarius Project: The subhalos of galactic halos. Mon. Not. R. Astron. Soc. 2008, 391, 1685–1711. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D. The Structure of cold dark matter halos. Astrophys. J. 1996, 462, 563–575. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D. A Universal density profile from hierarchical clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Lovell, M.R.; Eke, V.; Frenk, C.S.; Gao, L.; Jenkins, A.; Theuns, T.; Wang, J.; White, S.D.M.; Boyarsky, A.; Ruchayskiy, O. The haloes of bright satellite galaxies in a warm dark matter universe. Mon. Not. R. Astron. Soc. 2012, 420, 2318–2324. [Google Scholar] [CrossRef]
- Pieri, L.; Lavalle, J.; Bertone, G.; Branchini, E. Implications of High-Resolution Simulations on Indirect Dark Matter Searches. Phys. Rev. D 2011, 83, 023518. [Google Scholar] [CrossRef]
- Ghigna, S.; Moore, B.; Governato, F.; Lake, G.; Quinn, T.R.; Stadel, J. Density profiles and substructure of dark matter halos. Converging results at ultra-high numerical resolution. Astrophys. J. 2000, 544, 616. [Google Scholar] [CrossRef]
- Bullock, J.S.; Kolatt, T.S.; Sigad, Y.; Somerville, R.S.; Kravtsov, A.V.; Klypin, A.A.; Primack, J.R.; Dekel, A. Profiles of dark haloes. Evolution, scatter, and environment. Mon. Not. R. Astron. Soc. 2001, 321, 559–575. [Google Scholar] [CrossRef]
- Diemand, J.; Moore, B. The structure and evolution of cold dark matter halos. Adv. Sci. Lett. 2011, 4, 297–310. [Google Scholar] [CrossRef]
- Bartels, R.; Ando, S. Boosting the annihilation boost: Tidal effects on dark matter subhalos and consistent luminosity modeling. Phys. Rev. D 2015, 92, 123508. [Google Scholar] [CrossRef]
| 1 | Which are not affected by tidal forces. |
| 2 |
| Box | 100 Mpc | 17,481 | 27,973 | 125,704 | 197,208 | ||
| LGs | 15 Mpc/h | 1606 | 11,092 | 10,513 | 40,874 |
| IDM | 6.04 | 0.27 | 6.74 | 0.068 | ||
| CDM | 7.22 | 1.10 | 0.36 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moliné, Á.; Schewtschenko, J.A.; Sánchez-Conde, M.A.; Aguirre-Santaella, A.; Cora, S.A.; Abadi, M.G. Properties of Subhalos in the Interacting Dark Matter Scenario. Galaxies 2019, 7, 80. https://doi.org/10.3390/galaxies7040080
Moliné Á, Schewtschenko JA, Sánchez-Conde MA, Aguirre-Santaella A, Cora SA, Abadi MG. Properties of Subhalos in the Interacting Dark Matter Scenario. Galaxies. 2019; 7(4):80. https://doi.org/10.3390/galaxies7040080
Chicago/Turabian StyleMoliné, Ángeles, Jascha A. Schewtschenko, Miguel A. Sánchez-Conde, Alejandra Aguirre-Santaella, Sofía A. Cora, and Mario G. Abadi. 2019. "Properties of Subhalos in the Interacting Dark Matter Scenario" Galaxies 7, no. 4: 80. https://doi.org/10.3390/galaxies7040080
APA StyleMoliné, Á., Schewtschenko, J. A., Sánchez-Conde, M. A., Aguirre-Santaella, A., Cora, S. A., & Abadi, M. G. (2019). Properties of Subhalos in the Interacting Dark Matter Scenario. Galaxies, 7(4), 80. https://doi.org/10.3390/galaxies7040080






