PKS 2155-304: A Case Study of Blazar Variability Power Spectrum at the Highest Energies and on the Longest Timescales
Abstract
1. Introduction
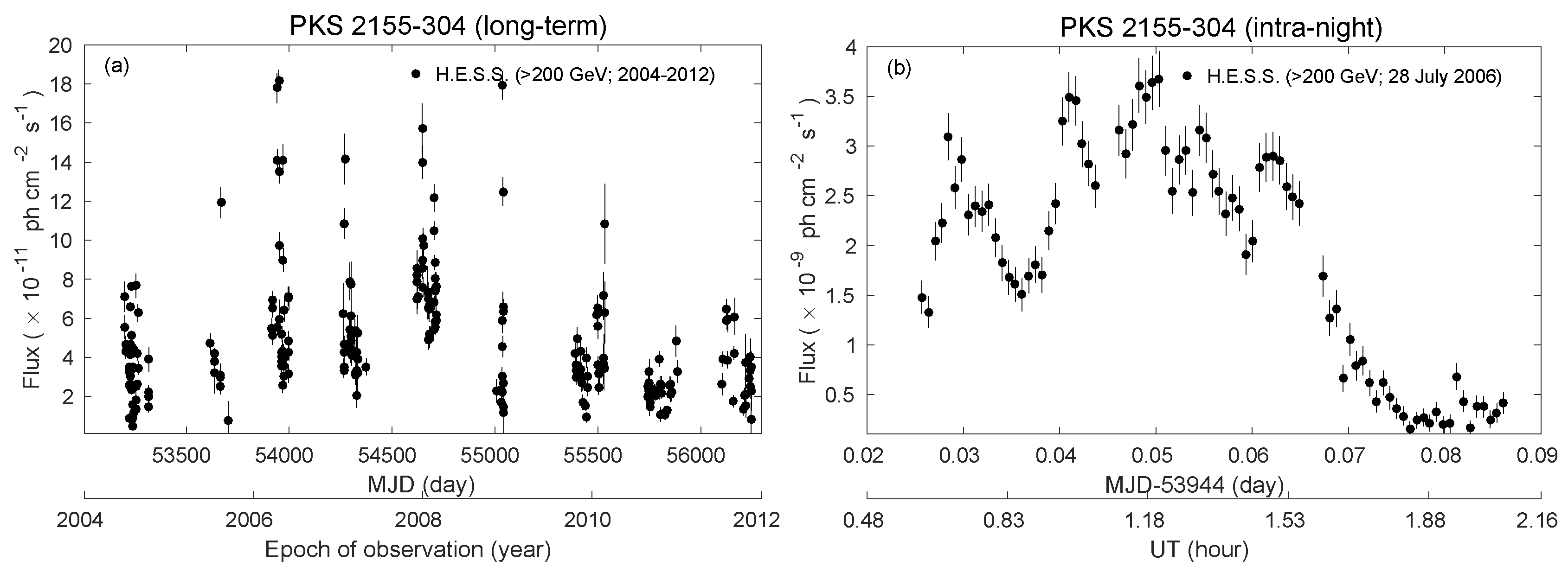
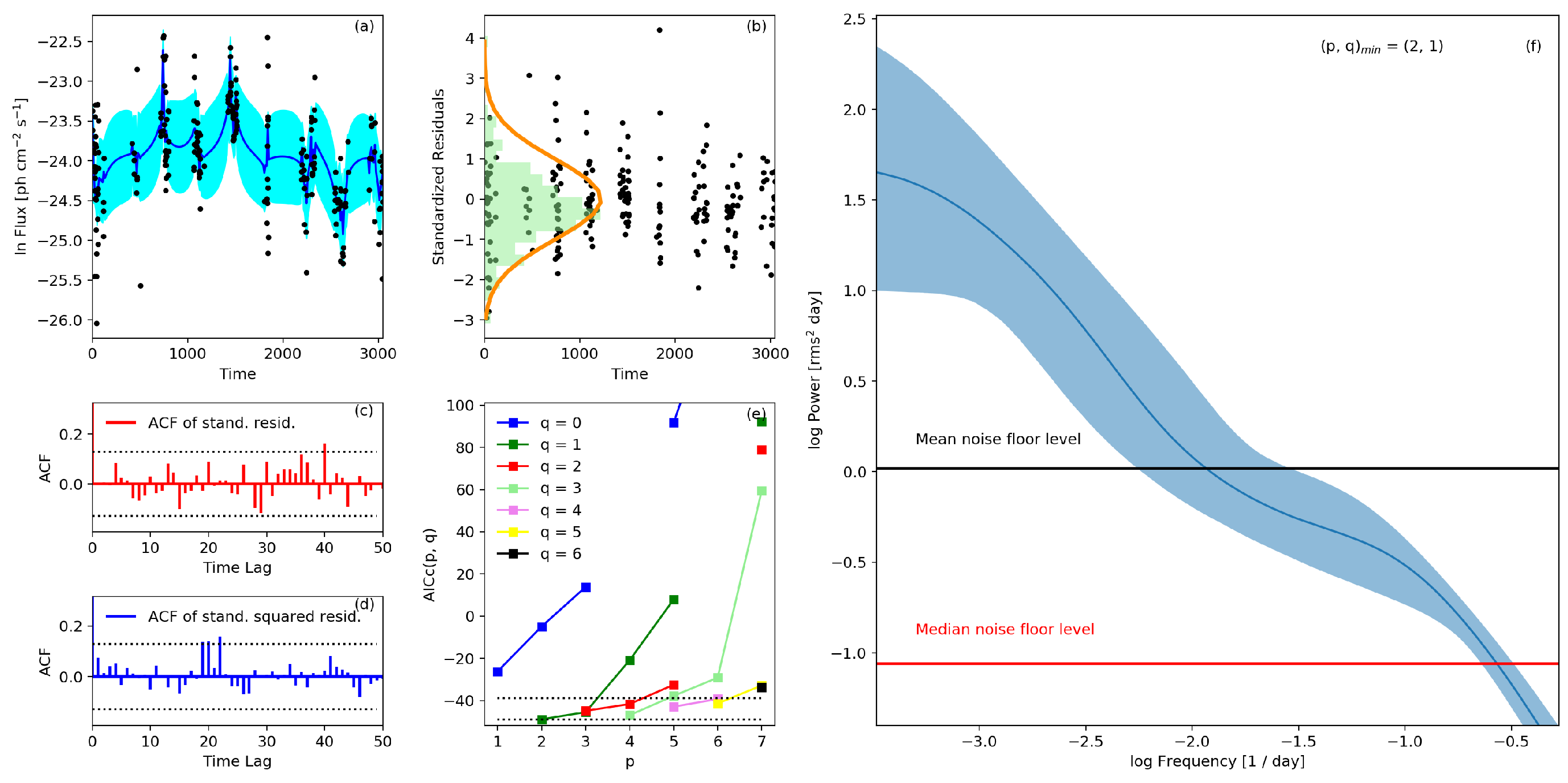
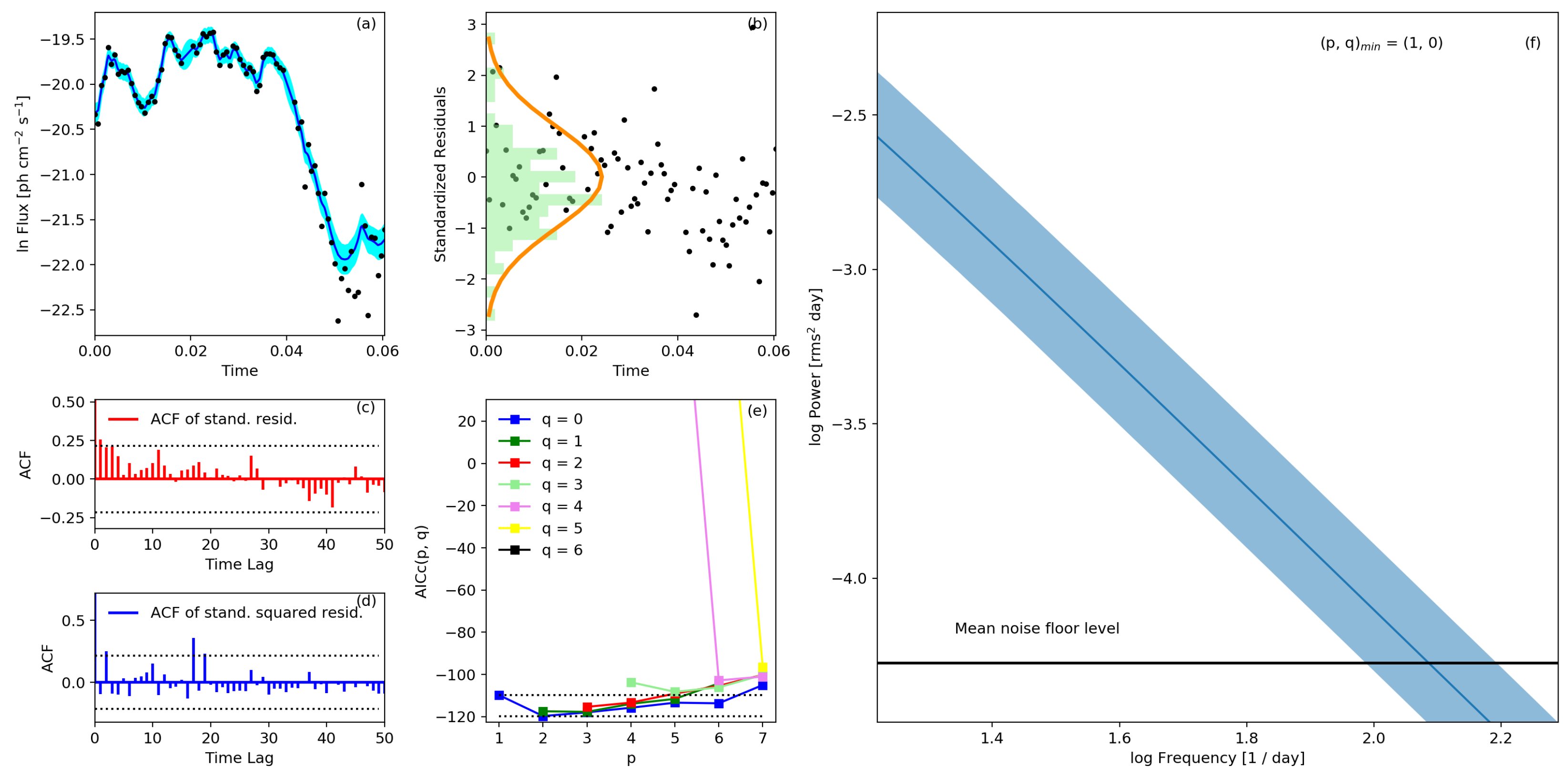
2. Methodology: CARMA Modeling of the H.E.S.S. Light Curves
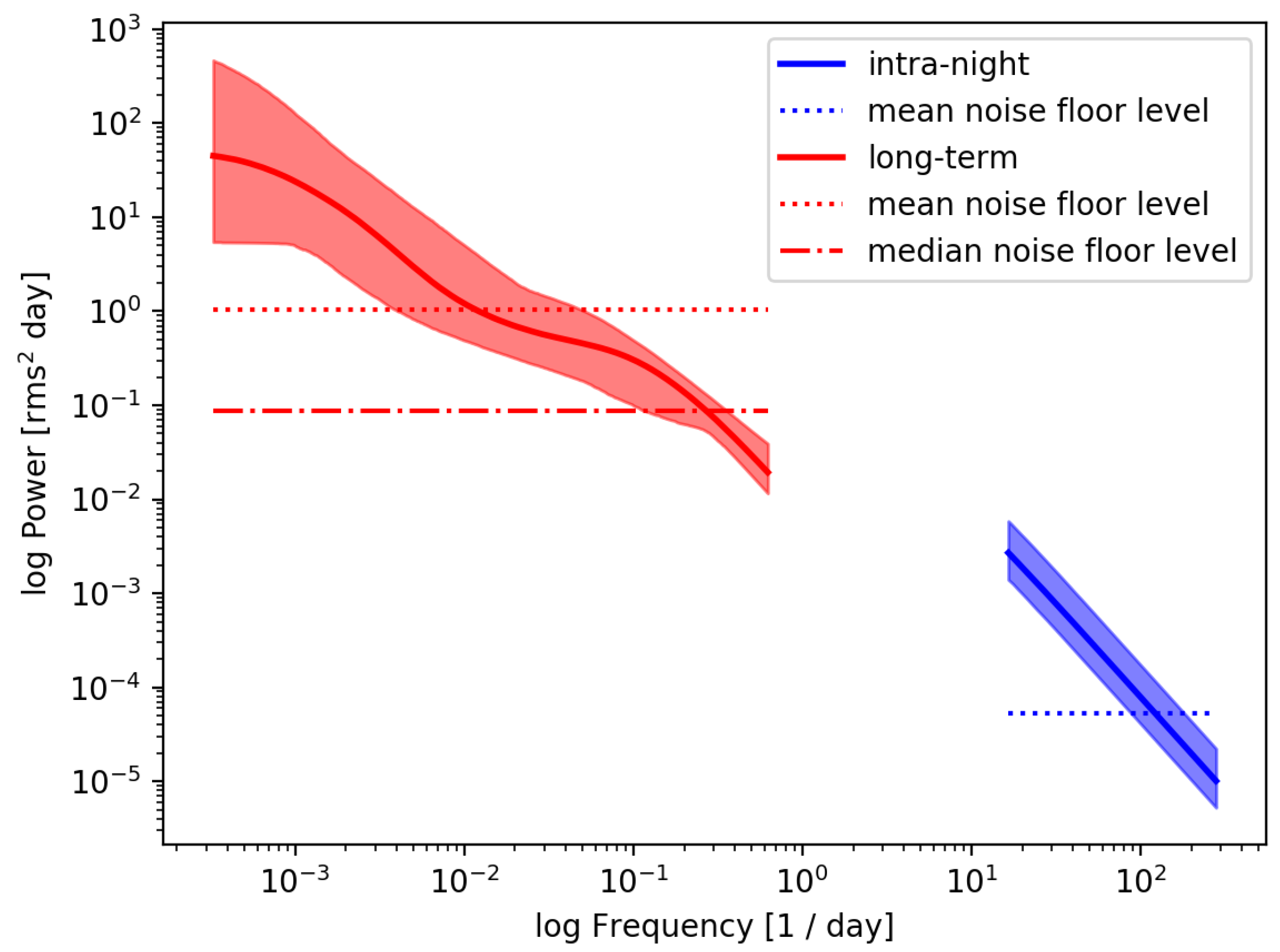
3. Results
4. Discussions and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PSD | Power Spectral Density |
| CARMA | Continuous-time Auto-Regressive Moving Average |
References
- The Fermi-LAT collaboration. Fermi Large Area Telescope Fourth Source Catalog. arXiv 2019, arXiv:1902.10045. [Google Scholar]
- Marscher, A.P. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780, 87. [Google Scholar] [CrossRef]
- Sironi, L.; Petropoulou, M.; Giannios, D. Relativistic jets shine through shocks or magnetic reconnection? Mon. Not. R. Astron. Soc. 2015, 450, 183–191. [Google Scholar] [CrossRef]
- Sikora, M.; Stawarz, Ł.; Moderski, R.; Nalewajko, K.; Madejski, G.M. Constraining Emission Models of Luminous Blazar Sources. Astrophys. J. 2009, 704, 38–50. [Google Scholar] [CrossRef]
- Ghisellini, G.; Celotti, A.; Fossati, G.; Maraschi, L.; Comastri, A. A theoretical unifying scheme for gamma-ray bright blazars. Mon. Not. R. Astron. Soc. 1998, 301, 451–468. [Google Scholar] [CrossRef]
- Böttcher, M.; Reimer, A.; Sweeney, K.; Prakash, A. Leptonic and Hadronic Modeling of Fermi-detected Blazars. Astrophys. J. 2013, 768, 54. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F.; Maraschi, L.; Celotti, A.; Sbarrato, T. The power of relativistic jets is larger than the luminosity of their accretion disks. Nature 2014, 515, 376–378. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.F.; Xue, Y.Q.; Brandt, W.N.; Cui, W.; Wang, Y.J. Extremely rapid X-ray flares of tev blazars in the rxte era. arXiv 2017, arXiv:astro-ph.HE/1712.00459. [Google Scholar]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. An Exceptional Very High Energy Gamma-Ray Flare of PKS 2155-304. Astrophys. J. Lett. 2007, 664, L71–L74. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F. Rapid variability in TeV blazars: The case of PKS 2155-304. Mon. Not. R. Astron. Soc. 2008, 386, L28–L32. [Google Scholar] [CrossRef]
- Begelman, M.C.; Fabian, A.C.; Rees, M.J. Implications of very rapid TeV variability in blazars. Mon. Not. R. Astron. Soc. 2008, 384, L19–L23. [Google Scholar] [CrossRef]
- McKinney, J.C.; Blandford, R.D. Stability of relativistic jets from rotating, accreting black holes via fully three-dimensional magnetohydrodynamic simulations. Mon. Not. R. Astron. Soc. 2009, 394, L126–L130. [Google Scholar] [CrossRef]
- Goyal, A.; Stawarz, Ł.; Zola, S.; Marchenko, V.; Soida, M.; Nilsson, K.; Ciprini, S.; Baran, A.; Ostrowski, M.; Wiita, P.J.; et al. Stochastic Modeling of Multiwavelength Variability of the Classical BL Lac Object OJ 287 on Timescales Ranging from Decades to Hours. Astrophys. J. 2018, 863, 175. [Google Scholar] [CrossRef]
- Rieger, F. Gamma-Ray Astrophysics in the Time Domain. Galaxies 2019, 7, 28. [Google Scholar] [CrossRef]
- Goyal, A.; Stawarz, L.; Ostrowski, M.; Larionov, V.; Gopal-Krishna; Wiita, P.J.; Joshi, S.; Soida, M.; Agudo, I. Multi-wavelength variability study of the classical BL Lac object PKS 0735+178 on timescales ranging from decades to minutes. arXiv 2017, arXiv:astro-ph.HE/1702.02504. [Google Scholar]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Ajello, M.; Aller, H.D.; Aller, M.F.; Angelakis, E.; Arkharov, A.A.; Axelsson, M.; Bach, U.; et al. The Spectral Energy Distribution of Fermi Bright Blazars. Astrophys. J. 2010, 716, 30–70. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Allafort, A.; Schady, P.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Blandford, R.D.; et al. The Imprint of the Extragalactic Background Light in the Gamma-Ray Spectra of Blazars. Science 2012, 338, 1190. [Google Scholar] [CrossRef]
- Franceschini, A.; Rodighiero, G.; Vaccari, M. Extragalactic optical-infrared background radiation, its time evolution and the cosmic photon-photon opacity. Astron. Astrophys. 2008, 487, 837–852. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Albert, J.; Aliu, E.; Anderhub, H.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; et al. Very-High-Energy gamma rays from a Distant Quasar: How Transparent Is the Universe? Science 2008, 320, 1752. [Google Scholar] [CrossRef]
- Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Balenderan, S.; Balzer, A.; Barnacka, A.; Becherini, Y.; Becker Tjus, J.; et al. Measurement of the extragalactic background light imprint on the spectra of the brightest blazars observed with H.E.S.S. Astron. Astrophys. 2013, 550, A4. [Google Scholar] [CrossRef]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Babić, A.; Banerjee, B.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Bednarek, W.; et al. Multiwavelength observations of a VHE gamma-ray flare from PKS 1510-089 in 2015. Astron. Astrophys. 2017, 603, A29. [Google Scholar] [CrossRef]
- Dorner, D.; Ahnen, M.L.; Bergmann, M.; Biland, A.; Balbo, M.; Bretz, T.; Buss, J.; Einecke, S.; Freiwald, J.; Hempfling, C.; et al. FACT-Monitoring Blazars at Very High Energies. arXiv 2015, arXiv:astro-ph.IM/1502.02582. [Google Scholar]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Ayala Solares, H.A.; Barber, A.S.; Bautista-Elivar, N.; et al. Search for Very High-energy Gamma Rays from the Northern Fermi Bubble Region with HAWC. Astrophys. J. 2017, 842, 85. [Google Scholar] [CrossRef]
- Falomo, R.; Pesce, J.E.; Treves, A. The Environment of the BL Lacertae Object PKS 2155-304. Astrophys. J. 1993, 411, L63. [Google Scholar] [CrossRef]
- Abdalla, H.; Abramowski, A.; Aharonian, F.; Benkhali, F.; Andersson, A.G.; Andersson, T.; Arrieta, M.; Aubert, P.; Backes, M.; Balzer, A.; et al. Characterizing the γ-ray long-term variability of PKS 2155-304 with H.E.S.S. and Fermi-LAT. Astron. Astrophys. 2017, 598, A39. [Google Scholar] [CrossRef]
- Wierzcholska, A.; Zacharias, M.; Jankowsky, F.; Wagner, S.; H.E.S.S. Collaboration. H.E.S.S. Monitoring of PKS 2155-304 in 2015 and 2016. Galaxies 2019, 7, 21. [Google Scholar] [CrossRef]
- Rieger, F.M.; Volpe, F. Short-term VHE variability in blazars: PKS 2155-304. Astron. Astrophys. 2010, 520, A23. [Google Scholar] [CrossRef]
- Max-Moerbeck, W.; Richards, J.L.; Hovatta, T.; Pavlidou, V.; Pearson, T.J.; Readhead, A.C.S. A method for the estimation of the significance of cross-correlations in unevenly sampled red-noise time series. Mon. Not. R. Astron. Soc. 2014, 445, 437–459. [Google Scholar] [CrossRef]
- Kelly, B.C.; Becker, A.C.; Sobolewska, M.; Siemiginowska, A.; Uttley, P. Flexible and Scalable Methods for Quantifying Stochastic Variability in the Era of Massive Time-domain Astronomical Data Sets. Astrophys. J. 2014, 788, 33. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Sobolewska, M.A.; Siemiginowska, A.; Kelly, B.C.; Nalewajko, K. Stochastic Modeling of the Fermi/LAT γ-Ray Blazar Variability. Astrophys. J. 2014, 786, 143. [Google Scholar] [CrossRef]
- Uttley, P.; McHardy, I.M.; Vaughan, S. Non-linear X-ray variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 2005, 359, 345–362. [Google Scholar] [CrossRef]
- Liodakis, I.; Pavlidou, V.; Hovatta, T.; Max-Moerbeck, W.; Pearson, T.J.; Richards, J.L.; Readhead, A.C.S. Bimodal radio variability in OVRO-40 m-monitored blazars. Mon. Not. R. Astron. Soc. 2017, 467, 4565–4576. [Google Scholar] [CrossRef]
- Shah, Z.; Mankuzhiyil, N.; Sinha, A.; Misra, R.; Sahayanathan, S.; Iqbal, N. Log-normal flux distribution of bright Fermi blazars. Res. Astron. Astrophys. 2018, 18, 141. [Google Scholar] [CrossRef]
- Biteau, J.; Giebels, B. The minijets-in-a-jet statistical model and the rms-flux correlation. Astron. Astrophys. 2012, 548, A123. [Google Scholar] [CrossRef]
- Chevalier, J.; Sanchez, D.A.; Serpico, P.D.; Lenain, J.P.; Maurin, G. Variability studies and modelling of the blazar PKS 2155-304 in the light of a decade of multi-wavelength observations. Mon. Not. R. Astron. Soc. 2019, 484, 749–759. [Google Scholar] [CrossRef]
- Kastendieck, M.A.; Ashley, M.C.B.; Horns, D. Long-term optical variability of PKS 2155-304. Astron. Astrophys. 2011, 531, A123. [Google Scholar] [CrossRef]
- O’Riordan, M.; Pe’er, A.; McKinney, J.C. Blazar Variability from Turbulence in Jets Launched by Magnetically Arrested Accretion Flows. Astrophys. J. 2017, 843, 81. [Google Scholar] [CrossRef]
- Kushwaha, P.; Chandra, S.; Misra, R.; Sahayanathan, S.; Singh, K.P.; Baliyan, K.S. Evidence for Two Lognormal States in Multi-wavelength Flux Variation of FSRQ PKS 1510-089. Astrophys. J. Lett. 2016, 822, L13. [Google Scholar] [CrossRef]
- Ackermann, M.; Anantua, R.; Asano, K.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Becerra Gonzalez, J.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; et al. Minute-timescale >100 MeV γ-Ray Variability during the Giant Outburst of Quasar 3C 279 Observed by Fermi-LAT in 2015 June. Astrophys. J. Lett. 2016, 824, L20. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. The 2009 multi-wavelength campaign on Mrk 421: Variability and correlation studies. Astron. Astrophys. 2015, 576, A126. [Google Scholar] [CrossRef]
| 1. | |
| 2. | |
| 3. | |
| 4. | Data for the period 2004–2012 were obtained upon request from David Sanches. |
| 5. | |
| 6. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goyal, A. PKS 2155-304: A Case Study of Blazar Variability Power Spectrum at the Highest Energies and on the Longest Timescales. Galaxies 2019, 7, 73. https://doi.org/10.3390/galaxies7030073
Goyal A. PKS 2155-304: A Case Study of Blazar Variability Power Spectrum at the Highest Energies and on the Longest Timescales. Galaxies. 2019; 7(3):73. https://doi.org/10.3390/galaxies7030073
Chicago/Turabian StyleGoyal, Arti. 2019. "PKS 2155-304: A Case Study of Blazar Variability Power Spectrum at the Highest Energies and on the Longest Timescales" Galaxies 7, no. 3: 73. https://doi.org/10.3390/galaxies7030073
APA StyleGoyal, A. (2019). PKS 2155-304: A Case Study of Blazar Variability Power Spectrum at the Highest Energies and on the Longest Timescales. Galaxies, 7(3), 73. https://doi.org/10.3390/galaxies7030073



