Relativistic Aspects of Accreting Supermassive Black Hole Binaries in Their Natural Habitat: A Review
Abstract
1. Introduction
1.1. : Galaxy Mergers and Relaxation, Key Physics: Newtonian Self-Gravity
1.2. : The Final-Parsec Problem, Key Physics: Newtonian Self-Gravity + Hydrodynamics
1.3. sub--: Gravitational Wave-Driven Regime, Key Physics: GR + Magnetohydrodynamics (MHD)
1.4. Binary–Disk Decoupling
1.5. Lessons Learned from Single Black Hole Accretion
2. Results
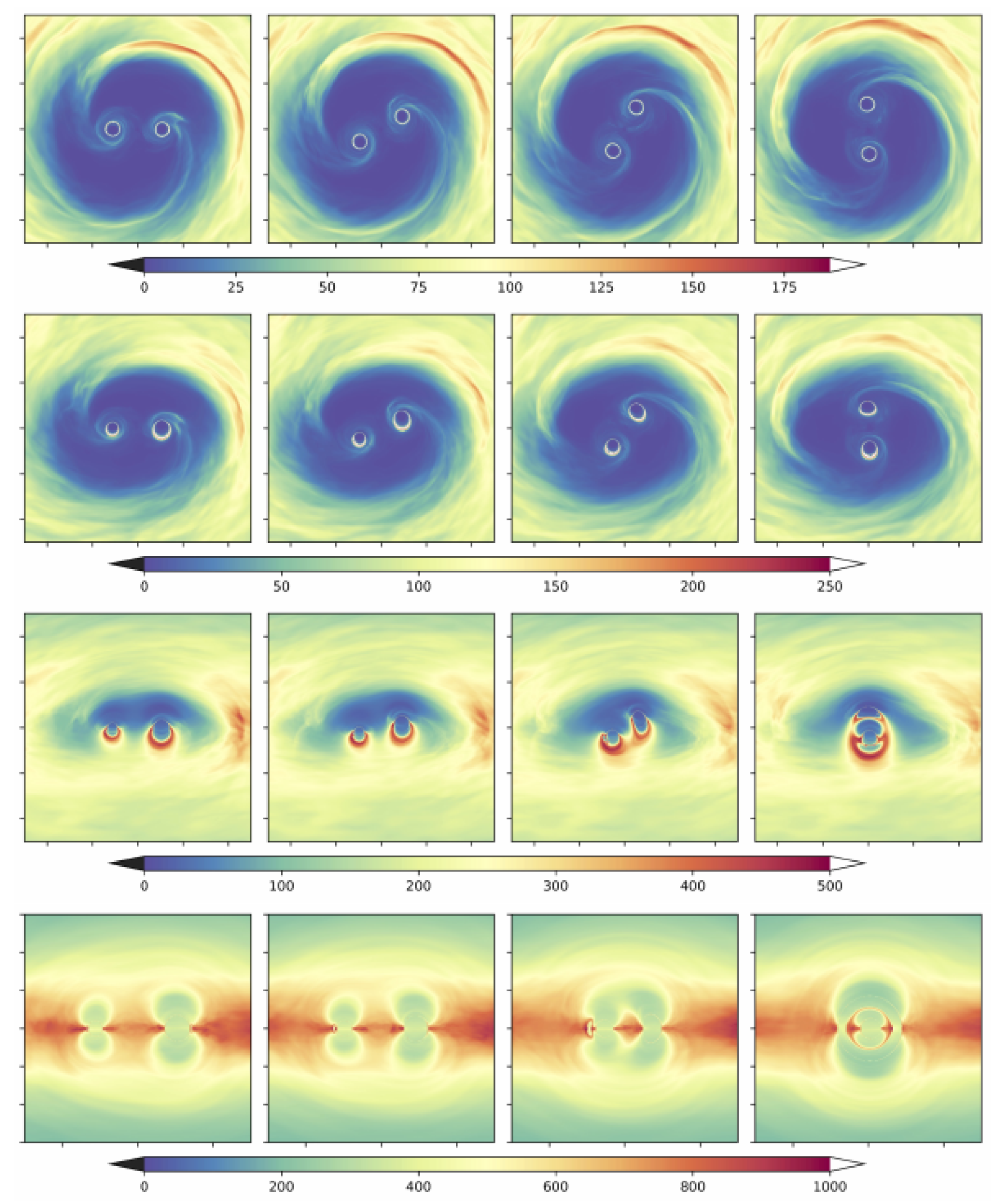
2.1. New Structural Features in the Binary Case
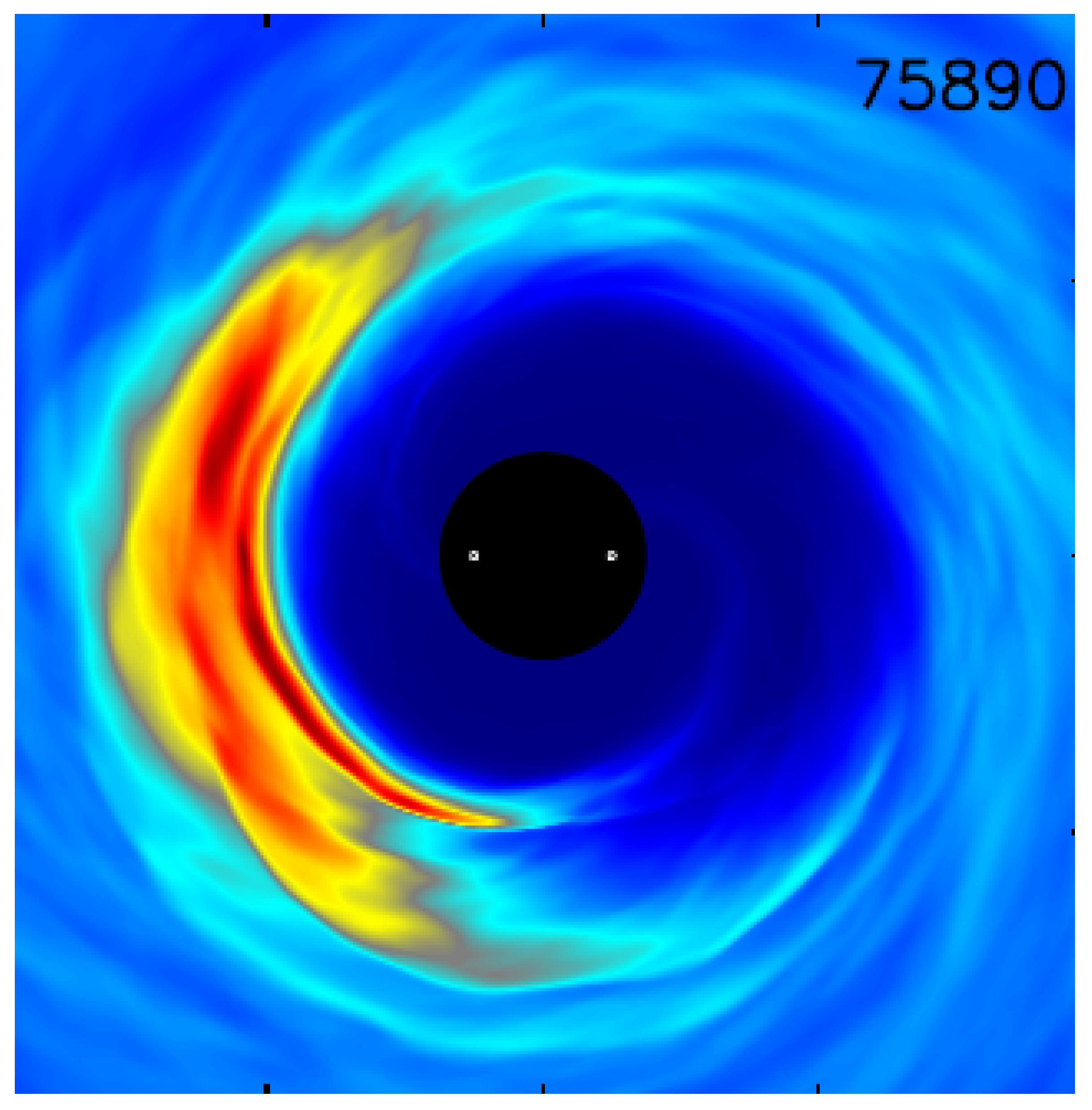
2.1.1. Cavity and Pile-Up
2.1.2. Non-Axisymmetric Structures: Streams and Lumps
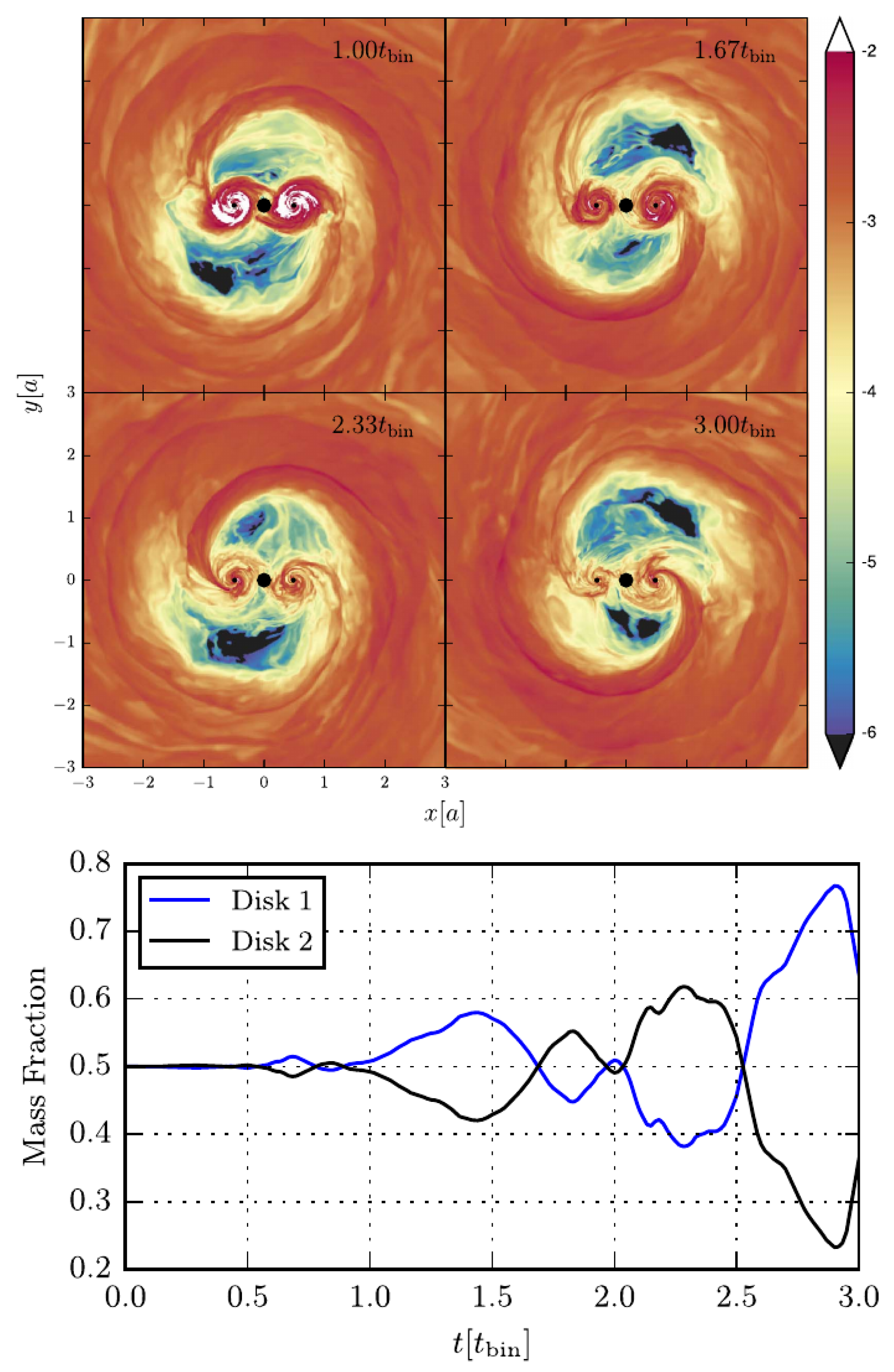
2.1.3. Mini-Disks and Mass Sloshing
2.1.4. Enhanced Variability
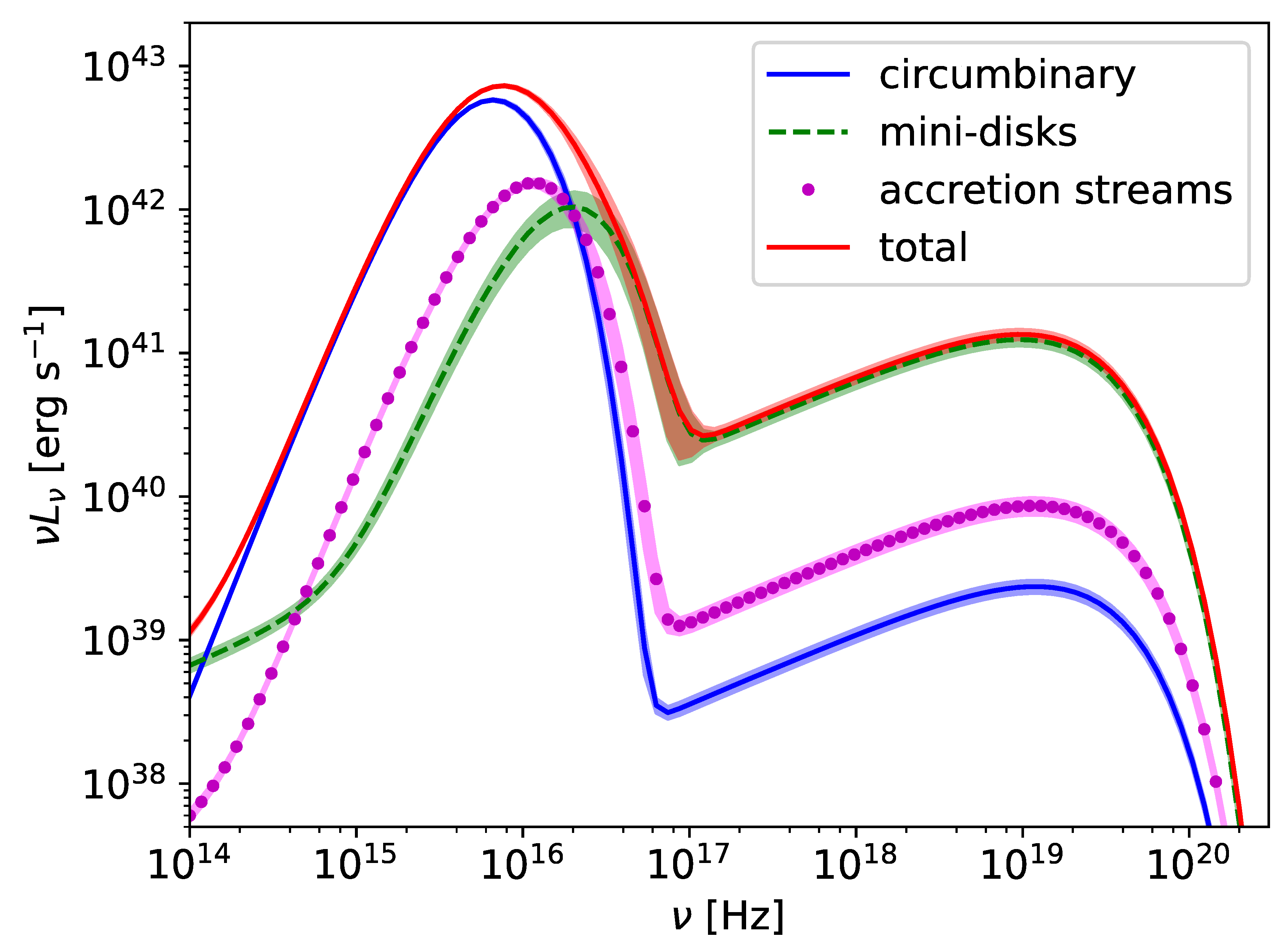
2.2. Connecting Theoretical Models and Observational Data
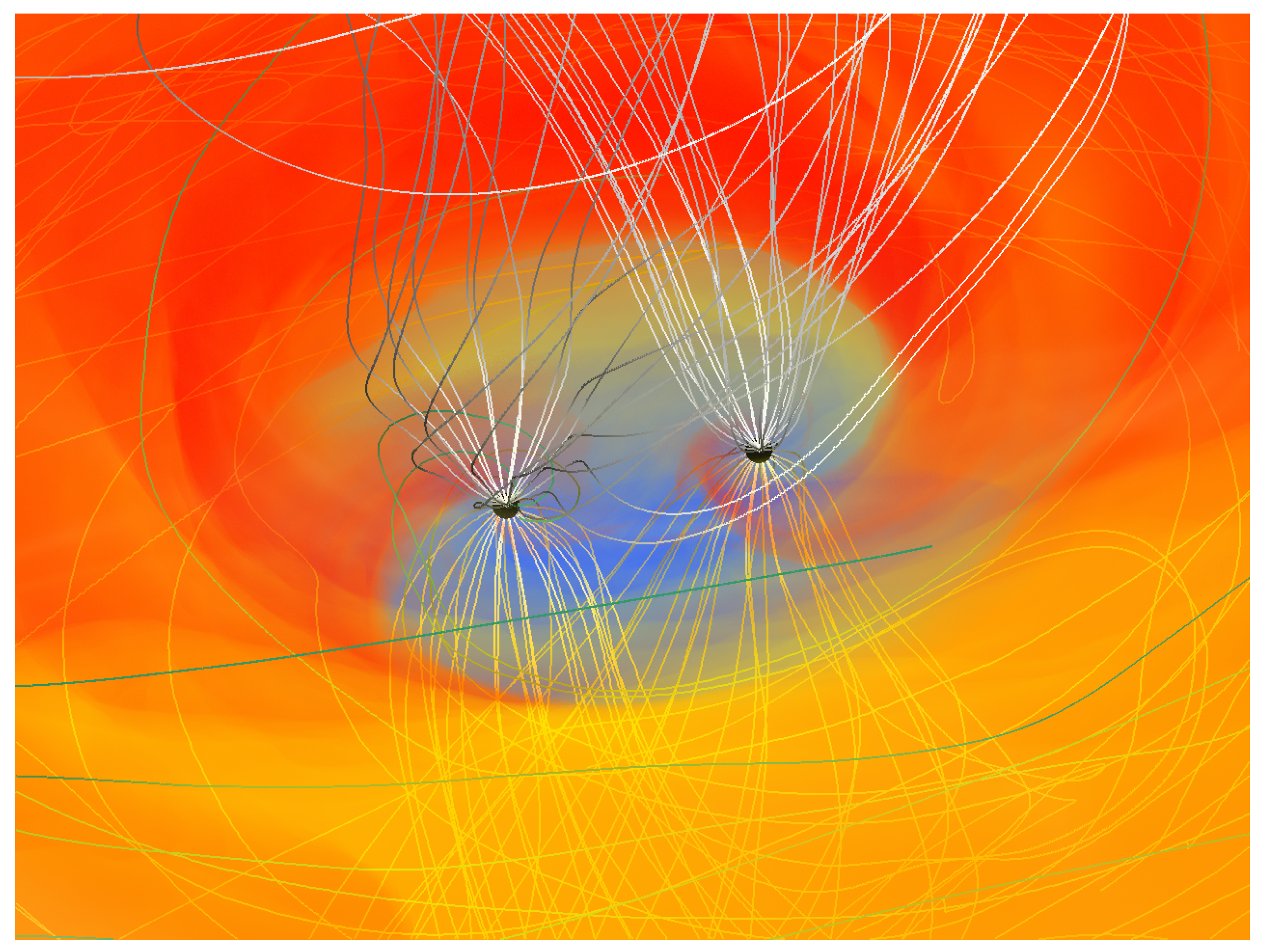
2.3. GRMHD in Dynamic Spacetime
2.4. During and Post Merger
2.5. Distinguishability of Single vs. Binary AGN
3. Discussion/Conclusions
Funding
Conflicts of Interest
References
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Massive black hole binaries in active galactic nuclei. Nature 1980, 287, 307. [Google Scholar] [CrossRef]
- Roos, N. Galaxy mergers and active galactic nuclei. Astron. Astrophys. 1981, 104, 218–228. [Google Scholar]
- Mohamed, Y.H.; Reshetnikov, V.P. Interacting galaxies in deep fields of the Hubble Space Telescope. Astrophysics 2011, 54, 155–161. [Google Scholar] [CrossRef]
- Eracleous, M.; Boroson, T.A.; Halpern, J.P.; Liu, J. A Large Systematic Search for Close Supermassive Binary and Rapidly Recoiling Black Holes. Astrophys. J. Suppl. Ser. 2012, 201, 23. [Google Scholar] [CrossRef]
- Reynolds, C.S. Observing black holes spin. Nat. Astron. 2019, 3, 41–47. [Google Scholar] [CrossRef]
- Harrison, F.A.; Craig, W.W.; Christensen, F.E.; Hailey, C.J.; Zhang, W.W.; Boggs, S.E.; Stern, D.; Cook, W.R.; Forster, K.; Giommi, P.; et al. The Nuclear Spectroscopic Telescope Array (NuSTAR) High-energy X-ray Mission. Astrophys. J. 2013, 770, 103. [Google Scholar] [CrossRef]
- Ayre, M.; Bavdaz, M.; Ferreira, I.; Wille, E.; Lumb, D.; Linder, M. ATHENA: System design and implementation for a next generation X-ray telescope. UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XIX. Proc. SPIE 2015, 9601, 96010L. [Google Scholar] [CrossRef]
- Decarli, R.; Dotti, M.; Fumagalli, M.; Tsalmantza, P.; Montuori, C.; Lusso, E.; Hogg, D.W.; Prochaska, J.X. The nature of massive black hole binary candidates—I. Spectral properties and evolution. Mon. Not. R. Astron. Soc. 2013, 433, 1492–1504. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.; Kocsis, B.; Haiman, Z. Ripple effects and oscillations in the broad FeKa line as a probe of massive black hole mergers. Mon. Not. R. Astrono. Soc. 2013, 32, 1468–1482. [Google Scholar] [CrossRef]
- Pflueger, B.J.; Nguyen, K.; Bogdanović, T.; Eracleous, M.; Runnoe, J.C.; Sigurdsson, S.; Boroson, T. Likelihood for Detection of Subparsec Supermassive Black Hole Binaries in Spectroscopic Surveys. Astrophys. J. 2018, 861, 59. [Google Scholar] [CrossRef]
- Sillanpaa, A.; Haarala, S.; Valtonen, M.J.; Sundelius, B.; Byrd, G.G. OJ 287—Binary pair of supermassive black holes. Astrophys. J. 1988, 325, 628–634. [Google Scholar] [CrossRef]
- Lehto, H.J.; Valtonen, M.J. OJ 287 Outburst Structure and a Binary Black Hole Model. Astrophys. J. 1996, 460, 207. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Lehto, H.J.; Nilsson, K.; Heidt, J.; Takalo, L.O.; Sillanpää, A.; Villforth, C.; Kidger, M.; Poyner, G.; Pursimo, T.; et al. A massive binary black-hole system in OJ287 and a test of general relativity. Nature 2008, 452, 851–853. [Google Scholar] [CrossRef] [PubMed]
- Valtonen, M.; Ciprini, S. OJ 287 Binary Black Hole System. In Proceedings of the Multifrequency Behaviour of High Energy Cosmic Sources, Sicily, Italy, 23–28 May 2011. [Google Scholar]
- Britzen, S.; Fendt, C.; Witzel, G.; Qian, S.J.; Pashchenko, I.N.; Kurtanidze, O.; Zajacek, M.; Martinez, G.; Karas, V.; Aller, M.; et al. OJ287: Deciphering the ‘Rosetta stone of blazars’. Mon. Not. R. Astron. Soc. 2018, 478, 3199–3219. [Google Scholar] [CrossRef]
- Liu, F.K.; Li, S.; Komossa, S. A Milliparsec Supermassive Black Hole Binary Candidate in the Galaxy SDSS J120136.02+300305.5. Astrophys. J. 2014, 786, 103. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Stern, D.; Glikman, E.; Drake, A.J.; Mahabal, A.A.; Donalek, C.; Larson, S.; Christensen, E. A possible close supermassive black-hole binary in a quasar with optical periodicity. Nature 2015, 518, 74–76. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Gezari, S.; Heinis, S.; Magnier, E.A.; Burgett, W.S.; Chambers, K.; Flewelling, H.; Huber, M.; Hodapp, K.W.; Kaiser, N.; et al. A Periodically Varying Luminous Quasar at z = 2 from the Pan-STARRS1 Medium Deep Survey: A Candidate Supermassive Black Hole Binary in the Gravitational Wave-driven Regime. Astrophys. J. Lett. 2015, 803, L16. [Google Scholar] [CrossRef]
- Charisi, M.; Bartos, I.; Haiman, Z.; Price-Whelan, A.M.; Graham, M.J.; Bellm, E.C.; Laher, R.R.; Márka, S. A population of short-period variable quasars from PTF as supermassive black hole binary candidates. Mon. Not. R. Astron. Soc. 2016, 463, 2145–2171. [Google Scholar] [CrossRef]
- Runnoe, J.C.; Eracleous, M.; Pennell, A.; Mathes, G.; Boroson, T.; Sigurdsson, S.; Bogdanović, T.; Halpern, J.P.; Liu, J.; Brown, S. A large systematic search for close supermassive binary and rapidly recoiling black holes—III. Radial velocity variations. Mon. Not. R. Astron. Soc. 2017, 468, 1683–1702. [Google Scholar] [CrossRef]
- Milosavljević, M.; Merritt, D. Formation of Galactic Nuclei. Astrophys. J. 2001, 563, 34–62. [Google Scholar] [CrossRef]
- Milosavljević, M.; Merritt, D. The Final Parsec Problem. AIP Conf. Proc. 2003, 686, 201–210. [Google Scholar] [CrossRef]
- Milosavljević, M.; Merritt, D. Long-Term Evolution of Massive Black Hole Binaries. Astrophys. J. 2003, 596, 860–878. [Google Scholar] [CrossRef]
- Lodato, G.; Nayakshin, S.; King, A.R.; Pringle, J.E. Black hole mergers: Can gas discs solve the ‘final parsec’ problem? Mon. Not. R. Astron. Soc. 2009, 398, 1392–1402. [Google Scholar] [CrossRef]
- Cuadra, J.; Armitage, P.J.; Alexander, R.D.; Begelman, M.C. Massive black hole binary mergers within subparsec scale gas discs. Mon. Not. R. Astron. Soc. 2009, 393, 1423–1432. [Google Scholar] [CrossRef]
- Roedig, C.; Dotti, M.; Sesana, A.; Cuadra, J.; Colpi, M. Limiting eccentricity of subparsec massive black hole binaries surrounded by self-gravitating gas discs. Mon. Not. R. Astron. Soc. 2011, 415, 3033–3041. [Google Scholar] [CrossRef]
- Khan, F.M.; Holley-Bockelmann, K.; Berczik, P.; Just, A. Supermassive Black Hole Binary Evolution in Axisymmetric Galaxies: The Final Parsec Problem is Not a Problem. Astrophys. J. 2013, 773, 100. [Google Scholar] [CrossRef]
- Khan, F.M.; Fiacconi, D.; Mayer, L.; Berczik, P.; Just, A. Swift Coalescence of Supermassive Black Holes in Cosmological Mergers of Massive Galaxies. Astrophys. J. 2016, 828, 73. [Google Scholar] [CrossRef]
- Ryu, T.; Perna, R.; Haiman, Z.; Ostriker, J.P.; Stone, N.C. Interactions between multiple supermassive black holes in galactic nuclei: A solution to the final parsec problem. Mon. Not. R. Astron. Soc. 2018, 473, 3410–3433. [Google Scholar] [CrossRef]
- Danzmann, K. LISA: Laser interferometer space antenna for gravitational wave measurements. Classical Quant. Grav. 1996, 13, A247. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Dotti, M.; Sesana, A.; Decarli, R. Massive black hole binaries: Dynamical evolution and observational signatures. Adv. Astron. 2012, 2012, 940568. [Google Scholar] [CrossRef]
- Peters, P.C.; Mathews, J. Gravitational radiation from point masses in a Keplerian orbit. Phys. Rev. 1963, 131, 435–440. [Google Scholar] [CrossRef]
- Peters, P.C. Gravitational Radiation and the Motion of Two Point Masses. Phys. Rev. 1964, 136, B1224–B1232. [Google Scholar] [CrossRef]
- Hobbs, G.; Archibald, A.; Arzoumanian, Z.; Backer, D.; Bailes, M.; Bhat, N.D.R.; Burgay, N.; Burke-Spolaor, S.; Champion, D.; Cognard, I.; et al. The international pulsar timing array project: Using pulsars as a gravitational wave detector. Class. Quantum Grav. 2010, 27, 084013. [Google Scholar] [CrossRef]
- Sesana, A.; Volonteri, M.; Haardt, F. LISA detection of massive black hole binaries: Imprint of seed populations and extreme recoils. Class. Quantum Grav. 2009, 26, 094033. [Google Scholar] [CrossRef]
- Haiman, Z.; Kocsis, B.; Menou, K. The Population of Viscosity- and Gravitational Wave-Driven Supermassive Black Hole Binaries Among Luminous AGN. Astrophys. J. 2009, 700, 1952–1969. [Google Scholar] [CrossRef]
- Sesana, A.; Roedig, C.; Reynolds, M.T.; Dotti, M. Multimessenger astronomy with pulsar timing and X-ray observations of massive black hole binaries. Mon. Not. R. Astron. Soc. 2012, 420, 860–877. [Google Scholar] [CrossRef]
- Tanaka, T.; Haiman, Z.; Menou, K. Electromagnetic counterparts of supermassive black hole binaries resolved by pulsar timing arrays. Mon. Not. R. Astron. Soc. 2012, 420, 705–719. [Google Scholar] [CrossRef]
- Komossa, S.; Baker, J.G.; Liu, F.K. Growth of Supermassive Black Holes, Galaxy Mergers and Supermassive Binary Black Holes. Proc. Int. Astron. Union 2016, 29, 292–298. [Google Scholar] [CrossRef]
- Sesana, A.; Haiman, Z.; Kocsis, B.; Kelley, L.Z. Testing the Binary Hypothesis: Pulsar Timing Constraints on Supermassive Black Hole Binary Candidates. Astrophys. J. 2018, 856, 42. [Google Scholar] [CrossRef]
- Kocsis, B.; Haiman, Z.; Menou, K. Pre-Merger Localization of Gravitational-Wave Standard Sirens With LISA: Triggered Search for an Electromagnetic Counterpart. Astrophys. J. 2008, 684, 870–888. [Google Scholar] [CrossRef]
- Corrales, L.R.; Haiman, Z.; MacFadyen, A. Hydrodynamical response of a circumbinary gas disc to black hole recoil and mass loss. Mon. Not. R. Astron. Soc. 2010, 404, 947–962. [Google Scholar] [CrossRef]
- Zanotti, O.; Rezzolla, L.; Del Zanna, L.; Palenzuela, C. Electromagnetic counterparts of recoiling black holes: General relativistic simulations of non-Keplerian discs. Astron. Astrophys. 2010, 523, A8. [Google Scholar] [CrossRef]
- Lousto, C.O.; Campanelli, M.; Zlochower, Y.; Nakano, H. Remnant masses, spins and recoils from the merger of generic black hole binaries. Classical Quant. Grav. 2010, 27, 114006. [Google Scholar] [CrossRef]
- Schnittman, J.D.; Buonanno, A. The Distribution of Recoil Velocities from Merging Black Holes. Astrophys. J. Lett. 2007, 662, L63–L66. [Google Scholar] [CrossRef]
- Kesden, M.; Sperhake, U.; Berti, E. Relativistic Suppression of Black Hole Recoils. Astrophys. J. 2010, 715, 1006–1011. [Google Scholar] [CrossRef]
- Yuan, F.; Narayan, R. Hot Accretion Flows Around Black Holes. Annu. Rev. Astron. Astrophys. 2014, 52, 529–588. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Fragile, P.C. Foundations of Black Hole Accretion Disk Theory. Living Rev. Relat. 2013, 16, 1. [Google Scholar] [CrossRef]
- Schnittman, J.D. Astrophysics of super-massive black hole mergers. Class. Quantum Grav. 2013, 30, 244007. [Google Scholar] [CrossRef]
- Bode, T.; Haas, R.; Bogdanovic, T.; Laguna, P.; Shoemaker, D. Relativistic Mergers of Supermassive Black Holes and their Electromagnetic Signatures. Astrophys. J. 2010, 715, 1117–1131. [Google Scholar] [CrossRef]
- Farris, B.D.; Liu, Y.T.; Shapiro, S.L. Binary black hole mergers in gaseous disks: Simulations in general relativity. Phys. Rev. 2011, D84, 024024. [Google Scholar] [CrossRef]
- Bode, T.; Bogdanovic, T.; Haas, R.; Healy, J.; Laguna, P.; Shoemaker, D. Mergers of Supermassive Black Holes in Astrophysical Environments. Astrophys. J. 2011, 744, 45. [Google Scholar] [CrossRef]
- Bogdanović, T.; Bode, T.; Haas, R.; Laguna, P.; Shoemaker, D. Properties of accretion flows around coalescing supermassive black holes. Class. Quantum Grav. 2011, 28, 094020. [Google Scholar] [CrossRef][Green Version]
- Noble, S.C.; Mundim, B.C.; Nakano, H.; Krolik, J.H.; Campanelli, M.; Zlochower, Y.; Yunes, N. Circumbinary MHD Accretion into Inspiraling Binary Black Holes. Astrophys. J. 2012, 755, 51. [Google Scholar] [CrossRef]
- Farris, B.D.; Gold, R.; Paschalidis, V.; Etienne, Z.B.; Shapiro, S.L. Binary black hole mergers in magnetized disks: Simulations in full general relativity. Phys. Rev. Lett. 2012, 109, 221102. [Google Scholar] [CrossRef] [PubMed]
- Gold, R.; Paschalidis, V.; Etienne, Z.B.; Shapiro, S.L.; Pfeiffer, H.P. Accretion disks around binary black holes of unequal mass: General relativistic magnetohydrodynamic simulations near decoupling. Phys. Rev. D 2014, 89, 064060. [Google Scholar] [CrossRef]
- Gold, R.; Paschalidis, V.; Ruiz, M.; Shapiro, S.L.; Etienne, Z.B.; Pfeiffer, H.P. Accretion disks around binary black holes of unequal mass: General relativistic MHD simulations of postdecoupling and merger. Phys. Rev. D 2014, 90, 104030. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A powerful local shear instability in weakly magnetized disks. I—Linear analysis. II—Nonlinear evolution. Astrophys. J. 1991, 376, 214–233. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 1998, 70, 1–53. [Google Scholar] [CrossRef]
- Shi, J.M.; Krolik, J.H.; Lubow, S.H.; Hawley, J.F. Three-dimensional Magnetohydrodynamic Simulations of Circumbinary Accretion Disks: Disk Structures and Angular Momentum Transport. Astrophys. J. 2012, 749, 118. [Google Scholar] [CrossRef]
- Bowen, D.B.; Campanelli, M.; Krolik, J.H.; Mewes, V.; Noble, S.C. Relativistic Dynamics and Mass Exchange in Binary Black Hole Mini-disks. Astrophys. J. 2017, 838, 42. [Google Scholar] [CrossRef]
- Khan, A.; Paschalidis, V.; Ruiz, M.; Shapiro, S.L. Disks around merging binary black holes: From GW150914 to supermassive black holes. Phys. Rev. D 2018, 97, 044036. [Google Scholar] [CrossRef] [PubMed]
- Macfadyen, A.I.; Milosavljevic, M. An Eccentric Circumbinary Accretion Disk and the Detection of Binary Massive Black Holes. Astrophys. J. 2008, 672, 83–93. [Google Scholar] [CrossRef]
- Kocsis, B.; Haiman, Z.; Loeb, A. Gas pile-up, gap overflow, and Type 1.5 migration in circumbinary disks: Application to supermassive black hole binaries. Mon. Not. R. Astron. Soc. 2012, 427, 2680–2700. [Google Scholar] [CrossRef]
- Armitage, P.J. Physical processes in protoplanetary disks. arXiv 2015, arXiv:1509.06382. [Google Scholar]
- Armitage, P.J.; Natarajan, P. Eccentricity of supermassive black hole binaries coalescing from gas rich mergers. Astrophys. J. 2005, 634, 921–928. [Google Scholar] [CrossRef]
- Armitage, P.J.; Natarajan, P. Accretion during the merger of supermassive black holes. Astrophys. J. 2002, 567, L9–L12. [Google Scholar] [CrossRef]
- Bowen, D.B.; Mewes, V.; Campanelli, M.; Noble, S.C.; Krolik, J.H.; Zilhão, M. Quasi-periodic Behavior of Mini-disks in Binary Black Holes Approaching Merger. Astrophys. J. Lett. 2018, 853, L17. [Google Scholar] [CrossRef]
- Bowen, D.B.; Mewes, V.; Noble, S.C.; Avara, M.; Campanelli, M.; Krolik, J.H. Quasi-Periodicity of Supermassive Binary Black Hole Accretion Approaching Merger. arXiv 2019, arXiv:1904.12048. [Google Scholar]
- Ryan, G.; MacFadyen, A. Minidisks in Binary Black Hole Accretion. Astrophys. J. 2017, 835, 199. [Google Scholar] [CrossRef]
- Ireland, B.; Mundim, B.C.; Nakano, H.; Campanelli, M. Inspiralling, nonprecessing, spinning black hole binary spacetime via asymptotic matching. Phys. Rev. D 2016, 93, 104057. [Google Scholar] [CrossRef]
- Giacomazzo, B.; Baker, J.G.; Miller, M.C.; Reynolds, C.S.; van Meter, J.R. General Relativistic Simulations of Magnetized Plasmas around Merging Supermassive Black Holes. Astrophys. J. 2012, 752, L15. [Google Scholar] [CrossRef]
- D’Ascoli, S.; Noble, S.C.; Bowen, D.B.; Campanelli, M.; Krolik, J.H.; Mewes, V. Electromagnetic Emission from Supermassive Binary Black Holes Approaching Merger. Astrophys. J. 2018, 865, 140. [Google Scholar] [CrossRef]
- Palenzuela, C.; Lehner, L.; Liebling, S.L. Dual Jets from Binary Black Holes. Science 2010, 329, 927–930. [Google Scholar] [CrossRef] [PubMed]
- Sperhake, U.; Berti, E.; Cardoso, V.; Pretorius, F.; Yunes, N. Superkicks in ultrarelativistic encounters of spinning black holes. Phys. Rev. D 2011, 83, 024037. [Google Scholar] [CrossRef]
- Lousto, C.O.; Zlochower, Y. Hangup Kicks: Still Larger Recoils by Partial Spin-Orbit Alignment of Black-Hole Binaries. Phys. Rev. Lett. 2011, 107, 231102. [Google Scholar] [CrossRef] [PubMed]
- Lousto, C.O.; Zlochower, Y. Nonlinear gravitational recoil from the mergers of precessing black-hole binaries. Phys. Rev. D 2013, 87, 084027. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C.; Zlochower, Y.; Merritt, D. Large Merger Recoils and Spin Flips from Generic Black Hole Binaries. Astrophys. J. Lett. 2007, 659, L5–L8. [Google Scholar] [CrossRef]
- Bogdanović, T.; Reynolds, C.S.; Miller, M.C. Alignment of the Spins of Supermassive Black Holes Prior to Coalescence. Astrophys. J. 2007, 661, L147–L150. [Google Scholar] [CrossRef]
- Komossa, S. Recoiling Black Holes: Electromagnetic Signatures, Candidates, and Astrophysical Implications. Adv. Astron. 2012, 2012, 364973. [Google Scholar] [CrossRef]
- Pesce, D.W.; Braatz, J.A.; Condon, J.J.; Greene, J.E. Measuring Supermassive Black Hole Peculiar Motion Using H2O Megamasers. Astrophys. J. 2018, 863, 149. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. 2019, 875, L5. [Google Scholar] [CrossRef]
- Kelly, B.J.; Baker, J.G.; Etienne, Z.B.; Giacomazzo, B.; Schnittman, J. Prompt electromagnetic transients from binary black hole mergers. Phys. Rev. D 2017, 96, 123003. [Google Scholar] [CrossRef]
- Charisi, M.; Haiman, Z.; Schiminovich, D.; D’Orazio, D.J. Testing the relativistic Doppler boost hypothesis for supermassive black hole binary candidates. Mon. Not. R. Astron. Soc. 2018, 476, 4617–4628. [Google Scholar] [CrossRef]
- Drake, A.J.; Djorgovski, S.G.; Mahabal, A.; Prieto, J.L.; Beshore, E.; Graham, M.J.; Catalan, M.; Larson, S.; Christensen, E.; Donalek, C.; et al. The Catalina Real-time Transient Survey. Proc. Int. Astron. Union 2011, 7, 306–308. [Google Scholar] [CrossRef]
- LSST Science and LSST Project Collaborations. LSST Science Book, Version 2.0. 2009. Available online: https://www.lsst.org/scientists/scibook (accessed on 29 May 2019).
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. Publ. ASJ 2003, 55, L69–L72. [Google Scholar] [CrossRef]
- McKinney, J.C.; Dai, L.; Avara, M.J. Efficiency of super-Eddington magnetically-arrested accretion. Mon. Not. R. Astron. Soc. 2015, 454, L6–L10. [Google Scholar] [CrossRef]
- Marshall, M.D.; Avara, M.J.; McKinney, J.C. Angular momentum transport in thin magnetically arrested discs. Mon. Not. R. Astron. Soc. 2018, 478, 1837–1843. [Google Scholar] [CrossRef]
- Johnson, M.D.; Fish, V.L.; Doeleman, S.S.; Marrone, D.P.; Plambeck, R.L.; Wardle, J.F.C.; Akiyama, K.; Asada, K.; Beaudoin, C.; Blackburn, L.; et al. Resolved magnetic-field structure and variability near the event horizon of Sagittarius A*. Science 2015, 350, 1242–1245. [Google Scholar] [CrossRef]
- Gold, R.; McKinney, J.C.; Johnson, M.D.; Doeleman, S.S. Probing the Magnetic Field Structure in Sgr A* on Black Hole Horizon Scales with Polarized Radiative Transfer Simulations. Astrophys. J. 2017, 837, 180. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. 2019, 875, L2. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. Astrophys. J. 2019, 875, L3. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. 2019, 875, L4. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. 2019, 875, L6. [Google Scholar] [CrossRef]
- Burke-Spolaor, S.; Blecha, L.; Bogdanovic, T.; Comerford, J.M.; Lazio, T.J.W.; Liu, X.; Maccarone, T.J.; Pesce, D.; Shen, Y.; Taylor, G. The Next-Generation Very Large Array: Supermassive Black Hole Pairs and Binaries. arXiv 2018, arXiv:1808.04368. [Google Scholar]
- D’Orazio, D.J.; Loeb, A. Imaging Massive Black Hole Binaries with Millimeter Interferometry: Measuring black hole masses and the Hubble constant. arXiv 2017, arXiv:1712.02362. [Google Scholar] [CrossRef]
| 1. | We have normalized to a separation of as was used in studies with full general relativistic magnetohydrodynamics (GRMHD). This value is only slightly smaller than the decoupling radius in Equation (5). After all, these time scales only give crude estimates and due to the steep scaling of with a the resulting inspiral time scales can seem prohibitively large. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gold, R. Relativistic Aspects of Accreting Supermassive Black Hole Binaries in Their Natural Habitat: A Review. Galaxies 2019, 7, 63. https://doi.org/10.3390/galaxies7020063
Gold R. Relativistic Aspects of Accreting Supermassive Black Hole Binaries in Their Natural Habitat: A Review. Galaxies. 2019; 7(2):63. https://doi.org/10.3390/galaxies7020063
Chicago/Turabian StyleGold, Roman. 2019. "Relativistic Aspects of Accreting Supermassive Black Hole Binaries in Their Natural Habitat: A Review" Galaxies 7, no. 2: 63. https://doi.org/10.3390/galaxies7020063
APA StyleGold, R. (2019). Relativistic Aspects of Accreting Supermassive Black Hole Binaries in Their Natural Habitat: A Review. Galaxies, 7(2), 63. https://doi.org/10.3390/galaxies7020063




