The Truncated Lindley Distribution with Applications in Astrophysics
Abstract
1. Introduction
- Is it possible to find the constant of normalization for a left and right truncated Lindley PDF?
- Is it possible to derive an analytical expression for the mean of a left and right truncated Lindley PDF
- Is a left and right truncated Lindley PDF a model for the IMF and for a sample of masses?
2. The Lindley Family
2.1. Lindle Distribution
2.2. The Lindley Distribution with Scale
2.3. The Truncated Lindley Distribution with Scale
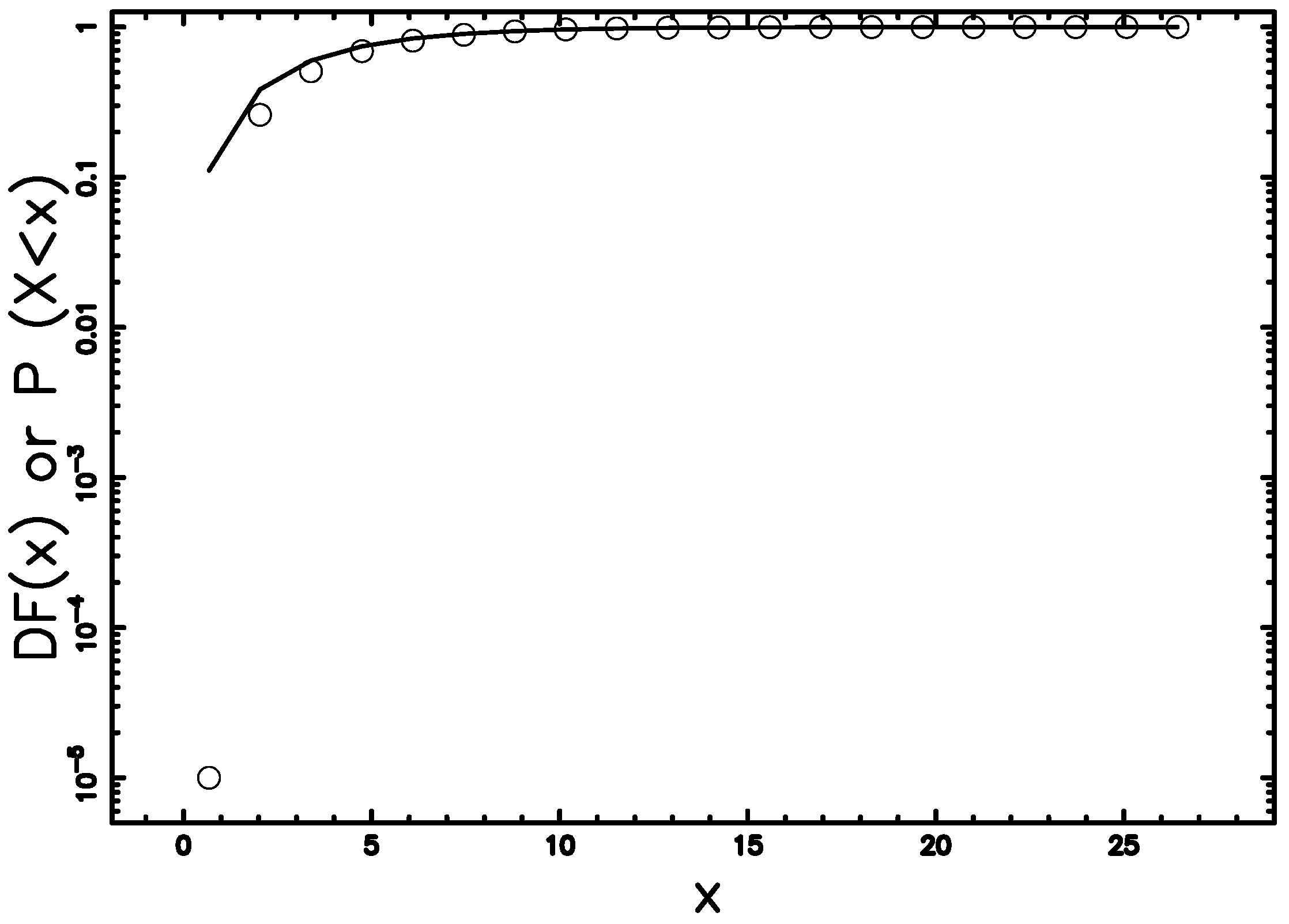
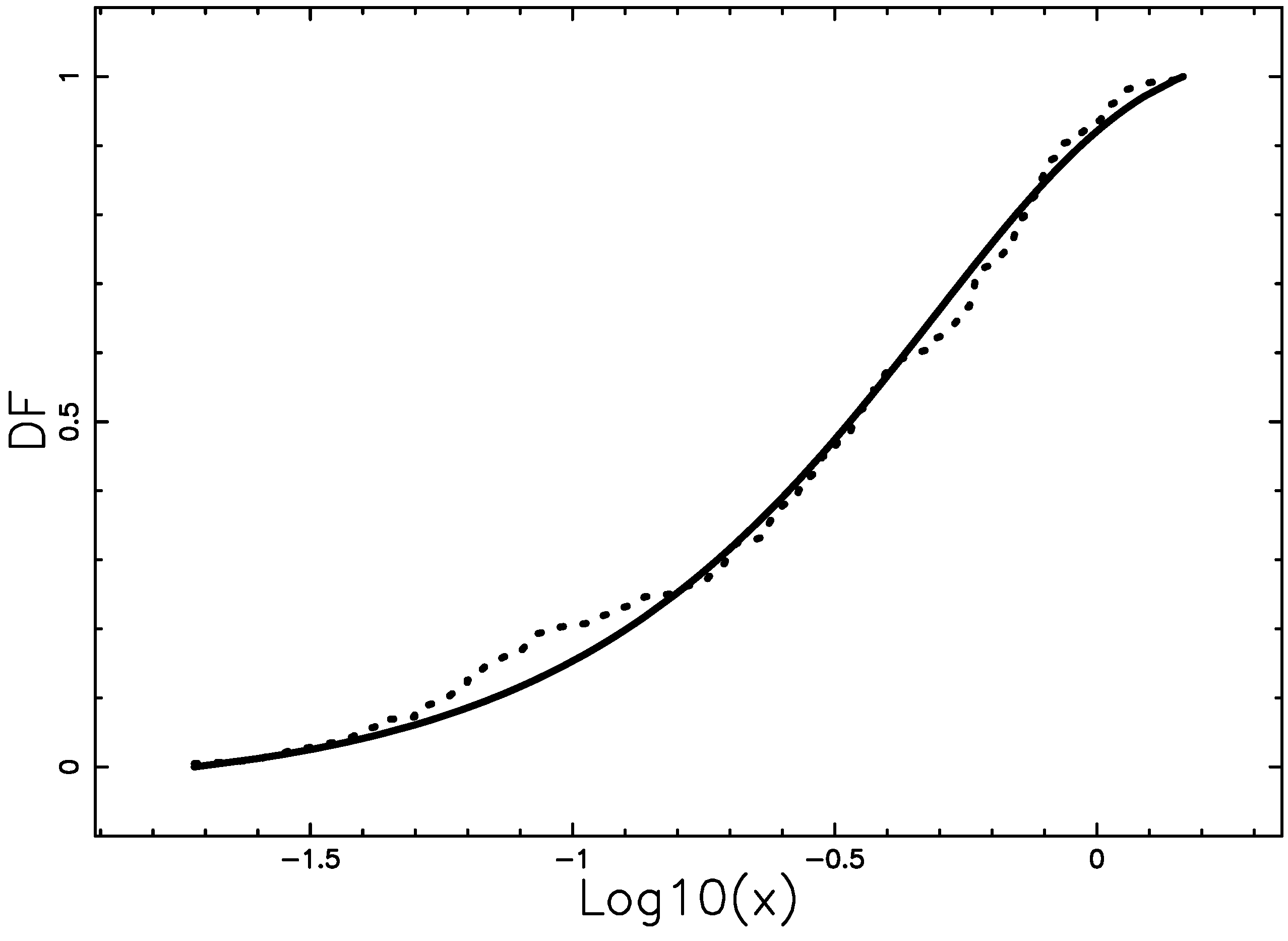
3. The IMF for Stars
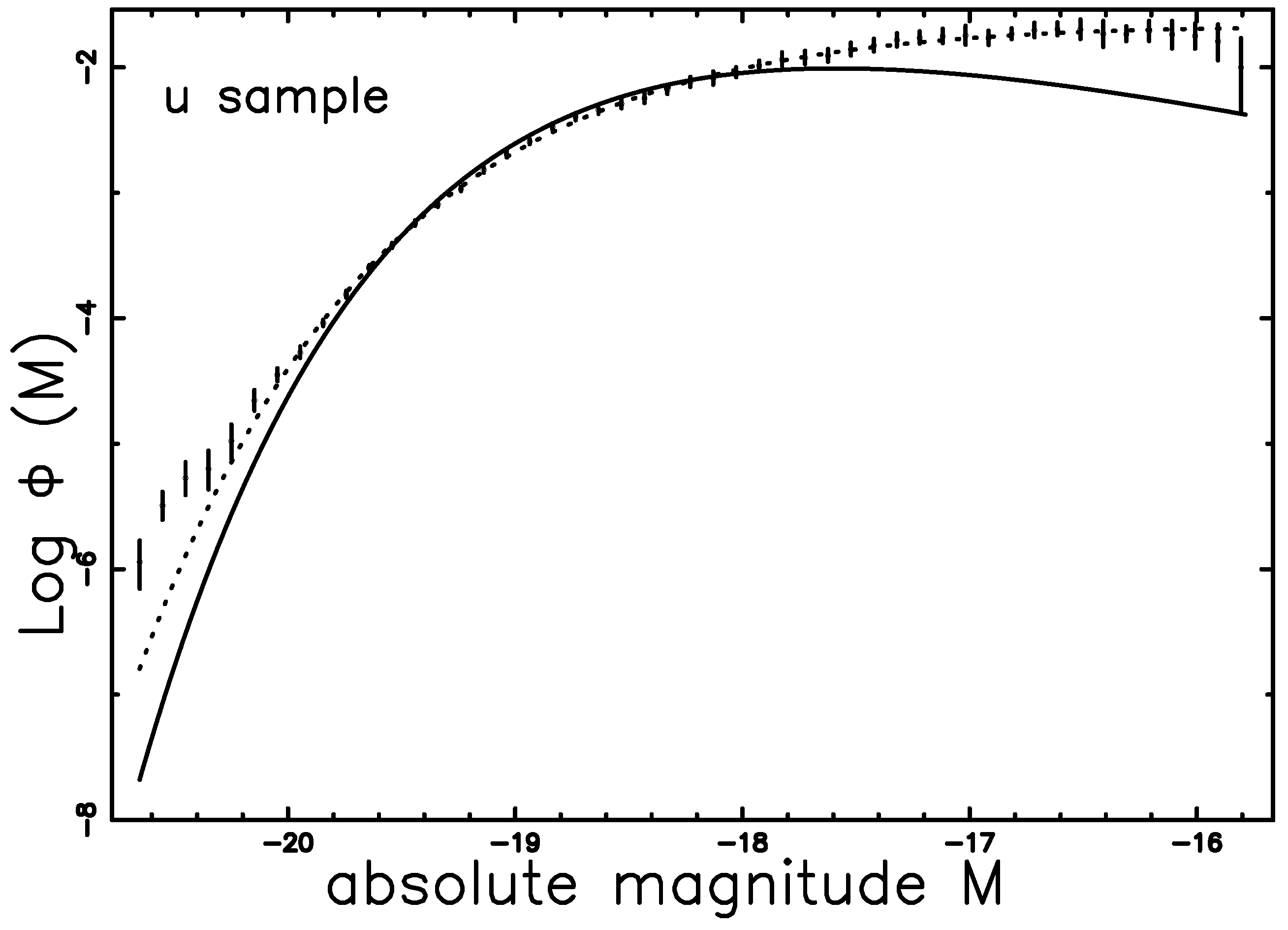
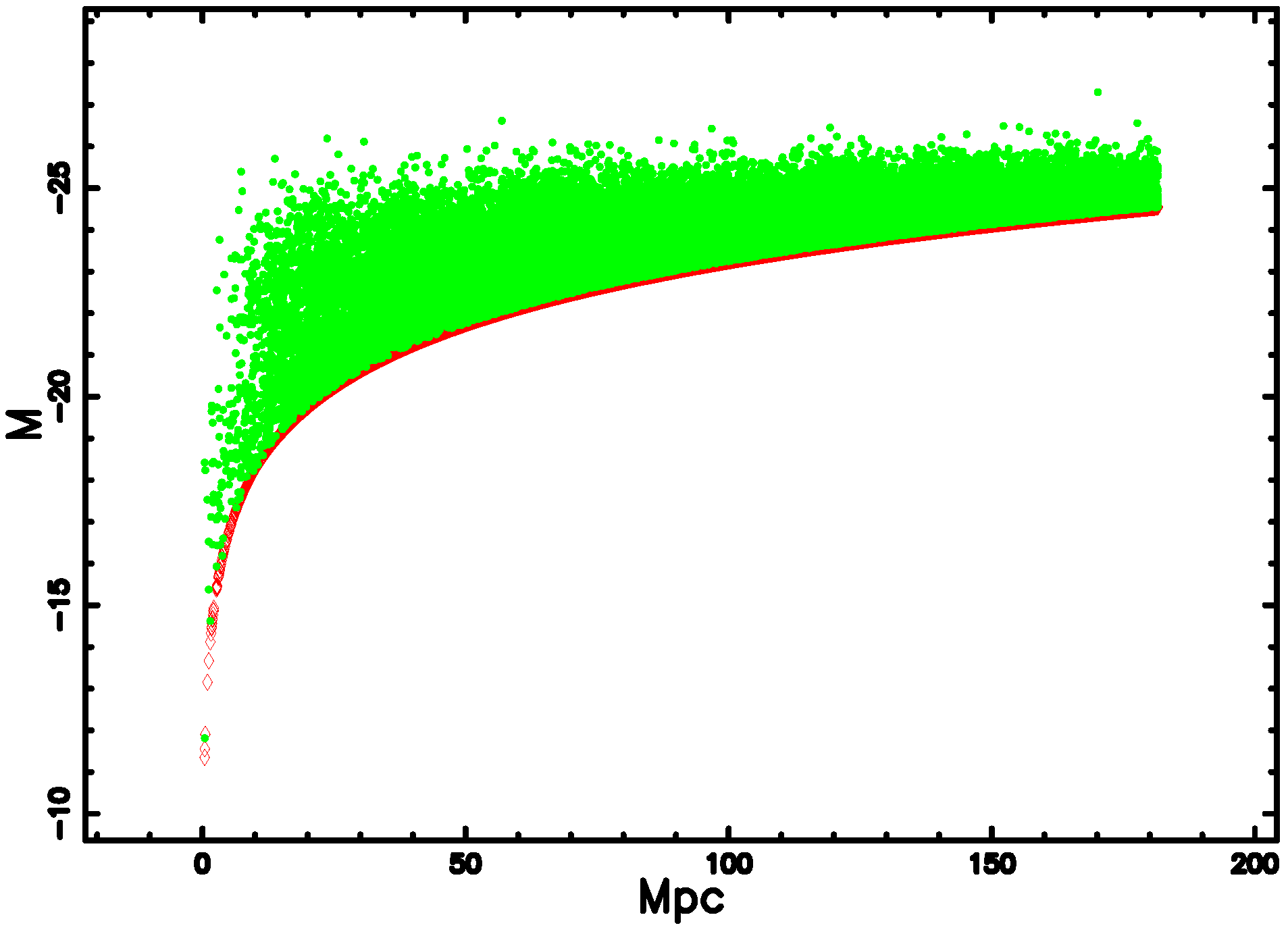
4. The Luminosity Function for Galaxies
4.1. The Schechter Function
4.2. The Lindley LF
4.3. The Truncated Lindley LF
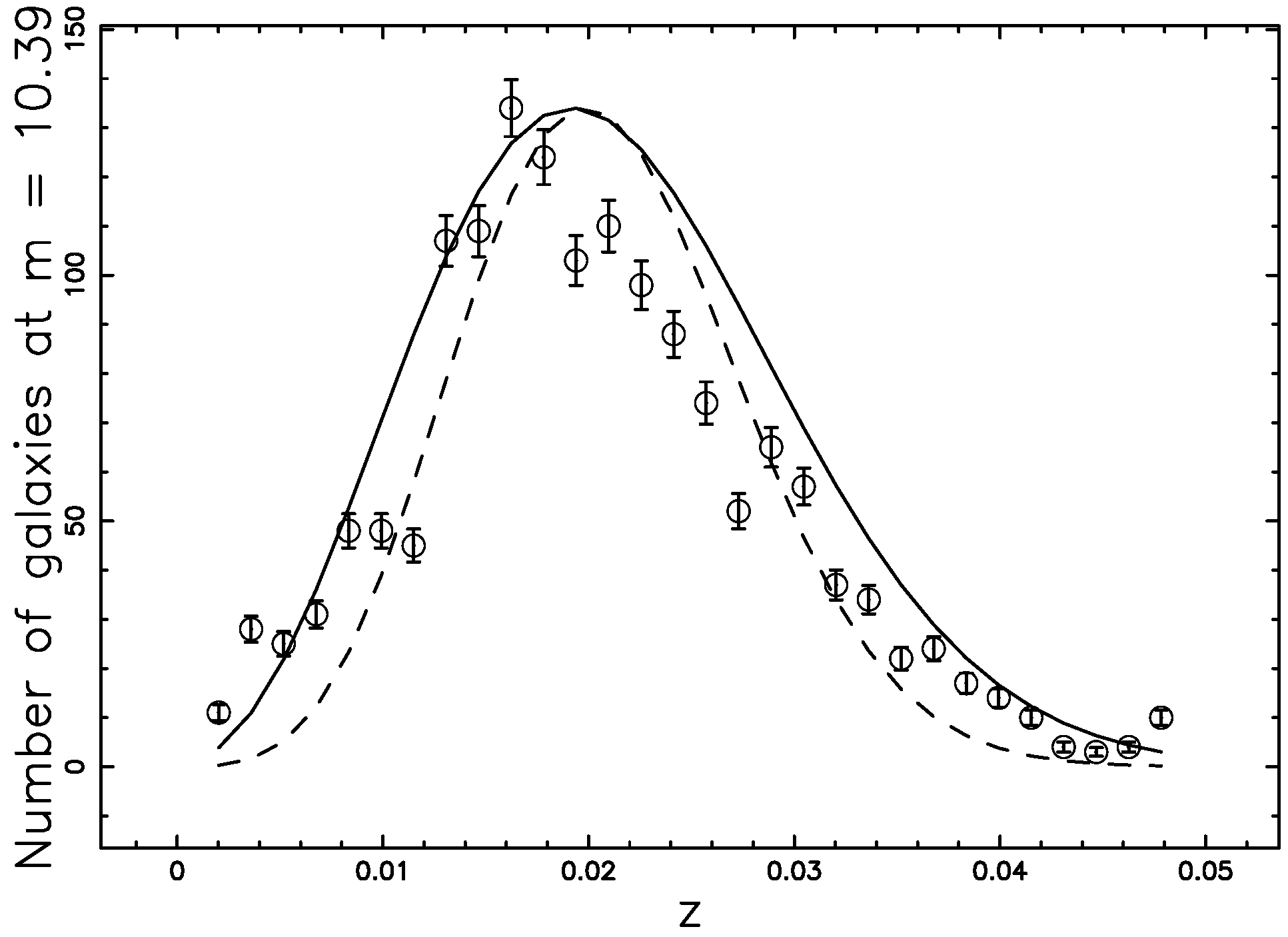
4.4. The Photometric Maximum
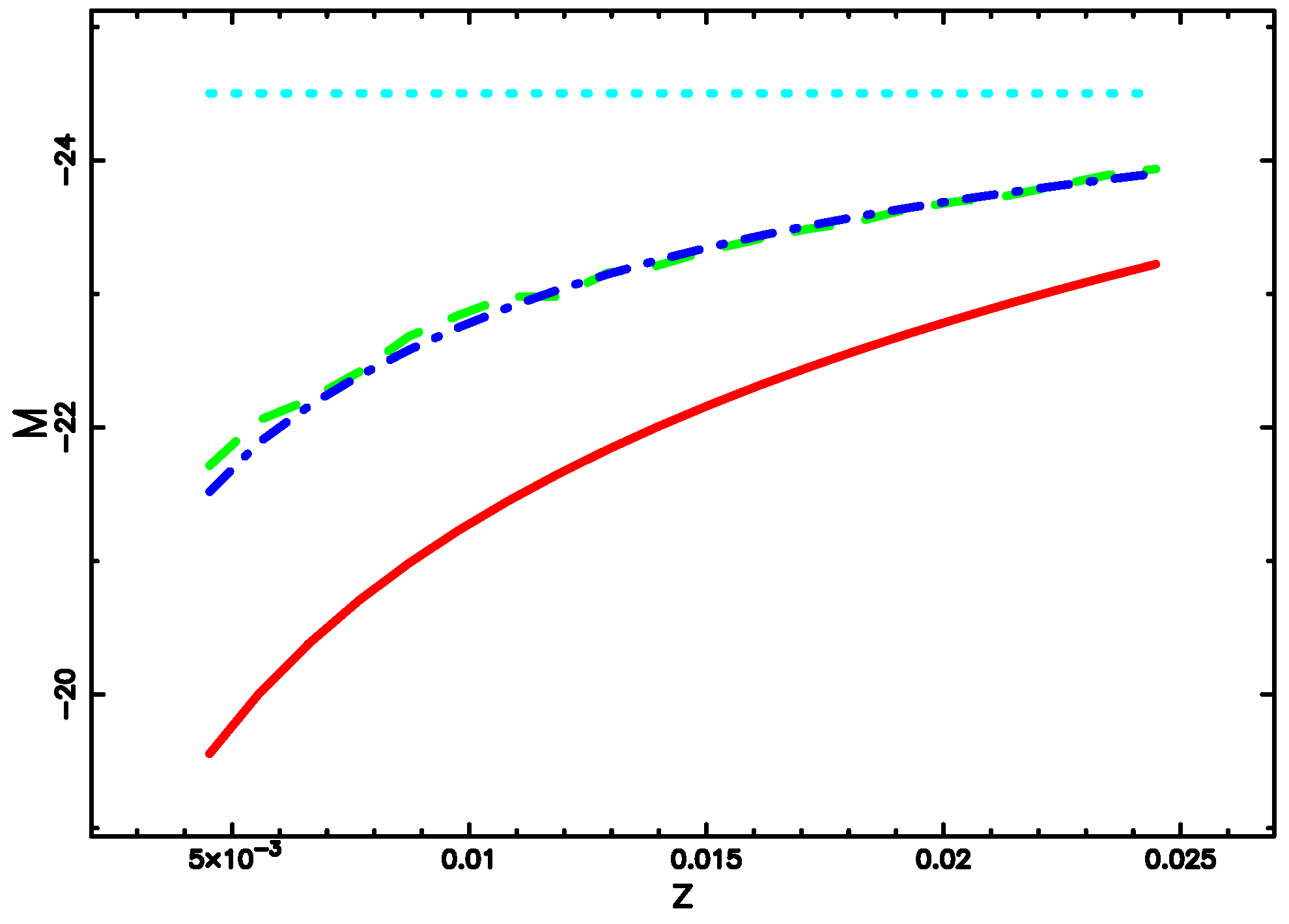
4.5. Averaged Absolute Magnitude
5. Conclusions
Funding
Conflicts of Interest
Appendix A. Other Parameters of the Lindley Distribution
Appendix B. Moments for the Lindley Distribution with Scale
Appendix C. The Parameters of the Truncated Lindley Distribution
References
- Lindley, D.V. Fiducial distributions and bayes’ theorem. J. R. Stat. Soc. Ser. B 1958, 20, 102–107. [Google Scholar] [CrossRef]
- Lindley, D.V. Introduction to Probability and Statistics from a Bayesian Viewpoint; Cambridge University Press: Cambridge, UK, 1965. [Google Scholar]
- Ghitany, M.; Atieh, B.; Nadarajah, S. Lindley distribution and its Application. Math. Comput. Simul. 2008, 78, 493–506. [Google Scholar] [CrossRef]
- Zakerzadeh, H.; Dolati, A. Generalized Lindley Distribution. J. Math. Ext. 2009, 3, 1–17. [Google Scholar]
- Singh, S.K.; Singh, U.; Sharma, V.K. The truncated lindley distribution: Inference and application. J. Stat. Appl. Probab. 2014, 3, 219–228. [Google Scholar] [CrossRef]
- Gui, W.; Chen, M. Parameter estimation and joint confidence regions for the parameters of the generalized lindley distribution. Math. Prob. Eng. 2016, 2016, 7946828. [Google Scholar] [CrossRef]
- Shanker, R.; Shukla, K.K.; Shanker, R.; Tekie, A. A three-parameter lindley Distribution. Am. J. Math. Stat. 2017, 7, 15–26. [Google Scholar]
- Salpeter, E.E. The Luminosity Function and Stellar Evolution. Astrophys. J. 1955, 121, 161. [Google Scholar] [CrossRef]
- Scalo, J.M. The stellar initial mass function. Fundam. Cosm. Phys. 1986, 11, 1. [Google Scholar]
- Kroupa, P.; Tout, C.A.; Gilmore, G. The distribution of low-mass stars in the Galactic disc. Mon. Not. R. Astron. Soc. 1993, 262, 545–587. [Google Scholar] [CrossRef]
- Binney, J.; Merrifield, M. Galactic Astronomy; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Kroupa, P. On the variation of the initial mass function. Mon. Not. R. Astron. Soc. 2001, 322, 231–246. [Google Scholar] [CrossRef]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Publ. ASP 2003, 115, 763–795. [Google Scholar] [CrossRef]
- Zaninetti, L. The initial mass function modeled by a left truncated beta distribution. Astrophys. J. 2013, 765, 128–135. [Google Scholar] [CrossRef]
- Zaninetti, L. A right and left truncated gamma distribution with application to the stars. Adv. Stud. Theor. Phys. 2013, 23, 1139–1147. [Google Scholar] [CrossRef][Green Version]
- Zaninetti, L. A left and right truncated lognormal distribution for the Stars. Adv. Astrophys. 2017, 2, 197–213. [Google Scholar] [CrossRef]
- Schechter, P. An analytic expression for the luminosity function for galaxies. Astrophys. J. 1976, 203, 297–306. [Google Scholar] [CrossRef]
- Driver, S.P.; Phillipps, S. Is the Luminosity Distribution of Field Galaxies Really Flat? Astrophys. J. 1996, 469, 529. [Google Scholar] [CrossRef]
- Bell, E.F.; McIntosh, D.H.; Katz, N.; Weinberg, M.D. The Optical and Near-Infrared Properties of Galaxies. I. Luminosity and Stellar Mass Functions. Astrophys. J. Suppl. 2003, 149, 289. [Google Scholar] [CrossRef]
- Blanton, M.R.; Lupton, R.H.; Schlegel, D.J.; Strauss, M.A.; Brinkmann, J.; Fukugita, M.; Loveday, J. The Properties and Luminosity Function of Extremely Low Luminosity Galaxies. Astrophys. J. 2005, 631, 208–230. [Google Scholar] [CrossRef]
- Alcaniz, J.S.; Lima, J.A.S. Galaxy Luminosity Function: A New Analytic Expression. Braz. J. Phys. 2004, 34, 455–458. [Google Scholar] [CrossRef]
- Coil, A.L.; Blanton, M.R.; Burles, S.M.; Cool, R.J.; Eisenstein, D.J.; Moustakas, J.; Wong, K.C.; Zhu, G.; Aird, J.; Bernstein, R.A.; et al. The PRIsm MUlti-object Survey (PRIMUS). I. Survey Overview and Characteristics. Astrophys. J. 2011, 741, 8. [Google Scholar] [CrossRef]
- Jimeno, P.; Broadhurst, T.; Coupon, J.; Umetsu, K.; Lazkoz, R. Comparing gravitational redshifts of SDSS galaxy clusters with the magnified redshift enhancement of background BOSS galaxies. Mon. Not. R. Astron. Soc. 2015, 448, 1999–2012. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Padmanabhan, T. Cosmology and Astrophysics through Problems; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Padmanabhan, P. Theoretical Astrophysics. Volume III: Galaxies and Cosmology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Zaninetti, L. The Luminosity Function of Galaxies as Modeled by a Left Truncated Beta Distribution. Int. J. Astron. Astrophys. 2014, 4, 145–154. [Google Scholar] [CrossRef]
- Zaninetti, L. A left and right truncated schechter luminosity function for Quasars. Galaxies 2017, 5, 25. [Google Scholar] [CrossRef]
- Lambert, J.H. Observations variae in Mathesin Puram. Acta Helvitica 1758, 3, 128. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
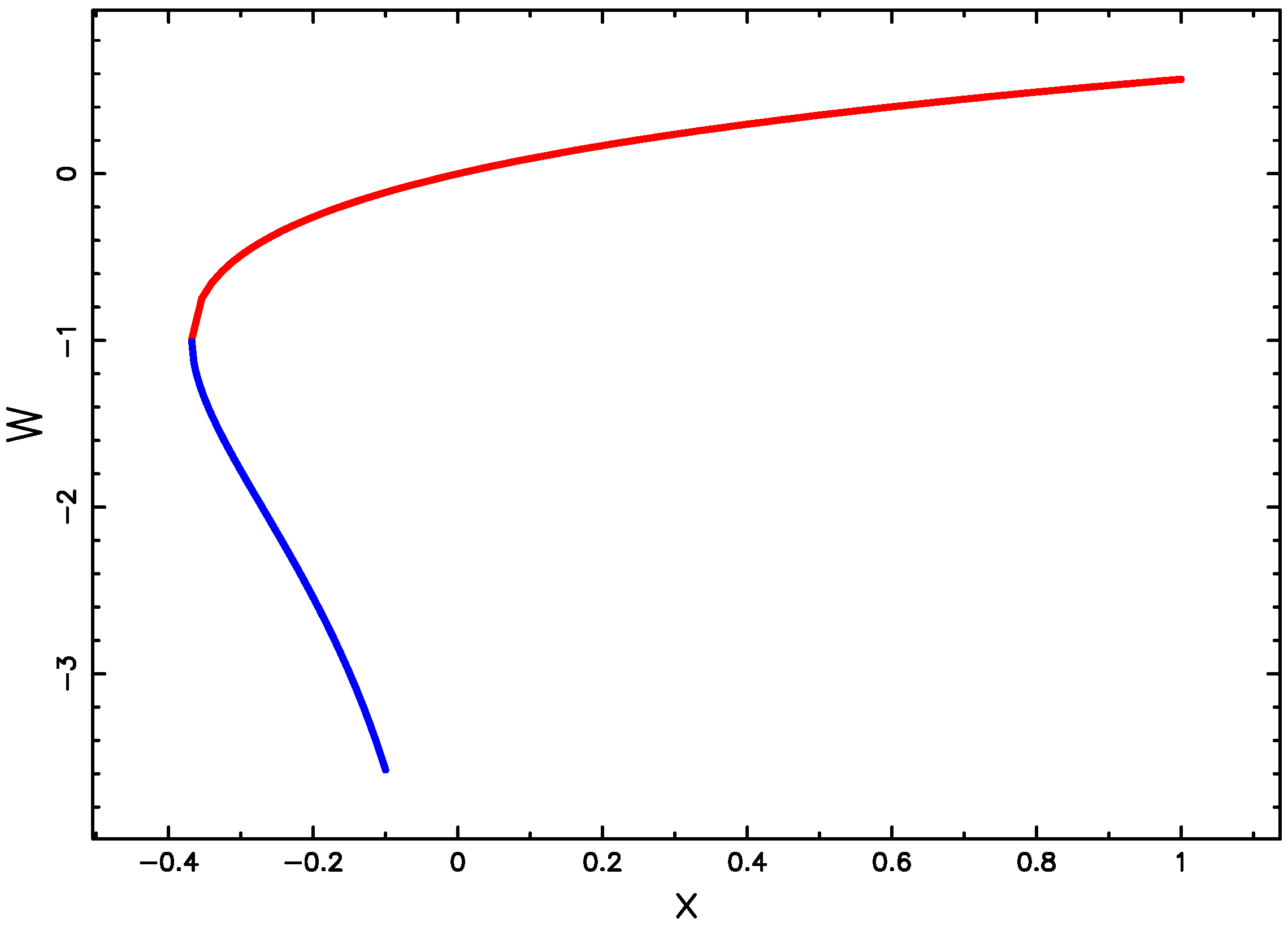
- Corless, R.M.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, D.E. On the lambertw function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Corless, R.M.; Jeffrey, D.J.; Knuth, D.E. A sequence of series for the lambert w function. In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation (ACM), Maui, HI, USA, 21–23 July 1997; pp. 197–204. [Google Scholar]
- Dence, T.P. A brief look into the lambert w function. Appl. Math. 2013, 4, 887–892. [Google Scholar] [CrossRef]
- Hassanein, W.A.; Elhaddad, T.A. Truncated lindley gamma distribution. Pak. J. Stat. 2016, 32, 227–246. [Google Scholar]
- Hopkins, A.M. The Dawes Review 8: Measuring the Stellar Initial Mass Function. Publ. Astron. Soc. Aust. 2018, 35, e039. [Google Scholar] [CrossRef]
- Hosek, M.W.J.; Lu, J.R.; Anderson, J.; Najarro, F.; Ghez, A.M.; Morris, M.R.; Clarkson, W.I.; Albers, S.M. The Unusual Initial Mass Function of the Arches Cluster. Astrophys. J. 2019, 44, 870. [Google Scholar]
- Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions, 3rd ed.; John Wiley & Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Larson, R.B. A simple probabilistic theory of fragmentation. Mon. Not. R. Astron. Soc. 1973, 161, 133–143. [Google Scholar] [CrossRef]
- Miller, G.E.; Scalo, J.M. The initial mass function and stellar birthrate in the solar neighborhood. Astrophys. J. Suppl. 1979, 41, 513–547. [Google Scholar] [CrossRef]
- Zinnecker, H. Star formation from hierarchical cloud fragmentation—A statistical theory of the log-normal Initial Mass Function. Mon. Not. R. Astron. Soc. 1984, 210, 43–56. [Google Scholar] [CrossRef][Green Version]
- Cox, A.N. Allen’s Astrophysical Quantities; Springer: New York, NY, USA, 2000. [Google Scholar]
- Zaninetti, L. The Luminosity Function of Galaxies as modelled by the Generalized Gamma Distribution. Acta Phys. Pol. B 2010, 41, 729. [Google Scholar]
- Blanton, M.R.; Hogg, D.W.; Bahcall, N.A.; Brinkmann, J.; Britton, M. The Galaxy Luminosity Function and Luminosity Density at Redshift z = 0.1. Astrophys. J. 2003, 592, 819–838. [Google Scholar] [CrossRef]
- Hubble, E. A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae. Proc. Natl. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Zaninetti, L. A near infrared test for two recent luminosity functions for galaxies. Rev. Mex. Astron. Astrofis. 2014, 50, 7–124. [Google Scholar]
- Padé, H. Sur la représentation approchée d’une fonction par des fractions rationnelles. Annales Scientifiques de l’École Normale Supérieure 1892, 9, 3–93. [Google Scholar] [CrossRef]
- Kahaner, D.; Moler, C.; Nash, S. Numerical Methods and Software; Prentice Hall Publishers: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
| Method | Parameters | AIC | Q | D | |||
|---|---|---|---|---|---|---|---|
| truncated Lindley | MLE | b = 0.666, , = 0.0189, = 1.46 | 47.75 | 2.48 | 0.065 | 0.332 | |
| lognormal | MLE | = 1.029, m = 0.284 | 71.24 | 3.73 | 0.09366 | 0.04959 | |
| truncated lognormal | MLE | = 1.499, m = 0.478, = 0.0189, = 1.46 | 50.96 | 2.68 | 0.0654 | 0.372 |
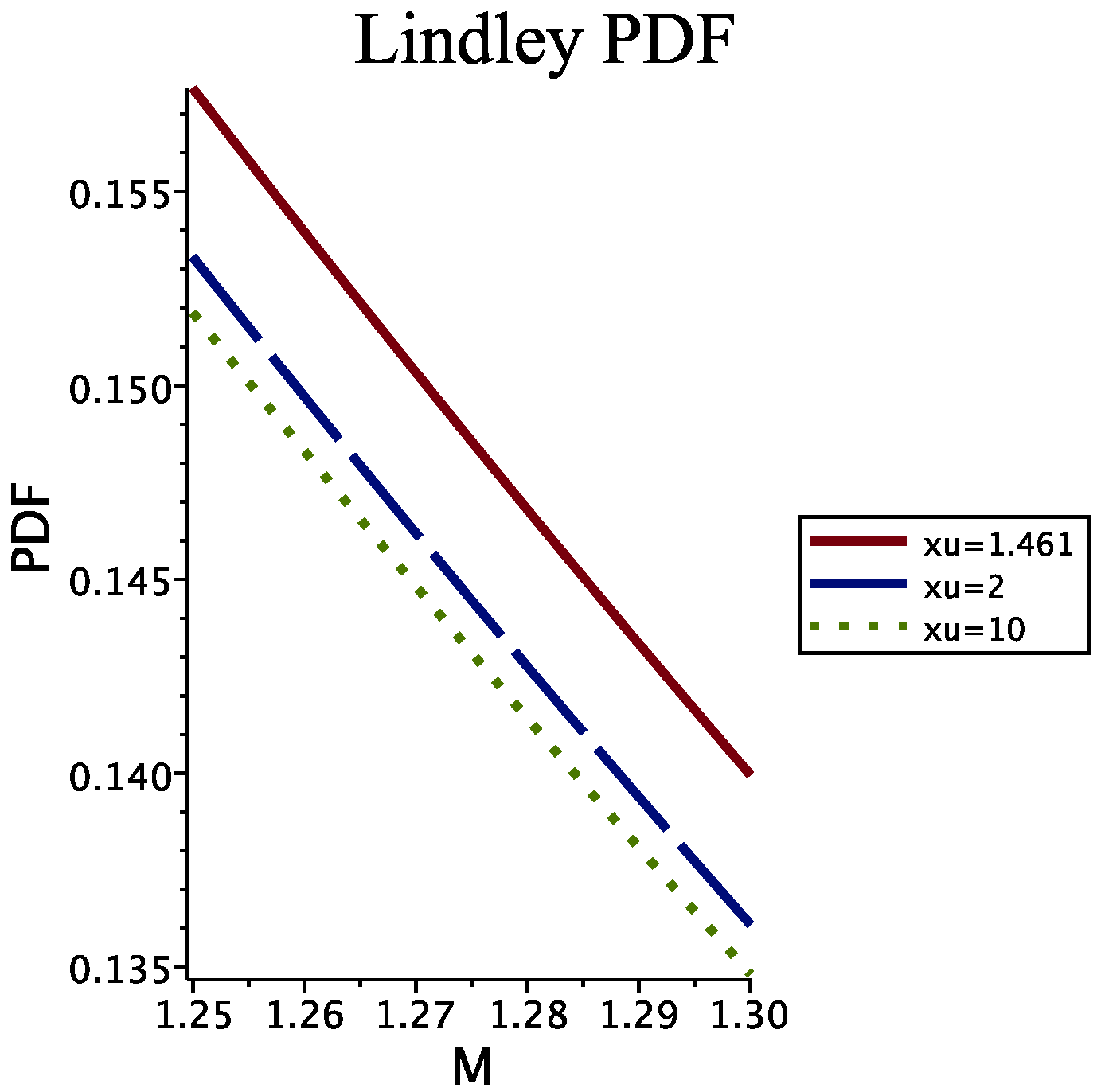
| Mass in Solar Units | Lifetime (Year) |
|---|---|
| 1.461 | |
| 2 | |
| 10 |
| LF | Parameters | |
|---|---|---|
| Schechter | = −17.92, = −0.9, = 0.0114/Mpc3 | 0.689 |
| Lindley | = −23.40, c = 214.1, = 0.0289/Mpc3 | 6.6741 |
| truncated Lindley | = −23.458; c = 224.47; = 0.0239/Mpc3; = −20.653; = −15.785 | 6.6739 |
| LF | Parameters | |
|---|---|---|
| Schechter | = −23.289, = −0.794, = 0.0128/Mpc3 | 7.08 |
| Lindley | = −23.7, c = 2.8, = 0.0289/Mpc3 | 6.84 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaninetti, L. The Truncated Lindley Distribution with Applications in Astrophysics. Galaxies 2019, 7, 61. https://doi.org/10.3390/galaxies7020061
Zaninetti L. The Truncated Lindley Distribution with Applications in Astrophysics. Galaxies. 2019; 7(2):61. https://doi.org/10.3390/galaxies7020061
Chicago/Turabian StyleZaninetti, Lorenzo. 2019. "The Truncated Lindley Distribution with Applications in Astrophysics" Galaxies 7, no. 2: 61. https://doi.org/10.3390/galaxies7020061
APA StyleZaninetti, L. (2019). The Truncated Lindley Distribution with Applications in Astrophysics. Galaxies, 7(2), 61. https://doi.org/10.3390/galaxies7020061





